The implications of changing education distributions for life expectancy gradients

Abstract

Recent research has proposed that shifting education distributions across cohorts are influencing estimates of educational gradients in mortality. We use data from the United States and Finland covering four decades to explore this assertion. We base our analysis around our new finding: a negative logarithmic relationship between relative education and relative mortality. This relationship holds across multiple age groups, both sexes, two very different countries, and time periods spanning four decades. The inequality parameters from this model indicate increasing relative mortality differentials over time. We use these findings to develop a method that allows us to compute life expectancy for any given segment of the education distribution (e.g., education quintiles). We apply this method to Finnish and American data to compute life expectancy gradients that are adjusted for changes in the education distribution. In Finland, these distribution-adjusted education differentials in life expectancy between the top and bottom education quintiles have increased by two years for men, and remained stable for women between 1971 and 2010. Similar distribution-adjusted estimates for the U.S. suggest that educational disparities in life expectancy increased by 3.3 years for non-Hispanic white men and 3.0 years for non-Hispanic white women between the 1980s and 2000s. For men and women, respectively, these differentials between the top and bottom education quintiles are smaller than the differentials between the top and bottom education categories by 18% and 39% in the U.S. and by 39% and 100% in Finland. Had the relative inequality parameters of mortality governing the Finnish and U.S. populations remained constant at their earliest period values, the difference in life expectancy between the top and bottom education quintiles would – because of overall mortality reductions – have declined moderately. The findings suggest that educational expansion may bias estimates of trends in educational differences in life expectancy upwards.

1. Introduction

The measurement of inequality and its consequences is one of the primary enterprises of social demography, and accordingly much attention has been focused on whether growing social inequality is driving inequality in life expectancy and health. Life expectancy is an absolute measure of wellbeing, and absolute differentials in life expectancy have implications for inequalities in non-health related outcomes such as wealth accumulation and the receipt of social security and pension income. Given the importance of social inequalities in mortality, whether measured by educational attainment, income, or occupational status and changes therein over time, it is important to consider how cohort-specific changes in the distribution of these social indicators contribute to changing period measures of inequality in mortality. The focus of this paper is to illustrate how cohort-specific changes in educational distributions influence period estimates of disparities in mortality by educational attainment.

Many prior studies have documented educational gradients in mortality and attempted either to explain factors that contribute to their existence or document how educational disparities have changed over time (Elo et al., 2006; Elo and Preston 1996; Hayward et al., 2015; Hendi 2015, 2017; Ho and Fenelon 2015; Mackenbach et al., 1999; Meara et al., 2008; Montez and Zajacova 2013a; Sasson 2016). However, recent research has raised questions about whether studying changes in educational differentials in mortality without consideration of the impact of shifting educational distributions on estimated trends is appropriate (Begier et al., 2013; Dowd and Hamoudi 2014; Goldring et al., 2016; Hendi 2015). There are two main issues that arise when education distributions are shifting. First, over-time comparisons of the difference in mortality between education groups may be biased measures of the change in social gradients in mortality. It is hypothesized that unmeasured characteristics of various education groups, which are related to health, are changing over time as the fraction of individuals reaching specific educational thresholds is shifting over time (e.g., the percentage of those with a high school education becomes smaller and the percentage with higher levels of education becomes larger) (Dowd and Hamoudi 2014). Second, cross-sectional summary measures of mortality consist of the mortality experience of multiple birth cohorts, each having a different educational distribution, such that period estimates may not correspond to the real experience of any cohort with a given level of schooling (Hendi 2017). Consider, for example, the experience of cohorts that provide input for estimates for an age-standardized mortality rate or period life expectancy by educational attainment. Currently, individuals with the lowest level of education aged 80–84 years might be at the 45th percentile of the education distribution for their cohort, whereas people in the same education category aged 30–34 years might be only at the 5th percentile of the educational distribution for their birth cohort. These cross-sectional estimates for people in the lowest education category would combine younger individuals with very low relative education and older individuals with a much higher relative education.

Most studies of the association between education and mortality categorize educational attainment by educational milestones, such as less than high school, high school, some college, and college graduate and above, or some variation of these categories. This choice may be justified by the relatively rigid demands for educational certificates for most occupations in modern societies. However, when educational attainment is improving across birth cohorts, the shift in the education distribution leads to changes in the composition of the education categories such that selection on observed and unobserved characteristics that are also likely to be health-related is changing over time. Thus, comparisons of period mortality measures by static categories of educational attainment may lead to a misleading interpretation of trends in the education-mortality gradient over time.

Several prior studies that have addressed the issue of changing education distributions have relied on the slope index of inequality (SII), which accounts for differences in the education distribution over time or between populations (Pamuk 1985; Preston et al., 1981). It does so by plotting the percentile rank of an education category against the age-standardized death rate or life expectancy for that category, and then estimating the weighted linear association between those two variables, where the weights are equal to the relative size of the education categories (Mackenbach and Kunst 1997; Moreno-Betancur et al., 2015; Valkonen 1989). In the United States, the results from analyses based on the SII typically show smaller changes in the educational gradient in mortality over time than when the changes in the education distribution are not considered (Preston and Elo 1995). Others have addressed the issue by not relying on educational thresholds but rather allocating individuals to equally sized rank-ordered education categories over time (Bound et al., 2015; Hendi 2015). Findings from such analyses suggest that the conclusions regarding changes in the education-mortality gradient in the United States depend on how educational attainment is classified. When changes in the education distribution are accounted for in mortality inequality measures, changes in the education-mortality gradient are smaller than without such adjustment.

In this paper, we demonstrate how educational expansion affects measurement of inequality in mortality in Finland and the U.S., two countries with very different education transition timings and vastly different welfare states. We introduce a methodological approach that allows us to measure educational gradients in period life expectancy (or any other summary measure of mortality) while adjusting for changes in the education distribution across cohorts. This approach is based on our finding of a negative logarithmic relationship between education-specific mortality ratios and the education category’s percentile rank in the education distribution. We use high-quality Finnish registry and U.S. survey data to show that this logarithmic relationship holds across age and sex groups and over time. We show that while educational differences in mortality have indeed steepened over time, this steepening is overestimated when the shifting education distribution is not taken into account. Much of the increase in the relative education-mortality gradient over time is due to stagnant or only very slowly improving mortality at the low end of the education distribution, where fewer and fewer people are concentrated over time.

1.1. The changing education distribution in Finland and the United States

Although today Finland is considered one of the most forward-thinking countries in terms of education, for much of the twentieth century, it was a largely agrarian society with low levels of formal education. It was not until the latter half of the twentieth century that educational attainment improved rapidly, producing large differences in educational attainment by cohort. This transformation can be seen clearly in Figs. 1 and 2 with birth cohorts separated by only a decade having very different education profiles.

Fig. 1.

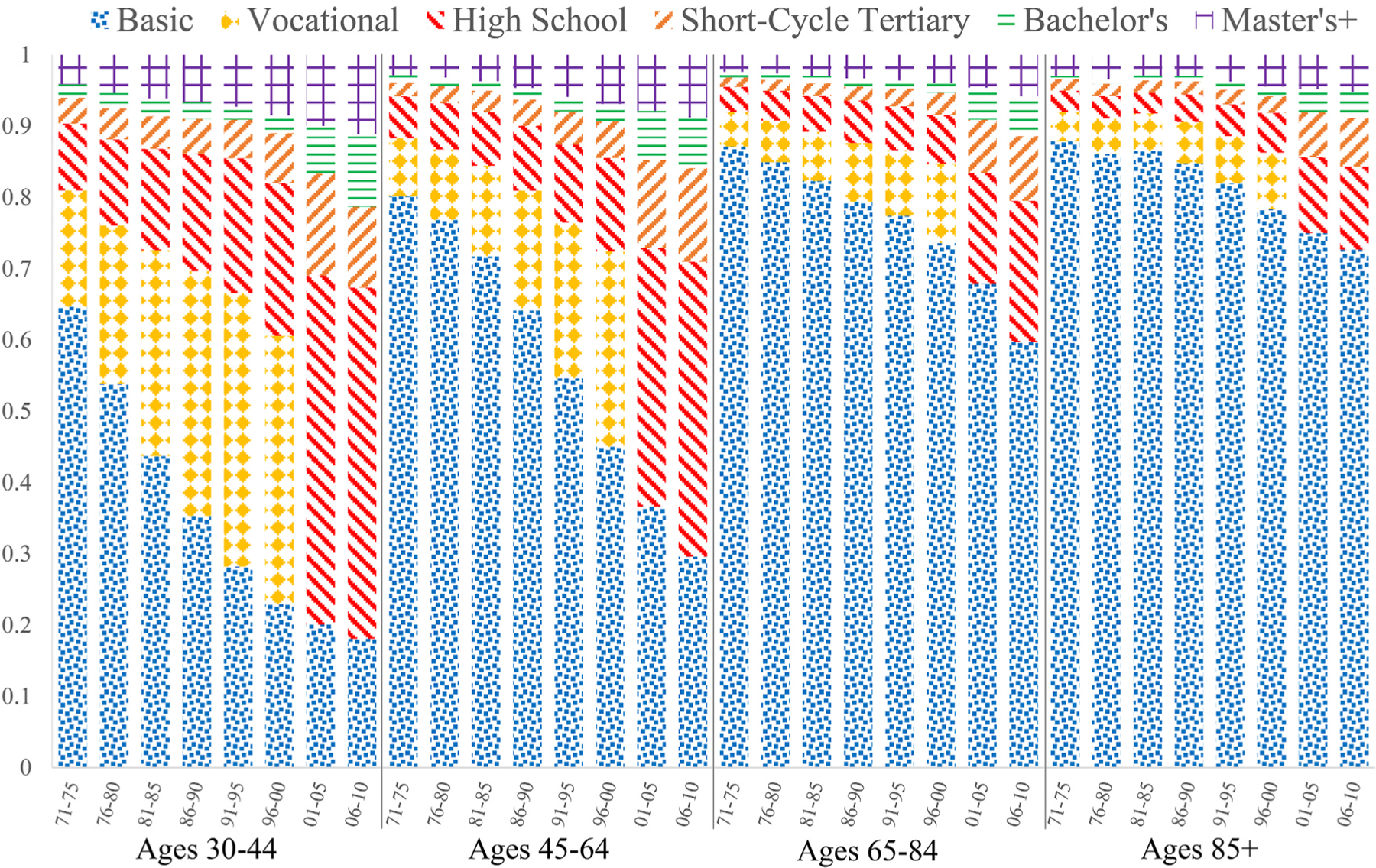
Education Distribution by Age and Period, Finnish Men, 1971–2010. Source: Authors’ calculations based on Finnish registry data and censuses.

Note: The education categorization for 2001–2005 and 2006–2010 combines vocational and high school into one category.

Fig. 2.

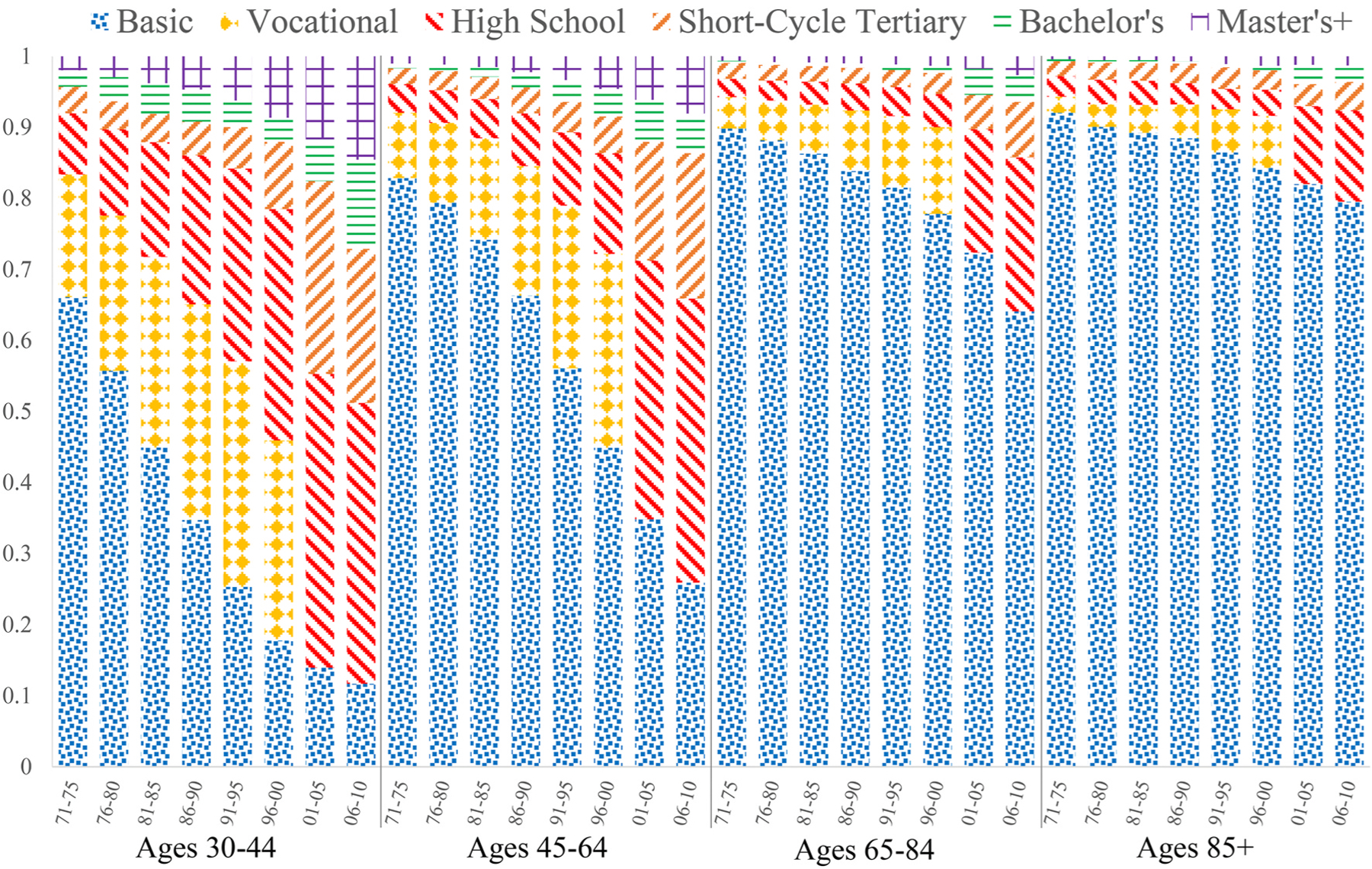
Education Distribution by Age and Period, Finnish Women, 1971–2010

Source: Authors’ calculations based on Finnish registry data and censuses.

Note: The education categorization for 2001–2005 and 2006–2010 combines vocational and high school into one category.

The changing education distribution of the US population is shown in Figs. 3 and 4. In comparison to Finland, the educational expansion in the United States occurred earlier. The changes from the 1980s to the 2000s were less pronounced in the U.S., with the expansion happening somewhat later for women than for men. These country-specific differences would be expected to have a differential impact in Finland and the United States on trends in mortality by educational attainment, with larger contributions in Finland.

Fig. 3.

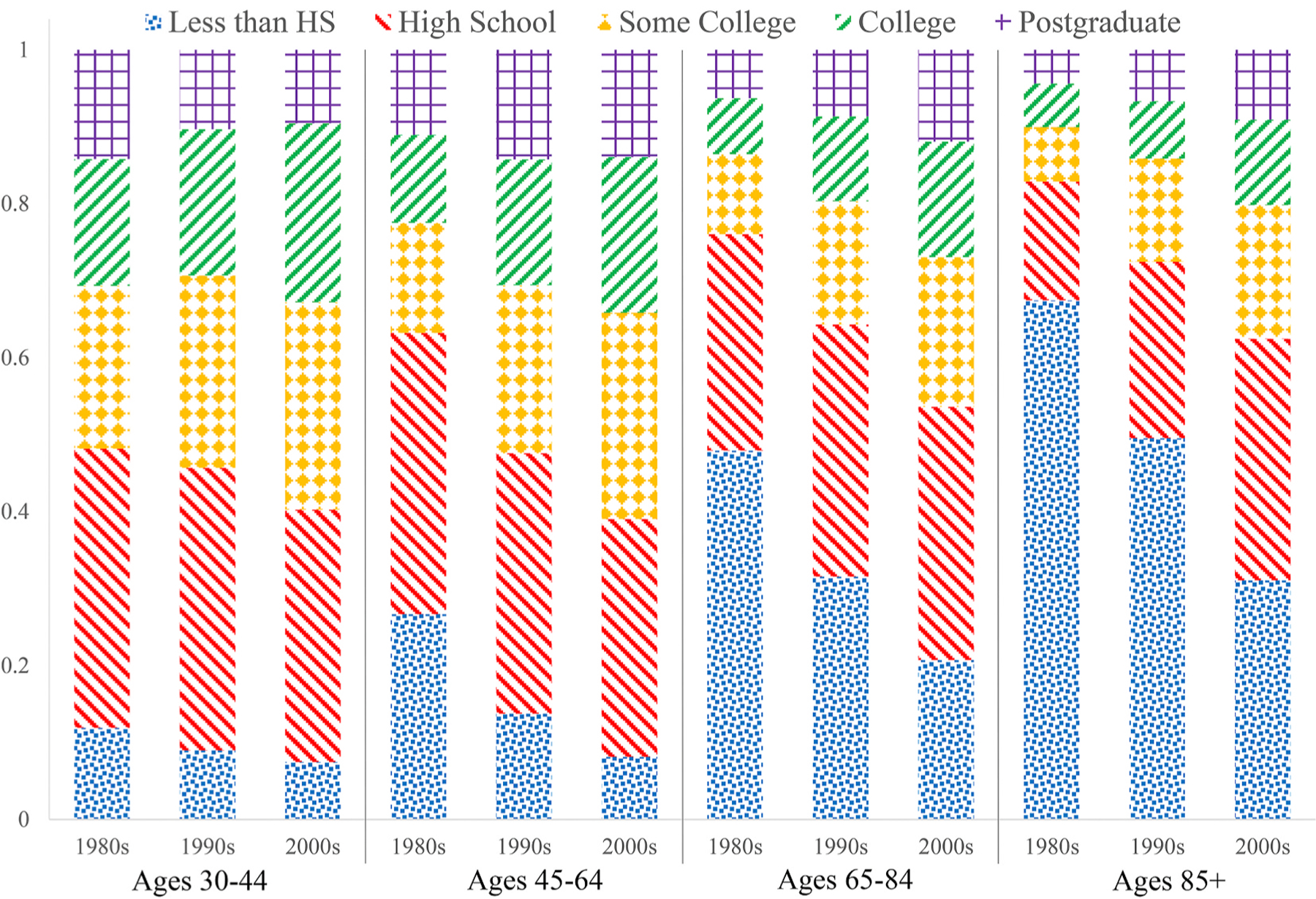
Education Distributions by Age and Period, non-Hispanic White American Men, 1980s-2000s

Source: U.S. National Longitudinal Mortality Study (NLMS) Release 5.

Fig. 4.

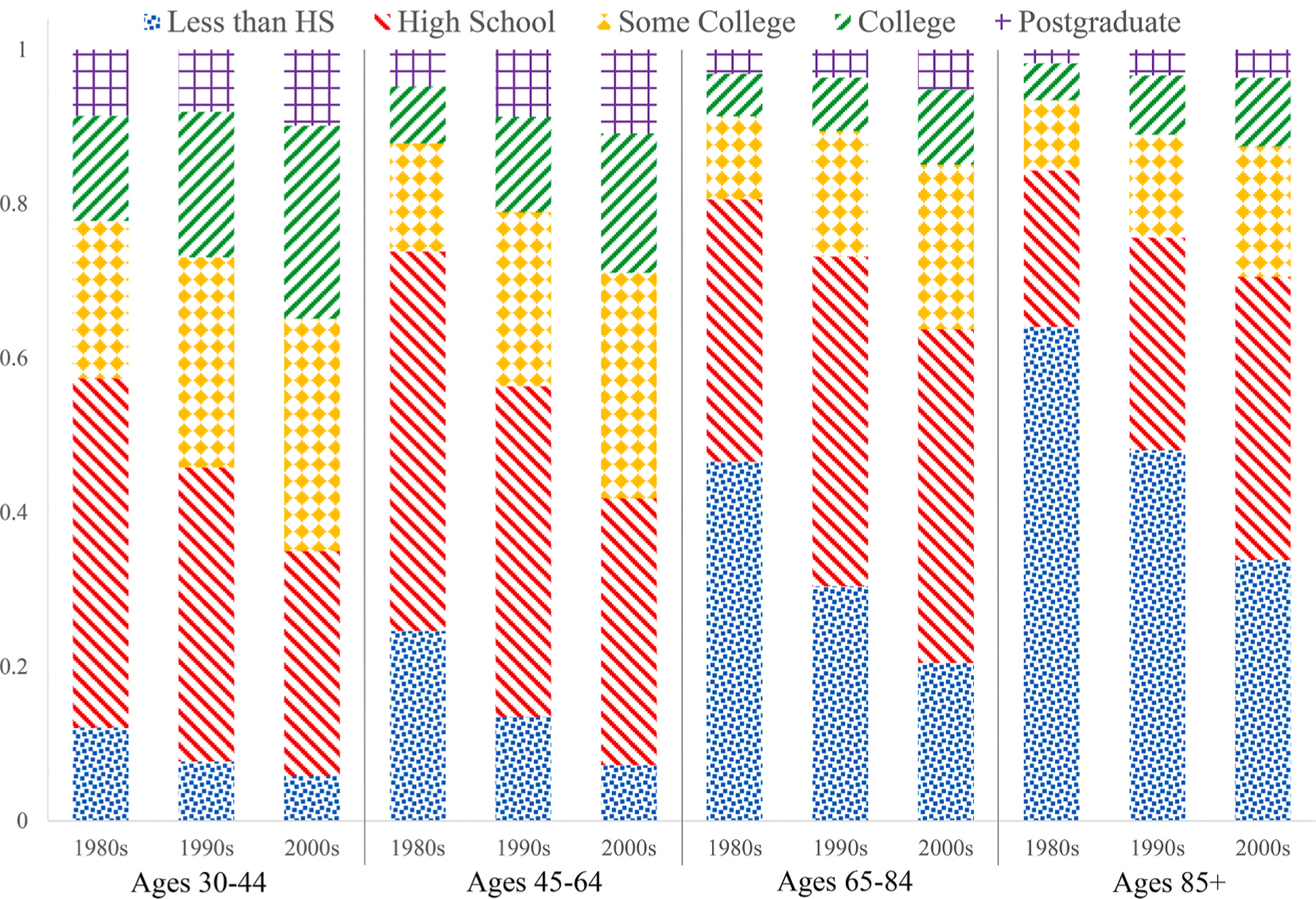
Education Distributions by Age and Period, non-Hispanic White American Women, 1980s-2000s

Source: U.S. National Longitudinal Mortality Study (NLMS) Release 5.

The changes in educational distribution by birth cohort shown above in both Finland and the United States together with changing occupational structures and labor markets that have increasingly rewarded those with higher levels of education suggest that a given level of schooling does not confer the same social status at different points in time (Berg 1970; Collins 1971, 1979; Spence 1973). For example, as seen in Appendix Fig. 1 for Finland, the educational distribution of male employment by occupational class has shifted considerably over time. An increasing proportion of low-skill occupations employ men with educational credentials beyond a basic education. Men with a basic level of schooling are increasingly relegated to unskilled occupations while the lower and upper white-collar occupations are dominated with those who have obtained education beyond secondary school. Individuals who obtained higher status occupations in earlier periods needed less schooling than individuals in later birth cohorts. In other words, the educational qualifications required for the same types of jobs became higher for later birth cohorts. Thus, part of the widening of the educational gradient in mortality may be due to cohort-specific educational differences that are related to occupational and status competition (Collins 1971, 1979). For all its virtues, educational level is thus unlikely to be a consistent measure of socioeconomic status across cohorts when educational distributions are changing over time. In this article, we present a parameterization of the relationship between relative position in the education distribution and mortality that allows us to generate estimates of status gradients in life expectancy that are consistent across time.

1.2. Data and methods

We use data from the U.S. National Longitudinal Mortality Study (NLMS) (Rogot et al., 1992) and linked Census and vital statistics register data from Finland (Martikainen et al., 2013) on deaths and exact person-days lived cross-tabulated by sex, age, period and educational attainment for those aged 30+. The NLMS consists of multiple waves of the Current Population Surveys (CPS) from the 1980s, 1990s, and 2000s linked to the National Death Index (NDI) for up to six years of mortality follow-up. The CPS is a nationally representative household survey of the civilian, non-institutionalized population of the United Sates designed to provide detailed data on unemployment and socioeconomic and demographic characteristics of the U.S. population. Because the U.S. population is more heterogeneous in its racial and ethnic composition than the Finnish population, we restricted the U.S. data to non-Hispanic whites. For Finland, we use the Finnish Longitudinal Census Data File restricted to the non-institutionalized population to make it comparable with the U.S. data. The Finnish data covers each five-year period between 1971 and 2010, while the American data covers three periods: the 1980s, 1990s, and 2000s. Age is collapsed into five-year groups. Education is categorized into a 6-category measure for Finland, roughly translating to: basic education; upper secondary, vocational school; upper secondary, high school; short-cycle tertiary; bachelor’s degree; and master’s degree or higher. For the 2001–2005 period and later, the education categorization changes slightly and collapses the second group with a portion of the third group (the categorization for the lowest and the highest education groups remains the same). For the U.S., education is measured by highest grade or credential completed, covering the following categories: less than high school; high school graduate; some college; college degree; and postgraduate. The person-years measure in both datasets is the total number of days lived by people within a sex-age-education group in a given period. Individuals are allowed to age out of and into adjacent age groups. Mortality follow-up begins at time of the CPS or the Census enumeration.

1.3. Death rates and life tables

We compute age-sex-education-specific mortality rates by five-year age groups for each of the aforementioned eight time periods for Finland and three time periods for the U.S., for age groups 30–34, …, 90–94, 95+ years (top-coded at 90+ for the U.S.). We do not compute death rates for people aged younger than 30 since many are unlikely to have completed their education. Each rate is multiplied by 365.25 to measure the rates in terms of deaths per person-year. Abridged life tables starting at age 30 are computed using standard methods with graduated _na_x values (Preston et al., 2001).

1.4. Modeling the relationship between SES and mortality

Since our goal is to examine the relationship between education percentile (position in the education distribution) and mortality, we computed age-sex-period-specific education distributions and mortality ratios. Within an age-sex group in a given period, we divided each of the education-specific death rates by the overall mortality rate (the age-sex-specific mortality rate for that period). For Finland, this produced six mortality ratios for each age-sex group in each period (with the exception of the 2001–2005 and 2006–2010 periods, which had only five education categories):

$$R_i=\raisebox{1ex}{${}_{n}m{}_x^i$}\!\left/ \!\raisebox{-1ex}{${}_{n}m{}_x$}\right.i=1,\dots ,6$$ (1)

where ${}_{n}m{}_x^i$ is the death rate for education group i, and _nm_x is the death rate for the entire population aged x to x + n. For the United States, these tabulations produced five mortality ratios for each age-sex group for each of the three periods (1980s, 1990s, and 2000s). We then computed the education distribution for each age-sex group in each period by tabulating the number of person-years lived by each education group and dividing by the total person-years lived across all education groups within the age-sex group in that period. The education percentile for each age-sex-education group in a given year is the percentile corresponding to the halfway point for the education group within the education distribution in that period. For example, in 1971–1975 the upper secondary vocational education group for males aged 30–34 in Finland ranged from the 56th percentile to the 77th percentile. The midway point for this group is (0.56 + 0.77)/2 = 0.67, so the education percentile value for 30–34-year-old Finnish males in 1971–1975 with an upper secondary vocational education is 0.67. By 1996–2000, the upper secondary vocational education group for males aged 30–34 ranged from the 20th percentile to the 55th percentile. The midway point for this group is (0.20 + 0.55)/2 = 0.38, so the education percentile value for 30–34-year-old males in 1996–2000 with an upper secondary vocational education is 0.38. We then plotted the mortality ratios against the education percentile values to trace out the socioeconomic gradient in mortality.

Based on the observed relationship between the mortality ratios and the education percentiles, we estimated regressions of the following form:

$$\text{log}\left(R_i\right)=\alpha +\beta e_i+u_{i}i=1,\dots ,6$$ (2)

where i represents an education group, R_i is the education-specific mortality ratio for a given age-sex group in a particular period, e_i is the education percentile corresponding to education group i in that year and for that age-sex group, and u_i is a mean-zero error term. Since there are 14 age groups, 2 sexes, and eight five-year periods in Finland, we compute a total of 14 × 2 × 8 = 224 regressions, each with two parameters (α and β). Similarly, we compute 13 × 2 × 3 = 78 regressions for the United States.

The α and β parameters are the skewness and inequality parameters, respectively, pertaining to the education-mortality relationship. e^α can be interpreted as the mortality ratio relative to the entire population for people at the bottom of the education distribution. All else being equal, a higher α value indicates that mortality is more concentrated (skewed) toward the lower end of the education spectrum. If α increases over time, then there is evidence that the mortality of the most poorly educated is diverging from the overall level of mortality. If α decreases over time, then the mortality of the most poorly educated is converging to the overall level of mortality — mortality is less skewed towards lower levels of the education distribution. The β parameter reflects relative mortality inequality by educational attainment and (e^β −1) can be interpreted as the average percent difference in mortality between the 0^th and 100th percentiles of the education distribution. For example, a β value of −1.8 means that individuals with the highest level of education have mortality rates that are around 83% lower than individuals with the lowest level of schooling (e^−1.8 − 1 ≈ −0.83). A decrease in β over time indicates that the relative difference in mortality between individuals with the highest and lowest level of schooling is growing. A mean-preserving change in α requires that β changes in the opposite direction. In other words, if the situation of the worst-off is improving relative to the total population (α is decreasing) but the overall mortality rate in the population remains constant, then by necessity the most highly educated must shoulder a greater portion of the mortality burden (β must increase) and educational inequality in mortality will decrease. Together, these two parameters summarize the main features of the educational gradient in relative mortality: the relative difference in mortality between the most and least educated and the degree of concentration of mortality at the lower end of the education distribution.

1.5. Computing life tables by educational quintile

The objective of this analysis is to compute life tables that account for the changing education distribution across birth cohorts in a given time period and across time. To do so, we must be able to compare a fixed set of education categories—for example, quintiles of educational attainment—and compute life tables based on the mortality rates corresponding to those fixed quintiles. We can use the regression estimates (α and β) to compute mortality rates that correspond to the education quintiles or any other range of the education distribution. If an education quintile ranges between education percentiles a and b, then the average mortality ratio corresponding to that quintile is:

$${\overline{R}}_{\left(a,b\right)}=\frac{1}{b-a}\underset{a}{\overset{b}{\int }}{e}^{\alpha +\beta x}dx=\frac{e^{\alpha }}{\beta \left(b-a\right)}\left(e^{\beta b}-e^{\beta a}\right)$$ (3)

which means that the average mortality rate corresponding to that quintile is just the age-sex-specific general mortality rate multiplied by ${\overline{R}}_{\left(a,b\right)}$. Since the second education quintile ranges from 0.20 to 0.40, b = 0.40 and a = 0.20 for that quintile. If, for a given age-sex group in a particular period, α = 0.8 and β = −1.8 then ${\overline{R}}_{\left(0.2,0.4\right)}=1.3$. For example, males aged 30–34 in 1986–1990 in Finland had a death rate of 0.002, so if their α and β parameters were 0.8 and −1.8, respectively, then their second-quintile-specific death rate is 1.3 × 0.002 = 0.0026.

Using the two model parameters we compute quintile-specific death rates for each age-sex group in each of the eight periods for Finland and three periods for the United States to produce a full set of age-specific death rates for 80 distinct life tables (five quintiles over eight periods for two sexes) for Finland and 30 distinct life tables (five quintiles over three periods for two sexes) for the United States.¹ We then compute the life tables using iteration to calculate the _na_x values (Preston et al., 2001). We describe how to implement the method introduced in this article in additional detail and provide an example in an online supplementary methodological appendix.

1.6. Counterfactuals

Finally, we also compute counterfactual life table estimates. These counterfactual estimates allow us to make statements like: “If relative educational inequalities in mortality hadn’t changed over time (but overall mortality rates evolved as observed), what would be the difference in life expectancy between the first and fifth quintile of the education distribution?” To do so, we can simply borrow the α and β estimates from 1971 to 1975 for Finland and apply them to the 1976–1980, 1981–1985, 1986–1990, 1991–1995, 1996–2000, 2001–2005, and 2006–2010 overall mortality rates to compute the counterfactual life table. Similarly, for the United States we take the α and β estimates for the 1980s and apply them for 1990s and 2000s overall mortality rates to obtain counterfactual life tables.

2. Results

2.1. Trends in educational inequality in mortality in Finland

As discussed previously and shown in Figs. 1 and 2, there were large changes in the education distribution among both male and female birth cohorts in Finland over time.

Table 1 shows life expectancy at age 30 by educational category for Finland for the eight time periods for men and women. Life expectancy increased for all education categories, though not at an equal pace. People with higher levels of education tended to experience faster increases in life expectancy than people with lower levels. This led to an increase in the difference in life expectancy between graduate degree holders and people with basic education. Between 1971–1975 and 2006–2010, this differential increased from 5.1 years to 8.3 years for men (a 3.3-year increase) and from 3.6 years to 4.6 years for women (a 1.0-year increase).

Table 1.

Life Expectancy at Age 30 by Education and Year, Finland 1971–2010.

Education Level	Time Period								Change Over Time
Men	71–75	76–80	81–85	86–90	91–95	96–00	01–05	06–10	71–75 to 06–10
1. Basic education	38.6	39.5	40.7	41.1	42.0	43.0	43.9	44.4	5.7
2. Upper secondary, vocational school	42.1	42.9	43.1	43.5	44.5	45.4	–	–	–
3. Upper secondary, high school	41.5	42.8	44.1	44.8	46.1	47.4	46.8a	47.5a	–
4. Short-cycle tertiary	43.4	44.7	45.8	46.8	48.1	49.6	49.5	50.3	7.0
5. Bachelor’s degree	43.2	43.3	45	45.8	47.4	49.1	50.7	51.8	8.6
6. Master’s degree or higher	43.7	45	46.2	47.6	48.9	50.3	51.4	52.7	9.0
Total	39.3	40.4	41.7	42.4	43.6	44.8	46.3	47.3	8.0
Difference (6–1)	5.1	5.5	5.4	6.5	6.9	7.3	7.5	8.3	3.3
Women	71–75	76–80	81–85	86–90	91–95	96–00	01–05	06–10	71–75 to 06–10
1. Basic education	46.6	48.0	49.0	49.2	49.7	50.4	51.0	51.5	4.9
2. Upper secondary, vocational school	49.2	50.1	50.8	51.0	51.7	52.5	–	–	–
3. Upper secondary, high school	49.2	50.0	51.2	51.1	52.2	53.1	53.4a	54.2a	–
4. Short-cycle tertiary	49.3	50.9	51.8	52.2	53.2	54.4	54.6	55.8	6.5
5. Bachelor’s degree	49.1	51.3	51.6	52.4	52.9	53.7	55.2	56.0	6.9
6. Master’s degree or higher	50.2	51.0	51.9	52.4	53.8	53.8	55.1	56.1	5.9
Total	46.9	48.4	49.4	49.7	50.5	51.5	52.5	53.6	6.7
Difference (6–1)	3.6	3.0	2.9	3.3	4.1	3.4	4.1	4.6	1.0

^aDue to a change in Finland’s educational system, the “Upper secondary, high school” category from 2001 forward corresponds to the combined “Upper secondary, vocational school” and “Upper secondary, high school” categories in prior years.

Source: Authors’ calculations based on Finnish registry data and censuses.

Fig. 5 plots the relationship between education percentile and mortality ratios (the ratio of education-specific mortality to overall mortality) for Finnish men and women. The point markers represent the period and 5-year age groups, and the colors highlight the first (red) and last (blue) year of observation. We find a strikingly regular negative logarithmic relationship. Relative mortality is highest for people with the lowest level of schooling, and lowest for those with the highest level of education, following a smooth diminishing-returns relationship. This relationship holds for both men and women and for all age groups and time periods, although the relationship is clearer for individuals aged 30–84. This is consistent with the lack of a large educational gradient in mortality among people aged 85+. The points cross the 1.0 (equality) line at around the 50th percentile of education for men and the 40th percentile for women, indicating a slightly greater concentration of inequality at the lower educational percentiles for men than for women. These patterns are also evident in Appendix Figs. 2–5, which graph the values of (e^β −1) (Appendix Figs. 2–3) and e^α (Appendix Figs. 4–5) from the estimated regressions. These figures show that inequality in relative mortality has increased for the younger age groups and remained stable for the older age groups.

Fig. 5.

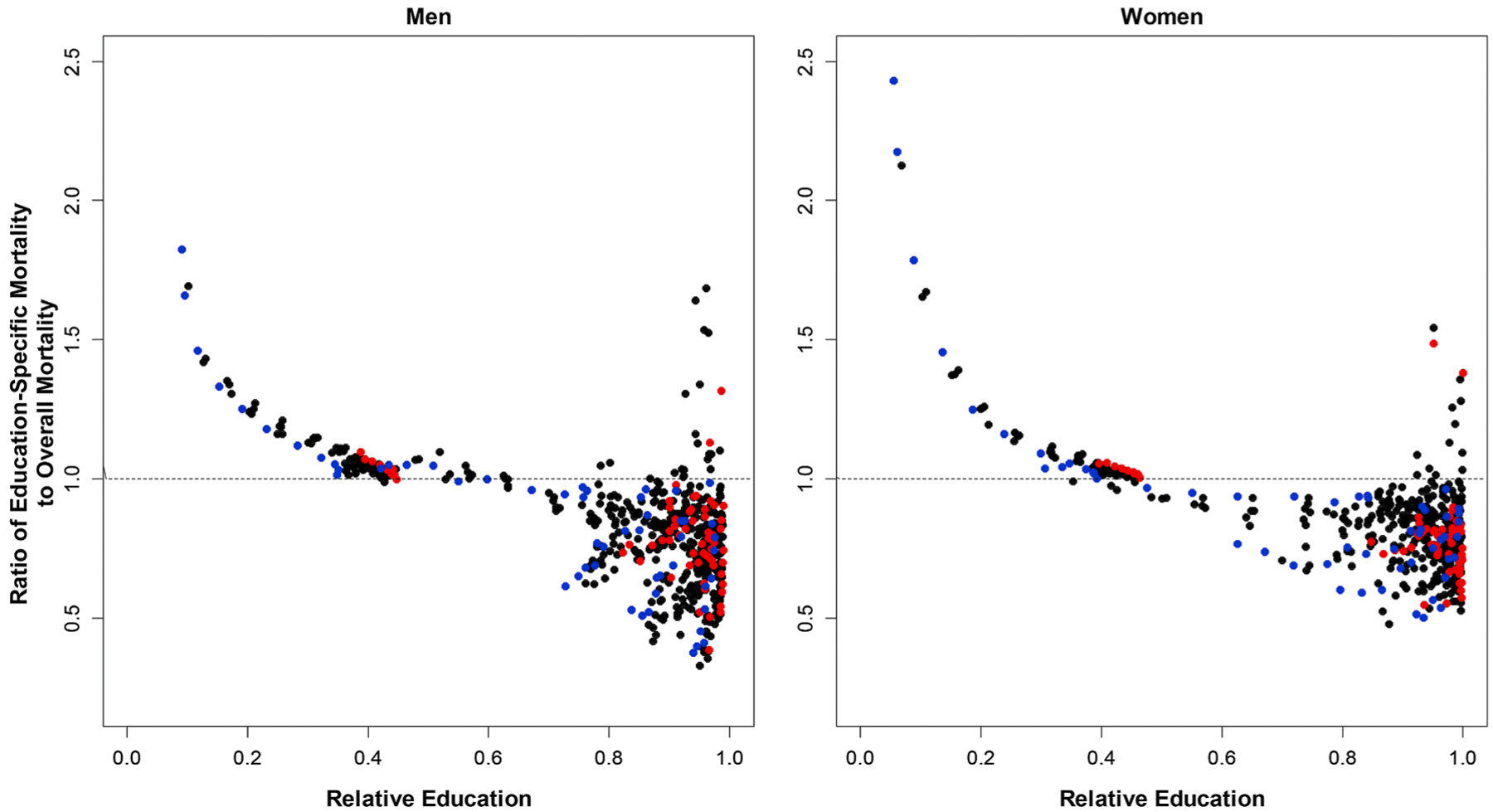
Relationship between Relative Education and Relative Mortality among Finnish Men and Women

Source: Authors’ calculations based on Finnish registry data and censuses.

Note: The colored points correspond to the periods 1971–1975 (red) and 2006–2010 (blue), and each of the intervening five-year periods (black). (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Table 2 presents life expectancy at age 30 for Finland by education quintile. These values are computed using the overall age-specific mortality rates and the estimates of α and β described earlier. Life expectancy increased for all education quintiles for both men and women. Similar to the estimates by educational thresholds shown in Table 1, male life expectancy increased more quickly for those in the higher education quintiles than for those in the lower quintiles, although the increase in the difference in life expectancy between the top and bottom education quintiles is somewhat smaller than the increase in the difference between the top and bottom education categories—2.0 years versus 3.3 years—between 1971–1975 and 2006–2010. The pattern, however, differs for women. Women in all five education quintiles experienced similar increases in life expectancy ranging from 6.6 to 6.8 years and the difference between the first and fifth education quintile did not change between 1971–1975 and 2006–2010. Women did experience a slight decrease in the difference between 1971–1975 and 1986–1990, and subsequently a slight increase from 1996 to 2000 to 2001–2005.

Table 2.

Life Expectancy at Age 30 by Education Quintile and Year, Finland 1971–2010.

Education Level	Time Period								Change Over Time
Men	71–75	76–80	81–85	86–90	91–95	96–00	01–05	06–10	71–75 to 06–10
1. First Quintile	36.1	37.1	38.6	39.0	39.9	41.0	42.2	42.9	6.8
2. Second Quintile	37.9	38.9	40.3	40.9	42.0	43.2	44.6	45.6	7.7
3. Third Quintile	39.5	40.5	41.8	42.6	43.8	45.2	46.6	47.8	8.3
4. Fourth Quintile	41.0	42.1	43.3	44.1	45.5	46.9	48.4	49.6	8.6
5. Fifth Quintile	42.4	43.6	44.6	45.6	47.0	48.5	50.0	51.2	8.8
Total	39.3	40.4	41.7	42.4	43.6	44.8	46.3	47.3	8.0
Difference (5–1)	6.3	6.4	6.0	6.6	7.1	7.5	7.8	8.3	2.0
Women	71–75	76–80	81–85	86–90	91–95	96–00	01–05	06–10	71–75 to 06–10
1. First Quintile	44.7	46.5	47.6	47.9	48.6	49.5	50.3	51.4	6.6
2. Second Quintile	45.9	47.5	48.6	48.9	49.6	50.6	51.6	52.6	6.8
3. Third Quintile	47.0	48.5	49.4	49.8	50.6	51.6	52.7	53.8	6.8
4. Fourth Quintile	48.0	49.4	50.3	50.6	51.5	52.6	53.7	54.8	6.7
5. Fifth Quintile	49.1	50.3	51.1	51.4	52.4	53.4	54.6	55.7	6.6
Total	46.9	48.4	49.4	49.7	50.5	51.5	52.5	53.6	6.7
Difference (5–1)	4.3	3.8	3.5	3.5	3.8	3.9	4.3	4.3	0.0

Source: Authors’ calculations based on Finnish registry data and censuses.

Table 3 shows counterfactual life expectancies at age 30 for Finland by education quintile. The counterfactual scenario fixes the α and β parameters to their 1971–1975 levels and allows overall mortality rates to improve as observed. This table, coupled with the results in Table 2, answers the question: “How much of the widening in the educational gradient in life expectancy is due to changes in the inequality parameters in Finland (net of secular mortality declines)?” We find that if the inequality parameters remained fixed, then individuals with the lowest level of schooling would experience greater increases in life expectancy than those with the highest level of schooling. For men, life expectancy at age 30 among the first quintile would increase from 36.1 to 44.6 years (8.5-year increase), whereas life expectancy among the fifth quintile would increase from 42.4 to 49.8 years (7.4-year increase). This would shrink the difference in life expectancy between the first and fifth quintiles by 1.0. The respective figures for women are 44.7 and 51.6 for the first quintile and 49.1 to 55.5 in the fifth quintile, reducing the life expectancy gap by 0.4 years. Since overall mortality rates were allowed to vary as observed in the actual population, total life expectancy in the counterfactual scenario is equal to total life expectancy in the factual scenario. When coupled with Table 2, these results suggest that, net of secular declines in mortality, the growth in inequality is responsible for a widening of the life expectancy gradient on the order of 3.0 years for men (2.0 − ( − 1.0) = 3.0) and 0.5 years for women (0.0 − ( − 0.5) =0.5). Additional decompositions suggest that 76% of the widening in the longevity gradient between the top and bottom education quintiles for men is due to increasing mortality inequality between the most- and least-educated (beta effects), while 24% is due to greater concentration of mortality among the least educated (alpha effects). For women, the alpha and beta effects cancel each other out.

Table 3.

Counterfactual Life Expectancy at Age 30 by Education Quintile and Year Assuming No Change in Inequality Parameters, Finland 1971–2010.

Education Level	Time Period								Change Over Time
Men	71–75	76–80	81–85	86–90	91–95	96–00	01–05	06–10	71–75 to 06–10
1. First Quintile	36.1	37.3	38.7	39.3	40.6	42.0	43.5	44.6	8.5
2. Second Quintile	37.9	39.0	40.3	41.0	42.2	43.5	45.0	46.0	8.2
3. Third Quintile	39.5	40.5	41.8	42.5	43.7	44.9	46.4	47.4	7.9
4. Fourth Quintile	41.0	42.0	43.2	43.9	45.0	46.3	47.6	48.7	7.7
5. Fifth Quintile	42.4	43.4	44.5	45.2	46.3	47.5	48.8	49.8	7.4
Total	39.3	40.4	41.7	42.4	43.6	44.8	46.3	47.3	8.0
Difference (5–1)	6.3	6.1	5.9	5.9	5.7	5.4	5.3	5.3	−1.0
Women	71–75	76–80	81–85	86–90	91–95	96–00	01–05	06–10	71–75 to 06–10
1. First Quintile	44.7	46.2	47.3	47.6	48.4	49.5	50.5	51.6	6.9
2. Second Quintile	45.9	47.4	48.4	48.7	49.5	50.5	51.6	52.6	6.8
3. Third Quintile	47.0	48.5	49.4	49.8	50.5	51.5	52.6	53.6	6.7
4. Fourth Quintile	48.0	49.5	50.5	50.8	51.6	52.5	53.5	54.6	6.6
5. Fifth Quintile	49.1	50.6	51.5	51.8	52.5	53.5	54.5	55.5	6.4
Total	46.9	48.4	49.4	49.7	50.5	51.5	52.5	53.6	6.7
Difference (5–1)	4.3	4.3	4.3	4.2	4.1	4.0	4.0	3.9	−0.4

Source: Authors’ calculations based on Finnish registry data and censuses.

2.2. Comparison to the United States

Fig. 6 demonstrates that the negative logarithmic relationship observed for Finland also holds for the U.S. The results for educational categories (Table 4), education quintiles (Table 5), and the counterfactual scenario (Table 6) are also broadly similar to those we documented in Finland in that life expectancy differentials across education categories were typically larger than differentials between the top and bottom education quintiles. In contrast to Finland, however, the increase in the gap between the top and bottom education categories was greater for women (4.9 years) than for men (4.0 years) (Table 4). These differentials were reduced to 3.0 years for women, by 1.9 years, and to 3.3 years for men, by 0.7 years, when comparing the top and bottom quintiles in the education distribution (Table 5). These results suggest that for non-Hispanic whites, educational expansion appears to have had a larger impact on estimates of educational inequality in mortality for women than for men when measured by education categories compared to the relative position in the education distribution from the 1980s–2000s. This seems sensible, since white women had a more recent and rapid educational transition than did white men, as reflected in Figs. 3 and 4.

Fig. 6.

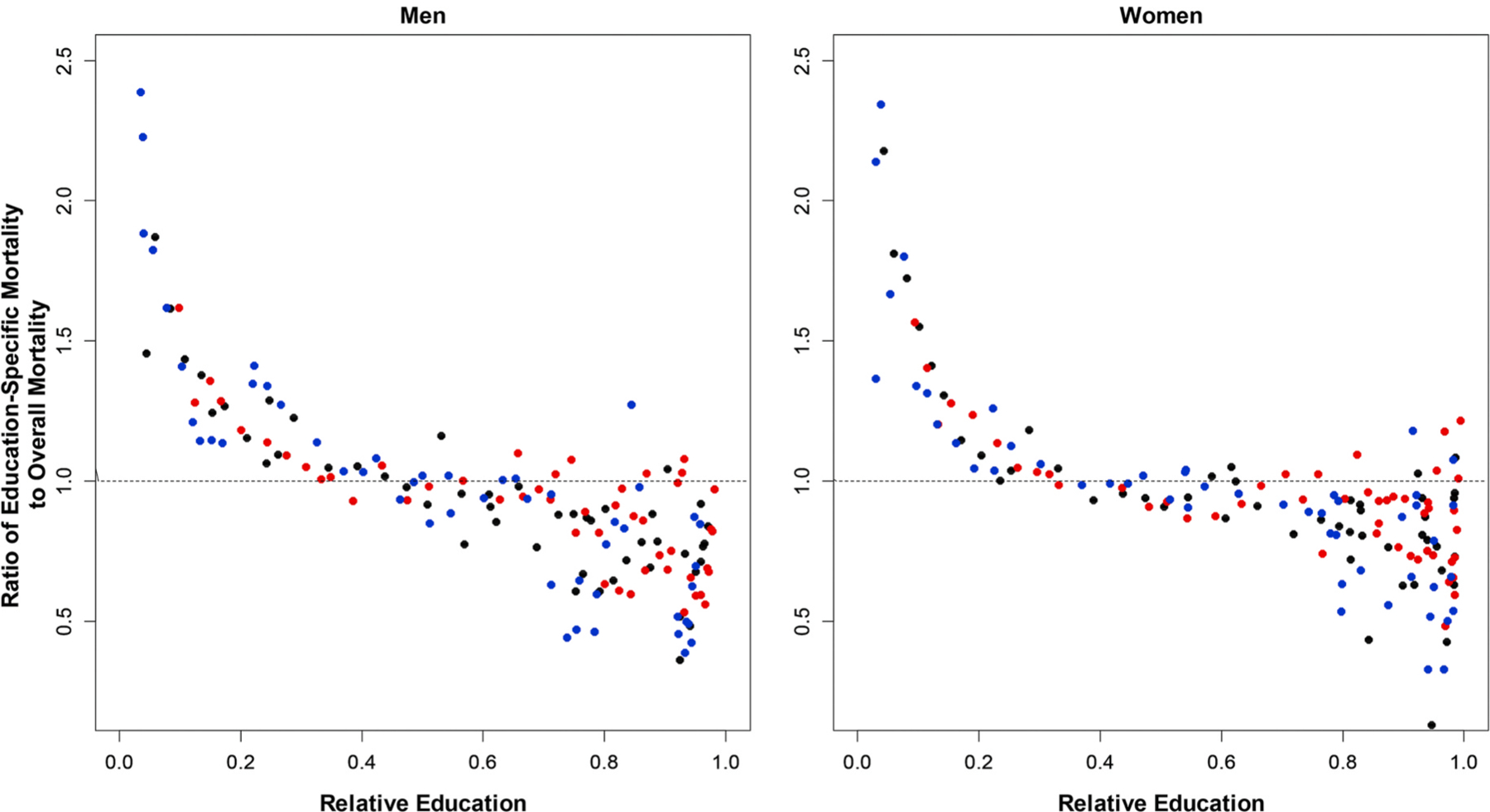
Relationship between Relative Education and Relative Mortality among non-Hispanic White American Men and Women

Source: Authors’ calculations based on U.S. NLMS.

Note: The red, black, and blue points correspond to the 1980s, 1990s, and 2000s, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

Table 4.

Life Expectancy at Age 30 by Year, Sex, and Education Category, non-Hispanic Whites, United States 1980s–2000s.

Education Level	Males				Females
	Time Period			Change Over Time	Time Period			Change Over Time
	1980s	1990s	2000s	1980s-2000s	1980s	1990s	2000s	1980s-2000s
1. Less than High School	42.7	42.8	44.7	1.9	50.7	48.9	49.8	−0.9
2. High School	45.5	46.8	48.6	3.1	53.0	52.8	54.6	1.6
3. Some College	46.1	48.4	51.5	5.4	53.4	54.3	55.4	2.0
4. College	48.5	50.3	53.3	4.8	53.6	55.0	56.5	2.8
5. Postgraduate	49.9	51.0	55.9	6.0	54.7	56.3	58.7	4.0
Total	45.3	46.9	50.2	4.9	52.4	52.6	54.5	2.1
Difference (5–1)	7.2	8.2	11.2	4.0	4.0	7.4	9.0	4.9

Source: Authors’’ calculations based on NLMS Release 5.

Table 5.

Life Expectancy at Age 30 by Year, Sex, and Education Quintile, non-Hispanic Whites, United States 1980s–2000s.

Education Level	Males				Females
	Time Period			Change Over Time	Time Period			Change Over Time
	1980s	1990s	2000s	1980s-2000s	1980s	1990s	2000s	1980s-2000s
1. First Quintile	42.1	43.2	45.3	3.2	50.7	49.8	51.3	0.6
2. Second Quintile	43.9	45.3	48.3	4.4	51.7	51.5	53.2	1.5
3. Third Quintile	45.6	47.3	50.8	5.3	52.6	52.9	54.9	2.3
4. Fourth Quintile	47.1	49.1	53.1	6.0	53.4	54.2	56.4	3.0
5. Fifth Quintile	48.5	50.8	55.0	6.6	54.1	55.4	57.7	3.5
Total	45.3	46.9	50.2	4.9	52.4	52.6	54.5	2.1
Difference (5–1)	6.4	7.6	9.7	3.3	3.4	5.5	6.4	3.0

Source: Authors’ calculations based on NLMS Release 5.

Table 6.

Counterfactual Life Expectancy at Age 30 by Year, Sex, and Education Quintile Assuming No Change in Inequality Parameters, non-Hispanic Whites, United States 1980s–2000s.

Education Level	Males				Females
	Time Period			Change Over Time	Time Period			Change Over Time
	1980s	1990s	2000s	1980s-2000s	1980s	1990s	2000s	1980s-2000s
1. First Quintile	42.1	43.8	47.2	5.1	50.7	51.0	52.9	2.2
2. Second Quintile	43.9	45.6	48.9	5.0	51.7	51.9	53.8	2.1
3. Third Quintile	45.6	47.2	50.5	4.9	52.6	52.7	54.6	2.1
4. Fourth Quintile	47.1	48.6	51.8	4.7	53.4	53.5	55.4	2.0
5. Fifth Quintile	48.5	50.0	53.1	4.6	54.1	54.2	56.0	1.9
Total	45.3	46.9	50.2	4.9	52.4	52.6	54.5	2.1
Difference (5–1)	6.4	6.1	5.9	−0.5	3.4	3.3	3.2	−0.3

Source: Authors’ calculations based on NLMS Release 5.

In Table 6, we show the counterfactual scenario for the United States and answer the following question: “How much of the widening in the educational gradient in life expectancy is due to changes in the inequality parameters in the United States (net of secular mortality declines and changing educational composition)?” We find that net of secular declines in mortality, the growth in inequality is responsible for a widening of the life expectancy gradient on the order of 3.8 years for men (3.3 − (− 0.5) = 3.8) and 3.2 years for women (3.0 − (− 0.3) ≈ 3.2 due to rounding). Decompositions suggest that among white men, approximately 90% of the increase in the inequality across quintiles was due to increasing inequality between the most- and least-educated (the beta effect) and approximately 10% was due to the increasing concentration of mortality among the least-educated (the alpha effect). This is consistent with the finding for Finland. The equivalent proportions for white women are 87% due to beta effects and 13% due to alpha effects.

3. Discussion and conclusion

The great majority of contemporary research on the education-mortality gradient has used fixed educational thresholds, whereas some have tried to account for shifting education distributions in various ways (Ho 2017; Ho and Fenelon 2015; Miech et al., 2011; Montez and Zajacova 2013b, 2014; Östergren et al., 2017). We propose a unique but relatively simple method to address this issue and demonstrate its utility using high-quality survey and register-based data in two different contexts with variation in the timing of educational expansion.

Perhaps the most striking finding is a remarkably regular, negative logarithmic relationship between educational percentiles and mortality. This relationship holds across multiple age groups, both sexes, two different countries, and multiple time periods spanning 40 years. Our findings are relevant for the literature concerning the education/health gradient and the broader social science literature on the construction of status. At first blush, our finding of a negative log relationship might seem at odds with prior studies that have identified a piecewise-linear relationship between years of schooling and mortality in the U.S. (Backlund et al., 1999; Hayward et al., 2015; Montez et al., 2012; Sheehan et al., 2018). In actuality, it is consistent with the prior findings. The negative logarithmic relationship suggests that the presence of a large education category should be accompanied by a large stepwise change in relative mortality. This is consistent with prior findings that there is a stepwise decline in mortality at educational credential thresholds (e.g., high school and college graduation).

One of the most widely reported findings in the mortality literature is that the education-mortality gradient has widened over time in a number of countries (Hendi 2017; Mackenbach et al., 2016; Meara et al., 2008; Montez et al., 2011), while some other studies have shown that changes in the education distributions (i.e., educational expansion) are responsible for a part of this widening (Begier et al., 2013; Bound et al., 2015; Dowd and Hamoudi 2014; Goldring et al., 2016; Hendi 2015, 2017; Östergren et al., 2017). Relative to this study, Hendi (2015) finds a larger role for educational expansion in driving increasing inequality for white men. That study focuses on different time periods, uses different methods, and restricts analyses to people aged 25–84 as opposed to 30+ used here. Hendi (2015) solves the problem that education distributions within age groups change over time. The present study additionally solves the problem that education distributions vary across age groups within time periods. Our findings are consistent with these prior studies in that estimates of educational inequality in mortality are affected by how educational attainment is measured and that holding the relative position in the education distribution constant over time will result in smaller increase in the education-mortality gradient than when the gradient is based on educational categories. We further show that the size of the difference between these estimates depends in part on the timing of the educational expansion and overall mortality decline. Our findings further point to the role of changing selectivity into education categories. Both Finland and the United States experienced rapid education transitions, which allowed an increasing proportion of young people to attain higher education that dramatically altered the education distribution across birth cohorts over time.

If we focus on education categories as opposed to position in the education distribution, then educational expansions will by necessity result in increasing inequality in mortality. Part of the increase in inequality comes from actual increases in underlying inequality (summarized in this study by the α and β parameters). Another part of the increase in inequality may come from decreased barriers to higher education. The latter process is actually one of increased socioeconomic equality—people are finding it easier to gain a secondary or tertiary education; however, because of the decline in selectivity into higher education, this process would lead to higher relative mortality in the low education categories, which would tend to increase inequality.

One potential remaining question is how researchers should think about inequality with respect to education quintiles. While it is more straightforward to think about income in terms of quintiles, education quintiles do not admit as ready an interpretation. One way to interpret education quintiles is to posit education as representing the observed outcome of some underlying, latent continuous variable. If there is a monotonic relationship between this latent variable and educational attainment, then education quintiles correspond to the education categories that would prevail if the latent variable were divided into five equal-sized groups. Another way to think about education quintiles is to recognize that education categories are simply blunt measures of exact educational attainment. For example, in the U.S., the “less than high school” group usually consists of people who have had one, two, or three years of high school education without earning a diploma. The number of years is a closer approximation of the exact amount of educational attainment, which is itself a continuous variable that admits quintile (or other quantile) groupings.

Future studies of educational inequalities in mortality should pay attention to the potential impact of changing education distributions across birth cohorts when measuring educational gradients in mortality. We further note that the impact of changing education distributions is not specific to mortality, but also should be taken into account when studying the association of educational attainment and other outcomes over time, such as fertility and marriage, or when studying trends and differentials in other social determinants of health with distributional change, such as occupational social class or living arrangements.

The method developed in this paper can be thought of as an extension of the slope-index of inequality (Pamuk 1985; Preston et al., 1981). The latter measures mortality inequality by modeling the relationship between relative education and either life expectancy or age-standardized death rates within education categories. Our method allows the mortality-education relationship to vary by age group and additionally allows for non-linearity in this relationship. Another advantage of our method is that it doesn’t require any additional data than what is typically used to compute the education-specific mortality measures—namely, deaths and person-years for each education category by sex and age group. This method has further applications in terms of making comparisons across populations (e.g., international comparisons or comparisons across states), since different populations have differing education distributions.

Much of the literature on the education-mortality relationship has attempted to assess the extent to which this association is “causal” (Behrman et al., 2011; Lleras-Muney 2005; Lundborg et al., 2016). Our study does not make any claims as to the causality of the relationship. However, our findings do suggest that studies wishing to precisely identify such a relationship should do so separately for each birth cohort (since different birth cohorts have different levels of selectivity into education) and also account for the negative logarithmic relationship discussed above. One may be tempted to interpret the findings of the present study as an endorsement of the idea that education has no direct relationship with mortality in the causal sense. We do not believe our findings would substantiate such an interpretation. Rather, we would interpret our findings as suggesting that both the magnitude and direction of the causal relationship will vary across birth cohorts and across time as educational expansion occurs.

This study is also connected to the broader social scientific literature on the construction of status. Scholarship arising out of the mid-20th century status attainment literature have variously treated education as an absolute measure or a relative measure of status. Sociologists have argued since the 1970s that an educational credentialing process has been underway, with consequences for the link between education and status (Berg 1970; Collins 1971, 1979). Increased status competition linked to the labor market has driven an increasing number of young people to seek out a high school diploma or a college degree. In other words, this literature would suggest that education is not a static measure of status. This line of thinking is not restricted to sociology – economists have also theorized that increased educational attainment may be a strategy for signaling quality in the job market (Spence 1973). Our findings contribute to this line of thought by suggesting that both absolute and relative education may matter for the determination of status. If we believe that there will always be a status-mortality gradient and that education is a reasonable proxy for status, then a divergence between the trends in the absolute education gradient in mortality and the relative education gradient in mortality as observed in this study and elsewhere (Mackenbach et al., 2019) would suggest that the education-status relationship (i.e., the construction of status) is itself changing.

In summary, we provide two new findings to the literature. First, we identify a strikingly regular negative logarithmic relationship between relative education and relative mortality. This relationship holds across age groups, sexes, contexts, and time periods. Second, we use this negative logarithmic relationship to develop a new method that allows us to calculate period summary measures of mortality (e.g., life expectancy, age-standardized mortality rate) that correspond to any given segment of the education distribution. We apply this method and find that part of the widening of the absolute education differences in life expectancy appears to originate from educational expansion and the associated changes in the patterns of selection into educational categories. Future studies can use the methods developed in this article to assess whether changes in the education gradient in mortality using both absolute and relative education measures hold in other contexts where rapid education transitions have occurred.