Abstract
Following successful non-pharmaceutical interventions (NPI) aiming to control COVID-19, many jurisdictions reopened their economies and borders. As little immunity had developed in most populations, re-establishing higher contact carried substantial risks, and therefore many locations began to see resurgence in COVID-19 cases. We present a Bayesian method to estimate the leeway to reopen, or alternatively the strength of change required to re-establish COVID-19 control, in a range of jurisdictions experiencing different COVID-19 epidemics. We estimated the timing and strength of initial control measures such as widespread distancing and compared the leeway jurisdictions had to reopen immediately after NPI measures to later estimates of leeway. Finally, we quantified risks associated with reopening and the likely burden of new cases due to introductions from other jurisdictions. We found widely varying leeway to reopen. After initial NPI measures took effect, some jurisdictions had substantial leeway (e.g., Japan, New Zealand, Germany) with > 0.99 probability that contact rates were below 80% of the threshold for epidemic growth. Others had little leeway (e.g., the United Kingdom, Washington State) and some had none (e.g., Sweden, California). For most such regions, increases in contact rate of 1.5–2 fold would have had high (> 0.7) probability of exceeding past peak sizes. Most jurisdictions experienced June–August trajectories consistent with our projections of contact rate increases of 1–2-fold. Under such relaxation scenarios for some regions, we projected up to 100 additional cases if just one case were imported per week over six weeks, even between jurisdictions with comparable COVID-19 risk. We provide an R package covidseir to enable jurisdictions to estimate leeway and forecast cases under different future contact patterns. Estimates of leeway can establish a quantitative basis for decisions about reopening. We recommend a cautious approach to reopening economies and borders, coupled with strong monitoring for changes in transmission.
Keywords: SARS-CoV-2, COVID-19, Non-pharmaceutical interventions, Bayesian, SEIR
1. Introduction
The novel severe acute respiratory syndrome–coronavirus 2 (SARS-CoV-2 virus), which emerged at the end of 2019, has caused a global pandemic with over 28 million confirmed cases of coronavirus disease 2019 (COVID-19) and 911,000 confirmed deaths worldwide as of September 11, 2020 (Johns Hopkins University, 2020). Wide-ranging non-pharmaceutical interventions (NPIs) such as hand hygiene, face masks, physical (social) distancing, banning mass gatherings, and strict lockdowns have been among the primary tools for reducing COVID-19’s spread throughout 2020 (Gandhi et al., 2020, Ferguson et al., 2020, Hellewell et al., 2020, Hernandez et al., 2020, Dehning et al., 2020).
As a result, incidence in many jurisdictions outside China followed a similar pattern. After an initial phase of occasional detection (typically during late January to February and commonly due to imported cases), case counts grew rapidly (typically during early March). At this point, NPIs were put in place, in the form of “lockdowns” or other requirements for social and physical distancing. Case counts generally continued to rise for several weeks until the impact of NPIs became observable as a flattening and then decline of the epidemic curve. The economic, social, and health costs of NPIs have been significant.
Following declines in incidence, many jurisdictions partially lifted restrictions and reopened their economies, and allowed travel across regional and international boundaries (Cousins, 2020, Nordling, 2020, Kupferschmidt, 2020). Large studies undertaken in high-prevalence settings do not indicate that herd immunity has been reached (New York State Department of Health, 2020, Havers et al., 2020), and consistent with that observation, there have been large resurgences in COVID-19 cases in some jurisdictions, particularly in the United States (Johns Hopkins University, 2020). The degree of flexibility, or “leeway”, that exists to increase activity without causing a major resurgence or “second wave” of cases is largely unknown. The flexibility that exists in a given location is dependent on the local circumstances governing transmission, as well as the restrictions that are currently in place (Liu et al., 2020a, Imai et al., 2020). It is essential to estimate the risk associated with increased social and economic activity, and to understand this risk within and between particular jurisdictions, before making decisions around reopening.
We propose that discussions of COVID-19 risk in the context of reopening local economic activity, and of reopening borders and trade, should consider three aspects of transmission dynamics: (1) the probability that infections are rising at the current time in a jurisdiction, even if reported cases are declining; (2) the probability that a given increase in social and economic activity in the general population will lead to a substantial growth in cases over the coming weeks, and (3)—with regards to travel and border reopening—the number of introduced cases and their likely impact in the destination.
Using a mathematical model fit to local case data for a selection of jurisdictions with differing epidemics, we estimated the leeway for reopening without causing increasing COVID-19 cases, and the probabilities that reopening would lead to cases increasing above thresholds after a fixed time. We used case data prior to June 7, 2020 and compared the results to subsequent epidemic dynamics. The model includes a portion of the population engaging in distancing and related measures: these individuals are at reduced risk of encountering infectious individuals and are less likely to be encountered themselves—for example because they are able to work from home, consistently wear masks, or avoid social situations (see Methods).
For each of 12 jurisdictions worldwide, selected for their diversity of epidemic trajectories and NPIs, we first estimated the impact of widespread NPIs in the period between March and late April, 2020, and then calculated how close the estimated contact rate was to the threshold for epidemic growth. These jurisdictions were chosen to be illustrative rather than a global comparison. We included some European, Asian, and North American jurisdictions with varying epidemic trajectories and included some nations and some states or provinces that are likely to be sources of importations for each other. We estimated this both in the period immediately following NPI measures (late March to the end of April) and after May 1, as some jurisdictions began to reopen in May. We refer to these time frames as “post-NPI” and simply “May 2020” (though data go to June 7). We use the idea of leeway to describe the room between their state after May 2020 and the threshold beyond which cases would begin to grow.
2. Methods
2.1. Data
We obtained reported case data from publicly available sources (Table S1). In some cases, we performed additional data processing to account for data anomalies prior to model fitting (Supplement). We used Google mobility data (Google, 2020), along with segmented regression (Fig. S1; Supplement), to inform Bayesian priors for the start and end dates of physical distancing measures.
2.2. SEIR model
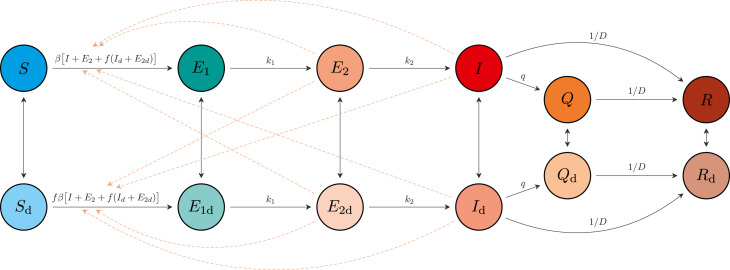
We extended the SARS-CoV-2 susceptible–exposed–infectious- recovered (SEIR) model developed in Anderson et al. (2020b). The model allows for self-isolation and quarantine through a quarantine compartment and a reduced duration of infection (compared to the clinical course of disease). We modeled a fixed portion of the population that is able to participate in physical distancing; each of the SEIR compartments has an analogous compartment in the distancing group (Fig. 1). We extended the model (Anderson et al., 2020b) here by estimating additional parameters: the timing of the physical distancing ramp, the scale of the initial cases, the fraction of the population engaging in physical distancing, and multiple contact rates through time for those practicing distancing.
Fig. 1.
Schematic of the epidemiological model. Compartments: susceptible to the virus (); exposed (); exposed, pre-symptomatic, and infectious (); symptomatic and infectious (); quarantined (); and recovered or deceased (). Recovered individuals are assumed to be immune. The model includes analogous variables for individuals practicing physical distancing: , , , , , and . Solid arrows represent flow of individuals between compartments at rates indicated by the mathematical terms. Dashed lines show which compartments contribute to new infections. An individual in some compartment can begin distancing and move to the corresponding compartment at rate . The reverse transition occurs at rate . The model quickly settles on a fraction participating in distancing, and dynamics depend on this fraction, rather than on the rates and .
Reproduced from Anderson et al. (2020b) for clarity.
The model describes the time dynamics of susceptible (), exposed () exposed and infectious (), symptomatic and infectious (), quarantined () and recovered or deceased () individuals (Fig. 1). It assumes that recovered individuals are immune to the virus. The model has analogous states for individuals practicing physical distancing, given by , , , , , and . Physical distancing is implemented by reducing the contact rate, thereby lowering the spread of the virus. The model is fitted separately for each jurisdiction.
The system of differential equations (Anderson et al., 2020b) for the non-physical-distancing population is given by:
| (1) |
where is the transmission rate, is the physical distancing parameter, is the average infectious period, and are the rates individuals move to and from the physical distancing compartments, is the rate of moving from to , is the rate of moving from to , and is the quarantine rate for movement from compartment to (Anderson et al., 2020b). In the model without interventions (neither distancing nor quarantine), the basic reproductive number is , namely the transmission rate times the mean duration of the infectious state period. We explicitly estimated not , and so is given by . The analogous system of equations for the physical-distancing population (Anderson et al., 2020b) is given by:
| (2) |
In this model, the probability of quarantine is , as the times from onset of symptoms to quarantine and from onset of symptoms to removal are independent exponential random variables. Quarantined individuals are unable to infect others in our model, so this would imply isolation outside of the household or a similar situation. The incubation period in our model is the sum of the duration of states and , which is 5 days on average, consistent with published estimates (McAloon et al., 2020, Tindale et al., 2020). The duration of the infectious state is on average 4 days, given and , plus an average of 1 day pre-symptomatic infectiousness. This results in serial intervals on average of 4–9 days (5 days from incubation period in the infectee, plus between −1 and 4 days from symptom onset of infector to exposure of infectee, exponentially distributed), consistent with published estimates (Griffin et al., 2020). While many individuals with symptoms will isolate immediately upon noticing COVID-19 symptoms, others may not show symptoms at all; a 4-day duration is an average over this variability.
The force of infection for this population is a fraction of that of the non-distancing population Eq. (1). In addition, note that the factor appears twice in the force of infection. This is due to the fact that physical distancing helps in reducing the rate that “distancers” move about and contact others, and the rate at which they are contacted by anyone (distancing or otherwise) who is experiencing population contact. This factor changes with time to model the introduction and strength of NPI measures that reduce contact rates:
| (3) |
where and are the start and end times of the initial implementation of physical distancing measures such that declines from 1 to during this period, and is the value of after May 1 as physical distancing starts potentially relaxing. For each jurisdiction, , and are estimated (see below).
Our overall approach was to estimate and using Bayesian inference. We also estimated the fraction of the population engaged in NPI or distancing, the times and , and the starting introduction size (prevalence at the model starting time 30 days before the first day). We used data from reported cases, despite the issues inherent in this (García-Basteiro et al., 2020), and compensate for variable testing through time where possible (Supplement) and for the delay between symptom onset and case reporting (next section).
We determined the threshold that would result in epidemic growth () by projecting with the model under a sequence of values and determining the minimum value that would result in an increase in infectious individuals over time () (Anderson et al., 2020b). We then calculated “threshold ratios”, or leeway, as and .
2.3. Reported cases and testing model
We let denote the number of recorded cases on day . The number of people who become symptomatic on a given day is the number moving from the exposed pre-symptomatic ( and ) to the symptomatic ( and ) compartments, namely . The expected number of reported cases on day is a weighted sum of those who become symptomatic in previous days, where the weights are determined by the delay between symptom onset and reporting (Anderson et al., 2020b):
| (4) |
where represents the sampling fraction on day and we use a Weibull distribution with shape and scale for . If , then all estimated infectious people are tested and then become reported cases; represents a reduction in expected cases on day due to not everyone being tested. See Anderson et al. (2020b) for further details on fitting from data. We used and as estimated for British Columbia in Anderson et al. (2020b) for the other regions (due to a lack of the necessary data), except for New Zealand for which A. Lustig and M. Plank (pers. comm.) fitted non-public data using our code (Edwards, 2020a).
2.4. Statistical model fitting
We fit our SEIR models with Stan 2.21.2 (Carpenter et al., 2017, Stan Development Team, 2020b) and R 4.0.2 (R Core Team, 2019) using our R package covidseir (Anderson et al., 2020a). We sampled from six chains with 500 iterations per chain and discarded the first half of each chain as warm-up. We assessed chain convergence with trace plots and via ensuring (the potential scale reduction factor) and (the effective sample size) (Stan Development Team, 2020b) (Table S6). Code to reproduce our analysis is available at https://github.com/carolinecolijn/leeway-reopen-covid19 and https://doi.org/10.5281/zenodo.4628345.
3. Results
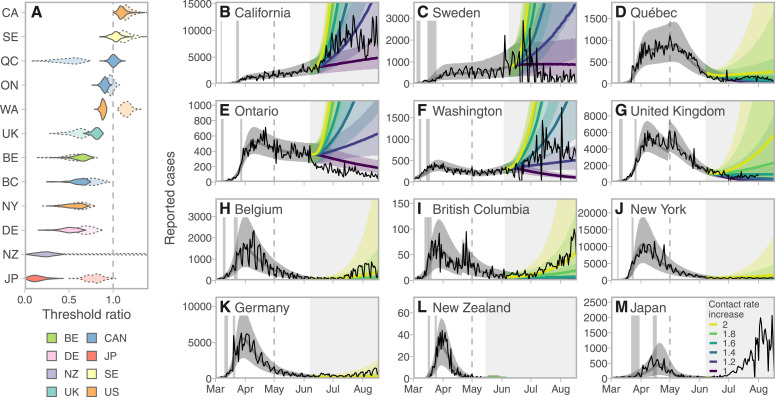
We found that after initial NPI measures took effect, some jurisdictions had substantial leeway to re-open (Japan, New Zealand, New York, Germany, Belgium, and British Columbia), with an above-0.99 probability that contact rates were below 80% of the threshold for epidemic growth (Fig. 2A). Japan and New Zealand had the most leeway, with contact rates well below half the threshold. In contrast, some jurisdictions had little leeway (the United Kingdom [UK], Washington, and Ontario) and some had none, as cases were still rising (Quebec, Sweden, and California). Estimates for the period after May 1 found that some jurisdictions had little or no leeway for further re-opening (California, Sweden, Washington, Ontario) as they were at or above the critical threshold. Some had used part of their leeway already (Japan, Germany, New York, and British Columbia; Fig. 2A). Several had more leeway after May 2020 than they did immediately after NPI measures took effect (the UK, and Quebec, with Quebec well below the threshold and the UK with 0.99 probability of being 80% of the threshold). New Zealand had so few cases that estimation with this modeling framework left considerable uncertainty. These leeway results are relatively robust to assumptions about the duration of infection and the prior on the fraction of individuals distancing (Fig. S4) as well as the mean of the delay distribution (Fig. S5, S6). Changes to the delay distribution mainly affected estimates of (the date at which distancing was fully implemented; Fig. S5). The estimates of and were near in time to dates of known policy changes in many, but not all, jurisdictions (Table S7, Fig. S2).
Fig. 2.
Projected cases given scenarios of relaxed control measures strongly depend on the leeway between the estimated contact rate and the threshold for increase. A: Posterior densities of the ratio between the contact rate and the threshold (the value above which exponential increases are expected). Darker violins represent the post-measures period and paler dotted violins represent the post-May 1 estimates. Jurisdictions with contacts well below the threshold have more leeway to relax control measures. Colors represent countries (to group the three Canadian provinces and three US states together). B–M: Model fits and projections at 6 multiplicative contact rate increases, from a baseline from the lower of the estimates from the two time periods. Solid lines represent posterior medians and ribbons represent 90% credible intervals. Thin lines represent reported case data. Vertical gray bands indicate 90% credible intervals for the start and end times of initial control measures ramp. Dashed vertical lines indicate the start of the “recent” period (May 1). The choice to project from a baseline of the lower of the post-measures and recent estimates means that projections are based on measures at the stricter time period in all jurisdictions. Gray shaded areas indicate time periods for which data were not used for estimation. Regions are arranged by decreasing mean threshold ratio in the immediate post-measures period.
We forecasted the impact of relaxing distancing measures by increasing contact rates among those engaged in distancing, starting from a baseline of the lower of the post-NPI and May estimates (Fig. 2B–M). The UK, Belgium, and Quebec moved to stricter control after May 1. All had some leeway by early June, though we found that increasing contact beyond 60% above the recent estimate would likely lead to a growing epidemic in the UK and Quebec. Belgium had substantial leeway to re-open. The remaining jurisdictions had used some of their leeway already by early June, 2020. Those with little to no leeway to begin with now showed rapid forecasted increases if contact were to increase (California, Sweden, Washington, and Ontario). British Columbia had some leeway to re-open and did so; a doubling of contact compared to the post-measures baseline predicted rises in case numbers. Germany, New York, New Zealand, and Japan showed low risks of rising cases with moderate increases in contact rates. Comparing our forecasted cases from early June to late August with realized cases, most jurisdictions experienced trajectories consistent with our projections of contact rate increases from one- to two-fold (Fig. 2B–M).
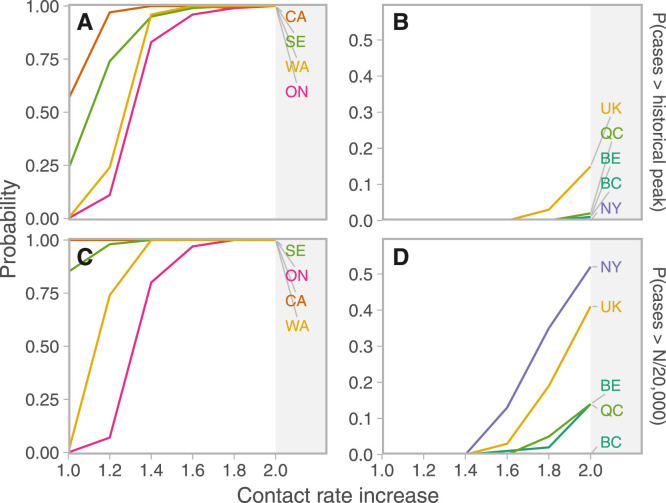
We estimated the probability of exceeding the peak number of cases in March and April, and the probability of reaching one incident reported case per 20,000 individuals under different increases in contact rates (again from a baseline of the time period in which control was stricter) (Fig. 3). Given similar increases in contact rate, Ontario, Washington, Sweden, and California were most likely to exceed both one incident case per 20,000 and their historical peaks in June and July. The UK had a small risk of exceeding its previous peak (probability of 0.06 with a doubling of contact rates from the post-measures period). New York, the UK, and Quebec had some risk of exceeding one case per 20,000 given these increases; New York’s previous peak was high and the risk of exceeding it was correspondingly low.
Fig. 3.
Probabilities that cases would exceed reference thresholds over the 6 weeks following June 7, 2020 depend on contact rate increases and jurisdiction. Projections are from a baseline of the lower of the post-NPI and May 2020 estimates. A, B: Probability of exceeding the historical “first wave” maximum. C, D: Probability of reported cases per day exceeding 1/20,000 of the population (). ON: Ontario, WA: Washington, CA: California, QC: Quebec, BC: British Columbia, NY: New York, SE: Sweden, UK: United Kingdom, BE: Belgium, DE: Germany, NZ: New Zealand, JP: Japan.
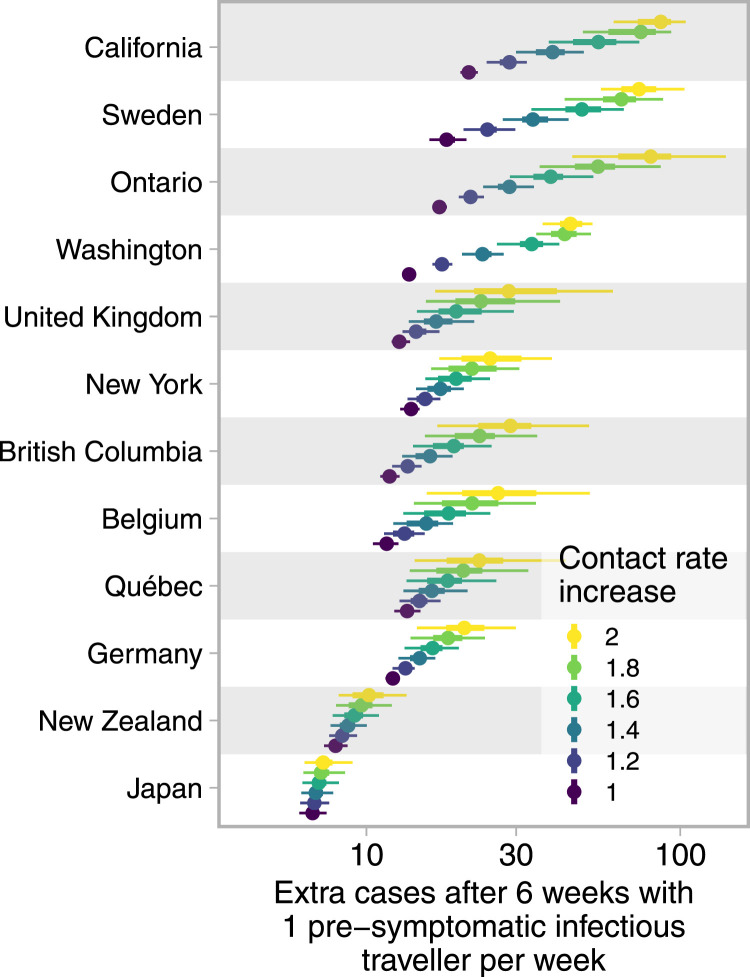
There has been pressure to reopen borders to business and leisure travelers due to the social and economic costs of travel restrictions. We modeled the impact of introducing successful imported cases (cases that result in a secondary infection) at a constant rate to estimate the impact on total cases in each jurisdiction, taking uncertainty in the contact ratios (and other posterior estimated quantities; see Supplement) into account (Fig. 4). Our results illustrate the expected extra cases resulting from one successful imported case per week over six weeks. Assuming independence of imported cases, these results can be scaled to realistic rates of importation (e.g., for 100 successfully imported cases, multiply expected extra cases by 100). In Japan, where the dynamics were well below the threshold in all posterior samples, each importation results in few additional cases. Meanwhile, in California or Sweden, because there was a high posterior probability that transmission was above the threshold, introduced cases were more likely to cause extended chains of transmission and contribute large case volumes. The result is that up to approximately 100 new cases may result (over six weeks) from a weekly introduction of a single case. Fig. 4 is generated under the assumption that successfully introduced cases join the general population, have access to its testing and control procedures, and engage in its broader distancing and NPI behaviors.
Fig. 4.
Cases resulting from one successful import per week over 6 weeks range from fewer than ten to hundreds and depend on contact in the destination population. Dots represent medians and thick and thin line segments represent 50% and 90% credible intervals; the -axis is log distributed. Contact rate increases are based on the lower of the post-measures and recent contact ratio estimates. Regions are ordered by the average extra cases across contact rate increases. Extra cases are compared to a projection that does not include weekly successful imports; travelers themselves have not been removed from the totals.
4. Discussion
Our forecasted cases from early June to late August with contact rate increases from one- to two-fold were consistent with realized cases in most jurisdictions. California proceeded with reopening in June, under a mandate to wear masks indoors and outdoors if distancing was not possible (June 18 (The Associated Press, 2020)), but with virus counts and hospitalizations rising, closed bars and other venues at the end of June. Cases peaked in late July at over 12,000 daily cases following a new statewide closure of all indoor businesses on July 13 (Pereira, 2020). Cases in New York continued to decline. Quebec saw a rise through July and reopened with an extensive array of control measures in place (Gouvernement du Québec, 2020) including mask mandates and measures for bars, restaurants and other indoor social venues. British Columbia proceeded with reopening through the summer and saw increases in community transmission, initially among younger age groups (B.C. Centre for Disease Control, 2020). Washington saw similar rises in young adults who were gathering in large numbers. Reopening was paused in response and indoor service at venues selling alcohol was stopped (Stone, 2020); a decline in cases began in late July. Germany’s case counts remained low until late July when a rise began, attributed to summer travel and increased mobility and contact (Deutsche Welle, 2020).
In contrast, some jurisdictions experienced trajectories outside or towards the extremes of our projections. Sweden had restrictions on gatherings (Krisinformation.se, 2020), half the workforce working at home, widespread voluntary distancing (Henley, 2020), and high schools were operating with distance learning (Folkhälsomyndigheten, 2020, Sundholm, 2020). In June and July, municipalities took over ensuring that restaurants and bars were following guidelines (The Local, 2020); elementary schools closed for the summer and testing and contact tracing were enhanced (June 4) (Edwards, 2020b). Sweden’s case trajectory was lower than it would have been had contact rates increased according to our forecast, as was the trajectory in Ontario. Whereas in Japan, following reopening of schools, theaters, cinemas, gyms and other indoor events with fewer than 100 people (June 1), 1000 people (June 19), and 5000 people (July 10), and increases in testing by about 30%, there was a considerable resurgence of cases likely driven in part by increases in local tourism (subsidized as of July 22) (KPMG, 2020). Belgium resumed schools on May 18, reopened bars and restaurants on June 8th and EU borders on June 15 (while also beginning to test close contacts of cases rather than focusing on symptomatic individuals only). Pools, wellness centers, theaters, casinos, conferences and other indoor venues with limits of 50 people (200 with approval) were opened July 1. There was then a quick response to rising cases, with social contact limited to 15 per week (July 7) and then only 5 per family (July 29), mandatory masks and other measures, after which case numbers returned to a decline by late August.
The estimated dates that NPI measures took effect ( and ) matched dates of policy changes such as mass gatherings or stopping essential services in many but not all jurisdictions. The difference in some cases is understandable as these measures do not capture infectious contact in the population. The most pronounced differences between inferred dates when distancing ramped up and timings of these particular measures were in Quebec and Ontario, where the model estimated that distancing continued to ramp up well after the time that essential services were closed, and in Japan, where the model estimated distancing ramping up well after when mass gatherings were stopped. In Quebec and Ontario, transmission within the health care system (MacFarlane, 2020) was captured in our model to some extent with health care in the non-distancing population, but this was probably not greatly impacted by changes in mass gatherings and non-healthcare activities. In Japan, returning travelers in late March contributed to the rise in cases (Al Hasan et al., 2021), which was then suppressed by further distancing measures.
To interpret these results with reference to borders and travel requires consideration of the individual jurisdictions involved. Consider a border opening from jurisdiction A to jurisdiction B. If both jurisdictions are well below their thresholds, then the probability of a large volume of new cases resulting from introductions is low, primarily because general transmission will be prevented in jurisdiction B, but also because prevalence is likely to be low in A, though this depends on the epidemic, testing, reporting, and population dynamics in A. Conversely, if A is near its own threshold, then there may be as-yet-unobserved exponential growth of cases in A, affecting the rate of introduction to B. If the destination is near its threshold, then introduced cases could result in exponential growth in B (Russell et al., 2021). Furthermore, travel itself may result in additional transmissions. These effects could be amplified if travelers join a congregate setting or are less socially distanced than the general population due to tourism or work activities, or if they have reduced access to local health care and control measures such as contact tracing. Indeed, Ontario, California, Washington and other jurisdictions all saw COVID-19 outbreaks among farm workers (Bogart, 2020, Newman, 2020, Sturgill, 2020) and more than 600 workers tested positive in Ontario in the weeks up to mid-July, 2020 (Doyle, 2020).
The COVID-19 pandemic has seen an unprecedented number of travel restrictions and border measures, in spite of WHO recommendations against unnecessary closures, weak evidence that these are effective in preventing pandemic influenza (Mateus et al., 2014) (though they do reduce spread and buy time (Wells et al., 2020)), and concerns about their impact on movement of medical supplies and personnel (Devi, 2020). There has been a notion of “travel bubbles” in which countries or jurisdictions experiencing comparable levels of risk open borders to travel and commerce (European Commission, 2020). As jurisdictions with low case numbers reopen their economies (likely approaching the epidemic threshold as measures are relaxed), they will be at renewed risk of introductions. We suggest that the highest-risk borders arise when a source jurisdiction has prevalent cases and the destination jurisdiction is near or above its threshold, or is reopening to the extent that cases could now spread widely despite earlier successes (Russell et al., 2021). Due to variations in testing, we do not know the relative prevalence (Dempsey, 2020), but we would predict, among the locations in our study, that introductions into California, Sweden, Ontario, and Washington carry the highest risk, followed by the UK. Interactions among these jurisdictions would carry the highest risk, despite that by some indicators the overall COVID-19 control in several of these is similar. Interactions among the UK, Quebec, BC, NY, Germany, and Belgium are lower risk but the probability of causing dozens of new cases per introduced case per week remains considerable. Furthermore, jurisdictions with small historical peaks (e.g., British Columbia, New Zealand) could easily be put in a position of exceeding their historical peak as a result of introduced cases from a region with higher prevalence.
The model and underlying data have limitations. The data are provided by jurisdictions and depend on testing protocols and capacity, delays to reporting, different base populations being tested, and other variations (García-Basteiro et al., 2020). Indeed, this motivates using inferred summaries like the leeway, in lieu of direct comparisons of case counts. Our approach accounts as much as possible for differences in testing through time, for the local dynamics of distancing behavior, and different starting intensity and timing of different epidemics. However, our model estimates are oriented towards widespread NPI and distancing measures, and implicitly attribute changes in case dynamics to contact rates. Transmission dynamics involve a complex interplay of outbreak control, management of COVID-19 in health care settings, reduction in community transmission, testing and reporting, contact tracing and other public health measures. Our notion of contact rates combines both rate of interaction and probability of infection during interaction; thus, increased rates of interaction during reopening may, to a certain degree, be possible without increased transmission if key public health measures are in place and highly functional. Our model also assumes a simple population structure—data for more complex population structures being largely lacking. The numbers of reported cases per prevalent case will change as testing is widened, and this is not modeled in our forecasts. Finally, facing rising case numbers, policy-makers are likely to act as they did in California, Washington, Belgium and other areas. Model forecasts based on constant estimated parameters do not take policy and societal reactions into account, though control theory models can do so (Stewart et al., 2020). Our projections are not intended to be predictions, as any prediction would require some knowledge of the public health and broader responses to the state of the pandemic.
The effective reproduction number (the average number of secondary infections per infection) is the leading concept playing the role of leeway in pandemic reporting and discourse. When , infections decline on average, and they grow when . is simple and interpretable and one might ask whether leeway has any advantage given the speed and simplicity of estimating , for example with packages such as EpiEstim (Cori, 2021). Even more simply, one could fit a regression of to estimate a rate of growth, . How much below zero the slope is would be akin to the leeway. This would require even fewer assumptions than ; estimates rely on a generation interval distribution, and generation intervals are hard to measure and are known to change over outbreaks and epidemics (Ali et al., 2020). Our model is more complex still, estimating not just a rate or a number but a set of parameters attached to a mechanism—contact rate among those distancing. Our approach can therefore, in principle, explore what happens if increased screening or testing reduce the duration of infectiousness and continued social distancing measures (for which one now has an estimate of ) are in place. Conversely, the model can project the leeway afforded by expanded testing, improved support for distancing, or other measures. In other words, estimation in a mechanistic model carries advantages in interpretability and use. An estimate, or a growth rate estimate, cannot be used in the same way. This increased interpretability has proven useful to government agencies in practice: the British Columbia provincial government and the Canadian federal government have both been using estimates of and leeway from these models for decision making since April 2020 and September 2020, respectively.
Amidst differing epidemics and control measures, each jurisdiction has a leeway—the room between the current state and the threshold—and this is comparable from place to place. The leeway, together with model fits that are informed by data and which describe the uncertainty in how much leeway there is, can provide a quantitative basis for decisions about reopening. We are at a unique time in this pandemic, with a so-called “first wave” receding not due to immunity, but due to widespread behavioral change. Given that reopening is occurring, this left populations vulnerable to resurgence of cases, driven both by local transmission and sparked by introductions. To mitigate risks associated with imported cases and reopening borders, it is important to account for the risk of growth in the general population together with the likelihood that imported cases will arrive in high-risk settings. We recommend that policy-makers carefully consider (i) whether imported cases and seeded outbreaks are likely to be identified and managed to the same degree as those in the local population; (ii) whether travelers will engage in high-risk or high-contact activities, especially within marginalized populations; and (iii) whether local trace and test strategies have the capacity to manage imported cases and nascent outbreaks.
CRediT authorship contribution statement
Sean C. Anderson: Data analysis and interpretation, Model development, Implementation, Model fitting, Figures, Study design, Conceiving, Writing - original draft. Nicola Mulberry: Data analysis and interpretation, Model fitting, Figures, Conceiving, Writing - original draft. Andrew M. Edwards: Data analysis and interpretation, Model fitting, Figures, Writing - original draft. Jessica E. Stockdale: Data analysis and interpretation, Model fitting, Figures, Writing - original draft. Sarafa A. Iyaniwura: model fitting, Conceiving, Writing - original draft. Rebeca C. Falcao: model fitting, Conceiving, Writing - original draft. Michael C. Otterstatter: Study design, Interpretation, Conceiving, Writing - original draft. Naveed Z. Janjua: Study design, Interpretation, Conceiving, Writing - original draft. Daniel Coombs: Study design, Interpretation, Conceiving, Writing - original draft. Caroline Colijn: Data analysis and interpretation, Conceiving, Writing - original draft, Model development, Study design.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported by funding from the Michael Smith Foundation for Health Research, Canada (grant 18933), from Genome BC (project code COV-142), and from the Peter Wall Institute for Advanced Studies. C.C. and J.S. are funded by the Federal Government of Canada’s Canada 150 Research Chair program . We thank two anonymous reviewers for comments that greatly improved this manuscript.
Footnotes
Supplementary material related to this article can be found online at https://doi.org/10.1016/j.epidem.2021.100453.
Appendix A. Supplementary data
The following is the Supplementary material related to this article.
Supplementary methods, figures, tables.
References
- Al Hasan Syed Mahfuz, Saulam Jennifer, Kanda Kanae, Ngatu Nlandu Roger, Hirao Tomohiro. Trends in COVID-19 outbreak in Tokyo and Osaka from January 25 to May 6, 2020: a joinpoint regression analysis of the outbreak data. Jpn. J. Infect. Dis. 2021;74(1):73–75. doi: 10.7883/yoken.JJID.2020.332. [DOI] [PubMed] [Google Scholar]
- Ali Sheikh Taslim, Wang Lin, Lau Eric H.Y., Xu Xiao-Ke, Du Zhanwei, Wu Ye, Leung Gabriel M., Cowling Benjamin J. Serial interval of SARS-CoV-2 was shortened over time by nonpharmaceutical interventions. Science. 2020;369(6507):1106–1109. doi: 10.1126/science.abc9004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson S.C., Edwards A.M., Yerlanov M., Mulberry N., Stockdale J.E., Iyaniwura S.A., Falcao R.C., Otterstatter M.C., Irvine M.A., Janjua N.Z., Coombs D., Colijn C. 2020. Covidseir: Bayesian SEIR model to estimate physical-distancing effects. https://github.com/seananderson/covidseir. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson Sean C, Edwards Andrew M, Yerlanov Madi, Mulberry Nicola, Stockdale Jessica, Iyaniwura Sarafa A, Falcao Rebeca C, Otterstatter Michael C, Irvine Michael A, Janjua Naveed Z, Coombs Daniel, Colijn Caroline. Quantifying the impact of COVID-19 control measures using a Bayesian model of physical distancing. PLOS Comput. Biol. 2020;16(12):e1008274. doi: 10.1371/journal.pcbi.1008274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- B.C. Centre for Disease Control . 2020. COVID-19 case counts and press statements. http://www.bccdc.ca/health-info/diseases-conditions/covid-19/case-counts-press-statements, Accessed: 2020-4. [Google Scholar]
- Bogart Nicole, CTV News . 2020. Advocates demand Ontario shut down farms as COVID-19 cases soar among workers. https://www.ctvnews.ca/health/coronavirus/advocates-demand-ontario-shut-down-farms-as-covid-19-cases-soar-among-workers-1.5004897, Accessed: 2020-8-18. [Google Scholar]
- Carpenter Bob, Gelman Andrew, Hoffman Matthew D., Lee Daniel, Goodrich Ben, Betancourt Michael, Brubaker Marcus, Guo Jiqiang, Li Peter, Riddell Allen. Stan: a probabilistic programming language. J. Stat. Softw. 2017;76(1) doi: 10.18637/jss.v076.i01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cori Anne. 2021. Epiestim: Estimate time varying reproduction numbers from epidemic curves. https://CRAN.R-project.org/package=EpiEstim, R package version 2.2-4. [Google Scholar]
- Cousins Sophie. New Zealand eliminates COVID-19. Lancet. 2020;395(10235):1474. doi: 10.1016/S0140-6736(20)31097-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehning Jonas, Zierenberg Johannes, Spitzner F. Paul, Wibral Michael, Neto Joao Pinheiro, Wilczek Michael, Priesemann Viola. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science. 2020:eabb9789. doi: 10.1126/science.abb9789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dempsey Walter. 2020. The hypothesis of testing: Paradoxes arising out of reported coronavirus case-counts. arXiv:2005.10425. [Google Scholar]
- Deutsche Welle . 2020. Coronavirus: Sweden records highest death tally in 150 years. https://www.dw.com/en/coronavirus-digest-sweden-records-most-deaths-in-150-years-in-first-6-months-of-2020/a-54618997, Accessed: 2020-8-19. [Google Scholar]
- Devi Sharmila. Travel restrictions hampering COVID-19 response. Lancet. 2020;395(10233):1331–1332. doi: 10.1016/S0140-6736(20)30967-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doyle Sabrina. Migrant workers falling through cracks in health care coverage. CMAJ. 2020;192(28):E819–E820. doi: 10.1503/cmaj.1095882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edwards Andrew M. 2020. Righttruncation: Likelihood calculations for right-truncated data as used for delay distributions during COVID-19. https://github.com/andrew-edwards/rightTruncation. [Google Scholar]
- Edwards Catherine. 2020. Sweden announces major overhaul of coronavirus testing strategy. https://www.thelocal.se/20200604/sweden-announces-major-overhaul-of-coronavirus-testing-strategy, Accessed: 2020-9-8. [Google Scholar]
- European Commission, ., European Commission Press Release: Tourism and transport: Commission’s guidance on how to safely resume travel and reboot Europe’s tourism in 2020 and beyond, 2020. https://ec.europa.eu/commission/presscorner/api/files/document/print/en/ip_20_854/IP_20_854_EN.pdf.
- Ferguson Neil, Laydon Daniel, Nedjati Gilani Gemma, Imai Natsuko, Ainslie Kylie, Baguelin Marc, Bhatia Sangeeta, Boonyasiri Adhiratha, Cucunuba Perez ZULMA, Cuomo-Dannenburg Gina. 2020. Report 9: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand. [DOI] [Google Scholar]
- Folkhälsomyndigheten . 2020. Lärosäten och gymnasieskolor uppmanas nu att bedriva distansundervisning. https://www.folkhalsomyndigheten.se/nyheter-och-press/nyhetsarkiv/2020/mars/larosaten-och-gymnasieskolor-uppmanas-nu-att-bedriva-distansundervisning/, Accessed: 2020-9-8. [Google Scholar]
- Gandhi K.R.R., Murthy K.V.R., Rao P., Casella F. 2020. Non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality. [DOI] [PMC free article] [PubMed] [Google Scholar]
- García-Basteiro Alberto L, Chaccour Carlos, Guinovart Caterina, Llupià Anna, Brew Joe, Trilla Antoni, Plasencia Antoni. Monitoring the COVID-19 epidemic in the context of widespread local transmission. Lancet Respir. Med. 2020;8(5):440–442. doi: 10.1016/S2213-2600(20)30162-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Google . 2020. Community mobility reports. https://www.google.com/covid19/mobility Accessed: 2020-5. [Google Scholar]
- Gouvernement du Québec . 2020. Gradual resumption of activities under the COVID-19-related pause. https://web.archive.org/web/20200819103128/https://www.quebec.ca/en/health/health-issues/a-z/2019-coronavirus/gradual-resumption-activities-covid19-related-pause/, Accessed: 2020-8-19. [Google Scholar]
- Griffin John, Casey Miriam, Collins Áine, Hunt Kevin, McEvoy David, Byrne Andrew, McAloon Conor, Barber Ann, Lane Elizabeth Ann, More Simon. Rapid review of available evidence on the serial interval and generation time of COVID-19. BMJ Open. 2020;10(11) doi: 10.1136/bmjopen-2020-040263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Havers Fiona P, Reed Carrie, Lim Travis, Montgomery Joel M, Klena John D, Hall Aron J, Fry Alicia M, Cannon Deborah L, Chiang Cheng-Feng, Gibbons Aridth, Krapiunaya Inna, Morales-Betoulle Maria, Roguski Katherine, Rasheed Mohammad Ata Ur, Freeman Brandi, Lester Sandra, Mills Lisa, Carroll Darin S, Owen S Michele, Johnson Jeffrey A, Semenova Vera, Blackmore Carina, Blog Debra, Chai Shua J, Dunn Angela, Hand Julie, Jain Seema, Lindquist Scott, Lynfield Ruth, Pritchard Scott, Sokol Theresa, Sosa Lynn, Turabelidze George, Watkins Sharon M, Wiesman John, Williams Randall W, Yendell Stephanie, Schiffer Jarad, Thornburg Natalie J. Seroprevalence of antibodies to SARS-CoV-2 in 10 sites in the United States, March 23-May 12, 2020. JAMA Intern. Med. 2020;180(12):1576–1586. doi: 10.1001/jamainternmed.2020.4130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hellewell Joel, Abbott Sam, Gimma Amy, Bosse Nikos I, Jarvis Christopher I, Russell Timothy W, Munday James D, Kucharski Adam J, Edmunds W John, Sun Fiona. Feasibility of controlling COVID-19 outbreaks by isolation of cases and contacts. Lancet Global Health. 2020;8(4):E488–E496. doi: 10.1016/S2214-109X(20)30074-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Henley Jon, The Guardian . 2020. Critics question Swedish approach as coronavirus death toll reaches 1,000. https://www.theguardian.com/world/2020/apr/15/sweden-coronavirus-death-toll-reaches-1000. [Google Scholar]
- Hernandez Andres, Correa-Agudelo Esteban, Kim Hana, Branscum Adam J, Miller F DeWolfe, MacKinnon Neil, Cuadros Diego F. 2020. On the impact of early non-pharmaceutical interventions as containment strategies against the COVID-19 pandemic. medRxiv. [DOI] [Google Scholar]
- Imai Natsuko, Cori Anne, Dorigatti Ilaria, Baguelin Marc, Donnelly Christl A, Riley Steven, Ferguson Neil M. 2020. Report 3: transmissibility of 2019-nCoV. https://www.imperial.ac.uk/media/imperial-college/medicine/sph/ide/gida-fellowships/Imperial-College-COVID19-transmissibility-25-01-2020.pdf. [Google Scholar]
- Johns Hopkins University . 2020. Coronavirus resource center. https://coronavirus.jhu.edu/ [Google Scholar]
- KPMG . 2020. Japan. Government and institution measures in response to COVID-19. https://home.kpmg/xx/en/home/insights/2020/04/japan-government-and-institution-measures-in-response-to-covid.html, Accessed: 2020-9-9. [Google Scholar]
- Krisinformation.se . 2020. Förbud mot allmänna sammankomster med fler än 50 personer. https://www.krisinformation.se/nyheter/2020/mars/ytterligare-begransning-sammankomster, Accessed: 2020-9-8. [Google Scholar]
- Kupferschmidt K. Ending coronavirus lockdowns will be a dangerous process of trial and error. Science. 2020 doi: 10.1126/science.abc2507. [DOI] [Google Scholar]
- Liu Yang, Gu Zhonglei, Xia Shang, Shi Benyun, Zhou X-N, Shi Yong, Liu Jiming. What are the underlying transmission patterns of COVID-19 outbreak?–An age-specific social contact characterization. EClinicalMedicine. 2020;22 doi: 10.1016/j.eclinm.2020.100354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacFarlane John, CBC News . 2020. COVID-19 in Quebec: ’there will continue to be many deaths,’ says premier, insisting spread is under control. https://www.cbc.ca/news/canada/montreal/covid-19-quebec-april-30-1.5550311. [Google Scholar]
- Mateus Ana LP, Otete Harmony E, Beck Charles R, Dolan Gayle P, Nguyen-Van-Tam Jonathan S. Effectiveness of travel restrictions in the rapid containment of human influenza: a systematic review. Bull. World Health Organ. 2014;92:868–880D. doi: 10.2471/BLT.14.135590. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McAloon Conor, Collins Áine, Hunt Kevin, Barber Ann, Byrne Andrew W., Butler Francis, Casey Miriam, Griffin John, Lane Elizabeth, McEvoy David, Wall Patrick, Green Martin, O’Grady Luke, More Simon J. Incubation period of COVID-19: A rapid systematic review and meta-analysis of observational research. BMJ Open. 2020;10(8) doi: 10.1136/bmjopen-2020-039652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- New York State Department of Health . 2020. COVID-19 testing. https://coronavirus.health.ny.gov/covid-19-testing, Accessed: 2020-5-29. [Google Scholar]
- Newman Jesse, The Wall Street Journal . 2020. Coronavirus hits nation’s key apple, cherry farms. https://www.wsj.com/articles/coronavirus-hits-nations-key-apple-cherry-farms-11594027802, Accessed: 2020-8-18. [Google Scholar]
- Nordling Linda. South Africa flattens its coronavirus curve—and considers how to ease restrictions. Science. 2020 doi: 10.1126/science.abc2689. [DOI] [Google Scholar]
- Pereira Ivan. 2020. How california lost control over COVID-19 despite early successes. https://abcnews.go.com/Health/california-lost-control-covid-19-early-successes/story?id=72008022, Accessed: 2020-8-19. [Google Scholar]
- R Core Team . 2019. R: A language and environment for statistical computing. R Foundation for Statistical Computing. [Google Scholar]
- Russell Timothy W., Wu Joseph T., Clifford Sam, Edmunds W. John, Kucharski Adam J., Jit Mark. Effect of internationally imported cases on internal spread of COVID-19: A mathematical modelling study. Lancet Public Health. 2021;6(1):e12–e20. doi: 10.1016/S2468-2667(20)30263-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stan Development Team . 2020. RStan: the R interface to Stan. http://mc-stan.org/, R package version 2.19.3. [Google Scholar]
- Stewart Greg, van Heusden Klaske, Dumont Guy A, IEEE Spectrum . 2020. How control theory can help us control COVID-19. https://spectrum.ieee.org/biomedical/diagnostics/how-control-theory-can-help-control-covid19, Accessed: 2020-9-9. [Google Scholar]
- Stone Will, NPR . 2020. How bars are fueling COVID-19 outbreaks. https://www.npr.org/sections/health-shots/2020/08/18/902328016/how-bars-are-fueling-covid-19-outbreaks. [Google Scholar]
- Sturgill Kristi, Los Angeles Times . 2020. At least 176 test positive for coronavirus at Ventura County farmworker housing complex. https://www.latimes.com/california/story/2020-06-30/at-least-176-positive-coronavirus-tests-at-ventura-county-farmworker-housing-complex. [Google Scholar]
- Sundholm Marianne. 2020. Gymnasieskolor och universitet i sverige går över till distansundervisning. https://svenska.yle.fi/artikel/2020/03/17/gymnasieskolor-och-universitet-i-sverige-gar-over-till-distansundervisning, Accessed: 2020-9-8. [Google Scholar]
- The Associated Press . 2020. Timeline of events during california’s coronavirus outbreak. https://apnews.com/ad28f59dbebc94cd80868cb5761a7702, Accessed: 2020-8-19. [Google Scholar]
- The Local . 2020. What changes about life in Sweden in July 2020? https://www.thelocal.se/20200701/what-changes-about-life-in-sweden-from-july-1st, Accessed: 2020-9-8. [Google Scholar]
- Tindale Lauren C, Stockdale Jessica E, Coombe Michelle, Garlock Emma S, Lau Wing Yin Venus, Saraswat Manu, Zhang Louxin, Chen Dongxuan, Wallinga Jacco, Colijn Caroline. Evidence for transmission of COVID-19 prior to symptom onset. eLife. 2020;9 doi: 10.7554/eLife.57149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wells Chad R, Sah Pratha, Moghadas Seyed M, Pandey Abhishek, Shoukat Affan, Wang Yaning, Wang Zheng, Meyers Lauren A, Singer Burton H, Galvani Alison P. Impact of international travel and border control measures on the global spread of the novel 2019 coronavirus outbreak. Proc. Natl. Acad. Sci. USA. 2020;117(13):7504–7509. doi: 10.1073/pnas.2002616117. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary methods, figures, tables.