Photoacoustic microscopy with sparse data by convolutional neural networks

Abstract

The point-by-point scanning mechanism of photoacoustic microscopy (PAM) results in low-speed imaging, limiting the application of PAM. In this work, we propose a method to improve the quality of sparse PAM images using convolutional neural networks (CNNs), thereby speeding up image acquisition while maintaining good image quality. The CNN model utilizes attention modules, residual blocks, and perceptual losses to reconstruct the sparse PAM image, which is a mapping from a 1/4 or 1/16 low-sampling sparse PAM image to a latent fully-sampled one. The model is trained and validated mainly on PAM images of leaf veins, showing effective improvements quantitatively and qualitatively. Our model is also tested using in vivo PAM images of blood vessels of mouse ears and eyes. The results suggest that the model can enhance the quality of the sparse PAM image of blood vessels in several aspects, which facilitates fast PAM and its clinical applications.

1. Introduction

Photoacoustic (PA) microscopy (PAM), as a hybrid imaging technique based on the PA effect, has been widely used in the field of biomedical imaging [1], [2], [3], [4], [5], [6]. Optical-resolution PAM (OR-PAM), as one implementation of PAM, offers high spatial resolution at the expense of penetration depth and has demonstrated many potential applications [6], [7], [8]. For image acquisition in OR-PAM, since a sample typically has spatially distinct optical absorption, the sample's optical absorption map is obtained by performing point-by-point scanning over the sample. As a result, the imaging speed of OR-PAM is highly restricted due to the point-by-point scanning mechanism, especially for high-resolution OR-PAM that performs scanning in smaller steps and thus has more scanning points (i.e., more scanning pixels) in a given region of interest (ROI). A low imaging speed may hamper selected applications such as monitoring dynamic biological systems.

In recent years, efforts have been made to speed up OR-PAM scanning, which mainly focus on fast scanning mechanisms. Components such as a high-speed voice-coil stage, a galvanometer scanner, a microelectromechanical system (MEMS) scanning mirror, a micro lens array together with array ultrasonic transducers were used for fast-scanning OR-PAM [9], [10], [11], [12], [13], [14]. A random-access scanning method was also applied in OR-PAM to accelerate the imaging speed by employing a digital micromirror device to scan only a selected region [15]. In these works, sophisticated and expensive hardware was used. Alternatively, sparse-scanning OR-PAM with post image processing offers a solution to improve imaging speed by scanning fewer points (in contrast to full-scanning). Methods such as compressive sensing technologies have been applied to sparse-scanning OR-PAM, which is formulated as a low-rank matrix recovery problem [16]. A high-quality image can be recovered from an OR-PAM image with sparse data. However, due to the relatively high sampling density (e.g., the sampling density of 0.5 mainly demonstrated in [16]) and the complex realization of compressive sampling in experiments, enhancement of imaging speed is limited. Therefore, there is still a need for more efficient and practical algorithms to accelerate the imaging speed of OR-PAM.

Significant advances have been made recently in image processing, mainly using deep learning algorithms (or convolutional neural networks (CNNs)). After AlexNet achieved much better performance than the conventional algorithms in the image classification task in 2012 [17], CNNs have been widely utilized to handle various vision tasks such as de-haze, de-noise, image classification, and image segmentation [18], [19], [20], [21]. In addition to dealing with these problems, super resolution (SR) is another popular topic in the computer vision area, aiming to restore low-resolution pictures. The SR problem is ill-posed because a low-resolution image theoretically corresponds to multiple high-resolution images. Therefore, CNNs are trained to learn the most reasonable mapping, which can generate a high-resolution image with vivid and clear details based on a low-resolution image. SRCNN is the first to implement SR with a simple and shallow CNN [22]. Then, SRGAN applied the concept of generative adversarial networks (GANs) together with CNNs to generate images with highly intuitive fidelity, instead of the plain pixel-wise similarity [23], [24].

More recently, CNNs have also been applied to PA imaging, primarily for PA computed tomography (PACT), which is another implementation of PA imaging [3]. Antholzer et al. used the U-Net architecture to remove the artifacts in sparse PACT [25], [26], [27]. PA source detection and reflection artifact removal can also be achieved by CNN-based methods [28]. Emran et al. demonstrated fast LED-based PACT imaging based on CNN and recurrent neural network approaches and achieved an 8-fold increase in PACT imaging speed [29]. However, studies of CNN-based methods to improve PAM imaging speed are still lacking.

Enhancing the quality of a low-sampling sparse OR-PAM image, i.e., restoring it to approach the latent full-sampling one, can be categorized as an SR problem. Similar to the usage in [22], [24], the term “SR problem” here is not explicitly related to breaking the diffraction limit in physics. Instead, the term implies generating high-quality images from sparse OR-PAM with limited digital pixels. Hence, the problem is also ill-posed. Therefore, in this work, we propose a CNN-based method to improve the quality of the sparse OR-PAM image with the following advancement. First, efforts have been made to acquire an experimental dataset of 268 OR-PAM images ($256\times 256\times 180$ pixels) of leaf veins that are used to train the CNN model in this work, and the rarely-seen OR-PAM dataset will be accessible online for further studies by other researchers. Secondly, high-quality images are restored from 1/4 or 1/16 low-sampling images with poor quality, which may facilitate fast OR-PAM imaging. Thirdly, we extend our method to in vivo applications and achieved high-quality OR-PAM images of blood vessels of mouse ears and eyes, showing the feasibility of applying the method in biomedical research and potentially in clinics. It is worth mentioning that although OR-PAM is demonstrated in this work, the proposed method may also be applied to acoustic-resolution PAM (AR-PAM) and other point-by-point scanning imaging modalities, such as optical coherence tomography and confocal fluorescence microscopy. Note that in the following of this paper, PAM refers to OR-PAM unless otherwise specified.

2. Methods

2.1. PAM system

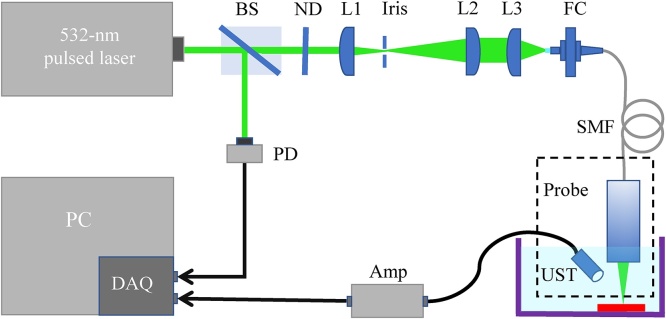
The schematic of our PAM system is illustrated in Fig. 1. A 532-nm pulsed laser (FDSS532-Q4, CryLaS, Germany) with a pulse repetition frequency (PRF) of 1 kHz and a pulse duration of $<$2 ns was used to excite PA signals. The laser beam emitted from the laser head was split into two paths by a beam splitter (BS025, Thorlabs). The reflected light detected by a photodiode (DET10A2, Thorlabs) served as the trigger signal, which was fed to a data acquisition card (CSE1422, GaGe) with a 14-bit resolution. The transmitted light passed a beam-shaping set (consisting of lens #1, lens #2, and an iris) to obtain an expanded collimated light beam. Note that the light intensity was controlled by neutral density filters in front of lens #1. The light beam was then focused by lens #3 and coupled into a single-mode fiber (SMF) via a fiber coupler (F-915, Newport). A probe mainly consisting of the SMF and the lens for light focusing was fabricated and used for PA excitation. We prepared the probes with different high resolutions of $\sim$2-4 $\mu$m to acquire images in this work. PA signals were detected by a custom-made ultrasound transducer (central frequency: 35 MHz; bandwidth: $\sim$40 MHz) and amplified by a preamplifier (ZFL-500LN-BNC+, Mini-Circuits). The data acquisition card was then used for signal digitization at a sampling rate of 200 MS/s. In this system, both the probe and ultrasound transducer, as the PAM scan head (the dashed box in Fig. 1), were mounted on a two-dimensional (2D) motorized stage (M-404, Physik Instrumente [PI], Germany) for scanning during image acquisition.

Fig. 1.

Schematic of the PAM system. BS, beam splitter; PD, photodiode; ND, neutral density filter; L1, lens #1; L2, lens #2; L3, lens #3; FC, fiber coupler; SMF, single mode fiber; UST, ultrasound transducer; Amp, preamplifier; DAQ, data acquisition card; PC, personal computer.

2.2. Dataset preparation

In this work, a dataset of PAM images of bodhi and magnolia leaf veins was used to train and validate our CNN model. First, we immersed the prepared leaf samples in black ink in a container for at least 7 h. Then, the leaves were taken out of the container, and the remained ink (i.e., not within leaf vein networks) was removed by blowing. The leaves were then placed on a glass slide and sealed with silicone glue (GE Sealants). Secondly, the leaf samples were imaged by PAM. The probe with a resolution of 2 $\mu$m (measured by a beam profiler and a $10\times$ beam expander) was used to scan the leaf samples with a data size of $256\times 256$ pixels and a step size of 8 $\mu$m, corresponding to a scanning range of $\sim$2.05 mm. For each PA A-line, 180 pixels were acquired, corresponding to the depth range of $\sim$1.35 mm considering the sound speed of 1500 m/s in water. That is, each three-dimensional PAM image has $256\times 256\times 180$ pixels. We acquired a dataset of 268 original full-scanning (or full-sampling) PAM images in total.

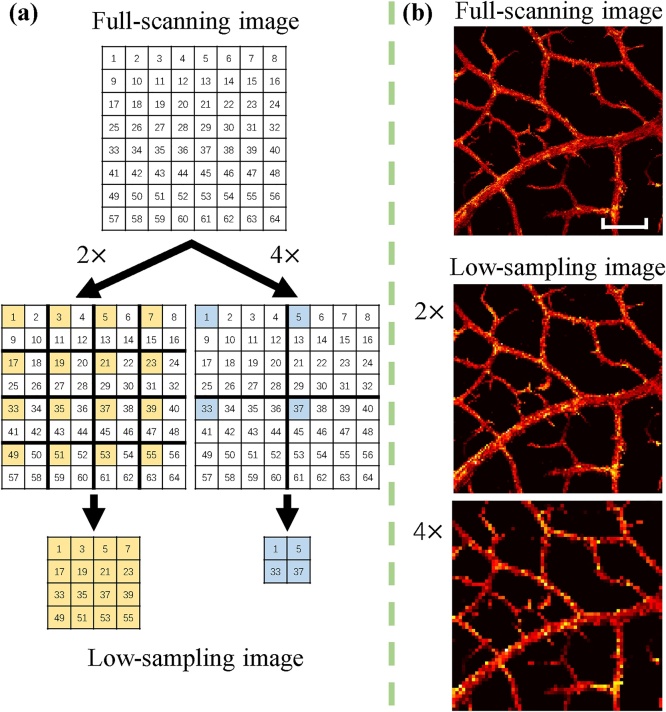
The low-sampling sparse data were obtained by down-sampling the above full-scanning data. The process is illustrated in Fig. 2. Specifically, with $2\times$ scaling in step size, only 1/2 pixels in one lateral dimension were selected and used (as indicated by the yellow-colored pixels in Fig. 2(a)) in the low-sampling image. That is, the low-sampling image ($128\times 128\times 180$ pixels) has only 1/4 pixels of the full-scanning image. In this regard, a 4-fold reduction in the image acquisition time can be expected to the first approximation. Similarly, with $4\times$ scaling in step size, the low-sampling image ($64\times 64\times 180$ pixels) has only 1/16 pixels and is expected to need only 1/16 image acquisition time, similarly, to the first approximation, compared to the full-scanning case. Considering that the resolution is much smaller than the step size (2 $\mu$m vs. 8 $\mu$m, 16 $\mu$m, and 32 $\mu$m), the down-sampling method used here will digitally produce a good approximation of the experimentally-acquired low-sampling images. Then, the maximum amplitude projection (MAP) along the depth direction was applied to obtain 2D images, which is commonly used for the OR-PAM image display. Fig. 2(b) shows one example by applying the down-sampling method. As can be seen, the image quality is degraded in the low-sampling images (e.g., blurs and discontinuities). Finally, the 268 sets of 2D PAM images were used for our CNN model, where the low-sampling PAM image ($128\times 128$ or $64\times 64$ pixels) was used as input and the full-scanning one ($256\times 256$ pixels) as the ground truth.

Fig. 2.

The process of generating low-sampling images from the full-scanning ones. (a) Illustration of the down-sampling method. (b) An example by applying the down-sampling method. Scale bar: 500 $\mu$m. All images in (b) share the same scale bar.

For each scaling rate ($2\times$ and $4\times$), we split the dataset into training, validation, and test sets with a ratio of 0.8:0.1:0.1. All the pixel values were linearly scaled to the range of ($-$1, 1). Regular data augmentation operations, including flipping and rotation, were applied for training.

2.3. Network architecture and settings

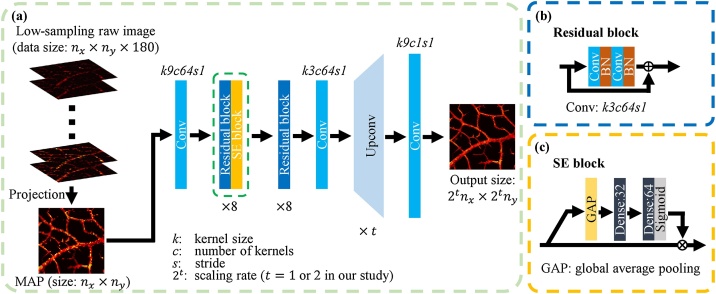
The architecture of the proposed CNN is shown in Fig. 3. We utilized 16 residual blocks [24] and 8 Squeeze-and-Excitation (SE) blocks [30] as the key parts of feature extraction. Inspired by SRGAN [24], the residual blocks elaborated in Fig. 3(b) can well extract features in SR tasks. Moreover, we found that the SE block [30] (shown in Fig. 3(c)) with the channel-wise attention mechanism contributed to network convergence and performance. The “Upconv” block consisted of a $2\times$ up-sampling layer and a standard convolutional layer (with a kernel size of 3, number of filters of 256, and stride of 1). For the $2\times$ scaling experiments (i.e., 1/4 pixels for the low-sampling data), only one “Upconv” block was applied, while for the $4\times$ scaling experiments (i.e., 1/16 pixels for the low-sampling data), two “Upconv” blocks were adopted successively. The Tanh activation function was used for the final output layer, and the Sigmoid activation function was used for the second dense layer (also called a fully connected layer) in each SE block. Other convolutional layers and dense layers all adopted ReLU activation functions.

Fig. 3.

The architecture of the proposed CNN model. (a) The overview of the proposed CNN model. (b) The details of each residual block. (c) The details of each SE block. The Tanh activation function follows the last convolution layer, and the second dense layer in each SE block uses the Sigmoid activation function, while all the other convolutional layers and dense layers adopt ReLU activation functions. Different $t$ values correspond to various scaling rates.

The perceptual loss was applied to train the CNN model. As indicated in [24], [31], [32], [33], [34], although pixel-wise mean squared error (MSE) and mean absolute error (MAE) loss functions significantly improve the pixel-wise metrics like peak signal-to-noise ratio (PSNR) and structural similarity index (SSIM) [35], the generated image is likely to be too smooth and the quality is poor from a subjective point of view. This phenomenon was found to be quite severe for PAM images (demonstrated later in Section 3.3). Hence, a perceptual loss function was adopted to train the CNN model. Specifically, we calculated the MSE based on the output feature map of the 7th convolutional layer of VGG19 [24], [31], [34], [36], [37], which can give a high-level feature description of the image. The VGG19 model was pretrained on the ImageNet dataset [38]. With the prediction $I^{\mathrm{pred}}$ and the ground truth projection $I^{\mathrm{gt}}$ to calculate the perceptual loss, the two feature maps from the 7th convolutional layer of VGG19 can be expressed as $\varphi (I^{\mathrm{pred}})$ and $\varphi (I^{\mathrm{gt}})$, respectively. Thus, the perceptual MSE loss should be:

$$\mathrm{Loss}=\frac{1}{n_x\times n_y\times n_f}\sum _{x=1}^{n_x}\sum _{y=1}^{n_y}\sum _{f=1}^{n_f}{(\varphi (I^{\mathrm{gt}})}_{x,y,f}-\varphi {{(I^{\mathrm{pred}})}_{x,y,f})}^2,$$ (1)

where $n_x$, $n_y$, and $n_f$ denote the dimensions of the feature map.

In our experiments, the proposed CNN model was implemented using the Keras framework with the TensorFlow backend. Adam optimizer was applied with ${\beta }_1=0.5$ and ${\beta }_2=0.999$. The learning rate was 2e$-$4. A single Nvidia 2080Ti GPU was used for training. We trained the model for 40000 iterations with a batch size of 8. During training, the intermediate models were evaluated every 200 iterations using the validation set. The intermediate model with the best validation performance was selected and used as the final model in this work.

3. Results and analysis

3.1. Leaf vein experiment by the down-sampling method for testing

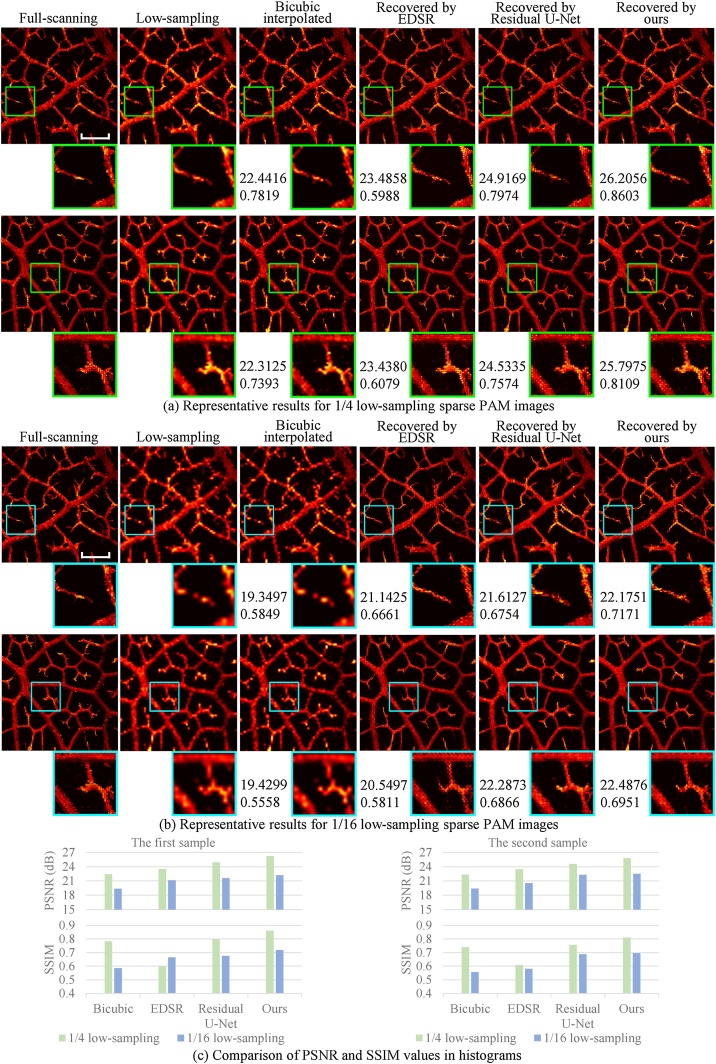
As detailed in Section 2, the CNN model was trained using the dataset generated by the down-sampling method. Representative results of the recovered PAM images are shown in Fig. 4, and the quantitative statistical results for the test set are listed in Table 1, where PSNR and SSIM (by comparing the recovered PAM images with the corresponding ground truth) metrics were both calculated.

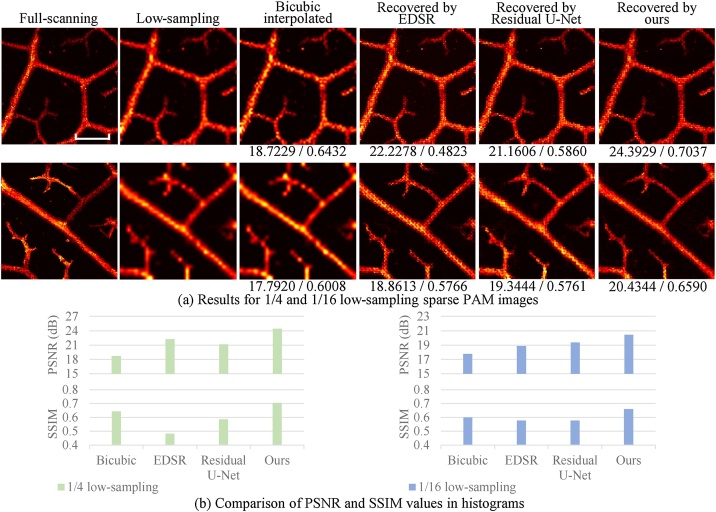
Fig. 4.

Results of the leaf vein experiment by the down-sampling method. The recovered PAM images are obtained from 1/4 (a) and 1/16 (b) low-sampling sparse PAM images. The numbers below the images indicate the PSNR (dB) and SSIM values (by comparing the entire image with the corresponding ground truth). In both (a) and (b), the top row shows the results from a magnolia leaf (the first sample), and the bottom row from a bodhi leaf (the second sample). Scale bar: 500 $\mu$m. All images, excluding zoom images, share the same scale bar. (c) Comparison of PSNR and SSIM values of the two samples in histograms.

Table 1.

Leaf vein experiment: comparison of PSNR and SSIM values.

	$2\times$		$4\times$
	PSNR (dB)	SSIM	PSNR (dB)	SSIM
Bicubic	23.4936 $\pm$ 1.8718	0.7721 $\pm$ 0.0457	19.9941 $\pm$ 1.9204	0.5773 $\pm$ 0.0683
EDSR	24.2356 $\pm$ 1.7999	0.5955 $\pm$ 0.0115	21.5557 $\pm$ 2.0176	0.6264 $\pm$ 0.0808
Residual U-Net	25.2166 $\pm$ 1.8106	0.7657 $\pm$ 0.0282	22.4960 $\pm$ 1.6238	0.6817 $\pm$ 0.0592
Ours	26.1431 $\pm$ 1.7022	0.8183 $\pm$ 0.0599	23.1760 $\pm$ 1.9290	0.7159 $\pm$ 0.0602

In Fig. 4, besides our restoration method, three other representative methods, the conventional bicubic interpolation, a re-trained EDSR model [39], and a re-trained Residual U-Net model [40], were applied for comparison. EDSR is a typical and effective CNN-based method originally designed for natural image SR problems. Residual U-Net is another well-known CNN architecture that has been widely adopted for various image restoration problems. The recovered PAM images were obtained from 1/4 and 1/16 (Fig. 4(a) and 4 (b), respectively) low-sampling sparse PAM images. For each scaling rate, two representative results are provided in Fig. 4. Zoom images (denoted by the green and cyan boxes for $2\times$ and $4\times$ scaling cases, respectively) are also displayed for better comparison. Fig. 4(c) shows the comparison of PSNR and SSIM values in histograms.

By checking the zoom images in Fig. 4, the three CNN-based methods are superior to bicubic interpolation from the intuitive view. Specifically, first, the results by bicubic interpolation are blurred and overly smoothed. Secondly, the low-sampling image suffers from discontinuities, which are not recovered by bicubic interpolation. By contrast, no such issues are observed by CNN methods, and the recovered images look more natural and closer to the full-scanning ones. Bicubic interpolation (and other conventional methods) uses the weighted average values of a local area, while the CNN models can learn more high-level (or more global) information to predict pixel values better. It is worth noting that the above issues (blurring, over smoothing, and discontinuity) of the recovered images using bicubic interpolation become obviously severer for the recovery from the 1/16 low-sampling case (Fig. 4(b)) compared with that from the 1/4 low-sampling case (Fig. 4(a)), while the consistently high quality and high fidelity for the recovered images using the CNN methods are achieved for the recovery from both the 1/4 and 1/16 low-sampling cases. That is, as the scaling increases, the advantages of the CNN methods become more apparent than the bicubic interpolation. Furthermore, as shown in Fig. 4(c), the recovered images by our CNN method have the highest PSNR and SSIM values compared with those by the other two CNN methods.

A similar trend can be found in the statistical results (mean and standard deviation values) on the test set, as shown in Table 1. For the $4\times$ scaling case, compared with bicubic interpolation, our model's PSNR and SSIM values (average of the test set) are greatly improved by 3.1819 dB and 0.1386. Besides, according to the two metrics, our model outperforms the re-trained EDSR model and Residual U-Net model for both $2\times$ and $4\times$ scaling cases. Therefore, our method can provide relatively high-quality PAM images from very sparse data, which was demonstrated quantitatively and subjectively.

3.2. Leaf vein experiment using experimentally-acquired sparse data for verification

To further verify the feasibility of our method, besides the low-sampling images obtained from the operation in Fig. 2, experimentally-acquired sparse PAM images were also fed to our trained CNN, which is closer to practical applications. We scanned the same ROI with a scanning step size of 8 $\mu$m and 16 $\mu$m (or 8 $\mu$m and 32 $\mu$m). In this demonstration, the full-scanning PAM image with $128\times 128$ pixels and the corresponding low-sampling PAM image with $64\times 64$ (or $32\times 32$) pixels were experimentally scanned over the same ROI. The low-sampling PAM images were used as the input and the corresponding images with $128\times 128$ pixels as the reference. Two representative results are shown in Fig. 5(a), where the top and bottom rows show the 1/4 and 1/16 low-sampling cases, respectively. In Fig. 5(a), the advantages of our CNN model (no issues of blurring, over smoothing, and discontinuity) are also observed. Our CNN model also achieves the highest PSNR and SSIM values, as shown in Fig. 5(b). The results verify that by using our CNN model for sparse-scanning and post processing, fast PAM imaging can be realized, and the images with similar quality to the very time-consuming full-scanning corresponding image can be recovered.

Fig. 5.

Results of the leaf vein experiment by experimentally-acquired low-sampling data for verification. (a) The top and bottom rows show the 1/4 and 1/16 low-sampling cases, respectively. The low-sampling images are collected by using a larger scanning step size. The numbers below the images indicate the PSNR (dB) and SSIM values (by comparing the image with the corresponding full-scanning reference image). Note that noise and laser fluctuations lead to some difference between pixel values of the same position from different scans of the full-scanning and low-sampling images. Scale bar: 300 $\mu$m. All images share the same scale bar. (b) Comparison of PSNR and SSIM values of the two cases in histograms.

3.3. Ablation investigation

The ablation investigation of the proposed CNN was elaborated. Two essential components (SE blocks and perceptual loss) of our method were analyzed to show their effectiveness.

As shown in Fig. 3(a) and (c), we applied the SE block [23] after some residual blocks. With the channel-wise attention design, the SE block is thought to be useful for channel information selection. The investigation results (including mean and standard deviation) are shown in Table 2. We found that the CNN without SE blocks was hard to converge during training and showed relatively poor results. For example, for $4\times$ scaling test set, the PSNR and SSIM values for the CNN without SE blocks are reduced by 1.3876 dB and 0.0936, respectively.

Table 2.

Ablation investigation of the existence of SE blocks.

	$2\times$		$4\times$
	PSNR (dB)	SSIM	PSNR (dB)	SSIM
Without SE blocks	24.9429 $\pm$ 1.7847	0.8124 $\pm$ 0.0444	21.7884 $\pm$ 1.8139	0.6223 $\pm$ 0.0655
With SE blocks	26.1431 $\pm$ 1.7022	0.8183 $\pm$ 0.0599	23.1760 $\pm$ 1.9290	0.7159 $\pm$ 0.0602

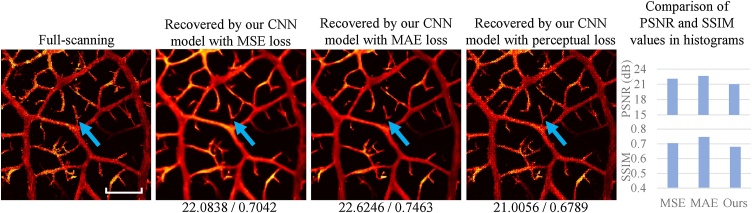
The perceptual loss is one of the most critical parts of our method. As explained previously, training with pixel-wise MSE and MAE contributes to getting higher PSNR and SSIM values. However, it probably results in finding a pixel-wise average solution that loses the fine texture [24], [31], [32], [33], [34]. To illustrate the argument, we trained three models with one different setting: one used the perceptual loss function while the other two utilized the conventional pixel-wise MSE and MAE loss functions, individually. We compared the recovered images by the three models with the ground truth. Representative results for the 1/16 low-sampling case are shown in Fig. 6. Images from left to right in Fig. 6 show the full-scanning image (ground truth) and the recovered PAM images by our CNN model with pixel-wise MSE loss, with pixel-wise MAE loss, and with perceptual loss, respectively. Similarly, PSNR and SSIM values were calculated, as shown below the recovered images.

Fig. 6.

Comparison between the CNN models with pixel-wise MSE / MAE loss and perceptual loss. The recovered PAM images are obtained from a 1/16 low-sampling sparse PAM image. The numbers below the images indicate the PSNR (dB) and SSIM values (by comparing the image with the corresponding ground truth). Scale bar: 500 $\mu$m. All images share the same scale bar. Comparison of PSNR and SSIM values in histograms is provided.

According to Fig. 6, PSNR and SSIM values of the cases of MSE loss and MAE loss are higher than those from the case of perceptual loss. However, the recovered PAM images of the cases of MSE loss and MAE loss are so smooth that they differ from the ground truth a lot from the perceptive point of view. Some small branches even disappear (e.g., the parts indicated by the blue arrows in Fig. 6). By contrast, although the recovered PAM image of the case of perceptual loss has relatively low metric values, it looks very much like the corresponding ground truth (e.g., more textures in the ground truth restored), which may be more critical for biomedical applications. In this regard, it is essential to apply such a perceptual loss function.

It is also important to point out that both assessments of the perceptive point of view and pixel-wise metrics should be considered to evaluate the effects of image recovery. In Fig. 4, Fig. 5, we are able to attain excellent results by our CNN model in terms of both assessments, which would be the best outcome.

3.4. In vivo experiment

We also extended our verification to in vivo experiment to better demonstrate the practical applications of our model. The CNN models trained on the leaf vein dataset were further fine-tuned (i.e., by transfer learning) by some additional in vivo PAM vascular images, which were acquired using the probe with a resolution of $\sim$3-4 $\mu$m and a scanning step size of 4 $\mu$m. Specifically, 101 in vivo PAM vascular images of mouse ears were used, with 90 images for transfer learning and 11 images for testing. The training settings for the transfer learning were the same as those for the leaves described previously. No layers were frozen for transfer learning.

PSNR and SSIM values calculated based on the in vivo test set are listed in Table 3. According to Table 3, our method also achieves the highest metric values compared with the other techniques. Similar to Table 1, our method has more improvements for the $4\times$ scaling case than those for the $2\times$ scaling case compared with bicubic interpolation.

Table 3.

In vivo mouse ear vessel experiment: Comparison of PSNR and SSIM values.

	$2\times$		$4\times$
	PSNR (dB)	SSIM	PSNR (dB)	SSIM
Bicubic	25.0855 $\pm$ 1.7853	0.7709 $\pm$ 0.0249	21.3115 $\pm$ 2.0410	0.5743 $\pm$ 0.0695
EDSR	25.0279 $\pm$ 1.6590	0.7507 $\pm$ 0.0212	21.4274 $\pm$ 1.6949	0.5526 $\pm$ 0.0574
Residual U-Net	25.0937 $\pm$ 1.4864	0.7767 $\pm$ 0.0180	22.4326 $\pm$ 2.0770	0.6355 $\pm$ 0.0559
Ours	26.3509 $\pm$ 1.6034	0.7880 $\pm$ 0.0192	23.3825 $\pm$ 2.3061	0.6483 $\pm$ 0.0839

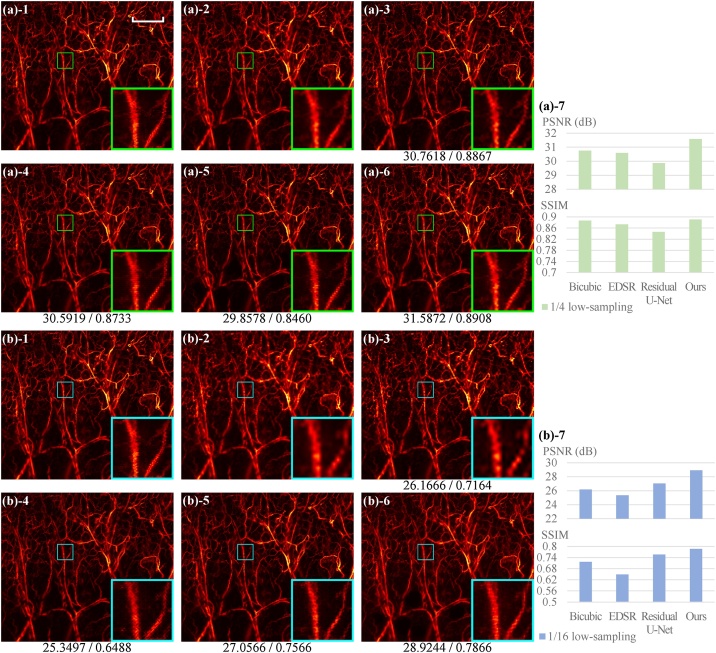
Besides quantitative comparison, the comparison from the perceptive point of view was conducted by checking PAM images. One representative result is shown in Fig. 7. The full-scanning image, acquired previously [41], has a size of $704\times 608$ pixels. Because the main body of our CNN architecture (excluding SE blocks) is a fully convolutional network, it can handle images with arbitrary input sizes without any cropping and montage operations. As can be seen, the qualitative advantages of CNN methods (sharper edges, high fidelity, and more continuous patterns) over bicubic interpolation are still preserved in the in vivo images of mouse ear blood vessels. The advantages can be much better appreciated in the 1/16 low-sampling case (Fig. 7(b)) than in the 1/4 low-sampling case (Fig. 7(a)). Although the other two CNN methods, EDSR and Residual U-Net, also show good visual performance as our CNN model in Fig. 7, our CNN model attains the highest metric values (Figs. 7(a)-7 and (b)-7), as also described above (statistical results in Table 3). That is, compared with EDSR and Residual U-Net, our method reaches the best outcome in both assessments of the perceptive point of view and pixel-wise metrics.

Fig. 7.

Demonstration of in vivo PAM images of blood vessels of the mouse ear. (a) The 1/4 low-sampling case. (b) The 1/16 low-sampling case. (a,b)-1 Full-scanning; (a,b)-2 Low-sampling; (a,b)-3 Bicubic interpolated; (a,b)-4 Recovered by EDSR; (a,b)-5 Recovered by Residual U-Net; (a,b)-6 Recovered by ours; (a,b)-7 Comparison of PSNR and SSIM values in histograms. The numbers below the images indicate the PSNR (dB) and SSIM values (by comparing the entire image with the corresponding ground truth). Scale bar: 500 $\mu$m. All images, excluding zoom images, share the same scale bar.

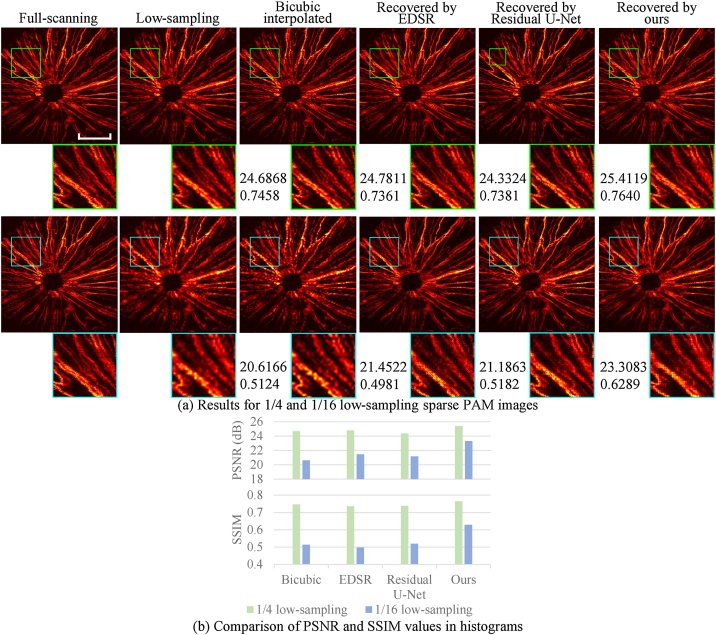
Further, we attempt to test our model for different patterns other than the tree-like patterns (e.g., with branches and subbranches) that have been demonstrated so far. Therefore, an in vivo PAM image of blood vessels of a mouse eye, which have radial patterns, was also tested. The PAM image with $448\times 448$ pixels was acquired previously by the probe with a resolution of $\sim$3 $\mu$m and a scanning step size of 4 $\mu$m [42]. The CNN model used for Fig. 7 (i.e., for PAM vascular images of mouse ears) was directly applied to the PAM vascular images of mouse eyes without further training.

The results are shown in Fig. 8. Similarly, we compared the full-scanning PAM image (ground truth) and the PAM images recovered by bicubic interpolation and by the three CNN methods. The recovered PAM images were also obtained from the 1/4 and 1/16 low-sampling sparse PAM images. As shown in Fig. 8, our method achieves the highest metric values among the four methods. From the perceptive point of view, our method renders a recovered PAM image with sharper edges and more continuous patterns than bicubic interpolation, especially for the 1/16 low-sampling case. This can be appreciated more clearly by comparing the zoom images. Therefore, even if using the CNN model trained by images with tree-like patterns, we still achieve good performance when applying our model to images with radial patterns, showing the robustness of the CNN method to some degree.

Fig. 8.

Demonstration of in vivo PAM images of blood vessels of the mouse eye. (a) The top and bottom rows show the 1/4 and 1/16 low-sampling cases, respectively. The numbers below the images indicate the PSNR (dB) and SSIM values (by comparing the entire image with the corresponding ground truth). Scale bar: 500 $\mu$m. All images, excluding zoom images, share the same scale bar. (b) Comparison of PSNR and SSIM values of the two cases in histograms.

4. Discussion

To speed up PAM imaging speed, fast-scanning PAM has been extensively investigated by employing sophisticated and expensive hardware. Alternatively, sparse-scanning PAM offers an elegant solution to realize fast PAM imaging utilizing software-based post processing. We proposed a CNN method to deal with the sparse data as an SR problem, specifically to recover from the low-sampling sparse PAM images. We adopted several key settings, including residual blocks, SE blocks, and perceptual loss function, in our method. As a result, our method produced excellent results in both the perceptive point of view and pixel-wise metrics.

In our work, we applied different full-scanning step sizes for leaf veins and mouse vessels (i.e., 8 $\mu$m and 4 $\mu$m, respectively). This is in part because the feature size of leaf veins is larger than that of mouse vessels. Different parameters and patterns (such as different full-scanning step sizes, different resolutions of PAM, and tree-like and radial patterns) used in our demonstrations also show the robustness of our CNN method. On the other hand, as expected, to apply our CNN method to low-sampling sparse PAM images with fine features, a small scanning step size for acquiring the low-sampling image has to be adopted accordingly. Otherwise, when the scanning step size is larger than the feature size (e.g., 2:1), some originally isolated pixels (i.e., disconnected from adjacent pixels) cannot be recovered by our CNN method. Interestingly, we found that for originally continuous patterns (in contrast to isolated pixels) such as tortuous blood vessels, our CNN method can excellently recover the patterns even when the scanning step size is larger than the feature size (e.g., the two samples in Fig. 4(b)). Specifically, for example, for the first sample in Fig. 4(b), by comparing the zoom images of the cases of “Low-sampling” and “Recovered by ours” with that of “Full-scanning,” the recovered PAM image by our method enables the recovery of fine features (the branch tip (at the center of the zoom images) whose feature size is smaller than the scanning step size of 32 $\mu$m) and continuous patterns, showing the SR ability and fidelity of our CNN method for selected applications such as blood vessels with continuous line patterns. This is because part of the continuous branch was still scanned, and the CNN methods produce images based on high-level and global information.

In practice, other than the total scanning pixels, factors such as laser PRF, scanning mechanisms (e.g., a motorized stage or a MEMS scanner), and data storage in the computer will affect and limit the ultimate scanning speed of PAM. Given certain laser PRF, the scanning time is approximately proportional to the total scanning pixels if the time taken for other parts is relatively short and can be neglected. In this regard, by reducing the sampling density to 1/4 or 1/16 in the low-sampling PAM images, the scanning time can be reduced to 1/4 or 1/16, respectively, compared with the full-scanning counterpart. Together with the post processing by the CNN methods, high-quality PAM images similar to the full-scanning counterpart can be obtained. It should be noted that the post-processing time is much shorter than the 2D scanning time, and therefore negligible. With our current PAM system (PRF of 1 kHz), the time taken for other parts mainly lies in the response time of the motorized stage. Thus, the scanning time will be closely proportional to the total scanning pixels when the scanning range in a B-scan is sufficiently long, which makes the time taken for other parts relatively short. For better illustration, we studied the relation between the scanning time and the total scanning pixels for two scanning ranges of 0.768 mm and 6.144 mm. Each scanning range used a 3 $\mu$m (full-scanning) and 12 $\mu$m ($4\times$ scaling rate or low-sampling) scanning step size. That is, the total scanning pixels were reduced by 4 times from the full-scanning to the low-sampling for each scanning range. For the case of the scanning range of 0.768 mm, the B-scan time is reduced by $\sim$2 times from the full-scanning to the low-sampling (0.453 s vs. 0.228 s). On the other hand, for the case of the scanning range of 6.144 mm, the B-scan time is reduced by $\sim$3.4 times (2.553 s vs. 0.760 s), which is closer to the scaling rate of 4. Investigation of the speed improvement with our CNN model on a high-speed PAM system (e.g., using a MEMS scanner) is of interest for future work.

Enhancing the quality of low-sampling sparse PAM images has been studied based on the alternating direction method of multipliers algorithm (ADMM). In our work, instead, a deep learning-based method was employed to deal with such enhancement of sparse PAM images. The deep learning-based method has advantages in regular scanning (in image acquisition) and fast processing speed (in post processing). First, regular scanning is much easier to implement than random scanning that is required for using a compressive sampling scheme [16]. For regular scanning, one can simply change to a larger scanning step, as demonstrated in this work. Secondly, to generate an image of about 1M pixels from the sparse data (i.e., the recovered latent full-scanning image has 1M pixels), the proposed CNN method costs about 0.35 s (with a single Nvidia 2080Ti GPU), while the ADMM requires 475.09 s (with the Intel Core 3.60 GHz). More importantly, we verified that our CNN method provides excellent performance even for the 1/16 low-sampling data, while the method in [16] mainly demonstrated the case with 1/2 low-sampling data to guarantee the quality of the recovered images. In other words, our method can significantly boost the PAM imaging speed. Fast PAM imaging would benefit in vivo imaging applications such as mitigating motion blurs due to, for example, animal breathing.

A work similar to ours has been published very recently [43]. Comparison of the two works is elaborated. (i) Both CNN models have typical architecture. Specifically, Residual Blocks to avoid vanishing gradient and SE blocks to further improve the performance are adopted in our CNN model, while a variation of U-Net, consisting of Dense Blocks to make the CNN deeper without vanishing gradient is used in [43]. (ii) The two CNN models have different advantages in terms of input sparse PAM image size and scaling rate. Our CNN model can accept arbitrary input sparse PAM image size, whereas the CNN model in [43] cannot due to the architecture characteristics of U-Net. On the other hand, the scaling rate in our CNN model has to be an integer (as shown in this work), while that in the CNN model in [43] can be a non-integer. (iii) Further, more samples and patterns (leaf veins, mouse ear blood vessels, mouse eye blood vessels) were demonstrated in this work, while only mouse brain vasculature was studied in [43]. (iv) We noticed that a low-sampling rate of 1/16 (i.e., 6.25%) was demonstrated in this work, while a smaller low-sampling rate of 2% was reported in [43]. We compared the full-scanning feature size (the smallest vessel diameter) in this work (Fig. 7(a)-1) and in [43] (Fig. 5(a)-1 in [43]) and found that $\sim$2 pixels and $\sim$4 pixels in one dimension are sampled for the full-scanning feature size in this work and in [43], respectively. This may explain that the CNN model in [43] can still work well at a smaller low-sampling rate. Therefore, in this regard, it can be considered that the performance of our CNN model is still comparable to the recent study [43].

5. Conclusion

We proposed a novel CNN-based method to improve the quality of sparse PAM images, which can equivalently improve PAM imaging speed. The CNN model was trained on the dataset of PAM images of leaf samples. Residual blocks, SE bocks, and perceptual loss function are essential in our CNN model. Both 1/4 and 1/16 low-sampling sparse PAM images were tested, and the proposed CNN method show remarkable performance in terms of perceptive point of view compared with conventional bicubic interpolation. PSNR and SSIM values using our method are also better than those using bicubic interpolation, EDSR, and Residual U-Net. We have also extended our method to in vivo PAM images of blood vessels of mouse ears and eyes, and the recovered PAM images have a high resemblance to the full-scanning ones. The CNN method to deal with sparse PAM images may also be applied to AR-PAM and other point-by-point scanning imaging modalities such as optical coherence tomography and confocal fluorescence microscopy. Our work opens up new opportunities for fast PAM imaging.

Declaration of competing interest

The authors declare no conflicts of interest.

Biographies

Jiasheng Zhou received his B.S. degree in Electronic Science and Technology from Shandong University and M.S. degree in Optics from East China Normal University. In 2018, he joined the University of Michigan-Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University, Shanghai, China, as a graduate student. His research interests include fast scanning photoacoustic imaging and non-contact photoacoustic imaging.

Da He received his B.S. degree in Optoelectronic Information Science and Engineering from Nankai University. In 2018, he joined the University of Michigan-Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University, Shanghai, China, as a graduate student. He is interested in biomedical image processing and computer vision.

Xiaoyu Shang received the B.S. degree in Optoelectronic Information of Science and Engineering from Sun Yat-Sen University. In 2018, she joined the University of Michigan-Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University, Shanghai, China, as a graduate student. Her research interest is biomedical image processing with deep learning, especially for photoacoustic imaging denoising.

Zhendong Guo received his B.S. degree in Opto-electronics Information Engineering and M.S. degree in Optical Engineering from Tianjin University. In 2016, he joined the University of Michigan-Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University, Shanghai, China, as a graduate student. His research interest includes development of Fabry – Perot sensor and photoacoustic imaging systems for biomedical applications.

Sung-Liang Chen received the Ph.D. degree in electrical engineering from the University of Michigan, Ann Arbor, MI, USA, and post-doctoral training at the University of Michigan Medical School, USA. He is currently an Associate Professor with the University of Michigan-Shanghai Jiao Tong University Joint Institute, Shanghai Jiao Tong University, Shanghai, China. His research interests include photoacoustic imaging technology and applications, optical imaging systems, and miniature photoacoustic transducers and ultrasound sensors. He was a recipient of the Shanghai Pujiang Talent Award.

Jiajia Luo received his Ph.D. degree in mechanical engineering from the University of Michigan, Ann Arbor, USA. He is currently an Assistant Professor at the Biomedical Engineering Department, Peking University, Beijing, China. His research interests include biomedical imaging, biomechanics, and machine learning. He was a recipient of a career development award in Michigan Institute for Clinical & Health Research, National Natural Science Foundation of China General Grant Award, as well as Peking University Clinical Medicine + X Young Investigator Grant Award.

Appendix B. Supplementary Data

The following are the supplementary data to this article: