Evaluation of denoising strategies for task‐based functional connectivity: Equalizing residual motion artifacts between rest and cognitively demanding tasks

Abstract

In‐scanner head motion represents a major confounding factor in functional connectivity studies and it raises particular concerns when motion correlates with the effect of interest. One such instance regards research focused on functional connectivity modulations induced by sustained cognitively demanding tasks. Indeed, cognitive engagement is generally associated with substantially lower in‐scanner movement compared with unconstrained, or minimally constrained, conditions. Consequently, the reliability of condition‐dependent changes in functional connectivity relies on effective denoising strategies. In this study, we evaluated the ability of common denoising pipelines to minimize and balance residual motion‐related artifacts between resting‐state and task conditions. Denoising pipelines—including realignment/tissue‐based regression, PCA/ICA‐based methods (aCompCor and ICA‐AROMA, respectively), global signal regression, and censoring of motion‐contaminated volumes—were evaluated according to a set of benchmarks designed to assess either residual artifacts or network identifiability. We found a marked heterogeneity in pipeline performance, with many approaches showing a differential efficacy between rest and task conditions. The most effective approaches included aCompCor, optimized to increase the noise prediction power of the extracted confounding signals, and global signal regression, although both strategies performed poorly in mitigating the spurious distance‐dependent association between motion and connectivity. Censoring was the only approach that substantially reduced distance‐dependent artifacts, yet this came at the great cost of reduced network identifiability. The implications of these findings for best practice in denoising task‐based functional connectivity data, and more generally for resting‐state data, are discussed.

We showed the inefficacy of many denoising strategies in balancing motion‐related artifacts between functional conditions that are differently prone to motion, such as rest and cognitively demanding conditions. While no pipeline was able to completely suppress motion artifacts and simultaneously maximize network identifiability, we found that strategies exploiting an optimized aCompCor yielded the best results. Importantly, we advocate the use of censoring with caution, since we found the method to be cost ineffective, prone to introduce biases and to reduce network identifiability.

1. INTRODUCTION

In‐scanner head motion is one of the major confounders in functional connectivity (FC) studies employing the blood oxygenation level dependent (BOLD) signal (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012; Satterthwaite et al., 2012; Van Dijk, Sabuncu, & Buckner, 2012). Two critical issues make the technique highly susceptible to motion. The first is intrinsic to FC itself, which is defined as statistical dependencies among remote neurophysiological events (Friston, 2011), and is commonly estimated as temporal correlations between BOLD time series of different brain regions. Regrettably, any non‐neuronal source of variance can introduce spurious correlations that may completely obscure neuronally‐driven correlations. In addition, motion acts by adding both global and spatially‐dependent variance (Power, Schlaggar, & Petersen, 2015), mimicking true functional connections. Second, investigators lack any a priori information regarding the exact temporal characteristics of neuronal‐related variance, which makes the reliability of FC estimates dependent on the ability of researchers to detect, model and remove physiological noise, reducing its magnitude below the threshold that systematically affects results.

Consequently, a great effort has been made to develop (Behzadi, Restom, Liau, & Liu, 2007; Jo, Saad, Simmons, Milbury, & Cox, 2010; Patriat, Reynolds, & Birn, 2017; Power et al., 2014; Power et al., 2015; Pruim, Mennes, van Rooij, et al., 2015; Salimi‐Khorshidi et al., 2014; Satterthwaite et al., 2013) and compare (Ciric et al., 2017; Muschelli et al., 2014; Parkes, Fulcher, Yucel, & Fornito, 2018; Pruim, Mennes, Buitelaar et al., 2015; Shirer, Jiang, Price, Ng, & Greicius, 2015; Siegel et al., 2017; Weissenbacher et al., 2009; Yan et al., 2013) numerous strategies for denoising BOLD data. There is substantial heterogeneity in the performance of these strategies, and even the most effective approaches were not able to fully account for motion‐related artifacts in FC estimates (Parkes et al., 2018). While a relatively low residual motion‐related variance may be considered acceptable when in‐scanner motion is evenly distributed among factors of interest, it can still create concerns when it correlates with the investigated factors. Such situations are common in neuroscience research since they are often found in developmental, aging (Harms et al., 2018, and references therein) and clinical studies (Pardoe, Kucharsky Hiess, & Kuzniecky, 2016).

Another class of FC studies in which head motion is particularly serious is the one focused on network dynamics induced by cognitive engagement, which is generally assessed by comparing resting state to one or multiple task conditions. Indeed, it has been reported that subjects tend to move less when they are engaged in a cognitive task than when they are under unconstrained conditions (Huijbers, Van Dijk, Boenniger, Stirnberg, & Breteler, 2017). Even passive movie watching, which requires minimal attention, has been associated with lower head movement compared to rest (Vanderwal, Kelly, Eilbott, Mayes, & Castellanos, 2015), especially in young children (Greene et al., 2018). While such a behavioral trait may be exploited to reduce the detrimental effect of motion on image acquisitions, particularly on structural or diffusion images, it is prone to bias task‐based FC studies. Therefore, whereas evidence from fMRI studies indicate that the brain accommodates task demands with specific and systematic network reconfigurations (reviewed in Gonzalez‐Castillo & Bandettini, 2018), it is not clear to what extent such modulations are compounded by the different amount of motion between the functional conditions being compared. Moreover, denoising strategies have been specifically developed for study designs involving one condition per subject, and in particular for resting‐state data. Their effectiveness has not been evaluated in the context of multiple steady‐state conditions that are differently prone to motion, as during different prolonged cognitive engagements or physiological conditions.

In the current work, we sought to identify the appropriate procedures for mitigating and balancing residual motion‐related effects across protracted functional conditions in task‐based connectivity studies. Specifically, we employed a set of benchmark measures to investigate how popular denoising strategies perform in cleaning up BOLD data that span different steady‐state functional conditions characterized by distinct amounts of head motion. To this aim, we analyzed data from our previous study (Tommasin et al., 2017; Tommasin et al., 2018) in which we collected BOLD fluctuations in a block‐design fashion employing prolonged epochs of alternated resting‐state and sustained working‐memory task conditions. Leveraging on the peculiar acquisition protocol, both long and with multiple conditions within the same run, we evaluated the condition‐specific performance of the pipelines according to benchmarks based either on minimizing motion‐related artifacts or at maximizing network identifiability. In addition, in order to corroborate our findings, we evaluated the pipelines in a further, larger dataset, composed of two separate acquisitions of resting‐state and stop‐signal task scans (Poldrack et al., 2016). Finally, we examined the robustness of previously reported task‐associated modulations in within‐network FC (Tommasin et al., 2018) by exploring its variability under different denoising strategies and under stringent exclusion of motion‐contaminated volumes.

2. MATERIALS AND METHODS

2.1. Subjects and datasets

Denoising strategies were evaluated in two fMRI datasets. The first, which we refer to as “Centro Fermi” (CF) dataset (40 runs from 20 healthy subjects), is composed of data collected at our laboratory for the evaluation of FC modulations following sustained task execution (Tommasin et al., 2017; Tommasin et al., 2018). Each CF run comprises multiple long‐lasting epochs of either rest or working‐memory task. Despite the limited sample size, the CF dataset was used as our primary dataset given its peculiar paradigm (detailed in the following section). For the second dataset, which serves for result corroboration and to counteract the sample‐size limitation of the CF dataset, we used a subset of data from the Consortium for Neuropsychiatric Phenomics (CNP Poldrack et al., 2016). The CNP dataset comprises resting‐state scans as well as six scans of BOLD acquisitions under different task conditions. We chose to compare the resting state to the stop‐signal task since such task showed the greatest difference in motion compared to rest, as reported in a previous study (Huijbers et al., 2017). From the entire pool of healthy subjects (130 subjects), we selected 120 subjects that included (a) a complete resting‐state acquisition, (b) a complete stop‐signal task acquisition, and (c) a T1‐weighted structural scan.

The CF data were collected on a 3T MRI Scanner (Magnetom Allegra, Siemens Healthineers, Erlangen, Germany) equipped with a standard birdcage coil. Functional images were acquired using a Gradient‐Echo Planar Imaging (GE‐EPI) sequence (TR = 2,100 ms, TE = 30 ms, FA = 70°, voxel size 3 × 3 × 2.5 mm³, 1.25 mm skip). Each run lasted 24 min and 38 s yielding 704 volumes (four dummy scans included). The slices were positioned starting from the vertex of the brain and covered the whole cerebrum. The cerebellum was not consistently included in the field of view of each subject. High‐resolution T1‐weighted images were acquired for anatomic reference and tissue segmentation purpose using a Magnetization Prepared Rapid Acquisition Gradient Echo (MPRAGE, TE = 4.38 ms, TI = 910 ms, TR = 2000 ms, FA = 8°, voxel size 1 × 1 × 1 mm³). Subjects gave written informed consent in accordance with the Declaration of Helsinki and European Union regulations.

The CNP data were collected on one of two Siemens Trio 3T scanners. Rest and task runs were acquired on the same day with a GE‐EPI sequence (TR = 2000 ms, TE = 30 ms, FA = 90°, voxel size 3 × 3 × 4 mm³). The resting run lasted for 304 s (∼5 min), for a total of 152 volumes, while the stop‐signal task was longer, lasting 368 s (∼6 min) for a total of 184 volumes. Four dummy scans preceded functional acquisitions and were not included in the data. T1‐weighted images were acquired with MPRAGE (TE = 3.31 ms, TI = 1,100 ms, TR = 2,530 ms, FA = 7°, voxel size 1 × 1 × 1 mm³).

2.2. Functional paradigms

2.2.1. CF dataset

CF functional images were acquired during a block‐design stimulation paradigm consisting of alternated long‐lasting epochs of eyes‐open resting state and sustained auditory working memory task (4 min and 54 s each, starting with a resting‐state epoch). The auditory working memory task involved continuous n‐back trials administered in epochs at either “high” load (2‐back) or “low” load (1‐back). Each trial was composed of a 500‐ms window, in which subjects were aurally presented with a vowel (pseudo‐randomly chosen among A, E, or O), and a subsequent 1,600‐ms response window, during which subjects had to report, via an MRI compatible 2‐button keyboard, whether the current vowel was the same as the one presented one stimulus prior (1‐back) or two stimuli prior (2‐back). During the entire functional run, subjects were asked to maintain their gaze on the center of the screen, which was marked by a one‐degree diameter circle over a uniform black background. The stimulation paradigm started at the beginning of the third dummy scan (i.e., was overall shifted backward by two TR) to roughly account for hemodynamic delay. More detailed information on the stimulation paradigm can be found in (Tommasin et al., 2018).

Two functional runs were acquired for each subject during the same experimental session, with epoch ordering: rest/1‐back/rest/2‐back/rest or rest/2‐back/rest/1‐back/rest, counterbalanced across subjects. Since we found no significant difference in motion between 1‐back and 2‐back epochs (see Figure S1), we lumped the two load conditions together, thus, from here on we will simply refer to both n‐back epochs as task epochs.

2.2.2. CNP dataset

The CNP rest and task data were acquired in separate runs, yet within the same acquisition session. During resting‐state acquisitions, no stimulation was presented and subjects were asked to remain relaxed and keep their eyes open. The stop‐signal task runs consisted of 128 trials in which a “go” stimulus (left or right pointing arrow) was visually presented with or without an aurally presented “stop” signal (a 500 Hz tone). Subjects were required to respond to the go stimulus (via a left or right button press) as quickly and accurately as possible, but to withhold the response in case of the stop tone. Trials were separated by rest periods (with a black screen) whose duration was pseudorandomly chosen between 0.5 and 4 s, with a mean of 1 s. While the experimental design is aimed at identifying the specific response to the stop signal, we treated the runs as block‐designed, thus ignoring potential instantaneous changes of motion associated with the different structure of the trials (i.e., with or without the stop signal). More detailed information about the stimulation can be found in Poldrack et al. (2016).

2.3. Functional image preprocessing

Image preprocessing was performed with FC toolbox (CONN 18.a, Whitfield‐Gabrieli & Nieto‐Castanon, 2012), which is based on SPM12 routines (http://www.fil.ion.ucl.ac.uk/spm), and was run on Matlab 2016b (The Mathworks Inc., Natick, MA). Preprocessing of functional data included the following steps: (a) rigid body registration for inter‐frame head motion, (b) application of the unwarp algorithm to reduce the susceptibility‐by‐movements effects (Andersson, Hutton, Ashburner, Turner, & Friston, 2001), (c) compensation of systematic slice‐dependent time shifts by phase shift in the Fourier domain, (d) direct normalization to Montreal Neurological Institute (MNI) space (voxel size 3 × 3 × 3 mm³) using as source image the EPI mean volume obtained from step a, and (e) intensity normalization to global mode 1,000 units. The direct normalization to MNI space (i.e., without using high‐resolution structural information) was chosen in order to mitigate the impact of geometric distortion artifacts, as shown in (Calhoun et al., 2017). Subject‐specific whole‐brain (WB) masks were defined to retain voxels fully covered by the field of view of the EPI sequence. Such masks were obtained by intersecting an a priori brain mask with subject‐specific masks composed of voxels with a mean intensity above the 20% of the global mode. The WB mask was also used to compute the global signal.

To allow a fair comparison between rest and task conditions, scans were trimmed so that the two functional conditions had the same number of volumes. In the CF dataset, we discarded the first resting‐state epoch, since there were three rest and two task epochs. Following the cut, the final number of volumes in the run was 560 (280 volumes per condition, approximately 10 min). In the CNP dataset, we discarded the first 32 volumes of the task run, so that each functional condition was composed of 152 volumes (approximately 5 min).

Finally, after removing constant and linear trends, the rest and task runs of the CNP dataset were concatenated, yielding a total run length of 304 volumes.

2.4. Structural image processing

T1 weighted images were segmented with SPM12 to obtain gray matter, white matter (WM), and cerebrospinal fluid (CSF) probability maps in native space (Ashburner & Friston, 2005). From tissue probability maps we derived WM and CSF masks for later extracting confounding signals. In constructing these masks, great care was applied to minimize partial volume errors that can yield confounding signals contaminated with signals from gray matter voxels (Power, Plitt, Laumann, & Martin, 2017). For each subject, the WM probability map was thresholded at 99% and underwent a 3‐voxel level erosion (AFNI's 3dmask_tool, Cox, 1996). Depending on the quality of the structural images, the 99% threshold may result in small holes in the deep white matter voxels that, once the image is eroded, substantially reduce the spatial extension of the final mask. To prevent this from happening, we applied the “fill_holes” function of 3dmask_tool before the erosion step. The eroded mask was normalized to MNI space (voxel size 3 × 3 × 3 mm³) using the transformation obtained from the segmentation of the T1 weighted image. To further reduce the contamination from gray matter signals, the MNI‐normalized mask was deprived of the brainstem, since this region is characterized by a scarce contrast between the two tissue types. CSF masks, encompassing only the ventricles, were constructed with a similar procedure. For each subject, the CSF probability map was first deprived of voxels in close proximity to the gray matter by intersecting the map with a gray matter mask (obtained from the GM probability map with threshold at 95% and applying a 2‐voxel level dilation; 3dmask_tool). Subsequently, the ensuing map was thresholded at 99% (95% for the CNP dataset, since in such dataset the 99% threshold resulted in a few subjects with empty masks) and underwent a 2‐voxel level erosion. The resulting mask was normalized to MNI space and was deprived of any nonventricle structure using an a priori mask. In case the final mask contained less than 10 voxels, the procedure was replicated using a 1‐voxel level erosion. Additional information regarding the constructed masks are reported in Figure S2 and Table S1.

Once confounding signals were extracted with the above‐defined masks, we further masked functional data by retaining voxels with a gray matter probability >75%. Such last masking aimed at increasing the specificity of FC estimates and at lightening the computational burden.

2.5. Assessment of in‐scanner motion

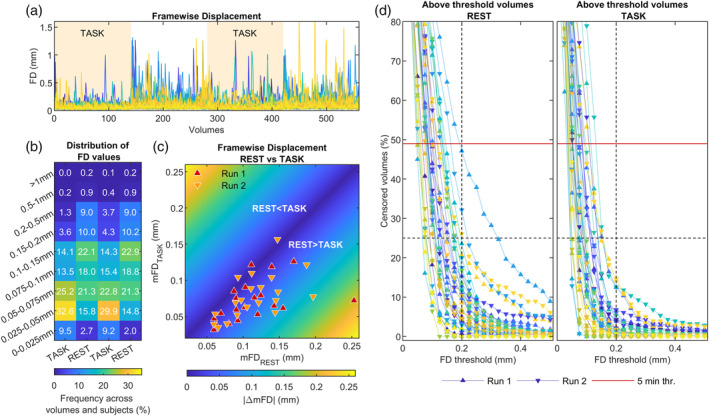
The realignment transformation matrices, estimated during the interframe rigid‐body registration, were used to compute the framewise displacement (FD), defined as the root mean square deviation of the relative transformation matrices (i.e., the transformation “error” between two consecutive volumes), over an 80‐mm radius sphere (Jenkinson, Bannister, Brady, & Smith, 2002). Although there are several alternative FD metrics, we adopted the one defined by Jenkinson and colleagues as it has been shown to be the most closely related to voxel‐specific metrics of displacement (Yan et al., 2013).

For the CF dataset, we split the FD series in its five epochs, according to the experimental paradigm. As for the EPI series, the FD series of the first epoch was discarded. The remaining four epochs were merged according to the functional condition, resulting in one series at rest (FD_rest) and one at task (FD_task). Similarly, for the CNP dataset we discarded the first 32 points of the task FD series, so that the FD series matched the trimmed EPI series.

The metric used to summarize the subject's head movement during the two functional conditions was the mean FD (mFD).

2.6. Denoising pipelines

2.6.1. The general framework

Different denoising pipelines were evaluated in their ability to remove motion‐related artifacts. All the considered denoising pipelines were applied within a common framework, which employs a multiple linear regression model to perform simultaneous nuisance regression, band‐pass filtering and, if included in the pipeline, censoring of volumes highly contaminated by motion (Jo et al., 2013). Each denoising model was composed of a set of regressors common to all pipelines, which included (a) Legendre polynomials up to order 1 to account for constant and linear trends and (b) a basis of sines and cosines to regress out frequencies outside the band 0.008–0.1 Hz. This common set of regressors was accompanied by pipeline specific confounding variables (see next section for their definitions), that consumed a variable number of temporal degrees of freedom (tDoF). When censoring was required, the marked volumes were put to zero value both in the data and in the regressor matrix, consuming a number of tDoF equal to the number of excised volumes. For the CNP dataset, in order to take into account the phase shift between the concatenated rest and task runs, two orthogonal sets of trend and band‐pass blocks were used (see Figure S3 for CF and CNP representative denoising matrices). The linear regression was calculated via ordinary least squares method using the functional run as dependent variable and the above defined regressor matrix as explanatory variables. The denoised series was obtained by computing the residuals of the regression model.

The simultaneous denoising approach is available in AFNI via the function 3dTproject (Cox, 1996), however, for speeding up calculations (e.g., by avoiding loading multiple times the same dataset that undergoes different regression models) we rewrote the algorithm in Matlab. The function is freely available from GitHub (https://github.com/dmascali/fmri_denoising), along with code to construct suitable regressors for denoising.

We note that the range of frequency selected for bandpass filtering is slightly wider compared to similar previous denoising studies (e.g., Parkes et al., 2018; Yan et al., 2013). The cut‐off frequencies were selected to minimize the impact of the filter on the residual tDoF while at the same time allowing for low‐pass filtering below 0.1 Hz, which in previous studies has shown to be effective in mitigating motion artifacts (Satterthwaite et al., 2013).

2.6.2. Volume censoring

As part of data denoising, it is a common approach to remove volumes corrupted by in‐scanner motion, where the corrupted volumes may be selected using the FD series or similar data quality metrics. While censoring has been shown to mitigate the impact of motion on FC estimates (Power et al., 2014; Satterthwaite et al., 2013; Yan et al., 2013), it also reduces the accuracy of FC estimates due to the dependency of the sample correlation variance on the number of observations (Davey, Grayden, Egan, & Johnston, 2013). For the same reason, censoring can also introduce heteroscedasticity when the number of excised volumes is variable across the sample, since the variance of correlations tends to increase with the number of excised volumes. Heteroscedasticity may be particularly problematic when the studied effects covary with in‐scanner motion, as in our case, comparing functional conditions differently affected by motion.

We adopted two censoring variants, one based on an FD threshold, which we will refer to as threshold‐based censoring (T‐censoring), and one that removes volumes based on the top‐percentage FD values, which we will refer to as percentage‐based threshold (P‐censoring). In T‐censoring, which is commonly applied in the literature (Power et al., 2015; Satterthwaite et al., 2013), we marked for deletion all volumes within the run with an FD above 0.2 mm. In P‐censoring, we censored a fixed number of volumes for each subject by marking volumes having an FD within the top 25%, separately for task and rest conditions. T‐censoring ensures FC to be computed on scans with no gross motion, at the cost of a variable loss of tDoF between rest and task conditions, possibly inducing between‐condition biases. Conversely, P‐censoring ensures a fair comparison between conditions, but removes potentially good volumes in the condition with less motion. In the CF dataset, the 0.2 mm and 25% thresholds were chosen so to leave at least 39 tDoF and at least 5 min of data in each functional condition, which has been shown as an adequate amount of data to achieve stable estimates of FC (Van Dijk et al., 2010). Given the short acquisition, the CNP dataset could not meet these two criteria for any sensible threshold, therefore, we did not explore censoring in this dataset.

2.6.3. Denoising models

We evaluated the performance of numerous popular denoising pipelines, which are listed in Table 1. Each pipeline was a composition of the following confounding variables:

TABLE 1.

Characteristics of the 12 evaluated denoising pipelines

Model number	Name	Trends	Band‐pass filter	RP	WM/CSF‐derived signals	ICA‐AROMA	GSR	T/P‐censoring	Total	Residual tDoF
1	12RP	2/4	343/190	12	—	—	—	—	357/206	203/98
2	24RP	2/4	343/190	24	—	—	—	—	369/218	191/86
3	24RP+8WM&CSF	2/4	343/190	24	8	—	—	—	377/226	183/78
4	24RP+aCompCor	2/4	343/190	24	10	—	—	—	379/228	181/76
5	24RP+aCompCor50%	2/4	343/190	24	60.7 ± 4.0/35.3 ± 4.2	—	—	—	429.7 ± 4.0/253.3 ± 4.2	130.3 ± 4.0/50.7 ± 4.2
6	ICA‐AROMA	2/4	343/190	—	2	81.7 ± 20.7/29.8 ± 10.9	—	—	428.7 ± 20.7/225.8 ± 10.9	131.3 ± 20.7/78.2 ± 10.9
GSR based
7	24RP+8WM&CSF+4GSR	2/4	343/190	24	8	—	4	—	381/230	179/74
8	24RP+aCompCor + 2GSR	2/4	343/190	24	10	—	2	—	381/230	179/74
9	24RP+aCompCor50% + 2GSR	2/4	343/190	24	61.9 ± 3.8/35.5 ± 4.1	—	2	—	432.9 ± 3.8/255.5 ± 4.1	127.1 ± 3.8/48.5 ± 4.1
10	ICA‐AROMA + 2GSR	2/4	343/190	—	2	81.7 ± 20.7/29.8 ± 10.9	2	—	430.7 ± 20.7/227.8 ± 10.9	129.3 ± 20.7/76.2 ± 10.9
Censoring based
11	24RP+8WM&CSF+4GSR+Tcens	2/‐	343/‐	24/‐	8/‐	—	4/‐	36.3 ± 31.8/‐	417.3 ± 31.8/‐	142.7 ± 31.8/‐
12	24RP+8WM&CSF+4GSR+Pcens	2/‐	343/‐	24/‐	8/‐	—	4/‐	140/‐	521/‐	39/‐

Note: For each pipeline the table shows the number of explanatory variables used by each set of confounders, along with the total number of variables (including the number of censored volumes) and the residual nominal tDoF. When more than one number is present in a cell, the first refers to the CF dataset, the second to the CNP dataset; when this distinction is absent, the number is common to both datasets. When the number of confounders is variable across the dataset, the mean and the standard deviation are reported.

• RP. The 6‐realignment parameters (RP; three‐rotational and three‐translational parameters), estimated during the interframe rigid‐body registration step, plus their temporal derivatives (12RP; temporal derivatives are always calculated via backward difference). We also considered an additional expansion of the 12RP set by including also the squared terms, for a total of 24 explanatory variables (Satterthwaite et al., 2013).

• WM&CSF. Based on the argument that signals from WM and CSF compartments primarily reflect a mixture of artifacts and physiological noise, these signals are commonly exploited to construct confounders to be regressed out from data (Giove, Gili, Iacovella, Macaluso, & Maraviglia, 2009). Two explanatory variables (2WM&CSF) were obtained by extracting the mean tissue signal separately from WM and CSF masks. Similar to the 24RP set, we also considered an expanded set of confounders that included the two average time series, their first temporal derivatives and the squares of the resulting four terms (8WM&CSF).

• aCompCor. Introduced by Behzadi et al. (2007), anatomical component correction (aCompCor) defines a set of orthogonal confounders by extracting the first n‐principal components (PCs) from regions representative of physiological noise, such as WM and CSF compartments, and it has been shown to outperform mean tissue‐based regression in removing motion artifacts (Muschelli et al., 2014). We performed temporal PC analysis on the mean‐centered BOLD time series enclosed in each nuisance mask (i.e., WM and CSF). Then, following (Muschelli et al., 2014), we evaluated two different aCompCor variants that differed in the number of extracted PCs. We either retained a fixed number of PCs, 5 for each tissue type resulting in a total of 10 explanatory variables (aCompCor method), or we extracted a variable number of PCs so that the selected components explained at least 50% of the variance in each tissue mask (aCompCor50% method).

  Differently from previous evaluation studies (Ciric et al., 2017; Muschelli et al., 2014; Parkes et al., 2018; Shirer et al., 2015), before running PC analysis, we orthogonalized the BOLD signals with respect to the sine/cosine basis functions and with respect to any other confounders in the model (e.g., to the 24RP in case of the model 24RP + aCompCor). Such an approach ensures that the extracted PCs are maximally predictive. The developed Matlab code is available from the GitHub repository (https://github.com/dmascali/fmri_denoising).

• ICA‐AROMA (ICA‐based strategy for Automatic Removal of Motion Artifacts). ICA‐AROMA is a data‐driven method to identify and remove motion‐related artifacts (Pruim, Mennes, Buitelaar, et al., 2015; Pruim, Mennes, van Rooij, et al., 2015). The method employs spatial ICA decomposition followed by an automatic classification of noise independent components (ICs) based on four theoretically motivated features: (1) robust correlation with realignment‐derived time series, (2) high frequency content, (3) brain edge, and (4) CSF spatial overlap. Then, ICs classified as noise are removed from the data using ordinary least squares partial regression (including into the model the entire set of ICs). This approach ensures that only the variance uniquely associated with noise‐classified ICs is removed. The ICA‐AROMA cleaned time series is complemented by the additional regression of tissue‐mean signals (i.e., the 2WM&CSF confounding set, yet now extracted from the cleaned series). The number of regressors required by ICA‐AROMA is variable across subjects, being dependent on the number of ICs classified as noise. In order to comply with the advised processing stream (Pruim, Mennes, van Rooij, et al., 2015), ICA‐AROMA was applied to data in native space, motion and slice‐timing corrected, global 4D mean intensity normalized and spatially smoothed (full width at half maximum = 6 mm). Notwithstanding smoothing is required by ICA‐AROMA to better identify structured artifacts, it also introduces an additional variable in model comparison. To overcome such issue, we discarded the ICA‐AROMA output time series (smoothed) and we reconstructed the cleaned series using the mixing matrix and the component classification on the unsmoothed and MNI normalized data (via partial regression).

• GSR (Global Signal Regression). The subject‐specific WB masks were used to extract the global signal defined as the averaged time series from all voxels within the mask. We considered either a two‐term set composed of the mean signal plus its temporal derivative (2GSR) or an additional expansion including also the squared terms (4GSR).

The denoising pipelines were designed to investigate the effects of the above‐defined confounding signals and/or some of their combinations (Table 1). Comparison of models 1 and 2 investigates the effect of employing an extensive expansion of realignment parameters; models 3–5 the use of signals from tissue compartments. Models 4–6, based on PCA and ICA data decomposition respectively, represent the most promising no‐GSR‐based pipelines according to previous studies focused on resting‐state connectivity (Ciric et al., 2017; Muschelli et al., 2014; Pruim, Mennes, Buitelaar, et al., 2015). For Pipelines 3–6, we also studied the effect of GSR (models from 7 to 10). Censoring was applied to Pipeline 7, as suggested in (Satterthwaite et al., 2013), either using T‐censoring (model 11) or P‐censoring (model 12).

2.7. FC estimates

Before estimating FC, the denoised series were split and merged in order to obtain two functional series, one for the rest and one for the task condition, from which we extracted condition‐specific FC estimates. If the pipeline included censoring, the censored volumes, originally set to zero value, were removed. ¹ In order to compute benchmark measures, we parcellated the cortex in 333 node regions using the Gordon and colleagues parcellation, which provides higher homogenous FC than other available parcellations (Gordon et al., 2016). Five (34) node regions were discarded because they did not overlap consistently with the EPI data in the CF (CNP) dataset, resulting in a total of 328 (299) exploitable nodes. Average time series were extracted from each node and a FC matrix was obtained by calculating the Pearson's correlation coefficient between average time series of each pair of nodes, resulting in 53,628 (44,551) unique FC estimates. Before computing any statistics, the correlation values were z‐Fisher transformed.

2.8. Outcome measures

We computed a set of benchmarks designed to highlight residual artifacts. Specifically, we evaluated (a) the change in signal intensity from one volume to the next (DVARS, see below for its definition), (b) the intersubject correlation between a quality control (QC) metric and FC estimates (QC–FC correlations), and (c) the residual effect of censoring high‐motion volumes (Δr plots). The benchmarks were computed separately for rest and task conditions and for the change in FC; they were also evaluated to the extent that they yield comparable results between the two functional conditions, providing an additional indicator of pipeline efficacy. Since the above defined metrics are not sensitive to possible overfitting, we adopted a fourth benchmark (d) based on the ability to identify densely connected sub‐networks (modularity metrics). Finally, we explored the robustness against in‐scanner motion of a commonly reported finding in studies of task‐based dynamic FC, namely, the reduction of within‐network FC (Gonzalez‐Castillo & Bandettini, 2018). Each measure is detailed in the following sections.

2.8.1. DVARS investigation

DVARS is an intensity‐based data‐quality metric that indexes the change in signal intensity from one volume to the next (Power et al., 2014; Smyser et al., 2010). A DVARS series is obtained by computing, for each time frame, the root mean square (rms) value over the entire brain, or within a mask, of the differentiated BOLD time series (via backward difference). Differently from FD, which is only related to head motion, DVARS is sensitive to various physiological noises, including for example, breathing‐related variance. DVARS can be computed before any denoising is performed and might be used as an index for censoring noisy volumes, but it can also be computed after denoising has been performed to assess the quality of the denoised data. In order to do the latter, we computed DVARS within a noise only mask (DVARS_NOISE) following each considered denoising pipeline ² ; then, we summarized the QC series by extracting the rms value from each functional condition, and finally plotting the task‐associated change, that is, Δrms(DVARS_NOISE) = rms(DVARS_NOISE|TASK) − rms(DVARS_NOISE|REST). The noise only mask contained voxels on the edge of the brain and was constructed by applying a 3 voxel‐level dilation to the subject‐specific whole‐brain mask (3dmask_tool, AFNI) and subsequently removing any voxels in the original mask; by construction, the NOISE mask does not contain voxels used to compute FC or to extract confounding signals. Ideally, in the case of a perfectly cleaned dataset, no difference in rms(DVARS_NOISE) between the two functional conditions is expected. Thus, effective pipelines should yield zero‐centered distributions of Δrms(DVARS_NOISE).

Moreover, in order to examine how movements translate into MR signal changes within the region of interest, we compared the DVARS_GM time courses to the FD series, where DVARS_GM was calculated in the subject‐defined GM mask.

2.8.2. QC‐FC correlations

A possible benchmark measure for assessing residual motion‐related variance in FC is the correlation between per‐subject mFD and per‐subject estimates of FC (Burgess et al., 2016; Ciric et al., 2017; Parkes et al., 2018; Power et al., 2014). We computed the intersubject Pearson's correlation between mFD and FC for all possible pairs of nodes, yielding a distribution of QC‐FC correlations. Such distribution was computed separately for each functional condition (i.e., mFD_rest vs. FC_rest and mFD_task vs. FC_task). In addition, in order to understand to what extent the task‐associated changes in FC are related to the task‐associated difference in head movement, we computed a QC‐FC distribution by correlating the per‐subject ΔmFD = mFD_task − mFD_rest with the per‐subject ΔFC = FC_task − FC_rest. In perfectly cleaned dataset, no intersubject variability in FC is expected to be explained by in‐scanner motion, thus, a good cleaned dataset should yield a zero‐centered QC‐FC distribution with small standard deviation. We extracted the median of the absolute distribution to evaluate both the centering and spread of the distribution.

We also quantified possible distance‐dependence artifacts in QC‐FC distributions by computing the Spearman's correlation between the QC‐FC values and the associated Euclidian distance between each pair of nodes (Parkes et al., 2018). Indeed, prior studies have shown that in‐scanner motion differently impacts FC depending on the distance between regions, with short‐range connections showing greater association with motion (Power et al., 2012; Satterthwaite et al., 2012; Van Dijk et al., 2012); likely due to the greater similarity of motion‐added variance for nearby voxels compared with the similarity of motion‐added variance for distant regions (Power et al., 2015).

2.8.3. Δr plots

In addition of being employed as a cleanup strategy, censoring has also been adopted as a benchmark tool (Burgess et al., 2016; Power et al., 2014). The basic idea is that the difference in FC obtained with and without censoring (Δr) should reflect the extent to which motion‐contaminated volumes influence FC estimates. In contrast to QC‐FC correlations, that index motion‐related artifacts using across‐subjects variance in FC and motion estimates, Δr analyses explore the specific effect of motion‐contaminated volumes at the subject level.

Compared to previous work (Burgess et al., 2016; Power et al., 2014), we applied some modifications to this benchmark. First, we used a P‐censoring approach, instead of the common T‐censoring method, to avoid tDoF‐related variability in FC estimates both across subjects and across conditions. Second, to improve the sensitivity of the benchmark, as well as to avoid introducing a bias between censored and uncensored estimates, we calculated Δr as the difference between FC computed censoring the 20% top FD volumes minus FC computed censoring the 20% bottom FD volumes, that is, FC obtained from the least motion‐affected volumes (LM, low motion) and one estimated from the most motion‐contaminated volumes (HM, high motion), respectively. We computed Δr _REST = FC_REST|LM − FC_REST|HM and Δr _TASK = FC_TASK|LM − FC_TASK|HM, while to assess the task‐related change in FC we computed ΔFC_LM − ΔFC_HM, where ΔFC = FC_TASK − FC_REST. This procedure yielded for each subject a distribution of Δr values, one for each pair of nodes. From the subject‐specific Δr distribution we extracted the mean, which indexes global artifacts, as well as the Spearman's correlation between Δr values and the associated Euclidian distance between each pair of nodes, which indexes distance‐dependent artifacts.

Due to the limited number of volumes in the CNP dataset, this benchmark was evaluated solely for the CF dataset.

2.8.4. Network modularity

A good denoising pipeline should remove physiological artifacts while preserving signal of interest. Indeed, while removing motion artifacts does increase the detection power of the true neuronal effect, an over aggressive denoising may lose this benefit by removing the very signal of interest. Thus, we computed modularity, an index that quantifies the extent to which a graph can be partitioned in densely connected sub‐networks, also called communities. It is expected that motion would decrease modularity (Satterthwaite et al., 2012), and similarly, we expect that pipelines that remove real signal would decrease the modular structure of the brain (Ciric et al., 2017). For each subject, we identified communities in the connectivity matrix, separately for rest, task and for their difference, using the Louvain algorithm (Blondel, Guillaume, Lambiotte, & Lefebvre, 2008) and maximizing a modularity function defined for fully connected, weighted and undirected graph (Rubinov & Sporns, 2011). To address degeneracy of community partitions, we iterated the algorithm to obtain 250 optimal partitions and finally selected the partition with the greatest similarity with respect to all other partitions (Doron, Bassett, & Gazzaniga, 2012). Likewise, we selected as the best representative modularity value the average modularity across the 250 iterations, which was then evaluated as a function of denoising pipelines. Given that modularity by definition tends to favor graphs whose distribution of correlations is centered to zero, we expect that denoising strategies adopting GSR would be favored. Consequently, we extracted a second outcome that does not suffer from this limitation, that is, the similarity of the identified network partitions across subjects, that we quantified as the average of the z‐score of Rand index calculated over all pairs of subjects' partitions. In a homogenous sample, we expect that effective and efficient denoising pipelines would increase the partitions' similarity across subjects.

2.8.5. Effect of motion on task‐associated change in within‐network FC

One of the main findings we obtained analyzing the CF dataset was a marked task‐associated reduction of the internal synchronization of several large‐scale networks (Tommasin et al., 2018). Here, we re‐evaluated this finding using different pipelines in order to assess the extent to which the processing may influence the reported reduction in FC. With this aim, we computed the within‐network FC of six ICA‐derived networks (dorsal attention (DAN), default mode (DMN), frontoparietal (FPN), somatomotor (SMN), ventral attention (VAN), and visual (VIS) network) as described in (Tommasin et al., 2018). We further explored the stability of within‐network FC under progressive elimination of motion‐contaminated volumes, both with the T‐ and P‐censoring approach. In case of progressive T‐censoring, in order to rule out the possibility that the reduction in FC may be driven by the most moving subjects, we explored lower FD thresholds (<0.2 mm) that progressively resulted in the elimination of subjects with not enough tDoF after censoring.

3. RESULTS

3.1. Subject's in‐scanner movement

As expected, the analysis of the FD series showed a marked tendency for subjects to move more during the resting periods than when they were engaged in the working‐memory (Figure 1) or in the stop‐signal task (Figure S4). The motion characteristics of the two datasets are reported in Table 2.

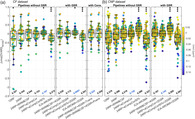
FIGURE 1.

Evaluation of in‐scanner head movement for the CF dataset. (a) FD series for each session and subject, with sessions from the same subject plotted with the same color. (b) Distribution of FD values in 9 bins of different width, showing the marked difference in the distribution of FD values between rest and task epochs. (c) Task‐averaged mFD versus rest‐averaged mFD. (d) Percentage of volumes above various FD thresholds computed separately at rest (left panel) and task (right panel). The dotted vertical and horizontal lines mark, respectively, the 0.2 mm and 25% threshold that we used in denoising pipelines employing censoring. Percentage values above the red lines have less than 5 min of residual data

TABLE 2.

Motion characteristics for the CF and CNP datasets

	CF dataset			CNP dataset
Measure	Functional condition		p‐values	Functional condition		p‐values
	Rest	Task		Rest	Task
mFD (mm)
Number of runs (subjects)	40 (20)	40 (20)		120 (120)	120 (120)
Mean	0.114	0.074	7.8 × 10−5	0.106	0.080	4.4 × 10−8
SD	0.042	0.029		0.072	0.061
Min	0.060	0.032		0.033	0.024
Max	0.25	0.16		0.49	0.44
Percentage of volumes with FD >0.2
Number of runs (subjects)	40 (20)	40 (20)		120 (120)	120 (120)
Mean	10.1	2.9	.0027	9	5	5.4 × 10−5
SD	9.8	4.0		15	10
Min	0	0		0	0
Max	47	15		83	79
FD series across all runs (mm)
Number of volumes	11,200	11,200		18,240	18,240
SD	0.10	0.064		0.15	0.16
Skewness	5.1	5.5		12	21
Kurtosis	50	61		323	754

Note: p‐values are obtained via two‐sample paired t‐tests (in the case of CF, after averaging runs belonging to the same subjects).

Considering the CF dataset (Figure 1), the resting epochs were characterized both by more volumes with extreme FD values and by an overall shift of the FD distribution toward higher values (Figure 1b). As shown in Figure 1c, the mFD was found significantly greater at rest than at task (mFD_task: 0.074 ± 0.029 mm; mFD_rest: 0.114 ± 0.042 mm paired t‐test, mFD_rest > mFD_task: t = 5.0, p = 7.8 × 10⁻⁵, dof = 19, after averaging the two runs). As the result of the pronounced difference in the distribution of FD values for the two functional conditions, a simulation of censoring at several thresholds resulted in more volumes above threshold at rest than at task, for all considered thresholds (Figure 1d). Figure 1d also shows that the 0.2 mm threshold, chosen for T‐censoring, resulted in at least 5 min of retained data free from gross motion, at both rest and task. The 25% threshold, selected for the P‐censoring, resulted in all task series below 0.2 mm of FD, while 2 out 40 rest series had some volumes with FD above 0.2 mm. Similar motion characteristics were found in the CNP dataset (mFDtask: 0.080 ± 0.061 mm; mFDrest: 0.106 ± 0.072 mm; paired t‐test, mFDrest > mFDtask: t = 5.9, p = 4.4 × 10^–8, dof = 119), yet it showed a few subjects with extreme motion (mFD >0.25 mm).

The two datasets did not significantly differ in the average motion (t‐test mFD_CF > mFD_CNP: p = .96, t = 0.06, dof = 138), nor they differed in the disparity of motion between task and rest conditions (t‐test ΔmFD_CF > ΔmFD_CNP: p = .22, t = −1.2, dof = 138).

3.2. DVARS results

Head motion induces spurious signal changes that are apparent in DVARS series. Given the differential impact of head motion between rest and task conditions, we expect DVARS to reflect such differences by showing higher values for the resting state. Here, we used a balanced DVARS value between the two functional conditions as an indicator of pipeline efficacy.

Figure 2 shows the distribution of Δrms(DVARS_NOISE) for each considered pipeline and dataset, with functional runs color‐coded based on the task‐associated difference in head motion. The distribution of Δrms(DVARS_NOISE) was shifted or skewed toward negative values for many investigated models, indicating greater rms(DVARS_NOISE) values at rest than at task. Generally, negative Δrms(DVARS_NOISE) values were associated with high differences in head motion between function conditions (see blue dots). Considering the CF dataset (Figure 2a), the worst performing methods were those based exclusively on the regression of realignment parameters (i.e., 12RP and 24RP), as indicated by the median absolute Δrms(DVARS_NOISE). Adding nuisance signals derived from WM and CSF compartments decreased the median absolute Δrms(DVARS_NOISE), with the aCompCor models performing better than the simple tissue‐averaged signals. In particular, aCompCor50% yielded the best median absolute value and was the only method that was able to invert the sign of Δrms(DVARS_NOISE) for the functional runs with the greatest disparity in motion between conditions (see blue dots now laying on the upper quadrant). On the contrary, ICA‐AROMA performed poorly, with a distribution almost comparable to those of simpler models. Adding GSR provided minor to modest benefits and adding censoring, either T‐ or P‐censoring, provided almost no benefit compared to the respective uncensored version.

FIGURE 2.

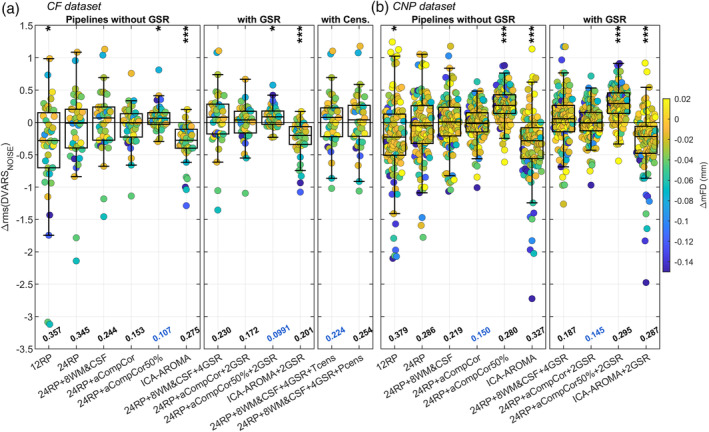
Task‐associated changes in DVARS_NOISE. The box plots show the distribution of the difference in rms(DVARS_NOISE) between task and rest—i.e., Δrms(DVARS_NOISE) = rms(DVARS_NOISE|TASK) − rms(DVARS_NOISE|REST)—for all considered pipelines, separately for CF (a) and CNP (b) datasets. Δrms(DVARS_NOISE) values, calculated separately for each run (40 and 120 runs for the CF and CNP dataset, respectively), are color‐coded based on the task‐associated difference in mFD. At the bottom of each box is reported the median of the absolute Δrms(DVARS_NOISE), with the smallest value highlighted in blue. On top of each box the asterisks mark whether the mean of the distribution is significantly different from zero as indicated by a one‐sample t‐test (performed after averaging runs from the same subjects); ***p <.001, **p <.01, *p <.05

Convergent results were obtained with the CNP dataset (Figure 2b), yet with one exception. The most noticeable is the drop in performance of aCompCor50%, which showed a much higher median absolute value due to a distribution of Δrms(DVARS_NOISE) markedly shifted toward positive values, indicating greater DVARS during task than at rest. Such an inversion may be the result of an overaggressive denoising that may have overfitted the data.

To investigate the type and the time course of variance removed by different models, we compared, subject by subject, the FD series against the DVARS_GM series. Figure 3 shows the FD series from two typical high‐motion subjects (mFD_REST ∼0.2 mm, one for each dataset) alongside DVARS_GM series extracted from four denoising models plus a simple model with only trends and band‐pass regressors (BP, black line). Large FD‐concurrent fluctuations in BOLD intensity, which were prominent during rest epochs, were largely suppressed by 24RP regression. A further, albeit less marked, improvement was obtained by adding aCompCor and even more by switching to aCompCor50%. ICA‐AROMA showed a good but not consistent performance, occasionally failing to decouple the fluctuations in the two QC series (see e.g., volumes ∼150, ∼430, and ∼550 in Figure 3a, and volumes ∼125 in Figure 3b). On the contrary, fluctuations in BOLD intensity not ostensibly related to fluctuations in FD series, mostly present during task epochs (especially in the CF dataset), were effectively mitigated both by aCompCor‐based models and by ICA‐AROMA, while they were mainly unaffected by 24RP regression. Another noticeable feature is the suppression of DVARS_GM values under the baseline level occurring simultaneously with huge movements, which can be observed with 24RP regression and, even more, with aCompCor‐based pipelines but not with ICA‐AROMA (see for example volumes ∼150, ∼430, and ∼550 in Figure 3a). This kind of depression in DVARS series has already been reported (Hallquist, Hwang, & Luna, 2013) and may indicate the goodness of these kinds of models in removing BOLD signal fluctuations following head movements that heavily affect the entire brain. The effect, being particularly marked for aCompCor50%, may explain the change in the sign of Δrms(DVARS_GM) for the 24RP + aCompCor50% pipeline seen in the CNP dataset. Similar patterns can be seen in the other subjects. For each cohort, the series for the stillest subject and for an average‐moving subject are reported in Figures S5 and S6, respectively.

FIGURE 3.

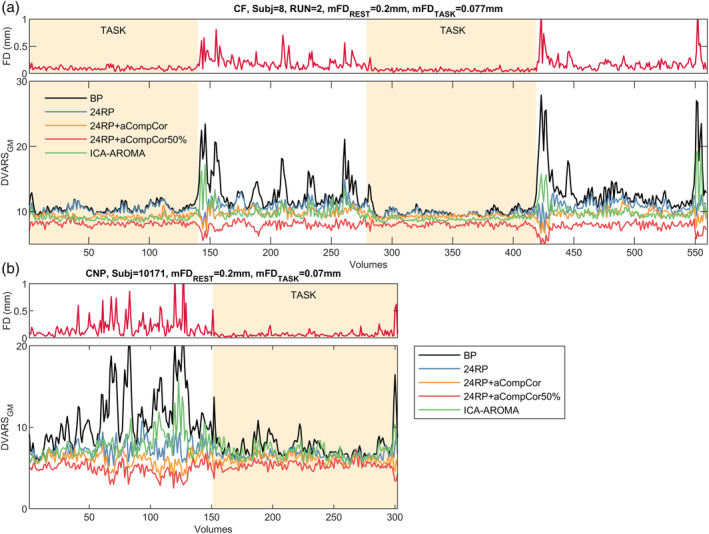
QC series for a representative high‐motion subject within the (a) CF and (b) CNP dataset. In each main panel, the first row shows the FD series, while the second row shows DVARS_GM series calculated after applying five different denoising models. BP (band‐pass, black line) is a denoising model containing only trends and band‐pass regressors

3.3. QC‐FC correlations

The results of the QC‐FC analyses, designed to assess the association between FC estimates and in‐scanner motion, are reported in Figure 4 for the CF dataset (similar results were obtained with the CNP dataset and are reported in Figure S7). The top panels (Figure 4a) show the distributions of the correlations between the FC estimates from the 53,628 edges (Gordon's parcellation) and the mFD, while the middle panels (Figure 4b) show the median values of the absolute distributions. Pipeline without GSR showed a large variability in QC‐FC correlations, with the mean of the distributions ranging from .36 to .0045. Methods based solely on realignment‐derived regressors (12RP and 24RP) showed the greatest association with motion, exhibiting distributions of QC‐FC correlations markedly shifted toward positive values and with high median absolute correlations, both indicating the presence of strong global motion‐related effects. These pipelines also showed a pronounced differential motion effect between conditions, with FC estimates from task epochs showing a higher association with motion compared to FC estimates from rest epochs. The use of signals extracted from tissue compartments improved results, with the extension of the benefits that depended on the type of signals extracted. PCA‐based methods (i.e., aCompCor models) outperformed the mean‐based method (i.e., 24RP + 8WM&CSF) both in centering the distributions and in decreasing the median absolute correlations. The best centering of the QC‐FC distributions, the lowest median absolute correlations as well as the best evenness across conditions was achieved with 24RP + aCompCor50%, which substantially outperformed the 24RP + aCompCor model, indicating that increasing the number of extracted PCs had a great impact on reducing motion artifacts. In general, ICA‐AROMA demonstrated intermediate performance between the two aCompCor models.

FIGURE 4.

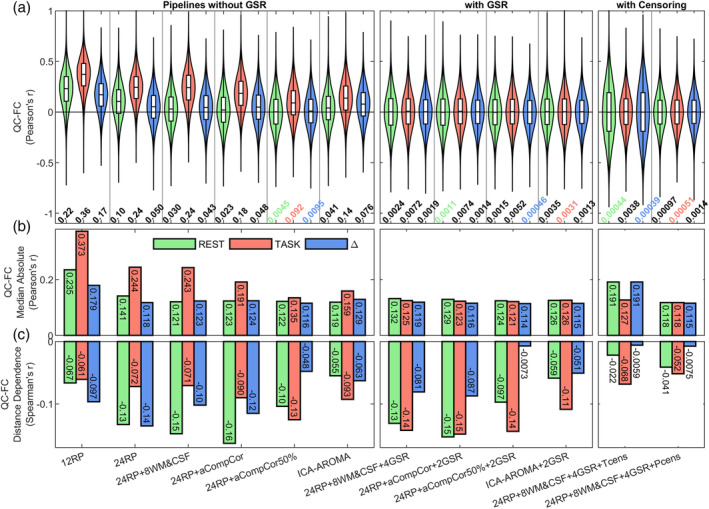
QC‐FC plots for evaluating the across‐subject relationship between motion (mFD) and connectivity estimates under different denoising strategies for the CF dataset. The top panels (a) show the distribution of QC‐FC correlations along with the absolute mean value of the correlations, aiming at quantifying the centering of the distributions. The middle panels (b) show the median value of the absolute QC‐FC correlations, which takes into account both the centering and the spread of the distribution. The bottom panels (c) show the Spearman's correlation between QC‐FC correlations and the Euclidean distance between pairs of nodes, indexing distance‐dependent artifacts. QC‐FC results are displayed for REST and TASK separately. For the task‐based change in FC (ΔFC = FC_task − FC_rest), the residual relationship with motion was evaluated with respect to the change in mFD (mFD = mFD_task − mFD_rest)

The addition of GSR was greatly effective in removing global motion artifacts. Regardless of the pipeline on which it was applied (tissue‐based average, PCA or ICA) or of the number of considered terms (2 or 4), GSR yielded almost perfectly centered QC‐FC distributions (|mean[r] <.0074) and median absolute correlations highly comparable across functional conditions (maximum difference across conditions = .013). Although the performance of the considered GSR‐based models were rather similar, 24RP + aCompCor50% + 2GSR ranked as the best pipeline according to the median absolute correlations.

Censoring applied on the 24RP + 8WM&CSF + 4GSR pipeline further improved the centering of the distributions (|mean[r]| <.0038 and <.0014, for T‐ and P‐censoring, respectively). Yet, T‐censoring, but not P‐censoring, produced a severe increase of the spread of the distributions for the resting condition and for the task‐based change, which resulted in inflated median absolute values (median |r| ∼.19). Finally, among all considered pipelines, P‐censoring yielded the lowest median absolute correlations (median |r| <.118).

Figure 4c shows the residual distance‐dependent artifacts, quantified as the Spearman's correlation between FC estimates and the Euclidean distance between pairs of nodes. For all considered models, the correlation was negative, indicating a higher association between FC and motion at short distance rather than at longer distances. Among pipelines without censoring, models that were effective at minimizing global artifacts were generally not as effective with distance‐dependent artifacts. No pipeline was associated with correlations both low and even across conditions, although, even in the worst case, the magnitude of the effect was modest (Spearman's r <.16). The addition of censoring markedly reduced distance‐dependent artifacts, irrespective of the censoring approach (T‐ or P‐censoring).

3.4. Δr plots

The effect of the most motion‐affected volumes on subject‐level FC estimates can be appreciated in the Δr plots (Figure 5). From the difference between FC estimates obtained from the least (FC_|LM) and the most (FC_|HM) motion‐affected volumes we explored the average motion effect across all pairs of nodes (distribution of means, Figure 5a) and distance‐dependent artifacts (Figure 5b).

FIGURE 5.

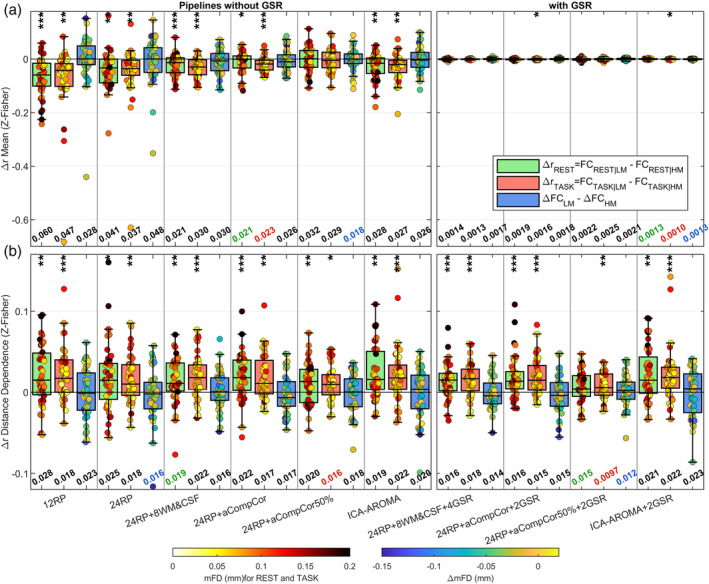
Censoring analysis (Δr) to evaluate residual artifacts in the CF dataset associated with the most moving volumes of each subject. For each run, Δr values were obtained by subtracting FC estimated using the least motion‐affected volumes (FC_|LM) from FC estimated using the most motion‐contaminated volumes (FC_|HM), where in both cases the top/bottom 20% of volumes were discarded. From the run‐specific Δr values, two quantities were extracted: (a) the mean, which indexes residual global artifacts, and (b) the distance‐dependent effect of motion of FC estimates, obtained by calculating the Spearman's correlation between Δr and the Euclidean distance between pairs. This analysis was run separately for rest (Δr _REST) and task (Δr _TASK), while the effect on task‐related change in FC was estimated by computing ΔFC_LM − ΔFC_HM, where ΔFC = FC_TASK − FC_REST. The box plots contain the distribution of the means (a) and distance‐dependent effects (b) across 40 points (20 subjects × 2 runs). Each data point is color‐coded based on mFD, for rest and task conditions, or based on ΔmFD, for the ΔFC comparison. At the bottom of each panel is reported the median absolute of the distribution, which takes into account both the centering and the spread of the distribution; the smallest median absolute values are color‐coded based on the functional condition. On top of each panel the asterisks mark whether the mean of the distributions are significantly different from zero as indicated by one‐sample t‐tests (performed after averaging the two runs); ***p <.001, **p <.01, *p <.05

The majority of the investigated pipelines yielded a distribution of means significantly (p <.05) shifted toward negative values (Figure 5a), indicating that high motion volumes increased FC estimates, irrespective of the distance between pairs of nodes. In general, the pipeline ranking was similar to that seen in QC‐FC correlations. Complex methods, such as PCA or ICA‐based strategies, yielded more centered and narrower distributions of means than realignment‐based models. Among pipelines without GSR, 24RP + aCompCor yielded the lowest median absolute values for both rest and task conditions (0.021 and 0.023, respectively), yet the distributions of means were still significantly shifted toward negative values. The only non‐GSR based approach that resulted in centered distributions of means with no significant group effect was 24RP + aCompCor50%. Using GSR greatly reduced the spread of the distributions, yielding approximately 10 times‐lower median absolute values. Among GSR‐based pipelines, 24RP + 8WM&CSF + 4GSR and 24RP + aCompCor50% + 2GSR resulted in no significant group effect.

The distribution of distance dependence was generally shifted toward positive values (Figure 5b), which indicates that high motion volumes differentially affected FC estimates depending on the internode distance, increasing short‐ more than long‐distance connections. Significant distance‐dependent effects were reported for all investigated pipelines. Considering the median absolute values, the distance dependence was generally mitigated by more effective strategies, at odds with what reported for the distance‐dependent effect of QC‐FC correlations (Figure 4c). The best median absolute values were obtained using GSR on 24RP + aCompCor50%.

3.5. Network modularity

Results of the community‐based analyses are reported in Figures 6 and 7 for the CF and CNP dataset, respectively. Each figure shows the subject‐specific modularity (Panels a) and the across‐subject similarity of the identified network partitions (Panels b). In general, these metrics exhibited patterns in agreement with those reported for QC‐FC correlations and Δr plots, indicating that the removal of motion artifacts was also associated with better sub‐network identifiability. Specifically, pipelines that were effective in mitigating global motion artifacts were associated with high modularity values and high similarities of the network partitions across subjects. Nevertheless, some deviations from such a general pattern were noted. The most notable exception was volume censoring that yielded worse results than the uncensored version (i.e., 24RP + 8WM&CSF + 4GSR) for all metrics (Figure 6). In particular, censoring produced a strong decrease in the across‐subject similarity of network partitions, with the effect that was more pronounced for P‐censoring, the most expensive approach in terms of tDoF (39 residual tDoF, see Table 1), than for T‐censoring. This result highlights the critical role of tDoF in the across‐subject reproducibility of network structures.

FIGURE 6.

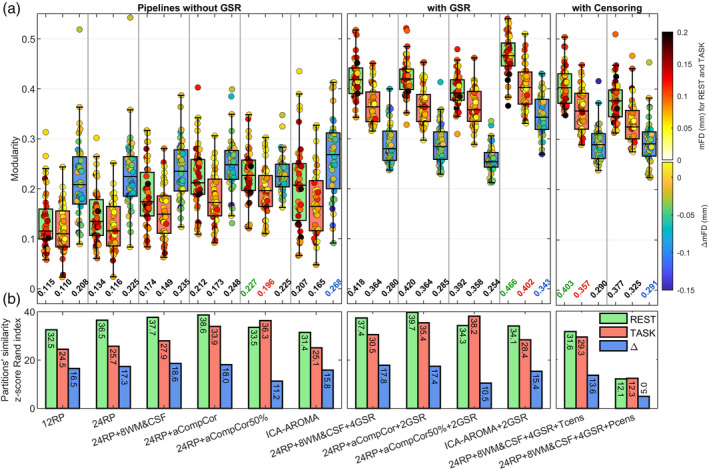
Results of the network modularity analysis for the CF dataset. (a) The box plots show the across‐subject distribution of modularity for each functional condition (REST and TASK) and for the differential condition (Δ = TASK − REST). The 40 runs (20 subjects × 2 runs) composing the box plots are color‐coded based on mFD, for rest and task conditions, or based on ΔmFD, for the Δ comparison. At the bottom of each box plot is reported the median of the distribution, with the largest values that are color‐coded based on the functional condition. (b) Partitions' similarity across subject, assessed via z‐score of Rand index

FIGURE 7.

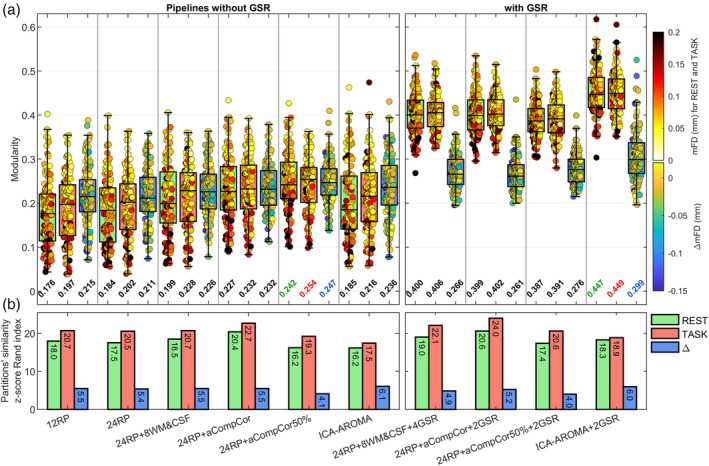
Results of the network modularity analysis for the CNP dataset. (a) The box plots show the across‐subject distribution of modularity for each functional condition (REST and TASK) and for the differential condition (Δ = TASK − REST). The 120 runs composing the box plots are color‐coded based on mFD, for rest and task conditions, or based on ΔmFD, for the Δ comparison. At the bottom of each box plot is reported the median of the distribution, with the largest values that are color‐coded based on the functional condition. (b) Partitions' similarity across subject, assessed via z‐score of Rand index

Among pipelines without GSR, aCompCor‐based models demonstrated relatively good results, particularly in maximizing modularity, with 24RP + aCompCor50% that showed the highest values in both rest and task conditions. Nevertheless, divergent results were seen when comparing the partitions' similarity of the aCompCor50% model between the CF (Figure 6) and CNP (Figure 7) dataset. Indeed, while in the CF dataset switching between aCompCor to aCompCor50% improved the partitions' similarity for the task condition, the same switching in the CNP dataset yielded reduced similarity for both functional conditions and for their difference. Such discrepancy between the datasets may once again be related to a low number of residual tDoF. Indeed, the shortest dataset, CNP, had ∼51 tDoF left after the application of 24RP + aCompCor50%, a much lower number compared to that of the longest dataset, CF (∼130 tDoF).

Regardless of the dataset, ICA‐AROMA pipelines exhibited mixed results. In combination with GSR, ICA‐AROMA showed the highest modularity, whereas without GSR it demonstrated intermediate performance in agreement with benchmarks based on motion‐related artifacts. Nevertheless, the partitions' similarity was relatively low, with values that were comparable to those of RP‐based models.

When evaluating partitions' similarity, it should be considered that noise could inflate such a metric in case motion‐induced connectivity patterns are reproducible across subjects. This possibility cannot be excluded a priori, especially considering that previous studies have shown motion to increase test–retest reliability of FC (Parkes et al., 2018; Shirer et al., 2015), probably due to a trait‐like nature of motion‐related noise. In order to mitigate such concerns, we recalculated the across‐subject partitions' similarity using a weighted average, where each pair of z‐score Rand index was weighted with 1/mFD, so that partitions estimated from high motion subjects were penalized. Results of the weighted similarity, reported in Figure S8, are in agreement with the unweighted variant, which suggests that partitions' similarity results are not driven by stereotyped patterns of motion.

3.6. Effect of motion on task‐associated changes in within‐network FC

Using the CF dataset, we previously reported a marked reduction of within‐network FC in several large‐scale networks following the execution of the working‐memory task (Tommasin et al., 2018). Here, the task‐associated reduction in within‐network FC was found to be modulated in magnitude depending on the denoising model applied, but it was always significantly different from zero (see Figure S9). In addition, the incremental censoring analysis showed the stability of the effect sign under progressive elimination of the most motion‐affected volumes. Results of such analysis applied to the best performing pipeline, 24RP + aCompCor50%, are reported in Figure S10, while in Figure 8 we show results for the 24RP + aCompCor pipeline, that, demanding fewer tDoF, allowed us to explore a wider range of censoring thresholds. Results are reported with and without GSR and show that the effect sign was always negative, irrespective of the censoring approach (T‐ or P‐censoring). Not only the sign was preserved, but also the relative magnitude of the effect among networks was reasonably stable. In P‐censoring mode, Δwithin‐network FC tended toward zero as soon as the tDoF approach zero. In T‐censoring mode, the progressive elimination of the subjects who moved most highlighted the reduction of Δwithin‐network FC even at very low FD thresholds, ruling out the possibility that the effect was driven by motion.

FIGURE 8.

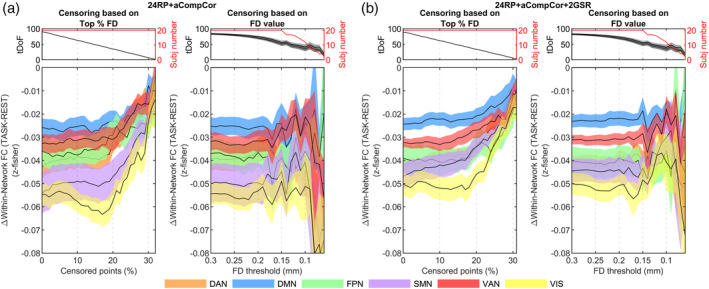
Incremental censoring analysis for within‐network FC considering models (a) RP24 + aCompCor and (b) RP24 + aCompCor + 2GSR. In each panel, the left plot shows a P‐censoring analysis while the right plot a T‐censoring analysis. In P‐censoring an equal number of volumes were excised from rest and task conditions ensuring condition comparability in terms of tDoF, yet at the expense of removing potentially good volumes in the task condition. In T‐censoring a more efficient data cleaning comes at the expense of variable tDoF among conditions and, in case of severe thresholds, at the progressive elimination of subjects with the highest motion. For each network, the mean across subjects of FC is shown as a black line along with shades representing the standard error of the mean (SEM), color‐coded based on the network. Likewise, tDoF for the T‐censoring variant are represented with the mean and SEM (light‐gray shade for task, darker for rest). DAN, dorsal attention; DMN, default mode, FPN, frontoparietal; SMN, somatomotor; VAN, ventral attention; and VIS, visual network

4. DISCUSSION

The current study evaluated the efficacy of commonly adopted denoising pipelines in balancing the residual motion‐related artifacts between functional conditions differently prone to in‐scanner motion. First, we confirmed the marked difference in subjects' motion between resting epochs and epochs of continuous performance of either a working‐memory task or a stop‐signal task, with task epochs characterized by a minor number of bulky movements and lower average motion. Second, we found that many denoising pipelines performed poorly according to the selected benchmarks, displaying either high association between motion and FC or unbalanced residual motion artifacts between functional conditions. The inclusion of the global signal among confounding variables substantially improved many benchmarks and virtually equalized global motion artifacts between conditions. Among no GSR‐based pipelines, aCompCor‐based models, particularly aCompCor50%, performed well across nearly all benchmarks. However, pipelines that were effective in mitigating global motion artifacts were associated with higher distance‐dependent artifacts compared with less efficient pipelines. Censoring was the only approach that was effective in mitigating distance dependence, yet at the expense of a great loss of tDoF accompanied by reduced network identifiability and similarity across network partitions. Moreover, in case the number of censored volumes was not balanced between rest and task, censoring increased the correlation between motion and task‐based changes in FC. Finally and most importantly, we showed the robustness against head motion of a common result in task‐based FC studies, namely the reduction of within‐network FC during task performance. These findings are discussed in detail in the following sections.

4.1. Realignment‐ and tissue‐based models

The simple 12RP model was overly ineffective, showing strong global artifacts as highlighted by QC‐FC correlations and Δr plots. The expansions of 12RP, that is, models 24RP, 24RP + 8WM&CSF and the aCompCor‐based models, yielded the same pattern across all considered benchmarks, with each expansion generating some benefits with respect to the previous ones. The first great improvement is obtained by expanding the 12 motion‐based model with its squared terms that model nonlinearities in the motion‐BOLD relation and remove the dependency on the sign of motion‐derived parameters (Satterthwaite et al., 2013). The improvement generated by this model is in agreement with previous reports (Satterthwaite et al., 2013; Yan et al., 2013) and, although the increase in effectiveness may be dependent on the amount of motion in the dataset, the modest reduction in tDoF (12 additional explanatory variables compared with 12RP), supports its use as default set of realignment‐based regressors. Adding mean tissue‐based signals with expansion terms (i.e., 8WM&CSF) to the 24RP model yielded a minor but consistent improvement, which, however, was outranked by the use of aCompCor. Of note, 24RP + 8WM&CSF and 24RP + aCompCor pipelines have a similar cost in terms of tDoF, being composed of 8 and 10 confounding signals extracted from tissue compartments, respectively. Thus, results from our multiple‐condition datasets suggest that exploiting signals from tissue compartments that encompass various orthogonal sources of variance is both more effective and more efficient than accounting for phase lags (first derivatives) and nonlinear effects (squared terms) in tissue‐mean signals.

Despite each of the above‐described pipelines provided incremental benefits in reducing global motion artifacts, they all showed a relatively high differential efficacy in cleaning the two functional conditions, especially in the CF dataset. The effect was markedly reduced by using the 24RP + aCompCor50% pipeline, that is, by increasing the number of PCs used as confounding variables. Indeed, among pipelines without GSR, the 24RP + aCompCor50% model provided the best results in nearly every benchmark, particularly in minimizing global motion artifacts, in balancing the residual artifacts across conditions and at maximizing metrics based on network identifiability. Yet, the latter effect was not seen in the CNP dataset, where the application of aCompCor50% resulted in reduced across‐subject partitions' similarity compared to the aCompCor variant. The discrepancy between the two datasets is likely to be tDoF related. Indeed, aCompCor50% had a great cost in terms of tDoF, which resulted in a poor residual nominal tDoF for the CNP but not for the CF dataset. In light of such results, the application of aCompCor50%, despite its good efficacy in removing global motion artifacts, should be evaluated in concert with the consumed and available tDoF, especially in short acquisition protocols.

One interesting feature that emerged from the inspection of QC‐FC plots in the CF dataset (Figure 4) is that the above‐described condition‐dependent pipeline efficacy fostered the functional condition most affected by motion, that is, the rest condition. While the lack of physiological recordings hamper any firm conclusion, we speculate that the effect may be related to condition‐dependent respiratory fluctuations that are differentially coupled to motion. Indeed, in the case of a stronger coupling at rest than at task, regression of realignment‐derived parameters may remove more respiration‐related variance at rest than at task.

4.2. aCompCor‐based pipelines

As highlighted above, aCompCor‐based pipelines were found to be superior to the mean‐tissue based method in every considered benchmark. The strength of the aCompCor approach lies in its data‐driven capability of defining confounding variables encompassing multiple orthogonal sources of variance, which, compared to the mean signals, are more likely to explain the different types of physiological noise in the two functional conditions. Indeed, the striking difference in head motion between task and rest epochs may result in condition specific patterns of BOLD signal change that may be inadequately represented by solely mean signals.

We found that the number of PCs used as regressors played a critical role. Indeed, the aCompCor variant, which used a total of 10 confounding signals, was striking outperformed by the aCompCor50% variant, which used a much larger number of confounders (around 61 and 35 for CF and CNP, respectively). Such result indicates that five PCs for tissue type are not sufficient to evenly clean the datasets. While we cannot generalize the statement to different dataset types, we suspect that the need for a large set of PCs in order to effectively minimize motion artifact is due to the specific complexity of multiple‐condition experiments or of long‐acquisition scans. Indeed, this type of experiments tends to be affected by a richer spectrum of physiological noise compared to single‐condition or short‐acquisition scans. Nonetheless, a clear advantage of aCompCor50% is the data‐driven selection of the number of PCs, which makes the method particularly flexible, being able to tune the number of regressors according to the specific physiological noise within the data.

Compared to previous evaluation studies, we optimized aCompCor by extracting PCs from tissue signals orthogonalized with respect to the confounding variables that composed the model, yielding a set of PCs with a greater noise prediction power compared to the standard variant. The benefits of this optimization are illustrated in Figure S11 for the aCompCor50% variant of the CF dataset. Figure S11a–c shows QC‐FC plots for the standard aCompCor50% approach and for two different optimizations obtained by preorthogonalizing WM and CSF signals with respect to either the sine/cosine basis functions (i.e., filtering the signals before computing PCs) or to the sine/cosine basis functions plus realignment‐derived variables (the actual model used for pipeline comparisons). Both preorthogonalization schemes produced benefits compared to the standard approach, with the complete orthogonalization yielding the best results, particularly in shifting the QC‐FC correlations toward zero. A second and critical benefit of such an optimization is specific to the aCompCor50% variant. When the optimization was used, we saw a marked reduction of the number of extracted PCs, that is, a reduction of the components required to fulfill the 50% variance criteria, as illustrated in Figure S11d. This result shows that the majority of the components extracted without the optimization explained variance that was already accounted for by the other regressors within the model, particularly by the sine/cosine basis functions. The number of used PCs has a direct impact on the nominal tDoF, which is a critical parameter particularly in short acquisitions, such as in the CNP dataset. Indeed, we note that without the optimization we could not perform aCompCor50% on the CNP dataset, since without the gain in residual tDoF provided by the preorthogonalization scheme the denoised matrix was not invertible. In summary, the optimization we adopted increased both the efficacy of the method and, in the case of the aCompCor50% variant, its efficiency. While the optimized approach was first introduced with connectivity toolbox (Whitfield‐Gabrieli & Nieto‐Castanon, 2012), research in denoising optimization surprisingly has not explored it thus far (Ciric et al., 2017; Muschelli et al., 2014; Parkes et al., 2018; Shirer et al., 2015). Our results encourage the use of the optimized aCompCor approach also in resting‐state experiments. We provide code to perform it in Matlab (https://github.com/dmascali/fmri_denoising).

4.3. ICA‐AROMA

ICA‐AROMA demonstrated intermediate performance, ranking between the 24RP + 8WM&CSF and 24RP + aCompCor50% pipelines for most of the benchmarks, but it performed poorly according to DVARS‐based outcomes. Even small differences in head motion resulted in greater rms(DVARS_NOISE) at rest than at task (see green dots in Figure 2). From the inspection of QC series (Figure 3, and Figure S5 and S6), ICA‐AROMA effectively reduced signal changes during task epochs, performing better than the 24RP model, but was less effective at suppressing motion‐related signal changes occurring during resting epochs, especially those occurring in coincidence with bulky movements.

ICA‐AROMA is appealing because it uses a conservative denoising approach that is achieved by avoiding direct regression of realignment‐derived parameters and by using partial regression in a model containing both “good” and “bad” ICs. These precautions mitigate the possibility of removing signal of interest that may covary with confounding variables. Thus, it might be possible that ICA‐AROMA preserved signals of interest otherwise removed by other pipelines, possibly leading to a physiological task‐induced reduction of rms(DVARS). However, we ruled out such possibility since Δrms(DVARS) was calculated in a noise‐only mask where no neuronal meaningful difference is expected.

ICA‐AROMA was also associated with a considerable loss of tDoF, particularly for the CF dataset where the number of explanatory variables matched that of 24RP + aCompCor50% (an average of ∼82 ICs were classified as noise), while for the CNP dataset the number was similar to that of 24RP + 8WM&CSF (∼30 noise‐classified ICs). These numbers are at odds with previous evaluation studies focused on resting‐state data, where an average of ∼10 to 20 ICs were classified as noise in ∼5 to 8 min‐long datasets (Ciric et al., 2017; Parkes et al., 2018). The discrepancy is mainly related to the different run lengths, being the CNP and CF datasets roughly two and four times longer than those of previous studies, respectively. Indeed, while the number of ICs classified as noise naturally tends to increase with the complexity of the structured noise, it also increases as a function of the number of components in which the data are decomposed (due to the more likely splitting of noise ICs in sub components with similar features). The algorithm for automatic dimensional estimation used in ICA‐AROMA (which is the same of MELODIC, FSL, Beckmann & Smith, 2004; Jenkinson, Beckmann, Behrens, Woolrich, & Smith, 2012) tends to decompose longer datasets in higher dimensionalities, thus explaining the discrepancy with previous studies. Setting an a priori dimension for data decomposition may help in reducing the loss of tDoF in long or short‐TR experiments, yet further research is needed to both determine the optimum decomposition number and to evaluate the ensuing classification performance. As an alternative approach to preserve tDoF, it is possible to divide the acquisition in epochs and then running ICA‐AROMA on each epoch separately, thereby reducing the series length from 20 to 5 min. We explored this possibility in a supplementary analysis, the results of which are shown in Figure S12. ICA‐AROMA ran on single‐epochs reduced the average number of noise classified components from ∼82 to 60. As a consequence of the less aggressive denoising, the efficacy in removing motion‐related variability was slightly reduced, yet the across‐sample partitions' similarity was increased for the resting and differential condition. While we did not find strong evidence to favor one approach over the other, they should be carefully evaluated in different acquisition schemes, as with shorter TR or longer epochs/runs.

4.4. Global signal regression

In line with previous reports (Ciric et al., 2017; Parkes et al., 2018; Yan et al., 2013), the inclusion of the whole‐brain signal markedly reduced global motion artifacts. Additionally, we showed that GSR is particularly effective in balancing the residual motion artifacts across the two functional conditions, even when applied to pipelines that per se showed a great differential residual artifacts (e.g., 24RP + 8WM&CSF). Despite its clear efficacy, GSR remains controversial (see e.g., Murphy & Fox, 2017). One of the main arguments concerns the fact that the global signal is a mixture of neuronal and non‐neuronal signals, with their relative contribution that depends on the amount of noise in the data. As a consequence of the unbalanced noise level between task and rest conditions, it is possible that GSR removed more neuronal signal at task than at rest, introducing artifactual differences in FC between conditions. While this possibility cannot be ruled out by our study, the fact that both the modularity and the similarity among network partitions were maximized by the use of GSR (Figures 6 and 7), partially mitigates the concern. A second caveat that must be considered when adopting GSR is that the ensuing distribution of correlations, among all possible voxels, becomes centered to zero. Depending on the investigated metrics, such redistribution of correlations may have important repercussions on result interpretations. In our data, considering the task‐based changes in within‐network FC (Figure 8), the addition of GSR reduced the standard error of the mean but did not substantially affect the absolute and the relative magnitude of the effect among networks. The similarity of the within‐network results, with or without GSR, is likely to be due to the large networks used to compute the metric. More spatially localized metrics may be more influenced by the redistribution of correlations by GSR.

4.5. Distance dependence

Depending on the denoising strategy, our data showed small to modest distance‐dependent artifacts. Interestingly, among pipelines without censoring, the application of models that were effective at minimizing the global (i.e., spatially delocalized) association between mFD and FC (i.e., QC‐FC metric; Figures 4a,b) resulted in an increased distance dependence between motion and connectivity estimates (Figure 4c). In other words, the residual association between motion and connectivity was more distance‐dependent after the application of effective denoising strategies. For instance, one of the pipelines that showed the smallest QC‐FC distance‐dependence in both functional conditions was the simple 12RP model, which ranked as the worst model for removing global artifacts. These results suggest that distance‐dependent artifacts are at least partially a consequence of a fragmentary denoising. Indeed, while head motion has a tendency to impact short‐ more than long‐distance connections (e.g., Satterthwaite et al., 2013), a denoising model performing differentially between nearby and distant connections can introduce similar artifacts, in the same way as GSR has been implied to exacerbate distance‐dependence (Ciric et al., 2017). This effect was particularly evident when using signals from tissue compartments or when using GSR, however, it was also evident when expanding the 12RP set to include the squared terms. Overall, motion‐related variance with a spatially variable profile was not effectively represented by the evaluated confounding variables, that, with the exclusion of ICA‐AROMA, were all representative of large‐scale effects (volume‐wise realignment parameters or signals from tissue compartments). One class of methods that we did not consider but that deserves further consideration is that of voxel‐wise confounders. Voxel‐wise motion parameters (e.g., Yan et al., 2013) or locally derived confounding signals (e.g., Jo et al., 2010), although have shown moderate efficacy in removing global artifacts (Ciric et al., 2017; Yan et al., 2013), have the potential to target distant‐dependent artifacts and may benefit from the association with methods that are more effective at minimizing global artifacts, such as GSR or CompCor.

In our study, the only approach that was effective at minimizing both spatially delocalized and distance‐dependent artifacts was volume censoring, irrespective of the modality (P‐ or T‐censoring). However, censoring was greatly expensive in terms of tDoF, with important repercussions on FC estimates and network identifiability.

4.6. Volume censoring

Excising volumes to decrease the impact of motion on FC has the side effect of decreasing the accuracy of FC estimates, increasing the likelihood of extreme values (Yan et al., 2013). When the number of excised volumes is variable across the sample or across conditions, censoring may introduce a bias due to the different accuracy of FC estimates. To explore such a potential effect, we compared the commonly used censoring based on thresholding FD series (T‐censoring) to a censoring approach that constrains the amount of excised volumes to be equal across both subjects and conditions (P‐censoring). While both censoring variants were effective at improving the centering of QC‐FC distributions (Figure 4a) and at minimizing the distance‐dependent effect (Figure 4c), they behaved differently with respect to the spread of the QC‐FC distributions. In particular, T‐censoring, but not P‐censoring, increased the spread of the distribution and consequently the median absolute value (Figure 4b) for the resting condition and for the task‐based change. In addition to affecting the task‐based change in FC, such bias may alter any other behavioral correlation that shares variability with motion. The bias is mainly driven by few runs showing the highest mFD during the rest condition (see runs with mFD_rest above ∼0.175 mm in Figure 1c), that after T‐censoring were characterized by FC estimates with a wider distribution. Previous studies have shown that the major benefit of adopting censoring comes from a stringent selection of subjects (Parkes et al., 2018). While discarding subjects may be feasible in resting‐state experiment where large cohort of data are publicly available, this may not be viable for task‐based experiments, which are less common and generally require more complex and long acquisition protocols (in our study, each run lasted 25 min). Therefore, discarding potentially valid acquisitions may not be an option in this kind of studies. Notably, despite the subjects that drove this bias were outliers with respect to the number of excised volumes, after censoring they had an adequate number of volumes for FC computation, as recommended in the field (Van Dijk et al., 2010).

Irrespective of the bias introduced by the variability in the number of excised volumes, censoring was highly expensive in terms of tDoF, particularly when using P‐censoring. The detrimental effect of reducing the number of available tDoF was evident in the reduced network identifiability (Figure 6). Indeed, both censoring modalities reduced the modularity and the similarity of across‐sample network partitions. The latter was particularly affected by P‐censoring (the most tDoF‐consuming modality), showing a similarity across partitions that was even lower than that of the worst performing pipeline (i.e., 12RP). The critical role of tDoF was also evident in the incremental censoring analysis for the task‐based change in within‐network FC (Figure 8), which tended sharply to zero as soon as tDoF went below ∼30.

Overall, our findings suggest adopting censoring with caution in task‐based experiments. Censoring may be a sensible approach when the scientific goals dictate the use of metrics or comparisons that are particularly sensitive to distance‐dependent artifacts. In this case, to alleviate the side effects of censoring, researchers may use more lenient thresholds. Indeed, in a supplementary analysis we found that the mitigation of distance‐dependent artifacts was also achieved with less aggressive threshold, as an FD threshold of 0.3 mm or discarding the 15% of the most moving volumes (Figure S13), sparing a considerable number of tDoF. On the contrary, when the scientific goals dictate the use of metrics that are not sensitive to distance‐dependent effects (e.g., within‐network FC), we discourage the use of censoring, so to preserve tDoF and, consequently, to increase the accuracy of FC estimates.

4.7. Considerations on the denoising framework

A critical aspect in BOLD data cleaning is the order and method used for frequency filtering, nuisance regression, and volume censoring. In the current work, we opted for a single linear regression model that performs the three steps simultaneously, as recommended in (Jo et al., 2013). The simultaneous approach provides several benefits. When censoring is used, the simultaneous denoising avoids spreading motion‐contaminated signals back and forward in time as in the case of filtering followed by volume deletion (Carp, 2013). Moreover, the simultaneous denoising provides an upper limit on the number of censored volumes, because the estimation of the model is constrained by the nominal tDoF; namely, it is not possible to obtain a residual series when there are fewer observations (i.e., time points, excluding censored volumes) than model parameters (i.e., confounding variables). While the tDoF of the linear model do not reflect the effective tDoF (e.g., they do not take into account the autocorrelation structure of the data), still, they provide a useful tool for decreasing the risk of using statistically meaningless time series. Regardless of the use of censoring, the simultaneous approach has shown to outperform the popular regression‐followed‐by‐filtering in attenuating nuisance related variability and in removing motion‐related fluctuations in resting‐state data (Hallquist et al., 2013). The advantage is possible because the simultaneous approach mitigates the frequency mismatch existing between nuisance variables and the nuisance‐induced variability in the MR signal.

It is important to note that when censoring is not used, the simultaneous approach is equivalent to a two‐step processing in which confounding signals and MRI data are filtered separately, and then nuisance regression is performed on the filtered series (Hallquist et al., 2013). Despite the numerical equivalence of the two methods, the two‐step method offers the possibility of using different filtering strategies, such as IIR filters, while the simultaneous approach is restricted to sinusoidal‐based filters (equivalent to FIR filters). Nonetheless, we advise the use of the simultaneous (1‐step) approach to take into account the residual nominal tDoF, even when censoring is not performed.

The use of MRI data acquired during multiple functional conditions allows for two different data‐cleaning strategies: either denoising the functional run as a whole (“full‐run” method), or denoising each functional condition separately by splitting the run in its composing epochs (“single‐epoch” method). In the current work, we opted for the former strategy, since the latter required a number of explanatory variables that was not compatible with censoring pipelines. Indeed, one key difference between the two approaches is the number of confounding variables, which is n times greater when splitting the run, where n is the number of epochs. For instance, in the CF dataset, the RP24 set requires 24 confounding variables in the full‐run method, whereas 96 are required in the single‐epoch method (an RP24 set for each epoch). The single‐epoch strategy has the potential to provide a better control for nuisance related variability, yet at the cost of reducing FC sensitivity due to the marked loss in tDoF. Indeed, in a supplementary analysis we compared the two methods using noncensoring based pipelines and found a marked reduction in the residual tDoF, ranging from −19% to −62%. This reduction was accompanied with lower QC‐FC correlations (average median absolute change = −9 ± 10%, min = −37%, max = 3%), indicating a more effective cleaning of motion‐related variability. However, this benefit was accompanied with a strong reduction in the across‐sample partitions' similarity (average z‐score Rand index change = −42 ± 20%, min = −77%, max = 0%), indicating lower sensitivity to FC. The only exception was ICA‐AROMA, where the lower dimensional decomposition (due to the division of the run, see Section 4.3 for details), played a major role compared to the expansion of the 2WM&CSF set. In summary, when multiple conditions are collected within the same functional run, we advocate the use of the “full‐run” approach for sparing tDoF and increasing FC sensitivity.

4.8. Limitations

One important limitation of the present study is the impossibility of disentangling genuine task‐related changes in connectivity from those arising from task‐related changes in head motion. Since we lack any ground truth regarding the effect of the task on FC, we based most of our evaluation on detecting residual motion artifacts. Exploiting the paired design of the study, we used as an indicator of effective cleaning a low and balanced residual artifact between the two functional conditions. Nonetheless, the employed benchmarks have limitations. QC‐FC analyses are only capable of identifying linear relationships between motion and connectivity estimates; for instance, they might fail if motion results in a ceiling effect on connectivity. Moreover, in comparing rest and task, QC‐FC analyses may suffer from the slight difference in across‐sample variance between rest and task motion, with the higher variability at rest that is more likely to explain variance in connectivity. The information contained in Δr plots is also limited, since the plots convey insights solely about the selected censored volumes. Pushing further the threshold, so that even volumes characterized by smaller amounts of motion are excised, might have disclosed further residual artifacts. While such a strategy was not feasible due to the limited number of tDoF, we partially mitigated this limitation by increasing the sensitivity of Δr plots (i.e., comparing the “best” against the “worst” volumes).

The entire set of denoising strategies evaluated in this work was complemented with bandpass filtering. We did not explore different cutoff frequencies nor the possibility of removing the lowpass filter. Indeed, while lowpass filtering has been shown to mitigate motion‐related variability (e.g., Satterthwaite et al., 2013), it has also shown to remove neuronal‐related signals occurring beyond typical cutoff frequencies (Chen & Glover, 2015; Niazy, Xie, Miller, Beckmann, & Smith, 2011), which is suggestive of a general trade‐off between adequately modeling noise and preserving neuronal‐related signals. In addition, in the current work, FC was estimated by calculating Pearson's correlations between pairs of nodes, but other techniques, such as partial correlation or ICA‐based methods, are available. The choice of the method for extracting FC can strongly interact with the optimal frequency range for filtering, since different methods have different sensitivity to spurious variance and different requirements in terms of tDoF. Further studies are needed to define the optimal trade‐off for frequency filtering under different experimental conditions.

Finally, while we explored an extensive set of denoising strategies including many popular techniques, we did not fully cover the copious assortment of denoising methods developed so far. Many of these approaches (reviewed in Caballero‐Gaudes & Reynolds, 2017) deserve further consideration.

4.9. Conclusion

In this work, we evaluated popular denoising strategies in the challenging pursuit of balancing residual‐motion artifacts between steady‐state cognitive conditions that are inherently affected by different amounts of motion. Exploiting a paired design, where the same subject undergoes two levels of a single treatment, we underscored the inefficacy of many approaches, especially those based exclusively on realignment‐derived parameters. The best strategy employed a combination of realignment‐derived parameters along with aCompCor50% signals, which further benefited from GSR. Importantly, we encourage the use of the optimized aCompCor to obtain the best from this approach. We also advise to use censoring with caution in these types of experiments since it has the potential to introduce additional biases. Furthermore, censoring provided minor benefits compared to GSR and came at the great cost of reduced network identifiability.

These results provide important indications for denoising data composed of multiple steady‐state conditions (see Table 3), yet many of these observations naturally extend to the more common resting‐state fMRI. Importantly, while this study was not specifically designed to deal with patients, it finds a natural albeit indirect application to the identification of best practices in studies contrasting populations intrinsically affected by different degrees of motion, as is the case of many neurological diseases. Moreover, our conclusions should be carefully evaluated in the context of dynamic FC studies, where the use of a much short temporal scale (from 30 to 60 s) poses great challenges to specificity and sensitivity. Finally, as highlighted in similar studies, our results demonstrate further the importance of inspecting, and possibly reporting, the residual relation between motion and FC.

TABLE 3.

Overview of major findings and recommendations

Denoising framework
	Recommendations	Benefits
Filtering/regression/censoring	Use a linear regression model to perform all steps simultaneously	Better control for nuisance‐related variability (see Hallquist et al., 2013) Better control for residual nominal tDoF Provides an upper limit to the number of censored volumes
Treatment of multiple epochs within the same functional run	Avoid splitting the functional run in epochs	Denoising the whole run reduces the number of confounding variables, increasing network identifiability metrics
Nuisance mask creation	Extract masks from high‐resolution segmentation maps using conservative probability thresholds and multiple erosion cycles	Prevents contamination from gray matter voxels (see Power et al., 2017). Otherwise, the extracted signals might behave like GSR

Pipeline evaluation
Pipelines	Strengths	Weaknesses	Recommendations
GSR (e.g., 24RP + 8WM&CSF + GSR)	The most effective strategy for balancing motion‐related effects across functional conditions	GSR remains controversial
Censoring (24RP + 8WM&CSF + GSR + T/P‐cens)	The best approach for controlling distance dependent artifacts	Reduced network identifiability metrics, especially with P‐censoring T‐censoring is prone to introduce additional biases	If possible, exclude high‐moving subjects (see Parkes et al., 2018) Distance‐dependent artifacts can also be controlled with lenient thresholds (FDjenk >0.2; see figure S13)
aCompCor50% (24RP+ aCompCor50%)	Best non‐GSR based pipeline	It might overfit the data, depending on the number of observations.	Use the preorthogonalization procedure to increase the noise prediction power and to reduce the number of extracted components (see Figure S11)
aCompCor (24RP+ aCompCor)	Lower number of consumed tDoF compared to aCompCor50%		Use the preorthogonalization procedure to increase the noise prediction power (see Figure S11)
ICA‐AROMA	Good control of motion‐related artifacts No direct regression of motion parameters Nonaggressive denoising	Depending on the number of observations, it might require a considerable number of tDoF	In long multiple‐condition experiment, evaluate the possibility of performing ICA‐AROMA in each epoch separately in order to reduce the number of noise‐classified components (see Figure S12)
RP (RP12, RP24)	Effective in combination with other strategies	It might remove true signals covarying with head motion	Prefer 24RP over 12RP

CONFLICT OF INTEREST

The authors declare no potential conflict of interest.

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are either available in the OpenFMRI database at https://openneuro.org/datasets/ds000030/ (CNP dataset) or are available from the corresponding author upon reasonable request (CF dataset).

Supporting information

Appendix S1: Supporting Information

Mascali D, Moraschi M, DiNuzzo M, et al. Evaluation of denoising strategies for task‐based functional connectivity: Equalizing residual motion artifacts between rest and cognitively demanding tasks. Hum Brain Mapp. 2021;42:1805–1828. 10.1002/hbm.25332