Molecular switch architecture determines response properties of signaling pathways

Significance

Molecular switches are key components of intracellular signal-transduction pathways. Experimental work has established that the activity of molecular switches is regulated by three distinct mechanisms: 1) activation, 2) derepression, and 3) concerted (activation and derepression). However, it remains unclear how the choice of signaling mechanism influences the performance properties of the switch. Here, we characterize each switch design in terms of dose–response relationship, response time, and abilities to process upstream fluctuations. Our results highlight unique features of each mechanism and provide insight into the operating principles that underlie many different signaling pathways.

Abstract

Many intracellular signaling pathways are composed of molecular switches, proteins that transition between two states—on and off. Typically, signaling is initiated when an external stimulus activates its cognate receptor that, in turn, causes downstream switches to transition from off to on using one of the following mechanisms: activation, in which the transition rate from the off state to the on state increases; derepression, in which the transition rate from the on state to the off state decreases; and concerted, in which activation and derepression operate simultaneously. We use mathematical modeling to compare these signaling mechanisms in terms of their dose–response curves, response times, and abilities to process upstream fluctuations. Our analysis elucidates several operating principles for molecular switches. First, activation increases the sensitivity of the pathway, whereas derepression decreases sensitivity. Second, activation generates response times that decrease with signal strength, whereas derepression causes response times to increase with signal strength. These opposing features allow the concerted mechanism to not only show dose–response alignment, but also to decouple the response time from stimulus strength. However, these potentially beneficial properties come at the expense of increased susceptibility to upstream fluctuations. We demonstrate that these operating principles also hold when the models are extended to include additional features, such as receptor removal, kinetic proofreading, and cascades of switches. In total, we show how the architecture of molecular switches govern their response properties. We also discuss the biological implications of our findings.

Several molecules involved in intracellular signaling pathways act as molecular switches. These are proteins that can be temporarily modified to transition between two conformations, one corresponding to an on (active) state and another to an off (inactive) state. Two prominent examples of such switches are proteins that are modified by phosphorylation and dephosphorylation and GTPases that bind nucleotides. For phosphorylation–dephosphorylation cycles, it is common for the covalent addition of a phosphate by a kinase to cause activation of the modified protein. A phosphatase removes the phosphate to turn the protein off. In the GTPase cycle, the protein is on when bound to guanosine triphosphate (GTP) and off when bound to guanosine diphosphate (GDP). The transition from the GDP-bound state to the GTP-bound state requires nucleotide exchange, whereas the transition from the GTP-bound to the GDP-bound state is achieved via hydrolysis of the $\gamma$ phosphate on GTP. The basal rates of nucleotide exchange and hydrolysis are often small. These reaction rates are increased severalfold by Guanine Exchange Factors (GEFs) and GTPase Accelerating Proteins (GAPs), respectively (1, 2).

A signaling pathway is often initiated upon recognition of a stimulus by its cognate receptor, which then activates a downstream switch. In principle, a switch may be turned on by three mechanisms: (a) activation, by increasing the transition rate from the off state to the on state; (b) derepression, by decreasing the transition rate from the on state to the off state; and (c) concerted activation and derepression. Examples of these three mechanisms are found in the GTPase cycles in different organisms. In animals, signaling through many pathways is initiated by G-protein-coupled receptors (GPCRs) that respond to a diverse set of external stimuli. These receptors act as GEFs to activate heterotrimeric G proteins (3–6). Thus, pathway activation relies upon increasing the transition rate from the off state to the on state. There are no GPCRs in plants and other bikonts; the nucleotide exchange occurs spontaneously, without requiring GEF activity (7–9). G proteins are kept in the off state by a repressor such as a GAP or some other protein that holds the self-activating G protein in its inactive state. In this scenario, the presence of a stimulus results in derepression, i.e., removal of the repressing activity (10–12). Concerted activation and dererpression occur in the GTPase cycle of the yeast mating-response pathway (13, 14), in which the inactive GPCRs recruit a GAP protein and act to repress, whereas active receptors have GEF activity and act to activate. Thus, perception of a stimulus leads to concerted activation and derepression by increasing GEF activity while decreasing GAP activity.

These three mechanisms of signaling through molecular switches also occur in many other systems. For example, the activation mechanism described here is a simpler abstraction of a linear signaling cascade, a classical framework used to study general properties of signaling pathways (15–19), as well as to model specific signaling pathways (20–22). While derepression may seem like an unusual mechanism, it occurs in numerous important signaling pathways in plants (e.g., auxin, ethylene, gibberellin, and phytochrome), as well as gene regulation (23–27). In many of these cases, derepression occurs through a decrease in the degradation rate of a component instead of its deactivation rate. Concerted mechanisms are found in bacterial two-component systems, wherein the same component acts as kinase and phosphatase (28–35).

Many previous studies have focused on the properties of a single switch mechanism without drawing comparisons between the three potential ways for initiating signaling. For example, the classical Goldbeter–Koshland model studied zero-order ultrasensitivity of an activation mechanism (15). Further analyses examined the effect of receptor numbers (36–38), feedback mechanisms (39, 40), and removal of active receptors via endocytosis and degradation (41, 42). Similarly, important properties of the concerted mechanism have been elucidated, such as its ability to perform ratiometric signaling (13, 14), to align dose responses at different stages of the signaling pathway (43), as well as its robustness (29, 44). The derepression mechanism is relatively less studied. Although there are models of G-signaling in Arabidopsis thaliana (45–47), these models have a large number of states and parameters and do not specifically examine distinct behaviors conferred by derepression.

What are the evolutionary constraints that may favor activation over derepression and vice versa? Seminal studies have investigated this question for gene-regulatory networks (48–50). However, an analysis of differences in the functional characteristics of activation, derepression, and concerted mechanisms in the context of cell signaling is still lacking. To address this deficiency, we perform a systematic comparison of the three mechanisms using the following metrics: 1) dose–response, 2) response time, and 3) ability to suppress or filter stochastic fluctuations in upstream components. The rationale behind comparing dose–response curves is that they provide information about the input sensitivity range and the output dynamic range, both of which are of pharmacological importance. We supplement this comparison with response times, which provide information about the dynamics of the signaling activity. The third metric of comparison is motivated from the fact that signaling pathways are subject to intrinsic fluctuations that occur due to the stochastic nature of biochemical reactions (51–56).

We construct and analyze both deterministic ordinary differential equation (ODE) models and stochastic models based on continuous-time Markov chains. We show that activation has the following two effects: It makes the switch response more sensitive than that of the receptor, and it speeds up the response with the stimulus strength. In contrast, derepression makes the switch response less sensitive than the receptor occupancy and slows down the response speed as stimulus strength increases. These counteracting behaviors of activation and derepression lead to intermediate sensitivity and intermediate response time for the concerted mechanism. In the special case of a perfect concerted mechanism (equal activation and repression), the dose–response curve of the pathway aligns with the receptor occupancy, and the response time does not depend upon the stimulus level. The noise comparison reveals that the concerted mechanism is more susceptible to fluctuations than the activation and derepression mechanisms, which perform similarly. We further show that these results qualitatively hold for more complex models, such as those incorporating receptor removal and proofreading. We finally discuss our findings to suggest reasons that might have led biological systems to evolve one of these mechanisms over the others, a question that has received considerable attention in the context of gene regulation (48–50).

Model Formulation

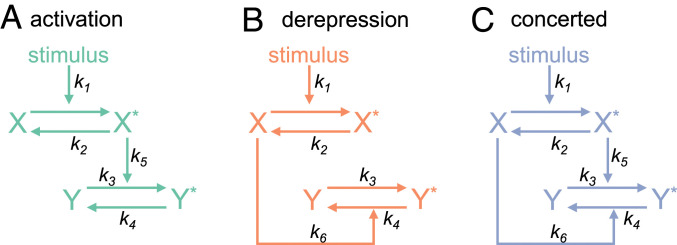
We consider a two-tier model for each of three mechanisms of signaling through a molecular switch (Fig. 1). The first tier is common for all mechanisms, where an inactive receptor ($X$) becomes active ($X^{*}$) when its corresponding input (stimulus) is presented. The second tier is the molecular switch that transitions between off ($Y$) and on ($Y^{*}$) states. In the activation mechanism, the transition rate from the off state to the on state increases as the number of active receptor molecules increases (Fig. 1A). In the derepression mechanism, the transition rate from the on state to the off decreases with a decrease in the number of inactive receptor molecules (Fig. 1B). In the concerted mechanism, both activation and derepression occur simultaneously (Fig. 1C). We model these mechanisms using ODEs, assuming mass-action kinetics. To this end, we denote the time by $t$, the stimulus level by $S$, the total number of receptors by $X_T$, and the total number of switches by $Y_T$. We use $X^{*}$ and $Y^{*}$ to denote the number of active receptors and the number of active switches, respectively. The rate constants are as follows: $k_1$ is the rate of receptor activation per unit stimulus, $k_2$ is the rate of receptor deactivation, $k_3$ is the basal rate of activation of the switch, $k_4$ is the basal rate of deactivation of the switch, $k_5$ is the strength of activation of an individual active receptor, and $k_6$ is the strength of repression of an individual inactive receptor. Thus, the (total) activation strength is $k_5{X}_T$, and the (total) repression strength is $k_6{X}_T$. Lastly, we assume that $X_T$ and $Y_T$ are conserved and that each model is in steady state before presentation of the stimulus at $t=0$.

Fig. 1.

Mechanisms for signaling through molecular switches. Presentation of a stimulus activates a receptor ($X\to X^{*}$). The reverse reaction causes deactivation of the receptor ($X^{*}\to X$). These transitions govern the activity of a molecular switch downstream. (A) In the activation mechanism, $X^{*}$ increases the rate at which the inactive switch ($Y$) becomes active ($Y^{*}$). The opposite reaction $Y^{*}\to Y$ has a constant rate. (B) In the derepression mechanism, the transition $Y\to Y^{*}$ occurs at a constant rate. Activity of the switch is controlled through $X$: The stimulus decreases $X$ and consequently increases $Y^{*}$. (C) In the concerted paradigm, both activation and derepression simultaneously control the downstream component.

Note that the concerted mechanism encompasses both activation and derepression. Therefore, writing ODEs for the concerted mechanism is sufficient to capture all three mechanisms. The number of active receptors and the number of active switches evolve over time according to the following ODEs (SI Appendix, section S1):

$$\frac{d{X}^{*}}{dt}=k_{1}S{X}_T-\left(k_{1}S+k_2\right)X^{*},$$ [1a]

$$\begin{array}{ll}\hfill \frac{d{Y}^{*}}{dt}& =k_3{Y}_T+k_5{Y}_T{X}^{*}-\left(k_3+k_4+k_6{X}_T\right)Y^{*}\hfill \\ \hfill & \hspace{1em}-\left(k_5-k_6\right)X^{*}{Y}^{*}.\hfill \end{array}$$ [1b]

The activation and derepression mechanisms represent limiting cases in which $k_6=0$ and $k_5=0$, respectively. Solving Eq. 1 requires rate constants and initial conditions to be specified. We assume that initial conditions are given by the prestimulus $\left(S=0\right)$ steady state:

$$X_0^{*}=0,\hspace{1em}{Y}_0^{*}=\frac{k_3}{k_3+k_4+k_6{X}_T}{Y}_T.$$ [1c]

With the models described by Eq. 1, we next compare the three signaling mechanisms in terms of their dose responses and response times.

Dose Responses

We begin our analysis by examining the steady-state dose responses of activation, derepression, and concerted mechanisms. The steady-state solution to Eq. 1 is

$$\overline{X^{*}}=\frac{S{X}_T}{S+\frac{k_2}{k_1}},$$ [2a]

$$\overline{Y^{*}}=\frac{\frac{k_2{k}_3}{k_1\left(k_3+k_4+k_5{X}_T\right)}+\frac{k_3+k_5{X}_T}{k_3+k_4+k_5{X}_T}S}{\frac{k_2\left(k_3+k_4+k_6{X}_T\right)}{k_1\left(k_3+k_4+k_5{X}_T\right)}+S}{Y}_T,$$ [2b]

where $\overline{X^{*}}$ and $\overline{Y^{*}}$ represent the steady states for the number of active (occupied) receptors and the number of active switches, respectively. Notably, both $\overline{X^{*}}$ and $\overline{Y^{*}}$ have the form

$$R=\frac{R_0{\mathrm{\Theta }}_R+R_{\infty }S}{{\mathrm{\Theta }}_R+S},$$ [3]

where $R_0$ is the minimum response corresponding to $S=0$, $R_{\infty }$ is the maximum response corresponding to $S\gg {\mathrm{\Theta }}_R$, and ${\mathrm{\Theta }}_R$ is the stimulus concentration that produces half-maximal response $\frac{R_0+R_{\infty }}{2}$. The dynamic range of the response is given by $R_{\infty }-R_0$, signifying the maximum the output can change in response to the input. Eq. 3 shows that shapes of dose–response curves are the same for the three signaling mechanisms. Hence, comparison between them can be carried out in terms of $R_0$, $R_{\infty }$, and ${\mathrm{\Theta }}_R$.

At the receptor level, $X_0^{*}=0$ and $X_{\infty }^{*}=X_T$. The ratio $\frac{k_2}{k_1}$, which equals the binding affinity of the stimulus with the receptor, determines the half-maximal stimulus (${\mathrm{\Theta }}_{X^{*}}=\frac{k_2}{k_1}$) and the fractional receptor occupancy ($\frac{X}{X_T}=\frac{k_{1}S/k_2}{1+k_{1}S/k_2}$). For the switch, the response ($\overline{Y^{*}}$) is specified by:

$$Y_0^{*}=\frac{k_3{Y}_T}{k_3+k_4+k_6{X}_T},$$ [4a]

$$Y_{\infty }^{*}=\frac{\left(k_3+k_5{X}_T\right)Y_T}{k_3+k_4+k_5{X}_T},$$ [4b]

$${\mathrm{\Theta }}_{Y^{*}}={\mathrm{\Theta }}_{X^{*}}\frac{k_3+k_4+k_6{X}_T}{k_3+k_4+k_5{X}_T}.$$ [4c]

These expressions show that the dose–response of the switch depends upon the basal rates as well as activation strength ($k_5{X}_T$) and repression strength ($k_6{X}_T$). A careful examination of Eq. 4 provides the following insights:

• 1.The activation strength ($k_5{X}_T$) does not affect the minimum response ($Y_0^{*}$), but affects the maximum response ($Y_{\infty }^{*}$). In particular, increasing $k_5{X}_T$ increases $Y_{\infty }^{*}$. The repression strength ($k_6{X}_T$) decreases $Y_0^{*}$ and does not affect $Y_{\infty }^{*}$.
• 2.Relative values of the repression and activation strengths dictate the relationship between the half-maximal stimulus for the switch response (${\mathrm{\Theta }}_{Y^{*}}$) vis-á-vis the half-maximal stimulus for the receptor occupancy (${\mathrm{\Theta }}_{X^{*}}$). More specifically, ${\mathrm{\Theta }}_{Y^{*}}<{\mathrm{\Theta }}_{X^{*}}$ when $k_5{X}_T>k_6{X}_T$, ${\mathrm{\Theta }}_{Y^{*}}={\mathrm{\Theta }}_{X^{*}}$ when $k_5{X}_T=k_6{X}_T$, and ${\mathrm{\Theta }}_{Y^{*}}>{\mathrm{\Theta }}_{X^{*}}$ when $k_5{X}_T<k_6{X}_T$. Increasing $k_6{X}_T$ increases ${\mathrm{\Theta }}_{Y^{*}}$, while increasing $k_5{X}_T$ does the opposite.
• 3.The limiting case of $k_3=0$ implies $Y_0^{*}=0$, and that of $k_4=0$ leads to $Y_0^{*}=Y_T$. Thus, nonzero basal rates reduce the dynamic range $Y_{\infty }^{*}-Y_0^{*}$ because $Y_{\infty }^{*}<Y_T$ and $Y_0^{*}>0$. In the same vein, the relationship between ${\mathrm{\Theta }}_{Y^{*}}$ and ${\mathrm{\Theta }}_{X^{*}}$ is most sensitive to the ratio $k_6{X}_T/k_5{X}_T$ when $k_3=0$ and $k_4=0$.

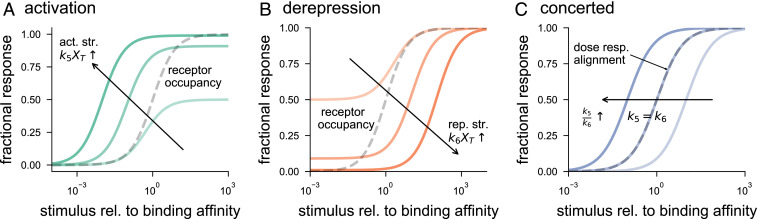
Fig. 2 illustrates the features of the dose–response curves for the three mechanisms described above. For many signaling pathways, it is reasonable to assume negligible signaling activity in the absence of stimulus ($Y_0^{*}\ll Y_T$) and almost full activity for high stimulus levels ($Y_{\infty }^{*}\approx Y_T$). To meet these physiological constraints requires $k_3\ll k_4+k_6{X}_T$ and $k_4\ll k_3+k_5{X}_T$, respectively. Additionally, note that, for simplicity, we set basal rates equal to zero where possible. Thus, we use the following parameters for Fig. 2: $k_3=0$ and $k_6=0$ for activation; $k_4=0$ and $k_5=0$ for derepression; and $k_3=0$ and $k_4=0$ for concerted. As shown in Fig. 2A, activation makes the switch response more sensitive to stimulus than the receptor occupancy (${\mathrm{\Theta }}_{Y^{*}}<{\mathrm{\Theta }}_{X^{*}}$). Increasing the activation strength ($k_5{X}_T$) increases $Y_{\infty }^{*}$ and decreases ${\mathrm{\Theta }}_{Y^{*}}$, increasing the dynamic range (vertical expansion) and sensitivity (leftward shift) of the dose–response curve. The derepression mechanism exhibits an opposite behavior with ${\mathrm{\Theta }}_{Y^{*}}>{\mathrm{\Theta }}_{X^{*}}$. In this scenario, increasing the repression strength increases the dynamic range by decreasing $Y_0^{*}$ and decreases sensitivity by increasing ${\mathrm{\Theta }}_{Y^{*}}$ (Fig. 2B).

Fig. 2.

Dose–response curves for signaling mechanisms through molecular switches. The response is measured in terms of fraction of active switches $Y^{*}/Y_T$ as the stimulus level varies. The receptor-occupancy curve denotes the fraction of active receptors $X^{*}/X_T$. The stimulus is normalized by its binding affinity to the receptor (${\mathrm{\Theta }}_{X^{*}}$). (A) For the activation mechanism, the half-maximal stimulus (${\mathrm{\Theta }}_{Y^{*}}$) of a dose–response curve is less than ${\mathrm{\Theta }}_{X^{*}}$. Each dose–response curve (solid line) is for a fixed activation strength (act. str.) $k_5{X}_T$. Increasing $k_5{X}_T$, depicted by the solid arrow, causes an upward expansion and leftward shift in dose–response. For these plots, the following values for parameters were used: $k_3=0,k_4=1$ and $k_6=0$. The activation strength ($k_5{X}_T$) was varied to take values from $\left(\mathrm{1,10,100}\right)$. (B) For the derepression mechanism, the dose–response of the switch for a given repression strength (rep. str.) ($k_6{X}_T$) has half-maximal stimulus (${\mathrm{\Theta }}_Y$) greater than ${\mathrm{\Theta }}_{X^{*}}$. Increasing $k_6{X}_T$, shown by the solid arrow, leads to a downward expansion and rightward shift in the dose–response curve. The repression strength $k_6{X}_T$ takes values from $\left(\mathrm{1,10,100}\right)$. The rest of the parameters were set as $k_3=1$, $k_4=0$, and $k_5=0$. (C) In the case of concerted mechanism, ${\mathrm{\Theta }}_{Y^{*}}$ may be greater than, equal to, or less than ${\mathrm{\Theta }}_{X^{*}}$, depending upon the relative (rel.) values of the activation strength and the derepression strength. Increasing the ratio $k_5/k_6$, depicted by the solid arrow, shifts the dose response (resp.) to the left. Dose–response alignment (${\mathrm{\Theta }}_{Y^{*}}={\mathrm{\Theta }}_{X^{*}}$) occurs when $k_5=k_6$. The parameters used for the plots are $k_3=0$ and $k_4=0$. The ratio $k_5/k_6$ was varied over $\left(0.1,\mathrm{1,10}\right)$.

Because we ignore the basal rates, changing activation and derepression strengths only influence ${\mathrm{\Theta }}_{Y^{*}}$ in the case of a concerted mechanism. As expected, the switch response is more (less) sensitive than the receptor occupancy if activation (derepression) dominates derepression (activation). There is a perfect alignment of the fractional receptor-occupancy curve with the dose–response curve of the switch when $k_5=k_6$ (Fig. 2C). Another important property of the concerted model is that it exhibits ratiometric signaling, in which the response of the switch ($Y^{*}$) is determined by the ratio of active receptors to the total number of receptors ($X^{*}/X_T$) (13, 14). The absolute value of the total number of receptors ($X_T$) has no bearing on $\overline{Y^{*}}$. This may be seen by setting $k_3=0$ and $k_4=0$ in the expression of $\overline{Y^{*}}$ in Eq. 2:

$$\overline{Y^{*}}=\frac{S{Y}_T}{S+\frac{k_2{k}_6}{k_1{k}_5}}.$$ [5]

In reality, $k_3$ and $k_4$ are likely to be small, but nonzero. Therefore, ratiometric signaling does not hold in a strict sense.

Our theoretical results above show how the dose–response curves behave differently for activation, derepression, and concerted mechanisms. Are some of these behaviors observed in biological systems? One example where the signaling response becomes maximal when only a small fraction of receptors are bound (${\mathrm{\Theta }}_{Y^{*}}<{\mathrm{\Theta }}_{X^{*}}$) is the EGFR–MAPK pathway, which elicits a full MAPK response at less than $5\%$ receptor occupancy (57). Our analysis explains this by an activation mechanism or a concerted mechanism, in which the activation strength dominates the repression strength. A contrasting behavior is seen in the ethylene pathway of A. thaliana, in which a loss-of-function mutation of one of the ethylene receptors, etr1, shows increased sensitivity to etylene (58). This points to a derepression mechanism in which the decreased amount of the receptor ($X_T$) lowers the repression strength $k_6{X}_T$ and shifts the dose–response curve to the left in comparison to that of the wild-type system. A suggested example of concerted mechanism is the yeast G-signaling pathway, which exhibits both ratiometric signaling (13, 14) and dose–response alignment (43).

Response Times

Our analysis thus far focused on the steady-state properties of the activation, derepression, and concerted mechanisms. In this section, we study these mechanisms in terms of their response times; that is, the time it takes for a signaling output to reach its steady state. We use the following definition of response time:

$${\mathcal{T}}_R=\frac{{\int }_0^{\infty }t\left|\overline{R}-R\left(t\right)\right|dt}{{\int }_0^{\infty }\left|\overline{R}-R\left(t\right)\right|dt},$$ [6]

where $R\left(t\right)$ is the time-dependent response of the pathway component under consideration and $\overline{R}$ represents its value at steady state (59). For this definition, ${\mathcal{T}}_R$ represents the “center of mass” of the response $R\left(t\right)$ and is well-defined when $R\left(0\right)\hspace{0.17em}\ne \hspace{0.17em}\overline{R}$. We may also think of $1/{\mathcal{T}}_R$ as the speed of the response in the sense that if the response is determined by a single kinetic step, ${\mathcal{T}}_R$ is the reciprocal of the rate constant for that step. For example, the response time for the receptor is given by (SI Appendix, section S2):

$${\mathcal{T}}_{X^{*}}=\frac{1}{k_{1}S+k_2}.$$ [7]

Thus, the response time decreases (i.e., response speeds up) if $k_{1}S+k_2$ increases. Because the response time depends upon the sum $k_{1}S+k_2$ and the steady-state receptor occupancy depends upon the ratio $k_{1}S/k_2$, these quantities can be tuned independently.

In the absence of stimulus, the response time of the switch follows the same form as Eq. 7:

$${\left.{\mathcal{T}}_{Y^{*}}\right|}_{S=0}=\frac{1}{k_3+k_4+k_6{X}_T}.$$ [8]

When the stimulus is present, analytic solutions to the integrals in Eq. 6 for the response time of $Y^{*}\left(t\right)$ do not exist, except for a special case of the perfect concerted model $k_5=k_6$. It is, however, possible to approximate ${\mathcal{T}}_{Y^{*}}$ by linearizing the ODE system in Eq. 1 around its steady state:

$$\begin{array}{ll}\hfill {\mathcal{T}}_{Y^{*}}& \approx \underset{\text{resp. time of}{Y}^{*}\text{when}{X}^{*}\text{is in steady}-\text{state}}{\underbrace{\frac{1}{k_3+k_4+k_6{X}_T+\left(k_5-k_6\right)\frac{k_{1}S{X}_T}{k_{1}S+k2}}}}+\underset{\text{resp. time of}{X}^{*}}{\underbrace{\frac{1}{k_{1}S+k_2}}}\hfill \\ \hfill & \times \underset{\text{time}-\text{averaging}}{\underbrace{\frac{k_3+k_4+k_6{X}_T+\left(k_5-k_6\right)\frac{k_{1}S{X}_T}{k_{1}S+k2}}{k_{1}S+k_2+k_3+k_4+k_6{X}_T+\left(k_5-k_6\right)\frac{k_{1}S{X}_T}{k_{1}S+k2}}}}.\hfill \end{array}$$ [9]

This equation is exact for the special case when $k_5=k_6$ (SI Appendix, section S3C). The first term in Eq. 9 can be interpreted as the response time of the switch when the receptors are at steady state, because in that case, the switch would be turned on at a rate $k_3+k_5\frac{k_{1}S{X}_T}{k_{1}S+k_2}$ and turned off at a rate $k_4+k_6{X}_T-k_6\frac{k_{1}S{X}_T}{k_{1}S+k_2}$; so, the inverse of their sum would give the response time. The second term represents the response time of the receptor (${\mathcal{T}}_{X^{*}}$) multiplied by a time-averaging factor, which computes the ratio of ${\mathcal{T}}_{X^{*}}$ to the sum of ${\mathcal{T}}_{X^{*}}$ and the response time of the switch when $X^{*}=\overline{X^{*}}$. The time-averaging term lies between zero and one; its value approaches zero if the receptor response is much faster than the switch response when $X^{*}=\overline{X^{*}}$ and approaches one if the receptor response is much slower than that of the switch.

If the receptor response is much faster than that of the switch, we expect that the latter does not depend upon the former (time-averaging term $\to 0$). Indeed, in this limit, Eq. 9 gives

$${\mathcal{T}}_{Y^{*}}\approx \frac{1}{k_3+k_4+k_6{X}_T+\left(k_5-k_6\right)\frac{k_{1}S{X}_T}{k_{1}S+k2}}.$$ [10]

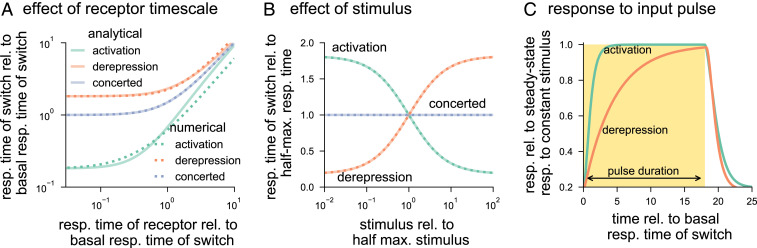
Comparing Eq. 10 with the basal response time in Eq. 8 shows that for a given stimulus level, activation speeds up the response in comparison with the basal response. In contrast, derepression slows down the response, and a perfect concerted mechanism does not affect the response time (Fig. 3A). In the other limiting case, when the receptor timescale is much slower than that of the switch, we expect the receptor dynamics to dictate the response time (time-averaging term $\to 1$). Indeed, in this case, Eq. 9 reduces to ${\mathcal{T}}_{Y^{*}}\approx {\mathcal{T}}_{X^{*}}$, such that choice of the mechanism to control the switch has little effect on the response time. Our analytical as well as numerical calculations confirm this behavior (Fig. 3A).

Fig. 3.

Response times of molecular switches governed by activation, derepression, and concerted mechanisms. (A) The response (resp.) time of the switch increases as the response time of the receptor increases. Differences in the signaling mechanisms are more prominent when the receptor response is fast (i.e., the relative [rel.] response time of the receptor goes to zero). In this limit, activation decrease the response time, derepression increases the response time, and the concerted mechanism leaves it unchanged in comparison to the basal response time. For each signaling mechanism, the response time is computed by using the analytical result in Eq. 9 (solid lines) and numerically validated by using Eq. 6 (dashed lines). To ensure the same basal response and basal response time of the switches across signaling mechanisms, we chose the parameters as $k_3=1/9$, $k_4=1$, $k_6=0$, and $k_5{X}_T=10$ for activation; $k_3=1/9$, $k_4=0$, $k_5=0$, and $k_6{X}_T=1$ for derepression; and $k_3=1/9$, $k_4=0$, and $k_5{X}_T=k_6{X}_T=1$ for concerted. The receptor response time was $k_{1}S+k_2$ varied through $k_2$, while maintaining $k_{1}S/k_2=1$. (B) With increase in the stimulus level, response time decreases for activation, increases for derepression, and does not change for the concerted mechanism. The comparison is controlled by setting same response time at half-maximal (half-max.) stimulus ${\mathrm{\Theta }}_{Y^{*}}$. The following parameters were chosen to have same basal response, but different basal response times: $k_3=1$, $k_4=9$, $k_5{X}_T=90$, and $k_6=0$ for activation; $k_3=10,k_4=0,k_5=0$, and $k_6{X}_T=90$ for derepression; and $k_3=10$, $k_4=0$, and $k_5{X}_T=k_6{X}_T=90$ for concerted. The receptor occupancy was varied by changing $k_{1}S/k_2$ while maintaining the receptor response time $1/\left(k_{1}S+k_2\right)$, which was chosen to be 100 times faster than the response time of the switches at their respective half-maximal stimulus levels. (C) Comparing the system’s response to a pulse of stimulus provides a method for distinguishing mechanisms. The response time for activation (derepression) following exposure to stimulus is shorter (longer) than following removal of stimulus. The time series for each mechanism is normalized to its steady state in the presence of stimulus. We used parameters such that each mechanism has the same response time of the switch in the absence of the stimulus and the stimulus strength produced a half-maximal response. Specific values of parameters are: $k_1=1$, $k_2=1$, $X_T=100$, and $Y_T=100$ for both mechanisms; $k_3=1/9$, $k_4=1$, $k_5=0.1$, and $S=0.1$ for activation; and $k_3=1/9$, $k_4=0$, $k_6=0.01$, and $S=10$ for derepression.

An intuitive explanation for why activation is faster than derepression is as follows. Activation shortens the average lifetime of the off state, without affecting the average lifetime of the on state. Derepression operates differently; it does not affect the average lifetime of the off state, but increases the lifetime of the on state. Thus, activation responds faster than derepression. The concerted mechanism simultaneously decreases the lifetime of the off state and increases the lifetime of the on state. Therefore, its response time lies between those of activation and derepression.

Next, we examine how the response time varies with stimulus level ($S$). Because changing the stimulus affects the response time of the receptor, which, in turn, affects the response time of the switch, we control for this effect by keeping $k_{1}S+k_2$ constant. We find that activation shortens the response time (speeds up the response) with increasing stimulus levels, whereas derepression increases the response time (slows down the response) (Fig. 3B). Importantly, the response time of the concerted mechanism is independent of the stimulus strength and, therefore, able to respond rapidly over the whole range of stimulus levels. To better understand this behavior, consider the response time for the limiting case of fast receptor dynamics. Eq. 10 can be rewritten as

$${\mathcal{T}}_{Y^{*}}\approx \frac{\frac{1}{k_3+k_4+k_6{X}_T}{\mathrm{\Theta }}_{Y^{*}}+\frac{1}{k_3+k_4+k_5{X}_T}S}{S+{\mathrm{\Theta }}_{Y^{*}}},$$ [11]

which changes from $\frac{1}{k_3+k_4+k_6{X}_T}$ at $S=0$ to $\frac{1}{k_3+k_4+k_5{X}_T}$ as $S\to \infty$. The half-maximal stimulus ${\mathrm{\Theta }}_{Y^{*}}$ is the same as defined in Eq. 4. For the activation mechanism, $\frac{1}{k_3+k_4+k_6{X}_T}>\frac{1}{k_3+k_4+k_5{X}_T}$, so the response time decreases with stimulus. Moreover, $\frac{1}{k_3+k_4+k_6{X}_T}<\frac{1}{k_3+k_4+k_5{X}_T}$ for the derepression mechanism and $\frac{1}{k_3+k_4+k_6{X}_T}=\frac{1}{k_3+k_4+k_5{X}_T}$ for the perfect concerted mechanism. Therefore, the response time increases with the stimulus for the derepression mechanism and is independent of the stimulus for the concerted case. It is also worth pointing out that activation is faster than derepression only if the basal response times are equal. Therefore, to construct a switch that responds rapidly using derepression, it is necessary for the switch to undergo fast basal cycling (Fig. 3B).

Our analysis of dose–response properties for ratiometric signaling given in Eq. 5 reveals that this mechanism is independent of the total number of receptors $X_T$ when the basal rates of the switch are zero ($k_3=0$ and $k_4=0$). Using these values in the expression for the response time in Eq. 9 demonstrates that this property does not hold for the response time. Specifically, the response time decreases with an increase in $X_T$ (SI Appendix, section S3E).

Up to this point, we have assumed that the input signal is constant in time. However, cells are often faced with environmental conditions that change in time, and challenging signaling pathways with time-dependent inputs is a powerful experimental technique for revealing the network motifs that regulate these systems (60, 61). To investigate how molecular switches respond to dynamic inputs, we first considered how each mechanism responds to a single pulse of stimulus in the form of a square wave. Using a time-dependent signal of this form provides a technique for distinguishing the activation and derepression mechanisms (Fig. 3C). If the response time following exposure to the stimulus is shorter (longer) than the time for the system to relax once the stimulus is removed, then the switch is primarily controlled by activation (derepression). We also consider the responses of receptor as well as switch governed by either of the three mechanisms to periodic input signals consisting of sequences of square wave pulses with varying frequency. We find that these architectures filter high-frequency inputs (SI Appendix, section S5).

Processing Upstream Fluctuations

The deterministic models used to compare the signaling mechanisms thus far ignore the stochastic nature of biochemical reactions, which becomes relevant when the abundance of receptor and switch proteins are small (51–56, 62, 63). Therefore, we formulate a stochastic model of the concerted mechanism and analyze the other two mechanisms as its special cases. Our model consists of four reactions: activation of receptor upon recognizing the stimulus, deactivation of receptor, on-to-off transition of the molecular switch, and off-to-on transition of the molecular switch. The stochastic model is characterized by the probabilistic nature of each reaction, and the discreteness of changes in population counts upon occurrence of a reaction, as tabulated in Table 1.

Table 1.

Transitions and associated rates for the stochastic model

Reaction	Population update	Transition rate
$X\to X^{*}$	$X^{*}\mapsto X^{*}+1$	$k_{1}S\left(X_T-X^{*}\right)$
$X^{*}\to X$	$X^{*}\mapsto X^{*}-1$	$k_2{X}^{*}$
$Y\to Y^{*}$	$Y^{*}\mapsto Y^{*}+1$	$\left(k_3+k_5{X}^{*}\right)\left(Y_T-Y^{*}\right)$
$Y^{*}\to Y$	$Y^{*}\mapsto Y^{*}-1$	$\left(k_4+k_6\left(X_T-X^{*}\right)\right)Y^{*}$

Our goal is to analyze the noise properties of activation, derepression, and concerted mechanisms. We quantify noise using coefficient of variation squared ($C{V}^2$), which is computed by normalizing the variance by ${\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}}^2$ and is a dimensionless quantity. To this end, we use the ODEs that describe the time evolution of the first- and second-order moments and solve them in steady state to obtain the stationary moments (64–66) (SI Appendix, section S4A). In particular, moments for the number of active receptors ($X^{*}$) are given by

$$⟨X^{*}⟩=\frac{k_{1}S{X}_T}{k_{1}S+k_2},\hspace{1em}C{V}_{X^{*}}^2=\frac{⟨{X^{*}}^2⟩-{⟨X^{*}⟩}^2}{{⟨X^{*}⟩}^2}=\frac{1}{X_T}\frac{k_2}{k_{1}S}.$$ [12]

Here, $⟨.⟩$ denotes the expected value (average) of its argument. These moments correspond to a binomial distribution with parameters $X_T$ and $\frac{k_{1}S}{k_{1}S+k_2}$ (SI Appendix, section S4A). The stochastic mean $⟨X^{*}⟩$ is same as the steady-state value for $X^{*}$ in the deterministic model in Eq. 1. The coefficient of variation squared increases as the number of receptors ($X_T$) decreases. Therefore, the noise analysis is important when $X_T$ is small. In addition, the noise decreases with the ratio $k_{1}S/k_2$. Recall that $k_{1}S/k_2$ is the stimulus level relative to the binding affinity. Thus, the noise diminishes when the stimulus level is much higher than the binding affinity.

Closed-form expressions for the moments are not available for $Y^{*}$, owing to the nonlinear term $X^{*}{Y}^{*}$ in reaction rates, except for the special case of a perfect concerted model ($k_5=k_6$). We approximate the mean response and the noise by considering a linearized system around the steady state

$$⟨Y^{*}⟩\approx \frac{k_3+k_5\frac{k_{1}S}{k_{1}S+k_2}{X}_T}{k_3+k_4+k_6\frac{k_2}{k_{1}S+k_2}{X}_T}{Y}_T,$$ [13a]

$$C{V}_{Y^{*}}^2\approx \underset{\text{contribution from act./deact. of}{Y}^{*}}{\underbrace{\frac{1}{Y_T}\frac{k_4+k_6{X}_T\frac{k_2}{k_{1}S+k_2}}{k_3+k_5{X}_T\frac{k_{1}S}{k_{1}S+k_2}}}}+$$

$$C{V}_{X^{*}}^2\times \underset{\text{time}-\text{averaging}}{\underbrace{\frac{k_3+k_4+k_5\frac{k_{1}S{X}_T}{k_{1}S+k_2}+k_6\frac{k_2{X}_T}{k_{1}S+k_2}}{k_{1}S+k_2+k_3+k_4+k_5\frac{k_{1}S{X}_T}{k_{1}S+k_2}+k_6\frac{k_2{X}_T}{k_{1}S+k_2}}}}$$

$$\times \underset{\text{coupling}}{\underbrace{\frac{{\left(\frac{k_{1}S}{k_{1}S+k_2}\right)}^2{\left(k_4{k}_5{X}_T+k_6{X}_T\left(k_3+k_5{X}_T\right)\right)}^2}{{\left(k_3+k_5\frac{k_{1}S{X}_T}{k_{1}S+k_2}\right)}^2{\left(k_3+k_4+k_5\frac{k_{1}S{X}_T}{k_{1}S+k_2}+k_6\frac{k_2{X}_T}{k_{1}S+k_2}\right)}^2}}}.$$ [13b]

We validate these approximations using exact semianalytical approach based on ref. 67 (SI Appendix, section S4D). The formula for $C{V}_{Y^{*}}^2$ above is written in terms of various sources of noise, as previously done for gene-regulation models (68–70). Specifically, the noise in the signaling activity of the switch arises from two sources: activation/deactivation reactions of the switch, and noise in the number of active receptors $\left(C{V}_{X^{*}}^2\right)$. The contribution from activation/deactivation of the switch in Eq. 13 has a similar form as $C{V}_{X^{*}}^2$ in Eq. 12. Accordingly, the contribution of this term decreases with an increase in $Y_T$ or increase in the ratio of the total activation rate $\left(k_3+k_5{X}_T\frac{k_{1}S}{k_{1}S+k_2}\right)$ with total deactivation rate $\left(k_4+k_6{X}_T\frac{k_2}{k_{1}S+k_2}\right)$. This ratio increases if the activation strength increases or the repression strength decreases. The contribution of $C{V}_X^2$ to $C{V}_{Y^{*}}^2$ is scaled by time-averaging and coupling terms. The time-averaging term is the same as that in Eq. 9; it varies between zero and one, depending upon the relative timescales of the receptor and the switch. Thus, in the limiting case where receptor dynamics is very fast, the contribution from $C{V}_{X^{*}}^2$ to $C{V}_{Y^{*}}^2$ becomes negligible due to efficient time-averaging of fluctuations in $X^{*}$. The coupling term in Eq. 13 determines how strongly $X^{*}$ affects $Y^{*}$. For example, this term is zero when the stimulus is absent ($S=0$) or when both $k_5$ and $k_6$ are zero. In both these cases, the switch is decoupled from the receptor.

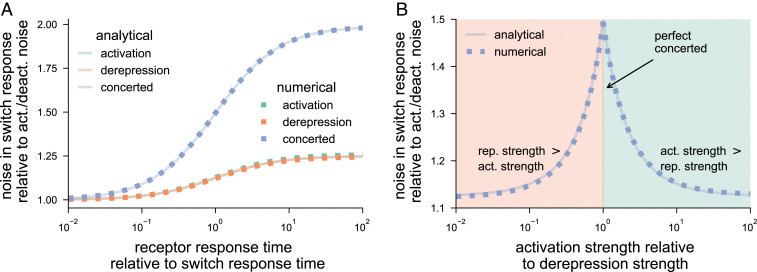
Next, we compare the noise properties of activation, derepression, and concerted mechanisms. To mathematically control the comparison, we assume that the receptor dynamics is same across the three strategies. In addition, we maintain the same average rate at which the switch turns on from the off state—i.e., $k_3+k_5\frac{k_{1}S{X}_T}{k_{1}S+k_2}$—and the same average rate at which the switch turns off from the on state—i.e., $k_4+k_6\frac{k_2{X}_T}{k_{1}S+k_2}$. These assumptions ensure that differences in the noise properties, if any, are solely due to the architecture of the molecular switch, and not dependent on the parameters. With this setup, we examine the effect of relative timescales (response times) of the receptor and the switch. We observe that in Eq. 13, varying $k_{1}S+k_2$ while maintaining $k_{1}S/k_2$ only affects the time-averaging term; all other terms are not affected. As shown in Fig. 4A, the noise properties of these signaling mechanisms are similar when the receptor timescale is fast. This is expected because the dominant contribution in $C{V}_{Y^{*}}^2$ comes from its own activation and deactivation. However, when the receptor timescale is slower than that of the switch, the overall noise increases, regardless of the signaling mechanism, and the noise performance of the concerted mechanism becomes worse than the other two mechanisms.

Fig. 4.

Noise in the number of active switch molecules. Noise is quantified by using coefficient of variation squared ($C{V}_{Y^{*}}^2$) as in Eq. 13. The overall $C{V}_{Y^{*}}^2$ is shown relative to the contribution from activation/deactivation (act./deact.) of $Y^{*}$. The analytical result is computed by using Eq. 13, which is validated numerically. (A) Noise with change in response time of the receptor. The noise increases as receptor response time increases, i.e., as the receptor slows down in comparison with the switch response time. The concerted model has a higher noise than activation and derepression, which perform similarly. The difference is negligible when receptor dynamics is fast and is more prominent when receptor is slow. The receptor response time ($k_{1}S+k_2$) is varied by changing $k_2$, while keeping the same receptor occupancy through the ratio $k_{1}S/k_2$, so as to keep the same number of switches. The differences across signaling mechanisms are controlled by ensuring the same total activation rate of the switch $k_3+k_5\frac{k_{1}S{X}_T}{k_{1}S+k_2}$ and same total deactivation rate $k_4+k_6\frac{k_{2}S{X}_T}{k_{1}S+k_2}$. We used the following parameters: $k_3=0$, $k_4=1$, $k_5=0.02$, and $k_6=0$ for activation; $k_3=1$, $k_4=0$, $k_5=0$, and $k_6=0.02$ for derepression; and $k_3=0$, $k_4=0$, and $k_5=k_6=0.02$ for concerted. In addition, $X_T$ and $Y_T$ were taken to be 100 each. The receptor occupancy was maintained by $k_{1}S/k_2=1$. (B) Noise strength as a function of the relative (rel.) strengths of activation and derepression for a concerted mechanism. The noise is highest when the activation and derepression strengths match (perfect concerted mechanism). Deviating from the perfect concerted mechanism toward either stronger activation (shaded green region) or stronger derepression (shaded orange region) leads to smaller noise. Parameters were chosen such that total activation and the total deactivation rates were the same across signaling mechanisms. For derepression, the activation (act.) strength was kept constant, and the repression (rep.) strength $k_6{X}_T$ was varied with a commensurate change in the basal deactivation rate $k_4$. For activation, the repression strength was kept constant, and the activation strength $k_5{X}_T$ was increased with appropriate change in the basal activation rate $k_3$. We used the following parameters: $k_1=1$, $S=1$, $k_2=1$, $k_3+k_5\frac{k_{1}S{X}_T}{k_{1}S+k_2}=1$, $k_4+k_6\frac{k_2{X}_T}{k_{1}S+k_2}=1$, $X_T=100$, and $Y_T=100$.

The observation that activation and derepression both have similar noise and their concerted action has higher noise is surprising in light of our analyses of dose–response and response time. In terms of these properties, activation and derepression counteract to enable intermediate response for the concerted mechanism. Intuitively, the increase in fluctuations occurs because in the concerted mechanism, fluctuations in the upstream component affect both transitions $Y\to Y^{*}$ and $Y^{*}\to Y$. In the case of activation and derepression, however, only one of these transitions is coupled with the upstream component. As a result, the concerted mechanism performs worse in terms of noise. We further highlight this observation by varying the relative strengths of activation ($k_5{X}_T$) and derepression ($k_6{X}_T$) in Fig. 4B. The noise is greatest for the concerted mechanism when $k_5{X}_T=k_6{X}_T$.

We also analyze the special case of ratiometric signaling. Our deterministic analysis shows that for a concerted mechanism without basal rates ($k_3=0$ and $k_4=0$), the steady-state response ($\overline{Y^{*}}$) does not depend upon the total number of receptors ($X_T$). However, similar to the response time, the $C{V}_{Y^{*}}^2$ also depends upon $X_T$ through the time-averaging term and $C{V}_{X^{*}}^2$, both of which decrease with increases in $X_T$ (SI Appendix, section S4B). To summarize, ratiometric signaling only holds for the steady-state response. A cell that has higher $X_T$ would respond faster as well as with less noise than a cell with a smaller $X_T$.

Model Generalizations

The two-tier models of signaling systems shown in Fig. 1 are purposely simplified for analytical tractability. In practice, signaling pathways comprise multiple tiers and frequently employ feedback regulation. Furthermore, one or more of the assumptions used to simplify the model equations are likely not to hold for any given pathway. Therefore, in this section, we examine how the models perform in more complicated situations.

Receptor Removal.

The models shown in Fig. 1 assume conservation of receptor molecules ($X_T$) and switch molecules ($Y_T$). However, in many cases, ligated receptors are removed from the cell surface and subsequently degraded (42, 71–73). To account for this effect, we reformulated the models in Fig. 1 to include receptor production at a rate $k_p$, removal of inactive receptors with rate $k_d$, and removal of active receptors with rate $k_d^{*}$.

Inclusion of receptor removal results in the following modification of the ODE system in Eq. 1:

$$\frac{dX}{dt}=k_p-k_{d}X-k_{1}SX+k_2{X}^{*},$$ [14a]

$$\frac{d{X}^{*}}{dt}=k_{1}SX-k_2{X}^{*}-k_d^{*}{X}^{*},$$ [14b]

$$\frac{d{Y}^{*}}{dt}=\left(k_3+k_5{X}^{*}\right)\left(Y_T-Y^{*}\right)-\left(k_4+k_{6}X\right)Y^{*}.$$ [14c]

The initial conditions are: $X\left(0\right)=\frac{k_p}{k_d}$, $X^{*}\left(0\right)=0$, and $Y^{*}\left(0\right)=\frac{k_3{Y}_T}{k_3+k_4+k_6{k}_p/k_d}$. As before, setting $k_6=0$ and $k_5=0$, respectively, results in ODEs for the activation and derepression mechanisms. When receptor production and removal are included in the model, the key qualitative differences between the activation and derepression mechanisms remain unchanged. For example, the functional forms of the dose–response curves are similar to those of Eq. 2 (SI Appendix, section S6). Some key features of the dose–response curves are:

• 1.The total number of receptors at steady-state $\overline{X}+\overline{X^{*}}$ remains $k_p/k_d$ (prestimulus level) if $k_d=k_d^{*}$, becomes greater than $k_p/k_d$ if $k_d>k_d^{*}$, and becomes less than $k_p/k_d$ if $k_d<k_d^{*}$.
• 2.The half-maximal stimulus for the receptor response is ${\mathrm{\Theta }}_X={\mathrm{\Theta }}_{X^{*}}=\frac{k_2+k_d^{*}}{k_1}\frac{k_d}{k_d^{*}}$, which now differs from the binding affinity of the receptor $k_2/k_1$.
• 3.The half-maximal stimulus for the switch response ${\mathrm{\Theta }}_{Y^{*}}$ equals ${\mathrm{\Theta }}_{X^{*}}$ if $k_6=k_5{k}_d/k_d^{*}$. Moreover, ${\mathrm{\Theta }}_{Y^{*}}>{\mathrm{\Theta }}_{X^{*}}$ if $k_6>k_5{k}_d/k_d^{*}$, and ${\mathrm{\Theta }}_{Y^{*}}<{\mathrm{\Theta }}_{X^{*}}$ if $k_6<k_5{k}_d/k_d^{*}$.

In terms of the response time, when the removal rates of inactive and active receptors are the same $k_d=k_d^{*}$, the response time of $Y^{*}$ is similar to that in Eq. 9. As expected, activation speeds up the response, and derepression slows it down. However, when the receptor removal rates differ ($k_d\hspace{0.17em}\ne \hspace{0.17em}{k}_d^{*}$), then the expressions for response time become quite complicated (SI Appendix, section S6). In this case, a further assumption of fast receptor dynamics leads to the same conclusions for the three signaling mechanisms. As we discuss next, when the timescales of the receptor and switch are similar, more interesting behavior is possible.

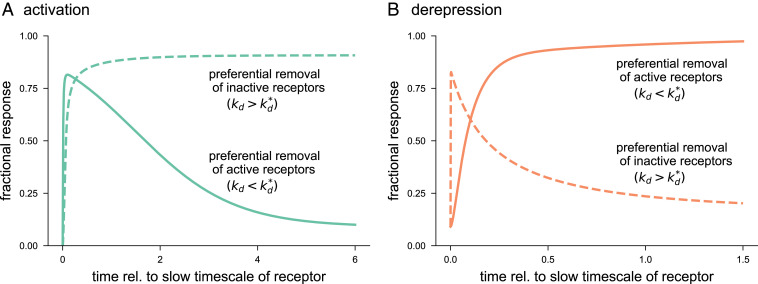
Receptor removal has been shown to generate adaptive behavior in response to sustained stimulus. That is, the response is transient, eventually returning to near basal levels (74, 75). Our analysis revealed that if $k_d=k_d^{*}$, then both inactive receptors, $X\left(t\right)$, and active receptors, $X^{*}\left(t\right)$, monotonically approach their respective steady states. However, if $k_d\hspace{0.17em}\ne \hspace{0.17em}{k}_d^{*}$, then it is possible for $X\left(t\right)$ to transiently undershoot and for $X^{*}\left(t\right)$ to transiently overshoot steady state, producing an adaptive response. In particular, adaptation by $X^{*}\left(t\right)$ occurs when $k_d^{*}>k_d$, i.e., active receptors are removed at a faster rate than inactive receptors. In contrast, adaptation by $X\left(t\right)$ occurs when $k_d^{*}<k_d$ (SI Appendix, section S6C). If the kinetics of the switch is fast as compared to those of the receptor, the switch follows the transient changes in $X\left(t\right)$ and $X^{*}\left(t\right)$. Thus, for the activation mechanism to exhibit adaptive behavior requires that the active form of the receptor be preferentially removed $\left(k_d<k_d^{*}\right)$ (Fig. 5A). Alternatively, for the derepression mechanism to exhibit an adaptive response requires the inactive form of the receptor to be preferentially removed $\left(k_d>k_d^{*}\right)$ (Fig. 5B). For completeness, we examine the scenarios where the inactive receptors are preferentially removed for an activation mechanism and active receptors are preferentially removed for a derepression mechanism. Interestingly, in both these cases, the responses are sustained and do not adapt. These results thus provide another set of differences between activation and derepression mechanisms.

Fig. 5.

Effect of receptor removal on responses of activation and derepression mechanisms. The response is measured in terms of fraction of active switch molecules ($Y^{*}/Y_T$) over time which is normalized to the slow timescale of the receptor (SI Appendix, section S6). (A) For an activation mechanism, the switch response adapts, i.e., returns toward basal response after a transient, if the rate of removal of active receptors ($k_d^{*}$) is higher than that of inactive receptors ($k_d$). In contrast, if inactive receptors are removed at a faster rate, then the response sustains. For the adaptive response, we chose $k_p=0.11$, $k_d=0.0011$, and $k_d^{*}=0.11$. For the sustained response, we set $k_p=101$, $k_d=1.01$, and $k_d^{*}=0.01$. The remaining parameters were selected as $k_1=1$, $k_2=1$, $k_3=0$, $k_4=10$, $k_5=1$, $k_6=0$, $S=1$, and $Y_T=100$. (B) For the derepression mechanism, preferential removal of $X$ results in adaptation, whereas preferential removal of $X^{*}$ causes sustained response. For the adaptive response, we used $k_p=101$, $k_d=1.01$, and $k_d^{*}=0.01$. For the sustained response, we chose $k_p=1$, $k_d=0.01$, and $k_d^{*}=1$. The remaining parameters were taken as $k_1=1$, $k_2=1$, $k_3=10$, $k_4=0$, $k_5=0$, $k_6=1$, $S=100$, and $Y_T=100$. Rel., relative.

Kinetic Proofreading.

Another simplification of the models shown in Fig. 1 is that the receptor kinetics is considered to be a single-step process. Recent work suggests that receptor kinetics is often more complex and may involve kinetic proofreading, in which a ligated receptor undergoes a series of transformations before becoming signaling competent (76–78). To study the effects of kinetic proofreading, we extend the model equations as follows:

$$\frac{d{X}_1^{*}}{dt}=k_{1}S\left(X_T-\sum _{i=1}^n{X}_i^{*}\right)-\left(k_2+k_f\right)X_1^{*},$$ [15a]

$$\frac{d{X}_i^{*}}{dt}=k_f{X}_{i-1}^{*}-\left(k_2+k_f\right)X_i^{*},\hspace{1em}i=\mathrm{2,3},\dots ,N-1,$$ [15b]

$$\frac{d{X}_N^{*}}{dt}=k_f{X}_{N-1}^{*}-k_2{X}_N^{*},$$ [15c]

$$\frac{d{Y}^{*}}{dt}=\left(k_3+k_5{X}_n^{*}\right)\left(Y_T-Y^{*}\right)-\left(k_4+k_6\left(X_T-X_n^{*}\right)\right)Y^{*}.$$ [15d]

Here, $n\ge 2$ is the total number of configurations for a ligated receptor, and $k_f$ is the rate at which a ligated receptor transitions to the next configuration. We assume that all receptor states are capable of repressing the downstream switch, except $X_n^{*}$, which is the only competent state for activating the downstream switch (SI Appendix, section S7). Moreover, all receptors are assumed to be unligated before the arrival of the stimulus. Therefore, the initial conditions are $X_i^{*}=0\hspace{0.17em}\forall i\in \left\{\mathrm{1,2},\dots ,n\right\}$ and $Y^{*}=\frac{k_3{Y}_T}{k_3+k_4+k_6{X}_T}$.

Including multiple states for the receptor does not change the qualitative behavior of dose–response curves of the three signaling mechanisms. However, now, only a fraction of the total ligated receptors are signaling competent. This fraction is given by ${\left(\frac{k_2}{k_2+k_f}\right)}^{n-1}$ and depends on the rate at which a ligated receptor transitions toward the signaling-competent state, $k_f$, the rate of ligand release, $k_2$, and the number of configurations of the ligated receptors, $n$. The response time at the receptor level differs from that for the model in Fig. 1 and is given by

$${\mathcal{T}}_{X_n^{*}}=\frac{1}{k_{1}S+k_2}+\frac{1}{k_f+k_2}\frac{\left(n-1\right)\left(k_{1}S+k_2\right)}{k_f+k_2+\left(n-1\right)\left(k_{1}S+k_2\right)}.$$ [16]

Yet, the response time of the switch still has a similar decomposition as that in Eq. 9 (SI Appendix, section S7).

Cascades.

Given that activation and derepression shift dose–response in opposite directions, a natural question to ask is whether dose–response alignment can occur in a signaling cascade where activation and derepression operate sequentially? To explore this possibility, we constructed a three-tier model where the response $Y^{*}$ in Fig. 1A leads to derepression of a downstream component. Our analysis shows that, indeed, the dose response of the downstream component is better aligned with the receptor occupancy than the dose response of $Y^{*}$ (SI Appendix, section S8). An alternate mechanism where derepression is followed by activation by modifying Fig. 1B also exhibits a similar behavior. For each of these cascades, as expected, the response time of the downstream component depends less strongly on the stimulus than that of $Y^{*}$ (SI Appendix, section S8). It is worth noting that nonlinear regulation, such as feedback and feedforward loops, can also be used to compensate for undesirable characteristics of a given signaling mechanism. For example, negative feedback can align the dose–response curve with receptor occupancy for signaling pathways that operate through activation (43, 79, 80).

Having studied dose–response and response time of model generalizations, we next investigate the wider applicability of the results on the switch architectures’ abilities to process upstream fluctuations. Instead of looking at specific generalizations, we assume that the inactive receptors $X\left(t\right)$ and the active receptors $X^{*}\left(t\right)$ are unspecified stochastic processes that are correlated with the number of active switches $Y^{*}\left(t\right)$. Specifically, we assume a positive correlation between $X^{*}\left(t\right)$ and $Y^{*}\left(t\right)$, and a negative correlation between $X\left(t\right)$ and $Y^{*}\left(t\right)$. This assumption is consistent with the models in Fig. 1 as well as models consisting of receptor removal and kinetic proofreading. We show that in such a setup, the steady-state noise in $Y^{*}$ is highest for the concerted mechanism (SI Appendix, section S9). Thus, our findings on processing of upstream fluctuations by different signaling mechanisms are generalizable.

Discussion

Molecular switches are important components of most signaling pathways. Typically, these switches can exist in two states, on and off, and the presence of an external stimulus biases the switch toward the on state. This transition can occur either by increasing the off-to-on rate (activation), decreasing the on-to-off rate (derepression), or both (concerted). We characterized these three mechanisms in terms of their dose–response curves, response times, and abilities to process upstream fluctuations. We further examined how these three mechanisms were affected by some generalizations of the receptor dynamics. The following list summarizes key differences in the performance of switches based on activation, derepression, and concerted mechanisms:

• $•$Both activation and derepression cannot align signaling activity with receptor occupancy. In particular, activation reduces the stimulus level required for half-maximal signaling as compared to $50\%$ receptor occupancy (${\mathrm{\Theta }}_{Y^{*}}<{\mathrm{\Theta }}_{X^{*}}$), whereas derepression produces a rightward shift of the dose–response curve (${\mathrm{\Theta }}_{Y^{*}}>{\mathrm{\Theta }}_{X^{*}}$). The dose–response curve aligns with the receptor-occupancy curve (${\mathrm{\Theta }}_{Y^{*}}={\mathrm{\Theta }}_{X^{*}}$) for a perfect concerted mechanism (Fig. 2).
• $•$A concerted mechanism is capable of ratiometric signaling, where the steady-state signaling output only depends upon fractional receptor occupancy, and not on the total number of receptors.
• $•$The response time for the activation mechanism decreases with signal strength, whereas it increases for the derepression mechanism. Importantly, the response time for a perfect concerted mechanism is independent of signal strength (Fig. 3).
• $•$Activation and derepression mechanisms respond similarly to upstream fluctuations, whereas the concerted mechanism is more susceptible to fluctuations (Fig. 4). Unlike the mean steady-state response, fluctuations in the output signal for the ratiometric signaling do depend on the total number of receptors.
• $•$These results generalize to models that include more complex receptor dynamics, e.g., receptor removal and kinetic proofreading.
• $•$Preferential removal of active (inactive) receptors leads to an adaptive response for the activation (derepression) mechanism and a sustained response for the derepression (activation) mechanism (Fig. 5).

These results suggest performance trade-offs in the operating characteristics for each mechanism. The activation mechanism can increase the sensitivity of the pathway and generate response times that decrease with signal strength, but at the cost of dose–response curves that do not align with receptor occupancy, potentially limiting the pathway’s ability to transfer information (79). In this sense, the activation mechanism operates as an “eager” system that is sensitive to small receptor occupancy and accelerates the response for stronger signals. Therefore, activation seems appropriate for situations in which the cost of a false negative is greater than a false positive. For example, the adrenaline response to imminent danger should be sensitive and fast because cost of a false positive is small, but a false negative can be deadly.

Similar to the activation mechanism, derepression leads to misalignment of the dose–response curve and receptor occupancy. However, for derepression, the dose–response curve is shifted to the right. Another difference between these mechanisms is that for derepression, the response time increases with signal strength. Therefore, derepression acts as a “measured” system that does not respond to low receptor occupancy, waiting for a strong signal before committing to a response. Derepression seems appropriate for scenarios where the cost of a false positive is greater than a false negative. Interestingly, derepression-based signaling is found in many plants’ pathways. We speculate that it happens because plants have to continually allocate their limited resources between growth in competition with their neighbors and immunity to survive pathogen attack (81, 82). For example, plants would perhaps ignore growth of a low level of pathogenic bacteria before allocating resources to fight them. Other possible scenarios where derepression may be used include irreversible cell-fate decisions such as the WNT pathway for embryo development (83) and fail-safe mechanisms such as the hypoxia-inducible factor in face of oxygen deprivation (84).

The concerted mechanism is better able to align with the receptor-occupancy curve than either the activation or derepression mechanisms. Therefore, it has better information fidelity (79). The concerted mechanism also can generate response times that are independent of the strength of the input signal. However, these features come at the cost of higher susceptibility to upstream fluctuations. We note that in a recent study, it was shown that ratiometric (concerted) signaling provided an advantage for gradient sensing, because it could compensate for spatial variations in the receptor concentration (14). The system under consideration in that study was the mating response of yeast. For this case, the spatial fluctuations in the receptor concentration were larger than downstream fluctuations in signaling, allowing the concerted mechanism to outperform an activation-based mechanism.

While misalignment of the dose–response curve with receptor occupancy can cause loss of information, it may also offer some advantages. Consider a scenario where active receptors are preferentially removed, resulting in adaptation of the signaling response (Fig. 5). Recent work has shown that it is possible to exploit this feature to perform relative sensing (fold-change detection) if the receptor removal is a multistep process (42). Alternatively, a negative feedback may also result in an adaptive response and thereby a fold-change detection (59). A key feature of fold-change detection is that the sensitivity of the system decreases each time the system adapts (59, 85). Our results suggest that a relative sensing mechanism may be implemented with a derepression if the receptor removal operates on inactive receptors. We speculate that a negative feedback operating on inactive receptors would also yield the same effect.

Understanding the evolutionary constraints that favor either activation or derepression in the context of gene regulation is a long-standing question that has been addressed (48–50). Under the assumption that both mechanisms are functionally equivalent, these investigations theorized that activation is selected when demand for the gene product is high, whereas derepression is favored when demand is low. Our results reveal that these mechanisms have different operating characteristics. In particular, our analysis demonstrates that activation operates as an eager system and derepression as a measured system, thus providing a functional perspective when considering evolutionary advantages of each mechanism.

A limitation of our investigations is that the models we considered assumed mass-action kinetics for enzymatically driven reactions, and therefore do not capture saturation effects. While we do not anticipate that the qualitative features of our main results will change when this assumption is relaxed, it is possible that including saturation effects will produce behavior not captured by the current model. Therefore, extending our model to include saturation effects will be the subject of future investigations. Another future direction is to analyze the performance of the three switches when they are subjected to feedback and feedforward regulation. We end by noting that while we focused our investigations on signaling pathways, our results are likely to be relevant for understanding other intracellular systems, such as gene-regulatory networks and metabolic pathways.

Data Availability

Data have been deposited in GitHub (https://github.com/elstonlab/2021PNAS_SwitchComparison).