Rapidly deployable and morphable 3D mesostructures with applications in multimodal biomedical devices

Significance

The ability to miniaturize deployable and morphable structures could significantly broaden their applications in biomedical, healthcare, and electronics devices, but remains to be very challenging, due to the difficulty to achieve considerable actuation deformations at small scales (e.g., several millimeters). Here, we present actuation schemes and design strategies to enable assembly of three-dimensional (3D) mesostructures that actively, rapidly, and reversibly deform (by nearly an order of amplitude in size) and switch among various stable states. These schemes provide routes to multimodal devices that actively change their functions following changes in shapes. A skin sensor that can actively switch between the deep and shallow sensing modes serves as an example to demonstrate the promising potential toward developments of multimodal biomedical devices.

Abstract

Structures that significantly and rapidly change their shapes and sizes upon external stimuli have widespread applications in a diversity of areas. The ability to miniaturize these deployable and morphable structures is essential for applications in fields that require high-spatial resolution or minimal invasiveness, such as biomechanics sensing, surgery, and biopsy. Despite intensive studies on the actuation mechanisms and material/structure strategies, it remains challenging to realize deployable and morphable structures in high-performance inorganic materials at small scales (e.g., several millimeters, comparable to the feature size of many biological tissues). The difficulty in integrating actuation materials increases as the size scales down, and many types of actuation forces become too small compared to the structure rigidity at millimeter scales. Here, we present schemes of electromagnetic actuation and design strategies to overcome this challenge, by exploiting the mechanics-guided three-dimensional (3D) assembly to enable integration of current-carrying metallic or magnetic films into millimeter-scale structures that generate controlled Lorentz forces or magnetic forces under an external magnetic field. Tailored designs guided by quantitative modeling and developed scaling laws allow formation of low-rigidity 3D architectures that deform significantly, reversibly, and rapidly by remotely controlled electromagnetic actuation. Reconfigurable mesostructures with multiple stable states can be also achieved, in which distinct 3D configurations are maintained after removal of the magnetic field. Demonstration of a functional device that combines the deep and shallow sensing for simultaneous measurements of thermal conductivities in bilayer films suggests the promising potential of the proposed strategy toward multimodal sensing of biomedical signals.

Deployable and morphable structures capable of changing their sizes and shapes significantly are essential in engineering (e.g., aerocrafts) and daily life (e.g., tents, umbrellas, and folding fans) (1, 2). Miniaturizing such structures to be comparable to the small scale in natural and/or human-engineered living systems such as arteries (1∼10 mm) (3), early-stage lesions (4), and organoids (∼1 mm) (5), and in minimally invasive surgeries (4) could broaden their applications in biomedical, healthcare, and electronic devices (6, 7). Recent advances in manufacture, fabrication, and assembly techniques enable the use of materials that respond to irradiation (8–12), magnetic field (13–21), electric field (22–27), electromagnetic field (28, 29), heat (17, 30–36), chemicals (37, 38), and pressures (39, 40) to remotely actuate large structural deformations (41–47). For example, the three-dimensional (3D) printing technique of programmed ferromagnetic domains developed by Kim et al. (13) realized the fast transformation between complex 3D configurations using magnetic field. By programming the magnetic configurations of nanomagnets, the micromachines developed by Cui et al. (19) could be transformed among multiple configurations. Mao et al. (28) presented soft electromagnetic actuators driven by Lorentz forces to fold two-dimensional (2D) precursors into various 3D shapes in spatially varying magnetic field. The silicon-lithium alloying reaction was exploited by Xia et al. (38) to drive the transformation of silicon-coated microlattices whose deformed shapes could be locked via plastic deformations.

Despite the significant progress, most of the existing strategies are demonstrated only at relatively large sizes (>1 cm), while the ability to scale the deployable and morphable structures down to small sizes, such as millimeter and submillimeter scales, is crucial for many applications, such as the minimally invasive surgery and the sensing of early-stage lesion. With the reduction of the structural size, the integration of actuation components with 3D structures becomes more challenging, and many types of actuation forces, especially those (e.g., Lorentz forces and magnetic forces) that can be controlled remotely, decrease significantly compared to the structural rigidity. Therefore, the strategies that work effectively at relatively large sizes (>1 cm) may not be applicable at millimeter and submillimeter scales. In particular, the following two aspects are worthy of further exploration. On one hand, while a few different strategies have been developed to lock the deformed shape after removing the external stimuli, such as those based on plastic deformations (38, 48), shape-memory effects (49–52), and multistable structures (53–61), none is without limitations. For example, plastic deformations could reduce the durability of 3D architectures, and the prolonged period of phase transition in the shape-memory effect limits the speed of the reconfiguration (49–51). For specially engineered 2D patterns, the mechanics-guided, deterministic 3D assembly through the use of diverse release paths of biaxial prestrain allowed the transformation of assembled structures among multiple stable states (53–55), but applying a mechanical force to the underlying elastomeric substrate in situ is difficult. Incorporating dielectric elastomers that deform under an applied electric field as the assembly platform allows the formation of reconfigurable 3D mesostructures but requires high voltages and patterned electrodes (62, 63). Other strategies including the bistable Kresling patterns in response to the distributed magnetic actuation (15) were demonstrated at relatively large scales (>1 cm). A rapid, robust, and reversible shape reconfiguration at a small scale requires an actuation source that can be easily controlled, as well as a tailored design of low-rigidity structures. On the other hand, many deployable and morphable structures adopted intrinsically soft materials, such as elastomers (modulus ≤ 10 MPa) (64), which limits their applications in microelectronics and biomedical devices. This is because the inorganic functional materials (e.g., metals, silicons, and piezoelectric ceramics) often have large moduli (≥50 GPa) and may not be directly incorporated into those soft structures, due to the incompatibility of the fabrication technique and the increased structural rigidity. Three-dimensional structures made of intrinsically hard functional materials have been previously reported by our group (65–68), but active, large deformations are not accessible, due to the large rigidity and/or the lack of actuation components.

Here, based on the mechanics-guided, deterministic 3D assembly (69–82), we introduce schemes of electromagnetic actuation and strategic structural designs to overcome the above limitations. The 3D assembly technique enables the integration of actuation components such as current-carrying metals (66) and magnetic materials (71) into small-scale 3D architectures to generate driving forces with portable magnets, as well as functional components ranging from silicons (67, 68), commercial chips (83–86), to piezoelectric ceramics/polymers (65, 87, 88). The design of low-rigidity structures guided by the finite element analysis (FEA) allows access to large deformations driven by those forces that are otherwise too small for conventional structures (89) at small sizes (e.g., <5 mm). The proposed strategies enable the assembly of millimeter-scale structures of various geometric configurations with submillimeter-scale feature sizes (e.g., ribbon width), ranging from 3D serpentines, kirigami patterns, to pop-up books that can switch rapidly and reversibly among multiple stables states. In particular, combined computational and experimental studies allow the formation of millimeter-scale deployable structures that can rapidly change their sizes by approximately one order of amplitude, which are unachievable previously. Furthermore, we demonstrate a functional device for detection of the thermal conductivities of a bilayer material, which can be actively switched between the deep and shallow sensing modes.

Results and Discussion

Schemes of Electromagnetic Actuation for 3D Reconfiguration.

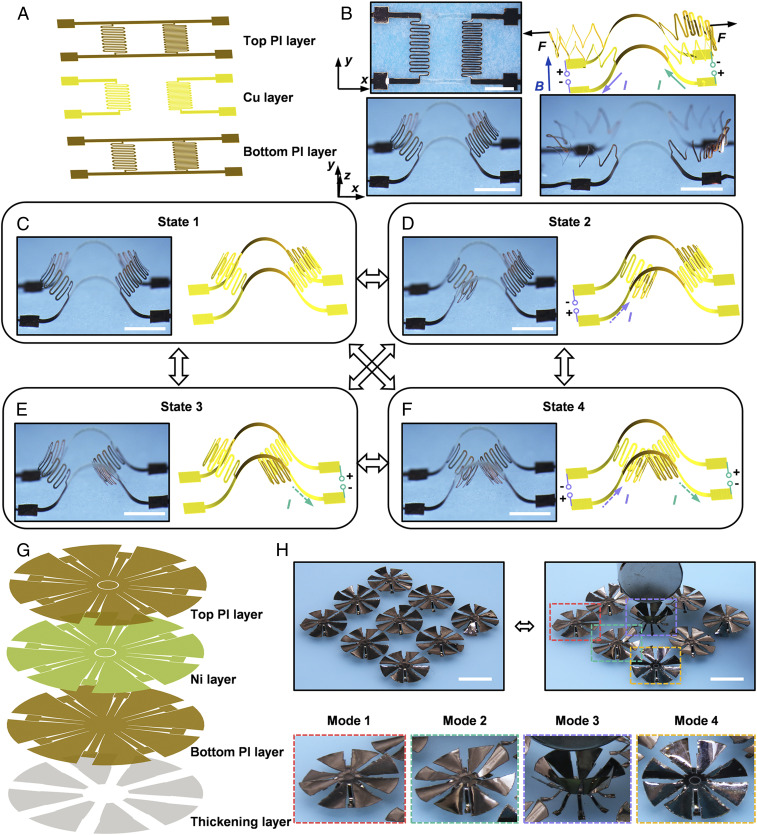
Fig. 1 presents combined experimental and numerical results that illustrate two representative schemes of electromagnetic actuation, relying on the use of either Lorentz forces or magnetic materials. Fig. 1A provides a schematic illustration of a 2D precursor design, where the functional component crucial to the generation of Lorentz force is a patterned copper (Cu) layer (300 nm) sandwiched between two polyimide (PI) layers (∼3 μm each; see Materials and Methods for details). The four square anchors serve as bonding sites with a prestretched elastomeric substrate, while the other region of the 2D film forms a weak interface governed by van der Waals interactions. Release of the biaxial prestrain (∼36%) results in a controlled compressive buckling that converts the 2D precursor to a double-layer, multistable 3D architecture consisting of two reconfigurable serpentine ribbons and two supportive ribbons (Fig. 1 B, Left). The assembled 3D mesostructure is then placed in a uniform magnetic field (magnetic flux density B ∼ 0.4 T) applied by a couple of portable, disk-shaped magnets (diameter, 60 mm; SI Appendix, Fig. S1). Connecting the exposed metal layers at the bonding sites to external current sources generates Lorentz forces that can enable the 3D reconfiguration among various stable and/or temporary states. Here, the patterned metal film divides the electrical current (I) into two independently addressable channels, each flowing past one serpentine ribbon in the buckled structure (SI Appendix, Fig. S2A). The amplitude and the direction of the current in each channel can be adjusted remotely and rapidly, therefore enabling a remote and accurate control of the Lorentz force applied to each serpentine ribbon. Note that the 3D configuration formed through the buckling-guided assembly corresponds to the first-order buckling mode, which is referred to as the stable state 1 (Fig. 1C and SI Appendix, Fig. S2B). Starting from the stable state 1, the electrical currents, shown in Fig. 1D, generate Lorentz forces that push the left serpentine ribbon inwards. When the electrical current exceeds a critical value to overcome the energy barrier of the structure, the left serpentine ribbon snaps to the other side to form the stable state 2 that corresponds to the second-order buckling mode. After turning off the current, the mesostructure remains in stable state 2, due to the energy barrier. Applying Lorentz forces in the opposite direction returns the mesostructure to the stable state 1. Similarly, the mesostructure can be reversibly switched into two other stable states 3 and 4 (Fig. 1 E and F). Based on this strategy, the mode switch between any of the two stable states among 1∼4 can be realized directly (SI Appendix, Fig. S2 C and D). Moreover, by applying Lorentz forces that push the serpentines outwards, a temporary configuration (Fig. 1 B, Right) can be reached, where the distance between two serpentine ribbons is maximized (∼1 cm). This strategy enables the structure to switch between a folded shape (Fig. 1F) and an extended shape (Fig. 1 B, Right), with the overall size (measured by the distance between two serpentine ribbons) changing by approximately one order of amplitude. The above processes of state switch can be well predicted by FEA (see SI Appendix, Finite element analysis for details). According to FEA calculations, the maximum strain in both the Cu and the PI layers is below the threshold of plastic deformations, which ensures the robustness and durability of the mesostructure (SI Appendix, Fig. S3A). This is also evidenced by the cyclic experiment (SI Appendix, Fig. S3B), where the mesostructure can be switched between the folded and extended shapes (i.e., the configurations in Fig. 1F and the right panel of Fig. 1B) for 3,000 times without fracture.

Fig. 1.

Schematic illustrations of 3D mesostructures actuated by Lorentz forces and magnetic forces. (A) Schematic illustration of the 2D precursor in an exploded view to show the layer construction. (B–F) Optical images and FEA results of a deployed 3D ribbon mesostructure, actuated by applying the Lorentz force. (Scale bar, 2 mm.) (C–F) Optical images and FEA results of four different stable configurations for the assembled 3D mesostructure, which can be triggered by applying different Lorentz forces (through control of the electrical current). (Scale bars, 2 mm.) (G) Schematic illustration of the 2D precursor in an exploded view to show the layer construction, including a nickel layer (600 nm) sandwiched between two polyimide (PI) layers (∼7 μm each) with a thickening layer (PI, ∼8 μm). (H) Array of magnetic architectures deformed under an external magnetic field, with the Bottom illustrating deformations of four unit cells. (Scale bars, 10 mm.)

An alternate scheme relies on the use of a magnetic material (nickel, 600 nm) that is deposited between two PI layers to generate magnetic forces in the gradient magnetic field (Materials and Methods), without the need to use any power source (Fig. 1G). Here, a thickening layer (PI, ∼8 μm) is added below the bottom PI layer to ensure the flatness of the 2D precursor after the microfabrication, which is important for the integration of functional, commercial units into 3D devices. This design adopts the design of a spatially varying magnetic field to deform the same structure into diverse shapes. To illustrate this capability, Fig. 1H shows an array of identical mesostructures formed by compressive buckling, which can be reshaped into different 3D configurations when placed near a magnet (diameter, ∼20 mm; thickness, ∼10 mm), following the gradient of the magnetic field. Four typical modes are zoomed in at the bottom of Fig. 1H. In the middle of array, all petals of the 3D mesostructure are lifted up, as shown in Fig. 1H (mode 3, purple frame). At the sides of array, the petals that are close to the magnet are also lifted (mode 2, green frame).

Reconfigurable and Deployable 3D Mesostructures Actuated by Lorentz Forces.

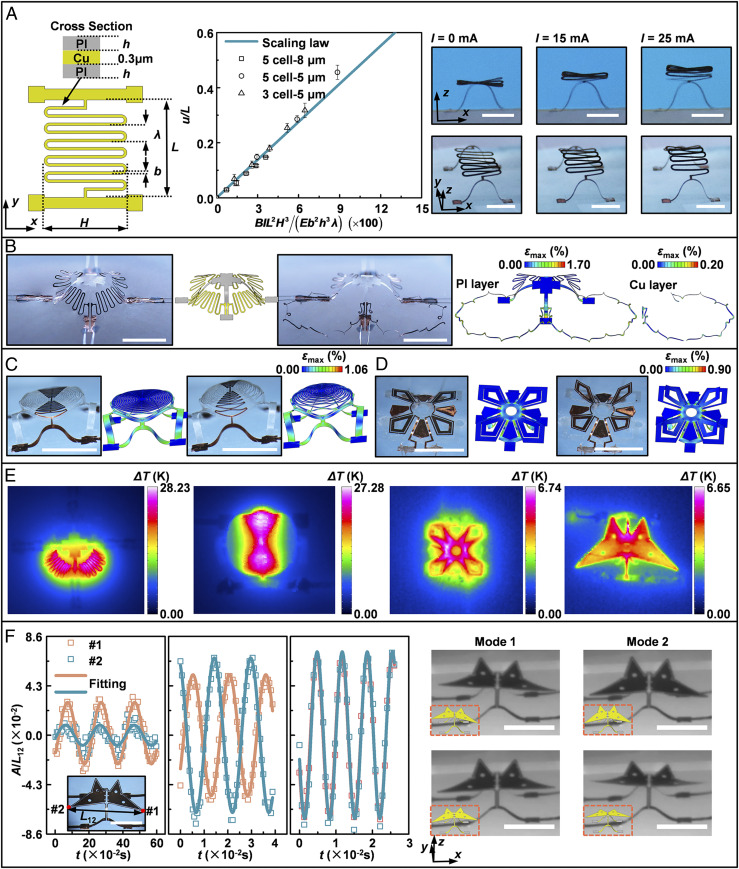
To shed light on the key parameters that control the capability of electromagnetic actuation, we focus on the mechanics analyses of a representative design with a suspended serpentine configuration, as shown in Fig. 2A. The 2D precursor (Fig. 2 A, Left) consists of two straight ribbons and a serpentine ribbon in the middle to enhance the flexibility of the mesostructure. By adjusting the prestrain components in the x and y directions, the serpentine ribbon could maintain a roughly flat state during the buckling-guided assembly. Here, we use the maximum deflection [i.e., the out-of-plane displacement (u) at the center point of the structure, as shown in SI Appendix, Fig. S4A] of suspended serpentine mesostructure to measure the capability of electromagnetic actuation. In the simulation, five repeating unit cells are selected for the serpentine ribbon. The copper layer (∼300 nm) is sandwiched between two PI layers (each layer with a thickness >5 µm). Considering the much smaller thickness of Cu layer than the PI layer, the contribution of Cu layer to the effective bending stiffness can be neglected. Based on a series of parameter analysis using FEA (SI Appendix, Derivation of the scaling law for the normalized out-of-plane displacement actuated by Lorentz force), a scaling law of normalized displacement (u/L) is given by the following:

$$\frac{u}{L}=4.6\times {10}^{-4}\frac{BI{L}^2{H}^3}{E{b}^2{h}^3\lambda },\left(\frac{u}{L}>5\%\right).$$ [1]

Fig. 2 A, Middle, presents measurement results for the normalized out-of-plane displacement (u/L) versus the combined parameters, showing an excellent proportional correlation. Here, each of the eight parameters varies independently in its representative range. The dots are for FEA with the baseline values of eight parameters, including Young’s modulus E = 2.5 GPa, thickness h = 7 μm, width b = 300 μm, unit cell length λ = 1,800 μm, height H = 9120 μm, representative length L = 16,200 μm, I = 10 mA, and B = 0.1 T, as shown in SI Appendix, Fig. S4B. Fig. 2 A, Right, provides optical images of the raised serpentine mesostructure (five cells, h = 8 μm, B = 0.15 T) under different levels (0, 15, and 25 mA) of current. Good agreements can be observed between the scaling law and measurements, suggesting that Eq. 1 can accurately predict the normalized out-of-plane displacement of the serpentine mesostructure under large deformations. It is noteworthy that the deformed configuration of the suspended serpentine ribbon can be adjusted by changing the direction of magnetic field (SI Appendix, Fig. S5). Fig. 2B and SI Appendix, Fig. S6A show the design and deformation of a deployable mesostructure with four serpentine ribbons. The projected area of deployed flexible mesostructure to the x–y plane is nearly 6.2 times larger than that of the initial state. Even at such large level of deformations, the maximum strains of PI and Cu layers are both well below their plastic limits, as shown in Fig. 2 B, Left. Diverse actuation deformations driven by Lorentz forces are possible with appropriate choices of structural pattern and circuit design. Experimental and computational studies of two examples appear in Fig. 2 C and D, and their 2D precursors are in SI Appendix, Fig. S6 B and C. A kirigami structure with symmetric cuts on a circular membrane is shown in Fig. 2C, where the circuits are distributed at part of the disk. By applying external magnetic field and current, the relative flat membrane is deformed into a curved surface. In Fig. 2D, the circuits are distributed along the edge of four petals, such that the actuation deformations can be triggered only at these local regions. Another example (SI Appendix, Fig. S7) shows the actuation deformations of a cartoon dog face driven by Lorentz forces. The temperature distributions of electromagnetic 3D mesostructures were detected by infrared camera (VarioCAM HD head; InfraTec), with a few representative results presented in Fig. 2E. The currents applied to the deployable mesostructure (Fig. 2B) and kirigami mesostructure (Fig. 2C) are I = 70 mA and I = 50 mA, resulting in a relatively high temperature rise (up to ∼28.2 K), as shown in the Left two panels of Fig. 2E. However, this level of temperature increase does not cause any plastic deformations in the structures, as evidenced by the almost complete recovery of 3D configuration when the magnetic field (or electrical current) is removed. In the other two examples (Right two panels, Fig. 2E), the temperature changes (up to ∼6.7 K) are much lower, in part due to the lower current (I = 40 mA).

Fig. 2.

Programmable deformations in mechanically assembled 3D mesostructures actuated by Lorentz forces. (A) Scaling laws and experimental results for the maximum out-of-plane displacement of the suspended serpentine mesostructure as a function of the combined parameter, BIL²H³/(Eb²h³λ). (Scale bars, 4 mm.) (B) Optical images and FEA results for a highly deployable 3D mesostructure. The rightmost panel shows the distribution of the maximum principal strain. (Scale bars, 4 mm.) (C and D) Experimental and FEA results that illustrate actuated deformations in two 3D mesostructures, controlled by the Lorentz force. (Scale bars, 4 mm.) (E) Measured temperature distribution of 3D mesostructures when the electrical currents are applied. (F) Time responses of vibrational amplitudes at two endpoints of wings (marked as #1 and #2) in a butterfly-shaped mesostructure, for alternating currents with three different frequencies (5, 65, and 145 Hz, from Left to Right). The images on the Right show vibrational modes at the two lowest resonant frequencies. (Scale bars, 4 mm.)

Fig. 2F, Left, presents time responses of vibrational amplitudes in a butterfly-shaped mesostructure subjected to a sine wave current with three different frequencies (f = 5, 65, and 145 Hz, from Left to Right; AFG2021; Tektronix). The 2D precursor of this mesostructure is in SI Appendix, Fig. S6D. Here, the vibrational modes can be described using the out-of-plane displacement component at the two endpoints of wings. The optical images and FEA predictions (in red frame) of the two lowest order modes appear in the Right of Fig. 2F. According to these results, the first-order and second-order modes correspond to the left–right vibration and front–back vibration, respectively. Although we focus on the combination of the electromagnetic actuation with the mechanics-guided, deterministic 3D assembly technique in this study, the approaches and design principles could be extended to other scenarios (e.g., the actuation of a free-standing, initially flat precursor without prestrain in the substrate).

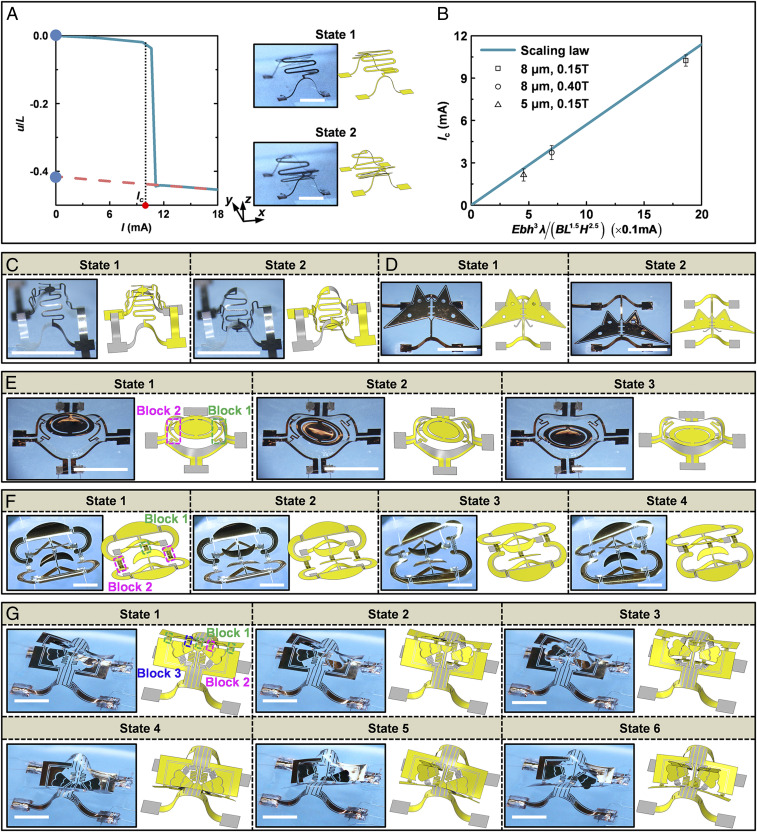
The Lorentz force can be also utilized to trigger the mode transition of reconfigurable 3D mesostructures assembled through compressive buckling. Fig. 3A and SI Appendix, Fig. S8A provide a simple example of suspended serpentine mesostructure assembled using a biaxial prestrain (ε_x-pre = 50% and ε_y-pre = 11%). Here, the normalized, maximum out-of-plane displacement (u/L) is plotted as a function of the current (Fig. 3A) to capture the deformation process between different stable states. Starting from the stable state 1 with a pop-up serpentine mesostructure, the magnitude of u/L increases slightly with increasing the current, until a critical current (I_c) is reached. Across this critical current (I_c), the mesostructure undergoes an abrupt transition into another stable state with a pop-down serpentine mesostructure, resulting in a sharp drop of u/L, as shown in the Right of Fig. 3A (optical images and FEA results). If the current is removed after the mode transition, the magnitude of out-of-plane displacement decreases slightly, since the serpentine mesostructure maintains the pop-down state. According to the theoretical analyses and FEA calculations, a scaling law of the critical current (I_c) (SI Appendix, Fig. S8B and Derivation of the scaling law for the critical current of state switching) can be given by the following:

$$I_{\mathrm{c}}=5\text{.}7\frac{Eb{h}^3\lambda }{B{L}^{1.5}{H}^{2.5}}.$$ [2]

Fig. 3B presents measurement results of the critical current, which agree reasonably well with the results based on Eq. 2, verifying the proportional dependence of I_c on the combined parameter, $\frac{Eb{h}^3\lambda }{B{L}^{1.5}{H}^{2.5}}$. This scaling law also suggests that the critical current increases with increasing the rigidity of suspended serpentine mesostructure.

Fig. 3.

Reconfigurable 3D mesostructures that can be reshaped by Lorentz forces. (A) FEA results that show the normalized maximum out-of-plane displacement versus the current applied to the suspended serpentine mesostructure. (Scale bars, 4 mm.) (B) Scaling laws and experimental results for the critical current of the suspended serpentine mesostructure as a function of the combined parameter, Ebh³λ/(BL^1.5H^2.5). (C–E) Optical images and FEA results that illustrate different stable configurations of reconfigurable 3D mesostructures. (Scale bars, 4 mm.) (F) Similar results for an origami-shaped reconfigurable mesostructure with four stable states. (Scale bars, 4 mm.) (G) Similar results for a reconfigurable origami mesostructure with six stable states. (Scale bars, 4 mm.)

Compared with the loading-path controlled strategy (53, 55), the presented scheme based on Lorentz forces can complete the mode switch more rapidly (e.g., <1 s), since it does not involve the stretch and release of the elastomer substrate. Fig. 3 C and D presents two bistable mesostructures that can be switched rapidly between different stable configurations by adjusting the magnitude of electrical currents (the circuits shown in SI Appendix, Fig. S9 A and B). A further extension of these design concepts allows the assembly of complex 3D mesostructures that can be switched among more (≥3) different stable configurations. Fig. 3 E–G provides three examples of multistable 3D mesostructures that incorporate appropriate designs of electrical circuits (SI Appendix, Fig. S9 C–E) and structural components that can either buckle upward or downward. Here, the structural components are the building blocks for achieving the mode transition. In Fig. 3E, the mesostructure has two such building blocks, i.e., the arc parts (in green and purple frames) labeled as “block 1” and “block 2,” respectively, and correspondingly two separate electrical circuits, labeled as “channel 1” and “channel 2” (SI Appendix, Fig. S9C), respectively. The stable state 1 denotes the configuration formed through compressive buckling. By adjusting the magnitude of electrical current in channel 1 and fixing the magnetic field based on this configuration (state 1), a downward Lorentz force is applied to the block 1, leading to its mode switch from the pop-up to the pop-down state. In the meanwhile, the other part of the reconfigurable 3D mesostructure (Fig. 3E) undergoes a slight level of deformations due to the mechanical coupling, resulting in the formation of a distinct stable configuration (state 2). By further adjusting the magnitude of electrical current in channel 2, this mesostructure deforms from state 2 to state 3, due to the mode transition of block 2. Note that a fourth state that is essentially the same as state 2 (due to the structural symmetry) exists, where the block 1 pops up and the block 2 pops down. This stable state is not shown in Fig. 3E. Following a similar design strategy, Fig. 3F shows a reconfigurable origami-shaped mesostructure with two building blocks controlled by two independent electrical circuits (SI Appendix, Fig. S9D). Four stable states are accessible by individually controlling the stable states of two building blocks (block 1 and block 2, in green and purple frames, respectively). In this design, serpentine ribbons serve as the building blocks for the mode transition. Two sets of serpentine ribbons marked by the purple frame in Fig. 3F are designed to be in the same electrical circuit, and therefore, undergo deformations simultaneously, such that they can be regarded as a combined building block. By turning on the electrical circuits (from channel 1 to channel 2 to channel 1) in a certain order, the stable configuration of this 3D mesostructure can be programmed to be state 1, state 2, state 3, and state 4, in sequence. In Fig. 3G, a reconfigurable origami mesostructure with six stable states is achieved by controlling motions of three building blocks, with the design of electrical circuits illustrated in SI Appendix, Fig. S9E. Note that three sets of serpentine ribbons highlighted by the green frame in Fig. 3G runs in parallel and can be regarded as a combined building block. Two additional stable states that show geometric symmetry with respect to state 2 and state 5 are not shown in Fig. 3G. In principle, more stable states can be realized by increasing the number of building blocks (and accordingly, controlled electrical circuits) in the design. Theoretically, if there are N building blocks (each with two stable states) in a reconfigurable 3D mesostructure, the maximum number of stable states for the reconfigurable mesostructure is 2^N. In practical designs, this number (2^N) might not be reached, due to certain levels of geometric symmetry. In all of above demonstrations, optical images and FEA predictions of reconfigurable mesostructures show remarkably good agreements. Our experiments and scaling laws suggest that this actuation scheme and design strategy can also be implemented across a broad range of lengths scales (from 1 to 10 mm; SI Appendix, Fig. S10).

Reconfigurable and Deployable 3D Mesostructures Consisting of Magnetic Materials.

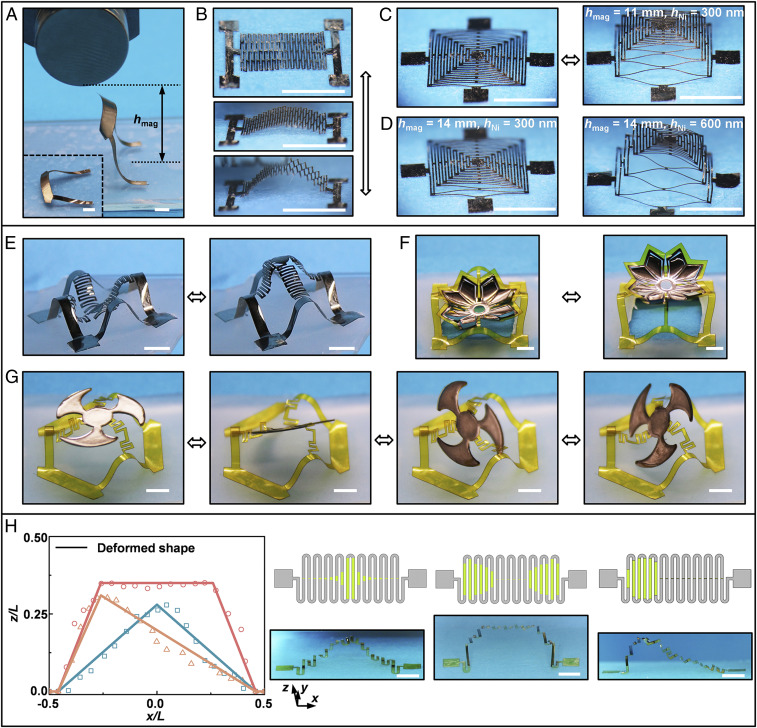
Excluding the electromagnetic actuation-based Lorentz forces, a more straightforward route relies on the use of magnetic metals (i.e., iron or nickel) that can be deposited at strategic locations of 2D precursors (SI Appendix, Fig. S11) to enable reconfigurable 3D mesostructures without a power source, as shown in Fig. 4. Fig. 4A shows such an actuation in a C-shaped mesostructure consisting of a sandwich construction of PI/Ni/PI. The as-assembled configuration (Fig. 4 A, Lower Left) is formed through use of a uniaxial prestrain (∼70%), and has a small height (2 mm), compared to the lateral dimension (14.5 mm). Applying an external magnetic field results in a large out-of-plane displacement (10 mm) in the C-shaped mesostructure. Similarly, Fig. 4 B and C shows large deformations in kirigami mesostructures, which drives the transformation of 2D precursors into 3D configurations. The raised height of kirigami mesostructures increases gradually when the magnet approaches the structures, as shown in Fig. 4B. Due to the low rigidity of kirigami mesostructures, the raised height is close to in-plane characteristic dimensions (Fig. 4C). Additionally, the raised height can be increased by increasing the Ni thickness to generate enhanced magnetic forces. Fig. 4D shows that when the Ni thickness increases from ∼300 nm (left frame) to ∼600 nm (right frame), the raised height of the mesostructure increases more than twice for the same external magnetic field (h_mag = 14 mm). Above examples illustrate that with proper designs of mesostructures, sufficient magnetic forces can be produced to drive large deformations of mesostructures. The magnetic forces can also enable the mode switch of reconfigurable mesostructures. Fig. 4 E and F shows two bistable mesostructures that can be switched rapidly (<1 s) between pop-up and pop-down states using an external magnetic field. Fig. 4G presents a design that can be switched among four different stable shapes, mainly resulting from the different spatial rotation of the flat patterned membrane in the 3D mesostructure. By depositing magnetic material (Ni) at selective regions and placing the magnet at various locations with respect to the structure, the distribution of magnetic force can be also controlled, providing an abundant degree of design freedom to achieve diverse structural deformations. For the serpentine mesostructure with the same 2D pattern, 3D mesostructures with a diversity of 3D profiles can be achieved by designing the distribution of Ni patterns (Fig. 4 H, Upper Right), with three representative examples shown in Fig. 4H. Here, different manufacturing and preparation processes can be used to form reconfigurable 3D mesostructures (Fig. 4 E–H and see Materials and Methods for details).

Fig. 4.

Deployable and reconfigurable 3D mesostructures achieved through use of magnetic materials. (A) Optical images of the as-assembled and actuated configurations for a C-shaped structure. (Scale bars, 4 mm.) (B) Optical images that show actuated deformations in a 2D kirigami mesostructure with unidirectional cuts. (Scale bars, 4 mm.) (C) Similar results for another 2D kirigami mesostructure with bidirectional cuts. (Scale bars, 4 mm.) (D) Optical images of the kirigami mesostructure with the same pattern as that in C, and two different metal thicknesses (300 and 600 nm). (Scale bars, 4 mm.) (E–G) Optical images that illustrate different stable configurations of reconfigurable 3D mesostructures that can be reshaped by applying external magnetic fields. (Scale bars, 4 mm.) (H) Optical images and 2D precursors for the serpentine mesostructures with different distribution of magnetic material on each straight ribbon. The leftmost panel shows the profiles of deformed shapes. (Scale bars, 4 mm.)

A Biomedical Device Capable of Both Deep and Shallow Thermal Sensing.

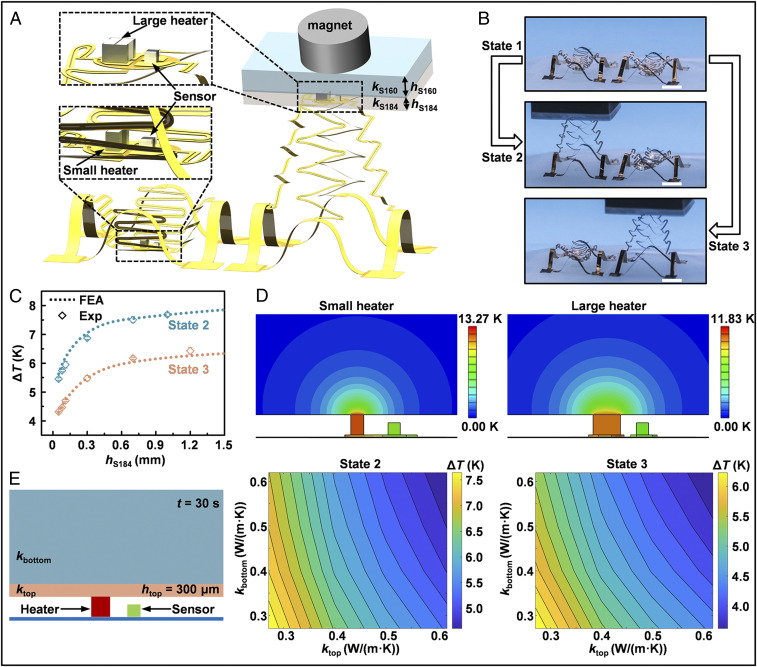
The integration of functional components in the deployable and morphable mesostructures described above allows practical applications in multimodal biomedical and healthcare devices. Fig. 5 provides a device demonstration for the simultaneous measurement of the thermal conductivity of each material component in a bilayer film (such as the epidermis and dermis in human skins). The device has two separate sensing units (Fig. 5 A, Top Left), each of which consists of a heater and a temperature sensor, as supported by a small disk connected to serpentine ribbons (cross-sectional profile: ∼5 μm PI/∼300 nm Cu/∼5 μm PI). The unit with a relatively large heater is designed for a deep sensing, and the other with a small heater is for a shallow sensing. A thickening layer (∼8 μm) is added below the small disk to ensure the flatness of the 2D precursor after the microfabrication. Under an external magnetic field, magnetic forces can be generated in the Ni layer in terminal electrodes of the commercial heater (thick film chip resistor) and sensor (chip NTC thermistor), and therefore, each unit can be pulled up or down, following the same strategy described in Fig. 4. By tailoring the pattern of the 2D precursor and placing the magnet in appropriate locations, the deformations of two sensing units can be controlled almost independently. In the rest mode, both sensing units are in the pop-down states (Fig. 5B, state 1) due to the gravity effect. Each of these units can be switched to the pop-up state and further deformed, such that the top surface of the heater is conformally in contact with the target material (Fig. 5B, states 2 and 3), without evidently interfering with the configuration of the other unit. Compared with the 2D device that is flat as fabricated, the deformation of each sensing unit is better controlled independently owing to the existence of energy barrier (E_barrier = E_peak − E_initial; SI Appendix, Fig. S12). Experiments on an artificial skin made of bilayers of Sylgard 184 silicone elastomer [k_S184 = 0.27 W/(m·K); Dow] and Sylgard 160 silicone elastomer [k_S160 = 0.62 W/(m·K); Dow] show that the temperature changes of the two sensing units are distinguishable for different Sylgard 184 thicknesses (h_S184). Here, the total heating power and heating time are fixed, and experimental measurements match reasonably well with FEA results (Fig. 5C).

Fig. 5.

A biomedical device for simultaneous measurements of thermal conductivities of bilayer materials. (A) Schematic illustration of the deployable, biomedical device for deformable process and measurement. (B) Optical images of biomedical device in different operational modes (states 1, 2, and 3). (Scale bars, 4 mm.) (C) Changes in temperature (ΔT) as a function of the thickness of Sylgard 184 silicone elastomer (h_S184) for two different states at a measurement time of 30 s. (D) Heat penetration depth induced by sensing units with small and large heaters on a semi-infinite, homogeneous medium. (E) Cross-sectional schematic image (Left) for measuring the thermal conductivities of a bilayer film, and contour plots of ΔT in terms of k_top and k_bottom for states 2 and 3 (Middle and Right).

The difference in the sensing depth of the two units mainly results from the heater size. For a simplified steady-state thermal conduction model consisting of a heater on a semi-infinite, homogeneous medium (SI Appendix, Fig. S13), the normalized temperature change below the heater (r = 0, where r is the distance to the center of the heater, as shown in SI Appendix, Fig. S13B) follows the scaling law (see SI Appendix, The sensing depth analysis and Fig. S13C for details) given by the following:

$$\frac{\mathrm{\Delta }T}{\mathrm{\Delta }{T}_{\max }}=F\left(\frac{z}{a}\right),$$ [3]

where ΔT_max = ΔT(z = 0, r = 0). This suggests that the heat penetration depth increases with increasing the heater size (a). Full-scale FEA on the device in Fig. 5A also shows that the sensing unit with a larger heater leads to a larger heat penetration depth than that with a smaller heater (Fig. 5D).

The measurement based on these two sensing units allows simultaneous detection of thermal conductivities of a bilayer material (e.g., epidermis and dermis). For a bilayer material with the top layer depth h_top = 300 μm (Fig. 5 E, Left), FEA shows distinguishable sensitivities of temperature changes (measured by the two sensing units) to changes in thermal conductivities of two different layers (in Middle and Right panels of Fig. 5E). In particular, the unit with a small heater is more sensitive to the change in the thermal conductivity (k_top) of the top layer than that with a large heater, while the latter is more sensitive to the change in the thermal conductivity (k_bottom) of the bottom layer. As such, both thermal conductivities of k_top and k_bottom can be determined by solving two coupled nonlinear equations. An error analysis (see SI Appendix, Error analysis for the thermal conductivities for details.) suggests that the errors in predictions of k_top and k_bottom are ∼3% and 10%, respectively (SI Appendix, Tables S1 and S2), for 0.1 K error in the temperature measurement (estimated from experiments).

Conclusion

The schemes of electromagnetic actuation and design methods of structure/circuit layouts presented here provide means to 3D mesostructures capable of changing their shapes significantly and rapidly. Integration of multiple independently addressable, current-carrying channels into the 3D mesostructure allows generation of precisely controlled Lorentz forces. Via the remote control of the amplitude and direction of current in each channel, the 3D mesostructure can be switched rapidly among various stable or temporary states. An alternate strategy that exploits magnetic forces induced by integrated magnetic materials under a spatially varying magnetic field provides an approach to drive the deformation of 3D mesostructure without an external power source. Guided by rational designs based on FEA and proposed scaling laws, around 20 morphable 3D mesostructures are presented, showing the applicability of proposed strategies. A functional device capable of switching between the deep and shallow sensing modes serves as an example to demonstrate the application of deployable and morphable mesostructures in multimodal, biomedical measurements.

Materials and Methods

Fabrication of Reconfigurable and Deployable 3D Mesostructures by Photolithography.

Preparation of 2D precursors in PI/metal/PI began with spin-coating a thin sacrificial layer of poly(methyl methacrylate) (950 PMMA A4; MicroChem; ∼200 nm in thickness) and a layer of PI (PI paa1002; Furunte; ∼3 μm in thickness) on a silicon wafer in sequence. Depositing a thin layer of Cu (∼300 nm in thickness) or Ni (∼300 nm in thickness) by electron beam evaporation, followed by the photolithography, realized the pattern of metal. Spin-coating another layer of PI (∼3 μm in thickness) on the PMMA/PI/metal pattern, depositing a thin layer of Ti (∼35 nm in thickness), and conducting the second photolithography process realized the pattern of hard mask. Then, the reactive ion etching (RIE Plasma System; Nordson MARCH) defined the 2D structures (2D precursors). Removing the hard mask by immersion in HF solution, and dissolving the underlying PMMA layer by immersion in acetone for 5 min, allowed the retrieval of 2D structures onto a piece of water-soluble tape (Water-Soluble Wave Solder 5414; 3M). The 2D structures were laminated onto a prestrained substrate (Dragon Skin; Smooth-On) by immersion in deionized water and then washing the water-soluble tape. Dispensing a commercial adhesive (Super Glue; Gorilla Glue Company) yielded strong interfaces only at the bonding sites. Slowly releasing the prestrain in the substrate completed the fabrication of 3D mesostructures (SI Appendix, Fig. S14).

Fabrication of Reconfigurable and Deployable 3D Mesostructures by Laser Cutting.

Preparation of 3D mesostructures in PI/metal/PI began with spin-coating a bilayer of poly(methyl methacrylate) (950 PMMA A4; MicroChem; ∼200 nm in thickness) and PI (PI paa1002; Furunte; ∼7 μm in thickness) on a silicon wafer, followed by depositing Cu (∼300 nm in thickness) or Ni (∼300/400/600 nm in thickness) by electron beam evaporation, and then spin-coating another layer of PI (∼7 μm in thickness). Laser cutting (VLS2.30; Universal Laser Systems) the PI/metal/PI membrane defined the 2D precursors. The following transfer printing and 3D assembly processes are the same as the fabrication of reconfigurable and deployable 3D mesostructures by photolithography (SI Appendix, Fig. S15A).

Preparation of 3D mesostructures in PI/Ni began with laser cutting the commercial PI film (∼8 μm in thickness) on a water-soluble tape to define the 2D precursors of the mesostructures, followed by depositing a thin layer of Ni (∼300 nm in thickness) at selective regions by electron beam evaporation through a shadow mask (PET; ∼250 μm in thickness). Dissolving the underlying water-soluble tape on a prestrained substrate and conducting the 3D assembly process completed the fabrication of 3D mesostructures (SI Appendix, Fig. S15B).

Fabrication and Measurement of 3D Biomedical Device.

Fabrication of 3D biomedical device capable of both deep and shallow thermal sensing began with preparation of 2D precursors in PI/Cu/PI as described in the fabrication of reconfigurable and deployable 3D mesostructures by photolithography. Additional steps involved the integration of heater (1 kΩ; thick film chip resistor; Panasonic) and sensor (10 kΩ at 25 °C; Chip NTC thermistor; TDK) on the 2D precursor of biomedical device, followed by adding a thickening layer (∼8 μm in thickness) below the small disk of the 2D precursor. A single thick film chip resistor was used as the small heater in the biomedical device, and two resistors in parallel as the large heater. The transfer and buckling steps followed the same procedures mentioned above.

The measurement hardware included a regulated direct-current (DC) power supply (TD1326; TASI), a translation stage (LWZ4060; MISI), and a digit multimeter (34465A; Keysight). The translation stage produced a motion of the sample that was close to the sensing units. The DC power supply was used to provide energy for the heaters. The digit multimeter recorded the resistance values of the sensor during heating.

Data Availability

All study data are included in the article and/or supporting information.