Shedding Light on the Black Box: Explaining Deep Neural Network Prediction of Clinical Outcomes

Abstract

Introduction:

Deep neural network models are emerging as an important method in healthcare delivery, following the recent success in other domains such as image recognition. Due to the multiple non-linear inner transformations, deep neural networks are viewed by many as black boxes. For practical use, deep learning models require explanations that are intuitive to clinicians.

Methods:

In this study, we developed a deep neural network model to predict outcomes following major cardiovascular procedures, using temporal image representation of past medical history as input. We created a novel explanation for the prediction of the model by defining impact scores that associate clinical observations with the outcome. For comparison, a logistic regression model was fitted to the same dataset. We compared the impact scores and log odds ratios by calculating three types of correlations, which provided a partial validation of the impact scores.

Results:

The deep neural network model achieved an area under the receiver operating characteristics curve (AUC) of 0.787, compared to 0.746 for the logistic regression model. Moderate correlations were found between the impact scores and the log odds ratios.

Conclusion:

Impact scores generated by the explanation algorithm has the potential to shed light on the “black box” deep neural network model and could facilitate its adoption by clinicians.

1. Introduction

In recent years, a special type of machine learning (ML) method called deep neural network (DNN) has brought breakthroughs to a wide range of artificial intelligence tasks including computer vision, speech recognition, and authentic games because DNN showed superior performance over traditional ML methods on those tasks [1–6]. Clinical applications of DNN quickly followed [7–9], with anticipation that DNN would revolutionize healthcare delivery, and there have been some early signs of success [7, 10–13].

DNN models are black boxes to most clinicians; understanding and explaining their behaviors is the subject of ongoing research [14, 15]. To gain clinical acceptance and implementation, we need to explain DNN models in a way that is clinically understandable [16, 17]. Traditional statistical models, especially linear models like logistic regression, are widely used because they provide explanations of the impact of each independent variable on the prediction (e.g. in the form of odds ratio), despite suboptimal performance. However, DNN models are particularly difficult to explain due to the highly complex transformations carried out between the “deep” layers in the DNN [14].

Compared to clinical data, natural scene images, speech recordings, or game board layouts are much easier for humans to understand. A human can quickly recognize a dog in an image, but cannot quickly interpret lab values, radiologic images, and clinical notes as sepsis. As a result, the limited DNN explanation studies that have been published are mostly intended to confirm human interpretation, e.g., if an image feature critical to the prediction of being a dog looks like the outline of a dog [18]. With clinical prediction, human users may not have such prior knowledge and expect the model to return clinical features that justify the prediction.

We are working on tackling the challenging problem of explaining DNN models. In this study, based on a cohort of over 20,000 patients with cardiovascular diseases, we built a DNN model to predict death within one year of a major cardiovascular procedure (MCVP) and provided explanations for the outcome prediction by the DNN model. To generate the explanation, we defined a new concept, referred to as the impact score. The impact score is based on the presence/value of clinical conditions’ impact on the predicted outcome. Similar to the (log) odds ratio generated by logistic regression models, impact scores are continuous variables intended to shed light on the black-box DNN models. For comparison, we fitted a logistic regression model on the same data. The logistic regression performance and the log odds ratios were compared with the DNN model performance and the impact scores.

2. Methods

2.1. Data

The data source for this study was the clinical data warehouse administered by Veteran Affairs Information and Computing Infrastructure (VINCI). We identified 21,355 veterans who had their first major cardiovascular procedure (MCVP) in 2014. The hospitalization during which the patient received the first MCVP was called the index hospitalization. The primary outcome was mortality within one year of the discharge date of the index hospitalization. The patient data used by the prediction model included demographic data as well as medical data from the two years prior to the index hospitalization and including the index hospitalization.

The demographic data included

• age (at the index hospitalization),

• gender,

• race,

• ethnicity.

The medical data included

• all ICD-9 diagnosis codes,

• all ICD-9 procedure codes used for MCVP,

• all medication orders,

• all-cause hospitalizations,

• clinical notes.

All the medical data except MCVP codes were obtained from the two years prior to the index hospitalization; the MCVP codes were obtained from the index hospital when the patients had their first MCVP in life. All the data except the clinical notes were structured (i.e., coded) data. Seven frailty indicators (e.g., mobility) were extracted from the notes using a natural language processing (NLP) program we previously developed [19].

2.2. Major cardiovascular procedures (MCVP)

Providers can now offer invasive and aggressive treatments to patients with cardiovascular disease - implantable cardioverter defibrillators, mechanical support devices, valve replacements, and other surgical procedures [20–22]. These interventions (i.e. MCVP), are invasive, involve risk, and can be painful; a careful patient selection is imperative [23–26]. Ideally, patients who receive these treatments should have a reasonable life expectancy to benefit from aggressive treatment, without substantial peri-procedural complication risk. The treatment intensity should match the expected patient outcome, yet providers do not have a reliable method to estimate prognosis as most clinical trials do not include older, frail patients. Older patients, in particular, comprise a growing proportion of the cardiac surgery population, but existing risk scores are inaccurate -- they overestimate risk in robust, older patients, and underestimate risk in frail, older patients [27].

2.3. Variables used for prediction

Model features were divided into two categories: temporal and non-temporal. The temporal variables were created based on the patient history data, whose values were always associated with a time stamp. The temporal variables included all-cause hospitalization, diagnostic classes, drug classes, and frailty indicators. The diagnostic classes were the major ICD-9 diagnostic code categories (e.g. neoplasm, mental disorders, etc.) [28]. The drug classes were the RxClasses [20] built upon the RxNorm codes. These variables, except for the frailty indicator variables, were binary with value 1/0 representing the presence/absence of the condition in the patient’s record at a given time. The frailty variable had continuous values ranging from 0 and 1, representing the severity of frailty status. The non-temporal variables included demographic variables (age, gender, race, etc.) and the types of surgery the patient had at index hospitalization. For the complete list of variables, see Table A (1^st column) in the Appendix.

2.4. Temporal data representation

To make temporal data suitable for use by the deep neural network, we proceeded as follows. First, we discretized time in the 2-year window prior to the index hospitalizations into 52 time points, with each time point representing a time slice of 2 weeks. For each temporal variable that took binary values, it took value 1 at a time point if the corresponding condition was present in the 2 weeks; otherwise, it took value 0. For each frailty variable, the maximum of the value(s) within the 2 weeks were used as its value at the time point. Thus, every temporal variable had a sequence of 52 values along with the time points on each patient. Next, we arranged the temporal variables in a fixed order so that each patient’s temporal data were represented by a matrix: the rows corresponded to the variables, and the columns corresponded to the time points. This matrix was further visually represented by an image, called a temporal image, as follows: every pixel of the image corresponded to an entry of the matrix, with color white/black representing value 0/1, and various gray scales representing values between 0 and 1. A sample image is provided in Fig. 1. Similar representations of patient data were used for feature embedding [29] and risk prediction [30].

Fig. 1.

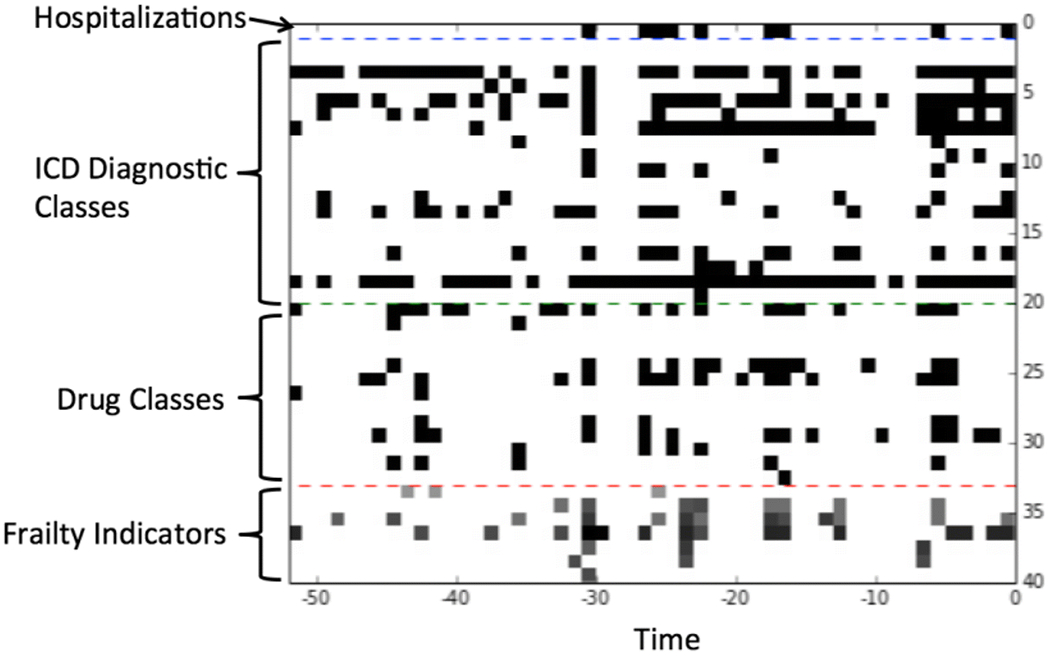
An example of the temporal images. The x-axis is the time (in weeks) within the 2 years prior to the discharge date of the index hospitalization. The y-axis is the list of temporal variables.

2.5. Building a deep neural network

The deep neural network had 2 branches at the input end (Fig. 2). One branch took temporal data as input and the other branch took non-temporal data as input. The branch taking temporal data as input was a convolutional neural network (CNN). This branch was composed of a sequence of layers as follows:

• an input layer (A) receiving temporal images/matrices as input

• a 1-D convolutional layer (B)

• a 1-D max-pooling layer (C)

• a 1-D convolutional layer (D)

• a 1-D max-pooling layer (E)

• a fully-connected layer (F)

Fig. 2.

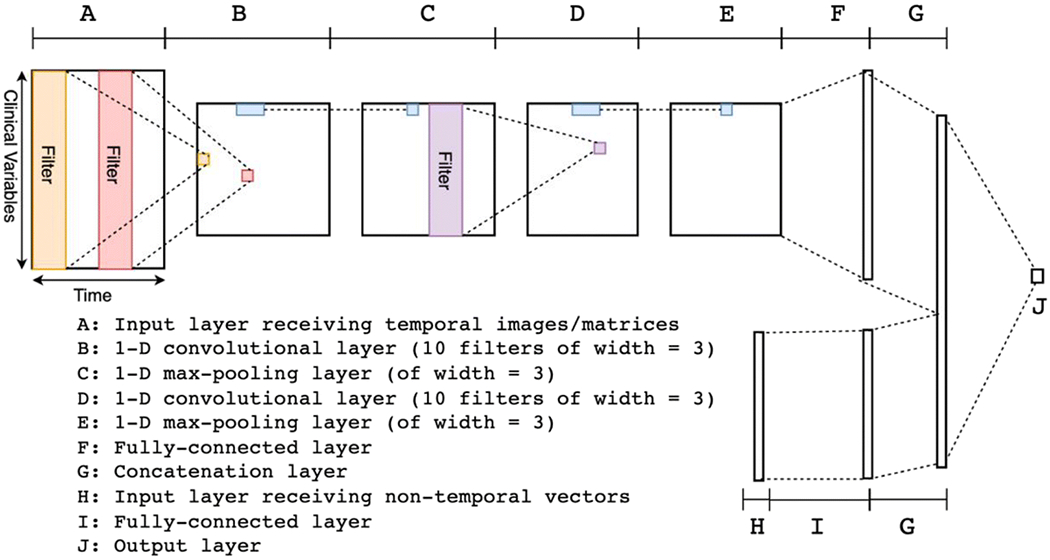
Architecture overview of the deep neural network (see description in text).

For each of the layers, the modifier “1-D” meant that the operations (convolution and max-pooling) were applied along the time-direction. Both of the convolutional layers (B and D) used 10 filters with a width of 3. Both of the max-pooling layers (C and E) had a width of 3 as well. The convolutional layers combined with the max-pooling layers were able to automatically extract higher level features from the raw data [31]. The other branch was composed of two layers as follows:

• an input layer (G) receiving non-temporal vectors as input,

• a fully-connected layer (H).

The last layers (F and H) from the two branches were joined using a simple concatenation to form the last hidden layer (I) of the whole network. The last layer, or the output layer (J), was a fully connected layer producing a single number as the output. All the non-linear activation functions for the hidden layers were the rectified linear function, defined as f(x) = max(x, 0). The non-linear function for the output layer was the sigmoid function, defined as $\sigma \left(x\right)=\frac{1}{1+e^{-x}}$, which transforms an arbitrary value into a value between 0 and 1. We used the binary cross-entropy function as the loss function and added both L1 and L2 regularizations. The weights were updated using the algorithm of stochastic gradient descent with Nesterov momentum. The DNN was implemented in a Python library called Theano [32] together with a helper library called Lasagne [33].

2.6. Training and evaluation

We divided the 21,355 patients into 3 sets: training (70%), validation (10%), and testing (20%). The initial weights in all the hidden layers and the output layer of the DNN were randomly assigned with small numbers. Then the DNN was trained on the training set with weights updated iteratively using backpropagation. The weights were updated using the method of mini-batched stochastic gradient descent. The size of each mini-batch was 50. After each epoch i.e., a single pass over the whole training set, the DNN model was evaluated on the 10% validation set to measure the performance. The training stopped when no improvements in the validation performance were observed over 10 consecutive epochs. The model with the best validation performance before training was stopped was used as the final model. This final model was then applied to the 20% testing set to measure the final performance. The main performance metric was area under the receiver operating characteristics curve (AUC).

2.7. Explain the outcome prediction

It is a difficult task to explain the prediction process inside a DNN due to the multiple layers of non-linear transformations from input to output. For the clinical domain, a key concern is the relationship between variables and outcomes; in logistic regression models, odds ratios describe such relationships. For DNN, we set out to measure the “impact” of each variable on the predicted outcome.

Observation-level impact score.

In our representation of temporal data, a temporal variable corresponds to a row of pixels, and every pixel with a nonzero value in the row means a presence (a value = 1) or a severity level (a value between 0 and 1) of the corresponding condition, hence represents an observation. To measure the impact of an observation on the outcome, we defined the impact score as follows. For each pixel with a nonzero value, we changed the value to zero and calculated the change on the prediction. The value 0 here is called the reference value. Recall that the last layer of the DNN outputs a value p between 0 and 1 through a sigmoid function p = σ(χ). The change of prediction was not the change in p but the change in x. One way to obtain x from p was to use the logit function: $x=\mathrm{logit}\left(p\right)=\log \frac{p}{1-p}$ Therefore, the observation-level impact score was defined as

$$\frac{\mathrm{logit}\left(p_{\mathrm{current}}\right)-\mathrm{logit}\left(p_{\mathrm{reference}}\right)}{\left(\mathrm{current\; pixel\; value}\right)-\left(\mathrm{reference\; pixel\; value}\right)}$$

where p_reference was the new value of p after changing the pixel value to the reference value 0.

Individual-level impact score.

To measure the impact of a temporal variable for an individual patient, we defined the individual-level impact score of a temporal variable as

$$\frac{\mathrm{logit}\left(p_{\mathrm{current}}\right)-\mathrm{logit}\left(p_{\mathrm{reference}}\right)}{\left(\mathrm{current\; max.\; pixel\; value\; in\; the\; row}\right)-\left(\mathrm{reference\; pixel\; value}\right)}$$

where p_reference was the new value of p after changing all pixel values in the row corresponding to the temporal variable to the reference value 0, and the “current max pixel value in the row” was the maximal pixel value along the same row.

For non-temporal variables, since each variable took a single value, the impact score followed the same way as the observation-level definition.

Population-level impact score.

We also defined the impact score of temporal or non-temporal variables at the population level simply as the mean of all the impact scores of the variable on all those patients in the training set who had an impact score. Note that a variable did not necessarily have an impact score on every patient: if a patient had no presence of a condition throughout the 2-year window, then according to the above definitions, there would be neither observation-level nor individual-level impact score for this variable, and this patient would not be included in the population to calculate of the mean of the impact scores.

2.8. Comparison with logistic regression model

Logistic regression models are widely accepted in the medical domain because they provide easy explanations/interpretations for the prediction. Specifically, the log odds ratios of a logistic regression model also describe the impact of the corresponding variables on the predicted results. Therefore, we built a logistic regression model on the same training set and evaluated its prediction performance (AUC) on the same testing set. Then we compared the impact scores we calculated based on the DNN model with the log odds ratios of the logistic regression model in terms of their correlations. The signs of the impact scores/log odds ratios also matter, so we also counted the number of variables whose impact scores and log odds ratios had both positive/negative signs or opposite signs. This comparison would provide, to a certain extent, a validation for using the impact scores to explain the DNN model. We did not expect the impact scores to be exactly the same as the log odds ratios but hypothesized that there would be moderate to strong correlations because both types of scores reflect the relationship between the variables and the outcome.

3. Results

Among 21,355 patients who underwent an MCVP in 2014, 6.8% died within one year following the index hospitalization. The AUC for the DNN was 0.787, compared to 0.746 for the logistic regression (LR) model (Fig. 3).

Fig. 3.

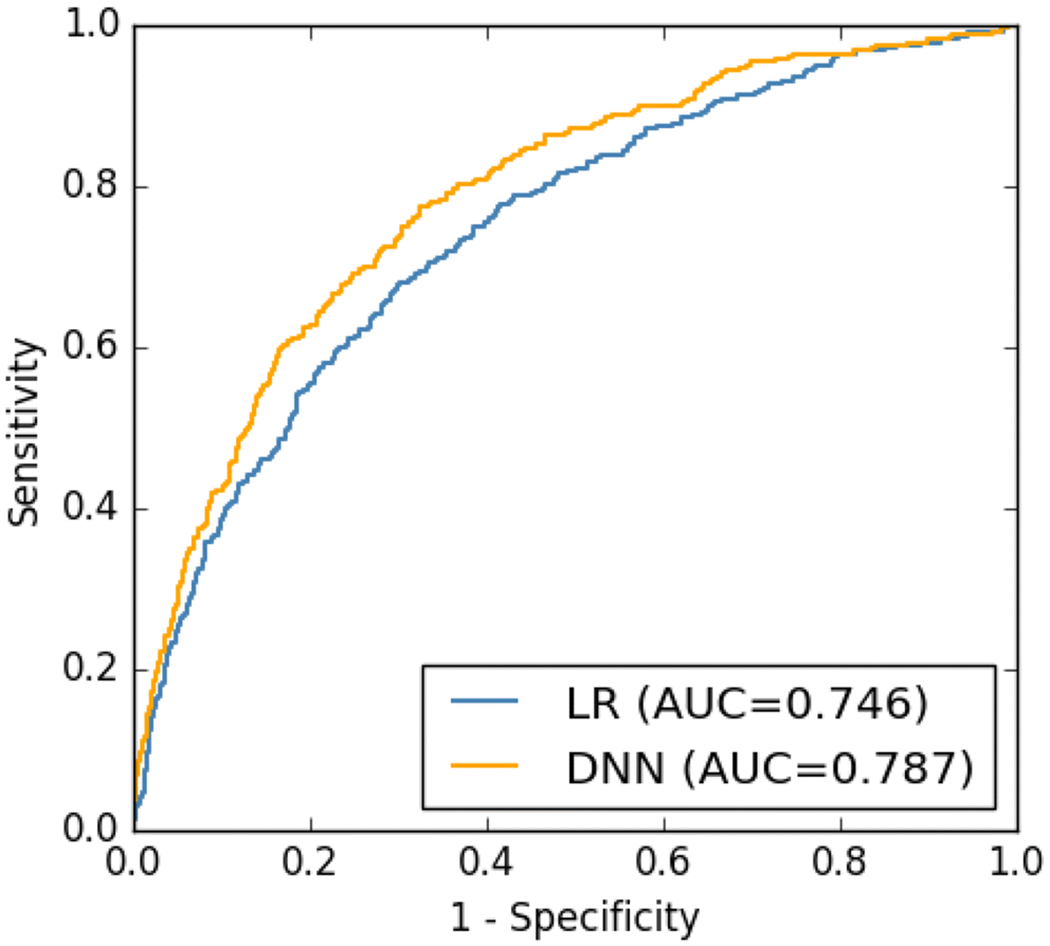
The ROCs of the DNN model and LR model calculated on the testing dataset.

In Fig. 4, we show the top 10 variables ranked by the magnitude (i.e., absolute value) of the impact scores (at the population level) and the top 10 variables ranked by the magnitude of the log odds ratios. These variables were the most important factors “decided” by the DNN model or the LR model.

Fig. 4.

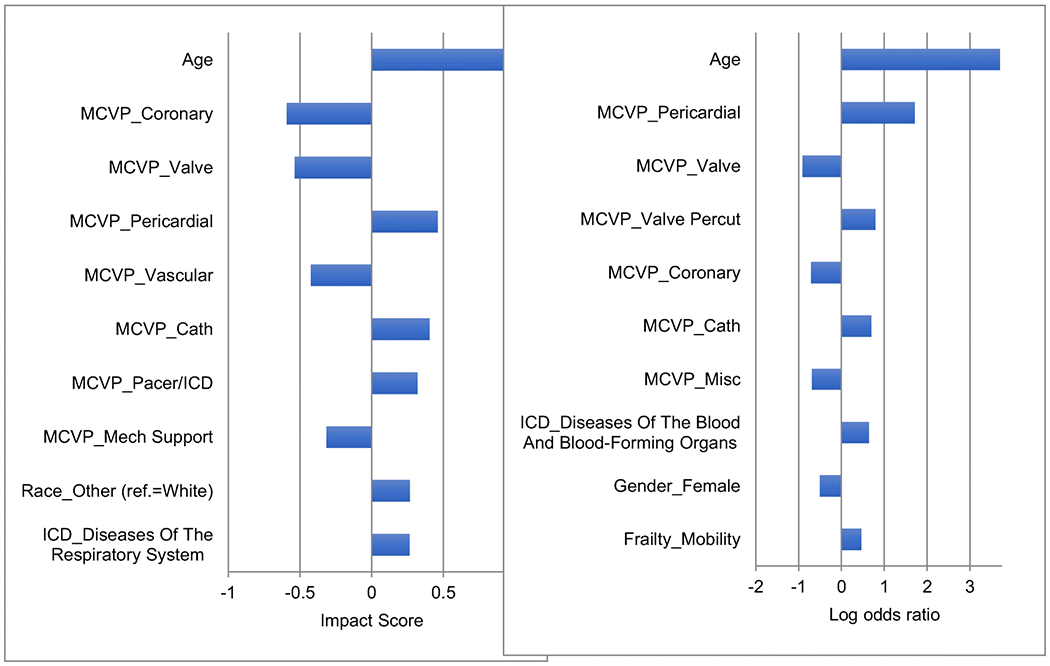
List of top 10 variables ranked by the magnitude of impact scores (left chart) and list of top 10 variables ranked by the magnitude of log odds ratio (right chart).

A complete list of numerical values of the population-level impact scores and log odds ratios are reported in Appendix, Table A.

We calculated 3 types of correlations – the Pearson’s correlation, the Spearman’s rank correlation, and the sign-agreement – between the impact scores and the log odds ratios. The sign-agreement is defined as the proportion of the variables on which the impact score and log odds ratios agree on the signs (positive or negative). We first calculated the 3 correlations on all the 37 variables (excluding the variables which were unused by the logistic regression model). The result is reported in Table 1.

Table 1.

The correlations between the population-level impact scores and the log odds ratios

Correlation Type	Value
Pearson	0.69
Spearman	0.63
Sign agreement	0.78

Next, we calculated the same 3 types of correlations on the top 18 (50%) variables ranked by the magnitudes of the impact scores. The result is shown in Table 2.

Table 2.

The correlations between the population-level impact scores and the log odds ratios on the top 18 variables ranked by the magnitudes of the impact scores.

Correlation Type	Value
Pearson	0.81
Spearman	0.79
Sign-agreement	0.89

We can see from Table 1 that the impact scores and log odds ratios had moderate agreements, while from Table 2 that they had stronger agreements. This suggests that the DNN model and LR model used similar key variables, i.e., those of large magnitudes, in their predictions. A more direct confirmation is in Fig. 4.

4. Discussion and Conclusion

DNN models can often outperform traditional machine learning and statistical predictive models. However, models like logistic regression and support vector machine with a linear kernel are more transparent and easier to understand, while a neural network is usually deemed as a black box. When we present the results of DNN models to clinicians and clinical researchers, a recurring question is how the model makes the prediction. Detailed descriptions of the layers of the neural network and weights of the nodes in the layers are not helpful; clinicians and clinical researchers want to understand the variables’ role in the prediction and how they are combined.

In this study, we developed a DNN model to predict death during the first year following MCVP. The DNN model outperformed the logistic regression model by nearly 4 percentage points. The goal of this research is to support patient and physician decision making before MCVP by providing accurate outcome prediction. While we still need more accurate models we have provided clinically meaningful explanations to help with implementation. The explanation approach we developed is a first step toward shedding light on the DNN black box.

DNN models are useful because they can model complex non-linear relationships, which is particularly applicable to human disease. To decipher these relationships, we proposed using impact scores. The impact scores are comparable to the log odds ratios for logistic regression. The impact score of a temporal variable can be calculated at two levels: at the level of clinical observation/finding, represented by a pixel with black or gray color on the temporal image, and at the level of an individual patient (over the whole 2-year time period). The impact score of a non-temporal variable is only calculated at the individual level. The population-level impact score was calculated as the mean of individual-level impact scores over all patients. This allows an explanation both on the individual level and on the population level. The importance of a clinical observation/finding is expected to vary for each patient. At the same time, it is desirable to understand the importance of a clinical observation/finding on the population level. For example, older patients are more likely to be frail, but frailty differs dramatically among patients of the same age. Both age and frailty are strong risk factors for post-surgical outcomes. How they factor into a patient’s actual and predicted outcome still differs at the individual level.

We calculated the correlations between the impact scores from the DNN model and log odds ratios from the logistic regression model in order to provide a partial validation to our approach. Logistic regression models are generally trusted by clinicians as a tool to understand the relationships between the variables and the outcome [34]. We also know that a logistic regression model and a DNN model trained on the same data both reflect/approximate the true underlying relationship in the data. Therefore, we expected that the two models would have some agreements in considering what variables were the key variables for predictions. The agreements could be measured by various correlations. We must stress that this “validation” does not consider the logistic regression model as the “gold standard”, and therefore one should not state that “the stronger the correlations are, the more correct the impact scores are.” We calculated 3 types of correlations – Pearson’s correlation, Spearman’s rank correlation, and the sign-agreement, which represent the agreements between the impact scores and the log odds ratios at different levels. The sign-agreement is the coarsest measure of agreement among the three as it completely ignores the magnitude. The Pearson’s and the Spearman’s correlations are both finer measures, but from two different perspectives: Pearson’s is more affected by magnitudes while Spearman’s is more affected by relative rankings. We see from the results that when calculated on all the variables, all the 3 correlations are moderate, but when calculated on only the half most important variables “considered” by the DNN model, all the 3 correlations become stronger. An explanation for this may be that the variables having impact scores of larger magnitudes were considered as more important features by the DNN model, and the two models had higher agreements on the more important variables.

The ultimate evaluation of impact scores will require an understanding of the “ground truth.” Such ground truth is typically unavailable in real patient data. As an alternative, we are currently generating a number of simulated datasets to validate the impact scores. We admit that simulated data cannot reach the complexity of real patient data and models trained on any dataset cannot completely capture the ground truth. Nevertheless, simulation provides us an approach to further validate the impact scores.

One limitation is that we did not use an extremely large sample for training DNN. The sample size of 20,000 is not small, though complex DNNs can handle and perform better with even larger data sets. We plan to repeat our experiment on a larger dataset with the goal to improve predictive performance. Another limitation is the lack of differentiation between unknown/missing values and values representing negative findings/observations in our temporal data representation, as both were represented by zero. While it is common for a clinical study to assume that the absence of positive findings implies negative findings, the assumption is not always true. A patient with chronic illness still has the illness on the days of not visiting a hospital.

More work is needed to explain DNN models that are used for clinical outcome predictions. We have not yet explained how the individual values and variables are combined in the DNN model to make predictions. Since we represent clinical data using temporal images, we have an opportunity to discover complex patterns not only across variables but also within a variable over time. Arguably the trained DNN model has captured some of these relationships. We plan to develop new methods to reveal these patterns. We also plan to experiment with other DNN architectures such as LSTM and Transformer and develop methods to explain these models.