Quantitative Systems Pharmacology Approaches for Immuno‐Oncology: Adding Virtual Patients to the Development Paradigm

Abstract

Drug development in oncology commonly exploits the tools of molecular biology to gain therapeutic benefit through reprograming of cellular responses. In immuno‐oncology (IO) the aim is to direct the patient’s own immune system to fight cancer. After remarkable successes of antibodies targeting PD1/PD‐L1 and CTLA4 receptors in targeted patient populations, the focus of further development has shifted toward combination therapies. However, the current drug‐development approach of exploiting a vast number of possible combination targets and dosing regimens has proven to be challenging and is arguably inefficient. In particular, the unprecedented number of clinical trials testing different combinations may no longer be sustainable by the population of available patients. Further development in IO requires a step change in selection and validation of candidate therapies to decrease development attrition rate and limit the number of clinical trials. Quantitative systems pharmacology (QSP) proposes to tackle this challenge through mechanistic modeling and simulation. Compounds’ pharmacokinetics, target binding, and mechanisms of action as well as existing knowledge on the underlying tumor and immune system biology are described by quantitative, dynamic models aiming to predict clinical results for novel combinations. Here, we review the current QSP approaches, the legacy of mathematical models available to quantitative clinical pharmacologists describing interaction between tumor and immune system, and the recent development of IO QSP platform models. We argue that QSP and virtual patients can be integrated as a new tool in existing IO drug development approaches to increase the efficiency and effectiveness of the search for novel combination therapies.

Cancer originates from changes in the DNA of a single cell in an individual patient. Development of molecular biology knowledge and tools over the last 6 decades have enabled tackling this disease at the molecular level. Next Generation Sequencing offers unprecedented insight into genomes and transcriptomes of individual patients, tumors, and cells informing our understanding of the origins of cancer variability and increasingly providing diagnostic tools allowing selection of personalized therapies. The wealth of knowledge on molecular and cellular mechanisms and an arsenal of molecular tools allowing their modulation opens an avenue toward development of drugs reprogramming cellular behavior to treat and cure the disease. Immuno‐oncology (IO), ¹ in particular, is a relatively old concept only recently enabled by molecular characterization of tumor‐immune interactions, which has revolutionized treatment options. Rudolph Virchow first proposed to mobilize the patient’s own immune system to fight cancer in late 19th century. ² Later, William Coley tested this idea with the crude approach available at the time of bacterial broth injection. ³ More than a century later, understanding of immune system checkpoints at the molecular level and an advent of monoclonal antibody drugs enabled development of the first therapies truly reprogramming immune response for the benefit of patients with cancer. Compounds specifically targeting PD1/PD‐L1 and CTLA4 receptors induced immune response to achieve long‐term benefit, where standards of care failed and their success precipitated the rise of IO to the fastest growing area of pharmaceutical research and development. ⁴ Despite initial success, PD1/PD‐L1 and CTLA4 checkpoint inhibitors are not effective in all patient populations. This prompted the need for mechanistic understanding of the reasons for patient variability and development of diagnostic methods for patient selection. On the basis of these insights, the focus of IO drug development has now shifted toward combination therapy, where features of an individual disease or even an individual tumor are exploited by administration of multiple compounds with specific doses and timings, due to the rationale of additive efficacy.

There are currently more than 2,000 active clinical trials in IO. ⁴ This vast number is a testimony to the combinatorial explosion of possible target and dosing regimen combinations emerging from contemporary knowledge on tumor immunobiology and capabilities to design compounds specifically to modulate players in complex molecular networks that determine cellular behavior. Unfortunately, to date, most of the combination trials have failed to demonstrate improvement with respect of standard of care. The unprecedented number of clinical trials poses unique challenges and may become an impediment for progress in the field. In addition to rising drug development costs, further growth in the number of combination therapy trials may be limited by the shortage of patients. The 2,000 clinical trials, which started in 2017, ⁴ required ~ 600,000 patients, whereas there were only about 50,000 patients participating in research across all areas of oncology. It is clear that efficient and effective experimental exploitation of the combination therapy space in IO is severely limited and that new approaches are required to prioritize and optimize trials and direct limited resources toward drug development areas with highest probability of success.

One of the reasons for failure of IO combination therapy trials is a lack of quantitative understanding of complex dynamic factors determining efficacy leading to the selection of suboptimal combinations and dosing regimens. Translation of the vast literature on basic cancer immunobiology to actual choice of multiple compounds, dose amounts, and timings is challenging. Complex, dynamic feedbacks underlying immune response and tumor growth in the patient are very difficult to understand intuitively, without the use of quantitative mathematical models. Conventional pharmacokinetic and pharmacodynamic (PK/PD) models, which typically connect modulation of target pharmacology to clinical outcomes through empirical models, do not fully capitalize on existing mechanistic knowledge. In contrast, quantitative systems pharmacology (QSP) ⁵ integrates knowledge of molecular and cellular interactions involved in the tumor growth and immune response linking PK/PD with clinical outcomes. QSP models support target/combination selection and validation in early discovery as well as optimal trial design through identification of patient subgroups, dosing regimens, and biomarkers using so‐called virtual patients (VPs; see later). Moreover, quantitative representation of existing knowledge allows formal testing of different mechanistic assumptions and parameters, thus supporting decisions by quantitative account of uncertainty. As such, QSP models are a valuable new tool for clinical pharmacologists to make better use of existing mechanistic biological knowledge in combination therapy selection and personalized therapy.

In this review, we will first describe a general framework for QSP in IO combination therapy development. We will then provide a comprehensive review of mathematical models describing interaction between tumor and the immune system at different levels of granularity. Subsequently, we will then describe how these models have provided the basis for current efforts on the development of large‐scale IO QSP platforms applicable for selection and validation of combination therapies in drug development projects. We hope that the review will contribute to the uptake of QSP approaches by clinical pharmacologists and others in IO drug development, improve the efficiency of the current paradigm, and speed up the approval of novel therapies for patients.

QSP APPROACH TO COMBINATION THERAPY SELECTION

QSP supports drug development by providing mechanistic in silico models of the biology underlying disease, drug PKs as well as target binding and drug effect. The field originated from the combination of well‐established PK/PD approaches describing drug absorption, distribution, metabolism, elimination, and drug action with systems biology, focusing on understanding of complex biological processes in health and disease. ⁵ QSP models represent in a quantitative framework existing literature knowledge on the molecular, cellular, and physiological mechanisms, which perturbation in healthy individuals leads to disease. The models are initially typically inferred only to a minor extent from retrospective fitting of clinical data, but rather formulated and parameterized based on the mechanistic knowledge available before the trial is conducted. A major application of QSP is a more personalized prediction of clinical outcome for a specific compound or combination of compounds, dose and dosing regimen. Other applications involve examination of what‐if scenarios and alternative mechanistic hypotheses to aid experimental design through understanding of underlying biological complexity. The vast majority of QSP models are developed in an ordinary differential equation (ODE) framework and simulated with off‐the‐shelf numerical solvers, but other approaches, such as agent based models, ⁶ are also proposed. Figure 1 shows a typical example QSP model, developed for illustration purposes and described in detail in our recent Tutorial in this journal. ⁷

Figure 1.

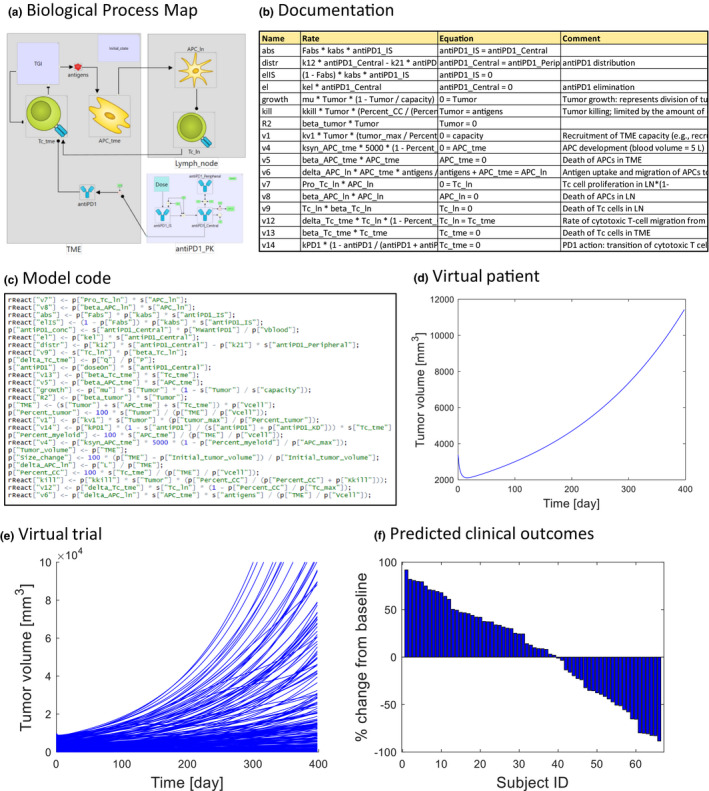
Example quantitative systems pharmacology immuno‐oncology model published by Lazarou et al. ⁷ (a) Biological process map representing molecular and cellular processes underlying disease, drug action, and pharmacokinetics. (b) Documentation containing variable and parameter definitions, rate laws, and literature references. (c) The model represented as a set of ordinary differential equations and compiled to executable code. (d) Simulation tumor growth in an individual virtual patient. (e) Virtual trial simulation of a sample of virtual patients. (f) Predicted clinical outcomes. Waterfall plot of a percentage change from baseline in virtual patients. LN, lymph node; TME, tumor microenvironment.

The mechanistic, bottom‐up, literature‐based approach to model‐informed drug discovery and development has already been successfully applied in physiologically‐based pharmacokinetics (PBPK). ⁸ The knowledge on anatomy, physiology, and physical chemistry of the processes involved in drug absorption, distribution, metabolism, and elimination is represented in an ODE framework and used for the simulation of the time profile of drug concentration (e.g., at the site of action). PBPK illustrates how a mechanistic approach increases the scope of extrapolation beyond the data used to build the model, in some cases enabling replacement of the clinical trial with its virtual equivalent. For example, PBPK is an industry standard, with regulatory acceptance, in an evaluation of the effect of drug‐drug interactions (DDIs) after being extensively evaluated with a diverse set of drugs. ⁹ When concentration of the drug at the site of action is affected by co‐administration of another drug, metabolized by the same enzyme, the PBPK models validated for both drugs, can be combined and used to predict the extent of the interaction and formulate label recommendation for dosing. In this context of use, the PBPK simulation can be accepted in lieu of clinical trial for DDIs, thus decreasing number of clinical trials, patient risk, and drug development costs. ⁹ The key feature of PBPK models that enable this important application is the incorporation of the detailed mechanistic knowledge and in vitro assays available before a trial is conducted (i.e., binding and processing of compounds by drug metabolizing enzyme). If drug metabolism was empirically accounted for, by inferring clearance from clinical data, extrapolation would not have been possible and a full DDI trial would have to be conducted. There are numerous other applications, such as extrapolation between different drug formulations, where mechanistic PBPK models are used with high confidence. The QSP approach is based on the same general methodology of representing knowledge on underlying biology as a mechanistic model and then using the model for extrapolation. Although it is still much less established than PBPK, the number of regulatory submissions supported by QSP models is growing and some experts, perhaps generously, believe that the QSP will reach the level of maturity and acceptance of PBPK in the very near future. ¹⁰ In summary, we propose that PBPK provides a clear and compelling precedence for what can be achieved by mechanistic modeling in drug development and regulatory decision making and believe that the field of QSP can leverage this experience to speed up application and impact.

Consideration of patient variability is crucial for successful drug development in any therapeutic area, but oncology poses exceptional challenges, due to the molecular diversity of individual tumors. Incorporation of mechanistic variables into the model enables simulation of VPs, where each individual has its own unique combination of parameter values, in principle covering the entire biological scope of the model. A VP is a variant of a mechanistic model, where selected parameters and variable values at initial state are randomly generated following experimentally known population distribution of these quantities ¹¹ (Figure 1d ). In a virtual trial simulation, a sample of VPs is generated and subjected to the same dosing regimen as in an actual trial (Figure 1e ). Simulation of VPs outputs a sample of individual time profiles, which reflects subject variability of clinical outcomes (Figure 1f ). Results from individual patients from actual clinical trials can subsequently be mapped onto VPs, for example, to identify mechanistic hypothesis for heterogeneous biomarker responses. Moreover, repeated simulations of trials of set number of subjects can be used to predict between‐trial variability and inform power calculations. Again, this methodology is very well established in PBPK, where known distributions of physiological parameters (e.g., body weight, cardiac output, and blood and organ volumes) are used to generate VPs. Moreover, parameter correlations are taken into account to create physiologically plausible individuals (e.g., it is unlikely to observe a tall man with a liver volume of a child). PBPK also demonstrates the use of genetic variability—allele frequencies of drug transporters and drug metabolizing enzymes in specific populations are used to obtain VPs with different enzyme activities. A common application of virtual trials is extrapolation to a specific population of interest (ethnicity, gender, disease, and pediatric). In the context of IO, mechanistic models enable use of recent high‐throughput molecular biology data for a virtual trial simulation to account for molecular variability of tumors. The Cancer Genome Atlas (TCGA) ¹² alone contains genome and transcriptome sequences of over 20,000 primary cancer and matched normal samples spanning 33 cancer types, amounting to about 1 petabyte of data. We recently demonstrated ⁶ how to use a QSP virtual trial approach to translate the wealth of molecular data to variability of clinical outcomes in IO trials.

Figure 2 summarizes main applications of QSP in IO. We believe that the features of the QSP approach described above make it a valuable tool for target prioritization and hypothesis generation in the discovery stage and an attractive alternative for commonly used animal models with poor translational track records. ¹³ Mechanistic detail and understanding are needed to include multiple potential molecular targets and account for the complex network of molecular and cellular interactions linking these targets to clinical biomarkers and determining their interactions. The model needs to be quantitative and time dependent to predict longitudinal response of quantitative clinical biomarkers to variable dosing regimens of multiple compounds. The model needs to be created based on existing literature knowledge, ex vivo and in vitro assays on human cells to enable prediction of clinical outcomes before clinical trial is conducted. In the following sections, we will review the legacy of mechanistic models describing interactions among immune system and tumor and recently developed QSP models in IO. We will then discuss challenges and critique of the approach.

Figure 2.

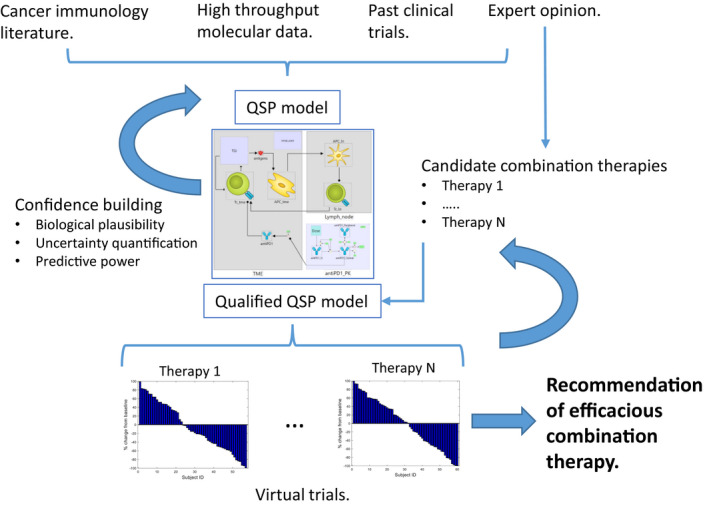
Knowledge integration with quantitative systems pharmacology (QSP) model to support efficacious combination therapy selection in immuno‐oncology. Mechanistic model is created based on cancer immunology literature. High throughput molecular data on tumor biopsies can be used to calibrate model for specific disease. ⁷ The model can be further calibrated using past clinical data on therapies similar to those which are under investigation. The model is subjected to the iterative process of simulation and comparison with experimental data to evaluate biological plausibility of model behaviors and predictive power. Parameter space is extensively exploited to quantify uncertainty. Expert opinion from an interdisciplinary drug development team is key at every stage of this process. Experts formulate the list of candidate therapies, which are evaluated in virtual trials. Iteration of this process leads to recommendation of efficacious combination therapy, based on integrated mechanistic knowledge, data, and expert opinion.

LEGACY MODELS OF CANCER IMMUNOBIOLOGY

The complexity of the immune system dynamics, emerging from the network of positive and negative feedbacks, has been recognized very early and attracted interest of the mathematical modeling community long before application in clinical pharmacology. Models of the interaction between immune system and tumor have been created since early 1990s and their development paralleled growing understanding of the mechanistic detail of molecular and cellular interactions. Because therapeutic modalities were not available yet, this research was conducted mostly by the academic community hypothesizing about potential future therapeutic relevance, but not yet being able to perform virtual trials and relate models to drug development pipelines. Nevertheless, the legacy of mathematical models in immunology provides an invaluable knowledge base for current development of QSP models for drug development. First, mathematical models developed over 3 decades constitute a comprehensive library of rate‐law equations describing complex, nonlinear interactions at different levels of mechanistic granularity. Second, authors of modeling papers analyzed the large corpus of basic immunobiology data to justify parameters of their models. Although new technologies and data became recently available and the models should refer to original experimental sources rather than modeling papers, the collection of basic experimental literature and model parameterization strategies constitutes a valuable resource for QSP modelers. However, the large number of papers is not easy to identify and review by an individual modeler at the start of each drug development project in a timely manner. Here, we provide such a comprehensive and systematic review, which was generated through a precompetitive collaboration among seven pharmaceutical research organizations (the “IO QSP Consortium”). Because we identified nearly 150 models, we do not describe all of them in detail. Instead, we focus on analyzing the coverage of the fundamental processes of the Cancer Immunity Cycle (CIC) ¹ —a commonly used conceptual framework in cancer immunobiology. Moreover, to further inform the choice of references to examine in detail, we provide a classification of models based on the similarity of formalism, mechanistic granularity, and biological coverage.

We systematically searched literature for mathematical models describing the dynamic interactions between the cancer and immune cells using combinations of terms such as “cancer immunity cycle,” “cancer immunotherapy,” “immuno‐oncology,” “checkpoint inhibitors,” “cytokine‐based immunotherapy,” “tumor microenvironment,” “anti‐PD‐1,” “anti‐PD‐L1,” “anti‐CTLA4,” “mathematical models,” “predictive models,” “quantitative systems pharmacology,” “QSP,” and a few other specific searches using names of the cell‐types, cytokines, and other molecular entities involved in CIC. Information regarding the following topics were captured from the 141 papers identified: (i) the purpose for which the model was developed, (ii) model variables (cell‐types, cytokines, growth‐factors, cell‐surface receptors, and other molecular signatures) and their interactions, (iii) treatment types (mono or in combination), (iv) study type (animal/clinical data), and (v) the biomarkers used for model validation. Figure 3 shows an overview of the relationships among the 141 articles in terms of biological coverage, formalism, and authorship. The full list of references is provided in the Supplementary Material . For the sake of completeness, Figure 3 also includes full‐scale QSP models, which will be reviewed in more detail in a later section.

Figure 3.

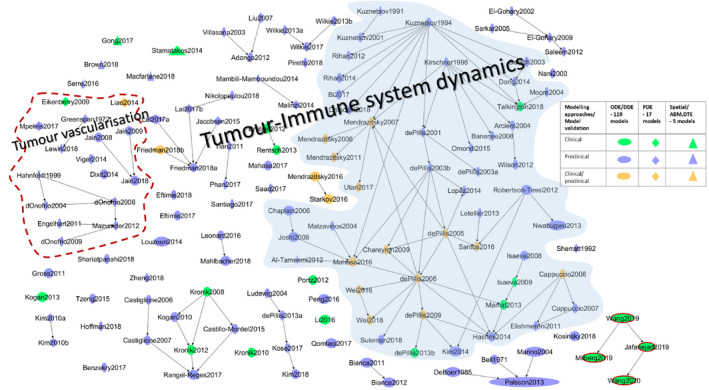
Mechanistic models of cancer‐immunity cycle and immunotherapies. An overview of the literature‐based models of cancer and immune system dynamics that is reviewed in this study. Although most of the models belong to the tumor and immune system dynamics, few models that describe the dynamics of specific processes in tumor microenvironment are also included. For example, a model that describes macrophage dynamics, tumor‐stromal cross‐talk, T‐helper cell differentiation in the context cancer are included (see Supplementary Material S1 for details of these models). The four models on the bottom right corner where the nodes are highlighted in red are immuno‐oncology quantitative systems pharmacology platform models that were published recently. The models highlighted in blue shade are a chunk of models that are derived and expanded from the first generation of models (see the main text for details). Modeling approaches and the study type used for model validation are reflected as shapes and colors as defined in the key table. The node size represents the model size (i.e., the number of cell‐types, cytokines, and other molecular entities included in the models). Model size is not always the number of variables in the models. For example, the intermediate variables and protein complexes are not taken into account. The size of the models ranges from 2 to 21. The “Fully‐integrated Immune Response Model – FIRM” model is the biggest model in our list with 21 different cell types and cytokines. ODE, ordinary differential equation.

The concept of immunological surveillance against cancer was substantially developed by Burnett ¹⁴ following the original proposal by Ehrlich in 1909, ¹⁵ and later rephrased by Thomas. ¹⁶ The concept states that a normal function of the immune system, or more precisely the cell‐mediated immunity carried out by thymus‐derived lymphocytes, is to recognize and destroy newly appearing tumor cells in situ. Mathematical models to describe the concept of immune surveillance started to emerge as simple “two‐ODE” systems in the early 1990s, which then developed into the current state‐of‐the‐art multiscale QSP models describing the dynamics of several components in the cancer‐immunity cycle. In this section, we will focus on the evolution of these models describing the cancer and immune system interplay, and the effect of immunotherapies.

Models, which include only immune stimulation

In the first generation of “two‐ODE” models, the dynamics of the tumor and cytotoxic cells follows a classical “predator‐prey” behavior introduced by Alfred Lotka and Vito Volterra. The early models described by Kuznetsov introduced a number of phenomena, including immune stimulation of tumor growth, “sneaking through” of the tumor, and formation of a tumor “dormant state” as seen in vivo. ¹⁷ , ¹⁸ , ¹⁹ With the growth of experimental data surrounding the complexity of tumor and immune cells interactions mediated by cytokines, Kirschner and Panetta developed a “three‐ODE” system model that describes the dynamics of effector and tumor cells, and the cytokine IL‐2. The effect of adoptive cellular immunotherapy on the model was explored using a treatment term that represents an external source of effector cells, such as LAK or TIL cells. ²⁰ Given the simplicity and applicability of the above models to examine several hypothesis underlying the fundamental principles of cancer progression, they gained immense popularity and formed a hub for the evolution for several other models. By following the aspects of the above models, de Pillis and Radunskaya ²¹ developed a model to explore the effect of chemotherapy by including normal, tumor, and immune cells. Although the healthy tissue and tumor cells compete for available resources, the immune and tumor cells compete in a predator‐prey fashion. This model then became a base for a big cluster of models (Figure 3 ) where it was expanded to include CD8+ T‐cells, NK cells, circulating T‐lymphocytes, and dendritic cells to investigate mono and combinations of several immune modulating agents, such as chemotherapy, IL‐2, IL‐12, INF‐α, IL‐21, DC vaccine, and TIL. ²² , ²³ , ²⁴ , ²⁵ , ²⁶ , ²⁷ , ²⁸ , ²⁹ , ³⁰ , ³¹ , ³²

Models taking into account immune suppression by regulatory T cells

Tumors evade the immune‐mediated elimination by producing substances, such as TGF‐β and IL‐10, that stimulate the expansion of immunosuppressive cells, in particular, T‐regulatory cells, MDSCs, and M2 macrophages. One of the major limitations in the above cited models are the lack of immune suppressive components, which plays a critical role in shaping the tumor microenvironment to restrain antitumor immunity by restricting effector cells infiltration. In order to account for this, de Pillis et al. ³³ introduced regulatory T cells (Tregs) into their previous models and examined the effect of sunitinib in reducing the immunosuppressive effect in tumor microenvironment (TME). In addition to its anti‐angiogenic effects, sunitinib is found to directly inhibit the immunosuppressive environment by reducing the number of Tregs. It has also been reported that sunitinib modulates Treg activity by decreasing T‐helper cell differentiation into Tregs rather than killing Tregs directly. TGF‐β released mainly from Tregs and other immunosuppressive cells has a dual effect in cancer biology. In early stages, it acts directly on cancer cells to suppress their growth. As the tumor progresses, it stimulates tumor progression by suppressing and blocking effector cells from infiltrating into the TME. Along this line, Arciero et al. ³⁴ added TGF‐β mediated immunosuppressive and tumor growth stimulatory effect to the model by Kirschner and Panatte, ²⁰ and investigated the effect of siRNA treatment that suppresses TGF‐β production by inhibiting the TGF‐β mRNA. This model was expanded by Wilson ³⁵ to quantify the effects that anti‐TGF‐β and peptide vaccine treatments might have on the stability of tumor‐immune dynamics and how the combined treatment might contribute to tumor clearance as opposed to tumor escape. Their investigation suggested that monotherapy with anti‐TGF‐β did not have a significant impact on tumor growth. However, it significantly enhanced the efficacy of the peptide vaccine by inducing an increased number of tumor antigen‐specific cytotoxic T cells, which is critical for the effective elimination of tumor cells. Interestingly, it has been shown that TGF‐β attenuates tumor response to PD‐L1 blockade by contributing to exclusion of T cells. ³⁶ Hence, for immune excluded phenotypes, the inhibition of TGF‐β enhances the efficacy of immune‐checkpoint blockade therapies, which is observed in preclinical studies of murine breast and colon carcinoma models. ³⁷

Models including immune suppression by myeloid cells

Cancer cells are highly effective at evading immune responses by inducing polarization of pro‐inflammatory M1 macrophages into anti‐inflammatory M2 macrophages, and promoting expansion of myeloid derived suppressor cells (MDSCs) through the secretion of several immunosuppressive molecules, such as TGF‐β and IL‐10. In order to evaluate macrophage interactions within the TME and assess how their interactions affect tumor progression, Mahlbacher et al. ³⁸ integrated M1, M2, and Tie2 expressing macrophages (TEMs) and their properties into a model of tumor growth. The main properties of these macrophage variants included in this model are M1, which release nitric oxide, M2, which release growth promoting factors, such as VEGF‐A, TGF‐β, and IL‐10, and TEM, which facilitates angiogenesis via angiopoietin‐2 and promote M2 differentiation from monocytes. The model result showed that the presence of M2 lead to larger tumor growth regardless of TEM effects, suggesting that immunotherapeutic strategies that lead to TEM ablation may not work to restrain tumor growth when a sizeable population of M2 is present. Macrophage polarization within the changing TME mediated by cytokines, recruitment/function of MDSCs, and polarization toward M2 macrophages mediated by factors, such as MCSF and GMCSF, how these mechanisms affect effectors cells in killing tumor cells are studied by several other models. ³⁹ , ⁴⁰ , ⁴¹ Colony stimulating factor‐1 receptor (CSF1R) is a critical receptor on macrophages and offers a promising therapeutic strategy for high‐grade gliomas. Inhibiting CSF1R promotes macrophages to switch from protumorigenic M2 phenotype to antitumorigenic M1 phenotype that promote tumor cell death. However, acquisition of drug resistance during CSF1R inhibition was observed in preclinical mouse models. To understand how resistance emerges during this therapy, Zheng et al. ⁴² developed a spatio‐temporal model of macrophage‐mediated drug resistance to understand the interplay between glioma cells and macrophages targeted by CSF1R inhibitors through CSF1 and IGF1 pathways. Macrophages and glioma cells interact through the CSF1/CSF1R and IGF1/IGF1R pathways, and inhibiting CSF1R would limit the secretion of IGF1, which is a resource to sustain the survival and growth of glioma cells. However, they found that during prolonged treatment with CSF1R inhibitors, IGF1 was elevated through alternate pathway that in turn sustains the survival of glioma cells. The model then quantitatively evaluated the effects of combined CSF1R inhibition and IGF1R receptor inhibition. Shariatpanahi et al. ⁴³ developed a model to study the expansion and immunosuppressive effect of MDSCs, and evaluated the effect of anti‐MDSC drugs, such as L‐arginine and 5‐fluorouracil (5‐FU) on restoring antitumor immunity. Tumor cells stimulate the production and expansion of MDSCs, and these cells suppress antitumor immunity by producing arginase 1, an enzyme that inhibits effector T cells and NK cells antitumor activity. The model simulation showed that the addition of L‐arginine supplementation to the intermittent 5‐FU therapy reduced the time of the tumor eradication and the number of iterations for 5‐FU treatment.

Models accounting for tumor vascularization

Tumor vascularization is an inevitable process in tumor growth and progression. This is often accomplished by the release of several immunosuppressive cytokines and pro‐angiogenic growth factors. Wang et al. ⁴⁴ established through a J558 mouse model that an immunosuppressive cytokine IL‐35 (a member of IL‐12 family of cytokines) promotes tumor growth by enhancing MDSC accumulation, inhibiting the infiltration of cytotoxic T cells and stimulating angiogenesis. To explore the mechanism of IL‐35 in tumor growth and immune evasion, Liao et al. ⁴⁵ developed a model consisting of a system of partial differential equations that involve the interaction among different cell‐types (tumor cells, MDSCs, T cells, Tregs, and endothelial cells) and cytokines (M‐CSF, TGF‐β, VEGF, and IL‐35). The key interactions include the secretion of IL‐35 by tumor, Tregs, and MDSCs that promote the secretion of VEGF by tumor cells, which in turn attracts endothelial cells to trigger angiogenesis. The model was also evaluated numerically to establish the level IL‐35 inhibition that is needed to reduce tumor growth. On a similar note, Jain and Jackson ⁴⁶ , ⁴⁷ , ⁴⁸ expanded their previous models to investigate the bidirectional communication between tumor cells and endothelial cells on treatments targeting VEGF and its receptors that inhibit cell proliferation via downregulating Bcl‐2. The expression of VEGF by tumor cells under hypoxia initiates an autocrine‐signaling and paracrine‐signaling cascade that results in enhanced expression of Bcl‐2 and promotes proliferation. The increase in vascular endothelial cells in TME results in the decrease in hypoxia. There are several other models that address tumor vascularization by studying the interaction among tumor cells, stromal cells, immune cells, and some of the key molecular players (Figure 3 and Supplementary Material ).

Models of Bacillus Calmette‐Guerin and oncolytic viral immunotherapy

Immunotherapy using Bacillus Calmette‐Guerin (BCG) is an established clinical treatment for superficial bladder cancer. BCG is believed to cause tumor elimination by stimulating immune response via initiating inflammatory reaction. The inflammation attracts innate immune cells that subsequently triggers the adaptive immune response to work against cancer cells. However, some patients do not respond to this protocol, hence Bunimovich‐Mendrazitsky et al. ⁴⁹ adopted the early models by Kirschner and Panatte ²⁰ and Kuznetsov et al. ¹⁷ to investigate BCG‐tumor‐immune interplay. Based on this foundational work, several models were developed to understand the mechanism of BCG action in bladder cancer, where a suggestion for combination of BCG with IL‐2 to improve the success rate was made by Bunimovich‐Mendrazitsky et al. ⁵⁰ On a similar ground, oncolytic viral (OV) therapy is an effective strategy to destroy cancer cells, as shown in clinical trials. In OV therapy, oncolytic viruses infect tumor cells and replicate in tumor cells; upon lysis of infected tumor cells the new viral particles burst out and proceed to infect additional tumor cells. On the other hand, the viral peptides are immunogenic and, hence, stimulate anticancer immune response, which presents a major challenge in maximizing efficacy. Therefore, the effectiveness of these therapies depends on the interactions between the oncolytic viruses and the host immune response. In order to understand the basic dynamics of OV therapy, Tian ⁵¹ proposed a simple model to represent the interactions among tumor cells, infected tumo cells, and oncolytic viruses, and concluded that the viral therapeutic dynamics is largely determined by the viral burst size. This model was further expanded with immune cells to understand the effects of the innate and adaptive immune response on OV therapy. ⁵² As macrophages are the first line of defense against infections, Eftimie and Eftimie ³⁹ developed a mathematical model to investigate the possible outcome of the interactions between two extreme macrophage phenotypes (M1 and M2) and oncolytic virus in the context of B16F10 melanoma. They concluded that macrophage polarization toward M1 or M2 phenotypes could enhance the efficacy of OV therapy either through the activation of antitumor immune response or through enhancing oncolysis.

Models including NK cells and antibody‐dependent cell‐mediated cytotoxicity

Targeting surface antigens expressed on tumor cells, and checkpoint receptors expressed on cancer and immune cells by monoclonal antibodies has revolutionized cancer therapeutics. One mechanism of action of antibody‐based immunotherapy is the activation of immune effector cells, particularly NK cells, to mediate antibody‐dependent cell‐mediated cytotoxicity (ADCC). To address this mechanism, Hoffman et al. ⁵³ developed a very simple model in which NK cells kill cancer cells at a rate, which depends on the amount of antibody bound to each cancer cell. The model was calibrated using an in vitro study on SKBr3 breast cancer cells, and the results show how the processes involved in ADCC change as the initial concentration of antibody and NK‐cancer cell ratio are varied. Similarly, Tzeng et al. ⁵⁴ developed a model based on the previous knowledge that ADCC plays an important role in immunocytokine efficacy. The model hypothesized that IL‐2 efficacy could be enhanced without introducing toxicity by the administration of additional tumor‐specific antibody. The hypothesis was also shown in a syngeneic mouse melanoma model that IL‐2 indeed synergized with antitumor antibodies to significantly prolong survival. There are increasing evidences that the efficacy of monoclonal antibodies designed to target checkpoint receptors on tumor cells and immune cells are enhanced through NK‐mediated ADCC mechanism. For example, there are several studies that suggest regulatory T cells depletion by NK‐mediated ADCC may play a significant role in increasing the efficacy of ipilimumab treatment. ⁵⁵

Other models

Other modeling formalisms that describe and investigate different mechanisms of cancer and immune cell dynamics include: (i) a spatial model that accounts for the difference in trajectories between pre‐activated and activated immune cells, ⁵⁶ (ii) a model that accounts for the interaction between multiple tumors competing for resources and immune response, ⁵⁷ and (iii) models that investigate the roles of oncogenes and anti‐oncogenes in controlling cell proliferation, and that explores how immune cells respond to inactivation of the driving oncogene. ⁵⁸ , ⁵⁹ , ⁶⁰ Not all models listed in the lineage map Figure 1 are reviewed in this section; however, the entire list of these models is available in the Supplementary Material.

Summary

Most of the models summarized above are developed to understand specific aspects of cancer and immune system interplay, and, hence, are structurally small with only essential cellular/molecular component. This limits applicability for investigation of other IO mechanisms and treatment scenarios, for example, a combination involving immune modulators in different stages of CIC. In recent years, knowledge base integration of CIC mechanisms involving different cell‐types (tumor cells, innate and adaptive immune cells, and stromal cells) and molecular components (cytokines, cell‐surface receptors, etc.) are put together in a large‐scale QSP platform model for predicting combinations of different cancer therapies. ⁶¹ , ⁶² , ⁶³ , ⁶⁴ , ⁶⁵ These models are reviewed in the next section.

Our survey includes 141 mechanistic models, which describe different aspects of CIC. The models have grown significantly in size and complexity in the past 2 decades by incorporating the advances in cancer‐immune biology. Even though there were several overlapping models that describe the same aspect of the cancer‐immunity cycle, the level of granularity in describing the underlying mechanisms differed, and together they cover a vast majority of cell‐types and molecular signatures involved in the cancer‐immune system biology. The models together describe the mechanisms involving 15 different cells types (includes cancer cells, immune cells, and stromal cells) and 36 molecular signatures (includes cytokines, chemokines, cell‐surface receptors, growth factors, and intracellular molecules), applied to predict different treatment scenarios (with both immunotherapy and nonimmunotherapy agents; Figure 4 a,b). Cell‐cell interactions and molecular players mediating them, which are covered by the corpus of mechanistic models reviewed here are visualized in Figure 5 .

Figure 4.

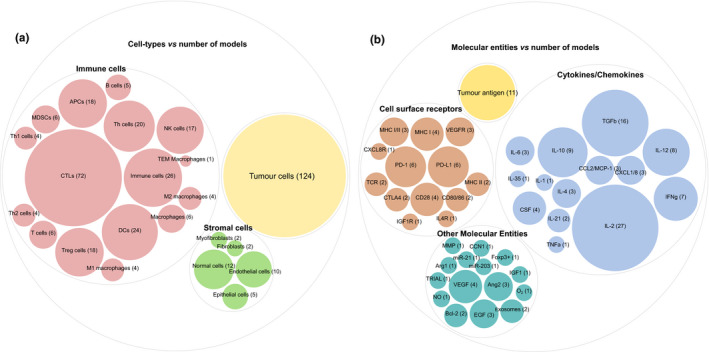
Cell‐types and molecular entities usage in the models. (a) Cell‐types vs. number of models: there are about 18 different cell types that include tumor cells, 12 types of immune cells, and 5 types of stromal cells. The number in the bracket adjacent to the cell‐type name denote the number of models in which these cell‐types are used. For models that do not differentiate between different immune cells, a common name is used. For example, the predator‐prey type models use effector cells (which is a combination of NK cells and CTLs, here referred to as immune cells) and tumors. (b) Molecular entities vs. number of models: there are about 43 molecular entities that include tumor antigens, cytokines and chemokines, cell‐surface receptors, and, in addition, molecules that are involved in tumor angiogenesis (VEGF and Ang2), intracellular signaling, and other molecular functions are listed as “Other Molecular Entities.”

Figure 5.

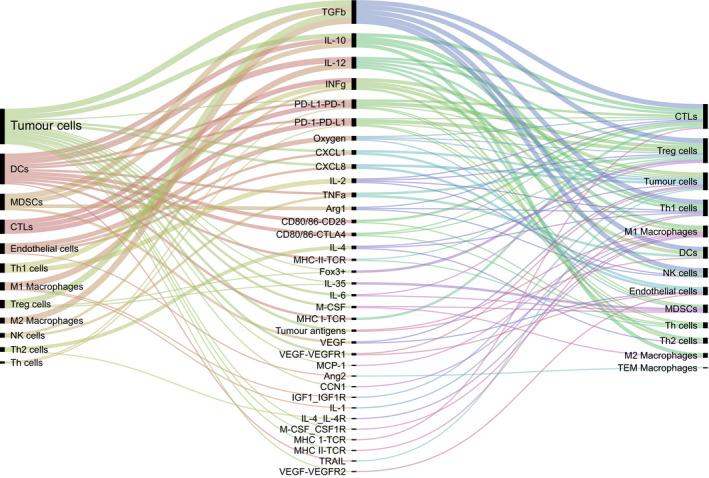
Cell‐cell communication mediated by molecular players. Cytokines, chemokines, growth factors, cell‐surface receptors, and other molecular players (middle) that mediate cell‐cell communication as described in the models reviewed in this paper.

QSP PLATFORM MODELS IN IO

As presented above, modeling the dynamics of the interaction between the immune system and cancer at cellular and molecular levels has been a long‐standing topic in mathematical and systems biology. However, simulation of a virtual trial in IO, with a model of sufficient mechanistic detail to inform selection of combination therapies, has become available to clinical pharmacologists only recently.

In our view, the model developed by Popel’s group constitutes one of the first full‐scale QSP platforms in IO, validated by the simulation of anti‐PD1, anti‐PD‐L1, anti‐CTLA4, and epigenetic inhibitor drug combinations in melanoma, breast cancer, and non‐small cell lung carcinoma. ⁶¹ , ⁶³ , ⁶⁴ , ⁶⁵ The model describes biology of the disease by a detailed description of the interactions among the following cellular species: tumor, effector T cells, primed T cells, antigen presenting cells (APCs), mature APCs, resident APCs, naïve T cells, Tregs, and MDSCs. The following surface receptors mediating cellular interactions are explicitly considered: TCR, MHCI, CD28, CD80, CD86, PD1, PD‐L1, PD‐L2, and CTLA4. To incorporate receptors, the authors created large number of quantities representing different cellular and molecular complexes formed in immune synapses. The compartment structure of the model is complex and varies, depending on application. There are four major compartments: tumor, tumor draining lymph node, peripheral, and central. Leukocyte circulation model is more detailed and uses lymph node, lungs, gastrointestinal, spleen, remaining peripheral tissues, venous blood, and arterial blood compartments. The authors describe PKs of therapeutic antibodies with a PBPK model including plasma, lymph, tumor, tight tissues, and leaky tissues. Depending on model variant, the platform contains ~ 280 differential equations.

Publications of Milberg et al., ⁶³ Wang et al., ⁶⁴ , ⁶⁵ and Jafarnejad et al. ⁶¹ exemplify application of QSP platform models for multiple mechanisms and different diseases: breast cancer treatment with anti‐CTLA4, anti‐PD1/L1 checkpoint inhibitors ⁶⁴ and epigenetic modulators, ⁶⁵ checkpoint inhibitor therapy of melanoma, ⁶³ and lung cancer. ⁶¹ Instead of building a new model for each trial, it was demonstrated that the same core mechanistic model of the disease describing tumor growth and interaction with immune system can be applied to different scenarios. The platform model is expanded, rather than created from scratch, to include mechanisms specific to a particular target. For example, Wang et al. ⁶⁵ incorporated a PK/PD model of entinostat, a histone deacetylase inhibitor, and studied combinations of this breast cancer therapeutic with immune checkpoint inhibitors. Moreover, additional modules were incorporated to account for genotypes or biomarkers of interest, including PD‐L1 expression and TMB. Jafarnejad et al. ⁶¹ incorporated a detailed model of APC antigen presentation, including binding of antigenic peptides to MHCII receptors, thus providing mechanistic link to patients’ HLA genotype in virtual trial simulations, the output of which can be analyzed in exactly the same manner as an actual clinical trial. Thus, the VPs were classified according to Response Evaluation Criteria in Solid Tumors and percent changes from baseline are summarized in waterfall plots. This allows direct comparison of simulation results with previous clinical trials to build confidence in the model as well as prospective predictions for candidate combination therapies.

The QSP platform model described above was applied in a number of case studies demonstrating feasibility and benefit of including VPs into drug development pipeline. Milberg et al. ⁶³ demonstrated that they can accurately predict median longitudinal time profile and number of patients showing partial or complete response for anti‐PD1 and anti‐CTLA4 combinations in melanoma. Although most of the model parameters were literature‐based, a selected set of parameters were adjusted using data from anti‐PD1 and anti‐CTLA4 monotherapies. The model was then applied to make predictions for combination therapy, including different doses and administration sequences and validated by comparison with combination trial data. In a case study on breast cancer, Wang et al. ⁶⁴ demonstrated how their QSP model can be used to make personalized predictions for individual patients for whom clinical measurements were available. The authors used available clinical measurements of initial tumor size and PD‐L1 expression for individual clinical subjects to instantiate VPs specific to these subjects. The model was then used to predict a longitudinal time profile for each of the subjects and results were compared with available data. They concluded that although the clinical data fall within confidence intervals of the predictions and trends are instructive, the model overpredicted efficacy. Nevertheless, this case study constitutes an important demonstration of a “virtual twin” ⁶⁶ methodology, where each VP represents an actual clinical subjects for whom sufficient data are available to instantiate the model and predict an individual tumor trajectory. In another case study on breast cancer, Wang et al. ⁶⁵ presented application of their QSP model to combination of immunotherapy with another class of drugs—epigenetic inhibitors. Model predictions suggest synergistic effect of anti‐PD1 and entinostat therapies. Jafarnejad et al. also applied the QSP model to non‐small‐cell lung carcinoma, to predict individual patient biomarkers response. They identified tumor mutational burden as a biomarker of patient response, in agreement with clinical knowledge and predicted that the number of helper and regulatory T cells in blood and tumor biopsy can be used to further improve selection of individual patients for whom immunotherapy is likely to be beneficial. In summary, the seminal work of Popel’s group and extensions thereof demonstrates methodology, feasibility, and benefit of using QSP platform models in IO drug development pipelines.

Following the original developments in academia, the QSP approach to IO has now started to attract significant interest and investments from industry for application in drug discovery and development. However, it is recognized that significant investment is required to develop a large‐scale QSP platform and that the time and resources this may take poses a practical barrier for individual research and development organisations. ⁶⁷ The organizations co‐authoring this publication have, therefore, decided to tackle this problem through a consortium model, where currently seven companies share resources, expertise, information, and data in a precompetitive manner to create and validate an industry standard, clinical IO QSP platform model. Members of our consortium have full access to the model code and details, ensuring transparency and scientific and technical rigor. Following completion of this most challenging and effort‐intensive initial stage in the QSP workflow, the completed core model, which has been qualified for specific use cases can be adapted and used by individual members outside the consortium in internal projects, where novel mechanisms and compounds can be integrated in a relative short period of time with limited resources. The entinostat case study described by Wang et al. ⁶⁵ demonstrates this method of working. One of the priorities is to use mechanistic‐modeling approaches to fully capitalize on the unprecedented wealth of tumor biopsy–omics data available from TCGA. ¹² In particular, the Immune Landscape of Cancer ⁶⁸ resource provides data on the infiltration of TME by 22 immune cell types in 11,080 TCGA samples from 33 cancer types. These unique data are sufficient to not only derive parameters specific to cancer types, but also infer distributions describing biological variability of tumors and use them in generation of the VPs. ⁷ Through this approach, the required complexity of the biological scope of the model can continuously be aligned with the step change in data availability, which allows us, for example, to incorporate more cell types than previously described models and describe dynamics of every individual cytokine and chemokine involved in cellular interactions.

In summary, recent work demonstrates the feasibility and potential of applying QSP approaches for selection of combination therapy in IO drug development. Moreover, most recent advances have shown that the next generation of IO QSP platforms can, for the first time, integrate in a quantitative manner large volumes of data generated through technological advances in molecular biology, sequencing of genomes, and transcriptomes of individual tumors. This provides the basis for a virtual twin approach in IO where VPs can be created to guide choice of treatment and dosing regimen in individual patients.

CHALLENGES AND CRITIQUE OF QSP APPROACH

A major challenge in the application of QSP models in drug development is building confidence in the values of a very large number of parameters. The platform models described above usually involve several hundreds of parameters, which values are set based on experimental data, mainly from diverse literature for different cellular and molecular interactions. In our view, well‐established criteria to assess pharmacometric models are often not relevant for QSP models. An example is parameter correlation or more general identifiability analysis (i.e., a proof that there is no other parameter set that fits data equally well), given a stated likelihood function. ⁶⁹ We believe that because parameters of QSP models are based on experimental data on individual interactions, rather than statistically inferred from comparison of model outputs with data, this requirement is often not relevant. The purpose of developing mechanistic QSP models is to extrapolate, rather than to interpolate. In the area of systems biology, it has been suggested that “sloppy” parameters are universal and indeed a fundamental characteristic of complex pathways. This is almost certainly also the case in QSP and we agree with Gutenkunst et al. ⁷⁰ that “The prevalence of sloppiness highlights the power of collective fits and suggests that modelers should focus on predictions rather than on parameters.” The context of use is to prospectively predict the data, which are outside of the range of the data used for model calibration. For example, in a well‐established application, a PBPK model parameterized by in vitro assays of drug metabolizing enzyme and transporter activities is used to predict clinical PKs, before any clinical data are available. This is a very different context of use from statistical inference of parameters obtained from a compartmental PK model fitted to existing clinical data and their empirical correlation with patient and study covariates. In the context of IO, the aim is often to predict clinical data for a candidate combination therapy, before a clinical trial is conducted. There may be preclinical data available as well as past clinical data on the tumor growth or monotherapies, and comparison of model prediction with these data can be used to increase confidence and calibrate a few selected parameters. However, the final aim is a prospective prediction of the clinical outcomes for a novel scenario.

The definition of what constitutes a “calibrated” QSP model is still subject to debate in the field and outside the scope of the present paper and we refer to a recent review of common current practices by Bai and coworkers. ⁶⁹

We appreciate that quantitative data on individual molecular and cellular interactions are sparse and that parameterization of large‐scale mechanistic models in IO is challenging. Often, quantitative experimental data on parameters is lacking and where it is available it is available from different experimental settings (e.g., in vitro experiments using different cell lines). Moreover, a translational challenge exists when using information from animal experiments for parameterization of human in silico models. In current practice, unknown parameters still have to be identified by fitting to experimental data and with this identifiability problems can arise. However, we believe that given the large‐scale experimental investments in oncology and immunology motivated not just by cancer but also infectious and auto‐immune diseases, this situation is quickly changing. In our recent article, ⁷ we have demonstrated that the high‐throughput, quantitative, –omics data cover all stages of the CIC, which form the basis of our IO QSP platform. Moreover, one of the benefits of mechanistic modeling is generation of hypotheses about mechanisms underlying disease and therapy. These hypotheses will motivate further application of existing quantitative measurement methods and perhaps development of new approaches. We expect that quantitative mechanistic modeling and experimentation will develop in parallel ⁷¹ and that the QSP approach in IO will be gaining prominence.

Another frequent criticism of QSP platform models is the seemingly redundant level of detail and biological scope. ⁷² Usually, when QSP model prediction is compared with clinical data and published, one can easily demonstrate that much simpler models could describe the relationship between variables considered in a particular prediction. However, as argued before, the application of a QSP model in IO is very different from this retrospective, descriptive analysis. The QSP platform is used to examine a large number of candidate therapies to predict clinical outcomes, before clinical data are available, select the combination, dose, dosing regime, and sequence, which maximizes chances of efficacious treatment and inform decision about which therapy should be taken forward to the clinical trial (Figure 2 ). This context of use necessitates a wide biological scope and detailed description. The model needs to contain large number of variables describing potential targets and biomarkers to allow testing of a large number of combinations. It needs to include a comprehensive model of interactions between these targets to allow predictions for any possible combination and differential efficacy in different patient groups (i.e., responders vs. nonresponders). Apart of achieving certain predictive power in validation case studies, the model must also provide description of the biology, which is recognized as a plausible, and comprehensive representation of knowledge by molecular and cell biology experts. The biology and clinical expert input and assessment constitutes a critically important stage in QSP platform development and qualification and is arguably the most important contributor to increasing confidence in the model. Furthermore, the model must be quantitative to allow consideration of dose amount, timing, longitudinal tumor size profile, percent of responders, and quantitative variables describing other biomarkers. However, to define and limit the biological scope and level of detail to be represented in an IO QSP model is challenging, and it is not easy to decide which processes shall be considered for a certain application. ⁷³

Another advantage of a large‐scale mechanistic model is that although its creation may be slow, the application is very fast. With a mature model, hundreds of virtual trials exploring a wide range of study designs, patient characteristics, dosing regimens etc., can be explored in a matter of days. Ideally, the QSP platform should be made available through a user‐friendly and validated user interface, which can be used by a wider group of quantitative clinical pharmacologists. When such a platform model is submitted to the regulator, the sponsor may refer to previous submission and documentation that the regulator is already familiar with and qualification may only have to be provide for the model extension. This brings us back to the point about how QSP can leverage from the PBPK discipline, where familiarity of the regulator with a limited number of mechanistic platform models has arguably one of the main reasons for its impact in drug development decision making.

Of course, QSP is still a novel approach and its methodology is intensively debated. Over the last 5 years, a number of papers have been dedicated to qualification, a formalized process of building confidence in QSP platform. ⁶⁹ , ⁷³ , ⁷⁴ , ⁷⁵ Although precise guidelines have not yet been agreed by the community and regulators, authors appreciate that qualification should be done with consideration of the risk of following model predictions in a particular context of use. The uses cases for model qualification have to be carefully selected to allow a valid application of the model. This follows a framework already recommended by the US Food and Drug Administration (FDA) for the modeling of medical devices. ⁷⁶ Justification of parameter values shifts focus from identifiability analysis to stating parameter ranges, where the model exhibits behaviors recognized as plausible by biology experts. Following the practice of computer simulation established in engineering and climate sciences, a lot of attention is devoted to global sensitivity analysis and uncertainty quantification.

Last, but not least, any new approach should be evaluated by comparison with existing state‐of‐the‐art. Currently, it is our experience that most decisions about which combination therapies should be tested experimentally and clinically are typically made by a relatively small group of immunobiology and oncology domain experts based on qualitative and at times selective interpretation of literature, preclinical results, and, when available, previous clinical data on monotherapies. In contrast to this somewhat intuitive and subjective approach, a QSP model represents the literature and expert knowledge in an explicit, transparent, and quantitative framework, and through virtual trial simulation enables extrapolation from this knowledge to quantitative clinical outcomes and the exploration of numerous “what if” scenarios. In our view, this already provides substantial advantage over the current ways of working and increases the chances of selecting efficacious patient‐oriented combinations.

CONCLUSIONS

In light of the unprecedented number of ongoing and planned clinical trials and preclinical programs for IO combination therapies and the emergence of examples of late‐stage attrition, there is an urgent need to improve the process of selecting candidate therapies and improve the design of trials to increase the chances of success and terminate low‐value programs prior to clinical testing. QSP models integrate existing mechanistic knowledge on disease and drug PK/PD in a quantitative framework allowing simulation of virtual trials, where candidate drug combinations are evaluated in silico before being tested in the clinic. Although development of full‐scale platform models allowing virtual screening of large numbers of candidate therapies became possible only recently, the current QSP approaches capitalize on the legacy of 3 decades of progress in mathematical and systems biology. Recently developed QSP models have started to demonstrate their potential in actual drug development case studies that indicate both feasibility and benefit of the approach. Based on these early results, we predict that QSP models will increasingly be used in IO drug development and that it will soon become standard practice to run virtual trials ahead of and in parallel with clinical trials to more quickly bring better therapeutics to patients with cancer.

Funding

No funding was received for this work.

Conflict of Interest

The authors declared no competing interests for this work. As Editor‐in‐Chief for Clinical Pharmacology & Therapeutics, Piet van der Graaf was not involved in the review or decision process for this paper.

Supporting information

Supplementary Material