Force-velocity and tension transient measurements from Drosophila jump muscle reveal the necessity of both weakly-bound cross-bridges and series elasticity in models of muscle contraction

Abstract

Muscle contraction is a fundamental biological process where molecular interactions between the myosin molecular motor and actin filaments result in contraction of a whole muscle, a process spanning size scales differing in eight orders of magnitude. Since unique behavior is observed at every scale in between these two extremes, to fully understand muscle function it is vital to develop multi-scale models. Based on simulations of classic measurements of muscle heat generation as a function of work, and shortening rate as a function of applied force, we hypothesize that a model based on molecular measurements must be modified to include a weakly-bound interaction between myosin and actin in order to fit measurements at the muscle fiber or whole muscle scales. This hypothesis is further supported by the model’s need for a weakly-bound state in order to qualitatively reproduce the force response that occurs when a muscle fiber is rapidly stretched a small distance. We tested this hypothesis by measuring steady-state force as a function of shortening velocity, and the force transient caused by a rapid length step in Drosophila jump muscle fibers. Then, by performing global parameter optimization, we quantitatively compared the predictions of two mathematical models, one lacking a weakly-bound state and one with a weakly-bound state, to these measurements. Both models could reproduce our force-velocity measurements, but only the model with a weakly-bound state could reproduce our force transient measurements. However, neither model could concurrently fit both measurements. We find that only a model that includes weakly-bound cross-bridges with force-dependent detachment and an elastic element in series with the cross-bridges is able to fit both of our measurements. This result suggests that the force response after stretch is not a reflection of distinct steps in the cross-bridge cycle, but rather arises from the interaction of cross-bridges with a series elastic element. Additionally, the model suggests that the curvature of the force-velocity relationship arises from a combination of the force-dependence of weakly- and strongly-bound cross-bridges. Overall, this work presents a minimal cross-bridge model that has predictive power at the fiber level.

1. Introduction

Muscle contraction is a multi-scale biological process that drives essential physiological functions. At the smallest scale, contraction is a result of interactions between two proteins, actin and myosin, contained in thin and thick filaments, respectively. Coupled to the hydrolysis of ATP, transient interactions occur between these proteins, whereby a myosin molecule binds to an actin filament and forms a cross-bridge. Once bound, myosin undergoes a conformational change (the power-stroke), which results in one filament sliding past the other. The binding of ATP to the myosin active site causes the myosin molecule to detach from actin. ATP is then hydrolyzed while myosin is detached from actin, and the process repeats. Direct and indirect measurements of these molecular interactions in vitro provide insight into this process.

Optical trapping experiments with isolated actin filaments and a single myosin molecule provide direct measurements of the lifetime of myosin binding and the size of the power-stroke [1, 2, 3, 4]. Similar experiments provide measurements of the force-dependence of myosin’s detachment from actin [5, 6, 7, 8]. Additionally, small ensembles of (~ 10) myosin molecules can be used in optical trapping protocols, resulting in measurements of actin sliding rate as a function of force [9, 10] or the duration and maximum force of multiple molecule binding events [11, 12, 13]. Though these small ensemble results are not direct measurements of single molecule properties, the presence of multiple myosin both increases the temporal resolution of the measurement by increasing the lifetime of binding events, and also provides information about how myosin molecules interact with each other through a common actin filament. Additionally, the in vitro motility assay, which measures the velocity of actin filaments displaced by an ensemble of ~ 100 myosin molecules [e.g. 14, 15], provides complementary information about how groups of myosin function while moving a common actin filament.

At a larger scale, experiments with whole muscle or isolated muscle fibers can provide steady-state measurements of the force a muscle produces as a function of shortening velocity [e.g. 16], as well as transient measurements of force produced throughout time [e.g. 17]. In addition, energetics measurements inform on how the energy liberated by a muscle is related to the work produced [e.g. 18]. While all of these techniques lead to an extensive amount of experimental data across ~eight orders of magnitude, it is challenging to make direct comparisons between measurements at different scales, because unique behavior emerges at each level [19, 20, 21, 22, 23, 24, 25]. Thus, it is unclear how to directly associate molecular in vitro measurements to larger fiber and whole muscle measurements [e.g. 26].

One way to make connections across scales is through development of mathematical models. In 1957, shortly after the sliding filament theory was proposed [27, 28], A.F. Huxley developed a molecular-scale cross-bridge model which replicates steady-state, whole muscle measurements [16]. This model was later adjusted in various ways to replicate transient muscle measurements [17], to be thermodynamically consistent [29], and to fit biochemical measurements [30]. Subsequently, as experimental techniques at the muscle fiber scale advanced, these mathematical models have evolved to be consistent with some subset of muscle measurements, typically at the fiber or whole muscle scale [e.g. 31, 32, 33, 34, 35].

Though they differ in their details, these models are all formulated in a similar manner. In particular, myosin molecules transition between some number of discrete chemical states. Each state is associated with a particular conformation, and in some, myosin is bound to actin. The rate constants that govern the transitions between these states are force-dependent and, since myosin is assumed to act as a linear spring, are proportional to myosin’s molecular extension, x. However, until molecular measurements became possible, the x-dependence of these rates was unknown, so modelers had to rely on either intuition or mathematical convenience.

Molecular measurements of the x-dependence of myosin’s reaction rates significantly constrain these models. ADP release (k_D(x)), for example, depends exponentially on molecular extension in smooth [5, 6] and cardiac [7, 8] myosin, consistent with theoretical predictions [e.g. 36]. Thus, recent models no longer must define an entire function (k_D(x)), but rather two parameters ($k_D^0$ and E) that define it $\left(k_D\left(X\right)=k_D^0{e}^{EX}\right)$. Of the current models that are informed by these molecular measurements [e.g. 21, 35, 37], we focus on the model of Walcott et al. 2012 (Fig. 1A), due to its relative simplicity and its ability to describe in vitro measurements from the scale of single molecules to ~100 molecules, all with a single set of parameters [24]. In addition, the model is able to fit force-velocity measurements from muscle fibers, and infer molecular properties from these cellular measurements [38].

Figure 1:

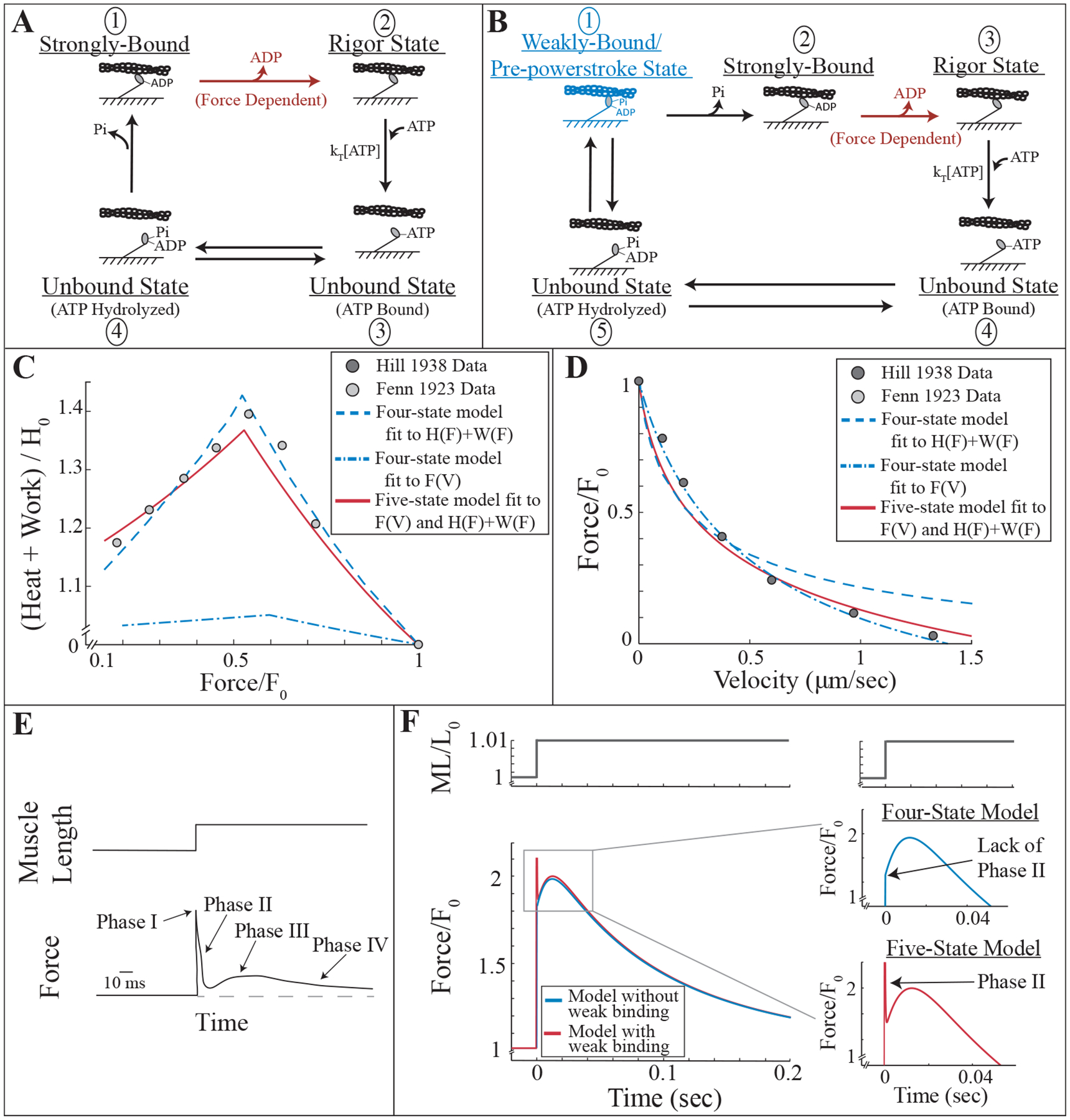
Motivation for weakly-bound cross-bridges in a model of muscle contraction based on molecular measurements. A) Four-state kinetic scheme of myosin’s interaction with actin including two bound states (states 1 and 2) and two unbound states (states 3 and 4). B) Five-state kinetic scheme that is the same as that in A, except with the addition of a weakly-bound state labeled in blue (state 1), where myosin is bound to actin but has not undergone its power-stroke. C, D) Measurements of the heat produced and work done by a muscle as a function of load (C, [18]) and force produced as a function of shortening velocity (D, [16]). The four-state model was fit to the energetics data (dashed blue line in C), and the corresponding force-velocity relationship is plotted in D. The four-state model was also fit to the force-velocity measurements (dash-dotted blue line in D), and the corresponding energetics relationship is plotted in C. The five-state model is able to simultaneously fit both measurements (red lines, C and D). E) Illustration of a typical skeletal muscle force transient response to a quick stretch. F) Four- and five-state model response to quick stretch (blue and red lines, respectively). Insets illustrate the lack of phase II in the four-state model response, and the clear phase II in the five-state model response.

While the success of such modeling approaches in bridging the molecular to cellular scale is exciting, all models neglect some details. For example, Walcott et al. 2012 [24] neglect a rapid, transient interaction between myosin and actin (the weakly-bound state) that occurs prior to myosin’s strong binding to actin and power-stroke [39, 40, 41]. Although this interaction is too fast to be observed with standard single molecule techniques (though see [42]), its presence has been inferred from solution [43, 44, 45, 46] and muscle fiber measurements [47, 48, 49]. Given that this model without weakly-bound cross-bridges is validated across size scales, it is of interest to understand the effect and necessity of a weakly-bound interaction.

With this in mind, we aim to develop a minimal cross-bridge model based on well-defined molecular mechanisms that is able to scale up and have predictive power at the fiber and cellular levels. The organization of the paper is as follows: In the Motivation section (section 2), we hypothesize that such a model must include both weakly- and strongly-bound cross-bridges, based on fits to steady-state force-velocity and force-energetics experiments performed on frog muscle fibers under similar, but not identical, conditions. We propose a five-state model that can fit both experiments. Adding support to this hypothesis, this model qualitatively reproduces the delayed increase in force following a rapid lengthening of a muscle fiber (stretch-activation). However, in the Results section (section 3), we show that this model is not consistent with our measurements of steady-state force-velocity and tension transients performed with Drosophila muscle fibers under identical experimental conditions. To reproduce our measurements, both force-dependent detachment of weakly-bound cross-bridges and an elastic element in series with the cross-bridges are necessary. In the Discussion section (section 4), we describe the implications of these results on inferring molecular mechanisms from muscle fiber measurements.

2. Motivation

How does myosin’s weakly-bound state contribute to force production? Under what circumstances, if at all, can it be neglected? These are the central questions we wish to address. To do so, we consider two alternative models: the first (Fig. 1A) is a four-state model of myosin’s interaction with actin that is based solely on molecular measurements [24]. This model reproduces measurements at the single molecule to large ensemble scale in vitro [24] and is consistent with some fiber measurements [38]. The second (Fig. 1B) is a five-state model, identical to the first, but including a fifth state in which myosin has bound to actin but has not undergone a power-stroke, and is therefore not producing force. We have organized our results into two separate sections. In the first (this section), we motivate our hypothesis that this fifth, weakly-bound state is necessary to consistently model muscle measurements at the fiber scale. In the next section (the Results section), we describe experiments and modeling that test our hypothesis.

2.1. Weak Binding is Necessary for Consistent Force-Dependence

As a first test of the effect of myosin’s weakly-bound state on muscle measurements, we fit the model to two classic experiments, both of which are influenced by myosin’s force-dependent reaction rates: 1) the Fenn effect and the energetics of muscle contraction, and 2) the Hill relationship between steady-state muscle force and shortening velocity.

In the first set of measurements we consider, W. O. Fenn measured the relationship between energy liberation and work performed during muscle contraction [18]. With this work, Fenn determined that the excess heat, i.e. the heat produced by a muscle during an isotonic experiment minus the heat produced during an isometric experiment, was proportional to the work done by the muscle. This phenomenon, known as the Fenn Effect, is attributed to myosin’s force-dependent reaction rates [5]. In the second set of data we model, A.V. Hill measured the relationship between force and velocity during isotonic contractions [16]. Hill’s measurements suggest an approximately hyperbolic relationship between force and velocity, with shortening rate decreasing as load on the muscle increases (Fig. 1D). The nonlinearity of this relationship is also attributed to myosin’s force-dependent reaction rates [38, 50].

Given that the Hill and Fenn data were collected under similar experimental conditions and are both influenced by myosin’s force-dependent reaction rates, we compared our two models, without (Fig. 1A) and with (Fig. 1B) weak binding, to the measurements. To do so, we expressed each model mathematically, solving for force as a function of velocity and ATP consumption as a function of shortening velocity to compare to Hill and Fenn’s data, respectively (see Methods and Supplementary Material, SM). In all of our calculations, myosin’s force-dependence is defined by a single non-dimensional parameter, E = κδd/k_BT, where κ is the stiffness of myosin, δ is a parameter (with units of distance) that describes myosin’s force-dependent chemistry, d is myosin’s power-stroke size, and k_BT is Boltzmann’s constant times temperature.

By varying the parameters of the four-state model (without weak binding) we optimized the fit to each of the two measurements individually (see SM). The agreement between model and data is good (dashed blue line in Fig. 1C and dash-dotted blue line in Fig. 1D). However, the parameters that optimize the model fit to Fenn’s energetics measurements are not consistent with Hill’s shortening velocity measurements as a function of load, predicting a relationship that is too curved (dashed blue line in Fig. 1D). Similarly, the parameters that optimize the model fit to Hill’s shortening velocity measurements are not consistent with Fenn’s heat plus work measurements as a function of load, predicting a linear relationship that is not sufficiently steep (dash-dotted blue line in Fig. 1C). The inconsistency between the fits is due to a difference in force-dependence, with the force-velocity measurements predicting a smaller force-dependence (E = 0.57) and the force-energetics measurements predicting a larger one (E = 1.88).

The five-state model (with weak binding), however, is able to simultaneously fit both data sets with a single force-dependence (E = 1.42, red curves in Figs. 1C, D) and generates a significantly better fit than the four-state model (F-test, p < 0.05). This improved fit is made possible by the weakly-bound cross-bridges, which act as a viscous drag on the system (see SM), providing a resistive force that varies linearly with shortening velocity. Thus, in the simulations of the force-velocity measurements, force comes from both the weakly-bound cross-bridges, with a linear force-velocity relationship, and the strongly-bound cross-bridges, with a curved force-velocity relationship whose curvature depends on E. Fitting Hill’s data with the five-state model therefore requires a greater curvature for the force from the strongly-bound cross-bridges (i.e. a larger E) to balance the absence of curvature from the force of the weakly-bound cross-bridges. For Fenn’s energetic measurements, however, weak binding has a minimal effect. In particular, although the muscle must do more work to overcome the resistive force of the weakly-bound cross-bridges, the magnitude of this work is small compared to the work done by the muscle raising the weight (see SM). Thus, weakly-bound cross-bridges effectively mask the force-dependence predicted from force-velocity measurements, allowing both fiber level data sets to be fit together.

2.2. Weak Binding is Necessary to Reproduce Force Transient Response

While the Fenn and Hill measurements provide preliminary motivation for weak-binding, these experiments are nearly 100 years old and are done under similar, but not identical conditions. Additionally, heat measurements are challenging to interpret, because other ATP-consuming reactions besides cross-bridge cycling occur in a muscle [51]. Thus, to further understand the contribution of weakly-bound cross-bridges to muscle force, we consider the transient behavior produced by a muscle (or muscle fiber) after a quick stretch [e.g. 17]. In this experiment, the muscle (or fiber) is activated isometrically. It is then rapidly stretched a small percentage of its length, and held isometric again. The response after stretch is often called the tension transient [17, 52, 53, 54, 55, 56], presumably because the measured quantity is the tension in the muscle or muscle fiber. Here, we will refer to the response after stretch as the force transient, because our model makes predictions of the force generated from the interaction of myosin with actin. The force response of a muscle, or muscle fiber, post-stretch is a peak in force at the time of stretch (phase I), followed by a rapid decay (phase II), a delayed increase in force (phase III/stretch-activation) and finally a slower recovery period (phase IV) (Fig. 1E) [17, 52, 54, 57, 58]. The molecular mechanism behind this force response is unknown [52, 58, 59, 60, 61].

Simulating this quick stretch (see Methods), we find that the four-state model is unable to reproduce all of the qualitative behavior of the force response, and in particular, is lacking the quick decay of phase II. This model predicts a large increase in force at the time of stretch (i.e. phase I), followed by a transient increase in force (i.e. phase III), and finally a subsequent decay (i.e. phase IV) (Fig. 1F, upper inset). This response is due to the fact that strongly-bound cross-bridges are extended with stretch and, since they act as linear springs in the model, therefore experience a proportional increase in force. This force decreases the ADP release rate (transition from state 1 to 2 in Fig. 1A, see Eq. 2), which therefore slows the rate at which the cross-bridge detaches. The attachment rate of cross-bridges is unaffected, so new cross-bridges continue to attach. This results in a net increase in the amount of bound cross-bridges, and thus the transient increase in force post-stretch. This result suggests that phase III is attributable to strong binding, and in particular the force-dependent decrease in ADP release rate post-stretch.

The five-state model, however, is able to reproduce each of the four phases of the force response (Fig. 1F, lower inset). In this model, both strongly-bound and weakly-bound cross-bridges are extended with stretch. The strongly-bound cross-bridges have the same effect as in the four-state model, with a decreased detachment rate resulting in a net increase of bound cross-bridges and thus phase III. The weakly-bound cross-bridges, however, act on much faster time scale. Post-stretch, these cross-bridges rapidly re-equilibrate, resulting in the quick decay of phase II.

Taken together, our simulation results show that the four-state model, without weak binding, cannot simultaneously fit Hill’s force-velocity and Fenn’s energetics measurements, nor does it reproduce the qualitative behavior of force transients following a rapid stretch. In contrast, the five-state model, with weak binding, simultaneously fits Hill’s and Fenn’s measurements and reproduces the four phases of the force transient post-stretch. Given these results, we hypothesize that a weakly-bound interaction between actin and myosin is necessary to consistently model muscle across scales. To test this hypothesis, we performed force-velocity and force transient measurements on the same muscle fiber type under the same experimental conditions. We then fit our measurements with the four- and five-state models.

3. Results

We performed two different muscle mechanical experiments (force-clamps to obtain force-velocity curves and force transients in response to length steps) on permeabilized (skinned) Drosophila jump muscle fibers to test our hypothesis that a weakly-bound interaction between actin and myosin is necessary to consistently model muscle across scales. Note that the jump muscle is mechanically equivalent to a fast skeletal muscle type with maximum shortening velocity and tension generation similar to mouse fast-twitch muscle type 2B [62]. In the first experiment, we performed force transient measurements on fibers at a sarcomere length of 3.6 μm with length increase amplitudes ranging from 0.25% to 2% of the muscle fiber length (e.g. Fig. 2A). We varied the stretch amplitudes to ensure that the muscle fiber gave a linear force response to the stretch. A non-linear response would indicate some yielding behavior (i.e. the forcible detachment of myosin from actin), which is not included in our model. We observe a linear relationship for stretches less than 1% of muscle fiber length (Fig. 2B), and only fit the model to measurements with stretch amplitudes in this linear range, to ensure that cross-bridges are not being forcibly detached.

Figure 2:

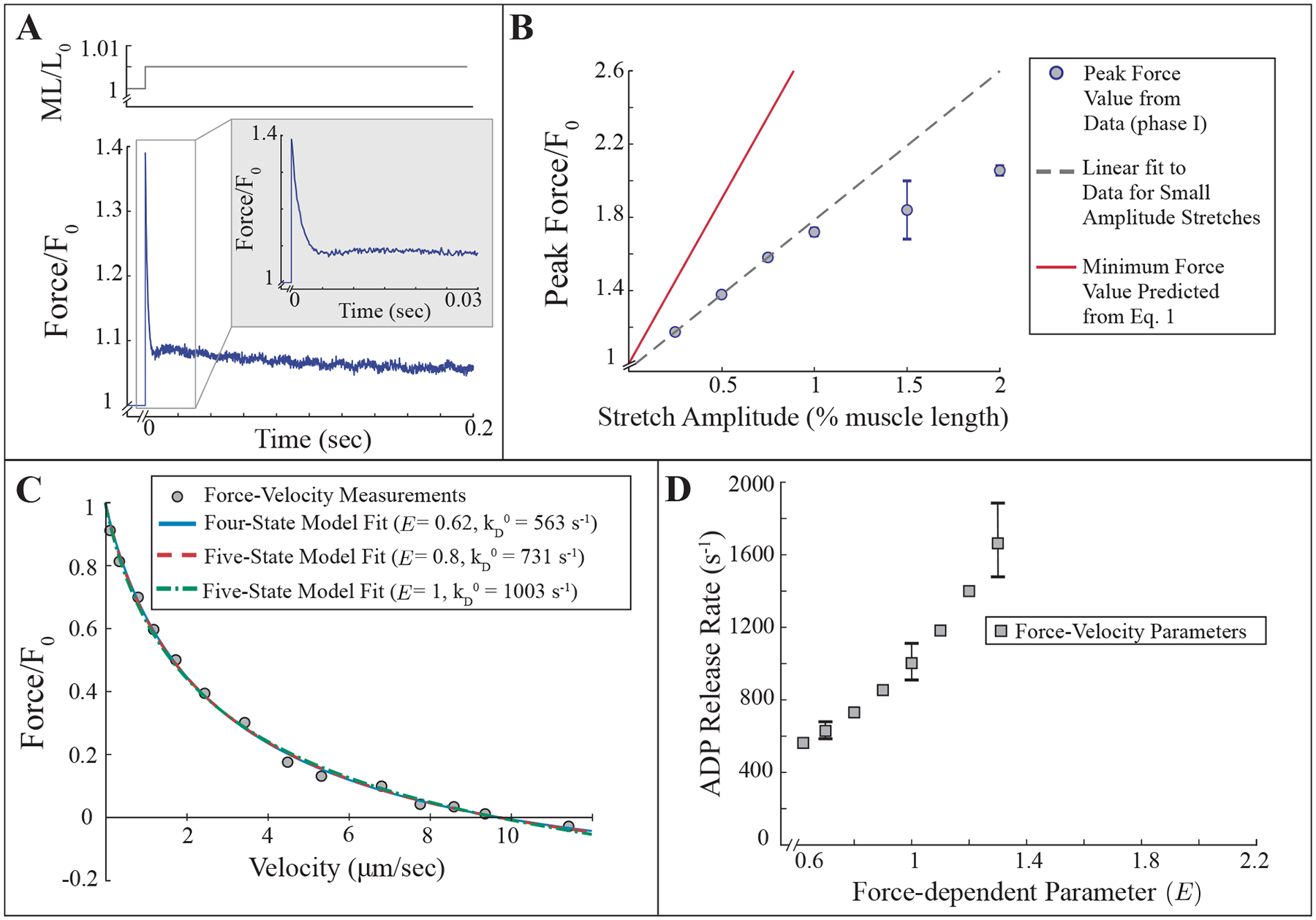
Comparison between our measurements and model simulations show that the model can fit force-velocity measurements but is inconsistent with force transient measurements. A) Force transient measurement from a jump muscle fiber that was stretched 0.5% of its fiber length over 0.5 ms. Inset is the same force transient on a smaller time scale. B) Relationship between peak force post-stretch (phase I) and stretch amplitude. Each data point (blue circles) is the mean ± SD of transients from three different fiber preparations. The dashed line is a linear fit to measurements of stretch amplitudes less than 1%. The red line is the model prediction (Eq. 1). C) Force-velocity measurements from an equivalent jump muscle fiber preparation are well-fit by the four- and five-state models. D) Lower bound on combinations of unloaded ADP release rate and the force-dependent parameter that fit force-velocity measurements with the five-state model (see SM).

In the second experiment, we performed force-velocity measurements on fibers under the same conditions as the force transient measurements (Fig. 2C, see Methods). These measurements produced force-velocity curves that are comparable to our previous measurements with jump muscle fibers from the same fly line, pwMhc2 [e.g. 38, 62, 63], and can be well-fit with the four-state model with an E = 0.62, or with the five-state model with a range of E values above E = 0.62 (Fig. 2C, D, see SM).

Given that either the four- or five-state model reproduces these force-velocity measurements, we further test our hypothesis by fitting the force transient measurements with both of our models. If the four-state model fits our force transient measurements and our force-velocity measurements with a consistent set of parameters, then we reject the hypothesis that weakly-bound cross-bridges are necessary to model muscle. If the five-state model fits the force transient measurements and the force-velocity measurements with a consistent set of parameters, but the four-state model does not, then we cannot reject the hypothesis. If neither model fits both measurements, we cannot reject the hypothesis as stated, but we can reject both models and conclude that the models do not capture some effect contributing to muscle force.

3.1. Mismatch Between Force Transient Data and Model

We fit the four- and five-state models to both the force transient and force-velocity measurements. While both models could reproduce our force-velocity measurements, neither model was able to reproduce our force transient measurements. One obvious difference between the modeled and measured force transients was a discrepancy in the peak force obtained post-stretch (phase I). This discrepancy is surprising, since this peak in force occurs over such a rapid time scale (Stretch duration: 0.5 ms, Measurement resolution: 0.125 ms) that myosin molecules would likely not undergo chemical state transitions, and therefore the force response should represent the elastic stretching of myosin molecules bound to actin. Given this simple interpretation, we investigated this difference between the peak force predicted by model and measurement in more detail; however, as we will show, even if this discrepancy is explained, neither the four-nor the five-state model can simultaneously fit our measurements.

A simple calculation allows us to understand the mismatch between the peak force we measured, and that which was predicted by the model. In the experiments, the half-sarcomere of the muscle fiber is set at a length of 1.8 μm. The muscle fiber is then stretched a particular fraction, s, of its length (e.g. a 0.5% stretch corresponds to s = 0.005). Assuming each sarcomere stretches equally, a stretch of s muscle lengths is equivalent to stretching each sarcomere s sarcomere lengths, and therefore s of each half-sarcomere length. The length of stretch in nanometers at the half-sarcomere level is therefore $\mathcal{S}=1800\text{ nm}\cdot s$. We can calculate a lower bound on the peak force post-stretch for a given stretch amplitude by considering the force from cross-bridges that are strongly-bound before stretch. Pre-stretch, these cross-bridges have undergone a power-stroke and therefore have an average extension of d = 10 nm. Post-stretch, these cross-bridges have now been stretched an additional $\mathcal{S}$ nm, giving an average extension of $\mathcal{S}+d$ nm. Assuming linear cross-bridge elasticity and myosin stiffness of κ, the force produced by a cross-bridge post-stretch is $F_p=\left(\mathcal{S}+d\right)\kappa$. Normalizing this to the pre-stretch value, we get,

$$\frac{F_p}{F_0}=\frac{\left(\mathcal{S}+d\right)\kappa }{d\kappa }=\frac{\mathcal{S}}{d}+1=\frac{1800\cdot s}{d}+1$$ (1)

We emphasize that this estimate is a lower bound because we neglect the contribution of weakly-bound cross-bridges, which (if present) would also be stretched and would add to this force.

The measured values of peak force following stretch are much less than this estimated lower bound (Fig. 2B). Importantly, only a few model assumptions lead to this model prediction, namely linear cross-bridge elasticity, a power-stroke size of d = 10 nm, and the assumption that a particular length change at the fiber level corresponds to the same relative change at the sarcomere level. While it might be argued that estimates of power-stroke size vary [e.g. 1, 3, 4, 31, 64], we would need a power-stroke size of d > 25 nm in order to reproduce the experimental measurement, since Eq. 1 is a lower bound. Thus, with the assumptions of linear elasticity, a power-stroke size of 10 nm (or less), and the same relative stretch amplitude across scales, the model and data are inconsistent.

While a discrepancy between model and data means that we reject both models and neither reject nor support our hypothesis, this conclusion depends on all of the assumptions that led to Eq. 1. We therefore consider two explanations for the discrepancy that would adjust the result from Eq. 1: (1) the relative change in sarcomere length is smaller than the relative change in fiber length, resulting in an overestimation of stretch amplitude of the half-sarcomere, and (2) the force transient data includes an “unexplained” force due to factors other than actin and myosin. We discuss these two possibilities below, keeping in mind that they are not mutually exclusive.

3.2. Explanation 1: Overestimated Stretch Amplitude

Our calculation of peak force (phase I) following stretch (Eq. 1) relies on the assumption that a relative change in fiber length results in an equivalent relative change in sarcomere length. However, it is possible that the change in sarcomere length is smaller than that measured at the fiber level, due to the elasticity of structures in series with the cross-bridges. There are a variety of elastic elements that are in series with cross-bridges (e.g. titin, Z-disks), in series with the muscle fiber (e.g. the thin-filament), in the experimental equipment, and at the fiber ends from sarcomeres that are damaged when the fiber is clamped. When a muscle fiber is stretched, these elastic structures (which we refer to as the series elastic element) are also stretched, and therefore the change in sarcomere length is smaller than the corresponding change in fiber length.

To account for this overestimation of stretch amplitude, we let stretch amplitude be a parameter of fit, along with the other unknown model parameters (see SM). In doing so, we account for the effect of the series elastic element on the stretch amplitude, but neglect any dynamic interaction between the cross-bridges and the series elastic element (also see section 3.4). Additionally, in the force transient measurements, the isometric force post-stretch is slightly higher than the pre-stretch isometric force (residual force enhancement). Since the model does not include a mechanism for residual force enhancement, we account for this by adding a small force to the model post-stretch, so that the modeled force returns to the measured post-stretch isometric force for long time (see SM). With these specifications, we fit the model to our measurements. The optimization converges to a good fit to the entire force transient measurement, reproducing all parts of the force response (i.e., phases I-IV, Fig. 3A).

Figure 3:

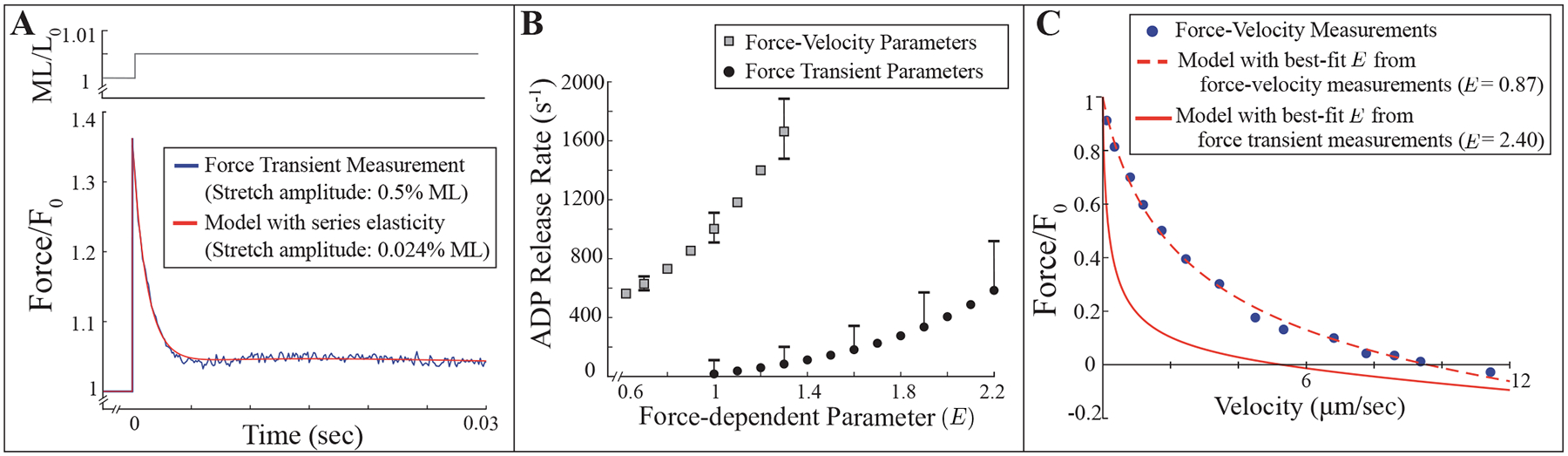
With a decreased stretch amplitude, the model reproduces force transient measurements, but the results are inconsistent with force-velocity measurements. A) The five-state model fits our force transient measurements for a 0.5% muscle length stretch with a best-fit half-sarcomere stretch amplitude of 0.437 nm (compared to a 9 nm stretch without series elasticity). B) Combinations of unloaded ADP release rate and the force-dependent parameter that fit force-velocity (gray squares) and force transient (black circles) measurements with the stretch amplitude fixed at Δs = 0.437 nm. Error bars denote parameter values that give results within one standard deviation of the best-fit error. C) Model fits to force-velocity measurements with $k_D^0$ fixed from the best-fit to the force transient measurement, and E from the best-fit to the force transient measurement (sold line) and best-fit to the force-velocity measurements (dashed line).

Though the model reproduces the force transient measurements, there are two reasons that we reject this explanation. The first is that the best-fit predicts that the stretch amplitude at the sarcomere level is an order of magnitude smaller than that imposed experimentally at the fiber level (experimental stretch amplitude: 9 nm for a 0.5%ML stretch, predicted stretch amplitude: 0.437 ± 0.08 nm, see SM). While series elastic elements can result in an overestimation of the stretch amplitude at the sarcomere level, it is unlikely that the effect is of this magnitude.

The second reason that an overestimation of stretch amplitude is unlikely to explain the discrepancy between simulation and measurement is that, with this small stretch amplitude, the model requires a large force-dependence to fit the force transient measurements. This is because in the model, phase III of the force transient response arises from stretching strongly-bound cross-bridges. Since the cross-bridges act as linear springs, this stretch results in a proportionate force on the cross-bridge, which then decreases that cross-bridge’s ADP release rate (via the parameter E). Thus, if the stretch amplitude is decreased by an order of magnitude, the force-dependent parameter E must be increased by an order of magnitude in order to obtain the same decrease in ADP release rate. This large force-dependence required to fit force transient measurements is inconsistent with the force-dependence predicted from force-velocity measurements (Fig. 3B), resulting in a force-velocity relationship that is too curved (Fig. 3C). Thus, we reject the explanation that series elasticity results in an overestimation of stretch amplitude, and instead consider the effect of an “unexplained” force on our calculation.

3.3. Explanation 2: Unexplained Force

In our calculation of peak force following stretch (Eq. 1), we also assume that all of the measured muscle force arises from the interaction of myosin cross-bridges with actin. While we account for the force contribution of passive elements by measuring the force production in experiments at low calcium concentrations (see SM), it is possible that other calcium-dependent, non-cross-bridge elements contribute to force. Indeed, such a mechanism has been proposed to account for the increase in isometric force following a stretch (i.e. residual force enhancement, [65, 66, 67, 68, 69, 70, 71]).

To account for this potential non-cross-bridge force, we let it be a parameter in the model. With this addition, we find that the optimization converges to a good fit to the entire force transient measurement (SM Fig. S13). However, we find that these results mirror the inconsistencies we found with stretch amplitude as a model parameter (Sec. 3.2 and Fig. 3), and thus we must reject this hypothesis. In particular, the best-fit predicts an implausibly large post-stretch unexplained force of over 28 times the isometric force from cross-bridges. Additionally, this large magnitude of unexplained force then requires a large force-dependence to fit our force transient measurements, which is then inconsistent with our force-velocity measurements (see SM for details).

The net result of the comparison of our model to our measurements is that neither the four-state nor the five-state model can reproduce both our force-velocity and force transient measurements, allowing us to reject both models as stated. We can therefore infer that neither model captures all of the effects contributing to muscle force in these experiments, and conclude that at least one of our model assumptions is wrong.

However, the success of the five-state model in fitting Fenn’s and Hill’s measurements and reproducing both our force transient and force-velocity measurements (albeit with different parameters), suggests that some modification of the five-state model might successfully fit both of our measurements. We therefore considered various alternative model assumptions. We found that none of these alternative assumptions, individually, allows the model to fit our measurements. Neither non-linear elasticity of myosin, force-dependent detachment of weakly-bound cross-bridges, nor thin-filament activation could explain the discrepancy (see SM for details). However, when we allow the series elastic element to interact dynamically with the cross-bridges and include force-dependent detachment of weakly-bound cross-bridges, we can fit our measurements with the five-state model.

3.4. Model with Force-Dependent Detachment of Weakly-Bound Cross-Bridges and Series Elasticity is able to Consistently Model Muscle Measurements

In section 3.2, we invoked a series elastic element to motivate our efforts to fit our measurements with a stretch amplitude at the sarcomere level that is smaller than the imposed stretch. In doing so, we made the assumption that this series elastic element does not change length after the initial stretch. However, this elasticity, possibly due to a variety of factors (e.g. titin, Z-disks, the experimental apparatus; see Sec. 3.2), may be more dynamic. If we relax our original assumption, allowing a dynamic interplay between the contractile element and the series elastic element, the model remains unable to fit the data. However, if we additionally include force-dependence in the detachment from the weakly-bound state [42], the model is consistent with our measurements (Fig. 4, see SM for details of the fitting procedure and the model).

Figure 4:

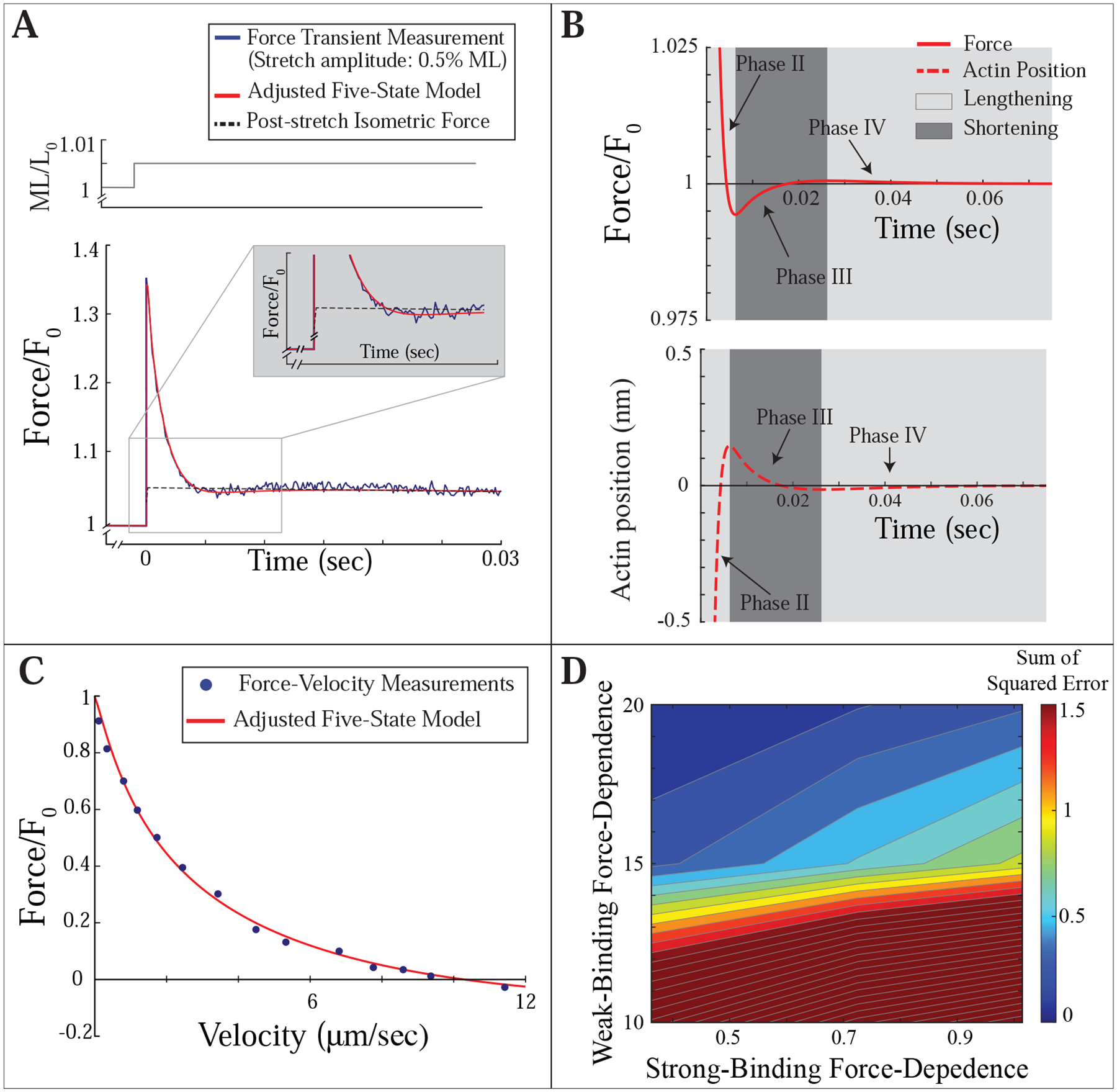
The five-state model adjusted to include force-dependent detachment of weakly-bound cross-bridges and an elastic element in series with the cross-bridges is able to reproduce our measurements. A) The adjusted model reproduces all four phases of the force transient response. Inset shows that the force in both measurement and model briefly drops below the post-stretch isometric force (dashed line). B) Force (relative to isometric, top panel), and actin position (relative to a steady-state position of 0, bottom panel), as a function of time during the force transient response. The light grey regions represent time during which actin is moving in the lengthening direction relative to myosin. The dark grey regions represent time during which actin is moving in the shortening direction relative to myosin. C) The adjusted model replicates our force-velocity measurements. D) Sum of the squared error in comparing model to measurements for combinations of the magnitude of force-dependence of weakly- and strongly-bound cross-bridge detachment, model parameters E_wb and E, respectively. Each axis plots the non-dimensional values of the respective force-dependencies (see Sec. 4.3). The model requires a small force-dependence for strong-binding and a large force-dependence for weak-binding to accurately fit our measurements.

To fit our force transient measurements, we must again account for residual force enhancement, the increase in isometric force post-stretch. Adding a small force post-stretch (as discussed in section 3.2), allows the model to fit phase I and II of the force transient. However, adding a slightly larger force allows the model to fit phases I-III of the force transient, and to partially reproduce phase IV (Fig. 4A, dashed line shows added force, Fig. 4B shows the four phases of the simulated force transient). With the same parameters, the model fits our force-velocity measurements (Fig. 4C). To our knowledge, this is the first cross-bridge model that accurately captures both the dynamics of the force transient after stretch and steady-state force-velocity measurements.

4. Discussion

Bridging the molecular to cellular (and larger) scales has been a central focus in the study of muscle contraction. Such a multi-scale understanding would have a profound impact on both science and medicine, e.g. improving the understanding of human movement [72] and the treatment of genetic heart disease [73]. Over fifty years ago, the sliding filament theory [27, 28] and A. F. Huxley’s mathematical model [50] suggested that this multi-scale understanding was within reach. Subsequent successful predictions of the sliding filament theory [e.g. 74], biochemical and structural measurements of myosin interacting with actin [e.g. 43, 75] and molecular-scale measurements [e.g. 1, 14] further contributed to the idea that a multi-scale understanding of muscle contraction was at hand. Nevertheless, to our knowledge, there is still no mathematical muscle model capable of explaining all (or even more than a little) of muscle phenomenology at the cellular scale.

We aim to develop a cross-bridge model that consistently describes muscle measurements across scales. To do so, we start with a molecular-scale model that incorporates many molecular measurements [24], but we make a few critical assumptions motivated by mathematical convenience when we apply our model to the fiber scale (e.g. that sarcomeres are uniform and contain a large number of myosin molecules). This allows us to employ a suite of mathematical tools (see Methods and SM) and perform global parameter optimization when we fit our experimental measurements. Optimization of this form is powerful, because it allows us to rule out specific models. Here, for example, we can conclude that the model assumptions in our four and five-state models (Fig. 1A,B) are wrong, since neither are able to reproduce our data for any parameter choice.

Upon rejection of these proposed models, we tested some of the assumptions we made when we applied the five-state model to our measurements. In particular, we found that including either non-linear elasticity of myosin, force-dependent detachment of weakly-bound cross-bridges, or thin-filament activation did not allow the model to fit our measurements. However, extending the five-state model to include force-dependent detachment of weakly-bound cross-bridges as well as a dynamic interaction with a series elastic element allows the model to simultaneously fit our measurements. As with any successful model fit, this does not guarantee that the model is correct; however, given the difficulty in fitting the model to the data and the large number of alternative models we were able to reject, it is an attractive hypothesis that the force transient response after a small amplitude stretch is due the interaction of a series elastic element and weakly-bound cross-bridges that detach from actin in a force-dependent manner. This result has implications to the connection between cross-bridge dynamics and muscle fiber measurements.

4.1. Strongly-Bound Cross-Bridges are Unlikely to Cause Stretch-Activation

Our preliminary simulations of force transients using our two proposed models led us to hypothesize that strongly-bound cross-bridges are responsible for the delayed increase in force of phase III (stretch-activation). In the model, this occurs due to the force-dependence of strongly-bound cross-bridges, which, upon stretch, experience forces that decrease their detachment rate, resulting in a net increase in bound cross-bridges and therefore increased force (section 2.2). However, we reject this hypothesis as described by the models, because neither model can fit our force transient and force-velocity measurements. Adjusting for the possible effects of series elasticity or an unexplained force allows the five-state model to fit our measurements of the force transient, but then it cannot also fit our force-velocity measurements (section 3.2, 3.3).

The failure of the five-state model is due to significant differences in the force-dependence required to fit our two experiments. In the force transient fits, large force-dependence is needed to decrease the detachment rate of the strongly-bound cross-bridges enough to get a sufficient increase in force to fit the stretch-activation response. These large values are then inconsistent with those predicted from force-velocity measurements (Fig. 3B). This discrepancy persists even when the model is adjusted to include either non-linear elasticity of myosin, force-dependent detachment of weakly-bound cross-bridges, or thin-filament activation (see SM). Thus, we conclude that strongly-bound cross-bridges cannot be solely responsible for the stretch-activation response.

When we adjust the model to include both a series elastic element interacting dynamically with cross-bridges and force-dependent detachment of weakly-bound myosin, it can simultaneously reproduce both the force transient response and the force-velocity relationship (Fig. 4A, C). Interestingly, in the simulated force response, cross-bridge force drops below isometric at the end of phase II (Fig. 4A, inset). This drop in force occurs because, even though the fiber length is held constant, both the length of the series elastic element and the length of the contractile element (i.e., the position of actin relative to myosin) are changing. The drop in force coincides with a time when actin moves beyond its steady-state position relative to myosin. Actin moving beyond its steady-state position causes the series elastic element to relax, producing less force. Actin then moves in the shortening direction, extending the series elastic element and causing force to rise in phase III. There is another small overshoot and drop in force which produces phase IV (Fig. 4B). In the simulations of the force from the fiber, this drop is masked by the small force we add post-stretch to account for residual force enhancement (dashed line, Fig. 4A). However, in some measurements of stretch-activation, particularly at larger stretch amplitudes, a clear drop in force below even the initial isometric force is observed [76, 77, 78]. Such sub-isometric force could not occur if stretch-activation were caused by prolonged attachment of strongly-bound cross-bridges. After stretch, there would be at least as many strongly-bound cross-bridges as pre-stretch, and each cross-bridge would produce more force. Thus, strongly-bound cross-bridges cannot cause sub-isometric forces post-stretch, since together they will result in more, and not less, force. This observation further strengthens our conclusion that stretch-activation is not solely caused by prolonged binding of strongly-bound myosin molecules, and that the major contributor is more likely a dynamic interaction between cross-bridges and a series elastic element.

4.2. Series Elasticity Results in a Complex Connection Between the Rates of the Force Transient Response and Cross-Bridge Kinetics

Force transient measurements have been employed to make direct connections between force decay rates and the kinetic steps of the interaction between actin and myosin [17, 32, 57, 76]. Our results, however, suggest that the connection between force transients and molecular kinetics may not be straightforward. In particular, in our simulations, the extension rate of the series elastic element, and therefore the velocity of actin relative to myosin, varies post-stretch on the same time scale as phase I and II of the force transient response. Thus, the rate at which the phase II decay occurs reflects both the kinetics of cross-bridge unbinding and also this rapidly changing actin velocity. This result provides further insight into why our original five-state model, without a dynamic series elastic element, was unable to fit our force transient measurements (Fig. 3). In this model, there is a mismatch in time scales between our force transient and force-velocity measurements, with the former requiring slower ADP release than the latter (Fig. 3B). The addition of a dynamic series elastic element resolves this discrepancy (Fig. 4).

This result fits with previous modeling studies that have highlighted the importance of series elasticity in other contexts. For example, myofilament elasticity has been shown to have a significant effect on cross-bridge dynamics and force in computational muscle models [79, 80, 81]. Similarly, a computational model used to reproduce the stress relaxation response of muscle illustrates that series elasticity has a large effect on the resulting force transient [82]. This previous modeling work highlights the necessity of appropriately modeling filament elasticity in cross-bridge models, and that time scales of force production do not directly relate to kinetic steps in the cross-bridge cycle. Our findings expand these results to the context of stretch-activation. We show that the individual phases of the force transient response cannot be directly linked to specific kinetic steps, and further, that series elasticity must be included in cross-bridge models to accurately capture stretch-activation.

4.3. Strongly and Weakly-Bound Cross-Bridges Contribute to Force-Velocity Curvature

It is generally thought that the curvature of the force-velocity relationship is due to the force-dependent chemistry of myosin molecules [e.g. 38]. In particular, it has been shown experimentally that ADP release rate and myosin detachment are dependent on the load the molecule experiences [5, 6], and that even small ensembles of myosin molecules can produce force-velocity curves that are similar to those from entire muscle fibers [9]. Additionally, muscle models that include force-dependent ADP release produce force-velocity relationships with appropriate curvature both at the molecular scale [24], and at the fiber scale [38]. Quantitatively, this force-dependence can be described by a single non-dimensional parameter, E (see Sec.2.1), generally ranging between 0.7–1.9 for skeletal muscle [5, 6, 24, 38]. Thus, it is at least a plausible hypothesis that the curvature of the force-velocity relationship is determined by the force-dependence of ADP release. While other steps in myosin’s cross-bridge cycle have also been measured to be force-dependent [42], the contribution of these states to force production is unclear.

Our fits to Fenn’s [18] and Hill’s [16] data required, in addition to force-dependent ADP release, force-independent weakly-bound cross-bridges that act as a viscous drag (Figs. 1C, D). While the viscous drag has little impact on the Fenn effect, overall force-velocity curvature is a combination of the curved force from the force-dependent strongly-bound cross-bridges, and the linear drag from the force-independent weakly-bound cross-bridges. In effect, the weakly-bound cross-bridges are masking the force-dependence that would be predicted from strong binding alone.

In contrast, fits to our measurements of force transients and force-velocity were possible only with significant force-dependence in unbinding of the weakly-bound state, and minimal force-dependence in unbinding of the strongly-bound state (Fig. 4D). Our best fit has a non-dimensional force-dependence of E = 0.36 for strongly-bound cross-bridges, a bit smaller than previously reported values [5, 6, 24, 38]. The model also includes a single non-dimensional parameter that describes the force-dependence of weakly-bound cross-bridges, E_wb. By non-dimensionalizing these two force-dependencies, they are directly comparable (note, however, that while an increase in force slows the rate of detachment for strongly-bound cross-bridges, it increases the detachment rate of weakly-bound cross-bridges, so they have opposite sign). The large best-fit force-dependence for weakly-bound cross-bridges, E_wb = 20, indicates that the curvature of the force-velocity relationship in the model is largely due to the force-dependence of the weakly-bound state.

In fitting both of our data sets, we find that the curvature of the force-velocity relationship represents a combination of the force-dependence of the weakly- and strongly-bound states. Therefore, in interpreting force-velocity curvature, it is critical to consider the contributions and force-dependencies of both weakly- and strongly-bound cross-bridges.

5. Conclusion

Over the past two decades, the molecular picture of muscle contraction has been brought sharply into focus by single molecule techniques. However, a gap remains between that molecular picture and the behavior of muscle at the cellular and larger scale. Modeling approaches are critical in bridging this gap. We have demonstrated that the addition of a weakly-bound state allows a cross-bridge model, extensively validated with molecular-scale data, to describe several whole muscle experiments. Further, we show that this model, even with a weakly-bound state, cannot explain our own measurements on Drosophila jump muscle fibers. However, if both elastic elements in series with the cross-bridges and force-dependent unbinding from a weakly-bound state are included in the model, it is able to simultaneously fit our measurements. Taken together, the successes and failures of our cross-bridge models in describing fiber level measurements provide insight into the molecular mechanism of stretch-activation, demonstrate a lack of a direct connection between the force transient response and kinetic steps in the cross-bridge cycle, and suggest that the curvature of the classic force-velocity relationship results from a combination of the force-dependencies (or lack thereof) of weakly- and strongly-bound cross-bridges. This work represents a step toward a minimal cross-bridge model that has predictive power at the fiber level.

6. Materials and Methods

6.1. Experiments

We used jump muscles from the Drosophila line pwMhc2 [83], which we have used as a control line in all of our previous jump muscles experiments. This provided us with a large data pool with which to compare our current results and enabled accurate determination of the quality of our current experimental results. Skinned jump muscle fiber bundles were prepared as previously described [38, 62, 63]. Briefly, jump muscles were removed from three-day-old female flies and chemically demembranated (skinned) for one hour. Muscles were pared down to 6 – 8 fibers and aluminum T-clips were attached to either end resulting in a fiber bundle of approximately 150 μm in length, 100 μm width, and 50 μm depth. The bundle was mounted on a muscle mechanics apparatus and attached to a force transducer and a piezo motor while bathed in relaxing solution (pCa 8.0, 12 mM MgATP, 30 mM creatine phosphate, 600 U/ml creatine phosphokinase, 1 mM free Mg²⁺, 5 mM EGTA, 20 mM BES (pH 7.0), 200 mM ionic strength, adjusted with Na methane sulfonate, 1 mM DTT) at 15°C. Starting sarcomere length was set to 3.6 micro;m by lengthening the fiber bundle. The fiber bundle was transferred to pre-activating solution (same as relaxing solution, but no EGTA) for two minutes and then into activating solution (same as relaxing solution, but pCa 5.0). Isometric tension was measured once force reached a steady-state maximum level.

To obtain force transients in response to rapid length increases, fiber bundles were first activated as described above and then rapidly lengthened over 0.5 ms and held at the increased length for 500 ms before returning to the starting fiber length. The length increases tested ranged from 0.25% to 2% fiber length. The same length increases were performed at pCa 8.0 to determine if passive properties contributed significantly to force amplitudes (see SM).

Separate jump muscle fiber bundles were used to obtain force-velocity curves. Force-velocity curves were performed using the force-clamp technique as previously described [38, 62, 63]. Briefly, after the fiber reached its maximum activated tension level the fiber bundle was initially rapidly shortened for 0.5 ms and then the velocity of shortening adjusted until the velocity of shortening produced the desired tension level based on feedback from the force transducer. 14 different tension levels were chosen starting with low tension loads, and increased load in each subsequent force clamp. To produce a force-velocity data point from each force-clamp, the average velocity and tension between 5 ms and 13 ms was calculated, the earliest time following the initiation of shortening that tension was consistently clamped.

6.2. Modeling Details

We model the interaction between actin and myosin with the kinetic schemes detailed in Fig. 1A and B. In the five-state model, myosin and actin interact in the following consecutive steps: (1) myosin binds to actin in a pre-power-stroke state with inorganic phosphate (P_i) and ADP in its active site, (2) in some order, P_i is released and myosin undergoes a conformational change, transitioning into a strongly-bound, post-power-stroke state, (3) ADP is released and myosin stays strongly-bound to actin in a rigor state, (4) ATP binds to the empty active site of myosin, causing dissociation of myosin from actin, (5) ATP is hydrolyzed into P_i and ADP, and the cycle repeats. The four-state model is identical to the five-state, with the exception that it does not include a weakly-bound state.

To quantitatively compare the models to cellular level data, we express each kinetic scheme as a system of integro-PDEs. Each equation corresponds to a particular state in the model, and describes the dynamics of myosin in that state. For unbound states, myosin and actin do not interact, and thus the probability of being in one of these states is simply a function of time. However, when myosin is bound to actin, it is bound with a particular extension, which determines the force on the molecule. Thus, the equations corresponding to bound states describe the probability density that myosin is in a bound state with a particular extension. Transitions between states are defined by constant rates except for: (1) the transition between a bound and unbound state is defined as a rate density, since this is dependent on the extension with which myosin binds, and (2) ADP release rate is force-dependent with the following form based on Bell’s approximation [5, 6, 36]:

$$k_D\left(F\right)=k_D^0\text{ exp}\left(-\frac{\delta F}{k_{B}T}\right)$$ (2)

where δ is a parameter that describes myosin’s force-dependent chemistry, k_BT is Boltzmann’s constant times temperature and $k_D^0$ is the reaction rate in the absence of force. All other transition rates in the model are independent of force.

To compare the model to experimental measurements, we solve the system using a variety of numerical and analytical techniques. Numerically, we implement a standard ODE solver, together with a root find for the integral constraint, to solve the system under steady-state conditions (as in force-velocity and heat measurements). To solve the system without a steady-state assumption (as in force transients), we use a method of characteristics to transform the system of PDEs into one of ODEs. These ODEs are then solved along the characteristics using another standard ODE solver, e.g. fourth-order Runge-Kutta. To simulate the quick stretch of the force transient protocol, we solve the ODEs using an initial condition of steady-state shifted by the half-sarcomere stretch amplitude.

While these numerical techniques provide accurate solutions, they are too inefficient to perform global parameter optimization. Thus, in order to fit the model to experimental data, we additionally need analytical solutions. We implement a matched asymptotic expansion to solve the system analytically under steady-state conditions. Without the steady-state assumption, we use a separation of time scales and a moment approximation to reduce the system to a set of ODEs [84]. While this does not allow for an explicit analytical solution, it does result in a system that is efficient enough to optimize with standard techniques.

Once the system is solved, we have expressions for the probability that myosin is in each state. This lends to a calculation for force, given that the force produced per myosin molecule is the probability that myosin is bound times the force produced when it is. With this, the model results can be related back to measurements from a variety of experimental protocols. Thus, with this mathematical formulation of the kinetic schemes in Fig. 1A and B, we have connected the molecular interactions to cellular behavior in a way that is robust enough to optimize parameters and fit the model to experimental measurements. (See SM for a detailed discussion of the modeling techniques used.)