Yeast optimizes metal utilization based on metabolic network and enzyme kinetics

Significance

Metal ions are essential to all living cells, as they can serve as cofactors of enzymes to drive catalysis of biochemical reactions. We present a constraint-based model of yeast that relates metabolism with metal ions via enzymes. The model is able to capture responses of metabolism and gene expression upon iron depletion, suggesting that yeast cells allocate iron resource in the way abiding to optimization principles. Interestingly, the model predicts up-regulation of several iron-containing enzymes that coincide with experiments, which raises the possibility that the decrease in activity due to limited iron could be compensated by elevated enzyme abundance. Moreover, the model paves the way for guiding biosynthesis of high-value compounds (e.g., p-coumaric acid) that relies on iron-containing enzymes.

Abstract

Metal ions are vital to metabolism, as they can act as cofactors on enzymes and thus modulate individual enzymatic reactions. Although many enzymes have been reported to interact with metal ions, the quantitative relationships between metal ions and metabolism are lacking. Here, we reconstructed a genome-scale metabolic model of the yeast Saccharomyces cerevisiae to account for proteome constraints and enzyme cofactors such as metal ions, named CofactorYeast. The model is able to estimate abundances of metal ions binding on enzymes in cells under various conditions, which are comparable to measured metal ion contents in biomass. In addition, the model predicts distinct metabolic flux distributions in response to reduced levels of various metal ions in the medium. Specifically, the model reproduces changes upon iron deficiency in metabolic and gene expression levels, which could be interpreted by optimization principles (i.e., yeast optimizes iron utilization based on metabolic network and enzyme kinetics rather than preferentially targeting iron to specific enzymes or pathways). At last, we show the potential of using the model for understanding cell factories that harbor heterologous iron-containing enzymes to synthesize high-value compounds such as p-coumaric acid. Overall, the model demonstrates the dependence of enzymes on metal ions and links metal ions to metabolism on a genome scale.

Metabolism plays a key role in all cellular processes. To maintain metabolic activities, cells take up nutrients from the environment, including macronutrients and minerals. Macronutrients such as carbohydrates and amino acids are primary substrates of metabolic reactions to provide energy and precursors for other biological processes. Many minerals (e.g., metal ions) are essential but appear to be less related with metabolism as they do not directly participate in metabolic reactions as either substrates or products. Instead, they serve as cofactors on enzymes to ensure proper function. The BRENDA database (1) summarizes experimental evidence of metal ions being stimulatory or even essential for ion-containing enzyme activities. Although many individual enzymes have been experimentally identified to interact with metal ions (2, 3), there is a lack of quantitative relationships between metal ions and metabolism from a holistic perspective.

Predicting cellular behavior with quantitative models is of particular interest (4), which could hopefully aid in uncovering the mechanisms and driving forces by which cells adapt to perturbations (e.g., reduced availability of metal ions). Genome-scale metabolic models (GEMs) together with constraint-based approaches enable predicting the optimal state of cells subject to external and internal constraints based on optimization principles (5, 6). Using GEMs as a framework, many other biological processes than metabolism have been mathematically described, especially protein synthesis processes (7–9). The integration of protein synthesis with metabolism allows for imposing proteome constraints by enzyme kinetics, which has shown wider applications, such as predictions of protein levels (7, 10) and proteome allocation (9, 11). Given that enzyme kinetics could be affected by metal ion availability, it will be possible to apply proteome-constrained frameworks to establish quantitative relationships between metal ions and metabolism.

Besides serving as an important cell factory, the yeast Saccharomyces cerevisiae has shown to be a powerful model organism for experimentally investigating metal ions (12, 13) and could also infer targets on metal ion–related diseases in humans based on homology (14). In addition, a wealth of information of metal ions has been accumulated for S. cerevisiae [e.g., a large number of yeast proteins have been identified as iron-containing (15) and zinc-containing (16) proteins]. Therefore, yeast would also be a promising model organism to mathematically explore the effect of metal ions on metabolism.

Here, we present a mathematical framework that integrates protein synthesis and incorporation of enzyme cofactors into a GEM of the yeast S. cerevisiae and name the resulting model CofactorYeast. We show the model’s capability of estimating abundances of metal ions binding on enzymes, capturing representative proteins of distinct metal ions, and simulating metabolic responses upon reduced availability of metal ions, especially iron. At last, we illustrate its application in metabolic engineering of yeast for producing para-coumaric acid (also called p-hydroxycinnamic acid [p-HCA]), which could be dependent on optimal iron and proteome allocation.

Results

Integration of Enzyme Cofactors with Proteome-Constrained Model.

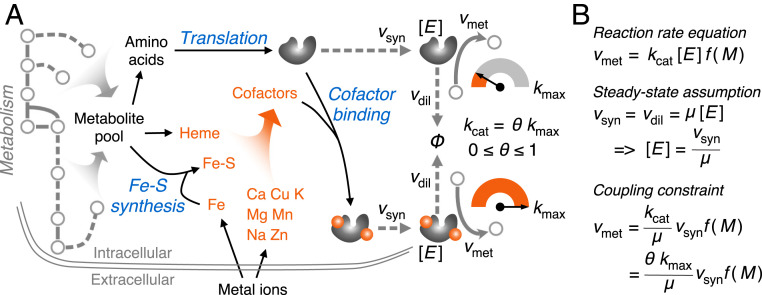
We constructed the model CofactorYeast based on a consensus GEM of S. cerevisiae Yeast8 (17) (Fig. 1A). Firstly, we expanded the metabolic part by adding iron-sulfur cluster (ISC) synthesis reactions as well as transport and exchange reactions of metal ions (Dataset S1). To account for enzyme synthesis in the model, we formulated translation reactions with amino acids as substrates and adenosine triphosphate as energy cost. Subsequently, we added cofactor binding reactions for the proteins that contain cofactors, which required collecting information about cofactors binding to enzymes with a high coverage. Accordingly, we generated a comprehensive dataset of cofactor information for S. cerevisiae (Dataset S2) based on databases, including PDBe (18), BRENDA, and UniProt (19), and the literature. We focused on eight metal ions and iron-containing compounds (i.e., heme and ISCs) as cofactors (Fig. 1A), although others (e.g., vitamins) are also available in the dataset, and they can therefore easily be integrated in future studies. From our dataset, we see that zinc is the most widely used metal ion that serves as a protein cofactor across the yeast proteome as it is present in more than 10% of the total of about 6,000 proteins, followed by magnesium (9%) and iron (2%) (SI Appendix, Fig. S1A). These three minerals are also the top three most widely used metal ions that bind on metabolic proteins, among which magnesium accounts for the most with binding to more than 150 enzymes (SI Appendix, Fig. S1B).

Fig. 1.

Overview of the model CofactorYeast. (A) Scope of the model. In addition to metabolism, the model accounts for synthesis of iron-sulfur (Fe-S) clusters, translation, and cofactor binding processes. In this study, the enzyme cofactors include eight metal ions, ISCs, and heme. Notably, the parameter θ can be used to decrease turnover rates for the enzymes losing cofactors. (B) Coupling constraint. The mathematical relationship between metabolic reaction rates and enzyme synthesis rates can be established based on reaction rate equation with the steady-state assumption. V_met, metabolic reaction rate; k_cat, turnover rate; [E], enzyme concentration; f(M), a function of metabolite concentrations; V_syn, enzyme synthesis rate; V_dil, enzyme dilution rate; μ, growth rate; k_max, the maximal turnover rate.

Considering the cases in the BRENDA database that an enzyme would have a basal level of activity without metal ions rather than being completely inactive, we introduced a flexible parameter θ to adjust the turnover rate based on the binding state (i.e., the enzyme would have the maximal turnover rate if it is bound with all metal ions while a reduced value without binding of the metal ions) (Fig. 1A). This is, however, not applicable to heme and ISCs, as these compounds are essential for enzyme activity and stability (20–22) (i.e., an enzyme would not function if it loses them).

In addition to the basic constraints used in normal GEMs [e.g., bounds on reaction rates and stoichiometric balance (23)], we adopted coupling constraints (8) to relate metabolic reaction rates with enzyme synthesis rates according to enzyme kinetics and steady-state assumption (Fig. 1B), which enables imposing proteome constraints. With proteome constraints, the model is able to predict growth rates on diverse carbon sources and the Crabtree effect of S. cerevisiae (SI Appendix, Fig. S2), which have also been predicted by other models with protein or enzyme constraints (10, 24, 25). Furthermore, the integration of cofactors enables exploring the combined effect of proteome constraints and cofactor availability on metabolism.

Prediction of Metal Ion Abundance and Usage.

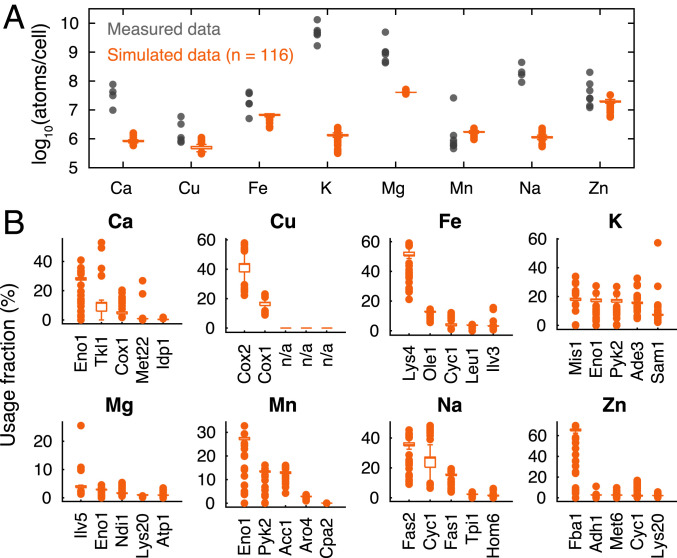
We used the model to simulate aerobic growth on different carbon, nitrogen, phosphorus, and sulfur sources. Among the simulations, we only selected true positives (116 simulations) [i.e., simulated growth is consistently observed on Biolog plates (17)] to estimate abundances of metal ions binding on enzymes. We found that the model is capable of predicting varying abundances of bound metal ions under diverse conditions (Fig. 2A). This cannot be achieved by normal GEMs, which would predict a constant metal ion composition for any conditions, as metal ions in these models are integrated into the biomass equation with fixed coefficients (17). To evaluate the simulations, we collected experimentally measured metal ion compositions under different culture conditions (Dataset S3). Although these culture conditions do not involve all simulated conditions, they account for distinct metabolic states (e.g., growth on different carbon sources and culture media) (Dataset S3). We can see that the ranges of simulated abundances of some metal ions, such as copper, iron, manganese, and zinc, overlap with the ranges of measurements (Fig. 2A), showing that the model performs well in predicting metal ion levels. It should be noted that the simulated values are mostly lower than the measured data, which is due to the fact that the model only predicts bound metal ions while measurements might also account for free forms. Still, we found that potassium and sodium show much lower simulated abundances than the measured data (Fig. 2A). This is likely due to the fact that these two metal ions cannot only act as cofactors on enzymes but also participate in other biological processes beyond the model scope (e.g., maintenance of membrane potential and osmotic stress) (12).

Fig. 2.

Abundance and usage of metal ions. (A) Simulated abundances of metal ions that bind on enzymes of cells under 116 conditions compared with measured metal ion contents of cells from various studies (Dataset S3). A single cell dry weight of 13 pg (26) was used to convert cell weight to cell count. (B) Proteins that account for high usage of each metal ion across the 116 simulated conditions.

We also used the simulated fluxes to estimate metal ion usage of each protein in the 116 simulations, which would show the allocation of metal ions under diverse conditions. The box plots (Fig. 2B) display the top five proteins that account for the greatest fraction of each metal ion, based on the median across simulations. We can see that the model is able to capture representative metal ion-containing proteins in S. cerevisiae (Fig. 2B) [e.g., copper-dependent cytochrome c oxidase (COX) (12), iron-containing proteins involved in amino acid pathway (27), the most abundant zinc-containing proteins including Fba1, Adh1, and Met6 (16)]. Taken together, these evaluations show a good performance of the model in terms of predicting metal ions with proteome constraints.

Metabolic Responses to Reduced Availability of Metal Ions.

To investigate the effect of metal ion limitation on metabolism, we used the model to predict metabolic responses to reduced uptake rates of eight metal ions. We first simulated growth at unlimited conditions as the reference state, where all metal ions were exactly sufficient. By doing so, we obtained the reference uptake rates of all metal ions, referred to as 100% uptake. Subsequently, we simulated growth by reducing the uptake rate of each metal ion proportionally while maintaining the other metal ions unlimited. As expected, the reduced uptake of metal ions resulted in decreased growth rates (SI Appendix, Fig. S3). The simulations suggest that these metal ions are essential for growth, and some are in line with experimental observations [e.g., decreased growth was observed with reduced availability of iron (28), zinc (29), and magnesium (30)].

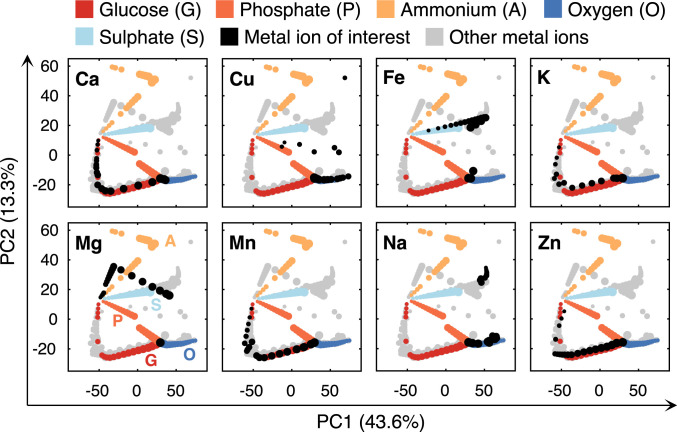
We further compared the metabolic responses to reduced availability among metal ions. To do so, we performed principal component analysis (PCA) on simulated metabolic flux distributions by gradually decreasing uptake rates of various metal ions. From the PCA plots, we found clear variabilities in the simulated flux distributions upon limitation of various metal ions (Fig. 3), suggesting that the metal ions affect growth by adjusting various metabolic pathways. Furthermore, we integrated into PCA plots the simulated flux distributions in response to reduced uptake of other nutrients, including glucose, phosphate, ammonium, and sulfate, as well as oxygen (Fig. 3). By comparing all the flux distributions, we found that limitation of a few metal ions behaves similarly with limitation of other nutrients and oxygen. First, limitation of manganese and zinc displayed a similar response with glucose limitation, which could coincide with the major effect of those metal ions on glycolytic enzymes. For example, the activity of zinc-containing protein Fba1 was greatly reduced in zinc deficient conditions (16). Second, copper deficient simulations are in part overlapping with oxygen limitation (Fig. 3), which could be due to the role of copper in the electron transport chain (ETC) [e.g., COX (12)]. Third, iron limitation is similar to sulfate limitation (Fig. 3). This is due to the requirement for both iron and sulfur for the biosynthesis of ISCs, which are predominant iron-containing compounds in iron deficient conditions (31). Altogether, the model enables to predict distinct metabolic changes upon reduced availability of metal ions.

Fig. 3.

PCA of flux distributions under reduced availability of eight metal ions, four nutrients, and oxygen. Each dot represents a simulated flux distribution. The dots in the same color (except gray) represent the flux distributions of changed uptake rates of a certain metal ion, nutrient, or oxygen, which were from 100 to 5% of the optimum, represented by dot size (i.e., 100% corresponds to the largest while 5% the smallest). In each subplot, the flux distributions of the metal ion of interest are marked in black, while gray dots represent the other metal ions.

Proteome and Iron Reallocation upon Iron Deficiency.

In order to explore further the predictive power of the model, we decided to focus on the role of iron. We did this for several reasons. First, iron is one of the most widely used metal ions (SI Appendix, Fig. S1). Second, iron plays irreplaceable roles in many cellular processes, especially energy metabolism, due to its special ability to donate and accept electrons. Third, iron has various forms besides the ionic state, such as heme and ISCs, which are synthesized with the involvement of metabolic pathways. Altogether, iron is of particular interest, and accordingly there are more published studies and datasets of iron than the other metal ions (13), which could be used to test our model predictions.

Here, we focused on response of S. cerevisiae upon iron deficiency. It was reported that yeast cells exhibited a 20% increase in doubling time upon iron deficiency (28). This corresponds to the simulation with reducing the iron uptake to 50% of the reference, which showed ∼80% of the reference growth rate (SI Appendix, Fig. S3). We therefore selected iron uptake to be at 50% of the uptake at unlimited conditions as representing iron deficient conditions in our simulations. In addition, we used various θ values ranging from 0 to 0.9 to assess the impact of the parameter θ on simulation results.

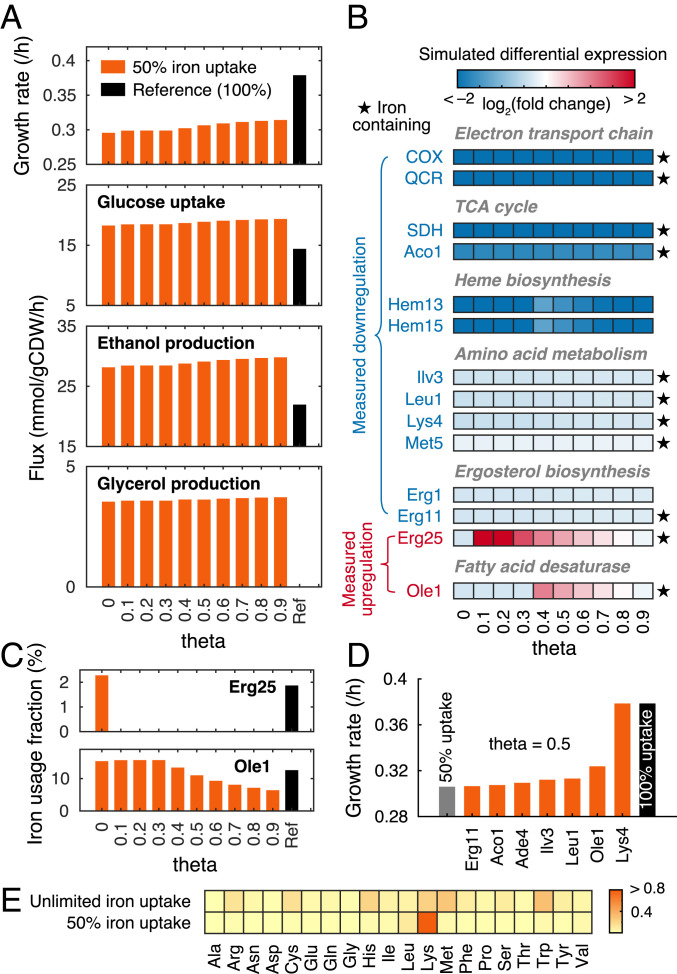
In terms of metabolic level, the simulations showed that iron deficiency led to decreased growth while increased glucose uptake and ethanol and glycerol production (Fig. 4A), indicating an elevated glycolytic flux and cytosolic reduced form of nicotinamide adenine dinucleotide accumulation. The predictions are consistent with metabolomics measurements of iron deficient cells that show elevated glycolytic intermediates associated with increased flux through this pathway (28) and that the glycerol production rate was increased by iron starvation (32). Notably, the changes in exchange rates and growth rates for different θ values are much lower than the changes between conditions of iron deficiency and unlimited conditions (reference case) (Fig. 4A). This shows that the parameter θ has little effect on the simulated metabolic level.

Fig. 4.

Simulations of iron deficiency. (A) Simulated growth rates and exchange fluxes with various θ values for 50% iron uptake compared with the reference. (B) Experimentally measured differential expression compared with simulations upon 50% reduction in iron uptake with various θ values. The color of the enzyme name represents measured differential expression upon iron deficiency (i.e., blue means measured down-regulation and red up-regulation). Heatmap represents simulated differential expression based on predicted protein abundances. Complex abbreviations: QCR, ubiquinol cytochrome-c reductase; SDH, succinate dehydrogenase. (C) Iron usage of Erg25 and Ole1 with various θ values. (D) Sensitivity analysis of iron-containing proteins with 50% iron uptake and θ value of 0.5. (E) Reduced cost analysis of amino acid uptake for growth under unlimited and 50% iron uptake conditions with θ value of 0.5. Color represents the reduced cost value. A higher value indicates a greater impact of an increase in the amino acid uptake on growth rate.

To explore molecular mechanisms on how iron affects metabolism, we used the model to predict changes in gene expression levels based on protein abundances upon iron deficiency, which were compared with measured transcriptional responses (28, 33, 34). We found that the model captured key changes in agreement with measurements, including down-regulation of enzymes in the ETC, the tricarboxylic acid (TCA) cycle, heme biosynthesis, amino acid metabolism, and ergosterol biosynthesis (Fig. 4B), suggesting that yeast cells liberate iron resource by reducing the level of iron-containing enzymes. Notably, the predicted down-regulations seem to be conserved for different θ values (Fig. 4B). However, the predicted expression changes of two proteins (i.e., Erg25 and Ole1) are dependent on the parameter θ (Fig. 4B). We found that the model, with some nonzero values of the parameter θ, predicted up-regulation of these proteins (Fig. 4B), which is consistent with measured increase in their transcript or protein levels upon iron limitation (33–35). In addition, we found that these proteins showed decreased iron usage when up-regulated (Fig. 4C). This indicates that the model optimizes iron utilization at the expense of proteome resource upon iron deficiency. Taken together, the model identified two types of responses upon iron deficiency (i.e., down-regulate iron-containing proteins to liberate and spare iron and up-regulate iron-containing proteins to compensate for the decreased activity caused by low iron).

To identify key iron-containing proteins on growth upon iron deficiency, we performed a sensitivity analysis. For each iron-containing protein in the model, we assumed it to be a non-iron-containing protein (i.e., it does not contain any iron, ISC, or heme but can operate at the maximal turnover rate) and then simulated again iron deficiency using 50% iron uptake. The simulations show that if Lys4, homoaconitase, was not an iron-containing protein, the growth would not be affected even with 50% iron uptake (Fig. 4D), suggesting that Lys4 might dominate iron utilization, which could be attributed by its essential role in amino acid biosynthesis carrying high fluxes and inclusion of four iron atoms per protein copy as a 4Fe-4S cluster. This might be in line with the finding that Lys4 is present in excess in iron replete cells (28), which could allow for rapid adaption to iron depletion. In addition, the analysis identified other proteins (e.g., Ole1, Leu1, and Ilv3), which would recover growth slightly if assumed to be a non-iron-containing protein (Fig. 4D). The result (Fig. 4D) suggests the essential impact of those iron-containing proteins on growth, and most of them were regulated upon iron deficiency (Fig. 4B). Therefore, the analysis shows that these iron-containing proteins might be sensitive to iron availability and accordingly regulated upon iron limitation.

Considering the vital role in iron utilization of Lys4, which participates in lysine biosynthesis, we expected that addition of lysine to the medium could relieve iron deficiency. To test this, we performed reduced cost analysis of uptake of each amino acid for growth under both unlimited and limited iron conditions, which was calculated as increase in growth rate over increase in amino acid uptake rate. We found that lysine exhibited the highest reduced cost toward growth with limited iron uptake (Fig. 4E), meaning that lysine is more important than other amino acids upon iron deficiency, although this does not hold when iron is in excess (Fig. 4E).

Metabolic Engineering of p-HCA upon Iron Availability.

There is much interest in expressing complex plant biosynthetic pathways in yeast with the objective to enable scalable production of plant natural products that are difficult to source from nature. Many different plant pathways have thus been expressed in yeast [e.g., biosynthesis of opioids (36), cannabinoids (37), and tropane alkaloids (38)]. In line with this, it was recently demonstrated that p-HCA, a bioactive plant compound serving as precursor for many commercially valuable chemicals, could be produced by S. cerevisiae through the introduction of heterologous enzymes from Arabidopsis thaliana (39). Among them, the cinnamic acid hydroxylase, as a plant cytochrome P450, requires heme as its enzyme cofactor. We therefore evaluated whether the model could be used to gain insight into potential strategies for optimization of the pathway and, in particular, how there will be competition between iron usage for enzymes in this pathway and endogenous enzymes required for growth.

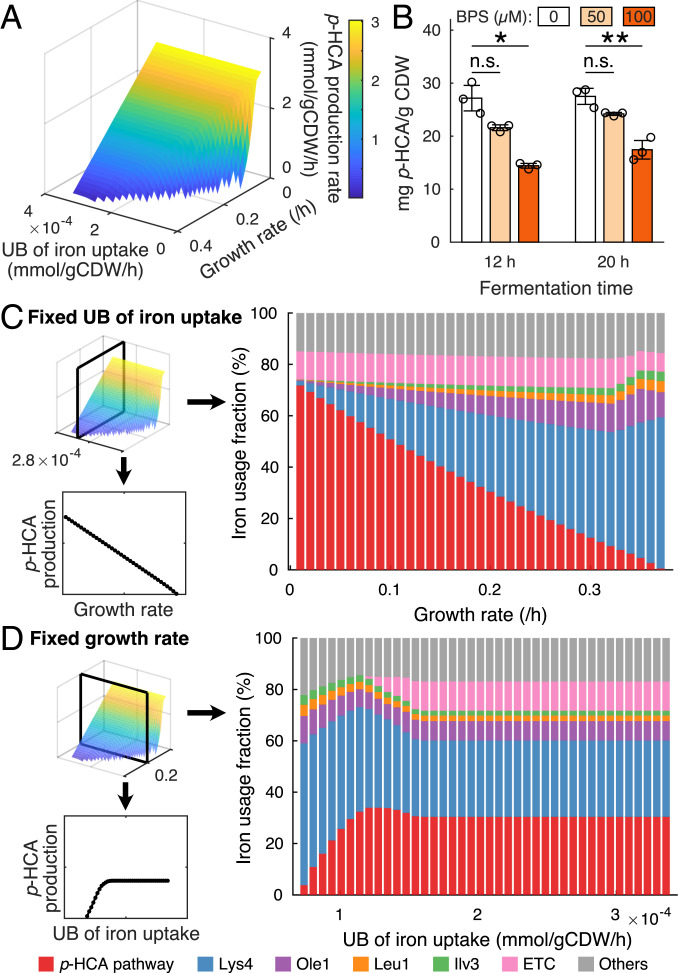
Based on the original study (39), we introduced the p-HCA production pathway in our model for simulating the starting strain QL01, which includes a phenylalanine ammonia lyase, a cinnamic acid hydroxylase and a cytochrome P450 reductase from A. thaliana. Additionally, we collected information about the enzymes, including sequences, cofactor usage, and turnover rates (Dataset S4). With the model, we investigated the combined effect of growth and iron availability on p-HCA production. To do so, we maximized the production rate of p-HCA by changing simultaneously growth rate and the upper bound (UB) of iron uptake rate. As expected, growth is an essential factor with its decrease leading to improved p-HCA production at any iron uptake rate (Fig. 5A), which is caused by a trade-off between growth and p-HCA production due to carbon source and proteome resource allocation. On the other hand, we found that at most of the simulated growth rates p-HCA production rate started to decline once the UB of iron uptake rate was below a certain value (Fig. 5A), indicating that iron could limit p-HCA production if it is insufficient.

Fig. 5.

Iron-dependent biosynthesis of p-HCA. (A) p-HCA production rate changes with various growth rates and UBs of iron uptake. (B) Shake-flask cultures with addition of bathophenanthroline disulfonate (BPS) were sampled at 12 h and 20 h for determining p-HCA yield on biomass. Statistical analysis was performed by using Student’s t test (two-tailed; two-sample unequal variance; n.s. (not significant): P ≥ 0.05; *: 0.01 ≤ P < 0.05; **: P < 0.01). All data represent the mean of n = 3 biologically independent samples, and error bars show SDs. (C) Iron usage of key proteins and pathways changes with various growth rates at a fixed UB of iron uptake rate. (D) Iron usage of key proteins and pathways changes with various UBs of iron uptake at a fixed growth rate.

To validate the simulations, we carried out batch fermentations by growing the p-HCA producing strain QL01 in iron limited media, which was achieved by the addition of bathophenanthroline disulfonate, a chelator of Fe²⁺ ions (31), at different concentrations, including 0 µM (unlimited), 50 µM (mildly limited), and 100 µM (severely limited). We determined biomass and p-HCA concentrations after 12 h and 20 h and found that they both decreased upon iron limitation (SI Appendix, Fig. S4). Notably, we found that the p-HCA yield on biomass was significantly decreased upon severe iron limitation (Fig. 5B), suggesting that strain capability of synthesizing p-HCA is also weakened. This means that biomass formation could have a higher priority for utilizing iron than p-HCA synthesis. Accordingly, we demonstrated that iron is essential for p-HCA production, which can support our model simulations.

Furthermore, we used the model to estimate iron allocation with changing growth and iron uptake rates. For a fixed UB of iron uptake rate, it is obvious that the majority of iron is allocated to biomass formation pathways, including the enzymes Lys4, Ole1, Leu1, and Ilv3 as well as the p-HCA production pathway (Fig. 5C) and that p-HCA production rate relies highly on the amount of iron allocated to the p-HCA pathway (Fig. 5C). For a fixed growth rate, once the iron uptake becomes limiting, we can see the first reallocation of iron resource from the ETC to the p-HCA production when it is maximized (Fig. 5D), meaning that ETC could be sacrificed to save iron consumption, which appears to be a similar strategy with the down-regulation of the ETC in wild-type strains upon iron deficiency (28, 33, 34). With more limited iron uptake, we can see another reallocation of iron resource from p-HCA to biomass production (Fig. 5D), suggesting the priority of iron utilization for biomass formation by fixing the growth rate.

Taken together, the model is able to predict the influence of iron on biosynthesis of p-HCA in yeast, which could be due to optimal allocation of iron resource among native and heterologous pathways. This suggests that integration of metal ions with proteome-constrained metabolic model would provide a promising framework, with the aid of advanced computational tools (40), to understand and optimize cell factories in the field of metabolic engineering.

Discussion

Here, we integrated metal ions as enzyme cofactors within a GEM of S. cerevisiae, resulting in the mathematical model CofactorYeast. We formulated cofactor binding reactions by adding metal ions onto enzymes with stoichiometric information. Accordingly, the abundance of each metal ion is represented by the abundances of individual metabolic enzymes that contain the metal ion. The model was able to estimate total abundances of metal ions that are consistent with experimental data (Fig. 2A), suggesting the assumption to be reasonable. As the first step, this proves that we establish a quantitative relationship between metal ions and metabolism. Next, we used the model to predict metabolic states with changed uptake rates of various metal ions, resulting in distinct metabolic responses (Fig. 3). Therefore, we demonstrate that with the bottom-up integration of metal ions the model could describe the effect of metal ions on metabolism from a holistic perspective.

In particular, the model is capable of capturing metabolic responses upon iron deficiency (Fig. 4). Interestingly, with a 50% reduction in the iron uptake rate, there is only an about 20% reduction in growth rate (Fig. 4A), indicating that the model appears to maximize biomass yield on iron once iron becomes limiting as can be seen analogously in iron-limited chemostat growth of Escherichia coli (41). To this end, the model finds two main strategies to optimize iron utilization, including 1) down-regulation of iron-containing enzymes in the ETC and TCA cycle (Fig. 4B) and 2) up-regulation of Erg25 and Ole1 (Fig. 4B), which are key iron containing enzymes required for lipid biosynthesis. Both of the strategies are consistent with experimental observations (33–35). The first strategy results in a shift from iron-dependent to iron-independent energy-producing pathways (i.e., from respiration to fermentation) (Fig. 4 A and B). We thus show in this study that iron cost of enzymes could be another factor leading to the shift between the two energy-producing pathways, while we showed previously that such a shift could also be caused by the protein cost of enzymes (25). The second strategy shows the possibility that iron could be saved at the cost of proteome resource even though the proteome is also constrained in fast-growing cells (8), suggesting that iron might be more limiting than the proteome resource at the simulated conditions. Taken together, we demonstrate with the model that optimal resource allocation is able to explain cellular behavior upon iron deficiency.

From a modeling point of view, we propose the modeling framework of yeast that accounts for enzyme synthesis and enzyme cofactor integration for metabolic catalysts. Recently, the GEM of the yeast S. cerevisiae was extended to include iron metabolism, permitting estimation of iron requirements roughly based on metabolic fluxes (42). This model would be less explicit due to the lack of proteome constraints and enzyme kinetics, while our framework takes the advantage of the proteome-constrained concept and is accordingly able to account for constraints of both the proteome and metal ions. In addition, given the accurate predictions as a proteome-constrained model (SI Appendix, Fig. S2), the model is suitable to be extended by adding synthesis of machineries such as ribosome in gene expression processes, leading to a more explicit model (7–9). Notably, in this framework we introduced the parameter θ to adjust activity of enzymes losing metal ions. Although it remains to be proven whether or not every enzyme would maintain a basal nonzero activity once it loses metal ions, we showed in simulations that the exchange rates and most enzyme levels are conserved across θ values (Fig. 4 A and B). However, we did observe up-regulation of the iron-containing enzymes Erg25 and Ole1 only by adjusting θ values (Fig. 4B), which is consistent with experimental observations (33–35), illustrating the necessity of introducing the parameter θ. Moreover, the parameter θ could hopefully be used for modeling other processes that function on enzyme activity (e.g., for describing the effect of protein phosphorylation on enzyme activity) (43). Therefore, given the mathematical relationship between protein phosphorylation and activity (44, 45), our framework together with the parameter θ could integrate protein phosphorylation in future studies.

While our model is able to predict cellular responses to metal ion limitation, it is also possible to account for metal toxicity upon extremely high levels in the environment. The metal ion with toxic levels could bind to noncognate sites in metalloenzymes (46) to preclude the binding of the correct metal ion and therefore inhibit the activity (12). This can be formulated in the current framework by assuming that the toxic metal ion can bind on a set of enzymes to inhibit activity, which, however, requires more information. In addition, interchangeability among metal ions might also happen even in normal media where all metal ions are in sufficient but nontoxic levels, and this could also be readily formulated with available information.

In conclusion, we develop the model CofactorYeast by linking metal ions to metabolic enzymes with proteome constraints, which allows for quantitative and systematic investigation of relationship between metal ions and genome-scale metabolism. We show that the model with optimization principles is capable of interpreting metabolic remodeling upon iron deficiency and describing iron-dependent production of p-HCA by yeast. We expect that the model will also be used as a framework for analysis of omics data such as ionomics (47).

Materials and Methods

All the materials and methods are detailed in SI Appendix, including construction of CofactorYeast, simulations of CofactorYeast and simulations of p-HCA production, which were performed in MATLAB with the COBRA toolbox (48), and experimental validations.

Data Availability

The model and codes are available at https://github.com/SysBioChalmers/CofactorYeast. All other study data are included in the article and/or supporting information.