Significance
Many biological networks are modeled with multivariate discrete dynamical systems. Current theory suggests that the network of interactions captures salient features of system dynamics, but it misses a key aspect of these networks: some interactions are more important than others due to dynamical redundancy and nonlinearity. This unequivalence leads to a canalized dynamics that differs from constraints inferred from network structure alone. To capture the redundancy present in biochemical regulatory and signaling interactions, we present the effective graph, an experimentally validated mathematical framework that synthesizes both structure and dynamics in a weighted graph representation of discrete multivariate systems. Our results demonstrate the ubiquity of redundancy in biology and provide a tool to increase causal explainability and control of biochemical systems.
Keywords: biochemical regulation, Boolean network, canalization, complex networks, complex networks
Abstract
The ability to map causal interactions underlying genetic control and cellular signaling has led to increasingly accurate models of the complex biochemical networks that regulate cellular function. These network models provide deep insights into the organization, dynamics, and function of biochemical systems: for example, by revealing genetic control pathways involved in disease. However, the traditional representation of biochemical networks as binary interaction graphs fails to accurately represent an important dynamical feature of these multivariate systems: some pathways propagate control signals much more effectively than do others. Such heterogeneity of interactions reflects canalization—the system is robust to dynamical interventions in redundant pathways but responsive to interventions in effective pathways. Here, we introduce the effective graph, a weighted graph that captures the nonlinear logical redundancy present in biochemical network regulation, signaling, and control. Using 78 experimentally validated models derived from systems biology, we demonstrate that 1) redundant pathways are prevalent in biological models of biochemical regulation, 2) the effective graph provides a probabilistic but precise characterization of multivariate dynamics in a causal graph form, and 3) the effective graph provides an accurate explanation of how dynamical perturbation and control signals, such as those induced by cancer drug therapies, propagate in biochemical pathways. Overall, our results indicate that the effective graph provides an enriched description of the structure and dynamics of networked multivariate causal interactions. We demonstrate that it improves explainability, prediction, and control of complex dynamical systems in general and biochemical regulation in particular.
Increasing evidence indicates that nonlinear interactions between biochemical variables—such as cell signaling, protein interactions, and genetic regulation and suppression—are pervasive (1–5), yet linear models of biochemical regulation fail to capture these key features of network causality (6). The simplest way to model such causal interdependent nonlinear dynamics is with multivariate discrete dynamical systems, also known as automata networks. Boolean networks (BNs), for instance, are canonical models of complex systems that exhibit a wide range of dynamical behaviors (3, 7). They have been successfully used to reveal insights into the dynamics of biochemical regulation (8), cell signaling (9), metabolism (10), anticancer drug response (11), and neuronal action potentials (12), among other things (13). In addition, BNs provide a convenient modeling framework to explore general properties of complex systems, such as self-organization, criticality, causality, canalization, robustness, and evolvability (3, 14–19).
The success of BNs can be attributed largely to three features of these models (7, 13, 20, 21): 1) qualitative thresholds to measure transitions in concentration/expression of biochemical molecules in experimental data without the need for precise parameter estimation; 2) interaction graphs that synthesize complex multivariate dynamics to reveal the topology of the causal organization of biological systems; and 3) discrete dynamics that facilitate the prediction of critical behavior, self-organization, robustness, evolvability, and controllability. The first feature makes BNs very useful for estimating predictive systems biology models from data, especially because many processes in biology—such as gene expression and immune or neuron activation—are characterized by switch-like transitions between the presence or absence of a biochemical molecule or signal (13, 21). The second and third features of BNs make them ideal models to explore the interplay between the organization and the dynamics of complex systems (22, 23). Traditionally, the organization and dynamics of BNs are captured by general probabilistic parameters of the system variables (e.g., the mean number of interactions between variables or mean node bias) that are used to predict features of system-wide behavior, such as the transition from order to chaos (14, 18). Interactions between BN variables are usually represented as directed graphs, with arrows indicating when one node variable is an input to the logical rules governing another node variable. Thus, interaction graphs treat all inputs to a variable with equal importance, even though each input may have a weaker or stronger role in determining state transitions.
In reality, the states of almost all biochemical node variables are robust to dynamic perturbations from many of their input variables but highly responsive to just a few (3, 19). Such dynamical redundancy is a ubiquitous hallmark of the third feature of BNs that has been used to study canalization in biological complexity (17, 24)—a concept Waddington (25) introduced to characterize the mechanisms organisms use to buffer development, regulation, and evolution against perturbations. Indeed, the presence of canalization can drastically alter the functional interaction topology of BNs, with profound consequences to the stability and controllability of biological systems (17, 20, 24).
To better capture the functionally relevant pathways of BN models of biochemical regulation and signaling, we introduce the effective graph. It uses a measure of collective canalization to take into account nonlinear effects present when several inputs are needed to regulate a variable. This way, the effective graph integrates all of the dynamical redundancy present in BN dynamics, thus revealing the most important interactions and pathways in determining state transitions. Through an analysis of 78 experimentally validated biological models across a wide range of different biochemical systems and cell types (SI Appendix, section 2), we show that interactions in biological networks are on average much less effective at generating state transitions than interactions in random Boolean automata. For instance, in gene regulation, this means that a gene on its own is less likely to regulate the expression of another gene it interacts with than what would be expected from the set of possible gene–gene interactions.
The effective graph provides a probabilistic characterization of multivariate interactions and dynamics in a causal graph form. It also captures how conditioning the system on known input states, such as when administering a drug intervention, can modify the remaining biochemical interactions. The conditional effective graph thus provides a mechanistic explanation for how control propagates through biochemical models and how causal, nonlinear, microlevel interactions integrate to define macrolevel biological function. We leverage this analytical tool to study a model of signal transduction in ER+ breast cancer (26) to reveal why and how certain drugs drive cancer cells to proliferate or die and identify the modular pathway dynamics that facilitate or hinder this control.
Finally, the redundancy observed in BN models from systems biology also reveals that only a fraction of causal interactions is typically needed to determine convergence to dynamical attractors, which represent biological function in these models. This suggests that the regulatory dynamics of biological networks are robust to random dynamical perturbations yet controllable via the most effective pathways revealed by the effective graph. To demonstrate this observation, we show that the effective graph is consistently better than the original interaction graph at predicting the impact of dynamical perturbations across random networks, a model of floral organ specification in the flowering plant Arabidopsis thaliana (27, 28), and the ER+ breast cancer model (26). Given the widespread applicability of BNs, our framework opens a promising research direction in the control of complex dynamical systems and can facilitate the design of interventions in systems biology models, especially those for development and disease. By synthesizing structure and dynamics into a single-graph formalism, the effective graph increases the predictability and explainability of actionable models of biochemical regulation and signaling and causal automata models in general.
Canalization of Boolean Automata
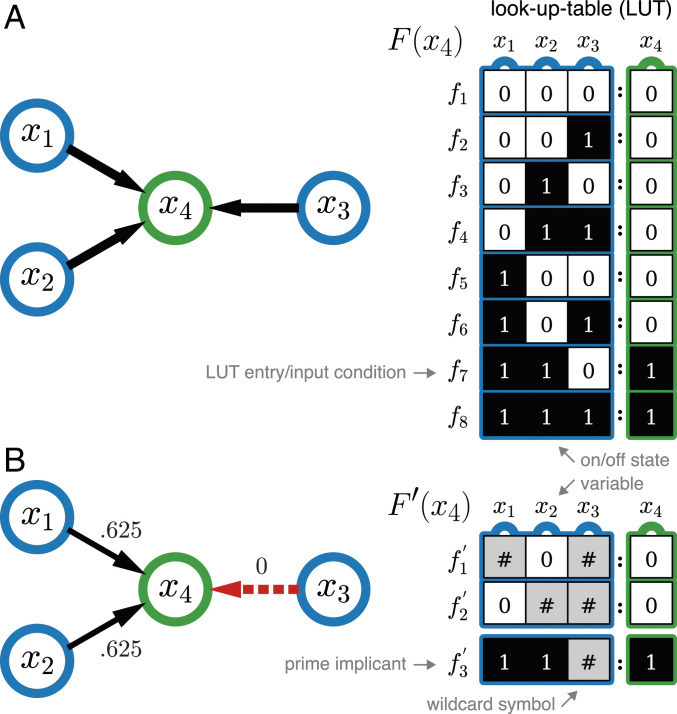
A Boolean automaton is a binary variable, , whose state is updated in discrete time steps, , according to a deterministic state-transition function relating the states of inputs to its own state at the next time step: . This logical function, , is defined by a look-up (truth) table (LUT), , with one entry for each of the combinations of input states and a mapping to the automaton’s next state (transition or output), . The bias, , of the automata is the fraction of transitions to state 1 in the output column of the LUT. An exemplar Boolean automaton with its LUT is shown in Fig. 1A.
Fig. 1.
Constructing the effective graph. (A, Left) The interaction graph of automaton (green node), with input variables (blue nodes, ) and (A, Right) its corresponding Boolean logic given by the LUT, with bias . (B, Left) The effective graph of automata is built from the wild card redescription of the LUT (B, Right), , which shows that input is always redundant (only wild cards in its column) and that . Edge thickness denotes edge effectiveness, , with the fully redundant edge shown in dashed red. The total input redundancy of automaton is , and therefore, its effective connectivity is .
A BN is a graph , where is a set of Boolean automata nodes and is a set of directed edges, , that represent the interaction network, denoting that automaton is an input to automaton , as computed by with LUT : for example, the interaction graph for the BN model of the floral organ development in the A. thaliana plant (28) (see Fig. 4A). The set of inputs into automaton is denoted by , and its cardinality, , is the in-degree of node . At any given time , is in a specific configuration of automata states, —we use the terms state for individual automata () and configuration () for the collective network state (i.e., the vector of states of all automata of the BN at time ). The set of all possible network configurations is denoted by , where . BNs update synchronously (all automata simultaneously at time ) or asynchronously (some automata are selected randomly or via a schedule at time ). However, the effective graph does not depend on the chosen update policy since it is constructed from the redundancy parameters of each automaton considered separately.
Fig. 4.
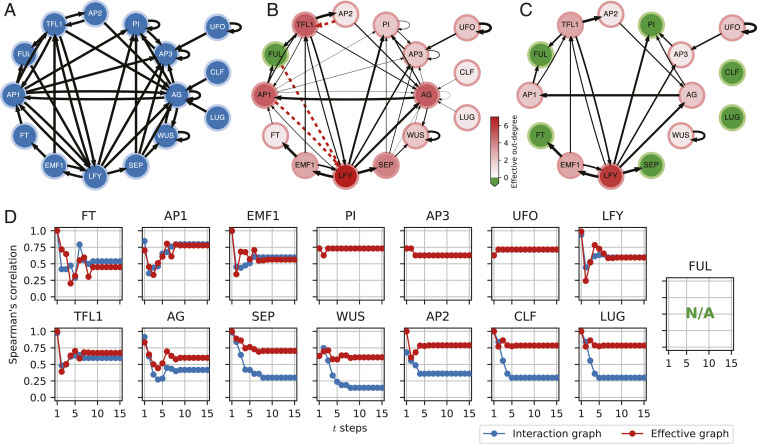
Study of the A. thaliana BN model. (A) The interaction graph for the A. thaliana BN. (B) The effective graph. Edge thickness denotes effectiveness, ; dashed red indicates fully redundant edges (Table 1 shows parameter values); node color intensity denotes effective out-degree; and green nodes denote cases of null effective out-degree (). (C) A threshold effective graph showing only edges with to enhance visibility of the largest connected component that allows to function as a master regulator and reveals that functions simply as an autoregulator; green nodes denote cases of null effective out-degree at this threshold level. (D) Spearman’s rank correlation (vertical axis) between the true impact of perturbing each node [] and respective path-length approximation predictions using the interaction (blue) and effective (red) graphs after steps (horizontal axis); cannot be computed (N/A, not available) because it has null impact on other variables (validating our observation of a fully redundant output).
The canalization of an automaton reflects the fact that not all input states are equally important for determining its state transition (3). We follow Marques-Pita and Rocha (17) by quantifying canalization through the amount of logical redundancy present in the automata. Specifically, we use the first step of the Quine–McCluskey Boolean minimization algorithm (29) to identify inputs of an automaton , which are redundant given the state of its other inputs. This procedure compresses an LUT into the set of all distinct prime implicants of , represented as a set of wild card schemata, , in which the wild card or “don’t care” symbol, #, denotes an input whose state is redundant for determining the automaton transition given the states of other necessary inputs. For instance, schema in the Fig. 1B example specifies that when input , the states of inputs and are redundant to determine the next state of , which is guaranteed to be 0. In this process, the original LUT is redescribed into a complete set of schemata (Fig. 1).
Every wild card schema redescribes a subset of entries in the original LUT, denoted by , where means “is redescribed by.” For example, schema in the Fig. 1 example redescribes the set of LUT entries . The set of (overlapping) schemata is complete since it contains all unique prime implicants that redescribe all entries of the original LUT, here described as wild card schemata. In Boolean minimization, the set of prime implicants can be further reduced (via the additional steps of the Quine–McCluskey algorithm or equivalent methods), but because our goal is to tally all possible minimal transition conditions of an automaton, we preserve all prime implicants; ref. 17 and SI Appendix have details. Notice that all measures that ensue are computed from the entire population of prime implicants and are thus parameters, not sampled statistics, of logical functions .
The amount of canalization present in the logic of an automaton can be quantified by probabilistic parameters derived from the schema redescription of its LUT. Input redundancy, , measures the number of inputs that, on average, are not needed to determine the state of automaton , assuming that all input combinations are equally likely. It is quantified by tallying the mean number of wild card symbols present in schemata set that redescribes LUT :
| [1] |
where is the number of # symbols in schema . In computing , we assume that each entry of LUT can be redescribed with equal likelihood by any of the schemata in that includes it (). Thus, we use the average operator () in Eq. 1. This is the same as assuming that any schema (or prime implicant) is a viable intervention possibility to change the state of automaton . Other redundancy aggregations are possible (17), but averaging over all possible schemata allows the per-edge separation of redundancy we pursue below (SI Appendix, section 1 has additional discussion).
A complementary parameter of the redundancy of automaton is its effective connectivity:
| [2] |
which yields the number of inputs that are on average necessary to determine the automaton’s state. Whereas is the number of inputs to automaton present in the interaction graph of the BN (in-degree), measures the number of such inputs that are actually (on average) necessary to determine the state of —the effective connectivity of . In the Fig. 1B example, because six entries of LUT () are redescribed by schemata with two wild cards () and two entries () are redescribed by schemata with one wild card (), via Eqs. 1 and 2 we obtain and . In other words, on average, 1.75 inputs to are redundant, and thus, its effective connectivity is 1.25—in contrast to its in-degree of three.
Other automata parameters, distinct from Eqs. 1 and 2, can be used to measure canalization. For instance, sensitivity (30) also aims to measure the effective dynamics of a Boolean automaton, but as we discuss below, it does not capture the nonlinear effects of collective canalization. We can also extract additional redundancy from the symmetries that exist in the schemata set , thus providing a further compression of this set (17, 31), but we do not consider symmetry redundancy in the present analysis. Additional algorithmic details as well as relationships between canalization, control, robustness, and modularity of BN models are presented in refs. 17 and 20 and SI Appendix.
Most automata contain some amount of input redundancy; only the two parity functions for any have (e.g., the exclusive OR, function and its negation for ). Therefore, the original interaction graph of a BN misses the high amount of redundancy present in most BNs and does not capture how automata truly influence one another in a network.
The Effective Graph and Redundancy in Models of Biochemical Regulation and Signaling
The input redundancy and effective connectivity of Eqs. 1 and 2 reveal that, on average, the interaction graph overestimates the number of inputs needed to determine transitions. However, these parameters do not specify which of the interactions are actually more effective and how they combine to form pathways that transmit signals through the network. To measure how input redundancy is distributed over the individual inputs to an automaton, we introduce the per-input parameters of redundancy and effectiveness. The latter is then used to compute the edge weights of the effective graph, which provides a (probabilistic) synthesis of the canalizing dynamics of a BN.
Edge redundancy, , tells us, on average, how redundant an incoming edge from automaton is in determining the state of automaton . This is computed by counting the average number of schema in in which input is specified by a wild card symbol:
| [3] |
where is a logical condition that assumes the truth value one if input is a wild card in schema and zero otherwise; is the average operator. Similarly, edge effectiveness, , captures the extent to which an incoming edge from automaton is on average necessary to determine the value of automaton :
| [4] |
Naturally, and , meaning that the canalization of an automaton is additive over its incoming edges.
We can now define the effective graph of a BN to capture the varying influence of each input edge on the dynamics of automata nodes. Specifically, , where is the set of automata and is the set of directed edges, weighted by their effectiveness as defined by Eq. 4. Note that an edge (interaction) can be fully redundant if its effectiveness is null, . This is the case of input in the Fig. 1B example, which is always redescribed by a wild card in and thus, . In practice, fully redundant edges should be completely removed, but in this article, to catalog their existence, we emphasize them as red dashed edges (e.g., edge in Fig. 1B).
One may think that fully redundant edges should not occur in well-constructed networks; however, they are fairly common in systems biology models. Indeed, we analyzed 78 Boolean models stored on the Cell Collective (9) and found that 17 of them () contained at least one fully redundant edge, with 87 fully redundant edges in total. The inclusion of fully redundant edges in these models may result from inference methods based on information theory that can fail to capture polyadic relationships (32), but the most likely reason is an incomplete record of experimental observation. Typically, systems biology models integrate many experimental studies conducted by many different teams in different scenarios, which are available in interaction databases and the published literature (33). Modelers who integrate such scientific evidence have to make decisions about conflicting or weak evidence (13). For instance, the A. thaliana model studied below (see Fig. 4) contains three fully redundant edges, which ultimately result from “subjective decisions given alternatives with equivalent results” (27). SI Appendix, section 2.B has a more detailed discussion of how these issues can lead to fully redundant edges in systems biology models. Certainly, our methodology can serve as a logical check on these models to remove completely redundant interactions.
The effective graph is a probabilistic synthesis of the dynamical redundancy of a BN model given all its possible initial conditions. However, in systems biology we often want to study a model under specific initial conditions: for example, cells in a cancer state or under the influence of a particular drug, as pursued below in the analysis of the estrogen receptor positive (ER+) breast cancer model. Since the set of possible initial conditions in such cases is reduced, the interaction topology of the effective graph changes. This is easily captured in our methodology by conditioning the effective graph on a set of variables, , that are fixed to specific constant states. The resulting conditional effective graph, , can have a drastically altered effective topology, for instance, with many more interactions revealed to be fully redundant.
The computational complexity of our canalization parameters and the effective graph scale linearly with the number of nodes and can thus be computed for large BNs (17), unlike most methodologies used to analyze the dynamics of BNs. Instead, the computational complexity bottleneck to derive the effective graph is bounded by the Quine–McCluskey algorithm (29) on the largest degree node in the BN: that is, the automaton with the largest . When this value is very large, one can sample the prime implicant population, but none of the analysis here pursued required such estimation. We provide a full implementation of all canalization parameters (Eqs. 1–4) and the effective graph in the open-source CANA python package (31).
Effectiveness of Biochemical Interactions
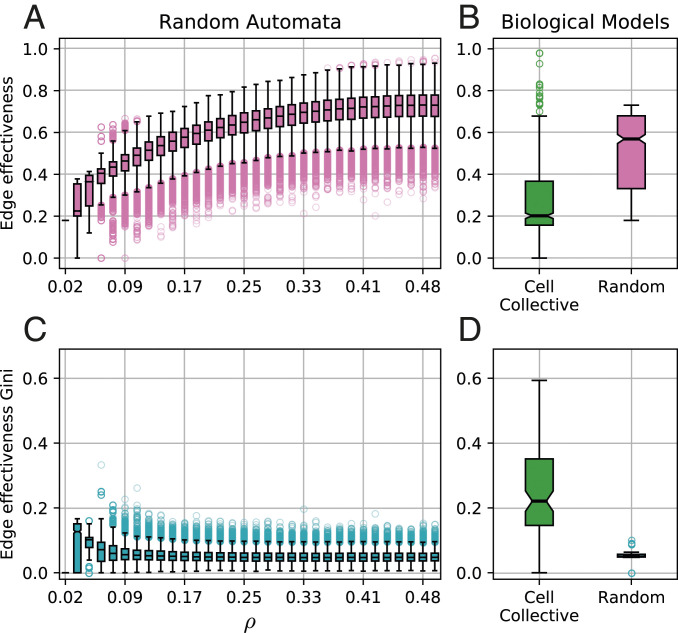
Input redundancy (Eq. 1) is prevalent in random Boolean automata. In BNs, this leads to a lower effective connectivity (Eq. 2) for automata nodes than the interaction graph (in-degree) specifies, with varying edge effectiveness (Eq. 4) distributed across inputs. The prevalence and variation of edge redundancy are shown in Fig. 2A for random Boolean automata of degree . For all values of bias (), we observe much variation in edge effectiveness, although its median value goes from at the lowest bias () to at the highest bias (). The upward shift of the distribution of edge effectiveness indicates that inputs tend to become more important for determining the state transition of the automata as bias increases. The behavior for automata with other is similar (SI Appendix, Fig. S3).
Fig. 2.
Central tendency, variation, and heterogeneity of edge effectiveness of Boolean automata in biochemical regulation and random ensembles. (A) The distributions of edge effectiveness for ensembles of automata with degree at each bias . (B) The distribution of edge effectiveness of the 630 incoming interactions to 105 automata with degree in Cell Collective models (green) compared with a bias-matched sample of random Boolean automata (pink). (C) The distributions of edge effectiveness Gini coefficients for inputs to automata in each of the random ensembles from A. (D) The distribution of edge effectiveness Gini coefficients for inputs to the 105 automata with degree in the Cell Collective models (green) compared with the bias-matched ensemble of random Boolean automata (cyan).
The observed distribution of edge effectiveness for random Boolean automata provides context for next question: how much redundancy is present in experimentally validated biochemical interactions? To answer this question, we calculated the edge effectiveness of all 8,220 interaction edges from the 78 BN models in the Cell Collective (SI Appendix, section 2). We compare this distribution with an ensemble of random automata matching the degree () and bias () of the Cell Collective automata. Specifically, for each automaton from the systems biology models, we sample random automata with exactly the same degree and bias. We observe that the mean edge effectiveness of interactions in the biochemical networks is much smaller than that of interactions in the random ensemble (Fig. 2B). For simplicity but without loss of generality, Fig. 2B depicts the distribution of effectiveness for 630 incoming edges to 105 automata of degree in the systems biology models, as compared with that of the bias-matched random ensemble of same ; distribution comparisons for other values of are shown in SI Appendix, Fig. S3. A two-sample independent t test for the difference in the means between the experimentally validated biochemical (0.27) and the random interactions (0.51) confirms the statistical differences between these distributions for automata, with a P value .
Edge effectiveness allows us to differentiate network interactions based on how much they contribute to determining automata transitions and to identify the inputs that most control a given automaton. In contrast, the original interaction graph of a BN does not differentiate the inputs to an automaton. Let us look at how edge effectiveness differentiates input importance with an example. Consider two automata, (balanced) and (unbalanced), each with inputs: . In the first case, the transition function is specified by , a symmetric logic since all inputs are interchangeable. In this balanced case, the edge effectiveness is the same for all incoming edges . In the second case, the transition function is specified by , a logic where input primarily determines the transition. Accordingly, in this unbalanced case the edge effectiveness varies by incoming edge: and , which reflect the importance of input in determining the state of the automaton.
To ascertain the heterogeneity of effectiveness in biochemical interactions, we again compare the systems biology models in the Cell Collective with similar random ensembles. For each automaton, we compute the Gini inequality coefficient to obtain a real number between zero and one, where zero denotes that all inputs have exactly the same effectiveness and one denotes maximum inequality among the inputs (i.e., one input completely dominates over the others) (SI Appendix, section 3). When applied to the balanced and unbalanced example automata, we obtain Gini coefficients of 0 and 0.31, respectively. This accurately reflects the effectiveness equality of the inputs to and the effectiveness inequality of the inputs to .
The Gini coefficient calculated for the automata in the Cell Collective database reveals greater effectiveness inequality in their interaction than in comparable random automata. In other words, a smaller subset of inputs plays a more important role in controlling the biochemical variables in these models than is expected by chance. Consider first Fig. 2C, where edge effectiveness in random automata with degree is characterized by a relatively small Gini coefficient for all biases. This indicates that in random automata, while redundancy is pervasive (Fig. 2A), it is distributed similarly over the inputs—incoming edges are roughly equally effective in determining the state of the random automata. In contrast, as shown in Fig. 2D, the Gini coefficient of the edge effectiveness of automata with in the 78 biological models varies much more but is consistently higher than the bias-matched random automata. This is further supported by a two-sample independent t test for the difference in the means of the automata distributions in biochemical models (0.22) and in the random ensemble (0.05), which confirms the statistical differences between these distributions with a P value .
In summary, our analysis of edge effectiveness demonstrates not only that automata used to model biochemical regulation in the Cell Collective contain more redundancy than expected in random automata but also, that this redundancy is unevenly distributed over their inputs. In other words, in the models of biochemical regulation, only a few interactions are effective in controlling variable transitions, while most interactions are redundant and not very dynamically effective.
Collective Canalization in Dynamical Regulation
A crucial feature of Boolean automata is the potential for highly nonlinear integration over their inputs (14, 15). Canalization is one such nonlinear phenomenon whereby a subset of inputs jointly determines the state of an automaton while rendering redundant the complement subset of inputs (3, 17). However, existing measures of canalization do not consider the full range of nonlinear joint interaction.
We can measure the extent to which nonlinear collective canalization is present in an automaton by comparing our per-input canalization and redundancy parameters—that capture joint dependencies—with parameters that consider each input independently. One such measure assuming independence is the activity of an input to a Boolean automaton : . It is the probability, , that automaton flips its state at when its input flips its state at , given a uniform distribution of input states at (30). In turn, the sensitivity of automaton is the sum of all its input activities .
Interestingly, our formulation of canalization via schema redescription also yields the activity of an input with a simple modification to formula (Eqs. 3 and 4), by substituting the maximum operator () for the average operator ():
| [5] |
SI Appendix, section 1.C has a proof of this formulation of activity. From here, it follows that and . This fact allows us to measure how much of the effective connectivity of an automaton and the effectiveness of its inputs derives from joint interactions among the inputs:
| [6] |
In other words, and measure the portion of canalization that derives from collective canalization at the node and input levels of a BN—in excess of sensitivity and activity, respectively.
Because collective canalization is very common, especially as the number of inputs () increases (3), the distinction between effective connectivity and sensitivity is quite relevant for understanding the true regulatory dynamics in BNs, especially in systems biology models. Indeed, even for Boolean automata of , the sensitivity parameter does not discriminate between such common Boolean functions as conjunction/disjunction and proposition/negation: . In contrast, effective connectivity correctly accounts for the additional collective canalization that is present in the conjunction/disjunction (and other) functions: , while .
Collective canalization is at play even in the small BN shown in Fig. 1. The edges of its effective graph are , , whereas the activity measured for the same interactions is , . The discrepancy occurs because and jointly determine with a collective canalization of . Indeed, on average one input is not sufficient to determine the state of , as sensitivity implies. For one-quarter of the input configurations (two of eight entries in the LUT redescribed by schema ), both inputs and are needed to jointly determine the state of , and thus, its collective canalization is . Clearly, the effective connectivity value of is a more accurate characteristic of how inputs jointly determine the state of , by aggregating both their individual and collective contributions. On average, 1.25 inputs are needed to specify the transition of (conversely, inputs are on average redundant); SI Appendix, section 1 has an additional example. While the concept of “ sensitivity” (34) extends sensitivity to subsets of inputs, it results in a vector of values, which is less intuitive in a network context than the scalar parameter .
Collective canalization is measured at node and edge levels unequivocally via Eq. 6 and characterizes differences in the canalization of Boolean functions that sensitivity and activity do not measure. The question of how much the collective canalization captured by our parameters affects the dynamics of BNs is beyond the scope of this paper. However, collective canalization has already been shown to lead to more accurate predictions of critical behavior across a wide range of BN connectivity and dynamical behavior (19).
Together, our results show that our canalization parameters (Eqs. 1–4) capture redundancy and dynamical effectiveness in BNs at the automaton node and edge levels. They encompass parameters such as sensitivity and activity and importantly, also account for the nonlinear effects of collective canalization. One goal of the effective graph is to precisely quantify the true impact of interactions in spreading perturbations and control signals in BN models of biochemical regulation. The edges, therefore, are weighted according to their dynamical effectiveness (Eq. 4) to capture both their activity and (nonlinear) collective canalization contributions (Eq. 6). Next, we study the utility of the effective graph in predicting the spread of dynamical perturbations and identifying control pathways.
Effective Graph Predicts the Spread of Perturbations
An important goal of systems biology is to quantify and predict the spread of perturbations and control signals across networked regulatory pathways (35, 36). While the interaction graph of a BN is useful for a theory of perturbations because it specifies which automata are topologically reachable in a given number of time steps, it fails to capture the varying effectiveness of each interaction in propagating signals through network pathways. The effective graph, on the other hand, provides enriched information about dynamical redundancy and canalization from each constituent automaton. In this section, we demonstrate that the effective graph’s enriched portrait better captures the spread of perturbations in both random BNs and experimentally validated systems biology models.
Many types of perturbations can be considered, including those that change the structure or logic of the original model such as edge shuffling or deletion (22). Here, we focus on how specific, fixed models of biochemical regulation respond to different dynamical conditions—such as cellular response to drug regimens in ER+ breast cancer. Thus, unless otherwise noted, by perturbation we mean negating the logical state of an automaton at time (also known as bit-flip perturbation). The impact of such a perturbation to an automaton in a BN is quantified by the Boolean analogue of the partial derivative (37):
| [7] |
where denotes the state (truth value) of automaton node at time when the BN is initiated with configuration at time and denotes configuration with the state of automaton negated. The partial derivative yields one if flipping the state of in initial configuration leads to flipping its state at time and zero otherwise. The total impact on automaton of perturbations to automaton after steps is the average over all initial configurations:
| [8] |
For large BNs, must be estimated by averaging over a random sample of initial network configurations.
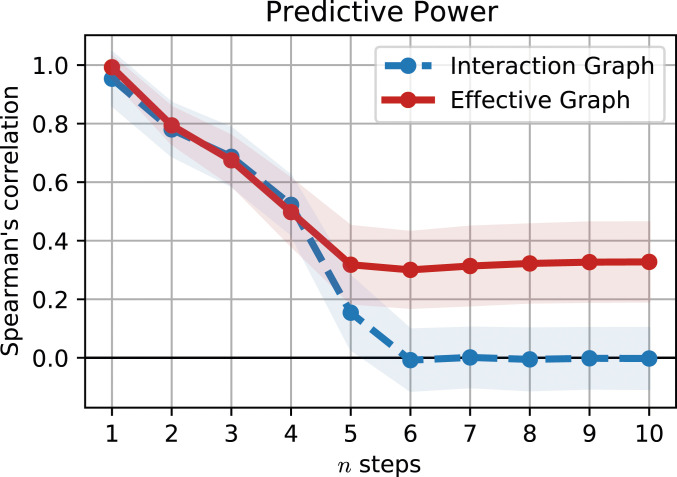
We now study how well the interaction and effective graphs predict the total impact of perturbations, using a different spreading model for each: and , respectively. To set up , we consider that all nodes connected via a path of at most edges starting from node are equally impacted by a perturbation to node , where is the number of time steps since the perturbation—the “light cone” of as signals to any cannot travel faster than the minimum number of edges (SI Appendix, Fig. S1). The second model is similar except that the (weighted) effectiveness edges in the effective graph are assumed to proportionally constrain the spread of a perturbation (SI Appendix, section 4). This constraint is given by the product of edge weights in the strongest path between and (SI Appendix, Fig. S1), limited by the light cone such that the number of edges in the path is smaller than the number of elapsed time steps. By choosing the path with maximum product of edge weights as a surrogate measure for the total impact of perturbations, we assume [as in linear control (38)] that a signal can propagate without restriction via a connected path in the interaction graph model (), but edge effectiveness deferentially restricts propagation in the effective graph model (). To measure how well each model predicts which nodes are most affected by perturbations to node , we compute the average Spearman’s rank correlation between each model and the true at each time step.
We illustrate the superior predictive power of first with an experiment using random BNs of nodes, fixed degree , and average bias (SI Appendix, section 4). For each BN, we select 10 nodes at random to perturb, approximating the total impact on the other nodes with a sample of random initial configurations. As shown in Fig. 3, the rank correlation of with the effective graph model, (red), is consistently better than with the interaction graph model, (blue). Indeed, after the full network is encompassed in the light cone, is unable to differentiate which nodes might have been impacted by the perturbation, and Spearman’s correlation is zero. In contrast, the effective graph retains predictive information about which variables are impacted by perturbations as measured by a significant positive Spearman correlation with the true dynamical impact. As shown below, the ability of the effective graph to predict perturbation spread in experimentally validated models of biochemical regulation is even more striking.
Fig. 3.
The effective graph captures the spread of perturbations. The predictive power of the edge-product approximation using the two models, (blue) and (red), measured by the Spearman rank correlation (vertical axis) with the total impact, , sampled from trajectories, after steps (horizontal axis). The shaded region denotes one SD for a sample of 100 random networks and 10 perturbed nodes per network.
Effective Graph Reveals How Control Pathways Function in Models of Biochemical Regulation
The characterization of control strategies in biomedicine can help focus experiments, aid the design of advanced disease therapeutics (1, 39), and even suggest intervention strategies to reprogram cells (40) (e.g., to revert a mutant cell to a wild-type state). It is well known that when the set of automata nodes of a BN is large, enumeration of all configurations of its state-transition graph (STG) becomes difficult, making the controllability of BNs a nondeterministic-polynomial-time hard problem (41). Therefore, control methodologies that leverage the interaction graph or otherwise approximate the dynamics are highly desirable since they can greatly simplify the complexity of BN control (1, 17).
Effective Graph Enhances Structure-Only Control Inference.
Several recent methodologies aim to determine the controllability of complex dynamical systems based solely on the graph of interactions between variables: structural controllability (SC) (38), minimum dominating set (MDS) (42), and feedback-vertex set control (FVC) (1, 43). By using only the interaction graph to predict minimum sets of variables (driver nodes) that are needed to control a network, these methods make predictions about the entire ensemble of dynamical systems that fit the same interaction graph (20). In contrast, since the effective graph is obtained by removing dynamical redundancy in a specific BN, the ensemble of possible dynamical systems that can fit is much smaller. Therefore, the effective graph is likely to lead to more precise inferences of control pathways in specific systems biology (BN) models than those derived from structure-only methods, such as SC, MDS, and FVC.
The removal of fully redundant edges from the interaction graph can reduce the number of feedback loops, revealing a smaller or distinct set of driver nodes than those predicted by FVC (SI Appendix, section 5). Consider the interaction and effective graphs of the A. thaliana flower development BN (27, 28) (TBN) in Fig. 4 A and B. This gene regulatory model integrates experimental evidence of causal relationships among 15 genes (and the proteins they encode) that regulate cell-fate determination during floral organ specification in this plant. The loop between Terminal Flower 1 (TFL1) and Floral homeotic Apetala 2 proteins disappears because the edge from the latter to the former is completely redundant. While FVC predicts that TFL1 is required to control the network (to control this nonexistent loop), analysis of its STG (SI Appendix, section 6) reveals that TFL1 can be replaced by the AP1 (Floral homeotic Apetala 1) protein, which is not in this loop, to control the network. Interestingly, AP1 is not in the set of driver nodes FVC predicts are needed for control. Similarly, the completely redundant interaction between AP1 and LFY (Leafy) removes the loop between these two proteins, allowing LFY to be replaced by the EMF1 (Embryonic flower 1) protein to control the network under the (pinning) control conditions assumed by FVC (SI Appendix, section 6).
Importantly, edges do not need to be fully redundant to make interaction loops dynamically irrelevant. The drastic reduction in effective connectivity observed by comparing the TBN interaction and effective graphs is summarized in Table 1. It underscores how canalized the dynamics of the TBN model is and how such canalization alters the effective or true interaction structure. Consider the case of the Floral homeotic Pistillata (PI) protein, a transcription factor in the Thaliana flower development model in Fig. 4. FVC predicts that PI is required for dynamical control of this BN. However, the PI self-regulation loop has very low effectiveness (). Analysis of this model’s STG (SI Appendix, section 6) reveals that PI is not in fact needed to control this network; indeed, PI has a very low effective out-degree () and thus, very little influence on dynamics (Table 1).
Table 1.
Canalization parameters for variables with in the A. thaliana model (SI Appendix, Table S4)
| AG | 9 | 6.9 | 2.1 | 0.77 | 0.23 | 5 | 1.9 | 0.38 |
| AP3 | 7 | 4.7 | 2.3 | 0.68 | 0.32 | 2 | 0.8 | 0.4 |
| PI | 6 | 3.8 | 2.2 | 0.64 | 0.36 | 2 | 0.47 | 0.24 |
| AP1 | 4 | 2.4 | 1.6 | 0.59 | 0.41 | 6 | 1.4 | 0.23 |
| LFY | 4 | 2.8 | 1.2 | 0.69 | 0.31 | 7 | 4.8 | 0.69 |
| TFL1 | 4 | 2.8 | 1.2 | 0.69 | 0.31 | 5 | 2.8 | 0.57 |
| WUS | 3 | 1.4 | 1.6 | 0.48 | 0.52 | 2 | 0.91 | 0.46 |
| FUL | 2 | 0.75 | 1.2 | 0.38 | 0.62 | 1 | 0 | 0 |
, , and denote in-degree, input redundancy, and effective connectivity, respectively; and denote versions of and normalized by; and and denote out-degree and effective out-degree, respectively.
Other features of a very canalized dynamics are also striking. While transcription factors Agamous (AG), Floral homeotic Apetala 3 (AP3), and PI are seemingly regulated by many other proteins (in-degrees of nine, seven, and six, respectively), their effective connectivity is considerably smaller (2.1, 2.3, and 2.2, respectively). In other words, unlike what is assumed in the interaction graph, these transcription factors are on average regulated by little more than two other proteins at any given time. In general, all variables with have much input redundancy (variables with a single input, by definition, cannot have redundancy). Indeed, except for the Fruitful (FUL) DNA-binding protein, all have more than input redundancy and less than effective connectivity, as seen in columns and in Table 1.
Effective Graph Aids Explanation of Biological Mechanism.
Structure-only control theories yield a set of driver nodes that are needed for control, but they do not provide a mechanistic explanation of how those nodes control the network or which nodes are more effective at control and signal propagation. The examples above demonstrate that the effective graph includes important dynamical redundancy information pertaining to the specific BN being analyzed. It reveals a more accurate portrait of how control operates, including alternative, actionable intervention strategies—such as the possibility of using AP1 or instead of or , respectively, in the set of driver nodes that control the TBN (by pinning).
Beyond identification of accurate driver variables, an analysis of the strongest paths of the effective graph reveals a more precise mechanistic understanding of how control propagates in biochemical regulation models. Consider the control roles of the and (Wuschel) transcription factor proteins in the Thaliana model. The most general form of BN control allows perturbations at any stage of the dynamics (to any configuration of the STG)—a more general form of control than the FVC pinning control assumptions (SI Appendix, section 5). In this case, via an STG enumeration method (20), we observe that the TBN is fully controllable by interventions to the trivial inputs {UFO, LUG, CLF} and additional driver set alone. This makes sense because in the interaction graph in Fig. 4A, there is a path from or to any other node (except the three input nodes); so, in principle, signals from these nodes could reach any other node. However, in the effective graph in Fig. 4B, is connected to the remainder of the network via a single very low-effectiveness edge with (AG transcription factor): . Therefore, is, in effect, dynamically decoupled from the remainder of the network. In contrast, preserves paths with high edge effectiveness to all other nodes in the effective graph. The threshold effective graphs in Fig. 4C and SI Appendix, Fig. S4 clarify the very distinct functional roles of these two proteins in the dynamics of this development model.
We validate these inferences with the analysis of perturbation spread on the TBN effective graph, as shown in Fig. 4D. The predictive power of the path-length approximation is very similar for both the interaction and effective graphs in the case of , but it is completely different for where the effective graph leads to a much higher correlation with the true impact of perturbing the latter variable. In other words, does not behave at all like the original interaction graph would suggest. The effective graph reveals that these two transcription factors function very differently in how they control the TBN dynamics of this model. While is only an autoregulator, is a master regulator mechanism (44). Thus, even though the driver set for this network is , except to control itself, is sufficient and a much more effective candidate for experimental intervention.
Also striking in the TBN effective graph is the case of the DNA-binding protein. The interaction graph, built from published pairwise experiments, depicts that it causally affects . However, this interaction is completely redundant in the model’s logic for . The protein, therefore, has no impact in this model, as shown in the effective graph in Fig. 4B and confirmed by our perturbation analysis. Notice that because perturbations to lead to null impact on other variables, we cannot compute Spearman’s correlation to its predictive power for the interaction and effective graphs (hence, the N/A in Fig. 4D). Although the interaction graph implies that signals from can reach almost all other variables in the model, the effective graph clearly reveals it reaches none.
We note that the effective graph is a probabilistic representation of the underlying dynamics, so even an edge with very low effectiveness may on rare occasions play a key role in determining dynamics. Still, statistically, edges with very low effectiveness are likely to play a reduced role in propagating control signals. This is demonstrated by the fact that the effectiveness-weighted paths of the effective graph are much more predictive of (correlated with) spreading dynamics after variable perturbation than paths of the original interaction graph, for both random graphs in Fig. 3 and the Thaliana network in Fig. 4D. Thus, strong paths in the effective graph are likely good control channels in systems biology models because they are better at propagating signals than other paths in the original interaction graph.
Effective Graph Enhances Understanding of Signaling in Large Network Cancer Models.
The effective graph reveals multivariate canalizing dynamics by removing redundancy from automata networks and allows for a more precise characterization of perturbation and control signals. Since the effective graph is computed from the scalable schema redescription methodology, we can apply it to large networks for which full enumeration of the configuration space, and thus, computation of true control behavior or identification of all attractors, is not possible (17, 31). To demonstrate how it allows us to understand canalizing dynamics and identify effective control pathways, we study two large signal transduction networks involved in leukemia (45) and ER+ breast cancer (26), whose interaction and effective graphs are shown in Fig. 5 and SI Appendix, Figs. S7–S13.
Fig. 5.
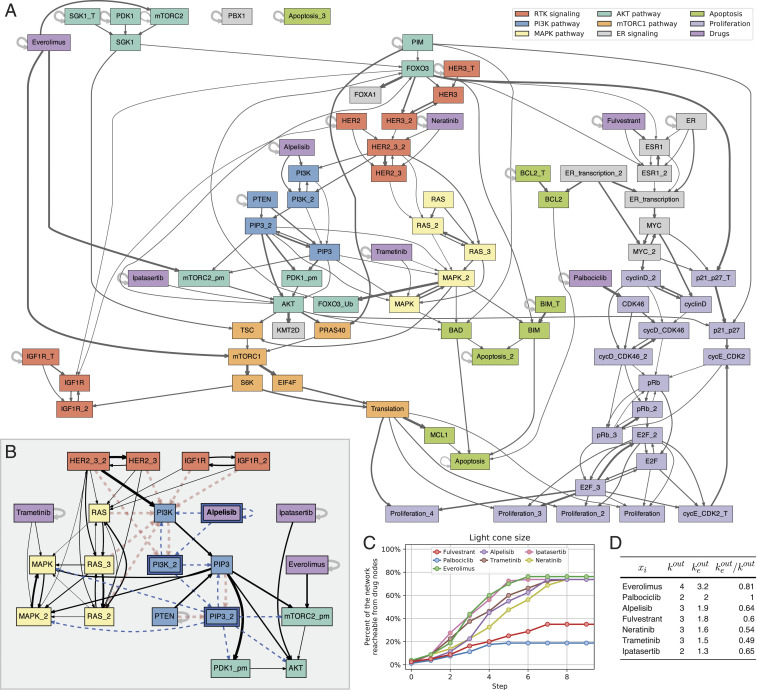
Study of the ER+ breast cancer BN model. (A) Hierarchical rendering of the effective graph for the BN model of ER+ breast cancer. Edge thickness denotes its effectiveness, thresholded to ; node color denotes constituent pathways (legend is in the top right corner). (B) Conditional effective graph with Alpelisib= ON (pinned state denoted with bold text and blue border), revealing how it renders much of the influence from (receptor tyrosine kinases) pathway redundant (red dashed edges) while fixing the state of several variables in the pathway, such as the phospholipid (phospholipid); variables whose state becomes fixed (constants) are denoted by a blue border, and edges that transmit a constant input state are denoted by a dashed blue color. (C) Spreading dynamics of perturbations to each of the seven drugs in the model and the proportion of network effectively reachable. (D) Effectiveness of outgoing edges of drug variables; and denote out-degree and effective out-degree, respectively.
The ER+ breast cancer network is a multistate automata network that has been converted to a fully equivalent, 80-variable BN (26). The goal of this model, built from experimental evidence, is to study resistance mechanisms to PI3K (phosphatidylinositol 3-kinase) inhibitors in ER+, HER2+, and PIK3CA-mutant breast cancer cells. Seven drugs that inhibit specific targets of interest are included in the model. For instance, alpelisib is a PI3K inhibitor (a drug that inhibits phosphoinositide 3-kinase enzymes involved in cell growth signaling pathways). The model is used to study known and novel combinatorial interventions that combine PI3K inhibition with other strategies (26). The objective is not so much to find the attractors of the entire multivariate dynamical system but simply to identify the final state of specific outcome nodes that model cancer cell death (apoptosis) or proliferation. In other words, the model is constructed to study which dynamical interventions control cancer cells to their programmed death or at least inhibit their proliferation.
The effective graph of this model (SI Appendix, Fig. S11) reveals that much redundancy is present in its dynamics, and edge effectiveness is highly variable. Some interactions are almost completely redundant with effectiveness as small as 0.065. The maximum edge effectiveness, 1.0, is only observed for automata with a single input, where redundancy cannot exist by definition. SI Appendix, Table S7 shows canalization parameters for all of the variables in this model; Fig. 5D shows key parameters for the seven drugs included in this model.
The interaction graph (80 nodes) has 23 () autoregulator (self-loop) nodes, of which 18 () are input nodes (SI Appendix, Fig. S10). This means that a large proportion of nodes cannot be controlled via other nodes. Still, reachability is ultimately formed by a single weakly connected component and 45 strongly connected components, the largest of which has 24 nodes (SI Appendix, Tables S2 and S3). This implies that signals from input nodes could in principle reach the entire network via the weakly connected component and of the nodes could regulate each other via the largest strongly connected component.
The effective graph, however, reveals a different, clearer understanding. The network dynamics is effectively separated into various modules, perhaps because the model is a synthesis of six pathways implementing distinct resistance mechanisms to PI3K inhibition that affect the apoptosis and proliferation pathways (26). Indeed, the most effective edges form very few connections among subsystems that can effectively propagate signals. This is shown by the existence of many strongly connected components (and input nodes) when only the reasonably effective edges are considered—especially in comparison with other models studied (SI Appendix, Tables S2 and S3). Consider the threshold effective graph with edge effectiveness greater than or equal to 0.2 shown in Fig. 5A. The largest strongly connected component is composed of only 17 () nodes, and 45 () nodes form strongly connected components of a single node. This means that there is little effective cross-regulation dynamics or long-range signaling in the model. Most of the effective dynamics can only be driven by direct intervention to many individual nodes or short pathways involving few nodes. The network becomes even more splintered at a threshold of 0.4 (SI Appendix, Figs. S12 and S13), resulting in the largest strongly connected component of only 3 () nodes, with 61 () nodes forming strongly connected components of a single node. Reachability is also quite diminished; for an edge effectiveness threshold of 0.4, there are 12 weakly connected components, the largest of which is composed of only 52 nodes ( of the network). Indeed, two of the apoptosis nodes and one of the proliferation nodes, all key targets of the model, become isolated at effectiveness threshold 0.4, and one of the apoptosis nodes becomes isolated at effectiveness threshold 0.2.
These results are consistent with the known behavior of the model, whereby control of cancer apoptosis or inhibition of proliferation requires interventions to many nodes, including the PI3K inhibitor, other drugs, and every input node (26). The effective graph, however, reveals that the dynamics of this network is very robust to perturbation and hard to control because its subsystems are effectively decoupled. That is, canalization works by preventing propagation of signals and cross-regulation. Indeed, most of the (nondrug) variables that have an impact on cancer apoptosis or proliferation, when working in tandem with the PI3K inhibitor and baseline (table 3 in ref. 26), have short paths to those target variables (at most three edges) in the effective graph.
The connectivity of the effective graph thus reveals that the overall dynamics of the ER+ breast cancer network is very modular with many effectively decoupled subsystems—substantially more than the other experimentally validated biochemical models considered, as seen in SI Appendix, Tables S2 and S3. In contrast, in the TBN discussed above, canalization enables to function as a single master regulator gene that can effectively propagate signals (effectiveness at or above 0.4). It reaches all other nodes in a large, weakly connected component of 12 nodes ( of network), except for (which remains in a decoupled component) and the input nodes. Similarly, in the case of the T cell survival in leukemia network (45), the effective graph maintains a single weakly connected component of 58 nodes ( of the network), even for a high 0.4 effectiveness, which reveals a greater ability to propagate effective control signals through this network.
Let us now use the effective graph to study how differently the seven drugs are capable of controlling cancer cells to apoptosis or proliferation in this model. The goal of the original model is to find interventions—especially single-node interventions—that synergize with the PI3K inhibitor Alpelisib (26). Focusing on the remaining six drugs, the model reveals that Fulvestrant and Palbociclib best synergize with Alpelisib to increase apoptosis or decrease proliferation of cancer cells. Everolimus also modestly increases apoptosis, although not as much as the other two drugs. In contrast, Neratinib, Trametinib, and were shown to not synergize with Alpelisib (table 3 in ref. 26).
An initial observation of the effective graph, summarized in Fig. 5D, is consistent with those results: Alpelisib and the three drugs that best synergize with it are the top four with the largest effective out-degrees (). Thus, the most outwardly effective drugs are also those previously shown to lead to greatest control of cancer apoptosis or proliferation. More importantly, the effective graph reveals why the seven drugs affect the cancer dynamics the way they do. The hierarchical rendering of the (0.2) threshold effective graph shown in Fig. 5A clearly reveals why Fulvestrant and Palbociclib synergize so well with the inhibitor Alpelisib: they act on the estrogen () signaling and cell proliferation pathways that Alpelisib cannot effectively reach [except by indirectly reaching the terminal proliferation nodes via the (mechanistic target of rapamycin complex 1) pathway]. This is demonstrated by comparing the conditional effective graph for Alpelisib= ON with those for a combined intervention Alpelisib=Fulvestrant= ON or Alpelisib=Palbociclib= ON (SI Appendix, Figs. S16, S18, and S21): only the combination interventions are capable of fully resolving the state of the proliferation variables. This explains why these drugs in combination with Alpelisib can drive cancer proliferation to zero in this model, while Alpelisib on its own cannot (table 3 in ref. 26). Moreover, Fulvestrant can also effectively reach some of the apoptosis pathway, which explains why, in combination with Alpelisib, it can increase apoptosis of cancer cells in this model but Palbociclib does not—the latter is only effective on the proliferation pathway and is not effective on apoptosis. These observations are also corroborated by the study of spreading perturbations. In Fig. 5C, we can see that Fulvestrant and Palbociclib reach a distinct, smaller part of the network, with Fulvestrant reaching more of the network ( signaling, proliferation, and apoptosis pathways) than palbociclib (only the proliferation pathway).
The drugs that were shown not to synergize with Alpelisib (Ipasertib, Neratinib, and Trametinib) not only have the lowest values of in Fig. 5D but are also shown in Fig. 5A and the respective conditional effective graphs (SI Appendix, Figs. S19, S20, and S22) to only contribute to the same pathways that Alpelisib already acts on. Fig. 5C also shows perturbing these three drugs ultimately spreads only to the same subgraph of the network that Alpelisib already acts upon. Indeed, the conditional effective graph for an intervention to Alpelisib alone (plus the baseline cancer-state input variables) shown in SI Appendix, Fig. S16 reveals that the drugs Ipasertib, Neratinib, and Trametinib are rendered completely redundant—interestingly, Neratinib is actually redundant even without Alpelisib but just with the cancer cell-state baseline (SI Appendix, Fig. S15). This highlights how the effective graph methodology provides an analytical explanation of the causal relationships in the model; one does not need to run ensemble Monte Carlo simulations of the BN model to know that Ipasertib, Neratinib, and Trametinib have no effect on apoptosis and proliferation of ER+ cancer cells in this model when Alpelisib is present.
Finally, the case of Everolimus is also well explained by the effective graph. While it is very outwardly effective (largest in Fig. 5D), it also acts mostly on pathways already under downstream control by Alpelisib, as can be seen in Fig. 5A and in comparisons between the respective conditional effective graphs in SI Appendix, Figs. S16 and S17. Thus, while the simulations in ref. 26 report a very modest effect on apoptosis in synergy with Alpelisib ( increase), our results predict that, in this model, the effect on apoptosis of a combined intervention (Alpelisib alone) is causally negligible. It is noteworthy that Everolimus retains an effective edge to the (protein kinase B) pathway (via ), providing some control of a subset of this pathway not under Alpelisib control (the top left in Fig. 5A and SI Appendix, Fig. 19). Indeed, the spreading dynamics experiments summarized in Fig. 5C show that perturbations to Everolimus spread just a little farther than perturbations to Alpelisib. Everolimus is therefore not as redundant to the overall dynamics as are Ipasertib, Neratinib, and Trametinib. Moreover, it preserves very effective pathways to both the and pathways even at a high effectiveness threshold of 0.4 (SI Appendix, Fig. S13), which can play a part if Alpelisib becomes inactive.
It should be noted, similarly to the TBN model (Fig. 4D), that perturbation analysis of the ER+ breast cancer network for the seven drugs studied shows that the effective graph is always more correlated with impact on dynamics than is the interaction graph (SI Appendix, Fig. S14). Therefore, the inferences derived above from the effective graph are grounded on a more realistic description of the model’s true dynamics than inferences made directly from the interaction graph.
In summary, analysis of the effective graph and its dynamics provides a more complete understanding of why the seven drugs behave as reported in previous experiments with this model (26)—including why some are redundant. Removal of redundancy, furthermore, reveals analytically how canalization affects the mechanisms of apoptosis and proliferation of cancer cells in this model. In particular, some drugs are more effective than others due to how decoupled from overall dynamics their pathways become. Indeed, the breast cancer network is one of the most “fractured” of all of the experimentally validated biochemical models we studied—an issue we discuss in detail in SI Appendix, section 7 by studying their dynamical modularity via the analysis of strongly and weakly connected network components for all effectiveness threshold levels.
Discussion and Conclusion
The effective graph we introduce synthesizes both the causal interaction structure and the nonlinear dynamics of BNs into a single scalable graph formalism. We use 78 experimentally validated BN models from systems biology to demonstrate that biochemical interactions contain significantly more redundancy than expected by chance, and this leads to very canalized nonlinear dynamics. This observation is consistent with Waddington’s idea that canalization is pervasive in biological systems (25), whereby most random dynamical perturbations are not effective and only a few interactions control changes in network dynamics. This suggests that evolution in biological regulation has selected for redundancy, which has long been hypothesized as a requirement for the robustness to random perturbations that is necessary for evolvability (46, 47).
In addition to systems biology models, we use artificial models to show that effective graphs provide a more precise characterization of the (nonlinear) causal interaction logic of automata networks than do interaction graphs. These examples demonstrate that the effective graph is a better predictor of how perturbation signals propagate than is the original interaction graph, and thus, it is a useful construct to predict how control signals propagate. The effective graph can greatly aid the construction, refinement, and analysis of systems biology models by revealing how evidence from pairwise biochemical regulation experiments is integrated. Indeed, 22% of the biological models from the Cell Collective contain at least one fully redundant edge, and all contain much redundancy (19). Thus, the effective graph can aid in the simplification of biochemical network models to reveal their most essential regulatory pathways.
In comparison with the original automata networks, edge effectiveness reflects a loss of causal detail about which specific input combinations result in downstream variable-state changes. However, the effective graph is not proposed as a substitute for the causal interaction details that the original automata network contains. It is rather a revision of the original interaction graph that provides a much more precise, probabilistic accounting of causal dynamics and can be conditioned on different input assumptions with the conditional effective graph. Therefore, the loss of specific causal detail yields a powerful approach for analysts who want to identify the most effective intervention strategies, those most likely to steer dynamics to desirable behavior.
Other methods have been proposed to integrate structure and dynamics into enhanced network representations. The general idea is to capture all of the possible roles that variables and interactions play in the logic of automata networks with additional formalism such as hyperedges (48) or distinct node types for variable states (49). The removal of redundancy via Boolean minimization can also be used to obtain parsimonious enhanced network representations, as shown in previous work (17). While these methods can preserve all possible causal interactions, even the rarest ones, they increase the complexity of the network representation. In contrast, the effective graph is a directed, weighted graph with a single node type, which is simpler and more amenable to the well-known graph-theoretical analysis and methods of network science (50). Moreover, the node- and edge-level effectiveness parameters are directly interpretable and provide an aggregate but accurate quantification of the causal pathways that are of greater interest for analysis and intervention in biochemical networks.
Without additional knowledge, our probabilistic characterization first assumes a uniform distribution over the likelihood of all input-state combinations to a given automaton. While this assumption is valid for automata in isolation, the presence of a biologically relevant subset of states or the convergence of dynamics onto attractors can alter the distribution of input states. The conditional effective graph allows us to explore such distinct input assumptions—as we do to study the causal roles of specific drugs in the cellular processes involved in ER+ breast cancer. It also provides a promising direction for future work toward integrating the dynamically evolving likelihood of input states into a temporal effective graph.
Because we are interested in studying the (ontogenetic) dynamics of specific biochemical regulation systems, we focus on dynamical perturbations that change the state of biochemical variables. In future work, the effective graph is likely to be very useful to study the impact of structural perturbations, such as edge deletions or changes in logical transition rules (14). Indeed, one would expect greater dynamical disruptions from structural perturbations to effective pathways than to redundant pathways (20). Thus, our methodology can also be a tool to study the robustness and evolvability of function in biochemical networks—including developmental and disease control—especially in synergy with methods that hitherto have used only the original interaction graph (1, 38, 42, 43).
To demonstrate that the effective graph is useful in designing interventions in a specific systems biology model of development, disease, and biochemical regulation, we focus on the analysis of a small BN model of flower development, A. thaliana, as well as a large BN model of signal transduction in a model of ER+ breast cancer. In these models, the effective graph allows us to demonstrate how different biochemical molecules or signals control dynamics. Whereas existing methods can identify driver variables that control dynamics, we show that by removing dynamical redundancy, the effective graph not only can help identify a more precise (smaller) set of driver variables but can also show how these variables function. For instance, our method distinguishes between an autoregulator gene () that is only needed to control itself and a master regulator gene () that controls most of the A. thaliana network. This enhanced explainability can also be used to reveal alternative, actionable control strategies, such as using or instead of or to control the Thaliana model.
Similarly, the effective graph of the ER+ breast cancer model allows us to understand why and how some PI3K inhibitor drugs are more effective than others at controlling apoptosis or growth. Specifically, the methodology provides an analytical explanation of the causal relationships that arise in the macrolevel network dynamics rather than observations from Monte Carlo simulations. This allows us to show analytically how Fulvestrant synergizes with Alpelisib to best control the cancer cell line model, as well as why several drugs in the model are completely redundant. Such accurate explanations of how control interventions propagate throughout a biochemical system are important for the design of advanced disease therapeutics (39). Indeed, explainability is an important feature to derive actionable complex systems models in biomedicine and elsewhere. It can lead not only to model refinement (for example, by testing and potentially removing interactions predicted to be redundant) but also, to a deeper understanding of how causal, nonlinear, microlevel interactions integrate to define macrolevel biological functions. Our approach thus enhances understanding of multilevel complexity in biochemical regulation and multivariate dynamical systems at large.
Data and Code Availability
All simulations and data used to support the findings of this study are freely available in the CANA package (31) or the Cell Collective (9).
Supplementary Material
Acknowledgments
We thank Santosh Manicka and Manuel Marques-Pita for helpful discussions, Deborah Rocha for editing the manuscript, and Alice Grishchenko for graphics consultation. R.B.C. was partially funded by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) Grant 18668127 and Fundação para a Ciência e a Tecnologia (FCT) Grant PTDC/MEC-AND/30221/2017. L.M.R. was partially funded by NIH, National Library of Medicine Grant 1R01LM012832; by a Fulbright Commission fellowship; and by National Science Foundation Research Traineeship “Interdisciplinary Training in Complex Networks and Systems” Grant 1735095. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
See online for related content such as Commentaries.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2022598118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or SI Appendix.
References
- 1.Zanudo J. G. T., Yang G., Albert R., Structure-based control of complex networks with nonlinear dynamics. Proc. Natl. Acad. Sci. U.S.A. 114, 7234–7239 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Klamt S., Haus U. U., Theis F., Hypergraphs and cellular networks. PLoS Comput. Biol. 5, e1000385 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Reichhardt C. J. O., Bassler K. E., Canalization and symmetry in Boolean models for genetic regulatory networks. J. Phys. Math. Theor. 40, 4339–4350 (2007). [Google Scholar]
- 4.Gates A. J., Gysi D. M., Kellis M., Barabási A. L., A wealth of discovery built on the human genome project—by the numbers. Nature 590, 212–215 (2021). [DOI] [PubMed] [Google Scholar]
- 5.Perez-Perez J. M., Candela H., Micol J. L., Understanding synergy in genetic interactions. Trends Genet. 25, 368–376 (2009). [DOI] [PubMed] [Google Scholar]
- 6.Davidson E., Levin M., Gene regulatory networks. Proc. Natl. Acad. Sci. U.S.A. 102, 4935 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bornholdt S., Boolean network models of cellular regulation: Prospects and limitations. J. R. Soc. Interface 5, S85–S94 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Li F., Long T., Lu Y., Ouyang Q., Tang C., The yeast cell-cycle network is robustly designed. Proc. Natl. Acad. Sci. U.S.A. 101, 4781–4786 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Helikar T., et al. , The cell collective: Toward an open and collaborative approach to systems biology. BMC Syst. Biol. 6, 96 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chechik G., et al. , Activity motifs reveal principles of timing in transcriptional control of the yeast metabolic network. Nat. Biotechnol. 26, 1251–1259 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Choi M., Shi J., Zhu Y., Yang R., Cho K. H., Network dynamics-based cancer panel stratification for systemic prediction of anticancer drug response. Nat. Commun. 8, 1940 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kurten K. E., Correspondence between neural threshold networks and Kauffman Boolean cellular automata. J. Phys. Math. Gen. 21, L615 (1988). [Google Scholar]
- 13.Albert R., Thakar J., Boolean modeling: A logic-based dynamic approach for understanding signaling and regulatory networks and for making useful predictions. Wiley Interdiscip. Rev. Syst. Biol. Med. 6, 353–369 (2014). [DOI] [PubMed] [Google Scholar]
- 14.Kauffman S. A., The Origins of Order: Self-Organization and Selection in Evolution (OUP USA, 1993). [Google Scholar]
- 15.Gershenson C., Guiding the self-organization of random Boolean networks. Theor. Biosci. 131, 181–191 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Marshall W., Kim H., Walker S. I., Tononi G., Albantakis L., How causal analysis can reveal autonomy in models of biological systems. Phil. Trans. Math. Phys. Eng. Sci. 375, 20160358 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Marques-Pita M., Rocha L. M., Canalization and control in automata networks: Body segmentation in Drosophila melanogaster. PloS One 8, e55946 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Aldana M., Boolean dynamics of networks with scale-free topology. Phys. Nonlinear Phenom. 185, 45–66 (2003). [Google Scholar]
- 19.Manicka S., Marques-Pita M., Rocha L. M., Effective connectivity determines the critical dynamics of biochemical networks. arXiv[Preprint] (2021). https://arxiv.org/abs/2101.08111 (Accessed 22 January 2021). [DOI] [PMC free article] [PubMed]
- 20.Gates A. J., Rocha L. M., Control of complex networks requires both structure and dynamics. Sci. Rep. 6, 24456 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bérenguier D., et al. , Dynamical modeling and analysis of large cellular regulatory networks. Chaos 23, 025114 (2013). [DOI] [PubMed] [Google Scholar]
- 22.Kauffman S. A., Metabolic stability and epigenesis in randomly constructed genetic nets. J. Theor. Biol. 22, 437–467 (1969). [DOI] [PubMed] [Google Scholar]
- 23.Thomas R., Boolean formalization of genetic control circuits. J. Theor. Biol. 42, 563–585 (1973). [DOI] [PubMed] [Google Scholar]
- 24.Kauffman S., Peterson C., Samuelsson B., Troein C., Genetic networks with canalyzing Boolean rules are always stable. Proc. Natl. Acad. Sci. U.S.A. 101, 17102–17107 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Waddington C. H., Canalization of development and the inheritance of acquired characters. Nature 150, 563–565 (1942). [Google Scholar]
- 26.Zañudo J., Scaltriti M., Albert R., A network modeling approach to elucidate drug resistance mechanisms and predict combinatorial drug treatments in breast cancer. Canc. Converg. 1, 5 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Espinosa-Soto C., Padilla-Longoria P., Alvarez-Buylla E. R., A gene regulatory network model for cell-fate determination during Arabidopsis thaliana flower development that is robust and recovers experimental gene expression profiles. Plant Cell 16, 2923–2939 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chaos Á., et al. , From genes to flower patterns and evolution: Dynamic models of gene regulatory networks. J. Plant Growth Regul. 25, 278–289 (2006). [Google Scholar]
- 29.McCluskey E. J., Minimization of Boolean functions. Bell. Syst. Tech. J. 35, 1417–1444 (1956). [Google Scholar]
- 30.Shmulevich I., Kauffman S. A., Activities and sensitivities in Boolean network models. PRL 93, 048701 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Correia R. B., Gates A. J., Wang X., Rocha L. M., Cana: A python package for quantifying control and canalization in Boolean networks. Front. Physiol. 9 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.James R., Crutchfield J., Multivariate dependence beyond Shannon information. Entropy 19, 531 (2017). [Google Scholar]
- 33.Kolchinsky A., Lourenco A., Wu H. Y., Li L., Rocha L. M., Extraction of pharmacokinetic evidence of drug-drug interactions from the literature. PloS One 10, e0122199 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kadelka C., Kuipers J., Laubenbacher R., The influence of canalization on the robustness of Boolean networks. Phys. Nonlinear Phenom. 353, 39–47 (2017). [Google Scholar]
- 35.Kolchinsky A., Gates A. J., Rocha L. M., Modularity and the spread of perturbations in complex dynamical systems. Phy. Rev. E 92, 060801 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Santolini M., Barabási A. L., Predicting perturbation patterns from the topology of biological networks. Proc. Natl. Acad. Sci. U.S.A. 115, E6375–E6383 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Luque B., Solé R. V., Lyapunov exponents in random Boolean networks. Phys. Stat. Mech. Appl. 284, 33–45 (2000). [Google Scholar]
- 38.Liu Y. Y., Slotine J. J., Barabási A. L., Controllability of complex networks. Nature 473, 167–173 (2011). [DOI] [PubMed] [Google Scholar]
- 39.Zhang R., et al. , Network model of survival signaling in large granular lymphocyte leukemia. Proc. Natl. Acad. Sci. U.S.A. 105, 16308–16313 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wang R. S., Albert R., Elementary signaling modes predict the essentiality of signal transduction network components. BMC Syst. Biol. 5, 44 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Akutsu T., Hayashida M., Ching W. K., Ng M. K., Control of Boolean networks: Hardness results and algorithms for tree structured networks. J. Theor. Biol. 244, 670–679 (2007). [DOI] [PubMed] [Google Scholar]
- 42.Nacher J. C., Akutsu T., Structural controllability of unidirectional bipartite networks. Sci. Rep. 3, 1647 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Fiedler B., Mochizuki A., Kurosawa G., Saito D., Dynamics and control at feedback vertex sets. I. Informative and determining nodes in regulatory networks. J. Dynam. Differ. Eq. 25, 563–604 (2013). [DOI] [PubMed] [Google Scholar]
- 44.Chan S. S. K., Kyba M., What is a master regulator? J. Stem Cell Res. Ther. 3, 1000e114 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Saadatpour A., et al. , Dynamical and structural analysis of a T cell survival network identifies novel candidate therapeutic targets for large granular lymphocyte leukemia. PLoS Comput. Biol. 7, e1002267 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Conrad M., The geometry of evolution. Biosystems 24, 61–81 (1990). [DOI] [PubMed] [Google Scholar]
- 47.Pigliucci M., Is evolvability evolvable? Nat. Rev. Genet. 9, 75–82 (2008). [DOI] [PubMed] [Google Scholar]
- 48.Klamt S., Saez-Rodriguez J., Lindquist J. A., Simeoni L., Gilles E. D., A methodology for the structural and functional analysis of signaling and regulatory networks. BMC Bioinf. 7, 56 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yang G., Gómez Tejeda Zañudo J., Albert R., Target control in logical models using the domain of influence of nodes. Front. Physiol. 9, 454 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Barabási A. L., et al. , Network Science (Cambridge University Press, 2016). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All simulations and data used to support the findings of this study are freely available in the CANA package (31) or the Cell Collective (9).
All study data are included in the article and/or SI Appendix.