Abstract
Accurate description of finite-temperature vibrational dynamics is indispensable in the computation of two-dimensional electronic spectra. Such simulations are often based on the density matrix evolution, statistical averaging of initial vibrational states, or approximate classical or semiclassical limits. While many practical approaches exist, they are often of limited accuracy and difficult to interpret. Here, we use the concept of thermo-field dynamics to derive an exact finite-temperature expression that lends itself to an intuitive wavepacket-based interpretation. Furthermore, an efficient method for computing finite-temperature two-dimensional spectra is obtained by combining the exact thermo-field dynamics approach with the thawed Gaussian approximation for the wavepacket dynamics, which is exact for any displaced, distorted, and Duschinsky-rotated harmonic potential but also accounts partially for anharmonicity effects in general potentials. Using this new method, we directly relate a symmetry breaking of the two-dimensional signal to the deviation from the conventional Brownian oscillator picture.
Multidimensional optical spectroscopy is an emerging experimental method for studying molecular photochemistry and photophysics, but its further development and the interpretation of new experiments rely heavily on theoretical modeling.1−7 To this end, a number of theoretical methods8−15 were developed to account for typical vibrational–electronic effects occurring in molecular systems, such as anharmonicity, different curvatures of the ground- and excited-state potential energy surfaces, or mode–mode mixing (Duschinsky rotation).16−20 In its original formulation, the second-order cumulant expansion21−24 is exact only for the Brownian oscillator (i.e., displaced harmonic) model and cannot treat the intermode coupling in the excited state. Although this basic molecular model shaped our understanding of steady-state, ultrafast, and multidimensional electronic spectroscopy in the past decades, it is inadequate for many molecules that exhibit Duschinsky and anharmonicity effects.12,14 Similar limitations are met when using the semiclassical phase averaging,22,25 also known as the Wigner-averaged classical limit26−30 or dephasing representation.31−34 The recently developed third-order cumulant approach seems to overcome these limitations,10,13,14 yet it is accurate only in systems with weakly coupled or distorted modes.14
In contrast, quantum dynamics methods35−40 are well suited for describing the evolution of nuclear wavepackets but often neglect temperature effects. To avoid the impractical Boltzmann averaging over the initial states, a number of alternative strategies for including temperature in wavepacket-based methods have been proposed.41−47 We turn to the so-called thermo-field dynamics,48,49 which transforms the von Neumann evolution of a density matrix to a Schrödinger equation with a doubled number of degrees of freedom. This approach has only recently been introduced in chemistry for solving the electronic structure,50−52 vibronic,53−56 and spectroscopic57 problems at finite temperature. Here, we show how it could be used to compute two-dimensional vibronic spectra. The finite-temperature treatment is combined with the thawed Gaussian approximation,58 an efficient first-principles59,60 method for wavepacket propagation, and applied to the stimulated emission and ground-state bleach signals of azulene.
In two-dimensional spectroscopy, a nonlinear time-dependent polarization22,61
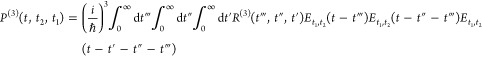 |
1 |
is induced in the sample through interaction with the electric field Et1,t2(t) comprised of three light pulses centered at times –t2 – t1, −t2, and 0, where t1 is the delay between the first two pulses, t2 is the delay between the second and third pulses, and R(3)(t‴, t″, t′) is the third-order response function.22 In a heterodyne detection scheme, the measured signal is61
| 2 |
where ELO(t) is the fourth, local oscillator pulse centered at time t3 after the third pulse. The two-dimensional spectrum is obtained by scanning S(t3, t2, t1) as a function of the three time delays and Fourier transforming over t1 and t3. We focus on the absorptive two-dimensional spectrum62,63
| 3 |
and assume ultrashort and nonoverlapping pulse approximations, where the rephasing and nonrephasing spectra61
| 4 |
| 5 |
are defined through
| 6 |
| 7 |
and
| 8 |
In eq 8, Ĥj terms
are the vibrational Hamiltonians corresponding to the ground (j = 1) and excited (j = 2 or 3) electronic
states, ρ̂ = exp(−βĤ1)/Tr[exp(−βĤ1)] is the vibrational density operator at temperature T = 1/kBβ, and 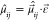 is the electronic transition dipole moment
between electronic states i and j projected on the polarization unit vector ε⃗ of the external electric field. Correlation function C1 corresponds to the stimulated emission and ground-state
bleach processes, while C3, which involves
a higher excited electronic state, corresponds to the excited-state
absorption (see section 1 of the Supporting Information). Although the excited-state absorption term involves, in general,
a sum over several higher excited states (i ≥
3), here, for the sake of brevity, we consider only one such state.
is the electronic transition dipole moment
between electronic states i and j projected on the polarization unit vector ε⃗ of the external electric field. Correlation function C1 corresponds to the stimulated emission and ground-state
bleach processes, while C3, which involves
a higher excited electronic state, corresponds to the excited-state
absorption (see section 1 of the Supporting Information). Although the excited-state absorption term involves, in general,
a sum over several higher excited states (i ≥
3), here, for the sake of brevity, we consider only one such state.
An intuitive physical interpretation of eq 8 is available in the zero-temperature limit, where the density operator ρ̂ = |1,g⟩⟨1,g| is given in terms of the ground vibrational state |1,g⟩ of the ground electronic state. Then40
| 9 |
where
| 10 |
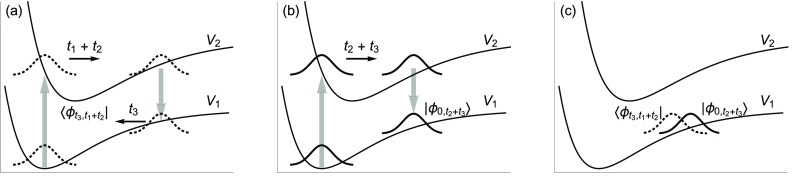
Ĥi′ = Ĥi – ℏω1,g, and ℏω1,g = ⟨1,g|Ĥ1|1,g⟩. In Figure 1, we illustrate how eq 9 is evaluated for stimulated emission contribution C1(t1 + t2, t3, t2 + t3) (eq 8) to the rephasing signal (eq 6). The bra nuclear wavepacket is first evolved for a time τa = t1 + t2 in the excited electronic state and then for a time τb = t3 in the ground state; the ket wavepacket is in the ground electronic state during t1 and evolves in the excited state for a time τc = t2 + t3. In general, during time delays t1 and t3, also known as coherence and detection times, the bra and ket wavepackets evolve on different potential energy surfaces; during the so-called population time t2, the two wavepackets are in the same electronic state: in the ground state for the ground-state bleach contribution and in the excited electronic state for the stimulated emission and excited-state absorption components.
Figure 1.
Evolution of the bra (a, dotted line) and ket (b, solid line) wavepackets of eq 9 for τa = t1 + t2, τb = t3, and τc = t2 + t3. Their overlap (c) is stimulated emission term C1(t1 + t2, t3, t2 + t3) (eq 8) of rephasing signal SR(t3, t2, t1) (eq 6).
We now address the question of whether it is possible to retain the simple wavepacket picture without neglecting finite-temperature effects. To answer this question in the affirmative, we employ thermo-field dynamics, which maps the evolution of a density operator at finite temperature to the evolution of a wave function with a doubled number of coordinates. In the thermo-field dynamics theory,48 the thermal vacuum is defined as
| 11 |
where |kk̃⟩ = |k⟩|k̃⟩ is the basis vector of the tensor-product space obtained from the physical (with basis {|k⟩}) and “fictitious” (with basis {|k̃⟩}) Hilbert spaces. We note that physical operators (denoted only by a hat ^, such as ρ̂ or μ̂) act only on the physical subspace. With these definitions, eq 8 can be rewritten as
| 12 |
where
| 13 |
is the analogue of |ϕτ,t(i)⟩ from eq 10
| 14 |
is the Hamiltonian acting in the full, tensor-product
space, and 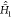 is the ground-state
vibrational Hamiltonian
acting in the fictitious space only. The proof of eq 12 goes as follows:
is the ground-state
vibrational Hamiltonian
acting in the fictitious space only. The proof of eq 12 goes as follows:
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
| 20 |
Equation 15 is obtained from eq 12 by inserting the definition (eq 13) of 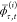 , while eq 16 results upon substituting eq 11 for |0̅(β)⟩; in going from eq 16 to eq 17, we used
the fact that operators acting in different subspaces commute. In
going from eq 17 to eq 18, we used the conjugation
rules relating the physical and fictitious spaces (see section 2 of the Supporting Information). The
resolution of identity and commutation of ρ̂1/2 with Ĥ1 were used to obtain eq 19, and the definition
and cyclic property of the trace to obtain eq 20.
, while eq 16 results upon substituting eq 11 for |0̅(β)⟩; in going from eq 16 to eq 17, we used
the fact that operators acting in different subspaces commute. In
going from eq 17 to eq 18, we used the conjugation
rules relating the physical and fictitious spaces (see section 2 of the Supporting Information). The
resolution of identity and commutation of ρ̂1/2 with Ĥ1 were used to obtain eq 19, and the definition
and cyclic property of the trace to obtain eq 20.
Remarkably, the result (eq 12) has exactly the same form as the zero-temperature expression (eq 9) and can be interpreted as in Figure 1. It also allows finite-temperature effects to be included in regular wave function-based codes, by modifying only the definition of the initial state and the Hamiltonians under which this state is evolved. In section 3 of the Supporting Information, we prove that the same wavepacket picture can be justified even beyond the Born–Oppenheimer approximation, which was invoked implicitly in eqs 6–8. To avoid exponentially scaling exact quantum methods on precomputed potential energy surfaces64−67 or computationally demanding multiple-trajectory68−82 approaches, we propose using the simple, yet efficient, single-trajectory thawed Gaussian approximation, which can be interfaced with on-the-fly ab initio evaluation of potential energy information.83
Let us consider a Gaussian wavepacket
| 21 |
where qt and pt are the real, D-dimensional expectation values of the position and momentum, respectively, At is a D × D complex symmetric matrix with a positive-definite imaginary part, γt is a complex scalar whose imaginary part ensures normalization of the wavepacket, and D is the number of coordinates. Within the thawed Gaussian approximation,58 one replaces true potential energy V(q) by its local harmonic approximation
| 22 |
about the center qt of the wavepacket, which leads to the following equations of motion for the Gaussian’s parameters:58,84
| 23 |
| 24 |
| 25 |
| 26 |
where Lt = ptT·(2m)−1·pt – V(qt) is the Lagrangian along the trajectory (qt, pt) and m is the symmetric mass matrix. According to eqs 23–26, the position and momentum of the Gaussian wavepacket evolve classically, while matrix At depends on the Hessians along the classical trajectory. The described evolution of the Gaussian wavepacket is exact for a harmonic potential because the local Taylor expansion of eq 22 becomes exact in this case. For more general, anharmonic potentials, the method is only approximate, but typically accurate for moderate anharmonicity and short times, which makes it practical in spectroscopic applications.58−60,85,86 Although the thawed Gaussian propagation is not suited for nonadiabatic dynamics, it can treat accurately the effects that arise due to different force constants of the ground- and excited-state potential surfaces: mode distortion, i.e., the change in the frequency of a normal mode, and intermode coupling or Duschinsky rotation. The on-the-fly ab initio thawed Gaussian approximation, which uses electronic structure calculations to compute potential energies, gradients, and Hessians only when needed, was recently validated for the simulation of finite-temperature linear57 and zero-temperature two-dimensional spectra.40
To construct the initial state, we approximate
the ground-state
potential energy surface by a harmonic potential and use the corresponding
mass-scaled normal mode coordinates. Then, in the zero-temperature
limit, the initial state ψ0(q) =
⟨q|1,g⟩ is a Gaussian
(eq 21) and D = F, where F is the
number of vibrational degrees of freedom. In the thermo-field dynamics
formulation, D = 2F, the initial
state ψ̅0(q̅) = ⟨q̅|0̅(β)⟩ is also a Gaussian, and q̅ = (q, q̃) is the 2F-dimensional coordinate vector.57 To solve the equations of motion in the finite-temperature
picture, we need the potential energies, gradients, and Hessians in
the extended coordinate space, which can be easily formulated in terms
of the energies, gradients, and Hessians of the two potential energy
surfaces, as shown in ref (57). Remarkably, the thermo-field dynamics under Hamiltonian 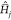 (eq 14) requires exactly the same classical
trajectory, in electronic
state j, as the conventional, zero-temperature thawed
Gaussian propagation with Hamiltonian Ĥj.57 No further
ab initio evaluations are needed for the finite-temperature implementation,
meaning that, within the thawed Gaussian approximation, the temperature
effects can be included almost for free. The only difference in the
computational cost is in solving the equations of motion with 2F rather than F coordinates, which is approximately
23 = 8 times more expensive due to the roughly cubic scaling
of the involved matrix operations, including matrix–matrix
multiplication and matrix inverse. This cost is, however, negligible
compared to the cost of electronic structure calculations.
(eq 14) requires exactly the same classical
trajectory, in electronic
state j, as the conventional, zero-temperature thawed
Gaussian propagation with Hamiltonian Ĥj.57 No further
ab initio evaluations are needed for the finite-temperature implementation,
meaning that, within the thawed Gaussian approximation, the temperature
effects can be included almost for free. The only difference in the
computational cost is in solving the equations of motion with 2F rather than F coordinates, which is approximately
23 = 8 times more expensive due to the roughly cubic scaling
of the involved matrix operations, including matrix–matrix
multiplication and matrix inverse. This cost is, however, negligible
compared to the cost of electronic structure calculations.
Formally, the propagation of the wavepacket according to eqs 23–26 requires not only the potential energies and gradients but also the Hessians at each step of the dynamics. In this work, we employed the single-Hessian method,87 which further approximates V″(qt) ≈ V″(qref) in eq 25, where qref is a reference geometry at which the Hessian of the excited-state potential surface is evaluated once and reused during the excited-state dynamics. Because the center of the wavepacket still follows the fully anharmonic classical trajectory, the single-Hessian version partially includes anharmonicity effects; in several examples studied in ref (87), the accuracy of this method was shown to be similar to that of the thawed Gaussian approximation. Here, we chose qref as the excited-state minimum. The ground-state potential surface was assumed to be harmonic in all simulations.
To analyze the effects of the excited-state anharmonicity, we compare the anharmonic calculations, based on the on-the-fly single-Hessian thawed Gaussian approximation for the excited-state propagation, with the harmonic model (also called the generalized Brownian oscillator model), where the excited-state potential surface is approximated by a harmonic potential fitted to the surface at its minimum (so-called adiabatic harmonic or adiabatic Hessian scheme). In the mass-scaled normal mode coordinates of the ground state, the excited-state force constant is a symmetric, nondiagonal matrix, whose off-diagonal terms reflect intermode couplings, also known as Duschinsky mixing. To study the effects of the difference between the excited- and ground-state force constants on linear and two-dimensional spectra, we construct the displaced harmonic model (also called the Brownian oscillator model), where the excited-state force constant is approximated by the force constant in the ground electronic state. This model neglects mode distortion and Duschinsky effects. The two-dimensional spectra can be computed exactly with the thawed Gaussian propagation, as described above, for both harmonic and displaced harmonic oscillator models. Whereas the exact solution to the displaced harmonic oscillator model was known before in the form of the second-order cumulant expansion,22 to the best of our knowledge, no method has been published for computing exactly the two-dimensional spectra of the global harmonic (or generalized Brownian oscillator) model.14
Azulene is a well-known example of a Kasha-violating molecule,88 as it emits light from the second, rather than first, excited electronic state. This is due to the interplay of two factors:89 (i) weak nonadiabatic coupling between states S1 and S2 and (ii) fast (≈1 ps) nonradiative decay from S1 to S0. These properties make azulene one of the key building blocks in the synthesis of novel optoelectronic materials.90 Although nonadiabatic couplings between the ground and first excited states play an important role in the photoinduced dynamics of azulene,89 they do not affect its vibrationally resolved S1 ← S0 absorption spectrum. Indeed, the linear absorption spectrum can be reproduced well using adiabatic, Born–Oppenheimer approaches that neglect nonadiabatic effects.89,91,92 Here, we also ignore the nonadiabatic effects on the two-dimensional spectra, which we compute only at short t2 delay times. In the results, we focus on the ground-state bleach and stimulated emission contributions to the two-dimensional spectrum (the first two terms on the right-hand sides of eqs 6 and 7); according to the oscillator strengths of the S1–S0 (0.009)93−95 and S2–S1 (≈10–5)94,95 transitions, the excited-state absorption is expected to be ∼3 orders of magnitude weaker.
In Figure 2 (top), we compare linear absorption spectra simulated at 300 and 0 K with the experimental spectrum recorded at room temperature. One of the main effects of temperature is the broadening of the spectral features, which also affects the relative intensities of vibronic peaks, namely, those at 14300 and 15800 cm–1. These intensities are overestimated in the zero-temperature spectrum but corrected by the finite-temperature treatment.
Figure 2.
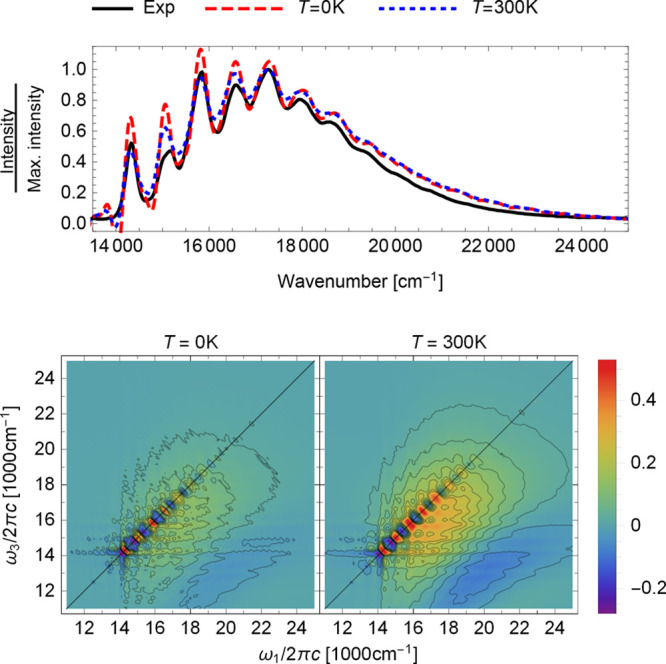
S1 ← S0 absorption spectra of azulene (top) computed with the on-the-fly ab initio single-Hessian thawed Gaussian approximation at zero temperature (red, dashed) and at 300 K (blue, dotted), compared with the experimental spectrum (black, solid) recorded at room temperature in cyclohexane.89 Absorptive two-dimensional electronic spectra (bottom) (eq 3) at zero delay time (t2 = 0), computed at zero temperature (left) and 300 K (right). Each two-dimensional spectrum shows the sum of the ground-state bleach and stimulated emission terms (first two terms on the right-hand sides of eqs 6 and 7) corresponding to the S1–S0 electronic transition in azulene. See Figure S1 for the rephasing and nonrephasing contributions to these spectra and Figures S3 and S4 for the spectra at delays t2 > 0.
A non-zero temperature has an even stronger effect on the two-dimensional spectrum (Figure 2, bottom). The zero-temperature spectrum is composed of sharp vibronic peaks, which are broadened and less resolved in the spectrum computed at 300 K. As in the linear spectrum, the temperature effects modify not only the resolution of the spectrum but also the relative intensities of the peaks. However, in contrast to the linear absorption spectrum, where these differences affect only a few peaks and could still be considered acceptable, the two-dimensional spectrum is strongly affected due to the increased complexity of spectral features.
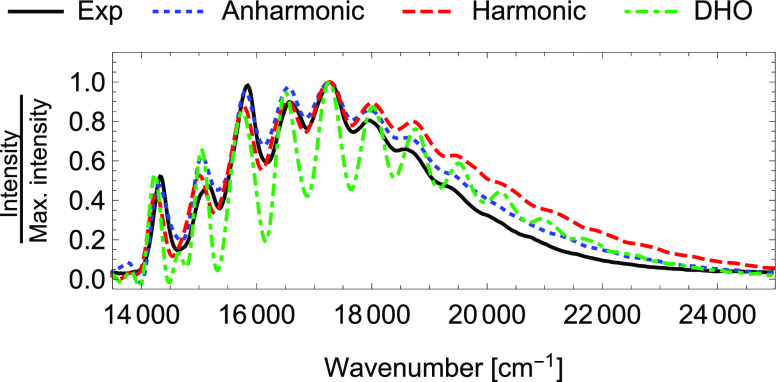
To investigate the effects of anharmonicity, mode distortion, and mode–mode coupling, we first compare the linear absorption spectra computed using three models with different accuracies (see Figure 3). The spectrum computed with the displaced harmonic oscillator model displays a highly regular intensity pattern, as opposed to the irregular intensities found in the experiment, and overestimates the frequency spacing between the peaks. The results are largely improved by including Duschinsky coupling and changes in the mode frequencies through the global harmonic model. However, the harmonic approximation suffers from an overly broad tail in the high-frequency region. This is further corrected by accounting for the anharmonicity effects with the on-the-fly thawed Gaussian approximation.
Figure 3.
S1 ← S0 absorption spectra of azulene computed with the on-the-fly ab initio single-Hessian thawed Gaussian approximation (“Anharmonic”, blue, dotted), harmonic approximation (red, dashed), and displaced harmonic oscillator (DHO) model (green, dashed–dotted) at 300 K, compared with the experimental spectrum (black, solid) recorded at room temperature in cyclohexane.89
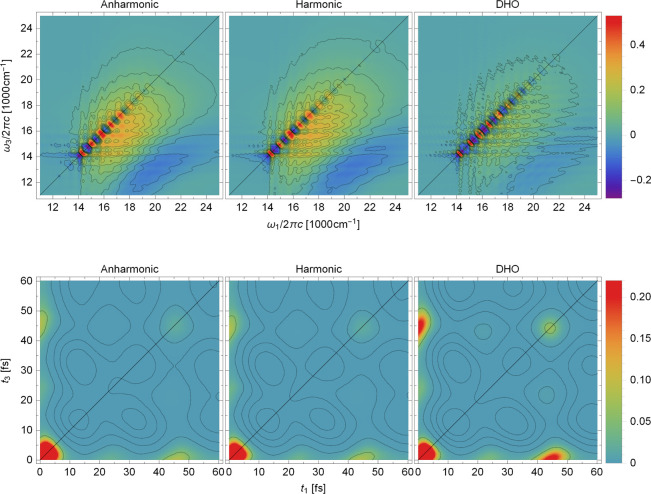
The corresponding two-dimensional spectra (Figure 4, top) exhibit similar differences, which we can conveniently analyze in the time domain [see Figure 4, bottom, for |SR(t3, 0, t1)| and Figure S6 for |SNR(t3, 0, t1)|]. The displaced harmonic oscillator model results in stronger recurrences after 45 fs (in t1, t3, or both t1 and t3) than the harmonic or anharmonic approaches. This translates into sharper peaks in the two-dimensional spectrum. The anharmonic spectrum extends less into the high-frequency region, compared to the harmonic and displaced harmonic oscillator models, because the thawed Gaussian propagation gives a slower initial decay (for t1 and t3 < 6 fs) in the time domain than the models that neglect anharmonicity (see Figure S5). Subtle differences between the harmonic and anharmonic excited-state dynamics affect the peak intensities in the region between 15000 and 18000 cm–1.
Figure 4.
Absorptive two-dimensional electronic spectra (top) (eq 3) at zero delay time (t2 = 0), computed with the on-the-fly ab initio single-Hessian thawed Gaussian approximation (“Anharmonic”, left), harmonic approximation (middle), and displaced harmonic oscillator (DHO) model (right) at 300 K. Each spectrum shows the sum of the ground-state bleach and stimulated emission terms (first two terms on the right-hand sides of eqs 6 and 7) corresponding to the S1–S0 electronic transition in azulene. See Figure S2 for the rephasing and nonrephasing contributions to these spectra and Figures S3 and S4 for the spectra at delays t2 > 0. First 60 fs of |SR(t3, 0, t1)| (bottom) (eq 6). See Figure S6 for |SNR(t3, 0, t1)|.
Interestingly, for the displaced harmonic oscillator model, |SR(t3, 0, t1)| is symmetric with respect to the diagonal (Figure 4, bottom right), which does not hold when mode distortion, rotation, and anharmonicity are included (Figure 4, bottom left and middle). We prove this analytically in sections 7 and 8 of the Supporting Information, where we also demonstrate that the asymmetry can appear only in rephasing signal |SR(t3, 0, t1)|. Moreover, we show that the (incorrect) symmetry of |SRDHO(t3, 0, t1)| with respect to the diagonal t1 = t3 is, more generally, imposed by the second-order cumulant approximation,22 which is exact for the displaced harmonic oscillator model and is employed regularly to model two-dimensional spectra.23,24,96,97 Hence, the second-order cumulant method cannot account for the asymmetry induced by the deviation from the displaced harmonic oscillator model. This erroneous qualitative behavior was difficult to study in the past, partly due to the absence of practical methods that could easily go beyond the second-order cumulants or Brownian oscillators.
In conclusion, we derived a general and exact expression for computing finite-temperature vibrationally resolved two-dimensional electronic spectra with wave function-based methods. The inclusion of temperature is the key to simulating spectra of larger systems or solvated molecules, due to the multitude of low-frequency modes that are thermally excited at room temperature. By combining the exact expression with the thawed Gaussian approximation, we developed a practical and efficient method for computing two-dimensional spectra beyond zero temperature and beyond the displaced harmonic oscillator model. With the help of the newly developed method, we identified an asymmetry in the time domain signal that could serve as evidence for the changes in mode frequencies, mode–mode coupling, or anharmonicity. This asymmetry cannot be described with the conventional and widely used second-order cumulant approach.
Computational Methods
The ground electronic state of azulene was modeled at the second-order Møller–Plesset (MP2) perturbation theory level; the first excited state was modeled using the second-order Laplace-transformed density-fitted local algebraic diagrammatic construction [LT-DF-LADC(2)] scheme,98−101 as implemented in the Molpro 2015 package.102 The cc-pVDZ basis set was used throughout (see ref (89)). We first evaluated the Hessians in the ground and excited states at the respective optimized geometries. Then, starting from the minimum of the ground state, an on-the-fly ab initio classical trajectory was evolved in the excited electronic state for 1130 steps with a time step of 8 au ≈ 0.19 fs (total time of ≈219 fs).
Linear spectra were computed by Fourier transforming the first 500 steps of the wavepacket autocorrelation function (see ref (83)). With regard to the simulation of two-dimensional spectra, t1 and t3 times were propagated up to ≈106 fs (500 steps); t2 delays ranged from 0 (results shown in the main text) to 25 fs (130 steps), in intervals of 5 fs or 26 steps. Condon approximation, which was justified for the S1 ← S0 absorption of azulene in ref (89), was employed. Gaussian broadening with a half-width at half-maximum of 90 cm–1 was used in both linear and two-dimensional spectra. Linear spectra were shifted in frequency and scaled in intensity to match at the maximum intensity peak of the experiment; two-dimensional spectra were shifted by the same frequency shifts as the linear absorption spectra and scaled according to the maximum of the fully absorptive two-dimensional spectrum (eq 3).
Data supporting this publication can be found at 10.5281/zenodo.4552858.
Acknowledgments
The authors acknowledge the financial support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement 683069-MOLEQULE) and from the Swiss National Science Foundation through the NCCR MUST (Molecular Ultrafast Science and Technology) Network.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.1c00123.
Derivation of eqs 6–8, conjugation rules in thermo-field dynamics, thermo-field dynamics expression beyond the Born–Oppenheimer approximation, rephasing and nonrephasing contributions to the spectra of Figures 2 (bottom) and 4 (top), two-dimensional spectra at t2 > 0, |SR(t3, 0, t1)| at short times, (a)symmetry of the rephasing and nonrephasing spectra in the time domain, and proof of the symmetry of the two-dimensional signal within the second-order cumulant approximation (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Yuen-Zhou J.; Aspuru-Guzik A. Quantum process tomography of excitonic dimers from two-dimensional electronic spectroscopy. I. General theory and application to homodimers. J. Chem. Phys. 2011, 134, 134505. 10.1063/1.3569694. [DOI] [PubMed] [Google Scholar]
- Kreisbeck C.; Kramer T.; Aspuru-Guzik A. Disentangling electronic and vibronic coherences in two-dimensional echo spectra. J. Phys. Chem. B 2013, 117, 9380–9385. 10.1021/jp405421d. [DOI] [PubMed] [Google Scholar]
- Yuen-Zhou J.; Krich J. J.; Kassal I.; Johnson A. S.; Aspuru-Guzik A.. Ultrafast Spectroscopy; IOP Publishing, 2014. [Google Scholar]
- Zhou N.; Chen L.; Huang Z.; Sun K.; Tanimura Y.; Zhao Y. Fast, Accurate Simulation of Polaron Dynamics and Multidimensional Spectroscopy by Multiple Davydov Trial States. J. Phys. Chem. A 2016, 120, 1562–1576. 10.1021/acs.jpca.5b12483. [DOI] [PubMed] [Google Scholar]
- Ikeda T.; Tanimura Y. Probing photoisomerization processes by means of multi-dimensional electronic spectroscopy: The multi-state quantum hierarchical Fokker-Planck equation approach. J. Chem. Phys. 2017, 147, 014102. 10.1063/1.4989537. [DOI] [PubMed] [Google Scholar]
- Xiang B.; Ribeiro R. F.; Dunkelberger A. D.; Wang J.; Li Y.; Simpkins B. S.; Owrutsky J. C.; Yuen-Zhou J.; Xiong W. Two-dimensional infrared spectroscopy of vibrational polaritons. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 4845–4850. 10.1073/pnas.1722063115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conti I.; Cerullo G.; Nenov A.; Garavelli M. Ultrafast Spectroscopy of Photoactive Molecular Systems from First Principles: Where We Stand Today and Where We Are Going. J. Am. Chem. Soc. 2020, 142, 16117. 10.1021/jacs.0c04952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kano H.; Saito T.; Kobayashi T. Observation of Herzberg-Teller-type wave packet motion in porphyrin J-aggregates studied by sub-5-fs spectroscopy. J. Phys. Chem. A 2002, 106, 3445–3453. 10.1021/jp012493f. [DOI] [Google Scholar]
- Kobayashi T.; Wang Z.; Otsubo T. Classification of dynamic vibronic couplings in vibrational real-time spectra of a thiophene derivative by few-cycle pulses. J. Phys. Chem. A 2007, 111, 12985–12994. 10.1021/jp076750d. [DOI] [PubMed] [Google Scholar]
- Fidler A. F.; Engel G. S. Nonlinear spectroscopic theory of displaced harmonic oscillators with differing curvatures: A correlation function approach. J. Phys. Chem. A 2013, 117, 9444–9453. 10.1021/jp311713x. [DOI] [PubMed] [Google Scholar]
- Bizimana L. A.; Carbery W. P.; Gellen T. A.; Turner D. B. Signatures of Herzberg-Teller coupling in three-dimensional electronic spectroscopy. J. Chem. Phys. 2017, 146, 084311. 10.1063/1.4976995. [DOI] [PubMed] [Google Scholar]
- Anda A.; Abramavičius D.; Hansen T. Two-dimensional electronic spectroscopy of anharmonic molecular potentials. Phys. Chem. Chem. Phys. 2018, 20, 1642–1652. 10.1039/C7CP06583C. [DOI] [PubMed] [Google Scholar]
- Zuehlsdorff T. J.; Montoya-Castillo A.; Napoli J. A.; Markland T. E.; Isborn C. M. Optical spectra in the condensed phase: Capturing anharmonic and vibronic features using dynamic and static approaches. J. Chem. Phys. 2019, 151, 074111. 10.1063/1.5114818. [DOI] [PubMed] [Google Scholar]
- Zuehlsdorff T. J.; Hong H.; Shi L.; Isborn C. M. Nonlinear spectroscopy in the condensed phase: The role of Duschinsky rotations and third order cumulant contributions. J. Chem. Phys. 2020, 153, 044127. 10.1063/5.0013739. [DOI] [PubMed] [Google Scholar]
- Shedge S. V.; Zuehlsdorff T. J.; Khanna A.; Conley S.; Isborn C. M. Explicit environmental and vibronic effects in simulations of linear and nonlinear optical spectroscopy Explicit environmental and vibronic effects in simulations of linear and nonlinear optical spectroscopy. J. Chem. Phys. 2021, 154, 084116. 10.1063/5.0038196. [DOI] [PubMed] [Google Scholar]
- Fuji T.; Saito T.; Kobayashi T. Dynamical observation of Duschinsky rotation by sub-5-fs real-time spectroscopy. Chem. Phys. Lett. 2000, 332, 324–330. 10.1016/S0009-2614(00)01278-1. [DOI] [Google Scholar]
- Bizimana L. A.; Brazard J.; Carbery W. P.; Gellen T.; Turner D. B. Resolving molecular vibronic structure using high-sensitivity two-dimensional electronic spectroscopy. J. Chem. Phys. 2015, 143, 164203. 10.1063/1.4934717. [DOI] [PubMed] [Google Scholar]
- Galestian Pour A.; Lincoln C. N.; Perlík V.; Šanda F.; Hauer J. Anharmonic vibrational effects in linear and two-dimensional electronic spectra. Phys. Chem. Chem. Phys. 2017, 19, 24752–24760. 10.1039/C7CP05189A. [DOI] [PubMed] [Google Scholar]
- Zhu R.; Zou J.; Wang Z.; Chen H.; Weng Y. Electronic state-resolved multimode-coupled vibrational wavepackets in oxazine 720 by two-dimensional electronic spectroscopy. J. Phys. Chem. A 2020, 124, 9333–9342. 10.1021/acs.jpca.0c06559. [DOI] [PubMed] [Google Scholar]
- Fumero G.; Schnedermann C.; Batignani G.; Wende T.; Liebel M.; Bassolino G.; Ferrante C.; Mukamel S.; Kukura P.; Scopigno T. Two-dimensional impulsively stimulated resonant Raman spectroscopy of molecular excited states. Phys. Rev. X 2020, 10, 11051. 10.1103/PhysRevX.10.011051. [DOI] [Google Scholar]
- Mukamel S. Dressed-cluster and hydrodynamic expansions for line broadening in simple fluids. Phys. Rev. A: At., Mol., Opt. Phys. 1982, 26, 617. 10.1103/PhysRevA.26.617. [DOI] [Google Scholar]
- Mukamel S.Principles of nonlinear optical spectroscopy, 1st ed.; Oxford University Press: New York, 1999. [Google Scholar]
- Segarra-Martí J.; Mukamel S.; Garavelli M.; Nenov A.; Rivalta I. Towards Accurate Simulation of Two-Dimensional Electronic Spectroscopy. Top. Curr. Chem. 2018, 376, 24. 10.1007/s41061-018-0201-8. [DOI] [PubMed] [Google Scholar]
- Picchiotti A.; Nenov A.; Giussani A.; Prokhorenko V. I.; Miller R. J. D.; Mukamel S.; Garavelli M. Pyrene, a Test Case for Deep-Ultraviolet Molecular Photophysics. J. Phys. Chem. Lett. 2019, 10, 3481–3487. 10.1021/acs.jpclett.9b01325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukamel S. On the semiclassical calculation of molecular absorption and fluorescence spectra. J. Chem. Phys. 1982, 77, 173–181. 10.1063/1.443638. [DOI] [Google Scholar]
- Egorov S. A.; Rabani E.; Berne B. J. Vibronic spectra in condensed matter: A comparison of exact quantum mechanical and various semiclassical treatments for harmonic baths. J. Chem. Phys. 1998, 108, 1407–1422. 10.1063/1.475512. [DOI] [Google Scholar]
- Egorov S. A.; Rabani E.; Berne B. J. Nonradiative relaxation processes in condensed phases: Quantum versus classical baths. J. Chem. Phys. 1999, 110, 5238–5248. 10.1063/1.478420. [DOI] [Google Scholar]
- Shi Q.; Geva E. A derivation of the mixed quantum-classical Liouville equation from the influence functional formalism. J. Chem. Phys. 2004, 121, 3393–3404. 10.1063/1.1771641. [DOI] [PubMed] [Google Scholar]
- McRobbie P. L.; Hanna G.; Shi Q.; Geva E. Signatures of nonequilibrium solvation dynamics on multidimensional spectra. Acc. Chem. Res. 2009, 42, 1299–1309. 10.1021/ar800280s. [DOI] [PubMed] [Google Scholar]
- McRobbie P. L.; Geva E. A benchmark study of different methods for calculating one- and two-dimensional optical spectra. J. Phys. Chem. A 2009, 113, 10425–10434. 10.1021/jp905305t. [DOI] [PubMed] [Google Scholar]
- Mollica C.; Vaníček J. Beating the Efficiency of Both Quantum and Classical Simulations with a Semiclassical Method. Phys. Rev. Lett. 2011, 107, 214101. 10.1103/PhysRevLett.107.214101. [DOI] [PubMed] [Google Scholar]
- Wehrle M.; Šulc M.; Vaníček J. Time-Resolved Electronic Spectra with Efficient Quantum Dynamics Methods. Chimia 2011, 65, 334–338. 10.2533/chimia.2011.334. [DOI] [PubMed] [Google Scholar]
- Šulc M.; Vaníček J. Accelerating the calculation of time-resolved electronic spectra with the cellular dephasing representation. Mol. Phys. 2012, 110, 945–955. 10.1080/00268976.2012.668971. [DOI] [Google Scholar]
- Zambrano E.; Šulc M.; Vaníček J. Improving the accuracy and efficiency of time-resolved electronic spectra calculations: Cellular dephasing representation with a prefactor. J. Chem. Phys. 2013, 139, 054109. 10.1063/1.4817005. [DOI] [PubMed] [Google Scholar]
- Schubert A.; Engel V. Two-dimensional vibronic spectroscopy of coherent wave-packet motion. J. Chem. Phys. 2011, 134, 104304. 10.1063/1.3560165. [DOI] [PubMed] [Google Scholar]
- Krčmář J.; Gelin M. F.; Domcke W. Calculation of third-order signals via driven Schrödinger equations: General results and application to electronic 2D photon echo spectroscopy. Chem. Phys. 2013, 422, 53–62. 10.1016/j.chemphys.2013.01.002. [DOI] [Google Scholar]
- Krčmář J.; Gelin M. F.; Domcke W. Simulation of femtosecond two-dimensional electronic spectra of conical intersections. J. Chem. Phys. 2015, 143, 074308. 10.1063/1.4928685. [DOI] [PubMed] [Google Scholar]
- Picconi D.; Cina J. A.; Burghardt I. Quantum dynamics and spectroscopy of dihalogens in solid matrices. I. Efficient simulation of the photodynamics of the embedded I2Kr18 cluster using the G-MCTDH method. J. Chem. Phys. 2019, 150, 064111. 10.1063/1.5082650. [DOI] [PubMed] [Google Scholar]
- Picconi D.; Cina J. A.; Burghardt I. Quantum dynamics and spectroscopy of dihalogens in solid matrices. II. Theoretical aspects and G-MCTDH simulations of time-resolved coherent Raman spectra of Schrödinger cat states of the embedded I2Kr18 cluster. J. Chem. Phys. 2019, 150, 064112. 10.1063/1.5082651. [DOI] [PubMed] [Google Scholar]
- Begušić T.; Vaníček J. On-the-fly ab initio semiclassical evaluation of third-order response functions for two-dimensional electronic spectroscopy. J. Chem. Phys. 2020, 153, 184110. 10.1063/5.0031216. [DOI] [PubMed] [Google Scholar]
- Matzkies F.; Manthe U. Accurate reaction rate calculations including internal and rotational motion: A statistical multi-configurational time-dependent Hartree approach. J. Chem. Phys. 1999, 110, 88–96. 10.1063/1.478128. [DOI] [Google Scholar]
- Manthe U.; Huarte-Larrañaga F. Partition functions for reaction rate calculations: Statistical sampling and MCTDH propagation. Chem. Phys. Lett. 2001, 349, 321–328. 10.1016/S0009-2614(01)01207-6. [DOI] [Google Scholar]
- Gelman D.; Kosloff R. Simulating dissipative phenomena with a random phase thermal wavefunctions, high temperature application of the Surrogate Hamiltonian approach. Chem. Phys. Lett. 2003, 381, 129–138. 10.1016/j.cplett.2003.09.119. [DOI] [Google Scholar]
- Nest M.; Kosloff R. Quantum dynamical treatment of inelastic scattering of atoms at a surface at finite temperature: The random phase thermal wave function approach. J. Chem. Phys. 2007, 127, 134711. 10.1063/1.2786088. [DOI] [PubMed] [Google Scholar]
- Lorenz U.; Saalfrank P. Comparing thermal wave function methods for multi-configuration time-dependent Hartree simulations. J. Chem. Phys. 2014, 140, 044106. 10.1063/1.4862739. [DOI] [PubMed] [Google Scholar]
- Wang L.; Fujihashi Y.; Chen L.; Zhao Y. Finite-temperature time-dependent variation with multiple Davydov states. J. Chem. Phys. 2017, 146, 124127. 10.1063/1.4979017. [DOI] [PubMed] [Google Scholar]
- Werther M.; Grossmann F. Including temperature in a wavefunction description of the dynamics of the quantum Rabi model. J. Phys. A: Math. Theor. 2018, 51, 014001. 10.1088/1751-8121/aa94a1. [DOI] [Google Scholar]
- Suzuki M. Thermo Field Dynamics in Equilibrium and Non-Equilibrium Interacting Quantum Systems. J. Phys. Soc. Jpn. 1985, 54, 4483–4485. 10.1143/JPSJ.54.4483. [DOI] [Google Scholar]
- Takahashi Y.; Umezawa H. Thermo Field Dynamics. Int. J. Mod. Phys. B 1996, 10, 1755–1805. 10.1142/S0217979296000817. [DOI] [Google Scholar]
- Harsha G.; Henderson T. M.; Scuseria G. E. Thermofield Theory for Finite-Temperature Coupled Cluster. J. Chem. Theory Comput. 2019, 15, 6127–6136. 10.1021/acs.jctc.9b00744. [DOI] [PubMed] [Google Scholar]
- Harsha G.; Henderson T. M.; Scuseria G. E. Thermofield theory for finite-temperature quantum chemistry. J. Chem. Phys. 2019, 150, 154109. 10.1063/1.5089560. [DOI] [PubMed] [Google Scholar]
- Shushkov P.; Miller T. F. Real-time density-matrix coupled-cluster approach for closed and open systems at finite temperature. J. Chem. Phys. 2019, 151, 134107. 10.1063/1.5121749. [DOI] [PubMed] [Google Scholar]
- Borrelli R.; Gelin M. F. Quantum electron-vibrational dynamics at finite temperature: Thermo field dynamics approach. J. Chem. Phys. 2016, 145, 224101. 10.1063/1.4971211. [DOI] [PubMed] [Google Scholar]
- Borrelli R.; Gelin M. F. Simulation of Quantum Dynamics of Excitonic Systems at Finite Temperature: An efficient method based on Thermo Field Dynamics. Sci. Rep. 2017, 7, 9127. 10.1038/s41598-017-08901-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelin M. F.; Borrelli R. Thermal Schrödinger Equation: Efficient Tool for Simulation of Many-Body Quantum Dynamics at Finite Temperature. Ann. Phys. 2017, 529, 1700200. 10.1002/andp.201700200. [DOI] [Google Scholar]
- Chen L.; Zhao Y. Finite temperature dynamics of a Holstein polaron: The thermo-field dynamics approach. J. Chem. Phys. 2017, 147, 214102. 10.1063/1.5000823. [DOI] [PubMed] [Google Scholar]
- Begušić T.; Vaníček J. On-the-fly ab initio semiclassical evaluation of vibronic spectra at finite temperature. J. Chem. Phys. 2020, 153, 024105. 10.1063/5.0013677. [DOI] [PubMed] [Google Scholar]
- Heller E. J. Time-dependent approach to semiclassical dynamics. J. Chem. Phys. 1975, 62, 1544–1555. 10.1063/1.430620. [DOI] [Google Scholar]
- Wehrle M.; Šulc M.; Vaníček J. On-the-fly Ab Initio Semiclassical Dynamics: Identifying Degrees of Freedom Essential for Emission Spectra of Oligothiophenes. J. Chem. Phys. 2014, 140, 244114. 10.1063/1.4884718. [DOI] [PubMed] [Google Scholar]
- Wehrle M.; Oberli S.; Vaníček J. On-the-fly ab initio semiclassical dynamics of floppy molecules: Absorption and photoelectron spectra of ammonia. J. Phys. Chem. A 2015, 119, 5685. 10.1021/acs.jpca.5b03907. [DOI] [PubMed] [Google Scholar]
- Schlau-Cohen G. S.; Ishizaki A.; Fleming G. R. Two-dimensional electronic spectroscopy and photosynthesis: Fundamentals and applications to photosynthetic light-harvesting. Chem. Phys. 2011, 386, 1–22. 10.1016/j.chemphys.2011.04.025. [DOI] [Google Scholar]
- Khalil M.; Demirdöven N.; Tokmakoff A. Obtaining absorptive line shapes in two-dimensional infrared vibrational correlation spectra. Phys. Rev. Lett. 2003, 90, 047401. 10.1103/PhysRevLett.90.047401. [DOI] [PubMed] [Google Scholar]
- Johnson P. J. M.; Koziol K. L.; Hamm P. Intrinsic phasing of heterodyne-detected multidimensional infrared spectra. Opt. Express 2017, 25, 2928. 10.1364/OE.25.002928. [DOI] [PubMed] [Google Scholar]
- Meyer H.-D., Gatti F., Worth G. A., Eds. Multidimensional Quantum Dynamics: MCTDH Theory and Applications, 1st ed.; Wiley-VCH: Weinheim, Germany, 2009. [Google Scholar]
- Roulet J.; Choi S.; Vaníček J. Efficient geometric integrators for nonadiabatic quantum dynamics. II. The diabatic representation. J. Chem. Phys. 2019, 150, 204113. 10.1063/1.5094046. [DOI] [PubMed] [Google Scholar]
- Choi S.; Vaníček J. Efficient geometric integrators for nonadiabatic quantum dynamics. I. The adiabatic representation. J. Chem. Phys. 2019, 150, 204112. 10.1063/1.5092611. [DOI] [PubMed] [Google Scholar]
- Choi S.; Vaníček J. A time-reversible integrator for the time-dependent Schrödinger equation on an adaptive grid. J. Chem. Phys. 2019, 151, 234102. 10.1063/1.5127856. [DOI] [PubMed] [Google Scholar]
- Tatchen J.; Pollak E. Semiclassical on-the-fly computation of the S0 → S1 absorption spectrum of formaldehyde. J. Chem. Phys. 2009, 130, 041103. 10.1063/1.3074100. [DOI] [PubMed] [Google Scholar]
- Conte R.; Ceotto M. In Quantum chemistry and dynamics of excited states; González L., Lindh R., Eds.; John Wiley & Sons, Ltd., 2020; Chapter 19, pp 595–628. [Google Scholar]
- Buchholz M.; Grossmann F.; Ceotto M. Mixed semiclassical initial value representation time-averaging propagator for spectroscopic calculations. J. Chem. Phys. 2016, 144, 094102. 10.1063/1.4942536. [DOI] [PubMed] [Google Scholar]
- Buchholz M.; Grossmann F.; Ceotto M. Application of the mixed time-averaging semiclassical initial value representation method to complex molecular spectra. J. Chem. Phys. 2017, 147, 164110. 10.1063/1.4998510. [DOI] [PubMed] [Google Scholar]
- Curchod B. F. E.; Martínez T. J. Ab Initio Nonadiabatic Quantum Molecular Dynamics. Chem. Rev. 2018, 118, 3305–3336. 10.1021/acs.chemrev.7b00423. [DOI] [PubMed] [Google Scholar]
- Makhov D. V.; Glover W. J.; Martinez T. J.; Shalashilin D. V. Ab initio multiple cloning algorithm for quantum nonadiabatic molecular dynamics. J. Chem. Phys. 2014, 141, 054110. 10.1063/1.4891530. [DOI] [PubMed] [Google Scholar]
- Makhov D. V.; Symonds C.; Fernandez-Alberti S.; Shalashilin D. V. Ab initio quantum direct dynamics simulations of ultrafast photochemistry with Multiconfigurational Ehrenfest approach. Chem. Phys. 2017, 493, 200–218. 10.1016/j.chemphys.2017.04.003. [DOI] [Google Scholar]
- Thompson A. L.; Martínez T. J. Time-resolved photoelectron spectroscopy from first principles: Excited state dynamics of benzene. Faraday Discuss. 2011, 150, 293–311. 10.1039/c1fd00003a. [DOI] [PubMed] [Google Scholar]
- Šulc M.; Hernández H.; Martínez T. J.; Vaníček J. Relation of exact Gaussian basis methods to the dephasing representation: Theory and application to time-resolved electronic spectra. J. Chem. Phys. 2013, 139, 034112. 10.1063/1.4813124. [DOI] [PubMed] [Google Scholar]
- Zimmermann T.; Vaníček J. Efficient on-the-fly ab initio semiclassical method for computing time-resolved nonadiabatic electronic spectra with surface hopping or Ehrenfest dynamics. J. Chem. Phys. 2014, 141, 134102. 10.1063/1.4896735. [DOI] [PubMed] [Google Scholar]
- Worth G. A.; Robb M. A.; Burghardt I. A novel algorithm for non-adiabatic direct dynamics using variational Gaussian wavepackets. Faraday Discuss. 2004, 127, 307–323. 10.1039/b314253a. [DOI] [PubMed] [Google Scholar]
- Richings G. W.; Polyak I.; Spinlove K. E.; Worth G. A.; Burghardt I.; Lasorne B. Quantum Dynamics Simulations Using Gaussian Wavepackets: the vMCG Method. Int. Rev. Phys. Chem. 2015, 34, 269–308. 10.1080/0144235X.2015.1051354. [DOI] [Google Scholar]
- Bonfanti M.; Petersen J.; Eisenbrandt P.; Burghardt I.; Pollak E. Computation of the S1 S0 vibronic absorption spectrum of formaldehyde by variational Gaussian wavepacket and semiclassical IVR methods. J. Chem. Theory Comput. 2018, 14, 5310–4323. 10.1021/acs.jctc.8b00355. [DOI] [PubMed] [Google Scholar]
- Polyak I.; Richings G. W.; Habershon S.; Knowles P. J. Direct quantum dynamics using variational Gaussian wavepackets and Gaussian process regression. J. Chem. Phys. 2019, 150, 041101. 10.1063/1.5086358. [DOI] [PubMed] [Google Scholar]
- Chen L.; Sun K.; Shalashilin D. V.; Gelin M. F.; Zhao Y. Efficient simulation of time- and frequency-resolved four-wave-mixing signals with a multiconfigurational Ehrenfest approach. J. Chem. Phys. 2021, 154, 054105. 10.1063/5.0038824. [DOI] [PubMed] [Google Scholar]
- Vaníček J.; Begušić T. In Molecular Spectroscopy and Quantum Dynamics; Marquardt R., Quack M., Eds.; Elsevier, 2021; pp 199–229. [Google Scholar]
- Lasser C.; Lubich C. Computing quantum dynamics in the semiclassical regime. Acta Numerica 2020, 29, 229–401. 10.1017/S0962492920000033. [DOI] [Google Scholar]
- Rohrdanz M. A.; Cina J. A. Probing intermolecular communication via lattice phonons with time-resolved coherent anti-Stokes Raman scattering. Mol. Phys. 2006, 104, 1161–1178. 10.1080/00268970500525515. [DOI] [Google Scholar]
- Begušić T.; Roulet J.; Vaníček J. On-the-fly ab initio semiclassical evaluation of time-resolved electronic spectra. J. Chem. Phys. 2018, 149, 244115. 10.1063/1.5054586. [DOI] [PubMed] [Google Scholar]
- Begušić T.; Cordova M.; Vaníček J. Single-Hessian thawed Gaussian approximation. J. Chem. Phys. 2019, 150, 154117. 10.1063/1.5090122. [DOI] [PubMed] [Google Scholar]
- Beer M.; Longuet-Higgins H. C. Anomalous light emission of azulene. J. Chem. Phys. 1955, 23, 1390–1391. 10.1063/1.1742314. [DOI] [Google Scholar]
- Prlj A.; Begušić T.; Zhang Z. T.; Fish G. C.; Wehrle M.; Zimmermann T.; Choi S.; Roulet J.; Moser J.-E.; Vaníček J. Semiclassical Approach to Photophysics Beyond Kasha’s Rule and Vibronic Spectroscopy Beyond the Condon Approximation. The Case of Azulene. J. Chem. Theory Comput. 2020, 16, 2617–2626. 10.1021/acs.jctc.0c00079. [DOI] [PubMed] [Google Scholar]
- Xin H.; Gao X. Application of azulene in constructing organic optoelectronic materials: New tricks for an old dog. ChemPlusChem 2017, 82, 945–956. 10.1002/cplu.201700039. [DOI] [PubMed] [Google Scholar]
- Dierksen M.; Grimme S. Density functional calculations of the vibronic structure of electronic absorption spectra. J. Chem. Phys. 2004, 120, 3544–3554. 10.1063/1.1642595. [DOI] [PubMed] [Google Scholar]
- Niu Y.; Peng Q.; Deng C.; Gao X.; Shuai Z. Theory of excited state decays and optical spectra: Application to polyatomic molecules. J. Phys. Chem. A 2010, 114, 7817–7831. 10.1021/jp101568f. [DOI] [PubMed] [Google Scholar]
- Thulstrup E. W.; Case P. L.; Michl J. Azulene: polarized absorption in stretched polymers and magnetic circular dichroism. Chem. Phys. 1974, 6, 410–418. 10.1016/0301-0104(74)85025-1. [DOI] [Google Scholar]
- Gillispie G. D.; Lim E. C. Vibrational analysis of the S2-S1 fluorescence of azulene in a naphthalene mixed crystal at 4.2 K. J. Chem. Phys. 1978, 68, 4578–4586. 10.1063/1.435563. [DOI] [Google Scholar]
- Foggi P.; Neuwahl F. V. R.; Moroni L.; Salvi P. R. S1-Sn and S2-Sn Absorption of Azulene: Femtosecond Transient Spectra and Excited State Calculations. J. Phys. Chem. A 2003, 107, 1689–1696. 10.1021/jp021313e. [DOI] [Google Scholar]
- Nenov A.; Giussani A.; Fingerhut B. P.; Rivalta I.; Dumont E.; Mukamel S.; Garavelli M. Spectral lineshapes in nonlinear electronic spectroscopy. Phys. Chem. Chem. Phys. 2015, 17, 30925–30936. 10.1039/C5CP01167A. [DOI] [PubMed] [Google Scholar]
- Farfan C. A.; Turner D. B. Interference among multiple vibronic modes in two-dimensional electronic spectroscopy. Mathematics 2020, 8, 157. 10.3390/math8020157. [DOI] [Google Scholar]
- Kats D.; Schütz M. A multistate local coupled cluster CC2 response method based on the Laplace transform. J. Chem. Phys. 2009, 131, 124117. 10.1063/1.3237134. [DOI] [PubMed] [Google Scholar]
- Ledermüller K.; Kats D.; Schütz M. Local CC2 response method based on the Laplace transform: Orbital-relaxed first-order properties for excited states. J. Chem. Phys. 2013, 139, 084111. 10.1063/1.4818586. [DOI] [PubMed] [Google Scholar]
- Ledermüller K.; Schütz M. Local CC2 response method based on the Laplace transform: Analytic energy gradients for ground and excited states. J. Chem. Phys. 2014, 140, 164113. 10.1063/1.4872169. [DOI] [PubMed] [Google Scholar]
- Schütz M. Oscillator strengths, first-order properties, and nuclear gradients for local ADC(2). J. Chem. Phys. 2015, 142, 214103. 10.1063/1.4921839. [DOI] [PubMed] [Google Scholar]
- Werner H.-J.; Knowles P. J.; Knizia G.; Manby F. R.; Schütz M.; Celani P.; Györffy W.; Kats D.; Korona T.; Lindh R.; et al. MOLPRO, version 2015.1, a package of ab initio programs; 2015. (http://www.molpro.net).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.