Bioelectrical domain walls in homogeneous tissues

Abstract

Electrical signaling in biology is typically associated with action potentials, transient spikes in membrane voltage that return to baseline. Hodgkin-Huxley and related conductance-based models of electrophysiology belong to a more general class of reaction-diffusion equations which could, in principle, support spontaneous emergence of patterns of membrane voltage which are stable in time but structured in space. Here we show theoretically and experimentally that homogeneous or nearly homogeneous tissues can undergo spontaneous spatial symmetry breaking through a purely electrophysiological mechanism, leading to formation of domains with different resting potentials separated by stable bioelectrical domain walls. Transitions from one resting potential to another can occur through long-range migration of these domain walls. We map bioelectrical domain wall motion using all-optical electrophysiology in an engineered cell line and in human induced pluripotent stem cell (iPSC)-derived myoblasts. Bioelectrical domain wall migration may occur during embryonic development and during physiological signaling processes in polarized tissues. These results demonstrate that nominally homogeneous tissues can undergo spontaneous bioelectrical symmetry breaking.

Introduction

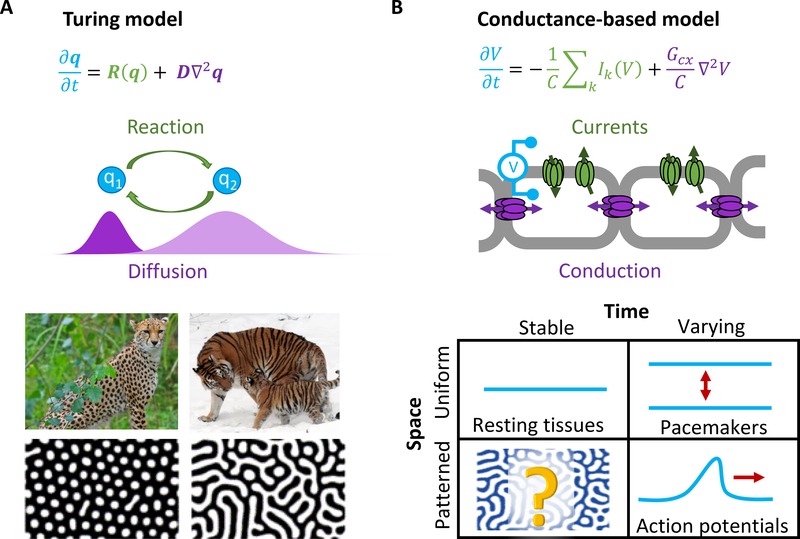
In 1952, Hodgkin and Huxley introduced a mathematical model of action potential propagation in the squid giant axon, based on nonlinear dynamics of electrically coupled ion channels.¹ In the same year, Alan Turing proposed a model for biological pattern formation, based on diffusion and nonlinear reaction dynamics of chemical morphogens.² These two seemingly unrelated models have an underlying mathematical kinship: both are nonlinear reaction-diffusion equations, first order in time and second order in space. Thus, from a mathematical perspective, one expects parallel classes of solutions. These solutions can be organized by whether they are uniform or patterned in space, and stable or varying in time (Fig. 1). All four combinations of spatial and temporal structure have been observed in chemical reaction-diffusion systems³, but only three of the four have been reported in nominally homogeneous systems governed by Hodgkin-Huxley-like conductance-based models. We thus sought to observe the fourth class of electrophysiological dynamics: spontaneous spatial symmetry breaking in a nominally homogeneous tissue to create patterns of membrane voltage that are static in time but that vary in space.

Figure 1. Biochemical and bioelectrical spontaneous pattern formation.

A) In chemical Turing patterns, a nonlinear chemical reaction coupled to diffusion leads to spontaneous formation of stable concentration patterns from homogeneous initial conditions, similar to ones seen in Nature. Here q = (q₁, q₂) is the vector of reagent concentrations, R(q) is the nonlinear relation between concentration and reaction rate, and D is the vector of diffusion coefficients. B) Conductance-based models have the same structure as the Turing equation. Here V is the membrane voltage, C is the membrane capacitance, I_k is the current through the k^th ion channel, and G_cx is the connexin conductivity. The chart shows possible solutions to an initially homogeneous conductance-based model, classified by variation in space and time. Spontaneous patterns that vary in space but not in time are a little-explored possibility in electrophysiology. Images of natural and simulated patterns adapted from Wikipedia and Kondo et al³.

Spatial symmetry breaking might emerge during slow transitions in membrane potential, such as occur during embryonic development and in signaling processes in peripheral organs. While spontaneous pattern-forming processes in electrophysiology have been contemplated,^4–8 unambiguous observations with clear mechanistic interpretations have been lacking. Part of the experimental challenge comes from the difficulty of spatially mapping membrane voltage. Patch clamp measurements of membrane potential probe the voltage at only discrete points in space, and are thus ill-suited to mapping spatial structure. Recent advances in voltage imaging facilitate spatially resolved measurements ^9,10, and optogenetic stimulation offers the prospect to tune the electrophysiological state of a tissue and perhaps to drive it into a regime of spontaneous symmetry breaking.

Here, we explore these ideas experimentally in engineered cells expressing the inward-rectifying potassium channel K_ir2.1 and the channelrhodopsin CheRiff (Fig. 2A,B). While this two-component cellular model is so simple as to appear almost trivial, we find that coupled ensembles of these cells show richly diverse transitional behaviors, including electrical bistability, bioelectrical domain walls, and noise-induced breakup into discrete electrical domains. We further show that similar dynamics occur in human induced pluripotent stem cell (iPSC)-derived myocytes during differentiation. Our results demonstrate bioelectrical pattern formation and domain wall motion as generic mechanisms by which tissues can switch from one membrane voltage to another.

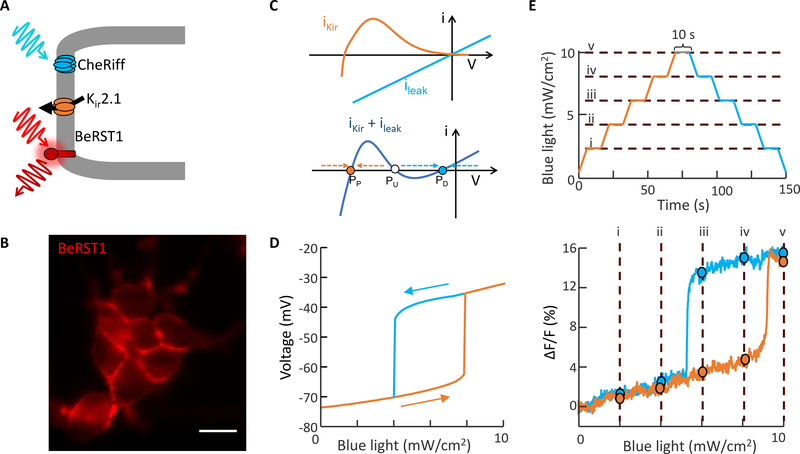
Figure 2. Electrophysiological bistability in an engineered cell line.

A) Bi-HEK cells expressed an inward-rectifier potassium channel, K_ir2.1, and a light-gated ion channel, CheRiff. A far-red voltage-sensitive dye, BeRST1, reported membrane potential. B) Fluorescence image of bi-HEK cells labeled with BeRST1. Scale bar 20 μm. C) Expression of an inward rectifier potassium channel (e.g. K_ir 2.1) and a non-selective leak conductance (e.g. channelrhodopsin) are sufficient, together, to produce electrical bistability. D) Numerical simulations showing hysteresis of steady-state membrane potential under ramped optogenetic stimulation. Simulations were based on measured I-V curves of bi-HEK cells (Methods). E) Top: optogenetic stimulus waveform. Epochs of constant illumination intensity have been indicated with Roman numerals. Bottom: Optical measurements of membrane voltage in a small cluster of bi-HEKs, exposed to the stimulus waveform above. Circles denote points where the optogenetic stimulus strength was held constant for 10 s.

Bistable membrane voltages

The lipid bilayer cell membrane behaves, electrically, as a parallel plate capacitor. Transmembrane protein channels can pass ionic currents which alter the intracellular charge, and hence the membrane voltage. In a single cell or a small isolated patch of tissue, the membrane voltage follows:

$$C_m\frac{dV}{dt}=-I$$ [Eq. 1]

where C_m is the membrane capacitance and I is the current through all ion channels (outward positive). Channel gating dynamics can impose a nonlinear and history-dependent relation between I and V which causes complex dynamics in excitable cells.

Resting potential $\left(\frac{dV}{dt}=0\right)$ in most polarized cells is set by an inward rectifier potassium channel, K_ir. The current through the K_ir channel is $I_{Kir}=g_K{x}_{\infty }\left(V\right)(V-E_K)$, where g_K is the conductance (proportional to the number of channels in the membrane), and x_∞(V) captures the voltage-dependent gating of the channel (shut at depolarized voltages, open at polarized voltages).¹¹ The term (V − E_K), where E_K ∼ −90 mV is the potassium Nernst potential, accounts for the electrochemical driving force for ions to cross the membrane. The function I_Kir(V) crosses the x-axis at the potassium reversal potential. Inward rectification implies a drop in K_ir current at more positive potentials. Together these attributes give K_ir channels a non-monotonic I-V relationship (Fig. 2C).^4,12 To a good approximation, the K_ir conductance depends on present voltage only, not on history.

Cells typically have one or more leak conductances. We consider the simplest case: an Ohmic leak with reversal potential 0 mV and conductance g_l, leading to a straight line I-V relation, I_leak = g_l V. Leak conductances can be gated by external variables, e.g. by chemical ligands or mechanical forces. Below we use a non-selective cation-conducting channelrhodopsin, CheRiff, as a leak conductance where the value of g_l is readily tunable via blue light ⁹.

The total current is the sum of the K_ir and leak currents (Fig. 2C). When g_l dominates, one has a single depolarized fixed point (I = 0) near 0 mV (P_D). When g_K dominates, one has a single polarized fixed point near −90 mV (P_P). When g_l and g_K are approximately balanced, one has an N-shaped I-V curve which crosses the x-axis three times. This situation implies coexistence of stable fixed points P_D and P_P with an unstable fixed point (P_U) in between, leading to overall bistability.^13,14 From a dynamical systems perspective, this situation is analogous to the bistability observed in the famous E. coli Lac operon system.^15,16

We genetically engineered a HEK293 cell line that stably expressed K_ir2.1 and CheRiff (Methods).^17,18 We call these bistable-HEK cells (bi-HEKs). Patch clamp measurements on small clusters (~50 μm diameter) of bi-HEKs revealed a non-monotonic I-V curve, which could be driven through two saddle-node bifurcations by light (Supplementary Fig. 1). We performed numerical simulations of a cell governed by Eq. 1, using the measured I-V curve (Methods). Under continuous variation in blue light the simulated membrane potential underwent sudden jumps at saddle node bifurcations where P_U annihilated either P_D or P_P. The jumps occurred at different values of blue light in the polarizing and depolarizing directions, leading to hysteresis (Fig. 2D), i.e. within the hysteretic region, the membrane voltage was bistable.

We used a far-red voltage-sensitive dye, BeRST1 ¹⁹, to report the membrane voltage in small clusters of bi-HEKs. Homogeneous blue illumination was slowly increased (0 to 10 mW/cm² over 75 s) and then decreased using a piecewise-continuous waveform comprising linear ramps alternating with 10 s intervals of constant intensity (Fig. 2E, top). The 10 s periods of constant intensity were ~10³-fold longer than the membrane electrical time constant (~10 ms), sufficient to ensure that the membrane voltage reached steady state. The optically recorded membrane voltage showed abrupt transitions and hysteresis, in close agreement with the numerical simulations (Fig. 2E, bottom). Furthermore, we did not detect drift in the membrane voltage during the periods of constant optogenetic drive, confirming that the dynamics were quasi-static. Thus, cells expressing K_ir + leak exhibited a form of non-genetic electrophysiological memory: the steady-state membrane voltage was not uniquely specified by the ion channels alone. Rather, in the hysteretic regime the steady-state voltage depended on the history of ionic currents, which could in turn depend on the history of stimuli to the cell or, in principle, on the history of gene expression (e.g. whether the leak or the K_ir channel was expressed first).⁴

Bioelectrical domains in extended tissues

In an extended tissue, neighboring cells can be coupled by gap junctions. When the voltage on a cell deviates from the mean of its neighbors, ionic currents flow through the gap junctions to minimize this deviation. The dynamics then become:

$$C_m\frac{\partial V}{\partial t}=-I+G_{cxn}{\nabla }^{2}V,$$ [Eq. 2]

where G_cxn is the sheet conductance due to gap junction channels. When the membrane potential is bistable (i.e. the ratio g_l/g_K is in the hysteretic portion of Fig. 2E), different regions of the tissue may sit at different resting potentials, P_U and P_D.²⁰ A domain wall then emerges at the interface between these regions (Fig. 3A). In a homogeneous tissue, the domain wall is stationary only when the K_ir and leak conductances are perfectly balanced, i.e. when the areas of the positive and negative portions of the I-V curve between P_U and P_D are equal.²¹ Otherwise the domain wall migrates to expand the territory of the stronger conductance (Supplementary Fig. 2A–C).

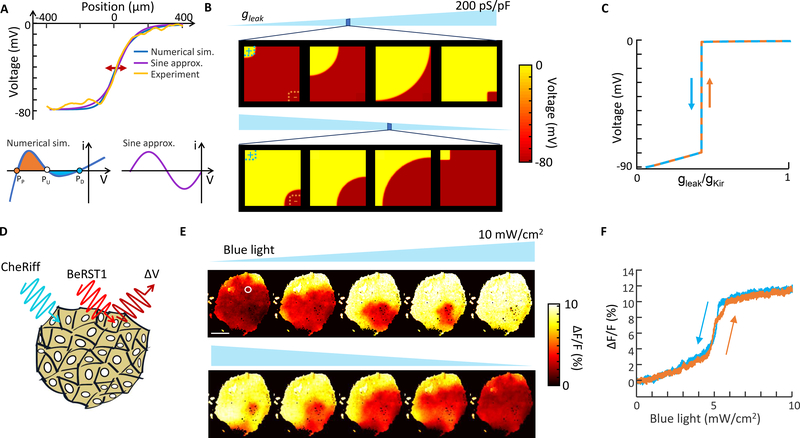
Figure 3. Bioelectric domain walls in an engineered cell line.

A) Top: Profile of a bioelectrical domain wall in one dimension, comparing numerical simulations based on a balanced K_ir and leak current, an analytical approximation based on a sinusoidal I-V relation, and experimental data. Bottom: I-V curves based on a detailed biophysical model of K_ir + leak (left) or a sinusoidal approximation (right). In a homogeneous tissue, the domain wall migrates in a direction set by the relative areas of the orange and blue shaded regions of the I-V curve, favoring the fixed point with the larger shaded region. B) Simulation of domain wall growth in a homogeneous tissue with two discrete defects to nucleate transitions (clamped at V = 0 on the top left, clamped at V = −90 mV on the bottom right). The transitions in the bulk tissue occurred over a narrow range of g_leak. See Supplementary Movie S1. C) Simulation of membrane voltage in the tissue in (B) as a function of leak conductance. D) Confluent islands of bi-HEK cells were illuminated with uniform blue light to stimulate CheRiff, and with red light to elicit voltage-dependent fluorescence of BeRST1. E) Fluorescence images of an island of bi-HEKs under gradually increasing optogenetic stimulation. Scale bar 1 mm. See Supplementary Movies S2 and S3. White circle denotes region with voltage plotted in (F). F) Fluorescence as a function of optogenetic stimulus strength from the region circled in white in (E). Domain wall migration in the large island led to a step-like change in membrane potential without hysteresis.

To aid intuition, we introduce a simple analytical model of a bioelectrical domain wall. We approximate the I-V relation by a sinusoidal function, $I\left(V\right)=A\sin \left(\frac{2\pi V}{\left|E_K\right|}\right)$. While the sinusoidal approximation does not replicate the detailed shape of the I-V curve, it correctly captures the three zero-crossings between E_k and 0 mV (Fig. 3A). In one dimension, the steady-state domain wall profile ($\frac{\partial V}{\partial t}=0$) obeys

$$G_{cxn}\frac{d^{2}V}{d{x}^2}=A\sin \left(\frac{2\pi V}{\left|E_K\right|}\right).$$ [Eq. 3]

Differential equations of this form appear in many contexts, perhaps most famously to describe the dynamics of a physical pendulum (with time replacing position as the independent variable).²² The domain wall profile is described by the separatrix solution which delineates the oscillatory from the rotatory solutions:

$$V\left(x\right)=\frac{2E_K}{\pi }{\tan }^{-1}\left[\exp \left(\sqrt{\frac{2\pi A}{G_{cxn}{E}_K}}x\right)\right]$$ [Eq. 4]

The domain wall width scales as $\lambda \sim \sqrt{\frac{G_{cxn}{E}_K}{2\pi A}}$. The parameter A is a measure of the strength of the (non-gap junction) ionic currents, i.e. g_K and g_l in the more detailed biophysical model.

Fig. 3A compares the analytical approximation (Eq. 4) with numerical simulation using the complete expression for the K_ir2.1 + leak I-V relation (Methods). The numerical and analytical domain wall profiles differ by at most 3.5 mV for a domain wall of height 77.5 mV.

Dual patch clamp measurements have shown that G_cxn is maximal at zero voltage difference between adjoining cells and decreases when the intercellular voltage exceeds approximately ±40 mV.²³ Our simulations showed that in the domain walls the maximal nearest-neighbor voltage difference was < 1 mV, implying that the voltage dependence of G_cxn could safely be neglected. This effect may be necessary to include when the width of the domain wall approaches the size of a cell.

In two dimensions, simulations predicted that bioelectrical domains nucleated at defects (e.g. cells that expressed only leak or only K_ir) and spread through the tissue (Fig. 3B, Supplementary Movie S1). In a tissue that was homogeneous but for an arbitrarily low density of nucleation points, the hysteresis vanished and the transition between depolarized and polarized states was abrupt (Fig. 3C). Thus the collective nature of the transition in an extended tissue was predicted to convert a gradual change in ionic currents into a highly sensitive phase change-like switch in membrane potential.

HEK cells endogenously express connexins 43 and 45 which mediate nearest-neighbor electrical coupling,^24,25 so we reasoned that confluent monolayers of bi-HEK cells might support bioelectrical domain walls. We performed optogenetic stimulation and voltage imaging experiments in confluent islands of bi-HEKs with dimensions ~2 × 2 mm, corresponding to ~4×10⁴ cells (Fig. 3D). Initially (in the absence of optogenetic stimulation) the tissue was homogeneously polarized. Illumination with dim blue light led to nucleation of depolarized domains near the tissue boundaries. We extracted the mean fluorescence intensity profile across the domain wall. When scaled to match the voltage axis, the profile agreed closely with the predictions of both the numerical simulation and the analytical approximation (Fig. 3A).

As the blue light further increased, the domain walls migrated across the tissue, until the whole tissue was depolarized (Fig. 3E, Supplementary Movies S2 and S3). The fluorescence intensity of most regions in the island showed step-like depolarization with little hysteresis, consistent with the theoretical predictions. Domain wall formation and migration were observed in 8 of 8 independently prepared and measured islands (Supplementary Fig. 3), though in some cases defects prevented depolarization of the entire island.

To test the stability of the domain walls, we applied a piecewise-continuous blue light waveform comprising linear ramps alternating with 10 s intervals of constant intensity, as in Fig. 2E. During each period of constant illumination the domain walls remained stationary. During each period of increasing or decreasing illumination, the domain walls advanced or retreated, respectively (Supplementary Fig. 4). The 10 s periods of domain wall stability were ~10³-fold longer than the membrane relaxation time constant of ~10 ms, demonstrating the quasi-static nature of the electrical patterns. These experiments confirmed the existence of stable domain walls in a nominally homogeneous tissue, a hallmark of spontaneous spatial symmetry breaking.

We confirmed the role of gap junctions in domain wall migration by adding a gap junction blocker 2-aminoethyl diphenylborinate (2-APB, 50 μM) to island cultures of bi-HEKs. Before adding the gap junction blocker, a ramp of blue light caused the island to depolarize over a narrow range of blue light levels via domain wall migration, and the membrane potential showed little hysteresis. After adding the blocker, individual cells showed discrete hysteretic switching, each with its own transition points set by the cell-specific expression levels of K_ir2.1 and CheRiff (Supplementary Fig. 5). Thus gap junctional coupling was necessary for the transition from zero-dimensional to two-dimensional behavior.

No tissue is perfectly uniform, so we explored via simulation tissues with cell-to-cell variations in expression of K_ir or leak (Methods). Noisy ion channel expression introduced an effective friction for domain wall motion, stabilizing droplet-like domains of high or low voltage and broadening the transition in tissue-average voltage under a ramp in g_l (Supplementary Fig. 6). Sufficiently strong heterogeneity led to stick/slip saltatory domain wall motion. The tissue-average voltage then showed Barkhausen-like fine-structure noise (Supplementary Fig. 7). Tissue heterogeneity also restored some degree of hysteresis in the tissue-average voltage, and, when strong enough, broke the tissue into discrete domains that switched independently. The predicted voltage dynamics of coupled cells expressing leak + K_ir thus exhibited many of the features found in magnetization of a disordered soft ferromagnet.²⁶

Signatures of noisy ion channel expression were observable in our experiments on island cultures. Due to regional variations in the depolarizing transition point, the voltage averaged over the whole island showed a broader transition than did local measurements (Supplementary Fig. 7). The island-average voltage showed Barkhausen-like fine-structure noise, and a small amount of hysteresis, indicative of stick-slip domain motion. Numerical simulations of islands with noisy gene expression recapitulated these effects (Supplementary Fig. 7). In cultures where transient transfection of K_ir2.1 led to enhanced cell-to-cell variability in g_K (Methods), we observed breakup into regions in which the voltage showed hysteretic zero-dimension-like behavior and regions which showed smooth and reversible depolarization, in concordance with simulations (Supplementary Fig. 7, Supplementary Movies S4 and S5).

Electrical bistability and hysteresis during myogenesis

Early embryonic tissue has a membrane voltage, V_m ~ 0 mV ²⁷. During myogenesis, myoblast precursors polarize electrically, exit the cell cycle, and fuse into myocytes whose resting potential is ~−85 mV.²⁸ Expression of K_ir2.1 initiates this hyperpolarization.²⁹ In mammals, myoblast precursors couple transiently via gap junctions during differentiation and prior to fusion.³⁰ We thus hypothesized that bistability and bioelectric domain wall motion might occur during myogenesis.

We performed all-optical electrophysiology experiments in human induced pluripotent stem cell (hiPSC) derived myoblasts as they differentiated into myocyte fibers in vitro (Fig. 4A). HiPSC myoblasts were seeded at low density, lentivirally transduced to expresses CheRiff, and then allowed to proliferate to form a confluent monolayer (Methods; Fig. 4A). The cells were then differentiated into myocytes. After one week of differentiation, cells expressed stained positive for myogenin, PAX7, and myosin heavy chain, and adopted an elongated fiber-like morphology, indicative of differentiation toward mature myocytes (Fig. 4B). RNAseq measurements on matched samples showed a significant increase in K_ir2.1 expression during the differentiation process (5.6-fold, p <0.001) and high expression of gap junction proteins Cx43 and Cx45 throughout (Methods). We performed voltage imaging under ramped wide-field optogenetic stimulation at two time-points during differentiation to test for signatures of electrical bistability in isolated cells and domain wall motion in confluent cultures.

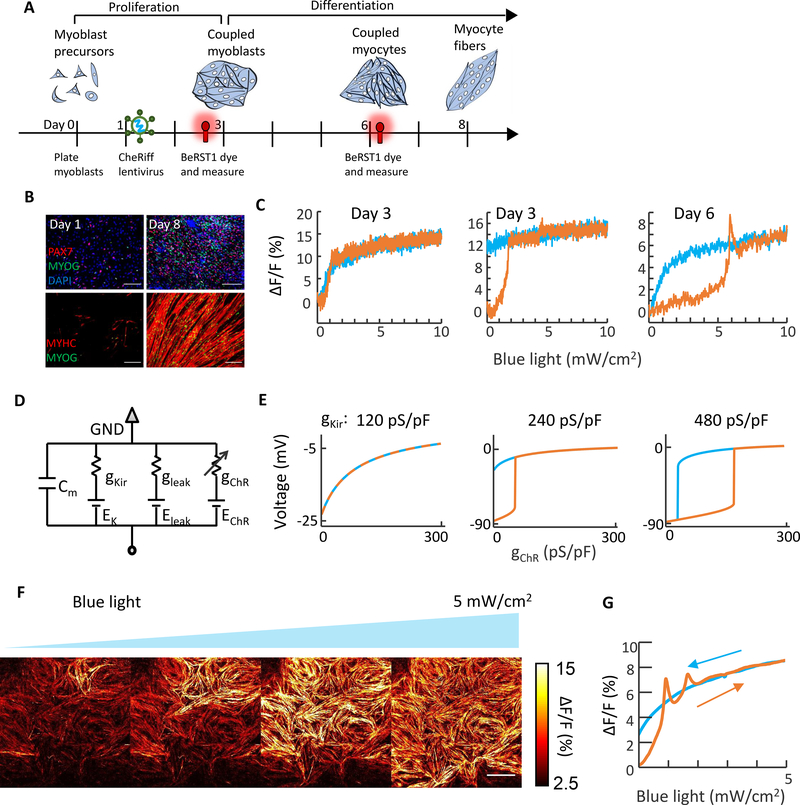
Figure 4: Bioelectric domain wall propagation in stem cell-derived myocytes.

A) Timeline for differentiation, viral transduction, and measurement. B) Immunocytochemistry staining of myocyte cultures during differentiation. Stains show PAX7, myogenin (MYOG), and myosin heavy chain (MYHC). Scale bars 200 μm. C) Optical measurements of membrane potential in individual isolated myoblasts at different times after differentiation. D) Simple electrical circuit model for myoblasts. The K_ir channel was modeled as a nonlinear conductance, the leak was treated as Ohmic with E_leak = −20 mV, and the channelrhodopsin was treated as Ohmic with E_ChR = 0 mV. E) Simulations of optogenetically induced changes in membrane voltage at different values of g_Kir. All other parameters of the simulation were kept constant between the three panels. F) Bioelectrical domain wall migration in a monolayer of electrically coupled myocytes (measured 3 days after start of differentiation). Scale bar 1 mm. See Supplementary Movie S6. G) Optical measurements of membrane voltage as a function of optogenetic stimulus strength in the confluent culture. Depolarization-activated inward currents led to spikes atop the optogenetically induced depolarizations.

In myoblast precursors that had not yet reached confluence (day 3), we observed heterogeneous responses to ramped optogenetic stimulation: Cells showed either a smooth response with saturation-like behavior and little hysteresis (67%, 34 of 51, Fig. 4C left) or a step-wise depolarization, which did not reverse upon cessation of the optogenetic stimulus (33%, 17 of 51, Fig. 4C middle). In immature myocytes mechanically dissociated from a confluent culture (day 6, 3 days after start of differentiation), we observed sub-populations with behavior similar to day 3 (smooth depolarization with no hysteresis: 47%, 42 of 89; step-wise, irreversible depolarization: 29%, 26 of 89). We also observed a new sub-population comprising cells with closed hysteresis loops that resembled the bi-HEKs (24%, 21 of 89, Fig. 4C right, Supplementary Fig. 8, Methods).

These three seemingly disparate behaviors could all be explained by a simple model containing a leak, a channelrhodopsin, and K_ir expression which increased on average between day 3 and 6 (Fig. 4D, S8). At the lowest K_ir level, the I-V curve was monotonically increasing, so channelrhodopsin activation shifted a single stable voltage fixed point along the I = 0 axis. This led to a continuous and reversible change in voltage (Fig. 4E). At intermediate K_ir level, the I-V curve was N-shaped and crossed the I=0 axis three times in the absence of channelrhodopsin activation. Blue light drove step-wise depolarization via a saddle node bifurcation. The depolarized state remained stable in the absence of optogenetic drive, leading to non-recovering depolarization. At the highest K_ir level, the hysteresis curve shifted to the right and the cells repolarized in the absence of optogenetic drive. Thus, a simple model with one tuning parameter captured the three qualitatively distinct single-cell responses to channelrhodopsin activation.

In confluent monolayers at day 6, we used patterned optogenetic stimulation to excite a portion of the tissue. The evoked action potentials propagated beyond the stimulated region, confirming the presence of gap junctional electrical coupling (Supplementary Fig. 9). Under spatially homogeneous ramped optogenetic stimulation, we observed optogenetically induced domain wall propagation (Fig. 4F, Supplementary Movie S6). The presence of domain wall propagation was surprising, considering that only a minority (24%) of the isolated cells were bistable. Simulations showed that the due to strong electrotonic coupling, the global behavior of a tissue could be dominated by a minority of cells expressing K_ir2.1 (Supplementary Fig. S6). As in the bi-HEKs, the whole-tissue average voltage showed little hysteresis as a function of optogenetic drive (Fig. 4G), consistent with depolarization via domain wall migration. These observations show that differentiating myoblasts exhibit electrical bistability when isolated and collective domain wall migration during an essential step of myogenesis.

In contrast to the bi-HEK cells, the myoblasts also supported propagation of regenerative action potential waves. These waves manifested as spikes in the whole-tissue fluorescence during a gradual optogenetic depolarization (Fig. 4G). The additional depolarizing drive associated with these spikes caused the waves to propagate rapidly across the tissue, without disruption from the defects which could pin the motion of domain walls.

Discussion

Quasi-static spatial variations in membrane potential are well known to arise in development (of animals^31–33, plants³⁴ and protists³⁵), in wound healing³⁶, and to persist in some mature tissues³⁷. In most cases the ion channels responsible for these potentials are not known, but it is generally assumed that the membrane voltage in each patch of tissue is set by the locally expressed ion channels, i.e. that the bioelectrical patterns are ‘baked in’ to the tissue via conventional morphogen signaling pathways which govern ion channel gene expression. Our work shows that this need not be the case. Electrical instabilities can amplify minute (possibly undetectable) variations in ionic currents in an otherwise homogeneous tissue. Thus the conventional view that patterns of gene expression drive patterns of electrophysiology might, in some cases, be reversed. The pathways by which patterns of membrane voltage could affect patterns of gene expression remain a topic of much current research.^33,38

In vitro, muscle cells must be aggregated to differentiate, a phenomenon called the “community effect”.³⁹ Our results show that electrical coupling can mediate community effects, i.e. that the collective electrical dynamics of coupled cells can be strikingly different from the individuals, even if all cells are identical. Domain wall migration mediates polarization in extended tissues, whereas isolated cells or small clumps must polarize all at once. Consequently, under ramped K_ir2.1 expression, an electrically coupled, extended tissue will polarize before an isolated cell or small patch, even if all other conditions are identical. K_ir2.1 expression is required for the expression of the myogenic transcription factors Myogenin (MyoG) and Myocyte Enhancer Factor-2 (MEF2).²⁹ Disruption of gap junction coupling is sufficient to disrupt myogenesis.⁴⁰ Together, these observations suggest that bioelectric domain walls might play a functionally important role in myogenesis. This prediction merits further mechanistic tests in cultured myocytes and in vivo. It will be interesting to relate the bioelectrical response properties of developing muscle to the shifts that occur as myocytes fuse and gap junctional coupling diminishes during maturation.

Many combinations of ion channels can produce N-shaped I-V curves and thereby mediate electrical bistability. For instance, the combination of a K⁺-selective leak current and the steady-state window current of T-type Ca_V channels mediates plateau potentials in thalamocortical neurons.^41,42 In this case, one would expect electrical bistability to be accompanied by bistability in intracellular Ca²⁺ concentration, which might then couple to downstream biochemical or genetic signaling pathways. The combination of a persistent voltage-gated sodium current and a K⁺-selective leak current can also drive bistability. Persistent Na_V currents have been observed in striated cardiac and skeletal muscle and in many types of mammalian neurons.⁴³ Persistent sodium and persistent L-type calcium currents contribute to sustained activation in a spinal cord injury model.⁴⁴ Finally, persistent sodium currents are thought to play a role in propagating and amplifying the influence of distal synaptic inputs during dendritic integration.⁴⁵ In principle, any of these bistable scenarios could produce bioelectrical domain walls in electrotonically extended systems, though we are not aware of any such direct observations.

Gap junctions are necessary for proper formation of many tissues during development, including in heart, liver, skin, hair, cartilage, bone, and kidney,^46,47 though the physiological roles of these gap junctions remain unclear. Our work suggests that gap junction-mediated bioelectrical domain wall motion may be an important feature in some of these systems. For instance, chondrocytes express K_ir channels⁴⁸, gap junctions⁴⁹, and the ionotropic serotonin receptor 5-ht3a⁵⁰ which is a nonselective cation channel electrically similar to channelrhodopsin. These conditions suggest that the ingredients are present for regulation of membrane potential via domain wall migration. Wounding in endothelial monolayers has been shown to induce slowly migrating zones of depolarization⁵¹, suggesting that these cells might also support bioelectrical domain walls. The phenomenon of spreading cortical depression may also reflect a form of electrical bistability, though the underlying mechanism is likely far more complex than the phenomena studied here.⁵² The presence of long-lived electrical bistability in tissues could provide a means to couple bioelectric patterns to biochemical and genetic signaling networks.^4–6

The shape of the I-V curve in our experiments is qualitatively captured by a cubic (Fitzhugh Nagumo-type) nonlinearity.^53,54 Models of this sort have been applied to describe similar dynamics (zero-dimensional hysteresis, domain nucleation, growth and disorder-driven breakup) in magnetic domain reversals in ferromagnets,⁵⁵ in the spread of forest fires,⁵⁶ in phase transitions,²¹ and in expanding species ranges with a strong Allee effect.⁵⁷ Spontaneous spatial symmetry breaking and pattern formation are well established in neural field theories⁵⁸ and in models of cardiac arrhythmias.^59,60 In these systems, however, the membrane voltage varies with time, i.e. the systems are described by the lower right quadrant of Fig. 1B. Our work shows that the reaction-diffusion formalism can be applied to purely spatial symmetry breaking in electrophysiology.

In the Turing model, formation of quasi-periodic patterns requires interaction of two or more morphogens, often described as an activator and an inhibitor. Conductance-based models describe the dynamics of voltage, a scalar quantity. The spatial symmetry breaking studied in this report does not constitute a classical Turing pattern, in that voltage is only a one-dimensional state variable. As a result, the patterns of membrane voltage did not have a characteristic finite spatial frequency. To achieve a classical Turing-like pattern would require coupling of voltage to another diffusible species, e.g. Ca²⁺. It is not known whether classical Turing-like patterns of membrane voltage can be created via purely electrophysiological means.

Methods

Numerical modeling of electrically bistable cells and tissues

In the conductance-based model, the voltage dynamics are governed by the equation:

$$C_m\frac{\partial V}{\partial t}=G_{Cxn}{\nabla }^{2}V-(I_{Kir}+{I_{leak}+I}_{ChR})$$

The gap junction sheet conductance is defined as G_Cxn = g_Cxn × l², where g_Cxn is the gap junction conductance between adjacent cells, and l is the linear dimension of a cell. If g_Cxn is measured as an areal conductance (S/m²), then the units of G_Cxn are S (i.e. sheet conductance, which has no spatial dimension). If C_m is measured as an areal capacitance (F/m²), then the ratio G_Cxn/C_m has units of a diffusion coefficient (m²/s), making explicit the connection between the conductance-based model and the reaction-diffusion equation.

For convenience in simulations, units of space were 10 μm (corresponding to linear size of one cell), units of time were ms, and units of voltage were mV. We assumed the capacitance of a cell was 10 pF. Conductances were measured in nS/pF, ionic currents in pA/pF, and voltage in mV. Parameters used in all simulations are given in the Tables in the Model parameters section of the Methods.

Simulations were run in Matlab using custom software. Single-cell voltages in 0D were determined by finding fixed points of cell-autonomous current-voltage curves. Extended tissues were numerically simulated as two-dimensional grids of 100 × 100 cells with periodic boundary conditions and one grid-point per cell. Simulations and experiments thus had similar spatial scales. For simulations of nucleation events in homogenous tissues (Fig. 3B), 300 × 300 cell grids with no-flux boundary conditions were implemented to match experimental conditions. The discrete Laplacian was implemented using the matlab del2 function (with default spacing) and solutions were time-integrated using Euler’s method with 10 kHz sampling.

The inward rectifying potassium current from K_ir2.1 was based on a model from ten Tusscher et al. ¹¹ as: $I_K=g_K{x}_{K\infty }\left(V\right)\left(V-E_K\right)$ with reversal potential at E_K = −90 mV. The parameter $x_{K\infty }\left(V\right)$ is a time-independent rectification factor that depends on voltage, with the following form:

$$x_{K\mathrm{\infty }}=x_0\frac{{\alpha }_K}{{\alpha }_K+{\beta }_K}$$

$${\alpha }_K=\frac{0.1}{1+e^{0.06(V-E_K-200)}}$$

$${\beta }_K=\frac{3e^{0.0002(V-E_K+100)}+e^{0.1\left(V-E_K-10\right)}}{1+e^{-0.5(V-E_K)}}$$

The scaling factor x₀ = 100 was introduced to make x_K∞ of order unity between −90 and −60 mV. In our simulations the conductance magnitude g_K was the only parameter varied to mimic changes in expression of K_ir2.1. The variable leak was modeled as an Ohmic conductance with reversal potential 0 mV. For homogeneous tissues all cells had identical K_ir2.1 and leak conductances.

To introduce disorder into the tissue, a fraction n_K of the cells were randomly assigned to express K_ir2.1 (all with conductance g_K) while the remaining cells had no K_ir2.1 expression (Supplementary Figs. 6, 7). Spatial correlations in K_ir2.1 expression were introduced by assigning a random number to each cell, independently sampled from a uniform distribution on [0, 1]. The values where then smoothed with a two-dimensional Gaussian kernel of width d. A threshold was selected so that a fraction n_K of the cells were above threshold. These cells were assigned to express K_ir2.1 with conductance g_K and cells below threshold did not express. The extent of the spatial correlations was tuned by varying d. In the simulation for Supplementary Figs. 7G,H, K_ir2.1 and CheRiff expression were heterogeneous, and independent of each other. The distribution of CheRiff expression was calculated following the same procedure as for K_ir2.1, using the same smoothing parameter, d, but different thresholds n_K, and n_ChR.

Cells in simulated tissues were first initialized to their cell-autonomous resting potential, i.e. the resting potential in the absence of influences from the neighbors. Bistable cells were initialized to the fixed point which had the greater area under the curve between it and the unstable fixed point. Tissues were then time-evolved to generate an initial steady state voltage profile. To simulate bioelectrical dynamics under changes in parameters, conductances were gradually changed over timescales slower than any of the internal relaxation dynamics. For simulations of domain boundary velocities in homogeneous tissues with bistable I-V curves (Supplementary Fig. 2), the left half of the tissue was initialized in a depolarized state and the right half in a hyperpolarized state.

Bi-HEK cell generation and culture

Genetic constructs encoding the inward rectifying potassium channel Kir2.1 and the blue-shifted channelrhodopsin CheRiff were separately cloned into lentiviral expression backbones (FCK-CMV) and then co-expressed in HEK 293T cells along with the lentiviral packaging plasmid PsPAX2 (Addgene) and the envelope plasmid VsVg (Addgene) via polyethylenimine transfection (Sigma). Lentiviral particles were harvest at 36 and 72 hours post-transfection, and then concentrated 20-fold using the Lenti-X concentrator system (Takara).

For experiments where nominally homogeneous expression was the goal (Figs. 2, 3), HEK cells were incubated with both K_ir2.1 and CheRiff lentiviral vectors for 48 hours prior to measurement, and then passaged and replated onto poly-D-lysine coated glass-bottom tissue culture dishes (MatTek). For patch clamp measurements (Supplementary Fig. 1), bi-HEKs were plated sparsely onto Matrigel coated dishes. For wide-field measurements (Fig. 3), adhesive islands were prepared by manually spotting poly-d-lysine onto MatTek plates. Bi-HEKs were plated onto these plates to create confluent patches of cells approximately 2 mm in diameter.

For experiments where disordered expression was the goal (Supplementary Fig. 7), K_ir2.1 and CheRiff constructs were transiently expressed (using Mirus 293T) in HEK cells which were then grown to confluence for an additional 72 hours prior to measurement. High-disorder samples were not replated prior to measurement.

hiPSC myoblast and myocyte differentiation

HiPSC-derived myoblasts were differentiated into myocyte fibers according to an established serum-free differentiation protocol.⁶¹ Briefly, 3–4 weeks old primary myogenic cultures generated from wild-type hiPSCs were dissociated as described and myogenic progenitors (myoblasts) were replated at low density (35–40k/cm²) onto Matrigel (Corning, Cat#354277)-coated dishes in skeletal muscle growth media (SKGM-2, Lonza CC-3245) with 10 μM ROCK inhibitor.⁶¹ After 24 hours, medium was changed to SKGM-2 media without ROCK inhibitor and incubated with low-titer lentivirus encoding CheRiff-CFP. Myoblast cultures were proliferated for up to 72 hours, at which point cultures reached ~90% confluence. Cultures were then induced for myogenic differentiation with DMEM/F12 supplemented with 2% knock-out serum replacement (Invitrogen, Cat. # 10828028), 10 μM of the TGFβ inhibitor SB431542 (Tocris, Cat. # 1614), 1 μM Chiron (Tocris, Cat. # 4423), 0.2% Pen/Strep (Life Technologies, Cat. # 15140122) and 1x ITS (Life Technologies, Cat. # 41400045). ⁶¹ Following induction, medium was changed on days 1 and 2 and then was refreshed every other day for up to 10 days post-differentiation to generate mature and fused myocyte fibers. Samples were measured between 0 and 3 days after start of differentiation (i.e., after 3 and 6 days in culture).

Immunostaining and imaging

Human iPSC-derived myocyte cultures were fixed for 20 minutes in 4% formaldehyde. Cultures were rinsed three times in phosphate-buffered saline (PBS), followed by blocking buffer composed of PBS supplemented with 10% fetal bovine serum (FBS) and 0.1% Triton X-100. Primary antibodies were then diluted in blocking buffer and incubated overnight at 4 °C. Cultures were then washed three times with PBST (PBS supplemented with 0.5% Tween-20) and incubated with secondary antibodies conjugated with an AlexaFluor dye (Molecular probes) and DAPI (5 μg/mL) in blocking buffer for 2 h at room temperature. Cultures were washed with PBST followed by PBS, followed by imaging. Antibodies were: anti-PAX7 (Developmental Studies Hybridoma Bank, DSHB), anti-Myogenin (Santa Cruz, SC-576X) and embryonic anti-MyHC (DSHB, F1.652).

Transcriptomic profiling: Library preparation and sequencing

RNA was extracted from cells using Trizol (Invitrogen) or with the RNeasy Mini Kit (Qiagen). Libraries were prepared using Roche Kapa mRNA HyperPrep sample preparation kits from 100 ng of purified total RNA according to the manufacturer’s protocol. The finished dsDNA libraries were quantified by Qubit fluorometer, Agilent TapeStation 2200, and RT-qPCR using the Kapa Biosystems library quantification kit according to manufacturer’s protocols. Uniquely indexed libraries were pooled in equimolar ratios and sequenced on two Illumina NextSeq500 runs with single-end 75bp reads by the Dana-Farber Cancer Institute Molecular Biology Core Facilities.

Transcriptomic profiling: RNAseq Analysis

Sequenced reads were aligned to the UCSC hg19 reference genome assembly and gene counts were quantified using STAR (v2.5.1b)⁶². Differential gene expression testing was performed by DESeq2 (v1.10.1)⁶³ and normalized read counts (FPKM) were calculated using cufflinks (v2.2.1)⁶⁴. RNAseq analysis was performed using the VIPER snakemake pipeline.⁶⁵

Patch clamp and all-optical electrophysiology

All electrophysiological measurements were performed in Tyrode’s solution, containing (in mM) 125 NaCl, 2 KCl, 2 CaCl₂, 1 MgCl₂, 10 HEPES, 30 glucose. The pH was adjusted to 7.3 with NaOH and the osmolality was adjusted to 305–310 mOsm with sucrose. Prior to measurements, 35-mm dishes were washed twice with 1 mL phosphate-buffered saline (PBS) to remove residual culture media, then filled with 2 mL Tyrode’s solution.

For patch clamp measurements, filamented glass micropipettes (WPI) were pulled to a resistance of 5–10 MΩ and filled with internal solution containing (in mM) 140 KCl, 1 MgCl₂, 10 EGTA, 10 HEPES, 3 Mg-ATP, pH adjusted to 7.3 with KOH. The patch electrode was controlled via a low-noise patch clamp amplifier (A-M Systems, model 2400). Voltage traces were collected under I = 0 current clamp mode, and current traces were collected in voltage clamp mode. Blue light for optical stimulation (Coherent Obis 488 nm) was modulated using an acousto-optic tunable filter (Gooch and Housego GH18A series). Patch clamp measurements were performed on small clusters of cells (approximately 6 cells).

Spatially resolved optical electrophysiology measurements were performed using a home-built upright ultra-widefield microscope⁶⁶ with a large field of view (4.6×4.6 mm², with 2.25×2.25 μm² pixel size) and high numerical aperture objective lens (Olympus MVPLAPO 2XC, NA 0.5). Fluorescence of BeRST1 was excited with a 639 nm laser (OptoEngine MLL-FN-639) at 100 mW/cm², illuminating the sample from below at an oblique angle to minimize background autofluorescence. BeRST1 fluorescence was separated from scattered laser excitation via a dichroic beam splitter (Semrock Di01- R405/488/561/635-t3-60×85) and an emission filter (Semrock FF01-708/75-60-D). Images were collected at 100 Hz frame rate on a Hamamatsu Orca Flash 4.2 scientific CMOS camera. Optogenetic stimulation was performed by exciting CheRiff with a blue LED (Thorlabs M470L3) with a maximum intensity of at 10 mW/cm².

Prior to measurement, cells were incubated with 1 μM BERST1 dye in phosphate buffered saline for 30 minutes in a tissue culture incubator. Samples were then washed and prepared in Tyrode’s solution immediately before imaging.

Data Analysis and Image Processing

Optical recordings of voltage-sensitive BeRST1 fluorescence were acquired for isolated cells, small clusters of cells (4–12 cells), and extended tissues (>2 mm linear size). Recordings were processed using custom MATLAB software. Briefly, to minimize uncorrelated shot-noise, movies were subjected to 4×4 binning, followed by pixel-by-pixel median filtering in the time domain (9 frame kernel). A background signal was calculated from a cell-free region of the field of view and subtracted from the region containing the cells. Mean sample images were generated by measuring the average fluorescence of the tissue prior to optogenetic stimulation. Functional recordings were divided pixel-wise by this baseline to generate movies of ΔF/F. Plots of voltage-dependent fluorescence were generated by averaging the time-lapse movies over the relevant region of interest (e.g. small clusters for 0D data; localized spots within extended cell culture islands for 2D local measurements; and over entire cell culture islands for 2D mean measurements).

Statistical Analysis

Statistical analysis was performed on optical electrophysiology recordings from immature myocyte precursors to assess the significance of population-level differences in electrophysiological phenotypes at different time points. Measurements were performed on populations of isolated cells taken at 3 and 6 days in culture (see hiPSC myoblast and myocyte differentiation methods above). Fluorescent recordings of voltage were acquired for 100 ms prior to illumination, during a 40 s ramp of blue light (increasing from 0 to 10 mW/cm² for 20 s, then decreasing for 20 s), and then for 5 s after the blue light was turned off. Raw acquisitions were converted to ΔF/F for further analysis.

Electrophysiological phenotypes were parameterized by calculating the total endpoint hysteresis and the mean integral hysteresis for each identified cell (Supplementary Fig. 8). Endpoint hysteresis was defined as the difference in ΔF/F between the 5 s at the end of the acquisition and the 100 ms at the start of the acquisition. Integral hysteresis was defined as the difference between the mean ΔF/F over the decreasing phase of the blue light ramp and the mean ΔF/F during the increasing phase of the blue light ramp (each averaged over the corresponding full 20 s ramp).

In each sample, individual cells which responded to CheRiff stimulation were first manually identified via an overall mean ΔF/F image. 51 and 89 cells were identified in the day 3 and day 6 measurements, respectively. Endpoint hysteresis and mean hysteresis were then calculated for each identified cell, and a cell was sorted as hysteresis-positive if it demonstrated a value greater than 0.3 for either measure (Supplementary Fig. 8). Cells which showed endpoint hysteresis > 0.3 were sorted into the endpoint hysteresis cluster, regardless of their integral hysteresis value. Cells with integral hysteresis > 0.3 and endpoint hysteresis < 0.3 were sorted into the integral hysteresis cluster.

Model parameters

Default model parameters were as follows:

Parameter	Explanation
Cm = 10 pF	Single cell capacitance
l = 10 μm	Size of an individual cell; discretization size of simulated tissues
EK = −90 mV	Potassium reversal potential
EChR = 0 mV	Channelrhodopsin reversal potential
Eleak = −20 mV	Additional leakage reversal potential. Used for myocyte models (Fig. 4) and for model of disorder-induced domain formation (Supplementary Fig. 7).
GCxn = 2 nS/pF × l2  = 200 (nS/pF) × μm2	Strength of gap junction coupling between bi-HEK cells
nKir = 0 – 1	Proportion of cells initialized to express Kir2.1
nChR = 0.75 – 1	Proportion of cells initialized to express CheRiff. Expression is uniform (nChR = 1) in all panels except for Supplementary Fig. 7H (in which nChR = 0.75).
d = 0.001 to 10 cells	Width of gaussian smoothing kernel used to introduce spatial correlations in Kir2.1 expression
gK = 0 – 500 pS/pF	Kir2.1 conductance. This conductance is multiplied by the inward rectifying function xK∞.
x0 = 100	Scaling factor to set xK∞ to order unity between EK and the point of maximum outward current (Vmax ∼ −69 mV)
gChR, = 0 to 100 pS/pF	Conductance of the channelrhodopsin CheRiff. Varied continuously in simulations of blue light intensity ramps.
gleak = 5 pS/pF	Additional leak conductance added to myocyte model

Model parameters for figure panels:

Figure panel	Parameters
2C	gChR, = 50 pS/pF, gK = 200 pS/pF
2D	gChR, = 1 to 200 pS/pF, gK = 200 pS/pF
3A	imax = 0.54 pA/pF gChR = 50 pS/pF, gK = 200 pS/pF, nKir = 1
3B, top	gChR = 70 pS/pF, gK = 200 pS/pF, nKir = 1
3B, bottom	gChR = 60 pS/pF, gK = 200 pS/pF, nKir = 1
3C	gChR, = 1 to 200 pS/pF, gK = 200 pS/pF, nKir = 1
4E	gleak, = 100 pS/pF, gChR = 0.1 to 300 pS/pF (ramped), gK = 120, 240, 480 pS/pF (left, middle, and right panels)
S2B	gChR = 24.5 pS/pF, gK = 60, 72.5, 85, 97.5 pS/pF (top to bottom)
S2C	gChR = 22 pS/pF, nKir = 1
S6B	gK = 1 to 500 pS/pF, gChR = 20 pS/pF, nKir = 1
S6D,E	gK = 500 pS/pF, gChR = 20 pS/pF, d = 0.001, nKir = 0 to 1
S6G,H	gK = 500 pS/pF, gChR = 20 pS/pF, d = 10, nKir = 0 to 1
S7C,D	gK = 50 pS/pF, gleak = 20 pS/pF, Eleak = −20 mV, d = 3, nKir = 0.25, gChR= 0 to 250 pS/pF
S7G,H	gChR, = 1 to 300 pS/pF, gK = 600 pS/pF, nKir = 0.5, nChR = 0.75, d = 1.5
S8A	gleak, = 100 pS/pF, gChR = 0.1 to 300 pS/pF (ramped), gK = 120, 240, 480 pS/pF (left, middle, and right panels)

For simulations in S2 and S6, the channelrhodopsin and leak conductances were equivalent (i.e. there was a single ohmic leak conductance in the model with E_leak = E_ChR = 0 mV. For simulations of the three-conductance myocyte model in Figs. 4, S7 and S8, two separate Ohmic conductances were included (with E_leak = −20 mV, E_ChR = 0 mV).