Abstract
Iterative neural networks (INN) are rapidly gaining attention for solving inverse problems in imaging, image processing, and computer vision. INNs combine regression NNs and an iterative model-based image reconstruction (MBIR) algorithm, often leading to both good generalization capability and outperforming reconstruction quality over existing MBIR optimization models. This paper proposes the first fast and convergent INN architecture, Momentum-Net, by generalizing a block-wise MBIR algorithm that uses momentum and majorizers with regression NNs. For fast MBIR, Momentum-Net uses momentum terms in extrapolation modules, and noniterative MBIR modules at each iteration by using majorizers, where each iteration of Momentum-Net consists of three core modules: image refining, extrapolation, and MBIR. Momentum-Net guarantees convergence to a fixed-point for general differentiable (non)convex MBIR functions (or data-fit terms) and convex feasible sets, under two asymptomatic conditions. To consider data-fit variations across training and testing samples, we also propose a regularization parameter selection scheme based on the “spectral spread” of majorization matrices. Numerical experiments for light-field photography using a focal stack and sparse-view computational tomography demonstrate that, given identical regression NN architectures, Momentum-Net significantly improves MBIR speed and accuracy over several existing INNs; it significantly improves reconstruction quality compared to a state-of-the-art MBIR method in each application.
Keywords: Iterative neural network, deep learning, model-based image reconstruction, inverse problems, block proximal extrapolated gradient method, block coordinate descent method, light-field photography, X-ray computational tomography
1. INTRODUCTION
Deep regression neural network (NN) methods have been actively studied for solving diverse inverse problems, due to their effectiveness at mapping noisy signals into clean signals. Examples include image denoising [1]–[4], image deconvolution [5], [6], image super-resolution [7], [8], magnetic resonance imaging (MRI) [9], [10], X-ray computational tomography (CT) [11]–[13], and light-field (LF) photography [14], [15]. However, regression NNs with a greater mapping capability have increased overfitting/hallucination risks [16]–[19]. An alternative approach to solving inverse problems is an iterative NN (INN) that combines regression NNs – called “refiners” or denoisers – with an unrolled iterative model-based image reconstruction (MBIR) algorithm [20]–[27]. This alternative approach can regulate overfitting of regression NNs, by balancing physical data-fit of MBIR and prior information estimated by refining NNs [16], [18]. This “soft-refiner” approach has been successfully applied to several extreme imaging systems, e.g., highly undersampled MRI [20], [25], [28]–[30], low-dose or sparse-view CT [16], [19], [24], [27], [31], and low-count emission tomography [18], [32]–[34].
1.1. Notation
This section provides mathematical notations. We use f(x; y) to denote a function f of x given y. We use ∥·∥p to denote the ℓp-norm and write ⟨·,·⟩ for the standard inner product on . The weighted ℓ2-norm with a Hermitian positive definite matrix A is denoted by . The Frobenius norm of a matrix is denoted by ∥ · ∥F. (·)T, (·)H, and (·)∗ indicate the transpose, complex conjugate transpose (Hermitian transpose), and complex conjugate, respectively. diag(·) denotes the conversion of a vector into a diagonal matrix or diagonal elements of a matrix into a vector. For (self-adjoint) matrices , the notation B ⪯ A denotes that A − B is a positive semidefinite matrix.
1.2. From block-wise optimization to INN
To recover signals from measurements , consider the following MBIR optimization problem:
| (P0) |
where is a set of feasible points, f(x; y) is data-fit function, γ is a regularization parameter, and is some high-quality approximation to the true unknown signal x. The data-fit f(x; y) measures deviations of model-based predictions of x from data y, considering models of imaging physics (or image formation) and noise statistics in y. In (P0), the signal recovery accuracy increases as the quality of z improves [17, Prop. 3]; however, it is difficult to obtain such z in practice. Alternatively, there has been a growing trend in learning sparsifying regularizers (e.g., convolutional regularizers [24], [35]–[38]) from training datasets and applying the trained regularizers to the following block-wise MBIR problem: . Here, a learned regularizer quantifies consistency between x and refined sparse signal ζ via some learned operators . Recently, we have constructed INNs by generalizing the corresponding block-wise MBIR updates with regression NNs without convergence analysis [25], [27]. In existing INNs, two major challenges exist: convergence and acceleration.
1.3. Challenges in existing INNs: Convergence
Existing convergence analysis has some practical limitations. The original form of plug-and-play (PnP [23], [39]–[41]) is motivated by the alternating direction method of multipliers (ADMM [42]), and its fixed-point convergence has been analyzed with consensus equilibrium perspectives [23]. However, similar to ADMM, its practical convergence depends on how one selects ADMM penalty parameters. For example, [22] reported unstable convergence behaviors of PnP-ADMM with fixed ADMM parameters. To moderate this problem, [41] proposed a scheme that adaptively controls the ADMM parameters based on relative residuals. Similar to the residual balancing technique [42, §3.4.1], the scheme in [41] requires tuning initial parameters. Regularization by Denoising (RED [22]) is an alternative that moderates some such limitations. In particular, RED aims to make a clear connection between optimization and a denoiser , by defining its prior term by (scaled) . Nonetheless, [43] showed that many practical denoisers do not satisfy the Jacobian symmetry in [22], and proposed a less restrictive method, score-matching by denoising.
The convergence analysis of the INN inspired by the relaxed projected gradient descent (RPGD) method in [31] has the least restrictive conditions on the regression NN among the existing INNs. This method replaces the projector of a projected gradient descent method with an image refining NN. However, the RPGD-inspired INN directly applies an image refining NN to gradient descent updates of data-fit; thus, this INN relies heavily on the mapping performance of a refining NN and can have overfitting risks, similar to non-MBIR regression NNs, e.g., FBPConvNet [12]. In addition, it exploits the data-fit term only for the first few iterations [31, Fig. 5(c)]. We refer the perspective used in RPGD-inspired INN and its related works [26], [44] as “hard-refiner”: different from soft-refiners, these methods do not use a refining NN as a regularizer. More recently, [26] presented convergence analysis for an INN inspired by a proximal gradient descent method. However, their analysis is based on noiseless measurements, which is typically impractical.
Fig. 5.
RMSE minimization comparisons between different INNs for sparse-view CT (fan-beam geometry with 12.5% projections views and 105 incident photons; averaged RMSE values across two test reconstructed images).
Broadly speaking, existing convergence analysis largely depends on the (firmly) nonexpansive property of image refining NNs [22], [23], [43], [31, PGD], [26]. However, except for a single-hidden layer convolutional NN (CNN), it is yet unclear which analytical conditions guarantee the non-expansiveness of general refining NNs [27]. To guarantee convergence of INNs even when using possibly expansive image refining NNs, we proposed a method that normalizes the output signal of image refining NNs by their Lipschitz constants [27]. However, if one uses expansive NNs that are identical across iterations, it is difficult to obtain “best” image recovery with that normalization scheme. The spectral normalization based training [45], [46] can ensure the non-expansiveness of refining NNs by single-step power iteration. However, similar to the normalization method in [27], refining NNs trained with the spectral normalization method [46] degraded the image reconstruction accuracy for an INN using iteration-wise refining NNs [19]. In addition, there does not yet exist theoretical convergence results when refining NNs change across iterations, yet iteration-wise refining NNs are widely studied [20], [21], [25], [28]. Finally, existing analysis considers only a narrow class of data-fit terms: most analyses consider a quadratic function with a linear imaging model [26], [31] or more generally, a convex cost function [23], [43], [46] that can be minimized with a practical closed-form solution. No theoretical convergence results exist for general (non)convex data-fit terms, iteration-wise NN denoisers, and a general set of feasible points.
1.4. Challenges in existing INNs: Acceleration
Compared to non-MBIR regression NNs that do not exploit the data-fit f(x; y) in (P0), INNs require more computation because they consider the imaging physics. Computation increases as the imaging system or image formation model becomes larger-scale, e.g., LF photography from a focal stack, 3D CT, parallel MRI using many receive coils, and image super-resolution. Thus, acceleration becomes crucial for INNs.
First, consider the existing methods motivated by ADMM or block coordinate descent (BCD) method: examples include PnP-ADMM [23], [41], RED-ADMM [22], [43], MoDL [30], BCD-Net [16], [18], [25], etc. These methods can require multiple inner iterations to balance data-fit and prior information estimated by trained refining NNs, increasing total MBIR time. For example, in solving such problems, each outer iteration involves x(i+1) = argminx F(x; y, z(i+1)), where F is given as in (P0) and z(i+1) is the output from the ith image refining NN. For LF imaging system using a focal stack data [47], solving the above problem requires multiple iterations, and the total computational cost scale with the numbers of photosensors and sub-aperture images. In addition, nonconvexity of the data-fit term f(x; y) can break convergence guarantees of these methods, because in general, the proximal mapping is no longer nonexpansive.
Second, consider the existing works motivated by gradient descent methods [21], [26], [28], [31]. These methods resolve the inner iteration issue; however, they lack a sophisticated step-size control or backtracking scheme that influences convergence guarantee and acceleration. Accelerated proximal gradient (APG) methods using momentum terms can significantly accelerate convergence rates for solving composite convex problems [48], [49], so we expect that INN methods in the second class have yet to be maximally accelerated. The work in [44] applied PnP to the APG method [49]; [50] applied PnP to the primal-dual splitting (PDS) algorithm [51]. However, similar to RPGD [31], these are hard-refiner methods using some state-of-the-art denoisiers (e.g., BM3D [52]) but not trained NNs. Those methods lack convergence analyses and guarantees may be limited to convex data-fit function.
1.5. Contributions and organization of the paper
This paper proposes Momentum-Net, the first INN architecture that aims for fast and convergent MBIR. The architecture of Momentum-Net is motivated by applying the Block Proximal Extrapolated Gradient method using a Majorizer (BPEG-M) [24], [35] to MBIR using trainable convolutional autoencoders [24], [25], [37]. Specifically, each iteration of Momentum-Net consists of three core modules: image refining, extrapolation, and MBIR. At each Momentum-Net iteration, an extrapolation module uses momentum from previous updates to amplify the changes in subsequent iterations and accelerate convergence, and an MBIR module is noniterative. In addition, Momentum-Net resolves the convergence issues mentioned in §1.3: for general differentiable (non)convex data-fit terms and convex feasible sets, it guarantees convergence to a point that satisfies fixed-point and critical point conditions, under some mild conditions and two asymptotic conditions, i.e., asymptotically nonexpansive paired refining NNs and asymptotically block-coordinate minimizer.
The remainder of this paper is organized as follows. §2 constructs the Momentum-Net architecture motivated by BPEG-M algorithm that solves MBIR problem using a learnable convolutional regularizer, describes its relation to existing works, analyzes its convergence, and summarizes the benefits of Momentum-Net over existing INNs. §3 provides details of training INNs, including image refining NN architectures, single-hidden layer or “shallow” CNN (sCNN) and multi-hidden layer or “deep” CNN (dCNN), and training loss function, and proposes a regularization parameter selection scheme to consider data-fit variations across training and testing samples. §4 considers two extreme imaging applications: sparse-view CT and LF photography using a focal stack. §4 reports numerical experiments of applications where the proposed Momentum-Net using extrapolation significantly improves MBIR speed and accuracy, over the existing INNs, BCD-Net [22], [25], [30], Momentum-Net using no extrapolation [21], [28], ADMM-Net [20], [23], [41], and PnP-PDS [50] using refining NNs. Furthermore, §4 reports numerical experiments where Momentum-Net significantly improves reconstruction quality compared to a state-of-the-art MBIR method in each application.
2. MOMENTUM-NET: WHERE BPEG-M MEETS NNS FOR INVERSE PROBLEMS
2.1. Motivation: BPEG-M algorithm for MBIR using learnable convolutional regularizer
This section motivates the proposed Momentum-Net architecture, based on our previous works [24], [37]. Consider the following approach for recovering signal x from measurements y (see the setup of block multi-(non)convex problems in §A.1.1):
| (1) |
where is a closed set, f(x; y) + γr(x, {ζk}; {hk}) is a (continuosly) differentiable (non)convex function in x, is a learnable convolutional regularizer [24], [36], {ζk : k=1, …, K} is a set of sparse features that correspond to {hk ∗x}, is a set of trainable filters, and R and K denote the size and number of trained filters, respectively.
Problem (1) can be viewed as a two-block optimization problem in terms of the image x and the features {ζk}. We solve (1) using the recent BPEG-M optimization framework [24], [35] that has attractive convergence guarantee and rapidly solved several block optimization problems [24], [35], [53]–[55]. BPEG-M has the following key ideas for each block optimization problem (see details in §A.1):
-
Mb-Lipschitz continuity for the gradient of the bth block optimization problem, ∀b:
Definition 1 (M-Lipschitz continuity [24]).
A function is M-Lipschitz continuous on if there exists a (symmetric) positive definite matrix M such thatDefinition 1 is a more general concept than the classical Lipschitz continuity.
-
A sharper majorization matrix M that gives a tighter bound in Definition 1 leads to a tighter quadratic majorization bound in the following lemma:
Lemma 2 (Quadratic majorization via M-Lipschitz continuous gradients [24]). Let . If ∇f is M-Lipschitz continuous, thenHaving tighter majorization bounds, sharper majorization matrices tend to accelerate BPEG-M convergence.
- The majorized block problems are “proximable”, i.e., proximal mapping of majorized function is “easily” computable depending on the properties of bth block majorizer and regularizer, Mb and rb, where the proximal mapping operator is defined by
(2) Block-wise extrapolation and momentum terms to accelerate convergence.
Suppose that 1) gradient of f(x; y) + γr(x, {ζk}; {hk}) is M-Lipschitz continuous at an extrapolated point , ∀i; 2) filters in (1) satisfy the tight-frame (TF) condition, , ∀u for some boundary conditions [24]. Applying the BPEG-M framework (see Algorithm A.1) to solving (1) leads to the following block updates:
| (3) |
| (4) |
| (5) |
where E(i+1) is an extrapolation matrix that is given in (8) or (9) below, is a (scaled) majorization matrix for ∇F(x; y, z(i+1)) that is given in (7) below, ∀i, the proximal operator in (5) is given by (2), and is the characteristic function of set (i.e., equals to 0 if , and ∞ otherwise).
Proximal mapping update (3) has a single-hidden layer convolutional autoencoder architecture that consists of encoding convolution, nonlinear thresholding, and decoding convolution, where flip(·) flips a filter along each dimension, and the soft-thresholding operator is defined by
| (6) |
for n = 1, …, N, in which sign(·) is the sign function. See details of deriving BPEG-M updates (3)–(5) in §A.1.4. The BPEG-M updates in (3)–(5) guarantee convergence to a critical point, when MBIR problem (1) satisfies some mild conditions, e.g., lower-boundedness and existence of critical points; see Assumption S.1 in §A.1.3.
The following section generalizes the BPEG-M updates in (3)–(5) and constructs the Momentum-Net architecture.
2.2. Architecture
This section establishes the INN architecture of Momentum-Net by generalizing BPEG-M updates (3)–(5) that solve (1). Specifically, we replace the proximal mapping in (3) with a general image refining NN , where θ denotes the trainable parameters. To effectively remove iteration-wise artifacts and give “best” signal estimates at each iteration, we further generalize a refining NN to iteration-wise image refining NNs , where θ(i+1) denotes the parameters for the ith iteration refining NN , and Niter is the number of Momentum-Net iterations. The iteration-wise NNs are particularly useful for reducing overfitting risks in regression, because is responsible for removing noise features only at the ith iteration, and thus one does not need to greatly increase dimensions of its parameter θ(i+1) [16], [18]. In low-dose CT reconstruction, for example, the refining NNs at the early and later iterations remove streak artifacts and Gaussian-like noise, respectively [16].
Algorithm 1.
Momentum-Net
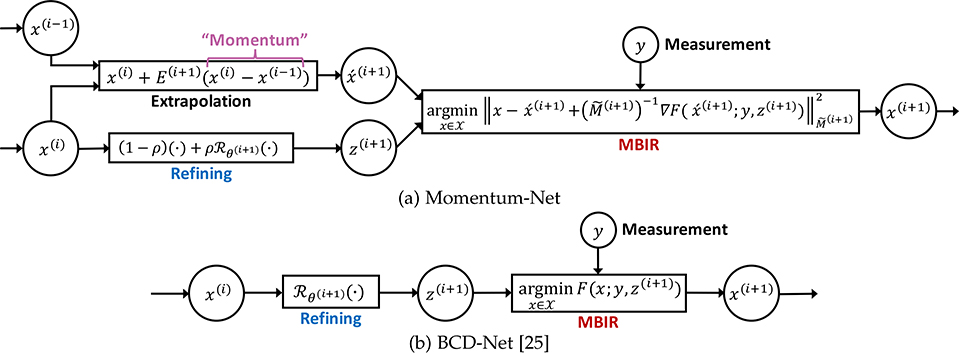
Each iteration of Momentum-Net consists of 1) image refining, 2) extrapolation, and 3) MBIR modules, corresponding to the BPEG-M updates (3), (4), and (5), respectively. See the architecture of Momentum-Net in Fig. 1(a) and Algorithm 1. At the ith iteration, Momentum-Net performs the following three processes:
Fig. 1.
Architectures of different INNs for MBIR. (a–b) The architectures of Momentum-Net and BCD-Net [25] are constructed by generalizing BPEG-M and BCD algorithms that solve MBIR problem using a convolutional regularizer trained via convolutional analysis operator learning (CAOL) [24], [36], respectively. (a) Removing extrapolation modules (i.e., setting the extrapolation matrices {E(i+1) : ∀i} as a zero matrix), Momentum-Net specializes to the existing gradient-descent-inspired INNs [21], [28]. When the MBIR cost function F(x; y, z(i+1)) in (P1) has a sharp majorizer , ∀i, Momentum-Net (using ρ≈1) specializes to BCD-Net; see Examples 5–6. (b) BCD-Net is a general version of the existing INNs in [20], [22], [23], [30], [39]–[41] by using iteration-wise image refining NNs, i.e., , or considering general convex data-fit f(x; y).
Refining: The ith image refining module gives the “refined” image z(i+1), by applying the ith refining NN, , to an input image at the ith iteration, x(i) (i.e., image estimate from the (i − 1)th iteration). Different from existing INNs, e.g., ADMM-Net [20], PnP-ADMM [23], [41], RED [22], MoDL [30], BCD-Net [25] (see Fig. 1(b)), TNRD [21], [28], we apply ρ-relaxation with ρ ∈ (0, 1); see (Alg.1.1). The parameter ρ controls the strength of inference from refining NNs, but does not affect the convergence guarantee of Momentum-Net. Proper selection of ρ can improve MBIR accuracy (see §A.10).
Extrapolation: The ith extrapolation module gives the extrapolated point , based on momentum terms x(i) −x(i−1); see (Alg.1.2). Intuitively speaking, momentum is information from previous updates to amplify the changes in subsequent iterations. Its effectiveness has been shown in diverse optimization literature, e.g., convex optimization [48], [49] and block optimization [24], [35].
MBIR: Given a refined image z(i+1) and a measurement vector y, the ith MBIR module (Alg.1.3) applies the proximal operator to the extrapolated gradient update using a quadratic majorizer of F(x; y, z(i+1)), where F is defined in (P0). Intuitively speaking, this step solves a majorized version of the following MBIR problem at the extrapolated point :
| (P1) |
and gives a reconstructed image x(i+1). In Momentum-Net, we consider (non)convex differentiable MBIR cost functions F with M-Lipschitz continuous gradients, and a convex and closed set . For a wide range of large-scale inverse imaging problems, the majorized MBIR problem (Alg.1.3) has a practical closed-form solution and thus, does not require an iterative solver, depending on the properties of practically invertible majorization matrices M(i+1) and constraints. Examples of combinations that give a noniterative solution for (Alg.1.3) include scaled identity and diagonal matrices with a box constraint and the non-negativity constraint, and matrices decomposable by unitary transforms, e.g., a circulant matrix [56], [57], with . The updated image x(i+1) is the input to the next Momentum-Net iteration.
The followings are details of Momentum-Net in Algorithm 1. A scaled majorization matrix is
| (7) |
where is a symmetric positive definite majorization matrix of ∇F(x; y, z(i+1)) in the sense of M-Lipschitz continuity (see Definition 1). In (7), λ = 1 and λ > 1 for convex and nonconvex F(x; y, z(i+1)) (or convex and nonconvex f(x; y)), respectively. We design the extrapolation matrices as follows:
for convex F,
| (8) |
for nonconvex F,
| (9) |
for some δ < 1 and {0 ≤ m(i) ≤ 1 : ∀i}. We update the momentum coefficients {m(i+1) : ∀i} by the following formula [24], [35]:
| (10) |
if F(x; y, z(i+1)) has a sharp majorizer, i.e., ∇F(x; y, z(i+1)) has M(i+1) such that the corresponding bound in Definition 1 is tight, then we set m(i+1) = 0, ∀i. §A.11 lists parameters of Momentum-Net, and summarizes selection guidelines or gives default values.
2.3. Relations to previous works
Several existing MBIR methods can be viewed as a special case of Momentum-Net:
Example 3. (MBIR model (1) using convolutional autoencoders that satisfy the TF condition [24]). The BPEG-M updates in (3)–(5) are special cases of the modules in Momentum-Net (Algorithm 1), with flip (i.e., single hidden-layer convolutional autoencoder [24]) and ρ ≈ 1. These give a clear mathematical connection between a denoiser (3) and cost function (1). One can find a similar relation between a multi-layer CNN and a multi-layer convolutional regularizer [24, Appx.].
Example 4. (INNs inspired by gradient descent method, e.g., TNRD [21], [28]). Removing extrapolation modules, i.e., setting {E(i+1) = 0 : ∀i} in (Alg.1.2), and setting ρ ≈ 1, Momentum-Net becomes the existing INN in [21], [28].
Example 5. (BCD-Net for image denoising [25]). To obtain a clean image from a noisy image corrupted by an additive white Gaussian noise (AWGN), MBIR problem (P1) considers the data-fit with the inverse covariance matrix , where σ2 is a variance of AWGN, and the box constraint with an upper bound U > 0. For this f(x; y), the MBIR module (Alg.1.3) can use the exact majorizer and one does not need to use the extrapolation module (Alg.1.2), i.e., {E(i+1) = 0}. Thus, Momentum-Net (with ρ ≈ 1) becomes BCD-Net.
Example 6. (BCD-Net for undersampled single-coil MRI [25]). To obtain an object magnetization from a k-space data obtained by undersampling (e.g., compressed sensing [58]) MRI, MBIR problem (P1) considers the data-fit with an undersampling Fourier operator A (disregarding relaxation effects and considering Cartesian k-space), the inverse covariance matrix , where σ2 is a variance of complex AWGN [59], and . For this f(x; y), the MBIR module (Alg.1.3) can use the exact majorizer that is practically invertible, where Fdisc is the discrete Fourier transform and P is a diagonal matrix with either 0 or 1 (their positions correspond to sampling pattern in k-space), and the extrapolation module (Alg.1.2) uses the zero extrapolation matrices {E(i+1) = 0}. Thus, Momentum-Net (with ρ ≈ 1) becomes BCD-Net.
The following section analyzes the convergence of Momentum-Net.
2.4. Convergence analysis
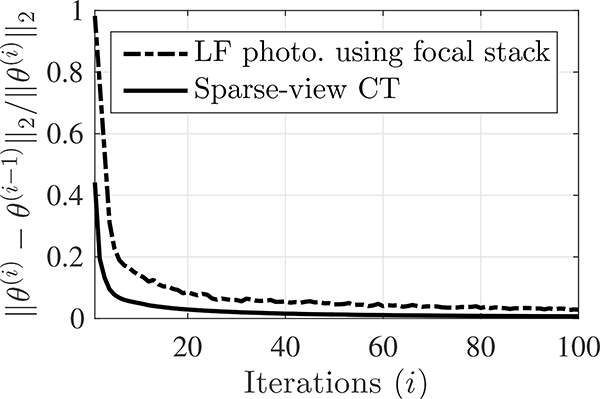
In practice, INNs, i.e., “unrolled” or PnP methods using refining NNs, are trained and used with a specific number of iterations. Nevertheless, similar to optimization algorithms, studying convergence properties of INNs with Niter → ∞ [23], [31], [46] is important; in particular, it is crucial to know if a given INN tends to converge as Niter increases. For INNs using iteration-wise refining NNs, e.g., BCD-Net [25] and proposed Momentum-Net, we expect that refiners converge, i.e., their image refining capacity converges, because information provided by data-fit function f(x; y) in MBIR (e.g., likelihood) reaches some “bound” after a certain number of iterations. Fig. 2 illustrates that dCNN parameters of Momentum-Net tend to converge for different applications. (The similar behavior was reported for sCNN refiners in BCD-Net [16].) Although refiners do not completely converge, in practice, one could use a refining NN at a sufficiently large iteration number, e.g., Niter = 100 in Momentum-Net, for the later iterations.
Fig. 2.
Convergence behavior of Momentum-Net’s dCNNs refiners in different applications (θ(i) denotes the parameter vector of the ith iteration refiner , for i=1, …, Niter; see details of in (19) and §4.2.1; Niter = 100). Sparse-view CT (fan-beam geometry with 12.5% projections views): quickly converges, where majorization matrices of training data-fits have similar condition numbers. LF photography using a focal stack (five detectors and reconstructed LFs consists of 9×9 sub-aperture images): has slower convergence, where majorization matrices of training data-fits have largely different condition numbers.
There are two key challenges in analyzing the convergence of Momentum-Net in Algorithm 1: both challenges relate to its image refining modules (Alg.1.1). First, image refining NNs change across iterations; even if they are identical across iterations, they are not necessarily nonexpansive operators [60], [61] in practice. Second, the iteration-wise refining NNs are not necessarily proximal mapping operators, i.e., they are not written explicitly in the form of (2). This section proposes two new asymptotic definitions to overcome these challenges, and then uses those conditions to analyze convergence properties of Momentum-Net in Algorithm 1.
2.4.1. Preliminaries
To resolve the challenge of iteration-wise refining NNs and the practical difficulty in guaranteeing their non-expansiveness, we introduce the following generalized definition of the non-expansiveness [60], [61].
Definition 7 (Asymptotically nonexpansive paired operators). A sequence of paired operators is asymptotically nonexpansive if there exist a summable nonnegative sequence such that1
| (11) |
When and , Definition 7 becomes the standard non-expansiveness of a mapping operator . If we replace the inequality (≤) with the strict inequality (<) in (11), then we say that the sequence of paired operators is asymptotically contractive. (This stronger assumption is used to prove convergence of BCD-Net in Proposition A.5.) Definition 7 also implies that mapping operators converge to some nonexpansive operator, if the corresponding parameters θ(i+1) converge.
Definition 7 incorporates a pairing property because Momentum-Net uses iteration-wise image refining NNs. Specifically, the pairing property helps prove convergence of Momentum-Net, by connecting image refining NNs at adjacent iterations. Furthermore, the asymptotic property in Definition 7 allows Momentum-Net to use expansive refining NNs (i.e., mapping operators having a Lipschitz constant larger than 1) for some iterations, while guaranteeing convergence; see Figs. 3(a3) and 3(b3). Suppose that refining NNs are identical across iterations, i.e., , ∀i, similar to some existing INNs, e.g., PnP [23], RED [22], and other methods in §1.3. In such cases, if is expansive, Momentum-Net may diverge; this property corresponds to the limitation of existing methods described in §1.3. Momentum-Net moderates this issue by using iteration-wise refining NNs that satisfy the asymptotic paired non-expansiveness in Definition 7.
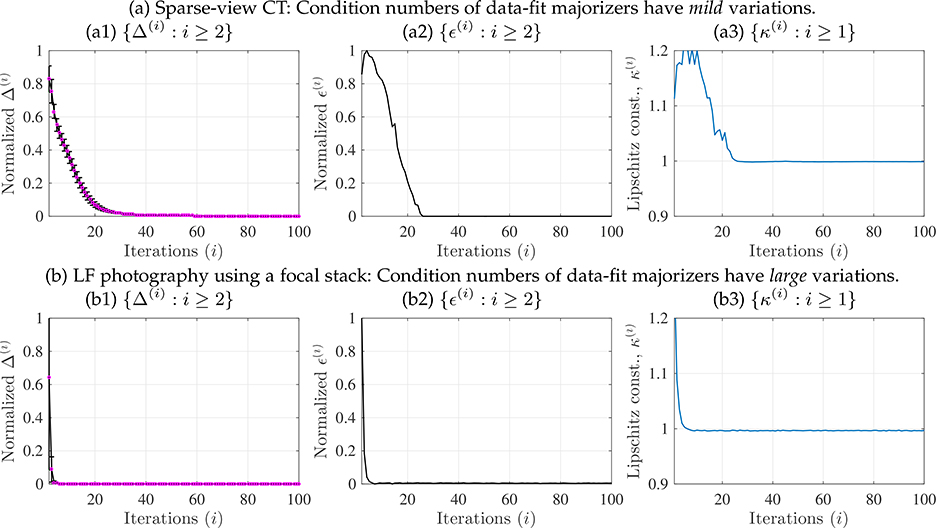
Fig. 3.
Empirical measures related to Assumption 4 for guaranteeing convergence of Momentum-Net using dCNNs refiners (for details, see (19) and §4.2.1), in different applications. See estimation procedures in §A.2. (a) The sparse-view CT reconstruction experiment used fan-beam geometry with 12.5% projections views. (b) The LF photography experiment used five detectors and reconstructed LFs consisting of 9×9 sub-aperture images. (a1, b1) For both the applications, we observed that Δ(i) → 0. This implies that the z(i+1)-updates in (Alg.1.1) satisfy the asymptotic block-coordinate minimizer condition in Assumption 4. (Magenta dots denote the mean values and black vertical error bars denote standard deviations.) (a2) Momentum-Net trained from training data-fits, where their majorization matrices have mild condition number variations, shows that ϵ(i) → 0. This implies that paired NNs in (Alg.1.1) are asymptotically nonexpansive. (b2) Momentum-Net trained from training training data-fits, where their majorization matrices have mild condition number variations, shows that ϵ(i) becomes close to zero, but does not converge to zero in one hundred iterations. (a3, b3) The NNs, in (Alg.1.1), become nonexpansive, i.e., its Lipschitz constant κ(i) becomes less than 1, as i increases.
Because the sequence {z(i+1) : ∀i} in (Alg.1.1) is not necessarily updated with a proximal mapping, we introduce a generalized definition of block-coordinate minimizers [53, (2.3)] for z(i+1)-updates:
Definition 8 (Asymptotic block-coordinate minimizer). The update z(i+1) is an asymptotic block-coordinate minimizer if there exists a summable nonnegative sequence such that
| (12) |
Definition 8 implies that as i → ∞, the updates {z(i+1) : i ≥ 0} approach a block-coordinate minimizer trajectory that satisfies (12) with {Δ(i+1) = 0 : i ≥ 0}. In particular, Δ(i+1) quantifies how much the update z(i+1) in (Alg.1.1) perturbs a block-coordinate minimizer trajectory. The bound always holds, ∀i, when one uses the proximal mapping in (3) within the BPEG-M framework. While applying trained Momentum-Net, (12) is easy to examine empirically, whereas (11) is harder to check.
2.4.2. Assumptions
This section introduces and interprets the assumptions for convergence analysis of Momentum-Net in Algorithm 1:
Assumption 1) In MBIR problems (P1), (non)convex F(x; y, z(i+1)) is (continuously) differentiable, proper, and lower-bounded in dom(F),2 ∀i, and is convex and closed. Algorithm 1 has a fixed-point.
Assumption 2) ∇F(x; y, z(i+1)) is M(i+1)-Lipschitz continuous with respect to x (see Definition 1), where M(i+1) is a iteration-wise majorization matrix that satisfies with 0 < mF,min ≤ m F,max < ∞, ∀i.
Assumption 3) The extrapolation matrices E(i+1) ⪰ 0 in (8)–(9) satisfy the following conditions:
for convex F,
| (13) |
for nonconvex F,
| (14) |
Assumption 4) The sequence of paired operators is asymptotically nonexpansive with a summable sequence {ϵ(i+i) ≥ 0}; the update z(i+1) is an asymptotic block-coordinate minimizer with a summable sequence {Δ(i+i) ≥ 0}. The mapping functions are continuous with respect to input points and the corresponding parameters {θ(i+1) : ∀i} are bounded.
Assumption 1 is a slight modification of Assumption S.1 of BPEG-M, and Assumptions 2–3 are identical to Assumptions S.2–S.3 of BPEG-M; see Assumptions S.1–S.3 in §A.1.3. The extrapolation matrix designs (8) and (9) satisfy conditions (13) and (14) in Assumption 3, respectively.
We provide empirical justifications for the first two conditions in Assumption 4. First, Figs. 3(a2) and A.1(a2) illustrate that paired refining NNs of Momentum-Net appear to be asymptotically nonexpansive in an application that has mild condition number variations across training data-fit majorization matrices. Figs. 3(a3), 3(b3), A.1(a3), and A.1(b3) illustrate for different applications that refining NNs become nonexpansive: their Lipschitz constants at the first several iterations are larger than 1, and their Lipschitz constants in later iterations become less than 1. Alternatively, the asymptotic non-expansiveness of paired operators can be satisfied by a stronger assumption that the sequence converges to some nonexpansive operator. (Fig. 2 illustrates that dCNN parameters of Momentum-Net appear to converge.)
Figs. 3(a3), 3(b3), A.1(a3), and A.1(b3) illustrate for different applications that the z(i+1)-updates are asymptotic block-coordinate minimizers. Lemma A.4 and §A.3 in the appendices provide a probabilistic justification for the asymptotic block-coordinate minimizer condition.
2.4.3. Main convergence results
This section analyzes fixed-point and critical point convergence of Momentum-Net in Algorithm 1, under the assumptions in the previous section. We first show that differences between two consecutive iterates generated by Momentum-Net converge to zero:
Proposition 9 (Convergence properties). Under Assumptions 1–4, let {x(i+1), z(i+1) : i ≥ 0} be the sequence generated by Algorithm 1. Then, the sequence satisfies
| (15) |
and hence .
Proof. See §A.4 in the appendices.
Using Proposition 9, our main theorem provides that any limit points of the sequence generated by Momentum-Net satisfy critical point and fixed-point conditions:
Theorem 10 (A limit point satisfies both critical point and fixed-point conditions). Under Assumptions 1–4 above, let {x(i+1), z(i+1) : i ≥ 0} be the sequence generated by Algorithm 1. Consider either a fixed majorization matrix with general structure, i.e., M(i+1) = M for i ≥ 0, or a sequence of diagonal majorization matrices, i.e., {M(i+1) : i ≥ 0}. Then, any limit point of {x(i+1)} satisfies both the critical point condition:
| (16) |
where is a limit point of {z(i+1)}, and the fixed-point condition:
| (17) |
where , denotes performing the ith updates in Algorithm 1, and and is a limit point of {θ(i+1)} and {M(i+1)}, respectively.
Proof. See §A.5 in the appendices.
Observe that, if or is an interior point of , (16) reduces to the first-order optimality condition , where ∂F(x) denotes the limiting subdifferential of F at x. With additional isolation and boundedness assumptions for the points satisfying (16) and (17), we obtain whole sequence guarantees:
Corollary 11 (Whole sequence convergence). Consider the construction in Theorem 10. Let be the set of points satisfying the critical point condition in (16) and the fixed-point condition in (17). If {x(i+1) : i ≥ 0} is bounded, then , where denotes the distance from u to , for any point and any subset . If contains uniformly isolated points, i.e., there exists η > 0 such that ∥u−v∥ ≥ η for any distinct points , then {x(i+1)} converges to a point in .
Proof. See §A.6 in the appendices.
The boundedness assumption for {x(i+1)} in Corollary 11 is standard in block-wise optimization, e.g., [24], [35], [53], [55], [62]. The assumption can be satisfied if the set is bounded (e.g., box constraints), one chooses appropriate regularization parameters in Algorithm 1 [24], [35], [55], the function F(x; y, z) is coercive [62], or the level set is bounded [53]. However, for general F(x; y, z), it is hard to verify the isolation condition for the points in in practice. Instead, one may use Kurdyka-Łojasiewicz property [53], [62] to analyze the whole sequence convergence with some appropriate modifications.
For simplicity, we focused our discussion to noniterative MBIR module (Alg.1.3). However, Momentum-Net practically converges with any proximable MRIR function (Alg.1.3) that may need an iterative solver, if sufficient inner iterations are used. To maximize the computational benefit of Momentum-Net, one needs to make sure that majorized MBIR function (Alg.1.3) is better proximable over its original form (P1).
2.5. Benefits of Momentum-Net
Momentum-Net has several benefits over existing INNs:
Benefits from refining module: The image refining module (Alg.1.1) can use iteration-wise image refining NNs : those are particularly useful to reduce overfitting risks by reducing dimensions of their parameters θ(i+1) at each iteration [16], [18], [19]. Iteration-wise refining NNs require less memory for training, compared to methods that use a single refining NN for all iterations, e.g., [63]. Different from the existing methods mentioned in §1.3, Momentum-Net does not require (firmly) nonexpansive mapping operators to guarantee convergence. Instead, in (Alg.1.1) assumes a generalized notion of the (firm) non-expansiveness condition assumed for convergence of the existing methods that use identical refining NNs across iterations, including PnP [20], [23], [39]–[41], [46], RED [22], [43], etc. The generalized concept is the first practical condition to guarantee convergence of INNs using iteration-wise refining NNs; see Definition 7.
Benefits from extrapolation module: The extrapolation module (Alg.1.2) uses the momentum terms x(i) − x(i−1) that accelerate the convergence of Momentum-Net. In particular, compared to the existing gradient-descent-inspired INNs, e.g., TNRD [21], [28], Momentum-Net converges faster. (Note that the way the authors of [43] used momentum is less conventional. The corresponding method, RED-APG [43, Alg. 6], still can require multiple inner iterations to solve its quadratic MBIR problem, similar to BCD-Net-type methods.)
Benefits from MBIR module: The MBIR module (Alg.1.3) does not require multiple inner iterations for a wide range of imaging problems and has both theoretical and practical benefits. Note first that convergence analysis of INNs (including Momentum-Net) assumes that their MBIR operators are noniterative. In other words, related convergence theory (e.g., Proposition A.5) is inapplicable if iterative methods, particularly with insufficient number of iterations, are applied to MBIR modules. Different from the existing BCD-Net-type methods [20], [22], [23], [25], [30], [39]–[41], [43] that can require iterative solvers for their MBIR modules, MBIR module (Alg.1.3) of Momentum-Net can have practical close-form solution (see examples in §2.2), and its corresponding convergence analysis (see §2.4) can hold stably for a wide range of imaging applications. Second, combined with extrapolation module (Alg.1.2), noniterative MBIR modules (Alg.1.3) lead to faster MBIR, compared to the existing BCD-Net-type methods that can require multiple inner iterations for their MBIR modules for convergence. Third, Momentum-Net guarantees convergence even for nonconvex MBIR cost function F(x; y, z) or nonconvex data-fit f(x; y) of which the gradient is M-Lipschitz continuous (see Definition 1), while existing INNs overlooked nonconvex F(x; y, z) or f(x; y).
Furthermore, §A.7 analyzes the sequence convergence of BCD-Net [25], and describes the convergence benefits of Momentum-Net over BCD-Net.
3. TRAINING INNS
This section describes training of all the INNs compared in this paper.
3.1. Architecture of refining NNs and their training
For all INNs in this paper, we train the refining NN at each iteration to remove artifacts from the input image x(i) that is fed from the previous iteration. For the ith iteration NN, we first consider the following sCNN architecture, residual single-hidden layer convolutional autoencoder:
| (18) |
where is the parameter set of the ith image refining NN, is a set of K decoding and encoding filters of size R, is a set of K thresholding values, and is the soft-thresholding operator with parameter α defined in (6), for i = 0, …, Niter −1. We use the exponential function exp(·) to prevent the thresholding parameters {αk} from becoming negative during training. We observed that the residual convolutional autoencoder in (18) gives better results compared to the convolutional autoencoder, i.e., (18) without the second term [18], [25]. This corresponds to the empirical result in [64], [65] that having skip connections (e.g., the second term in (18)) can improve generalization. The sequence of paired sCNN refiners (18) can satisfy the asymptotic non-expansiveness, if its convergent refiner satisfies that
where σmax(·) is the largest eigenvalue of a matrix, are limit point filters, and δR is the Kronecker delta filter of size R.
For dCNN refiners, we use the following residual multi-layer CNN architecture, a simplified DnCNN [4] using fewer layers, no pooling, and no batch normalization [46] (we drop superscript indices (·)(i) for simplicity):
| (19) |
for k = 1, …, K and l = 2, …, L−1, where is the parameter set of each refining NN, K is the number of feature maps, L is the number of layers, is a set of filters at the first and last dCNN layer, is a set of filters for remaining dCNN layer, and the rectified linear unit activation function is defined by .
The training process of Momentum-Net requires S high-quality training images, {xs : s=1, …, S}, S training measurements simulated via imaging physics, {ys : s=1, …, S}, and S data-fits {fs(x; ys) : s = 1, …, S} and the corresponding majorization matrices . Different from [16], [25], [66] that train convolutional autoencoders from the patch perspective, we train the image refining NNs in (18)–(19) from the convolution perspective (that does not store many overlapping patches, e.g., see [24]). From S training pairs , where is a set of S reconstructed images at the (i−1)th Momentum-Net iteration, we train the ith iteration image refining NN in (18) by solving the following optimization problem:
| (P2) |
where θ(i+1) is given as in (18), for i = 0, …, Niter − 1 (see some related properties in §A.8). We solve the training optimization problems (P2) by mini-batch stochastic optimization with the subdifferentials computed by the PyTorch Autograd package.
3.2. Regularization parameter selection based on “spectral spread”
When majorization matrices of training data-fits {fs(x; ys) : s=1, …, S} have similar spectral properties, e.g., condition numbers, the regularization parameter γ in (P1) is trainable by substituting (Alg.1.1) into (Alg.1.3) and modifying the training cost (P2). However, the condition numbers of data-fit majorizers can greatly differ due a variety of imaging geometries or image formation systems, or noise levels in training measurements, etc. See such examples in §4.1–4.2.
To train Momentum-Net with diverse training data-fits, we propose a parameter selection scheme based on the “spectral spread” of their majorization matrices . For simplicity, consider majorization matrices of the form , where the factor λ is selected by (7) and is a symmetric positive semidefinite majorization matrix for fs(x; ys), ∀s. We select the regularization parameter γs for the sth training sample as
| (20) |
where the spectral spread of a symmetric positive definite matrix is defined by for , and σmin(·) is the smallest eigenvalue of a matrix. For the sth training sample, a tunable factor χ controls γs in (20) according to , ∀s. The proposed parameter selection scheme also applies to testing Momentum-Net, based on the tuned factor χ⁎ in its training. We observed that the proposed parameter selection scheme (20) gives better MBIR accuracy than the condition number based selection scheme that is similarly used in selecting ADMM parameters [17] (for the two applications in §4). One may further apply this scheme to iteration-wise majorization matrices and select iteration-wise regularization parameters accordingly. For comparing different INNs, we apply (20) to all INNs.
4. EXPERIMENTAL RESULTS AND DISCUSSION
We investigated two extreme imaging applications: sparse-view CT and LF photography using a focal stack. In particular, these two applications lack a practical closed-form solution for the MBIR modules of BCD-Net and ADMM-Net [20], e.g., solving (Alg.2.2). For these applications, we compared the performances of the following five INNs: BCD-Net [25] (i.e., generalization of RED [22] and MoDL [30]), ADMM-Net [20], i.e., PnP-ADMM [23], [41] using iteration-wise refining NNs, Momentum-Net without extrapolation (i.e., generalization of TNRD [21], [28]), PDS-Net, i.e., PnP-PDS [50] using iteration-wise refining NNs, and the proposed Momentum-Net using extrapolation.
4.1. Experimental setup: Imaging
4.1.1. Sparse-view CT
To reconstruct a linear attenuation coefficient image from post-log sinogram in sparse-view CT, the MBIR problem (P1) considers a data-fit and the non-negativity constraint , where is an undersampled CT system matrix, is a diagonal weighting matrix with elements based on a Poisson-Gaussian model [17], [67] for the pre-log raw measurements with electronic readout noise variance σ2.
We simulated 2D sparse-view sinograms of size m = 888×123 – ‘detectors or rays’ × ‘regularly spaced projection views or angles’, where 984 is the number of full views – with GE LightSpeed fan-beam geometry corresponding to a monoenergetic source with 105 incident photons per ray and no background events, and electronic noise variance σ2 =52. We avoided an inverse crime in imaging simulation and reconstructed images of size N =420×420 with a coarser grid Δx=Δy =0.9766 mm; see details in [37, §V-A2].
4.1.2. LF photography using a focal stack
To reconstruct a LF that consists of C′ sub-aperture images from focal stack measurements that are collected by C photosensors, the MBIR problem (P1) considers a data-fit and a box constraint with U =1 (or 255 without rescaling), where is a system matrix of LF imaging system using a focal stack that is constructed blockwise with C · C′ different convolution matrices [47], [68], τc ∈ (0, 1] is a transparency coefficient for the cth detector, and N′ is the size of sub-aperture images, , ∀c′.3
Algorithm 2.
BCD-Net [25]
| Require: , γ > 0, x(0) = x(−1), y | ||
| for i = 0, …, Niter−1 do | ||
Image refining:
| ||
MBIR:
| ||
| end for |
In general, a LF photography system using a focal stack is extremely under-determined, because C ≪ C′.
To avoid an inverse crime, our imaging simulation used higher-resolution synthetic LF dataset [70] (we converted the original RGB sub-aperture images to grayscale ones by the “rgb2gray.m” function in MATLAB, for simplicity and smaller memory requirements in training). We simulated C =5 focal stack images of size N′ =255×255 with 40 dB AWGN that models electronic noise at sensors, and setting transparency coefficients τc as 1, for c=1, …, C. The sensor positions were chosen such that five sensors focus at equally spaced depths; specifically, the closest sensor to scenes and farthest sensor from scenes focus at two different depths that correspond to ‘dispmin+ 0.2’ and ‘dispmax− 0.2’, respectively, where dispmax and dispmin are the approximate maximum and minimum disparity values specified in [70]. We reconstructed 4D LFs that consist of S = 9 × 9 sub-aperture images of size N′ =255×255, with a coarser grid Δx=Δy =0.13572 mm.
4.2. Experimental setup: INNs
4.2.1. Parameters of INNs
The parameters for the INNs compared in sparse-view CT experiments were defined as follows. We considered two BCD-Nets (see Algorithm 2): for one BCD-Net, we applied the APG method [49] with 10 inner iterations to (Alg.2.2), and set Niter = 30; for the other BCD-Net, we applied the APG method with 3 inner iterations to (Alg.2.2), and set Niter = 45. For ADMM-Net, we used the identical configurations as BCD-Net and set the ADMM penalty parameter to γ in (P1), similar to [16]. For Momentum-Net without extrapolation, we chose Niter = 100 and ρ = 1 − ε. For the proposed Momentum-Net, we chose Niter = 100 and ρ = 0.5. For PDS-Net, we set the first step size to γ1 = γ−1 and the second step size to , per [50]. For performance comparisons between different INNs, all the INNs used sCNN refiners (18) with {R,K = 72} to avoid the overfitting/hallucination risks. For Momentum-Net using dCNN refiners, we chose L=4 layer dCNN (19) using R = 32 filters and K = 64 feature maps, following [46]. (The chosen parameters gave lower RMSE values than {L=6, R=33, K=64}, for identical regularization parameters.) For comparing different MBIR methods, Momentum used extrapolation, i.e., (Alg.1.2) with (8) and (10), and {R = 72, K = 92} for (18). We designed the majorization matrices as , using Lemma A.7 (A and W have nonnegative entries) and setting λ=1 by (7). We set an initial point of INNs, x(0), to filtered-back projection (FBP) using a Hanning window. The regularization parameters of all INNs were selected by the scheme in §3.2 with χ⁎ = 167.64. (This factor was estimated from the carefully chosen regularization parameter for sparse-view CT MBIR experiments using learned convolutional regularizers in [24].)
The parameters for the INNs compared in experiments of LF photography using a focal stack were defined as follows. We considered two BCD-Nets and two ADMM-Nets with the identical parameters listed above. For Momentum-Net without extrapolation and the proposed Momentum-Net, we set Niter = 100 and ρ = 1 − ε. For PDS-Net, we used the identical parameter setup described above. For performance comparisons between different INNs, all the INNs used sCNN refiners (18) with {R = 52, K = 32} (to avoid the overfitting risks) in the epipolar domain. For Momentum-Net using dCNN refiners, we chose L=6 layer dCNN (19) using R = 32 filters and K = 16 feature maps. (The chosen parameters gave most accurate performances over the following setups, {L = 4, R = 32, K = 16, 32, 64}, given the identical regularization parameters.) To generate in (Alg.1.1), we applied a sCNN (18) with {R=52, K =32} or a dCNN (19) with {L=6, R=32, K = 16} to two sets of horizontal and vertical epipolar plane images, and took the average of two LFs that were permuted back from refined horizontal and vertical epipolar plane image sets, ∀i.4 We designed the majorization matrices as , using Lemma A.7 and setting λ = 1 by (7). We set an initial point of INNs, x(0), to ATy rescaled in the interval [0,1] (i.e., dividing by its max value). The regularization parameters (i.e., γ in BCD-Net/Momentum-Net, the ADMM penalty parameter in ADMM-Net, and the first step size in PDS-Net) were selected by the proposed scheme in §3.2 with χ⁎ =1.5. (We tuned the factor to achieve the best performances).
For different combinations of INNs and sCNN refiner (18)/dCNN refiner (19), we use the following naming convention: ‘the INN name’-’sCNN’ or ‘dCNN’.
4.2.2. Training INNs
For sparse-view CT experiments, we trained all the INNs from the chest CT dataset with ; we constructed the dataset by using XCAT phantom slices [71]. The CT experiment has mild data-fit variations across training samples: the standard deviation of the condition numbers of is 1.1. For experiments of LF photography using a focal stack, we trained all the INNs from the LF photography dataset with and two sets of ground truth epipolar images, {xs,epi-h, xs,epi-v : s = 1, …, S, S = 21·(255·9)}; we constructed the dataset by excluding four unrealistic “stratified” scenes from the original LF dataset in [70] that consists of 28 LFs with diverse scene parameter and camera settings. The LF experiment has large data-fit variations across training samples: the standard deviation of the condition numbers of is 2245.5.
In training INNs for both the applications, if not specified, we used identical training setups. At each iteration of INNs, we solved (P2) with the mini-batch version of Adam [72] and trained iteration-wise sCNNs (18) or dCNNs (19). We selected the batch size and the number of epochs as follows: for sparse-view CT reconstruction, we chose them as 20 & 300, and 20 & 200 for sCNN and dCNN refiners, respectively; for LF photography using a focal stack, we chose them as 200 & 200, and 200 & 100, for sCNN and dCNN refiners, respectively. We chose the learning rates for (encoding/decoding) filters and thresholding values in sCNNs (18), as 10−3 and 10−1, respectively; we reduced the learning rates by 10% every 10 epochs. At the first iteration, we initialized filter coefficients with Kaiming uniform initialization [73]; in the later iteration, i.e., at the ith INN iteration, for i ≥ 2, we initialized filter coefficients from those learned from the previous iteration, i.e., (i−1)th iteration (this also applies to initializing thresholding values).
4.2.3. Testing trained INNs
In sparse-view CT reconstruction experiments, we tested trained INNs to two samples where ground truth images and the corresponding inverse covariance matrices (i.e., W in §4.1.1) sufficiently differ from those in training samples (i.e., they are a few cm away from training images). We evaluated the reconstruction quality by the most conventional error metric in CT application, RMSE (in HU), in a region of interest (ROI), where RMSE and HU stand for root-mean-square error and (modified) Hounsfield unit, respectively, and the ROI was a circular region that includes all the phantom tissues. The RMSE is defined by , where x⁎ is a reconstructed image, xtrue is a ground truth image, and NROI is the number of pixels in a ROI. In addition, we compared the trained Momentum-Net (using extrapolation) to a standard MBIR method using a hand-crafted EP regularizer, and an MBIR model using a learned convolutional regularizer [24], [37] which is the state-of-the-art MBIR method within an unsupervised learning setup. We finely tuned their regularization parameters to achieve the lowest RMSE. See details of these two MBIR models in §A.9.2.
In experiments of LF photography using a focal stack, we tested trained INNs to three samples of which scene parameter and camera settings are different from those in training samples (all training and testing samples have different camera and scene parameters). We evaluated the reconstruction quality by the most conventional error metric in LF photography application, PSNR (in dB), where PSNR stands for peak signal-to-noise. In addition, we compared the trained Momentum-Net (using extrapolation) to MBIR method using the state-of-the-art non-trained regularizer, 4D EP introduced in [47]. (The low-rank plus sparse tensor decomposition model [68], [74] failed when inverse crimes and measurement noise are considered.) We finely tuned its regularization parameter to achieve the lowest RMSE values. See details of this MBIR model in §A.9.3. We further investigated impacts of the LF MBIR quality on a higher-level depth estimation application, by applying the robust Spinning Parallelogram Operator (SPO) depth estimation method [75] to reconstructed LFs.
For comparing Momentum-Net with PDS-Net, we measured quality of refined images, z(i+1) in (Alg.1.1), because PDS-Net is a hard-refiner.
The imaging simulation and reconstruction experiments were based on the Michigan image reconstruction toolbox [76], and training INNs, i.e., solving (P2), was based on PyTorch (for sparse-view CT, we used ver. 1.2.0; for LF photography using a focal stack, we used ver. 0.3.1). For sparse-view CT, single-precision MATLAB and PyTorch implementations were tested on 2.6 GHz Intel Core i7 CPU with 16 GB RAM, and 1405 MHz Nvidia Titan Xp GPU with 12 GB RAM, respectively. For LF photography using a focal stack, they were tested on 3.5 GHz AMD Threadripper 1920X CPU with 32 GB RAM, and 1531 MHz Nvidia GTX 1080 Ti GPU with 11 GB RAM, respectively.
4.3. Comparisons between different INNs
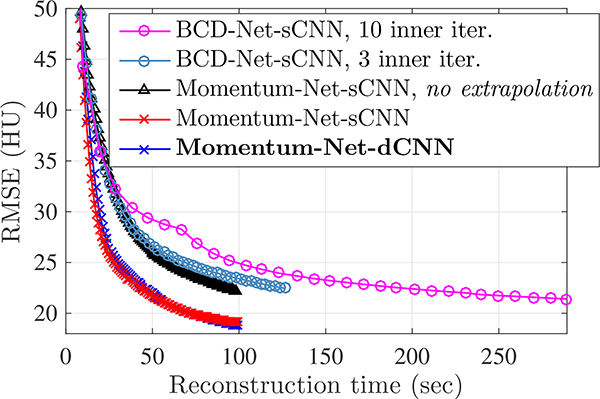
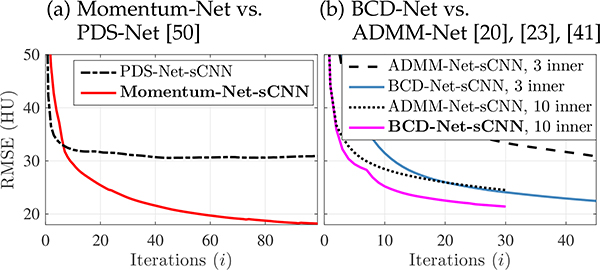
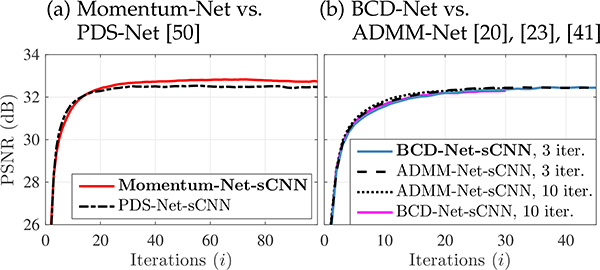
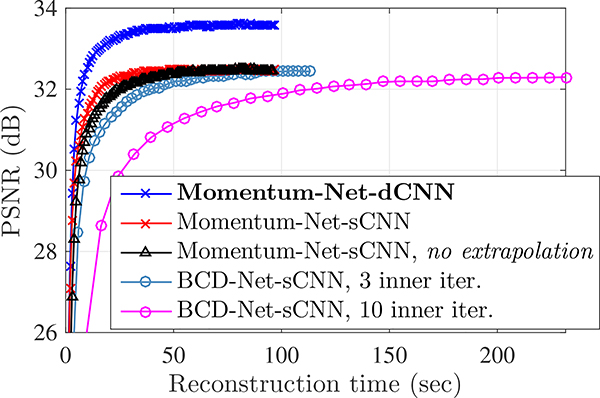
First, compare sCNN results in Figs. 4–5 and Figs. 6–7, for sparse-view CT and LF photography using a focal stack, respectively. For both applications, the proposed Momentum-Net using extrapolation significantly improves MBIR speed and accuracy, compared to the existing soft-refining INNs, [21]–[23], [28], [30] that correspond to BCD-Net [25] or Momentum-Net using no extrapolation, and ADMM-Net [20], [23], [41], and the existing hard-refining INN PDS-Net [50]. (Note that BCD-Net and Momentum-Net require slightly less computational complexity per INN iteration, compared to ADMM-Net and PDS-Net, respectively, due to having fewer modules.) Fig. 5 shows that to reach the 24 HU RMSE value in sparse-view CT reconstruction, the proposed Momentum-Net decreases MBIR time by 53.3% and 62.5%, compared to Momentum-Net without extrapolation and BCD-Net using three inner iterations, respectively. Fig. 7 shows that to reach the 32 dB PSNR value in LF reconstruction from a focal stack, the proposed Momentum-Net decreases MBIR time by 36.5% and 61.5%, compared to Momentum-Net without extrapolation and BCD-Net using three inner iterations, respectively. In addition, Figs. 5 and 7 show that using extrapolation, i.e., (Alg.1.2) with (8)–(10), improves the performance of Momentum-Net versus iterations.
Fig. 4.
RMSE minimization comparisons between different INNs for sparse-view CT (fan-beam geometry with 12:5% projections views and 105 incident photons; (a) averaged RMSE values across two test refined images; (b) averaged RMSE values across two test reconstructed images).
Fig. 6.
PSNR maximization comparisons between different INNs in LF photography using a focal stack (LF photography systems with C = 5 detectors obtain a focal stack of LFs consisting of S =81 sub-aperture images; (a) averaged RMSE values across two test refined images); (b) averaged RMSE values across two test reconstructed images.
Fig. 7.
PSNR maximization comparisons between different INNs in LF photography using a focal stack (LF photography systems with C = 5 detectors obtain a focal stack of LFs consisting of S =81 sub-aperture images; averaged PSNR values across three test reconstructed images).
We conjecture that the larger performance gap between soft-refiner Momentum-Net and hard-refiner PDS-Net, in Fig. 4(a) compared to Fig. 6(a), is because the LF problem needs stronger regularization, i.e., a smaller tuned factor χ⁎ in (20), than the CT problem. Similarly, comparing Fig. 4(b) to Fig. 6(b) shows that the LF problem has small performance gaps between BCD-Net and ADMM-Net.
For both the applications, using dCNN refiners (19) instead of sCNN refiners (18) has a negligible effect on total run time of Momentum-Net, because reconstruction time of MBIR modules (Alg.1.3) (in CPUs) dominates inference time of image refining modules (Alg.1.1) (in GPUs). Compare results between Momentum-Net-sCNN and -dCNN in Figs. 5 & 7 and Tables A.1 & A.2.
4.4. Comparisons between different MBIR methods
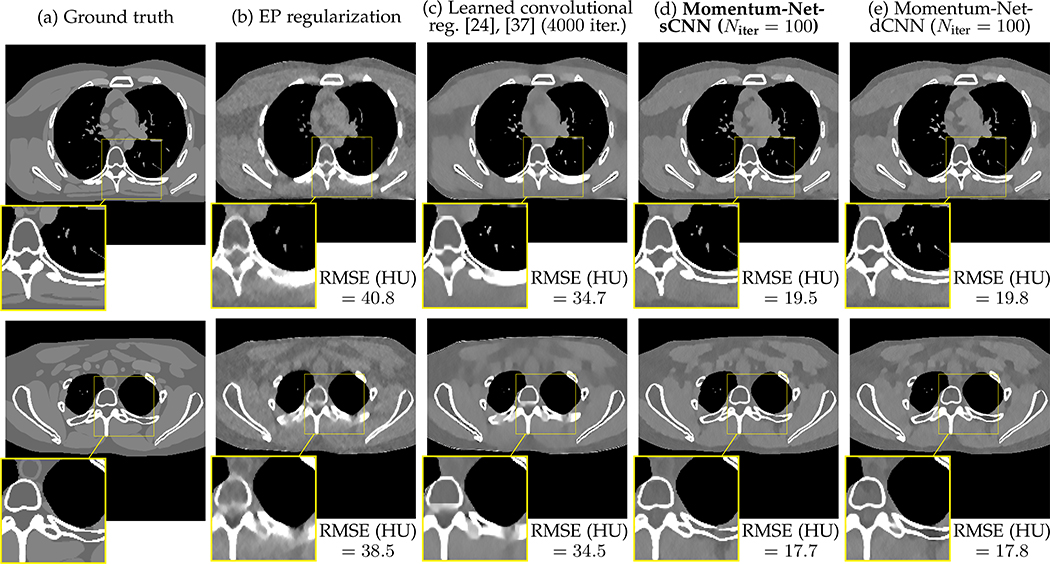
In sparse-view CT using 12.5% of the full projection views, Fig. 8(b)–(e) and Table A.1(b)–(f) show that the proposed Momentum-Net achieves significantly better reconstruction quality compared to the conventional EP MBIR method and the state-of-the-art MBIR method within an unsupervised learning setup, MBIR model using a learned convolutional regularizer [24], [37]. In particular, Momentum-Net recovers both low- and high-contrast regions (e.g., soft tissues and bones, respectively) more accurately than MBIR using a learned convolutional regularizer; see Fig. 8(c)–(e). In addition, when their shallow convolutional autoencoders need identical computational complexities, Momentum-Net achieves much faster MBIR compared to MBIR using a learned convolutional regularizer; see Table A.1(c)–(d).
Fig. 8.
Comparison of reconstructed images from different MBIR methods in sparse-view CT (fan-beam geometry with 12.5% projections views and 105 incident photons; images outside zoom-in boxes are magnified to better show differences; display window [800,1200] HU). See also Fig. A.2.
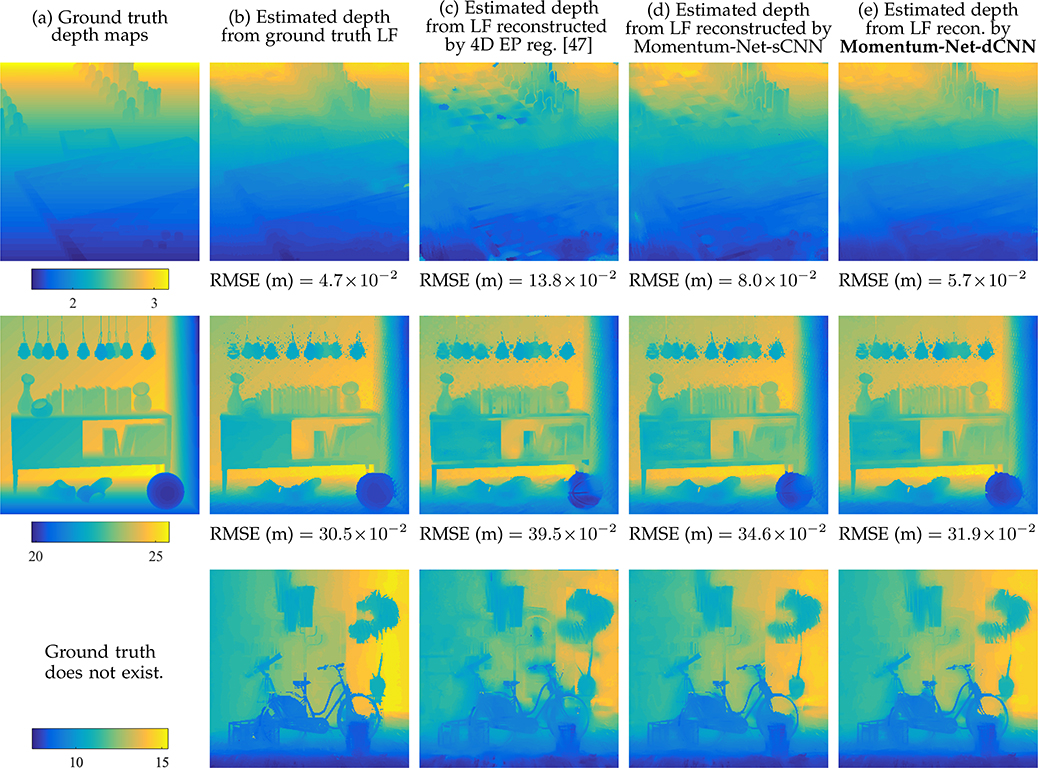
In LF photography using five focal sensors, regardless of scene parameters and camera settings, Momentum-Net consistently achieves significantly more accurate image recovery, compared to MBIR model using the state-of-the-art non-trained regularizer, 4D EP [47]. The effectiveness of Momentum-Net is more evident for a scene with less fine details. See Fig. 9(b)–(d) and Table A.2(b)–(d). Regardless of the scene distances from LF imaging systems, the reconstructed LFs by Momentum-Net significantly improve the depth estimation accuracy over those reconstructed by the state-of-the-art non-trained regularizer, 4D EP [47]. See Fig. 10(c)–(e) and Table A.3(c)–(e).
Fig. 9.
Error map comparisons of reconstructed sub-aperture images from different MBIR methods in LF photography using a focal stack (LF photography systems with C = 5 detectors capture a focal stack of LFs consisting of S = 81 sub-aperture images; sub-aperture images at the (5,5)th angular coordinate; the PSNR values in parenthesis were measured from reconstructed LFs). See also Fig. A.2.
Fig. 10.
Comparisons of estimated depths from LFs reconstructed by different MBIR methods in LF photograph using a focal stack (LF photography systems with C = 5 detectors capture a focal stack of LFs consisting of S = 81 sub-aperture images; SPO depth estimation [75] was applied to reconstructed LFs in Fig. 9; display window in meters). See also Fig. A.2.
In general, Momentum-Net needs more computations per iteration than EP MBIR, because its refining NNs use more and larger filters than the small finite-difference filters in EP MBIR, and EP MBIR algorithms can be often further accelerated by gradient approximations, e.g., ordered-subsets methods [77], [78].
5. CONCLUSIONS
Developing rapidly converging INNs is important, because 1) it leads to fast MBIR by reducing the computational complexity in calculating data-fit gradients or applying refining NNs, and 2) training INNs with many iterations requires long training time or it is challenging when refining NNs are fixed across INN iterations. The proposed Momentum-Net framework is applicable for a wide range of inverse problems, while achieving fast and convergent MBIR. To achieve fast MBIR, Momentum-Net uses momentum in extrapolation modules, and noniterative MBIR modules at each iteration via majorizers. For sparse-view CT and LF photography using a focal stack, Momentum-Net achieves faster and more accurate MBIR compared to the existing soft-refining INNs, [21]–[23], [28], [30] that correspond to BCD-Net [25] or Momentum-Net using no extrapolation, and ADMM-Net [20], [23], [41], and the existing hard-refining INN PDS-Net [50]. When an application needs strong regularization strength, e.g., LF photography using limited detectors, using dCNN refiners with moderate depth significantly improves the MBIR accuracy of Momentum-Net compared to sCNNs, only marginally increasing total MBIR time. In addition, Momentum-Net guarantees convergence to a fixed-point for general differentiable (non)convex MBIR functions (or data-fit terms) and convex feasible sets, under some mild conditions and two asymptotic conditions. The proposed regularization parameter selection scheme uses the “spectral spread” of majorization matrices, and is useful to consider data-fit variations across training/testing samples.
There are a number of avenues for future work. First, we expect to further improve performances of Momentum-Net (e.g., MBIR time and accuracy) by using sharper majorizer designs. Second, we expect to further reduce MBIR time of Momentum-Net with the stochastic gradient perspective (e.g., ordered subset [77], [78]). On the regularization parameter selection side, our future work is learning the factor χ in (20) from datasets while training refining NNs.
Supplementary Material
Acknowledgments
This work is supported in part by the Keck Foundation, NIH U01 EB018753, NIH R01 EB023618, NIH R01 EB022075, and NSF IIS 1838179.
Biography

Il Yong Chun (S’14–M’16) is a tenure-track Assistant Professor of EE at the University of Hawai’i, Mānoa (UHM). He received B.Eng. degree from Korea University in 2009, and the Ph.D. degree from Purdue University in 2015, both in electrical engineering. During his Ph.D., he worked with Intel Labs, Samsung Advanced Institute of Technology, and Neuroscience Research Institute, as a Research Intern or a Visiting Lecturer. Prior to joining UHM, he was a Postdoctoral Research Associate in Mathematics, Purdue University, and a Research Fellow in EECS, the University of Michigan, from 2015 to 2016 and from 2016 to 2019, respectively. His research interests include machine learning & artificial intelligence, optimization, compressed sensing, and adaptive signal processing, applied to medical imaging, computational photography, and biomedical image computing.

Zhengyu Huang received the B.S. degree in Physics from Hong Kong Baptist University in 2015 and is now pursuing Ph.D. degree in electrical and computer engineering at the University of Michigan. His research interests include image reconstruction, optics and deep learning. In particular, he is interested in applying deep learning methods to novel imaging systems for light field reconstruction and depth estimation.

Hongki Lim (S’17) received the B.S.E.E. degree from Inha University in 2012 and the Ph.D. degree in electrical and computer engineering from the University of Michigan in 2020. Before starting PhD program at University of Michigan, he worked at the strategic planning team of Samsung Electronics for two years. His research interest includes image reconstruction, medical image analysis, and deep learning.

Jeffrey A. Fessler (F’06) is the William L. Root Professor of EECS at the University of Michigan. He received the BSEE degree from Purdue University in 1985, the MSEE degree from Stanford University in 1986, and the M.S. degree in Statistics from Stanford University in 1989. From 1985 to 1988 he was a National Science Foundation Graduate Fellow at Stanford, where he earned a Ph.D. in electrical engineering in 1990. He has worked at the University of Michigan since then. From 1991 to 1992 he was a Department of Energy Alexander Hollaender Post-Doctoral Fellow in the Division of Nuclear Medicine. From 1993 to 1995 he was an Assistant Professor in Nuclear Medicine and the Bioengineering Program. He is now a Professor in the Departments of Electrical Engineering and Computer Science, Radiology, and Biomedical Engineering. He became a Fellow of the IEEE in 2006, for contributions to the theory and practice of image reconstruction. He received the Francois Erbsmann award for his IPMI93 presentation, and the Edward Hoffman Medical Imaging Scientist Award in 2013. He has served as an associate editor for the IEEE Transactions on Medical Imaging, the IEEE Signal Processing Letters, the IEEE Transactions on Image Processing, the IEEE Transactions on Computational Imaging, and is currently serving as an associate editor for SIAM J. on Imaging Science. He has chaired the IEEE T-MI Steering Committee and the ISBI Steering Committee. He was co-chair of the 1997 SPIE conference on Image Reconstruction and Restoration, technical program co-chair of the 2002 IEEE International Symposium on Biomedical Imaging (ISBI), and general chair of ISBI 2007. His research interests are in statistical aspects of imaging problems, and he has supervised doctoral research in PET, SPECT, X-ray CT, MRI, and optical imaging problems.
Footnotes
One could replace the bound in (11) with (and summable {ϵ(i+1) : ∀i}), and the proofs for our main arguments go through.
is proper if domF ≠ ∅. F is lower bounded in if .
Traditionally, one obtains focal stacks by physically moving imaging sensors and taking separate exposures across time. Transparent photodetector arrays [47], [69] allow one to collect focal stack data in a single exposure, making a practical LF camera using a focal stack. If some photodetectors are not perfectly transparent, one can use τc < 1, for some c.
Epipolar images are 2D slices of a 4D LF LF(cx, cy, cu, cv), where (cx, cy) and (cu, cv) are spatial and angular coordinates, respectively. Specifically, each horizontal epipolar plane image are obtained by fixing cy and cv, and varying cx and cu; and each vertical epipolar image are obtained by fixing cx and cu, and varying cy and cv.
This paper has appendices. The prefix “A” indicate the numbers in section, theorem, equation, figure, table, and footnote in the appendices.
Contributor Information
Il Yong Chun, Department of Electrical Engineering and Computer Science, The University of Michigan, Ann Arbor, MI 48019, USA; Department of Electrical Engineering, the University of Hawai’i at Mānoa, Honolulu, HI 96822 USA.
Zhengyu Huang, Department of Electrical Engineering and Computer Science, The University of Michigan, Ann Arbor, MI 48019 USA.
Hongki Lim, Department of Electrical Engineering and Computer Science, The University of Michigan, Ann Arbor, MI 48019 USA.
Jeffrey A. Fessler, Department of Electrical Engineering and Computer Science, The University of Michigan, Ann Arbor, MI 48019 USA.
REFERENCES
- [1].Vincent P, Larochelle H, Lajoie I, Bengio Y, and Manzagol P-A, “Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion,” J. Mach. Learn. Res, vol. 11, no. Dec, pp. 3371–3408, 2010. [Google Scholar]
- [2].Xie J, Xu L, and Chen E, “Image denoising and inpainting with deep neural networks,” in Proc. NIPS, Lake Tahoe, NV, Dec. 2012, pp. 341–349. [Google Scholar]
- [3].Mao X, Shen C, and Yang Y-B, “Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections,” in Proc. NIPS, Barcelona, Spain, Dec. 2016, pp. 2802–2810. [Google Scholar]
- [4].Zhang K, Zuo W, Chen Y, Meng D, and Zhang L, “Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising,” IEEE Trans. Image Process., vol. 26, no. 7, pp. 3142–3155, Feb. 2017. [DOI] [PubMed] [Google Scholar]
- [5].Xu L, Ren JS, Liu C, and Jia J, “Deep convolutional neural network for image deconvolution,” in Proc. NIPS, Montreal, Canada, Dec. 2014, pp. 1790–1798. [Google Scholar]
- [6].Sun J, Cao W, Xu Z, and Ponce J, “Learning a convolutional neural network for non-uniform motion blur removal,” in Proc. IEEE CVPR, Boston, MA, Jun. 2015, pp. 769–777. [Google Scholar]
- [7].Dong C, Loy CC, He K, and Tang X, “Image super-resolution using deep convolutional networks,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 38, no. 2, pp. 295–307, Feb. 2016. [DOI] [PubMed] [Google Scholar]
- [8].Kim J, Lee KJ, and Lee KM, “Accurate image super-resolution using very deep convolutional networks,” in Proc. IEEE CVPR, Las Vegas, NV, Jun. 2016. [Google Scholar]
- [9].Yang G, Yu S, Dong H, Slabaugh G, Dragotti PL, Ye X, Liu F, Arridge S, Keegan J, Guo Y et al. , “DAGAN: Deep de-aliasing generative adversarial networks for fast compressed sensing MRI reconstruction,” IEEE Trans. Image Process, vol. 37, no. 6, pp. 1310–1321, Jun. 2018. [DOI] [PubMed] [Google Scholar]
- [10].Quan TM, Nguyen-Duc T, and Jeong W, “Compressed sensing MRI reconstruction using a generative adversarial network with a cyclic loss,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1488–1497, June 2018. [DOI] [PubMed] [Google Scholar]
- [11].Chen H, Zhang Y, Kalra MK, Lin F, Liao P, Zhou J, and Wang G, “Low-dose CT with a residual encoder-decoder convolutional neural network (RED-CNN),” IEEE Trans. Med. Imag, vol. PP, no. 99, p. 0, Jun. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Jin KH, McCann MT, Froustey E, and Unser M, “Deep convolutional neural network for inverse problems in imaging,” IEEE Trans. Image Process, vol. 26, no. 9, pp. 4509–4522, Sep. 2017. [DOI] [PubMed] [Google Scholar]
- [13].Ye J, Han Y, and Cha E, “Deep convolutional framelets: A general deep learning framework for inverse problems,” SIAM J. Imaging Sci, vol. 11, no. 2, pp. 991–1048, Apr. 2018. [Google Scholar]
- [14].Wu G, Zhao M, Wang L, Dai Q, Chai T, and Liu Y, “Light field reconstruction using deep convolutional network on EPI,” in Proc. IEEE CVPR, Honolulu, HI, Jul. 2017, pp. 1638–1646. [Google Scholar]
- [15].Gupta M, Jauhari A, Kulkarni K, Jayasuriya S, Molnar AC, and Turaga PK, “Compressive light field reconstructions using deep learning,” in Proc. IEEE CVPR Workshops, Honolulu, HI, Jul. 2017, pp. 1277–1286. [Google Scholar]
- [16].Chun IY, Zheng X, Long Y, and Fessler JA, “BCD-Net for low- dose CT reconstruction: Acceleration, convergence, and generalization,” in Proc. Med. Image Computing and Computer Assist. Interven, Shenzhen, China, Oct. 2019, pp. 31–40. [Google Scholar]
- [17].Zheng X, Chun IY, Li Z, Long Y, and Fessler JA, “Sparse-view X-ray CT reconstruction using ℓ1 prior with learned transform,” submitted, Feb. 2019. [Online]. Available: http://arxiv.org/abs/1711.00905 [Google Scholar]
- [18].Lim H, Chun IY, Dewaraja YK, and Fessler JA, “Improved low-count quantitative PET reconstruction with an iterative neural network,” IEEE Trans. Med. Imag. (to appear), May 2020. [Online]. Available: http://arxiv.org/abs/1906.02327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Ye S, Long Y, and Chun IY, “Momentum-net for low-dose CT image reconstruction,” arXiv preprint eess.IV:2002.12018, Feb. 2020. [Google Scholar]
- [20].Yang Y, Sun J, Li H, and Xu Z, “Deep ADMM-Net for compressive sensing MRI,” in Proc. NIPS, Long Beach, CA, Dec. 2016, pp. 10–18. [Google Scholar]
- [21].Chen Y and Pock T, “Trainable nonlinear reaction diffusion: A flexible framework for fast and effective image restoration,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 39, no. 6, pp. 1256–1272, Jun. 2017. [DOI] [PubMed] [Google Scholar]
- [22].Romano Y, Elad M, and Milanfar P, “The little engine that could: Regularization by denoising (RED),” SIAM J. Imaging Sci, vol. 10, no. 4, pp. 1804–1844, Oct. 2017. [Google Scholar]
- [23].Buzzard GT, Chan SH, Sreehari S, and Bouman CA, “Plug- and-play unplugged: Optimization free reconstruction using consensus equilibrium,” SIAM J. Imaging Sci, vol. 11, no. 3, pp. 2001–2020, Sep. 2018. [Google Scholar]
- [24].Chun IY and Fessler JA, “Convolutional analysis operator learning: Acceleration and convergence,” IEEE Trans. Image Process, vol. 29, pp. 2108–2122, 2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].―, “Deep BCD-net using identical encoding-decoding CNN structures for iterative image recovery,” in Proc. IEEE IVMSP Workshop, Zagori, Greece, Jun. 2018, pp. 1–5. [Google Scholar]
- [26].Mardani M, Sun Q, Donoho D, Papyan V, Monajemi H, Vasanawala S, and Pauly J, “Neural proximal gradient descent for compressive imaging,” in Proc. NIPS, Montreal, Canada, Dec. 2018, pp. 9573–9583. [Google Scholar]
- [27].Chun IY, Lim H, Huang Z, and Fessler JA, “Fast and convergent iterative signal recovery using trained convolutional neural networkss,” in Proc. Allerton Conf. on Commun., Control, and Comput., Allerton, IL, Oct. 2018, pp. 155–159. [Google Scholar]
- [28].Hammernik K, Klatzer T, Kobler E, Recht MP, Sodickson DK, Pock T, and Knoll F, “Learning a variational network for reconstruction of accelerated MRI data,” Magn. Reson. Med, vol. 79, no. 6, pp. 3055–3071, Nov. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Mardani M, Gong E, Cheng JY, Vasanawala SS, Zaharchuk G, Xing L, and Pauly JM, “Deep generative adversarial neural networks for compressive sensing (GANCS) MRI,” IEEE Trans. Med. Imag, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Aggarwal HK, Mani MP, and Jacob M, “MoDL: Model based deep learning architecture for inverse problems,” IEEE Trans. Med. Imag, vol. 38, no. 2, pp. 394–405, Feb. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Gupta H, Jin KH, Nguyen HQ, McCann MT, and Unser M, “CNN-based projected gradient descent for consistent CT image reconstruction,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1440–1453, Jun. 2018. [DOI] [PubMed] [Google Scholar]
- [32].Kim K, Wu D, Gong K, Dutta J, Kim JH, Son YD, Kim HK, El Fakhri G, and Li Q, “Penalized PET reconstruction using deep learning prior and local linear fitting,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1478–1487, Jun. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Lim H, Fessler JA, Dewaraja YK, and Chun IY, “Application of trained Deep BCD-Net to iterative low-count PET image reconstruction,” in Proc. IEEE NSS-MIC, Sydney, Australia, Nov. 2018, pp. 1–4. [Google Scholar]
- [34].Lim H, Chun IY, Fessler JA, and Dewaraja YK, “Improved low count quantitative SPECT reconstruction with a trained deep learning based regularizer,” J. Nuc. Med. (Abs. Book), vol. 60, no. supp. 1, p. 42, May 2019. [Google Scholar]
- [35].Chun IY and Fessler JA, “Convolutional dictionary learning: Acceleration and convergence,” IEEE Trans. Image Process, vol. 27, no. 4, pp. 1697–1712, Apr. 2018. [DOI] [PubMed] [Google Scholar]
- [36].Chun IY, Hong D, Adcock B, and Fessler JA, “Convolutional analysis operator learning: Dependence on training data,” IEEE Signal Process. Lett, vol. 26, no. 8, pp. 1137–1141, Jun. 2019. [Online]. Available: http://arxiv.org/abs/1902.08267 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Chun IY and Fessler JA, “Convolutional analysis operator learning: Application to sparse-view CT,” in Proc. Asilomar Conf. on Signals, Syst., and Comput., Pacific Grove, CA, Oct. 2018, pp. 1631–1635. [Google Scholar]
- [38].Crockett C, Hong D, Chun IY, and Fessler JA, “Incorporating handcrafted filters in convolutional analysis operator learning for ill-posed inverse problems,” in Proc. IEEE Workshop CAMSAP, Guadeloupe, West Indies, Dec. 2019, pp. 316–320. [Google Scholar]
- [39].Sreehari S, Venkatakrishnan SV, Wohlberg B, Buzzard GT, Drummy LF, Simmons JP, and Bouman CA, “Plug-and-play priors for bright field electron tomography and sparse interpolation,” IEEE Trans. Comput. Imag, vol. 2, no. 4, pp. 408–423, Aug. 2016. [Google Scholar]
- [40].Zhang K, Zuo W, Gu S, and Zhang L, “Learning deep CNN denoiser prior for image restoration,” in Proc. IEEE CVPR, Honolulu, HI, Jul. 2017, pp. 4681–4690. [Google Scholar]
- [41].Chan SH, Wang X, and Elgendy OA, “Plug-and-play ADMM for image restoration: Fixed-point convergence and applications,” IEEE Trans. Comput. Imag, vol. 3, no. 1, pp. 84–98, Nov. 2017. [Google Scholar]
- [42].Boyd S, Parikh N, Chu E, Peleato B, and Eckstein J, “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Found. & Trends in Machine Learning, vol. 3, no. 1, pp. 1–122, Jan. 2011. [Google Scholar]
- [43].Reehorst ET and Schniter P, “Regularization by denoising: Clarifications and new interpretations,” IEEE Trans. Comput. Imag, vol. 5, no. 1, pp. 52–67, Mar. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Kamilov US, Mansour H, and Wohlberg B, “A plug-and-play priors approach for solving nonlinear imaging inverse problems,” IEEE Signal Process. Lett, vol. 24, no. 12, pp. 1872–1876, Dec. 2017. [Google Scholar]
- [45].Miyato T, Kataoka T, Koyama M, and Yoshida Y, “Spectral normalization for generative adversarial networks,” in Proc. ICLR, Vancouver, Canada, Apr. 2018. [Google Scholar]
- [46].Ryu E, Liu J, Wang S, Chen X, Wang Z, and Yin W, “Plug-and- play methods provably converge with properly trained denoisers,” in Proc. ICML, Long Beach, CA, Jun. 2019, pp. 5546–5557. [Google Scholar]
- [47].Lien M-B, Liu C-H, Chun IY, Ravishankar S, Nien H, Zhou M, Fessler JA, Zhong Z, and Norris TB, “Ranging and light field imaging with transparent photodetectors,” Nature Photonics, vol. 14, no. 3, pp. 143–148, Jan. 2020. [Google Scholar]
- [48].Nesterov Y, “Gradient methods for minimizing composite functions,” Math. Program, vol. 140, no. 1, pp. 125–161, Aug. 2013. [Google Scholar]
- [49].Beck A and Teboulle M, “A fast iterative shrinkage-thresholding algorithm for linear inverse problems,” SIAM J. Imaging Sci, vol. 2, no. 1, pp. 183–202, Mar. 2009. [Google Scholar]
- [50].Ono S, “Primal-dual plug-and-play image restoration,” IEEE Signal Process. Lett, vol. 24, no. 8, pp. 1108–1112, Aug. 2017. [Google Scholar]
- [51].Chambolle A and Pock T, “A first-order primal-dual algorithm for convex problems with applications to imaging,” J. Math. Imag. Vision, vol. 40, no. 1, pp. 120–145, 2011. [Google Scholar]
- [52].Dabov K, Foi A, Katkovnik V, and Egiazarian K, “Image denoising by sparse 3-d transform-domain collaborative filtering,” IEEE Trans. Image Process, vol. 16, no. 8, pp. 2080–2095, Jul. 2007. [DOI] [PubMed] [Google Scholar]
- [53].Xu Y and Yin W, “A block coordinate descent method for regularized multiconvex optimization with applications to nonnegative tensor factorization and completion,” SIAM J. Imaging Sci, vol. 6, no. 3, pp. 1758–1789, Sep. 2013. [Google Scholar]
- [54].―, “A fast patch-dictionary method for whole image recovery,” Inverse Probl. Imag, vol. 10, no. 2, pp. 563–583, May 2016. [Google Scholar]
- [55].―, “A globally convergent algorithm for nonconvex optimization based on block coordinate update,” J. Sci. Comput, vol. 72, no. 2, pp. 700–734, Aug. 2017. [Google Scholar]
- [56].Muckley MJ, Noll DC, and Fessler JA, “Fast, iterative subsampled spiral reconstruction via circulant majorizers,” in Proc. Int. Soc. Magn. Res. Med., Singapore, May 2016, p. 521. [Google Scholar]
- [57].McGaffin MG and Fessler JA, “Algorithmic design of majorizers for large-scale inverse problems,” ArXiv preprint stat.CO/1508.02958, Oct. 2015. [Google Scholar]
- [58].Chun IY and Adcock B, “Compressed sensing and parallel acquisition,” IEEE Trans. Inf. Theory, vol. 63, no. 7, pp. 1–23, May 2017. [Online]. Available: http://arxiv.org/abs/1601.06214 [Google Scholar]
- [59].Aja-Fernandez S, Vegas-Sanchez-Ferrero G, and Trist´ an-Vega A,´ “Noise estimation in parallel MRI: GRAPPA and SENSE,” Magn. Reson. Imaging, vol. 32, no. 3, pp. 281–290, Apr. 2014. [DOI] [PubMed] [Google Scholar]
- [60].Rockafellar RT, “Monotone operators and the proximal point algorithm,” SIAM J. Control Optm, vol. 14, no. 5, pp. 877–898, Aug. 1976. [Google Scholar]
- [61].Ryu EK and Boyd S, “Primer on monotone operator methods,” Appl. Comput. Math, vol. 15, no. 1, pp. 3–43, Jan. 2016. [Google Scholar]
- [62].Bolte J, Sabach S, and Teboulle M, “Proximal alternating linearized minimization or nonconvex and nonsmooth problems,” Math. Program, vol. 146, no. 1–2, pp. 459–494, Aug. 2014. [Google Scholar]
- [63].Gilton D, Ongie G, and Willett R, “Neumann networks for linear inverse problems in imaging,” IEEE Trans. Comput. Imag, vol. 6, pp. 328–343, Oct. 2019. [Google Scholar]
- [64].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” in Proc. IEEE CVPR, Las Vegas, NV, June 2016. [Google Scholar]
- [65].Li H, Xu Z, Taylor G, Studer C, and Goldstein T, “Visualizing the loss landscape of neural nets,” in Proc. NIPS, Montreal, Canada, Dec. 2018, pp. 6389–6399. [Google Scholar]
- [66].Li Z, Chun IY, and Long Y, “Image-domain material decomposition using an iterative neural network for dual-energy CT,” in Proc. IEEE ISBI, Iowa City, IA, Apr. 2009, pp. 651–655. [Google Scholar]
- [67].Chun IY and Talavage T, “Efficient compressed sensing statistical X-ray/CT reconstruction from fewer measurements,” in Proc. Intl. Mtg. on Fully 3D Image Recon. in Rad. and Nuc. Med, Lake Tahoe, CA, Jun. 2013, pp. 30–33. [Google Scholar]
- [68].Blocker CJ, Chun IY, and Fessler JA, “Low-rank plus sparse tensor models for light-field reconstruction from focal stack data,” in Proc. IEEE IVMSP Workshop, Zagori, Greece, Jun. 2018, pp. 1–5. [Google Scholar]
- [69].Zhang D, Xu Z, Huang Z, Gutierrez AR, Chun IY, Blocker CJ, Cheng G, Liu Z, Fessler JA, Zhong Z, and Norris TB, “Graphene-based transparent photodetector array for multiplane imaging,” in Proc. Conf. on Lasers and Electro-Optics, San Jose, CA, May 2019, p. SM4J.2. [Google Scholar]
- [70].Honauer K, Johannsen O, Kondermann D, and Goldluecke B, “A dataset and evaluation methodology for depth estimation on 4D light fields,” in Proc. ACCV, Taipei, Taiwan, Nov. 2016, pp. 19–34. [Google Scholar]
- [71].Segars WP, Mahesh M, Beck TJ, Frey EC, and Tsui BM, “Realistic CT simulation using the 4D XCAT phantom,” Med. Phys, vol. 35, no. 8, pp. 3800–3808, Jul. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Kingma DP and Ba JL, “Adam: A method for stochastic optimization,” in Proc. ICLR 2015, San Diego, CA, May 2015, pp. 1–15. [Google Scholar]
- [73].He K, Zhang X, Ren S, and Sun J, “Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification,” in Proc. IEEE ICCV, Santiago, Chile, Dec. 2015, pp. 1026–1034. [Google Scholar]
- [74].Kamal MH, Heshmat B, Raskar R, Vandergheynst P, and Wetzstein G, “Tensor low-rank and sparse light field photography,” Comput. Vis. Image Und, vol. 145, pp. 172–181, Apr. 2016. [Google Scholar]
- [75].Zhang S, Sheng H, Li C, Zhang J, and Xiong Z, “Robust depth estimation for light field via spinning parallelogram operator,” Comput. Vis. Image Und, vol. 145, pp. 148–159, Apr. 2016. [Google Scholar]
- [76].Fessler JA, “Michigan image reconstruction toolbox (MIRT) for Matlab,” Available from http://web.eecs.umich.edu/~fessler, 2016.
- [77].Hudson HM and Larkin RS, “Accelerated image reconstruction using ordered subsets of projection data,” IEEE Trans. Med. Imag, vol. 13, no. 4, pp. 601–609, Dec. 1994. [DOI] [PubMed] [Google Scholar]
- [78].Erdogan H and Fessler JA, “Ordered subsets algorithms for transmission tomography,” Phys. Med. Biol, vol. 44, no. 11, p. 2835, Jul. 1999. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.