Fast decoding cell type–specific transcription factor binding landscape at single-nucleotide resolution

Abstract

Decoding the cell type–specific transcription factor (TF) binding landscape at single-nucleotide resolution is crucial for understanding the regulatory mechanisms underlying many fundamental biological processes and human diseases. However, limits on time and resources restrict the high-resolution experimental measurements of TF binding profiles of all possible TF–cell type combinations. Previous computational approaches either cannot distinguish the cell context–dependent TF binding profiles across diverse cell types or can only provide a relatively low-resolution prediction. Here we present a novel deep learning approach, Leopard, for predicting TF binding sites at single-nucleotide resolution, achieving the average area under receiver operating characteristic curve (AUROC) of 0.982 and the average area under precision recall curve (AUPRC) of 0.208. Our method substantially outperformed the state-of-the-art methods Anchor and FactorNet, improving the predictive AUPRC by 19% and 27%, respectively, when evaluated at 200-bp resolution. Meanwhile, by leveraging a many-to-many neural network architecture, Leopard features a hundredfold to thousandfold speedup compared with current many-to-one machine learning methods.

Transcription factors (TFs) play a fundamental role in regulating gene expression via binding to specific DNA sequences (Badis et al. 2009; Vaquerizas et al. 2009; Jolma et al. 2013). Precisely decoding the TF binding landscape at single-nucleotide resolution is crucial for understanding the regulatory mechanisms underlying many cellular processes and human diseases (Rhee and Pugh 2011; Albert and Kruglyak 2015; Corces et al. 2018; Lambert et al. 2018). Beyond the sequence preferences of TF binding represented as motifs (Khan et al. 2018; Kulakovskiy et al. 2018), the Encyclopedia of DNA Elements (ENCODE) Project has established that many TFs predominantly bind to open chromatin (Neph et al. 2012; Thurman et al. 2012). The TF binding landscapes therefore vary substantially across cell types, which are associated with their unique organization of accessible chromatin across the genome (Thurman et al. 2012; Heinz et al. 2015). Chromatin immunoprecipitation followed by DNA sequencing (ChIP-seq) is a common technique to measure the in vivo TF binding profile in a specific cell type (Johnson et al. 2007). However, in ChIP-seq, DNA fragments are typically long and have variable lengths, which hinders precise localization of the binding site. In addition, the contamination of immunoprecipitations from unbound DNA in ChIP-seq experiments further leads to the description of TF binding only at a relatively low resolution (Rhee and Pugh 2011; Furey 2012). An alternative approach, ChIP-exo, can precisely map the genome-wide TF binding locations and reduce the erroneous calls (Rhee and Pugh 2011; He et al. 2015). However, it is infeasible to experimentally measure the single-nucleotide-resolution TF binding landscapes in the enormous combinations of TF and cell type pairs owing to limits on time and resources.

Advancements in computational models show great promise to delineate the TF binding landscape in silico (Eraslan et al. 2019; Zou et al. 2019). Previous works such as gkmSVM (Ghandi et al. 2014) and CENTIPEDE (Pique-Regi et al. 2011) solve this problem through statistical learning. Recent works, including DeepSEA (Zhou and Troyanskaya 2015), DeepBIND (Alipanahi et al. 2015), Basset (Kelley et al. 2016), Basenji (Kelley et al. 2018), DanQ (Quang and Xie 2016), DeFine (Wang et al. 2018), and BPNet (Avsec et al. 2021), have modeled the relationships between DNA sequences and TFs using neural network models. However, without the cell type–specific information on chromatin accessibility, these models cannot distinguish the diverse TF binding profiles across different cell types and conditions. Recent methods, including Anchor (Li et al. 2019) and FactorNet (Quang and Xie 2019), address this problem by considering both DNA sequence and chromatin accessibility, greatly improving the prediction accuracy in a cross–cell type fashion. But these methods typically only provide the statistically enriched TF binding regions at ∼200-bp resolution. Therefore, there is a great demand for computational tools to both accurately and precisely model the TF binding status for every single genomic position.

In computer vision, a common pixel-level image segmentation task is to train a computer program to recognize objects in an image and assign the object label to each input pixel. A simple way to solve this task is using the many-to-one neural network, which uses “many” pixels as input to predict “one” label at a time. Because there could be tens of thousands of pixels in an image, this many-to-one neural network is less efficient. An alternative is the many-to-many neural network, which simultaneously generates predictions for all pixels in an image and tremendously accelerates the prediction speed. This pixel-level image segmentation task is similar to the single-nucleotide TF binding: Each single nucleotide can be treated as a pixel, and we need to predict the binding or not label for each nucleotide in the genome “image.” The many-to-one neural network has been used in many pioneering research efforts to investigate functional genomics (Alipanahi et al. 2015; Zhou and Troyanskaya 2015; Kelley et al. 2016). We here present a many-to-many nucleotide-level segmentation framework to generate predictions for multiple genomic positions simultaneously, not only improving the predictive performance but also allowing for a hundredfold to thousandfold speedup compared with state-of-the-art methods.

Results

Overview of experimental design

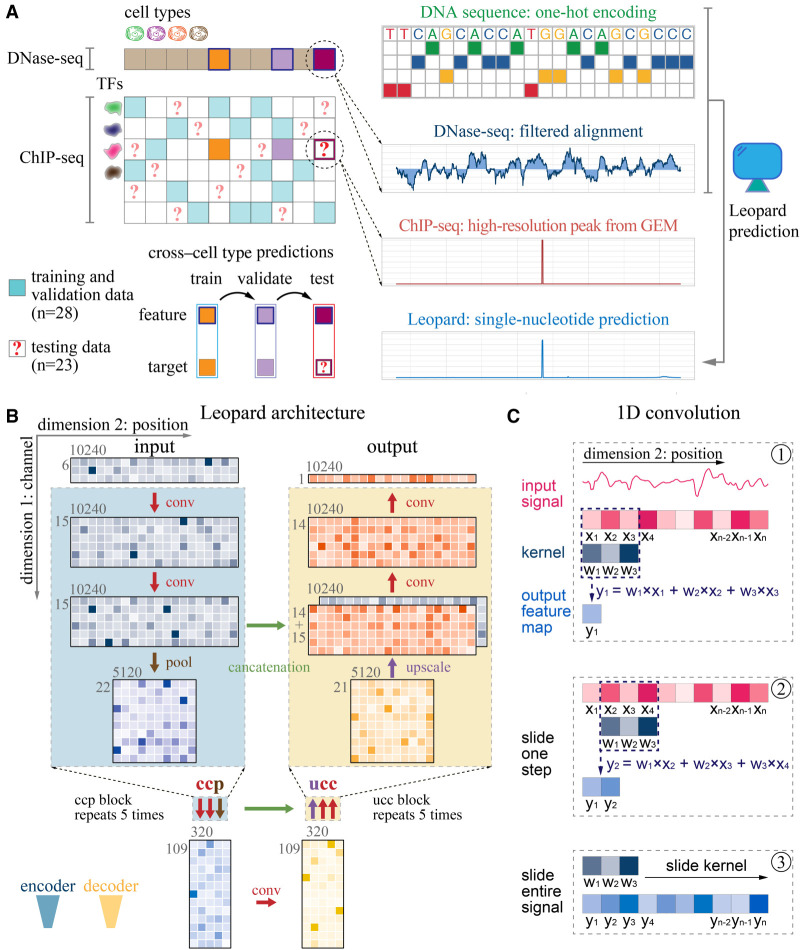
Leopard is designed to predict cross–cell type TF binding sites at a single-nucleotide level based on DNA sequence and chromatin accessibility from DNase-seq (Fig. 1A). For each TF–cell type pair, we used the real-valued DNase-seq filtered alignment signal as the primary feature. Meanwhile, DNA sequences were one-hot-encoded as additional input features to capture TF binding motifs. Leopard was designed to extract information from multiple ranges and resolutions for predicting TF binding locations. It has a deep convolutional neural network architecture, which accepts six-by-10,240 matrices as inputs (Fig. 1B). The six channels in the first dimension are signals from (1) DNase-seq, (2) ΔDNase-seq, and (3–6) one-hot-encoded DNA sequences. The ΔDNase-seq is the difference between a specific cell type and the average of all cell types used in this study, which is designed to capture potential sequencing biases (see Methods, “ΔDNase-seq Feature”). The columns in the second dimension correspond to the input length of 10,240 successive genomic positions. The core building block is the one-dimensional (1D) convolution operator (Fig. 1C). By scanning across all 10,240 positions, the convolutional layer can capture the upstream and downstream information, and key determinants of TF binding will trigger an activation, such as a motif match and open chromatin (see Methods, “The Neural Network Architecture of Leopard”). The details about all the network layers in the Leopard architecture can be found in Supplemental Table S1. To obtain genome-wide single-nucleotide TF binding events, we used GEM peak finder (Guo et al. 2012) to process the sequence alignment file of ChIP-seq reads. A total of 51 ChIP-seq data were used to build models (n = 28) and evaluate the cross-cell-type predictive performance (n = 23).

Figure 1.

Schematic illustration of Leopard workflow. (A) This study aims to decode the high-resolution transcription factor (TF) binding landscapes (ChIP-seq peaks extracted by GEM peak finder) based on chromatin accessibility (DNase-seq signals) in a cross–cell type fashion. A total of 28 ChIP-seq experimental results from the ENCODE Project were used to train and validate models, whereas the other 23 results were used to test the performance of our method. The DNase-seq signals of filtered alignments and one-hot-encoded DNA sequences were used as inputs for a deep convolutional neural network model. (B) Leopard accepts two-dimensional matrices as inputs, where the first dimension represents six channels (DNase-seq, ΔDNase-seq, and one-hot-encoded DNA sequence) and the second dimension represents 10,240 genomic positions. The 10,240 genomic positions correspond to randomly sampled consecutive segments in the human genome. Leopard has two components: the encoder (blue) and the decoder (yellow). The encoder contains five convolution-convolution-pooling (ccp) blocks, and the decoder has five upscaling-convolution-convolution (ucc) blocks. This architecture allows for generating outputs for multiple positions simultaneously, substantially boosting the prediction speed. In addition, the concatenation operations (horizontal green arrows) connect the encoder with the decoder, preventing information decay in deep neural networks. (C) The one-dimensional (1D) convolution operator calculates the inner product between the kernel (w1, w2, w3) and the input signal (x1, x2, x3), resulting in one feature map value (y1) in step 1. Then the kernel slides along the entire input signal (steps 2 and 3) and generates the output feature map vector, which has the same size in dimension 2 as the input.

Leopard accurately identifies cell type–specific TF binding profiles at single-nucleotide resolution

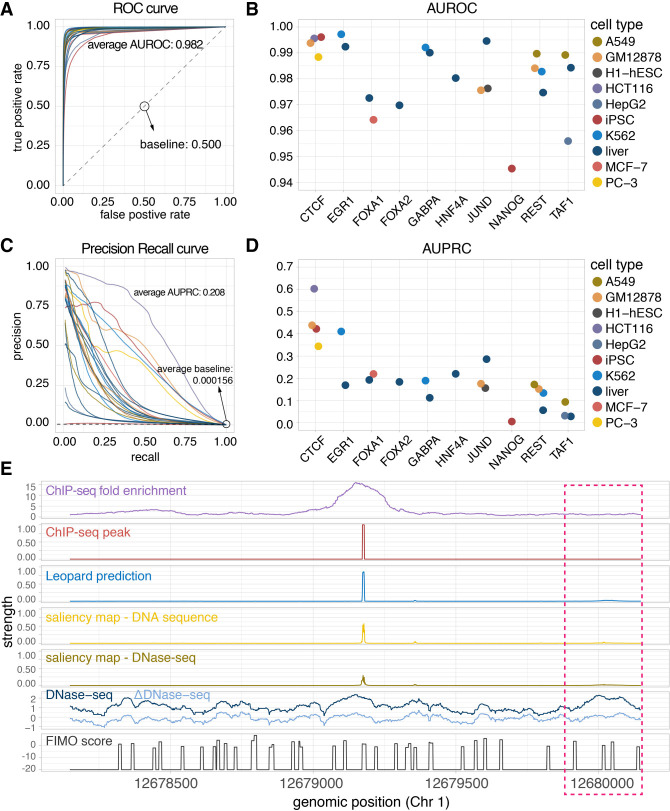
We first compared the Leopard prediction profiles with the high-resolution ChIP-seq peaks extracted by GEM in the 23 testing TF–cell type pairs. For each TF, we trained and validated our model in a subset of training cell types and then made predictions on the other subset of testing cell types. The complete train-test partition is shown in Supplemental Table S2. To further avoid potential overfitting to specific chromosomes (Chrs), the Chr 1, Chr 8, and Chr 21 were held out as the three testing chromosomes and the other 20 chromosomes (Chr 2–7, 9–20, 22, X) were used for training. Both the area under receiver operating characteristic curve (AUROC) and the area under precision recall curve (AUPRC) were calculated and compared (Fig. 2A–D). Leopard accurately identified TF binding profiles for the 10 TFs in this study, with a median prediction AUROC of 0.982. In 19 out of 23 (83%) testing TF–cell type pairs, Leopard achieved high AUROCs above 0.970 (Fig. 2A,B). The corresponding precision recall (PR) curves and AUPRCs are shown in Figure 2, C and D. Of note, identifying TF binding sites is an extremely difficult class imbalance problem; on average, only 0.0156% of all genomic positions were bound by TFs in the 23 testing TF–cell type pairs (Supplemental Table S3). The AUPRC baseline of random prediction was therefore very low, around 0.000156 (Fig. 2C, dashed line). Compared with the random prediction baseline, Leopard (average AUPRC = 0.208) had more than a thousandfold improvement. We also created a more stringent AUPRC baseline by overlapping DNase-seq signals with FIMO motif scanning results (Supplemental Table S3; Grant et al. 2011). This average AUPRC baseline is 0.0149, and Leopard had a 14-fold improvement. In general, single-motif-based scanning approaches are potentially problematic in identifying TF binding events, because many TFs have cognate motifs and some TFs may not have well-characterized motifs. It has been reported that ChIP-seq peaks may not contain cognate motifs (Wang et al. 2012), especially for indirect or tethered binding events. Therefore, instead of refining ChIP-seq signals with motif scanning, we extracted high-resolution ChIP-seq peaks using GEM, which is a peak calling and de novo motif discovery approach (Guo et al. 2012).

Figure 2.

Leopard identifies cell type–specific transcription factor binding events at single-nucleotide resolution. (A) The receiver operating characteristic (ROC) curves and (B) the areas under receiver operating characteristic curves (AUROCs) of the 23 testing TF–cell type pairs. Each dot represents the overall AUROC calculated from the testing chromosomes (Chr 1, Chr 8, and Chr 21). Different colors represent different cell types. (C) The precision recall (PR) curves and (D) areas under the precision recall curves (AUPRCs) of the 23 testing TF–cell type pairs. The average AUPRC baseline score of random prediction is 0.000156, shown as the horizontal dashed line, corresponding to the number of TF binding sites over the total number of base pairs in the testing chromosomes (Chr 1, Chr 8, and Chr 21). (E) An example 2000-bp segment is given to show the prediction results. This segment contains signals between genomic positions 12,678,147 and 12,680,147 of Chr 1 from the JUND binding profile in the liver cell. The first row is the original ChIP-seq fold enrichment generated through the standard ENCODE analysis pipeline. The second row is the high-resolution ChIP-seq peak created by the GEM peak finder. In the third row, Leopard generates single-nucleotide predictions and precisely provides the binding sites. The two saliency maps of DNA sequence and DNase-seq indicate positions contributing to the predictions. The corresponding DNase-seq and ΔDNase-seq signals, as well as the sequence-based motif scan scores using FIMO, are also shown here for comparison. Of note, the region in the pink rectangle also has open chromatin (high DNase-seq signals) and binding motifs (high FIMO scores), but no binding events were observed from the ChIP-seq experiment. Leopard is able to detect these nonbinding locations, no prediction peaks in this region.

Because the TF binding events are extremely sparse in the human genome space, the full areas under curves may not ideally reflect the predictive performance. We therefore calculated the partial areas under precision recall (PR) curves using multiple cutoffs of recall (1%, 5%, 10%, 50%, 80%, 90%) and the partial areas under receiver operating characteristic (ROC) curves using multiple cutoffs of false-positive rate (FPR; 0.01%, 0.1%, 0.5%, 1%, 5%, 10%), and the corresponding numbers of true positives, false positives, false negatives, precisions, recalls, and FPRs (Supplemental Tables S4, S5). In summary, these results showed the high prediction accuracy of our method.

To visualize the Leopard prediction results, we show a 2000-bp segment of JUND binding profile in the liver cell line as an example (Fig. 2E). The raw ChIP-seq data were processed through the standard ENCODE analysis pipeline, resulting in a broad region of putative binding sites between locations 12,678,147 and 12,680,147 in Chr 1, in terms of the fold enrichment (Fig. 2E, the first row “ChIP-seq fold enrichment”). After peak calling using GEM, we obtained a high-resolution peak (Fig. 2E, the second row “ChIP-seq peak”). Similarly, the predictions from Leopard clearly depicted the exact binding locations, aligning with the ChIP-seq peak (Fig. 2E, the third row “Leopard prediction”). We need to emphasize that Leopard is not a peak caller; it predicts the high-resolution TF binding events from only DNase-seq and DNA sequence. To visualize the genomic positions contributing to the predictions, we calculated the saliency maps (Zeiler and Fergus 2013) from these two inputs (Fig. 2E, “saliency map–DNA sequence” and “saliency map–DNase-seq”) and the peak regions contributed most. For comparison, we also aligned the DNase-seq signal, the ΔDNase-seq signal, and FIMO motif scanning score. As we expected, without the cell type–specific information on chromatin accessibility, the sequence-based motif scanning approach generates many false-positive binding sites (Fig. 2E, peaks in the bottom row). On the other hand, the DNase-seq and ΔDNase-seq signals indicated the open chromatin regions, which were a prerequisite for TF binding except for pioneering TFs. In general, a genomic site with the “open chromatin” status and a high motif match score is more likely, but not necessary, to be a binding site. In Figure 2E, Leopard distinguishes the putative binding events from nonbinding ones. For instance, the region around location 12,680,000 in the pink rectangle has high DNase-seq signals and multiple motif matches. However, no binding events were observed within this region based on the ChIP-seq experiment. Leopard correctly predicted no binding peaks within this region.

We further compared the above 2000-bp genomic region across three cell types (GM12878, H1-hESC, and liver) and observed distinct TF binding patterns across cell types. In liver (Fig. 2E) and H1-hESC (Supplemental Fig. S1), JUND had a similar binding peak in this region, and Leopard correctly predicted these binding events. In contrast, JUND did not bind to this region in GM12878 (Supplemental Fig. S1A), potentially owing to the relatively restricted chromatin accessibility in this specific cell line. Leopard successfully distinguished GM12878 from the other three cell types, because DNase-seq and ΔDNase-seq signals were the cell type–specific input features for Leopard. In contrast, computational methods only based on DNA sequences without DNase-seq features will not identify the differences across cell types. These results show the great advantage of Leopard over only DNA sequence-based methods for predicting TF binding sites.

Benchmarking Leopard prediction against the ChIP-exo data

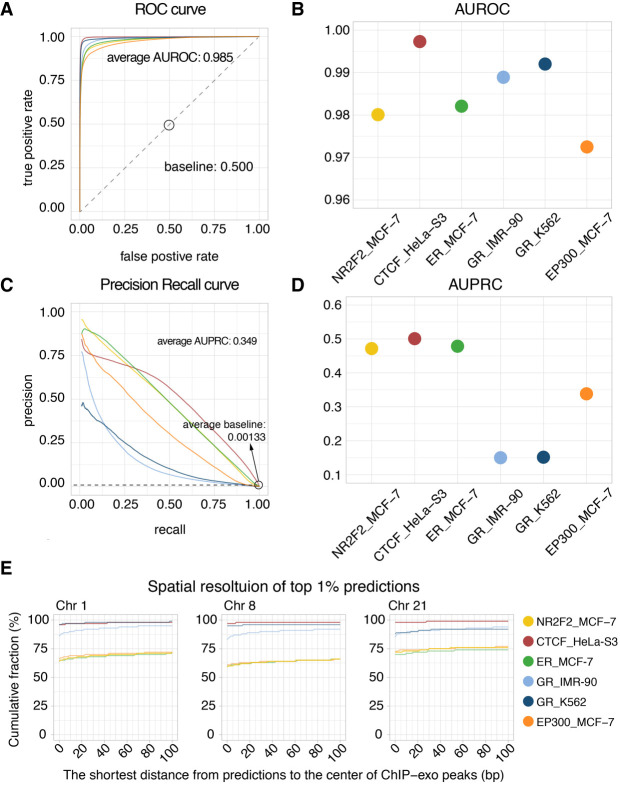
To evaluate the predictive performance of Leopard at single-base resolution, we further trained and evaluated Leopard models using ChIP-exo data, including CTCF in HeLa-S3 (Rhee and Pugh 2011); NR2F2, Estrogen Receptor (ER), and EP300 in MCF-7 (Serandour et al. 2013); and Glucocorticoid Receptor (GR) in IMR-90 and K562 (Starick et al. 2015). We built a within-cell-type model across chromosomes owing to the limited number of ChIP-exo data and used the same train-test chromosome partition as the previous ChIP-seq section. The predictive AUROCs and AUPRCs of Leopard are shown in Figure 3, A through D. Similar to the results on the ChIP-seq data, the average AUROC of 0.985 is very high, and the average AUPRC score is 0.349. The average AUPRC baseline of random prediction is only 0.00133 (Fig. 3C, dashed line). We also calculated the partial areas under PR curves at recall cutoffs of 1%, 5%, 10%, 50%, 80%, and 90%, and the partial areas under ROC curves at FPR cutoffs of 0.01%, 0.1%, 0.5%, 1%, 5%, and 10% (Supplemental Tables S6, S7). In addition to the areas under curves, we further investigated the spatial resolution of the top 1% predictions on the testing chromosomes (Chr 1, Chr 8, and Chr 21) (Fig. 3E). Specifically, for each center of ChIP-exo peak, we calculated the shortest distance to a predicted binding site among the top 1% Leopard predictions. For example in Chr 1, all six protein–cell type combinations achieved >70% fraction of 0-bp distance to the ChIP-exo peak center. As we expected, predictions of CTCF binding have the highest cumulative fractions and highest overlapping with ChIP-exo peaks in these three testing chromosomes. This is potentially because CTCF has a consensus motif, and it is easier to locate the precise binding sites, whereas other non-TF proteins do not necessarily have a well-characterized motif.

Figure 3.

Evaluating Leopard predictions based on TF binding profiles from ChIP-exo experiments. (A) The ROC curves and (B) the AUROCs of the six protein–cell type combinations. Different colors represent different combinations. (C) The PR curves and (D) AUPRCs of the six protein–cell type combinations. The average AUPRC baseline score of random prediction is 0.00133 shown as the horizontal dashed line. These results were calculated on the three testing chromosomes (Chr 1, Chr 8, and Chr 21). (E) The spatial resolution is defined as the shortest distance (in bp) between Leopard predictions and the center of ChIP-exo peaks. We focused on the top 1% predictions and calculated the cumulative fractions of peaks with different spatial resolutions, ranging from 0 bp to 100 bp in three testing chromosomes.

Leopard substantially outperforms state-of-the-art methods for predicting TF binding sites despite being evaluated at the low 200-bp resolution

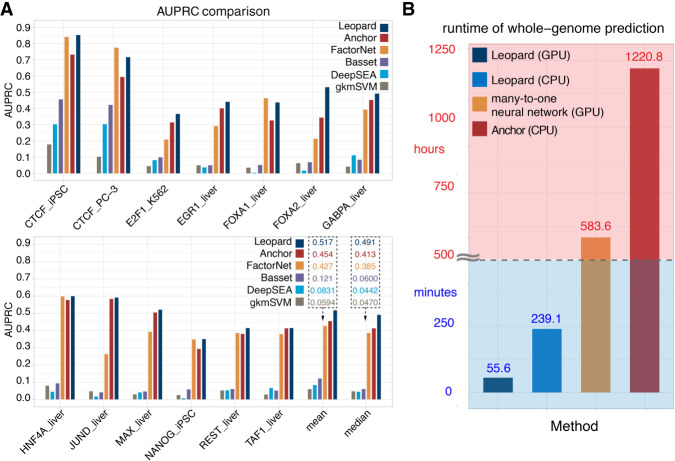
We further compared the recent state-of-the-art methods for TF binding site prediction, including the top performing methods named Anchor and FactorNet in the ENCODE-DREAM in vivo TF binding site prediction challenge. Anchor is based on a classical tree-based machine learning model, XGBoost, to predict TF binding sites through sophisticated feature engineering, whereas FactorNet is based on a many-to-one neural network model to address this problem. In addition, we compared earlier deep learning–based and svm-based methods, including DeepSEA, Basset, and gkmSVM. We benchmarked these methods on the same training and testing data sets in the ENCODE-DREAM challenge (Supplemental Table S8), which evaluated the predictive performance at 200-bp resolution with an offset of 50 bp. We adapted Leopard architecture to generate predictions at 200-bp resolution, which was called Leopard-200-bp (Supplemental Fig. S2).

The performance was evaluated in a cross–cell type and cross-chromosome fashion (for details, see Methods). Overall, Leopard achieved higher prediction AUPRCs than other methods (Fig. 4A). The mean and median AUPRCs show the improvement of Leopard predictions in the 13 testing TF–cell type pairs. Compared with the top performing methods in the ENCODE-DREAM challenge, Leopard improved the median prediction AUPRC by 19% and 27% over Anchor and FactorNet, respectively. We further performed pairwise statistical comparison of Leopard, Anchor, and FactorNet. For each testing TF–cell type pair, we randomly sampled 100 segments with a length of 100 kbp and then calculated the prediction AUPRC 100 times. The paired Wilcoxson signed rank test was performed. Leopard significantly outperformed Anchor and FactorNet in the 11 out of 13 (85%) testing TF–cell type pairs (Supplemental Fig. S3). In terms of AUROCs, Leopard, Anchor, and FactorNet had comparable performances, which were also higher than the other three methods (Supplemental Fig. S4). We also evaluated these three methods at 1-bp resolution. Because Anchor and FactorNet only provide predictions at the 200-bp interval, their predictions for each 200-bp interval were repeated 200 times to generate the “1-bp” predictions. The comparison results are shown in Supplemental Figure S5. Again, Leopard shows significantly higher AUPRCs than Anchor and FactorNet in the 13 testing TF–cell type pairs.

Figure 4.

Leopard substantially improves TF binding site prediction over state-of-the-art methods. (A) Leopard was benchmarked with the top performing classical tree-based model (Anchor), the top performing neural network model (FactorNet) in the ENCODE-DREAM in vivo TF binding site prediction challenge, two recent deep learning approaches (DeepSEA and Basset), and a classical machine learning method (gkmSVM). The same challenge training and testing data sets were used to train models and evaluate performance. Overall, Leopard achieved higher prediction AUPRCs than did the other methods. The mean and median AUPRCs on the bottom right clearly show the advantage of Leopard predictions in the 13 testing TF–cell type pairs. Leopard substantially improved the median prediction AUPRC by 19% and 27% over Anchor and FactorNet, respectively. (B) The runtime was tested for predicting the HNF4A binding profiles in the liver cell using different methods. Leopard shows a great advantage of speed and is flexible with both GPU and CPU.

In addition to higher prediction resolution and accuracy, Leopard has a great speed advantage over previous methods. Previous neural network approaches were typically based on the many-to-one architecture (Alipanahi et al. 2015; Zhou and Troyanskaya 2015; Quang and Xie 2016; Wang et al. 2018; Quang and Xie 2019), in which genomic segments containing hundreds or thousands of base pairs were used as inputs to predict only a single label at a time. Considering the fact that the human genome contains more than 3 billion bp, it requires a considerably long runtime for the genome-wide predictions using many-to-one models. In contrast, Leopard is based on a many-to-many neural network architecture, in which the base-wise labels for every nucleotide in the input genomic segment (10,240 bp) are generated simultaneously. This unique architecture tremendously boosts the prediction speed. To benchmark the runtimes of the many-to-one and many-to-many neural network structures, we modified Leopard and created a many-to-one version that accepted 10,240 bp as inputs and generated only one prediction value (Supplemental Fig. S6). For comparison, we also tested the runtime of Anchor, representing the speed of a tree-based XGBoost model. Leopard can finish prediction within 4.70, 2.80, and 0.95 min for predicting the single-nucleotide HNF4A binding sites on Chr 1, Chr 8, and Chr 21, respectively (Supplemental Fig. S7A). Yet Anchor and the many-to-one neural network require much longer runtimes, on the scales of hours. Meanwhile, Leopard is flexible with both graphics processing unit (GPU) and central processing unit (CPU) settings. When running Leopard on CPU, the prediction runtimes remain acceptable on the scale of minutes (Supplemental Fig. S7B). When making genome-wide predictions at single-nucleotide resolution, Leopard has a great advantage of speed; it only requires <1 h on GPU or 4 h on CPU. In contrast, it requires 583.6 h (>24 d) for the many-to-one neural network model and 1220.8 h (>50 d) for Anchor (Fig. 4B). Therefore, Leopard not only outperformed but also enabled a hundredfold to thousandfold speedup over the common many-to-one neural network and the Anchor model, respectively.

Discussion

Many studies have proposed computational models for predicting the sequence specificities of DNA-binding proteins and variant effects ab initio from DNA sequences (Alipanahi et al. 2015; Zhou and Troyanskaya 2015; Zhou et al. 2018, 2019). These approaches have advanced our understanding of the transcriptional regulation. However, in the new era of precision medicine, the context-dependent functional genomic and epigenomic landscapes across different cell types, tissues, and patients may not be completely encoded in the DNA sequence space. These genomic and epigenomic profiles provide crucial information for disease mechanism investigation and future treatment discovery. In this work, we develop a robust, scalable, and fast software, Leopard, to identify cell type–specific TF binding sites at the single-nucleotide level, which is a key challenge in computationally decoding functional elements of the human genome. Leopard leverages the cutting-edge deep learning framework for pixel-level image segmentation and large-scale data from the ENCODE Project, achieving high cross–cell type prediction accuracy. In addition to the ChIP-seq and ChIP-exo data used in this study, there are many alternative methods to study protein–DNA interactions. For example, CUT&RUN-seq is a recent technique with a higher signal-to-noise ratio, which requires less sequencing depth than ChIP-seq (Skene and Henikoff 2017). ChIP-nexus is an improved ChIP-exo approach with high resolution and enhanced robustness, which only requires similar amounts of cells as ChIP-seq (He et al. 2015). Similarly, SLIM-ChIP also provides high-resolution signals with small amounts of sample material (Gutin et al. 2018).

Unlike classical machine learning approaches that require complicated feature crafting and engineering (Li et al. 2018, 2019; Keilwagen et al. 2019), neural network models automatically learn the informative features and factors contributing to TF binding, largely increasing the flexibility and scalability (Jiang et al. 2019; Li and Guan 2021). For example, both Anchor (Li et al. 2019) and the method by J-Team (Keilwagen et al. 2019) calculated bin-level aggregate statistical features (maximum, mean, minimum, and other statistics) to represent the major signals instead of using the complete signals for the sake of computational efficiency. In contrast, Leopard accepts the complete DNase-seq signals of the input segments covering 10,240-bp positions without information loss, which may explain its higher predictive performance. Compared with many-to-one neural network models such FactorNet (one output at a time), the major advantages of Leopard include 1-bp resolution, high accuracy, and a hundredfold/thousandfold speedup (thousands of outputs at a time). Specifically, this speed boosting allows us to implement deep and complex neural network architectures such as U-Net to address the TF binding prediction problem, especially for huge data set at the scales of millions to billions (e.g., the human genome). If the speed is the bottleneck, it is impractical to build deep neural networks using the traditional many-to-one framework, and the depth of networks is one of the key parameters to achieve high performance. A recent DNA sequence-based neural network approach, Basenji, also leverages the idea of a many-to-many framework (Kelley et al. 2018). It accepts a 131-kbp bin as input and generates predictions of normalized coverage for the same length at a resolution of 128-bp bins, whereas the input and output length are both 10,240 bp in our model. Similarly, BPNet uses DNA sequence to predict base-resolution TF binding profiles on ChIP-nexus data, and the input and output lengths are 1 kb (Avsec et al. 2021). Dilated convolutions were also used to capture distal information in these methods. In terms of network structure tuning, we adapted the U-Net structure into the 1D version. Compared with a standard convolutional neural network, U-Net contains the unique “concatenation” operation to transfer information from the encoder to the decoder, which diminishes the information decay and proves to be powerful in computer vision tasks. Recent work in the field of neural architecture search indicates that neural networks based on randomly wired graphs achieved competitive performance to manually designed architectures on image classification (Xie et al. 2019). It would be interesting to see the future application of these models to bioinformatics research.

A unique feature of neural network models is that no specific TF motifs are needed as input. The TF motifs are implicitly contained in the ground truth, the ChIP-seq signal. During the neural network training process, the TF motifs are learned by the convolutional layers. In fact, the convolution operation on the one-hot-encoded DNA sequences is very similar to the motif scanning process. The difference is that for motif scanning, prior knowledge (e.g., position weight matrix of a specific TF) is required, whereas for convolution operation, no prior knowledge is required and the convolution weights (similar to position weight matrix) are learned during the training process. Traditional machine learning methods such as Anchor require TF motifs as a part of the input. The quality and potential biases of motifs (e.g., the data set, datatype, and algorithm for motif calculation) may affect the predictive performance. In addition, TF binding events are also associated with different TF–TF interactions. An algorithm relying on TF motifs may not be capable of considering all possible TF–TF interactions. In contrast, neural network models directly learn the potential binding patterns from DNA sequences, including patterns for both single-TF and multiple-TF bindings.

In this work, we use the saliency map approach to analyze feature importance in the neural network model, where the gradients of the output are back-propagated to calculate the input importance. It has been reported that comparing the activation of each neuron to its “reference activation” to obtain the contribution score could be a better alternative, especially in deep learning–based functional genomics studies using DeepLIFT (Shrikumar et al. 2017). We anticipate that the analysis of feature importance will further improve our understanding of deep learning models in the future studies.

Recent advancement in deep learning studies of genomic data has generated novel interpretations and biological hypotheses (Eraslan et al. 2019; Zou et al. 2019). Although the many-to-one neural network (with various convolutional, recurrent, and fully connected layers) has been actively explored, the many-to-many neural network remains to be developed. A major advantage of the many-to-many structure is the ultrafast prediction speed, which will accelerate the genomic research on the large genome-wide scale at single-nucleotide resolution. Here we show its very first application to identify TF binding events across cell types. We envision that our analysis framework and model can be flexibly adapted to investigate many other genomics modeling tasks in the future, including predicting various epigenetic modifications in different cell types.

Methods

Data collection and preprocessing

In this study, we used the data from the ENCODE Project, which consists of 51 ChIP-seq experiments and 13 DNase-seq experiments covering 10 TFs (CTCF, EGR1, FOXA1, FOXA2, GABPA, HNF4A, JUND, NANOG, REST, and TAF1) in 13 cell types (A549, GM12878, H1-hESC, HCT116, HeLa-S3, HepG2, iPSC, IMR-90, K562, liver, MCF-7, PANC-1, PC-3). The ChIP-seq data were downloaded from the ENCODE data portal (https://www.encodeproject.org/), with the accession numbers provided in Supplemental Table S9. The sequence alignment of ChIP-seq reads were processed using the GEM peak caller, with the parameters “‐‐s 2000000000 ‐‐k_min 6 ‐‐k_max 13.” A subset of 23 ChIP-seq experiments were held out as the evaluation testing set, and the remaining 28 ChIP-seq data were used for model training (Supplemental Table S2). For the 13 DNase-seq data, we downloaded them from the ENCODE-DREAM challenge website (https://www.synapse.org/#!Synapse:syn6176232). We used raw filtered alignment files without peak calling. Signals from multiple technical and biological replicates of the same cell type were summed and combined. To reduce the potential cell-specific cleavage and sequencing biases, we performed the quantile normalization following the same pipeline as described in Anchor (Li et al. 2019). In addition to ChIP-seq data, we downloaded the processed ChIP-exo peaks and ChIP-exo read alignments from the original studies. For CTCF in HeLa-S3 (Rhee and Pugh 2011), it was analyzed using the MACE pipeline (Wang et al. 2014). For NR2F2, ER, and EP300 in MCF-7 (Serandour et al. 2013), they were analyzed using MACS (Zhang et al. 2008). For GR in IMR-90 and K562 (Starick et al. 2015), we downloaded the sequence alignments of ChIP-exo reads and called peaks using GEM (Guo et al. 2012).

The ΔDNase-seq feature

The raw DNase-seq signals potentially have local sequencing biases (Madrigal 2015; Vierstra and Stamatoyannopoulos 2016). It has been well studied that the enzyme DNase I has an intrinsic cleavage preference for specific DNA sequence and/or shape (Dingwall et al. 1981; Lazarovici et al. 2013), and many computational approaches have been proposed to address the DNase-seq sequence biases (He et al. 2014; Gusmao et al. 2016; Martins et al. 2018). The strength of DNase-seq signals could be overestimated or underestimated owing to these local biases, which eventually affect the performance of machine learning models.

To alleviate the potential sequencing biases, we calculated the ΔDNase-seq signal by subtracting the reference DNase-seq signal (Li et al. 2019), which is the average across all 13 cell types under consideration. These 13 cell types include the training, validation, and testing cell types. Because DNase-seq and ΔDNase-seq are features, instead of the gold standard, for this TF binding prediction, this design will not lead to any contaminations. Contaminations will occur when the gold standard in the test set is involved in any phase of the training, such as selecting important features using the gold standard in the test.

The reference DNase signal only requires a one-pass calculation. When testing on new cell types, there is no need to recalculate this reference. This is because we already have many cell types to accurately estimate the average. To show this, we also calculated the references from randomly selected nine, 10, 11, and 12 cell types. These references are very similar, and the pairwise Pearson's correlations are all above 0.95 (Supplemental Fig. S8).

One-hot encoding of DNA sequence

The DNA sequence is a string of A/C/G/T characters, which cannot be directly understood by a computer program. A standard way of encoding the DNA sequence into numeric values is one-hot encoding, in which each nucleotide is assigned a specific channel, and the value is encoded as one only when a specific nucleotide occurs. For example, a 6-bp DNA sequence of “ACTGAT” can be encoded as a four-by-six matrix, where the four rows represent the four nucleotide channels (from top to bottom are the A, C, G, and T channels, respectively) and the six columns represent the six nucleotide positions. In Leopard, we used DNA sequences of 10,240 bp as input and encoded them into four-by-10,240 matrices. We also termed this as 10,240 successive genomic positions.

Stringent baseline by overlapping DNase-seq signals with motif scanning

A simple way to identify potential TF binding sites across the genome is calculating the TF motif matching score for each concessive genomic region. Find Individual Motif Occurrences (FIMO) is an efficient and fast software for scanning DNA sequences with motifs (Grant et al. 2011), which returns a motif matching score for each nucleotide in the input DNA sequence. By overlapping these motif scanning scores with DNase-seq filtered alignment signals, we define a more stringent AUPRC baseline than random predictions. Specifically, we scanned the hg19 reference genome using FIMO based on the TF motifs from HOCOMOCO v11 (Kulakovskiy et al. 2018). A relaxed cutoff of P = 0.01 was used to locate all the potential binding sites.

The neural network architecture of Leopard

The Leopard architecture has two components, the encoder and the decoder (Fig. 1B). The basic building unit of the encoder is the convolution-convolution-pooling (ccp) block, which contains two convolutional layers and one max-pooling layer. In each convolutional layer, the 1D convolution operation is applied to the data along the second dimension to extract the upstream and downstream information (Fig. 1C), and key determinants of TF binding will trigger an activation, including open chromatin and motif scanning hit. Of note, the users do not need to specify the TF motifs because the convolution operators can automatically learn and recognize the regulatory motifs and neighboring DNA sequences. Meanwhile, each max-pooling layer reduces the input length by half, allowing the subsequent convolutional layer to capture the information spanning longer genomic positions. For example, five successive points of the input matrix only cover five positions, whereas five successive points at the end of the encoder cover 5 × 2⁵ = 160 genomic positions. A total of five ccp blocks were used to gradually reduce the input length from 10,240 to 320 and increase the number of channels from six to 109, compensating for the loss of resolution along the genomic dimension. In contrast to the ccp blocks in the encoder, the counterpart upscaling-convolution-convolution (ucc) blocks were used in the decoder. They gradually increase the length but decrease the number of channels. In addition, the concatenation operation transfers the information from the encoder to decoder at each resolution (Fig. 1B, horizontal green arrows). The final output is a one-by-10,240 array, corresponding to the prediction of TF binding signals at each input position at single-base resolution. This neural network architecture effectively captures the long-range and short-range information at multiple scales. To show this, we compared Leopard models with five different input lengths (512 bp, 1024 bp, 5120 bp, 10,240 bp, and 20,480 bp) and evaluated the predictive performance of them in six TF–cell type pairs. In general, longer inputs lead to significantly better performance, which is also reported by previous studies (Kelley et al. 2016; Li et al. 2019; Kelley 2020). The 10,240-bp/20,480-bp models have the highest AUPRCs (Supplemental Fig. S9) and AUROCs (Supplemental Fig. S10). Because the 10,240-bp model requires fewer computational resources and remains comparable/has slightly worse performance than the 20,480 model, we used 10,240 bp in this study.

Cross–cell type and cross-chromosome training, validation, and testing

We used a “crisscross” training and validation strategy to build models and avoid overfitting (Li et al. 2019). For each TF, we first collected all the available training cell types. Then a pair of cell types was selected, one for model training and the other for model validation. Meanwhile, the 23 chromosomes (Chr 1–22 and X) were also partitioned into the training, validation, and testing sets. Chr 1, Chr 8, and Chr 21 were fixed throughout this study as the testing chromosome set, whereas the remaining 20 chromosomes were randomly partitioned into the training and validation sets.

During model training, we defined an epoch as 100,000 segments or samples randomly selected from the training chromosome set in the training cell type. Each time after the model was trained on one epoch of training samples, another epoch of validation samples was randomly selected from the validation chromosome set in the validation cell type to calculate the prediction losses, monitor the training progress, and avoid overfitting. The Adam optimizer was used. Each neural network model was first trained for five epochs with the learning rate of 1.0 × 10⁻³ and then trained for 15 epochs with the learning rate of 1.0 × 10⁻⁴ until the loss converged.

AUROC and AUPRC

We define a nucleotide position to be positive only when these two requirements are met: (1) this position falls in a conservative peak of ChIP-seq, and (2) this position is a FIMO motif scanning hit. If only one requirement or neither of these requirements is met, a nucleotide position will be defined as negative. The AUROC and the AUPRC between prediction and gold standard were used to evaluate the prediction performance. Because the predictions are continuous values between zero and one, a series of cutoff values, [0, 0.001, 0.002, …, 0.998, 0.999, 1.000], are used to binarize the predictions. At each cutoff, the true-positive rate (TPR) and the FPR are defined as

$$\mathrm{TPR}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}},$$

$$\mathrm{FPR}=\frac{\mathrm{FP}}{\mathrm{FP}+\mathrm{TN}},$$

where TP is true positive, FN is false negative, FP is false positive, and TN is true negative. Similarly, the precision and recall are defined as

$$\mathrm{Precision}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}},$$

$$\mathrm{Recall}=\mathrm{TPR}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}.$$

These values were calculated at each cutoff, forming the ROC curve and PR curve. The area under the curve therefore reflects the prediction performance of a model.

Overall AUPRC and AUROC

The overall AUPRC, or the gross AUPRC, is defined as

$$\mathrm{AUPRC}=\sum _j{P}_j(R_j-R_{j+1}),$$

$$P_j=\frac{\mathrm{number}\mathrm{of}\mathrm{TF}\mathrm{binding}\mathrm{nucleotides}\mathrm{with}\mathrm{predicted}\mathrm{probability}\left(j/1000\right)\mathrm{or}\mathrm{greater}}{\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{nucleotides}\mathrm{with}\mathrm{predicted}\mathrm{probability}\left(j/1000\right)\mathrm{or}\mathrm{greater}},$$

$$R_j=\frac{\mathrm{number}\mathrm{of}\mathrm{TF}\mathrm{binding}\mathrm{nucleotides}\mathrm{with}\mathrm{predicted}\mathrm{probability}\left(j/1000\right)\mathrm{or}\mathrm{greater}}{\mathrm{total}\mathrm{number}\mathrm{of}\mathrm{TF}\mathrm{binding}\mathrm{nucleotides}},$$

where precision (P_j) and recall (R_j) were calculated at each cutoff j and j = 0, 0.001, 0.002, …, 0.998, 0.999, 1. When multiple chromosomes are under consideration, this overall AUPRC is similar to the “weighted AUPRC,” which is different from simply averaging the AUPRC score of all chromosomes (Li and Guan 2021). This is because the overall AUPRC considers the length of each chromosome and because longer chromosomes contribute more to the overall AUPRC, resulting in a more accurate evaluation of the performance. The overall AUROC is defined in a similar way as the overall AUPRC.

Convolutional layer

The architecture of Leopard was adapted from a image segmentation neural network model, U-Net, which generates pixel-wise labels for every pixel in the input two-dimensional image (Ronneberger et al. 2015). Similarly, Leopard generates base-wise labels for every nucleotide in the input genomic segment (10,240 bp) simultaneously. In each convolutional layer, the kernel size of seven was used. In each pooling layer, max pooling was used. Each convolution operation was followed by a nonlinear activation, rectified linear unit (ReLU), which is defined as

$$f\left(x\right)=\max \left(0,x\right),$$

where x is the input and f(x) is the output. Only positive values activate a neuron, and ReLU allows for effective training of neural networks compared with other complex activation functions. In addition, batch normalization was used after each convolutional layer. In the final layer, we used the sigmoid activation unit to restrict the prediction value between zero and one. The sigmoid activation is defined as

$$f\left(x\right)=\frac{1}{1+e^{-x}},$$

where x is the input and f(x) is the output.

Training losses

The cross entropy loss was used for model training, which is defined as

$$H(y,\hat{y})=\sum _{i=1}^N[-y_i\cdot \log \widehat{y_i}-(1-y_i)\cdot \log (1-\widehat{y_i})],$$

where y_i is the gold standard label of TF binding = 1 or nonbinding = 0 at genomic position i, $\widehat{y_i}$ is the prediction value at position i, N = 10,240 is the total number of base pairs in each segment, y is the vector of the gold-standard labels, and $\hat{y}$ is the vector of predictions. Ideally, an “AUPRC loss” should be used for optimizing the AUPRC. However, the AUPRC function is not mathematically differentiable, which is required by the back-propagation algorithm during neural network model training. We therefore used the cross-entropy loss to approximate the “AUPRC loss.”

Method comparison at 200-bp resolution

When comparing our method with the top-ranking methods in the ENCODE-DREAM challenge, we used the same data set provided by the challenge, consisting of 43 and 13 ChIP-seq data for model training and held-out testing, respectively (Supplemental Table S8). Of note, in the challenge, the resolution of predictions was only 200 bp. For each 200-bp interval at 50-bp sliding window steps, a gold-standard binary label “bound” or “unbound” was assigned. The AUPRC between predictions and gold-standard labels was used as the scoring metric to compare different models, which was also used in the ENCODE-DREAM challenge. For this low-resolution prediction task, we created a Leopard 200-bp model (Supplemental Fig. S2), which directly generates predictions at the 200-bp resolution. In addition to the one-hot-encoded sequences and DNase-seq features, we also added the number of 5′ tag counts within each 200-bp bin as an extra feature, which was also named as frequency/Δfrequency feature in Anchor (Li et al. 2019).

Saliency map

For a 10,240-bp genomic region under consideration (for examples, see Fig. 2E; Supplemental Fig. S1), we used the cross-entropy loss of all 10,240 output positions to calculate the gradients for each input position with two types of channels: (1) four DNA sequence A/C/G/T channels, and (2) two open chromatin related DNase-seq/ΔDNase-seq channels. The original saliency map is a six-by-10,240 matrix. Then for each type of input, we calculated the maximum values along the channel dimension, resulting in two signals “saliency map–DNA sequence” and “saliency map–DNase-seq.” These saliency maps were calculated using the function “visualize_saliency” from the “keras-vis” module in Python. We used the parameter backprop_modifier = “guided,” through which only positive gradients were propagated positive activations.

The reference genome

In this work, we used GRCh37 as the reference genome, instead of GRCh38. One of the main improvements of GRCh38 over GRCh37 is the annotation of centromere regions. To the best of our knowledge, most TF binding sites are located outside the centromere regions. Therefore, if all the data in this work were lifted over to GRCh38, we surmise that our conclusions will not be significantly affected.

Software availability

The source code of our Leopard software is available on GitHub (https://github.com/GuanLab/Leopard) and as Supplemental Code.

Competing interest statement

Y.G. receives personal payment from Eli Lilly and Company, Genentech, F. Hoffmann-La Roche, and Merck & Co. and holds equity shares at Ann Arbor Algorithms.