Linear-time cluster ensembles of large-scale single-cell RNA-seq and multimodal data

Abstract

A fundamental task in single-cell RNA-seq (scRNA-seq) analysis is the identification of transcriptionally distinct groups of cells. Numerous methods have been proposed for this problem, with a recent focus on methods for the cluster analysis of ultralarge scRNA-seq data sets produced by droplet-based sequencing technologies. Most existing methods rely on a sampling step to bridge the gap between algorithm scalability and volume of the data. Ignoring large parts of the data, however, often yields inaccurate groupings of cells and risks overlooking rare cell types. We propose method Specter that adopts and extends recent algorithmic advances in (fast) spectral clustering. In contrast to methods that cluster a (random) subsample of the data, we adopt the idea of landmarks that are used to create a sparse representation of the full data from which a spectral embedding can then be computed in linear time. We exploit Specter's speed in a cluster ensemble scheme that achieves a substantial improvement in accuracy over existing methods and identifies rare cell types with high sensitivity. Its linear-time complexity allows Specter to scale to millions of cells and leads to fast computation times in practice. Furthermore, on CITE-seq data that simultaneously measures gene and protein marker expression, we show that Specter is able to use multimodal omics measurements to resolve subtle transcriptomic differences between subpopulations of cells.

Single-cell RNA sequencing (scRNA-seq) has increased the resolution at which important questions in cell biology can be addressed. It has helped to identify novel cell types based on commonalities and differences in genome-wide expression patterns, reconstruct the heterogeneous composition of cell populations in tumors and their microenvironment, and unveil regulatory programs that govern the dynamic changes in gene expression along developmental trajectories.

One of the most fundamental computational tasks in the context of scRNA-seq analysis is the identification of groups of cells that are similar in their expression patterns, that is, their transcriptomes, and which are at the same time distinct from other cells. Conceptually similar problems have been studied in anthropology (Driver and Kroeber 1932) and psychology (Zubin 1938) almost a century ago; since then, this so-called cluster analysis has become one of the most well-studied problems in unsupervised machine learning. Numerous methods have been proposed for clustering scRNA-seq data sets (Duò et al. 2018; Tian et al. 2019), with Seurat (Satija et al. 2015) and its underlying Louvain clustering algorithm (Blondel et al. 2008) being arguably the most widely used one. More recently, attempts have been made to design algorithms for the analysis of ultralarge scRNA-seq data sets, owing to the ever-increasing throughput of droplet-based sequencing technologies that allow profiling genome-wide expression for hundreds of thousands of cells at once. At the heart of such methods often lies a sampling technique that reduces the size of the data analyzed by a clustering algorithm. Cluster labels of cells in this so-called sketch are subsequently transferred to the remaining cells using, for example, a nearest neighbor algorithm. dropClust (Sinha et al. 2018), for example, includes a structure-preserving sampling step, but initially picks a small set of cells simply at random. Similarly, Seurat applies random subsampling before its nearest neighbor search.

The quality of the final clustering, however, strongly depends on how well the data sketch represents the overall cluster structure and how accurate the cluster labels of cells in the sketch can be inferred from incomplete data. Inaccurate labels of subsampled cells will likely lead to an inaccurate labeling of the full data. In addition, sampling cells proportional to their abundance might render rare cell types invisible to the algorithm. Geometric sketching was therefore recently proposed as an alternative sampling method that selects cells according to the transcriptomic space they occupy rather than by their abundance. Nevertheless, labels need to be inferred from partial data.

Spectral methods for clustering have been applied with great success in many areas such as computer vision, robotics, and bioinformatics. They make few assumptions on cluster shapes and are able to detect clusters that form nonconvex regions. On a variety of data types, this flexibility has allowed spectral clustering methods to produce more accurate clusterings than competing methods (Shi and Malik 2000). The high computational complexity, however, renders its application to large-scale problems infeasible. For n data points, spectral clustering computes eigenvectors of an n × n affinity matrix, which incurs a computational cost of $\mathcal{O}\left(n^3\right)$. For scRNA-seq data sets with n in the order of ten thousands up to the millions, this presents a prohibitive cost that has thus prevented the application of spectral clustering to large-scale single-cell data sets. Furthermore, spectral clustering methods are sensitive to the right choice of parameters used to model the similarity between data points (von Luxburg 2007), that is, RNA expression measurements of single cells. Data sets derived from different biological samples showing different cell population structures obtained using different sequencing technologies typically require a different set of parameter values to achieve accurate clustering results.

We introduce a new method, Specter, which addresses the challenges of computational complexity and parameter sensitivity to allow a tailored version of spectral clustering to be used in the analysis of large scRNA-seq data sets as well as measurements of multiple modalities of single cells (Zhu et al. 2020).

Results

Overview of Specter

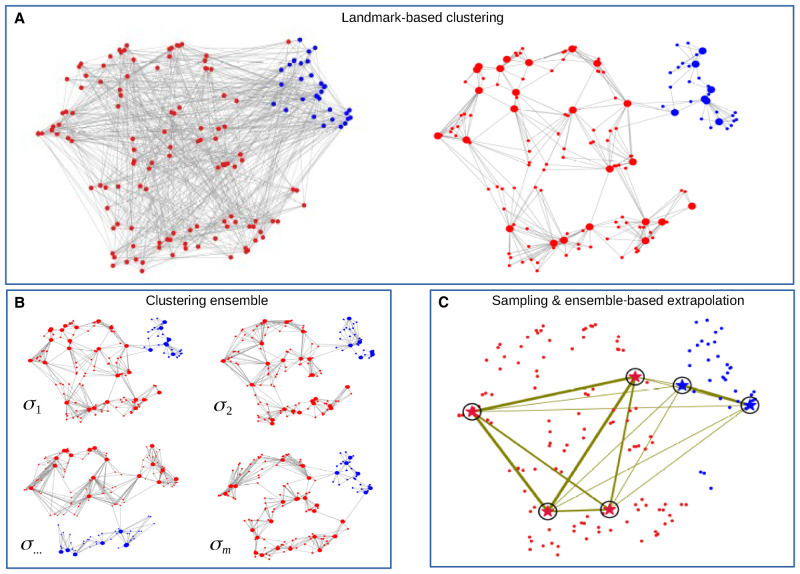
In contrast to methods that cluster only a (random) subsample of the data, Specter takes a fundamentally different approach that avoids learning from unlabeled partial data. We adopt the idea of landmarks (Cai and Chen 2015), a random sample of cells that are used to create a sparse representation of the full data from which a spectral embedding can then be computed in linear time. We use the speed of this approach to systematically explore the parameter space by a co-association-based consensus clustering scheme, also known in literature as cluster ensembles (Strehl and Ghosh 2003): Instead of picking one set of parameters, in Specter we explore different choices of parameters and reconcile the resulting clustering information into a single (consensus) clustering. In addition to aggregating clusterings obtained in different runs of the algorithm on the same data, consensus clustering can also be used to reconcile clusterings of cells based on different molecular features. CITE-seq (Stoeckius et al. 2017), for example, measures both gene expression and surface protein levels of individual cells, and Specter's consensus clustering scheme can help to resolve subpopulations of cells that cannot accurately be distinguished based on transcriptomic differences alone. We combine consensus clustering with a novel selective sampling strategy that uses clustering information obtained from the full data set to achieve overall linear-time complexity. Finally, we transfer cluster labels to the remaining cells using supervised k-nearest neighbors classification. We provide an overview of the approach in Figure 1A–C and a detailed description of our algorithm in Methods.

Figure 1.

Overview of Specter. Illustrations are based on t-SNE visualizations of a random subsample of scRNA-seq data by Grün et al. (2016). (A) Standard spectral clustering constructs an affinity matrix that captures (transcriptional) similarities between all pairs of cells (left), which renders its eigen decomposition prohibitively expensive for large data sets. (Right) In contrast, describing each cell (small circles) with respect to its nearby landmarks (big circles) that were initially selected as the means computed by k-means clustering, creates a sparse representation of the full data that speeds up the computation of a spectral embedding. Cells are colored to distinguish sorted hematopoetic stem cells (blue) from other mouse bone marrow cells (red) assayed by Grün et al. (2016). (B) Specter does not rely on a single set of parameters but performs multiple runs of landmark-based clustering using different sets of landmarks of different size and different measures of similarities between cells (parameterized by σ). Three clusterings closely resemble the true labeling shown in A, but one differs substantially. (C) Specter reconciles all individual clusterings into a consensus clustering. It clusters a carefully selected subset of cells (marked by circled stars) based on their co-association across all individual clusterings in B, indicated by the width of the corresponding edge. The thicker an edge, the more often its two end points were placed in the same cluster. Here, the four red stars and the two blue stars correctly form two groups of cells, whose labels are finally propagated to the remaining cells using one-nearest-neighbor classification. The final clustering shown in C closely resembles the true clustering in A.

Specter is more accurate than competing methods

We compared the performance of Specter to representative scRNA-seq clustering methods SC3 (v1.10.1) (Kiselev et al. 2017), Seurat (v2.3.4) (Satija et al. 2015), dropClust (v2.1.0) (Sinha et al. 2018), RCA (v2.0) (Li et al. 2017), TSCAN (v1.24.0) (Ji and Ji 2016), RaceID3 (v0.2.1) (Herman et al. 2018), CIDR (v0.1.5) (Lin et al. 2017), and RtsneKmeans (Duò et al. 2018) as well as to a geometric sketching–based clustering approach (Hie et al. 2019b). SC3 and Seurat consistently showed superior performance over competing methods in several clustering benchmarks (Duò et al. 2018; Tian et al. 2019) and are routinely used in scRNA-seq-based cell type analyses. The graph-based Louvain clustering approach used by Seurat has an additional speed advantage over SC3, which applies a consensus clustering scheme to obtain particularly accurate clusterings. dropClust was recently proposed for the analysis of ultralarge scRNA-seq data sets and follows a strategy outlined above. It first reduces the size of the data to a maximum of 20,000 cells using random sampling. After a second sampling step based on Louvain clusters, it applies average-linkage hierarchical clustering on the sampled cells. Cluster labels are then transferred to the remaining cells using a Locality Sensitive Hashing forest (Bawa et al. 2005) for approximate nearest neighbor searches. In contrast, the geometric sketching algorithm proposed in Hie et al. (2019b) samples cells evenly across the transcriptional space rather than proportional to the abundance of cell types as uniform sampling schemes do. Experiments by Hie et al. (2019b) showed that clustering a geometric sketch using the graph-based Louvain algorithm followed by propagating labels to the remaining cells via k-nearest-neighbor classification accelerates clustering analysis and yields more accurate results than uniform sampling strategies. We include the same geometric sketching–based clustering method in our benchmark and refer to it simply as geometric sketching throughout the text. We further included methods RCA, TSCAN, RaceID3, and CIDR to cover a diverse set of algorithms commonly used to cluster scRNA-seq data (for recent benchmarks, see Duò et al. 2018; Freytag et al. 2018; Tian et al. 2019), from nearest-neighbor-based graph clustering to hierarchical clustering to k-medoids to model-based clustering. Finally, we included general purpose k-means clustering (RtsneKmeans) as a baseline that performed well in Duò et al. (2018) compared to methods specifically developed for clustering scRNA-seq data.

Data sets and evaluation

We evaluated Specter and competing methods on 21 public scRNA-seq data sets and 24 simulated data sets (Supplemental Tables S1, S2). The former includes 16 data sets for which cell type labels were inferred in the original publication from clusterings of scRNA-seq measurements, which typically underwent manual refinement and annotation, as well as all real data sets except one that were used in Duò et al. (2018) to benchmark clustering methods based on cell phenotypes defined independently of scRNA-seq. Identically to Duò et al. (2018), we used “true” cell types annotated by FACS sorting in the Koh data set, and partitioned cells by genetic perturbation and growth medium in the Kumar data set. In data sets Zhengmix4eq and Zhengmix4uneq, Duò et al. (2018) randomly mixed equal and unequal proportions, respectively, of presorted B cells, CD14 monocytes, naive cytotoxic T cells, and regulatory T cells. Data set Zhengmix8eq additionally contained roughly equal proportions of CD56 NK cells, memory T cells, CD4 T helper cells, and naive T cells. Again, annotated cell types were used as reference partitioning of cells in the evaluation. We excluded a single data set from Duò et al. (2018) in which ground truth labels correspond to collection time points that all methods tested in Duò et al. (2018) failed to reconstruct. Data sets vary in size and number of cell populations and are described in Supplemental Table S1. We used Splatter (Zappia et al. 2017) to simulate 24 data sets that varied in the relative abundance of cell types that were either all equal (Geq), unequal (Gneq), or based on cell type abundances among peripheral blood mononuclear cells (PBMCs) in healthy individuals (Gpbmc), in number of cells (N1k, N2k, N5k), and in the probability of a gene being differentially expressed in a group, which was either 0.01 (DE1), 0.02 (DE2), 0.05 (DE5), or differed between groups (DEneq). Following the introduction to Splatter (https://bioconductor.org/packages/devel/bioc/vignettes/splatter/inst/doc/splatter.html), we set the number of genes to 1000 or 10, 000 (D10k). Supplemental Table S2 lists the characteristics of all simulated data sets.

We apply standard and uniform preprocessing (Duò et al. 2018) on all real and simulated data sets, including natural log-transformation of gene counts after adding a pseudocount of 1, selection of the top 2000 most variable genes (omitted for simulated data sets with fewer than 2000 genes), followed by dimensionality reduction to 100 principle components (https://www.mathworks.com/matlabcentral/fileexchange/47132-fast-svd-and-pca, retrieved October 30, 2020). We show results for Specter when using 20 ensemble members (Specter20E) and 50 ensemble members (Specter50E). We motivate this choice of the number of ensemble members below through experiments addressing the dependence of Specter's accuracy on this parameter. The results for these two variants are nearly identical and we therefore simply refer to them as Specter unless we explicitly distinguish these two settings. Owing to our clustering ensemble scheme, no additional tuning of parameters is required to apply Specter to the 45 data sets. Following the strategy in Duò et al. (2018), all methods were provided identical gene counts, but additional preprocessing steps were performed as recommended by each method. The geometric sketching–based Louvain clustering was provided the same preprocessed data as Specter. Consistent with the original publication (Hie et al. 2019b), geometric sketches ranging from 2% to 10% of the original number of cells were computed and clustered as described above. All methods were provided the correct number of clusters, or corresponding parameters were tuned accordingly. All experiments were run on an Intel Xeon CPU at 2.30 GHz with 320 GB memory. Methods SC3, RCA, RaceID3, and CIDR failed to run on the three largest data sets that included more than 450, 000 cells (Supplemental Table S1) because of insufficient memory. In fact, with a running time that grows cubic with the number of cells, SC3 is not designed for large data sets. On data set chen, for example, it takes SC3 5 h to cluster 14,000 cells. Similarly, on the three largest data sets we replaced the R (R Core Team 2020) implementation of the Louvain clustering algorithm called in the Seurat clustering pipeline by a more efficient Python implementation of the same algorithm in the scanpy package (v1.4.6) (Wolf et al. 2018). scanpy was specifically designed for the analysis of large-scale gene expression data sets and was used originally (Cao et al. 2019) to identify cell types in data set trapnell comprising more than 2 million cells.

Consistent with other benchmarks (e.g., Duò et al. 2018; Freytag et al. 2018; Sinha et al. 2018), we used the Adjusted Rand index (ARI) (Hubert and Arabie 1985) to measure the similarity between the inferred clusterings and the ground truth clustering that is based on the biological cell types annotated or presorted in the original study or was provided by the simulator. We additionally applied routinely used (Freytag et al. 2018) clustering metrics Normalized Mutual Information (NMI) (Studholme et al. 1999) and a homogeneity score (Rosenberg and Hirschberg 2007) to provide a more detailed analysis of clustering performance.

Evaluation on real data

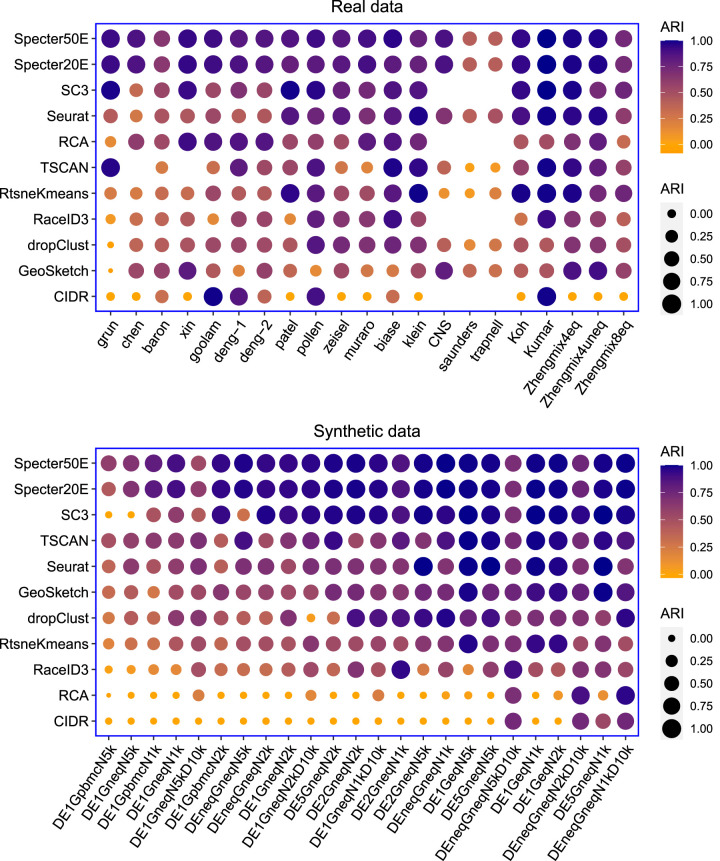
Consistent with previous benchmarks, SC3 and Seurat overall outperform existing methods, with RCA showing a competitive performance especially with respect to homogeneity scores (Fig. 2; Supplemental Figs. S1, S2). Specter, however, improves mean clustering accuracy over both methods in all three metrics. The biggest improvement can be observed with respect to ARI and homogeneity scores, whose mean values (excluding the three largest data sets for which SC3 failed to run) achieved by Specter (Specter50E) are 0.88 and 0.89, respectively, compared to 0.69 and 0.76 for Seurat and 0.78 and 0.84 for SC3. Overall, most methods achieved higher scores in NMI than in the other two metrics. On 17 of 21 real data sets, Specter obtained more accurate clusterings than Seurat in all three metrics and without exception achieved higher ARI scores than sampling-based methods dropClust and geometric sketching, even when sampling as many as 10% of cells in the latter approach. A similar preeminence can be observed when applying metrics NMI and homogeneity score. On many instances, the improvement was substantial. Results for smaller sketch sizes are shown in Supplemental Figure S3. In fact, on average, methods dropClust and geometric sketching achieved slightly lower scores with respect to all three metrics than baseline algorithm RtsneKmeans that simply applies standard k-means clustering on t-SNE projected cells. Note that the ground truth labeling of cell types in data sets trapnell, CNS, and saunders was obtained in the original publication using Seurat or its underlying Louvain clustering algorithm. Despite the additional manual refinement applied in some studies (Saunders et al. 2018; Zeisel et al. 2018; Cao et al. 2019), this might positively impact the evaluation results of Seurat and the geometric sketching–based Louvain clustering. On several instances, Specter achieved considerably higher ARI scores than SC3, whereas on others their performance was similar (within <10% difference in ARI). Note, however, that SC3 is not designed to cluster large data sets and had to be excluded from the comparison on the three largest data sets for computational reasons.

Figure 2.

Clustering performance measured in ARI of Specter and competing methods on real and synthetic scRNA-seq data sets. Methods are ordered by mean ARI score across data sets decreasing from top to bottom. In the calculation of mean scores, we excluded for each method the data sets for which the method did not run successfully. For the rightmost five real data sets, ground truth labels are based on cell phenotypes defined independently of scRNA-seq (Supplemental Table S1). Synthetic data sets are ordered from left to right by increasing mean ARI over all methods. SC3, RCA, RaceID3, and CIDR failed to run on the three largest data sets CNS, saunders, and trapnell because of insufficient memory. TSCAN failed to run on data sets chen and skin for unknown reasons. Geometric sketching refers to the Louvain clustering of 10% of the cells sampled using geometric sketching. Results for different sketch sizes are shown in Supplemental Figure S3.

Evaluation on simulated data

As expected, simulated data sets Gpbmc that reflect the unbalanced cell type composition among PBMCs pose the biggest challenge to clustering algorithms, whereas uniform cell type abundances (Geq) or a larger number of marker genes (DEneq*D10k or DE5) facilitate the detection of transcriptionally distinct groups of cells (Fig. 2; Supplemental Figs. S1, S2). Consistent with results on real data sets, Specter achieved the highest accuracy in terms of mean ARI, NMI, and homogeneity score across 24 simulated data sets, with scores in NMI being generally higher for most methods than in the other two metrics. Again, SC3 performed the best among the remaining methods in terms of mean ARI and mean homogeneity score, which may be attributed to a consensus clustering scheme that it applies similarly to Specter. With respect to NMI, Seurat and TSCAN achieved slightly higher mean scores than SC3, mainly owing to the two presumably most difficult instances in which SC3 returned clusterings with a score of 0 (in all three metrics) and is thus no better than a random partition of cells. Seurat performed well on data sets with equal cell type proportions (Geq) and on data sets in which groups are identified by a large number of marker genes (DE5), whereas a substantial drop in ARI and homogeneity score can be observed on the remaining data sets. Seurat's NMI scores show a similar but less pronounced pattern. Geometric sketching, which uses the same Louvain clustering algorithm as Seurat, behaves similarly. TSCAN performed better on synthetic than on real data sets (in all three metrics), but the opposite is true for RCA. The baseline algorithm RtsneKmeans yields accurate clusterings, especially on data sets with balanced cell type composition. On more difficult data sets, however, its accuracy drops significantly compared to several methods tailored to scRNA-seq analysis, especially in terms of ARI and homogeneity score. dropClust, on the other hand, achieved mean accuracy scores on synthetic data sets that are close to the baseline algorithm's ones (ARI 0.63 vs. 0.57, homogeneity score 0.65 vs. 0.63, NMI 0.67 vs. 0.71). We show in Supplemental Figure S4 how higher performance scores translate into a more meaningful representation of cell types.

In addition, we compared Specter to the original implementation of the landmark-based spectral clustering (LSC) algorithm to show the effectiveness of our hybrid landmark selection strategy, the clustering ensemble approach and the novel selective sampling scheme (Supplemental Note 1; Supplemental Figs. S5, S6). Finally, we show that Specter can use even a small number of ensemble members to improve clustering accuracy substantially and that Specter's performance is robust to the choice of parameter γ that controls the bandwidth of the Gaussian kernel (Supplemental Note 2; Supplemental Figs. S7, S8).

Specter identifies rare cell populations with high sensitivity

We evaluated Specter's sensitivity to rare cell populations by devising three simulation experiments with an increasing degree of difficulty. First, we repeated the experiment performed by Sinha et al. (2018) and randomly sampled a rare population of cells that comprise between 1% and 10% of total cells. More specifically, starting from two (equal size) groups of 2000 cells each that were simulated using Splatter (data set RareCellExp1 in Supplemental Table S2), we randomly down-sample one group to comprise 1% − 10% of the total number of cells. We repeat the experiment five times for each group; similar to Sinha et al. (2018), we report the average F₁ score over the 10 runs in Supplemental Figure S9. The F₁ score denotes the harmonic mean of the recall and precision, which we define identically to Sinha et al. (2018) with respect to the predicted cluster with the largest number of rare cells. Although several methods performed well on a sample of 10% of cells (SC3 being a notable exception), only Specter and Seurat are able to accurately detect a cell population composed of only 1% of cells. Additionally, we performed an experiment in which we randomly sampled cells from a group that is initially smaller (1000 cells) than the second group (9000 cells) (data set RareCellExp2 in Supplemental Table S2). Compared to the previous experiment, the rare population of cells will then occupy a smaller transcriptional space relative to the larger group, which may represent a more realistic, but also a more challenging scenario for clustering methods. The smaller group initially consists of 10% of total cells and was therefore down-sampled to comprise 1% − 5% of cells. Again, each sampling experiment was repeated 10 times and the average F₁ scores are shown in Supplemental Figure S10. Here, several methods obtained an F₁ score of close to 0 even when sampling 5% of cells, underlining the added difficulty of clustering unbalanced cell types. After further reducing the abundance of the rare cell type to 1%, only Specter achieved an almost perfect F₁ score (0.96), followed again by Seurat with an F₁ score of 0.78. In the most challenging scenario, we randomly down-sampled naive cytotoxic or regulatory T cells that partly overlap in the Zhengmix4eq data set (Supplemental Fig. S11) to comprise 1% − 10% of the total number of cells and repeated this experiment five times for each group. Average F₁ scores are shown over the 10 runs in Supplemental Figure S12. Even though Specter consistently shows the highest accuracy among all methods, its F₁ score monotonically decreases from close to 1 for 10%, to 0.26 for just 1% of cells, highlighting the intrinsic difficulty of detecting rare cell types that are transcriptionally similar to more abundant cell populations.

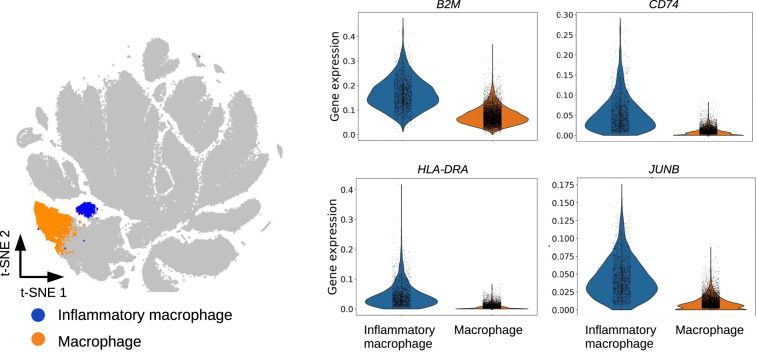
Finally, we confirmed Specter's sensitivity to rare cell types on a rare population of inflammatory macrophages that was reported and experimentally validated by Hie et al. (2019b), who applied Louvain clustering to a geometric sketch of 20,000 cells sampled from a data set of 254,941 human umbilical cord blood cells. In their experiments, Hie et al. (2019b) observed that this rare subtype is invisible to Louvain clustering, the algorithm used by Seurat, unless cells are initially sampled evenly across transcriptional space to better balance the abundance of common and rare cell types. In contrast, Specter reveals a similar population of inflammatory macrophages characterized by the same set of marker genes CD74, HLA-DRA, B2M, and JUNB (AUROC>0.9) without any prior preprocessing (Fig. 3).

Figure 3.

Clustering of 254,941 umbilical cord blood cells by Specter. (Left) Among macrophages defined by CD14 and CD68 marker gene expression, Specter detects a rare subpopluation of inflammatory macrophages that was recently discovered (Hie et al. 2019b). This rare subtype can be distinguished in Specter's clustering by the expression of the same set of inflammatory marker gene expression (CD74, HLA-DRA, B2M, and JUNB) used for its identification in Hie et al. (2019b).

Specter uses multimodal data to resolve subtle transcriptomic differences

We showed the ability of Specter to use complementary information provided by multimodal data to refine the clustering of single cells. More specifically, we reanalyzed two public data sets of 4292 healthy human PBMC (Mimitou et al. 2019) and 8617 cord blood mononuclear cells (CBMC) (Stoeckius et al. 2017), for which both mRNA and protein marker expressions (ADT, antibody-derived tags) were measured simultaneously using CITE-seq (Stoeckius et al. 2017). In these experiments, the investigators used 49 and 13 antibodies, respectively, that recognize cell-surface proteins used to classify different types of immune cells.

Consistent with previous analyses of CITE-seq data (https://satijalab.org/seurat/v3.1/multimodal_vignette.html; Kim et al. 2020), we used the Seurat R package (Butler et al. 2018) to preprocess RNA and ADT counts. We normalized ADT expression using centered log-ratio (CLR) transformation and log-transformed RNA counts after adding a pseudocount of 1. After selecting the top 2000 most variable genes, the expression of each gene was scaled to have mean expression 0 and variance 1, followed by dimensionality reduction to 20 principal components.

Doublets in the PBMC data set were removed using the same cell hashing-based approach with identical parameters as in Kim et al. (2020). Similar to the analysis in Stoeckius et al. (2017), a putative cluster of doublets coexpressing different RNA and protein lineage marker was removed from further analysis. On the CBMC data we relied on the doublet removal of Seurat performed in a prior analysis (https://satijalab.org/seurat/v3.1/multimodal_vignette.html) of this data set.

We annotated clusters based on differential expression of marker genes (Wilcoxon rank-sum test) for immune cell types listed in Supplemental Table S3. The analysis of both data sets is documented at GitHub (https://github.com/canzarlab/Specter).

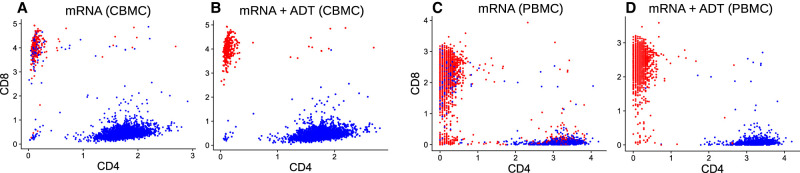
On both data sets, both Seurat and Specter fail to accurately distinguish naive CD4 T cells and CD8 T cells based on transcriptomic data alone (Fig. 4A,C; Supplemental Fig. S13). Many CD4⁻/CD8⁺ T cells identified by protein measurements (ADT) in the CBMC data set are wrongly grouped together with CD4 T cells by Seurat and Specter. Similarly, CD4 and CD8 T cells are mixed in the PBMC data set by both methods.

Figure 4.

Comparison of unimodal and joint clustering by Specter. CBMCs (A,B) and PBMCs (C,D) with coordinates of protein expression (ADT) along the CD4 and CD8 axes. Cells are clustered by Specter into CD4 T cells (blue) and CD8 T cells (red) either based on mRNA expression alone (A,C) or jointly from mRNA and surface protein expression (B,D). The mixing of CD4 T cells and CD8 T cells in the mRNA-based clustering is corrected through the co-association of both modalities by Specter.

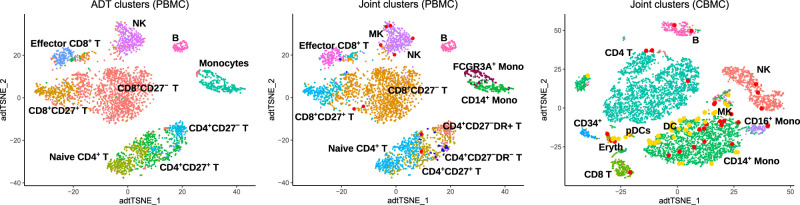
On the other hand, dendritic cells and megakaryocytes cannot be identified in the CBMC data set based on protein marker expression (see analysis using Seurat) (https://satijalab.org/seurat/v3.1/multimodal_vignette.html). Similarly, Figure 5 shows that ADT-based clustering by Specter is not able to separate CD14⁺ from FCGR3A⁺ monocytes nor megakaryocytes from other cell types in the PBMC data set. This can be analogously observed in the clustering by Seurat (Supplemental Fig. S13).

Figure 5.

t-SNE visualization of clusters identified by Specter. Clusters of PBM cells were inferred from protein expression (ADT) alone (left) or from combined mRNA and protein expression (middle). In contrast to the joint clustering of both modalities, ADT-based clustering cannot discriminate CD14⁺ and FCGR3A⁺ monocytes, does not detect megakaryocytes (red), and does not allow to discriminate between CD27⁻DR⁺ and CD27⁻DR⁻ subpopulations of CD4⁺ T cells. The simultaneous clustering of RNA and protein expresssion in CBM cells (right) additionally reveals a rare population of megakaryocytes (red).

We therefore aimed to correct and improve the individual clusterings of RNA and surface marker protein measurements by combining the two distinct species through our clustering ensemble approach. In particular, Specter first produces an identical number of clusterings (here 200) for each modality. It then combines the transcriptome-based clusterings and the protein-based clusterings through a co-association approach (Methods).

The joint clustering of RNA and protein expression by Specter profits from both modalities yet differs from both unimodal analyses: On the PBMC data set, an ARI score of 0.78 comparing multimodal and RNA-based clustering and a score of 0.72 between multimodal and ADT-based clustering indicate complementary aspects of cellular identity used in their joint clustering. On the CBMC data set, higher ARI scores of 0.87 and 0.91 between the multimodal clustering and RNA and ADT-based clusterings, respectively, reflect a higher agreement between the two modalities.

More specifically, the joint clustering of RNA and protein expression of CBM and PBM cells allows Specter to more accurately separate CD4 T cells and CD8 T cells compared to a simple transcriptome-based clustering (Fig. 4B,D). In contrast to ADT expression–based clustering of PBM cells, the joint clustering of RNA and surface protein expression by Specter correctly identifies megakaryocytes, CD14⁺, and FCGR3A⁺ monocytes (Fig. 5; Supplemental Table S3). In addition, only the combined clustering of ADT and RNA allows Specter to discriminate between CD27⁻ DR⁺ and CD27⁻ DR⁻ subpopulations of CD4⁺ memory T cells. In contrast to the clustering of protein data of CBM cells, Specter also correctly detects dendritic cells and megakaryocytes based on the markers listed in Supplemental Table S3 (see Fig. 5).

We compared the joint clustering by Specter to the results of CiteFuse (v0.99.10) (Kim et al. 2020), a method that was recently proposed specifically for the computational analysis of single-cell multimodal profiling data. As proposed initially for the combination of (bulk) genome-wide measurements across, for example, patients (Wang et al. 2014), CiteFuse applies the similarity network fusion algorithm to combine RNA and ADT expression of single cells and then clusters the fused similarity matrix using spectral clustering. We ran CiteFuse as originally described (Kim et al. 2020), including the removal of doublets and the (internal) selection of highly variable genes.

Overall, the clusters of CBM and PBM cells as computed by Specter and CiteFuse are highly similar, as indicated by a high ARI score of 0.94 and 0.86 for the two data sets (Supplemental Figs. S14, S15). In both data sets, however, only Specter is able to identify a rare population of megakaryocytes (Supplemental Table S3). Furthermore, in contrast to the analysis performed in Kim et al. (2020), CiteFuse was not able to discriminate between CD27⁻ DR⁺ and CD27⁻ DR⁻ subpopulations of CD4⁺ memory T cells in the PBMC data set, neither when using identical parameters as in Kim et al. (2020) nor when applying more conservative parameters in the doublet removal, using parameters taken from CiteFuse tutorial (Supplemental Fig. S16; https://sydneybiox.github.io/CiteFuse/articles/CiteFuse.html). Kim et al. (2020) attribute this discrepancy to a different selection of highly variable genes applied in an earlier version of the software used to produce the results in Kim et al. (2020).

The major advantage of Specter over CiteFuse, however, is its speed and scalability. CiteFuse requires 15 min and nearly 2 h to jointly cluster the 3880 PBM cells and 7895 CBM cells (after doublet removal), respectively, and is thus not expected to scale well on much larger data sets owing to the computational expensive fusion of networks. In contrast, Specter returns a high-resolution clustering of the two data sets in just 20 and 50 sec, respectively.

Scalability

Here, we show the scalability of Specter to large single-cell data sets. To experimentally confirm the theoretical linear-time complexity of our algorithm, we devised different size-simulated data sets containing between 1000 and 1 million cells (with characteristics DE1Geq) (Supplemental Table S2). As expected (Cai and Chen 2015), the landmark-based sparse representation of the data allows us to compute a spectral embedding in linear time (Supplemental Fig. S17). Furthermore, the experiment confirms that our novel selective sampling strategy reduces the quadratic complexity of the hierarchical clustering step that reconciles multiple ensemble members (Methods) to an overall linear dependence on the number of cells. As expected, the rate of increase in running time, that is, the slope of the lines shown in Supplemental Figure S17, is larger when Specter includes multiple clusterings (here 20) in the ensemble scheme. More precisely, we observed a linear increase in running time with the size of the clustering ensemble, that is, with the number of independent runs of the core algorithm (Supplemental Fig. S18). However, as shown in our experiments assessing the importance of individual algorithmic components in Specter, a relatively small number of runs is sufficient to improve accuracy of the resulting consensus clustering substantially. Even more, the independent computation of individual clusterings in an ensemble lends itself to parallel processing. In Supplemental Figure S19, we therefore explored how the use of multiple threads can speed-up the clustering ensemble approach and thus counterbalance the inclusion of an increasing number of ensemble members. With just four threads, the time required to compute a consensus clustering from 50 individual clusterings of 100,000 cells reduced from around 92 sec to just 34 sec. Increasing the number of threads further has a decreasing effect on total running time, reaching 15 sec total computation time using 20 threads. Again, we observed a roughly linear increase in running time with increasing sample size for a fixed number of threads (Supplemental Fig. S20), in which four threads reduced the running time of 50 runs in the clustering ensemble to a time that is nearly identical to the time a single thread needs to compute a consensus clustering from 20 ensemble members.

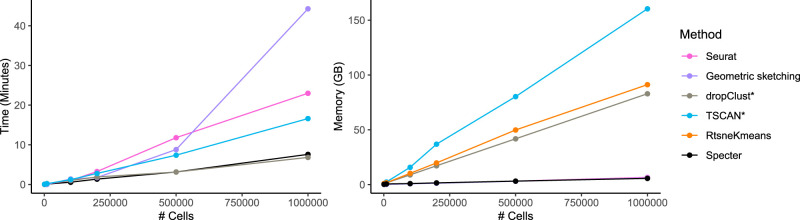
In Figure 6, we compared Specter's running time to all methods that ran successfully on the three largest real data sets. For all methods except TSCAN and dropClust, we measured the running time of the core algorithm and excluded preprocessing. The time Specter required to preprocess the data (using a single thread), including log-transformation, the selection of highly variable genes, and principle component analysis, is negligible (Supplemental Tables S4, S5). Seurat was run with a call to the more efficient scanpy implementation of the Louvain clustering algorithm. Even in single-threaded mode, Specter's running time that included 20 individual clusterings of 1 million cells is considerably faster (7.6 min) than Seurat which required 23 min for a single Louvain-based clustering of the same set of cells (Supplemental Table S4). Note that 20 ensemble members were used by Specter in Figure 2 (and Supplemental Figs. S1, S2) to achieve overall more accurate clusterings than competing methods. With just four threads, Specter's running time further drops to 3.2 min (Supplemental Fig. S20), whereas Seurat's clustering algorithm cannot be run with multiple threads. dropClust required 6.8 min to preprocess and cluster 1 million cells but is not able to make use of multiple threads. The running time of geometric sketching increases the fastest, whereas RtsneKmeans is as expected the slowest method (Supplemental Fig. S21). As one potential use of clustering results, visualization by FIt-SNE (Linderman et al. 2019) required ∼8 min for 1 million cells (Supplemental Table S5).

Figure 6.

Runtime and peak memory usage as a function of sample size. Seurat was run with a call to the more efficient scanpy implementation of the Louvain clustering algorithm. Running times exclude preprocessing for all methods except TSCAN and dropClust, whose implementation did not allow us to isolate the core algorithm. Memory usage of Specter, Seurat, and geometric sketching are nearly identical and cannot be distinguished in this plot. For ease of visualization, we show runtime results of method RtsneKmeans in Supplemental Figure S21.

Finally, Supplemental Table S6 gives the CPU times in minutes on the three largest real data sets used in this study. Again, we excluded preprocessing for all methods except TSCAN and dropClust. We additionally report the total running time of Specter including all prior preprocessing. In this analysis of real data sets, we exploited the full performance potential of Specter and used 20 threads to compute consensus clusterings from 50 individual runs, which outperformed all other methods in terms of accuracy in Figure 2 and Supplemental Figures S1 and S2. In this setting, Specter required around 15 min to cluster 2 million cells (23 min including single-threaded preprocessing) and was 5–10 times faster than Seurat that is unable to use multiple threads. On the largest data set, dropClust was the fastest method (12 min total computation time) even though it uses just a single thread. In contrast to Specter, however, dropClust considers only ∼1% of the data (20,000 cells) and its simplified model comes at the cost of a substantial loss in accuracy (Fig. 2; Supplemental Figs. S1, S2). Again, RtsneKmeans is the slowest among methods that terminate successfully on these large data sets.

Furthermore, Figure 6 shows peak memory usage as a function of number of cells on the same simulated data sets used to evaluate runtime performance. Together with Seurat and geometric sketching, Specter required the least amount of memory (<7 GB for 1 million cells), whereas the memory usage of methods TSCAN and dropClust increased rapidly for data sets containing more than 200,000 cells.

Discussion

We have introduced Specter, a novel method that identifies transcriptionally distinct sets of cells with substantially higher accuracy than existing methods. We adopt and extend algorithmic innovations from spectral clustering, to make this powerful methodology accessible to the analysis of modern single-cell RNA-seq data sets. We have shown the superior performance of Specter across a comprehensive set of public and simulated scRNA-seq data sets and illustrated that an overall higher accuracy also implicates an increased sensitivity toward rare cell types. At the same time, its linear-time complexity and practical efficiency makes Specter particularly well-suited for the analysis of large scRNA-seq data sets. Besides technological advances, the integration of cells from multiple experiments spanning different tissues or diseases may yield data sets with massive numbers of cells. Coupled with data integration methods such as Scanorama (Hie et al. 2019a) or Harmony (Korsunsky et al. 2019) that can remove, for example, tissue-specific differences, Specter can help to leverage such reference data sets to reveal hidden cell types or states. When combining different samples from the same experiment, simpler linear methods such as ComBat (Johnson et al. 2007) might be preferable (Luecken and Theis 2019) to correct for batch effects between samples before identifying groups of cells with distinct gene expression profiles using Specter.

Furthermore, we have illustrated how the flexibility of its underlying optimization model allows Specter to harness multimodal omics measurements of single cells to resolve subtle transcriptomic differences between subpopulations of cells. The application of our cluster ensemble scheme to the joint analysis of multimodal CITE-seq data sets yielded a slightly more fine-grained distinction of cell (sub)populations compared to the recently proposed multimodal clustering method CiteFuse. More importantly, in contrast to CiteFuse whose running time increased ≈ eightfold after doubling the number of cells, Specter will scale well to much larger data sets produced by droplet-based approaches that can measure multiple modalities of up to millions of cells together. Although the consensus clustering approach applied by Specter can in principle integrate the ensemble of clusterings generated from various molecular features, this work has focused on the combination of mRNA and protein marker expression as measured by CITE-seq or REAP-seq (Peterson et al. 2017). The practical suitability and potential limitations as well as necessary refinements of this strategy when applied to other assays that simultaneously measure, for example, accessible chromatin and gene expression (Cao et al. 2018), or more than two modalities at the same time (Clark et al. 2018), will need to be addressed in future experiments. Taken together, we believe that Specter will be useful in transforming massive amounts of (multiple) measurements of molecular information in individual cells to a better understanding of cellular identity and function in health and disease.

Methods

Spectral clustering uses eigenvectors of a matrix derived from the distance between points (here, cells) as a low-dimensional representation of the original data, which it then partitions using a method such as k-means. More precisely, given n data points x₁, x₂, …, x_n ∈ ℝ^m and a similarity matrix (affinity matrix) W = (w_ij)_n×n, where w_ij measures the similarity between points x_i and x_j, the graph Laplacian is defined as L = D − W or L = I − D^−1/2 WD^−1/2 in case of a (symmetric) normalized Laplacian. Here, D is a diagonal matrix whose entries are column sums (equivalently, row sums) of W. Spectral clustering then uses the top k eigenvectors of L to partition the data into k clusters using the k-means algorithm.

In the following description of our algorithm, we assume a given number of clusters k. In Specter we determine the number of clusters based on the Silhouette index (Rousseeuw 1987), which performed particularly well in recent benchmark studies (Arbelaitz et al. 2013; Chouikhi et al. 2015).

Landmark-based spectral clustering of single cells

Several methods have been proposed to accelerate the spectral clustering algorithm (Fowlkes et al. 2004; Shinnou and Sasaki 2008; Cai and Chen 2015). In particular, LSC has been shown to perform well in terms of efficiency and effectiveness compared to state-of-the-art methods across a large number of data sets (Cai and Chen 2015). In short, LSC picks a small set of p representative data points u₁, u₂, …, u_p ∈ ℝ^m, that is, the landmarks, which it then uses to create a representation matrix Z ∈ ℝ^p×n whose columns represent the original data with respect to the landmarks according to X ≈ UZ. Here, columns i of U ∈ ℝ^m×p contain landmarks u_i, and columns i of X contain the original input points x_i. Let the Gaussian kernel $K\left(x,y\right)=\exp \left(-\parallel x-y{\parallel }^2/2{\sigma }^2\right)$ measure the similarity between two points x and y, then matrix Z = (z_ji)_p×n is computed using Nadaraya-Watson kernel regression (Härdle 1990) as

$$z_{ji}=\{\begin{array}{cc}\frac{K(x_i,u_j)}{{\sum }_{j^{\mathrm{\prime }}\in U_{<i>}}K(x_i,u_{j^{\mathrm{\prime }}})}& \mathrm{if}j\in U_{<i>}\\ 0& \mathrm{otherwise},\end{array}$$

where $U_{<i>}$ is the set of r nearest landmarks of x_i. That is, z_ji is set to zero if u_j is not among the r nearest neighbors of x_i, which naturally leads to a sparse representation of the data. Motivated by non-negative matrix factorization that uses k (i.e., number of clusters) basis vectors to represent each data point (Xu et al. 2003), we set r to be equal to k in Specter (and in all experiments). Then each original point x_i can be approximated by

$${\hat{x}}_i=\sum _{j=1}^p{z}_{ji}{u}_j.$$

From this landmark-based representation of the complete data it computes the Laplacian matrix $L=\hat{Z}{\hat{Z}}^T$, where $\hat{Z}=D^{-1/2}Z$ and D is the diagonal matrix whose (i, i)-entry equals the sum of the ith row of Z. Then, this graph Laplacian L admits a fast eigen decomposition in time O(n) as opposed to O(n³) in the general case, which is described in more detail in Cai and Chen (2015).

Here, we tailor the idea of landmark-based spectral clustering to the characteristics and scale of modern scRNA-seq data sets. In particular, the choice of bandwidth σ used in the (Gaussian) kernel to smooth the measure of similarity between pairs of data points heavily depends on the type of data and can have a strong impact on the final clustering. In the original approach, parameter σ is set to the average Euclidean distance between data points and their k nearest landmarks, that is, to the average value of all elements in matrix Z. We empirically find that replacing the average by the maximum value, that is, by setting σ = γ ×mean [max(Z)], where max(Z) denotes a vector of maximum values for each row in Z and γ a randomly chosen parameter between 0 and 1, is able to better capture the transcriptional similarity between single cells and yields more accurate clusterings of cells.

Furthermore, we pair the theoretical reduction in time complexity from $\mathcal{O}\left(n^3\right)$ to $\mathcal{O}\left(n\right)$ with a practical speed-up of the LSC algorithm by applying a hybrid strategy when selecting the landmarks. The choice of representative data points (here, single cells), plays a crucial role in the quality of the final clustering. Random selection or k-means clustering were originally proposed as procedures for picking landmarks (Cai and Chen 2015). Random selection of representative cells is very efficient but often yields random sets of cells that do not represent the full data well, thus leading to poor clustering results. k-means, on the other hand, better takes into account the structure of the data when selecting landmark cells but its higher computational cost makes it impractical for large scRNA-seq data sets, where it accounts for ∼90% of the overall running time in our experiments. Our hybrid strategy seeks to balance the efficiency of random sampling and the accuracy of k-means-based landmark selection. It first picks a set of p′ candidate landmarks uniformly at random with p′ ≪ n (by default, p′ = 10p), from which it subsequently selects p < p′ final landmark cells using the k-means algorithm. Despite the initial random sampling, the full data are represented by the final set of landmarks.

Finally, for data sets that contain a small number of clusters, we adjust the spectral embedding based on which original data is clustered using k-means in the last step of spectral clustering. For a small number of clusters (e.g., k ≤ 4), the top k eigenvectors used in the original approach typically do not contain enough information to represent the full data well. In this case, we therefore use the top k + 2 eigenvectors to compute the spectral embedding.

Clustering ensembles across parameters and modalities

Different data types require a different choice of parameter values, and there is no general rule how to select the best one. To address this issue, we used consensus clustering, also known in literature as cluster ensembles (Strehl and Ghosh 2003), in the same way as ensemble learning is used in supervised learning. In particular, we generate a series of component clusterings by varying the number of selected landmarks p and the kernel bandwidth. We randomly select parameter γ, which controls the bandwidth of the Gaussian kernel from interval [0.1, 0.2] and choose p from interval

$$\left[\min \left(8k\log \left(k\right),\lceil n/3\rceil \right),\min \left(10k\log \left(k\right),\lceil n/2\rceil \right)\right].$$

This choice of p is motivated by a result by Tremblay et al. (2016), who used a sampling theory of bandlimited graph-signal developed in Puy et al. (2018) to prove that clustering a random subset of size O(k log(k)) is sufficient to accurately infer the cluster labels of all elements. To avoid sampling too many landmarks for small data sets (i.e., small number of cells n), we additionally set upper bounds $\lceil n/3\rceil$ and $\lceil n/2\rceil$ for the left and right boundaries of the interval, respectively. All clusterings produced by the different runs of our tailored LSC algorithm are then summarized in a co-association matrix H (Fred and Jain 2005) in which entry (i, j) counts the number of runs that placed cells i and j in the same cluster. We compute the final clustering through a hierarchical clustering of matrix H. Our LSC-based consensus clustering approach is summarized in Algorithm 1.

Different parameter choices (e.g., kernel bandwidths) provide different interpretations of the same data. In the same way as clustering ensembles can help unify these different views on a single modality, they can help reconcile the measurements of multiple modalities, such as transcriptome and proteome, of the same cell. More specifically, Specter produces an identical number of clusterings for each modality in step 2 of Algorithm 1, which it then combines through the same co-association approach (steps 3 and 4).

Algorithm 1: LSC ensemble —

1. Input: Cells x₁, …, x_n; number of clusters k.

2. Run the tailored LSC algorithm for different kernel bandwidths and varying numbers of landmarks.

3. Summarize all clusterings in a co-association matrix H.

4. Apply the single linkage hierarchical clustering algorithm to H to obtain the final k clusters.

Time complexity

The time complexity of the tailored LSC algorithm is O(n), and single linkage hierarchical clustering requires O(n²) time, yielding an overall complexity of O(n²) for Algorithm 1, assuming k is small enough to be considered a constant.

Selective sampling–based clustering ensemble

With a running time that scales quadratically with the number of cells, the application of Algorithm 1 to large-scale scRNA-seq data sets becomes infeasible. We therefore apply step 3 of our clustering ensemble approach (Algorithm 1) to a carefully selected sketch of the data. However, the co-association matrix H built in step 3 of the algorithm is based on cluster labels that were learned from the full data in step 2 using our tailored LSC algorithm. In addition, we propose a simple sampling technique that uses all clusterings computed in step 2 to guide the selection of cells.

Selective sampling

Sampling cells uniformly at random is naturally fast, because the decision to include a given cell into a sketch does not depend on any other cell. At the same time, these independent decisions ignore the global structure of the data such as the abundance of different cell types and may thus lead to a loss of rare cell types (Hie et al. 2019b). We therefore propose a sampling approach that uses the clusterings of the data computed in step 2 of Algorithm 1 to inform the (fast) selection of cells. More specifically, let Π = {π₁, π₂, …, π_m}, where π_i = (π_i1, π_i2, …, π_ik) is the ith clustering returned in step 2 of Algorithm 1, i = 1, 2, …, m. We select a sketch S of size $\left[k\sqrt{n}\right]$ that contains roughly the same number of cells in each cluster π_ij, for all i and j. This selective sampling procedure iterates through all clusters contained in all clusterings from which it randomly picks a cell not already contained in the sketch, until the size of the sketch reaches $\left[k\sqrt{n}\right]$ (see Algorithm 2).

Algorithm 2:  Selective sampling —

 1. Input: Component clusterings Π = {π₁, π₂, …, π_m}, number of clusters k.

 2. Initialization: $S=\mathrm{\varnothing }$.

 3. while $\left|S\right|<k\sqrt{n}$ do

 4  for i = 1 to m do

 5.   for j = 1 to k do

 6.    Randomly select a cell s from ${\pi }_{ij}\mathrm{\setminus }S$

 7.    $S=S\cup \left\{s\right\}$

 8.   end

 9.   end

10. end

Inference

Given a selectively sampled sketch S, we apply steps 3 and 4 in Algorithm 1 to cells in S, using labels obtained from the full data in step 2. That is, we construct a co-association matrix whose entries count the number of times the two corresponding cells in S were placed in the same cluster by a run of the LSC algorithm in step 2. From this matrix, we compute a consensus clustering of S using hierarchical clustering and finally transfer cluster labels to the remaining cells using supervised k-nearest-neighbors classification. That is, we assign each cell not in S to the cluster that the majority of its k nearest neighbors were placed in by the preceding consensus clustering of S. Our selective sampling-based cluster ensemble approach is summarized in Algorithm 3.

Algorithm 3:  Selective sampling-based clustering ensemble —

1. Input: Cells x₁, …, x_n; number of clusters k.

2. Run the tailored LSC algorithm for a varying number of landmarks and different kernel bandwidths. Let Π = {π₁, π₂, …, π_m} be the set of m clusterings.

3. Run selective sampling (Algorithm 2) on Π to obtain a sketch S of size $\left|S\right|=\left[k\sqrt{n}\right]$.

4. Summarize all clusterings of cells in S computed in step 2 in a co-association matrix H^S.

5. Apply single linkage hierarchical clustering to H^S to obtain k clusters for S.

6. Transfer labels to full data using k-nearest-neighbors classification.

Time complexity

Landmark-based spectral clustering performed in step 2 of Algorithm 3 takes O(n) (see above). Because we selectively sample a sketch of size $\left|S\right|=O\left(\sqrt{n}\right)$ in step 3, the complexity of steps 4 and 5 now reduces to O(n). Together with the k-NN classification that runs in O(n) in step 6, our selective sampling-based cluster ensemble scheme scales linearly with the number of cells n.

Publicly available data used in this study

The original publication of data sets used in this study to assess the accuracy of Specter in comparison to existing methods are listed in Supplemental Table S1. The real data sets in Duò et al. (2018) were downloaded from https://github.com/markrobinsonuzh/scRNAseq_clustering_comparison. All other real data sets smaller than 15,000 cells were downloaded from https://hemberg-lab.github.io/scRNA.seq.datasets; the three largest data sets from http://mousebrain.org (CNS), http://dropviz.org (saunders), and https://oncoscape.v3.sttrcancer.org/atlas.gs.washington.edu.mouse.rna/downloads (trapnell). The umbilical cord blood cell data (Hie et al. 2019b) were downloaded from http://cb.csail.mit.edu/cb/geosketch.

Software availability

The Specter software is available at GitHub (https://github.com/canzarlab/Specter) and as Supplemental Code under the open-source MIT license. The Specter repository also includes all code necessary to reproduce the results of this manuscript as well as a step-by-step documentation of the analysis of the PBMC and CBMC CITE-seq data sets (Stoeckius et al. 2017; Mimitou et al. 2019) as described in this study.

Competing interest statement

The authors declare no competing interests.