A unifying framework for rare variant association testing in family-based designs, including higher criticism approaches, SKATs, and burden tests

Abstract

Motivation

Analysis of rare variants in family-based studies remains a challenge. Transmission-based approaches provide robustness against population stratification, but the evaluation of the significance of test statistics based on asymptotic theory can be imprecise. Also, power will depend heavily on the choice of the test statistic and on the underlying genetic architecture of the locus, which will be generally unknown.

Results

In our proposed framework, we utilize the FBAT haplotype algorithm to obtain the conditional offspring genotype distribution under the null hypothesis given the sufficient statistic. Based on this conditional offspring genotype distribution, the significance of virtually any association test statistic can be evaluated based on simulations or exact computations, without the need for asymptotic approximations. Besides standard linear burden-type statistics, this enables our approach to also evaluate other test statistics such as variance components statistics, higher criticism approaches, and maximum-single-variant-statistics, where asymptotic theory might be involved or does not provide accurate approximations for rare variant data. Based on these P-values, combined test statistics such as the aggregated Cauchy association test (ACAT) can also be utilized. In simulation studies, we show that our framework outperforms existing approaches for family-based studies in several scenarios. We also applied our methodology to a TOPMed whole-genome sequencing dataset with 897 asthmatic trios from Costa Rica.

Availability and implementation

FBAT software is available at https://sites.google.com/view/fbatwebpage. Simulation code is available at https://github.com/julianhecker/FBAT_rare_variant_test_simulations. Whole-genome sequencing data for ‘NHLBI TOPMed: The Genetic Epidemiology of Asthma in Costa Rica’ is available at https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000988.v4.p1.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

With the increasing availability of whole-genome sequencing (WGS) studies, the development of region-based rare variant analysis approaches is becoming an important research question. Region-based approaches are motivated by the idea that, if we can combine association signals across rare variants in a pre-defined region, a suitable region-based association test has increased statistical power compared to single variant tests, which are typically underpowered for rare variant analysis. Simultaneously, the multiple testing problem is less severe as fewer association tests are computed. The power of a specific region-based association test statistic depends heavily on the underlying genetic architecture of the signal, which is typically unknown. For studies with unrelated samples, therefore, numerous region-based tests have been proposed. For example, burden tests and variance component tests (SKATs) (Li et al., 2008; Wu et al., 2011), combinations of both approaches (Lee et al., 2012a,b) and higher criticism or maximum statistic-based approaches for sparse signals (Barnett et al., 2017; Mukherjee et al., 2015). Recently, the aggregated Cauchy association test (ACAT) was proposed to efficiently combine information across different test statistics (Liu et al., 2019). The ACAT has the advantage that P-values can be evaluated quickly and weights based on prior biological knowledge can be incorporated (Li et al., 2020). However, population stratification is a potential problem in population-based designs that can be even more severe in the analysis of rare variants, since standard correction for population stratification often captures only the structure based on the common genetic variation (Bouaziz et al., 2020; Ma et al., 2020; Mathieson et al., 2012; Sha et al., 2016). In family-based association studies, the concept of Mendelian transmissions can be utilized to construct single variant association tests that are robust against genetic confounding [Transmission Disequilibrium Tests (TDTs) (Spielman et al., 1993) or Family-based Association Tests (FBATs) (Laird et al., 2006)]. For the region-based rare variant analysis, burden tests and the SKAT approach have been translated to the FBAT context (De et al., 2013; Ionita-Laza et al., 2013). As with their population-based equivalents, these two approaches estimate the correlation between the genetic loci empirically. Since family-based studies have often moderate sample sizes and the transmission structure introduces additional sparseness, this can lead to numerical instabilities, and asymptotic theory can provide imprecise approximations. This problem also translates to other potential approaches, such as higher criticism and maximum statistics, where asymptotic theory is even more involved. Motivated by the concerns regarding population stratification, the availability of several family-based cohorts in the TOPMed WGS program (Taliun et al., 2019), and the described technical issues with the translation of recent approaches to the family-based context, we propose a general FBAT framework for the region-based rare variant analysis that can evaluate the significance of any arbitrary test statistic without asymptotic theory. Based on the FBAT haplotype algorithm, we obtain the conditional offspring genotype distribution under the null hypothesis and given the sufficient statistic (Hecker et al., 2017b; Horvath et al., 2004). While the utilization of this conditional distribution provides robustness against population stratification, a second key advantage is that exact or simulation-based P-values can be obtained for virtually any test statistic. Multiple offspring per family can be used, founder/phase information can be missing, phenotypes can be dichotomous or quantitative, and pedigrees can be collected based on phenotype data. We describe the implementation of different test statistics such as Burden, SKAT (Ionita-Laza et al., 2013; Wu et al., 2011), higher criticism as well as maximum single variant statistic approaches (Barnett et al., 2017; Donoho et al., 2004; Mukherjee et al., 2015). As a referee suggested, based on the robust P-values for these four statistics that can be obtained by our approach, ACAT can efficiently summarize signals while reducing the multiple testing burden. For different scenarios, e.g. regions with sparse signals or varying local linkage disequilibrium (LD) structure, we compare our proposed FBAT framework to existing methodology, using extensive simulation studies. We also applied our methodology framework to a TOPMed whole-genome sequencing study for childhood asthma with 897 trios from Costa Rica.

2 Materials and methods

In a family-based WGS association study, genotype data for rare variants are available for a set of marker loci that define a genomic segment for region-based association analysis. We assume that the region is sufficiently small to neglect recombination events. The genotype information may be available for multiple offspring as well as for the parents. For the $\mathrm{i}$th nuclear family, we introduce the $p\mathrm{ }\times \mathrm{ }{n}_i$ genotype matrix $X_i$ and the $n_i$ dimensional phenotype vector $T_i$, where $n_i$ denotes the number of offspring in the $i$th nuclear family, and $p$ denotes the number of variants in the analysis region. The specific phenotype coding can increase power and was discussed in previous publications (Lange et al., 2002a,b). We assume an additive coding of $X_i$, e.g. the number of minor alleles, but other coding specifications reflecting recessive or dominant models can be considered as well. We regard $X_i\mathrm{ }$as random while $T_i$ is fixed in the FBAT approach.

2.1 FBAT sufficient statistic and simulation-based significance testing

For each region, using the haplotype algorithm for FBAT (Hecker et al., 2017b; Horvath et al., 2004), we obtain the conditional distribution of offspring genotypes $X_i$ in the $i$th nuclear family under the null hypothesis, given the sufficient statistic $S_i$ for the possible missing founder genotypes (Rabinowitz et al., 2000).

In words, for each nuclear family, the FBAT haplotype algorithm identifies a set of offspring genotype configurations such that the corresponding conditional distribution given any parental mating type, that is compatible with the observed genotypes, is the same and does not depend on any unknown nuisance parameter (e.g. allele frequencies, haplotype distribution etc.). This illustrates the sufficiency and provides robustness against population stratification and admixture. For more details and an example, we refer to Supplementary Appendix SA and SB. It is important to note that the FBAT haplotype algorithm does not require phased haplotypes and takes phase uncertainty into account (Horvath et al., 2004). Based on the conditional genotype distribution and the phenotype data, it is possible to determine the exact distribution of arbitrary test statistics (Schneiter et al., 2007) and compute specific moments such as the mean and variance of offspring genotypes, under the null hypothesis. This is an advantage, since asymptotic theory is not available for all potentially powerful test statistics and asymptotic approximations are often not accurate for rare variant data with limited sample size. Since exact computations can be complex, we propose to evaluate empirical association P-values based on a sufficiently large number of simulated draws from the conditional distribution. For this purpose, potential offspring genotypes are drawn from the conditional offspring genotype distribution and test statistics are re-evaluated as well as compared to the observed test statistic (see also Supplementary Appendix SB). This procedure can be combined with adaptive permutation/simulation-based P-value techniques, e.g. controlling the number of simulations depending on the estimated P-value and expected accuracy. In this context, stopping rules that are nearly optimal in terms of the required number of simulations are available (Hecker et al., 2017a). Due to subtle discreteness of this exact distribution of the test statistic, P-values in our framework can be slightly conservative. However, we demonstrate substantial power in the simulation studies and the real data analysis.

2.2 Test statistics

All test statistics under consideration are based on the following two objects. For the $\mathbf{i}$th family, we define the $\mathbf{p}$-dimensional vector of Mendelian residuals, weighted by the phenotype information, ${\mathbf{U}}_{\mathbf{i}}=\left({\mathbf{X}}_{\mathbf{i}}-\mathbf{E}\left[{\mathbf{X}}_{\mathbf{i}}|{\mathbf{S}}_{\mathbf{i}}\right]\right){\mathbf{T}}_{\mathbf{i}}$. Also, we define the corresponding $\mathbf{p}\times \mathbf{p}$ variance matrix ${\mathbf{V}}_{\mathbf{i}}=\mathbf{Var}\left({\mathbf{U}}_{\mathbf{i}}\right|{\mathbf{S}}_{\mathbf{i}},{\mathbf{T}}_{\mathbf{i}})$. Both objects are computed based on the conditional offspring genotype distribution, obtained by the FBAT haplotype algorithm. We use the notation $\mathbf{E}\left[{\mathbf{X}}_{\mathbf{i}}|{\mathbf{S}}_{\mathbf{i}}\right]$ and $\mathbf{Var}\left({\mathbf{U}}_{\mathbf{i}}\right|{\mathbf{S}}_{\mathbf{i}},{\mathbf{T}}_{\mathbf{i}})$ to emphasize that this conditional distribution equals the distribution under the null hypothesis, given the sufficient statistic ${\mathbf{S}}_{\mathbf{i}}$. Although we apply simulation-based testing and the respective moments are invariant for the same nuclear family throughout the replicates, their incorporation increases the power of the test statistics. The moments are utilized in all test statistics described in the following section, expressed through their dependency on ${\mathbf{U}}_{\mathbf{i}}$ and ${\mathbf{V}}_{\mathbf{i}}$. We also define the p-dimensional vector U=∑_iU_i and the p × p matrix V=∑_iV_i, with components U_j and V_(jl), 1 ≤ j, l ≤ p. 1 ≤ k, l ≤ p.

2.2.1 Burden-based approaches

Burden-type FBATs can be implemented by specifying a $\mathbf{p}$-dimensional weight vector $\mathbf{W}$ that collapses/summarizes the rare variant information of the region into a single scalar value. The weights could contain information about functional annotations, well suited choices increase the power of the test (Li et al., 2020). The contribution to the $\mathbf{FBA}\mathbf{T}\mathbf{\hspace{0.17em}}\mathbf{Burden}$statistic of the $\mathbf{i}$th family is then given by

$$U_i^{*}=W^T\left(X_i-E\left[X_i|S_i\right]\right)T_i$$

The corresponding FBAT-statistic for the simulation-based testing is computed by $\mathbf{FBAT}\mathbf{\hspace{0.17em}}\mathbf{Burden}={\left({\sum }_{\mathbf{i}}{\mathbf{U}}_{\mathbf{i}}^{\mathbf{*}}\right)}^2$.

2.2.2 Variance component/SKAT approaches

As an alternative to burden/collapsing association tests, SKAT/variance-component based region tests have been developed for rare variant data (Wu et al., 2011). They have the advantage that they do not require any assumptions about the effect configuration at the rare variant loci under the alternative hypothesis, but they are not as powerful as burden/collapsing approaches if one is certain about the alternative hypothesis. We define the general statistic

$$\mathrm{FBA}\mathrm{T} \mathrm{VC}={\mathrm{U}}^{\mathrm{T}}\mathrm{W}\mathrm{U}$$

where $\mathbf{W}$ is a fixed $\mathbf{p}\times \mathbf{p}$ weight matrix. Again, well-suited choices for the weight matrix could lead to increased power, whereas the default option is to use the identity matrix. In the scenario of affected offspring trios and a diagonal weight matrix $\mathbf{W}$, this test statistic equals the FB-SKAT statistic of Ionita-Laza et al. (2013), but in our framework, the P-value of the test statistic is obtained based on simulations from the conditional genotype distribution. If we set $\mathbf{W}={\mathbf{V}}^{-1},$ we obtain the multivariate FBAT (Rakovski et al., 2007).

2.2.3 Higher criticism and maximum statistics

Besides the commonly used burden and variance component approaches, we introduce the higher criticism and maximum statistic for region-based analysis in family-based studies. Both approaches are designed to identify sparse alternatives and have been introduced to genetic association studies of unrelated individuals recently (Barnett et al., 2017; Mukherjee et al., 2015). The optimality results related to the higher criticism/maximum statistic in the setting of unrelated case-control data and sparse signals developed in Mukherjee et al. (2015) can be used to motivate the application in, for example, affected offspring trios as well (Supplementary Appendix SC). Define the normalized single variant residuals ${\mathbf{U}}^{\mathbf{j}}\mathbf{/}\sqrt{{\mathbf{V}}^{\mathbf{jj}}}\mathbf{,} \mathbf{j}\mathbf{=}\mathbf{1}\mathbf{,}\mathbf{\dots }\mathbf{,}\mathbf{p}$ and denote the corresponding association P-value based on the asymptotic marginal normal distribution by ${\mathbf{q}}_{\mathbf{j}}$. We emphasize that the variance ${\mathbf{V}}^{\mathbf{j}\mathbf{j}}$ can be computed based on the conditional genotype distribution. Based on the available amount of information per variant, e.g. the number of informative transmissions/families, we restrict the set of variants to a subset of variants where the marginal variance is large enough (e.g. we require at least 5 informative nuclear families). Denote the number of variants in this subset by ${\mathbf{p}}^{\mathbf{\text{'}}}$. Given the ordered P-values ${\mathbf{q}}_{\left(1\right)}\le {\mathbf{q}}_{\left(2\right)}\le \dots \le {\mathbf{q}}_{\left(\mathbf{p}\mathbf{\text{'}}\right)}$, we define the HC statistic as

$$\mathrm{FBA}\mathrm{T} \mathrm{HC}=\underset{\mathrm{J}}{\max }\frac{\frac{j}{p\mathrm{`}}-q_{\left(j\right)}}{\sqrt{q_{\left(j\right)}(1-q_{\left(j\right)})}}$$

Here, the index set $\mathbf{J}$ could be $\{1,\dots ,\frac{\mathbf{p}\mathbf{\text{'}}}{2}\}$ or $\{1,\dots ,\mathbf{p}\mathbf{\text{'}}\}$, for example. It is important to note that, while $\mathbf{FBA}\mathbf{T} \mathbf{HC}$contains a transformation based on the single variant asymptotic distribution, the assessment of its significance based on simulations from the conditional distribution remains a valid approach regardless of whether the assumptions that motivated the transformation hold. The second approach to detect sparse signals in the tested genomic region is the MAX statistic which is simply defined as

$$\mathrm{FBA}\mathrm{T} \mathrm{MAX}=\underset{1\le j\le p}{\max }\left|\frac{U^j}{\sqrt{V^{jj}}}\right|$$

2.2.4 Aggregated Cauchy association test (ACAT)

As a referee noted, based on the four robust P-values for the different statistics described above, one could also compute an overall test statistic based on the aggregated Cauchy association test (ACAT) (Liu et al., 2019). Denoting the P-values by ${\mathrm{p}}_{\mathrm{Burden}}$, ${\mathrm{p}}_{\mathrm{SKAT}}$, ${\mathrm{p}}_{\mathrm{HC}}$ , and ${\mathrm{p}}_{\mathrm{MAX}}$, this test is based on

$${\mathrm{p}}_{\mathrm{ACAT}}=0.5-\frac{\mathrm{atan}\left(\frac{\mathrm{FBA}\mathrm{T} \mathrm{ACAT}}{4}\right)}{\mathrm{\pi }}$$

where $\mathrm{FBA}\mathrm{T} \mathrm{ACAT}=\tan \left(\right[0.5-{\mathrm{p}}_{\mathrm{Burden}}\left]\mathrm{\pi }\right)$ +$\mathrm{ }\tan \left(\left[0.5-{\mathrm{p}}_{\mathrm{SKAT}}\right]\mathrm{\pi }\right)+\tan \left(\right[0.5-{\mathrm{p}}_{\mathrm{HC}}\left]\mathrm{\pi }\right)$ +$\tan \left(\left[0.5-{\mathrm{p}}_{\mathrm{MAX}}\right]\mathrm{\pi }\right).$ The motivation of this combined statistic is to reduce the multiple testing burden while capturing significance if at least one the underlying statistics shows suitable evidence. We note that the direct application of the ACAT to single variant FBAT P-values is problematic. This is because single variant asymptotic P-values are most likely not reliable for rare variants with small minor allele counts and, for example, in the application to affected offspring trios, FBAT P-values can be exactly 1.0 if Mendelian expectations are matched. A P-value of 1.0 eliminates signals in the ACAT test.

3 Results

In this section, we describe the results of two simulation studies and the analysis of a whole-genome sequencing study of childhood-asthma with 897 affected offspring trios from Costa Rica.

3.1 Simulation studies

3.1.1 Settings and existing methods for comparison

We studied the performance of our proposed test statistics in two extensive simulation studies. In both studies, we compared the Type I error and power of our approach with existing methods for family-based region association analysis. In the first simulation study, we considered small genetic regions consisting of 30 or 50 rare genetic variants. This design roughly corresponds to suggested region sizes of 2–7 kb in the recent literature (Li et al., 2019, 2020). The second set of simulations looks at larger regions consisting of 1000 genetic rare variants. This reduces the multiple testing burden but requires test statistics that can detect sparse signals. In this second set of simulations, we utilized observed phased genotype data, e.g. haplotypes. We restricted all simulations to the scenario of trios with an affected offspring. However, it is important to note that our framework can be applied to any nuclear family and phenotype distribution. For the test statistics $\mathrm{FBA}\mathrm{T} \mathrm{Burden}$ and $\mathrm{FBA}\mathrm{T} \mathrm{VC}$, we applied equal weights to all variants, but more powerful approaches based on prior information can increase the power in practice (Li et al., 2020). In the following, we will denote the test statistics $\mathrm{FBA}\mathrm{T} \mathrm{Burden}$, $\mathrm{FBA}\mathrm{T} \mathrm{VC}$, $\mathrm{FBA}\mathrm{T} \mathrm{HC}$, $\mathrm{FBA}\mathrm{T} \mathrm{MAX}$, and $\mathrm{FBA}\mathrm{T} \mathrm{ACAT}$ by Burden, SKAT, HC, MAX, and ACAT for convenience. Depending on the scenario, we compared our test statistics with the gTDT (Chen et al., 2015), RV-GDT (He et al., 2017) and the RV-TDT BRV (He et al., 2014). The gTDT (Chen et al., 2015) offers five different test statistics for region-based affected offspring trio analysis, designed for different modes of inheritance and signal structures. The test statistics require phased haplotype data. If the phase information is not available, this information is reconstructed up to small uncertainties. We considered the test statistics gTDT-AD (additive), gTDT-DOM (dominant) and gTDT-CH (compound heterozygous) in our study. The RV-GDT (He et al., 2017) describes a generalization of the single variant GDT (Chen et al., 2009) for multiple variants in a genetic region. The RV-GDT can be applied to arbitrary pedigrees where affected and unaffected samples are collected; members can be missing. We note that this implies that the phenotype information for parents must be available in the trio scenario, whereas the classical TDT/FBAT test for offspring trios does not require this information. We also note that this approach can be vulnerable to population stratification (Hecker et al., 2019).

Simulation Study I: Moderately sized genetic regions with unphased data

To simulate based on real data LD and realistic population structure, we extracted haplotypes for two subpopulations (CEU and GBR) from the 1000 Genomes Project (1000 Genomes Project Consortium et al., 2015), consisting of 30 and 50 consecutive rare variants with a minor allele frequency (MAF) below 3%. Based on these haplotypes, we generated genotype data for trios using Mendelian transmissions. Using a standard relative risk disease model with a disease prevalence of ≈10%, we simulated offspring affection status and collected n = 1000 affected offspring trios. This simulation study is similar to the simulation studies described in the existing literature (Chen et al., 2015; He et al., 2017).

To check the Type I error rates and the robustness against population stratification, we simulated four different scenarios. In the ‘null’ scenario, we simulated no genetic signal and no within-family population stratification or admixture. That means, that the parental haplotypes were drawn uniformly from the combined CEU+GBR population. In ‘adm1’, one parent was simulated based on CEU haplotypes, and the other parent based on GBR haplotypes. Both parents were set to unaffected. This simulates population stratification in the parents which results in an admixed offspring. In ‘adm2’, the CEU parent phenotype was set to affected, and the GBR parent phenotype to unaffected. Scenario ‘adm3’ flipped these parental phenotypes.

For the power analysis, we simulated seven different scenarios where the number of causal variants and corresponding effect sizes differ. (i) three causal variants, effect sizes$\mathrm{ }0.4\left|{\log }_{10}\left(\mathrm{MAF}\right)\right|$, all corresponding minor alleles are risk alleles, (ii) three causal variants, effect sizes $0.4\left|{\log }_{10}\left(\mathrm{MAF}\right)\right|$, alternating effect direction, (iii) two causal variants, effect sizes $0.4\left|{\log }_{10}\left(\mathrm{MAF}\right)\right|$, all corresponding minor alleles are risk alleles, (iv) two causal variants, effect sizes $0.4\left|{\log }_{10}\left(\mathrm{MAF}\right)\right|$, different effect direction, (v) four very rare variants, effect sizes 1.0, all corresponding minor alleles are risk alleles, (vi) three causal variants, effect sizes $0.4\left|{\log }_{10}\left(\mathrm{MAF}\right)\right|$, all corresponding minor alleles are risk alleles, strong LD with other variants and (vii) scenario 6 but with the stratification from scenario ‘adm’. We note that given the effect sizes, certain exceedingly rare genotype configurations lead to a disease probability of 1. Empirical power rates were based on 1000 replicates, Type 1 error rates based on 10 000 replicates. In this set of simulations, we compared the FBAT statistics, gTDT statistics and the RV-GDT.

Simulation Study II: Large genetic regions with phased data

For our second set of simulation studies, we utilized the 1006 EUR population haplotypes from the 1000 Genomes Project based on 1000 consecutive rare genetic variants with MAF below 3%. In this simulation study, we consider a large number of variants in combination with a sparse signal, which means a small subset of causal variants that are not in strong LD with any other variants. We simulated affected offspring trios as described in the first simulation study but also stored the phased haplotypes for all members of the trio. In the scenario where the haplotypes are observed, the conditional distribution identified by the FBAT haplotype algorithm equals the distribution where both parents transmit one of the observed haplotypes with an equal probability of 0.5. We compared the performance of the FBAT statistics, the gTDT statistics and the RV-TDT BRV (He et al., 2014) statistics to demonstrate the potential advantage of non-burden tests in the presence of sparse signals. We simulated five different scenarios. The first scenario ‘null’ simulates the null hypothesis, without population stratification or admixture, based on 1000 trios. The four power scenarios are described as follows: (i) two causal variants, MAF∼0.2%, almost no LD to other variants, effect sizes 1.8, all corresponding minor alleles are risk alleles, 1000 trios, (ii) two causal variants, MAF∼2%, almost no LD to other variants, effect sizes 0.7, all corresponding minor alleles are risk alleles, 1000 trios (iii) 16 causal variants, MAF∼0.1%, almost no LD to other variants, effect sizes 0.7, all corresponding minor alleles are risk alleles, 10 000 trios and (iv) 16 causal variants, MAF∼0.1%, almost no LD to other variants, effect sizes 0.7, alternating effect directions, 10 000 trios. We note that, given the effect sizes, certain exceedingly rare genotype configurations lead to a disease probability of 1. In all these power scenarios, we did not simulate population stratification or admixture. Empirical P-values were based on 1000 replicates.

3.1.2 Results

In this section, we summarize the results of both simulation studies.

Simulation Study I: Moderately sized genetic regions with unphased data

Almost all test statistics controlled the Type I error appropriately (Table 1). The only exception is the RV-GDT in the scenario of population admixture with discordant parental phenotypes (adm2 and adm3). This is expected, as the GDT/RV-GDT test compares the frequencies between affected and unaffected family members and cannot distinguish between association and stratification in the parents. We note that the RV-GDT computes a one-sided P-value, which explains the deflation/inflation behavior, depending on the parental phenotypes. In Supplementary Appendix SD, we also report the Type 1 error rates for the significance level of $\mathrm{\alpha } = 0.005$ (Supplementary Table S3). The power results are visualized in Figure 1 and Supplementary Figure S1 and also reported in Supplementary Table S1 (Supplementary Appendix SD). Since the results for scenario 6 and 7 are very similar, Figure 1 and Supplementary Figure S1 are restricted to scenarios 1-6. We discuss the results of the four FBAT statistics Burden, MAX, HC, and SKAT, as well as the gTDT and RV-GDT first, and then consider the combined test ACAT for the FBAT statistics. The SKAT statistic shows the highest power in the first three scenarios and outperforms the other tests. However, the MAX and HC statistics also show substantial power. The results for scenario 4 are comparable between SKAT, MAX, and HC. In scenario 5, the HC statistics achieves the highest power, which is supported by our theoretical considerations as well (see Supplementary Appendix SC). In the last scenario 6, all FBAT tests achieve substantial power, as expected. The most powerful tests here are SKAT and RV-GDT, but MAX and HC test statistics achieve similar results. If we have different effect directions (scenario 2 and 4), the burden test loses power compared to the consistent effect direction scenarios 1 and 3, which is expected. The FBAT Burden test and gTDT-AD have almost no power in scenarios 4 and 5. It is important to note that the gTDT-AD and Burden are essentially based on the same test statistic idea, the only difference lies in the fact that the gTDT assigns haplotypes (with possible error) and our approach uses the robust conditional genotype distribution computed by the FBAT haplotype algorithm. Importantly, ACAT achieves similar power as the most powerful underlying FBAT statistic in each scenario. Our results demonstrate the advantages of non-burden tests in scenarios with sparse effects and alternating effect directions, as well as the advantage of using a combined statistic as ACAT.

Table 1.

Simulation Study I: Type I error rates at a significance level of 5%

		FBAT					gTDT			RV-GDT
	scenario	ACAT	Burden	HC	MAX	SKAT	gTDT-AD	gTDT-CH	gTDT-DOM	RV-GDT
p = 30	null	4.95%	4.58%	4.97%	4.48%	4.59%	4.85%	5.34%	5.53%	4.83%
	adm1	4.81%	5.06%	4.65%	4.24%	5.24%	5.48%	5.07%	5.08%	5.48%
	adm2	4.51%	4.64%	4.55%	4.04%	4.72%	5.04%	4.95%	5.24%	0.0%
	adm3	4.97%	4.37%	4.86%	4.19%	4.95%	4.7%	4.78%	4.94%	99.75%
p = 50	null	5.29%	4.71%	5.1%	4.74%	5.07%	4.95%	4.92%	4.69%	4.92%
	adm1	4.98%	4.64%	5.00%	4.95%	4.89%	4.99%	4.97%	4.93%	4.92%
	adm2	5.21%	4.74%	5.00%	4.97%	4.62%	5.07%	4.54%	5.28%	0.2%
	adm3	4.95%	4.79%	5.04%	4.93%	4.99%	4.98%	5.17%	5.15%	36.41%

Note: Type I errors at a significance level of 5% for the FBAT, gTDT and RV-GDT statistics. We considered four scenarios, separately for p = 30 and p = 50 variants. All results based on 10 000 replicates.

Fig. 1.

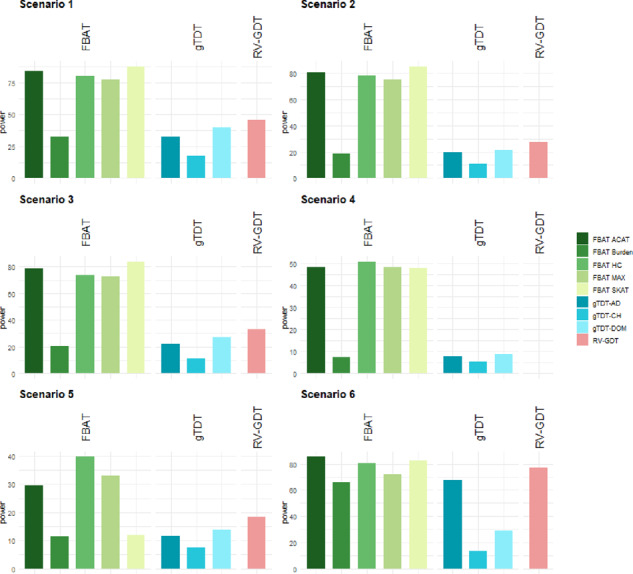
Simulation Study I: Power results for six different scenarios for genetic regions consisting of 30 variants at a significance level of α = 0.05. All results based on 1000 replicates

Simulation Study II: Large genetic regions with phased data

In Supplementary Table S2, we observe that all test statistics control the Type I error appropriately, whereas the gTDT-DOM is conservative. Since all P-values are evaluated empirically based on the conditional haplotype distribution by simulation, this is expected. Power results are reported in Supplementary Table S2 and Figure 2. Again, we consider the four individual FBAT statistics first and then consider the combined ACAT. In the first power scenario 1, the MAX test statistic achieves the highest power as we simulated a sparse and rare, but strong signal in the genetic region, consisting of two rare variants. The HC test statistic also achieves substantial power, whereas all other tests show almost no power in this scenario. In the second scenario, where the MAF of the two causal variants is much higher, the MAX test statistics still outperforms the other tests, but also the SKAT and the HC test statistics show good performances. In scenario 3, where many exceedingly rare causal variants have a relatively small effect size, the HC is the most powerful test. This is in line with the results in Mukherjee et al. (2015) that describe a lower detection boundary in the mild sparse regime compared to the MAX test statistics. However, the RV-TDT BRV and MAX test statistic also achieve substantial power in this scenario.

Fig. 2.

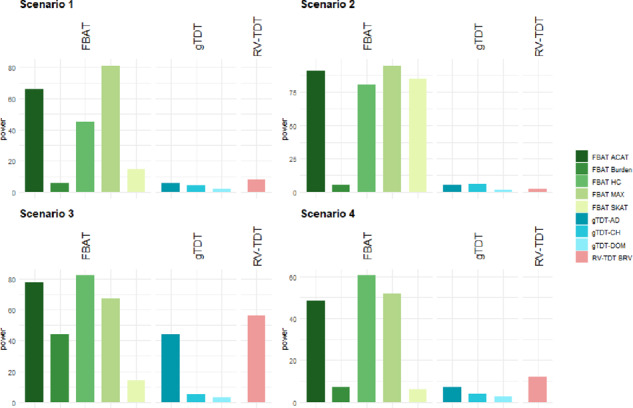
Simulation Study II: Power results for four different scenarios for genetic regions consisting of 1000 variants at a significance level of α = 0.05. All results based on 1000 replicates. Scenario 1 and 2 are based on 1000 trios, scenario 3 and 4 are based on 10 000 trios

The power behavior differs more in the last scenario 4, where the effects are pointing in different directions. Here, the MAX and HC statistics have a significantly increased power compared to the other tests, while the HC test statistic is the most powerful one. Again, the combined statistic ACAT controls the Type 1 error rate and achieves similar power as the top underlying FBAT statistic in each scenario. We note that the FBAT burden and the gTDT-AD test are close to the nominal level in scenarios 1, 2 and 4. Both tests are equivalent since the test statistics are the same in the phased haplotype scenario. Our results in this set of simulations demonstrate the advantage of non-standard test statistics such as HC or MAX in scenarios with very sparse signals, and their incorporation into the combined test ACAT.

3.2 Application to WGS study of childhood asthma

We analyzed a whole-genome sequencing dataset consisting of 897 Costa Rican asthmatic trios. Details regarding the study population and design were described previously (Hunninghake et al., 2007, 2008). This dataset is part of the TOPMed freeze 7 WGS data. Further details are described in Supplementary Appendix SF. After standard quality control, including removal of variants with multiple Mendelian errors, we excluded all variants with a MAF above 5%. The resulting 27 345 734 non-monomorphic variants were partitioned into approximately 547 000 consecutive windows of 50 rare variants. Other partitioning approaches could be considered (Fier et al., 2017; He et al., 2019), but, as the focus of this data analysis was to demonstrate the feasibility of our approach, we did not explore different window-strategies here. For each window, we computed the four FBAT statistics Burden, SKAT, MAX, and HC, as well as ACAT (based on the corresponding four P-values). We also applied the three gTDT test statistics (AD, DOM, and CH) to the same genetic windows. For Burden, SKAT, MAX, and HC, we applied a standard adaptive simulation procedure, similar as implemented in VEGAS2 (Mishra et al., 2015) or PLINK (Chang et al., 2015), where the maximum number of simulations was truncated at ${10}^9$. We could not apply the RV-GDT since parental phenotypes are missing. In Figure 3 and Supplementary Figure S2, we plotted the corresponding quantile-quantile-plots. We discuss the FBAT results in Figure 3 first.

Fig. 3.

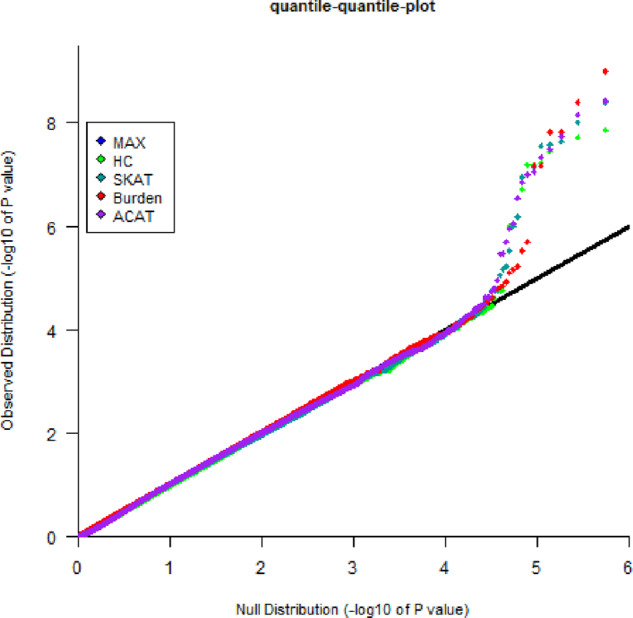
Quantile-quantile plot. Quantile-quantile plot for Burden, SKAT, MAX, HC, and ACAT test statistics based on approximately 547 000 windows of 50 consecutive rare variants in the analysis of 897 asthmatic trios from Costa Rica

Considering the four FBAT statistics Burden, SKAT, HC, and MAX jointly, based on the P-values for approximately 4*547 000 tests and a False Discovery Rate (FDR) at $\mathrm{\alpha } = 0.05$ (Benjamini et al., 1995), our approach identified three single significant regions on Chromosome 1, 12 and 21, as well as multiple consecutive significant regions on Chromosome 10. The significance of the three regions on Chromosomes 1, 12 and 21 was declared by the Burden test, whereas the single variant FBAT P-values within the regions were not in the classical range of genome-wide significance, e.g. $5\mathrm{*}{10}^{-8}$. The other regions on Chromosome 10 were identified by the MAX, HC, and SKAT tests. The lowest P-value of ${10}^{-9}$ was reached by the SKAT test. For these regions, the Burden test did not reach the magnitude of genome-wide significance. In Supplementary Figure S3 (Supplementary Appendix SE), we plotted the SKAT P-values against the Burden P-valued to demonstrate that the test statistics capture different aspects. Considering only the ACAT statistic and applying an FDR rate at $\mathrm{\alpha } = 0.05$, this approach identifies all regions described above, except the Chromosome 21 region that is mainly driven by the Burden statistic. As visualized in Supplementary Figure S4 (Supplementary Appendix SE), the results of Burden and gTDT-AD are very similar. This is expected since the test statistics are equal, the difference lies in the specification of the underlying haplotype distribution. Our approach accounts for the phase uncertainty. We note that all gTDT statistics can be incorporated into our framework as well. Based on an FDR rate at $\mathrm{\alpha } = 0.05$, the gTDT test statistics jointly identify the region on Chromosome 21 only.

4 Discussion

In this article, we propose a general framework for region-based association analysis in studies with family-based designs. The key advantage of the approach is that it combines robustness against population stratification/admixture with the possibility to evaluate significance of arbitrary rare variant test statistics without the need for asymptotic approximations. The framework incorporates burden tests, SKATs, maximum single variant, and higher criticism approaches. Furthermore, we described the implementation of $FBAT ACAT$, an application of the aggregated Cauchy association test (Liu et al., 2019) that combines the strengths of these underlying statistics. Given the flexibility of the framework, any future approach can straightforwardly be implemented. The basis of our approach is the conditional offspring genotype distribution obtained by the haplotype algorithm for FBATs (Hecker et al., 2017b; Horvath et al., 2004).

Our simulation results confirm that the optimal test for the region-based analysis depends on the specific genetic architecture of the disease, and any WGS analysis relying on just one single test statistic may not detect all associations contained in the data. While dense signals with consistent effect directions can be captured by burden tests, different effect directions and less dense signals can be identified by SKAT approaches. If the signal becomes more separated and sparser, the MAX and HC approaches can be the most powerful tests. This relationship between the architecture of the signal and the power of certain statistics is the same as in studies of unrelated samples. The ACAT statistic controls the Type 1 error and achieves similar power as the corresponding most powerful statistic in each of our simulation scenarios, while reducing the multiple testing burden.

The proposed implementation of the simulation-based P-values requires the user to pre-select the number of simulations that FBAT performs for each test. The computational burden can be decreased by adaptive strategies (Hecker et al., 2017a). A subject of future research will be to integrate the existing FBAT approaches to multivariate phenotypes, longitudinal data, age at onset (Ding et al., 2009; Lange, 2003; Lange et al., 2004), gene-environmental interactions, and testing strategies into the proposed framework (Ionita-Laza et al., 2007; Steen et al., 2005; Won et al., 2009).

As a limitation, we emphasize that, although our approach is robust against population stratification and admixture, the FBAT approach requires stringent quality control and the described approach relies on the absence of genotype errors. For details about variant quality control for sequencing data, we refer to (Taliun et al., 2019) and Supplementary Appendix SF. For imputed data, we recommend the application of a lower minor allele frequency cutoff to reduce genotype errors.

Finally, we note that another popular approach to association testing is the utilization of mixed models (Kang et al., 2010; Lippert et al., 2011; Loh et al., 2015; Yang et al., 2011; Zhou et al., 2012). Recent improvements enabled the analysis of dichotomous phenotypes, the incorporation of related samples and the extension from single variants to region-based analysis (Chen et al., 2016; Hayeck et al., 2017; Weissbrod et al., 2015; Zhou et al., 2018; 2019). However, pure family-based study designs often collect phenotype data for offspring only and select pedigrees based on the offspring phenotype, leading to substantial ascertainment bias. Whereas transmission-based approaches are valid in this scenario, standard mixed models cannot utilize genetic information of samples without phenotype data and can show skewed association P-values in these extreme-sampling scenarios (Hecker et al., 2019).