IMIX: a multivariate mixture model approach to association analysis through multi-omics data integration

Abstract

Motivation

Integrative genomic analysis is a powerful tool used to study the biological mechanisms underlying a complex disease or trait across multiplatform high-dimensional data, such as DNA methylation, copy number variation and gene expression. It is common to perform large-scale genome-wide association analysis of an outcome for each data type separately and combine the results ad hoc, leading to loss of statistical power and uncontrolled overall false discovery rate (FDR).

Results

We propose a multivariate mixture model (IMIX) framework that integrates multiple types of genomic data and allows modeling of inter-data-type correlations. We investigated the across-data-type FDR control in IMIX and demonstrated lower misclassification rates at controlled overall FDR than established individual data type analysis strategies, such as the Benjamini–Hochberg FDR control, the q-value and the local FDR control by extensive simulations. IMIX features statistically principled model selection, FDR control and computational efficiency. Applications to The Cancer Genome Atlas data provided novel multi-omics insights into the genes and mechanisms associated with the luminal and basal subtypes of bladder cancer and the prognosis of pancreatic cancer.

Availabilityand implementation

We have implemented our method in R package ‘IMIX’ available at https://github.com/ziqiaow/IMIX, as well as CRAN soon.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Integrative genomic analysis has become a powerful tool in biomedical research to study the biological mechanisms underlying a complex disease or trait. The mechanisms for a particular disease outcome, such as the prognosis or the molecular subtypes of cancer, may involve alterations in multiple pathways and biological processes, including copy number variations (CNV), epigenetic changes and transcriptomic changes. Therefore, it is appealing and imperative to integrate all the omics data together to analyze a disease outcome. A common strategy is to assess the associations between genes and an outcome separately for each data type using the family-wise error rate (FWER) or the false discovery rate (FDR) controlling procedures to adjust for multiple hypothesis testing. For example, Richard et al. (2017) conducted an epigenome-wide association study to identify DNA methylation loci for blood pressure regulation, where they used the Bonferroni correction to control the FWER in the methylation data analysis. To further study the functionally associated genes, they conducted a transcriptome-wide differential expression analysis using the RNAseq data separately. The results of each data type were combined ad-hoc by the simple intersection of significant genes, and additional correlation testing was performed between the two data types. A similar analysis strategy was employed to study the association of body mass index with DNA methylation and gene expression (Mendelson et al., 2017). These commonly adopted association analysis strategies assume that different data types are independent with each other, even if there may be strong inter-data-type correlations. A comprehensive study of data from The Cancer Genome Atlas (TCGA) has found that omics data, such as gene expression, DNA methylation and CNV, have several complex triangular dependence structures (Sun et al., 2018). Furthermore, it remains unclear whether the correlation structures between data types vary according to the associations between different genes and the outcome of interest through those data types. Therefore, the heuristic separate analysis strategy may lose statistical power by assuming that the data sources are independent of each other, as shown later in our simulation and real data applications. The integration of multiple types of omics data by identifying the unknown dependence structures becomes essential to understand the intricacy of the genomic mechanisms underlying complex diseases.

We propose a multivariate mixture model approach (IMIX) to integratively analyze the associations between genes and an outcome through multiple omics data types using summary statistics. The summary statistics are z-scores transformed from P-values obtained from association analysis between genes and an outcome. The P-values can be retrieved either from individual-level data or publicly available summary-level data in a target data type. IMIX incorporates the correlations and biological coordinations between various data sources to boost the statistical power for genomic discovery. We use the expectation-maximization (EM) algorithm to estimate the model parameters. IMIX can control the across-data-type FDR through an adaptive FDR control procedure, and it also features statistically principled model selection.

There has been some literature on integrative statistical methods that analyze the associations between genes and an outcome. One class of methods is the penalized regression analysis (Tibshirani, 1996; Zou and Hastie, 2005) for feature selection and prediction. However, these methods can rarely conduct rigorous error-control procedures and require individual-level data from the same sample set. Pineda et al. (2015) proposed a permutation-based strategy that enables the penalized regression models to assess statistical significance by using the permutation-based MaxT method. However, it also requires individual-level data from the same sample set and may increase the computation time. IMIX is versatile in data applications because it does not require the use of a common set of samples across data types. Recently, Gleason et al. (2020) proposed a new integrative omics method called Primo for quantitative trait loci (QTL) mapping based on genome-wide association study summary statistics. Our method shares a similar concept which uses the mixture model in data integration; however, there are several key differences. The main difference is how we approach the parameter estimation. Primo estimates the mixture model parameters by first assuming conditional independence between the data types given the latent state, estimating the marginal distributions of the test statistics under the null and alternative for each data type with a fixed proportion of non-null tests, and approximating the inter-data-type correlation matrices under certain assumptions. In contrast, IMIX directly estimates the multivariate mixture model parameters, including means, covariance matrices and mixing proportions, using the EM algorithm, which allows examining and relaxing the conditional independence assumption given the latent state. Furthermore, IMIX accommodates simultaneous model selection for both the number of mixture components and the correlation structure, a feature that is not included in Primo.

Through extensive simulation studies, we demonstrated that IMIX yielded better statistical power and overall FDR control than individual data type analysis strategies, such as the Benjamini–Hochberg FDR (BH-FDR) (Benjamini and Hochberg, 1995), the Bonferroni correction, the q-value (Storey, 2002; Storey et al., 2020 ) and the local FDR control (Efron, 2007). We also observed that IMIX is computationally efficient. We applied IMIX to study the molecular subtypes of bladder cancer through DNA methylation, CNV and gene expression, as well as the prognosis of pancreatic cancer through gene expression and CNV in the TCGA. Our applications of IMIX to the two TCGA datasets showed that different genomic data types could be correlated in both non-disease-associated and disease-associated genes, challenging the commonly adopted conditional independence assumption given the latent state in integrative analysis of multiplatform genomic data.

2 Materials and methods

In this section, we introduce the integrative multivariate mixture model approach to association analysis of multiple omics data (Section 2.1) and further propose several variants in the IMIX framework with different model assumptions (Section 2.2). Section 2.3 discusses model selection regarding the number of mixture components and the best model among proposed variants of the multivariate mixture model. We discuss the adaptive procedure for across-data-type FDR control in Section 2.4.

2.1 IMIX

We consider the problem of association analysis between gene $i,i=1,2,\dots ,N$ and an outcome through data type $h=1,2,\dots ,H$. For instance, we are interested in identifying which genes are associated with a binary outcome, basal or luminal molecular subtype of bladder cancer in our motivating TCGA data example, and assessing the associations through H = 3 genomic data types: DNA methylation, gene expression and CNV. The null hypothesis for each data type can be formulated as $H_{0,i}^{(h)}$: gene i is not differentially methylated/expressed/CNV changed in data type h.

The P-value p_ih for gene i in data type h is obtained from the hypothesis testing problem, e.g. based on regression analysis of omics data and the outcome. We further transform the P-values to z-scores x_ih by $x_{ih}={\Phi }^{-1}(1-p_{ih})$, where $\Phi$ is the cumulative distribution function of the standard normal distribution N(0, 1) (McLachlan et al., 2006; Wei and Pan, 2008). Note that this transformation ensures that smaller P-values are tranformed to larger z-scores, which correspond to the alternative hypothesis, i.e. the distribution of the z-scores under the alternative hypothesis (alternative distribution) has a larger mean than does the null distribution in data type h (McLachlan et al., 2006).

Then we group the genes into $K=2^H$ latent states based on their associations with the outcome through the H data types. We introduce a vector of binary variables to denote each latent state k of gene i: ${\mathit{z}}_{ik}=(z_{ik1},z_{ik2},\dots ,z_{\mathit{ikH}})$. If z_ikh = 1, gene i is associated with the outcome through data type h in class k; if z_ikh = 0, gene i is not associated with the outcome through data type h in class k. Without loss of generality, we assume H = 3. When $k=1,2,\dots ,8$, the potential latent states/classes of gene i are: ${\mathit{z}}_{i1}=(0,0,0),\hspace{0.17em}{\mathit{z}}_{i2}=(1,0,0),\hspace{0.17em}{\mathit{z}}_{i3}=(0,1,0),\hspace{0.17em}{\mathit{z}}_{i4}=(0,0,1),\hspace{0.17em}{\mathit{z}}_{i5}=(1,1,0),\hspace{0.17em}{\mathit{z}}_{i6}=(1,0,1),\hspace{0.17em}{\mathit{z}}_{i7}=(0,1,1)$ and ${\mathit{z}}_{i8}=(1,1,1)$. We fix the order of the latent state vectors and define a ‘global null’ as component 1, where gene i is not associated with the outcome through any of the H data types. Depending on the latent state of gene i, i.e. whether it belongs to latent state k or not, we have T_ik = 1 or T_ik = 0, respectively.

We assume that $X_i={(x_{i1},x_{i2},x_{i3})}^T$ comes from a mixture distribution with K = 8 mixture components:

$$f(X_i)=\sum _{k=1}^K{\pi }_k{f}_k(X_i),$$

where each component k follows an H-dimensional multivariate distribution f_k, and the mixing proportions are ${\pi }_k,k=1,\dots ,8$, subject to $\sum _{k=1}^8{\pi }_k=1$. To assess how likely gene i belongs to the latent state k, we estimate the posterior probability of the latent label T_ik:

$$Pr(T_{ik}=1|X_i)=\frac{{\pi }_k{f}_k(X_i)}{\sum _{j=1}^K{\pi }_j{f}_j(X_i)}.$$

We further assume the kth component distribution f_k to be multivariate normal. The normal mixture models are widely used to approximate different mixture distributions and account for heterogeneity in real data applications (McLachlan and Peel, 2004; Sun and Cai, 2007). The marginal mixture density $f({\mathit{X}}_{\mathit{i}})$ can then be written as $f({\mathit{X}}_{\mathit{i}};\mathit{\Psi })=\sum _{k=1}^K{\pi }_k{f}_k({\mathit{X}}_{\mathit{i}};{\mathit{\theta }}_{\mathit{k}}),$ where $f_k({\mathit{X}}_{\mathit{i}};{\mathit{\theta }}_{\mathit{k}})=\varphi ({\mathit{X}}_{\mathit{i}};{\mathit{\mu }}_{\mathit{k}},{\mathit{\Sigma }}_{\mathit{k}}).$ Here, the vector $\Psi ={({\pi }_1,{\pi }_2,\dots ,{\pi }_{K-1},{\mathit{\xi }}^T)}^T$ contains all the unknown parameters in the mixture model. $\mathit{\xi }$ is the vector containing all the elements of the component means, ${\mathit{\mu }}_1,\dots ,{\mathit{\mu }}_{\mathit{K}}$, and the elements of the covariance matrices, ${\mathit{\Sigma }}_1,\dots ,{\mathit{\Sigma }}_{\mathit{K}}$, known a priori to be distinct. We use the EM algorithm (Dempster et al., 1977) to estimate $\mathit{\Psi }$. We call this generic multivariate Gaussian mixture model IMIX-Cor. In the following sections we will describe three variants based on this model.

2.2 Variants of the IMIX

2.2.1. IMIX-Cor-Restrict: correlated mixture model with restrictions on mean

To tackle the possible unidentifiability problem of $\mathit{\Psi }$ due to the interchanging of component labels, we fix the order of the latent states as described in Section 2.1 and impose the following constraints on ${\mathit{\mu }}_k$:

$$\begin{array}{c}{\mathit{\mu }}_1=({\mu }_{10},{\mu }_{20},{\mu }_{30});{\mathit{\mu }}_2=({\mu }_{11},{\mu }_{20},{\mu }_{30});\hfill \\ \hfill & {\mathit{\mu }}_3=({\mu }_{10},{\mu }_{21},{\mu }_{30});{\mathit{\mu }}_4=({\mu }_{10},{\mu }_{20},{\mu }_{31});\hfill \\ \hfill & {\mathit{\mu }}_5=({\mu }_{11},{\mu }_{21},{\mu }_{30});{\mathit{\mu }}_6=({\mu }_{11},{\mu }_{20},{\mu }_{31});\hfill \\ \hfill & {\mathit{\mu }}_7=({\mu }_{10},{\mu }_{21},{\mu }_{31});{\mathit{\mu }}_8=({\mu }_{11},{\mu }_{21},{\mu }_{31}).\hfill \end{array}$$ (1)

These constraints correspond to the biological rationale that for each data type, we assume that the means of the test statistics from the null and non-null groups are the same across the K classes. For example, μ₁₀, the mean of the null distribution in data type 1, is the same in ${\mathit{\mu }}_1,\hspace{0.17em}{\mathit{\mu }}_3,\hspace{0.17em}{\mathit{\mu }}_4$ and ${\mathit{\mu }}_7$. The multivariate Gaussian mixture model with restrictions on the mean is denoted as IMIX-Cor-Restrict. Details of the parameter estimation using the EM algorithm are available in Supplementary Section S1.

2.2.2. IMIX-Ind: independent mixture model with restrictions on mean and variance

If we assume there is no correlation between any two data types given the latent state, i.e. conditional independence, then the covariance matrix in IMIX-Cor-Restrict, Σ_k, becomes diagonal. The model is reduced to

$$\begin{array}{c}f({\mathit{X}}_{\mathit{i}};\mathit{\Psi })=\sum _{k=1}^K{\pi }_k{f}_k({\mathit{X}}_{\mathit{i}};{\mathit{\theta }}_{\mathit{k}})\\ =\sum _{k=1}^K{\pi }_k{f}_{k1}({\mathit{x}}_{i1};{\theta }_{k1})f_{k2}({\mathit{x}}_{i2};{\theta }_{k2})f_{k3}({\mathit{x}}_{i3};{\theta }_{k3}),\end{array}$$

where $f_{kh}({\mathit{x}}_{\mathrm{ih}};{\theta }_{kh})=\varphi ({\mathit{x}}_{\mathrm{ih}};{\mu }_{kh},{\sigma }_{kh})$ is a normal probability density function with mean μ_kh and variance ${\sigma }_{kh}^2,\hspace{0.17em}k=1,\dots ,8;h=1,2,3$. Besides the constraints on the mean given in Equation (1), we impose the same constraints on the variance ${\sigma }_{kh}^2$ on the basis of the null and non-null genes for each data type. We call this model IMIX-Ind.

2.2.3. IMIX-Cor-Twostep: correlated mixture model with fixed mean

To reduce the model’s complexity, i.e. to create a more parsimonious model and ease the computation time, we propose a third modification based on the previous models, the correlated mixture model with fixed mean. This model is similar to the previous model with constraints on the means; however, with the replacement of the means estimated from the independent model IMIX-Ind, we ease the complexity of estimating the mean and the covariance matrices at the same time in the EM algorithm. In our simulation study to be detailed later on, IMIX-Ind performed well in estimating the means; thus, to facilitate the correlation estimation between data types, we introduce the correlated mixture model with fixed means, where we only estimate the covariance matrix for each component with a prespecified mean vector. We will show later in the simulation study that this model achieves the best computational efficiency and numerical stability among IMIX models that consider the correlation structures. We call this model IMIX-Cor-Twostep.

2.3 Model selection

In real data applications, one or a few classes out of K may be absent. For example, if there is no gene associated with the outcome across all three data types, then component 8 is absent in the true mixture distribution underlying the data. Using an eight-component mixture model to estimate a true seven-component mixture distribution will increase the number of unnecessary parameters to be estimated. In turn, this will negatively impact the parameter estimation and add more computation time or even makes it difficult to converge. Model selection improves the model fitting and parameter estimation; this idea is similar to ‘variable selection’ in machine learning, where we need to remove the unnecessary and redundant features. Model selection will also help provide a better understanding of the underlying biological processes between the genes and the outcome across multiple data types. This is closely related to the question of how many components K to include in the mixture distribution to prevent overfitting. As pointed out by previous works (Leroux, 1992; McLachlan and Peel, 2004), the penalized log-likelihood functions, including Akaike information criterion (AIC) and Bayesian information criterion (BIC), are adequate for selecting the number of components under a finite mixture distribution; in particular, under mild conditions, AIC and BIC do not underestimate the true number of components asymptotically. Specifically, AIC and BIC select the model that, respectively, minimizes $\text{AIC}=-2\times \text{loglik}+2d$ and $\text{BIC}=-2\times \text{loglik}+d\hspace{0.17em}\text{log}\hspace{0.17em}N$, where d is the number of unknown parameters (i.e. degrees of freedom), N is the number of genes and loglik is the maximized full log-likelihood.

Along with model selection for the number of components K, we also select the best model for a fixed K among the different methods introduced in Section 2.2 regarding mean and covariance structures. We introduce the IMIX framework, where the data are fitted for all four IMIX methods (IMIX-Ind, IMIX-Cor, IMIX-Cor-Twostep and IMIX-Cor-Restrict). Then AIC or BIC is used to select the best model among the candidate models, called IMIX-AIC or IMIX-BIC.

2.4 Adaptive procedure for across-data-type FDR control

We propose an across-data-type FDR control procedure in the IMIX framework based on an adaptive procedure introduced by Sun and Cai (2007). For each component k ($k\ne 1$), we construct the following hypotheses:

• $H_{0,i}^k$: Gene i does not belong to component k;

• $H_{1,i}^k$: Gene i belongs to component k.

Note that component 1 (the global null) is not considered as a ‘discovery’ and only components 2–8 are considered ‘discovery’ for which FDR is applicable. The across-data-type FDR for component k is defined as FDR_k=$E(F_k/R_k|R_k>0)Pr(R_k>0),k=2,\dots ,K$. Here F_k is the number of false discoveries in component k and R_k is the total number of hypotheses claimed significant in component k. When no hypothesis is claimed significant, FDR_k is 0. The estimated posterior probability that gene i belongs to component k is defined as ${\widehat{p}}_{i,k}=\widehat{Pr}(T_{ik}=1|X_i)$. The estimated local FDR for gene i is defined as ${\widehat{q}}_{i,k}=1-{\widehat{p}}_{i,k}=\widehat{Pr}(T_{ik}=0|X_i),k=2,\dots ,K$. The adaptive step-up procedure is described here: $\text{Let} m_k=\text{max}\{i:1/i\sum _{j=1}^i{\widehat{q}}_{(j),k}\le \alpha \},\text{then}\hspace{0.17em}\text{we}\hspace{0.17em}\text{reject}\hspace{0.17em}\text{all}\hspace{0.17em}{\mathrm{H}}_{0,(\mathrm{i})},\mathrm{i}=1,\dots ,{\mathrm{m}}_{\mathrm{k}}$, where ${\widehat{q}}_{(1),k},{\widehat{q}}_{(2),k},\dots ,{\widehat{q}}_{(n),k}$ are ranked in component k. The adaptive procedure controls the marginal FDR (mFDR) for each component at level α asymptotically. Here mFDR_k is defined as $E(F_k)/E(R_k)$. The estimated mFDR becomes ${\widehat{\text{mFDR}}}_k=\sum _{j=1}^{m_k}{\widehat{q}}_{(j),k}/m_k$. Genovese and Wasserman (2002) showed that under weak conditions, there exists an asymptotic relationship between mFDR and the across-data-type FDR of one component, in which mFDR_k = FDR_k + $O(N^{-1/2})$, where N is the number of hypotheses in component k and it is the same across all components. This adaptive procedure can be further used for a combination of components. For example, if we are interested in all the genes that are associated with the outcome through both DNA methylation and gene expression in a three-data type integration problem of DNA methylation (M), gene expression (E) and CNV, the procedure can be applied to the combination of components 5 and 8, i.e. (M+,E+,CNV-) and (M+,E+,CNV+).

3 Results

3.1 Simulation studies

We performed two sets of simulation studies. Simulation study 1 assessed the performance of IMIX in terms of across-data-type FDR control, misclassification rate and model calibration; simulation study 2 evaluated the information criteria we proposed for model selection. We consider the following multivariate normal mixture model for three data types:

$${\mathit{X}}_{\mathit{i}}\sim \sum _{k=1}^8{\pi }_k\varphi ({\mathit{\mu }}_{\mathit{k}},{\mathit{\Sigma }}_{\mathit{k}}),$$ (2)

where ${\mathit{\mu }}_{\mathit{k}}=({\mu }_{k1},{\mu }_{k2},{\mu }_{k3})$ with μ_kh corresponding to the mean of data type h in component k, and ${\mathit{\Sigma }}_{\mathit{k}}$ is a 3 × 3 matrix that contains the variance ${\sigma }_{kh}^2$ and the covariance ${\sigma }_{\mathit{khh}\prime }$ between data type h and $h\prime$ in component k.

3.1.1. Across-data-type FDR control and misclassification rate

To illustrate the lower misclassification rate while controlling for the across-data-type FDR of IMIX compared with the commonly used methods, we generated $1\hspace{0.17em}000$ simulated datasets of $N\times p=20\hspace{0.17em}000\times 3$  z-scores x_ih following (2) in six scenarios. Scenario 1 assumed all three data types were independent with ${\mathit{\Sigma }}_{\mathit{k}}$ = diag(1,1,1); the mean under the null was 0 and under the alternative was 3 for data type h; the proportion of each component was balanced as ${\pi }_k=0.125$. Scenarios 2–5 assumed the z-scores were correlated under the alternative hypothesis by adding covariances (they were also the correlations given the variances were 1) ${\sigma }_{k12}={\sigma }_{k13}={\sigma }_{k23}$ in ${\mathit{\Sigma }}_{\mathit{k}}$. Here we only set the covariances to be non-zero when at least two data types were both non-null in component $k=5,6,7,\hspace{0.17em}\text{and}\hspace{0.17em}8$. Each simulation scenario corresponded to a covariance of 0.1, 0.3, 0.5 and 0.8, respectively. The rest of the parameters in scenario 2–5 followed those of scenario 1. Scenario 6 mimicked the real data in Section 3.2.1, where we analyzed the luminal and basal molecular subtypes through DNA methylation, gene expression and CNV of the bladder cancer data in TCGA. We set the mean and covariance matrices in (2) equal to the empirical values estimated from z-scores classified by separate analysis of each data type using the BH-FDR method and an unbalanced proportion equal to the estimated $\widehat{\pi }$ using IMIX-Cor-Twostep (Supplementary Section S2.1). This simulation scenario thus did not favor either the separate analysis or the IMIX method.

We analyzed the simulated data by applying our proposed methods, including IMIX-Ind, IMIX-Cor-Restrict, IMIX-Cor, IMIX-Cor-Twostep, IMIX-AIC and IMIX-BIC. To compare the model’s performance with commonly used separate analysis methods, we applied the BH-FDR, the Bonferroni correction, the q-value and the local FDR procedure. We set $\alpha =0.2$ as the nominal error control level across all methods for comparisons. Note that we suggest an α value threshold between 0.05 and 0.2 for IMIX to discover interesting non-null genes while controlling the proportion of null genes (false positives) in the significant gene list.

The simulation results are presented in Figure 1a for the average of $1\hspace{0.17em}000$ simulations of the across-data-type FDR, which was the average of components 2–8 excluding the global null component 1; and in Figure 1b for the misclassification rate, which was the average of all components. Our proposed methods were able to robustly control the across-data-type FDR at the prespecified $\alpha =0.2$ level. The separate analysis q-value failed to control the FDR. The Bonferroni correction was designed to control the family-wise error rate. Still, we included it here to compare the misclassification rate with other methods, as it is a popular error control procedure among researchers in biomedical sciences. The local FDR procedure deflated the FDR in Scenarios 3–5, which behaved similarly to the IMIX-Ind. Both methods were based on independent mixture distributions, and the reason IMIX-Ind controlled the FDR slightly better than the local FDR procedure was that IMIX-Ind assumed a more flexible combination of mixing proportions while the local FDR procedure only considered the mixing proportions for one data type at a time. For example, the mixing proportion π₁ of component 1 in the IMIX-Ind is only subject to the constraint $\sum _{k=1}^8{\pi }_k=1$, while π₁ in the local FDR procedure is subject to ${\pi }_1={\pi }_{10}{\pi }_{20}{\pi }_{30}$, where ${\pi }_{h0}$ is the null mixing proportion for the separate analysis of data type $h=1,2,\hspace{0.17em}\text{and}\hspace{0.17em}3$. This was further illustrated in Scenario 6, where the underlying correlation structures and the generating model were more complicated: the local FDR procedure failed the across-data-type FDR control while IMIX-Ind controlled it robustly. The BH-FDR returned slightly inflated FDR in Scenarios 1–5, and the realized FDR increased as the correlations increased among the three data types. In Scenario 6, it failed to control the across-data-type FDR. IMIX steadily achieved a lower misclassification rate (Fig. 1b) in all scenarios than the commonly used methods. Our proposed methods can robustly control the across-data-type FDR and achieve a good operating characteristic under various scenarios.

Fig. 1.

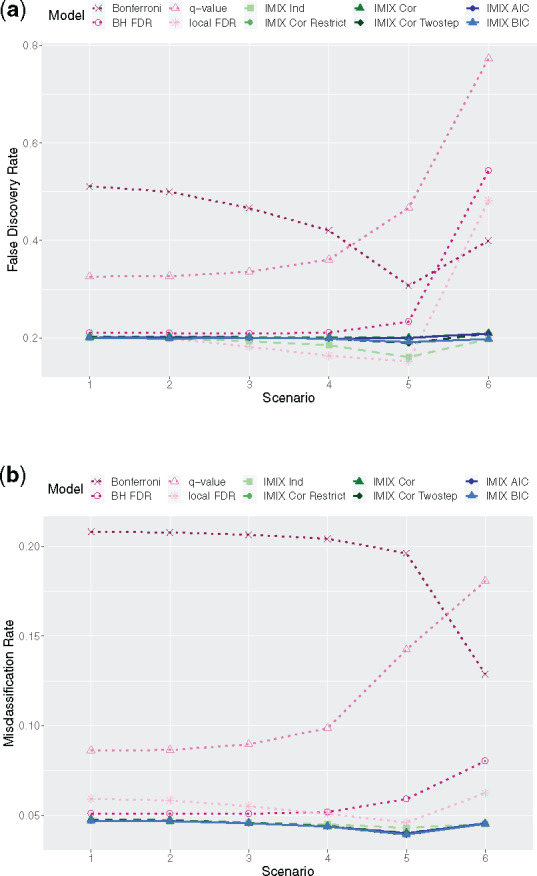
Comparison of IMIX-Ind, IMIX-Cor, IMIX-Cor-Restrict, IMIX-Cor-Twostep, IMIX-AIC, IMIX-BIC, Benjamini–Hochberg false discovery rate (BH-FDR), the Bonferroni correction, the q-value and the local FDR procedure at $\alpha =0.2$. (a) The realized across-data-type false discovery rate in the average of $1\hspace{0.17em}000$ simulations, the results in each scenario are of the average of components 2–8, excluding the global null component 1. (b) Misclassification rate in the average of $1\hspace{0.17em}000$ simulations, the results in each scenario are the average of all components

In addition, we compared the computation time needed for the four IMIX models (Supplementary Section S2.4: Supplementary Table S4) using the simulation Scenario 3, assuming three data types with correlation 0.3 based on $1\hspace{0.17em}000$ simulations. IMIX-Ind converged the fastest with only 4.50 s and 67 iterations on average. Moreover, IMIX-Cor-Twostep achieved great computational advantages with an average of 217.379 s with only 42 iterations over IMIX-Cor and IMIX-Cor-Restrict, with 970.901  and 417.531 s convergence time, and 161 and 71 iterations, respectively. This was processed on Intel(R) Xeon(R) CPU E5502 @ 1.87 GHz with max CPU 1866 MHz and min CPU 1600 MHz.

3.1.2. Model calibration and FDR control

Newton et al. (2004) showed that the performance of the estimated FDR based on equation $FD{R}_{\text{estimated}}(t)=\sum _{i=1}^N{q}_{i}I(q_i\le t)/\sum _{i=1}^{N}I(q_i\le t)$, relies on how well the model fitting is. Thus, we need to assess the model calibration to ensure that the IMIX framework is able to reliably control the realized FDR by the adaptive FDR procedures. We pursued this by comparing the realized and estimated FDRs on the results fitted using IMIX from the six scenarios in simulation study 1. We compared the estimated and realized FDRs averaged across the $1\hspace{0.17em}000$ simulated datasets for each non-null component 2–8, and the sum-up of non-nulls compared to the global null component 1. Supplementary Figures S1–S4 present the results of IMIX-Ind, IMIX-Cor-Restrict, IMIX-Cor and IMIX-Cor-Twostep in the six simulation scenarios. IMIX-Ind showed good model calibration in Scenarios 1 and 2, but as the correlation gradually increased from Scenario 3 to Scenario 5, the discrepancy between estimated FDR and realized FDR increased. In Scenario 6 where we mimicked the real data, IMIX-Ind was slightly conservative as the realized FDR was slightly smaller than the estimated FDR. IMIX-Cor and IMIX-Cor-Restrict performed similarly where the estimated and realized FDRs were coincident in scenarios 1–5. In scenario 6, component 4 and component 6 showed slightly inflated realized FDR. This was because the proportion of these two components got as small as $6.9\times {10}^{-3}$ and $8.9\times {10}^{-3}$. IMIX-Cor-Twostep also performed well in all scenarios except for a slight shift in Scenario 5, where the correlations between data types were as high as 0.8. Since this model utilizes the estimated mean parameters from IMIX-Ind, it may have slightly affected the model calibration. However, the computation time gain was much better and can be shown in real-data-based simulation Scenario 6.

In summary, the IMIX framework is rigorous and versatile with good model calibration under various data scenarios, leading to a reliable and accurate FDR estimation, and thus a robust adaptive FDR control procedure.

3.1.3. Model selection

We conducted simulation study 2 to evaluate how well AIC and BIC selected the number of components in the IMIX framework. We first generated $1\hspace{0.17em}000$ datasets following (2) for 16 scenarios that consisted of a combination of balanced and unbalanced mixing proportions of seven and eight components (Supplementary Table S1). The unbalanced mixing proportions were based on the proportions of genes in the real-data example; we used the estimated $\widehat{{\pi }_k}$ of the TCGA bladder cancer dataset fitted by IMIX-Cor as the unbalanced proportions for the eight-component mixture model. The seven-component mixture model simulation simply eliminated the eighth component from the eight-component mixture model, i.e. genes associated with the outcome through all three data types. For each mixing proportion and number of components combination, we generated four scenarios with the mean and covariance parameters equal to the simulated parameters in simulation study 1 Scenarios 2–5. We fitted the IMIX framework without adding any constraint on the mean, assuming models of one to eight components. Here, we were only interested in the final number of components of the selected model rather than the component each gene belongs to, for the purpose of model selection.

Supplementary Figures S5 and S6 show the number of components selected by AIC/BIC after averaging $1\hspace{0.17em}000$ simulation replications for the unbalanced seven- and eight component simulated models. AIC selected the correct number of components in both balanced and unbalanced settings (Supplementary Fig. S6a–d). BIC performed similarly (Supplementary Fig. S5a, b and d), but it selected a more conservative number, i.e. a more parsimonious model, under the extremely unbalanced eight-component scenario in Supplementary Figure S5c. We consider this unbalanced eight-component setting challenging for BIC or any model selection criterion because the smallest mixing proportion was only 4%. To further evaluate AIC and BIC’s ability to select the correct number of components when the mixing proportions were unbalanced, we conducted more simulation studies for an eight-component multivariate Gaussian mixture model with varying levels of unbalanced settings as shown in Supplementary Section S2.3. Both AIC and BIC performed well in identifying the correct number of components (Supplementary Fig. S7).

AIC and BIC were both reliable model selection criteria under relatively balanced mixing proportions. AIC could select up to eight components in extremely unbalanced situations; however, previous works (McLachlan and Peel, 2004; Steele and Raftery, 2009) showed that AIC is prone to overestimating the number of components. Fraley and Raftery (2002) showed that BIC performed well in choosing the number of components in a range of applications. The same group has implemented an R package ‘mclust’ that, by default, uses BIC for model selection (Scrucca et al., 2016). We consider BIC to be more stable as it takes into account the number of genes in the penalty term, which can be as large as tens of thousands under the whole-genome setting.

3.2 Real data applications

To demonstrate the proposed IMIX framework’s versatility and efficiency in different disease outcomes, we applied our method to a binary outcome, the luminal and basal molecular subtypes of muscle-invasive bladder cancer, as well as a survival outcome for the prognosis of pancreatic cancer in the TCGA dataset.

3.2.1 Molecular subtypes of bladder cancer in the TCGA

Previous studies in bladder cancer identified molecular signatures associated with the pathological and clinical outcomes (Choi et al., 2014; Guo et al., 2019); in particular, those molecular subtypes have important implications for prognostication and treatment. Twenty-three gene expression markers have been reported to play a major role in these molecular subtypes. We applied IMIX to analyze the TCGA bladder cancer patient cohort, which was profiled by three genomic platforms: DNA methylation, mRNA gene expression and CNV. We investigated: (i) whether those gene expression markers also demonstrated difference at the DNA methylation and CNV levels, and (ii) whether there were other genes associated with the molecular subtyping through any of the three data types. After quality control (Supplementary Section S3.1), we separately analyzed 373 DNA methylation samples, 391 RNA-Seq samples and 387 CNV samples with N=15 672 genes with respect to the molecular subtypes adjusting for the clinical covariates, including age, sex, race, smoking status and pathological stage. We applied IMIX, the Bonferroni correction and the BH-FDR to the final P-values obtained from the association tests of individual-level data. The nominal error control level of the Bonferroni correction and the BH-FDR for separate analysis was set at $\alpha =0.05$, and that of IMIX for integrative analysis was at $\alpha =0.2$. We used IMIX-BIC to perform model selection, with the optimal model selected as IMIX-Cor-Twostep and the best number of components as eight based on BIC values. Table 1 shows the point estimates and 95% bootstrap-based confidence intervals ($B=1\hspace{0.17em}000$) (McLachlan and Peel, 2004) for the parameters in the correlation matrices between DNA methylation, gene expression and CNV. DNA methylation and gene expression showed moderate correlations that involved non-null genes across both data types in component 5 (M+,E+,CNV–) and component 8 (M+,E+,CNV+). Another interesting finding was that DNA methylation and gene expression were correlated when genes were associated with the outcome through only one data type, as reflected in component 2 (M+ and E–) and component 3 (M– and E+). This also held for the correlations between methylation and CNV when genes were not associated with the outcome through either data type in component 1 (M–,CNV–) and component 3 (M–,CNV–), as well as gene expression and CNV in component 3 (E+,CNV–). These results further supported the IMIX model assumptions that the data types could be correlated, both under the alternative and the null hypothesis, thus reinforcing that the IMIX method was effective by assuming multivariate distributions in all components instead of the commonly adopted conditional independence, e.g. in the Primo method (Gleason et al., 2020).

Table 1.

Estimated correlations between the transformed z-scores (from P-value) across the data types with 95% bootstrap-based confidence intervals (B=1000) for TCGA bladder cancer data and TCGA pancreatic cancer data integration analysis by IMIX-BIC

TCGA bladder cancer				TCGA pancreatic cancer
Component	M & E	M & CNV	E & CNV	Component	E & CNV
1 (M-,E-,CNV-)	0.015 (-0.039, 0.072)	0.091 (0.037, 0.14)	−0.016 (-0.070, 0.043)	1 (E-,CNV-)	0.040 (-0.047, 0.13)
2 (M+,E-,CNV-)	0.070 (0.014, 0.12)	−0.012 (-0.060, 0.031)	0.0049 (-0.064, 0.075)	2 (E+,CNV-)	0.11 (-0.012, 0.21)
3 (M-,E+,CNV-)	0.14 (0.051, 0.23)	0.090 (0.016, 0.17)	−0.10 (-0.19, -0.022)	3 (E-,CNV+)	0.016 (-0.019, 0.049)
4 (M-,E-,CNV+)	−0.099 (-0.59, 0.40)	0.35 (-0.085, 0.73)	−0.059 (-0.53, 0.36)	4 (E+,CNV+)	0.12 (0.071, 0.18)
5 (M+,E+,CNV-)	0.25 (0.20, 0.31)	−0.037 (-0.082, 0.013)	0.038 (-0.023, 0.097)
6 (M+,E-,CNV+)	0.038 (-0.22, 0.25)	−0.037 (-0.27, 0.22)	−0.088 (-0.40, 0.26)
7 (M-,E+,CNV+)	0.21 (-0.16, 0.56)	0.13 (-0.27, 0.49)	0.12 (-0.29, 0.50)
8 (M+,E+,CNV+)	0.19 (0.021, 0.38)	0.10 (-0.049, 0.26)	0.080 (-0.13, 0.28)

Note: Confidence intervals not covering 0 are in boldface.

M, methylation; E, gene expression; CNV, copy number variation.

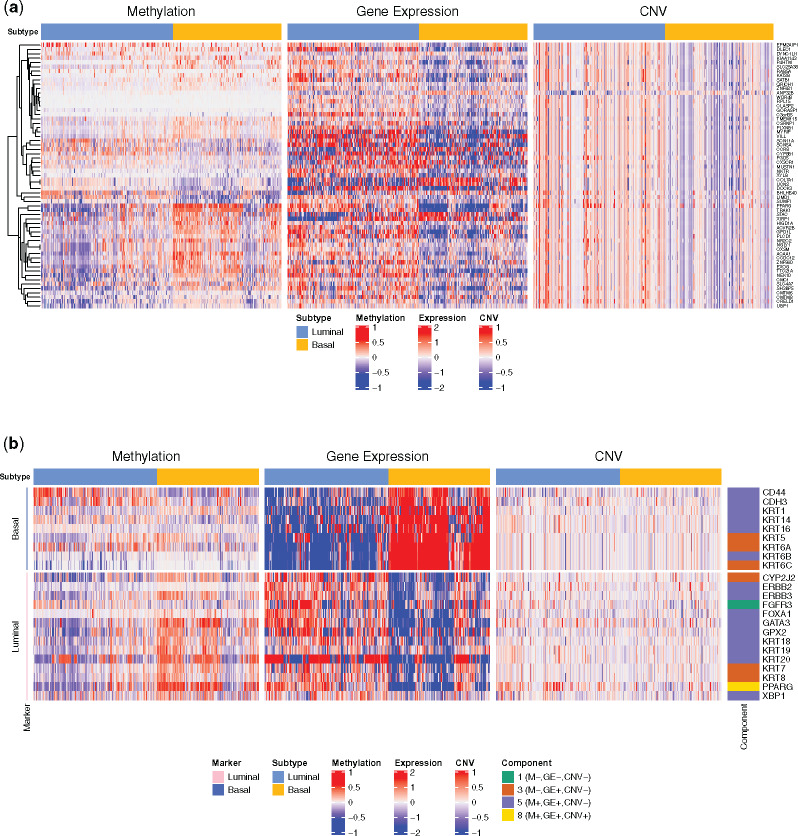
We compared the number of genes discovered in component 8 using the BH-FDR, the Bonferroni correction and our method (Supplementary Fig. S8a). The genes that were detected by the Bonferroni correction were identified by both our method and the BH-FDR. The genes detected by IMIX had an overlap of 146 genes with the BH-FDR and included 116 new genes not discovered by either the BH-FDR or the Bonferroni correction. The estimated ${\widehat{\text{mFDR}}}_8$ of IMIX was 0.1995, close to the prespecified across-data-type FDR control level alpha = 0.2. Through simulation studies in Section 3.1.1, our method was more effective in controlling the across-data-type FDR than other methods. We also showed the levels of DNA methylation, gene expression and CNV for the significant genes in component 8, i.e. genes that were associated with all three data types in Figure 2a; for the purpose of illustration, we only included the 61 significant genes after adaptive FDR control at $\alpha =0.01$. We conducted Ingenuity Pathway Analysis [IPA, Ingenuity Systems (www.ingenuity.com)] on the 61 significant genes in component 8 at $\alpha =0.01$. The results showed strong peroxisome proliferator activator receptor (PPAR) pathway activation (Supplementary Fig. S9) in luminal samples. This pathway was previously reported by Choi et al. (2014), who first proposed the molecular subtypes of muscle-invasive bladder cancer and showed that PPARα and PPARγ activation played essential roles in regulating gene expression signature for the luminal subtype. Specifically, they exposed the PPARγ-selective agonist rosiglitazone in two bladder cancer cell lines and further confirmed that rosiglitazone activated the PPAR pathway and enriched gene signatures in primary luminal samples. Furthermore, we estimated the causal relationships between DNA methylation, gene expression and CNV of the 61 genes in component 8 by applying Bayesian networks (Scutari, 2017) with the target nominal type I error rate at 0.01. Of those 61 genes, 51 showed significant dependent structures between the three data types. The directed acyclic graphs (DAGs) based on conditional independence tests with a restriction of causal direction from CNV to E showed six different causal structures (Supplementary Section S3.2).

Fig. 2.

Heatmaps of genes in IMIX analysis for bladder cancer molecular subtypes in TCGA. (a) Methylation, gene expression and copy number variation (CNV) patterns of top significant genes associated with the three data types (M+,GE+,CNV+) identified by IMIX in molecular subtypes of TCGA muscle-invasive bladder cancer patients, with adaptive FDR control at $\alpha =0.01$, estimated marginal FDR (${\widehat{\text{mFDR}}}_8$) = 0.0098. (b) Expression patterns of luminal and basal markers of TCGA bladder cancer cohort

We present the levels of the luminal and basal markers for DNA methylation, gene expression and CNV in Figure 2b. Among the 23 markers, we found that six, 15 and one gene belonged to component 3 (M-,E+,CNV-), component 5 (M+,E+,CNV-) and component 8 (M+,E+,CNV+), respectively. In particular, PPARG belonged to component 8, i.e. associated with the subtypes via all three molecular mechanisms. Bayesian networks further confirmed that PPARG had a full model with dependence structures of CNV → E, E–M, M–CNV [Supplementary Fig. S10(1)]. This gene was reported to be one of the driver genes for basal and luminal differentiation. As expected, the luminal samples showed a higher PPARG gene expression level than did the basal samples; furthermore, we discovered a concordant significant differential pattern in the methylation and CNV levels that has not been previously reported.

In summary, our analysis revealed that the luminal and basal markers demonstrated substantial differences in at least two data types (Fig. 2b). By applying the IMIX framework, we successfully discovered novel genes that were associated with the molecular subtypes across all three data types (Fig. 2a) and confirmed the PPAR/RXR activation canonical pathway that was previously reported to play a central role in luminal and basal differentiation (Choi et al., 2014).

3.2.2. Prognosis of pancreatic cancer in the TCGA

We further applied IMIX to a survival outcome to investigate the relationships between the prognosis of pancreatic cancer patients and two genomic datasets, gene expression and CNV in the TCGA. After quality control (Supplementary Section S3.1), we first applied the Cox proportional hazards model to each of the 15 472 genes respectively on 157 RNA-Seq samples and 161 CNV samples, adjusting for age, gender and smoking status. Next, we fitted IMIX, the BH-FDR and the Bonferroni correction on the summary statistics. After model selection based on BIC, IMIX-Cor-Twostep fitted the best. Table 1 shows the point estimates and 95% bootstrap-based confidence intervals ($B=1\hspace{0.17em}000$) of the parameters in the correlation matrices between gene expression and CNV. In component 4 (E+,CNV+), where the detected genes were significantly associated with survival outcomes through both gene expression and CNV, the correlation between gene expression and CNV was $\widehat{\rho }=0.120$ with 95% confidence interval $(0.071,0.18)$.

To assess the effect of the detected 104 genes in component 4 at $\alpha =0.05$, we used iCluster (Shen et al., 2009) to group the patients based on gene expression and CNV data into two classes; here, we only applied the 104 genes detected by IMIX with no feature selection in the clustering process. Figure 3 shows the gene expression and CNV levels of the identified 104 genes associated with the pancreatic cancer prognosis. The gene expression and CNV were positively correlated, as shown in the heatmap. Supplementary Figure S11 shows the Kaplan–Meier curve of the overall survival of pancreatic cancer patients. The log-rank test resulted in P = 0.016, and the Cox model adjusted for patient pathological stages resulted in P = 0.04. Furthermore, when we clustered the patients using the 991 genes discovered at adaptive FDR $\alpha =0.2$, all patients but one were grouped into the same clusters as using the 104 genes at $\alpha =0.05$; the Kaplan–Meier curve returned the same results. This indicates that IMIX captured the most important features and a controlled number of false discovered genes at $\alpha =0.05$. This result warrants further validation in an independent cohort.

Fig. 3.

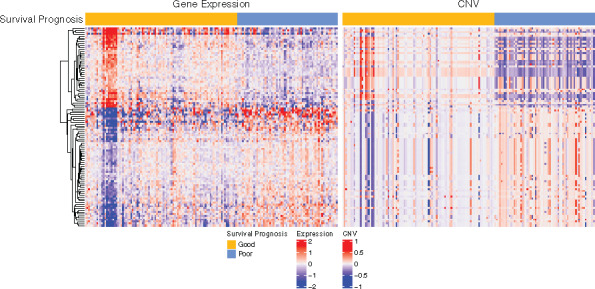
Gene expression and CNV patterns of the 104 genes selected by IMIX that were associated with the prognosis of the TCGA pancreatic cancer patients, with adaptive FDR control at $\alpha =0.05$, estimated marginal FDR (${\widehat{\text{mFDR}}}_4$) = 0.0498. Samples were clustered based on the 104 genes identified by IMIX. There were 94 samples in good prognosis group and 62 samples in poor prognosis group

We compared the results of IMIX, the Bonferonni correction and the BH-FDR for component 4, i.e. genes associated with the survival outcomes through both gene expression and CNV. The Bonferroni correction was not able to discover any significant genes at the nominal level, $\alpha =0.05$. IMIX detected 104 genes at $\alpha =0.05$ with an estimated ${\widehat{\text{mFDR}}}_4=0.0498$. The BH-FDR detected 271 genes at $\alpha =0.05$. IMIX identified fewer genes, but it captured the important features as evidenced by the Kaplan–Meier analysis/log-rank test with a controlled across-data-type FDR compared with the BH-FDR. We showed in Section 3.1.1 that the BH-FDR failed to control for FDR under the data integration settings. In addition, IMIX detected 991 genes at $\alpha =0.2$ with an estimated ${\widehat{\text{mFDR}}}_4=0.2$; and the 271 genes detected by the BH-FDR ($\alpha =0.05$) were all included in the genes discovered by our method as shown in the Venn diagram (Supplementary Fig. S8b).

4 Discussion

We have developed IMIX, a multivariate mixture model framework based on summary statistics for integrative genomic association analysis. Our model incorporates the correlation structures between different genomic datasets by assuming multivariate Gaussian mixture distribution of the z-scores (transformed from P-values) from association analysis of individual-level data. The IMIX framework includes four models: IMIX-Cor, IMIX-Ind, IMIX-Cor-Restrict and IMIX-Cor-Twostep, each of which best captures a specific type of mean and correlation structure arising from various data analysis problems. IMIX selects the optimal model based on AIC/BIC values among the four models. In addition, IMIX features simultaneous model selection for the number of underlying latent states/components of the optimal mixture model with a specific correlation structure. We use the EM algorithm in parameter estimation, and the mixture model naturally produces the local FDR for each gene, which is easily derived from the posterior probability. Our model features an adaptive procedure to control the across-data-type FDR, where we take into account both the multiple testing of the gene and the multiple data types under an integrative analysis setting. This error-control property for an integrative genomic model is the first of its kind, to our knowledge.

Our applications to the two TCGA datasets demonstrate that different genomic data types, such as DNA methylation, mRNA gene expression and CNVs, can be correlated in both null and non-null genes, as shown in the bootstrap-based confidence intervals (Table 1). Therefore, it is necessary to consider the inter-source correlations of multiple datasets in integrative analysis. Based on simulation studies under various settings of correlation structures, including the one based on the TCGA bladder cancer dataset, IMIX controlled the FDR precisely and yielded better statistical power than the independent separate analysis models, including the BH-FDR, the Bonferroni correction, the q-value and the local FDR procedure.

An important key feature of our proposed method using summary statistics is that the z-scores are based on the inverse standard normal transformation of P-values. For a given data type, the null distribution of the z-scores is the standard normal, referred to as the theoretical null (McLachlan et al., 2006). We relaxed this condition and used an empirical null with unspecified mean and variance to allow calibration differences. Larger z-scores (smaller P-values) correspond to the alternative hypothesis, i.e. the alternative distribution has a larger mean than the null distribution in each data type (McLachlan et al., 2006). An additional key feature of IMIX is its constraints on the mixture component means, which is not only more biologically plausible than unconstrained means, but together with the properties of z-scores have ensured model identifiability, a common challenge in mixture models. Another unique feature of IMIX is model selection: we let the data decide the number of mixture components and the correlation structure based on AIC or BIC.

In addition, IMIX is able to model summary statistics from independent or partially overlapping sample cohorts, as illustrated in the TCGA data examples (Section 3.2), which relaxes the conditions of previously published methods for the integration of multiple omics data requiring the same set of samples (Richardson et al., 2016). The robust results are shown in a sensitivity analysis (Supplementary Section S3.3) comparing the genes detected in each component using the same set of samples and non-overlapping samples. The implementation of IMIX employs the EM algorithm, which in general converges fast, leading to great computational efficiency.

IMIX can study various types of outcomes, including continuous, binary and time-to-event outcomes in integrative genomic analysis. We have applied IMIX to two kinds of problems, the prognosis of pancreatic cancer and the luminal and basal molecular subtypes of bladder cancer; both applications provided novel biological insights. The IMIX framework is not only applicable to cancer genomics but also to other complex diseases and traits as afforded by ongoing large-scale multiple-omics projects, such as the NIH Trans-Omics for Precision Medicine (TOPMed) project (Brody et al., 2017), consisting of more than 100 000 deeply phenotyped and sequenced individuals with multiple types of omics data, such as transcriptomic, epigenomic, metabolic, proteomic and whole-genome sequencing data. Therefore, this work has a wide range of potential applications to provide novel biological insights into disease mechanisms. We have implemented the integration model for two and three genomics data types in the simulation studies and data applications, which could be further generalized to four and more data types in the multivariate mixture model framework. We leave the details of this potential extension for future research. While we have relaxed the conditional independence assumptions for the data types in IMIX, we could further extend our method by assessing the correlations between genes within each data type, which is another important direction for future work.

We have implemented the proposed method in an R package ‘IMIX’, which is available at https://github.com/ziqiaow/IMIX and will be posted to R/CRAN.