Nav1.3 and FGF14 are primary determinants of the TTX-sensitive sodium current in mouse adrenal chromaffin cells

Martinez-Espinosa et al. show that FGF14 and the voltage-dependent Na⁺ channel Nav1.3 are the main regulators of rapidly inactivating currents and Nav channel availability in mouse adrenal chromaffin cells. Their results uncover a role for FGF14 in regulating Nav channel function.

Abstract

Adrenal chromaffin cells (CCs) in rodents express rapidly inactivating, tetrodotoxin (TTX)-sensitive sodium channels. The resulting current has generally been attributed to Nav1.7, although a possible role for Nav1.3 has also been suggested. Nav channels in rat CCs rapidly inactivate via two independent pathways which differ in their time course of recovery. One subpopulation recovers with time constants similar to traditional fast inactivation and the other ∼10-fold slower, but both pathways can act within a single homogenous population of channels. Here, we use Nav1.3 KO mice to probe the properties and molecular components of Nav current in CCs. We find that the absence of Nav1.3 abolishes all Nav current in about half of CCs examined, while a small, fast inactivating Nav current is still observed in the rest. To probe possible molecular components underlying slow recovery from inactivation, we used mice null for fibroblast growth factor homology factor 14 (FGF14). In these cells, the slow component of recovery from fast inactivation is completely absent in most CCs, with no change in the time constant of fast recovery. The use dependence of Nav current reduction during trains of stimuli in WT cells is completely abolished in FGF14 KO mice, directly demonstrating a role for slow recovery from inactivation in determining Nav current availability. Our results indicate that FGF14-mediated inactivation is the major determinant defining use-dependent changes in Nav availability in CCs. These results establish that Nav1.3, like other Nav isoforms, can also partner with FGF subunits, strongly regulating Nav channel function.

Introduction

Adrenal chromaffin cells (CC) express a rapidly inactivating tetrodotoxin (TTX)-sensitive voltage-gated sodium channel (Nav) current (Fenwick et al., 1982; Islas-Suárez et al., 1994; Vandael et al., 2015). Despite the rapid inactivation of CC Nav current and rapidly activated repolarizing K⁺ currents (Martinez-Espinosa et al., 2014; Lingle et al., 2018), depolarization-evoked action potential (AP) firing frequency in CCs is typically limited to ∼10–20 Hz (Solaro et al., 1995; Vandael et al., 2012; Martinez-Espinosa et al., 2014). In an associated paper (Martinez-Espinosa et al., 2021), following brief 5-ms inactivation steps, Nav current in rat CCs was shown to recover from inactivation with two separable processes, one with a fast recovery of ∼3–30 ms and the other ∼50–300 ms, each dependent on voltage. This dual fast-inactivation process is similar to that which has been termed “long-term inactivation” (Goldfarb, 2012; Barbosa and Cummins, 2016), for which the slow recovery component has been proposed to arise from inactivation involving the N termini of particular isoforms of intracellular fibroblast growth factor (FGF) homologous factors (FHFs; Dover et al., 2010). The fast inactivation process leading to slow recovery is thought to occur in a largely competitive fashion with conventional fast inactivation. The slow recovery process provides a potential mechanism by which Nav channel availability may be reduced during repetitive activity, perhaps influencing cell firing frequencies (Venkatesan et al., 2014; Navarro et al., 2020). To better understand the relationship between conventional fast inactivation and any competing fast-inactivation process, it is important that the underlying molecular entities be defined. Here, we address the question of the molecular identity of the Nav channel pore-forming subunits in rodent CCs and evaluate the role of FGF14 in the inactivation process.

The initial cloning of a neuroendocrine sodium channel, from both human and rat tissues (Klugbauer et al., 1995), demonstrated Nav1.7 (Scn9a) message in adrenal CCs. Subsequent work has supported this idea, demonstrating the presence of Nav1.7 message and protein, primarily in dissociated bovine CCs (Wada et al., 2004; Nemoto et al., 2013; Tamura et al., 2014), and has also identified pathways that can up- or downregulate Nav1.7 expression (Wada et al., 2008); however, a recent paper using quantitative reverse transcription PCR (RT-PCR) found that Nav1.3 message was more abundant than Nav1.7 in mouse CCs (Vandael et al., 2015). When both Nav1.3 and Nav1.7 currents have been found in the same cells, as in mouse pancreatic α and β cells, steady-state inactivation curves reveal two distinct Boltzmann components that are attributable to separate contributions of Nav1.7 and Nav1.3 currents, confirmed with Nav1.3 and Nav1.7 knockout (KO) mice (Zhang et al., 2014). In contrast, Nav currents in both rat and mouse CCs have steady-state inactivation properties seemingly consistent with a single Nav component (Lou et al., 2003; Vandael et al., 2015; Martinez-Espinosa et al., 2021). Heterologously expressed Nav1.3 and Nav1.7 have not been studied side by side in the same study, but comparison of Nav1.3 (Cummins et al., 2001) and Nav1.7 (Cummins et al., 1998; Herzog et al., 2003; Cummins et al., 2004) expressed in human embryonic kidney cells indicates that the steady-state inactivation curve for Nav1.7 is only slightly left shifted (voltage of half activation [V_0.5], ~ −75 mV) compared with Nav1.3 (V_0.5, approximately −65 mV). Whether a difference between Nav1.7 and Nav1.3 components would be readily resolvable is not clear. The utility of such comparisons can also be affected by which Nav β subunits may be present in native cells or employed in heterologous expression studies.

Motivated by the potential role of dual-pathway fast inactivation and the slow component of recovery from inactivation in the regulation of AP firing in rat CCs (Martinez-Espinosa et al., 2021), here we have turned to mouse CCs to begin to tease apart the molecular components of Nav current. Earlier work on mouse CCs has previously shown that Nav currents do exhibit two components of recovery from inactivation (Vandael et al., 2015), of which the slow component has been proposed to influence cell firing under certain conditions. Here, after establishing that the functional properties of Nav current in mouse and rat CCs are generally similar, we examine the impact of Nav1.3 KO on mouse CC Nav current. We find that that, although most CCs exhibit no or markedly reduced rapidly inactivating inward current, some Nav1.3 KO CCs do exhibit an inward current that is somewhat less than WT Nav current densities. Furthermore, by using FGF14 KO mice, we test whether an FGF14 isoform might be responsible for the slow component of recovery from inactivation in rodent CCs. We find that, in FGF14 KO mice, the slow component of recovery from inactivation is absent (>75% of tested cells) or markedly reduced. Given previous results establishing a role for FGF14A, but not FGF14B, in use-dependent inactivation and the kinetics of slow recovery from inactivation (Laezza et al., 2009; Dover et al., 2010), FGF14A is the most likely determinant of dual-pathway fast inactivation in mouse CCs. Overall, the results indicate that Nav1.3 and FGF14 together are the primary molecular components that underlie Nav channel inactivation behavior in mouse CCs. The results also demonstrate directly that the presence of FGF14 impacts substantially on changes in Nav channel availability during repetitive stimuli.

Materials and methods

Animals

Mice (8–12 wk old) were sacrificed by CO₂ inhalation following protocols approved by the Washington University in St. Louis Institutional Care and Use Committee. Animals were housed in accordance with the National Institutes of Health Committee on Laboratory Animal Resources guidelines. Nav1.3 KO mice (C57BL6j background) were kindly provided by Dr. Steven Waxman and D.-H. Sulayman (Yale University, New Haven, CT) with the kind permission of Dr. John Wood (University College London, London, UK) and maintained as homozygous global KO mice (Nassar et al., 2006). Control C57BL6 mice were obtained from The Jackson Laboratory. FGF14 KO mice (Wang et al., 2002) were kindly provided by Dr. Jeanne Nerbonne with permission of Dr. David Ornitz (both of Washington University School of Medicine, St. Louis, MO). The Fgf14 KO allele consists of replacement of exons 2 and 3 of Fgf14 with a β-Gal–neomycin cassette in frame with Fgf14 N-terminal exon 1 (Wang et al., 2002). Exons 2 and 3 encode the conserved core domains of FGFs that are implicated in binding to associated proteins (Olsen et al., 2003; Goetz et al., 2009). The resulting expressed protein product is thought to result in 70 N-terminal A isoform residues linked to β-Gal, with the residual Fgf14 N terminus influencing targeting of the β-Gal protein (Wang et al., 2002). Arguing that the presence of any residual FGF14–N-terminal–β-Gal protein does not affect Nav currents, shRNA-mediated knockdown of FGF14 had the same functional effects on Nav currents in adult cerebellar Purkinje neurons as observed in these FGF14 KO animals (Bosch et al., 2015), and that the WT phenotype can be rescued in KO Purkinje neurons with viral-mediated introduction of FGF14 (Bosch et al., 2015). For FGF14 KO mice in which a slow component of recovery from inactivation was noted, mice were genotyped multiple times by two individuals (one in the Lingle laboratory and one in the Nerbonne laboratory) using different sets of primers. In all cases, re-genotyping of the putative FGF14 KO mice confirmed the original genotype assignment.

Cell preparations

All experiments were done on CCs in adrenal medullary slices with slice preparation and solutions as described in the associated paper (Martinez-Espinosa et al., 2021). Given the smaller size of mouse adrenals, following removal of the surrounding adrenal cortex and embedding of the gland in agarose, typically five 200-µm-thick sections were obtained per gland. The top and bottom sections were not used to avoid any residual associated cortical cells.

Electrophysiological techniques

Whole-cell recordings from adrenal slices were done within 5 h after isolation of the adrenal gland. For recordings of Nav current, the standard open-pipette method (Hamill et al., 1981) was employed. Whole-cell voltage-clamp recordings were accomplished with a Multiclamp 700B amplifier (Molecular Devices). For measurements of excitability in Nav1.3 KO cells, the perforated patch-clamp method was used as previously described (Martinez-Espinosa et al., 2014). Command waveforms and data acquisition were done with the Clampex program from the pCLAMP 9.0 software package (Molecular Devices). Currents were evaluated without leak subtraction. The time constants of exponential relaxations in current records were fit using Clampfit algorithms. The fitting of Boltzmann functions or exponential recovery time course was done either by using Excel or with a custom program using a Levenberg-Marquardt algorithm for nonlinear least-squares fitting. Normalized GV curves were generated from G(V) = I / (V_m − V_r), with V_r = 66 mV, which assumes linearity in instantaneous current over voltages up to about +10 mV.

The typical membrane capacitance for mouse CCs included in this study was 8.95 ± 0.48 pF. Patch-clamp micropipettes were pulled from borosilicate glass (Drummond). Pipette resistances ranged from 1.5 to 2.5 MΩ. Electrodes were coated with Sylgard 184 (Dow Chemical) and fire polished. The reference electrode was an Ag/AgCl₂ pellet in direct contact with the bath.

Recording solutions

The internal saline had the following composition (in mM): 125 CsCl, 10 NaCl, 5 EGTA, 4 Mg-ATP, and 10 HEPES (pH 7.4 with CsOH). The standard extracellular solution contained (in mM) 119 NaCl, 23 NaHCO₃, 1.25 NaH₂PO₄, 5.4 KCl, 2.0 MgSO₄, 1.8 CaCl₂, 11 glucose, 2 sodium pyruvate, and 0.5 ascorbic acid (pH 7.4). Membrane capacitance and series resistance (R_s) were read from amplifier settings and R_s compensation was set to 90%. Analysis of currents has been limited to cells in which the estimated maximal voltage error resulting from residual uncompensated R_s was <10 mV (Martinez-Espinosa et al., 2021). Perfusion of external salines was performed by switching the solution flowing into the slice chamber.

RNA extraction and quantitative RT-PCR

For quantitative PCR measurements, four Sprague-Dawley rats (300–324 g, ∼70–75 d old) were ordered from Harlan Laboratories. Mice were C57/BL6 (8–12 wk old). Following sacrifice by CO₂ inhalation, adrenal glands were dissected under a microscope. The cortex was carefully removed and the adrenal medulla (AM) was quickly frozen in liquid nitrogen and then saved at −80°C. Total RNA from each pair of AMs from a single animal was isolated using the RNeasy Plus Mini Kit (Qiagen). cDNA was synthesized using the Bio-Rad iScript cDNA Synthesis Kit (cat. no. 170–8891). For the negative control groups, all components, except the reverse transcription, were included in the reaction mixtures. Real-time PCR was performed with specific primers purchased from Qiagen (Tables 1 and 2) and Power SYBR Green PCR Master Mix (cat. no. 4367659; Applied Biosystems) under reaction conditions identical to those described previously (Yang et al., 2009). PCR specificity was verified by a dissociation curve with a single peak that was run following the real-time PCR reaction. Message levels were normalized to the abundance of β-actin or glyceraldehyde 3-phosphate dehydrogenase message. The mean value was averaged from at least three separately prepared RNA samples, with each sample run in triplicate.

Table 1. Primers used for real-time PCR in rat tissues.

Rat gene	QuantiTect Primer Assay from Qiagen (cat. no.)	Amplicon length (bp)	Amplified exons
scn1a	QT02445618	134	20/21
scn2a	QT00190722	66	14/15
scn3a	QT01568126	86	3/4
scn4a	QT00184786	113	12/13
scn8a	QT00195496	67	7/8
scn9a	QT00194558	101	16/17
scn1b	QT00181559	96	3/4
scn2b	QT00193417	140	1/2
scn3b	QT00179459	118	4/5
scn4b	QT01581349	93	1/2
gapdh	QT00199633	149	1/3
actB	QT00193473	145	2/3

Table 2. Primers used for real-time PCR in mouse tissues.

Mouse gene	QuantiTect Primer Assay from Qiagen (cat. no.)	Amplicon length (bp)	Amplified exons
scn1a	QT01537991	150	8/9
scn2a1	QT01537466	122	2/3
scn3a	QT01750819	82	13/14
scn4a	QT01058414	114	11/12
scn8a	QT01044512	127	6/7/8
scn9a	QT02325337	119	14/15
gapdh	QT01658692	144	2/3
β-actin	Forward: 5′-TGG​AGA​AGA​GCT​ATG​AGC​TGC​CTG-3′	127
	Reverse: 5′-GTA​GTT​TCA​TGG​ATG​CCA​CAG​GAT-3′

Statistics

Unless otherwise indicated in a figure legend, most graphs display means ± SD for sets of measurements obtained from different cells from a given genotype. All reported n values refer to numbers of cells, although, in some cases, numbers of animals from which the cells were taken are also reported. Given that our results directly demonstrate that key aspects of the inactivation behavior under investigation involve heterogeneity among cells arising from unknown molecular components of the channels, the grouping of all cells from a single animal into an averaged measurement will artifactually lead to misinterpretation about the basic underlying phenomena. Thus, with regard to evaluating the behavior of a given type of current among cells and animals from a given genotype, a cell appears to be the appropriate experimental unit for consideration. In some cases, functions (Gaussian, exponential, or Boltzmann) were used to fit curves. In such cases, best fit parameters are reported along with the 90% confidence limit on the fitted parameter. For statistical tests, if >10 values are available for a comparison between two distributions, we employ a Kolgoromov-Smirov (KS) test, since this test makes no assumptions about normality. In other cases, we employ an ordinary ANOVA with Tukey’s corrections for multiple comparisons (GraphPad Prism 8; GraphPad Software). Exact P values are reported in the figure legends, except when P < 0.001. Readers will notice that different figures report results for recovery from inactivation at −80 mV with different numbers of WT cells. As is typical, not all protocols were tested on all cells. As such, in comparisons of voltage dependence of recovery from inactivation (see Figs. 2 and 3), we only included cells for which recovery was examined at more than one recovery voltage, resulting in a set of 16 WT cells for which recovery at −80 mV was obtained along with at least one other recovery voltage (−60, −100, or −120 mV). However, when comparing recovery between WT and FGF14 KO cells (see Figs. 6 and 7), we included all WT cells from which recovery was examined at −80 mV (a total of 33 WT cells), irrespective of whether recovery was examined at other voltages. Finally, Fig. 9 only includes cells (for WT, n = 22) for which recovery at −80 mV was measured both with the one pulse (1P) and ten pulse (10P) protocols.

Figure 2.

Nav current in mouse CCs exhibits two components of recovery from inactivation, generally similar to that in rat CCs. (A) Example paired-pulse recovery protocol with recovery at −80 mV following a 5-ms inactivation step at 0 mV. Right: Aligned P1 and P2 currents are shown. (B) Traces show the time course of recovery from inactivation at a −120-mV recovery potential for the same cell as in A. (C) Averaged time course (± SD) of recovery for mouse CCs at the indicated voltages along with best fit double exponential function given by I(t) = A_f*[1 − exp(−t / τ_f)] + A_s*[1 − exp(−t/τ_s)], where I(t) is fractional recovery, A_f and A_s are fraction fast and slow recovery, respectively, and τ_f and τ_s are time constants of fast and slow recovery, respectively. For −120 mV (n = 12 cells), A_f = 0.46 ± 0.02, τ_f = 2.17 ± 0.31 ms, A_s = 0.56 ± 0.02, τ_s = 83.3 ± 10.2 ms. For −100 mV (n = 12 cells), A_f = 0.48 ± 0.02, τ_f = 4.38 ± 0.49 ms, A_s = 0.54 ± 0.02, τ_s = 335.3 ± 43.1 ms. For −80 mV (n = 18 cells), A_f = 0.45 ± 0.01, τ_f = 9.38 ± 0.75 ms, A_s = 0.56 ± 0.02, τ_s = 660.5 ± 70.4 ms. For −60 mV (n = 8 cells), A_f = 0.29 ± 0.01, τ_f = 32.4 ± 2.7 ms, A_s = 0.49 ± 0.02, τ_s = 1,336.4 ± 176.0 ms. (D) Fits of recovery from inactivation in rat CCs from our associated paper (Martinez-Espinosa et al., 2021).

Figure 3.

Comparison of two-component recovery from inactivation in mouse and rat. (A) The time course of recovery from inactivation at −80 mV for 16 WT mouse CCs is shown, along with the averaged recovery time course (red line, from Fig. 2 C). (B) Recovery from inactivation at −120 mV for 12 WT CCs, along with averaged recovery (red line). (C) The A_f at −80 mV or −120 mV is plotted for both individual mouse (black) and rat (red) CCs. Dotted lines indicate values obtained in individual cells where both −80-mV and −120-mV recoveries were obtained. Statistical comparisons of distributions of fast recovery amplitude at −80 or −120 mV for both mouse and rat revealed no differences. (D) Mean values (± SEM) for fast (τ_f) and slow (τ_s) recovery time constants are plotted as a function of recovery potential for both mouse and rat CCs. Lines are derived from exponential fits but are only intended to highlight trends in the data. (E and F) Comparison of τ_f at −80 mV and −120 mV between mouse and rat CCs (E), with small symbols corresponding to values from individual cells (F) τ_s at −80 mV and −120 mV for mouse and rat CCs. Using ANOVA with a Bonferroni correction for multiple comparisons yielded P < 0.0001 for comparison of mouse and rat slow time constants at −80 mV, but all other comparisons (fast time constants, fraction fast amplitude, and slow time constants at −120 mV) were P > 0.85.

Figure 6.

FGF14 KO abolishes all or most slow recovery from inactivation, with little effect on fast recovery. (A) Standard paired-pulse recovery at −80 mV for a WT CC. (B) Paired-pulse recovery −80 mV for a CC from an FGF14 KO mouse. (C) Paired-pulse recovery at −120 mV for the cell shown in A. (D) Paired-pulse recovery at −120 mV for the FGF14 KO cell in B. (E) Time course of recovery from inactivation at −60 mV mV (means ± SD) for WT and FGF14 KO CCs (n indicates numbers of cells in all panels). Double exponential fit to WT recoveries was: A_f = 0.29 ± 0.01, τ_f = 32.4 ± 2.7 ms, A_s = 0.49 ± 0.02, τ_s = 1336.4 ± 176.0 ms. Single exponential fit to FGF14 KO recoveries: A_f = 0.48 ± 0.005 (normalized to full recovery at −80 mV), τ_f = 26.19 ± 1.07 ms. (F) Recoveries at −80 mV. This includes cells in addition to those in Fig. 2. For WT, A_f = 0.47 ± 0.01, τ_f = 6.95 ± 0.59 ms, A_s = 0.53 ± 0.02, τ_s = 584 ± 66.3 ms. For FGF14 KO and single exponential fit (blue line), A_f = 0.92 ± 0.01, τ_f = 8.40 ± 0.57 ms. For FGF14 KO and two exponential fit (red), A_f = 0.90 ± 0.01, τ_f = 7.92 ± 0.46 ms, A_s = 0.10 ± 0.05, τ_s = 1,129.4 ± 1,761.3 ms. (G) At −100 mV, for WT, A_f = 0.48 ± 0.02, τ_f = 4.38 ± 0.49 ms, A_s = 0.54 ± 0.02, τ_s = 335.3 ± 43.1 ms. For FGF14 KO, single exponential: A_f = 1.02 ± 0.01, τ_f = 3.83 ± 0.32 ms; for double exponential, A_f = 0.98 ± 0.02, τ_f = 3.55 ± 0.30 ms, A_s = 0.09 ±0.04, τ_s = 423.4 ± 650.3 ms. (H) At −120 mV, for WT, A_f = 0.46 ± 0.02. τ_f = 2.17 ± 0.31 ms, A_s = 0.56 ± 0.02, τ_s = 83.3 ± 10.2 ms. For FGF14 KO, single exponential, A_f = 0.99 ± 0.02, τ_f = 2.00 ± 0.28 ms; for double exponential, A_f = 0.89 ± 0.03, τ_f = 1.69 ± 0.16 ms, A_s = 0.17 ± 0.03, τ_s = 115.9 ± 62.2 ms. (I) Mean (+SD) time constants for slow (τ_s) and fast (τ_f) recovery time constants from WT CCs and single exponential recovery time constants for FGF14 KO cells are plotted as a function of recovery voltage.

Figure 7.

Variability in recovery from inactivation in WT and FGF14 KO cells: Some FGF14 KO CCs exhibit a residual component of slow recovery from inactivation. (A) Individual fractional recoveries for 16 WT CCs are shown based on the standard paired-pulse recovery at −80 mV. Red line shows best fit to averaged recoveries from WT cells. (B) The averaged recovery from the 33 cells (from 14 animals) in A, also shown in Fig. 6 F. Best fit of a double exponential: A_f = 0.47 ± 0.01, τ_f = 7.0 ± 0.6 ms, A_s = 0.53 ± 0.02, τ_s = 584.6 ± 66.3 ms. (C) Paired-pulse recoveries for 33 total CCs from FGF14 KO mice (recovery at −80 mV). Time courses plotted in black were best fit with a single exponential recovery, while those in blue required two exponential components. Red is the best fit to averages of all cells. (D) For FGF14 KO recoveries, recovery curves are plotted for all cells together (red, identical to FGF14 KO in Fig. 6 F), cells fit with only a single exponential time course (green), and cells for which the recovery curve required two exponentials. For grouping of all cells (33 cells from 12 animals) as in Fig. 6 F, A_f = 0.90 ± 0.01, τ_f = 7.9 ± 0.5 ms, A_s = 0.10 ± 0.05, τ_s = 1,129.4 ± 1,761.3 ms. For FGF14 KO cells in which only a single exponential was required, A_f = 0.97 ± 0.01, τ_f = 7.2 ± 0.4 ms. For FGF14 KO cells in which recovery required two exponentials, A_f = 0.76 ± 0.01, τ_f = 8.6 ± 0.5 ms, A_s = 0.24 ± 0.06, τ_s = 1,450.0 ± 956.6 ms. (E) Fractions of the fast recovery component for WT (gray) and FGF14 KO (red) were placed in 0.05-wide bins. Fast amplitude values for WT and FGF14 KO were compared by using a KS test because of the nonnormal distributions, yielding P = 0.000. (F) Mean ± SD and individual fast time constants are shown for WT and FGF14 KO CCs with adjusted P > 0.9999 (ANOVA with Bonferroni multiple comparisons test). (G) Mean ± SD and individual slow time constants; for WT versus FGF14 KO, P < 0.0001.

Figure 9.

Examination of slow recovery from inactivation in a fraction of FGF14 KO cells. (A and B) Recovery from inactivation in WT (A) and FGF14 KO (B) cells was compared for recovery at −80 mV from a standard single step (1P) to 0 mV, and then for recovery following a 10-Hz train of 10 steps to 0 mV (10P). (A) For 22 WT cells, recovery following a 10-Hz train results in a use-dependent decrease in the fast recovery component. For 1P, A_f = 0.47, τ_f = 6.03 ms, A_s = 0.53, τ_s = 549.4 ms. For 10P, A_f = 0.20, τ_f = 7.35 ms, A_s = 0.77, τ_s = 589.5 ms. (B) For averages of 19 FGF14 KO cells compared with 1P and 10P protocols, the 1P protocol primarily results in exclusively a fast recovery component, but some reduction in the fast component can occur in the 10P protocol (see Fig. S2). Note the large standard error associated with the 10P recoveries. For the 1P protocol, a single-exponential fit yielded: A_f = 0.95 ± 0.01, τ_f = 7.5 ± 0.9 ms; while, for a two-exponential fit, A_f = 0.94 ± 0.02, τ_f = 6.9 ± 0.5 ms, A_s = 0.05 ± 0.07, τ_s = 1,090.1 ±3,892.3 ms. For the 10P protocol, the two-exponential fit yielded A_f = 0.79 ± 0.01, τ_f = 7.4 ± 0.5 ms, A_s = 0.20 ± 0.1, τ_s = 1,664.0 ± 1,807.2 ms. Note the large confidence limits reflecting the parameters describing the slow component, given that the data do not strongly define this component. (C) Recoveries following the 10P protocol for 22 individual WT cells are plotted with the three cells with the largest fast recovery component highlighted in green. (D) Recovery following the 10P protocol is plotted for 19 FGF14 KO cells, with the 3 cells showing the most markedly reduced fast recovery highlighted in red. (E) Peak current diminution for the 22 WT cells during the 10P protocol are plotted. Green highlights cells in C with a larger component of fast recovery. (F) Peak current diminution during the 10-Hz train is plotted for the 19 FGF14 KO cells. For cells with exclusively fast recovery from inactivation (blue), there is little peak current diminution at 10 Hz. (G) The fraction of residual fast component (A_f) following the 10P protocol is plotted as a function of the peak Nav current diminution during the 10P train for WT (blue; green) and FGF14 (red) cells.

Online supplemental material

Fig. S1 shows the isolation of sodium current in Nav1.3 KO cells. Fig. S2 illustrates that Nav1.3 KO cells exhibit either of two forms of spontaneous electrical activity. Fig. S3 displays examples of two-component recovery from inactivation following 1P and 10P test stimuli for WT cells. Fig. S4 shows examples of recovery from inactivation following 1P and 10P test stimuli for FGF14 KO cells.

Figure S1.

Isolation of I_Na in Nav1.3 KO cells. (A) Noninactivating inward current (as shown in C) from seven Nav1.3 KO cells with no detectable fast inactivating inward current were used to provide an empirical description of macroscopic Ca²⁺ current. The rising phase of inward current was fit with a single exponential current to define maximal inward Cav current and the time constant of inactivation at membrane potentials from −40 through +20 mV. A plot of peak current density (mean ± SD) shows peak inward current from −10 to 0 mV. (B) Voltage dependence of average time constants (±SD) of Cav activation for seven cells. The averaged time constants were then used in conjunction with the empirically measured steady-state current to generate idealized Cav current for subtraction from individual cells as in C–E. (C) For a cell lacking observable fast inactivating inward current, panels show (left) raw current traces activated by steps from −40 through +20 mV, (center) fits of single exponential functions to the currents on the left, and (right) subtracted of best fits to the raw data reflecting removal of the Cav component from the traces. (D) For a cell with a modest fast inactivating inward current on the rising phase of Cav current, panels are as in C. Idealized Cav traces (center) generated based on measured activation time constants (B) were subtracted from raw current traces (left) to generate empirically isolated Nav currents lacking any contaminating Cav current. Red trace corresponds to voltage step to −10 mV, and blue trace to +10 mV. (E) For an Nav1.3 KO cell with one of the larger peak Nav currents, the same subtraction method was employed. Subtraction of the idealized Cav currents (center traces) from the measured currents (left traces) yielded isolated fast inactivated current without Cav contamination. (F) From traces with Cav currents removed (right panels in C–E), I-V curves were generated for voltages from −40 to +20 mV. Peak current was determined for each cell and current density (pA/pF) determined. Plot shows binned current densities. Cells with 0 Nav current were included in the bin corresponding to 0–25 pA/pF; bin width, 25 pA/pF. (G) Binned (100 pA/pF) current densities were normalized to generate separate probability density distributions for WT (gray) and Nav1.3 KO (red) cells, highlighting the lack of overlap between the two.

Figure S2.

Nav1.3 KO cells exhibit either of two forms of spontaneous electrical activity. (A) Spontaneous firing is illustrated for a WT CC recording by using the perforated patch method. Right trace shows faster time base examples of individual APs. (B) From the cell in A, the indicated voltage protocol was used to activate BK current, highlighting the inactivating nature of the current following a 50-ms depolarization to 0 mV to elevated cytosolic Ca²⁺ (Solaro et al., 1995). On the right, a faster time base example of the transient inward current immediately following depolarization to 0 mV is shown. (C) Spontaneous firing in an Nav1.3 KO cell at two different time bases. Peak AP amplitude is markedly reduced compared with WT cells, which is consistent with the role of voltage-dependent Cav channels in APs during blockade of Nav current (Vandael et al., 2015). (D) For the Nav1.3 KO cell in C, the Ca-loading protocol resulting in the activation of inactivating BK current, but no indication of any fast inactivating inward current (right trace). (E) Spontaneous slow wave burst firing in another Nav1.3 KO cell. (F) The Ca-loading protocol for the cell in E results in the activation of noninactivating BK current. Little or no inward current was observed during the initial step to 0 mV. The tendency of cells lacking inactivating BK channels to exhibit spontaneous slow wave bursts has been previously noted (Martinez-Espinosa et al., 2014).

Figure S3.

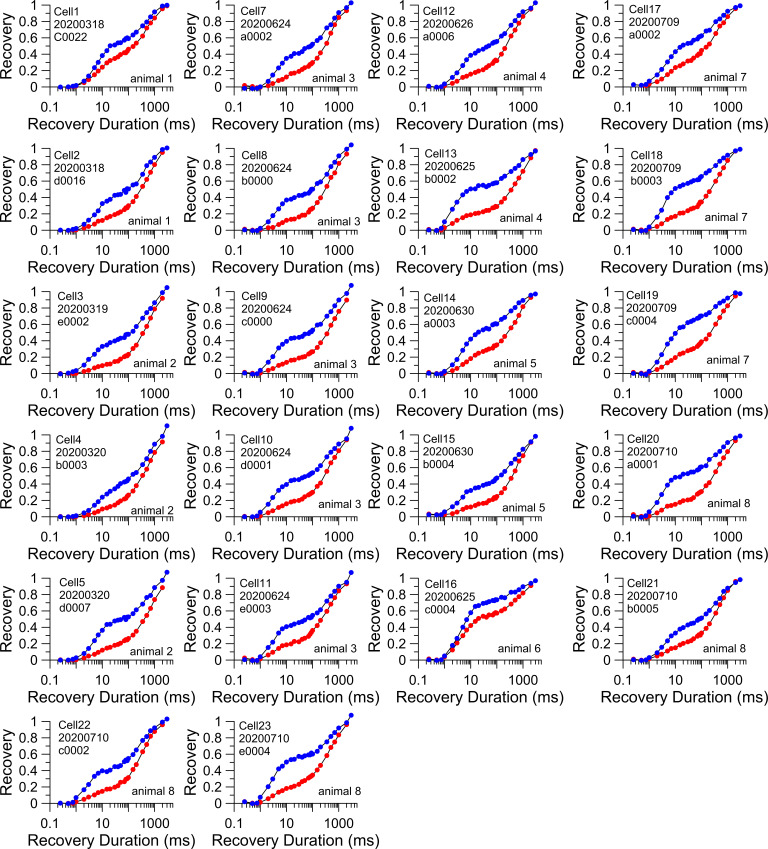
Examples of two-component recovery from inactivation following 1P and 10P test stimuli for WT cells. Each panel shows recovery from inactivation following a single 10-ms step to 0 mV (blue), and then following a 10-Hz train of 10 pulses to 0 mV (red). A total of 22 WT cells from 8 different animals were compared with the 1P and 10P protocols.

Figure S4.

Examples of recovery from inactivation following 1P and 10P test stimuli for FGF14 KO cells. Each panel shows recovery from inactivation following a single 10-ms step to 0 mV (blue), and then following a 10-Hz train of 10 pulses to 0 mV (red). A total of 24 FGF14 KO cells from 7 different animals were compared with the 1P and 10P protocols. Three cells in column 2 exhibited clear two-component recovery from inactivation following both 1P and 10P protocols. For these three cells, despite a smaller slow component of recovery following the 1P protocol, the 10P protocol resulted in a fraction of slow recovery comparable to or even larger than that observed in WT cells (Fig. S3).

Results

Properties of Nav currents in mouse CCs recorded in adrenal medullary slices

Fig. 1 A shows Nav current activated in a CC from a mouse adrenal medullary slice, with a 5-ms activation step over voltages from −70 to +50 mV, following a 1,000-ms conditioning step to −120 mV to remove any channel inactivation. Average peak Nav current density for mouse cells (n = 18) was compared with similar results for rat cells (Fig. 1 B), with average Nav current density in mouse CCs ∼70% of that in rat CCs. Normalized current amplitude (Fig. 1 C) shows that both mouse and rat Nav currents activate over a similar range of voltages, although the mouse currents are somewhat right shifted compared with rat cells. Conversion of the I-V relationship to G-V curves, assuming a +66-mV reversal potential, resulted in G-V curves that were similar, but not identical (Fig. 1 D). For mouse, the voltage of half-activation (V_0.5) of apparent conductance was −22.3 ± 0.3 mV with effective valence, z, = 5.3 ± 0.3e and, in rat, V_0.5 = −27.4 + 0.2 mV with z = 5.4 ± 0.2e (Table 3 for basic Nav properties between rat and mouse CCs). Although such G-V curves based on peak currents distort the true G-V properties of the current because of the effects of inactivation on the peak current, this apparent mouse G-V is shifted about +5 mV relative to rat (KS test P = 0.004). The rate of the onset of inactivation, measured from single exponential fits to the current decay phase, was similar to that in rat (Fig. 1 E). Comparison of the steady-state inactivation curves that were generated with 25-, 100-, 250-, and 1,000-ms conditioning durations over voltages from −100 through 0 mV (Fig. 1 F) exhibited a leftward shift with conditioning pulse duration qualitatively similar to that observed in rat CCs (Fig. 1 G; Martinez-Espinosa et al., 2021). However, over conditioning durations of 100–1,000 ms, the mouse fractional availability curve was shifted compared with rat cells about −5 to −9 mV (Fig. 1, G–H). With a 1,000-ms conditioning duration, for mouse, V_0.5 = −48.9 ± 1.0 mV, while, for rat, V_0.5 = −57.7 ± 0.6 mV. Some of this presumably reflects the shifted activation range of mouse Nav currents. Similar to rat cells, there was little indication that a double Boltzman function would better describe the steady-state inactivation behavior, except for a small indication of a more negative component with the 25-ms conditioning step. Peak current elicited from a conditioning potential of −80 mV versus that from −120 mV differed by <5% in both rat and mouse. This differs markedly from the behavior of mouse pancreatic β and α cells, which unambiguously express both Nav1.3 and Nav1.7 currents (Zhang et al., 2014).

Figure 1.

Basic properties of Nav current in mouse CCs are similar to those in rat CCs. (A) Example currents illustrating basic voltage-dependent activation in a mouse CC in a slice. (B) Plot of Nav current density (mean ± SD) from 18 mouse CCs. Red line corresponds to current density from rat CCs. (C) Points show normalized peak current amplitude for mouse CCs compared with rat CCs (red line). (D) Mouse (and rat) peak currents were converted to conductances assuming a reversal potential of +66 mV. For the G-V from mouse CCs, V_0.5 = −22.3 ± 0.3 mV with z = 5.3 ± 0.3e, while, for rat, V_0.5 = −27.4 ± 0.2 mV with z = 5.4 ± 0.2e. (E) Inactivation time constants (mean ± SD) as a function of command potential are plotted for 18 mouse CCs and compared with values from rat (red line). (F) Steady-state inactivation curves following 25-, 100-, 250-, and 1,000-ms conditioning steps at voltages from −110 to 0 mV for mouse. For 25 ms, V_0.5 = −35.5 ± 0.3 mV, z = 4.8 ± 0.3e; for 100 ms, V_0.5 = −42.6 ± 0.3 mV, z = 4.7 ± 0.2e; for 250 ms, V_0.5 = −46.7 ± 0.2 mV, 5.0 ± 0.2e; and for 1,000 ms, V_0.5 = −49.2 ± 0.3 mV, z = 4.8 ± 0.2e. (G) Comparison of mouse and rat (red) steady-state inactivation curves following 25-ms and 1,000-ms conditioning steps. At 25 ms for rat cells, V_0.5 = −37.8 ± 1.3 mV and, at 1,000 ms, V_0.5 = −57.7 ± 0.6 mV. (H) Comparison of V_0.5 of fractional availability following conditioning steps of differing durations for mouse and rat (red).

Table 3. Comparison of mouse and rat Nav channel properties.

Parameter	Mouse WTa	Mouse FGF14 KOa	Mouse Nav1.3 KOa	Mouse WTb	Ratc
G-V (V0.5) mV	−22.3 ± 0.3	−17.2 ± 1.9	−16.8 ± 2.7	−21.9	−27.4 ± 0.2
SS inact (V0.5) mV; 25 ms	−35.5 ± 1.1	−47.2 ± 2.1	n.d.	n.d.	−39.2 ± 0.4
SS inact (V0.5) mV; 1 s	−48.9 ± 1.0	−58.0 ± 1.4	−49.9 ± 3.3	−47.9 mV	−57.7 ± 0.2
Recovery voltage	−100 mV	−100 mV		−90 mV	−100 mV
τrec1 (ms; A1)	4.4 ± 0.5 (0.48)	3.8 ± 0.3 (1.0)	n.d.	4.8 (0.6)	6.4 ± 0.6 (0.5)
τrec2 (ms; A2)	335.3 ± 43.1 (0.54)	——	n.d.	156 (0.4)	162.9 ± 1.8 (0.53)
Recovery voltage	−60 mV	−60 mV		−50 mV	−60 mV
τrec1 (ms; A1)	32.4 ± 2.7 (0.29)	26.2 ± 1.1 (0.5)	n.d.	23.7 (0.34)	55.9 ± 1.1 (0.21)
τrec2 (ms; A2)	1,136.4 ± 176 (0.49)	——	n.d.	229 (0.22)	487.8 ± 7.6 (0.34)

Data are fitted parameter ± 90% confidence limit. n.d., not determined.

^aThis paper.

^bVandael et al. (2015; perforated patch).

^cMartinez-Espinosa et al., 2021

Comparison of fast and slower recovery from inactivation in rat and mouse CCs

The distinguishing feature of Nav current in rat CCs is a dual-pathway fast-inactivation process that leads to two distinct components of recovery from inactivation (Martinez-Espinosa et al., 2021). By using a standard paired pulse recovery protocol, Fig. 2 illustrates the time course of recovery from inactivation in a mouse CC for recovery at −80 (Fig. 2 A) and −120 mV (Fig. 2 B). The time course of recovery was well described by a double exponential recovery process (Fig. 2 C) at all recovery potentials comparable to that in rat CCs (Fig. 2 D), albeit with some differences in absolute time constants.

Variation in the time course of recovery from inactivation at −80 mV (Fig. 3 A) and −120 mV (Fig. 3 B) was compared among individual cells. The average fraction of the fast recovery component (A_f, with A_s representing fraction slow recovery) was near 0.5 at either −80 mV or −120 mV (Fig. 3 C). For individual cells, the amplitudes of fast recovery measured either at −80 or −120 mV were similar (dotted lines in Fig. 3 C). Overall, the fractional amplitude of the fast recovery component (Fig. 3 C) and mean time constants (Fig. 3, D–F) were similar between species, although slow recovery from inactivation at −80 mV is slower in mouse than in rat (P < 0.0001; Fig. 3 E). Overall, the key features of the two-component recovery are generally comparable between mouse and rat, suggesting they may have similar molecular underpinnings.

Evaluation of message for Nav subunits in mouse and rat AM

Earlier work on mouse AMs revealed a fivefold higher level of message for Nav1.3 (Scn3a) than Nav1.7 (Scn9a), and also reported the presence of bands on Western blots, perhaps corresponding to both Nav1.3 and Nav1.7 (Vandael et al., 2015). Here, we also tested for the presence of message in isolated mouse (Fig. 4 A) and rat (Fig. 4 B) AMs for known TTX-sensitive Nav variants, including Nav1.1 (Scn1a), Nav1.2 (Scn2a), Nav1.3 (Scn3a), Nav1.4 (Scn4a), Nav1.6 (Scn8a), and Nav1.7 (Scn9a). In mouse AMs, Nav1.3 message was predominant (Fig. 4 A), while Nav1.7 message was not clearly greater than other weakly expressed forms (Scn1a, Scn2a, Scn4a, and Scn8a). The levels observed here in mouse are similar to that observed previously (Vandael et al., 2015), with Nav1.3 message being 5–10-fold higher than Nav1.7 message. In rat, Nav1.3 (Scn3a) and Nav1.7 (Scn9a) were the most abundant of the TTX-sensitive Nav variants (Fig. 4 B), with Nav1.7 message levels exceeding that of Nav1.3.

Figure 4.

Nav1.3 (SCN3A) is the major contributor to inward Na⁺ current in mouse CCs. (A) Each point represents quantitative RT-PCR reactions run in triplicate for a single AM for the indicated Nav channel subunits from mouse AM, with message levels normalized to β-actin. (B) Similar reactions were run on rat AM. In both A and B, at least three AMs were examined for each message species. In A, P values (from ANOVA with Tukey’s post hoc test) <0.05 were: <0.0001 for Scn2a versus Scn3a, Scn3a versus Scn4a, Scn3a versus Scn8a, Scn3a versus Scn9a; and 0.0104 for Scn4a versus Scn9a. In B, adjusted P values <0.05 were: <0.0001 for Scn1a versus Scn9a; 0.0002 for Scn2a versus Scn9a; 0.0181 for Scn3a versus Scn9a; and 0.0003 for Scn8a versus Scn9a. (C) Example Nav current activation from a WT mouse CC. (D) Example current from a CC from an Nav1.3 KO mouse (typical of 26 Nav1.3 KO CCs) with clear Cav currents and no detectable Nav current. (E) Example current from an Nav1.3 KO CC with a mix of Nav current and Cav current (31 of 57 CCs exhibited at least some rapidly inactivating inward current). Traces in C–E were not leak subtracted. (F) Average peak inward current density (± SD) from 18 WT CCs, 26 Nav1.3 KO cells lacking Nav current (blue), and subtracted Nav current (Fig. S1) from 31 Nav1.3 KO cells. (G) Comparison of Nav current density for WT, Nav1.3 KO cells with detectable Nav current, and then all Nav1.3 KO (n = 57) cells. (H) Comparison of G-V curves for WT and Nav1.3 KO cells (16 cells with >750 pA peak Nav current). Fit parameters: for WT, V_0.5 = 22.3 mV, k = 5.3e; for Nav1.3 KO, V_0.5 = −17.2 mV, k = 4.9e. From averages of fits to individual cells, for WT, V_0.5 = −21.9 ± 2.9 mV, k = 5.8 ± 1.8e; for Nav1.3 KO, V_0.5 = −16.8 ± 2.7 mV, k = 4.8 ± 0.7e. V_0.5 and k values differ at P = 0.000 based on KS test. (I) Comparison of steady-state inactivation measured from 18 WT cells and 9 Nav1.3 KO cells with Nav currents. Note that the conditioning step duration was 500 ms for Nav1.3 KO cells and 1 s for WT cells. Fits to averaged data yielded, for WT, V_0.5 = −49.2 mV, with k = 4.8e, while for Nav1.3 KO cells, V_0.5 = −50.0 mV, with k = 5.0e. Averages of fits to individual cells yielded, for WT, V_0.5 = −48.9 ± 4.0 mV with k = 5.4 ± 0.7e, while for Nav1.3 cells, V_0.5 = −49.9 ± 3.3 mV, with k = 5.3 ± 0.7e. t test P values showed no differences for either V_0.5 values, P = 0.510, or k values, P = 0.771.

KO of Nav1.3 abolishes most Nav current in mouse CCs

To directly evaluate the molecular underpinnings of mouse CC Nav current, we took advantage of Nav1.3 KO mice (Nassar et al., 2006). Fig. 4 (C–E) compares whole-cell current recordings for a WT CC and two different categories of CC from Nav1.3 KO mice. For 26 of 57 CCs examined from Nav1.3 KO mice, a small, voltage-dependent inward current with little or no observable inactivation was seen (Fig. 4 D). This presumably reflects the Cav current expected in rodent CCs with 1.8 mM extracellular Ca²⁺ (Prakriya and Lingle, 1999; Marcantoni et al., 2007; Marcantoni et al., 2008). In 31 of 57 CCs, a component of rapidly inactivating inward current (Fig. 4 E and Fig. S1) could still be detected in CCs from the Nav1.3 KO mice, although in many cells the inactivating inward current was only barely detectable on the rising phase of the noninactivating Cav current (Fig. S1 D). To provide estimates of Nav current activation on the background of Cav current activation, we fit the Cav current activation time course in a set of seven CCs with no Nav current (Fig. S1, A–E). Idealized Cav current activation for each cell was then defined based on average activation time constants (Fig. S1 B) and the noninactivating inward current level associated with a given depolarization. Following the subtraction of the idealized Cav current from the raw current traces (Fig. S1, C–E), this provided a description of the rapidly inactivating component of inward current with the Cav component removed. Based on this procedure, the current density of Nav current in Nav1.3 KO cells was defined (Fig. 4, E and F). Considering only the Nav1.3 KO cells, which exhibited at least some detectable Nav current, the average peak current density was 98.4 ± 64.7 pA/pF compared with 725.0 ± 185.5 pA/pF in WT cells. If the 26 Nav1.3 KO cells exhibiting no detectable Nav current were included, overall average peak Nav current density in Nav1.3 KO cells was 53.5 ± 68.5 pA/pF. Even in Nav1.3 KO cells with the largest peak Nav current, the peak current density was still less than half that of any WT CC. To examine whether Nav current densities might group into separate categories, we binned the individual current densities, with cells lacking Nav current included in the 0–25 pA/pF bin (Fig. S1 F). The distribution only suggests a continuum of Nav expression with no clearly defined peak associated with those cells expressing Nav current. To highlight the differences between WT and Nav1.3 KO CCs, we also generated a probability distribution for WT and Nav1.3 KO current densities (Fig. S1 G), which highlights the absence of overlap in Nav current levels between the two genotypes.

We next tested whether the Nav current present in Nav1.3 KO cells might be functionally distinct from that in WT cells. By using a set of 16 Nav1.3 KO cells with the most robust Nav current, we generated G-V curves (Fig. 4 H) that suggested a slightly right-shifted V_0.5 (−16.8 ± 2.7 mV) compared with WT (−21.9 ± 2.9 mV). Importantly, steady-state inactivation curves (Fig. 4 I) for a set of nine Nav1.3 KO cells yielded a V_0.5 of −49.9 ± 3.3 mV (k = 5.3 ± 0.7e) compared with −48.9 + 4.0 mV (k = 5.4 ± 0.7e) for WT. Although our results do not allow for any conclusions regarding the likely molecular underpinnings for the non-Nav1.3 component of current, given the work cited above supporting the presence of Nav1.7 in AM of rat and cow, Nav1.7 seems to be the most likely candidate. Yet, that this non-Nav1.3 component has activation properties and, in particular, steady-state inactivation properties similar to Nav1.3 seems surprising given the distinction between the apparent Nav1.3 and Nav1.7 components of current in mouse pancreatic α and β cells (Zhang et al., 2014).

Although not the focus of this work, in 10 Nav1.3 KO CCs, we used perforated patch-clamp recordings to examine AP firing properties in such cells. In WT mouse CCs, two main kinds of behavior are observed, quiescent cells and cells that fire spontaneous APs at a frequency of ∼1 Hz (Marcantoni et al., 2010; Martinez-Espinosa et al., 2014). Certain conditions, such as a reduction of Nav current with TTX or slow depolarization, can elicit slow wave bursting (Vandael et al., 2015; Guarina et al., 2017), which also is more likely to be observed following KO of the β2 subunit of the Ca²⁺- and voltage-activated, large conductance K⁺ (BK) channel (Martinez-Espinosa et al., 2014). Fig. S2 A illustrates spontaneous firing in a WT mouse CC, exhibiting APs that strongly overshoot 0 mV. For this cell, a voltage protocol was employed to compare outward current with either a direct step to +100 mV or following a 50-ms step to 0 mV to produce robust Ca influx (Fig. S2 B). Following the Ca-loading step, an inactivating form of BK current is revealed, which is absent following the direct step to +100 mV (Solaro et al., 1995). Examination of the current trace immediately following depolarization to 0 mV reveals a rapidly inactivating inward current, consistent with the presence of a robust Nav current. Fig. S2, C and E, displays two different types of firing behavior observed among different Nav1.3 KO cells. In Fig. S2 C, the cell exhibits spontaneous APs, but with markedly more negative peak AP amplitude, consistent with depolarization-activated, low-voltage Ca²⁺ spikes. For this cell, the BK current (Fig. S2 D) was also inactivating, and no inward current was observed. In total, we recorded from five Nav1.3 KO cells with inactivating BK current. One showed spontaneous firing and four were quiescent. Fig. S2 E illustrates an Nav1.3 KO CC that exhibited spontaneous slow wave bursting. This occurred in a cell with noninactivating BK current (Fig. S2 F), and no inward current was noted during depolarization to 0 mV. For five Nav1.3 KO CCs which exhibit noninactivating BK current, three fired only with slow wave bursts, one was quiescent, and one fired spontaneous single APs. The resting potential for this set of 10 Nav1.3 KO cells was −44.7 + 1.9 mV, which was indistinguishable from earlier reports for WT cells (Martinez-Espinosa et al., 2014). For WT cells, peak AP amplitudes were previously measured as 29.9 ± 6.3 mV and 28.1 + 7.8 mV for CCs with inactivating and noninactivating BK currents, respectively (Martinez-Espinosa et al., 2014). For the Nav1.3 KO cells that exhibited some form of spontaneous firing, peak AP amplitude was −18.6 ± 6.1 mV (n = 5).

These results generally confirm earlier observations showing that, during inhibition of Nav current, mouse CCs can still exhibit spontaneous firing, that reduction of Nav current can favor repetitive slow wave burst firing (Vandael et al., 2015; Guarina et al., 2017), and that removal of BK inactivation also favors burst firing (Martinez-Espinosa et al., 2014).

FGF14 underlies the slow component of recovery from inactivation in mouse CCs

In neurons, long-term Nav inactivation (Dover et al., 2010; Venkatesan et al., 2014) has been shown to be mediated by intracellular FHFs (or FGFs; Smallwood et al., 1996; Munoz-Sanjuan et al., 2000). This FGF peptide family consists of four members (FGF11–14, also known as FHF3, FHF1, FHF2, or FHF4, respectively) with splice variation at the N terminus. These share a core segment with strong homology to secreted FGFs (Smallwood et al., 1996; Munoz-Sanjuan et al., 2000), but, in general, appear to not be secreted (but see Sochacka et al., 2020), instead interacting with Nav channels and potentially other cytosolic proteins (Pablo and Pitt, 2016). Structural information indicates that FGFs interact with Nav α subunits in a simple 1:1 stoichiometry, with the conserved core portion of FGFs binding to an interface on the Nav cytosolic C-terminal domain (Goetz et al., 2009; Wang et al., 2012).

As an initial test of whether an FGF variant might underlie dual pathway inactivation in CCs, we were fortunate to have access to FGF14 KO mice (kindly provided by Dr. Jeanne Nerbonne). Nav current in CCs from FGF14 KO mice was generally similar to that from WT CCs (Fig. 5 A versus Fig. 5 B), with comparable current densities (Fig. 5 C). The G-V for Nav current activation in FGF14KO cells was shifted by about +5 mV (Fig. 5 D). The time course of the onset of inactivation at voltages from −20 mV to +40 mV (Fig. 5, E and F) was faster for FGF14 KO CCs (at 0 mV, τ_i = 0.38 ± 0.02 ms) than WT cells (at 0 mV, τ_i = 0.50 ± 0.03 ms). The steady-state inactivation curve for mouse Nav current in the absence of FGF14 was shifted leftward about −10 mV (Fig. 5, G and H). This shift is qualitatively similar to the approximately −13-mV shift observed for granule cell Nav current following double KO of FGF12 and FGF14 (Goldfarb et al., 2007). As a corollary, heterologous expression of FGF14A produces an ∼10-mV positive shift in inactivation V_0.5 when coexpressed with Nav1.6 (Laezza et al., 2009).

Figure 5.

Nav currents in CCs from FGF14 KO animals. (A) Currents from a WT mouse CC activated with the indicated protocol with colored traces as indicated. (B) Currents from an FGF14 KO CC. (C) Voltage dependence of current density for CCs from FGF14 KO mice (red points; 10 cells) and those from WT mice (18 cells). Mean ± SD. (D) Normalized G-V curves (see Materials and methods) for WT (from Fig. 1 D) and FGF14 KO cells. For WT, V_0.5 = −22.3 ± 0.3 mV with z = 5.3 ± 0.3e and, for FGF14 KO, V_0.5 = −17.2 ± 1.9 mV with z = 4.5 ± 0.1e. (E) Traces of Nav current activated at 0 mV from WT (black) and FGF14 KO (red) cells were averaged and fit with single exponential functions, with faster onset of inactivation in FGF14 KO cells. (F) Mean values (± SD) for onset of inactivation for WT and FGF14 KO cells are plotted as a function of command potential. P values adjusted for multiple comparisons (ANOVA with Bonferroni correction) for comparison of WT and FGF14 KO inactivation time constants over the range of 0 to +40 mV were all P < 0.01. (G) Steady-state inactivation curves (mean ± SD) following either a 1-s or 25-ms conditioning step are compared for CCs from WT and FGF14 KO mice. With a 1-s conditioning step, for WT, V_0.5 = −48.9 ± 1.0 mV; for FGF14 KO, V_0.5 = −57.3 ± 0.3 mV, while for a 25-ms conditioning step, for WT, V_0.5 = −35.6 ± 1.1 mV and, for FGF14 KO, V_0.5 = −47.2 ± 2.1 mV. (H) Measured voltage of half availability (mean ± SD of individual cells) following 25-, 100-, 250-, and 1,000-ms conditioning potentials are plotted for cells from WT (15 cells) and FGF14 KO (14 cells). For comparisons between WT and KO at each conditioning duration, P < 0.0001 (ANOVA with Bonferroni correction for multiple comparisons).

We next examined recovery from inactivation, first comparing recovery at −80 mV in WT (Fig. 6 A) and FGF14 KO (Fig. 6 B) CCs. In the FGF14 KO cell, Nav current is about half recovered within 10 ms, while in WT cells, half recovery only occurs after ∼100 ms. Similarly, at a recovery potential of −120 mV, WT cells (Fig. 6 C) recover much more slowly than FGF14 KO cells, with recovery almost complete within 10 ms in FGF14 KO cells and only about half complete in 10 ms in WT cells. The averaged time course of recovery for CCs from FGF14 KO mice was plotted at voltages from −60 through −120 (Fig. 6, E–H) and compared with those from WT mice. The recovery time course for cells from FGF14 KO mice was generally well described by a single exponential recovery time constant (Fig. 6, E–H) in contrast to the double exponential characteristic of the recovery in WT CCs. However, the average recovery in FGF14 KO cells at −80 mV (Fig. 6 F), −100 mV (Fig. 6 G), and −120 mV (Fig. 6 H) was better fit with the addition of a small, slower recovery component of several hundred milliseconds that contributed a fractional recovery component of ∼0.05–0.1. This additional slow component will be addressed below; however, on balance, the slow component of recovery from inactivation is largely abolished when mice do not express FGF14. Furthermore, the remaining fast component of inactivation present in cells from FGF14 KO mice is indistinguishable from the fast component of recovery observed in WT cells (Fig. 6 I). This is consistent with the idea that the fast component simply reflects recovery from inactivation mediated by the conventional fast-inactivation process intrinsic to the Nav1.3 subunit. These results support the view that the entry into the slow recovery pathway arises primarily from FGF14. Given that previous results show that use-dependent inactivation and slow recovery is produced by FGF14A, but not FGF14B (Laezza et al., 2009; Dover et al., 2010), FGF14A is the most likely candidate as the major FGF partner of Nav1.3 in mouse CCs.

The similarity of the recovery time constant in FGF14 KO CCs to the fast component of recovery in WT CCs indicates that the presence of FGF14, in association with Nav1.3, has little impact on the fast-inactivation recovery process. This is consistent with a relative independence of the two inactivation pathways; however, we noted above that the onset of inactivation differed between WT and FGF14 KO cells (Fig. 5, E and F). If traditional fast inactivation and FGF14-mediated fast inactivation are strictly independent, competing inactivation pathways, with rates k_f and k_FGF, respectively, the expectation is that the inactivation time constant in WT cells would be τ_i = 1 / (k_f + k_FGF), while following removal of FGF14 τ_i(KO) = 1 / k_f. Thus, inactivation following FGF14 KO would be expected to be slower if the onset of inactivation involves two strictly independent, competing pathways. For present purposes, here we assume that all Nav channels contain an FGF subunit. Given that both slow and fast recovery pathways are likely entered at about equivalent rates (equal fast and slow recovery fractions following 5-ms inactivation steps), one would expect the inactivation time constant in FGF14 KO cells to be about twofold slower compared with WT cells. In contrast, we observed that the onset of inactivation was faster by ∼25% (Fig. 5 E, at 0 mV) over all tested inactivation voltages (Fig. 5 F). Although the magnitude of this difference may not be quite sufficient to approach statistical significance, it deviates from the expectation of a twofold prolongation. This result therefore suggests that the conventional fast and FGF14-mediated inactivation processes may not be entirely independent, but that the presence of FGF14 in the Nav1.3 channel complex may influence conventional fast-inactivation process. The relationship between intracellular FGF-mediated inactivation and fast inactivation will require more detailed evaluation of heterologously expressed Nav currents with and without FGF14 than has yet been done to date.

Some CCs from FGF14 KO mice exhibit a slow recovery component

As noted above, the averaged recovery from inactivation time course for FGF14 KO cells revealed a small, slow component of recovery from inactivation (Fig. 6, F–H). Here, we examine the issue of variability in recovery from inactivation among cells of each genotype (WT and FGF14 KO). For WT cells (Fig. 7 A), all cells were fit best with a double exponential recovery time course. Although the average amplitude of the fast component was ∼0.5 (Fig. 7 B), the fast component among individual cells varied from ∼0.3 to 0.75. In contrast, for cells from FGF14 KO mice (Fig. 7 C), 25 of 33 cells were best fit with a single exponential recovery time constant (cells with black lines in Fig. 7 C), while 8 cells (blue) were best fit with a double exponential time course. However, in all FGF14 KO cells for which a double exponential fit was required, the fast component was in excess of 0.5, which was markedly different than what was observed in WT cells (Fig. 7 A). Furthermore, the slow component of recovery in FGF14 KO cells, when present, appeared to be slower than that in WT cells (Fig. 7 G). To better evaluate this behavior, we grouped the FGF14 KO cells into those for which only a single exponential fit was sufficient and those for which two components of recovery were required (Fig. 7 D). Although this separation is somewhat arbitrary, the presence of a slow component in some FGF14 KO cells likely represents something distinct from the effects of FGF14. For those cells requiring two components (n = 8), the fitted values for amplitudes (A_f and A_s) and time constants (τ_f and τ_s) of the averaged recovery were A_f = 0.76 ± 0.01, τ_f = 8.6 ± 0.5 ms, A_s = 0.24 ± 0.06, τ_s = 1,450.0 ± 956.6 ms, and for those cells containing only a single exponential component, τ_f = 7.2 ± 0.4 ms. Despite the presence of a distinct slow component in 8 of the set of 33 FGF14 KO CCs, it can still be concluded that FGF14 is a major determinant of slow recovery from inactivation in essentially all CCs.

The individual values for A_f for WT and FGF14 KO cells were binned and their frequency of occurrence plotted (Fig. 7 E). FGF14 KO (red) cells are clearly shifted toward larger fractions of fast recoveries, even for those cells in which some slow recovery was observed. The fast time constants of recovery from inactivation (Fig. 7 F) were indistinguishable between WT and FGF14 KO. In contrast, for those FGF14 KO cells that exhibited slow recovery, the time constants of that slow recovery were slower than those in WT cells (P < 0.0001).

Slow recovery from inactivation is a major determinant of Nav channel availability

In our examination of the properties of Nav current in rat CCs, we examined the impact of the slow component of recovery on the availability of Nav current during repetitive stimuli (Martinez-Espinosa et al., 2021). The fractional diminution of Nav current either during trains of 5-ms depolarizations or via trains of AP waveforms could be accounted for by a simple model of two competing, independent fast-inactivation pathways. Furthermore, removal of the slow component of recovery from inactivation was predicted to abolish the use-dependent diminution of Nav current amplitude at 10-Hz trains (Martinez-Espinosa et al., 2021). Similarly, for Nav1.5 channels heterologously coexpressed with different FGF13 N-terminal variants (13S, 13U, and 13VY), slow recovery from inactivation arising from the FGF13S variant—also termed FGF13A—is associated with use-dependent diminution of Nav current during 10-Hz trains, while Nav1.5 channels without FGF13 subunits or those with FGF13U or FGF13VY exhibited no such diminution (Yang et al., 2016). Similarly, diminution of Nav peak current during trains has also been noted for heterologous expression of FGF13A in Nav1.6-expressing ND7/23 cells (Rush et al., 2006).

Here, for a set of WT (n = 22) and FGF14 KO (n = 19) cells (part of the set included in Fig. 7), we first tested each cell with the standard paired pulse inactivation protocol (1P protocol) with recovery at −80 mV (Fig. 8, A, C, and E). Then the same cell was subsequently tested with a protocol (10P protocol) in which a 10-Hz, 10-pulse train of 5-ms depolarizations preceded recovery intervals at −80 mV (Fig. 8, B, D, and F). For WT cells, the 10-Hz train drives channels into slow recovery pathways (Martinez-Espinosa et al., 2021), reducing the fast component of recovery from ∼0.5 to ∼0.3 (Fig. 8 G). In contrast, for FGF14 KO cells, we observed two types of behaviors. First, in most cells for which recovery from inactivation was well described by a single exponential (Fig. 8, C and D), recovery from inactivation following either the 1P or 10P protocol was essentially identical (Fig. 8 H). Furthermore, for such cells, during the 10-Hz train, there was little diminution in the amplitude of the Nav current elicited during each pulse in the train (Fig. 8, D and J), whereas, in the WT example (Fig. 8 B), peak Nav current was reduced to ∼40% of the initial amplitude. For those FGF14 KO cells that exhibited a slow component of recovery from inactivation (Fig. 8, E and F), the 10-pulse train produced an appreciable decrease in peak Nav current amplitude during the train (Fig. 8, F and J) and markedly slowed recovery from inactivation (Fig. 8 I). For these three example cells, comparison of the recoveries after the 1P and 10P protocols demonstrates three types of behaviors. The WT cell exhibits an appreciable use-dependent increase in the slow component of recovery from inactivation (Fig. 8 G). The FGF14 KO cell with no slow recovery shows no difference in recovery between the 1P and 10P protocols (Fig. 8 H). The FGF14 KO cell that exhibited a slow component of recovery shows an even more prominent use-dependent increase in the slow component than in the WT cell (Fig. 8 I). It is noteworthy that in this latter cell, although the initial slow component of recovery after the 1P protocol is less than the average in WT cells, it exhibits a much more prominent use-dependent increase in the slow component. This likely arises from the fact that, whatever the basis for that slow component of recovery, its time constant is slower than that found in WT cells (Fig. 7 G). The differences among these cells in terms of the diminution of peak Nav current amplitude during the 10P train are summarized in Fig. 8 J.

Figure 8.

Some CCs from FGF14 KO mice exhibit slow recovery from inactivation. (A) A standard paired-pulse protocol was applied to a CC from a WT mouse. Left (P1): Overlays of currents elicited by first pulse to 0 mV are shown. Right: Currents evoked by a second test pulse (P2) after recovery intervals at −80 mV are shown. (B) For the same cell as in A, recovery was examined after a 10-Hz train of 10 pulses, with P1 and P2 currents as indicated. The variable duration recovery interval was applied at the end of the 10-Hz train. (C and D) Identical protocols were applied to CC from a FGF14 KO mouse. Note marked fast recovery (C) and the absence of diminution of peak Nav current during train. (E and F) Another CC from an FGF14^−/− mouse that exhibited a slow component of recovery from inactivation. Cell was from same tissue slice as that in C and D. (G) Fractional recovery for the WT CC following a single step to 0 mV (1P) and following 10 steps to 0 mV (10P). Two exponential fit values were, for 1P, A_f = 0.52 ± 0.01, τ_f = 8.9 ± 0.7 ms, A_s = 0.48 ± 0.02, and τ_s = 572.6 ± 74.9 ms; while, after 10P, A_f = 0.35 ± 0.01, τ_f = 9.9 ± 0.8 ms, A_s = 0.63 ± 0.01, and τ_s = 604.3 ± 41.9 ms. (H) Fractional recovery following both 1P and 10P were fit with single exponentials. Following 1P, τ_f = 6.8 ± 0.3 ms, while following 10P τ_f = 7.1 ± 0.5 ms. (I) 1P recovery was fit with A_f = 0.65 ± 0.01, τ_f = 10.1 ± 0.6 ms, A_s = 0.41 ± 0.12, and τ_s = 2,252.5 ± 1,209.7 ms. After 10P, A_f = 0.28 ± 0.01, τ_f = 7.5 ± 0.5 ms, A_s = 0.88 ± 0.06, and τ_s = 2,379.6 ± 2,252.5 ms. (J) Diminution in peak Nav current amplitude during the 10P protocol shown in B, D, and F for the three cells.

The averaged recovery time courses for the 1P and 10P recoveries for WT (Fig. 9 A) and FGF14 KO (Fig. 9 B) emphasize the markedly reduced slow component of recovery in FGF14 KO cells. Individual 10P recoveries for all 22 WT cells (Fig. 9 C) and 19 FGF14 KO cells (Fig. 9 D) highlight the differences between the WT and FGF14 KO conditions. The 1P and 10P recoveries are plotted for all individual WT (Fig. S3) and FGF14 (Fig. S4) cells to highlight the generally complete removal of slow recovery in most FGF14 KO cells, but also the presence of some slow recovery in three FGF14 KO cells studied with both 1P and 10P protocols. All three of the FGF14 KO cells that exhibited a prominent slow component were from one animal (five additional cells with slow recovery were recorded from five other FGF14 KO animals, but studied only with the 1P protocols; Fig. 7 C). In the animal in which multiple cells with slow recovery were observed, other cells exhibited a clear single exponential recovery.

Although the limited number of cells and animals for which we have observed the unusual slow component of recovery precludes strong conclusions, a few other features of these cells are worth comment. For FGF14 KO cells that exhibited a slow recovery component following 1P stimulation, the slow fraction is smaller than that typically seen in WT cells; however, recovery following the 10P protocol is associated with a slow component of comparable amplitude to that seen in WT cells (Fig. 9 D), but of slower duration (Fig. 8 I). We propose that this strong use-dependent increase in the slow recovery fraction, despite a modest initial component of slow recovery, is responsible for a more slowly developing, but profound use-dependent diminution in peak Nav current during the 10-Hz train of stimuli compared with WT cells (Fig. 9 E versus Fig. 9 F). To highlight the relative importance of the accumulation of channels in slow recovery pathways for use-dependent changes in peak Nav amplitude, we plotted the A_f following the 10-Hz train versus the fractional Nav availability based on the measurement of relative Nav current amplitude during the 10th pulse in the train (Fig. 9 G). Although most FGF14 KO cells exhibited a large fast amplitude component along with little diminution in Nav availability, for FGF14 KO cells with a slow component of recovery, both the reduction in fast amplitude and reduction in Nav availability mirror the behavior seen in WT cells. Furthermore, three WT cells exhibiting the largest fast recovery component after the 10P protocol (Fig. 9 C, E, and G, green) exhibited the smallest use-dependent diminution of peak Nav current. Thus, it is the accumulation of channels in slow recovery pathways that dictates the extent of the diminution of peak Nav current during trains.

Dual-pathway inactivation and use-dependent changes in Nav availability

In the associated paper, a simple set of assumptions about the dual-pathway inactivation process described well the use-dependent diminution in Nav currents activated by either trains of square pulse depolarizations or AP voltage-clamp waveforms (Martinez-Espinosa et al., 2021). The basic assumptions were the following: (1) during a 5-ms depolarization or an AP, all activated channels inactivate with half entering traditional fast recovery states and half entering a slower recovery pathway; and (2) following inactivation, channels in either recovery pathway recover from inactivation into resting states in accordance with experimentally measured time constants. Therefore, beginning with 95% or more of the channels in resting states (assuming a −80-mV holding potential), fractional occupancy before any test pulse, immediately following any test pulse, and then after the recovery interval preceding the next test pulse can be readily calculated (Fig. 10 A). By using this approach and using the measured fast and slow time constants of recovery (τ_s) from inactivation at −80 mV, the occupancy of channels in closed, fast inactivated, or slow inactivated states was determined, first, for the WT condition at a time preceding each test depolarization in a 20-pulse train at 10 Hz (Fig. 10 B, 1), and then also following each 5-ms test depolarization where all channels have inactivated (Fig. 10 B, 2). Then, from the calculation of the channels that have returned to closed states between depolarizations, the calculated fractional decrease in peak Nav current amplitude was determined for the given set of recovery constants (Fig. 10 B, 3). Finally, based on the occupancies of channels in fast and slow recovery pathways following either a single test step (1P) or a train of 10 pulses (10P), the predicted 1P and 10P fractional recovery from inactivation was determined (Fig. 10 B, 4). Both the diminution of Nav amplitude and the relative changes between 1P and 10P recovery time courses match well with the experimental observations. To illustrate the impact of FGF14 KO in which no slow component of recovery from inactivation was observed, we repeated the calculations for a case in which only fast inactivation is observed (Fig. 10 C, 1–4). As trivially expected, there is no diminution of peak Nav amplitude during the train (Fig. 10 C, 3), as also observed experimentally (Fig. 8 D). Finally, we considered a case analogous to that of FGF14 KO cells in which a smaller fraction of initial slow recovery is also associated with a slower recovery time constant by using the experimentally measured values of A_f = 0.75 and τ_s = 1,591 ms (Fig. 10 D, 1–4). That 75% of channels inactivate into fast recovery pathways, an empirically based assumption, could arise from a number of mechanistically distinct factors about which we have no information. However, by using those values, peak Nav current amplitude can be seen to diminish to values comparable to the WT case, although with a slower approach to steady state (Fig. 10 D, 3). Similarly, the calculated 1P and 10P recoveries show the larger fractional increase in the slow recovery component (Fig. 10 D, 4) observed in those FGF14 KO cells, which exhibited a slow recovery component. These considerations show that the time constant of slow recovery in a dual-pathway inactivation system can impact profoundly the rate of use-dependent accumulation in slow recovery pathways and, correspondingly, the changes in Nav availability during trains of stimuli.

Figure 10.

Evaluation of the impact of slow and fast recovery from inactivation on use-dependent diminution of peak Nav amplitude. (A) The basic stimulation protocol for calculation of state occupancies, use-dependent peak current diminution, and 1P/10P recovery time course. From a −80 mV holding potential, a 10-Hz train of 20 5-ms steps to 0 mV was used to produce channel activation and inactivation. This corresponds to a 95-ms recovery interval between steps to 0 mV. Red triangles indicate time points before depolarization and green, after full inactivation. For calculations in B–D, fractional inactivation before P1 is assumed to be 0.05, with inactivated states split evenly between fast and slow recovery pathways. (B) Calculations assume that channels available for activation at the beginning of depolarization equally enter slow and fast recovery pathways, with no interconversion. Fraction of slow and fast recovery during each 95-ms recovery interval is calculated based on measured time constants of fast and slow recovery for WT cells at −80 mV (Fig. 7, F–G) and calculated initial fraction of channels in either fast or slow pathways. (B1) Black circles indicate fraction of channels available for activation before depolarization, red indicates channels in fast recovery pathways before depolarization, and blue indicates channels in slow recovery pathways before depolarization. (B2) Fractions of channels in slow recovery pathways (blue) and fast recovery pathways (red) immediately following inactivation (green arrows in A). (B3) Calculated fraction of peak Nav current normalized to P1 amplitude based on channels available for activation before each test pulse to 0 mV. (B4) Time course of recovery from inactivation based on calculated fraction of channels in fast and slow pathways following P1 or P10 and the measured time constants of recovery. (C) Calculations similar to those in B, but assuming that the slow component of recovery from inactivation is absent (most FGF14 KO cells). This yields no appreciable use-dependent diminution in Nav amplitude and identical single exponential time courses of recovery from inactivation following P1 or P10. (D) Calculations as in B and C, but assuming average fast and slow recovery time constants based on the set of FGF14 KO cells that exhibited a slow component of recovery.

To probe the potential roles of different aspects of the dual-pathway model on use-dependent changes in Nav availability, we first tested the impact of varying the fractions of channels entering A_f and A_s with each inactivating step (Fig. 11 A). This might arise because intrinsic rates of traditional fast inactivation and FGF-mediated inactivation differ. For example, the observed macroscopic inactivation time constant of ∼0.4 ms at 0 mV (Fig. 1 E) would be consistent with a range of combinations of intrinsic rates of entry into fast and slow pathways, all summing to 2,500/s, where τ_i = 1 / (k_i + k_FGF), where A_f = k_i / (k_i + k_FGF), where k_i is intrinsic rate of traditional fast inactivation and k_FGF is the rate of inactivation via FGF-mediated inactivation. A second factor affecting A_f and A_s could be a less-than-full stoichiometric presence of an FGF subunit in the Nav population; however, for the present calculations, this latter possibility is not considered. We used rates of fast and slow recovery from inactivation identical to those measured in WT CCs. The rates of recovery from inactivation following a single pulse (Fig. 11 A, 1) simply mirror the fraction of occupancy dictated by the assumption of a given A_f value. The diminution of peak Nav current varies considerably, as the relative entry into fast and slow recovery pathways varies (Fig. 11 A, 2), with the most dramatic effects on cumulative inactivation seen over A_f values from 0.5 to 0.95. Furthermore, the rate at which a steady-state level of Nav availability is attained varies considerably. As A_f increases, this naturally slows entry into slow recovery pathways during a train of stimuli. The accumulation of channels in slow recovery pathways is highlighted with the calculation of recovery following a standard 10P protocol (Fig. 11 A, 3). The impact of varying the time constant of recovery from fast inactivation from 6 to 30 ms was also evaluated (Fig. 11 B). In this case, although the shape of the recovery from inactivation following a 1P protocol (Fig. 11 B, 1) varies as expected for changes in τ_f, τ_f has no impact on the use-dependent accumulation of Nav channels in slow recovery pathways, as revealed in either the Nav peak current (Fig. 11 B, 2) or the 10P recovery protocol (Fig. 11 B, 3). When the τ_s is varied from 200 to 3,000 ms (Fig. 11 C, 1), slowing of τ_s results in a marked increase in the extent of use-dependent diminution of peak Nav current during a train (Fig. 11 C, 2), but with only modest impact on how much diminution occurs with each stimulus during a train. The latter effect, in contrast to what was observed with different values of entry into slow and fast recovery paths (Fig. 11 A), arises since τ_s does not impact how many channels enter slow recovery states with each stimulus, but only the persistence of channels in the slow recovery rates between stimuli. The 10P protocol also emphasizes the impact of τ_s on the shape of the time course of recovery from inactivation (Fig. 11 C, 3). Finally, we again examined the consequences of varying A_f (differential entry into fast and slow recovery pathways), but in association with a recovery time constant similar to what we observed in those FGF14 KO CCs with a slow component of inactivation (Fig. 11 D). Although the 1P recovery behaviors are generally similar to those with a faster τ_s (Fig. 11 D, 1), the calculations of peak Nav current diminution during a train further highlight the impact that a given τ_s can have on the approach to steady-state availability during a train, particularly in conjunction with reduced fraction of entry (e.g., A_f = 0.95) into slow recovery pathways (Fig. 11 D, 2). The greater accumulation of channels in slow recovery pathways is also highlighted in the 10P protocol (Fig. 11 D, 3).

Figure 11.

Impact of changes in inactivation properties on predicted Nav diminution during trains and increases in slow recovery fraction. Underlying assumptions are summarized in the text in association with Fig. 10. Based on Fig. 5 F, fast inactivation in the absence of FGF is ∼0.4 ms. Even if entry into slow recovery is 10-fold slower than normal fast inactivation, it is expected that inactivation will be complete during a 5-ms inactivation step, but that fewer channels will be in slow recovery pathways. (A) Impact of varying A_f (A_s = 1 − A_f) on predicted 1P recovery time course (A1), Nav diminution extent and time course (A2), and 10P recovery (A3). Blue: A_f = 0.95; red: A_f = 0.5; green: A_f = 0.05. Red corresponds to WT CC behavior. (B) As in A, but with predictions based on varying τ_f from 6 ms (blue) to 30 ms (green), with other constants as for WT. (C) As above, but with predictions based on varying τ_s from 200 ms (blue) to 3,000 ms (green) with red similar to WT measurements (600 ms). (D) Predictions based on variation in A_f from 0.95 (blue) to 0.05 (green), but with τ_s = 2,000 ms, highlighting the profound impact of τ_s on cumulative inactivation (D2 and D3).

The main point to be made from the above considerations is that, if there are specific molecular considerations that can influence either (1) relative rates of entry into slow and fast recovery pathway or (2) rates of recovery via the slow recovery pathway, such factors would dramatically affect use-dependent changes in Nav current availability during repetitive activity. Although a major portion of the use-dependent changes in Nav availability in mouse CCs clearly arises from the presence of FGF14 subunits, the presence of a slow recovery behavior of different properties (e.g., reduced slow component following a single depolarization and different τ_s), at least in some FGF14 KO CCs, suggests that there may be other factors, perhaps different FGF subunits, that can sculpt changes in Nav availability among different cells.

Discussion

The present results establish that the Nav1.3 isoform of sodium channel is the major Nav subunit contributing to Nav current in mouse CCs studied in adrenal medullary slices. Furthermore, FGF14 appears to be an integral component of all, or most, mouse CC Nav channels, being the primary determinant for the slow component of recovery from fast inactivation in most cells. This may be the first case for which an FGF is shown to partner with Nav1.3 in a native tissue, although, given the conservation of the FGF-binding surfaces among Navs, that is not surprising. Here, we will discuss four main issues: First, the relevance of the present observations to earlier work on Nav currents in CCs; second, possible explanations for slow recovery from inactivation present in a subset of CCs from FGF14 KO mice; third, implications of the present work concerning the independence of conventional fast inactivation in relationship to FGF-mediated inactivation; and, fourth, the potential impact of FGF-mediated inactivation and slow recovery from inactivation on Nav availability and excitability.

Molecular substrates of Nav currents in CCs

The present results establish that Nav1.3 is the predominant Nav current in mouse CCs. Although we cannot be sure of the identity of the non-Nav1.3 current in mouse cells, the prevalence of Nav1.7 message in rat and bovine CCs suggests that Nav1.7 suggests it is a reasonable candidate in mouse cells. The major presence of Nav1.3 in mouse cells runs counter to a long-standing view that Nav1.7 is the dominant neuroendocrine sodium channel (Wada et al., 2004; Yanagita et al., 2007; Wada et al., 2008). Much of this earlier body of work focused on bovine CCs and examined the up- or downregulation of Nav1.7 without assessing potential contributions of other Nav isoforms. Given the similarity in properties between the WT Nav current (mostly Nav1.3) in mouse CCs, and then the non-Nav1.3 current that is present in Nav1.3 KO cells, two different Nav isoforms with generally similar properties appear to be available for expression in CCs.

The presence of two different Nav isoforms of generally similar activation and steady-state inactivation properties contrasts with recent results on mouse pancreatic α and β cells. In those cells, both Nav1.3 and Nav1.7 have been shown to be expressed in the same cells (Zhang et al., 2014), and the two currents together result in two clearly separable components in their steady-state inactivation curves. Taking advantage of the general KO of Nav1.3 and a pancreatic-specific KO of Nav1.7 KO, it was shown that Nav1.7 KO removed the more negatively shifted component of availability, while Nav1.3 KO removed the more right-shifted component. In fact, the observed left-shifted properties of the Nav1.7 component of current would preclude it from contributing to Nav availability in cells with a resting potential of −50 mV or more positive (Zhang et al., 2014). This result raised some question about how a mouse Nav1.7 current could ever participate in AP generation in CCs; however, the results presented here on the residual Nav current in Nav1.3 KO cells leave open the possibility that an Nav1.7 current in mouse CCs may have properties similar to Nav1.3. This might also be the case in rat CCs for which Nav current properties are generally similar to mouse CCs, but Nav1.7 message is clearly more abundant than it is for Nav1.3.

FGF14 is the major determinant of the slow recovery from inactivation in mouse CCs, but other contributors may exist

The complete absence of slow recovery from inactivation in most CCs from FGF14 KO mice argues that FGF14 is an essential partner in the Nav1.3 channel complex in CCs. This most likely reflects the FGF14A isoform; however, a subset of FGF14 KO cells exhibited a slower component of recovery, which, on average, was smaller in relative amplitude and slower in time course than in WT cells, suggesting that the molecular basis of this residual slow recovery is distinct from that arising from FGF14.

What are the potential explanations for the residual slow recovery in some FGF14 KO cells? For 8 of 33 FGF14 KO cells exhibiting some slow recovery from inactivation, the initial fraction of slow recovery following a single inactivation step was ∼0.25, with an average time constant of slow recovery about twofold slower than in WT cells. One explanation, which we consider the most likely, is that this component may arise from the presence of another, as-yet-unidentified FGF isoform. That this residual component exhibits fast onset and slow recovery is a feature only shared among FGF isoforms, for all known mechanisms of Nav inactivation. This postulated additional isoform, although perhaps in lower abundance, may influence Nav inactivation behavior in WT cells along with FGF14; however, in WT cells, it would be virtually impossible to separate out multiple distinct slow recovery processes. This possibility will require evaluation with KO animals for additional FGF isoforms when they are available. However, that slow recovery mechanisms of different functional effect may exist has several intriguing aspects. First, the slower time constant of recovery of this persistent component suggests that this putative FGF subunit has kinetically distinct effects from that mediated by FGF14. Not only is the rate of recovery from FGF-mediated inactivation slower, but the smaller fraction of initial slow pathway occupancy following a single inactivation step suggests that the onset of inactivation mediated by the additional component may be slower. Second, the kinetically distinct behavior of the slow recovery was shown to be associated with a slower, but similarly deep development of use-dependent diminution of peak Nav current. This suggests that, if the slow component that is observed in some FGF14 KO CCs does arise from an additional FGF isoform, use-dependent changes in Nav variability may be differentially regulated by the expression of different FGF-A isoforms. An alternative explanation of the slow recovery of some FGF14 KO cells is that it arises from something other than an FGF subunit; however, given that the behavior of the slow component mirrors aspects of FGF14, we would not favor this possibility. Might the residual slow component reflect some aberrant assembly of the FGF14–N-terminal–β-gal peptide (see Materials and methods) that may be expressed in FGF14 KO animals? We consider this unlikely since the FGF14 N terminus lacks the key determinants for binding to the Nav C terminus. Furthermore, shRNA-mediated FGF14 knockdown has the same functional consequences on cerebellar Purkinje cell excitability as observed in FGF14 KO animals, suggesting that any residual FGF14–N-terminal–containing peptide does not influence cell excitability (Bosch et al., 2015). Any generalizations regarding the presence of slow recovery from inactivation in FGF14 KO cells are limited at this point, because such behavior was only observed in eight cells. Two key points are that (1) cells with slow recovery and cells completely without slow recovery were both observed in the same animals, and (2) slow recovery was observed in CCs from both male and female FGF14 KO mice.

The potential heterogeneity suggested by the FGF14 KO CCs is reminiscent of some other aspects of CCs. Rodent CCs are known to exhibit both inactivating and noninactivating BK channels, which can be completely segregated among different CCs based on the expression of the BK β2 regulatory subunit (Solaro et al., 1995; Martinez-Espinosa et al., 2014). Such differences impact the ability of CCs to fire more tonically or more phasically in response to constant current injection (Solaro et al., 1995; Sun et al., 2009). About 80% of rat CCs exhibit predominantly inactivating BK current, and a lesser percentage in mouse. Furthermore, CCs differ with regard to whether they express phenylethanolamine N-methyl-transferase, the enzyme essential for conversion of norepinephrine to epinephrine. In rat, up to 80% of CCs are thought to express phenylethanolamine N-methyl-transferase and preferentially secrete epinephrine (Verhofstad et al., 1985; Tomlinson et al., 1987). CCs may also be heterogeneous with regard to differences in sensitivity to secretagogues (González-Santana et al., 2020). Finally, the variation we observed in the contribution of the non-Nav1.3 current among mouse CCs may also reflect some heterogeneity in CC function. The possibility that secretory products of a given subpopulation of CCs may correlate with particular excitability properties dictated by underlying ion channels remains an intriguing topic for future investigation.

The relationship between FGF-mediated inactivation and conventional fast inactivation

Since the initial work of Goldfarb and associates, the prevailing hypothesis regarding dual-pathway fast inactivation—or long-term inactivation—has been that conventional fast inactivation intrinsic to the Nav channel subunit and inactivation mediated by the A isoform of an FGF compete to occupy overlapping positions of occupancy that occlude the ion permeation pathway (Dover et al., 2010; Goldfarb, 2012; Venkatesan et al., 2014). Based on current thinking, conventional fast inactivation, originally insightfully envisioned as a ball-and-chain mechanism (Armstrong and Bezanilla, 1977; Armstrong and Hollingworth, 2018), involves a peptide loop containing a conserved triplet of hydrophobic residues (IFM: Ile-Phe-Met) on the linker between domains III and IV of inactivating Nav channels. Although at one time the IFM loop was thought to act as a cap to hinder ion flux through the permeation pathway (West et al., 1992; Eaholtz et al., 1994), current structural evidence suggests that it may act allosterically to constrict ion flux (Yan et al., 2017). Furthermore, it is the movement of the domain IV (DIV) voltage sensor that is sufficient for fast inactivation in sodium channels and that also limits the rate of fast inactivation (Capes et al., 2013). For intracellular FGFs, a conserved homologous core domain present in all FGF isoforms has been shown to mediate binding to Nav α subunits, and mutations of that conserved surface disrupt the ability of FGFs to assemble with Navs (Goetz et al., 2009; Wang et al., 2012). The present understanding of how FGF-A isoform N termini produce inactivation has been largely based on functional tests of coexpression of FGF13A with Nav1.6 (Dover et al., 2010). This work (Dover et al., 2010) demonstrated that the N terminus of the FGF13A protein produces long-term inactivation of Nav1.6 channels, that mutation of basic residues in the N terminus abolishes long-term inactivation, and that synthetic peptides corresponding to residues 2–21 of the FGF13 subunit produce use-dependent inhibition of Nav1.6 current in a fashion similar to intact FGF13 subunits. In contrast, coexpression of FGF13B with Nav1.6 does not produce long-term inactivation. Together, these results led to the proposal that the mobile cytosolic N terminus of the FGF-A isoforms could occlude ion permeation in a fashion that competes with the normal fast-inactivation process, but involves a slower recovery from inactivation (Dover et al., 2010; Goldfarb, 2012). Although such evidence is consistent with channel occlusion models developed for fast inactivation of K⁺ channels (Hoshi et al., 1990, 1991), the specific molecular underpinnings of the FGF-mediated inhibition of ion permeation remain to be determined.

The present results and the associated paper (Martinez-Espinosa et al., 2021) address a few points that are pertinent to the relationship between the two inactivation pathways that have not been revealed in earlier work. First, results are generally consistent with the idea of independence between the two pathways, namely, once inactivation into one or the other pathway has occurred, channels are effectively precluded from equilibrating into the other pathway. The use-dependent accumulation in slow recovery pathways also strongly supports the idea that the two pathways are largely independent; however, one aspect of our results conflicts with this idea. Specifically, the onset of inactivation in CCs from FGF14 KO mice is more rapid than in CCs from WT mice (Fig. 5, E and F) and a simple shift in the activation G-V is unlikely to account for these differences. For FGF14-mediated fast inactivation in mouse CCs, our results indicate that about half the channels inactivate into each pathway. Assuming that all channels contain an inactivating FGF subunit, this requires that the rates of entry into each be quite similar. If two independent fast-inactivation mechanisms with comparable rates defined by k_f and k_FGF compete to produce inactivation, the expected time constant of inactivation would be defined by τ_i = 1 / (k_f + k_FGF). Since, at strong inactivation voltages, the entry into either inactivated state is largely absorbing, only a single exponential is expected. If the two pathways are independent, in the absence of FGF14, inactivation should then be defined simply by τ_i = 1 / k_f, which predicts a time constant twice as slow as in WT. Thus, that inactivation is actually faster in CCs from FGF14 KO mice raises the possibility that, at least for entry into inactivated states, there may be some interaction between the two pathways. This might reflect an allosteric effect or simply a steric effect whereby, for example, the presence of FGF14 might hinder but not prevent movement of the IFM-containing DIII–DIV linker. Such questions can most effectively be addressed with heterologous expression studies. Yet, this potential FGF14/Nav interaction does not contradict the key idea that, in large measure, the two pathways are largely independent.

FGFs, steady-state inactivation, slow recovery from inactivation, and cell firing

There is extensive literature concerned with various aspects of the specificity of interactions of different FGF isoforms with different Nav isoforms (Liu et al., 2003; Goetz et al., 2009; Laezza et al., 2009; Wang et al., 2012) and potential Nav/FGF partnerships in native tissues (Bosch et al., 2015; Wang et al., 2017; Effraim et al., 2019). Furthermore, there has been extensive attention paid to the physiological and pathophysiological consequences of different FGF isoforms and naturally occurring mutations (Liu et al., 2003; Laezza et al., 2007; Hennessey et al., 2013; Musa et al., 2015; Siekierska et al., 2016). Many of the functional studies have focused on the impact of FGFs on activation G-Vs, steady-state inactivation curves, channel localization, or current density (Goldfarb et al., 2007; Diwakar et al., 2009; Xiao et al., 2013; Pablo et al., 2016; Yang et al., 2016), suggesting that shifts in steady-state inactivation curves, by changing Nav channel availability at resting potentials, may impact cell firing. When examined in heterologous expression systems, both A and B FGF isoforms produce generally similar shifts in steady-state inactivation. There is no question that shifts in steady-state inactivation among cells will impact Nav availability, but such shifts, per se, are unlikely to underlie use-dependent alterations in availability, unless associated with specific kinetic behaviors that result in the accumulation of channels in states that only slowly recover from inactivation.

Thus, we would emphasize that, for FGF-A isoforms, it is the use-dependent accumulation in slowly recovering inactivated states that is the main determinant of use-dependent diminution of Nav channel availability during trains, which is in line with initial proposals from Goldfarb (Dover et al., 2010; Goldfarb, 2012; Venkatesan et al., 2014). Invariably, where it has been examined with heterologous expression, such use-dependent diminution of Nav channel availability has been specifically associated with FGF-A isoforms. This has been shown for FGF14A coexpression with Nav1.6 channels (Laezza et al., 2009), FGF-mediated spike accommodation in hippocampal pyramidal cells (Venkatesan et al., 2014), FGF13S-mediated coexpression with Nav1.5 channels (Yang et al., 2016), and FGF13A coexpression with Nav1.6 (Rush et al., 2006). The extent of the steady-state diminution of peak Nav current shows considerable variability among the various cases, ranging from ∼50% reduction to ∼90%, even at identical 10-Hz train frequencies. Ultimately, as supported by the present analysis, the specific kinetics of the FGF-mediated onset and recovery process are likely to be essential in defining the extent and time course of use-dependent diminution of Nav currents.

An important pair of papers on Nav currents in dorsal raphe neurons (Milescu et al., 2010; Navarro et al., 2020), almost certainly involving some as-yet-unidentified FGF, provides some of the more useful comparative information to the results presented here. Some interesting differences between the Nav currents in CCs and those in dorsal raphe are that, whereas in CCs inactivated channels are about equally distributed between fast and slow recovery pathways during a single depolarizing step, in dorsal raphe neurons only ∼20% of channels enter initially into slow recovery pathways (Milescu et al., 2010; Navarro et al., 2020). At present, quantitative information about the differential entry and rates of recovery among different cell types is lacking. Below we consider a few factors that will need to be considered in future work.

Are most Nav channels in native cells partnered with an FGF?

As mentioned above, a single FGF peptide binds to the C terminus of a given Nav α subunit (Goetz et al., 2009). Yet, in native cells, we cannot be certain how well populated the Nav C-terminal FGF binding motif may be. What can be measured are the initial fractions of channels in fast and slow recovery pathways following brief inactivation steps, which for both rat and mouse CCs is ∼0.5 each. As mentioned, this does not appear to be the case for raphe neurons (Navarro et al., 2020). For most other experimental work on FGFs to date, such quantitative information is not available. Although we have no direct information regarding the rates of entry into each recovery pathway in CCs, the equal distribution between slow and fast pathways would suggest a similarity in such rates at least at 0 mV and above. However, this assumes that all Nav channels in a cell are associated with FGF subunits, about which we have no direct information. Can we draw any inferences regarding the extent to which all Nav channels in CCs may partner with an FGF? Experimentally, the fact that perhaps 80–90% of channels can be driven into slow recovering pathways gives some confidence that most Nav channels are partnered with an FGF.

However, there are limitations in the use of the initial fractions of fast and slow recovery populations as an indicator of the extent of FGF assembly in a channel population. First, for those FGF14 KO cells that exhibited a slow component of recovery, the initial fraction of slow recovering channels was typically 0.25 or less, and ∼0.4 at most (Fig. S4), suggesting perhaps less assembly of any putative additional FGF in the channel population. Yet, in those cases, the 10P protocol could still drive as much as 0.8 of the channel population into slow recovery pathways, which indicates that, despite a modest initial fraction of entry into slow recovery pathways, most (or perhaps all) Nav channels still might contain a subunit mediating such slow recovery. A smaller initial slow recovery fraction with a large use-dependent increase in that fraction can also arise if rates of initial entry into an FGF-mediated inactivated state are substantially slower than conventional fast inactivation at 0 mV for a given type of FGF subunit. Second, in our calculations addressing the impact of different fractions of entry into fast and slow pathways, as well as the impact of different slow recovery time constants (Fig. 11), it is clear that modest initial fractional entry into slow recovery pathways can still be associated with very robust use-dependent occupancy of slow recovery pathways.

Slow inactivation properties conferred by specific FGFs may differentially tune use-dependent changes in Nav availability

Given that each FGF isoform appears competent to interact with a variety of different Nav isoforms (Goldfarb, 2005; Goetz et al., 2009), any functional differences among FGF-A subunits or specificity in interactions with particular Nav subunits are likely to generate profound differences in use-dependent changes in Nav availability. Based on the simple calculations presented here (Figs. 10 and 11), the two factors primarily affecting the extent and rate of development of use-dependent changes in Nav availability are, first, the initial differential rates of entry into fast and slow recovery pathways and, second, the rates of slow recovery from inactivation. Ultimately, careful understanding of such interactions of FGF-A isoforms with specific Nav variants will be required. We propose that specific differences in the onset of inactivation and recovery from inactivation mediated by specific FGF-A isoforms may have profound effects on the extent of the use-dependent accumulation of Nav channels in slow recovery from inactivation pathways. This, in turn, will differentially impact the time course and extent of Nav availability during repetitive stimuli.