Significance
Microfluidics is an important in vitro platform to gain insights into mechanics of blood flow and mechanisms of pathophysiology of human diseases. Extraction of 3D fields in microfluidics with dense cell suspensions remains a formidable challenge. We present artificial-intelligence velocimetry (AIV) as a general platform to determine 3D flow fields and a microaneurysm-on-a-chip to simulate blood flow in microaneurysms in patients with diabetic retinopathy. AIV is built on physics-informed neural networks that integrate seamlessly 2D images from microfluidic experiments or in vivo observations with physical laws to estimate full 3D velocity and stress fields. AIV could be integrated into imaging technologies to automatically infer key hemodynamic metrics from in vivo and in vitro biomedical images.
Keywords: blood flow in microaneurysm, diabetic retinopathy, three-dimensional flow fields, deep learning, image analysis
Abstract
Understanding the mechanics of blood flow is necessary for developing insights into mechanisms of physiology and vascular diseases in microcirculation. Given the limitations of technologies available for assessing in vivo flow fields, in vitro methods based on traditional microfluidic platforms have been developed to mimic physiological conditions. However, existing methods lack the capability to provide accurate assessment of these flow fields, particularly in vessels with complex geometries. Conventional approaches to quantify flow fields rely either on analyzing only visual images or on enforcing underlying physics without considering visualization data, which could compromise accuracy of predictions. Here, we present artificial-intelligence velocimetry (AIV) to quantify velocity and stress fields of blood flow by integrating the imaging data with underlying physics using physics-informed neural networks. We demonstrate the capability of AIV by quantifying hemodynamics in microchannels designed to mimic saccular-shaped microaneurysms (microaneurysm-on-a-chip, or MAOAC), which signify common manifestations of diabetic retinopathy, a leading cause of vision loss from blood-vessel damage in the retina in diabetic patients. We show that AIV can, without any a priori knowledge of the inlet and outlet boundary conditions, infer the two-dimensional (2D) flow fields from a sequence of 2D images of blood flow in MAOAC, but also can infer three-dimensional (3D) flow fields using only 2D images, thanks to the encoded physics laws. AIV provides a unique paradigm that seamlessly integrates images, experimental data, and underlying physics using neural networks to automatically analyze experimental data and infer key hemodynamic indicators that assess vascular injury.
Human blood, primarily comprising plasma, red blood cells (RBCs), white blood cells, and platelets, is a non-Newtonian fluid exhibiting shear-thinning behavior (1, 2). The effect of this non-Newtonian behavior becomes more pronounced in microcirculation (3). Understanding and quantifying the biorheology of blood is essential for gaining insights into the mechanisms that influence microcirculation in physiology and disease (4–6). The characteristics of hemodynamics also determine the vascular integrity and blood-cell transport in physiology, e.g., the margination of platelets (7, 8). Platelet margination refers to the phenomenon of formation of a cell-free layer near the vessel wall in blood flow, as RBCs accumulate in the center of the vessel. Compromised hemodynamics can result in pathologies such as endothelial-cell inflammation and dysfunction, undesired platelet activation, and the formation of clots within a blood vessel (9–11).
Scientific research over the past several decades has led to rapid advances in in vivo imaging techniques (12–14). Despite this progress, it is currently not feasible to observe in real time many in vivo biological processes in microcirculation, such as the rupture of a microaneurysm (MA) in the retinal microvasculature and the initiation and development of blood clots. To compensate for this void in our ability to track the origins and progression of disease states, in vitro experiments of blood flow within microfluidic channels have been developed to mimic in vivo circulation under both physiologically and pathologically relevant conditions (see reviews in refs. 15–17). Microfluidic devices and laboratory-on-a-chip platforms offer advantages in exploring the biophysical and biochemical characteristics of blood flow in microvessels. Benefits of these devices include the need for only small volumes of blood for analysis and precise control over temperature, concentrations of gas, and chemicals in the blood (18). Another distinct advantage of such microfluidic platforms is that they enable quantitative determination of various key parameters associated with hemodynamics, such as spatial distributions of velocity and stress fields, under well-controlled experimental conditions so that mechanistic insights could be extracted for transitions from healthy to pathological states.
A wide variety of experimental techniques are currently available to assess the hemodynamics of in vitro blood flow in microcirculation. The state-of-the-art optical whole-field velocity measurement technique is microparticle image velocimetry (PIV) (19, 20), a nonintrusive method used to estimate flow fields in microchannels. Various algorithms employing PIV have been well developed in recent years (21–23), and this technology has been successfully applied to a broad range of biological problems (see reviews in refs. 24–26). PIV can provide measurements of blood velocity along channels in microcirculation, with high spatial and temporal resolution, by analyzing the motion of laser-induced fluorescence tracers seeded into blood (27–29). However, the experimental apparatus requires elaborate calibration and may not be amenable for wide or easy deployment. Other approaches to monitor flow motion, such as advanced PIV methods (30–32) or optical flow monitoring techniques (33–36), are able to quantify hemodynamics from images of blood flow in the microchannels using RBCs and platelets as tracers, thereby requiring less hardware. However, their accuracy in providing near-wall flow measurements, which is critical for inferring the pathogenic basis of blood rheology and the estimation of wall shear stress, could be compromised, owing to the formation of cell-free layers in the vicinity of blood vessel walls.
Computational fluid dynamics (CFD) models have also been employed to simulate blood flow in microvessels or channels to investigate the pathophysiology of circulatory diseases (37, 38). By invoking laws of physics (e.g., Navier–Stokes equations) and specific boundary conditions (such as no-slip conditions at the blood-vessel wall), CFD models can simulate the flow field and extract key hemodynamic indicators. Several studies have employed CFD models to compute flow and stress fields in normal microvessels, as well as channels with various shapes, such as stenotic channels [in which constricted flow from plaques markedly alters flow characteristics (39, 40)], aneurysmal vessels containing a bulge in the vessel as a result of a weakened vessel wall (41, 42), and other vasculatures with complex geometries (43, 44). However, results extracted from CFD models are very sensitive to the flow-boundary conditions assumed at the inlets and outlets, which can be patient-specific. Even moderate errors in flow-boundary conditions could lead to large uncertainty in the estimation of the flow fields (45). In addition, CFD simulations could be computationally cumbersome for modeling flow field with moving boundaries or geometric variation, such as the hemodynamics changes due to accumulation of blood cells.
Problem Description
Accurate assessment of hemodynamics in microvessels requires both experimental data extracted from controlled in vitro or in vivo assays and application of relevant laws of physics. In this work, we propose artificial-intelligence velocimetry (AIV), a unique computational framework that infers velocity fields and stress fields from two-dimensional (2D) images that are interpreted by using artificial-intelligence techniques based on underlying physical principles. In particular, AIV is developed based on the physics-informed neural networks (PINNs) (47, 48), which can automatically infer these flow fields in arbitrary domains by seamlessly integrating data from in vivo or in vitro with the governing equations of fluid flow. As illustrated in Fig. 1, with spatial coordinates and time, , as inputs, AIV uses a fully connected network to approximate the functional solutions of image intensity , velocity field , and pressure field . The loss function for training the neural network is composed of three terms: the mismatch between the network predictions and data (); residuals of the governing equations (); and boundary conditions () on the channel surfaces. Here, we assume no-slip boundary conditions on the channel wall as cell-free layers are observed in the vicinity of the wall (see the bright-field images in Fig. 2 B and C). This observation is also consistent with the finding from studies of blood flow in a microchannel with similar dimensions (49). Slip boundary conditions can also be employed in AIV by modifying the formulations of in the case of blood flow in the capillary (50), where the membrane of the moving blood cells are constantly in contact with the vessel wall or when the permeability of the vessel wall needs to be considered, e.g., blood flow through atherosclerotic plaques where deposition of cholesterol could increase the permeability of the arterial wall (51, 52). More details of the AIV model can be found in Materials and Methods and SI Appendix.
Fig. 1.
Schematic diagram of AIV. A fully connected neural network is used to approximate solutions to desired output parameters, , by considering space and time coordinates as inputs (x, y, z, t). The governing equations are encoded in the network, where the derivatives are computed via automatic differentiation in the TensorFlow code [Google (46)]. No-slip boundary conditions on the channel surfaces (including upper, lower, and lateral walls) are also introduced, namely, . The activation function for each neuron is . The parameters of the neural network are trained by minimizing the loss function, which is composed of three terms: data mismatch, wall boundary conditions, and residuals of all conservation laws. More details of the proposed framework are described in Materials and Methods and SI Appendix.
Fig. 2.
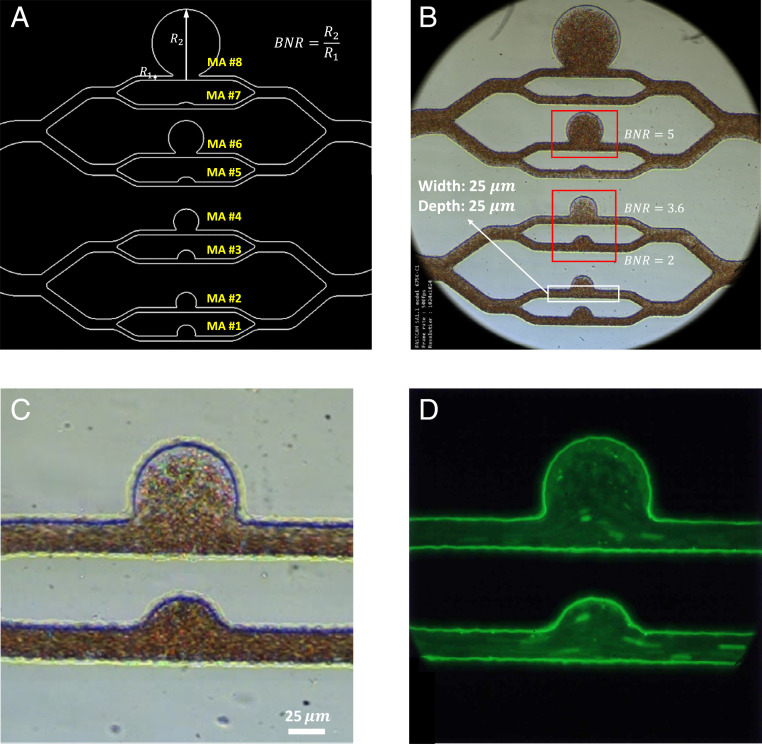
Design and microscopic images of the microfluidic platform, MAOAC. (A) Schematic diagram of the MA PDMS channels with different sizes. The size of the MA is characterized by the BNR, which is defined as the largest dimension of the MA body () divided by the diameter of feeding vessel (). The BNR of MA on MAOAC is varied from 1.5 to 12. The cross-section of the microchannel at the inlet and outlet portions is a square with an edge size of 25 . (B) An overview of a bright-field image illustrating blood flow in the microchip. (More details can be seen in Movie S1.) (C) A higher-magnification view of the bright-field image of two MA channels (BNR = 2 and BNR = 3.6). (D) A fluorescence-stained image of the same two MA channels shown in C. (More details can be seen in Movie S2.) AIV is used to extract velocity and pressure fields from the bright-field video images focusing on MAs with three typical sizes, namely, BNR = 2, 3.6, and 5, which are highlighted by the red rectangles in B. For MAs with BNR = 2 and 3.6, we perform platelet tracking on the fluorescence-stained video (D) for validation of AIV.
To demonstrate the capability of AIV based on a sequence of 2D microscopic blood-flow images, we first apply it to infer the velocity and stress fields in three-dimensional (3D) microchannels. As shown in Fig. 2 A and B, we design a microfluidic system, termed Micro-Aneurysm-On-A-Chip (MAOAC), to mimic MAs, which are the earliest clinically visible signs of diabetic retinopathy (DR), a complication of diabetes that could lead to visual impairment and blindness in diabetic patients (53). MAOAC contains eight straight microchannels intersecting with various sizes of cavities to mimic saccular-shaped MAs, the most prevalent shape of MAs observed in the retinal microvasculature of DR patients (54, 55). A high-speed camera is used to record blood flow in the microchannel (Fig. 2C). In addition, laser-induced fluorescence is employed to track the motion of platelets (Fig. 2D). More details of the experimental setup can be found in Materials and Methods. We adopt AIV to quantify key indicators of hemodynamics, such as velocity profiles, pressure, and wall shear stress, for various MAs and investigate alterations in hemodynamics induced by the change in size of MAs. In order to evaluate the performance of AIV, we compare the results from AIV with those obtained from five different experimental and computational methods: optical flow (36), Deep-PIV (56), single-cell tracking, CFD (57), and DPD (58).
Results
Inferring 2D Flow Fields.
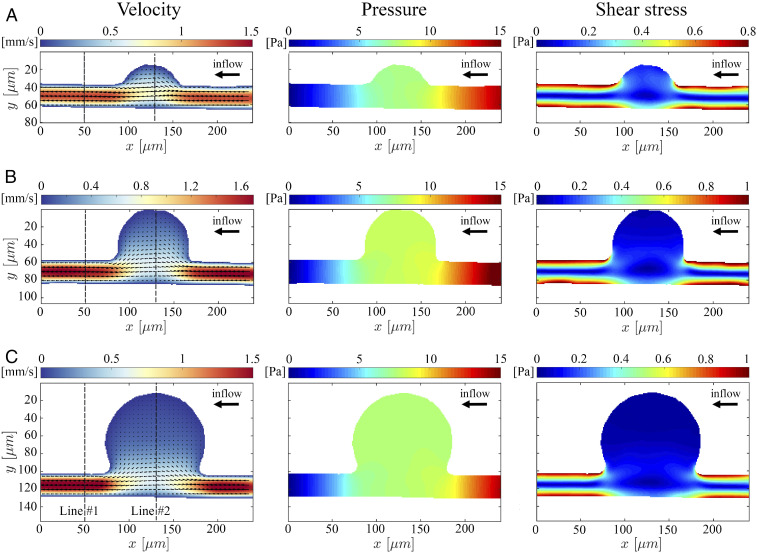
To demonstrate the capability of AIV to quantify the velocity and stress fields from microfluidic images during blood flow, we first extract 2D flow fields, such as velocity profile, pressure, and wall shear stress, from a sequence of 2D images taken in MAOAC and obtain the critical hemodynamic metrics. As shown in Fig. 2B, we select sequential images from three channels (MA3, MA4, and MA6), representing a small MA (body-to-neck ratio [BNR] = 2), an intermediate MA (BNR = 3.6), and a large MA (BNR = 5). Since the depth of these microchannels is only 25 m, we assume that the movement of RBCs captured by the microfluidic flow images occurs at the middle plane in the channel-depth direction such that the image data can be converted to a 2D spatiotemporal scalar field . Fig. 3 A–C show the 2D velocity fields, pressure fields, and shear stress profiles in the three MA channels based on the sequence of bright-field images in Fig. 2B. We observe that the maximum flow velocities in the inlet regions of the three MAOAC channels are about 1.5 mm/s, and the velocities drop along with pressure and shear stress when the flow enters the lumen of MAs. The decrease in velocity, pressure, and shear stress becomes more pronounced as the size of the MA increases. These alterations in hemodynamics are essential to gain a better understanding of the pathophysiology of MAs, since prior studies clearly suggest that reduced wall shear stress could cause endothelial dysfunction (59), which serves as a catalyst for the growth of aneurysms (60).
Fig. 3.
The 2D AIV predictions of velocity, pressure, and shear stress fields in MAOAC channels for BNR = 2 (A), BNR = 3.6 (B), and BNR = 5 (C). In Left, the arrows indicate the direction of the flow, whereas the color represents the magnitude of the velocity. AIV results are averaged over 100 image frames. The spatial distribution of the fields is represented by the colors in all of the plots.
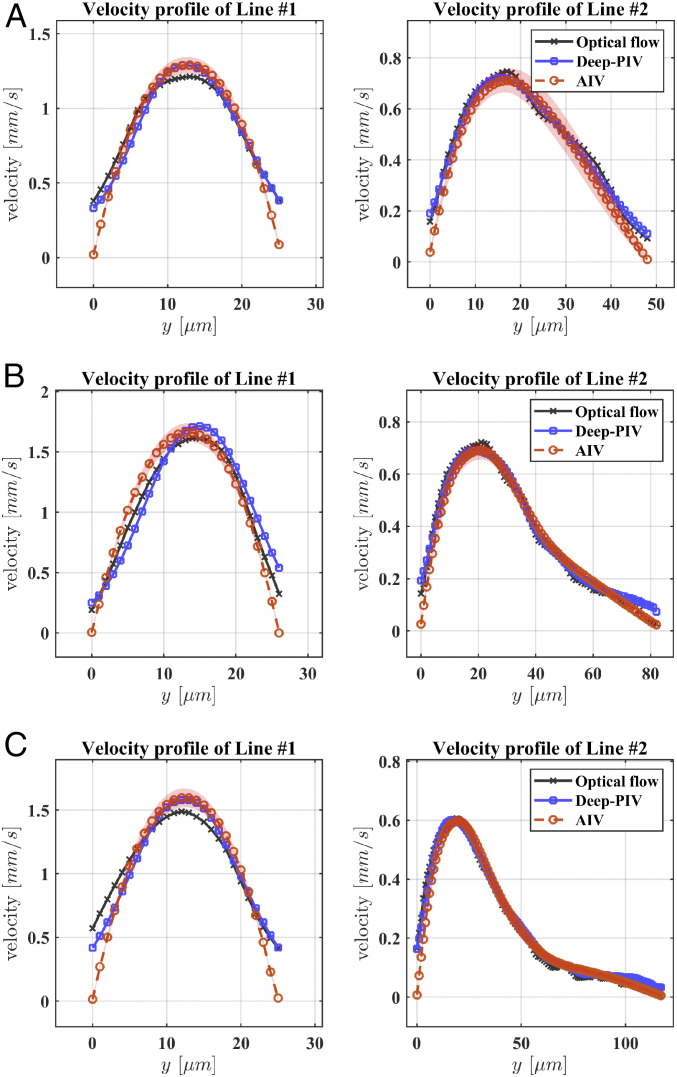
To further assess the reliability and accuracy of AIV, we compare our estimates with results obtained from three other independent approaches: the conventional optical flow method (36), Deep-PIV [an advanced PIV method with convolutional neural networks (32, 56)], and manual platelet tracking using the fluorescent images in our experiments. The implementation of the optical flow and Deep-PIV methods for predicting the fields in the present geometrical arrangements is described in SI Appendix. The velocity comparisons shown in Fig. 4 are performed at two points along vertical cross-lines of the microchannels: one located at the postaneurysm channel (Line #1, at m, as seen in Fig. 3) and the other one crossing the deepest region of the MA (Line #2, at m as seen in Fig. 3). The velocity profiles along Line #1 for the three microchannels (Fig. 4) show that our AIV model predictions of bulk flow velocities are consistent with the results from Deep-PIV and are less than 10% higher than the results from optical flow around the center of the channels. As for the near-wall velocity estimation, both Deep-PIV and optical flow techniques predict a nonvanishing velocity on the channel wall, whereas the AIV model gives zero velocity on the wall due to the imposition of the no-slip boundary condition. For velocity profile along Line #2, the AIV model predictions of the bulk flow velocity are in good agreement with the results of Deep-PIV and optical flow for all three MAOAC channels, but only AIV achieves zero velocity for near-wall predictions, as a consequence of the imposed boundary condition.
Fig. 4.
Comparison of the velocity profiles predicted by AIV, conventional optical flow, and Deep-PIV along two cross-lines in MAOAC channels with BNR = 2 (A), BNR = 3.6 (B), BNR = 5 (C). Comparisons are performed along two dotted lines marked at Fig. 3, Left. Line #1 is selected at the outlet portion of the microchannel, whereas Line #2 crosses the deepest region of the MAs. The symbols representing AIV predictions signify time-averaged values from 100 image frames, and the shadows represent SDs.
In addition to the above comparisons, we also performed a cross-validation of AIV by manually tracking the motion of platelets from fluorescence-stained video. As shown in Fig. 5A, four trajectories are identified for tracking the motion of four different platelets or platelet aggregates, with platelet velocities calculated along each of these trajectories. We also extract flow velocities along the same trajectories from velocity fields estimated by AIV in Fig. 5B for further comparison. To rationalize our approximation of local flow velocities using platelet velocities, we performed dissipative particle dynamics (DPD) simulations to model the transport of RBCs and platelets in channel MA#4 (BNR = 3.6), as shown in Fig. 6A. (Details of DPD simulation can be found in SI Appendix.) The trajectories of RBCs and platelets in Fig. 6B illustrate that in the straight channel, RBCs mostly travel in the core, where the flow velocity is high. This validates the assumptions, discussed earlier, that underlie our AIV framework. The platelets, however, flow in the cell-free layer near the vessel wall where the blood flow velocity is low, consistent with experimental and analytical studies (61–64). As a result, the displacement of platelets in the straight channel (Fig. 6C) is much smaller than that of RBCs during the same time interval. On the other hand, Fig. 6 B and C also show that the trajectories of RBCs and platelets overlap in the MA and that their displacements are comparable during the same time interval. These observations suggest that the velocities of platelets can be used to approximate local blood-flow velocities when platelets move within MAs.
Fig. 5.
Comparison of the velocities predicted by AIV and platelet tracking along four platelet trajectories in two MAOAC channels with BNR = 2 and 3.6. (A) Four platelet trajectories are tracked by using video images capturing experiments with fluorescence-staining. The velocity is computed as , where and are the positions of a platelet at two consecutive time steps with s. (B) The velocity magnitudes along these four trajectories are also extracted with AIV using bright-field video. (C) Magnitudes of velocity calculated along four trajectories using AIV and platelet tracking. The symbols representing AIV predictions signify the time-averaged values from 100 image frames, and the shadows represent the SDs.
Fig. 6.
Simulation of RBC and platelet transport in MAOAC channel with BNR = 3.6. (A) Three sequential snapshots (from left to right) of RBCs and platelets traveling in the microchannel. Red, RBCs; blue, platelets. Solvent particles are not plotted here to preserve clarity of presentation. (B) Trajectories of RBCs and platelets in the microchannel, as well as calculation of the displacements of RBCs and platelets based on their trajectories. Red curves, RBCs; blue curves, platelets. (C) Displacements of RBCs, platelets, and solvent particles as functions of time. The dotted lines signify displacements of RBCs, platelets, and solvent particles that do not travel into the MAs, whereas the solid lines designate the displacements of RBCs, platelets, and solvent particles that travel into the MAs. Each curve represents the average of 15 samples randomly selected from the simulation, except that the solvent particles which do not travel into the MAs were selected randomly around the centerline of the postaneurysm channel.
Velocity estimates along the four trajectories are plotted in Fig. 5C. These results show that the AIV predictions are in good agreement with velocities calculated from the two trajectories (Traj-3 and Traj-4) of platelets traveling in the MAs in channel MA#4. This demonstrates the capability of AIV to accurately infer flow fields in blood microcirculation. At platelet trajectories further away from the perimeter of the MA, such as those along Traj-1 and Traj-2, the differences between AIV (on RBC trajectories) and platelet tracking become more accentuated, as anticipated from the effect of platelet margination.
Extracting 3D Flow Field from 2D Images.
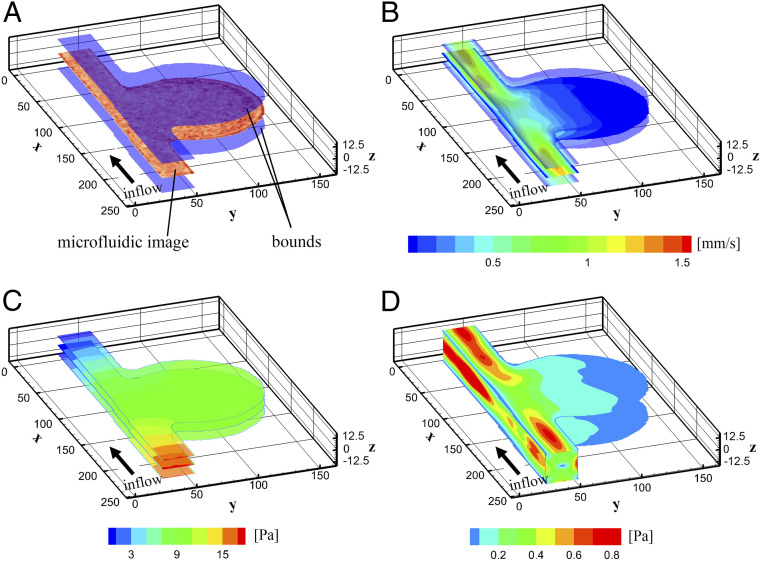
Next, we demonstrate that AIV can infer the full 3D flow velocity profiles along the entire depth of the microchannel using 2D images by invoking the underlying physical laws of fluid flow. Such estimation cannot be accomplished by using existing methods, such as Deep-PIV or optical flow, due to the lack of data at different depths of the channel. In order to obtain 3D velocity profiles, as shown in Fig. 7A, we extend our computational domain along the depth direction () by 25 m ( m), in line with the depth of the MAOAC channels. We enforce the no-slip boundary condition on the upper and lower surfaces ( m) and the lateral channel walls such that . Similar to the 2D case, we assume that the movement of RBCs occurs primarily at the middle plane along the channel depth, so that data from the images can be converted to a 3D spatiotemporal scalar field . A schematic of the AIV model, which is based on 3D physics-informed neural networks, is illustrated in Fig. 1 and in SI Appendix. Note that while the image data correspond to a 2D plane, the points for computing the residual loss are uniformly selected in the 3D domain. The training process for the 3D cases is similar to that for 2D, which can be found in SI Appendix.
Fig. 7.
The 3D AIV predictions for MAOAC channel with BNR = 5. (A) A 3D computational domain is constructed by extending the 2D domain along the depth direction () by 25 m ( m), consistent with the depth of the MAOAC channels. The images capture the motion of RBCs at the middle plane of the channel depth direction (). (B and C) Velocity (B) and pressure fields (C) at three different cross-sections ( m) along the depth of the channel. (D) Shear stress on the channel wall. AIV results are averaged over 100 image frames.
Fig. 7 B and C illustrate the velocity and pressure fields inferred by the AIV model at three different depth positions of the MA#6 channel (BNR = 5): z = 0 (middle plane) and z = 7.5 m. These results show that the flow velocities measured at z = 7.5 are significantly smaller than those at the middle plane, whereas no notable changes are observed in the flow pressure here in the depth direction. The shear stress on the channel wall is illustrated in Fig. 7D, and it shows a sudden drop of the wall shear stress from the parent vessel to the vessel wall of the MA. The wall shear stress continues to decrease in the region further away from the feeding channel, consistent with our 2D predictions and the findings reported from prior studies (42, 59, 65).
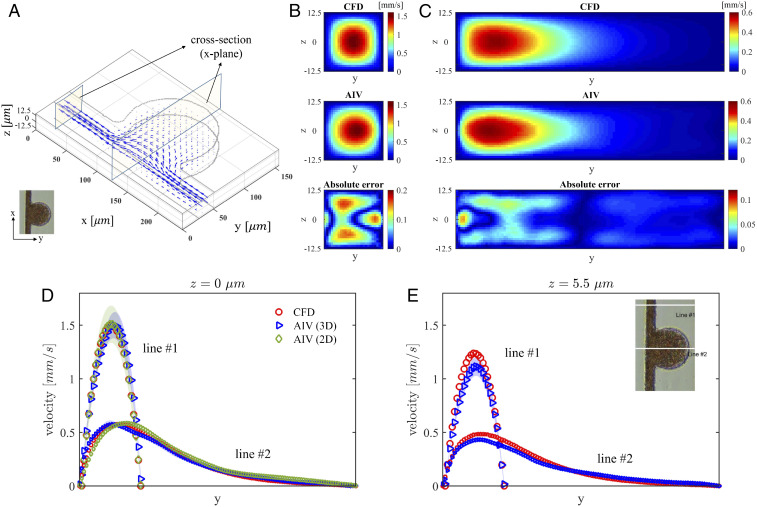
To evaluate the 3D results from AIV, we perform a companion 3D CFD simulation using the same governing equations (Eq. 2 in Materials and Methods) and computational domain as in the AIV method. We also employ the Carreau–Yasuda rheology model (Eq. 3) to capture the shear-thinning behavior of the blood. The governing equations are solved by using , a fast CFD solver based on the spectral element method (57). We use the pressure difference between the channel inlet and the outlet from the AIV model to drive blood flow in the channel. As shown in Fig. 8A, the velocity fields inferred from the 3D AIV and those obtained from the CFD simulations for MA#6 are compared at two cross-sections of the microchannels, with one located at the postaneurysm channel and the other one crossing the deepest region of MAs. The velocity maps of these two cross-sections in Fig. 8 B and C show that the predictions of AIV agree with the results of the CFD simulations. The maximum relative -norm errors for these two cross-sections are calculated to be and , respectively. We further plot the velocity profiles at these two cross-sections along the lines of m and m (Fig. 8 D and E). These results also show good agreement between the AIV model and 3D CFD simulation. In particular, Fig. 8 D and E demonstrate that 3D AIV can capture the expected decay of the velocity along the z-direction. There are some differences between the predictions of the AIV model and the CFD model, although both models invoke the same physical laws (Eq. 2), constitutive equation (Eq. 3), and boundary conditions. We also plot the AIV-prediction and the CFD-simulation results of shear stress along two lines on two different planes in the channel-depth direction (Z = 0 m and Z = 3.5 m), which can be found in SI Appendix, Fig. S3. Our results show that AIV predictions are comparable with the CFD simulation results with an averaged error of 10%. These differences are attributed to the fact that AIV directly incorporates the flow-image data of RBCs in estimating the fields and thus provides a more realistic picture of blood flow in the microchannel than CFD models. Similar trends are also observed for the 3D velocity estimates for the MA#3 channel, which can be found in SI Appendix.
Fig. 8.
Comparison of 3D AIV predictions with results of CFD simulations for the MAOAC channel with BNR = 5. (A) The 3D velocity vectors inferred from AIV. Two cross-sections along the x axis are selected for comparison with CFD simulations. (B) Velocity at the cross-section located at m in the microchannel. From top to bottom: CFD simulation, AIV model, and absolute error. The relative -norm error at this cross-plane is . (C) Velocity magnitudes at the cross-section located at m in the microchannel. From top to bottom: CFD simulation, AIV model, and absolute error. The relative -norm error is . (D and E) Velocity profiles along two cross-lines at planes m and m. The symbols representing AIV predictions signify the time-averaged values from 100 image frames, and the shadows represent the SDs.
Discussion and Concluding Remarks
In this work, we have developed a unique model to determine the 3D velocity, pressure, and stress fields associated with human blood flow in microcirculation by synergistically integrating the underlying physics with sequential images from microfluidics experiment and machine learning. The advantage of the proposed AIV model is that the conservation laws of the physics of blood flow and no-slip boundary conditions are encoded into a deep-learning neural network to interpret direct experimental observations from a microfluidics platform. We note that the flow velocity boundary conditions (slip or nonslip) on the channel wall in AIV can be specified by the user, depending on the particular case of interest. Therefore, the predictions of near-wall velocity by AIV are more physiologically relevant than those measured from optical flow and PIV. This feature is crucial for evaluating the wall shear stress, a hemodynamic metric that is associated with many vascular diseases (4, 6, 59). In distinct contrast to CFD methods, whose results are very sensitive to flow boundary conditions at the inlets and outlets, AIV does not require a priori knowledge of these boundary conditions to estimate flow fields. This unique feature overcomes the challenge in many applications, where the exact pressure profiles at the local inlet(s) and outlet(s) of an in vitro microfluidic device or a capillary bed in vivo are difficult or even impossible to measure directly or approximate. Moreover, the AIV model is more effective than CFD simulation when making a prediction of the flow field undergoing dynamic changes due to moving boundaries, such as the prediction of blood flow within deformable vessel wall or changes of hemodynamics in the MA due to blood clotting, as observed from high-resolution adaptive optics scanning laser ophthalmoscopy (AOSLO) images (42) and histology studies (66).
To validate the present approach, we compare the predictions of AIV models on the full spectrum of key hemodynamic parameters, such as pressure differential, shear rate, and wall shear stress, with results obtained from five different experimental and computational methods: optical flow (36), Deep-PIV (56), single cell tracking, CFD simulations (57), and DPD (58). Our results show that AIV predictions of bulk flow velocities in MAOAC with different geometries are in agreement with results from these other independent methods. In contrast to CFD models, AIV is capable of inferring flow field on-the-fly in microchannels because of its flexibility to incorporate data from sequential experimental images, particularly with fluids, such as blood, with a heterogeneous composition. On the other hand, we demonstrate that AIV can infer, owing to the encoded physics laws, full 3D flow fields along the depth of the microchannel from a sequence of 2D images. This is difficult to achieve with conventional PIV or other methods to estimate particle movement, which require advanced experimental apparatus, such as stereoscopic or holographic PIV (67, 68), to generate image data at different depths of the channel.
The present experimental results also provide insights and quantitative details to rationalize a variety of clinical findings pertaining to MAs in DR. The predictions of the flow field using MAOAC and AIV show reduced flow velocity and wall shear stress in the MAs with different BNR. Particularly, as the BNR of the MAs increases, the decrease in shear stress near the channel wall of the MAs becomes more significant. These results provide a rationale for the clinical finding that endothelial dysfunction, which is manifested as increased von Willebrand factor expression on the endothelial cell, is more likely to occur in MAs with larger BNR due to the reduced wall shear stress (59). We note that AIV can assess the blood-flow velocity for different shapes of MAs, such as focal bulging, fusiform, mixed saccular/fusiform, and so on. In this paper, we designed the microchannels to mimic various sizes of saccular-shaped MAs, because they are the most prevalent shape of MAs observed in the retinal microvasculature of DR patients. Future studies could employ additional microfluidic geometry designs to address different types of MAs.
The altered hemodynamics in MAs also contributes to thrombosis in the vascular lumen of MAs, a recently documented pathology of DR (42). In vivo images obtained from AOSLO have been used to classify the MAs’ morphologies into different groups (54), as well as to detect the blood clotting inside MAs (42). The AIV model can potentially be used to interpret the AOSLO images and predict the thrombus formation or rupture of MAs by monitoring the key hemodynamic metrics, such as wall shear stress, which is associated with the inflammation and dysfunction of endothelium cell, as well as the shear rate and the platelet residence time in the MAs, which can be used to predict the platelet activation and aggregation. We note that quantification of hemodynamic parameters from in vivo measurements in previous studies (42, 59, 65) were performed by using CFD models with assumed and general inflow and outflow boundary conditions since patient-specific inflow velocity was not readily available from in vivo images. The present AIV model, which does not require implementation of flow boundary conditions and mesh generation, can potentially learn the flow fields directly from in vivo video images and provide more accurate evaluation of hemodynamic indicators.
The AIV model proposed in this work can also be extended to accommodate various data sources through a multifidelity (MF) framework (69, 70), where additional neural networks are used to learn the correlation between the low-fidelity (e.g., simulation) and high-fidelity (e.g., experimental) data. The MF framework is very effective when there is a dearth of reliable, high-fidelity data and, thus, could be particularly useful for learning from in vivo images whose resolution and quality may be limited. For example, when only a portion of the flow field can be observed from in vivo images or only measurements of the velocity along a limited set of trajectories are available (e.g., by tracking local displacements of blood cells), we could first perform 3D CFD simulations to evaluate the flow field. These simulation data are considered low-fidelity data, as they are sensitive to the inflow and outflow boundary conditions, which are not always available from in vivo measurements. Following this, the 3D simulation data (low fidelity) could be integrated with the partial velocity field estimated by AIV based on in vivo images (high fidelity) using the MF framework to predict the entire flow field.
Although we have demonstrated several advantages of AIV over conventional methods, we also note some limitations of the AIV model. First, the computational cost of training the AIV model could be higher than the cost of optical flow or PIV methods because of the need to solve the governing equations of the underlying physics laws. Application of multi-graphics-processing unit training could help boost computational efficiency. Moreover, the trained AIV model could be used as a pretrained network to initialize the training of a new AIV model for other microfluidic experiments, thereby reducing the computational cost for future tasks. In this work, we assume that the flow of RBCs captured by sequential 2D images occurs at the middle plane in the channel-depth direction (). However, the 2D measurement plane generally has a certain finite thickness, which is determined by the depth of field of the objective lens. Incorporating the movement of RBCs out of the middle plane could lead to an underestimation of cross-sectional velocities. To extend the application of AIV to assess in vivo blood flow, we may need to consider the flow pulsatility as well as the dynamic deformation of the blood vessel wall. While AIV can naturally learn the pulsatile flow from image data, the underlying physics laws encoded in the AIV model need to be revised to account for the effect of deformable flow boundaries. For example, we can encode fluid-governing equations formulated on the basis of the arbitrary Lagrangian–Eulerian method, which is a standard approach to solve dynamic problems involving fluid–structure interaction and deformation of flow boundary (71, 72).
In summary, we present AIV, a unique platform that is capable of automatically inferring blood-flow field in microfluidic channels, and compute key hemodynamic parameters that are associated with the pathophysiology of MAs, one of the earliest clinically visible signs of DR. Encoded with physical laws and constitutive equations and integrated with neural-network training algorithms, AIV performs more effectively compared to the existing methods, particularly when the experimental data are limited. AIV also incorporates data from visual images, which is particularly important for investigation of blood flow (i.e., flow of RBCs and other blood components such as platelets) under pathological conditions where reliable constitutive laws may not be able to accurately describe hematological properties of blood for patient-specific disease states. AIV also can potentially facilitate scientific research in laboratories where systematic experiments alone, even with advanced tools, may not be sufficient to quantify all of the key parameters responsible for the pathogenesis of vascular injury. With continuous training, AIV offers a potentially powerful pathway to infer hemodynamics from in vivo examination and to develop quantitative metrics for patient diagnosis and monitoring.
Materials and Methods
Experimental Setup.
MA PDMS channel fabrication.
As illustrated in Fig. 2 A and B, eight microchannels that contain various sizes of cavities are designed to mimic different MAs. The BNR of the simulated MAs is defined as the largest caliber of the MA body divided by the size of feeding vessels and varies from 12 to 1.5. These MA channels were fabricated with polydimethylsiloxane (PDMS) using standard soft lithography. Each device was fabricated by using a master mold, lithographically patterned with SU-8 negative photoresist (Microchem Corporation) on a 4-inch silicon wafer (Silicon Connection), which was later placed inside a Petri dish. Commercial thermocurable PDMS (Sylgard 184, Dowsil) prepolymer was prepared by mixing the base and curing agent at a 10:1 weight ratio, following which the PDMS prepolymers were degassed under vacuum and cast onto the mold. Thermal cross-linking of PDMS was performed by curing at 80 °C for 2 h. The cured PDMS was cut and peeled off from the channel mold, following which the inlet and outlet access ports were created by using a 1.5-mm-diameter punch. Next, the PDMS channel was bonded with a cover slide under 80 °C for 2 h. Experiments were conducted after plasma pretreatment for 1 min.
Sample preparation.
Peripheral blood was drawn from a healthy donor by Venipuncture into a K2E EDTA tube, after which the whole blood was centrifuged at 200 × g for 12 min to extract platelet-rich plasma (PRP). The upper layer of PRP was further centrifuged at 1,200 × g for 5 min to acquire platelets, which were washed three times with platelet-washing solution and then resuspended in phosphate-buffered saline. The remaining blood cells were stored at 4 °C for later use. The platelets were then stained with DIOC6 (Sigma-Aldrich) (0.5 g/mL) for 1 h at room temperature. After being washed five times, the stained platelets were remixed with the remaining blood cells from the original whole blood at a 50% hematocrit for fluorescence imaging in the MA PDMS channels. The entire process was completed within 4 h to minimize the risk of time-dependent platelet malfunction.
All procedures on peripheral blood specimens were approved and performed in accordance with the Singapore National Health Group Domain Specific Review Board (the central ethics committee) and mutually recognized by Nanyang Technological University Institutional Review Board (IRB#2018/00671). All blood specimens were de-identified prior to use in the experiment.
Microfluidics experiment and visualization.
The microfluidic device was installed on a Nikon Eclipse T2000-U (Nikon) and visualized under a 40× objective. A blood sample, 20L in volume, was loaded into a reservoir (outlet) of the PDMS channel. A negative pressure of about −5 mbar was applied to the outlet, such that the blood cells flowed from the inlet into the direction of the outlet, thus generating the flow pattern recorded by the camera. Video images were recorded by a high-speed camera, FASTCAM SA1.1 (Photron). Bright-field images (Fig. 2 B and C), which are recorded at 500 frames per second (fps) and resolved with 1 m/pixel, served as the training data for the AIV model to infer velocity fields in microchannels. The fluorescent images (Fig. 2D), where the platelets or platelet aggregation were visualized as bright spots, were recorded at 60 fps, and they were used to perform cell-tracking measurements of platelets for AIV validation.
AIV Model.
Underlying physics laws.
To estimate the velocity and pressure fields from a sequence of images from microfluidic experiments (Fig. 2C), we follow the optical flow constraint (35), a basic assumption widely used in computer vision or fluid visualization. Here, it is assumed that the variation in the image brightness represents blood flow, and the image intensity is a spatiotemporal scalar field , whose transport can be described by an advection equation:
| [1] |
where is the 2D velocity projected onto the image plane, and is the spatial derivative operator. The fluid flow is taken to be governed by the incompressible Navier–Stokes equations:
| [2] |
where (1,060 kg/) and are the fluid density and pressure, respectively; is the dynamic viscosity. We also implemented the Carreau–Yasuda rheology model to capture the shear-thinning behavior of blood, which is expressed as
| [3] |
where Pas is the reference viscosity; , , s, and , all of which are parametrized for human blood (73). The shear rate, , which depends on the second invariant of the stress–strain rate tensor , is written as
| [4] |
In order to extract relevant nondimensional parameters, we define the characteristic length as m (which is equal to the channel width) and the characteristic velocity as mm/s (which is the mean velocity inside the vessel). As a result, the Reynolds number representative of the fluid flow problem considered here is .
Integrating physics with image data from microfluidic experiments using AIV.
The AIV technique employed here is based on PINNs, which were originally developed for solving forward and inverse problems for partial differential equations (47, 74) and were subsequently extended to solve fluid-mechanics problems (48, 75–77). AIV is capable of seamlessly assimilating the Navier–Stokes equations and the experimental data, and thus allows for the extraction of velocity and pressure fields by considering both the underlying physics of blood flow and the microfluidics or in vivo image data. As shown in Fig. 1, AIV contains a fully connected neural network, which is used to approximate the solutions, i.e., . This neural network takes the coordinates and time as inputs and provides as outputs the corresponding image intensity, velocity, and pressure. As the image intensity in the spatiotemporal domain can be obtained from the image data, the loss function of the neural network can be defined as
| [5] |
where and are the data from visual images and the output of neural network, respectively; and is the number of pixels in the investigated domain. In addition to loss from the mismatch between image data and neural-network predictions (), AIV introduces a residual loss () resulting from computing the residuals of the governing equations (Eq. 2) on random points to take into account the underlying physics of blood flow. is expressed as:
| [6] |
where is the number of residual points for evaluating the equations, which can be selected in the computational domain based on the location of interest. The no-slip boundary conditions on the channel walls are enforced by adding another loss term:
| [7] |
where denotes the boundaries of the channel wall; is the total number of pixels on the boundary. As a result, the parameters of the AIV model are obtained by minimizing the following total loss function:
| [8] |
where and are the weighing coefficients to account for the relative contributions of the three terms in the total loss function. We note that for AIV, using large values of and can accelerate the optimization because the image data can be quickly regressed, but it may also result in overfitting. More details of how to select the appropriate weighing coefficients in the loss function for training PINNs can be found in refs. 76 and 77. In our simulations, we chose and through a trial-and-run process. Details of the selection of these parameters can be found in SI Appendix. We train the network using the Adam optimizer (78), an adaptive algorithm for gradient-based, first-order optimization of stochastic objective functions. Once the training is accomplished, the AIV model can infer the full solutions of at any given point inside the computational domain and compute the shear rate and wall shear stress. More details of the hyperparameters of the AIV model and the training strategy can be found in SI Appendix.
Supplementary Material
Acknowledgments
S.C. and G.E.K. were supported by Department of Energy Physics-Informed Learning Machines Project No. DE-SC0019453. H.L., M.D., and G.E.K. were supported by NIH Grant R01HL154150. M.D. was supported by the Massachusetts Institute of Technology J-Clinic for Machine Learning and Health. F.K. and S.S. were supported by Nanyang Technological University, Singapore, through the Distinguished University Professorship (S.S.).
Footnotes
Competing interest statement: S.C., H.L., M.D., G.E.K., and S.S. have filed a patent application based on the research presented in this paper.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2100697118/-/DCSupplemental.
Data Availability
The data and codes used in this manuscript are publicly available on GitHub (https://github.com/shengzesnail/AIV_MAOAC) (79).
References
- 1.Lipowsky H. H., Microvascular rheology and hemodynamics. Microcirculation 12, 5–15 (2005). [DOI] [PubMed] [Google Scholar]
- 2.Popel A. S., Johnson P. C., Microcirculation and hemorheology. Annu. Rev. Fluid Mech. 37, 43–69 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Secomb T. W., Blood flow in the microcirculation. Annu. Rev. Fluid Mech. 49, 443–461 (2017). [Google Scholar]
- 4.Taylor C. A., Humphrey J., Open problems in computational vascular biomechanics: Hemodynamics and arterial wall mechanics. Comput. Methods Appl. Mech. Eng. 198, 3514–3523 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nixon A. M., Gunel M., Sumpio B. E., The critical role of hemodynamics in the development of cerebral vascular disease: A review. J. Neurosurg. 112, 1240–1253 (2010). [DOI] [PubMed] [Google Scholar]
- 6.Green D. J., Hopman M. T., Padilla J., Laughlin M. H., Thijssen D. H., Vascular adaptation to exercise in humans: Role of hemodynamic stimuli. Physiol. Rev. 97, 495–528 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sagel J., Colwell J. A., Crook L., Marta L., Increased platelet aggregation in early diabetes mellitus. Ann. Intern. Med. 82, 733–738 (1975). [DOI] [PubMed] [Google Scholar]
- 8.Jackson S. P., The growing complexity of platelet aggregation. Blood 109, 5087–5095 (2007). [DOI] [PubMed] [Google Scholar]
- 9.Kaiser D., Freyberg M. A., Friedl P., Lack of hemodynamic forces triggers apoptosis in vascular endothelial cells. Biochem. Biophys. Res. Commun. 231, 586–590 (1997). [DOI] [PubMed] [Google Scholar]
- 10.Gimbrone M. A. Jr, Topper J. N., Nagel T., Anderson K. R., Garcia-Cardeña G., Endothelial dysfunction, hemodynamic forces, and . Ann. N. Y. Acad. Sci. 902, 230–240 (2000). [DOI] [PubMed] [Google Scholar]
- 11.Casa L. D., Deaton D. H., Ku D. N., Role of high shear rate in thrombosis. J. Vasc. Surg. 61, 1068–1080 (2015). [DOI] [PubMed] [Google Scholar]
- 12.Kwan C. C., Fawzi A. A., Imaging and biomarkers in diabetic macular edema and diabetic retinopathy. Curr. Diabetes Rep. 19, 95 (2019). [DOI] [PubMed] [Google Scholar]
- 13.Choo Y. W., Jeong J., Jung K., Recent advances in intravital microscopy for investigation of dynamic cellular behavior in vivo. BMB Rep. 53, 357 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Courtie E., Veenith T., Logan A., Denniston A., Blanch R., Retinal blood flow in critical illness and systemic disease: A review. Ann. Intensive Care 10, 1–18 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Omori T., Imai Y., Kikuchi K., Ishikawa T., Yamaguchi T., Hemodynamics in the microcirculation and in microfluidics. Ann. Biomed. Eng. 43, 238–257 (2015). [DOI] [PubMed] [Google Scholar]
- 16.Hastings S. M., Griffin M. T., Ku D. N., Hemodynamic studies of platelet thrombosis using microfluidics. Platelets 28, 427–433 (2017). [DOI] [PubMed] [Google Scholar]
- 17.Herbig B. A., Yu X., Diamond S. L., Using microfluidic devices to study thrombosis in pathological blood flows. Biomicrofluidics 12, 042201 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Sebastian B., Dittrich P. S., Microfluidics to mimic blood flow in health and disease. Annu. Rev. Fluid Mech. 50, 483–504 (2018). [Google Scholar]
- 19.Santiago J. G., Wereley S. T., Meinhart C. D., Beebe D., Adrian R. J., A particle image velocimetry system for microfluidics. Exp. Fluid 25, 316–319 (1998). [Google Scholar]
- 20.Meinhart C. D., Wereley S. T., Santiago J. G., PIV measurements of a microchannel flow. Exp. Fluid 27, 414–419 (1999). [Google Scholar]
- 21.Wereley S. T., Gui L., Meinhart C., Advanced algorithms for microscale particle image velocimetry. AIAA J. 40, 1047–1055 (2002). [Google Scholar]
- 22.Raben J. S., Klein S. A., Posner J. D., Vlachos P. P., Improved accuracy of time-resolved micro-particle image velocimetry using phase-correlation and confocal microscopy. Microfluid. Nanofluidics 14, 431–444 (2013). [Google Scholar]
- 23.Kähler C. J., et al. , Main results of the 4th International PIV Challenge. Exp. Fluid 57, 97 (2016). [Google Scholar]
- 24.Lindken R., Rossi M., Große S., Westerweel J., Micro-particle image velocimetry (PIV): Recent developments, applications, and guidelines. Lab Chip 9, 2551–2567 (2009). [DOI] [PubMed] [Google Scholar]
- 25.Williams S. J., Park C., Wereley S. T., Advances and applications on microfluidic velocimetry techniques. Microfluid. Nanofluid. 8, 709–726 (2010). [Google Scholar]
- 26.Wereley S. T., Meinhart C. D., Recent advances in micro-particle image velocimetry. Annu. Rev. Fluid Mech. 42, 557–576 (2010). [Google Scholar]
- 27.Lima R., Ishikawa T., Imai Y., Yamaguchi T., “Blood flow behavior in microchannels: Past, current and future trends” in Single and Two-Phase Flows on Chemical and Biomedical Engineering, R. Dias, A. A. Martins, R. Lima, T. M. Mata, Eds. (Bentham Science, Sharjah, United Arab Emirates, 2012), pp. 513–547. [Google Scholar]
- 28.Pitts K., Mehri R., Mavriplis C., Fenech M., Micro-particle image velocimetry measurement of blood flow: Validation and analysis of data pre-processing and processing methods. Meas. Sci. Technol. 23, 105302 (2012). [Google Scholar]
- 29.Lima R., et al. , In vitro blood flow in a rectangular PDMS microchannel: Experimental observations using a confocal micro-PIV system. Biomed. Microdevices 10, 153–167 (2008). [DOI] [PubMed] [Google Scholar]
- 30.Champagnat F., et al. , Fast and accurate PIV computation using highly parallel iterative correlation maximization. Exp. Fluid 50, 1169 (2011). [Google Scholar]
- 31.Rabault J., Kolaas J., Jensen A., Performing particle image velocimetry using artificial neural networks: A proof-of-concept. Meas. Sci. Technol. 28, 125301 (2017). [Google Scholar]
- 32.Cai S., Liang J., Gao Q., Xu C., Wei R., Particle image velocimetry based on a deep learning motion estimator. IEEE Trans. Inst. Measur. 69, 3538–3554 (2020). [Google Scholar]
- 33.Horn B., Schunck B., Determining optical flow. Artif. Intell. 17, 185–203 (1981). [Google Scholar]
- 34.Corpetti T., Heitz D., Arroyo G., Mémin E., Santa-Cruz A., Fluid experimental flow estimation based on an optical-flow scheme. Exp. Fluid 40, 80–97 (2006). [Google Scholar]
- 35.Liu T., Shen L., Fluid flow and optical flow. J. Fluid Mech. 614, 253–291 (2008). [Google Scholar]
- 36.Heitz D., Mémin E., Schnörr C., Variational fluid flow measurements from image sequences: Synopsis and perspectives. Exp. Fluid 48, 369–393 (2010). [Google Scholar]
- 37.Gompper G., Fedosov D. A., Modeling microcirculatory blood flow: Current state and future perspectives. Wiley Interdis. Rev. Syst. Biol. Med. 8, 157–168 (2016). [DOI] [PubMed] [Google Scholar]
- 38.O’Connor J., Day P., Mandal P., Revell A., Computational fluid dynamics in the microcirculation and microfluidics: What role can the lattice Boltzmann method play? Integr. Biol. 8, 589–602 (2016). [DOI] [PubMed] [Google Scholar]
- 39.Westein E., et al. , Atherosclerotic geometries exacerbate pathological thrombus formation poststenosis in a von Willebrand factor-dependent manner. Proc. Natl. Acad. Sci. U.S.A. 110, 1357–1362 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Yazdani A., Li H., Humphrey J. D., Karniadakis G. E., A general shear-dependent model for thrombus formation. PLoS Comput. Biol. 13, e1005291 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Mountrakis L., Lorenz E., Hoekstra A., Where do the platelets go? A simulation study of fully resolved blood flow through aneurysmal vessels. Interf. Focus 3, 20120089 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bernabeu M. O., Lu Y., Abu-Qamar O., Aiello L. P., Sun J. K., Estimation of diabetic retinal microaneurysm perfusion parameters based on computational fluid dynamics modeling of adaptive optics scanning laser ophthalmoscopy. Front. Physiol. 9, 989 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lu Y., et al. , Computational fluid dynamics assisted characterization of parafoveal hemodynamics in normal and diabetic eyes using adaptive optics scanning laser ophthalmoscopy. Biomed. Optic Express 7, 4958–4973 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Perdikaris P., Grinberg L., Karniadakis G. E., Multiscale modeling and simulation of brain blood flow. Phys. Fluids 28, 021304 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Sankaran S., Marsden A. L., A stochastic collocation method for uncertainty quantification and propagation in cardiovascular simulations. J. Biomech. Eng. 133 (2011). [DOI] [PubMed] [Google Scholar]
- 46.Abadi M., et al. , “Tensorflow: A system for large-scale machine learning” in 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16) (USENIX Association, Berkeley, CA, 2016), pp. 265–283.
- 47.Raissi M., Perdikaris P., Karniadakis G. E., Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019). [Google Scholar]
- 48.Raissi M., Yazdani A., Karniadakis G. E., Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 367, 1026–1030 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Fedosov D., Caswell B., Suresh S., Karniadakis G., Quantifying the biophysical characteristics of plasmodium-falciparum-parasitized red blood cells in microcirculation. Proc. Natl. Acad. Sci. U.S.A. 108, 35–39 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ruckenstein E., Rajora P., On the no-slip boundary condition of hydrodynamics. J. Colloid Interface Sci. 96, 488–491 (1983). [Google Scholar]
- 51.Guha H., Chaudhury T., Flow in an arteriosclerotic blood vessel with rigid permeable wall. Bull. Math. Biol. 47, 613–627 (1985). [DOI] [PubMed] [Google Scholar]
- 52.Misra J., Shit G., Role of slip velocity in blood flow through stenosed arteries: A non-Newtonian model. J. Mech. Med. Biol. 7, 337–353 (2007). [Google Scholar]
- 53.Ting D. S. W., Cheung G. C. M., Wong T. Y., Diabetic retinopathy: Global prevalence, major risk factors, screening practices and public health challenges: A review. Clin. Exp. Ophthalmol. 44, 260–277 (2016). [DOI] [PubMed] [Google Scholar]
- 54.Dubow M., et al. , Classification of human retinal microaneurysms using adaptive optics scanning light ophthalmoscope fluorescein angiography. Invest. Ophthalmol. Vis. Sci. 55, 1299–1309 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Schreur V., et al. , Morphological and topographical appearance of microaneurysms on optical coherence tomography angiography. Br. J. Ophthalmol. 103, 630–635 (2019). [DOI] [PubMed] [Google Scholar]
- 56.Cai S., et al. , “Deep-PIV: A new framework of PIV using deep learning techniques” in 13th International Symposium on Particle Image Velocimetry: ISPIV 2019, C. J. Kähler, R. Hain, S. Scharnowski, T. Fuchs, Eds. (Universität der Bundeswehr, Munich, Germany, 2019).
- 57.Karniadakis G., Sherwin S., Spectral/hp Element Methods for Computational Fluid Dynamics (Oxford University Press, Oxford, UK, 2013). [Google Scholar]
- 58.Chang H. Y., et al. , Quantifying platelet margination in diabetic blood flow. Biophys. J. 115, 1371–1382 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ezra E., Keinan E., Mandel Y., Boulton M. E., Nahmias Y., Non-dimensional analysis of retinal microaneurysms: Critical threshold for treatment. Integr. Biol. 5, 474–480 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Boussel L., et al. , Aneurysm growth occurs at region of low wall shear stress: Patient-specific correlation of hemodynamics and growth in a longitudinal study. Stroke 39, 2997–3002 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Fahraeus R., Lindqvist T., The viscosity of the blood in narrow capillary tubes. Amm. J. Physiol. Leg. Cont. 96, 562–568 (1931). [Google Scholar]
- 62.Aarts P., et al. , Blood platelets are concentrated near the wall and red blood cells, in the center in flowing blood. Arteriosclerosis 8, 819–824 (1988). [DOI] [PubMed] [Google Scholar]
- 63.Zhao R., Kameneva M. V., Antaki J. F., Investigation of platelet margination phenomena at elevated shear stress. Biorheology 44, 161–177 (2007). [PubMed] [Google Scholar]
- 64.Kumar A., Graham M. D., Margination and segregation in confined flows of blood and other multicomponent suspensions. Soft Matter 8, 10536–10548 (2012). [DOI] [PubMed] [Google Scholar]
- 65.Li H., et al. , Predictive modelling of thrombus formation in diabetic retinal microaneurysms. R. Soc. Open Sci. 7, 201102 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Stitt A., Gardiner T., Archer D., Histological and ultrastructural investigation of retinal microaneurysm development in diabetic patients. Br. J. Ophthalmol. 79, 362–367 (1995). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Lindken R., Westerweel J., Wieneke B., Stereoscopic micro particle image velocimetry. Exp. Fluid 41, 161–171 (2006). [Google Scholar]
- 68.Satake S., et al. , Measurements of 3D flow in a micro-pipe via micro digital holographic particle tracking velocimetry. Meas. Sci. Technol. 17, 1647 (2006). [Google Scholar]
- 69.Meng X., Karniadakis G. E., A composite neural network that learns from multi-fidelity data: Application to function approximation and inverse PDE problems. J. Comput. Phys. 401, 109020 (2020). [Google Scholar]
- 70.Lu L., et al. , Extraction of mechanical properties of materials through deep learning from instrumented indentation. Proc. Natl. Acad. Sci. U.S.A. 117, 7052–7062 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Donea J., Giuliani S., Halleux J. P., An arbitrary Lagrangian-Eulerian finite element method for transient dynamic fluid-structure interactions. Comput. Methods Appl. Mech. Eng. 33, 689–723 (1982). [Google Scholar]
- 72.Hu H. H., Patankar N. A., Zhu M., Direct numerical simulations of fluid–solid systems using the arbitrary Lagrangian–Eulerian technique. J. Comput. Phys. 169, 427–462 (2001). [Google Scholar]
- 73.Boyd J., Buick J. M., Green S., Analysis of the Casson and Carreau-Yasuda non-Newtonian blood models in steady and oscillatory flows using the lattice Boltzmann method. Phys. Fluids 19, 093103 (2007). [Google Scholar]
- 74.Lu L., Meng X., Mao Z., Karniadakis G. E., DeepXDE: A deep learning library for solving differential equations. SIAM Rev., 63, 208–228 (2021). [Google Scholar]
- 75.Raissi M., Wang Z., Triantafyllou M. S., Karniadakis G. E., Deep learning of vortex-induced vibrations. J. Fluid Mech. 861, 119–137 (2019). [Google Scholar]
- 76.Jin X., Cai S., Li H., Karniadakis G. E., NSFnets (Navier-Stokes flow nets): Physics-informed neural networks for the incompressible Navier-Stokes equations. J. Comput. Phys. 426, 109951 (2021). [Google Scholar]
- 77.Wang S., Teng Y., Perdikaris P., Understanding and mitigating gradient pathologies in physics-informed neural networks. arXiv [Preprint] (2020) https://arxiv.org/abs/2001.04536 (Accessed 13 January 2020).
- 78.Kingma D. P., Ba J., Adam: A method for stochastic optimization. arXiv [Preprint] (2017) https://arxiv.org/abs/1412.6980 (Accessed 30 January 2017).
- 79.Cai S., et al. , AIV MAOAC. GitHub. https://github.com/shengzesnail/AIV_MAOAC. Deposited 4 February 2021. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data and codes used in this manuscript are publicly available on GitHub (https://github.com/shengzesnail/AIV_MAOAC) (79).