Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2021 Jan 11;12(2):869–875. doi: 10.1021/acs.jpclett.0c03581

Nature of Optical Excitations in Porphyrin Crystals: A Joint Experimental and Theoretical Study

Maurizia Palummo †, Luisa Raimondo ‡,*, Conor Hogan §,∥,*, Claudio Goletti ∥, Silvia Trabattoni ‡, Adele Sassella ‡
PMCID: PMC8023704  PMID: 33428409

Abstract

graphic file with name jz0c03581_0005.jpg

The nature of optical excitations and the spatial extent of excitons in organic semiconductors, both of which determine exciton diffusion and carrier mobilities, are key factors for the proper understanding and tuning of material performances. Using a combined experimental and theoretical approach, we investigate the excitonic properties of meso-tetraphenyl porphyrin-Zn(II) crystals. We find that several bands contribute to the optical absorption spectra, beyond the four main ones considered here as the analogue to the four frontier molecular orbitals of the Gouterman model commonly adopted for the isolated molecule. By using many-body perturbation theory in the GW and Bethe–Salpeter equation approach, we interpret the experimental large optical anisotropy as being due to the interplay between long- and short-range intermolecular interactions. In addition, both localized and delocalized excitons in the π-stacking direction are demonstrated to determine the optical response, in agreement with recent experimental observations reported for organic crystals with similar molecular packing.

The study of highly ordered and crystalline molecular thin films is of particular interest in view of the device integration of organic semiconductors. A microscopic understanding of their fundamental excited-state properties (in particular, origin and spectral and spatial extent) can indeed guide the design of devices with improved performance. For instance, the delocalization of excited states influences exciton–vibration interaction in the solid and can be directly related to the efficiency of devices.1,2

Among organic semiconductors, porphyrin-based materials have attracted a great deal of interest due to their importance in several fields ranging from biology to optoelectronics; for example, light harvesting, energy capture and transfer, gas sensing, and photocatalysis are some of the most intriguing and useful applications.3−6 The optical properties of porphyrin aggregates and crystals are generally treated in terms of the four frontier molecular orbitals of the Gouterman model7,8 (suitable for describing transitions in porphyrin molecules) and then adding the weak intermolecular interactions by means of the Kasha model.9 While these approaches give important qualitative or phenomenological insight,10,11 they cannot provide a fully quantitative and microscopic description of the nature of optical excitations. In addition, the numerous theoretical studies of porphyrin excited states present in the literature, including those based on ab initio quantum chemistry approaches or time-dependent density functional theory,12−14 deal mainly with single molecules, their derivatives, and small molecular aggregates.15−17

This study aims to go beyond this framework by unveiling the excitonic properties of crystalline π-stacked meso-tetraphenyl porphyrin-Zn(II) (ZnTPP) by means of a joint theoretical–experimental approach that combines state-of-the-art theoretical modeling with experimental measurements of highly crystalline and oriented ZnTPP nanowires. ZnTPP has been chosen because of its use as an active component in devices3,5 and as a model system for understanding the photophysical processes18−20 and the growth mechanisms in porphyrin nanostructures (nanowires, two-dimensional phases, etc.).21,22 The experimental optical spectra are interpreted by means of the use of quantum-mechanical parameter-free ground- and excited-state methods [density functional theory (DFT) and many-body perturbation theory (MBPT) simulations].23,24 Here, MBPT methods, which are able to tackle properties of both isolated molecules and oligomers as well as solid-state π-conjugated organic systems on an equal footing,25−31 are applied for the first time to porphyrin crystals giving a complete picture of the origin and the spatial extent of the excitons involved in their optical spectra. In particular, we demonstrate the presence of delocalized excitons, known to diffuse rapidly and contribute, e.g., to decrease the voltage losses in photovoltaic devices, especially in organic crystals with π-stacked molecules.1 The results presented here are particularly relevant because they can be extended to other π-stacked organic systems where short-range intermolecular interactions compete with long-range ones.32,33

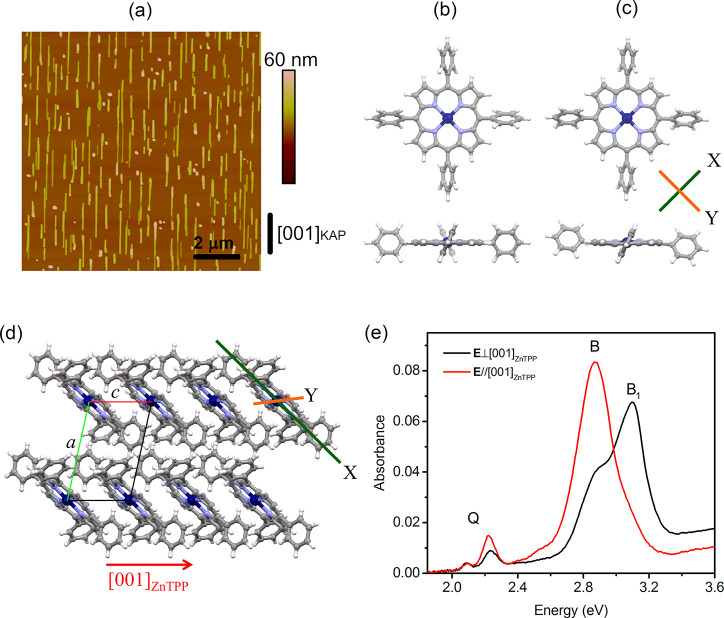
ZnTPP films are grown on freshly cleaved (010)-oriented potassium acid phthalate (KAP)34 substrates by means of organic molecular beam epitaxy. By a fine-tuning of the growth protocol, ZnTPP crystalline nanowires are selectively grown, uniformly distributed over the whole substrate surface, and well aligned along [001]KAP (Figure 1a). The wire size is rather homogeneous, with a length of 1–2 μm, a width of tens of nanometers, and a height of approximately tens of nanometers. The nanowires have been found to possess the known ZnTPP triclinic polymorphic structure determined at room temperature by Scheidt et al.,35 having the (100)ZnTPP plane in contact with the (010)KAP substrate.36 In this polymorph, the molecules take a different conformation with respect to the gas phase (Figure 1b,c)35,37 and are arranged in a layered motif with the molecules π-stacked along the c-axis, tilted by ∼43° with respect to (100)ZnTPP, and displaying a stacking distance of ∼3.85 Å (Figure 1d). The growth of such nanowires is driven by organic epitaxy36 through the double coincidence [001]ZnTPP//[001]KAP and [011]ZnTPP//[101]KAP; the alignment direction of the nanowires (Figure 1a) is therefore to be read as [001]ZnTPP, so that in the following, we simply refer to the ZnTPP crystal axes. Note that (1̅00)-oriented ZnTPP nanowires are also present (for further details, see refs (36) and (38)).

Figure 1.

Figure 1

Open in a new tab

(a) AFM (10 μm × 10 μm) height image of a 1 nm thick ZnTPP film grown on (010)KAP. The [001]KAP direction is reported in the panel. (b and c) Top and side views of the structure of a ZnTPP molecule in (b) the gas phase and (c) the triclinic crystal, respectively: H atoms in white, C in gray, N in light purple, and Zn in blue. (d) Structural model of the triclinic ZnTPP crystal with a perspective view along the [010]ZnTPP axis. X- and Y-axes in panels c and d are reference axes lying in the molecular plane (see the text). (e) Normal incidence absorption spectra of the sample in panel a, as collected for light polarization E//[001]ZnTPP and E⊥[001]ZnTPP (red and black lines, respectively). A constant background has been subtracted for better comparison.

The normal incidence absorption spectra of a ZnTPP film with a 1 nm nominal thickness are reported in Figure 1e as collected under linearly polarized light with electric field E along the two orthogonal directions giving the maximum optical anisotropy, here parallel and orthogonal to [001]KAP. Given the epitaxial relation illustrated above, the spectra represent a very good approximation of the normal incidence response of a (100)-oriented ZnTPP triclinic single crystal, collected under light-polarized parallel and perpendicular to [001]ZnTPP, i.e., the π-stacking direction (for further details, see the Supporting Information). The spectra are characterized by several peaks typical of porphyrins.7,8,18 At ∼2.1 and ∼2.2 eV, two peaks can be clearly distinguished, attributed to the lowest-energy Q-band and its phonon replica (probably the same attribution of the very weak peak at ∼2.4 eV)10 and characterized by some anisotropy. At 2.52 eV, a small polarized shoulder can also be detected only in the E//[001]ZnTPP-polarized spectrum. At higher energies, much more intense and broad peaks attributed to the B-bands are detected between 2.5 and 3.3 eV, showing a strong anisotropy. The broad B-bands are composed of nearly the same contributions in both polarized spectra, defined here as B and B1 peaks at ∼2.85 and ∼3.09 eV, respectively, with different relative intensities. Indeed, the B peak dominates the E//[001]ZnTPP-polarized spectrum where the B1 one is present just as a slight shoulder, possibly related to a poor coupling to the related transition dipole moment. On the contrary, for E⊥[001]ZnTPP, B1 is the most intense peak, notwithstanding a non-negligible contribution of the B peak.

Given the experimental characterization described above, we here aim to model the optical response of the ZnTPP triclinic crystalline phase by a theoretical study to gain insight into the nature of the excitations involved in the experimental spectra. Due to the large size of the nanowires composing the films, modeling the triclinic bulk phase is well-justified. We perform DFT and MBPT [namely GW and Bethe–Salpeter equation (BSE)] simulations to obtain the structural, electronic, and optical properties of ZnTPP, in both its gas- and solid-state triclinic phase (see the Supporting Information for a detailed description of the method).

First, the equilibrium geometry of the isolated ZnTPP molecule is determined using DFT.39 The atomic distances and angles are in good agreement (<0.05 Å difference in the bond lengths) with the existing literature;37,40 the opposite phenyl rings are rotated by 60° with respect to each other, and the porphyrinic core is planar, as expected (Figure 1b). Second, the molecular conformation of ZnTPP in the triclinic crystal has been similarly obtained through structural relaxation (see Figure 1c), starting from the geometry of the isolated molecule and using the experimental room-temperature lattice parameters of the crystal35 as constraints. There are two main effects: the spontaneous rotation of the opposite phenyl rings, which reach coplanarity, and a slight distortion of the final porphyrinic core with respect to the molecule in the gas phase. The latter distortion in particular occurs along the direction labeled Y in Figure 1c where a shift by approximately ±0.14 Å of the opposite N atoms is found with respect to the molecular plane, being negligible along X (the X and Y orthogonal directions are the projections onto the molecular plane of the directions connecting the opposite N atoms).

The calculated HOMO–LUMO gap of the molecule in the two conformations are similar, being 1.90 and 1.75 eV for the isolated molecule and for the molecule in the crystal, respectively. We then calculate the quasi-particle (QP) energy corrections within the perturbative GW approach to provide a better estimation of the electronic levels, thus obtaining QP gaps for the isolated molecule of 4.63 eV and for the crystal of 2.94 eV. Consistent with the literature,41−43 this difference can be explained as being due to the larger dielectric screening within the crystal, absent in the gas phase.

One further step at this point is the calculation of the GW band structure of the ZnTPP triclinic crystal, reported in Figure 2a. A clear dispersion of the first two conduction bands is visible along the ZΓ direction, which corresponds to the [001]ZnTPP direction in real space. This is the π-stacking direction, along which the molecules are closer and better packed (implying a stronger interaction). Looking at the bands at lower and higher energies (e.g., red and green bands in Figure 2a), we find clear and even higher dispersion. In this regard, in the four plots in Figure 2b, the charge density of several states in the crystal is shown: while the states in the a block are mainly localized in the porphyrinic core, several of the states in the b–e blocks are localized also on the external phenyl rings and some unoccupied states present charge density also between the molecules.

Figure 2.

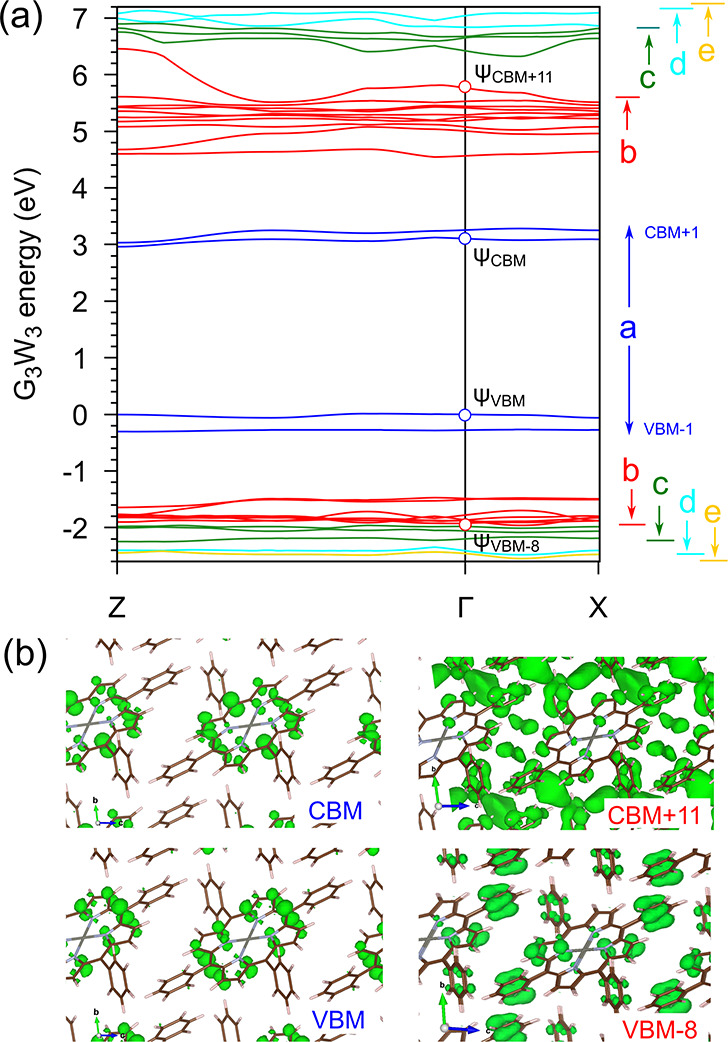
Figure 2

Open in a new tab

(a) GW band structure of ZnTPP crystal. Letters on the right indicate ranges of bands used in computing the optical spectra (see Figure 3d). Energy zero is set at the valence band maximum (VBM); CBM refers to the conduction band minimum. (b) |Ψ|2 of selected states calculated at Γ.

For simulating the optical spectra of the ZnTPP triclinic bulk phase, the BSE approach has been used. The BSE optical spectra are calculated through the diagonalization of the excitonic Hamiltonian,44,45 which also yields the exciton energies and spatial character. In Figure 3a, we report the BSE optical spectra (with a broadening of 0.05 eV) for E//[001]ZnTPP and E⊥[001]ZnTPP (red and black curves, respectively), directly comparable with the experimental data of Figure 1e. Both the energetic position and the anisotropy of the main experimental peaks indicated by Q, B, and B1 in Figure 1e are well-reproduced, while the intensity ratio is much different, probably due to the lack of electron–phonon interactions in the simulations.

Figure 3.

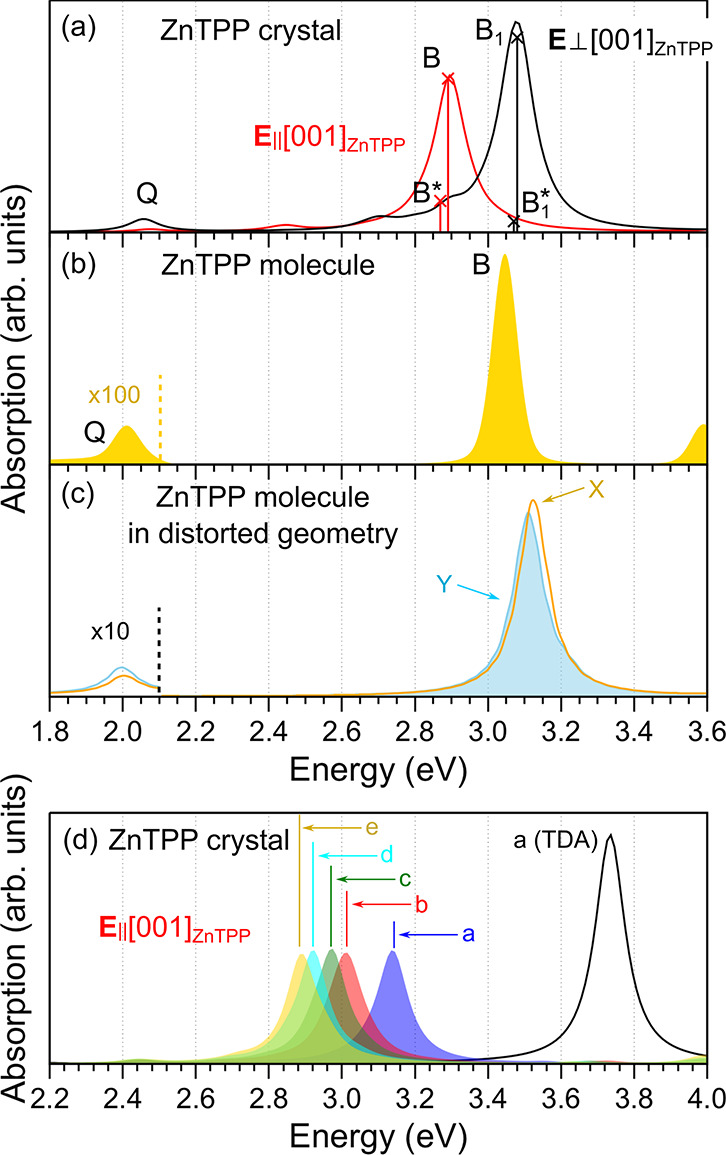
Figure 3

Open in a new tab

Computed absorption spectra of (a) the ZnTPP crystal for the two indicated orientations of the electric field, (b) the isolated gas-phase ZnTPP molecule, and (c) the isolated ZnTPP molecule having the conformation it takes in the bulk crystal, for light polarized along the X- and Y-axes (see Figure 1c). A broadening of 0.05 eV is used throughout. (d) Optical spectrum of the ZnTPP crystal calculated for polarization with E//[001]ZnTPP, as obtained by including an increasing number of states in the excitonic Hamiltonian (ranges a–e are indicated in Figure 2). Curves a–e include coupling; curve a(TDA) does not.

By comparing experimental and calculated spectra, we can reach several conclusions. First, we focus on the optical anisotropy observed in the ZnTPP nanowires and well reproduced by the BSE simulations and try to clarify whether it originates prevalently from the symmetry breaking effect of the crystal packing and/or from the distortion of the porphyrinic macrocycle. The ZnTPP molecule in the gas phase is centrosymmetric and isotropic; therefore, only a single intense B peak and a very weak Q peak (plus its phonon replica, not reproducible in our simulations) are normally visible (see Figure 3b). On the contrary, the isolated ZnTPP molecule in the distorted molecular conformation is anisotropic and the calculated optical spectra for light polarized along directions X and Y show indeed some anisotropy, but it is very weak (see Figure 3c). This demonstrates that the geometric distortion plays a negligible role in the strong optical anisotropy observed experimentally and calculated for the crystal (Figure 3a).

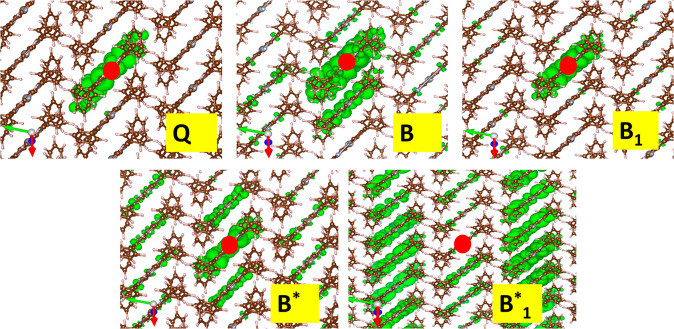
Second, the good convergence (<0.05 eV) in the energetic position of the main optical peaks has been obtained by diagonalization of the excitonic Hamiltonian built including 15 occupied and 18 unoccupied states (displaying the dispersion and charge density distribution discussed above). This result is particularly relevant and requires some discussion. Besides the three main excitons Q, B, and B1, several others exist in the B-band region, most of them with a very small oscillator strength (see Figure 3a, where the position and intensity of the most intense two, <0.05 eV apart, are reported and called here B* and B1*). Analysis of the origin of all excitons reveals that those labeled Q, B, and B1 are mainly due to a mixing of independent quasi-particle transitions among the four a bands in Figure 2a with a small contribution of transitions from or to b bands. The a bands can be thus considered as the counterpart in the crystal to the four frontier molecular orbitals of the Gouterman model for the molecules; they are indeed energetically well separated from any other bands, mainly contributing to the optical absorption in the ultraviolet–visible (UV–vis) region. On the contrary, the other excitons close to B and B1 (such as B* and B1* and those reported in Figure S4) have a larger contribution from bands in the b–e blocks in Figure 2a. For this reason, the inclusion of these bands in the excitonic Hamiltonian plays a fundamental role in the calculations, leading to a better agreement between the experimental and theoretical optical spectra, in terms of both energetic position and optical anisotropy (see Figure S3). To further clarify this point, in Figure 3d we report different BSE optical spectra (for only E//[001]ZnTPP) calculated including an increasing number of eh and he couples (single-particle transitions) in the excitonic Hamiltonian. An evident red-shift of the main optical peak (B peak) occurs as more bands are added (see spectra a–e), with a clear improvement in the energetic position in comparison with the experimental one. It is worth mentioning here that the need to include more bands in addition to the a block is another analogy with the results for isolated porphyrin molecules, where more states in addition to the four frontier states of the Gouterman model have to be considered.13,15 Finally, from the same figure, we can understand the effect of omitting the coupling terms in the excitonic Hamiltonian by comparing the black curve obtained within the Tamm–Dancoff approximation [labeled a(TDA)], with its counterpart obtained beyond this approximation (blue curve).

As a further, particularly interesting result, the nature of these excitons can be discussed within the general framework of excitations in molecular crystals. In the top panels of Figure 4, we plot the square modulus of the wave function of the Q, B, and B1 excitons obtained by fixing the hole position (indicated by a red dot) in a given molecule. While the Q and B1 states have a clear Frenkel character, with the electron and hole being localized in only one molecule, the B exciton shows a non-negligible probability to find the electron in other ZnTPP molecules with respect to the one where the hole is created. For the case of B* and B1* (see bottom panels in Figure 4), the delocalization is even higher, with the excitonic charge spread over several molecules along the π-stacking direction. It is worth noting that the other excitons present in the B-band region have similar delocalized character (not reported here). As mentioned above, in addition to the four a bands, these excitons also involve other states associated with bands in the b–e blocks, which show particularly strong dispersion along the π-stacking direction.27−29 Other theoretical studies2,25,46 have reported that in some organic molecular crystals, charge-transfer excitons (with charge delocalized on the first neighboring molecules) can be present and can be involved in optical and transport processes; nonetheless, those crystals are made of very different, rodlike molecules such as oligoacenes and display a completely different crystal packing. More recently, highly delocalized excitons are demonstrated by experimental observations in phthalocyanines,47 a class of molecules similar to porphyrins, where delocalization over >10 molecules along the π-stacking direction is observed in highly crystalline samples with a low degree of compositional disorder, like ours, thus lending support to the results discussed here.

Figure 4.

Figure 4

Open in a new tab

Square modulus of the excitonic wave function (green isosurface at 2% of the maximum value) obtained by fixing the hole position in a given molecule (large red circle). Top panels: Q, B, and B1 excitons. Bottom panels: B* and B1* excitons. The unit cell axes are reported: aZnTPP in green, bZnTPP in blue, and cZnTPP in red.

In conclusion, in this work, by applying MBPT methods, we have reproduced the experimental optical spectra of crystalline ZnTPP thin films. This approach has allowed us to analyze the origin of the huge optical anisotropy observed in the UV–vis region, demonstrated as being mainly due to intermolecular interactions along the π-stacking direction. We unveil a behavior of ZnTPP crystals that can be extended to other centrosymmetric porphyrin molecules whose electronic properties are known to be isotropic in the gas phase but become anisotropic in the crystalline state. Furthermore, an analysis in terms of single-particle transitions clearly demonstrates that other bands contribute to the excitonic optical peaks in the UV–vis region beyond the main ones, i.e., those we considered as the analogue of the four frontier molecular orbitals of the Gouterman model for the isolated molecule. Finally, we show that in the B-band region not only Frenkel-like excitons but also excitons with Wannier–Mott- and charge-transfer-like character, i.e., delocalized over several molecules, are present. These findings are particularly relevant as they can be considered a general behavior of π-stacked systems in which short intermolecular distances create competition between short- and long-range interactions, such as for other porphyrins and phthalocyanines. Although most of these excitons are optically inactive (at least in the theoretical framework used here, where we completely neglect the coupling with the vibrational degrees of freedom), their presence can be important in the exciton dynamics and transport properties of the material, in a manner similar to what has been recently found in other low-dielectric screening materials such as carbon nanotubes,48 layered transition metal dichalcogenides,49 and hybrid organic perovskites.50

Acknowledgments

M.P. acknowledges INFN for financial support through the National project Nemesys. M.P. and C.H. acknowledge CINECA for high-performance computational resources and support through the ISCRA initiative.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jpclett.0c03581.

  • Experimental methods, experimental configuration in optical measurements, theoretical methods, and BSE spectra (convergence, excitonic oscillator strengths, and Tamm–Dancoff approximation) (PDF)

The authors declare no competing financial interest.

Due to an ACS production error, this paper was originally published ASAP with incorrect pagination. This was corrected in the version published on January 14, 2021.

Supplementary Material

jz0c03581_si_001.pdf (914.4KB, pdf)

References

  1. Zhang G.; Chen X.-K.; Xiao J.; Chow P. C. Y.; Ren M.; Kupgan G.; Jiao X.; Chan C. C. S.; Du X.; Xia R.; et al. Delocalization of Exciton and Electron Wavefunction in Non-Fullerene Acceptor Molecules Enables Efficient Organic Solar Cells. Nat. Commun. 2020, 11, 3943. 10.1038/s41467-020-17867-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Alvertis A. M.; Pandya R.; Muscarella L. A.; Sawhney N.; Nguyen M.; Ehrler B.; Rao A.; Friend R. H.; Chin A. W.; Monserrat B. Impact of Exciton Delocalization on Exciton-Vibration Interactions in Organic Semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2020, 102, 081122(R) 10.1103/PhysRevB.102.081122. [DOI] [Google Scholar]
  3. Nwachukwu F. A.; Baron M. G. Polymeric Matrices for Immobilising Zinc Tetraphenylporphyrin in Absorbance Based Gas Sensors. Sens. Actuators, B 2003, 90, 276–285. 10.1016/S0925-4005(03)00047-9. [DOI] [Google Scholar]
  4. Jurow M.; Schuckman A. E.; Batteas J. D.; Drain C. M. Porphyrins as Molecular Electronic Components of Functional Devices. Coord. Chem. Rev. 2010, 254, 2297–2310. 10.1016/j.ccr.2010.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Min Park J.; Lee J. H.; Jang W.-D. Applications of Porphyrins in Emerging Energy Conversion Technologies. Coord. Chem. Rev. 2020, 407, 213157. 10.1016/j.ccr.2019.213157. [DOI] [Google Scholar]
  6. Mandal S.; Nayak S. K.; Mallampalli S.; Patra A. Surfactant-Assisted Porphyrin Based Hierarchical Nano/Micro Assemblies and Their Efficient Photocatalytic Behavior. ACS Appl. Mater. Interfaces 2014, 6, 130–136. 10.1021/am403518d. [DOI] [PubMed] [Google Scholar]
  7. Gouterman M. Spectra of Porphyrins. J. Mol. Spectrosc. 1961, 6, 138–163. 10.1016/0022-2852(61)90236-3. [DOI] [Google Scholar]
  8. Gouterman M.; Wagnière G. H.; Snyder L. C. Spectra of Porphyrins: Part II. Four Orbital Model. J. Mol. Spectrosc. 1963, 11, 108–127. 10.1016/0022-2852(63)90011-0. [DOI] [Google Scholar]
  9. Kasha M.; Rawls H. R.; Ashraf El-Bayoumi M. The Exciton Model in Molecular Spectroscopy. Pure Appl. Chem. 1965, 11, 371–392. 10.1351/pac196511030371. [DOI] [Google Scholar]
  10. Donker H.; Koehorst R. B. M.; Schaafsma T. J. Spectroscopy and Photophysics of Self-Organized Zinc Porphyrin Nanolayers. 1. Optical Spectroscopy of Excitonic Interactions Involving the Soret Band. J. Phys. Chem. B 2005, 109, 17031–17037. 10.1021/jp058054o. [DOI] [PubMed] [Google Scholar]
  11. Kalinowski J.; Stampor W.; Szmytkowski J.; Cocchi M.; Virgili D.; Fattori V.; Di Marco P. Photophysics of an electrophosphorescent platinum (II) porphyrin in solid films. J. Chem. Phys. 2005, 122, 154710. 10.1063/1.1878612. [DOI] [PubMed] [Google Scholar]
  12. Ghosh A. First-Principles Quantum Chemical Studies of Porphyrins. Acc. Chem. Res. 1998, 31, 189–198. 10.1021/ar950033x. [DOI] [Google Scholar]
  13. Parusel A. B.; Grimme S. DFT/MRCI Calculations on the Excited States of Porphyrin, Hydroporphyrins, Tetrazaporphyrins and Metalloporphyrin. J. Porphyrins Phthalocyanines 2001, 5, 225–232. 10.1002/jpp.310. [DOI] [Google Scholar]
  14. Shubina T. E. Computational Studies on Properties, Formation, and Complexation of M(II)-Porphyrins. Adv. Inorg. Chem. 2010, 62, 261–299. 10.1016/S0898-8838(10)62007-7. [DOI] [Google Scholar]
  15. Palummo M.; Hogan C.; Sottile F.; Bagalá P.; Rubio A. Ab Initio Electronic and Optical Spectra of Free-Base Porphyrins: The Role of Electronic Correlation. J. Chem. Phys. 2009, 131, 084102. 10.1063/1.3204938. [DOI] [PubMed] [Google Scholar]
  16. Blase X.; Attaccalite C.; Olevano V. First-Principles GW Calculations for Fullerenes, Porphyrins, Phtalocyanine, and Other Molecules of Interest for Organic Photovoltaic Applications. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 115103. 10.1103/PhysRevB.83.115103. [DOI] [Google Scholar]
  17. Hogan C.; Palummo M.; Gierschner J.; Rubio A. Correlation Effects in the Optical Spectra of Porphyrin Oligomer Chains: Exciton Confinement and Length Dependence. J. Chem. Phys. 2013, 138, 024312. 10.1063/1.4773582. [DOI] [PubMed] [Google Scholar]
  18. Edwards L.; Dolphin D.; Gouterman M.; Adler A. Porphyrins XVII. Vapor Absorption Spectra and Redox Reactions: Tetraphenylporphins and Porphin. J. Mol. Spectrosc. 1971, 38, 16–32. 10.1016/0022-2852(71)90090-7. [DOI] [Google Scholar]
  19. Yu H.-Z.; Baskin J. S.; Zewail A. H. Ultrafast Dynamics of Porphyrins in the Condensed Phase: II. Zinc Tetraphenylporphyrin.. J. Phys. Chem. A 2002, 106, 9845–9854. 10.1021/jp0203999. [DOI] [Google Scholar]
  20. Bonafé F. P.; Hernández F. J.; Aradi B.; Frauenheim T.; Sánchez C. G. Fully Atomistic Real-Time Simulations of Transient Absorption Spectroscopy. J. Phys. Chem. Lett. 2018, 9, 4355–4359. 10.1021/acs.jpclett.8b01659. [DOI] [PubMed] [Google Scholar]
  21. Rangan S.; Ruggieri C.; Bartynski R.; Martínez J. I.; Flores F.; Ortega J. Densely Packed ZnTPPs Monolayer on the Rutile TiO2(110)-(1 × 1) Surface: Adsorption Behavior and Energy Level Alignment. J. Phys. Chem. C 2016, 120, 4430–4437. 10.1021/acs.jpcc.5b12736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Zhang X.-L.; Jiang J.-W.; Liu Y.-T.; Lou S.-T.; Gao C.-L.; Jin Q.-Y. Identifying the Assembly Configuration and Fluorescence Spectra of Nanoscale Zinc-Tetraphenylporphyrin Aggregates with Scanning Tunneling Microscopy. Sci. Rep. 2016, 6, 22756. 10.1038/srep22756. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Kohn W.; Sham L. J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133. 10.1103/PhysRev.140.A1133. [DOI] [Google Scholar]
  24. Onida G.; Reining L.; Rubio A. Electronic Excitations: Density-Functional versus Many-Body Greens-Function Approaches. Rev. Mod. Phys. 2002, 74, 601–659. 10.1103/RevModPhys.74.601. [DOI] [Google Scholar]
  25. Cudazzo P.; Sottile F.; Rubio A.; Gatti M. Exciton Dispersion in Molecular Solids. J. Phys.: Condens. Matter 2015, 27, 113204. 10.1088/0953-8984/27/11/113204. [DOI] [PubMed] [Google Scholar]
  26. Cocchi C.; Draxl C. Optical Spectra from Molecules to Crystals: Insight from Many-Body Perturbation Theory. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 205126. 10.1103/PhysRevB.92.205126. [DOI] [Google Scholar]
  27. Kronik L.; Neaton J. B. Excited-State Properties of Molecular Solids from First Principles. Annu. Rev. Phys. Chem. 2016, 67, 587–616. 10.1146/annurev-physchem-040214-121351. [DOI] [PubMed] [Google Scholar]
  28. Cocchi C.; Breuer T.; Witte G.; Draxl C. Polarized Absorbance and Davydov Splitting in Bulk and Thin-Film Pentacene Polymorphs. Phys. Chem. Chem. Phys. 2018, 20, 29724–29736. 10.1039/C8CP06384B. [DOI] [PubMed] [Google Scholar]
  29. Rangel T.; Rinn A.; Sharifzadeh S.; da Jornada F. H.; Pick A.; Louie S. G.; Witte G.; Kronik L.; Neaton J. B.; Chatterjee S. Low-Lying Excited States in Crystalline Perylene. Proc. Natl. Acad. Sci. U. S. A. 2018, 115, 284–289. 10.1073/pnas.1711126115. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Sharifzadeh S. Many-Body Perturbation Theory for Understanding Optical Excitations in Organic Molecules and Solids. J. Phys.: Condens. Matter 2018, 30, 153002. 10.1088/1361-648X/aab0d1. [DOI] [PubMed] [Google Scholar]
  31. Blase X.; Duchemin I.; Jacquemin D. The Bethe-Salpeter Equation in Chemistry: Relations with TD-DFT, Applications and Challenges. Chem. Soc. Rev. 2018, 47, 1022–1043. 10.1039/C7CS00049A. [DOI] [PubMed] [Google Scholar]
  32. Fornari R. P.; Aragó J.; Troisi A. Exciton Dynamics in Phthalocyanine Molecular Crystals. J. Phys. Chem. C 2016, 120, 7987–7996. 10.1021/acs.jpcc.6b01298. [DOI] [Google Scholar]
  33. Hestand N. J.; Spano F. C. Molecular Aggregate Photophysics beyond the Kasha Model: Novel Design Principles for Organic Materials. Acc. Chem. Res. 2017, 50, 341–350. 10.1021/acs.accounts.6b00576. [DOI] [PubMed] [Google Scholar]
  34. Eremina T. A.; Furmanova N. G.; Malakhova L. F.; Okhrimenko T. M.; Kuznetsov V. A. Absolute-Configurations and Characteristics of Morphology of Potassium Biphthalate Crystal. Crystallogr. Rep. 1993, 38, 554–556. [Google Scholar]
  35. Scheidt W. R.; Mondal J. U.; Eigenbrot C. W.; Adler A.; Radonovich L. J.; Hoard J. L. Crystal and Molecular Structure of the Silver(II) and Zinc(II) Derivatives of Meso-Tetraphenylporphyrin. An Exploration of Crystal-Packing Effects on Bond Distance. Inorg. Chem. 1986, 25, 795–799. 10.1021/ic00226a014. [DOI] [Google Scholar]
  36. Raimondo L.; Trabattoni S.; Sassella A. Control of Post-Growth Processes for the Selection of Metallo-Tetraphenylporphyrin Nanowires. Phys. Chem. Chem. Phys. 2019, 21, 8482–8488. 10.1039/C8CP07747A. [DOI] [PubMed] [Google Scholar]
  37. Liao M.-S.; Scheiner S. Electronic Structure and Bonding in Metal Porphyrins, Metal = Fe, Co, Ni, Cu, Zn. J. Chem. Phys. 2002, 117, 205–219. 10.1063/1.1480872. [DOI] [Google Scholar]
  38. Campione M.; Capitani G. C.; Raimondo L.; Sassella A. Porphyrin Nanowires with Epitaxially Locked Uniaxial Orientation. J. Phys. Chem. C 2015, 119, 18210–18215. 10.1021/acs.jpcc.5b03848. [DOI] [Google Scholar]
  39. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  40. Irfan A.; Hina N.; Al-Sehemi A. G.; Asiri A. M. Quantum Chemical Investigations Aimed at Modeling Highly Efficient Zinc Porphyrin Dye Sensitized Solar Cells. J. Mol. Model. 2012, 18, 4199–4207. 10.1007/s00894-012-1421-4. [DOI] [PubMed] [Google Scholar]
  41. Ruini A.; Caldas M. J.; Bussi G.; Molinari E. Solid State Effects on Exciton States and Optical Properties of PPV. Phys. Rev. Lett. 2002, 88, 206403. 10.1103/PhysRevLett.88.206403. [DOI] [PubMed] [Google Scholar]
  42. Tiago M. L.; Northrup J. E.; Louie S. G. Ab Initio Calculation of the Electronic and Optical Properties of Solid Pentacene. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 67, 115212. 10.1103/PhysRevB.67.115212. [DOI] [Google Scholar]
  43. Hummer K.; Puschnig P.; Sagmeister S.; Ambrosch-Draxl C. Ab-Initio Study on the Exciton Binding Energies in Organic Semiconductors. Mod. Phys. Lett. B 2006, 20, 261–280. 10.1142/S0217984906010603. [DOI] [Google Scholar]
  44. Grüning M.; Marini A.; Gonze X. Exciton-Plasmon States in Nanoscale Materials: Breakdown of the Tamm-Dancoff Approximation. Nano Lett. 2009, 9, 2820–2824. 10.1021/nl803717g. [DOI] [PubMed] [Google Scholar]
  45. Sangalli D.; Ferretti A.; Miranda H.; Attaccalite C.; Marri I.; Cannuccia E.; Melo P.; Marsili M.; Paleari F.; Marrazzo A.; et al. Many-Body Perturbation Theory Calculations Using the Yambo Code. J. Phys.: Condens. Matter 2019, 31, 325902. 10.1088/1361-648X/ab15d0. [DOI] [PubMed] [Google Scholar]
  46. Sharifzadeh S.; Darancet P.; Kronik L.; Neaton J. B. Low-Energy Charge-Transfer Excitons in Organic Solids from First-Principles: The Case of Pentacene. J. Phys. Chem. Lett. 2013, 4, 2197–2201. 10.1021/jz401069f. [DOI] [Google Scholar]
  47. Manning L. W.; Rawat N.; Lamarche C.; Waterman R.; Headrick R. L.; Furis M. Exciton Delocalization in H2OBPc1-xMOBPcx (M = Co, Cu, Ni, Mn) Crystalline Thin-Film Organic Alloys. J. Phys. Chem. C 2016, 120, 11966–11976. 10.1021/acs.jpcc.6b02343. [DOI] [Google Scholar]
  48. Ishii A.; Machiya H.; Kato Y. K. High Efficiency Dark-to-Bright Exciton Conversion in Carbon Nanotubes. Phys. Rev. X 2019, 9, 041048. 10.1103/PhysRevX.9.041048. [DOI] [Google Scholar]
  49. Selig M.; Berghäuser G.; Richter M.; Bratschitsch R.; Knorr A.; Malic E. Dark and Bright Exciton Formation, Thermalization, and Photoluminescence in Monolayer Transition Metal Dichalcogenides. 2D Mater. 2018, 5, 035017. 10.1088/2053-1583/aabea3. [DOI] [Google Scholar]
  50. Meijerink A.; Rabouw F. T. Shedding Light on Dark Excitons. Nat. Mater. 2019, 18, 660–661. 10.1038/s41563-019-0376-6. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz0c03581_si_001.pdf (914.4KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES