Reconstruction of three-dimensional biventricular activation based on the 12-lead electrocardiogram via patient-specific modelling

Abstract

Aims

Non-invasive imaging of electrical activation requires high-density body surface potential mapping. The nine electrodes of the 12-lead electrocardiogram (ECG) are insufficient for a reliable reconstruction with standard inverse methods. Patient-specific modelling may offer an alternative route to physiologically constraint the reconstruction. The aim of the study was to assess the feasibility of reconstructing the fully 3D electrical activation map of the ventricles from the 12-lead ECG and cardiovascular magnetic resonance (CMR).

Methods and results

Ventricular activation was estimated by iteratively optimizing the parameters (conduction velocity and sites of earliest activation) of a patient-specific model to fit the simulated to the recorded ECG. Chest and cardiac anatomy of 11 patients (QRS duration 126–180 ms, documented scar in two) were segmented from CMR images. Scar presence was assessed by magnetic resonance (MR) contrast enhancement. Activation sequences were modelled with a physiologically based propagation model and ECGs with lead field theory. Validation was performed by comparing reconstructed activation maps with those acquired by invasive electroanatomical mapping of coronary sinus/veins (CS) and right ventricular (RV) and left ventricular (LV) endocardium. The QRS complex was correctly reproduced by the model (Pearson’s correlation r = 0.923). Reconstructions accurately located the earliest and latest activated LV regions (median barycentre distance 8.2 mm, IQR 8.8 mm). Correlation of simulated with recorded activation time was very good at LV endocardium (r = 0.83) and good at CS (r = 0.68) and RV endocardium (r = 0.58).

Conclusion

Non-invasive assessment of biventricular 3D activation using the 12-lead ECG and MR imaging is feasible. Potential applications include patient-specific modelling and pre-/per-procedural evaluation of ventricular activation.

What’s new?

• Reconstruction of three-dimensional (3D) activation map with only 12-lead electrocardiogram, patient-specific anatomy, and cardiovascular magnetic resonance-derived scar using a propagation model for the electric activation.

• Validation of reconstruction against endocardial and epicardial (coronary sinus/veins) invasive, high-density electroanatomic maps in 11 patients.

• Physiologically accurate conduction with heterogeneities (scar, fast endocardial layer) and anisotropy (fibres).

• Enabling technology for non-invasive individualization of patient-specific models.

Introduction

The standard 12-lead electrocardiogram (ECG) is the most routinely used, inexpensive, and non-invasive modality to record the electrical activity of the heart, but its diagnostic capability has acknowledged limits. In particular, the surface ECG does not provide quantitative information about the activation sequence in the heart.

Non-invasive electrocardiographic imaging, also called ECG mapping, overcomes at least some of the limitations of the standard ECG. ECG mapping combines information from many (usually 150–250) electrodes with knowledge of the geometry of the heart and torso of the patient to depict the electric activity of the heart.¹ It is a general-purpose tool that can reconstruct potentials, electrograms, and activation and repolarization patterns on either the epicardium or, less commonly, the endocardium. Some technologies based on ECG mapping have been extensively validated in experimental, animal, and clinical studies, with convincing results.^2–5 However, ECG mapping relies on a large number of electrodes, placed on the patient’s torso at the time of geometry acquisition using cardiac imaging as well as during the clinical intervention, thus requiring dedicated technical support and additional costs. Therefore, despite the advantages, its adoption in the clinical workflow is still limited.

In this study, we assess the possibility to reconstruct the activation map relying only on the 12-lead ECG for the electric data, by taking advantage of physiological and anatomical knowledge implemented in a patient-specific model. The parameters of the model, regional conduction velocities and sites of earliest activation, are automatically optimized to fit the simulated to the recorded QRS complex. The fitted patient-specific model can calculate almost real-time the activation sequence and may therefore enable model-assisted therapeutic intervention. Proof-of-principle validation was performed on a small, yet heterogeneous cohort of patients possibly with a scar by an extensive comparison of the calculated activation map against the invasively acquired high-density electro-anatomic endocardial map.

Methods

Study population

Eleven heart failure patients were retrospectively included in the study; of whom the following data were acquired: a 12-lead ECG, a clinically indicated magnetic resonance (MR) scan with late gadolinium-enhancement (LGE), and an electrophysiological study for measuring electro-anatomical maps (EAMs). The institutional review board approved the study protocol, and all patients gave written and oral informed consent for the investigation. The study was performed in compliance with the Declaration of Helsinki.

Construction of the patient-specific model from cardiovascular magnetic resonance and electrocardiogram

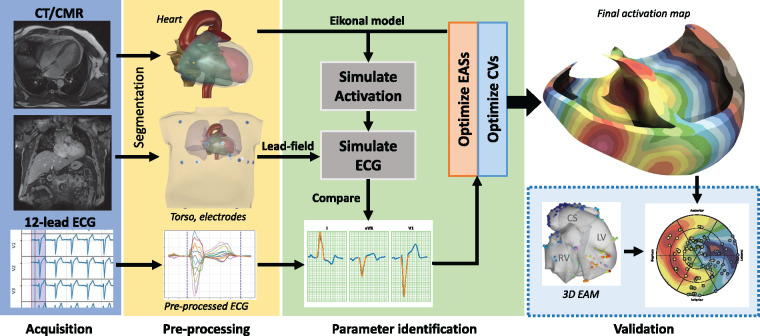
The overall workflow was based on a propagation model—the so-called ‘eikonal model’, previously described⁶—for simulating myocardial activation and the corresponding body surface 12-lead ECG. The model used a volumetric anatomical description of the heart and torso. The electrophysiological individualization of the model was achieved by identifying the early activation sites (EASs) and regional conduction properties of the myocardium by fitting the simulated QRS complex to the recorded one (Figure 1). The corresponding activation was eventually extracted from the propagation model using the identified parameters. Further details on the mathematical and computational aspects are available in Supplementary material online.

Figure 1.

Summary of the method. The workflow starts with the CMR acquisition of the anatomy of the heart and the torso (with electrode positions) and the standard 12-lead ECG (blue box). In the pre-processing phase (yellow box), a 3D anatomy of the patient is reconstructed from CMR/CT sequences. The parameter identification phase (light green box) aims at fitting the parameters of the model (CVs and EASs) to minimize the difference between recorded and simulated ECG. The reconstructed activation map was eventually validated against invasive EAM (dashed light blue box). CMR, cardiovascular magnetic resonance; CT, computed tomography; CV, conduction velocity; EASs, early activation sites; ECG, electrocardiogram.

Anatomical model

The patient anatomies were semi-automatically reconstructed from the cardiovascular magnetic resonance (CMR) images to create 1-mm resolution 3D volumetric computational grids.⁷ Scarred tissue was inferred from LGE-MRI sequences by manual contour drawing and alignment. Ventricular fibre orientation was assigned using a rule-based approach.⁷ A 1 mm thick fast conducting layer was included in both left ventricular (LV) and right ventricular (RV) endocardium. The torso model included lungs, blood masses, active myocardium with fibre orientation, connective tissue, skeletal muscles, and skin.

Propagation model and electrocardiogram simulation

In the propagation model, the electrical activation originated from a limited number (1–10 per chamber) of endocardial EASs and spread across the non-scarred myocardium with direction-dependent conduction velocity. The parameters of the model included the EASs, the surface-to-volume ratio of the cells, the intra- and extra-cellular conductivity, and a scaling parameter accounting for the ionic membrane model. The propagation was faster in the fibre direction than in the cross-fibre direction. The QRS complex of the 12-lead ECG was simulated by using the lead field theory.⁸ The transmembrane potential was a pre-computed template function shifted in time according to activation.

Fitting procedure

The parameter fitting procedure consisted of two phases. The first phase provided an initial estimate of the global CV and the number, location, and onset of the EASs, whereas the second phase further optimized the location of the EASs and the CV in four distinct regions (LV, RV and LV, RV fast endocardial layer). Several other parameters (electric conductivities, membrane model) were left unchanged from those reported in previous studies. Initial guesses for the parameters were the same for all patients.

Validation

Validation was performed by comparing the reconstructed activation maps at LV and RV endocardium and in the coronary sinus (CS) and veins with the EAMs as obtained from the electrophysiology study. The mapping system was the NOGA-XP system (Biologic Delivery Systems, Division of Biosense Webster, a Johnson&Johnson Company) equipped with a conventional 7-Fr deflectable-tip mapping catheter (NAVI-STAR, Biosense Webster). Unipolar electrograms and corresponding spatial positions of the tip of the catheter were simultaneously acquired at 1 kHz and 100 Hz, respectively, and aligned in time using the automatically detected R-peak of the 12-lead ECG. Points were accepted by the system according to a set of criteria for catheter stability and signal quality.

Electro-anatomical maps and patient-specific anatomy were spatially aligned by means of a translation and the acquired points were projected onto the corresponding anatomical region (LV or RV endocardium, LV epicardium). The LV earliest and latest activated regions (EAR and LAR) were presented using a bull’s-eye plot. The EAR and LAR were respectively defined as the earliest 10% and the latest 10% of activated endocardium. The endocardial breakthrough point (BP) and latest activated point (LAP) were defined as the centre of mass of the EAR and LAR, respectively. A trans-septal time (TST) was defined as the earliest LV breakthrough time, whereas the total activation time (TAT) was the maximal difference in activation within the LV endocardium. The overlap (OVL) between recorded and reconstructed activation was evaluated as area of the overlap when 20% of the total endocardium was activated, divided by 0.2.

Statistical analysis

Recorded and simulated ECGs were compared in terms of Pearson’s correlation, relative root-mean-square error and QRS duration. A similar analysis was applied to the pointwise comparison to EAMs. All distances were computed using the Euclidean distance. Bland–Altman analyses were carried out to evaluate the agreement between recorded and reconstructed activation times. All quantities are reported in mean ± SD or median and 1st and 3rd quartiles, if not indicated differently.

Results

The demographic characteristics of the cohort (Table 1) showed a median age of 69 years and a prevalence of males (73%). Scar was reported in three patients (27%). All patients had a long QRS duration (min 126 ms, max 185 ms). On average 265 ± 109 endocardial activation points per patient were acquired. In 11 patients, 186 ± 59 LV endocardial points were collected, in 6 patients an additional 71 ± 22 points in the RV, and in 7 patients 63 ± 19 points were recorded on the LV epicardium by introducing the mapping catheter into the CS and whenever possible in the coronary veins. The EAMs confirmed aleft bundle branch block condition in nine patients (82%). The median TST and TAT were, respectively, 54 ms (IQR 44–68 ms) and 76 ms (IQR 73–81 ms), and only two patients showed short TST (Table 1).

Table 1.

Characteristics of the patients

Patient ID	Sex	Age (years)	Scar	ECG	QRSd (ms)	TST (ms)	TAT (ms)
1	F	72	No	LBBB, SR	139	39	81
2	M	69	No	LBBB, AF	179	59	91
3	M	79	Yes (8)	IVCD, SR	138	3	81
4	M	57	Yes (6)	IVCD, SR	126	14	72
5	F	68	No	LBBB, SR	185	69	75
6	M	53	No	LBBB, SR	165	50	76
7	F	67	No	LBBB, SR, AVB1	156	72	48
8	M	68	No	LBBB, SR	154	54	63
9	M	73	Yes (1)	LBBB, SR, AVB1	176	77	77
10	M	84	No	LBBB, SR, AVB1	180	50	98
11	M	69	No	LBBB, SR, AVB1	170	68	74
Overall	73% M	69 ± 8.7	27% Yes	82% LBBB	160.7 ± 18.81	50.45 ± 22.6	76 ± 12.6

Statistics are reported in the last row as average ± standard deviation for numerical data and as percentage for categorical data.

AVB1, atrioventricular block first degree; ECG, electrocardiogram; F, female; IVCD, intraventricular conduction delay; LBBB, left bundle branch block; M, male; QRSd, QRS complex duration; SR, sinus rhythm; TST, trans-septal time; TAT, total activation time.

Detection of early activation sites

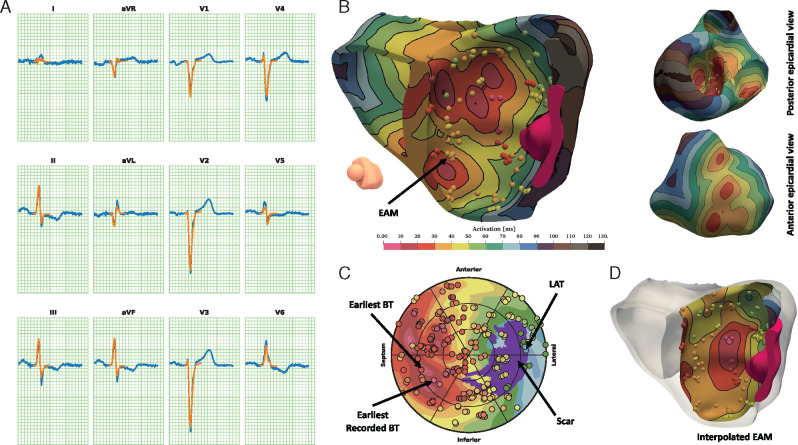
An illustrative example of the fitted patient-specific models is reproduced in Figure 2 for an IVCD patient with coronary artery disease (Patient #4). The patient has a non-LBBB QRS morphology and an extensive sub-endocardial scar located in the LV antero-lateral wall. The algorithm identified 14 EASs, 7 RV and 7 LV. No RV-LV delay was observed. In the LV, BPs were in the septal area both inferiorly and anteriorly, with a slightly higher occurrence in the inferior sectors. The simulated and recorded QRS complexes correlated excellently (r = 0.978). The BP and LAP localization errors were 11.1 and 8.9 mm, respectively. Notably, four EARs were correctly identified, with two EARs in the antero-septal area and two EARs in the inferior-septal area, very close to the recorded EAR in the same area. Pointwise correlation between calculated and measured points was 0.78 and OVL 0.4.

Figure 2.

Illustrative reconstruction. Example of the activation reconstruction for Patient #4. (A) Recorded (blue) and fitted (orange) ECG. (B) 3D cut view of the activation map with collected EAM points, and epicardial views. (C) LV bull’s-eye plot. (D) LV endocardial view of interpolated EAM (scar in purple). EAM, electro-anatomical maps; ECG, electrocardiogram; LV, left ventricular.

Overall accuracy of reconstructed activation

A pointwise comparison of reconstructed activation at points from EAM (Table 2) showed very high Pearson’s correlation (r = 0.815), particularly at LV endocardium (r = 0.833). In the RV endocardium and CS/veins the correlation was lower (r = 0.576 and 0.677). The Bland–Altman analysis showed no bias (0.45 ms) and limits of agreement (LoA) of −42.7 and +43.6 ms (2856 points). On the LV epicardium and endocardium, the reconstruction was good (r > 0.7) in 10 patients (91%) and modest only in Patient #3 (r = 0.33). On the RV endocardium Pearson correlation per patient was generally modest (r > 0.5 in four patients of the six) and poor in Patient #6 (r = 0.18). A relatively large bias of 27 ms was observed on the RV endocardium with LoA −18 and 72 ms.

Table 2.

Correlation between EAMs and reconstructed activation times for all points in the LV and RV endocardium and LV epicardium in all patients

Patient ID	LV endo	LV epi	RV endo	Overall
1	0.953	—	—	0.953
2	0.903	—	—	0.903
3	0.327	—	—	0.327
4	0.777	—	—	0.777
5	0.885	0.966	0.735	0.805
6	0.765	0.863	0.188	0.797
7	0.751	0.863	0.496	0.788
8	0.893	0.952	0.509	0.878
9	0.942	0.932	0.323	0.817
10	0.914	0.949	0.759	0.840
11	0.720	0.782	—	0.831
Overall	0.833	0.677	0.576	0.816

EAMs, electroanatomic maps; endo, endocardial; epi, epicardial; LV, left ventricular; RV, right ventricular.

The estimated TST obtained from the fitted model closely matched the measured TST (difference between reconstructed and recorded was −15.5 ± 16.5 ms) in all but one. The reconstructed TAT slightly overestimated the recorded one, with a difference of 25.7 ± 22 ms.

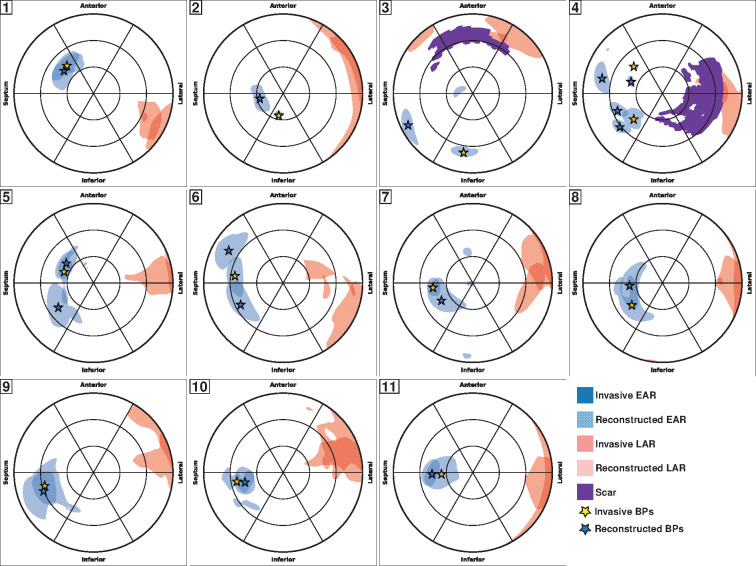
The BP and LAP in the LV were accurately identified in the correct AHA sector on the bull’s-eye plot in the majority of the patients (72%). In the remaining cases, BP was placed in the neighbouring segments (Figure 3). The distance between the calculated and the recorded BP was 13.5 (6.9–16.1) mm, and the OVL was 0.75 (0.56–0.79). The LAP was also accurately captured by the reconstructed activation map, 8.1 (6.1–14.5) mm off the recorded position.

Figure 3.

Validation against invasive mapping. Bull’s-eye plots for each patient showing the EAR (blue) and LAR (red) in the LV. The solid-coloured regions refer to the recorded maps, while the hatched-coloured regions are the reconstructed ones. Scar is in purple. BPs are marked by stars. BP, breakthrough point; EAR, earliest activated region; LAR, latest activated region; LV, left ventricular.

Accuracy of fitting the electrocardiogram

Overall, the fitted QRS complex was highly correlated to the recorded QRS complex (r = 0.92) and correlation was >0.9 in 9 of the 11 patients (82%). Per-patient correlation (Table 3) ranged from 0.84 (Patient #7) to 0.98 (Patient #6). The QRS duration was well captured, reporting an error (reconstructed minus recorded) of −3.0 [−17.37–5.28] ms. Overall, V1-V4 showed very high correlation while lead V6 and aVR showed modest correlation.

Table 3.

Correlation between recorded and fitted ECG, grouped by patient and lead

ID	I	II	III	V1	V2	V3	V4	V5	V6	aVF	aVL	aVR	All
1	0.941	0.886	0.918	0.979	0.947	0.972	0.863	0.375	0.889	0.852	0.935	0.939	0.934
2	0.191	0.920	0.928	0.849	0.885	0.991	0.949	0.754	−0.364	0.934	0.905	0.572	0.881
3	0.966	0.861	0.979	0.951	0.934	0.983	0.986	0.978	−0.301	0.958	0.984	0.432	0.944
4	0.707	0.969	0.961	0.975	0.995	0.993	0.989	0.882	0.973	0.971	0.916	0.940	0.978
5	0.899	0.623	0.879	0.968	0.996	0.986	0.981	0.469	0.646	0.799	0.919	0.630	0.963
6	0.979	0.959	0.938	0.978	0.990	0.984	0.914	0.853	0.907	0.847	0.971	0.978	0.981
7	0.800	0.591	0.935	0.964	0.991	0.940	0.930	0.759	0.246	0.852	0.942	0.341	0.843
8	0.908	0.732	0.914	0.979	0.961	0.988	0.985	0.981	0.941	0.869	0.937	−0.002	0.935
9	0.872	0.819	−0.687	0.967	0.937	0.982	0.975	0.817	0.306	0.518	0.081	0.864	0.917
10	0.870	0.858	0.418	0.941	0.953	0.946	0.622	0.767	0.905	0.622	0.819	0.878	0.932
11	0.918	0.930	0.666	0.981	0.978	0.956	0.877	−0.198	0.840	0.892	0.846	0.931	0.940
All	0.855	0.845	0.833	0.923	0.956	0.940	0.936	0.687	0.555	0.830	0.852	0.842	0.923

ECG, electrocardiogram.

Discussion

This study shows that a mathematical model can accurately reconstruct the volumetric propagation sequence of the ventricles in heart failure patients during sinus rhythm. In contrast to commercially available ECG mapping technologies, it does not require hundreds of electrodes; we obtained our results with only the 12-lead ECG and standard imaging data. The method can be easily integrated in existing EAM systems, possibly reducing mapping time, and increasing localization accuracy.

Our method is neither the first to require only a 12-lead ECG^9,10 nor the first to predict the activation sequence in the entire ventricular volume,¹¹ but it is the first to achieve both of these feats without compromising the physiological accuracy or strongly limiting the applicability of the approach. Our method combines the best of two worlds: ECG mapping^1,2,11–13 and patient-specific modelling.^14–16 Due to a highly optimized implementation the reconstruction is competitive in terms of time to solution to other ECG mapping approaches. At the same time, the accuracy of its ECG prediction is comparable with the gold standard, the bidomain model.⁶ We achieve this accuracy by using a volumetric conduction model, necessary to incorporate the effect of tissue anisotropy on the potential field generated by the activation wavefront. This automatically results in a fully 3D prediction of the activation sequence. The activation sequence itself was simulated realistically with an anisotropic eikonal equation.

Accuracy

The overall correlation of the activation map in the present study (r = 0.82) is comparable with those reported for ECG epicardial mapping in closed-chest pig experiments (r = 0.82 and 0.78)^3,4 and in clinical studies during pacing (r = 0.62 ± 0.16).⁵ Studies performed during sinus rhythm, better reflecting our cohort, showed significantly lower correlation (r=∼0).¹⁷ Importantly, we did not observe potentially unphysiological lines of block and U-shaped activation, often present in ECG mapping, because conduction velocity cannot change abruptly unless directly specified in the model.

The reconstruction of the activation was also accurate at the LV endocardium, which is inaccessible for potential-based ECG mapping approaches. Several ECG mapping methods for endocardial activation are available,^2,12,13 but validation data during sinus rhythm are scarce. Our localization error of BP and LAP in the LV (12.2 ± 8.8 mm) is comparable with those during atrioventricular conduction in patients with ventricular pre-excitation (18.7 ± 6.4 mm)² but higher than those during single pacing (6.5 ± 2.1 and 6 ± 5 mm).^12,13 For those methods only relying on the 12-lead ECG, localization error during pacing was significantly higher (>20 mm) but predicted the correct segment.^9,16 Our method also recorded a good similarity (in terms of overlap) between recorded and reconstructed earliest activation (0.69 ± 0.17) as a metric for accuracy in the reconstruction. While a small localization error suggests an accurate reconstruction of BP and LAP location, a large overlap indicates that conduction properties are also correct.

The reconstruction of the CS/veins map adequately reproduced the invasive recordings. In contrast, the RV activation reconstruction was modest in terms of correlation (r = 0.58) and showed on average a deviation from the EAM of 27 ms. A closer inspection of the Bland-Altman plot suggests that points in the earliest activated region were well reproduced while late-activated points were considerably delayed in the reconstructed map. The RV contributes less than the LV to the ECG, and the least-squares minimization used here tends to ignore small deviations in amplitude, hence limiting the accuracy. Additionally, the alignment of the recorded RV points to the anatomy is problematic and may be affected by large uncertainty, because of the concave shape of the chamber.

Patient-specific modelling

By virtue of its model-based nature, our approach has the potential to further improve the individualization in patient-specific modelling, an emerging paradigm aiming at supporting personalized therapeutic interventions.¹⁸ Personalization of cardiac models from 12-lead ECG has already been investigated by others.^10,14–16 Compared with those methods our approach is more general, being capable of identifying an optimal set of EAMs with no restriction on the number of sites, and very competitive in terms of time to solution, hence widening the spectrum of clinical applications.

Robustness of validation

The activation map extrapolated from the invasive mapping system may be affected by several uncertainties. The detection of the activation time from EGM could be difficult because of fractionation and far field signal in the unipolar readings and direction-dependency in bipolar signals.¹⁹ In addition, the spatial location of imaged points needs to be registered to the electrode positions. The combination of both these uncertainties (in space and in time) may affect the comparison, especially for BP and LAP localization. In this work, we opted for the more robust definition of BP (respectively LAP) as the centre of mass of the EAR (respectively LAR). In a Monte Carlo study, we found that the localization error of BP has significantly lower variance if defined as above instead of as the earliest activated point (see Supplementary material online).

Perspectives on clinical application

Our method could be included in the screening workflow of patients who are candidate to CRT as well as in selecting pacing targets. The measurement of the time interval between RV and LV, or the time between Q wave on surface ECG and LV at the time of CRT implantation has been predictive of both acute and chronic response to CRT.²⁰ The method could easily estimate both RV-LV timing and Q-LV time and thus provide a novel way for patient selection and pre-procedural planning of RV and LV lead placement. Patient-specific activation patterns can be calculated right at the time of pacing lead placement.

Study limitations

The patient-specific model has several parameters with considerable uncertainty. This is an undeniable problem of current cardiac models and, more generally, biological systems. Given the limited amount of data we use for the fitting and the complexity of the model, we had to minimize the number of free parameters. It is still possible however, that multiple combinations of parameters yield similar activation maps and surface ECG. The solution may therefore depend on the initial guess for the parameters and the optimization algorithm. To alleviate this problem, we designed the first phase of the algorithm to provide a robust initial guess.

The eikonal model does not cover the full spectrum of activation patterns. This may limit its applicability. Most notably, re-entrant activation is not admissible in our current formulation.

The study was admittedly based on a small patient cohort. However, this cohort was heterogeneous, with QRS duration ranging from 126 to 180 ms, different ventricular conduction abnormalities and variable underlying disease (e.g. scar). Importantly, the validation measurements consisted of high-resolution endocardial mapping in both ventricles and epicardial LV measurements (limited to CS/veins) in heart failure patients during sinus rhythm.

The validation analysis in this study was not performed blindly to the intracardial mapping. To avoid a possible bias, we used the same initial guess in the algorithm for all the patients, despite the heterogeneity of the cohort.

Currently, the model requires an accurate segmentation and mesh-construction from imaging data, which may require several hours per patient. For the majority of applications, a preparatory phase of several hours is reasonable and it does not disrupt the clinical workflow. Nonetheless, time to segmentation can nowadays be improved significantly by a combination of statistical atlases and machine learning.

Finally, scar was assessed by LGE-MRI acquisitions, which might not be routinely available. We also did not consider the border zone of the scar in the model, although the model can easily allow for it.

Conclusions

A 12-lead ECG-based technique for reconstructing cardiac activation was developed and validated. The methodology achieved very good endocardial accuracy, opening the possibility for a non-invasive pre- and peri-procedural evaluation of activation map during intrinsic sinus rhythm and, potentially, for guiding optimal lead placement.

Supplementary material

Supplementary material is available at Europace online.