How much deep learning is enough for automatic identification to be reliable?

Abstract

Objectives

To determine the optimal quantity of learning data needed to develop artificial intelligence (AI) that can automatically identify cephalometric landmarks.

Materials and Methods

A total of 2400 cephalograms were collected, and 80 landmarks were manually identified by a human examiner. Of these, 2200 images were chosen as the learning data to train AI. The remaining 200 images were used as the test data. A total of 24 combinations of the quantity of learning data (50, 100, 200, 400, 800, 1600, and 2000) were selected by the random sampling method without replacement, and the number of detecting targets per image (19, 40, and 80) were used in the AI training procedures. The training procedures were repeated four times. A total of 96 different AIs were produced. The accuracy of each AI was evaluated in terms of radial error.

Results

The accuracy of AI increased linearly with the increasing number of learning data sets on a logarithmic scale. It decreased with increasing numbers of detection targets. To estimate the optimal quantity of learning data, a prediction model was built. At least 2300 sets of learning data appeared to be necessary to develop AI as accurate as human examiners.

Conclusions

A considerably large quantity of learning data was necessary to develop accurate AI. The present study might provide a basis to determine how much learning data would be necessary in developing AI.

INTRODUCTION

In recent years, there has been growing interest in using artificial intelligence (AI) in the medical field.^1,2 Among the various applications of AI in orthodontics, effort has been applied to develop a fully automatic cephalometric analysis that would be capable of reducing the manpower burden of cephalometric analyses.^3–20 A recent study on fully automatic identification of cephalometric landmarks based on the latest deep-learning method showed higher detecting accuracy than other machine-learning methods.14 The AI system demonstrated perfect reproducibility and also performed landmark identification as accurately as human experts did.6 The latest AI was developed by applying 1028 sets of learning data during the training procedure.^6,14

Previous AI demonstrations commonly limited the quantity of learning and test data to 150 and 250 images, respectively. Conventionally, the images carried 19 annotated landmarks including 15 skeletal- and 4 soft-tissue anatomical points.^3,18,19 The improved accuracy of the latest AI studies was likely partly due to the increased quantity of learning data implemented during the AI training procedure. However, an important question was still remaining: How much learning data are actually necessary to sufficiently train AI? What would happen if the quantity of learning data doubled, tripled, or increased up to 10-fold? One could conjecture that a greater quantity of learning data in the AI training procedure would produce more accurate AI performance. However, manually detecting and annotating multiple landmarks on the massive original images for use during the training procedure for AI would be extremely laborious. When it comes to determining the sufficient quantity of learning data, the number of detecting targets per image (ie, the number of cephalometric landmarks in the cephalometrics example) was purported to play an important role and should also be taken into account.6

The purpose of this study was to investigate how much learning data might be necessary to sufficiently train a deep-learning system for practical use as AI. By comparing the accuracy of each AI according to (1) the quantity of learning data and (2) the number of detecting targets per image, an optimal quantity of learning data was attempted to be determined.

MATERIALS AND METHODS

Learning Data Sets

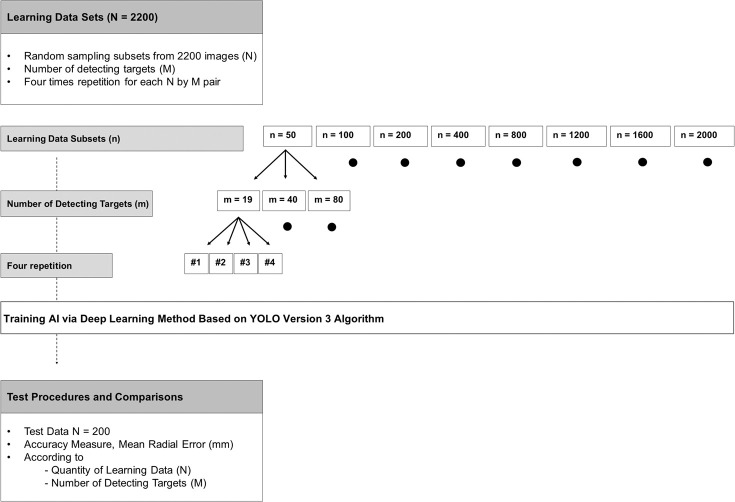
Figure 1 summarizes the experimental design implemented in this study. A total of 2400 lateral cephalometric radiographs were collected from the Picture Aided Communication System server (Infinitt Healthcare Co Ltd, Seoul, Korea) at Seoul National University Dental Hospital, Seoul, Korea. A total of 80 cephalometric landmarks in each of 2400 images were identified and annotated manually by a single examiner (examiner 1, SJL). Of these, 2200 images were chosen as the learning data to train AI. The institutional review board for the protection of human subjects at Seoul National University Dental Hospital reviewed and approved the research protocol (ERI 19007).

Figure 1.

Experimental design.

To measure intra- and interexaminer reliability, 200 images were selected, and landmark identification was repeated by a different examiner (examiner 2, HWH). The mean difference in identifying cephalometric landmarks within and between human examiners was 0.97 ± 1.03 mm and 1.50 ± 1.48 mm, respectively. The mean difference and the landmark detection error were measured in terms of radial error (also called the point-to-point error).

The characteristics of the learning and test data images used are listed in Table 1. These characteristics seemed to be consistent with the present trends regarding the malocclusion types among patients visiting a university hospital.^21,22 The subjects demonstrated a higher percentage of patients with severe dentofacial deformity.

Table 1.

Characteristics of the Learning and Test Data

Study Variable		n (%)
Learning data		2200 (100)
Gender	Female	1143 (52.0)
Skeletal classification	Class II	383 (17.4)
	Class III	1624 (73.8)
Test data		200 (100)
Gender	Female	103 (51.5)
Skeletal classification	Class II	28 (14.0)
	Class III	168 (84.0)

To compare the detection errors according to the quantity of learning data (N), subset data sizes of 50, 100, 200, 400, 800, 1200, 1600, and 2000 were selected by the random sampling method without replacement. These subsets were used during the AI training procedure. The data sizes of 100 and 200 were chosen to mimic the quantity of learning data from previous studies.^3,18,19

To compare the detection errors according to the number of detecting targets per image (M), subset landmarks sizes per image of 19, 40, and 80 were selected. The smallest number of detecting targets tested in this study was the 19 conventional landmarks widely used in previous public AI challenges.^3,12,18,19 The landmarks selected for the 40 subsets are generally used in clinical orthodontic practice. The greatest number of detecting targets (80) was selected because those were known to be essential for accurately predicting posttreatment outcomes.^23–27 A detailed description of landmarks is listed in Table 2.

Table 2.

List of 80 Landmarks^a

Landmark No.	Landmark Explanation	19	40	Landmark No.	Landmark Explanation	19	40
1	Vertical reference point 1 (arbitrary)			41	Pterygoid		√
2	Vertical reference point 2 (arbitrary)			42	Basion		√
3	Sella	√	√	43	U6 crown mesial edge
4	Nasion	√	√	44	U6 mesiobuccal cusp
5	Nasal tip		√	45	U6 root tip
6	Porion	√	√	46	L6 crown mesial edge
7	Orbitale	√	√	47	L6 mesiobuccal cusp
8	Key ridgeb			48	L6 root tip
9	Key ridge contour intervening point 1b			49	glabella		√
10	Key ridge contour intervening point 2b			50	glabella contour intervening pointb
11	Key ridge contour intervening point 3b			51	nasion		√
12	Anterior nasal spine	√	√	52	nasion contour Intervening point 1b		√
13	Posterior nasal spine	√	√	53	nasion contour intervening point 2b		√
14	Point A	√	√	54	supranasal tip		√
15	Point A contour intervening pointb			55	pronasale		√
16	Supradentale		√	56	columella
17	U1 root tip		√	57	columella contour intervening pointb
18	U1 incisal edge	√	√	58	subnasale	√	√
19	L1 incisal edge	√	√	59	cheekpoint
20	L1 root tip		√	60	point A		√
21	Infradentale		√	61	superior labial sulcus		√
22	Point B contour intervening pointb			62	labiale superius
23	Point B	√	√	63	upper lip	√	√
24	Protuberance menti			64	upper lip contour Intervening pointb
25	Pogonion	√	√	65	stomion superius		√
26	Gnathion	√	√	66	stomion inferius		√
27	Menton	√	√	67	lower lip contour Intervening pointb
28	Gonion, constructed	√	√	68	lower lip	√	√
29	Mandibular body contour intervening point 1b			69	labiale inferius
30	Mandibular body contour intervening point 2b			70	inferior labial sulcus
31	Mandibular body contour intervening point 3b			71	point B
32	Gonion, anatomic		√	72	protuberance menti
33	Gonion contour intervening point 1b			73	pogonion	√	√
34	Gonion contour intervening point 2b			74	gnathion		√
35	Articulare	√	√	75	menton		√
36	Ramus contour intervening point 1b			76	menton contour Intervening pointb
37	Ramus contour intervening point 2b			77	cervical point
38	Condylion		√	78	cervical point contour intervening point 1b
39	Ramus tip			79	cervical point contour intervening point 2b
40	Pterygomaxillary fissure			80	terminal point

^aThe 19 and 40 subsets are marked with the symbol √.

^bArbitrarily defined points for smooth delineation of anatomical structures. Capital letters represent hard-tissue landmarks, and lowercase letters represent soft-tissue landmarks.

Deep-Learning Method and Resultant AIs

The resolution of all images was 150 pixels per inch, and the image size was 1670 × 2010 pixels. The AIs were built on a desktop computer with ordinary specifications commonly available in the current market. The platform used was NVIDIA Computer Unified Device Architecture, a parallel computing platform for GPUs (Ubuntu 18.04.1 LTS with NVIDIA GeForce GTX 1050 Ti GPU, NVIDIA Corporation, Santa Clara, Calif). The AI algorithm was based on the latest deep-learning method, a modified You-Only-Look-Once version 3 algorithm. This is a deep-learning algorithm developed for real-time object detection.^6,14,28 The AI training time was about 12 hours when the number of learning data sets was greater than 1600. In cases in which the number of learning data sets was less than 1200, the training time varied approximately between 1 and 8 hours. During the training process, about 80% of the total memory of the GPU was occupied, which was approximately 3.2 GB.

According to the quantity of learning data and the number of landmarks, a total of 24 combinations (N × M = 8 × 3 = 24) of learning data sets were used in the AI training procedures. These procedures were repeated four times. In total, 96 different AIs were produced.

Test Procedure and Accuracy Measures

A total of 200 radiographs, which were not included in the 2200 learning data sets, were selected as test data in the present study. Each landmark in the 200 test images was identified by the 96 different AIs.

The accuracy of landmark identification of AI was evaluated by the mean radial error (MRE). The radial error (ie, the Euclidean distance between a landmark identified by human and by AI), was defined as

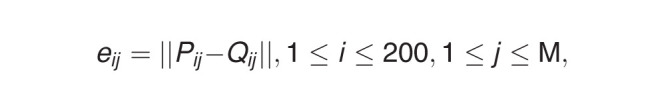where P_ij, Q_ij represented the position of j^th landmark of the i^th image identified by human and AI, respectively; M was the total number of landmarks used to train AI; and || || stands for the Euclidean distance measure calculated in millimeter units.

Statistical Analysis

To compare the accuracy according to the quantity of learning data and the number of detecting targets per image implemented during the training procedure of AI, and to determine the optimal number required to sufficiently train the AI, multiple linear regression analysis was conducted. The regression equation was formulated by setting MRE as a dependent variable and the quantity of learning data and the number of detecting targets as independent variables. All statistical analyses were performed by using Language R.29 The significance level was set at P < .05.

RESULTS

According to the Quantity of Learning Data

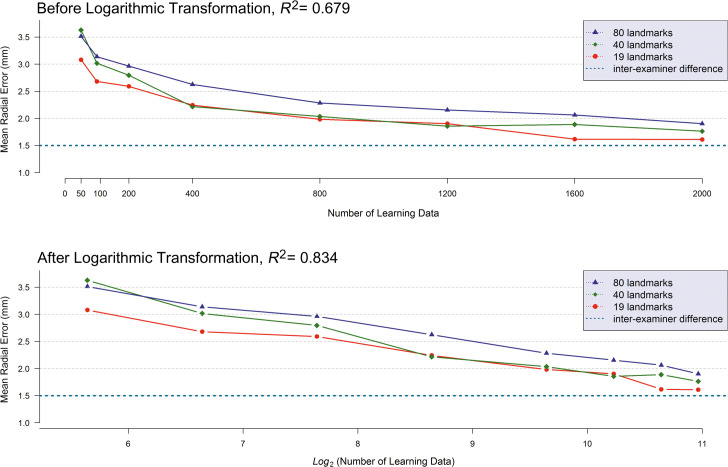
The relationship of the detection errors (or MRE) of AI to the quantity of learning data is illustrated in the top of Figure 2 by the number of detecting targets used in training. Multiple linear regression analysis showed that detection errors of the AI were significantly associated not only with the quantity of learning data but also with the number of detecting targets per image (P < .0001, Table 3). The more data that were implemented during the training procedure of AI, the smaller the detection errors observed. The resulting graph indicated that the relationship between the detection errors and the quantity of learning data seemed more likely to be nonlinear than linear. Upon inspecting the skewness of the graph, a logarithmic transformation was applied to the number of learning data sets. This resulted in a more plausible linear relationship (Figure 2, bottom). After applying the logarithmic transformation, the determination coefficient of the multiple regression model (R²), which is an indicator of the goodness-of-model-fit, also called the power of explanation, changed from R² = 0.679 to R² = 0.834. Consequently, the logarithmic transformation of the number of sample sizes indicated a more suitable explanation than the raw data modeling.

Figure 2.

(Top) Mean radial error (MRE) in millimeter units according to the quantity of learning data. (Bottom) Logarithmic transformation with base 2 was applied to the number of learning data sets.

Table 3.

Detection Errors of AI According to the Quantity of Learning Data and the Number of Detecting Targets Implemented During the Training Process^a

		Number of Learning Data (N)
Number of Landmarks (M)		n = 50	n = 100	n = 200	n = 400	n = 800	n = 1200	n = 1600	n = 2000
m = 19	First trial	3.74	2.54	2.80	1.89	2.19	1.84	1.66	1.63
	Second trial	2.78	2.71	2.39	2.07	1.73	1.96	1.55	1.64
	Third trial	2.82	2.88	2.68	2.56	2.17	2.09	1.76	1.59
	Fourth trial	2.98	2.59	2.49	2.45	1.84	1.72	1.50	1.58
	Average	3.08	2.68	2.59	2.24	1.98	1.90	1.62	1.61
m = 40	First trial	3.31	2.9	2.67	1.98	2.18	1.75	1.74	1.52
	Second trial	3.79	2.63	2.99	1.95	1.87	1.89	1.96	1.89
	Third trial	4.48	3.55	2.89	2.43	1.82	1.99	1.80	1.79
	Fourth trial	2.93	2.98	2.63	2.50	2.27	1.79	2.05	1.85
	Average	3.63	3.02	2.80	2.22	2.04	1.86	1.89	1.76
m = 80	First trial	3.51	3.38	3.08	2.52	2.14	1.98	2.27	1.76
	Second trial	3.21	3.27	2.43	2.55	2.26	2.13	1.98	1.94
	Third trial	3.75	2.78	3.15	2.44	2.32	2.15	2.09	2.15
	Fourth trial	3.58	3.12	3.19	2.99	2.41	2.36	1.91	1.76
	Average	3.51	3.14	2.96	2.63	2.28	2.16	2.06	1.90

^aThe values are mean radial error (MRE) by each trained AI in millimeter units for 200 test data sets. For each N, M combination, four random samples of size N were drawn from 2200 images.

According to the Number of Detecting Targets per Image

According to the number of detecting targets per image, the opposite relationship was observed; the detection errors increased as the number of detecting targets increased (Figure 2). The regression coefficients, β_{Number of Learning Data} and β_{Number of Detecting Targets} , from the multiple linear regression analysis underwent statistical tests under the null hypothesis if (1) β_{Number of Learning Data} ≥ 0 and (2) β_{Number of Detecting Targets} ≤ 0. This was to confirm statistically the previously mentioned relationships. As a result of the hypothesis tests, both null hypotheses were rejected. Consequently, this implied that the detection errors of AI decreased as the number of learning data sets increased, and the detection errors of AI decreased when the number of detecting targets decreased (Table 3).

Estimation of Optimal Quantity of Learning Data

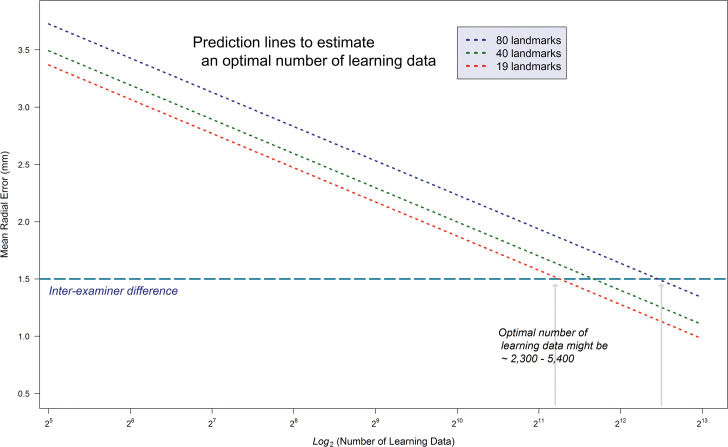
To estimate the optimal quantity of learning data, a prediction model based on the previously mentioned multiple linear regression model was built. Through the logarithmic transformation, there was a gain in the power of explanation from 67.9% to 83.4%. The decision criteria for clinically acceptable MRE was the interexaminer difference between human clinicians. Through the estimation procedure, at least 2300 learning data seemed to be necessary to develop AI as accurate as human examiners (Figure 3).

Figure 3.

Result of estimating an optimal number of learning data sets. To develop reliable AI that might be as accurate as human examiners, at least 2300 learning data sets seemed to be necessary.

DISCUSSION

The present study was the first study that examined the effect of the quantity of learning data and the number of detecting targets on the accuracy of AI. Most AI studies primarily focused on developing and improving accuracy.^2,3,6,14,20 However, previous studies implemented varying numbers of learning data sets and landmarks during the training procedure of AI, making it difficult to compare the resulting benchmarks among the studies (Table 4). Therefore, the primary purpose of the present study was shifted from the AI training method itself to the quantity of data that might sufficiently train AI, not only for research purposes, but also for use in clinical practice. As anticipated, the greater the quantity of learning data, the better the accuracy of AI. In addition, more detecting targets required a greater quantity of learning data to achieve a comparable level of accuracy (Figure 2). By applying a statistical simulation procedure, the study showcased how to determine the optimal quantity of learning data needed to develop AI as accurate as human examiners.

Table 4.

Previous Reports Regarding Automated Identification of Cephalometric Landmarks

Research Group	Year	Number of Learning Data	Number of Test Data	Number of Landmarks	Mean Radial Error, mm
Hwang et al.6	2019	1028	283	80	1.46
Lee et al.10	2019	935	100	33	Not reported
Wang et al.20	2018	150	150	19	1.69
Arik et al.3	2017	150	150	19	Not reported
Lindner et al.12	2016	400	None	19	1.2
Kaur and Singh9	2015	135	85	18	1.86
Lindner and Cootes11	2015	150	150	19	1.67
Ibragimov et al.8	2015	150	150	19	1.84
Ibragimov et al.7	2014	100	100	19	1.82–1.92
Vandaele et al.16	2014	100	100	19	1.95–2.20
Mirzaalian and Hamarneh13	2014	100	100	19	2.35–2.61
Chu et al.5	2014	100	100	19	2.68–2.92
Chen and Zheng4	2014	100	100	19	2.81–2.85

Prior to the beginning stage of the present study, the pattern of detection errors had been expected to decrease as the number of data sets increased. If a plateau with a significantly reduced error was detected, it could have been identified as an optimal point. However, there was no plateau. Instead, a linear relationship between the accuracy of AI and the log-transformed number of learning data sets was observed (Figure 2). In a previous deep-learning example based on picture files, the performance of image detection was reported to increase linearly over the log-transformed number of learning data sets.30 In mathematics, the logarithmic graph is one of the most well-known monotone increasing functions. Therefore, both in reality and in theory, it could be conjectured that the detection errors would gradually decrease as more and more data were implemented. However, in practice, because of the limitation of collecting and collating a huge amount of data, it might be reasonable to find an optimal point by examining the accuracy-data size tradeoffs. In the present study, this was accomplished by visually determining the optimal quantity of data on the graph. An interexaminer reliability measure could be applied that could be considered as a means to verify whether the AI created by a certain amount of data would result in accurate, practical, and clinically applicable AI. Taking the interexaminer difference of 1.50 mm between human examiners into consideration, the estimated quantity of learning data seemed to be at least 2300 data sets (Figure 3). Therefore, the sufficient quantity of learning data calculated in this study far outnumbered the learning data sizes (40– 1000) that were included in previous publications (Table 4).

Regarding the number of landmarks identified, most previous reports detected less than 20 anatomical landmarks (Table 4). This number might be sufficient to calculate the cephalometric measurements used in major orthodontic analyses. However, to obtain smooth realistic soft-tissue lines connecting neighboring soft-tissue landmarks and to be capable of predicting treatment outcomes, considerably greater numbers of landmarks (ie, more than 70 landmarks) were needed.^{6,14,23–27,31,32} To predict and visualize facial profile changes following orthodontic treatment, fewer than 20 landmarks could not provide sufficient soft-tissue information.^3,18–20 Although there have been significant advances in AI technology, the actual quantity of data needed for deep learning has not been given sufficient attention. The success of AI should be a model with high accuracy and also with considerably large-scale data sets.

CONCLUSIONS

• The accuracy of AI was directly proportional to the quantity of learning data and the number of detection targets.

• It could be conjectured that a considerable quantity of learning data, approximately at least 2300 learning data sets, would be required to develop accurate and clinically applicable AI.