The influence of awareness campaigns on the spread of an infectious disease: a qualitative analysis of a fractional epidemic model

Abstract

Mass-media coverage is one of the most widely used government strategies on influencing public opinion in times of crisis. Awareness campaigns are highly influential tools to expand healthy behavior practices among individuals during epidemics and pandemics. Mathematical modeling has become an important tool in analyzing the effects of media awareness on the spread of infectious diseases. In this paper, a fractional-order epidemic model incorporating media coverage is presented and analyzed. The problem is formulated using susceptible, infectious and recovered compartmental model. A long-term memory effect modeled by a Caputo fractional derivative is included in each compartment to describe the evolution related to the individuals’ experiences. The well-posedness of the model is investigated in terms of global existence, positivity, and boundedness of solutions. Moreover, the disease-free equilibrium and the endemic equilibrium points are given alongside their local stabilities. By constructing suitable Lyapunov functions, the global stability of the disease-free and endemic equilibria is proven according to the basic reproduction number $R_0$. Finally, numerical simulations are performed to support our analytical findings. It was found out that the long-term memory has no effect on the stability of the equilibrium points. However, for increased values of the fractional derivative order parameter, each solution reaches its equilibrium state more rapidly. Furthermore, it was observed that an increase of the media awareness parameter, decreases the magnitude of infected individuals, and consequently, the height of the epidemic peak.

Introduction

Epidemic outbreaks are usually caused by transmissible infections, commonly transmitted through animal-to-person, person-to-person, or from direct contact with potentially infected environments (van Seventer and Hochberg 2017). Many vital elements, including water, sanitation, food and air quality play an essential role in the spread of transmissible diseases (Musoke et al. 2016). According to World Health Organization (WHO), water supply, sanitation facilities, food and climate are the most important environmental factors influencing the transmission of infectious diseases. Besides, the irrational behavior of humans in the global environment promotes the emergence of infections (Nava et al. 2017). Indeed, the over-exploitation of natural resources, the upheavals of biodiversity and climate change may lead to the sudden appearance of new infectious diseases, particularly zoonotic diseases that are transmitted from animals to humans (Wilcox and Gubler 2005; Johnson et al. 2015). The emergence of SARS-CoV-1 in 2002, Ebola virus disease (EVD) and the emergence of MERS-CoV in 2012 have been designated as zoonotic diseases (Reperant and Osterhaus 2017). In addition, the current coronavirus disease pandemic 2019 (COVID-19), caused by SARS-CoV-2, has been similarly defined as an emerging infectious disease of animal origin (Abdel-Moneim and Abdelwhab 2020; Mahdy et al. 2020). However, for a long time, humans have invented several strategies to fight against epidemics such as quarantine, isolation and vaccination. On the other hand, mathematical modeling of infectious diseases has also been a valuable tool in the fight against epidemics outbreaks (Hethcote 2000). Kermack and McKendrick (1927) proposed the first modeling investigation of the course of an epidemic for a certain population in the early 20th century. Recently, modeling infectious diseases have generated significant interest in health research. Accordingly, modeling infectious diseases has been an interesting issue in mathematical epidemiology (Hethcote 2000; Venkatachalam and Mikler 2006; Area et al. 2015; Singh et al. 2016a, b; Tolles and Luong 2020; Aidoo et al. 2021). The authors have often used deterministic and stochastic versions of SIR-type compartment models (Buonomo et al. 2008; Jiang et al. 2011; Lin et al. 2014; Zhao 2016). However, in recent years many other researchers have used fractional extensions of mathematical models to study the dynamic of epidemics using fractional order derivatives (Ahmed et al. 2006; El-Saka 2013; Al-Sulami et al. 2014). Modeling by fractional-order differential equations has been an essential tool for describing dynamical processes involving memory effects that exist in many biological systems (Huo et al. 2015). During an epidemic, we can observe a biphasic decline behavior of infections or diseases at a slower rate due to population experiences and memory effects that cannot be modeled only by a natural derivative. For this reason, fractional modeling is more accurate than models based on ordinary differential equations. In recent years, many fractional SIR-type models involving Caputo fractional derivative have been developed and studied (Area et al. 2015; Saeedian et al. 2017; dos Santos et al. 2017; Mouaouine et al. 2018). Saeedian et al. (2017) studied the effect of memory on the evolution of an epidemic by means of the following model

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{D}^{\alpha }S(t)=\hfill & -\beta S(t)I(t),\hfill \\ D^{\alpha }I(t)=\hfill & \beta S(t)I(t)-\gamma I(t),\hfill \\ D^{\alpha }R(t)=\hfill & \gamma I(t),\hfill \end{array}\right)\end{array}$$ 1

in which, the population is divided into three compartments, depending on the epidemiological status of individuals: numbers of susceptible (S(t)), infectious (I(t)) and recovered (R(t)) at time t. $\beta$ and $\gamma$ are infection and recovery coefficients, respectively. $D^{\alpha }$ denotes the Caputo fractional derivative of order $\alpha$, where $\alpha \in (0,1)$. The authors showed that the dynamics of the system depends on the degree of memory effects, governed by the order of fractional derivatives $\alpha$, in which the evolution of an epidemic depends on the fraction of infected individuals at the onset of memory effects in the evolution. Recently, Mouaouine et al. (2018) investigated a fractional-order SIR epidemic model with nonlinear incidence function to cover various types of incidence rate that exist in literature. More recently, several studies have been conducted to study the dynamics of the COVID-19 pandemic using fractional-order mathematical models (Ahmad et al. 2020; Zeeshan et al. 2021; Oud et al. 2021; Chu et al. 2021). However, during an epidemic, awareness campaigns have been the most recommended Non-Pharmaceutical strategies used by the public health departments in order to slow down the spread of infections (Bergeron and Sanchez 2005; Cui et al. 2008; Liu and Ja 2008; Liu et al. 2007). The current crisis of COVID-19 pandemic has shown great interest of the media coverage as a means of health education through the dissemination of awareness programs and preventive measures. The health awareness campaigns have played an important role in influencing people’s behavior, and consequently, in controlling the force of the infection (Musa et al. 2021). In this paper, we enhance the model (1) by introducing the awareness campaign policy into the epidemic dynamics. For this end, we explore the following fractional SIR epidemic model with nonlinear incidence rate incorporating media coverage:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{D}^{\alpha }S(t)=\hfill & \Lambda -\left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}I(t)}{m+I(t)}}\right)S(t)I(t)-\mu S(t),\hfill \\ D^{\alpha }I(t)=\hfill & \left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}I(t)}{m+I(t)}}\right)S(t)I(t)-(\mu +d+r)I(t),\hfill \\ D^{\alpha }R(t)=\hfill & rI(t)-\mu R(t),\hfill \end{array}\right)\end{array}$$ 2

$\Lambda$ is the recruitment rate of the population, $\mu$ is the natural death rate, while d is the death rate due to disease and r is the recovery rate of the infectious individuals. ${\beta }_1$ is the maximal effective contact rate before media alert, ${\beta }_2$ is the maximal effective contact rate due to mass media alert in the presence of infected population. The half saturation $m>0$ reflects the reactive velocity of individuals and media coverage to epidemic disease. The function $\frac{I}{m+I}$ is a continuous bounded function that takes into account disease saturation or psychological effects (Tchuenche et al. 2011). The term $\frac{{\beta }_{2}I}{m+I}$ measures the effect of reduction of the contact rate when infectious individuals are reported in the media. Because the coverage report can slow, but cannot prevent disease from spreading completely, we have ${\beta }_1\ge {\beta }_2>0$. Since the two first equations in system (2) are independent of the third equation, we can reduce this system to the following equivalent model:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{D}^{\alpha }S(t)=\hfill & \Lambda -\left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}I(t)}{m+I(t)}}\right)S(t)I(t)-\mu S(t),\hfill \\ D^{\alpha }I(t)=\hfill & \left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}I(t)}{m+I(t)}}\right)S(t)I(t)-(\mu +d+r)I(t).\hfill \end{array}\right)\end{array}$$ 3

This study is organized as follows. In the next section, we present some background material and we show that our model is biologically and mathematically well posed. In the following section, we investigate the existence of equilibrium points and their local stability. Then we mainly study the global stability of the system and we present some numerical simulations to support our theoretical findings. Finally, we provide some conclusions.

Preliminary results

In this section, we recall some preliminary definitions of the fractional-order integral, Caputo fractional derivative, and Mittag–Lefller function (see Podlubny 1999), and the references therein). Therefore, we establish, the positivity and boundedness of solutions of the model (3).

Definition 1

The fractional integral of order $\alpha >0$ of a function $f:{\mathbb{R}}_{+}\to \mathbb{R}$ is defined as follows:

$$\begin{array}{c}\hfill I^{\alpha }f(t)=\frac{1}{\mathrm{\Gamma }(\alpha )}{\int }_0^t{(t-x)}^{\alpha -1}f(x)\mathrm{d}x,\end{array}$$ 4

where $\mathrm{\Gamma }(.)$ is the Gamma function.

Definition 2

The Caputo frational derivative of order $\alpha >0$ of a function $f:{\mathbb{R}}_{+}\to \mathbb{R}$ is given by

$$\begin{array}{c}\hfill D_t^{\alpha }f(t)=I^{n-\alpha }{D}_t^{n}f(t),\end{array}$$ 5

where $D\equiv \mathrm{d}/\mathrm{d}t$, with $\alpha \in (n-1,n)$ and $n\in {\mathbb{N}}^{\star }$. In particular, when $\alpha \in (0,1)$, we have

$$\begin{array}{c}\hfill D_t^{\alpha }f(t)={\displaystyle \frac{1}{\mathrm{\Gamma }(1-\alpha )}}{\int }_0^t{\displaystyle \frac{f^{\prime }(x)}{{(t-x)}^{\alpha }}}\mathrm{d}x.\end{array}$$ 6

Definition 3

Let $\alpha >0.$ The function $E_{\alpha }$ defined by

$$\begin{array}{c}\hfill E_{\alpha }(z)=\sum _{j=0}^{\infty }\frac{z^j}{\mathrm{\Gamma }(\alpha j+1)},\end{array}$$ 7

is called the Mittag–Lefller function of parameter $\alpha$.

It is well-known that both of infected population and susceptible individuals number should remain nonnegative and bounded. For this end, we explore the well-posedness of our proposed problem (3). Let $X(t)=\left(\begin{array}{c}S(t)\\ I(t)\end{array}\right)$, then we can reformulate the system (3) as follows:

$$\begin{array}{c}\hfill D^{\alpha }X(t)=F(X(t)),\end{array}$$ 8

where

$$\begin{array}{c}\hfill F(X(t))=\left(\begin{array}{c}\Lambda -\left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}I(t)}{m+I(t)}}\right)S(t)I(t)-\mu S(t)\hfill \\ \left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}I(t)}{m+I(t)}}\right)S(t)I(t)-(\mu +d+r)I(t)\hfill \end{array}\right).\end{array}$$ 9

For biological reasons, we assume that:

$$\begin{array}{c}\hfill S(0)\ge 0,I(0)\ge 0.\end{array}$$ 10

In order to establish the global existence of solutions for system (3) with initial condition (10), we need the following lemma:

Lemma 1

Assume that the vector function $F:{\mathbb{R}}^2\to {\mathbb{R}}^2$ satisfies the following conditions:

1. F(X) and $\frac{\partial F}{\partial X}$ are continuous.

2. $∥F,(,X,)∥\le \omega +\lambda ∥X∥$ $\forall X\in {\mathbb{R}}^2$, where $\omega$ and $\lambda$ are two positive constants.

Then system (3) has a unique solution defined on ${\mathbb{R}}_{+}$.

The proof of this lemma follows immediately from (Lin 2007).

Theorem 1

For any initial conditions satisfying (10), then system (3) has a unique solution on $[0,\infty )$, and this solution remains non-negative and bounded for all $t\ge 0$. In addition, we have

$$\begin{array}{c}\hfill N(t)\le N(0)+{\displaystyle \frac{\Lambda }{\mu }},\end{array}$$

where $N(t)=S(t)+I(t)$.

Proof

Using the results in (Hale and Lunel 1993), we establish the existence of solutions. Let

$$\begin{array}{cc}\hfill \epsilon =& \left(\begin{array}{c}\Lambda \\ 0\end{array}\right),A=\left(\begin{array}{cc}-\mu & 0\\ 0& -(\mu +d+r)\end{array}\right),\hfill \\ \hfill B_1=& \left(\begin{array}{c}-{\beta }_1\\ {\beta }_1\end{array}\right),B_2=\left(\begin{array}{c}{\beta }_2\\ -{\beta }_2\end{array}\right)\hfill \end{array}$$

then the system (3) can be written as follows:

$$\begin{array}{c}\hfill F(X)=\epsilon +AX+B_{1}SI+B_2{\displaystyle \frac{I}{I+m}}SI.\end{array}$$ 11

Then

$$\begin{array}{c}\hfill ∥F,(,X,)∥\le ∥\epsilon ∥+(∥B_1∥+∥B_2∥)∥S,I∥+∥A∥∥X∥.\end{array}$$ 12

Hence, the proprieties of Lemma 1 are satisfied. Then the system has a unique solution. Now, we establish the non-negativity of the solution, we have

$$\begin{array}{cc}& D^{\alpha }{S|}_{S=0}=\Lambda \ge 0,\hfill \end{array}$$ 13

$$\begin{array}{cc}& D^{\alpha }{I|}_{I=0}=0.\hfill \end{array}$$ 14

Therefore, the solution of system (3) remains non-negative in ${\mathbb{R}}_{+}^2$ for all $t\ge 0$.

Finally, we prove the boundedness of solution. From the model (3), and by adding all the equations, we obtain

$$\begin{array}{cc}\hfill D^{\alpha }N(t)=& \Lambda -\mu S(t)-(\mu +d+r)I(t)\hfill \\ \hfill \le & \Lambda -\mu N(t).\hfill \end{array}$$ 15

Solving (15), we get

$$\begin{array}{cc}\hfill D^{\alpha }N(t)\le & \left(-,{\displaystyle \frac{\Lambda }{\mu }},+,N,(0)\right)E_{\alpha }(-\mu t^{\alpha })+{\displaystyle \frac{\Lambda }{\mu }},\hfill \end{array}$$ 16

Since $0\le E_{\alpha }(-\mu t^{\alpha })\le 1$, we get

$$\begin{array}{c}\hfill N(t)\le N(0)+{\displaystyle \frac{\Lambda }{\mu }}.\end{array}$$ 17

This completes the proof. $\square$

Qualitative analysis of model (3)

Equilibria and local stability

In this subsection, we will determine the steady states of the model and investigate the local stability. We define the basic reproduction number $R_0$ (Van den Driessche and Watmough 2002) of our model by

$$\begin{array}{c}\hfill R_0={\displaystyle \frac{{\beta }_1\Lambda }{\mu (\mu +d+r)}}.\end{array}$$ 18

This quantity describes the average number of secondary infected individuals produced by one infected case in a susceptible population. First, we discuss the existence of equilibria for system (3). It is easy to see that system (3) has always a disease-free equilibrium $E_0(S_0,0)$ where $S_0=\frac{\Lambda }{\mu }$. In addition, we will show that the model (3) has an endemic steady state when $R_0>1$. Let $E^{\star }(S^{\star },I^{\star })$ be an endemic equilibrium such that $S^{\star }>0$, $I^{\star }>0$ and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\Lambda -\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)S^{\star }{I}^{\star }-\mu S^{\star }\hfill & =0,\hfill \\ \left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)S^{\star }{I}^{\star }-(\mu +d+r)I^{\star }\hfill & =0.\hfill \end{array}\right)\end{array}$$ 19

It follows that

$$\begin{array}{c}\hfill S^{\star }={\displaystyle \frac{\mu +d+r}{\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)}}\end{array}$$ 20

and

$$\begin{array}{c}\hfill {\displaystyle \frac{\Lambda }{\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)I^{\star }+\mu }}={\displaystyle \frac{\mu +d+r}{\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)}}.\end{array}$$ 21

Substituting (19) into the first equation of system (18), we obtain

$$\begin{array}{c}\hfill \Lambda -{\displaystyle \frac{\mu (\mu +d+r)}{\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)}}-(\mu +d+r)I^{\star }=0.\end{array}$$ 22

Let H be the function defined as

$$\begin{array}{c}\hfill H(x)=\Lambda -{\displaystyle \frac{\mu (\mu +d+r)}{\left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}x}{m+x}}\right)}}-(\mu +d+r)x.\end{array}$$ 23

We prove that the equation $H(x)=0$ has a unique solution. We have

$$\begin{array}{c}\hfill H^{\prime }(x)=-{\displaystyle \frac{m{\beta }_2\mu (\mu +d+r)}{{\left(m,+,x\right)}^2{\left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}x}{m+x}}\right)}^2}}-(\mu +d+r),\end{array}$$ 24

we can see that $H^{\prime }<0$, then H is a decreasing function. On the other hand, we have ${lim}_{x\to \infty }H(x)=-\infty$ and

$$\begin{array}{cc}\hfill H(0)=& \Lambda -{\displaystyle \frac{\mu (\mu +d+r)}{{\beta }_1}}\hfill \\ \hfill =& {\displaystyle \frac{\mu (\mu +d+r)}{{\beta }_1}}\left(R_0,-,1\right).\hfill \end{array}$$ 25

Since $R_0>1$ we have $H(0)>0$. Therefore, by means of the intermediate value theorem, and since F is decreasing, there is a unique solution of the equation $H(x)=0$. It follows that system (3) has unique endemic equilibrium $E^{\star }=(S^{\star },I^{\star })$. From the discussion above we get the following result:

Theorem 2

1. If $R_0\le 1$, then the system (3) has a unique disease-free equilibrium $E_0$ .

2. If $R_0>1$, the disease-free equilibrium is still present and system (3) has a unique endemic equilibrium $E^{\star }(S^{\star },I^{\star })$.

Next, we discuss the local stability of the disease-free equilibrium $E_0$ and the endemic equilibrium $E^{\star }$ respectively. We define the Jacobian matrix of system (3) at any equilibrium $\overline{E}(\overline{S},\overline{I})$ by

$$\begin{array}{c}\hfill J_{\overline{E}}=\left(\begin{array}{cc}-\mu -\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2\overline{I}}{m+\overline{I}}}\right)\overline{I}& {\displaystyle \frac{{\beta }_{2}m\overline{S}\overline{I}}{{(m+\overline{I})}^2}}-\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2\overline{I}}{m+\overline{I}}}\right)\overline{S}\\ \left({\beta }_1,-,{\displaystyle \frac{{\beta }_2\overline{I}}{m+\overline{I}}}\right)\overline{I}& \left({\beta }_1,-,{\displaystyle \frac{{\beta }_2\overline{I}}{m+\overline{I}}}\right)\overline{S}-{\displaystyle \frac{{\beta }_{2}m\overline{S}\overline{I}}{{(m+\overline{I})}^2}}-(\mu +d+r)\end{array}\right).\end{array}$$ 26

From Petráš (2011), Matignon (1996), a sufficient condition for the local stability of $\overline{E}$ is

$$\begin{array}{c}\hfill \left|arg,(,{\xi }_i,)\right|>{\displaystyle \frac{\alpha \pi }{2}},i=1,2,\end{array}$$ 27

where ${\xi }_i$ are the eigenvalues of $J_{\overline{E}}$. Thus, we have the following:

Theorem 3

If $R_0<1$, then the disease-free equilibrium $E_0$ is locally asymptotically stable and it is unstable whenever $R_0>1$.

Proof

At free-disease equilibrium $E_0$, (25) becomes

$$\begin{array}{c}\hfill J_{E_0}=\left(\begin{array}{cc}-\mu & {\displaystyle \frac{-{\beta }_1\Lambda }{\mu }}\\ 0& {\displaystyle \frac{{\beta }_1\Lambda }{\mu }}-(\mu +d+r)\end{array}\right).\end{array}$$ 28

Therefore, the eigenvalues of $J_{E_0}$ are ${\xi }_1=-\mu$ and ${\xi }_2=(\mu +d+r)(R_0-1)$. It is clear that ${\xi }_2$ satisfies condition (26) if $R_0<1$, and since ${\xi }_1$ is negative, this completes the proof. $\square$

Now, we investigate the local stability of $E^{\star }$. We have the following result.

Theorem 4

If $R_0>1$, then the endemic equilibrium $E^{\star }$ is locally asymptotically stable.

Proof

We assume that $R_0>1$. After evaluating (25) at endemic equilbrium $E^{\star }$ and calculating its characteristic equation, we get

$$\begin{array}{c}\hfill {\lambda }^2+a\lambda +b=0,\end{array}$$ 29

where

$$\begin{array}{cc}\hfill a=& \mu +{\displaystyle \frac{{\beta }_{2}m{S}^{\star }{I}^{\star }}{{(m+I^{\star })}^2}}+\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)I^{\star },\hfill \end{array}$$ 30

$$\begin{array}{cc}\hfill b=& {\displaystyle \frac{{\beta }_{2}m{S}^{\star }{I}^{\star }}{{(m+I^{\star })}^2}}\left(\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right),I^{\star },+,\mu \right).\hfill \end{array}$$ 31

It is obvious that $a>0$ and $b>0$. Hence, the Routh–Hurwitz conditions are satisfied. According to the results in Ahmed et al. (2006), the proof is complete. $\square$

Global stability

This subsection is devoted to the global stability of the two equilibria. To this end, we will use some suitable Lyapunov functions and fractional LaSalle’s invariant principle.

First, for the disease-free equilibrium $E_0$, we have the following result:

Theorem 5

If $R_0\le 1$, then the disease-free equilibrium $E_0$ is globally asymptotically stable.

Proof

We consider the following Lyapunov function:

$$\begin{array}{c}\hfill {\Phi }_0(t)=\left(S,-,S_0,-,S_0,ln,{\displaystyle \frac{S}{S_0}}\right)+I.\end{array}$$ 32

We calculate the fractional time derivation of ${\Phi }_0$ along with the solution of system (3). We obtain

$$\begin{array}{c}\hfill D^{\alpha }{\Phi }_0(t)=\left(1,-,{\displaystyle \frac{S_0}{S}}\right)D^{\alpha }S+D^{\alpha }I.\end{array}$$ 33

Using the fact that $\Lambda =\mu S_0$, we obtain

$$\begin{array}{cc}\hfill D^{\alpha }{\Phi }_0(t)\le & -{\displaystyle \frac{\mu }{S}}{(S-S_0)}^2-\left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}I}{m+I}}\right)(S-S_0)I\hfill \\ \hfill & +\left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}I}{m+I}}\right)SI-(\mu +d+r)I\hfill \\ \hfill =& -{\displaystyle \frac{\mu }{S}}{(S-S_0)}^2+\left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}I}{m+I}}\right)S_{0}I\hfill \\ \hfill & -(\mu +d+r)I\hfill \\ \hfill =& -{\displaystyle \frac{\mu }{S}}{(S-S_0)}^2\hfill \\ \hfill & -{\displaystyle \frac{{\beta }_{2}I}{m+I}}{S}_{0}I+(\mu +d+r)(R_0-1)I.\hfill \end{array}$$ 34

Since $R_0\le 1$, then $D^{\alpha }{\Phi }_0(t)\le 0$. Furthermore $D^{\alpha }{\Phi }_0(t)=0$ holds, if and only if $S=S_0$ and $I=0$. Consequently, the largest invariant set of $\{(S,I)\in {\mathbb{R}}_{+}^2:D^{\alpha }{\Phi }_0(t)=0\}$ is the singleton $\{E_0\}$. By fractional LaSalle’s invariance principle (Huo et al. 2015), $E_0$ is globally asymptotically stable. $\square$

For the second endemic equilibrium $E^{\star }$, we have the following result:

Theorem 6

The endemic equilibrium $E^{\star }$ is globally asymptotically stable whenever $R_0>1$.

Proof

We consider the following Lyapunov function:

$$\begin{array}{c}\hfill {\Phi }_1(t)={\displaystyle \frac{1}{2}}{(S-S^{\star }+I-I^{\star })}^2+a\left(I,-,I^{\star },-,I^{\star },ln,{\displaystyle \frac{I}{I^{\star }}}\right),\end{array}$$ 35

where a is a positive constant to be determined later.

We calculate the fractional time derivation of ${\Phi }_1$ along the solution of system (3). We get

$$\begin{array}{c}\hfill D^{\alpha }{\Phi }_1(t)=(D^{\alpha }S+D^{\alpha }I)(S-S^{\star }+I-I^{\star })+a\left(1,-,{\displaystyle \frac{I^{\star }}{I}}\right)D^{\alpha }I,\end{array}$$ 36

hence

$$\begin{array}{cc}\hfill D^{\alpha }{\Phi }_1(t)\le & (S-S^{\star }+I-I^{\star })\left(\Lambda ,-,\mu ,S,-,(,\mu ,+,d,+,r,),I\right)\hfill \\ \hfill & +a\left(1,-,{\displaystyle \frac{I^{\star }}{I}}\right)\left(\left({\beta }_1,-,{\displaystyle \frac{{\beta }_{2}I}{m+I}}\right),S,I\right)\hfill \\ \hfill & \left(-,(,\mu ,+,d,+,r,),I\right).\hfill \end{array}$$ 37

Using the fact that

$$\begin{array}{cc}\hfill \Lambda =& \mu S^{\star }+(\mu +d+r)I^{\star },\hfill \end{array}$$ 38

$$\begin{array}{cc}\hfill \left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)S^{\star }=& \mu +d+r,\hfill \end{array}$$ 39

we obtain

$$\begin{array}{cc}\hfill D^{\alpha }{\Phi }_1(t)\le & (S-S^{\star }+I-I^{\star })\left(\mu ,(,S^{\star },-,S,)\right)\hfill \\ \hfill & \left(+,(\mu +d+r),(I^{\star }-I)\right)\hfill \\ \hfill & +a(I-I^{\star })\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)(S-S^{\star })\hfill \\ \hfill & -a(I-I^{\star })\left({\displaystyle \frac{{\beta }_{2}I}{m+I}},-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)S\hfill \\ \hfill =& -\mu {(S-S^{\star })}^2-(\mu +d+r){(I-I^{\star })}^2\hfill \\ \hfill & +\left[a,\left({\beta }_1,-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)\right)\hfill \\ \hfill & \left(-,(,2,\mu ,+,d,+,r,)\right](S-S^{\star })(I-I^{\star })\hfill \\ \hfill & -a(I-I^{\star })\left({\displaystyle \frac{{\beta }_{2}I}{m+I}},-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)S.\hfill \end{array}$$ 40

Choose $a={\displaystyle \frac{2\mu +d+r}{{\beta }_1-{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}}}$ and notice that both $I-I^{\star }$ and ${\displaystyle \frac{{\beta }_{2}I}{m+I}}-{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}$ have the same sign, we get

$$\begin{array}{cc}\hfill D^{\alpha }{\Phi }_1(t)\le & -\mu {(S-S^{\star })}^2-(\mu +d+r){(I-I^{\star })}^2\hfill \\ \hfill & -a(I-I^{\star })\left({\displaystyle \frac{{\beta }_{2}I}{m+I}},-,{\displaystyle \frac{{\beta }_2{I}^{\star }}{m+I^{\star }}}\right)S\hfill \\ \hfill \le & 0.\hfill \end{array}$$ 41

Hence, the largest invariant set of $\{(S,I)\in {\mathbb{R}}_{+}^2:D^{\alpha }{\Phi }_1(t)=0\}$ is the singleton $\{E^{\star }\}$. By fractional LaSalle’s invariance principle (Huo et al. 2015), $E^{\star }$ is globally asymptotically stable. $\square$

Numerical simulations

In this section, we give some numerical simulations to illustrate our analytical results. For this end, we apply the algorithm presented by Erturk et al. (2008) to numerically solve the model (3). Let’s consider the following problem:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{D}^{\alpha }X(t)\hfill & =F(X(t)),\hfill \\ X(0)\hfill & =X_0\text{,}{X}_0\in {\mathbb{R}}_{+}^2.\hfill \end{array}\right)\end{array}$$ 42

where $X_0=\left(\begin{array}{c}S(0)\\ I(0)\end{array}\right)$ is the initial condition. The problem (42) is solved using the following numerical scheme

$$\begin{array}{cc}\hfill X(t_j)=& {\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\left({(j-1)}^{\alpha +1}\right)\hfill \\ \hfill & \left(-,(j-\alpha -1),j^{\alpha }\right)F(X(t_0))+X(0)\hfill \\ \hfill & +{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}\sum _{i=1}^{j-1}\left({(j-i+1)}^{\alpha +1}\right)\hfill \\ \hfill & \left(-,2,{(j-i)}^{\alpha +1},+,{(j-i-1)}^{\alpha +1}\right)F(X(t_i))\hfill \\ \hfill & +{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +2)}}F\left(X,(,t_{j-1},)\right)\hfill \\ \hfill & \left(+,{\displaystyle \frac{h^{\alpha }}{\mathrm{\Gamma }(\alpha +1)}},F,(X(t_{j-1}))\right),\hfill \end{array}$$ 43

with $t_{j+1}=tj+h$, for $j=0,1,\dots ,N-1$ and $X_0=\left(\begin{array}{c}40\\ 20\end{array}\right)$.

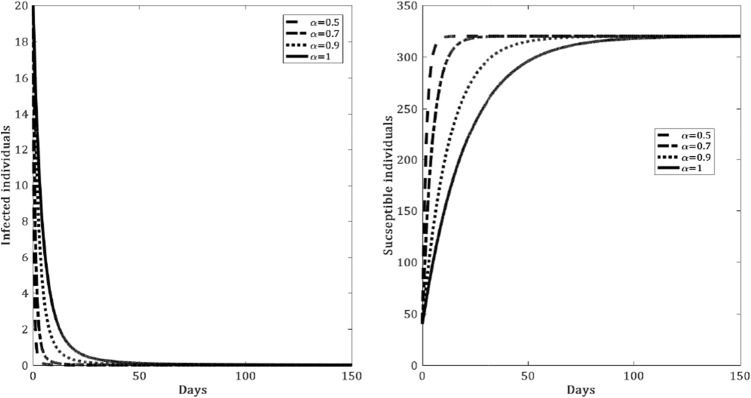
Figure 1 depicts the evolution of the infection during the first 150 days of observation. It is shown that the curves converge toward the disease-free-equilibrium $E_0=(320,0)$. In this case, the basic reproduction number is less than unity ($R_0=0.896<1$) which confirms the stability result of $E_0$.

Fig. 1.

Behavior of the infection as function of time for $\Lambda =16$, ${\beta }_1=0.0007$, ${\beta }_2=0.0005$, $\mu =0.05$, $d=0.1$, $r=0.1$, $m=20$, which corresponds to the stability of the disease-free equilibrium $E_0$

The evolution of the disease infection is represented in Fig. 2 for the endemic steady state $E^{\star }$. We observe that the curves converge to the endemic steady state $E^{\star }=(28,177)$. In this case, we calculate that $R_0=2.560>1$ which support our theoretical result about the stability of $E^{\star }$.

Fig. 2.

Behavior of the infection as function of time for $\Lambda =16$, ${\beta }_1=0.002$, ${\beta }_2=0.001$, $\mu =0.05$, $d=0.1$, $r=0.1$, $m=20$, which corresponds to the stability of the endemic equilibrium $E^{\star }$

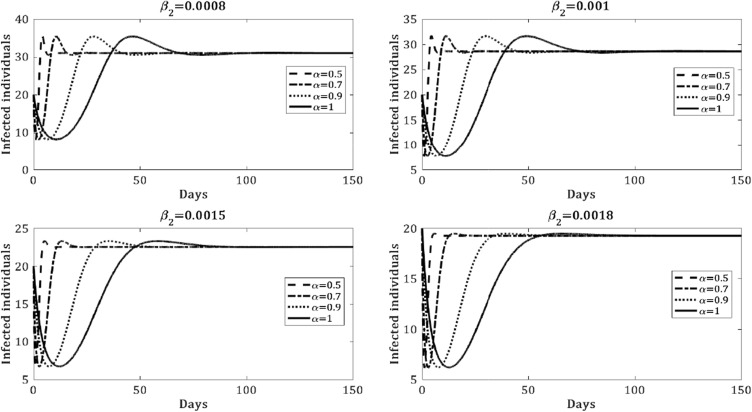
Figure 3 shows the dynamics of the infection illustrating the impact of media coverage on the spread of an epidemic in the case of disease persistence (when $R_0>1$) during the first 150 days of observation. Then we remark that increasing the values of the media coverage rate ${\beta }_2=0.0008;0.001;0.0015;0.0018$, decreases the magnitude of the infectious individuals.

Fig. 3.

Simulation of the media coverage impact on the behavior of the infection for $\Lambda =16$, ${\beta }_1=0.002$, $\mu =0.05$, $d=0.1$, $r=0.1$ and $m=20$

We notice that from the three previous illustrations, the order of the fractional derivative $\alpha$ has no effect on the stability of the equilibria. However, for higher values of $\alpha$, that describe the long memory term, the solutions converge more quickly to the steady states; this can support the fact that epidemic dynamics is directly related to the individuals’ experiences, memory and knowledge induced from epidemic (Saeedian et al. 2017).

Conclusion

In this work, a fractional order SIR epidemic model with the Caputo fractional derivative incorporating awareness campaigns strategy is presented and analyzed. The global existence, positivity and boundedness of solutions are established. The local stability of both disease free-equilibrium and the endemic-equilibrium are investigated. The global stability of both equilibria is explored by using Lyapunov method and fractional La-Salle invariance principle. Numerical simulations of the system are performed. It was shown that different values of $\alpha$ affect the time to reach the steady states, but have no effect on the stability of disease-free equilibrium and the endemic equilibrium. Also, it can be observed that an increase of the media effect parameter ${\beta }_2$, decreases the transmission rate, and consequently, the magnitude of infected individuals. It was found out that from both the analytical and numerical findings, the fractional-order derivative has no effect on the stability of equilibria. However, for increased values of the fractional derivative order, each solution curve converges more rapidly to its stationary state. Our proposed model may be useful to help in understanding the role of awareness programs to prevent the spread of disease during an outbreak, epidemic, or pandemic.

Author Contributions

All authors contributed equally to the writing of this paper. They read and approved the final version of the manuscript.

Funding Information

This research is supported by CNRST “Centre National pour la Recherche Scientifique et Technique”, N I003/018, Rabat, Morocco.

Declarations

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in the above mentioned paper.

Code availability

Available on request from the corresponding author.