DeepBAR: A Fast and Exact Method for Binding Free Energy Computation

Abstract

Fast and accurate calculation of standard binding free energy has many important applications. Existing methodologies struggle at balancing accuracy and efficiency. We introduce a new method to compute binding free energy using deep generative models and the Bennett acceptance ratio method (DeepBAR). Compared to the rigorous potential of mean force (PMF) approach that requires sampling from intermediate states, DeepBAR is an order-of-magnitude more efficient as demonstrated in a series of host-guest systems. Notably, DeepBAR is exact and does not suffer from approximations for entropic contributions used in methods such as the molecular mechanics energy combined with the generalized Born and surface area continuum solvation (MM/GBSA). We anticipate DeepBAR to be a valuable tool for computing standard binding free energy used in drug design.

Graphical Abstract

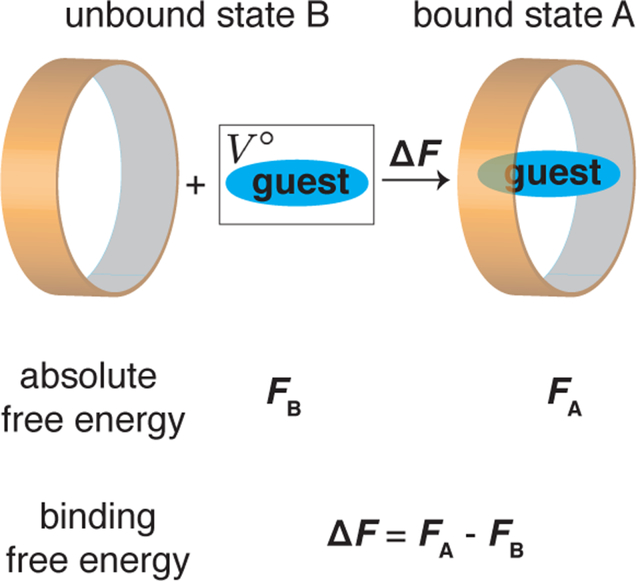
Non-covalent molecular binding is essential for many processes such as self-assembly¹ and signal transduction.² Accurate estimation of the absolute binding affinity could provide insight into the physicochemical interactions that drive these processes.³ Computing binding free energy also has important practical applications in drug discovery for in silico screening and design of small molecules that bind with a target protein.⁴

Numerous methods have been introduced for computing binding free energy. The alchemical double decoupling (ADD)⁵ and the potential of mean force (PMF) methods^6,7 are both exact. They rely on extensive molecular dynamics simulations and can, in principle, produce values directly comparable to experimental measurements, barring the approximations introduced in force field parameterization. Notably, these two methods require simulations for both the two end states (bound and unbound) and many alchemical/physical intermediate states that bridge them.^5–7 In addition to increasing the computational cost significantly, intermediate states are non-trivial to construct, and their definition varies greatly among systems. On the other hand, the molecular mechanics/Poisson–Boltzmann or generalized Born and surface area continuum solvation (MM/PBSA⁸ or MM/GBSA⁹) methods circumvent the need for intermediate states and only require sampling from the two end states. While computationally more efficient, MM/GBSA and MM/PBSA are less accurate due to the approximations introduced for estimating the entropic contributions.^8,9 The quality of such approximations is system-dependent, and their impact on the computed free energy values is hard to gauge a priori.

In this letter, we introduce a new method, DeepBAR, to compute the binding free energy as the difference of the absolute free energy for the bound state A and the unbound state B, i.e., ΔF_binding = F_A − F_B. Previously, we showed that absolute free energy could be calculated using deep generative models and the Bennett acceptance ratio (BAR) method with high accuracy.¹⁰ Like MM/GBSA and MM/PBSA, DeepBAR only requires sampling from the end states. A crucial difference from these methods is that DeepBAR is exact and can achieve the same accuracy as ADD and PMF. Therefore, it is designed to perform fast and accurate computations of binding free energy.

We first briefly review the method for calculating absolute free energy using reference states constructed with deep generative models.¹⁰ For conciseness in notation, we present the algorithmic details using state A as an example, but the procedure applies to state B equally. We define the reference state A° as a probabilistic model, q_A°(x; θ), and its energy function as U_A°(x) = −β⁻¹ log q_A°(x; θ). x represents the Cartesian coordinates of a molecular configuration and θ corresponds to the model parameters. β = 1/(k_BT) is the inverse of the product of the Boltzmann constant (k_B) and temperature (T). The benefit of defining the reference state as a probabilistic model is that because q_A°(x; θ) is normalized, the absolute free energy of this state is 0, i.e.,

$$F_{\text{A}°}=-{\beta }^{-1}\text{log }\int e^{-\beta U_{\text{A}°(\mathit{x})}}\text{ d}x=-{\beta }^{-1}\text{log}\int q_{\text{A}°}(x;\theta )\text{d}x=0.$$ (1)

Therefore, the absolute free energy for state A equals to its free energy difference from A°, ΔF_A°→A, and can be determined by solving the BAR equation:¹¹

$$\sum _{n=1}^{N_{\text{A}°}}f\left(\beta \left[\Delta U\left(x_{\text{A}°}^n\right)-M-\Delta F_{\text{A}°\to \text{A}}\right]\right)=\sum _{n=1}^{N_{\text{A}}}f\left(-\beta \left[\Delta U\left(x_A^n\right)-M-\Delta F_{\text{A}°\to \text{A}}\right]\right),$$ (2)

where f(t) = 1/(1 + e^t), ΔU(x) = U_A(x) − U_A°(x), and M = log(N_A/N_A°). A reliable estimation of the free energy difference, ΔF_A°→A, from the above equation requires (i) independent samples $\left\{x_{{\text{A}}^{°}}^n:n=1,\dots ,N_{{\text{A}}^{°}}\right\}$ from the reference state A° besides state A samples $\left\{x_{\text{A}}^n:n=1,\dots ,N_{\text{A}}\right\}$ that can be produced using molecular dynamics simulations and (ii) a significant phase space overlap between states A° and A. Both requirements can be satisfied if q_A°(x; θ) is designed as deep generative models, a special class of probabilistic models, with parameters (θ) that maximize the log-likelihood on samples $\left\{x_{\text{A}}^n:n=1,\dots ,N_{\text{A}}\right\}$ generated from state A. Deep generative models allow precise evaluation of the absolute probability for any molecular configuration and generating independent configurations at negligible computational cost. Log-likelihood maximization further ensures the similarity between configurations from deep generative models and those produced by molecular dynamics simulations for state A.

To demonstrate the efficacy of DeepBAR for computing binding free energy, we applied it to four host-guest systems (Figure 1).¹² These systems are small in size and permit exhaustive conformational sampling. They are widely used for benchmarking free energy calculation methods.¹³ The host molecule, cucurbit[7]uril (CB7),^14–17 is an achiral ring consisting of 7 glycoluril monomers. It features high binding affinities, especially for guests with a hydrophobic core that can fit tightly into its nonpolar binding pocket. To further simplify the system and eliminate sampling issues that might come from explicit water molecules, we used the OBC implicit solvent model¹⁸ in calculating the binding free energy.

Figure 1:

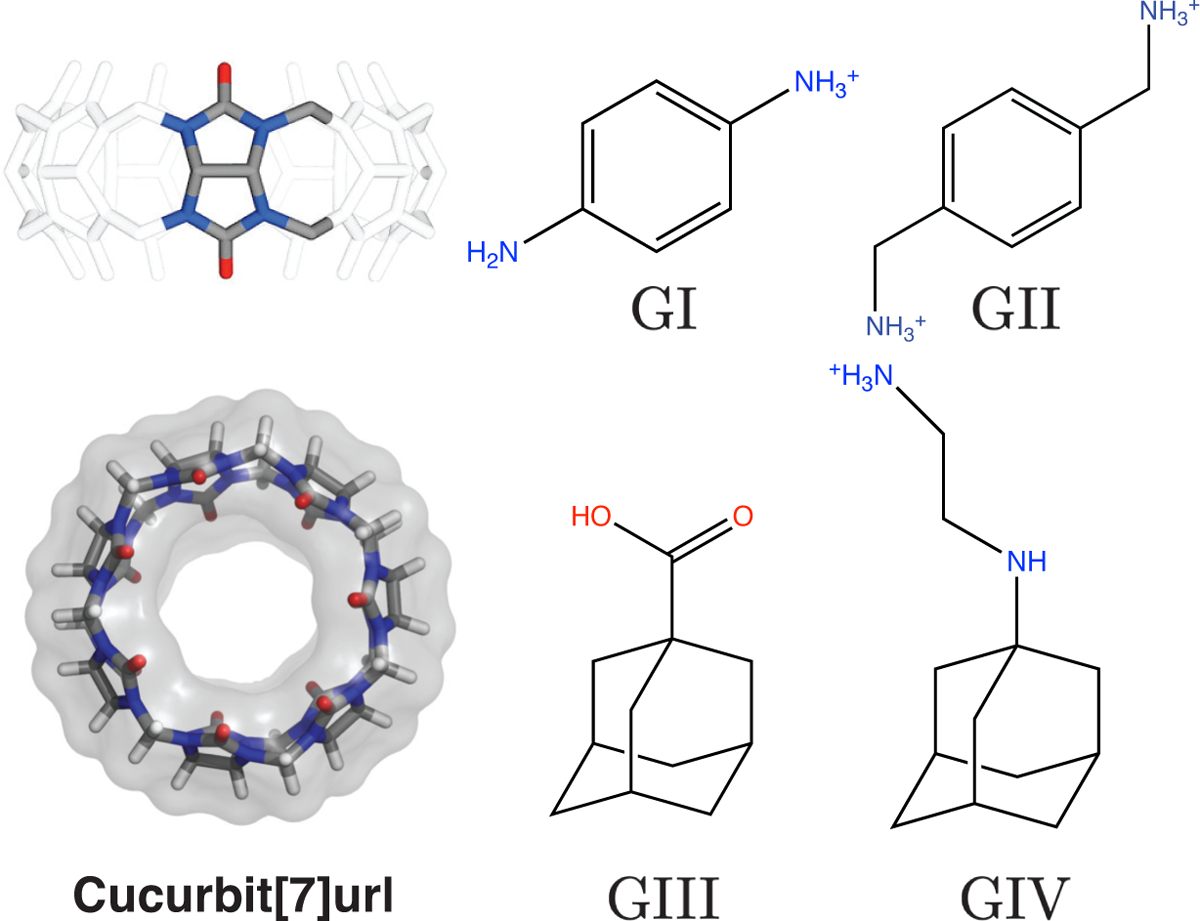
Illustration of the cucurbit[7]uril (CB7) host-guest system used for testing the DeepBAR method. The left two panels provide a side and top view of the host, with its periodic unit highlighted in the top panel. Structures of the four guests (GI-GIV) are shown in the right panels.

Molecular dynamics simulations were performed to collect sample configurations from state A and B. We removed the translational and rotational degrees of freedom for the host in state A and both the host and the guest in state B using restraining potentials. These potentials were defined with the use of fixed anchor particles (P1, P2, and P3) and virtual sites (H1, H2, and H3) of the host (Figure 2a and 2b). As detailed in the Supporting Information (SI), removing these degrees of freedom does not impact the accuracy of free energy calculations but facilitates conformational sampling. For notational purposes, we use x_h and x_g for the full phase space of host and guest and $x_h^{*}$ and $x_g^{*}$ for the ones with translational and rotational degrees of freedom removed.

Figure 2:

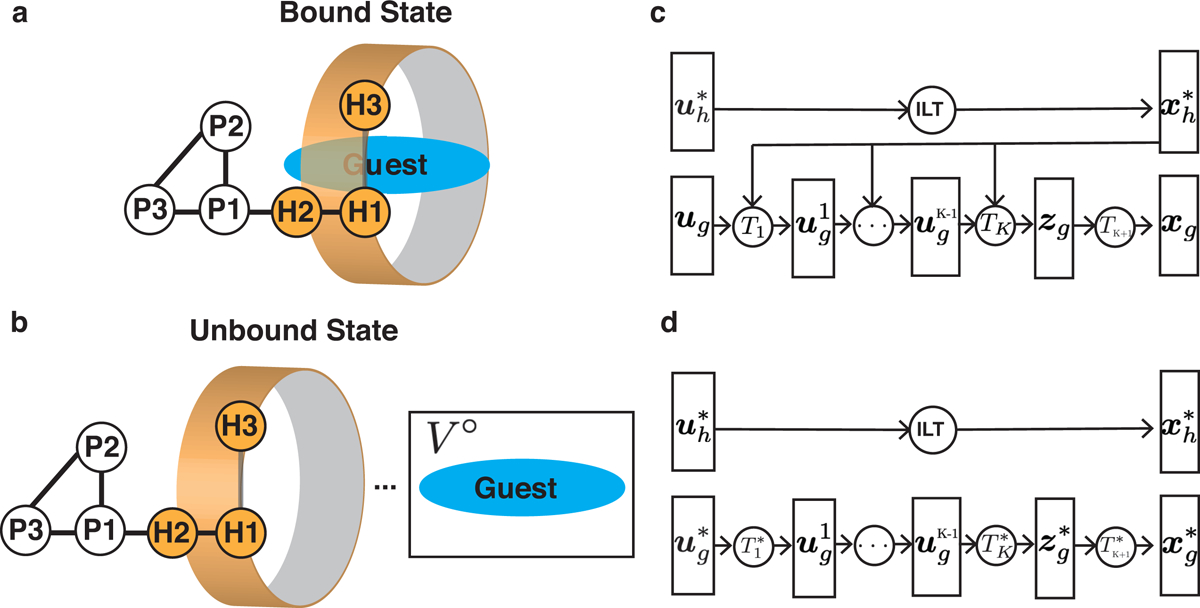
Parameterizing reference states with deep generative models using samples collected with restrained molecular dynamics simulations. (a, b) Illustration of the fixed anchor particles (P1, P2, and P3) and virtual sites (H1, H2, and H3) used to restrain the host in both bound and unbound states and guest molecules in the unbound state. Detailed definitions for these anchor particles and virtual sites are provided in the SI. (c and d) The flow-based deep generative models used for parameterizing reference state A° (c) and B° (d). The Cartesian coordinates for the host ($x_h^{*}$) and guest ($x_g/x_g^{*}$) are determined from normal random variables (${\mathbf{\text{u}}}_h^{*}$) via invertible linear transformations (ILT) and from multiple bijective transformations of uniformly distributed random variables ($u_g/u_g^{*}$), respectively.

Host-guest conformations from MD simulations were used to learn references states A° as $q_{\text{A}°}\left(x_h^{*},x_g\right)$ and B° as $q_{\text{B}°}\left(x_h^{*},x_g^{*}\right)$ using flow-based generative models.^19–22 Flow-based models produce molecular configurations by applying a series of bijective transformations to independent random variables that have normal or uniform distributions (Figure 2c and 2d). The transformations are often represented as neural networks to ensure the expressibility of the probabilistic models so that they can approximate the complex distributions from MD simulations well. Because random variable generation from both normal and uniform distributions is trivial to perform, sampling molecular configurations by applying transformations to these random samples is straightforward and computationally efficient. In contrast to MD simulations that only provide relative probability for molecular configurations due to the unknown partition function, flow-based models compute the absolute configurational probability by reweighting the probability of normal/uniform random variables with appropriate Jacobians. More details on the flow-based generative models are provided in the SI. The probability distribution for guest molecules in state A is dependent on the conformation of the host and we decomposed the joint probability distribution as $q_{\text{A}°}\left(x_h^{*},x_g\right)=q_{\text{A}°}\left(x_h^{*}\right)\cdot q_{\text{A}°}\left(x_g\mid x_h^{*}\right)$. On the other hand, the host and guest are independent from each other in state B, and correspondingly we decomposed the joint probability distribution as $q_{\text{B}°}\left(x_h^{*},x_g^{*}\right)=q_{\text{B}°}\left(x_h^{*}\right)\cdot q_{\text{B}°}\left(x_g^{*}\right)$.

After learning the reference states, we first evaluated their phase space overlap with the target states using marginal distributions of specific degrees of freedom. These marginal distributions can be estimated using sample configurations from reference and target states. Samples from the reference state were generated from the trained bijective transformations of random variables. Figure 3a and 3b show the distributions of x-y coordinates of atom C₄ on guest GIII for state A and state A°, respectively. Results for other systems and states are provided in Figure S1–S5. Because the host CB7 has a 7-fold rotational symmetry and its middle section plane is aligned with the x-y plane, the distribution of C₄ atom’s x-y coordinates in state A has a 7-fold rotational symmetry too (Figure 3a). Figure 3b shows that the corresponding distribution from the learned reference state A° matches quite well with that from state A even though the distribution has multiple modes. Figure S4a–S4d show similar agreement for the distributions of two representative dihedral angles between state A and A° for guest GIII.

Figure 3:

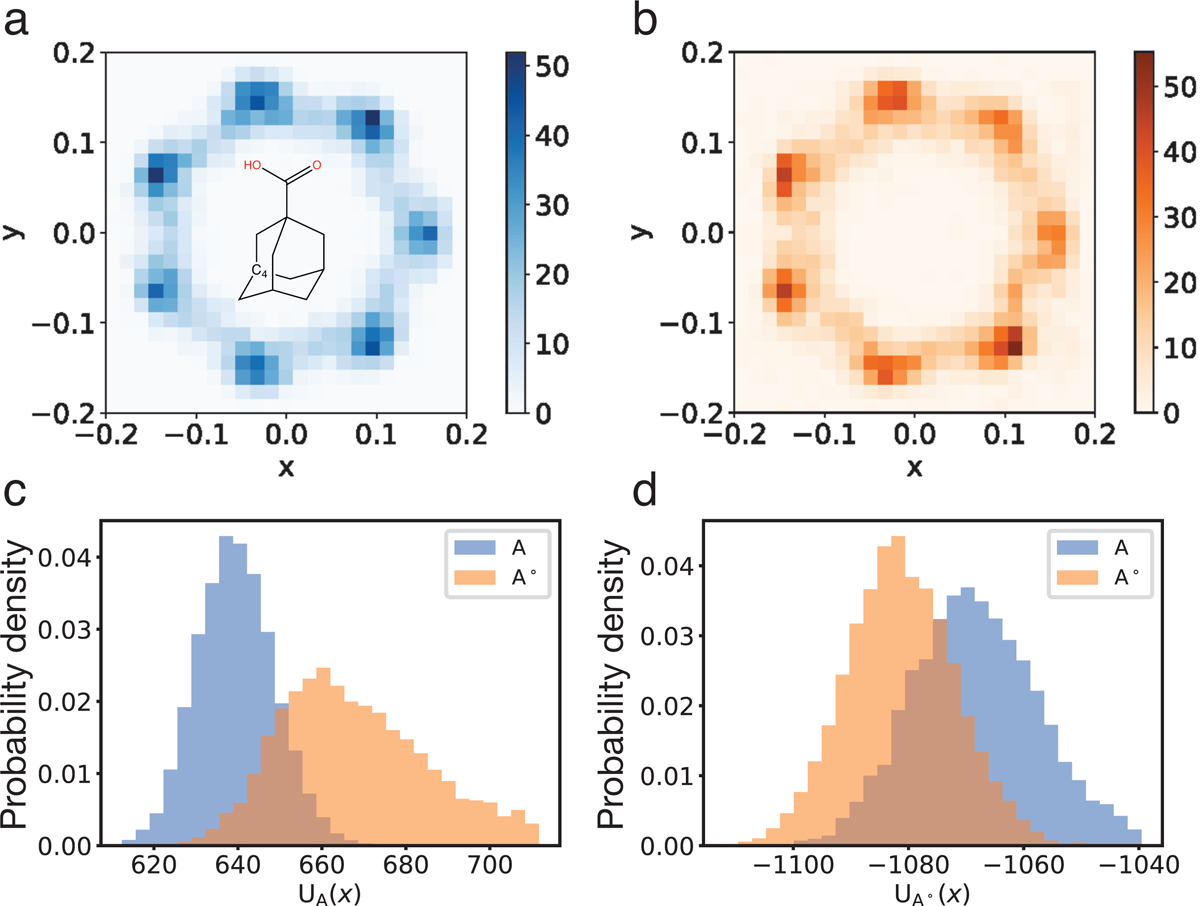
Phase space overlap between state A and A° for the CB7-GIII host-guest system. (a and b) Probability distribution of the x-y coordinates of atom C₄ on guest GIII for state A (a) and A° (b). Atom C₄ is one of the three spiro carbon atoms connecting the two rings, as shown in the embedded structure in part a. (c and d) Distributions of the value (in kcal/mol) of energy functions U_A (c) and U_A° (d) on samples from state A (blue) and state A° (orange).

In addition to the marginal distributions, we further examined the 3D conformations produced by generative models directly. The potential energy functions of the target states serve as a metric for the quality of these conformations as unphysical structures and even clashes between atoms will lead to high energy values. Figure 3c shows the probability distributions of the energy function U_A computed using sample configurations from state A (blue) and A°(orange) for the host-guest system with GIII. There is a significant overlap between the two distributions, supporting the ability of generative models in producing realistic molecular configurations with reasonable energy. In addition to the distributions of the target state energy function, we also computed and compared the distributions of the reference energy function U_A° (Figure 3d). Because the reference state was trained to maximize its likelihood on samples from state A, its energy function U_A°(x) has similar values on samples from itself and from state A. Correspondingly, the overlap between the two distributions for U_A°(x) is more significant than those for U_A(x). The corresponding results for state B and B° are provided in the Figure S4e and S4f and support similar conclusions. Similar overlaps are also observed for all other guest molecules (Figure S6–S8).

The significant phase space overlap between reference and target states allows robust estimation of their free energy difference with the BAR equation (Equation 2). Notably, for both state A and B, the estimations are relatively independent of the quality of the generative models. As shown in Figure 4c and 4d, the absolute free energy, F_A and F_B, converges by about 50 epochs, even though the generative models at this stage are less optimal and have smaller likelihood on the sample configurations from MD simulations (Figure 4a and 4b) compared to the final ones (80 epochs) that are used for making Figure 3. Similar results hold for all other guests, too (Figure S9–S11). Therefore, the free energy estimation is not very demanding on the phase space overlap between reference and target states and does not require the deep generative models to perfectly reproduce the probability distributions of target states.

Figure 4:

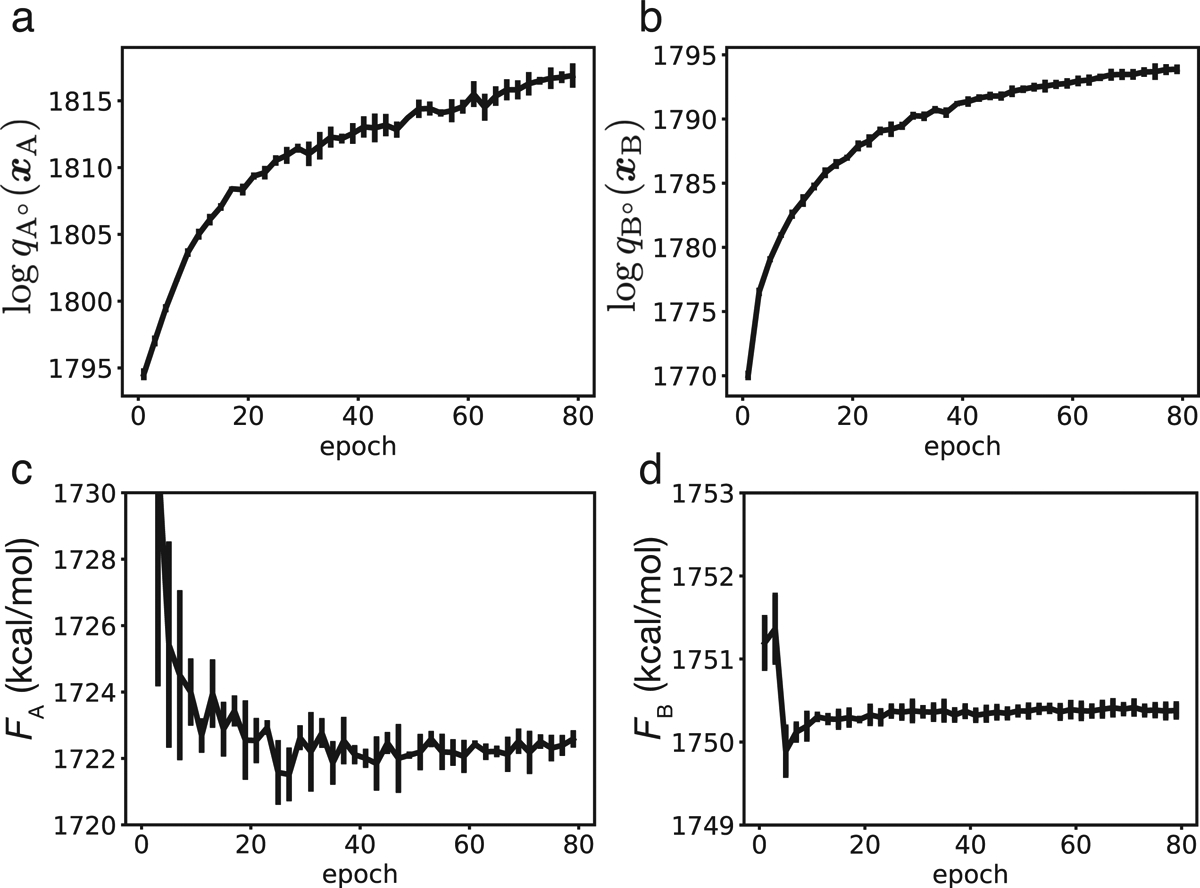
Free energy values estimated with DeepBAR are robust with respect to model quality. (a and b) Log-likelihood of the generative models for state A° (a) and B° (b) on training data as a function of the number of epochs used for model parameterization. (c and d) Values of the absolute free energy for state A (c) and B (d) calculated using models trained with different numbers of epochs.

With the absolute free energy of states A and B calculated, we can compute the binding free energy as their difference, i.e., ΔF_binding = F_A − F_B (Table 1). For comparison, we also computed the binding free energy of the four guest molecules using the PMF method.^6,7 In contrast to DeepBAR, PMF requires MD simulations for both end states and intermediate states in which the guest molecule is placed at increasing distances from the host. These intermediate states help bridge the two end states that do not have phase space overlap. They must be introduced at a slow pace to ensure sufficient overlap between any two adjacent states as well. For all four guests, we found that 95 intermediate states, corresponding to 97 windows in Table 2, are sufficient to produce converged results. There are significant overlaps between the probability distributions of collective variables for adjacent states (Figure S12–S23), and the computed binding free energy from three independent repeats shows small standard deviations (Table 2). We also computed the binding free energy using PMF with 49 and 33 windows. These results have much higher uncertainty. The binding free energy calculated using DeepBAR agrees well with that from PMF with 97 windows and reaches a similar statistical uncertainty level. The values are also comparable to results from prior studies.²³ On the other hand, the results computed using MM/GBSA show large systematic errors. Since 97 and 2 independent MD simulations are needed for the two methods, DeepBAR is almost 50 times more efficient than PMF in terms of the amount of sampling required to reach the same results with similar statistical uncertainty.

Table 1:

Absolute free energy of states A and B, F_A and F_B, and binding free energy ΔF_binding^a of the four guests calculated using the DeepBAR method.

guest	FA	FB	ΔFbinding
GI	1554.73±0.29	1567.37±0.22	−12.63±0.25
GII	1649.22±0.12	1664.05±0.18	−14.82±0.28
GIII	1722.73±0.17	1750.38±0.17	−27.65±0.15
GIV	1750.68±0.20	1780.54±0.24	−29.87±0.21

^aStandard deviations are computed using three independent repeats and the unit of free energy is kcal/mol.

Table 2:

Comparison of binding free energy ΔF_binding^a of the four guests calculated using the DeepBAR method, the PMF based method and the MM/GBSA method.

guest	DeepBAR	PMF			MM/GBSA
		97 windowsb	49 windows	33 windows
GI	−12.63±0.25	−12.76±0.27	−12.74±0.42	−13.47±1.83	−3.97±0.19
GII	−14.82±0.28	−15.29±0.09	−14.90±0.47	−14.69±4.64	−6.53±0.15
GIII	−27.65±0.15	−27.57±0.13	−27.32±0.60	−26.81±0.80	−20.61±0.16
GIV	−29.87±0.21	−30.61±0.32	−31.26±0.64	−29.26±0.67	−22.65±0.14

^aStandard deviations are computed using three independent repeats and the unit of free energy is kcal/mol;

^bThe PMF method with n windows means it samples from 2 end states and n − 2 intermediate states.

In summary, DeepBAR is exact and can accurately compute binding free energy using only a small fraction of the computational resource required by PMF. It does not suffer from the approximations that are inherent in other end state methods such as MM/GBSA and MM/PBSA^8,9 Although we benchmarked the method using host-guest systems, it can be readily applied to compute protein-ligand and protein-protein binding free energy.

We note that GB implicit solvent simulations¹⁸ were used to sample molecular configurations and parameterize deep generative models. Because explicit solvent simulations often provide better agreement with experiments for free energy calculations, it is desirable to couple them with the DeepBAR method. However, there can be challenges in modeling the ensemble distribution of all degrees of freedom in an explicit solvent system with generative models. Including solvent molecules dramatically increases the system size and introduces permutational symmetry (permutation of water molecules does not change the system’s energy) to the ensemble distribution. Encouraging progress is being made in designing flow-based generative models for systems with large sizes and permutational symmetry.^22,24–26 Combining these techniques with DeepBAR will be an exciting future direction.

Computational Methods.

MD simulations were used for conformational sampling in both DeepBAR and PMF. A cutoff distance of 1.4 nm was used for non-bonded interactions including both electrostatic and van der Waals interactions. The temperature of the simulations was maintained at 298 K using the Langevin dynamics with a friction coefficient of 1 ps⁻¹. The time step was set to 1 fs. For guest molecules GI, GII and GIII, 20 ns of simulations were performed and conformations were saved at every 0.1 ps. Because the guest GIV has a larger size and is slower to rotate inside the host, we used 100 ns of simulations to sample and collected conformations at every 0.5 ps. Therefore, 200,000 conformations were produced for all four guests to train generative models and reference states.

Invertible linear transformations (ILT) were used to model the transformation between $u_h^{*}$ and $x_h^{*}$ for both state A and state B, i.e., $x_h^{*}=\text{M}{u}_h^{*}+\mu$, where M is an invertible matrix. Rational quadratic neural spline flows²¹ (RQ-NSF) with 20 coupling layers, each of which has 32 hidden units, were used to model the transformation between $u_g^{*}$ and $z_g^{*}$ for state B and between $u_g\mid x_h^{*}$ and z_g for state A. The architectures of the RQ-NSF are the same as that used and also described in detail in our previous study.¹⁰ The 200,000 conformations sampled from state A (or B) were split into two sets, each of which has 100,000 conformations. 90,000 configurations of the first set were used as training data for learning RQ-NSF for state A° (or B°) and the remaining 10,000 conformations were used as validation data. The 100,000 conformations from the second set were used as x_A (or x_B) in computing ΔF_A°→A (or ΔF_B°→B) using Equation 2. The stochastic gradient descent method, Adam optimizer,²⁷ was used to optimize the RQ-NSF models by maximizing its likelihood on the training data. The learning rate was set to 0.001 and the training batch size was 512. After each epoch of training, the likelihood of the RQ-NSF model on the validation data was calculated and the training of the RQ-NSF model stopped when its likelihood on the validation data started to decrease, i.e., when the RQ-NSF model started to overfit. After learning, 100,000 conformations were sampled from state A° (or B°) and these conformations were used as x_A° (or x_B°) in computing ΔF_A°→A (or ΔF_B°→B) by solving the BAR equation (Equation 2) using the FastMBAR solver.²⁸

The PMF method used in this study follows the attach-pull-release (APR) framework presented in reference 7 for computing host-guest binding free energy. In this framework, the intermediate states are designed to open host cavity, remove guest and release host restraints in the three attachment, pulling, and release phases. Detailed information about restrain potentials used in the intermediate states is included in the SI. After sampling from both intermediate states and end states, the binding free energy was calculated by solving the multistate Bennett acceptance ratio equation.²⁹

The MM/GBSA calculations were conducted using the MMPBSA.py program³⁰ with the solute entropy calculated using the normal mode analysis (Table S1).