A Hi–C data-integrated model elucidates E. coli chromosome’s multiscale organization at various replication stages

Abstract

The chromosome of Escherichia coli is riddled with multi-faceted complexity. The emergence of chromosome conformation capture techniques are providing newer ways to explore chromosome organization. Here we combine a beads-on-a-spring polymer-based framework with recently reported Hi–C data for E. coli chromosome, in rich growth condition, to develop a comprehensive model of its chromosome at 5 kb resolution. The investigation focuses on a range of diverse chromosome architectures of E. coli at various replication states corresponding to a collection of cells, individually present in different stages of cell cycle. The Hi–C data-integrated model captures the self-organization of E. coli chromosome into multiple macrodomains within a ring-like architecture. The model demonstrates that the position of oriC is dependent on architecture and replication state of chromosomes. The distance profiles extracted from the model reconcile fluorescence microscopy and DNA-recombination assay experiments. Investigations into writhe of the chromosome model reveal that it adopts helix-like conformation with no net chirality, earlier hypothesized in experiments. A genome-wide radius of gyration map captures multiple chromosomal interaction domains and identifies the precise locations of rrn operons in the chromosome. We show that a model devoid of Hi–C encoded information would fail to recapitulate most genomic features unique to E. coli.

INTRODUCTION

The folding of the 4.64 Mb circular chromosome, with a contour length of 1.6 mm, inside 2-4 μm long spherocylindrical cell (1,2) of Escherichia coli (∼1.5 μm³ in volume) is a complex process, mediated by numerous factors and cues. Several decades’ investigations on chromosomal DNA of E. coli have rendered a picture of a highly condensed form called the nucleoid which is a dynamic macromolecular complex of the genetic material and nucleoid associated proteins (NAPs) along with proteins such as RNA polymerases (RNAP) (3). The multitude of experiments on E. coli chromosome have highlighted a ring-like architecture of nucleoid whose organization results from a combination of processes including DNA supercoiling (4), nucleotide associated proteins (NAPs)-induced condensation of DNA (5), crowding and non-equilibrium processes like transcription (3). In rapidly growing E. coli cells, nucleoid is severely compacted at the centre of cytoplasm with ribosomes being strongly concentrated at the periphery of the nucleoid (6). The multiscale organization underlying the E. coli nucleoid is only slowly getting recognized.

A set of classic experiments, including fluorescence microscopy (7,8) and site-specific recombination assays (9) had indicated spatial proximity and increased interactions among genetically distant DNA sites, giving birth to the idea of organization into a ring-like chromosomal architecture comprised of four large macrodomains, namely Ori (O), Ter (T), Left (L), Right (R) and two Non-Structured regions—Right (NS-R) and Left (NS-L). These macrodomains are considered to be spatially segregated from each other (7,8). Another investigation via fluorescence labeling of the genetic loci had proposed a model in which E. coli nucleoid displays a linear order of the loci distribution along the axial dimension of spherocylinder (10). More intriguingly, recent experimental studies brought into light the helical folding of the chromosome (11–14). In particular, it was found that the circular chromosome twists along the long axis to form a helix like, achiral conformation.

The complexity underlying bacterial chromosome has motivated a series of computer simulation studies and models to describe the architecture of E. coli chromosome. Some of them are based on coarse-grained models (6,15–17), while others used a more fine-grained approach for bacteria with base pair or approaching base-pair resolutions (18–21). While these models significantly contribute to our current understanding on E. coli chromosome, most of these models are phenomenological in nature and lack attempts in integrating experimental data.

In the first data driven model for E. coli chromosome, ChIP-chip data for RNAP was integrated into a fine grained polymer model (22). On the other hand, the emergence of high resolution chromosome conformation capture data in bacterial cells (23–26) has helped detect the interaction frequency between any two genomic loci in the whole genome of an organism and build data-informed models of bacterial chromosomes. Hi–C has the unique ability to determine the interaction frequency map of whole genome of an organism at high resolution (27). The ensemble nature of the resulting contact frequency matrices automatically incorporate the inherent stochasticity of the chromosome’s interactions. Using Hi–C and super-resolution microscopic imaging the 3D chromosome conformation of Mycoplasma pneumoniae was determined (26). Similarly, experimentally-restrained whole-chromosome models for Caulobacter cresentus had earlier been reported by Umbarger et al. (28), Le et al. (25) and Yildirim et al. (29). All of the above data driven approaches show that with emerging experimental techniques, one can enrich a computational model via integrating it with experimental data. Such theoretical studies can introduce specificity such as macrodomain formation, their locations and relative sizes for a bacterium into its model(s).

An early attempt at deducing the chromosome contact maps for E. coli was reported by Cagliero et al. (23) at a resolution of 20 kb. In this regard, the most recent report of 5 kb resolution Hi–C interaction maps of E. coli chromosome has been a key breakthrough (24). It brings out the salient features of the multiscale organization underlying the E. coli chromosome architecture. It also opens up promising opportunities for developing higher resolution and quantitative model for the same. In the current work, we present computer simulations of the E. coli chromosome by integrating beads-on-a-spring polymer model with recently reported Hi–C interaction matrix of E. coli chromosome (24). The Hi–C interaction maps are considered to be obtained from experiments involving a large ensemble of cells in nutrient rich condition (LB media, 37°C), each constituted of chromosome(s) at diverse replication stages in their respective phase of cell cycle. Accordingly, to account for the variability in the number of chromosomes and the amount of DNA present in a cell due to replication in rich growth condition in our model, we consider multiple distinct chromosomal architectures representative of different replication stages. As would be detailed in the article, the chromosome models of E. coli, developed at a 5 kb resolution, introduce replication forks or arms commensurate with the specific replication stage, unify multiple existing hypothesis related to E. coli chromosome’s architecture and demonstrates long-range organization into multiple macrodomains. In addition, the presented Hi–C integrated chromosome model unifies a wide array of independent experimental data such as fluorescence microscopy data (7), recombination assay (9) and precedent simulations. As would be revealed in the text that follows, the model vividly manifests the multiscale and multi-faceted organization of a replicating bacterial chromosome, namely a helical, macro-domain separated morphology and the CID boundaries in the vicinity of rRNA operons (22).

MATERIALS AND METHODS

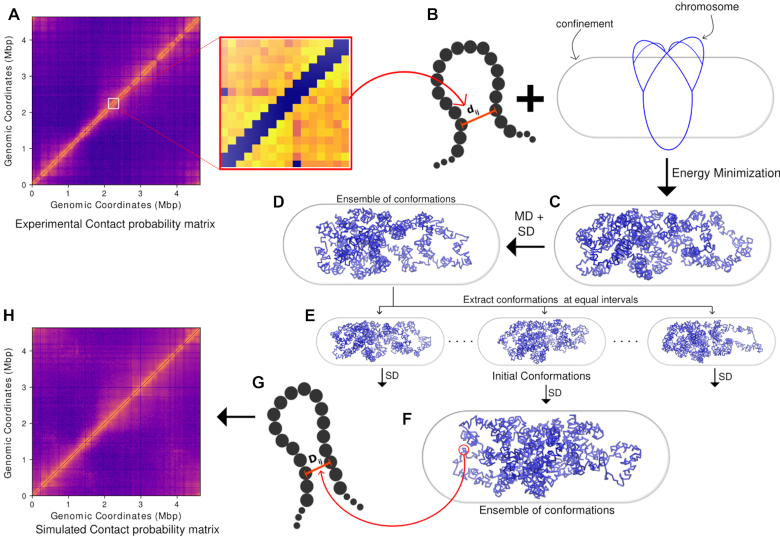
Figure 1 outlines the schematic of the integrative method used in the current work to generate the chromosome structures via combination of beads-on-a-spring model and Hi–C contact matrices. Below we detail different segments of the methods employed in the current work.

Figure 1.

A schematic of the method used to generate an ensemble of final chromosome structures. (A) Contact probability matrix from Hi–C experiment. (B) Expanded section of the matrix. (C) The experimental contact probabilities are mapped onto bond distances and bond strengths. d_ij is the initial distance between particles i and j. With Hi–C incorporated as harmonic restraints, the polymer is energy minimized along with the confining potential. (D) The energy minimized conformation is subjected first to molecular dynamics, then stochastic dynamics. (E) From the trajectory obtained via the stochastic dynamics, 200 snapshots were extracted at equal intervals from the last 1000 frames to get 200 initial conformations. (F) The initial conformations are subjected to another stochastic dynamics to obtain an ensemble of conformations. (G) The inter-particle distances obtained from the last 2000 frames of the 200 trajectories (2000 × 200) are used to calculate a simulated Hi–C contact probability matrix. (H) The simulated Hi–C contact probability is filtered and compared with the experimental matrix to validate the model.

Hi–C data processing

We used the data made available by Lioy et al. (24) with the GEO accession number GSE107301. SRA (Sequence Read Archive) files were splitted into both reads of pair-end sequences using fastq-dump. We used hiclib python library (https://bitbucket.org/mirnylab/hiclib) provided by Leonid Mirny’s group for further processing of the fastqs. Using hiclib, iterative mapping was performed with a minimum sequence length of 20 bp and a step length of 5 bp. Alignment reads were saved in BAM (Binary Alignment Map) files and processed according to 5 kb resolution and filtered using hiclib default fragment level filtering functions, namely: duplicates, large, extreme, dangling ends, etc. and they were binned into 928 bins according to 5 kb resolution. Further bin level filtering was performed to remove low coverage bins, bins with only small area sequenced and diagonal and adjacent to diagonals bins. Then the raw matrix was extracted using h5py python library from HDF5 file generated by hiclib library, we also set the two extreme elements on the off-diagonal of the matrix to zero, since they also are reads from adjacent regions of the chromosome, due to the chromosome being circular. The matrix is then normalized by using sequential component normalization (SCN) (30) in which, first all the column vectors were normalized to one using euclidian norm followed by each row vector and the whole process was iterated until the matrix become symmetric again (three iterations in our case). The normalized matrix is converted to a contact probability matrix by dividing each row by its maximum value (31) followed by a resymmetrization of the matrix (Figure 1A).

Model details and interaction potentials

Hi–C measurements involve a large ensemble of cells with chromosomes at diverse replication stages in their respective cell cycle. While in nutrient rich growth condition (LB media at 37°C), the cells would predominantly have two partially replicated chromosomes coexisting in the cell interior, there also would be simultaneous occurrence of chromosomes at other possible replication stages in diverse cells present in different phases of cell cycle. Specifically, we model three representative chromosomal architectures confined within a spherocylindrical cell (see SI Methods section 1.1 and Supplementary Figures S1–S3): non replicated single chromosome (G = 1.0), partially replicated single chromosome (G = 1.8) and partially replicated a pair of chromosomes (G = 3.6), with the topology of each architectures taken from the data compiled by Bremer and Dennis (32). Supplementary Figures S2 and S3 provide schematics of the topology of each chromosomal architecture employed in the current work. The amount of DNA present is denoted by the G value of the cell. G = 1.0 means that there is one single unreplicated chromosome present. Thus the total amount of DNA in a cell will be G × 4.64 × 10⁶ bp. For ease of explanation, we hereby define ‘backbone’ as the 4.64 Mb of the total DNA in the cell from which the rest of the DNA has replicated. The extent of partial replication is modeled by introducing replication fork following Bremer and Dennis (32) (see description in SI Methods section 1.2). We compute the Hi–C interaction map as an ensemble-average of that obtained from each of three chromosomal architecture. We modeled the E. coli chromosome(s) as a beads-on-spring polymer(s) with each bead representing a 5 × 10³ bp (i.e. 5 kb) nucleotides, which is the resolution of Hi–C interaction maps. The number of beads present in the system is G × 928 (G × 4.64 × 10⁶ bp/5 kb). The 5 kb nucleotides are indexed and annotated as per the genetic sequence of wild type E. coli MG1655 (GenBank ID: U00096.2) and modeled as non-overlapping van der Waals particles. The polymer beads are subjected to a spherocyllindrical confinement (see SI Methods section 1.3.1) commensurate with average dimension of E. coli at 37°C in LB media (axial length (including end-caps) of 2.482 μm and the diameter of 0.933 μm (1)) (See Supplementary Figure S1). As detailed in the SI Methods 1.1, based on an approximate volume fraction of the chromosome of 0.15 (33) (with respect to cell volume) and the spherocylindrical confinement dimensions, the individual bead diameter (σ) was determined to be 50.286 nm. All non-adjacent beads of the polymer, including those connected by Hi–C bonds, have been allowed to interact with each other via a purely repulsive potential 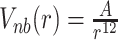, where A = 4εσ¹². For the simulations, A = 1.0 kJ mol⁻¹ σ¹² has been used (see SI Methods section 1.3.2).

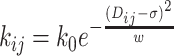(1)

Adjacent beads of the polymer(s) are connected by strong (300 kJ mol⁻¹σ⁻²) harmonic springs with σ as the equilibrium bond length. Hi–C contacts are also modeled as harmonic springs but with distance–dependent force constants and probability-dependent bond lengths (Figure 1B). Here it should be noted that beads belonging to a replication fork have Hi–C restraints present only among beads of that same fork. Beads from two different replication forks are not connected via any Hi–C restraints. The same assumption has been applied for inter chromosome Hi–C interactions, i.e. two independent replicated chromosomes do not have any Hi–C interactions between them. For beads present in replication forks, we mapped them to their corresponding bead in the ‘backbone’. To calculate Hi–C interactions among the beads of a fork, we used the indices of the backbone beads to which the fork beads have been mapped and calculated their respective Hi–C distances and bond strengths are per Equations (1) and (2). For multiple chromosomes coexisting together, we have defined the interaction among the fork beads in the manner stated above individually for each chromosome (polymer).

For Hi–C contact probability matrix P, we define the distance matrix, D as

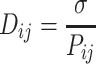(2)

where ij suggests the element in the ith row and jth column of the matrices. The restraining potential between a pair of Hi–C contacts at a separation of r_ij is given by 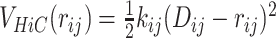. It should be noted that the matrix P is a sparse matrix with large number of the probability matrix elements being close to zero. Therefore a lot of the elements in D would be close to ∞. To take this into account, in our simulations, the force constants for the bonds incorporating the Hi–C contacts have been modeled as a gaussian function of the Hi–C distances (Equation 1) (as represented in Figure 1B and C). It should be noted that the choice of using Equation (1) is not arbitrary. For G = 1.0, we have also explored another possible equation (Supplementary Equation S1) in place of Equation (1) (see SI Methods section 1.3.3), but we found Equation (1) to be a better function for modeling (see SI Methods section 1.3.3 and Supplementary Figures S4– S6 for details).

Here, k₀ is an amplitude term that determines the upper limit to the force constants of the ‘Hi–C bonds’. This function essentially implies weaker values of force constant for larger distances. This function naturally takes V_HiC(D_ij) = 0 for D_ij = ∞. In Supplementary Equation (S1) in SI Methods section 1.3.3 and Supplementary Figure S7, k₀ and w are parameters that need to be optimized (see SI Methods section 1.4 and Supplementary Table S1). The metric used to optimize w is a Pearson correlation coefficient between the experimental and the filtered simulated contact probability matrices. Generation and filtering of simulated contact probability matrices has been performed as explained in SI Methods section 1.5 and 1.6. The protocol for comparing matrices has been described in SI Methods section 1.7. To speed up simulations, we did not harmonically restrain the specific ‘Hi–C bonds’ whose force constants are lower than 10⁻⁶ kJ mol⁻¹σ⁻² which correspond to gene pairs with contact probabilities lower than 0.33. Such bonds are very weak and do not impact the conformation(s) of the chromosome significantly. To implement the effect of spherocylindrical confinement induced by a E. coli cell, a restraining potential (Equation 3) has been used

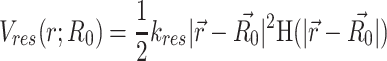(3)

H is a step function and gets activated only if any chromosome bead attempts to get out of the spherocylindrical confinement. R₀ is the center of the spherocylinder. k_res determines extent of elasticity of the cell boundary. For simulations, we have used 310 kJ mol⁻¹σ⁻².

Simulation details

All simulations are performed using the open source package GROMACS 5.0.7 (34). The source code of the program was modified by us to implement the interaction potential function of the spherocylindrical confinement. All other bonded and non-bonded interaction potentials were introduced by using default GROMACS utilities. To prepare the initial configurations, we used appropriate ring like topologies for three different values of G (1.0, 1.8, 3.6) (Supplementary Figures S2 and S3), as provided by the database of Bremer and Dennis (32). We energy minimized the topologies followed by 2 × 10⁶ step long molecular dynamics and another 2 × 10⁶ steps of stochastic dynamics (SD) (35). Then 200 snapshots were extracted from the last 1000 steps of the SD trajectory at equal intervals to obtain 200 independent initial configurations (see SI Methods section 1.8). Each of the 200 initial configurations were independently subjected to stochastic dynamics in NVT ensemble (Figure 1e and f). The temperature of the system was maintained using Langevin thermostat at 310K, corresponding to good growth condition of the bacteria. The time step for equilibration or production run is 0.001 t_red (see SI Methods section 1.9 for units). Each of the 200 simulations has been run for 2.5 × 10⁶ steps within which the system reached equilibration properly (Supplementary Figure S8). For all simulations, we saved the coordinates of the system at an interval of 1000 steps. Thus the number of configurations saved for each simulation will be , giving rise to 2500 frames from each of the 200 simulation trajectories. The time taken to simulate a single trajectory of 2× 10⁶ steps for G = 3.6 on a modest workstation (one single core of an Intel i5-8600K @ 3.6 GHz) took approximately only 1 h, suggesting a time-efficient protocol. The last 2000 frames from each trajectory (hence a total of 200 × 2000 frames) have been used for further analysis.

RESULTS AND DISCUSSION

Simulations reconstruct experimental Hi–C data

For E. coli in LB media at 37°C, corresponding to rapidly growing cell, the chromosome undergoes multiple rounds of replication before cell division. As mentioned in SI Methods section 1.2, we use a parameter called the G value of the chromosome to indicate the extent of replication of the chromosome (32). It is a ratio of the total DNA present in a given chromosome to the amount of DNA present in a non-replicated chromosome. In rapidly dividing cells, a distribution of G values is present in an ensemble of cells. To simulate a representative ensemble, we consider three distinct cases of G: G = 1.0 (non-replicated chromosome), G = 1.8 (partially replicated single chromosome) and G = 3.6 (partially replicated twin chromosomes).

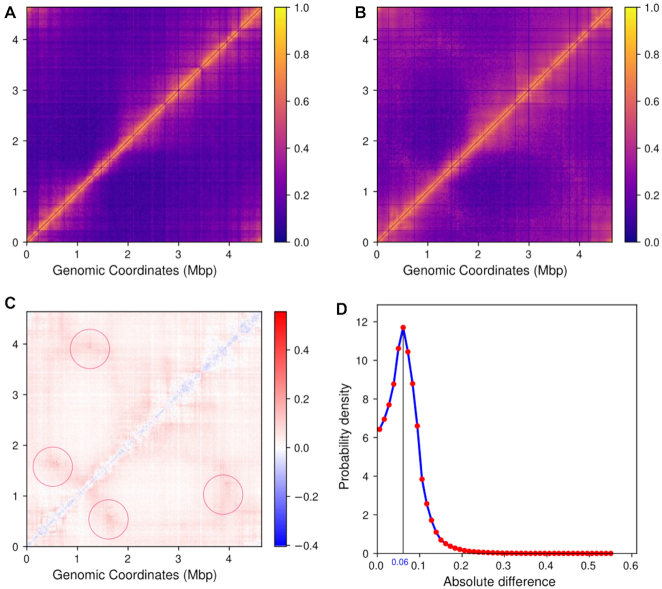
To verify our model, we first compare the simulated Hi–C contact probability map, which has been averaged over contact probability matrices obtained individually for G = 3.6, 1.8, 1.0, with the experimentally obtained contact probability map. Figure 2A and B compare the experimental Hi–C contact probability matrix of E. coli chromosome with that obtained from our simulations, respectively. A single intense diagonal indicates a smaller distance with a higher contact probability between neighbouring chromosomal regions. Absence of a secondary diagonal in the Hi–C interaction matrix reflects the lack of contacts between the two replication arms of the chromosome. A characteristic feature of prokaryotic chromosome is its circularity. High contact probabilities at the end regions of the Hi–C interaction matrix in Figure 2B (left most upper and right most lower corner) assure circularity of the chromosome in the current model as well.

Figure 2.

(A) Heatmap of experimental contact probability matrix. (B) Heatmap of simulated (filtered) Hi–C contact probability matrix. The matrix has been obtained by averaging over the ensemble of Hi–C matrices calculated for each G , namely G= 3.6, G= 1.8 and G = 1.0. (C) Heatmap of difference between contact probability matrix (simulated – experimental matrix), negative number or blue color indicates higher probability value in experimental matrix and positive number or red color indicates higher probability in simulated matrix. The regions of maximum divergence (encircled pink off-diagonal arms) appear near location of oriCs and difs and may be due to the presence of replication forks. (D) Distribution of absolute differences between the two contact probability matrices(experimental and simulated).

A Pearson correlation coefficient of 0.88 between experimental and simulated probability matrix indicates a very good agreement between simulated and in-vivo chromosome conformations. For a direct comparison, we also plotted the heatmap of the difference between the experimental and simulation-derived contact probability matrices (Figure 2C and the resulting histogram of absolute values from the difference heatmap (Figure 2D). The difference heatmap shows that for smaller genomic distances (i.e. bins near the diagonal) the contact probability is relatively higher in experimental matrix (blue regions). This can happen due to the inter-bead, repulsive, non-bonded potential we have used in our model to reduce chances of significant overlaps between beads. In practice, the nearby 5 kb regions of the chromosome may have higher overlaps among them than what we are estimating using our model. However, the distribution of absolute values of the difference heatmap in Figure 2D shows that the disagreement between experiment and simulation is considerably small as the major difference is <0.1, suggesting that there is reasonably a good correspondence between experimental and simulated Hi–C matrices, considering that there is also the presence of complex architecture involving replication fork. Thus our model is robust for three-dimensional reconstruction of the E. coli bacterial chromosome and can be explored for investigating and predicting key features of the chromosome at multiple length-scales.

As would be discussed in the rest of the article, we zoom into the details of chromosome conformations at different replication stages, with emphasis on G = 3.6.

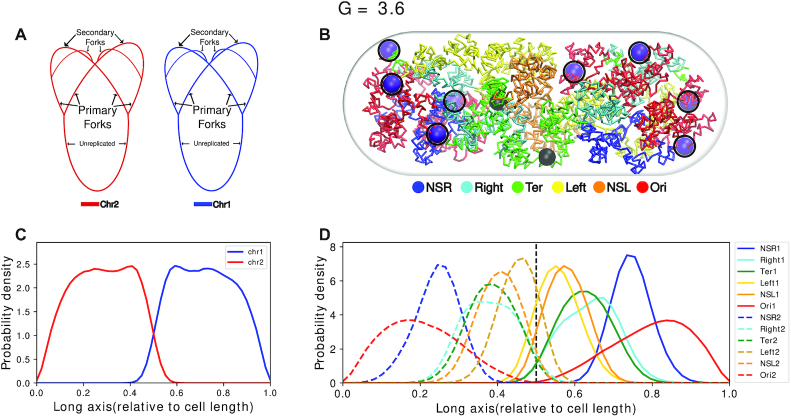
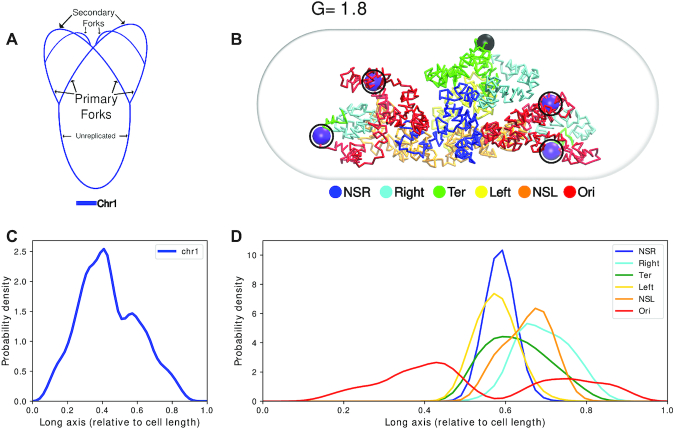
Chromosome conformations for G = 3.6

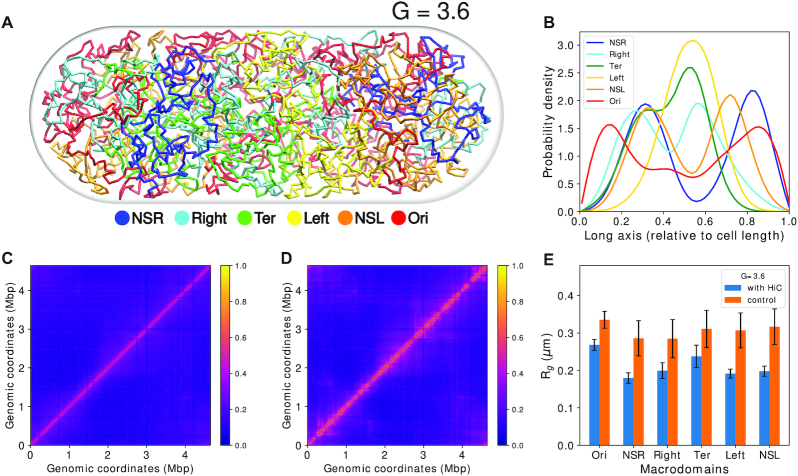
Figure 3A is a schematic of the topology of the chromosomes for G = 3.6. For G = 3.6 (32), we used two polymer chains each having 1672 beads (Figure 3A) (see SI Methods section 1.2 for calculation of number of beads). Each polymer chain has four OriCs and four replication forks. Thus, a total of eight OriCs(magenta) and two difs (black) (Figure 3B) are present inside the cell. Figure 3B is a representative configuration of the E. coli chromosome. It has been selected based on the closeness of the contact probability matrix averaged over the last 2000 frames of this trajectory to the experimental matrix. We can see that the two chromosomes have occupied each half of the cell and it is evident from the non-overlapping density profiles that both the chromosomes are mutually well segregated along the long axis of the cell. (Figure 3C and Supplementary Figure S9).

Figure 3.

(A) Schematic for the chromosome topology for G = 3.6. (B) Snapshot of the equilibrated chromosome from a representative trajectory with macrodomains colored. oriCs have been colored in magenta and also have been encircled. Dif loci have been colored in black. (C) Linear density of chromosomes along the long axis. (D) Average density of each macrodomain and non-structured regions, averaged over 200 trajectories and 2000 frames with respect to the cell’s long axis. The dashed black line denotes midcell.

Multiple experimental investigations involving E. coli chromosome have, in the past, proposed the existence of a set of macrodomains in its genome (7–9). Accordingly, in our model, we have color-coded the beads as per the annotation of proposed genetic sequences of chromosome macrodomains. We find that in each of the chromosomes, the four macrodomains and the two non-structured regions have been segregated along the long axis. This can also be inferred from the average densities of the macrodomains and the non-structured regions, shown in Figure 3D. Overall, we find a symmetrical orientation of the MDs in their respective cell halves about the mid-cell (denoted by the black dashed line in Figure 3D) with Ori MDs oriented toward poles and Ter located at mid-cell. Specifically, we observed that in our model, a macrodomain organization following a O1R1L1T1–T2L2R2O2 pattern has a higher probability of occurrence, apart from possibilities of other sequences of ordering of the macrodomains (Supplementary Figure S10). While the model captures the self-organized macro domains, the specific sequence of organization of these macrodomains found in the current model, differs slightly from L1R1L2R2 sequence of organization, which was reported in some experiments as the key sequence of organization of macrodomain (36,37). However, there is precedent report of a secondary population of organization having mirror-symmetric sequence order R1L1L2R2 by Wang and coworkers (36), which coincides with the prediction from current model. Any difference between the current model and the precedent report might arise from the dynamical nature of our model and lack of presence of other key components such as NAPs in the current model. Nonetheless, the features shown by a physics-based model, which only incorporates Hi–C restraints at a 5 kb resolution, is promising and the introduction of replication arms make this model more realistic. We also observe that the oriCs have localized themselves at the poles of the cells. This is an important event as just before cell division, which probably is the case for G = 3.6, oriCs orient themselves toward the poles (38) which our model recovered properly and will be discussed in details in the upcoming sections.

Reconciling with existing fluorescence and recombination measurements

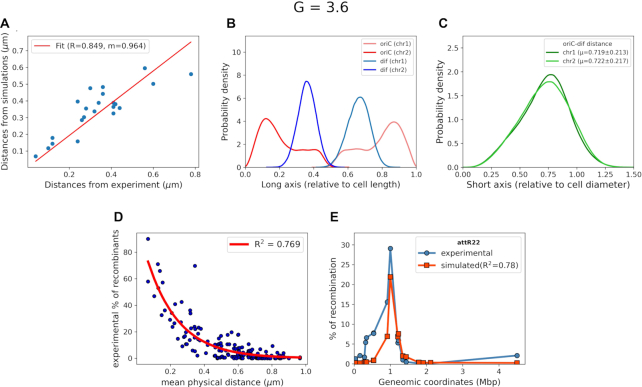
The existence of fluoroscence microscopy data for the inter-focal distances between various loci throughout E. coli chromosome (24) allowed us to compare distances from our simulated model with fluorescence mircroscopy-based measurement. A Pearson correlation coefficient of 0.85 (Figure 4A) shows reasonably good agreement between distance calculated from our model and fluorescence mircroscopy-determined inter-focal distances. Since the distances are calculated in real units (μm), the slope of the fit gives us the relative size of the simulated chromosome with the in-vivo counterpart.

Figure 4.

(A) Distances measured from our simulations (y-axis) for Hi–C data of E. coli at 37°C in LB media versus distances measured via fluorescence microscopy (x-axis), measured at 25°C in Minimal media. (B) Position distribution of oriC and dif with respect to the cell long axis. (C) Distribution of distance between oriC and dif relative to cell diameter. (D) Comparison between the recombination frequencies provided by Valens et al. (9) versus mean physical distance between recombination loci and red line indicates the single exponential fit. (E) A representative plot of recombination frequencies predicted by mean physical distance, blue: experimental data and red: predicted by simulated data.

Two loci, namely, oriC and dif are known to play a pivotal role in E. coli chromosome division and segregation (8,10,39). OriC is the origin of replication from where replication of chromosome starts and dif is another locus present in the Ter macrodomain and opposite to oriC in terms of genomic distance. Dif is the last region on the chromosome to be replicated after which the two chromosomes segregate. In exponentially dividing cells close to division, oriC is known to be localized at cell poles while dif should be opposite to oriC (36). To investigate the location of these two loci in our model, we plotted their average positional distributions, as obtained from the simulation trajectories. As we can see from Figure 4B, oriC is mainly localized near the poles (also labeled in snapshot in Figure 3B. The flat tail of the oriC comes from the replication forks present in each of the chromosomes. We also see that dif is mostly present, opposite to the oriC, at mid-cell. The distribution of distance between oriC and dif (Figure 4C) shows that the average distance between the two loci is also close to the diameter of the cell. Together, these distributions show that these two loci are axially present opposite to each other while oriCs localizes themselves to the cell’s poles, which is an important feature of the rapidly dividing E. coli cells near cell division. Upon clustering all the chromosome conformations based on the oriC-dif distance and distance based RMSD (DRMSD) as given in Equation (4) (40) (Supplementary Figure S11) we see that the chromosome conformations have very localized distributions of OriC-diff distances, with major values ranging between 0.6 and 0.8 times of the cell diameter. We also see that there is finite but small structural variability among the obtained conformations with respect to the cluster average Hi–C contact probability matrices. (Supplementary Figure S12).

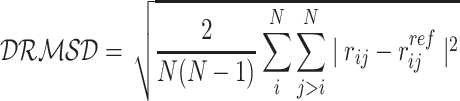(4)

where r_ij is the distance between beads i and j and 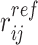is the distance between the same pair of beads in a reference conformation.

Using a method reported previously by Hacker et al. (22), our model has been able to predict recombination assay percentages. We first obtained an exponential fit between experimental percentage of recombinants and distances calculated for such loci pairs from simulations (Figure 4D). The fit suggests a good correlation with R² value of 0.769. Using the fit, we calculated the percentage of recombination for reported pairs of loci (9) and plotted the percentages with respect to their genomic distances. Figure 4E plots representative recombination data for loci attR22 and compares with the values predicted from the current model . We find that the prediction captures the peak position reasonably well. It is noteworthy that the model misses the small shoulder in the experimental data (orange), located to the left of the maximum, which the model is unable to reproduce. The genomic distance about which the shoulder is present is short and we speculate that overestimation of the inter-bead repulsion by our model might be a possible cause. However, if we compare the predicted recombination for other six loci (9), (Supplementary Figure S13) we find that there is an overall good correlation with the experimental data. Specifically, in some loci (in particular attr17 and attl29) the agreement between experiment and prediction from the model is very encouraging.

Conformations of chromosomes at other stages of replication

For G = 1.8, we employ a topology as depicted in Figure 5A with four oriCs and 1 dif (32). This is a special case of G = 3.6 where instead of two chromosomes there is only one partially replicated chromosome. From Figure 5B and D, we see that here also oriCs(magenta) have localized themselves toward the poles of the cell, while dif (black) remains at mid-cell.

Figure 5.

(A) Schematic for the chromosome topology for G = 1.8. (B) Snapshot of the equilibrated chromosome from a representative trajectory with macrodomains colored. oriCs have been colored in magenta and also have been encircled. Dif loci have been colored in black. (C) Linear density of chromosome along the long axis. (D) Average density of each macrodomain and non-structured regions, averaged over 200 trajectories and 2000 frames with respect to the cell’s long axis.

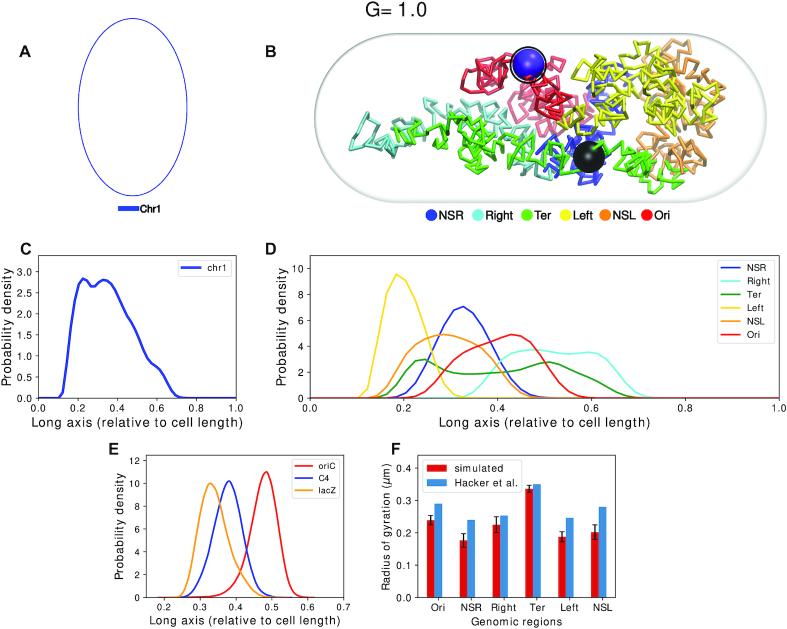
Finally, G = 1.0 corresponds to the scenario of unreplicated chromosome in the ensemble of cells, (Figure 6A). Figure 6B depicts that loci oriC(magenta) and dif(black) in chromosome corresponding to G = 1.0 are present close to mid-cell. We also see from Figure 6C that the chromosome stays mostly near the middle without populating the ends which has also been seen in experiments (41). Figure 6D indicates that macrodomain Ori occupies mid-cell and Ter is relatively more spread out along the long axis with an average position at mid-cell. Right is positioned to the right of Ori and Left is on the left of Ori. We also see that the Ter domain is the most extended of the MDs and has significant overlap along the long axis with its flanking domains. Such positioning of MDs are typical in cells which are far from division (36).

Figure 6.

(A) Schematic for the chromosome topology for G = 1.0. (B) Snapshot of the equilibrated chromosome from a representative trajectory with macrodomains colored. OriCs have been colored in magenta and also have been encircled. Dif loci have been colored in black. (C) Linear density of chromosome along the long axis. (D) Average density of each macrodomain and non-structured regions, averaged over 200 trajectories and 2000 frames with respect to the cell’s long axis. (E) Distribution of position of three loci: oriC, C4 and lacZ along the long axis (Z-axis) as mentioned by Wiggins et al. (10). (F) Average radius of gyration of each macrodomain from current model as compared to that given by Hacker et al. (22) for oriC@midcell, plectonemic model.

In a previous fluorescence based assay by Wiggins et al. (10), positions of multiple genetic loci in E. coli cells were monitored. From their spatial positioning a ‘linearly organized’ architecture of the chromosome was proposed. In particular, this investigation hypothesized that these loci are linearly positioned along the long axis of the chromosome. To test this hypothesis in our Hi–C encoded polymer model of the chromosome, we plot the distribution of three loci oriC, C4 and lac along long axis of cell (Figure 6E). These are the same loci position measured in Figure 2A by Wiggins et al. We find that in our model as well, these loci are linearly positioned along the long axis.

Since for G = 1.0, we have a single unreplicated chromosome, we are in a position to compare the radius of gyrations of macrodomains predicted by the current model with that of Hacker et al.’s predictions (22) (which also had modeled a single unreplicated chromosome, albeit at a nucleotide-level resolution). Figure 6F provides a comparative account of radius of gyration of each of the macro domains between these two models. We see that our model predicts slightly lower values than that of Hacker et al.’s (22) , but the trend of the R_gs remains same across both our model (for G = 1.0) and that of Hacker et al.’s (22).

The amount of DNA and stage of replication decide the positioning of oriC and dif

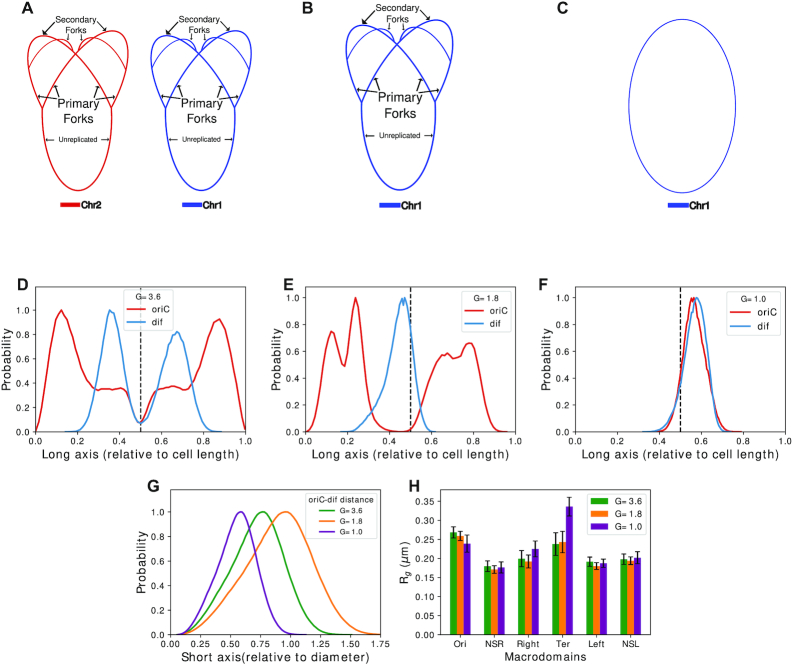
Figure 7 cumulatively compares how the relative positioning of oriC and dif in the bacterial cell varies with replication stages and chromosome architectures corresponding to G = 3.6, G = 1.8 and G = 1.0 (Figure 7A–C). Figure 7D and E depicts that for G = 3.6 and G = 1.8, the average probability densities are almost symmetrical about the mid-cell with oriC having higher probability toward the poles. This is more prominent for G = 3.6 than for G = 1.8. For G = 1.0, i.e. unreplicated chromosome, we see that both oriC and dif have aligned themselves near mid-cell, which is expected for exponentially growing E. coli when chromosome replication has not begun yet (36).

Figure 7.

(A) Schematic for G= 3.6. (B) Schematic for G= 1.8. (C) Schematic for G = 1.0. (D) Average probability of location of oriC and dif for G = 3.6, with respect to cell length. (E) Average probability of location of oriC and dif for G= 1.8, with respect to cell length. (F) Average probability of location of oriC and dif for G= 1.0, with respect to cell length. (G) Distributions of oriC-dif distances with respect to cell short axis. (H) Comparison of R_g of macrodomains among different G values.

From Figure 7D–F, we can see that as the amount of DNA being replicated increases, the oriC shifts more toward the poles of the cell. This might be caused due to the increased amount of DNA containing mostly Ori and its flanking regions, as replication starts from oriC and moves bidirectionally with almost equal speed (42). Thus, forks repelling each other might cause the replicated forks to orient toward the poles. This also explains the broad density of oriC as there are multiple oriCs present. Fluctuations from those oriCs should cause non-zero, albeit lower, average density at non-polar regions of the cell. Dif remains near mid-cell since it belongs to the non-replicated part of the ‘backbone’. Overall, we find that our model has been successful in reproducing the oriC and dif localizations expected during the replication of the chromosome. From Figure 7G, we can see that for all the chromosomes at diverse G values we have simulated, oriC and dif distances do not become more than the diameter of the cell, though they might not be oriented radially. Additionally, We find that the average size of the macrodomains do not change much across various replicated chromosomal architectures, except for Ter macro domain (Figure 7H). Specifically, Ter shows a much higher R_g for G = 1.0, which is a signature of a more expanded Ter conformation(Figure 6D and Supplementary Table S2).

The chromosome has no net chirality

Recent experimental investigations (11,13,26,28,29) have hypothesized that the bacterial chromosome, most likely, adopts an achiral, helical conformation. To corroborate predictions from our model with experimental observations by Marko et al. (11), we divide the cell along the long axis into 20 equal slices (referred to, from now on, as z-slicing) and plotted the centre of geometries (COGs) of each slice (Supplementary Figure S14). We find that the COGs obtained from the z-slices in our model are similar to those experimentally calculated (11). By fitting the coordinates obtained from z-slicing to a polygon, we calculated the average writhe of the polygon, as described by Klenin et. al (43). We then calculate the writhe of the fitted polygons to get an idea of the average chirality of the folded conformations. The writhe values we find have a sharp distribution (Supplementary Figure S15) about zero which signify that the chromosome adopts a helix like conformation, and is achiral. We think that it is also a characteristic feature of a helical chromosome structure.

Insights on global packing of the chromosome

A common approach for exploring global packing of chromosome, irrespective of its replication status, is the investigation of scaling of contact probability with respect to genomic distance (22,27) provided that cell division has not begun. Earlier, based upon similar analysis of intra-chromosomal contact probability as a function of genomic distance, a power law scaling of contact probability between 500 kb and 7 Mb for human chromosome was predicted (27). For the E. coli chromosome, a power law scaling of –1 was predicted by Hacker et al. (22). The inverse scaling of contact probability with genomic distance (∼s⁻¹) is in agreement with a previously proposed attribute that chromosomes are fractal in nature (44).

Fractal polymers are knot free which is important for the segregation of daughter chromosomes during cell replication (22,27,45). An analysis, similar to what Hacker et al. (22) had performed, to explore the intra-chromosome contact probability as a function of genomic distance, as extracted from experimentally determined Hi–C matrix, produces a scaling factor of ∼−0.77, suggestive of deviation from a perfect fractal. In our current model (Supplementary Figure S16a) the contact probability scales as ∼s^−0.55 in 10 kb to 1 Mb range. On the other hand, scaling of root-mean-squared (RMS) end-to-end distance with genomic distance suggests otherwise (Supplementary Figure S16b). RMS end-to-end distance scales as s^0.36 which is close to the expected value for scaling of RMS end-to-end distance with genomic distance for a fractal globule polymer which is s^1/3.

To confirm the fractal nature we explored the presence of knots in our ensemble of structures explicitly using an external python library (https://github.com/SPOCKnots/pyknotid). Knot analysis revealed that all conformations are knot free. Though our model has a resolution of only 5 kb per bead and that there are repulsive interactions among the beads, knots are still likely as we found some knots in simulations without Hi–C restraints. The fact that we found chromosome conformation predicted by the current model to be knot free is most likely because the Hi–C restraints did not allow the model chromosome to mix to an extent which could lead to formation of knots. The absence of knots implies that the chromosome is not an equilibrated globule, although it may not fold in a completely fractal manner.

Insights on local packing of the chromosome

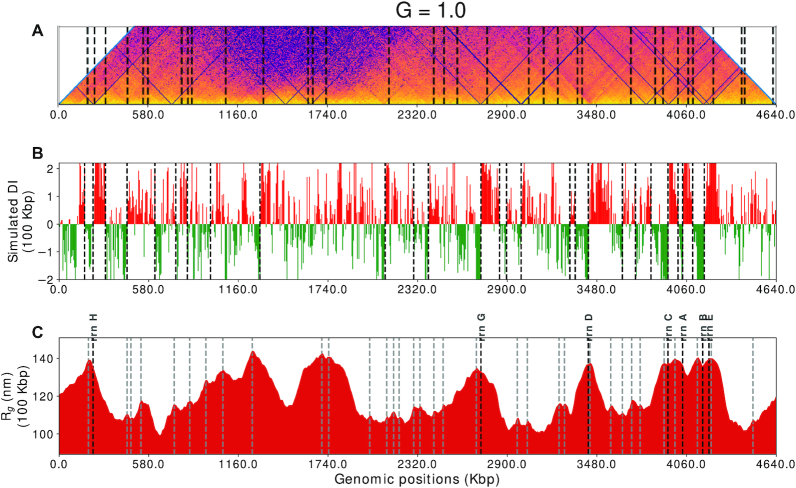
Figure 8A and Supplementary Figure S17 shows the CID boundaries calculated from the experimental contact probability matrix. The boundaries have been calculated using the Directionality Index (DI) algorithm (46) with a window size of 100 kb (Figure 8B).

Figure 8.

(A) The main diagonal of the average contact probability matrix rotated 45° clockwise with black vertical lines showing the position of CID boundaries. (B) Directionality index (100 kb) calculated from simulated matrix for wildtype E. coli (MG1655 in LB at 37°C in exponential growth phase) black vertical lines shows the CID (chromosome interaction domains) boundaries, (calculated as given by Le et al. (25)). (C) Radius of gyration map for wildtype E. coli (MG1655 in LB at 37°C in exponential growth phase) with respect to genomic coordinates with a moving window size of 20 beads (100 kb), gray and black vertical lines represent the peaks in the map and rrn operon sites respectively.

We see from Figure 8B that DI on the simulated contact probability matrix provides us with a lesser number of peaks. Therefore to calculate the boundaries directly from the structure, we developed a method which we call the R_g map method. In this method we use a moving window averaging of radius of gyration of continuous segments of chromosome. This approach gives rise to a ‘radius of gyration map’ (R_g map). Using this approach, we calculated the radius of gyration of fine-grained segments for each bead (e.g. for n_th bead: the R_g will be calculated for 20 beads starting from n − 10th to n + 9th bead) for all the beads in the chromosome. Here we calculated the R_g map at a window size of 20 beads, corresponding to 100 kb genomic segments to investigate the features of our model pertaining to the local density of chromosome. This method also enables us to probe the variation in local density of the chromosome along it’s contour.

Figure 8C shows the R_g map for a simple case, i.e. for G = 1.0, at a window size of 20 beads or 100 kb region. The black vertical lines, in the R_g map, highlight the most prominent peaks which were calculated with the help of a peak caller from scipy (47), which is tuned to get the exact number of peaks as predicted by directionality index (DI) at 100 kb size. We report a correlation of 0.99 between the positions of the CID boundaries detected by R_g map and DI (Supplementary Figure S18). Previously it was shown that the DI boundaries, when visualized with the heatmap of matrix, appear at the vertices of the triangles along the diagonal of the matrix. Therefore, we also compared our R_g map with the diagonal of the heatmap (shown in Figure 8A). The peak positions calculated from the Rg map are also marked in the Figure 8C and qualitatively we can see that these peaks are present at the vertices of triangles in most of the cases. Therefore, the comparison in Figure 8 suggests that our model is capable of capturing local chromosomal structures such as chromosomal interaction domains (CID). Together, R_g map comes out to be an effective tool in unraveling the local structure from our simulation model.

In a study on Caulobacter crescentus, it was found that, generally, one or many highly expressed genes were present at the CID boundaries (25). In rapidly dividing cells, the rrn operons are expressed at a higher rate than other metabolic genes due to the requirement of ribosomes for protein synthesis (48). Since the Hi–C experiment was also performed on rapidly dividing cells, high expression of rrn operons was expected. In another study, rrn operons showed higher transcriptional propensity, measured as RNA/DNA ratio, and overlap with CID boundaries (49). Therefore, motivated by previous experiments (25,48,49) and good agreement between peaks in R_g map and CID boundaries, we compared the peaks in R_g map with rrn operons’ genomic locations in E. coli. We found that six of the peaks in R_g map correspond to the genomic location of rrn operons as shown by bold, black vertical lines in Figure 8C.

Physically, higher R_g value indicates that the chromosome segment (in case of Figure 8C—20 beads) is occupying more volume than the adjacent segments of same length. Similarly, lower R_g value implies that the segment is compact and occupies lower volume than its adjacent segments. Therefore our results imply that the local DNA density is lower in the vicinity of highly expressed genes, a phenomenon earlier observed in the eukaryotic cells (50). These results suggest similarity with the ‘transcription centric’ approach used in a previous model (22). These low density regions, i.e. with high R_g value in R_g map are thus equivalent to plectoneme free regions (PFR) (22). Together, our model, via encoding Hi–C data, is able to capture all the spatial informations of the chromosome such as macrodomain structure, plectonemes, CIDs and transcription details.

Assessing the importance of the genomic contacts in chromosome organizations

While modeling the Hi–C contact probability data into distance restraints, we had made use of a sparse interaction matrix and by design, our model harmonically restrained only a fraction of the genomic pairs with high contact probability values in the contact probability matrix (≈7% of the total number of contacts). To assess the importance of the small percentage of the Hi–C contact probability matrix that has been used as an input in the model, we carried out ‘control simulations’ in which a self-avoiding polymer chain of same bead numbers (as in Hi–C informed ‘wild-type’ model) were simulated but no Hi–C restraints were applied within the chain. Figure 9A depicts a representative snapshot of the conformation obtained from such ‘control simulations’ corresponding to G = 3.6. Qualitatively, we can see from Figure 9B that all the macrodomains overlap significantly in control simulations. To quantify the extent of macrodomain overlaps, we divided the cell volume into a three-dimensional grid. For each macrodomain pair, we calculated the following ratio

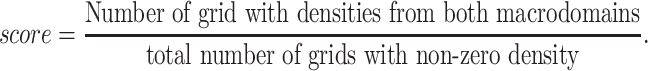Thus, the score will be 1 when there is complete overlap and 0 when there is no overlap. Using the score, we see that all the macrodomains are relatively well mixed in the control simulations compared to wild-type chromosome (Supplementary Table S3). They do not possess any localization and the polymer conformation is purely entropy-driven (6). Most macrodomains have become disorganized since the distribution is more spread out, than in wild-type cells. The polymer also is seen to have expanded to occupy all the volume available (Supplementary Figure S19). From this we conclude that presence of Hi–C restraints have induced a specificity into the polymer that forces it to arrange it’s various regions into a very particular order(s).

Figure 9.

(A) A color coded snapshot of the random-walk chromosome without Hi–C restraints (control). (B) Average densities of the four macrodomains and two non-structured regions with respect to the cell long axis. (C) Simulated contact probability matrix without Hi–C. (D) Simulated contact probability matrix with Hi–C. (E) Comparison of R_g of macrodomains between control and WT.

Upon comparison of the generated simulated Hi–C matrix from the control simulations with the experimental matrix, we see that the signature patterns along the diagonal are mostly absent in contact matrix obtained from the ‘control simulation’ (Figure 9C, D and S20a). Near diagonal, the simulated matrix looks much smoother (Figure S20a and Supplementary Figure S20b). These patterns correspond to CIDs on a smaller scale, and macrodomains on a larger genomic scale. This shows that the contacts, which are important, are relatively high in probability and constitute only a small fraction of the total chromosomal contact probability matrix. We also see from the difference heatmap (Supplementary Figure S20c) that the difference between corresponding probability values between the simulation without Hi–C and the experimental contact probability matrix is more prominent for regions which are genomically closer. The potential loss of the information in a chromosome model devoid of Hi–C contact probabilities data (as in the ‘control simulation’) can be further gleaned from Figure 9E. We see that all macrodomains derived from ‘control simulation’ have the same size, suggesting that the localized interactions are missing. The loss of key contacts also leads to expanded size for all Macrodomains in the control simulation.

CONCLUSION

In conclusion, we report a Hi–C data-integrated comprehensive model of E. coli chromosome at 5 kb resolution with replication forks. The model is able to recover and represent the extent of information Hi–C encodes at different stages of chromosome replication. The model captures the macrodomain segregation in unreplicated, partially replicated single and twin chromosomes precisely. The approach presented in the current work is distinct from other reconstruction algorithms recently used for modeling chromosomes (51–53) as the structures obtained from these algorithms do not produce an ensemble of structures and also requires scaling by another experimental data, such as fluorescence microscopy, to have the conformations commensurate with cell-sizes. On the contrary, the current model quantitatively reconciles numerous, independent experimental measurements on E. coli such as distances measured from flouroscence microscopy (7), experimental recombination assay percentages (9) and linear densities (41). The model predicts a roughly linear organization of chromosome regions, in line with experimental investigation (10). The model predicts that in oriC and dif are located at the mid-cell diametrically opposite to each other in exponentially dividing cells for non-replicated chromosome, while oriCs get localized at or toward the poles for replicating chromosomes, which was also seen from experiments (36). For the case of a non-replicating chromosome, our results are also consistent with the predictions the plectonemic model proposed by Hacker et al. (22) where oriC was located at the mid-cell. We also were able to predict CID boundaries and the location of rrn operons using an indigenous way of analyzing the radius of gyration of the chromosome segments for the non-replicating chromosome. All these results reflect upon the multitude of information Hi-C already encodes and our model being able to capture them properly. We claim that the protocol for conformation generation is simple and fast with a high efficiency in reproducing experimental observations.

Taken together, the model brings out the multiscale and multi-faceted organization of bacterial chromosome, manifesting a helical, macrodomain-segregated morphology at large scale and CIDs at a fine-grained scale. Finally, a control model, which does not incorporate Hi–C data, shows that the multiscale organization and domain-segregation do not appear in such model. Several proteins, such as NAPs, regulate these two factors for proper growth of the bacteria. The role of NAPs in maintaining overall chromosome conformation remains to be explored. Though we did not investigate the dynamics of the chromosome, but by incorporating mass of each bead one can, in practice, explore the chromosomal dynamics. Incorporation of other experimental data would act as refinements on the ensemble averaged Hi–C which has been used as the basis for the modeling. Multiscale simulations can also be attempted in which the coarse-grained interactions can be designed the way we incorporated bonds using Hi–C.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

This work was supported by computing resources obtained from shared facility of TIFR Centre for Interdisciplinary Sciences, India. We acknowledge support of the Department of Atomic Energy, Government of India, under Project Identification No. RTI 4007. Ramanujan Fellowship and Core Research grants provided by the Department of Science and Technology (DST) of India [CRG/2019/001219 to J.M.]. Funding for open access charge: Intramural fund of institute of the authors.

Conflict of interest statement. None declared.