Risk Assessment of Dengue Transmission in Bangladesh Using a Spatiotemporal Network Model and Climate Data

ABSTRACT

Vector-borne disease risk assessment is crucial to optimize surveillance, preventative measures (vector control), and resource allocation (medical supplies). High arthropod abundance and host interaction strongly correlate to vector-borne pathogen transmission. Increasing host density and movement increases the possibility of local and long-distance pathogen transmission. Therefore, we developed a risk-assessment framework using climate (average temperature and rainfall) and host demographic (host density and movement) data, particularly suitable for regions with unreported or underreported incidence data. This framework consisted of a spatiotemporal network-based approach coupled with a compartmental disease model and nonhomogeneous Gillespie algorithm. The correlation of climate data with vector abundance and host–vector interactions is expressed as vectorial capacity—a parameter that governs the spreading of infection from an infected host to a susceptible one via vectors. As an example, the framework is applied for dengue in Bangladesh. Vectorial capacity is inferred for each week throughout a year using average monthly temperature and rainfall data. Long-distance pathogen transmission is expressed with human movement data in the spatiotemporal network. We have identified the spatiotemporal suitability of dengue spreading in Bangladesh as well as the significant-incidence window and peak-incidence period. Analysis of yearly dengue data variation suggests the possibility of a significant outbreak with a new serotype introduction. The outcome of the framework comprised spatiotemporal suitability maps and probabilistic risk maps for spatial infection spreading. This framework is capable of vector-borne disease risk assessment without historical incidence data and can be a useful tool for preparedness with accurate human movement data.

INTRODUCTION

In modern times, threats posed by infectious diseases have become a significant public health concern due to increasing connectivity.¹ Emerging infectious diseases (e.g., H7N9, H5N1, and Ebola) as well as endemic diseases (e.g., dengue, chikungunya, and measles) pose a severe threat to human health and life.² Some infectious diseases have high mortality and morbidity rates (Ebola), and some of these diseases lack treatments or vaccines (dengue).^3,4 Infectious diseases are creating pandemics due to globalization. For example, 2019 had experienced major dengue outbreaks in many countries in the world, including Southeast Asia and Latin America. Other emerging and endemic infectious diseases had also shown to spread rapidly across the globe in recent times. Therefore, accurate risk assessment of disease outbreak is highly important for preparedness in this modern world. Risk has been defined by medical epidemiologists and health organizations⁵ as disease development probability within an individual in a specified time interval. Risk is also defined as the potential adverse consequences to human life, health, property, or the environment⁶ of unwanted phenomena (disease/event). Accurate risk-assessment models have the potential to improve epidemic prevention and control capabilities.

Because of the complexity in vector-borne disease spreading, risk is often associated with vector or host suitability, the basic reproduction number, vectorial capacity, vector prevalence, or incidence history.^5,7–9 One method to assess risk is by detecting disease outbreaks from surveillance data—a retrospective approach that has a limitation of allowing enough time for preparedness.¹⁰ However, some areas have limited resources for the surveillance system. Especially in developing countries, collected data may not be adequate as most people choose not to use medical facilities unless they have severe conditions. Therefore, disease surveillance data–dependent risk assessment is not always efficient with unreported or underreported incidences. Because of this, researchers have developed other risk-assessment methods to overcome the problem with retrospective methods. The impact of climate change on vector survival, suitability, and pathogen transmission has been assessed for vector-borne diseases in numerous research projects.^11–19 Unfortunately, very limited research has included spatial and temporal heterogeneity of weather conditions, population demography, and movement information in the risk-assessment models.

In this context, we develop a risk-assessment framework incorporating the aforementioned significant elements for vector-borne diseases. In this article, we focus on mosquito-borne diseases to demonstrate the risk-assessment framework as they comprise most of the vector-borne diseases. This article has three major contributions. The first is the formulation of a spatiotemporal, network-based risk-assessment framework by incorporating climate data and demographic information, especially for regions with unreported or underreported incidence data. The second is deriving a spatiotemporal suitability map of competent mosquito species in the disease transmission with only temperature data. The third is the development of spatial risk maps for disease transmission, showing the relative risk of each location compared with others. In addition, identification of the significant-incidence window and peak-incidence period is performed by comparing simulation results with data (when available). A serotype analysis is conducted to identify contributing factors for the year-to-year difference in incidence data. This novel risk-assessment method is capable of incorporating both human movement and contact patterns, as well as impacts of weather factors in human–mosquito interaction.

Finally, an application of the novel framework is presented for dengue spreading in Bangladesh. A spatiotemporal network is developed for human movement in Bangladesh using demographic information, and 1-month– and 2-month–lagged climate (temperature and rainfall) data. A map for the spatiotemporal suitability of human–mosquito interaction and spatial dengue transmission risk maps are obtained from simulation results. Simulation results match closely with the significant-incidence window and peak-incidence period with Bangladesh dengue transmission dynamics. The year-to-year data variability shows a correlation with the dominant serotype. The combined knowledge obtained from the framework (i.e., significant-incidence window, peak-incidence period, risk map, and spatiotemporal suitability map) provides a guideline to public health personnel in prioritizing spatiotemporal resource allocation to reduce/prevent dengue transmission. Risk maps are developed incorporating generalized human movement data in the spatiotemporal network, and have the adaptability to include actual and accurate movement data.

MATERIALS AND METHODS

Risk-assessment framework.

Our novel risk-assessment framework couples a spatiotemporal network-based approach with a compartmental disease model and a spatiotemporal spreading algorithm. The risk-assessment framework has the following five different components:

• 1.Compartmental model
• 2.Pathogen transmission model with climate data
• 3.Spatiotemporal network
• 4.Spatiotemporal spreading algorithm
• 5.Risk calculation

Each of these components is described in subsequent parts of this section.

Compartmental model.

Compartmental models express transitions of the host population from one disease state/compartment to another.²⁰ These compartments are, for example, susceptible, exposed, infectious, recovered, removed, vaccinated, and alert. Some parameters govern inter-compartmental transitions. The transition rate from susceptible to exposed/infected compartment (transmission rate) is the most crucial parameter for the vector-borne disease model. The transmission rate is correlated with climate/weather-dependent factors such as vector abundance and host–vector interactions. Therefore, we incorporate climate data in the transmission rate for the risk-assessment framework developed.

Pathogen transmission model with climate data.

The transmission rate for vector-borne diseases has a complicated relationship with the environment and the host. For example, mosquito abundance and its interaction with the host population cause the transition from susceptible to infected (or exposed) states. When the mosquito population is the vector for disease, temperature and rainfall data are used to develop the correlation between mosquito abundance and its interaction with the host population. This relationship can be expressed as vectorial capacity—a parameter governing the spread of infection from an infected to a susceptible host via vectors. Vectorial capacity is a parameter that governs the spreading of infection from an infected host to a susceptible host via vectors. During the 1960s, Garret-Jones formulated the vectorial capacity, the average number of secondary cases of a disease (e.g., malaria and dengue) arising from each primary infection in a defined population of susceptible hosts.^21,22 As vectorial capacity has been used to transmit the pathogen by Garret-Jones, subsequent literature has also used it for simulation using a network-based model. Scoglio et al.,²³ used vectorial capacity to express the pathogen transmission for Rift Valley fever in cattle using the vectorial capacity for Culex mosquitoes. Riad et al.²⁴ and Sekamatte et al.,²⁵ have also used vectorial capacity to express pathogen transmission via mosquitoes for Rift valley fever and Japanese encephalitis, respectively. The expression for vectorial capacity is given in Equation (1).

$$V_c=\frac{m{a}^2{b}_h{b}_m{c}^{-{\mathrm{\mu }}_{m}n }}{{\mathrm{\mu }}_m}.$$ (1)

Vector parameters used are 1) average daily vector biting rate (a), 2) probability of vector-to-human transmission per bite (b_h), 3) probability of human-to-vector infection per bite (b_m), 4) duration of the extrinsic incubation period (n), 5) vector mortality rate (µ_m), and 6) mosquito vector density with respect to the host (m).^21,22,26 These parameters are specific for the mosquito species and the concerned disease. We choose Aedes aegypti, one of the most competent mosquito species in transmitting dengue, Zika, chikungunya, yellow fever, and other severe diseases, to model the transmission rate/vectorial capacity. Except for mosquito vector density with respect to the host, all other parameters in Equation (1) can be calculated empirically using spatiotemporal temperature data.²⁶ The following empirical formulas are used to calculate temperature-dependent parameters, where T is the temperature in degrees Celsius.

• 1.
  Biting rate (a): Liu-Helmersson et al.²⁶ and Scott et al.²⁷ developed the following empirical equation from numerous experimental data to model the relationship between temperature and average blood meal frequency of the female A. aegypti.

  $$a\left(T\right)=0.0043T+0.0943 \left(\mathrm{da}{\mathrm{y}}^{-1}\right).$$ (2)

• 2.
  Probability of vector-to-human transmission per bite (b_h): The empirical equation for the probability of human infection was expressed with the following thermodynamic function.^26,28

  $$b_{h }\left(T\right)=0.001044T\left(T-12.286\right)\sqrt{32.461-T},\mathrm{for}12.286°\mathrm{C}\le T\le 32.461°\mathrm{C}.$$ (3)

• 3.
  Probability of human-to-vector infection per bite (b_m): Lambrechts et al.²⁹ derived the relationships between temperature and the probability of infection based on empirical data for several A. aegypti–borne diseases.

  $$b_m\left(T\right)=\{\begin{array}{cc}0.000729T-0.9037& \left(12.4°\mathrm{C}\le T\le 26.1°\mathrm{C}\right)\\ 1& \left(26.1°\mathrm{C}\le T\le 32.5°\mathrm{C}\right).\end{array}$$ (4)

• 4.
  Duration of the extrinsic incubation period (n): An exponential function was used to fit experimental data for the extrinsic incubation period.^29,30

  $$n\left(T\right)=4+e^{5.15-0.123T}.$$ (5)

• 5.
  Vector mortality rate (${\mathrm{\mu }}_{\mathit{m}}$): Yang et al.³¹ developed a fourth-order polynomial equation to fit experimental data to model the mortality rate in relation to temparature.

  $${\mathrm{\mu }}_m\left(T\right)=0.8692-0.1590T+0.01116T^2-3.408\ast {10}^{-4} T^3+3.809\ast {10}^{-6}{T}^4.$$ (6)

• 6.Mosquito vector density with respect to the host (m): The mosquito vector density with respect to the host mostly depends on the rainfall. Therefore, in this article, this parameter is expressed as proportional to the weekly average rainfall.³² We have normalized the average weekly rainfall in each location before using it in the vectorial capacity model.

Spatiotemporal network.

To account for the spatiotemporal heterogeneity of the disease transmission risk with changing weather conditions, we propose a spatiotemporal network. The spatiotemporal network is developed using host demographic information such as population density, distribution, and movement. In this network, nodes represent individuals within spatially homogeneous locations, and links represent movements within and between these locations. The network is spatially explicit and has multiple temporal realizations to represent heterogeneities in weather conditions with time and space. This network is then combined with a spatiotemporal spreading algorithm to simulate the spatiotemporal transmission of the infection. The network is periodically updated to reflect changing weather conditions in the spatiotemporal spreading algorithm.

Spatiotemporal spreading algorithm.

Nodes influence each other through statistically independent pairwise interactions in most network-based models. Sahneh et al.^33,34 developed the generalized epidemic modeling framework (GEMF) for stochastic spreading processes over complex networks based on these independent pairwise interactions. The GEMFsim tool was later developed for numerical simulation of GEMF-based models by implementing the Gillespie algorithm.³³ The combined state of all nodes in a network can be described as a random variable X_N(t) = x₁(t), x₂(t),…, x_i(t), where x_i(t) is the state (compartment) of node i at time t. Transition time from one state to another is expressed as an exponential distribution with a transition rate σ_n (x_n → J), where J is the destination state after the transition. This transition can be node based (dependent only on the node state x_i[t]) or edge based (dependent on the combined network state X_N[t]). After a transition occurs, the combined network state will change, and therefore, edge-based transition rates will change. However, node-based transition rates remain constant. Generalized epidemic modeling frameworksim accounts for changes in transition rates due to the change in the combined network state. However, the GEMFsim does not account for the temporal variation of the transition rates due to external factors (weather conditions or human activities).

The temporal variability of the transition rate is crucial for simulating vector-borne disease transmission. Therefore, it is required to adapt the Gillespie algorithm in the GEMFsim to account for the changing rates. In this article, we incorporate the nonhomogeneous Gillespie algorithm in the GEMFsim, which works for exponential event distributions and nonconstant transition rates.^4,35,36 The modified spreading algorithm is capable of periodically changing transition rates to reflect the temporal heterogeneity of vector-borne disease transmission.

Risk calculation.

As the spreading process in our spatiotemporal network is highly stochastic, we need to perform an adequate number of simulations. We keep track of each node’s status and count the numbers of simulations in which a particular node is infected. This count is later used to calculate the risk of the spatial disease spreading. The formula for risk calculation is $R_j=\frac{\frac{{{\displaystyle \sum }}_{n=1}^{N_j}{I}_n}{N_j}}{N_{\mathrm{simulation}}}$, where R_j = spreading risk in location j, I_n = number of simulations where node n is infected, N_simulation = number of simulations, and N_j = total number of population in jth location. The calculated risk is normalized for comparison with the risk of different spatial locations.

Application of the risk-assessment framework for Bangladesh dengue incidence.

Dengue is transmitted by Aedes mosquitoes in tropical and subtropical regions and may cause a wide range of manifestations from asymptomatic infections to deaths.³⁷ Arbovirus transmission is known to be driven by the interplay of gender, age, and travel of individuals. In addition, the transmission also depends on the type of host community (urban/rural), mosquito abundance, and use of mosquito control measures.^38–41 Understanding the relative importance of these factors is required for accurately assessing the risk of dengue.

A recent dengue outbreak in Bangladesh with a record number of cases drew close attention to assess the transmission risk. Bangladesh has a history of dengue incidence dating back to 1960, and a major outbreak occurred in 2000.^42–44 Since 2000, the Ministry of Health and Family Welfare of the People’s Republic of Bangladesh has been recording clinical cases, which are reported annually. Recent urbanization throughout the tropical world has accelerated dengue spreading as A. aegypti—the primary vector for dengue transmission—lives in densely populated human-made environments.⁴⁵ Bangladesh is a densely populated country with rapid urbanization, which provides a conducive environment for mosquito populations. Therefore, a risk-assessment tool for dengue transmission has become very important in Bangladesh.

Several studies have used historical time series data for reported dengue incidence. However, getting accurate data on dengue infection is surprisingly difficult. Only 11–32% of infected people are likely to have symptoms, with just a few being sick enough to require formal medical treatment.^45,46 Misdiagnosis and underreporting are common for cases requiring medical care as well. Therefore, risk assessments based on clinical case counts are not always useful, and may just reflect differences in access to healthcare, diagnostics, and the ability to report cases.⁴⁷ Record-keeping also requires significant resources not always available in Bangladesh. Therefore, our developed framework, which does not require incidence data, can be a useful tool for assessing spatial dengue transmission risk and spatiotemporal suitability in Bangladesh. The adapted framework for Bangladesh dengue spreading is presented in the following text.

Compartmental model for dengue.

When the dengue virus (DENV) enters the bloodstream of a susceptible person via infected mosquito bites, the individual becomes exposed to the disease. After a specific time for viral replication, the exposed individual becomes infectious. The infectious individual finally transitions to the removed state after recovery or death. Therefore, four specific phases/states concern the disease—susceptible, exposed, infected, and removed. The model is called SEIR. Its inter-compartmental transitions are independent Poisson processes with transitions rates expressed in Equations (7)–(9).

$$\mathit{Pr}\left(x_i\left[t+\Delta t\right]=E|x_i\left[t\right]=S,X_N\left[t\right]\right)={\mathrm{\beta }}_i\left(t\right)Y_i\Delta t+o\left(\Delta t\right),$$ (7)

$$\mathit{Pr}\left(x_i\left[t+\Delta t\right]=I|x_i\left[t\right]=E,X_N\left[t\right]\right)=\mathrm{\delta }\Delta t+o\left(\Delta t\right),$$ (8)

$$\mathit{Pr}\left(x_i\left[t+\Delta t\right]=R|x_i\left[t\right]=I,X_N\left[t\right]\right)=\mathrm{\gamma }\Delta t+o\left(\Delta t\right).$$ (9)

In these equations, x_i(t + Δt) = S, E, I, and R express the probability of node i occupying the susceptible, exposed, infected, or removed state at time (t + Δt), respectively. X_N(t) is the combined network state at time t. The transition rate from susceptible to exposed state is an edge-based transition, which is also time variant because of its dependency on weather conditions. We express this time-variant parameter β_i(t) with vectorial capacity for node i at time t, which is calculated from spatiotemporal weather conditions. Y_i is the set of infected neighbors of node i within the spatiotemporal network at time t. Parameter δ is the intrinsic incubation rate, which governs the transition from exposed to infected state. The transition from infected to removed state is expressed with the removal rate γ. Incubation rate δ and removal rate γ are node-based transition rates whose values are assumed equal to 0.17 and 0.14, respectively, and are time invariant in this work.^48,49 These values of δ and γ reflect the means of exponentially distributed parameter values used in the spatiotemporal spreading process.

Pathogen transmission model with Bangladesh climate data.

Transmission rate β is modeled with weekly average temperature and rainfall data in Bangladesh. Climate data for Bangladesh are collected from CLIMATE-DATA.ORG.⁵⁰ The upazila-level spatial unit is used in this work for network development. Climate data are used to calculate each parameter in the vectorial capacity in Equation (1). All parameters, except for mosquito vector density with respect to the host, are calculated from the weekly temperature data. The mosquito vector density parameter is assumed proportional to the weekly average rainfall, and a proportional constant is assumed to reflect a realistic outbreak scenario in Bangladesh.

An urbanization factor is assumed to reflect the suitability of an Aedes mosquito habitat for dengue transmission. The population density is used to classify the urbanization level of each location. Three urbanization factors are used to reflect back-country (population density < 1,000/km²), rural (1,000 ≤ population density < 3,000/km²), and urban (population density ≤ 3,000/km²) locations. The final transmission rate used in simulating dengue transmission is equal to vectorial capacity multiplied by the urbanization factor.

Spatiotemporal network for Bangladesh.

Developing a network is a crucial part of the risk assessment framework. The spatial structure in Bangladesh is as follows:

• 1.Administrative level 1, eight divisions.
• 2.Administrative level 2, 64 districts.
• 3.Administrative level 3, 544 upazila.

For network development, we have used the administrative level 3 spatial resolution. Therefore, Bangladesh is divided into 544 spatial locations before creating the network. Population data are collected for each spatial location from the city population website.⁵¹ The population in each location is scaled by 10,000 to reduce the computational burden during simulations.

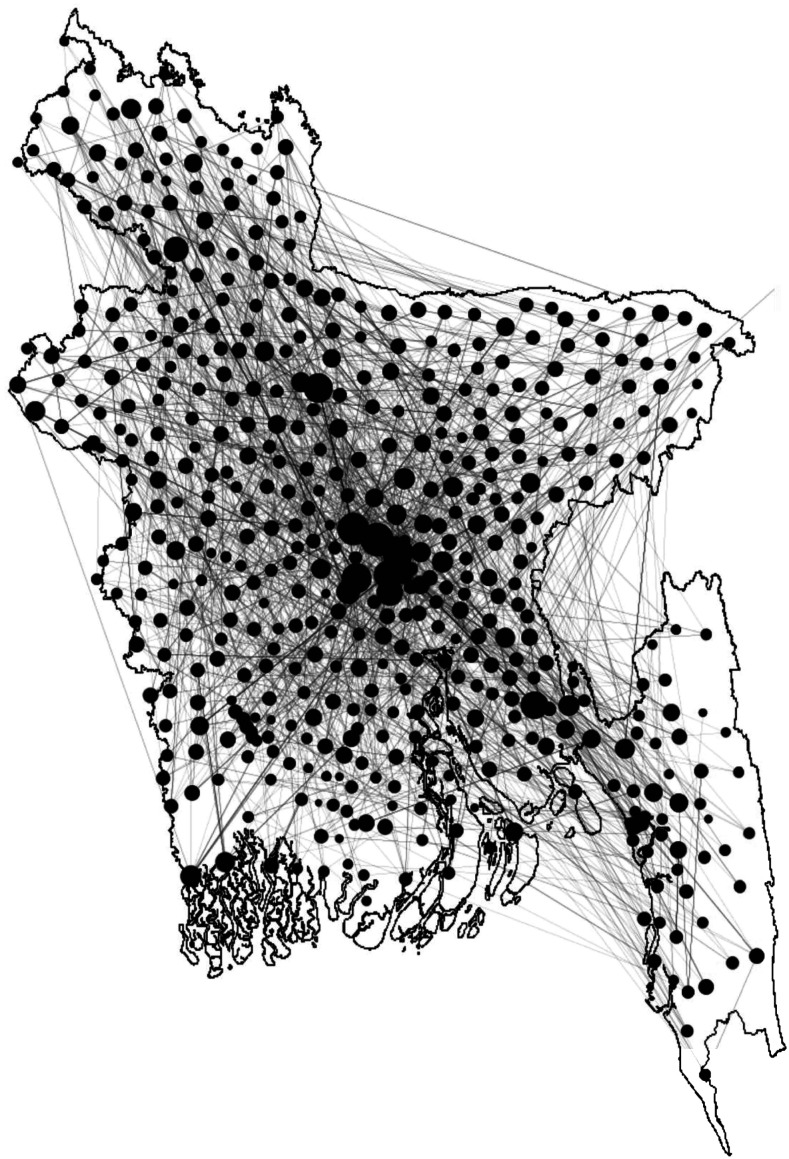
We assume an Erdos–Renyi network within each upazila, where links are created with a probability of 0.2. Inter-upazila links are created using an exponential dispersion kernel. We use the kernel function e^−kD for link generation, where k is a constant, and D is the distance between the source and destination location. We choose the value of k = 0.1 for creating the spatiotemporal network. District-level and division-level human movement, along with the exponential dispersion, are incorporated to reflect human movement patterns. District-level human movement is incorporated by generating links between the capital city Dhaka and all-district cities. Links are created between Dhaka and all-division cities to include division-level human movement in the network. Figure 1 demonstrates a simplified outline of the network.

Figure 1.

A simplified network diagram for Bangladesh. Each black circle represents the network within an upazila, whereas lines between circles express human movement. Circle sizes are scaled according to human movement (node degree) for that location. Greater circle size indicates a greater amount of human movement flow.

Bangladesh is a small country, having only 147,500 km² of area. However, there are still spatial and temporal difference between temperature and rainfall throughout the country. This spatiotemporal weather variation is very important for accurately representing dengue transmission. We included a spatiotemporal heterogeneity in the created network due to weather patterns, that is, pathogen transmission rates on each link. The literature shows the correlation between a 1-month– and 2-month– lagged temperature, rainfall, and dengue occurrence in Bangladesh.⁵² The heterogeneity in the weather patterns is reflected on a weekly value of transmission rate (β) calculated using both 1-month– and 2-month–lagged temperature and rainfall data.

We create two instances of the spatiotemporal network for two different outbreak types: first, major outbreaks spreading throughout the whole country, and second, minor outbreaks spreading only within major divisional cities. We explicitly incorporate district-level human movement for major outbreak scenarios with the exponential dispersion kernel. Division-level human movement is incorporated for minor outbreak scenarios along with the exponential dispersion. On developing the spatiotemporal network, we apply the stochastic spreading algorithm for risk assessment.

RESULTS AND DISCUSSION

Assessed risk in this work is a combination of weather-dependent spatiotemporal suitability and risk maps from the network-based model. Therefore, we present our results in the following two sections as

• 1.spatiotemporal suitability of dengue transmission in Bangladesh
• 2.risk maps for dengue transmission in Bangladesh

Spatiotemporal suitability of dengue transmission in Bangladesh.

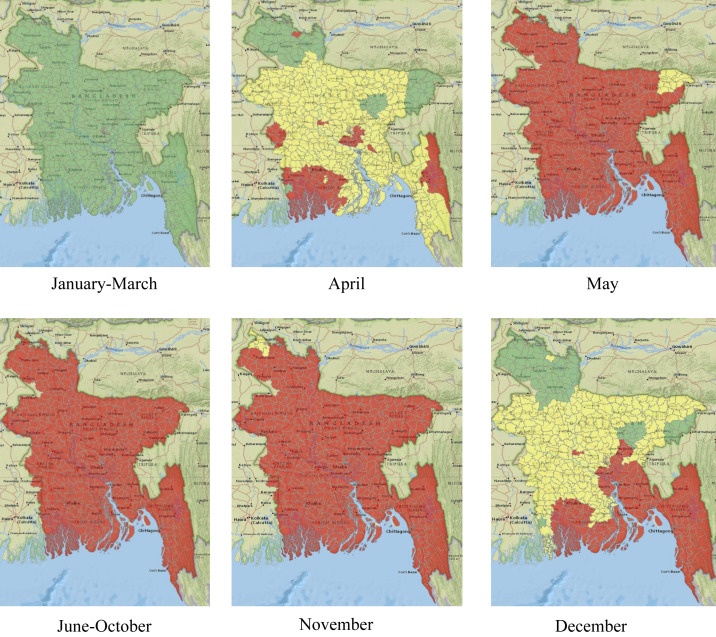
Spatiotemporal suitability expresses spatial and temporal suitability of the vector’s (mosquito’s) survival and function in pathogen transmission. When comparing dengue epidemic potential over time and space, it is preferable to use the relative vectorial capacity,²⁶ expressed as the vectorial capacity relative to the vector-to-human population ratio, and formulated as $r{V}_c=\frac{a^2{b}_h{b}_m{c}^{-{\mathrm{\mu }}_{m}n }}{{\mathrm{\mu }}_m}$.²⁶ All parameters are temperature dependent in the relative vectorial capacity definition. A higher relative vectorial capacity indicates a higher potential for a dengue epidemic. We calculate the relative vectorial capacity for the Aedes mosquito in Bangladesh to infer the suitability of dengue spreading. A threshold value for relative vectorial capacity exists beyond which Aedes mosquitoes can function properly in transmitting dengue infection. A relative vectorial capacity greater than 0.61 indicates the suitability of dengue spreading.²⁶ The spatiotemporal suitability maps for dengue spreading in Bangladesh are presented in Figure 2 for each month of the year. The relative vectorial capacity is found to be higher than the threshold value (0.61) for many months of the year in almost all locations (red and yellow regions).

Figure 2.

Spatiotemporal suitability maps for dengue transmission in Bangladesh based on temperature. The map represents suitability in the following manner: green (lowly suitable), yellow (moderately suitable), and red (highly suitable). This figure appears in color at www.ajtmh.org.

It is evident from Figure 2 that months between January and March are poorly suited for dengue transmission. In April, some southern parts of the country, as well as the capital city of Dhaka, become highly suitable. Other parts of the country, except the northern most corner, become moderately suitable. Starting from May, the whole country becomes highly suitable, and the situation remains similar until November. The most northern part of the country becomes poorly suitable, whereas the capital and southern part stay highly suitable in December. After December, the whole country becomes poorly suited again, which continues until April.

Dengue incidence data since 2000 show cases throughout the year, which supports our results for the suitability of dengue transmission. Bangladesh is a tropical country, which provides a suitable temperature for mosquito survival year-round. However, for temperate regions with widely varying temperatures, mosquitoes may not be able to survive in the coldest months.

Risk maps for dengue transmission in Bangladesh.

The network-based model enables us to simulate the spreading process within the spatiotemporal network described earlier. Every year, the dengue outbreak in Bangladesh shows a different trend. Some years cases are reported from most parts of the country, whereas some years outbreaks are mostly limited within divisional cities. Depending on the spreading, outbreaks are divided into two categories—major outbreaks, with widespread dengue cases, and minor outbreaks, with cases mostly in some divisional cities. Therefore, two distinct simulation scenarios are assumed to match the two different outbreak types. Simulations are performed with parameters calculated using both 1-month– and 2-month–lagged temperature and rainfall data, which are presented in the subsequent parts of this section.

Scenario 1: Major outbreak.

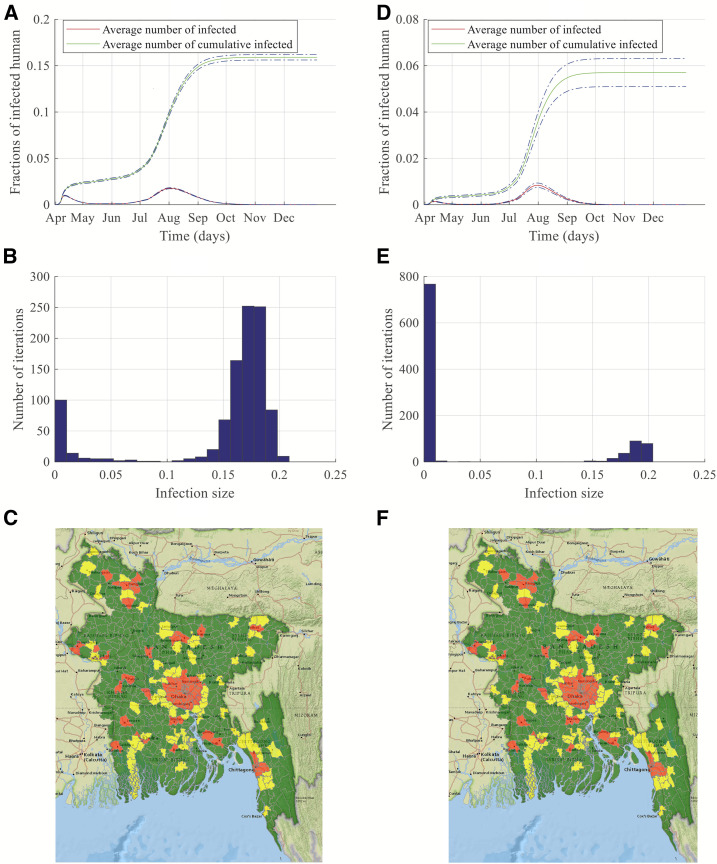
A major outbreak is defined when dengue cases are widespread throughout the whole country. For major outbreaks, the network is generated with district-level human movement incorporated. Dhaka is the capital of the country; therefore, frequent movement among all district towns is assumed to and from Dhaka. We performed 1,000 iterations for each scenario to account for stochasticity in the simulation results. Simulations are started with an entirely susceptible population with one infected human in the initial outbreak location. The initial outbreak location is also changed to see the impact of human movement on transmission risk. Simulation results for 1-month–lagged climate data, and two initial conditions—Dhaka and Chittagong outbreaks starting—are presented in Figure 3.

Figure 3.

Simulation results and risk maps for dengue transmission in Bangladesh for a major outbreak. Left-side panels are results of simulations started in Dhaka, whereas right-side panels are results of simulations started in Chittagong. (A and D) show dengue transmission dynamics, (B and E) present histograms of the number of simulations and infection size, and finally, (C and F) display risk maps for dengue infection. This figure appears in color at www.ajtmh.org.

Figure 3A and D show the fractions of infected people and cumulative infected people with a 95% CI when the simulation started in Dhaka and Chittagong, respectively. The curve for the average number of infected shows two peaks in Figure 3A and D. The first peak refers to the rapid spreading within the vicinity of the initial outbreak location, and the second peak represents the widespread outbreak. For novel vector-borne diseases, the infections start with a single infected human or a single infected mosquito. If we assume a single infected human started the infection, then the infection will start locally with competent mosquitoes biting the infected person. As mosquitoes have a short flying range, the infection will be local at the beginning, and this is evident from the smaller initial peak. Size of the peak depends on population size, level of urbanization, and area of the outbreak location. As Dhaka is densely populated, an outbreak starting there will result in a pronounced initial peak due to only local transmission (Figure 3A). We started our simulation in April as it is the first month of high suitability for the Aedes mosquito within the year for Bangladesh. However, the suitability increases with time, as shown in Figure 2, and the infection starts spreading to distant locations because of human movement as well as higher suitability. Hence, we have another peak in August with numerous cases countrywide. Although Figure 2 shows all locations are highly suitable from May to November, the underlying mosquito-dependent transmission rate keeps increasing until August and attains higher values in June–August. Therefore, despite human movement from Dhaka to other locations all year, because of the lower value of transmission rates, no widespread infections start until June. With the higher value of transmission rates, the number of infected individuals keeps increasing from June and attains its peak in August. Around 16% of the total population in the network becomes infected in this outbreak scenario. Almost 70% of the total infections are observed within the period of July–September. The peak consists of 2.5% of the entire population in our developed network. These infected people during August may require hospital care, which will be a huge burden on the healthcare system. Therefore, proper measures should be taken, and more resources should be allocated for dengue health care during July–September. Figure 3D shows the dynamics when dengue infection started in Chittagong. Total fractions of cumulative infected people and infected people during peak times are both significantly lower for this outbreak scenario, which can be attributed to the fact that Chittagong is not very densely populated as well as not well connected to the whole country as is Dhaka. Therefore, both the initial smaller peak and the second higher peak are smaller than the peaks in the Dhaka outbreak scenario. When the infection starts in Chittagong, around 6% of the population becomes infected compared with 16% in the Dhaka outbreak scenario. Therefore, starting location of the infection is a crucial determining factor of the extent and dynamics of the epidemic.

Figure 3B and E show the histogram with fractions of cumulative infected humans in the Bangladesh dengue network and the number of simulations performed. The x-axis represents fractions of infected humans in the simulation, and the y-axis shows the number of simulations where a particular infection size is obtained. Figure 3B shows that almost 80% of simulation results are in the 10–20% of infected humans in the representative network when the initial outbreak happens in Dhaka. This accounts for the narrower CI in Figure 3A and E expresses around a 20% probability of 10–20% of humans being infected. This variability in the fractions of infected individuals accounts for the wider CI in the simulation results in Figure 3D.

Transmission dynamics presented in Figure 3 are obtained using the network with district-level human movement incorporated, and 1-month–lagged temperature and rainfall data. However, when we perform simulations with 2-month–lagged temperature and rainfall data, the simulation is started in May, and the peaks are delayed by a month. The analysis of Bangladesh dengue incidence data since 2000 showed the occurrences of peaks in July–October.^42,43 Therefore, 2-month–lagged data also show significant similarity with the actual incidence data. Risk maps are similar for both 1-month–lagged and 2-month–lagged data. Simulation results for 2-month–lagged data are presented in the supporting materials.

Scenario 2: Minor outbreak.

Dengue infections are often confined within divisional cities, and a widespread outbreak does not happen. Therefore, we propose another scenario where we explicitly incorporate human movement from the city of Dhaka to other divisional cities, along with the distance-based exponential movement kernel. We call this scenario a minor outbreak as the infection does not spread countrywide. We perform simulations for both 1-month– and 2-month–lagged climate data.

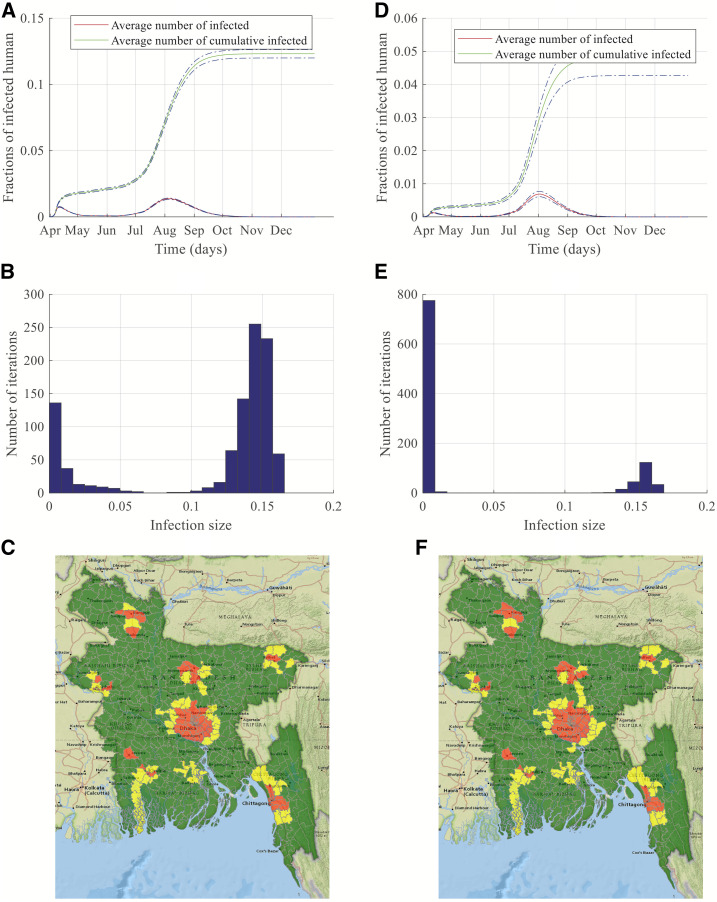
The results are presented in Figure 4, when simulations are performed with 1-month–lagged climate data and the same initial conditions as major outbreak scenarios, namely, starting simulations in Dhaka and Chittagong.

Figure 4.

Simulation results and risk maps for dengue transmission in Bangladesh for a minor outbreak. Left-side panels are results of simulations started in Dhaka, whereas right-side panels are results of simulations started in Chittagong. (A and D) show dengue transmission dynamics, (B and E) present histograms of the number of simulations and infection size, and finally, (C and F) display risk maps for dengue infection. This figure appears in color at www.ajtmh.org.

Figure 4A and D show a similar trend as shown in Figure 3A and D. For 1-month–lagged data, a major peak is observed in August with rapidly increasing infections from July–September. However, comparing Figures 3 and 4, we can see that both the value of the fraction of infected people during the peak infection time and the whole outbreak period are smaller during minor outbreaks.

Human movement can also be considered as a crucial factor in vector-borne disease spreading, although the pathogen transmission does not happen via direct physical contact. An exposed/infected person may move/travel to a different location and become infectious after reaching the destination. That person can be bitten by a competent local mosquito and may start a local outbreak in the destination location. Therefore, mosquitoes are responsible for local transmission, whereas human movement is mostly responsible for long-distance pathogen transmission during a period of higher suitability. The reduction in the number of infections in the minor outbreak scenario can be attributed to the reduced human movement volume within the network rather than with the major outbreak scenario.

It is evident from the comparison between panels (a) and (d) of Figures 3 and 4 that the major dengue-spreading period in Bangladesh is June–September. Identifying this time window for significant transmission is crucial for public health officials. Identification of the significant-incidence window will enable them to take prompt action during the surge of infection. The major action for controlling a vector-borne disease is always controlling the vectors. Therefore, control measures need to focus mostly on the significant-incidence months to reduce the mosquito population when resources are inadequate for the whole year.

Figure 4C and F show the normalized risk maps for dengue spreading during a minor outbreak. It is evident from the figures that high-risk areas are confined within major-division cities and their nearby locations in contrast to Figure 3C and F, where many locations throughout the country are at high risk. This reduction in the spreading risk can be attributed to reduced human movement in the minor outbreak scenario. Therefore, making people aware of human movement's impact on long-distance travel through social media or radio/TV broadcasting would help contain the epidemic. Simulations are also performed for 2-month–lagged climate data, and all results are like those obtained with 1-month–lagged data. These simulation results are presented in the supporting materials.

Our proposed framework is a generalized risk-assessment tool based on climate and demographic data, which can be used for risk assessment, especially in regions with unreported or underreported incidence data. Risk maps developed in this work are generated with the generalized concept of human movement within Bangladesh. The framework can incorporate more detailed and accurate human movement data. The incorporation of detailed movement data will provide a more accurate assessment of the transmission risk at each location. Once proper and accurate movement data are incorporated into the network, control measures should be applied to high-risk areas first, followed by medium- and low-risk areas, depending on availability of resources.

Serotype analysis.

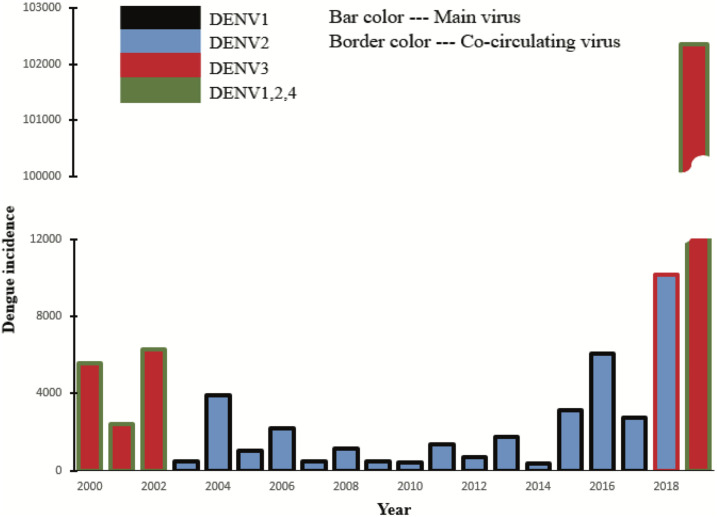
Since 2000, dengue cases arise every year in Bangladesh. However, the number of cases varies from year to year. Importantly, the available data concern only hospitalized and reported cases of dengue. In this section, we show the existence of a correlation between the number of cases and the circulating DENV serotypes. Dengue fever can be caused by any of four genetically related DENV serotypes (DENV1, DENV2, DENV3, and DENV4).⁵³ After recovering from infection with one dengue serotype, a person has immunity against that particular serotype.⁵³ Unfortunately, the person can be infected again with any of the remaining three dengue serotypes.⁵⁴ Subsequent infections often put individuals at greater risk for severe dengue illnesses than those who have not been previously infected.⁵⁵ A bar graph of yearly dengue incidences in Bangladesh with serotypes is presented in Figure 5.

Figure 5.

Serotype analysis of dengue spreading in Bangladesh since 2000. The bar chart presents the number of dengue cases with circulating serotypes each year in Bangladesh. The main bar color represents the dominant serotype, whereas the border represents other circulating serotypes. This figure appears in color at www.ajtmh.org.

The primary bar color represents the dominant circulating serotype, whereas the border color represents co-circulating serotypes. The x-axis shows the year, and the y-axis shows the number of reported dengue cases in Bangladesh. The bar and border colors are as follows: black for DENV1, blue for DENV2, red for DENV3, and green for DENV1, 2, and 4 together. The height of each bar corresponds to the number of cases in the corresponding year. Figure 5 shows the dominant circulating serotype was DENV3, with the other three co-circulating during the years 2000–2002. Within the period 2003–2016, DENV2 was the dominant serotype and DENV1 was co-circulating.⁵⁴ The DENV3 reemerging in 2017 resulted in a significant increase in the number of cases during 2018. However, DENV2 was still the dominant circulating serotype in 2018.⁵⁴ If a serotype is circulating long enough within a population, all recovered people may become immune to that specific serotype. An increase in the number of cases in 2018 can be attributed to the reemergence of DENV3. DENV3 became the dominant circulating serotype in 2019, which created an extreme and unprecedented surge in the number of infections. More than 100,000 cases were reported in 2019—which is more than double the number of combined cases in the previous 19 years—because of a vast susceptible population for DENV3 serotype. Currently, DENV3 is already in circulation in Bangladesh. Neighboring countries of Bangladesh have all four serotypes. Therefore, Bangladesh is always at risk for all four serotypes, including DENV4. Healthcare personnel should be vigilant to identify dengue patients before the significant-incidence period to identify the circulating serotypes. The introduction of a new serotype will produce a high probability of a surge in dengue infections.

Peak timing validation.

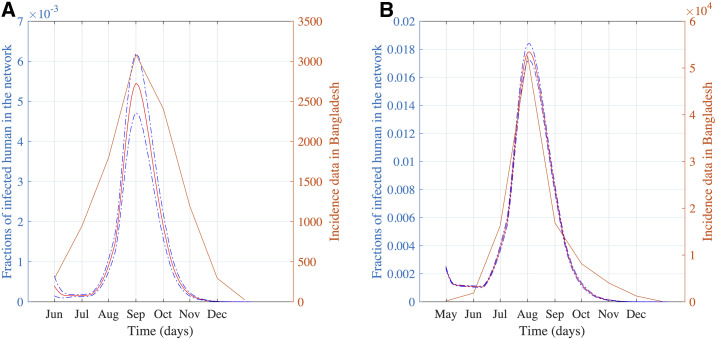
The yearly reported cases varied widely for dengue incidence in Bangladesh. For example, there were 10,148 cases in 2018, and more than 100,000 cases were reported in 2019.^54,56 Therefore, a high variability in year-to-year dengue cases exists. From the serotype analysis in the previous section, the unprecedented increase in 2019 can be attributed to the DENV3 circulation. The yearly number of dengue cases is a complex combination of circulating serotypes, movement patterns of the human population, and measures taken for mosquito control. For widely varying year-to-year case numbers, we used the peak-incidence time and transmission dynamics to compare our simulation results with the incidence data. Peak incidence happened mostly in August and September in Bangladesh.⁵⁴ Simulation results with 1-month–lagged climate data show incidence dynamics with the major peak in August. Two-month–lagged climate data resulted in a peak in September. We compare our simulation with actual incidence data for 2018 and 2019 in Figure 6.

Figure 6.

(A) Comparison of peak time from our simulation with incidence data during a minor outbreak in 2018 and (B) comparison of peak time from our simulation with incidence data during a major outbreak in 2019. This figure appears in color at www.ajtmh.org.

In 2018, the peak of incidence data was observed in September, as shown in Figure 6A. Simulation results for 2-month–lagged climate data show a peak in September in accordance with 2018 incidence data in Figure 6A. Disease dynamics from simulations with 1-month–lagged climate data shows a similar trend with a coinciding peak for 2019 (Figure 6B).

CONCLUSION

Climate data can be used to develop a generalized risk-assessment framework for vector-borne diseases together with demographic data—spatial distribution of individuals and their movement patterns. Therefore, we develop a novel risk-assessment framework with a spatiotemporal network model and a nonhomogeneous Gillespie algorithm, using both climate and demographic data. The assessed risk from this framework comprised spatiotemporal suitability maps and spatial risk maps. Spatiotemporal suitability maps show spatial and temporal suitability of vector-borne transmission. Spatial risk maps represent the disease transmission risk of each location compared with other locations on the map. This framework also identifies high-risk or elevated-risk months, as well as the peak-incidence period within a year.

On development, the framework is applied to the study of dengue transmission in Bangladesh for major and minor outbreak scenarios. The difference between major and minor outbreaks is defined by different levels of human movement to demonstrate the critical role of human dispersal on widespread pathogen transmission. Reduced human migration throughout the country will reduce the spread of infection to divisional cities. We generate the spatiotemporal suitability map and the risk maps for Bangladesh dengue transmission. Simulation results also showed a similar significant-incidence window as well as the peak-incidence period with reported dengue-incidence data in Bangladesh. Serotype analysis indicates the importance of identifying circulating DENV serotypes before the significant-incidence window. The possibility of a major outbreak is associated with the introduction and reemergence of new DENV serotypes. The proposed risk-assessment tool provides guidelines for public health officials to prioritize resource allocation and control measure application according to the estimated risk.

The network-based model has the flexibility to incorporate very detailed mitigation measures in the model. These mitigation measures can be social distancing, reduced human movement, or other disease-specific preventive measures. We will extend this work to explore different mitigation strategies in our future work.

Note: Supplemental material appears at www.ajtmh.org.