Compressed sensing velocity encoded phase contrast imaging: Monitoring skeletal muscle kinematics

Abstract

Purpose:

This study implements a compressed sensing (CS) 3-directional velocity encoded phase contrast (VE-PC) imaging for studying skeletal muscle kinematics within 40 s.

Methods:

Independent variable density random sampling in the phase encoding direction for each temporal frame was implemented for various combinations of CS-factors and views per segment. CS reconstruction was performed for the combined multicoil, temporal datasets using temporal Fourier transform followed by temporal principal component analysis sparsifying transformations. The method was tested on a flow phantom and in vivo, on velocity and strain rate of the medial gastrocnemius muscle of 11 subjects performing isometric contractions.

Results:

For the flow phantom, velocity from 8 undersampled sequences matched very well with the flowmeter values over a range of velocities spanning in vivo muscle velocities. Bland-Altman plots of the peak strain rate eigenvalues comparing 7 undersampled sequences was in good agreement with the reference (full k-space) scan. CS-factor of 4 combined with views per segment of 4 (scan times reduced by 4) yielded images with no visual artifacts allowing and yielded velocities and strain rate maps in the lower leg muscle in 40 s.

Conclusion:

This study shows that a reduction in scan time of velocity encoded phase contrast imaging up to a factor of 4 is possible using the proposed CS reconstruction.

1 |. INTRODUCTION

MRI has been established as a viable technique to study muscle kinematics (including strain mapping).^1–5 Several studies have established the feasibility of the velocity encoded phase contrast (VE-PC) -based MRI technique for monitoring muscle velocity and strain rate (SR) mapping during passive muscle motion and for different contraction modes (e.g., for isometric, concentric, and eccentric contraction patterns)^3–5 as well applied it to study differences in aging and young muscle as well as pre- and postunloading.^6,7 However, the limitation of the VE-PC is the long scan time that requires execution of ~75 consistent contractions for dynamic imaging (~2 min 40 s). Several methods have been developed to maintain the consistency of contraction for example, by providing a visual feedback of the measured force superposed on the target force curve.^6,7 However, this still limits the force that can be maintained for the duration of the scan; this is usually set at 30–35% maximum voluntary contraction (MVC) to enable ~75 consistent contractions. Studying muscle kinematics for several % MVCs including higher %MVCs may provide better insights into differences in muscle kinematics between normal and diseased (e.g., sarcopenia, disuse atrophy, dystrophy) conditions.^6,7 The long scan times also prevent acquisition of multiple slices to extract the full 3D strain or SR tensor. Furthermore, to decrease scan times, views per segment (vps) up to 4 are used, but this limits the acquired temporal resolution of the scans. A faster VE-PC sequence with improved temporal resolution could possibly expand the domain of exploration of muscle kinematics.

Compressed sensing (CS) has been applied successfully and extensively in MRI to accelerate scan times.⁸ CS allows for reconstruction of undersampled MRI data based on the concept that an image with a sparse representation in a known transform domain can be recovered (without artifacts) from randomly undersampled k-space data using a nonlinear reconstruction. The maximum acceleration (CS undersampling factor) will be determined by the image sparsity in the transform domain; the experimental observation is that the number of required samples is approximately ~4 times the number of nonzero coefficients in the transform domain. Various sparsifying transforms have been introduced, such as wavelet, principal component analysis (PCA), and Fourier transform (FT).⁸ For 2D imaging, practical considerations limit the randomness to the phase encode (PE) direction (k_y) while for 3D acquisitions, random undersampling can be performed in the 2 PE directions (k_y and k_z) allowing for higher acceleration factors. Furthermore, in 2D dynamic imaging as in 2D VE-PC, researchers have exploited the fact that each temporal frame can have a different random PE pattern and a joint reconstruction of all temporal frames exploits the randomness in 2 axes (k_y-t) allowing for higher acceleration factors compared with independent reconstructions of each temporal frame.

k_y-t CS reconstruction has also been integrated with multiple coil sensitivity profiles to perform a joint reconstruction of raw data from all the coils: this allows higher acceleration factors than CS without multiple coils that still yields images without significant artifacts. This latter technique, termed k_y-t SPARSE SENSE to reflect the combination of multicoil (parallel) imaging and CS techniques, has been applied to first-pass cardiac perfusion imaging as well as to studying cardiovascular and hepatoportal vascular dynamics.^9,10 However, the k_y-t SPARSE SENSE technique has not been applied to imaging muscle kinematics. It should be noted that muscle velocities are much lower than that encountered in cardiac or portal and hepatic veins blood flow imaging (velocity encoding [VENC] = 80 cm/s), so the VENC gradients are much larger for the VE-PC sequence to map muscle motion (VENC = 10 cm/s).

The larger VENC gradients result in noisier images, so that integrating CS with VE-PC sequences mapping lower velocities may pose additional challenges. One recent study reported 4D VE-PC integrated with CS applied to muscle dynamics.¹¹ The latter study performed 3D volume acquisition with undersampling in the k_y and k_z axes with 3-directional VENC. To leverage the undersampling in the slice direction, a fairly high number of partitions is required (e.g., ≥32) that results, for the best acceleration factor reported in the latter study (~×6.4), in scan times of ~2 min 46 s. Admittedly, the optimum approach for 3D SR tensor computation is to acquire in 3D with 3-directional VENC to cover the entire muscle.

However, the long acquisition time of the 3D sequence even with (~×6.4) undersampling¹¹ limits its application with regard to the goal of the current work to reduce the acquisitions to less than a minute. Furthermore, earlier experimental observation⁷ was that, with appropriate orientation of the acquisition slice in the plane of the muscle fibers (e.g., oblique sagittal for the medial gastrocnemius [MG]), 5 contiguous slices of 5-mm thickness allows the extraction of the 3D strain/SR tensor in 3 slices, and this is sufficient to capture the spatial variation of the 3D strain tensor along the length of the muscle.

The advantages of a faster VE-PC sequence for muscle imaging is that it will allow scans to be completed with a shorter number of contraction cycles; this will expand the applicability to cohorts that are limited in their ability to sustain consistent contraction levels for a large number of repetitions. These cohorts include older subjects (normal and sarcopenic) and subjects with skeletal muscle disorders, such as disuse atrophy dystrophy. Furthermore, a short VE-PC sequence will also enable acquisitions at higher %MVC (and at several %MVC) in contrast to current MRI based muscle kinematics studies limited to a single %MVC (~35%MVC) achievable using traditional longer VE-PC sequences.^6,7 Differences in muscle performance between normal and abnormal (sarcopenic, dystrophy, disuse atrophy) muscle function may be characterized better by investigating over a range of %MVCs to explore force-strain patterns.¹²

The objective of this study was to integrate CS and multicoil methods with 2D VE-PC imaging to decrease total scan time to less than a minute and implement this to study muscle kinematics. The new sequence was first validated with a constant flow phantom and velocity from the fully sampled and undersampled acquisitions (at different accelerations) were compared with reference flowmeter values. Calf muscle tissue motion (velocity and SR) under isometric contraction was monitored by the reference VE-PC sequence and compared with the undersampled VE-PC sequences for different acceleration factors (obtained by combinations of CS-factors and vps).

2 |. METHODS

2.1 |. VE-PC pulse sequence

The VE-PC pulse sequence with 3-directional VENC and the reference (without any VENC) is shown in Figure 1; the sequence schematic closely follows that in Markl.¹³ The VE-PC sequence shown in Figure 1 was modified for random undersampling with a different random pattern along the k_y direction at each temporal frame. The reference VE-PC sequence was implemented with 4 vps that resulted in an acquired temporal resolution of 285 ms (~8 acquired frames for the contraction cycle duration of 2.3 s); these acquired data were then interpolated using view sharing to reconstruct 17 temporal frames. As part of the current study, both CS acceleration factors and vps were modified to reduce scan time while maintaining/increasing the acquired temporal resolution.

FIGURE 1.

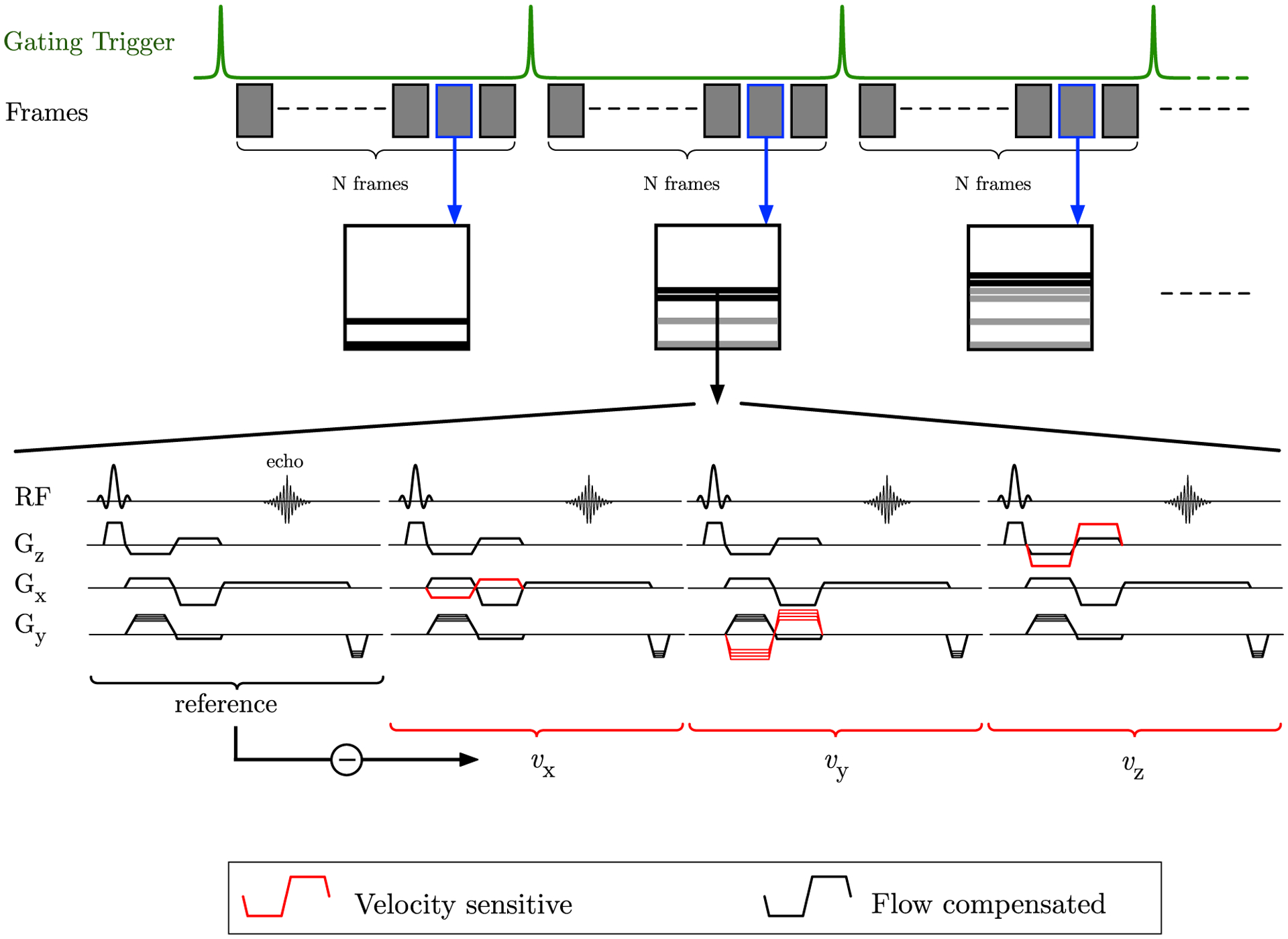
Pulse sequence diagram of the VE-PC sequence; the gating trigger shown on the top row is the external trigger from the force transducer attached to the foot restraining device. Each shaded block is expanded below in the pulse sequence; the pulse sequence includes the reference flow compensated acquisition followed by 3 acquisitions, which are VE along the z, x, and y-axis, respectively. The vps denotes the number of PE lines acquired in a temporal frame, here vps = 2 (e.g., if vps is set to 2, the above sequence is repeated at 2 PE levels and the data are assigned to the temporal frame suggests that the PE lines go toward creating the image at that temporal frame). Higher vps result in lower temporal resolutions

2.2 |. CS

2.2.1 |. k-space undersampling

Undersampling was performed along the k_y direction with a different random pattern at each temporal frame. The undersampling along the k_y was a random variable density pattern that yielded a dense sampling at the center of k-space. The pattern was drawn from a proton density fraction (Figure 2A) given by 10th order polynomial:

$$\text{PDF}={(1-\left|k\right|)}^{10}+m.$$ (1)

FIGURE 2.

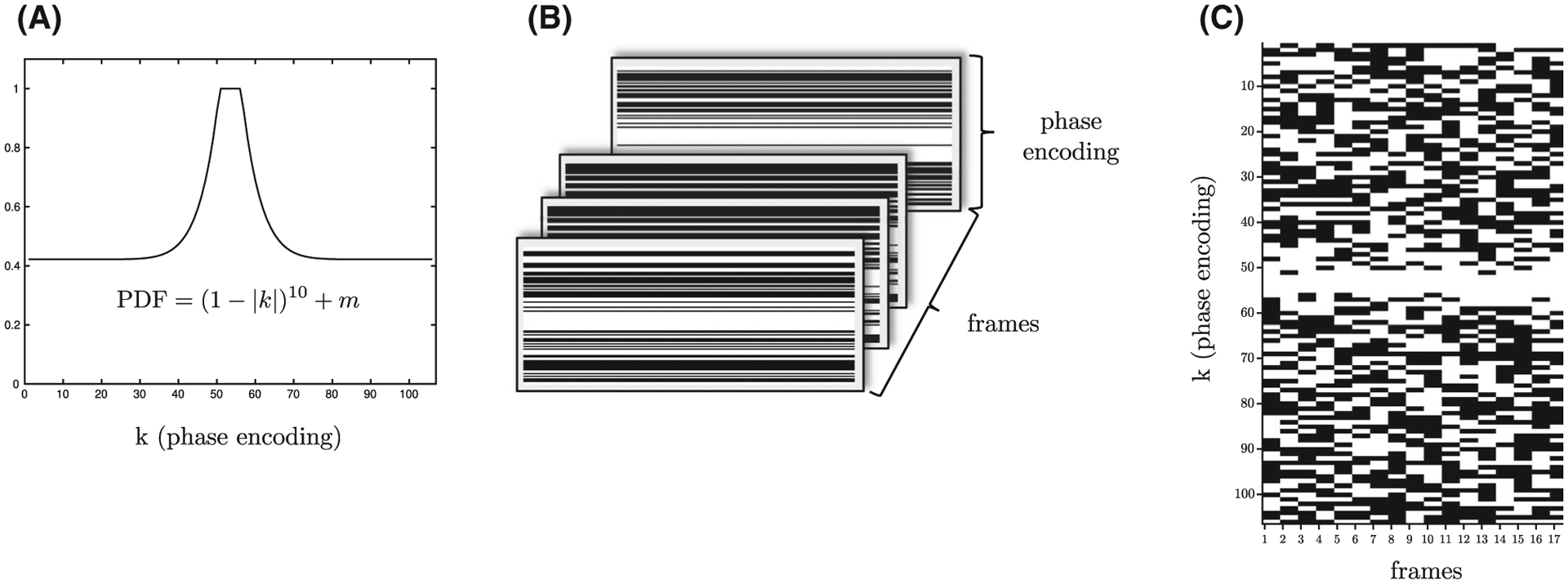
The proton density fraction (PDF) from which the random undersampling PE pattern is drawn (A). The PE undersampling pattern for each temporal frame with different random patterns for each frame; black indicates that the PE at that value is not acquired, while white indicates that the PE level is acquired (B). The PE levels for each temporal frame for all 17 temporal frames is shown here, with white indicating the line is acquired while the black shows it is not acquired (C) for undersampling factor 2 in this case. Note the dense sampling of the central k-space lines across all temporal frames

Here, k is the magnitude of k_y with the maximum and minimum values of k_y normalized to +1 and −1, respectively, and m is the sampling density computed by using an iterative bisection method, where the value in each iteration is divided successively by 2. This method ensured dense sampling at the center of k_y with decreasing k_y density toward the edges of k_y space.¹⁰ Dense sampling at the center has been established as providing better CS reconstructed images than uniform random undersampling.^8,9

The undersampling pattern for each temporal frame of the dynamic series was an independent random pattern (Figure 2B,C) selected as recommended by Lustig et al.⁸ In brief, an impulse at the origin in a 1D image is Fourier transformed to give a constant image. This constant 1D image is undersampled by the chosen random pattern, and then a 1D inverse fast FT (FFT) is performed to obtain the 1D image of the impulse. If no undersampling is performed, then the impulse is completely recovered while the undersampling results in side lobes, which are quantified as the sum of the coefficients not including the origin (denoted as interference) in the 1D image reconstructed by undersampling. The undersampling pattern with the lowest value for the interference (from 100 iterations) was chosen in separate iterations for a temporal frame. Different combinations of CS acceleration factors (CS-factors) and vps were tested for both in vitro phantom as well as for in vivo calf muscle studies (Figure 3).

FIGURE 3.

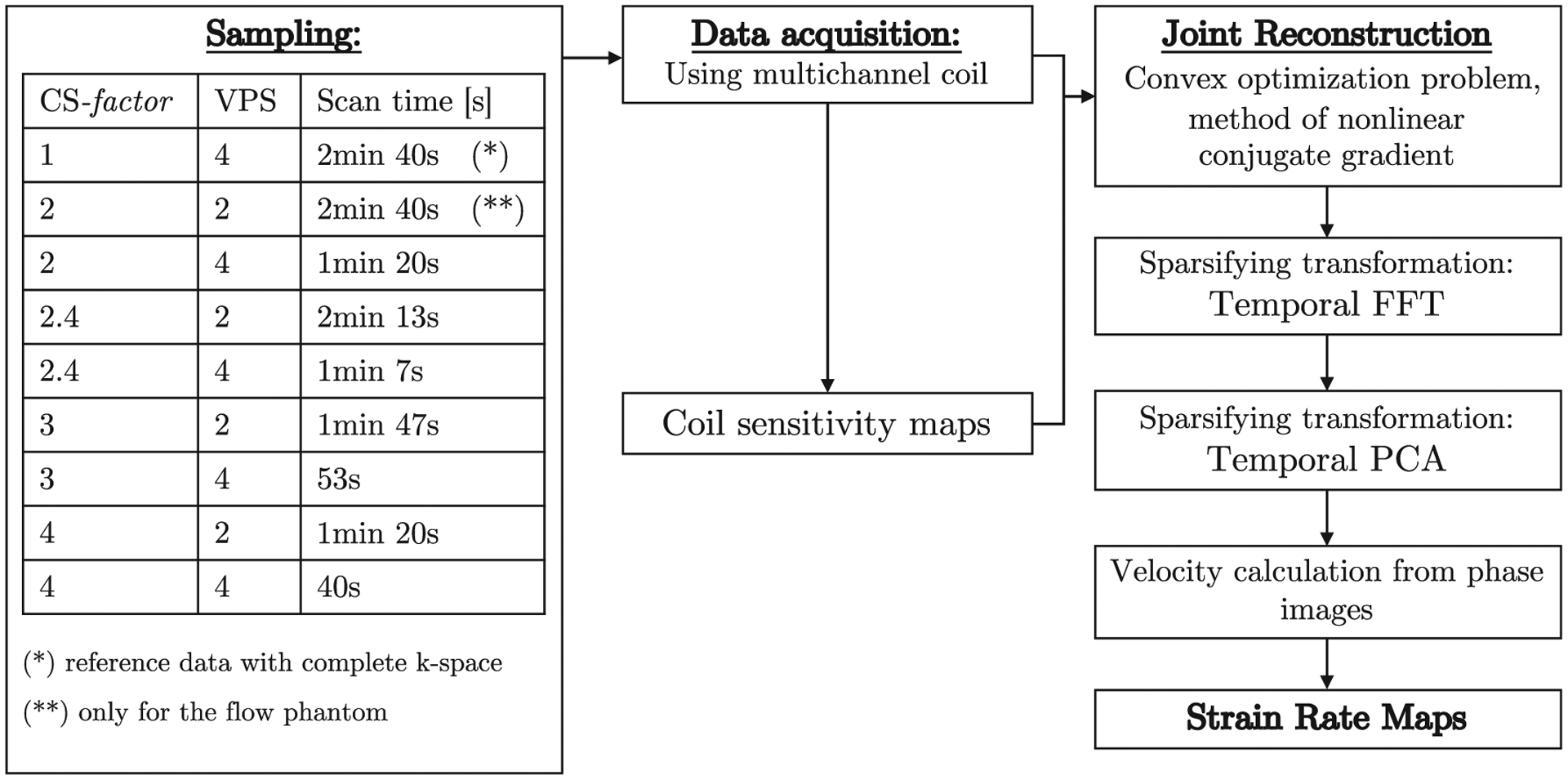
The k_y-t SPARSE SENSE acquisition and reconstruction pipeline. Different sampling patterns and vps were tested to identify the highest acceleration factors that would still produce artifact-free images after CS reconstruction. Complex raw k-space data were the input data for the algorithm, the zero filled inverse FT image was the start point for the temporal FFT stage

The undersampled patterns generated as detailed above were integrated into the VE fast gradient echo sequence by modifying the proprietary pulse sequence (GE Medical Systems, version 15M4, Milwaukee, WI) using the EPIC programming environment. The undersampled mask for each temporal frame was read from an external file. The entire sequence was tested on the simulation platform as well as during run-time to verify that the undersampled patterns were correctly reproduced.

2.2.2 |. CS iterative reconstruction

The flowchart for the iterative nonlinear reconstruction algorithm is shown in Figure 3 and follows the k_y-t SPARSE SENSE method reported earlier.^9,10,14 Data were downloaded from the scanner as the complex k-space data for each coil for each temporal frame. Data from the multiple channels were combined to form a self-calibrated coil sensitivity map C. The coil sensitivity map is obtained by a temporal average over all the phases followed by an adaptive array combination.¹⁵

A 2-stage process is used to reconstruct the image; the first stage uses the temporal Fourier transform as the sparsifying transform, while the second stage uses the temporal PCA as the sparsifying transform (Figure 3). The starting point of the first stage (temporal FT as the sparsifying transform) is the sensitivity-weighted multicoil image combination of the zero-filled Fourier reconstruction of the undersampled data. A joint reconstruction is performed over all coils and all temporal frames. CS reconstruction minimizes the functional shown in Equation 2.1:

$$f(I)=\underset{I}{\text{min}}{\Vert {\mathcal{F}}_{\text{su}}ℂ\cdot I-\mathbb{K}\Vert }_2^2+{\lambda }_{\mathcal{F}/\mathcal{P}C\mathcal{A}}{\Vert {\mathcal{W}}_{\mathcal{F}/\mathcal{P}C\mathcal{A}}\cdot I\Vert }_1$$ (2.1)

where I (current reconstructed image) and K (acquired undersampled k-space data) are defined according to Equations 2.2 and 2.3, respectively:

$$I=\left[\begin{array}{ccc}{i}_{11}& \dots & i_{t1}\\ ⋮& \ddots & \\ i_{1N}& & i_{tN}\end{array}\right]$$ (2.2)

$$\mathbb{K}={\mathcal{F}}_{\text{su}}ℂ\cdot I=\left[\begin{array}{ccc}{k}_{11}& \dots & k_{t1}\\ ⋮& \ddots & \\ k_{1N}& & k_{tN}\end{array}\right]$$ (2.3)

with N being the number of coils and t, the number of temporal frames and F_su and C are the spatially undersampled Fourier operator and coil sensitivity vector, respectively, defined by Equation 2.4:

$${\mathcal{F}}_{\text{su}}=\left[\begin{array}{c}{\text{F}}_{\text{su}}^1\\ ⋮\\ {\text{F}}_{\text{su}}^t\end{array}\right],ℂ=\left[{\text{C}}_1\dots {\text{C}}_N\right]$$ (2.4)

The functional in Equation 2.1 was minimized using a nonlinear conjugate gradient method.⁸ The l₁ norm term (second term on the left-hand side) maximizes the sparsity in the transform domain, W_F/PCA is the sparsifying transform (temporal FT in the first stage and PCA in the second stage of CS reconstruction), the l₂ norm (first term on the left-hand side) ensures data fidelity between the estimated image and the acquired data, and λ_F/PCA is the regularization parameter whose value controls the balance between image sparsity and image fidelity.

The CS reconstruction was performed off-line using in-house developed software developed in MATLAB (version R2018b. The MathWorks Inc., Natick, MA) running on Mac OSX (version 10.14.5 Apple Inc., Cupertino, CA). Using a computer equipped with Intel Core i5 CPU at 3.5 GHz with 16 GB global memory, the total computational time was ~30 min for each series.

2.2.3 |. Optimization

The regularization parameters λ and the number of iterations for the temporal FT and for the temporal PCA of the CS reconstruction were optimized independently for the flow phantom data and for the muscle data. The acquired undersampled images were used for phantom optimization, while simulated undersampled images were used in the muscle data optimization. The latter choice was based on the fact that comparing the reference to the acquired undersampled images may be biased by small differences in the contraction patterns in 2 separate acquisitions. Optimization was performed to minimize the root mean square error (RMSE) in velocity estimated from the difference between the velocity from the full k-space and from the undersampled k-space data. For the phantom, the velocity was estimated in the 3 flow tubes while for the muscle data, the velocity was estimated in a region of interest (ROI) (20 pixels × 7 pixels = 23 mm × 8 mm) placed in the MG. The optimization was performed for each CS acceleration factor stepping through a grid of values for λ and the number of iterations in the range shown in Equation 3:

$$\begin{gathered} {\lambda }_{\mathcal{F}}=[0.01,0.10],{\Delta }_{\lambda }=5\times {10}^{-3} \\ {\mathcal{F}}_{\text{ite}}=[10;30],{\Delta }_{\text{ite}}=5{\lambda }_{\mathcal{P}\mathcal{C}\mathcal{A}}=[0,0.10],{\Delta }_{\lambda }=5\times {10}^{-3} \\ \mathcal{P}\mathcal{C}{\mathcal{A}}_{\text{ite}}=[10;30],{\Delta }_{\text{ite}}=5. \end{gathered}$$ (3)

2.3 |. Static and flow phantom

Three tubes (diameter of 1 cm) with constant flow were wound around a static water phantom such that the flow in the tubes was perpendicular to the image plane and opposite to each other (Supporting Information Figure S1A–D, which is available online). Axial slices were acquired ensuring that the flow through the tubes was orthogonal to the plane of the image. The static/flow phantom was imaged with the full k-space acquisition and with the undersampled acquisitions (8 different combinations of CS acceleration factors and vps). Three different in-flow velocities were set for the phantom: 2.5, 5, and 7.5 cm/s and verified using the flowmeter 1G08 R3 (Cole-Parmer, Vernon Hills, IL), resulting in 6 different (3 velocity magnitudes × 2 opposite directions = 6) flow velocities available for measurements using VE-PC images.

2.4 |. In vivo human subject imaging

Eleven subjects (5 male / 6 female) were included in this study after written informed consent had been obtained. The criterion for inclusion was that subjects should be moderately active and those with any surgical procedures performed on the lower leg were excluded. All subjects were normal, healthy volunteers. The study was carried out under the approval of the Medical Research Ethics Board of University of California, San Diego, and conformed to all standards for the use of human subjects in research as outlined in the Declaration of Helsinki on the use of human subjects in research.

MRI was performed on a 1.5T Signa HD16 MR scanner (GE Medical Systems, Milwaukee, WI), with the subject lying supine, feet first, with the right leg (i.e., the dominant leg to be imaged) resting against a foot pedal.¹⁶ An optical fiber pressure transducer was glued to the foot pedal placed inside 8-channel radiofrequency coil. Pressure exerted against the foot pedal during isometric contraction was detected by the transducer, converted to a voltage by a spectrometer (Fiberscan, Luna Innovations, Roanoke, VA), and used to trigger the MR image acquisition using in-house built software developed in LabView (version 14.0.1.4008. National Instruments Inc, Austin, TX). For data analysis, the voltage output from the pressure transducer was later converted into units of force (Newtons) based on a calibration of the system using disc weights. Images were acquired during submaximal, isometric contraction at 35% of the individual MVC. The MR image acquisition was completed in approximately 53 cycles for the full k-space acquisition and the number of cycles ranged from 44 to 13 cycles for the accelerated scans; thus, it was important to ensure consistency of motion. This was ensured by providing the subject with real-time visual feedback of the actual force generated by the subject superposed on the target force curve to facilitate consistent contractions.⁷

2.5 |. MRI

The MR images used in this report included a localizer scan to identify the oblique sagittal orientation that best depicted the fascicles in the MG. The acquisition parameters for the reference full k-space VE-PC acquisition was: echo time, 7.7 ms; repetition time, 17.8 ms; averages, 2; flip angle, 20°; slice thickness, 5 mm; field of view, 30 cm × 22.5 cm (partial phase field of view, 0.55); 256 × 192 matrix (lower resolution in the phase direction); 4 vps; 1 slice; 17 temporal frames (with view sharing factor = 2); 10 cm/s 3-directional VENC. This resulted in 53 repetitions [(192 (PE) × 2 (averages) × 0.55 (phase field of view))/4 (vps) = 53] for each slice acquisition. The temporal resolution is calculated as: 17.8 (repetition time) × 4 (vps) × 4 (VENC directions)/2 (view sharing) = 142 ms. Seventeen temporal frames were collected within each isometric contraction-relaxation cycle of ~2.4 s (17 × 142 ms = 2.4 s). It should be noted that, in the reference sequence, the actual acquired number of temporal frames is only 8 with an acquired temporal resolution of 285 ms. For all the undersampled sequences, the geometry parameters were the same as in the original sequence, while the number of phase encode steps was decreased by the CS acceleration factors between 2 and 4 while varying vps between 2 and 4 as well. It should be noted that a vps of 2 in the CS acquisitions increased the acquired temporal resolution by a factor of 2 compared with full k-space acquisition (4 vps). The maximum CS-factor achievable was determined from a simulation of a full k-space data of muscle contraction.

Flow phantom acquisition parameters were same as for the human scans with the only difference being that the cycle length was 2 s resulting in 14 temporal frames.

2.6 |. Image and statistical analysis

Phase images were corrected for phase shading (mean background phase error) and denoised with a 2D anisotropic diffusion filter¹⁷ to yield the velocity images. Phase shading was estimated by averaging all of the dynamic images in the cine sequence. This was based on the assumption that the net change in position (and, therefore, net velocity) over the isometric contraction-relaxation cycle was zero. The average image was subtracted from the phase image at each temporal frame.

The (2 × 2) SR tensor was calculated from the spatial gradient of the velocity images and then diagonalized to obtain the eigenvalues and eigenvectors.^6,7 Eigenvalues (SR_fiber, SR_in-plane) were sorted on a voxel basis. SR_fiber denotes deformation approximately along the muscle fiber long axis and is negative during muscle fiber shortening (contraction during phases 1–8 of reference VE-PC sequence) and positive during relaxation (phases 9–17 of reference VE-PC sequence). SR_in-plane denotes deformation in the muscle fiber cross-section and is positive during muscle fiber shortening and negative during relaxation.

ROIs were placed in the anterior and posterior tubes of the flow phantom were used to measure the velocity in the tubes for a range of flow in the phantom. Bland-Altman plots were used to analyze the velocities from the acquisitions with different vps/CS combinations using the flowmeter velocity values as the reference. In vivo velocity and SR data were extracted and analyzed for the ROI [20 px × 7 px = 23 mm × 8 mm] placed in the MG. To ensure that the same anatomic region was sampled, each pixel in the ROI placed in the first temporal frame was tracked (with respect to the first frame) to locate the new pixel positions in successive frames, creating a frame-based ROI. Tracking was performed in 2D using the in-plane velocity information. The position in a subsequent frame was calculated based on the velocity information in the current frame. This allowed automated placement of an ROI in each frame that moved synchronously with the underlying anatomy. ROIs changed both location and shape (5 to 20% in successive frames) but the number of points was kept constant to ensure average values were based on the same number of points/frame. Bland-Altman analysis was performed on SR data comparing that derived from reference full k-space values to that obtained from undersampled sequences.

3 |. RESULTS

Supporting Information Figure S2 shows, for 1 example subject, the average of the force measured in a full reference acquisition and for the undersampled acquisition (vps/CS: 4/4) over the contraction cycle. The upper and lower bound curves were generated by plotting points at mean ± standard deviation (SD) at each sampled point of the force output. While the range of upper and lower bound of the force during the contractions was not significantly different between the undersampled and full k-space, the full width half maximum of the mean force is lower for the undersampled acquisition. Supporting Information Figure S3 shows an example velocity (phase) image from an undersampled acquisition (vps/CS: 2/4) and the denoised image after application of the 2D anisotropic diffusion filter. The reduction in velocity (phase) noise is visually evident in the denoised image. Supporting Information Figure S4 shows the efficacy of the phase correction using the temporally averaged phase map on select frames of the dynamic cycle: the corrected frames show that the first and last frames are close to zero velocity (small discrepancies in the first and last frame arise from the fact the first frame is shifted compared with the start of the acquisition).

Two sparsifying transforms were used in the current study to improve image quality in the reconstructed images. The fully sampled dynamic magnitude data were undersampled in the k_y-t plane to compare the sparsity provided by the temporal FT and temporal PCA transforms. Figure 4 shows the images after the temporal FT and after the temporal PCA transform, respectively, and these images illustrate the higher sparsity of the PCA transform. This is seen by the smaller number of images with nonzero coefficients in the PCA transform compared with the images in the FT transform.

FIGURE 4.

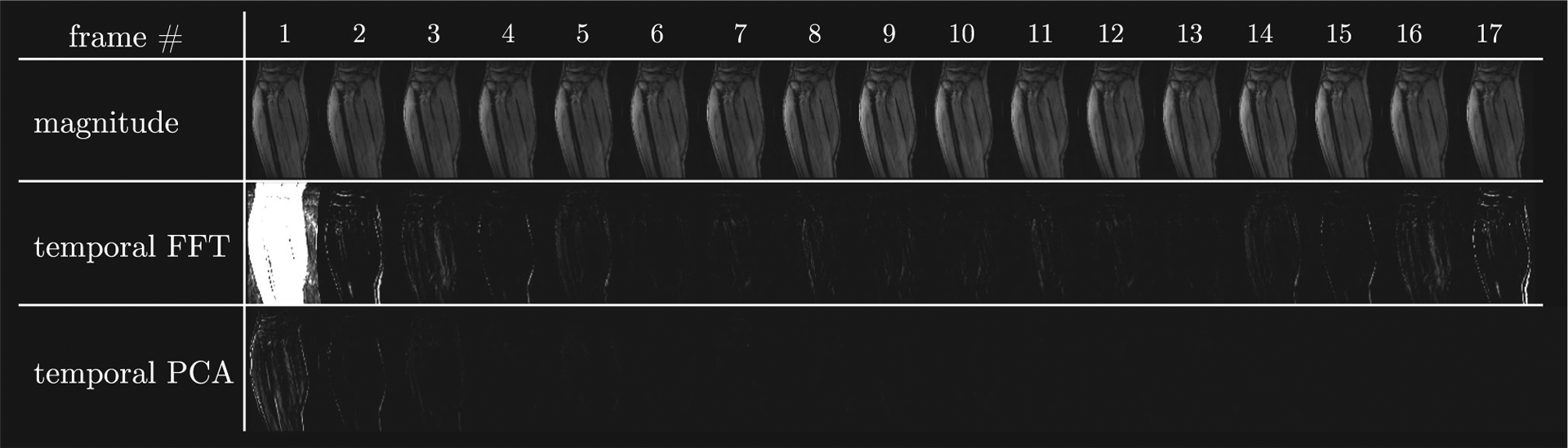
Top row, Magnitude images from a dynamic muscle scan based on the VE-PC sequence. Images after performing a temporal FT transform (middle row) and a temporal PCA (bottom row) on the magnitude images. The sparser transform will have fewer images with large coefficients; temporal FT has fewer nonzero images than temporal PCA. Middle (temporal FFT) and bottom (temporal PCA) have same intensity windowing

The results of the optimization of the regularization, λ_F and λ_PCA, and iteration parameters for each stage using the phantom image data are shown in Supporting Information Figures S1E, S1F. Supporting Information Figure S1E shows the optimization results for velocity estimated in the anterior tubes, while Supporting Information Figure S1F is the corresponding result for the tubes placed posteriorly. The RMSE in velocities (as a function of time in the dynamic cycle) measured in the constant flow phantom between reference full k-space and undersampled k-space was used as the metric for optimizing weights. The optimization was performed using undersampled data acquired with CS-factor of 4, and vps of 2. The plots are shown close to the minimum RMSE values because the total number of combinations of the parameters was large (503 combinations). At the optimal setting, the lowest values of 0.4% was seen for the anterior tubes and ~0.1% for the posterior tubes confirming that the CS reconstruction was able to accurately reproduce velocities. The combination of values that minimized the RMSE was chosen as optimal and used for the rest of the phantom CS reconstructions. Supporting Information Figure S5 is the Bland-Altman plot of the velocities from the full k-space acquisition and from undersampled acquisitions using 8 combinations of CS accelerations and vps factors with the flowmeter values as the reference velocities. The agreement is high with the mean of the differences close to zero or with a small underestimation of 0.1 cm/s for the different undersampled acquisitions compared with the flowmeter values. The 95% confidence intervals across the different vps/CS combinations range from ±0.25 cm/s to ±0.4 cm/s. Notably, the mean difference of the velocities is dependent on the mean velocity; this dependency was attributed to the errors in the reference flowmeter velocity that increased with velocity. However, the % difference between reference flowmeter and undersampled velocities was less than 2% for any of the vps/CS combinations.

The optimization for the muscle data for the CS factor of 4 is shown in Figure 5. The root-mean-square velocity at the peak of the contraction (in the large ROI placed in the MG) was used in calculating the RMSE for the optimization. Supporting Information Table S1 lists the regularization/iteration parameters for both steps of the reconstruction algorithm. The value of (λ_F/PCA) and number of iterations decreased with the decrease in acceleration factors. Once the optimization was performed on 1 subject’s muscle data, these parameters are used for the CS reconstruction of all in vivo data; the optimal parameters corresponding to each CS acceleration was chosen from Supporting Information Table S1.

FIGURE 5.

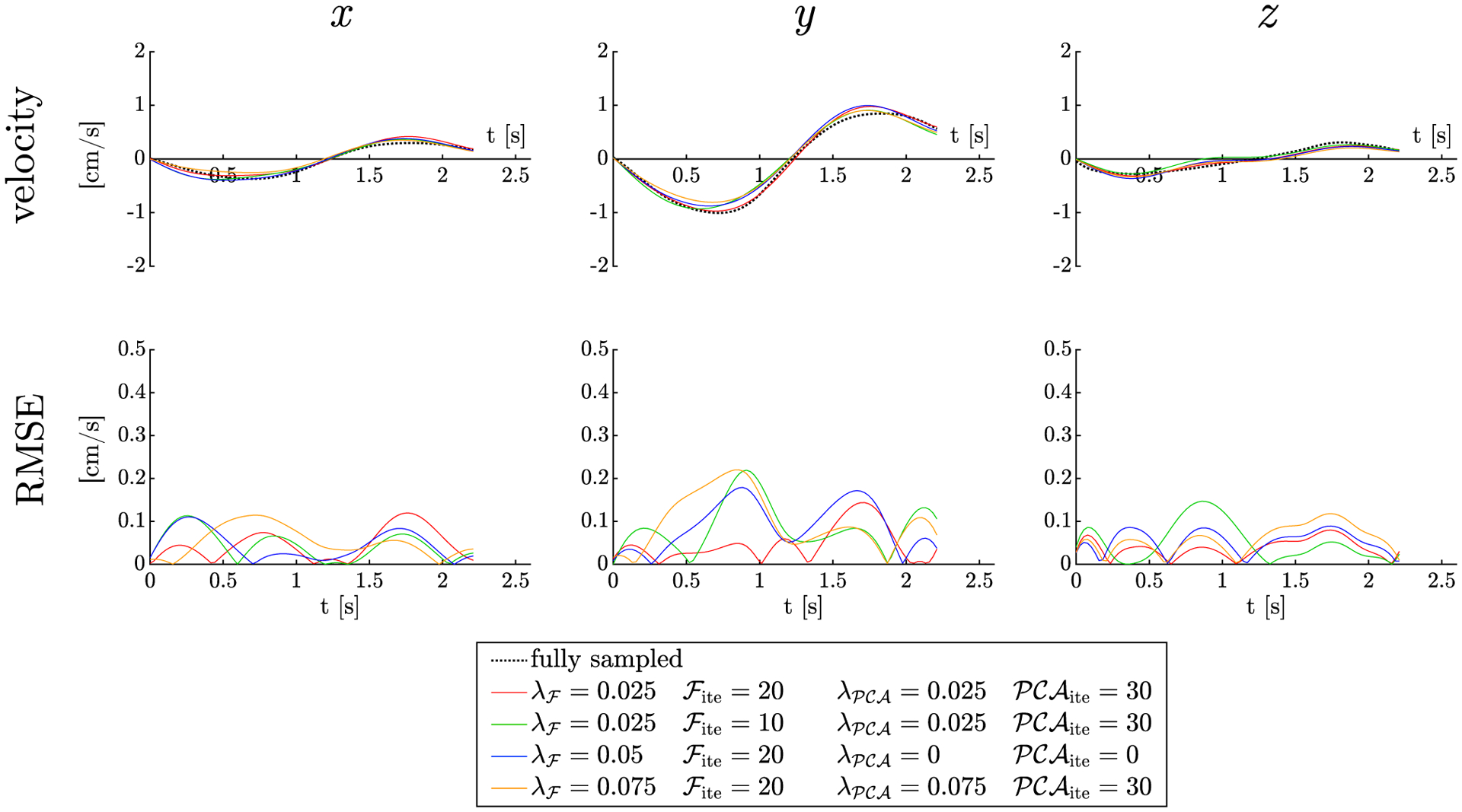
Optimization of the CS parameters in human subject: regularization factors and number of iterations for the ROI in MG muscle of the fully sampled data multiplied by the factor 4 undersampling mask. Each column represents each of the 3 orthogonal directions: x, y (in-plane), and z (out of plane). The plots of the velocities (top row) are shown as a function of time for different combinations of the regularization parameters and number of iterations. Bottom row is the RMSE for each of the velocities as a function of time. Plots with few best combinations only are shown here, but the algorithm stepped over the entire range of values (in main manuscript) to identify the best combination 20 and 30 iterations for temporal Fourier and temporal PCA, respectively, and regularization parameter λ = 0.025 for both

Figure 6 compares the phantom (static and flow) images acquired with the full k-space, simulated, and actual undersampled data acquired with CS-factor of 4 at select temporal frames. In the undersampled images, the static phantom is mapped correctly to values close to zero velocity (green shade in the color map), while flow out of the imaging plane is in red shade and into the imaging plane is in blue shade. The visual similarity of the fully sampled and undersampled velocity images is clearly evident. This is also confirmed by the RMSE map of the fully sampled and acquired undersampled images shown in the last row. The flow phantoms are not visible on the RMSE maps (showing very close agreement between the velocities from full k-space and undersampled k-space), and there is only the background static phantom with very small RMSE errors.

FIGURE 6.

Velocity images of the phantom at 5 temporal frames: static phantom is the large central object is green, while the anterior tubes (red) have water flowing perpendicular to and out of the imaging plane while the posterior tubes (blue) have water flowing perpendicular to and into the imaging plane. The first row (fully sampled) velocity data closely match (visual inspection) the simulated undersapmpled (second row) and the acquired undersampled (third row) velocity data. Quantitative comparison is provided in the RMSE maps of the difference in velocities of images in the first and third rows is shown in the last row of images. Values very close to zero are obtained for the velocity difference image between full k-space and the acquired undersampled (CS-factor = 4) data. Note, dark regions observed in the phantom colormap are locations with zero phase

Supporting Information Figure S6 shows simulated muscle data from random undersampling (CS-factors of 4 and 6) and the resultant magnitude images after CS reconstruction. The presence of artifacts at CS-factor of 6 is visually evident. Color-coded muscle velocity images of the fully sampled and the acquired undersampled images are shown in Figure 7 as a function of the isometric contraction cycle for 17 temporal frames. These are oblique sagittal images positioned to obtain the fibers of the MG in the plane of the image. The 2-stage CS reconstruction using the optimized parameters based on muscle velocity images resulted in undersampled images that were visually close to the images reconstructed from fully sampled k-space data. The spatial and temporal patterns of velocity are very similar for the full k-space and the undersampled acquisitions. The velocity in the image y-axis is the highest as this corresponds to the superior-inferior direction and the lowest velocity is in the z-direction, which maps the out-of-plane motion. The blue shades are negative velocities around the peak of the isometric contraction (temporal frames 4 to 8), and the red shades are positive velocities at the peak of the relaxation (temporal frames 12 to 16).

FIGURE 7.

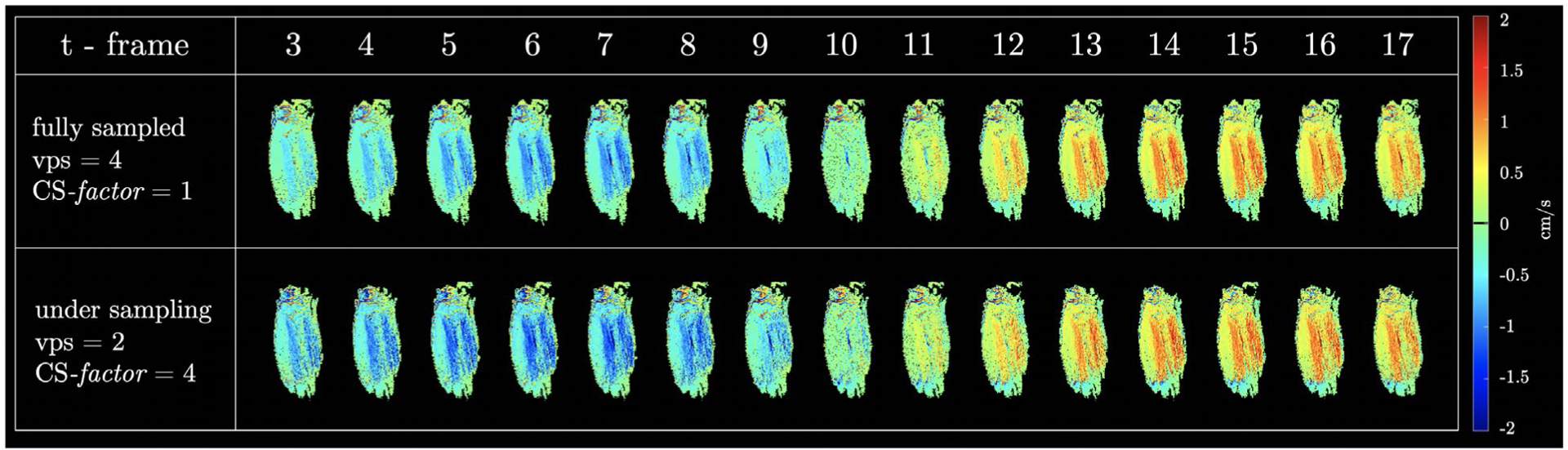
Velocity colormaps for the direction of maximum velocity in the oblique sagittal section through the calf muscles oriented to image the MG muscles in-plane of the image; images are shown at selected temporal locations through the contraction cycle. The fully sampled data is shown here (top section) followed by undersampled (by a factor of 4) reconstructed using the parameters obtained through the optimization process

Figure 8 is a plot of the v_y velocity component (averaged over the 11 subjects) as a function of the dynamic cycle measured in ROIs placed in the MG extracted from the full k-space as well as from the undersampled k-space with the different CS and vps factors. The good agreement between the v_y values from the reference and undersampled acquisitions is confirmed by the overlay of the mean v_y from full k-space on the v_y ± σ (average over 11 subjects) from the undersampled acquisitions.

FIGURE 8.

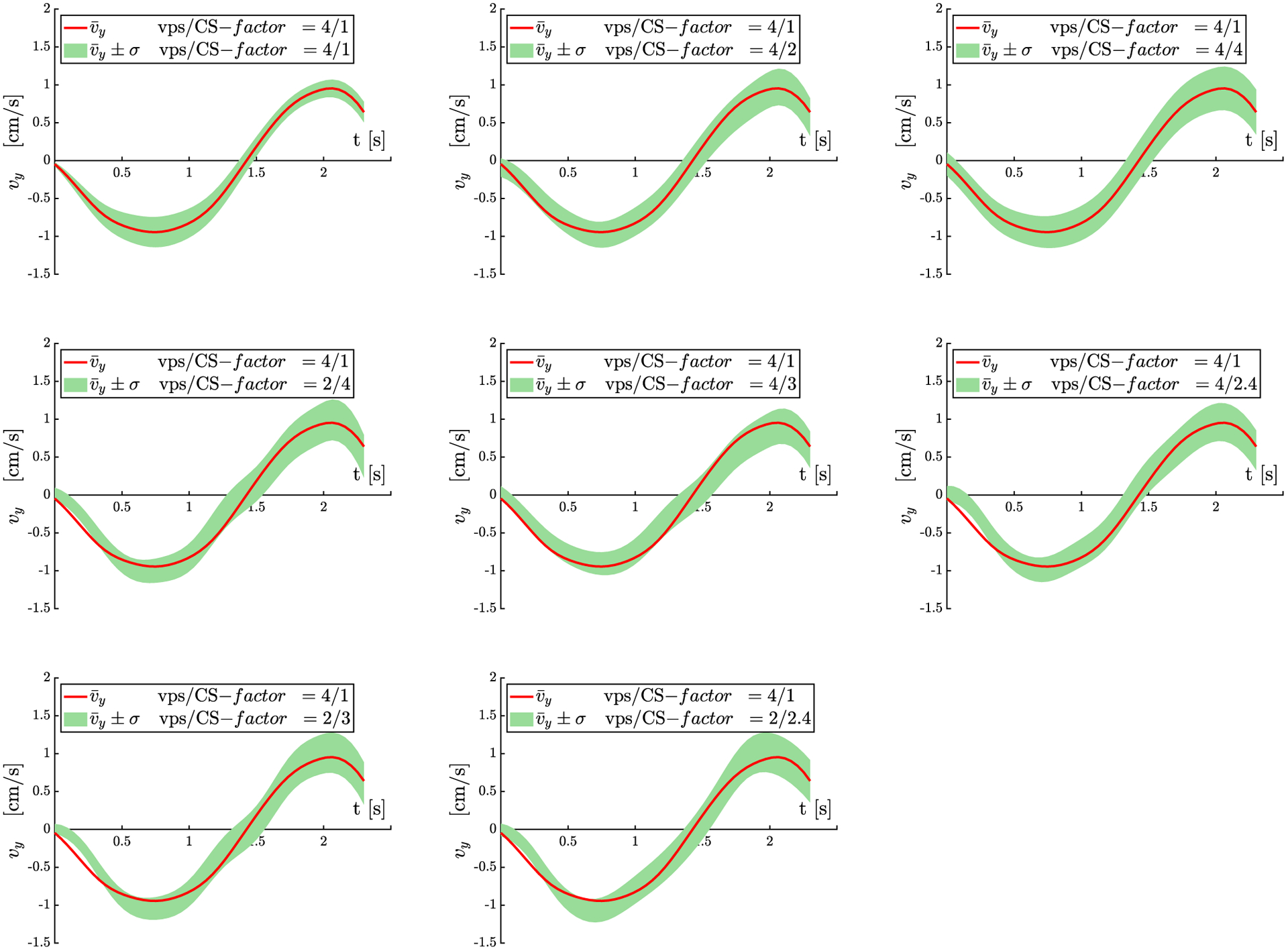
Superior-inferior velocity (v_y) plots as a function of the isometric contraction cycle for scans acquired with 8 different vps/CS-factors. Only the largest component of the velocity, v_y along the longitudinal axes of the muscle is shown here. The values shown here are the mean over the 11 subjects, the green shaded region reflects mean ± σ (SD) for each acquisition. The red line is the mean value (average of subjects) for the full k-space acquisition. This red line from the reference data is superposed on the shaded velocity regions for each CS-factor/vps combination as a visual guide to the overlap of the undersampled and full reference velocity values. Velocity values and temporal patterns closely track each other for all the combinations of vps and CS-factors

One of the goals of velocity mapping is to derive the strain or SR tensor to study muscle kinematics. It is important to note that both strain and SR are sensitive to noise as spatial gradients are calculated from the velocity or displacement maps to extract strain/SR; the use of the anisotropic diffusion filter to denoise was critical to the calculation of the SR maps (Supporting Information Figure S3). Figure 9 shows SR images (absolute values at the peak value in the contraction phase) calculated from the velocity maps acquired with different combinations of CS and vps factors; SR image quality is maintained at the highest acceleration factors. Bland-Altman plots (Figure 10) and the indices extracted from these plots (Supporting Information Table S2) show good agreement between the full k-space acquisition and the subsampled acquisitions (average of mean differences ranges from 0.5% to 6.7% across the vps/ CS combinations). The small mean differences confirm that the bias in the subsampled data compared with the full k-space data is small. The normalized coefficient of repeatability was ~24% for the CS = 4 undersampling.

FIGURE 9.

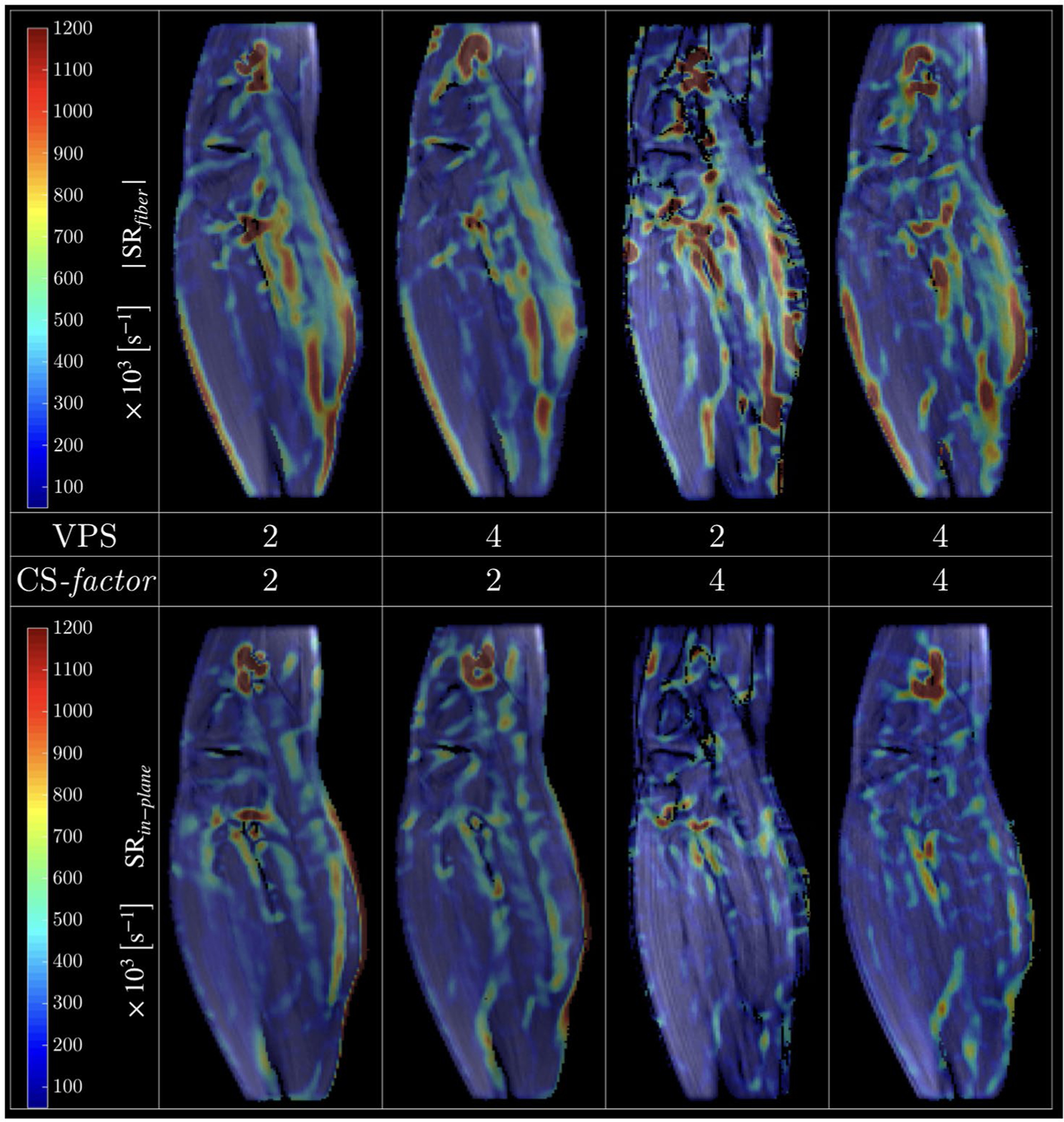
Absolute value SR tensor eigenvalue colormaps derived from velocity images for 4 different combinations of vps/CS-factor. The SR_fiber (negative) and SR_in-plane (positive) correspond to the SR maps along and perpendicular to the fiber direction, respectively; shown here is 1 temporal frame at the peak of the contraction phase for each CS scheme. The overall similarity of the colormaps as well as good image quality is evident for all the CS schemes. The colormaps will not be identical as each map is derived from a different acquisition and physiological/technical variabilities limit the exact reproducibility

FIGURE 10.

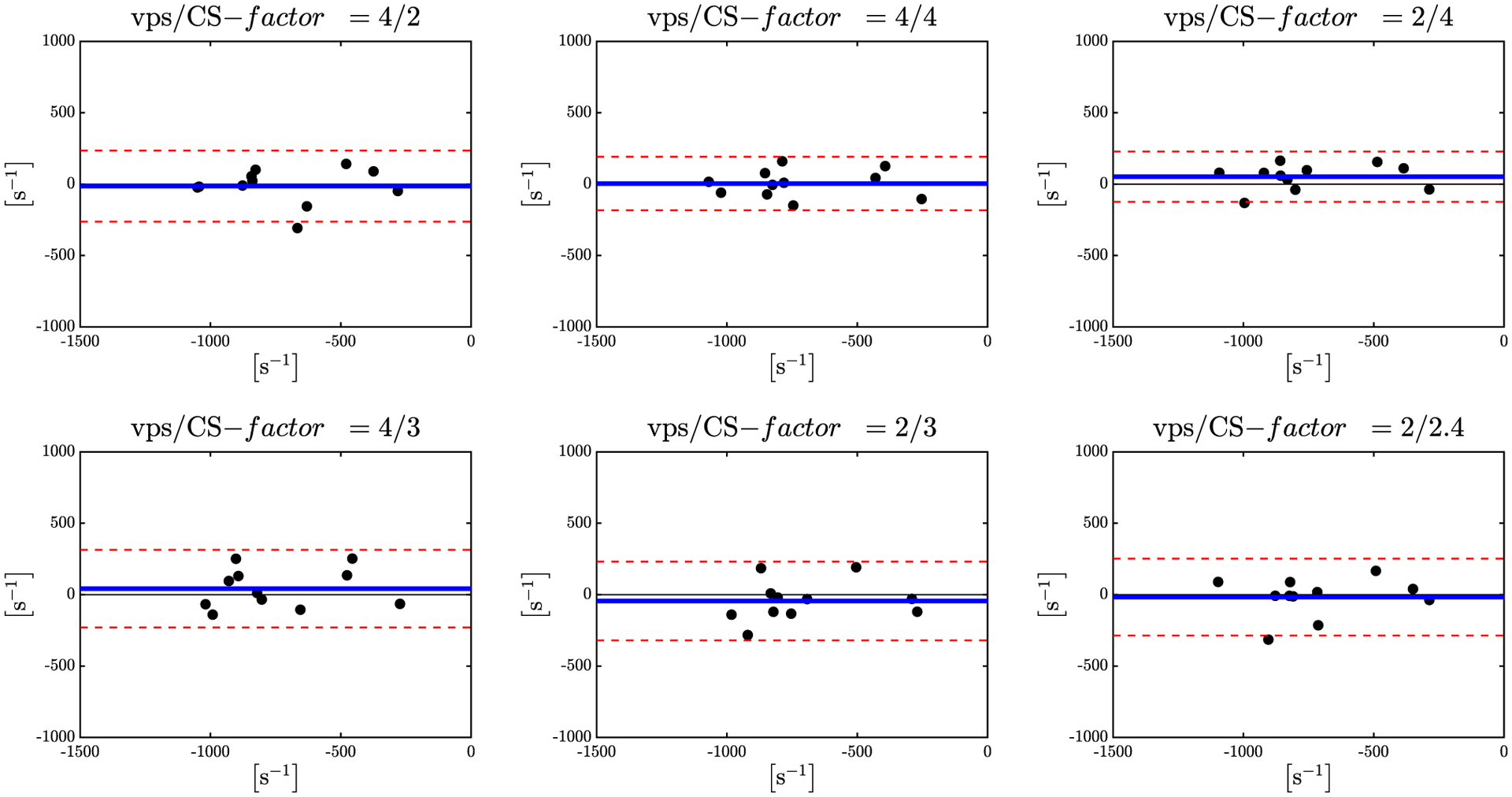
Bland-Altman plots for the peak SR_fiber values during the contraction part of the cycle for 6 different combinations of vps/CS-factor. Mean value between fully sampled and undersampled data is shown in blue, the 95% confidence intervals are shown in dotted red lines

4 |. DISCUSSION

CS has been integrated in VE-PC sequences^9,10 and applied to measuring flow in the cardiovascular system and offers a range of acceleration factors. One of the first report in combining CS with multicoil acquisition in a VE-PC sequence was the k_y-t SPARSE SENSE approach.^9,10 They used a 2-stage CS scheme with a temporal FT as the sparsifying transform for the first stage and a temporal PCA for the sparsifying transform for the second stage. A recent study reported a CS accelerated 4D (3-directional spatial with 3-directional VENC) phase contrast MRI using random undersampling patterns in the k_y-k_z plane.¹¹ The latter work reported acceleration factors of ~×6.4 without loss of accuracy in velocity or in the derived SR maps. 3D acquisition enables higher acceleration factors, but to realize the higher accelerations, it is important to have a large number of slices and this offsets the time gain from the higher acceleration factors. For example, the undersampled 3D VE-PC sequence discussed above reached an acceleration factor of ~×6.4 for a 32-slice acquisition (scan time, 2 min 46 s).¹¹ The undersampled 2D VE-PC sequence presented in the current study has an acceleration factor of 4 and is completed in 40 s.

The current work extends the k_y-t SPARSE SENSE method to 3-directional VE acquisition applied to the study of muscle kinematics (velocity and SR mapping) during isometric contraction to achieve scan times less than a minute. It should be noted that, for the current study, the imaging plane was chosen such that the MG fibers were in the imaging plane. This ensured that the velocity perpendicular to the slice was close to zero, and it should thus be possible to obtain the velocity information with 2-directional VENC. However, a 3-directional VENC was implemented as it is not always possible to choose the slice orientation to be in the plane of the muscle fibers. The goal of the undersampled VE-PC reported here is to enable the sequential acquisition of 3–5 slices to extract the full 3 × 3 strain/SR tensor. The reduction in scan time per slice will translate in the ability to image several slices.

The original studies that proposed PCA as the single sparsifying transform required training data.^18–20 Subsequently, a bootstrapping method was proposed that self-calibrated the PCA without the use of training data. This 2-step bootstrap reconstruction method using temporal FFT followed by temporal PCA was initially proposed by Jung and Ye¹⁴ and then applied for reconstructing undersampled cardiac T2 mapping²¹ and for cine phase contrast imaging.¹⁰ Comparison of the temporal FT and the temporal PCA in single step sparsifying transforms showed that temporal PCA was superior.^10,21 Furthermore, Feng et al²¹ reported that their preliminary results showed that the 2-step method was better than the direct PCA approach. This was attributed to the fact that an accurate PCA basis cannot be directly estimated because a set of low frequency k-space frequencies was not fully sampled.^10,21 Based on the results of these earlier studies, the current study implemented the 2-step reconstruction using the temporal FFT as the first step sparsifying transform and the temporal PCA as the second sparsifying transform.

Optimization of the regularization parameter and number of iterations for each step was performed using acquired undersampled data for the phantom, whereas the optimization for the human subject data was performed on simulated undersampled data from a full k-space acquisition. The approach for the human data was based on the fact that physiological variations in repeat dynamic studies of muscle contraction would influence the repeatability, and this would have biased the optimization. In the phantom, the minimum RMSE in velocity with the full k-space as the reference for the optimum values of the regularization parameters was less than 0.5%, whereas the corresponding minimum RMSE (averaged over the cycle) for v_y (velocity along the longitudinal muscle axis) from muscle data was around 5%. A comprehensive search of a matrix of combinations of λ_F, λ_PCA, and the corresponding number of iterations in each step was performed. The value of λ_PCA for optimizing the flow in the femoral artery^9,10 was 0.01 for a CS-factor of 6.3, while in the current study, for the flow phantom, it is 0.075 and for the in vivo muscle velocities, 0.025 for a CS-factor of 4. Furthermore, the regularization parameters changed with the acceleration factor. The optimization results emphasize the need for optimization for datasets with different velocities, background signals, and CS-factors.

The velocities derived from the VE-PC images of the flow phantom for the reference acquisition and for the different combinations of CS and vps were very well correlated with velocities measured by the flowmeter. This is also confirmed in the phantom images where the RMSE images obtained from the reference (full k-space) and undersampled acquired data (CS-factor = 4) show that the velocities in the undersampled images are accurately reconstructed (no difference in the velocities estimated by the 2 methods).

The average force curves at the MVC used in the current study (35% MVC) showed that the SD of the force (measure of the consistency of contractions) is comparable for the fully sampled k-space and the undersampled acquisition. It is highly likely though that differences in the SD of the force will be more pronounced at higher %MVCs, for the elderly and for subjects with compromise in muscle function; in all these cases, it will be harder to maintain consistency for larger repetitions. Visually good agreement of the muscle velocity images acquired with the full k-space and the undersampled k-space data (CS-factor = 4) confirm that the proposed 2-stage CS reconstruction accurately reproduces velocities without visual artifacts for in vivo undersampled data acquired in 40 s (compared with 2 min 40 s for the full k-space acquisition). A plot of the velocities, averaged over the 11 subjects shows good agreement with the reference velocities. However, a slightly larger variance in velocity is seen at the higher CS-factors (e.g., CS-factor = 4, vps = 4) presumably from the lower signal-to-noise ratio of the phase maps of the undersampled images. The effect of temporal sampling and CS reconstruction on smoothing peak velocities merits discussion. In the reference scan with a vps = 4, smoothing occurs due to the lower number of temporal frames that are collected (8 frames).

On the other hand, the undersampled data with vps = 2 has twice the temporal resolution, but the joint CS reconstruction along the temporal frames introduces smoothing of peak velocities¹⁰; the amount of smoothing will depend on the acceleration factor. However, the undersampled data with vps = 4 will have smoothing artifacts from both low temporal resolution as well as from the CS reconstruction. So, when comparing undersampled vps = 2 acquisitions with that of the reference scan (vps = 4), comparable extent of smoothing in the peak velocities is anticipated. However, it should be noted that the velocity peaks during the isometric contraction are not that sharp and have full width half maximum of ~700 ms (vps = 4/2 have a temporal resolution of 285 ms/142 ms), which may not result in significant smoothing of velocity peaks for any of the CS-factor/vps combinations tested here. Furthermore, in an earlier study, the reference full k-space data have been validated using a flow phantom with pulsatile flow profile similar to in vivo muscle motion.¹⁶

SR maps are particularly sensitive to noise in the original phase maps (i.e., the velocity maps). A good test of the quality (signal-to-noise ratio) of the undersampled VE-PC data is to assess the image quality of the SR maps generated from the undersampled velocity images. The quality of the SR maps generated from data acquired with different CS/vps factors confirms that image quality is good (in terms of signal-to-noise ratio as well as absence of artifacts) as the CS-factor changes from low to high acceleration factors. The Bland-Altman plots of reference SR values and undersampled SR values had good agreement and no bias for all combinations but the lowest confidence intervals were seen for the vps/CS-factor of 2/4 followed by the combination of 4/4. The 2/4 combination offers an increase in temporal resolution by a factor of 2 over the reference sequence and time savings factor of 2, while the 4/4 results in a time savings of 4. The normalized coefficient of repeatability is around 24% for the CS = 4 undersampled data, which is high and may arise from 2 other sources besides the differences between the full k-space and the undersampled acquisitions: higher noise in computed SR maps compared with velocity maps as well as the physiological variability in 2 separate acquisitions.

The choice of either sequence (vps: CS-factor of 2:4 or 4:4) will depend on the application. Increased temporal resolution VE-PC sequences will find application in monitoring blood flow and cardiac motion where rapid changes are anticipated at the systolic phase.^9,10 In studying skeletal muscle dynamics, a high temporal resolution VE-PC sequence may be useful to monitor muscle motion under nerve simulation where the initial rise of muscle strain is steep.¹² High temporal resolution may also be used to track the correlation of the force curve in submaximal voluntary contractions to the strain curve; strain appears to diminish more slowly than the force and the force-strain temporal correlation patterns may be used to explore myotonic disorders that are associated with delayed relaxation.¹² Considering a decrease in total scan time, applications can extend to study cohorts (e.g., in muscular dystrophies¹²) who cannot perform a large number of repeated contractions as well as increase the range of %MVCs.

To compare the maximum CS-factors achieved in the current study versus in earlier studies using the k_y-t SPARSE SENSE approach,^9,10 it is important to note the number of PE lines in the reference full k-space as well as the number of multicoils; both of these have an impact on the maximum CS achievable. Kim et al¹⁰ reported on undersampled VE-PC studies for flow imaging that achieved a CS-factor of 6.3 starting with the full k-space PE lines of 192 (~30 undersampled lines) and a 32-channel coil. Otazo et al⁹ achieved a CS-factor of 8 starting with the full k-space PE lines of 192 (~24 undersampled lines) and a 12-channel coil. In the current study, a 8-channel coil starting with a full k-space lines of 106 was used resulting in ~26 undersampled lines. The number of undersampled lines between the current and earlier studies is comparable, while the number of channels in the multicoil was the lowest in the current study.

There are several limitations to the study. The validation with the phantom experiments occurred with constant flow, in contrast to the in vivo situation in which a dynamically changing velocity profile in skeletal muscle was imaged. A 2D VE-PC sequence as proposed here is appropriate for certain muscles in which the imaging plane can be selected such that muscle fibers run in the imaging plane; this is possible for the MG, which is the focus of this study. If it is possible to select this orientation, a single slice at an orientation of the muscle fibers is sufficient because the deformation and strain in the direction orthogonal to the muscle fibers has been shown to be very small to zero from 3D strain measurements.^1,11

However, it is important to be able to extend the technique to monitor other muscles that have complex fiber trajectories. Future studies will explore CS methods for 4D VE-PC imaging to achieve under a minute scan time for 3D imaging as well. Recent innovations such as including random undersampling in the VENC directions termed multidimensional flow-preserving compressed sensing (MuFloCoS)²² may help achieve the high acceleration factors required to obtain 3D imaging with 3-directional VENC in acquisitions times of under a minute. Another limitation is that validation (for muscle data) using the velocities from the undersampled data compared with the reference data is difficult using acquired data, because the reproducibility of velocities acquired in separate dynamic scans will be limited by the subject’s ability to reproduce the same force patterns in the reference and in the undersampled patterns. Inclusion of a deformable phantom mimicking tissue deformation may help to accurately validate the undersampled acquisitions using the fully sampled acquisition as a reference.

In conclusion, this is a report of implementing a CS method for 2D VE-PC for monitoring muscle motion during contraction paradigms. CS reconstructions provided artifact-free images as well as accurate velocity values in phantoms and in in vivo human muscle during isometric contractions for acceleration factors up to 4 resulting in scan times of 40 s. This decrease in scan time extends the applicability of the technique to study muscle kinematics at higher %MVC and in cohorts such as aging, sarcopenic, or dystrophic subjects.

Supplementary Material

Supplementary Material ALL

FIGURE S1 Schematic of the constant flow phantom used to validate velocities calculated from the CS reconstructed images (A–D). Water flow directions are denoted by red and blue arrows for in and out of imaging plane directions respectively. Velocity measurements were performed in the axial orientation (D). Optimization of the CS parameters: regularization factor and number of iterations was performed on the phantom data. %_v, the % difference between velocity from CS reconstruction and the full k-space velocity was the objective function that was minimized. The plots of %_v are shows as a function of the dynamic frames for different combinations of the regularization parameters and number of iterations. Optimization plot (E) for flow in the anterior tubes (flow perpendicular and out the image plane) and (F) is a similar plot for flow in the posterior tubes (flow perpendicular and in the image plane). Selected regions of interest for which the velocity values were calculated are shown in blue. Plots with few best combinations only are shown here but the algorithm stepped over the entire range of values (in main manuscript) to identify the best combination

FIGURE S2 Averaged force curve with lower and upper boundary given as mean ± SD for the fully sampled acquisition with 52 contractions cycles (left) and undersampled acquisition with 13 contractions cycles (right)

FIGURE S3 Velocity maps before (A) and after (B) 2D anisotropic diffusion filter was applied for the frame corresponding to the peak of contraction cycle. Image shown on the left was acquired with a vps/CS-factor of 2/4. Parameters of anisotropic diffusion filter: κ = 2, Δ = 1/7 and 10 iterations

FIGURE S4 Selected frames of phase images for the direction of maximum velocity before (top row) and after (bottom row) correction for phase shading artifacts. The phase averaged image shown on the right is subtracted from each frame of the acquired images to generate the corrected images. The averaged image is the estimate for the phase shading

FIGURE S5 Bland-Altman plots for velocity measurements averaged in three regions of interest for the constant flow phantom for six different water flow velocities: −7.5, −5, −2.5, 2.5, 5, 7.5 [cm/s]. Measurements were performed for nine sequences with different combinations of views-per-segment (vps) and undersampling factors (CS-factor), flowmeter measurements are used as reference (model 1GO8 R3 by Cole-Parmer IL, USA). Fully sampled data set is shown in the central plot

FIGURE S6 Magnitude images of four selected time frames. Images reconstructed from the fully-sampled k-space (top row), undersampled with factor 4 (middle row) and undersampled with factor 6 (bottom row)

TABLE S1 Reconstruction parameters obtained for imaging sequences with different undersampling factors

TABLE S2 Parameters obtained from the Bland-Altman plots (Figure 10) of peak strain rates for seven different combinations of views per segment (vps) and undersampling factors (CS-factor). Mean strain rate (mean of reference and undersampled SR values) <SR>, mean of the paired differences: < SR >, % normalized mean of the paired differences: $<\widehat{SR}>\%100<SR>/<SR>$, Coefficient of Repeatability: CR 1/2 (upper 95% CI- lower 95%CI), % normalized $\widehat{CR}:CR\%100CR/\langle SR\rangle$. CI: Confidence Interval. Units of <SR>, <SR>, and CR are in s⁻¹ while the normalized quantities are unitless