Rapid MR relaxometry using deep learning: An overview of current techniques and emerging trends

Abstract

Quantitative mapping of MR tissue parameters such as the spin-lattice relaxation time (T₁), the spin-spin relaxation time (T₂), and the spin-lattice relaxation in the rotating frame (T_1ρ), referred to as MR relaxometry in general, has demonstrated improved assessment in a wide range of clinical applications. Compared with conventional contrast-weighted (eg T₁-, T₂-, or T_1ρ-weighted) MRI, MR relaxometry provides increased sensitivity to pathologies and delivers important information that can be more specific to tissue composition and microenvironment. The rise of deep learning in the past several years has been revolutionizing many aspects of MRI research, including image reconstruction, image analysis, and disease diagnosis and prognosis. Although deep learning has also shown great potential for MR relaxometry and quantitative MRI in general, this research direction has been much less explored to date. The goal of this paper is to discuss the applications of deep learning for rapid MR relaxometry and to review emerging deep-learning-based techniques that can be applied to improve MR relaxometry in terms of imaging speed, image quality, and quantification robustness. The paper is comprised of an introduction and four more sections. Section 2 describes a summary of the imaging models of quantitative MR relaxometry. In Section 3, we review existing “classical” methods for accelerating MR relaxometry, including state-of-the-art spatiotemporal acceleration techniques, model-based reconstruction methods, and efficient parameter generation approaches. Section 4 then presents how deep learning can be used to improve MR relaxometry and how it is linked to conventional techniques. The final section concludes the review by discussing the promise and existing challenges of deep learning for rapid MR relaxometry and potential solutions to address these challenges.

1 |. INTRODUCTION

MRI is a diverse and powerful imaging modality, with a broad range of applications both in clinical diagnosis and in basic scientific research.^1,2 Compared with other cross-sectional imaging modalities such as computed tomography (CT) or positron emission tomography (PET), MRI offers superior soft-tissue characterization and more flexible contrast mechanisms without radiation exposure. These unique advantages of MRI allow acquisitions of functional, hemodynamic, and metabolic information in addition to high-spatial-resolution anatomical images for a comprehensive examination.² However, despite an essential role in routine clinical diagnosis, the day-to-day use of MRI today is substantially limited to the qualitative assessment of contrast-weighted images, which are created based on the variation of underlying MR tissue parameters (eg T₁, T₂) across different types of tissue.³ The changes in these tissue parameters in lesions typically result in hyper-intense or hypo-intense features, thus generating useful information for routine clinical diagnosis.^4,5

MRI also allows quantitative measurements of inherent tissue T₁ and T₂ values, which are referred to as T₁/T₂ MR relaxometry or T₁/T₂ mapping. The estimation of spin-lattice relaxation in the rotating frame (T_1ρ)^6,7 (T_1ρ mapping) is also performed in some applications.⁸ Since the early history of MRI, there has long been an interest in the use of quantitative MR relaxometry to gain deeper insights into the disease environment.^9,10 The increased clinical value of MR relaxometry has been widely documented in diagnosis, stage, evaluation, and monitoring of various human diseases, including neurocognitive disorders,^11–15 neurodegeneration,^16–19 cancer,^20–23 myocardial and cardiovascular abnormalities,^24–27 degenerative musculoskeletal diseases,^28–32 and hepatic and pulmonary diseases.^33,34 Compared with conventional T₁-weighted or T₂-weighted images, MR relaxometry provides increased sensitivity to different diseases that could enable early identification of pathologies.¹⁰ It also delivers information that can be more specific to tissue composition and microenvironment.^10,35–38 Meanwhile, MR relaxometry is also more robust to surface coil effects, which may yield non-uniform signals unrelated to pathology and thus hinder clinical interpretation in conventional qualitative images. However, well known limitations of MR relaxometry include long scan times due to the need for repeated acquisitions with varying sampling parameters, cumbersome post-processing,^39–42 and sensitivity to different system imperfections.^43,44 For example, to estimate the T₂ value of an object, multiple images of the object need to be acquired first with varying T₂-decay contrast (eg different echo times (T_E)) for subsequent T₂ parameter fitting, thus leading to a several-fold increase of scan time compared with conventional T₂-weighted imaging.³⁹ A post-processing step is then performed to fit the acquired image series to a T₂ signal decay model so that corresponding T₂ values in selected regions of interest (ROIs) or a pixel-by-pixel T₂ map can be generated.^39,42 In addition, pre-calibration steps are sometimes needed to ensure that the prescribed imaging protocol (eg the flip angle (FA)) is as expected to ensure accurate and precise parameter generation.^45–47 These challenges and underlying complexity can all lead to the non-reproducible performance of MR relaxometry and can significantly restrict its routine clinical implementation and ultimate clinical translation.^48,49

The past two decades have seen remarkable advances in MR relaxometry in terms of scan times, quality, and robustness.³⁸ In particular, the imaging speed of MRI has been dramatically improved with faster imaging sequences, more efficient sampling trajectories, better gradient systems, and coil arrays with an increased number of elements. In the meantime, there has been an explosive growth of techniques to reconstruct undersampled MR data, from parallel imaging^50–56 to different spatiotemporal (k-t) acceleration techniques (including k-t parallel imaging and constrained k-t reconstruction methods).^57–66 Many of these techniques have been successfully demonstrated for rapid MR relaxometry with improved imaging performance.^67–72 In addition, MR relaxometry model-based reconstruction methods (simply referred to as model-based reconstruction hereafter) have also been proposed to embed corresponding parameter fitting models into iterative reconstruction for direct estimation of MR parameters from acquired k-space.^73–76 This synergistic reconstruction strategy combines traditionally separated imaging and parameter estimation steps into a single joint process, leading to significantly increased imaging efficiency. Moreover, the introduction of MR fingerprinting (MRF)⁷⁷ has further disrupted the way in which traditional MR relaxometry is performed, allowing an efficient generation of multiple MR parameters from a single acquisition. All of these efforts have resulted in improved imaging speed and performance that were previously inaccessible in MR relaxometry, and some of these methods have been extensively optimized and have seen early clinical translation for routine evaluation.

The recent rise of deep learning⁷⁸ has attracted substantial attention in the MRI community and has been revolutionizing many aspects of MRI research, including image reconstruction,^79–83 image analysis and processing,^84–86 and image-based disease diagnosis and prognosis.^86–88 Although the application of deep learning in quantitative MRI has been less explored compared with other techniques, a number of early studies have recently shown its great promise to improve MR relaxometry in terms of speed, efficiency, and quality. The goal of this paper is to discuss the potential application of deep learning for MR relaxometry, to review emerging deep-learning-based techniques that have been developed for MR relaxometry, and to highlight future directions. The remainder of the paper consists of four sections. In Section 2, we summarize and give a brief overview of the imaging models for MR relaxometry. In Section 3, we review current classical accelerated imaging methods for rapid MR relaxometry, and we mainly focus on techniques for reconstructing undersampled MR data towards parameter mapping. These techniques include state-of-the-art k-t acceleration approaches, model-based reconstruction methods, and novel methods for efficient generation of accurate MR parameters. In Section 4, we present how deep learning can be applied to improve rapid MR relaxometry with specific examples and how the use of deep learning is linked to conventional methods. In the last section, we illustrate the advantages and existing challenges of applying deep learning for rapid MR relaxometry, discuss potential solutions to address these challenges, and highlight potential directions to further improve their synergy. For simplicity and a more focused scope, this review paper is focused on the rapid mapping of T₁, T₂, and T_1ρ only (to which MR relaxometry typically refers), but it should be noted that these techniques could also be generalized to the quantification of other MR parameters.

2 |. MR RELAXOMETRY: THE IMAGING MODEL

2.1 |. Data acquisition and image reconstruction

Standard MR relaxometry involves acquisitions of a series of contrast-weighted images on the same object with varying imaging parameters and contrast, followed by fitting the signal evolution of each image pixel (or an ROI) across the dynamic/parameter dimension to a specific MR relaxometry model for generating corresponding parameters of interest. We begin with the MR forward model for acquiring MR data of a 2D + time dynamic image series, which can be written as

$$s\left(k_x,k_y,t\right)=\iint d(x,y,t)e^{-i2\pi \left(k_{x}x+k_{y}y\right)}\mathit{\text{dxdy}}.$$ (1)

Here, d denotes the dynamic image series to be acquired with varying contrast along the parameter dimension (size = n_x × n_y × n_p in the spatial dimension and the parameter dimension). s denotes the corresponding dynamic k-space with the same size. k_x and k_y are the spatial-frequency variables in k-space. x and y represent the coordinates in the image domain, and t represents the dynamic position along the parameter dimension. This signal equation can be extended into 3D by adding extra phase-encoding along the slice or partition dimension. With proper discretization, Equation 1 can be rewritten in matrix notation as

$$s=Fd$$ (2)

where F denotes the fast Fourier transform (FFT) operation to transform dynamic images into dynamic k-space. When the sampling of k-space satisfies the Nyquist rate (ie, the sampling frequency is at least twice the maximal signal frequency that is fulfilled if every k-space location is sampled, also known as full sampling), image reconstruction can be given by simply performing an inverse Fourier transform on acquired k-space under perfect imaging conditions (eg in the absence of B₀/B₁ inhomogeneities):

$$\tilde{d}=F^{\text{H}}s$$ (3)

where $\tilde{d}$ denotes the reconstructed dynamic images that can be later fitted to a signal model (see sections below) for generating quantitative parameters of interest.

Since MR relaxometry typically involves acquisitions of a dynamic image series, it requires much longer scan times compared with conventional qualitative contrast-weighted acquisitions that normally produce static images. As a result, accelerated imaging methods are usually needed to speed up the acquisition of dynamic images for quantitative parameter mapping. While the development of fast imaging sequences and more efficient imaging trajectories have been topics of interest, the imaging speed of MRI is fundamentally restricted by its sequential acquisition nature. As a result, undersampling (by skipping certain k-space measurements) remains a more effective way of accelerating MR data acquisitions. When undersampling is applied, Equation 2 is further extended by incorporating an undersampling operator (Λ) into the encoding operator:

$$s=\Lambda Fd.$$ (4)

Since the Nyquist sampling rate is no longer satisfied in this scenario, more advanced reconstruction algorithms beyond a simple FFT are needed for image reconstruction. These techniques include simple dynamic view-sharing methods,^66,89–91 various parallel imaging,^{50–53,56,92} temporal parallel imaging, and k-t acceleration approaches,^{54,55,57–59,66} and different constrained reconstruction strategies such as compressed sensing^{60–64,93,94} or low-rank-based methods.^65,68,95 Meanwhile, the MRF framework represents another direction of MR relaxometry to generate multiple quantitative parameters simultaneously without the need to reconstruct clean dynamic images.⁷⁷ A review of these classical techniques will be the main focus of discussion in the next section.

2.2 |. MR parameter fitting

Given the reconstructed dynamic image series, generation of MR parameters (MR parameter fitting) can be performed by fitting the image series into a relevant signal model with least-square minimization, which can be described as

$$\tilde{p}=\underset{p}{\text{argmin}}\Vert M(p)-\tilde{d}{\Vert }_2^2$$ (5)

where M and p = [p₁, p₂, …, p_n] represent the selected signal model (eg T₁ recovery or T₂ decay) and the corresponding parameters to be estimated, respectively. The fitting model is highly dependent on the sequence design and the parameters of interest. For example, a multiple-echo sequence (eg a turbo spin echo sequence) or a T₂-prepared sequence with different preparation lengths can be used for T₂ mapping, and an exponential T₂ decay mode can be used.⁹⁶ For T₁ mapping, an inversion recovery-prepared sequence^97–99 or a steady-state gradient echo sequence with variable flip angles (VFA)^100,101 can be used to capture the T₁ recovery rate to generate T₁ values.¹⁰² For T_1ρ mapping, a spin-lock-prepared sequence^103–105 with different preparation lengths is typically implemented to capture the decay rate of locked magnetization in a rotating frame.⁶ Recent studies have also suggested that a model from the Bloch equation can more accurately represent the T₂ signal decay by better accounting for system imperfections.⁴⁴ Moreover, one can also implement a sequence that is sensitive to different tissue parameters simultaneously (see MRF below) and design a multiparametric model based on the Bloch equation.⁷⁷ Discussion on the use of a specific sequence, the selection of models, and their accuracy of different models is beyond the scope of this study. The key point to deliver here is that, no matter which model is used, the fitting process generally follows Equation 5 to generate parameters of interest. This traditional two-step MR parameter mapping framework, including one step to acquire and reconstruct dynamic multi-contrast images and another step for parameter fitting, as shown in Figure 1A, is widely employed in a variety of studies.^67–72

FIGURE 1.

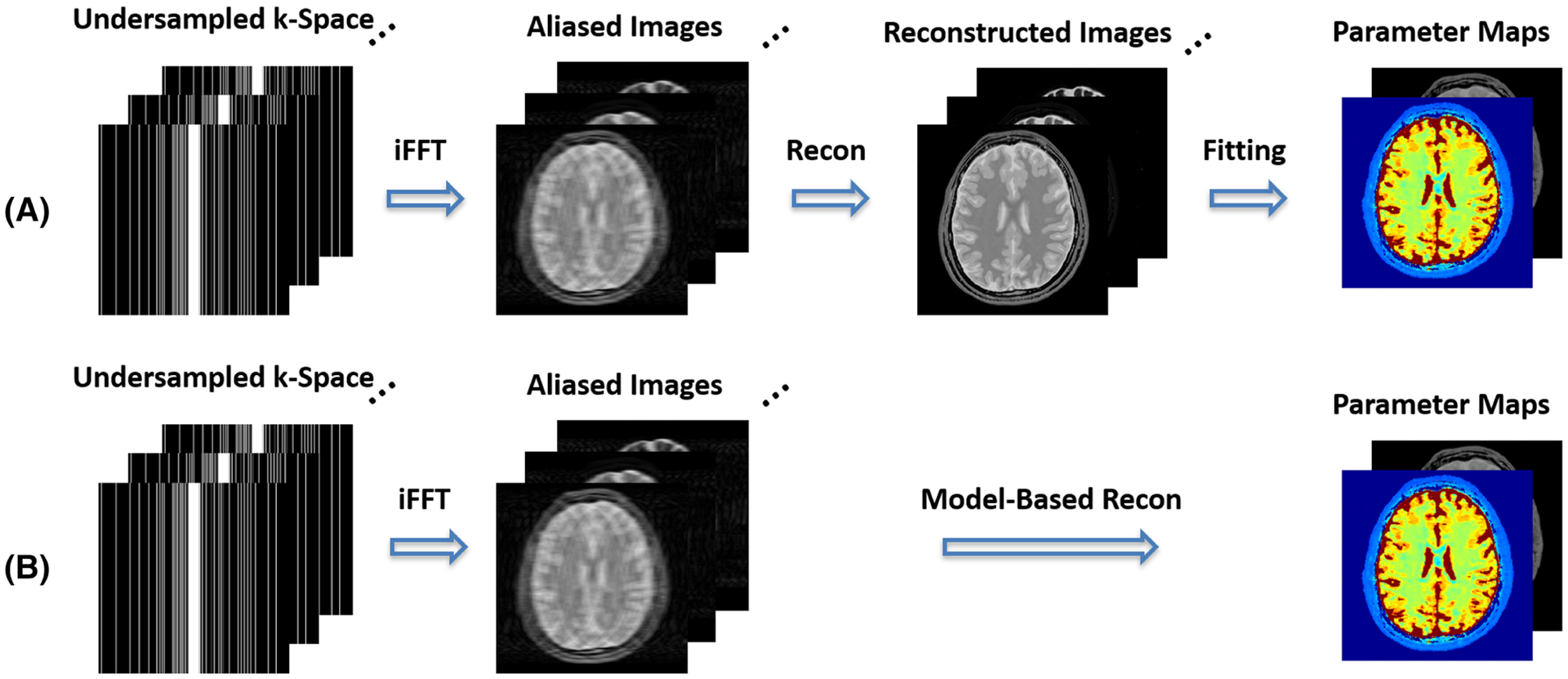
A, Standard MR parameter mapping is typically comprised of two separate steps, including one step to generate a dynamic multi-contrast image series and the next step to fit the dynamic images into a signal model to generate parameters of interest. B, MR parameter mapping can also be performed by combining the two separate steps into a model-based reconstruction framework, in which MR parameter maps can be directly estimated from undersampled dynamic k-space. A variable-density Cartesian undersampling scheme at a 4-fold acceleration is demonstrated in this schematic example

3 |. STATE-OF-THE-ART METHODS FOR RAPID MR RELAXOMETRY

This section briefly reviews the current state-of-the-art methods for reconstructing dynamic MR relaxometry images from undersampled data and for generating relevant MR parameters based on the imaging models described in the previous section.

3.1 |. Image reconstruction from accelerated MR relaxometry data

3.1.1 |. Parallel MRI

Multiple-coil arrays are widely used in modern MR scanners, and enable the reduction of scan times by skipping certain k-space measurements in most clinical applications using a technique known as parallel MRI.^{51,52,54,55,106} Mathematically, the undersampled signal equation described in Equation 4 can be adapted with additional coil sensitivity encoding as

$$s=\Lambda \mathit{\text{FCd}}=Ed$$ (6)

where C = [C₁, C₂, ⋯, C_j] represent coil sensitivities that can be pre-estimated or self-calibrated and E is called an encoding matrix, and combines the undersampling operator, Fourier encoding, and coil encoding. During the reconstruction process, parallel MRI aims to unfold aliased undersampled images (as in the sensitivity encoding (SENSE)-type methods⁵¹) or fill in the missing k-space data (as in the generalized autocalibrating partial parallel acquisition (GRAPPA)-type methods⁵²) using data simultaneously acquired with multiple coils. The choice of reconstruction strategy can be selected based on specific applications and the way in which coil sensitivity maps are generated. When coil sensitivity maps are available, the reconstruction of Equation 6 can be performed by minimizing the following least-square error in a generalized formalism⁵³:

$$\tilde{d}=\underset{d}{\text{argmin}}\Vert \mathit{\text{Ed}}-s{\Vert }_2^2.$$ (7)

Depending on the sampling schemes, the solution of Equation 7 can be found by computing the Moore-Penrose pseudoinverse directly⁵¹ or can be solved with iterative algorithms (eg the gradient descent algorithm) in a more generalized case.¹⁰⁷

Parallel MRI was introduced more than two decades ago and remained the cornerstone in most of the current routine clinical examinations. However, the maximum acceleration that can be achieved with parallel imaging alone is fundamentally limited by the number of coil elements and the design of coil arrays, and it is ultimately restricted by the electrodynamic principles.^51,53 However, as shown in the following subsections, parallel MRI can be synergistically combined with other more advanced image reconstruction methods for better reconstruction performance.

3.1.2 |. Constrained reconstruction

Additional regularizations can be incorporated into the parallel MRI framework to further increase acceleration rates and/or improve reconstruction performance.^{62,64,93,94,108–110} The incorporation of additional constraints inherently changes the weighting of competing considerations in the reconstruction problem and can result in more stable solutions (eg better suppression of artifacts/noise). In general, the combination of parallel imaging with constrained reconstruction can be represented by

$$\tilde{d}=\underset{d}{\text{argmin}}\Vert Ed-\mathbf{\text{s}}{\Vert }_2^2+\lambda R(d)$$ (8)

where R denotes a regularization (sometimes therecan be two or more regularizers) enforced on the dynamic relaxometry images to be reconstructed, and λ represents a weighting parameter to control the balance between data consistency (the left-hand term) and promotion of regularization (the right-hand term).

Among many regularizations that have been proposed for image reconstruction, ℓ₁-norm regularization, which is the basis of compressed sensing theory,^93,111,112 has received considerable attention and interest and has been extensively applied to accelerate MR relaxometry to exploit temporal image sparsity.^60,61,67,69 The ℓ₁-norm regularization can also be replaced by a low-rank constraint, which is another popular reconstruction scheme commonly applied for rapid MR relaxometry.^65,68,113 It can be further modified to enforce a so-called subspace constraint,¹¹⁴ which has received substantial interest in dynamic MRI reconstruction and has demonstrated superior performance to standard ℓ₁-norm constrained or low-rank-constrained reconstruction in many dynamic MRI studies.^{70–72,95,115–117}

Adding one or more regularizations (Equation 8) often makes the reconstruction problem non-linear, and thus an iterative reconstruction algorithm is needed. This prolongs reconstruction time compared with linear reconstruction (eg parallel MRI reconstruction), which can range from a few minutes to a few hours. When sparsity is exploited in reconstruction, incoherent undersampling, such as random Cartesian undersampling⁹³ or non-Cartesian undersampling,⁹⁴ is usually implemented to fulfill the requirement of incoherence in the compressed sensing theory.

3.2 |. Model-based reconstruction of MR parameters

A number of studies have proposed incorporating the MR parameter fitting models into image reconstruction so that corresponding parameter maps can be directly reconstructed from undersampled k-space in a single step with increased efficiency, performance, and robustness.^{73–75,118,119} The general framework of model-based reconstruction is shown in Figure 1B, and mathematically this can be expressed as

$$\tilde{p}=\underset{p}{\text{argmin}}\Vert EM(p)-s{\Vert }_2^2.$$ (9)

Here, the parameter fitting process previously described in Equation 5 is combined with Equation 7. The model-based reconstruction strategy has two specific advantages. First, it eliminates the parameter fitting step, which is traditionally treated as a separate process, is often cumbersome and is sensitive to residual noise and/or artifacts. Second, the parameter fitting model is employed as a constraint, which serves as an intrinsic regularizer for image reconstruction. This can lead to better suppression of noise and artifacts and thus potentially increased acceleration rates. In addition, an extra regularization can be further enforced on the parameters to be reconstructed to improve reconstruction performance^74,76:

$$\tilde{p}=\underset{p}{\mathrm{argmin}}\Vert EM(p)-s{\Vert }_2^2+\lambda R(p).$$ (10)

The main challenge of model-based reconstruction is the added computational complexity, which demands prolonged reconstruction time (eg 10–20 min or longer per 2D slice⁷⁵) and can restrict its clinical translation.

3.3 |. Efficient MR parameter mapping

Traditional MR parameter fitting, as shown in Equation 5, aims to find the least-square solution that minimizes the error between the underlying signal evolution and synthesized signal curve from the parameters to be fitted based on corresponding models. This is usually implemented through an iterative non-linear least-square fitting process, which is computationally expensive, particularly when pixel-by-pixel based fitting is desired and when additional considerations (eg correction of B₁⁺ profile or slice profile) need to be taken into account. To speed up parameter fitting, a number of studies have proposed pattern-recognition-based approaches.^44,120,121 In this type of algorithm, a dictionary containing signal evolutions from a range of possible parameters is simulated first using relevant signal models or the Bloch equations. During the parameter generation step, a pattern-recognition-based process is then performed to search for the element from the dictionary that best matches the signal evolution for a given image pixel (eg the element with the smallest least-square error with the signal to be fitted). Once the desired dictionary atom is found, its associated MR parameters are then assigned to this pixel, and this process is looped for all the pixels to generate parameter maps. The pattern-recognition-based fitting approach gives a couple of unique advantages over traditional iterative fitting methods. First, it involves only a linear searching step, thus enabling dramatically faster fitting speed. Second, since the dictionary can be pre-generated, it is well-suited for efficient parameter fitting using a complicated model.

MRF⁷⁷ is a more advanced framework that allows the simultaneous quantification of multiple tissue properties (eg joint T₁ and T₂ mapping) from a single MR scan in clinically feasible scan time (eg a few seconds to a few minutes). It is also based on pattern recognition to generate quantitative MRI parameter maps, as shown in Figure 2, and the dictionary in MRF is typically generated using the Bloch equations to cover a wide range of physiological tissue properties. In addition, an MRF sequence further employs randomized imaging parameters, such as FA, T_E, and time of repetition (T_R), to generate highly variable signal evolutions that simultaneously depend on different tissue properties. This also ensures that different dictionary elements can be better differentiable to reduce the chances of false dictionary matching. A combination of these new features provides much higher flexibility on simulating different encoding effects, such as FA and T_R/T_E, system imperfections, such as B₀ and B₁ inhomogeneities, and multiple tissue contributions, such as T₁, T₂, and diffusion.^122,123

FIGURE 2.

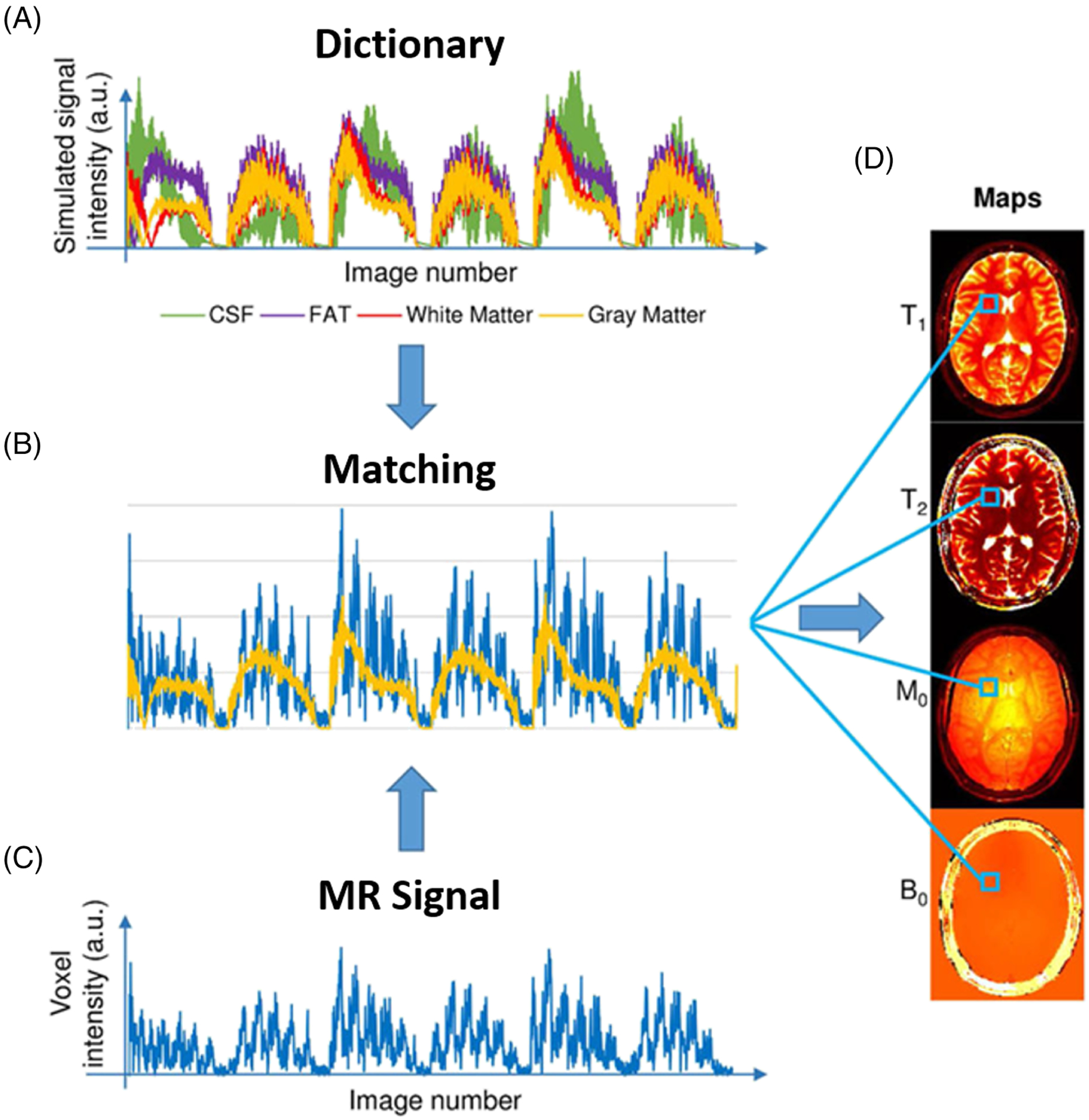
Schematic demonstration of pattern-recognition-based MR parameter generation in the MRF framework. A, Examples of four dictionary entries representing four primary tissues: cerebrospinal fluid (CSF), fat, white matter, and gray matter. B, Pattern matching of the voxel fingerprint in the dictionary, which allows retrieval of the tissue features represented by this voxel. C, The intensity variation of a voxel across the undersampled images. D, Parameter maps obtained by repeating the matching process for each voxel. (Image reproduced from Figure 1 in Panda et al. Magnetic resonance fingerprinting—an overview. Curr Opin Biomed Eng. 2017 Sep;3:56–66 with permission)

The pattern-recognition-based MR parameter generation, including the MRF framework, can be combined with previously described accelerated imaging techniques for improved imaging speed and performance. For example, standard non-Cartesian parallel image reconstruction, view-sharing approaches, or compressed sensing reconstruction have been used to improve MRF.^124–127 Imaging performance can be further improved with low-rank-based reconstruction methods^128–133 or subspace-based reconstruction methods.^{132,134–137} In addition, the model-based reconstruction strategy can also be incorporated to directly reconstruct desired MR parameters.^135,121,138

The main challenge of the pattern-recognition-based approach is the high computational demand to generate a dictionary and the large size of the dictionary that needs to be stored for signal matching, particularly when many parameters need to be considered simultaneously, as in MRF. This challenge can be alleviated by increasing the gap/footprint between consecutive dictionary elements, but this could lead to a reduction of fitting precision compared with conventional non-linear fitting approaches.

4 |. NEW GENERATION OF MR RELAXOMETRY: THE RISE OF DEEP LEARNING

4.1 |. Introduction of deep learning

Deep learning is one particular form of machine learning that uses a combination of weighted non-linear functions to represent complex learning functions.⁷⁸ Deep learning can be viewed as a multi-level feature representation model starting with learning simple linear features in initial network layers followed by more sophisticated features in deeper layers. The combination of a large number of learning modules leads to flexible and scalable learning capability. Along with the increase of computation power, deep learning has been revolutionizing computer vision and data science, and it has quickly expanded to many other modern scientific disciplines, including medical imaging research.⁷⁸

Deep learning utilizes a neural network to learn latent data information. Inspired by the anatomy of neurons and how they function in the brain to perform cognitive tasks, a neural network consists of multiple hidden layers, and each of them has interconnected artificial neurons with varying ‘weights’ representing the strength of connections. A basic artificial neural network architecture is the fully connected network (FCN), in which each node in one layer is interconnected to all other nodes in a subsequent layer (Figure 3). The connection weights can be updated during network training to form a complicated non-linear relationship between the input and output. To facilitate analysis of multi-dimensional image data, a set of processing modules is further introduced into neural networks for characterizing the inter-correlations among image pixels using convolution, where a set of kernels is used to identify image features such as intensity variations, edges, and patterns. The extracted features are then multiplied by activation functions, similar to real neuron activation, so that non-linearity is added to the learned features to increase model complexity and to enhance learning capability. In a typical neural network, the lth convolutional layer can be described as

$$f_u^l=\sigma \left(W_{n_l}^l*f_u^{l-1}+b_{n_l}^l\right).$$ (11)

Here, $f_u^l$ is the output of this convolutional layer with input $f_u^{l-1}$ as the output from the previous layer. * denotes multi-dimensional convolution. $W_{n_l}^l$ and $b_{n_l}^l$ are corresponding convolution kernels and biases, respectively, with a total of n_l filters. σ(·) denotes an activation function, such as the most commonly used rectified linear unit (ReLU). The size of the feature map can change throughout the network by using special convolutional processes such as dilated convolutions¹³⁹ and transposed convolutions,¹⁴⁰ or by using additional operators such as pooling¹⁴¹ and interpolations. Those operations can help maintain essential image information while diversifying learned features depending on study-specific learning purposes. Such a neural network structure is referred to as a convolutional neural network (CNN); it consists of many interconnected convolutional layers and allows learning of sophisticated features that are inherently embedded in a training database. The basic CNN can also be further extended to include many advanced processing modules, such as batch normalization,¹⁴² residual learning,¹⁴³ dense connection,¹⁴⁴ and dropout operation¹⁴⁵ to increase the learning capability, efficiency, and robustness.

FIGURE 3.

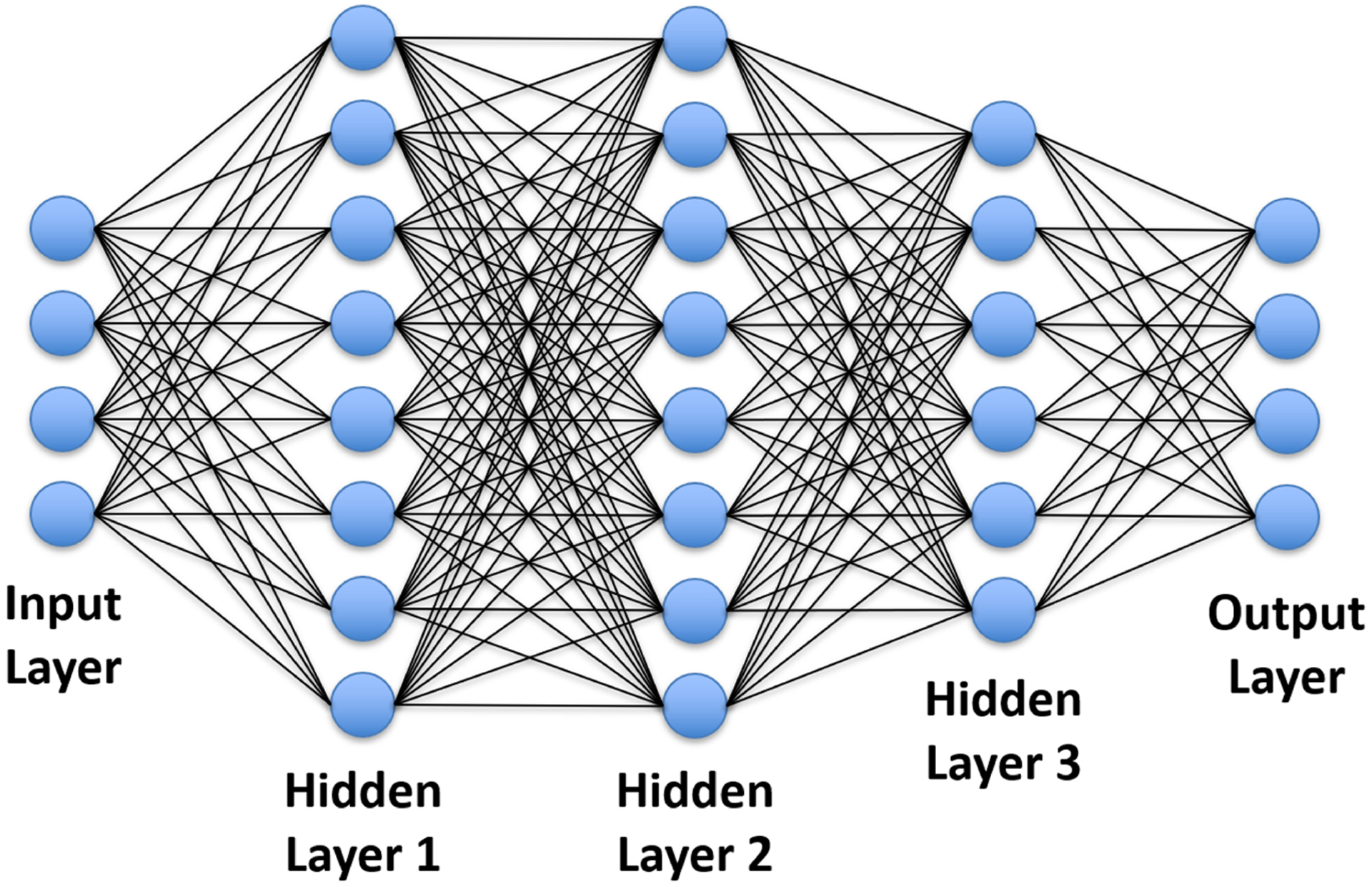
Schematic demonstration of an FCN with one input layer, one output layer, and three hidden layers. Each node in one layer is interconnected to all nodes in the following layer. This network can represent a complicated non-linear relationship between the input and the output

In recent years, different variants of CNN architectures have been proposed. In particular, U-Net¹⁴⁶ is an architecture that has been widely applied in medical image applications. The U-Net structure is an efficient CNN system to characterize pixel-wise dense image content using a paired encoder and decoder network. The encoder network consists of several convolutional layers, ReLU activation, batch normalization, and Max-pooling. It aims to characterize inherent image features while removing uncorrelated image structures and compressing image information. The decoder network uses a mirrored structure of the encoder to decompress the output of the encoder network. It recovers image resolution and then generates desirable image contrast through multiple levels of convolution operation. Multiple symmetric shortcut connections are also applied between the encoder and decoder networks to directly transfer image features with increased mapping efficiency.¹⁴⁷ Figure 4 shows an example of a customized U-Net architecture.

FIGURE 4.

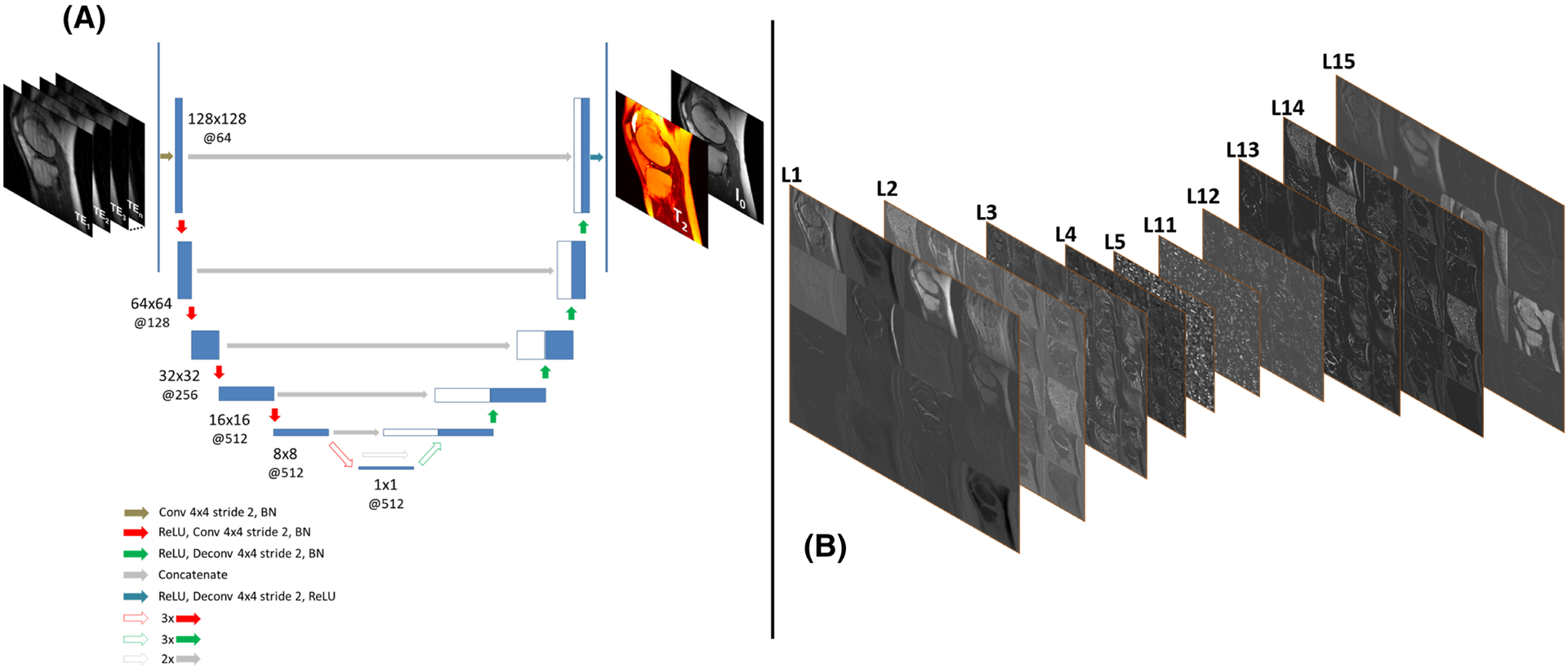
An example of mapping an undersampled knee MR image series into a pair of a T₂ map and proton density (I₀) map using an endto-end CNN structure in Reference 169. A, The network structure of a U-Net¹⁴⁶ implemented for the end-to-end mapping. The U-Net structure consists of an encoder network and a decoder network with multiple shortcut connections (eg concatenation) between them to enhance mapping performance. The encoder network is used to characterize robust and inherent image features while compressing image information, and the decoder network is applied to generate desirable image contrast using the extracted features of the encoder network. The abbreviations for the CNN layers include BN for batch normalization, Conv for 2D convolution, and Deconv for 2D deconvolution. The parameters for the convolution layers are labeled in the figure as image size @ the number of 2D filters. B, Schematic diagram of a set of extracted image features at different convolutional layers of the encoder (L1–L5) and decoder (L11-L15) networks. These connected processing modules allow the network to explore spatial-temporal correlation and to learn multi-level structural features to characterize complex image information for correcting image artifacts and removing image noise due to image undersampling

ResNet¹⁴³ is another popular CNN architecture that is also widely used in medical imaging applications. This architecture is often implemented for training a deep network. When a network has too many convolutional layers, a degradation problem can occur, causing rapid loss of network accuracy along with the increase of network depth. ResNet introduces a residual block where the layer input is connected to the layer output, thus forcing the layer to learn residual information with respect to the layer input. Compared with standard CNN, this turns out to be easier and less complex for network training, which potentially leads to improved network accuracy and performance.¹⁴³

CNN can also be extended to utilize spatial-temporal filters^148,149 or an architecture of recurrent CNN (RCNN)^150,151 for better capturing dynamic information and learning spatial-temporal information in dynamic images. RCNN introduces a ‘memory’ module to maintain an internal state of the network, which keeps active information from not only the current input but also its neighboring inputs over time. As a result, information learned from a dynamic frame can be used to help to learn about a different frame within the RCNN structure, and dynamic information can be propagated efficiently when the input changes with time.

The abovementioned network architectures usually use pixel-wise loss functions such as ℓ₁ or ℓ₂ norms to calculate the difference of network outputs with respect to training references. Recent studies have found that these simple loss functions are likely to cause image bias and blurring in imaging applications.¹⁵² To address this challenge, the generative adversarial network (GAN)¹⁵³ has been developed, and it has gained increasing attention in the deep learning field. With an adversarial learning scheme, GAN uses a separate network as a discriminator to evaluate the similarity between the outputs from the original neural network (typically referred to as a generator) and the training references. Such a training strategy enforces that the generator produces outputs that are indistinguishable from the training references. It enables assessment of network outputs from a perspective of multiple-level features, thus leading to better performance than standard ℓ₁ or ℓ₂ norm-based pixel-wise loss functions.

To this end, more content about network architectures can be found in the latest review articles.^154,155 The key point here is that the scalability and flexibility of constructing different networks with a large number of advanced processing modules provide a great many degrees of freedom to reformulate learning problems for MR relaxometry. These abovementioned network architectures and training strategies have been implemented and tested in recent deep-learning-based MR relaxometry applications and have demonstrated promising performance (Table 1), as will be seen in the following subsections.

TABLE 1.

Summary of recent representative studies on deep-learning-based rapid MR relaxometry

Reference	Method	Relaxation type	Network architecture	Image sequence	Training data	Testing data	Key results
Cai et al156	Deep OLED T2	T2 mapping	ResNet	Single-shot OLED planar imaging	Simulated data	Simulated phantom; in vivo brain	Reliable T2 mapping with higher accuracy and faster reconstruction than standard reconstruction method
Li et al158	MSCNN	T1ρ and T2 mapping	CNN	Magnetization-prepared angle-modulated partitioned k-space spoiled gradient echo snapshots T1ρ and T2 quantification	In vivo knee	In vivo knee	Up to 10-fold acceleration for simultaneous T1ρ and T2 maps with quantification results comparable to reference maps
Cohen et al164	MRF-DRONE	T1 and T2 mapping	FCN	Modified gradient-echo EPI MRF pulse sequence; fast imaging with steady-state precession MRF pulse sequence	Simulated data	Simulated phantom; phantom; in vivo brain	Accurate, 300 to 5000 times faster, and more robust to noise and dictionary undersampling than conventional MRF dictionary matching
Fang et al165	SCQ network	T1 and T2 mapping	FCN + U-Net	Fast imaging with steady-state precession MRF pulse sequence	In vivo brain	In vivo brain	Accurate quantification for T1 and T2 by using only 25% of time points of the original sequence
Liu et al169	MANTIS	T2 mapping	U-Net	Multi-echo spin-echo T2 mapping	In vivo knee	In vivo knee	Accurate and reliable quantification for T2 at up to eightfold acceleration, robust against k-space trajectory undersampling variation
Liu et al170	MANTIS-GAN	T2 mapping	GAN (generator, U-Net; discriminator, PatchGAN)	Multi-echo spin-echo T2 mapping	Simulated data	Simulated data	Up to eightfold acceleration for T2 mapping with accuracy and high image sharpness and texture preservation compared with the reference
Zha et al171	Relax-MANTIS	T1 mapping	U-Net	Variable flip angle spoiled gradient echo T1 mapping	In vivo lung	In vivo lung	Physics model regularized and self-supervised T1 mapping at reduced image acquisition time, robust against noise
Zibetti et al175	VN T1ρ	T1ρ mapping	VN	Modified 3D Cartesian turbo-FLASH sequence	In vivo knee	In vivo knee	Better T1ρ quantification using deep learning image reconstruction than compressed sensing
Jeelani et al177	DeepT1	T1 mapping	RCNN + U-Net	Modified Cartesian Look-Locker imaging	In vivo cardiac	In vivo cardiac	Noise-robust estimates compared with the traditional pixel-wise T1 parameter fitting at fivefold acceleration
Chaudhari et al178	MRSR	T2 mapping	CNN	DESS sequence	In vivo knee	In vivo knee	Minimally biased T2 from robust super-resolution in thin slice compared with the reference

Abbreviations:

DeepT₁, deep learning for T₁ mapping; MSCNN, model skipped convolutional neural network; Relax-MANTIS, reference-free latent map extraction MANTIS.

4.2 |. End-to-end deep learning for efficient MR parameter mapping

Neural networks can be constructed to learn spatial correlations and contrast relationships between input datasets and desirable outputs. This process is known as end-to-end deep learning or end-to-end mapping, which forms a non-linear transform function between two image domains. For MR relaxometry, a straightforward and effective application of end-to-end mapping is to directly translate dynamic MR relaxometry images (in domain D_u, typically undersampled images) to MR parameter maps (in domain P) through domain transform learning (denoted as D_u → P) given data pairs d_u and p representing the input image series and to-be-generated MR parameters. The data distribution in the training datasets can be denoted as d_u ~ P(d_u), and the corresponding learning process can then be formulated as

$$\tilde{\theta }=\text{arg }\underset{\theta }{\text{min}}\left({\text{E}}_{d_u-P\left(d_{\text{u}}\right)}\left[{\Vert C\left(d_{\text{u}}\mid \theta \right)-p\Vert }_p\right]\right)$$ (12)

where C(d_u|θ):d_u → p is a neural network mapping function conditioned on a network parameter set θ; ∥ ∥_p represents a p-norm function such as the ℓ₁-norm or ℓ₂-norm; and ${\text{E}}_{d_{\text{u}}~P\left(d_{\text{u}}\right)}[\cdot ]$ is an expectation operator given that d_u belongs to the data distribution P(d_u). It can be seen that Equation 12 is in a similar format to the parameter fitting model described in Equation 5, and the use of deep learning enables the direct generation of MR parameters from undersampled dynamic images. It should be noted that the optimization target in Equation 12 is fundamentally different from that in Equation 5. While Equation 5 aims to generate parameter maps that are consistent with the underlying dynamic signal evolution, Equation 12 attempts to estimate a network parameter set $\tilde{\theta }$, conditioned on which the neural network optimizes the mapping performance by minimizing the difference between the network outputs (eg deep-learning-generated parameters) and the training references (eg reference MR parameters). More specifically, the training process aims to characterize latent features that can be learned from the training datasets by updating network parameters. Once the training is completed, the learned parameter set $\tilde{\theta }$ for the neural network is fixed, and it can be used to convert newly acquired undersampled images to their corresponding parameter maps $\tilde{p}$ directly. This process is referred to as image inference:

$$\tilde{p}=C\left(d_u\mid \tilde{\theta }\right),d_u\in D_u.$$ (13)

Since the network structure and parameters are both fixed during the inference process, the forward operation in reconstruction can be achieved in a time-efficient fashion with computing time typically of the order of seconds using a modern graphics processing unit (GPU) or multi-threaded central processing unit (CPU). A number of recent studies have demonstrated the performance of end-to-end mapping to achieve efficient and accurate MR relaxometry with representative examples briefly summarized below.

Cai et al investigated the use of end-to-end CNN mapping to directly estimate the T₂ map from single-shot MR images of the brain¹⁵⁶ that were acquired using an overlapping-echo detachment (OLED) planar imaging sequence.¹⁵⁷ The proposed method applied a 2D ResNet to generate T₂ maps from input OLED images directly. The CNN was trained on simulated image datasets, and the trained network was applied for evaluation in real brain data. Compared with T₂ maps obtained from conventional constrained reconstruction, the T₂ maps generated with the proposed deep learning method produced reduced image artifact, noise, and blurring (Figure 5). Meanwhile, deep learning also led to increased accuracy in T₂ estimation with respect to reference T₂ maps.

FIGURE 5.

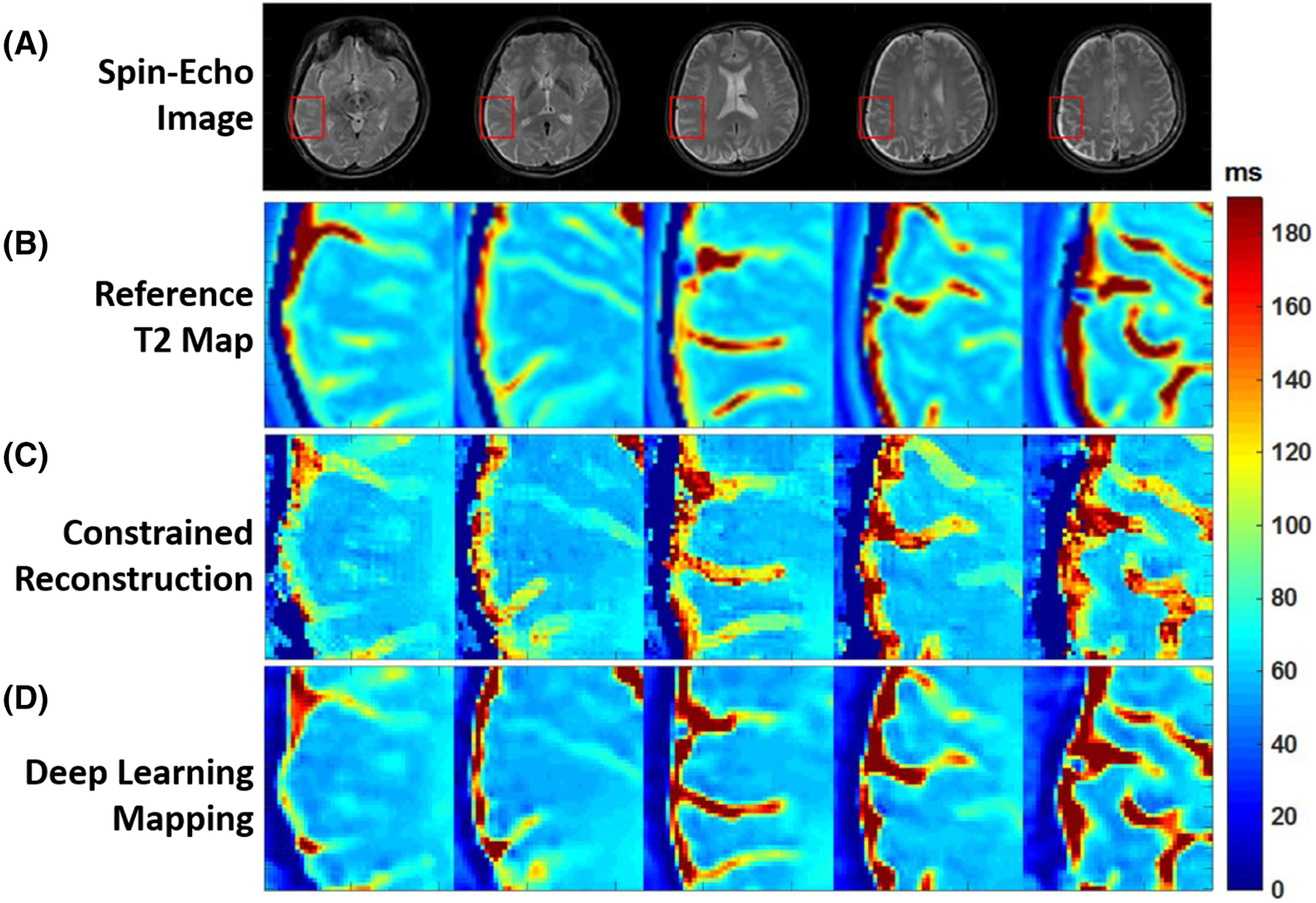
Examples showing the comparison of T₂ estimation between methods. A, Full FOV spin-echo images. B, Expanded reference T₂ maps. C, Expanded T₂ maps from constrained echo-detachment-based reconstruction method. D, Expanded T₂ maps from ResNet. Expanded ROIs are marked by the red rectangles in A. The reconstructed T₂ mappings from the echo-detachment-based method show much more noise (regular noise-like artifacts) and blurring around the texture edges. This indicates the difficulty of denoising and reducing the blurring effect at the same time for the echo-detachment-based method. However, the ResNet method simultaneously achieves both quite well, and the results show good agreement with the reference T₂ mappings. (Image reproduced from Figure 6 in Cai et al. Single-shot T₂ mapping using overlapping-echo detachment planar imaging and a deep convolutional neural network. Magn Reson Med. 2018. https://doi.org/10.1002/mrm.27205 with permission)

Li et al proposed rapid T_1ρ and T₂ mapping of the knee using an end-to-end CNN.¹⁵⁸ In this study, dynamic MR relaxometry images were acquired using a magnetization-prepared spoiled gradient echo snapshot sequence that was previously developed for T_1ρ and T₂ quantification. During the training process, the reference T_1ρ and T₂ maps were obtained by fitting fully sampled k-space datasets, and undersampled MR images were retrospectively generated using a 2D Poisson-disk random undersampling mask. An end-to-end 3D CNN was constructed to jointly learn spatial-temporal information and T_1ρ and T₂ contrast simultaneously. The learned CNN was then applied to convert newly acquired undersampled MR images to both T_1ρ and T₂ maps directly. The deep-learning-based method was found to provide accurate T_1ρ and T₂ quantification at 10-fold acceleration compared with the reference parameter maps.

End-to-end mapping has also been applied to improve MRF in several recent studies with different applications.^159–163 The first application is to help MRF with a better and more efficient generation of MR parameter maps. For example, Cohen et al developed a deep-learning-based method called MRF deep reconstruction network (MRF-DRONE), which uses an FCN to directly map MRF signal curves to T₁ and T₂ values on a pixel-by-pixel basis.¹⁶⁴ The network learning was performed on a large dictionary, and the FCN uses multiple hidden layers to characterize the correlations between MRF signal patterns and corresponding T₁ and T₂ values. The highly non-linear nature of the deep learning network allows sufficient feature compression and more efficient pattern recognition, which resulted in 300–5000 faster mapping speed compared with standard MRF matching.

In a later study, Fang et al developed a framework called spatially constrained tissue quantification (SCQ), which uses end-to-end mapping for both feature learning and signal matching in MRF,¹⁶⁵ as shown in Figure 6. Similarly to MRF-DRONE, an FCN was trained to compress MRF signal evolution curves into a low-dimensional feature vector to better characterize signal patterns and remove uncorrelated noise and artifacts. A set of feature maps was formed by concatenating all feature vectors for all pixels in MRF images. In addition, a U-Net structure was constructed to convert the low-dimensional features into T₁ and T₂ parameter maps. This method achieved accurate T₁ and T₂ estimation in the brain with only a quarter of the MRF data that are needed without deep learning, leading to a fourfold acceleration rate. Using deep learning, the same group has also demonstrated improved 2D MRF with an in-plane spatial resolution of 0.8 mm² in a scan time of 7.5 s (Reference 166) and improved 3D MRF with 1 mm³ isotropic spatial resolution in a scan time of 7 min.¹⁶⁷

FIGURE 6.

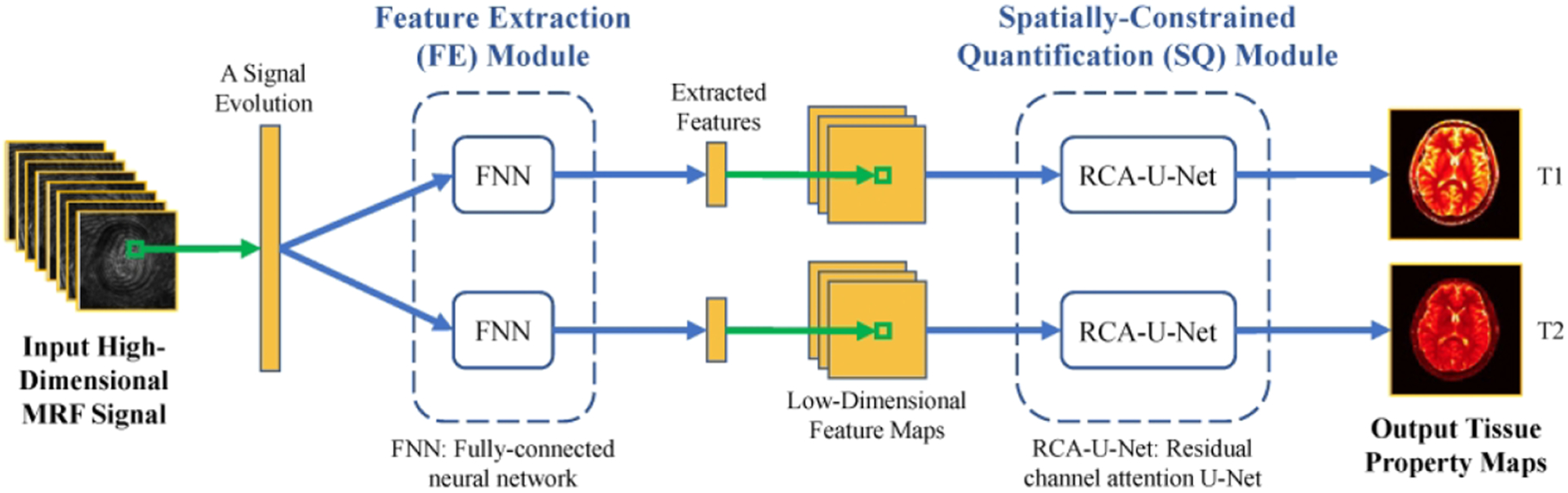
A diagram of the deep learning model for tissue quantification in MRF. First, the feature extraction module extracts a lower-dimensional feature vector from each MR signal evolution. A spatially constrained quantification module using end-to-end CNN mapping is then applied to estimate the tissue maps from the extracted feature maps with spatial information. This SCQ method achieved accurate T₁ and T₂ estimation using only a quarter of the required MRF signal initially, leading to an apparent fourfold acceleration for the brain. (Image reprinted from Figure 1 in Fang et al. Sub-millimeter MR fingerprinting using deep-learning-based tissue quantification. Magn Reson Med. 2019. https://doi.org/10.1002/mrm.28136 with permission)

Deep learning has also been used to help with the MRF dictionary generation. For example, Yang et al¹⁶⁸ developed a GAN-based method to learn to synthesize signal evolution curves from a reference MRF dictionary. The signal curves generated by deep learning were found to be consistent with those generated from the Bloch equations, and corresponding MR parameter maps generated from the learned dictionary were in a good agreement with those from the Bloch-equation-based dictionary for in vivo studies. The main advantage of using deep learning for MRF dictionary generation is the much faster computational speed (~1000-fold) compared with standard Bloch-equation-based simulation, particularly when a wide range of tissue parameters need to be covered.

4.3 |. Model-based deep learning reconstruction of MR parameters

In analogy to the model-based reconstruction shown in Equation 10, the end-to-end CNN mapping in Equation 12 can be further combined with a data fidelity term that enforces data/model consistency, and the CNN mapping can be treated as a deep-learning-based regularizer in this scenario as shown below:

$$\tilde{\theta }=\text{arg }\underset{\theta }{\text{min}}\left({\lambda }_1{\text{E}}_{d_u-P\left(d_{\text{u}}\right)}{\Vert EM\left(C\left(d_{\text{u}}\mid \theta \right)\right)-s\Vert }_2^2+{\lambda }_2{\text{E}}_{d_{\text{u}}-P\left(d_{\text{u}}\right)}\left[{\Vert C\left(d_{\text{u}}\mid \theta \right)-p\Vert }_p\right]\right).$$ (14)

Here, λ₁ and λ₂ are weighting parameters to balance the model fidelity (the left-hand term) and CNN mapping (the right-hand term), respectively. When multicoil arrays are employed, Equation 14 can also incorporate parallel imaging to enforce multicoil data/model consistency. The training of Equation 14 is equivalent to jointly learning two objectives. The first one (model fidelity) is to ensure that the reconstructed parameter maps from CNN mapping produce undersampled k-space data that match acquired k-space based on corresponding signal models. Similar to previous studies, the second objective (CNN mapping) is to ensure that undersampled MR relaxometry images produce parametric maps that are consistent with the reference parameter maps. The synergetic combination of these two loss terms inherits the advantage of high learning efficiency from end-to-end CNN mapping while incorporating prior MR physics knowledge into the training process, which can result in a more generalizable deep-learning-based image reconstruction model. The model-based deep learning reconstruction (Equation 14) forms a completely different problem to deep-learning-based parameter mapping (Equation 12). Strictly speaking, Equation 12 aims to map fully sampled or undersampled image series to parameters, while Equation 14 is more like a reconstruction problem that aims to reconstruct parameter maps consistent with acquired k-space, a process that is implemented in conventional iterative reconstruction as shown in Equations 8 and 10.

In a recent study, Liu et al demonstrated the performance of a model-based reconstruction framework using deep learning for rapid T₂ relaxometry.¹⁶⁹ The approach is called model-augmented neural network with incoherent k-space sampling (MANTIS), and aims to reconstruct T₂ maps from a series of undersampled multi-echo spin-echo MR images. As shown in Figure 7, the training of MANTIS aims to minimize the combined loss terms described in Equation 14 to enforce data/model consistency while removing undersampling-induced artifacts. Specifically, a U-Net was implemented as the CNN mapping function to learn spatial-temporal correlations between the undersampled input images and reference T₂ and proton density maps derived from fully sampled images. MANTIS was demonstrated for up to eightfold accelerated T₂ mapping of the knee with accurate T₂ estimation with respect to fully sampled references. Compared with conventional constrained reconstruction methods, MANTIS shows improved reconstruction performance with a lower error and higher structural similarity (Figure 8) and much faster reconstruction time.

FIGURE 7.

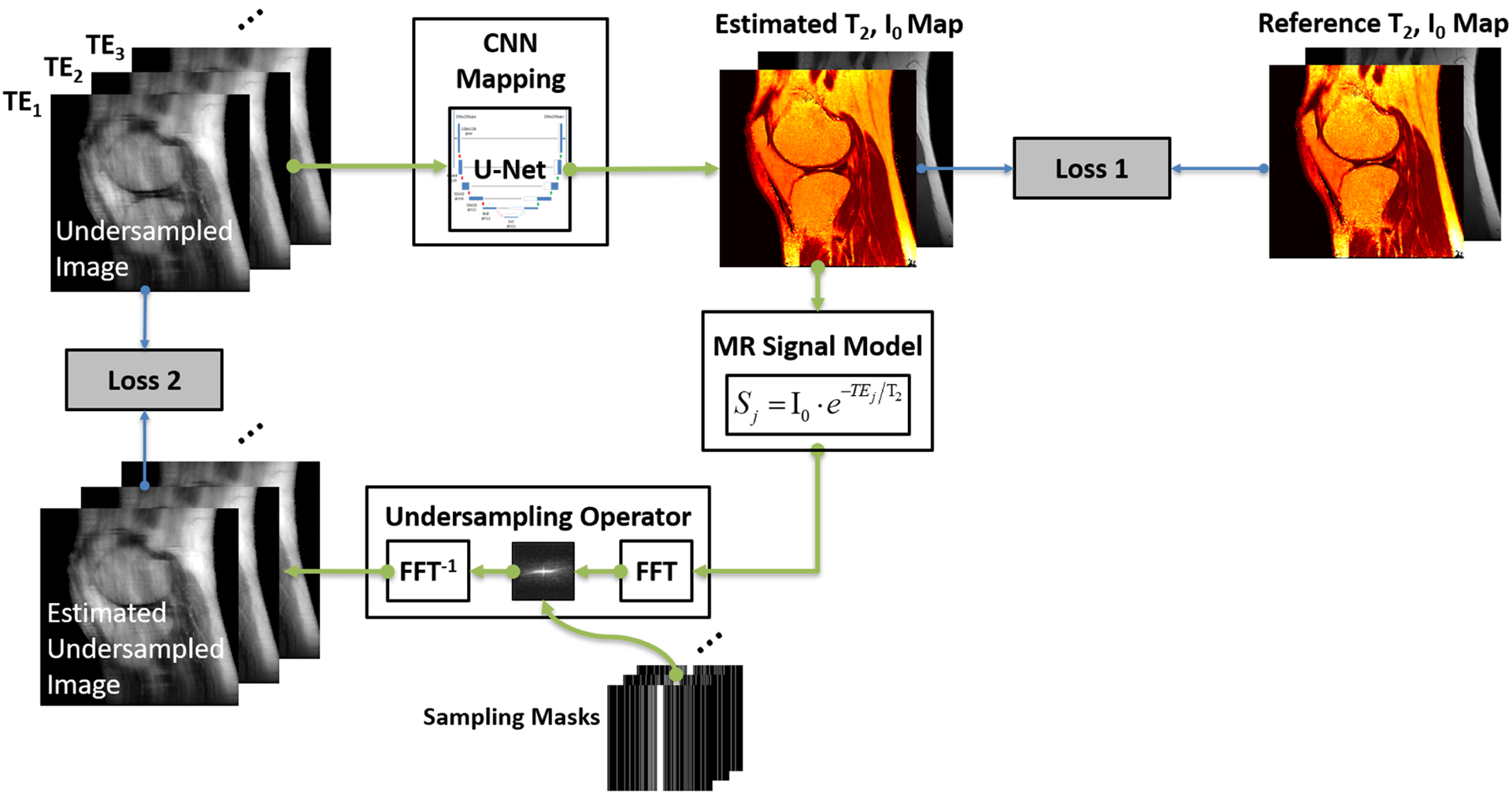
Illustration of the MANTIS framework for rapid MR parameter mapping, which features two loss components as shown in Equation 14. The first loss term (Loss 1) ensures that the undersampled multi-echo images produce parameter maps that are the same as the reference parameter maps generated from reference multi-echo images. The second loss term (Loss 2) ensures that the parameter maps reconstructed from the CNN mapping produce synthetic undersampled image data matching the acquired k-space measurements. This approach jointly implements both the data-driven deep learning component and the signal model from the fundamental MR physics. The framework can be extended to other types of parameter mapping with appropriate MR signal models. Other advanced CNN structures and loss functions can also be applied to augment the reconstruction performance

FIGURE 8.

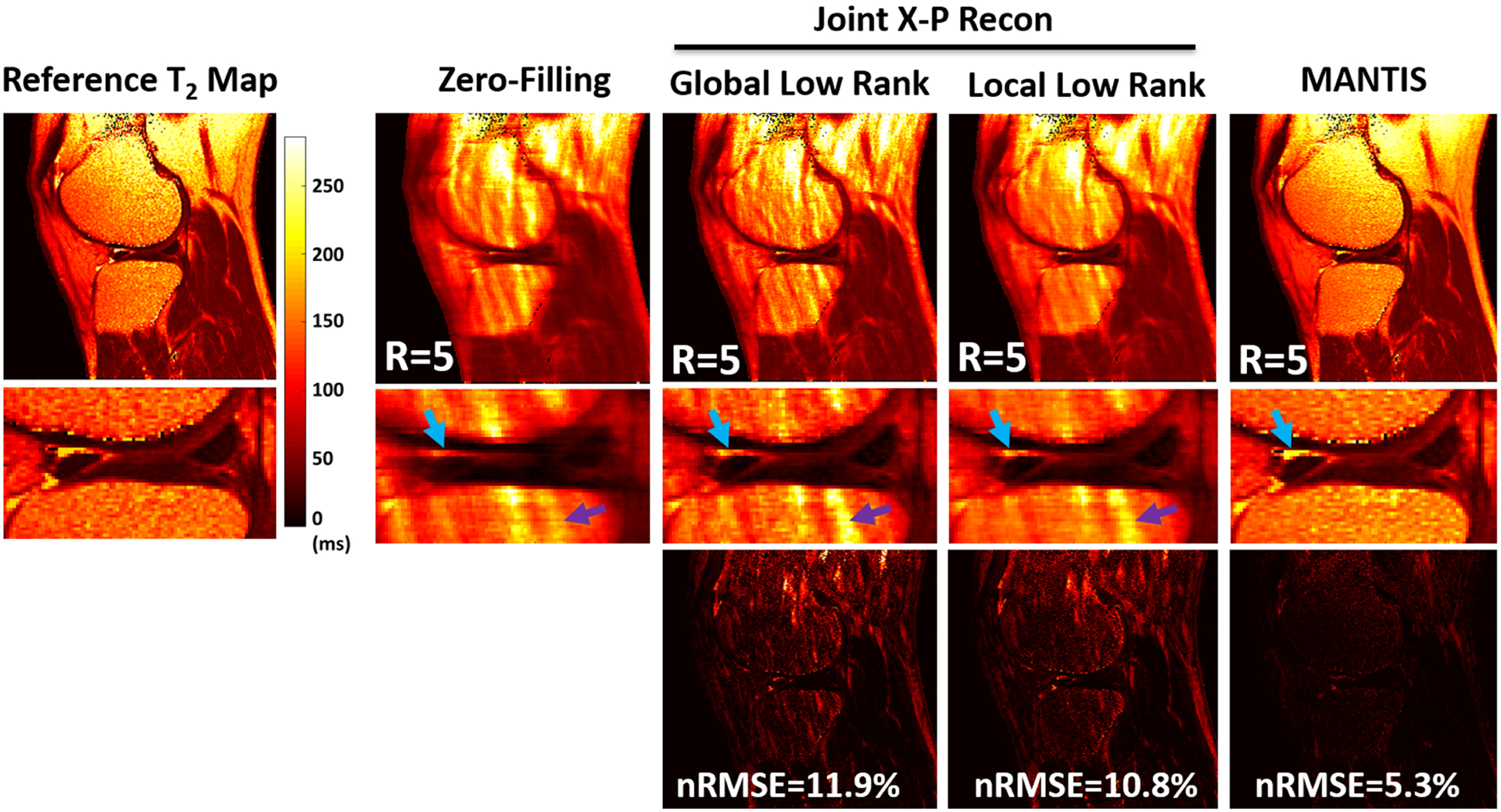
Comparison of T₂ maps estimated from MANTIS and different conventional sparsity-based reconstruction approaches at an acceleration rate of 5 (R = 5). MANTIS generated T₂ maps with well-preserved sharpness and texture comparable to the reference. Other methods created suboptimal T₂ maps with either reduced image sharpness or residual artifacts, as indicated by the arrows. The superior performance of MANTIS reconstruction was confirmed by the normalized root mean square error (nRMSE) and the residual error maps. The joint X-P constrained reconstruction methods, including global low rank and local low rank, were implemented based on Reference 68. (Image reproduced from Figure 3 in Liu et al. MANTIS: Model-Augmented Neural neTwork with Incoherent k-space Sampling for efficient MR parameter mapping. Magn Reson Med. 2019 Jul;82(1):174–188 with permission)

Liu et al have also further extended the MANTIS framework to an approach called MANTIS-GAN for rapid T₂ mapping of the brain by incorporating an additional adversarial loss function.¹⁷⁰ Specifically, based on the two loss terms in Equation 14, an additional adversarial loss is incorporated into the learning process to enable more realistic and accurate parameter maps. As shown in Figure 9 for a representative example, MANTIS-GAN maintains similar performance to standard MANTIS in suppressing artifacts and noise while enabling better preservation of tissue texture and image sharpness.

FIGURE 9.

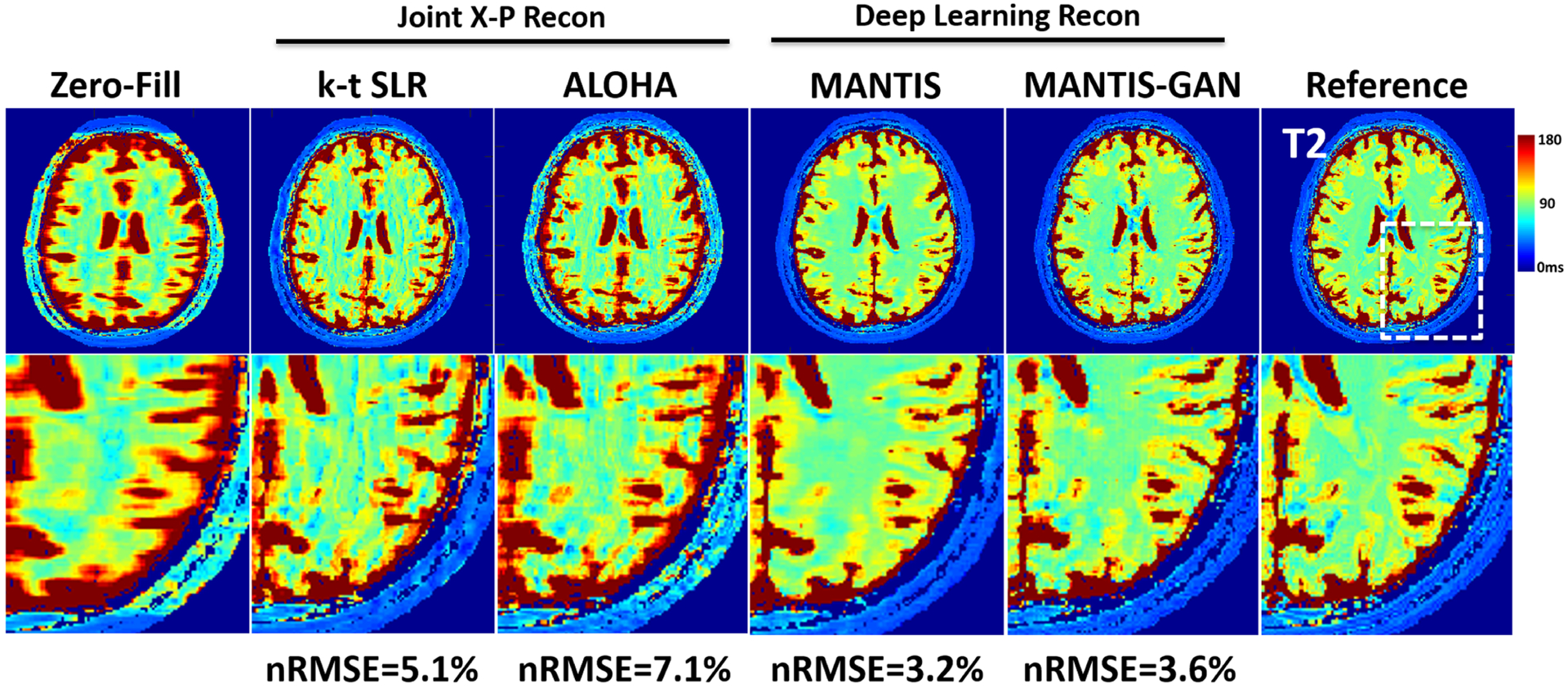
Representative examples of T₂ maps estimated from the different reconstruction methods at an acceleration rate of 8 (R = 8) in an axial brain slice. Undersampling at this high acceleration rate prevented the reliable reconstruction of a T₂ map with a simple inverse FFT (Zero-Fill) and advanced joint X-P compressed sensing methods, including k-t SLR⁶⁵ and ALOHA.¹¹³ The deep learning reconstruction MANTIS successfully removed aliasing artifacts and preserved better tissue contrast, which is similar to that of the reference but with some remaining blurring and loss of tissue texture. The deep learning reconstruction with adversarial training MANTIS-GAN provided not only accurate T₂ contrast but also much-improved image sharpness and tissue details that are superior to all other methods. The highest degree of correspondence between deep learning methods and the reference was confirmed by the nRMSEs, which were 3.2% and 3.6% for MANTIS and MANTIS-GAN, and 5.1% and 7.1% for k-t SLR and ALOHA, respectively

In some applications (such as MR relaxometry of the lung), it may be challenging to obtain an accurate and reliable reference for training due to low signal-to-noise ratio (SNR) and/or to motion. To address this issue, Zha et al proposed a model-based deep learning reconstruction approach¹⁷¹ by enforcing only the joint model/data consistency term from Equation 14, as shown below:

$$\tilde{\theta }=\text{arg }\underset{\theta }{\text{min}}\left({\text{E}}_{\mathbf{\text{d}}-P(\mathbf{\text{d}})}\Vert EM(C(d\mid \theta ))-s{\Vert }_2^2\right).$$ (15)

This leads to a ‘self-supervised’ deep learning method that does not require references during training. The authors of this study investigated its performance in rapid T₁ mapping of the lung that was based on a variable flip angle ultra-short echo time (UTE) spoiled gradient echo (SPGR) sequence following the driven equilibrium single pulse observation of T₁ (DESPOT1) method.¹⁷² Although the method was evaluated for fully sampled images only, it enabled accurate T₁ mapping from only three FA images compared with corresponding T₁ maps obtained from five FA images (Figure 10), thus leading to 40% reduction in scan time.

FIGURE 10.

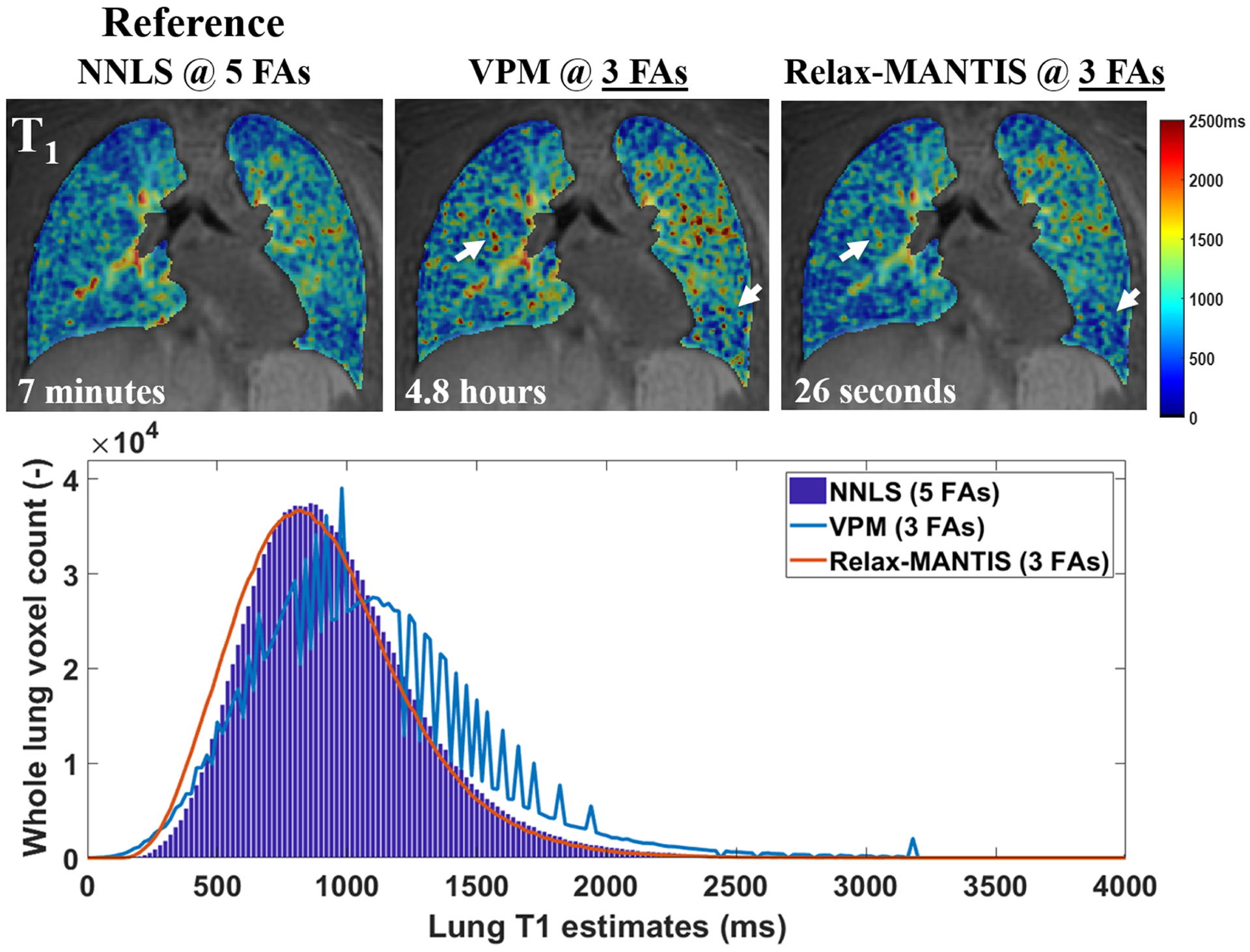
Examples of the estimated T₁ from UTE VFA lung data (SNR = 8.7) derived using standard non-linear least-squares fitting (NNLS)²¹⁵ with five FAs, the widely used maximum likelihood variable projection method (VPM)²¹⁶ with three FAs, and a self-supervised reference-free deep learning method (Relax-MANTIS) with three FAs. The T₁ values obtained with Relax-MANTIS showed similar regional variations as seen with NNLS with five FAs and less noisy measurements (white arrows) seen from VPM with three FAs. The lung T₁ histogram comparison suggests that whole lung T₁ distribution estimated using the deep learning method Relax-MANTIS with three FAs (orange curve) conforms much better to the distribution from the NNLS with five FAs (bar graph in blue). Relax-MANTIS provides good quantitative agreement with five-FA standard NNLS while using only three FAs, indicating a 40% scan time reduction for an accurate whole lung parenchymal T₁ quantification. The computing time for each 3D lung volume is significantly lower for the deep learning method at 26 s in comparison with the conventional methods at several minutes to hours. (Image courtesy of Wei Zha, PhD)

4.4 |. Deep-learning-based image reconstruction from accelerated MR relaxometry data

In analogy to the traditional two-step MR relaxometry method (one step for image reconstruction and the other step for parameter estimation), one can also focus on improving image reconstruction using deep learning for improved parameter estimation in the second step. Similarly to Equation 8, this type of image reconstruction using deep learning can be formulated as

$$\tilde{\theta }=\text{arg }\underset{\theta }{\text{min}}\left({\lambda }_1{\text{E}}_{{\mathbf{\text{d}}}_{\mathrm{u}}-P\left({\mathbf{\text{d}}}_{\mathrm{u}}\right)}{\Vert E\left(C\left(d_{\text{u}}\mid \theta \right)\right)-s\Vert }_2^2+{\lambda }_2{\text{E}}_{{\mathbf{\text{d}}}_u-P\left({\mathbf{\text{d}}}_{\mathrm{u}}\right)}\left[{\Vert C\left(d_{\text{u}}\mid \theta \right)-d\Vert }_p\right]\right).$$ (16)

Compared with Equation 8, Equation 16 aims to use deep learning as a data-driven regularizer, which is expected to provide better reconstruction performance compared with standard reconstruction employing a generic constraint. In addition, the deep-learning-based regularization can also be combined with traditional physics-based constraints, such as a low-rank constraint or a subspace-based constraint.^173,174 However, it should be noted that Equation 16 only reconstructs MR images, and an additional fitting process is still needed to produce MR parameter maps, which can be implemented following either Equation 5 (standard fitting) or Equation 12 (deep-learning-based mapping). Several studies have proposed different learning-based reconstruction methods within this category to improve MR relaxometry, as summarized below.

Zibetti et al investigated the use of a variational network (VN) for accelerated 3D T_1ρ mapping of the knee.¹⁷⁵ The reference in vivo T_1ρ datasets were acquired using a modified 3D Cartesian sequence with spin-lock preparation¹⁷⁶ at different spin-lock times. Images were retrospectively undersampled, and the learned network was applied to reconstruct each T_1ρ image separately. This study demonstrated that VN could provide better image reconstruction performance than conventional compressed-sensing-based reconstruction methods at an acceleration factor from 2 to 6. The improvement of image quality leads to the improved fitting of T_1ρ maps for cartilage quantification in the knee joint at different acceleration factors (Figure 11).

FIGURE 11.

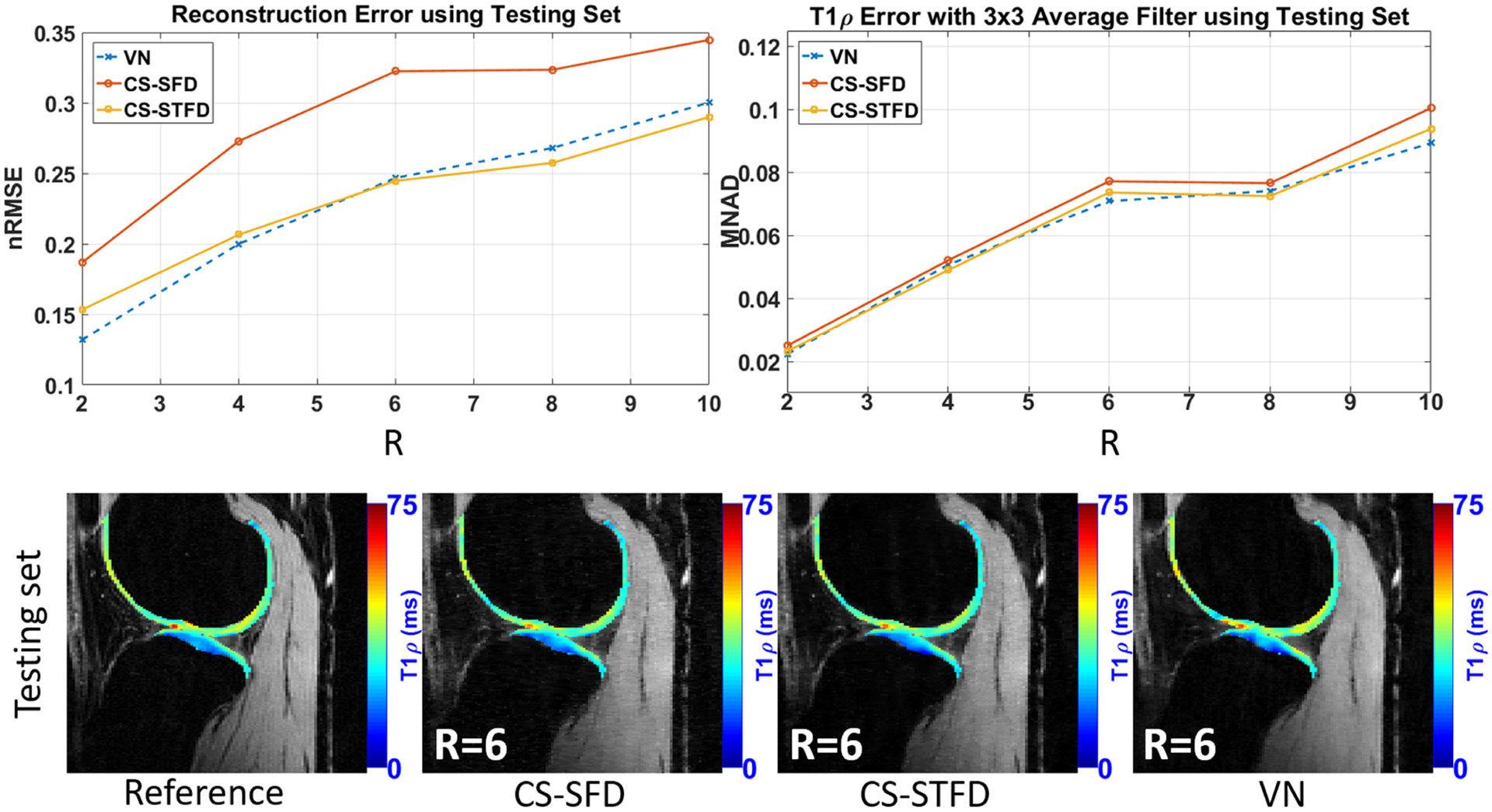
Comparison of T_1ρ maps estimated from VN and different compressed sensing reconstruction schemes. The advantages of VN over compressed sensing include faster image reconstruction and lower reconstruction error at acceleration factors R = 2–6. VN performed better than compressed sensing with lower error and bias in cartilage T_1ρ quantification under most of the acceleration factors. CS-SFD, compressed sensing using sparsity regularization on spatial finite differences; CS-STFD, compressed sensing using sparsity regularization on spatiotemporal finite differences; MNAD, median of normalized absolute deviation. (Image courtesy of Marcelo V. W. Zibetti, PhD)

Jeelani et al developed a deep-learning-based method for accelerated T1 mapping of the heart.¹⁷⁷ The proposed method consisted of a CNN for image reconstruction and a second CNN for generating T₁ maps using end-to-end mapping. Specifically, undersampled images acquired with a modified Look-Locker (MOLLI) sequence at eight inversion recovery time points were first sent to an RCNN reconstruction network¹⁵¹ to remove noise and artifacts by exploiting dynamic image information. The reconstructed MOLLI images were then used as the input for the second mapping network, a U-Net, which converts images directly to T₁ maps. This two-step reconstruction method has demonstrated better performance than conventional constrained reconstruction for cardiac T₁ mapping at fivefold acceleration.

Chaudhari et al proposed a deep-learning-based super-resolution technique for accelerated T₂ mapping of the knee.^178,179 Images were acquired using a dual-echo steady-state sequence (DESS), and a 3D CNN was constructed to improve through-plane resolution from thick slices using high-resolution thin-slice images as training references. This leads to increased volumetric coverage without prolonging times. This deep-learning-based super-resolution approach was found to outperform standard interpolation methods and sparsity-based super-resolution reconstruction methods¹⁷⁹ towards improved T₂ estimation with complete knee joint coverage. The proposed super-resolution method also enabled less biased T₂ measurements with respect to those obtained from the references using thick DESS images.¹⁸⁰

5 |. SUMMARY AND DISCUSSION

This review article discusses the potential of deep learning for rapid MR relaxometry and presents an overview of different pilot studies that have applied deep learning to improve MR parameter mapping. The paper first summarizes the basic imaging model for MR relaxometry, followed by different categories of traditional (non-deep-learning) approaches and deep-learning-based methods that have been applied to rapid MR relaxometry in terms of accelerated data acquisitions and/or efficient and accurate parameter fitting. This structure presents how deep-learning-based methods can be designed for rapid MR relaxometry and how they can be linked to conventional approaches.

The scope of this paper is limited to MR relaxometry, which typically refers to mapping of T₁, T₂, or T_1ρ parameters. However, the overall framework presented in this paper could also be extended to other quantitative imaging applications, such as diffusion imaging,^181,182 quantitative susceptibility mapping,^183–185 or perfusion imaging.^186–188 Meanwhile, the scope of deep learning for MR relaxometry is further limited to data acquisition, image reconstruction, and parameter fitting (eg using deep learning to generate better images and/or better parameter maps). The use of deep learning could also go beyond these applications and can help MR relaxometry from other perspectives. For example, recent studies have applied deep-learning-based segmentation approaches for automated analysis of cardiac T₁ mapping images¹⁸⁹ and knee joint T₂/T_1ρ mapping images.¹⁹⁰ The deep learning method was implemented to automatically segment the myocardial wall, and knee cartilage and meniscus, a process that is typically performed manually or semi-manually in conventional image analysis.

There has long been an interest in translating MR relaxometry into the clinical environment. However, this has been challenging due to its long acquisition times, slow reconstruction speed, and cumbersome overall imaging workflow. All of these have, in turn, restricted thorough clinical evaluation of MR relaxometry in terms of repeatability, reproducibility, and true added clinical value compared with conventional weighted images. As a relatively new direction, deep learning holds great promise in further pushing the translation of MR relaxometry into routine clinical evaluation. The improved imaging efficiency, including highly accelerated data acquisitions, faster image/parameter reconstruction, and more efficient parameter fitting, offered by deep learning would enable routine evaluation of MR relaxometry in large-scale clinical studies, so that its clinical value, repeatability, reproducibility, and robustness can be further investigated and evaluated in day-to-day MRI exams. However, this is a task that would require vendor involvement and close academic-industrial partnership.

The main challenge of deep learning is the requirement of training datasets, which are normally fully sampled MR images for training an image reconstruction algorithm. For conventional static MRI reconstruction, remarkable efforts have been made to address these issues, such as the recently proposed fastMRI project and its database that is released for free public use.¹⁹¹ However, this challenge is expected to be much greater and more complicated for quantitative MRI, including MR relaxometry, since quantitative MRI is not routinely performed in a current clinic environment, thus limiting the accumulation of training datasets. Image augmentation with MR simulation is a potential solution. Realistic numerical simulation using Bloch equations, Bloch-McConnell equations, or other physical models describing molecular diffusion and perfusion could generate training datasets that provide realistic MR signal variation for training deep learning networks.^122,192 However, it is important that the simulation can account for various system imperfection effects to mimic the realistic image data that are often seen in practice and can incorporate an adequate range of image features for creating robust and generalizable deep learning models. Alternatively, recent studies have also proposed the use of GAN to synthesize MR images for augmenting the training database.^193–199 While these approaches have shown promising results to generate pseudo-images for automated medical image segmentation and disease diagnosis, it is still unclear whether adequate dynamic information can be generated by using GAN to characterize sufficient signal variation for training a robust model for MR relaxometry. It should be noted that the training of GAN is a challenging task because the competing nature of the CNN generator and discriminator in GANs can cause unstable status and model collapse.^200–203 Additional care should also be taken to avoid GAN-induced image hallucination (eg pseudo image features), which can potentially degrade the overall training datasets and the resulting deep learning models. Moreover, transfer learning is a widely applied technique for training with a small database,^204,205 where a network can be pre-trained on datasets that are not related to the task to be performed and can then be fine-tuned with datasets that are related to the task. However, whether transfer learning can be applied to transfer quantitative MR information remains to be explored. Finally, the development of new deep learning architectures that work on limited training data might provide a solution to this problem. For example, instead of completely relying on training datasets to provide supervision for network, model-based deep learning approaches in the context of weak supervision or self-supervision use prior physical knowledge to regularize network training to learn useful image features.^169,171 Without compromising training performance, this could alleviate the demand on training datasets and provide more efficient learning capability with a small number of training datasets. A more comprehensive investigation on training deep-learning-based MR relaxometry with limited datasets would play an important role in facilitating its translation into clinical practice.

Another challenge of applying deep learning to MR relaxometry is the large image dimension size. MR relaxometry datasets are usually comprised of many dynamic frames, which would thus demand higher-performance computing hardware with more GPU memory and longer training time compared with application in static images. This issue is expected to be overcome by the rapid evolution of computing technologies and the development of new deep learning algorithms for handling multidimensional datasets. Recent efforts have been made in both industry and academia to develop more powerful parallel computing devices, cloud computing, and large-scale servers to address this bottleneck in applications of large computing problems. Meanwhile, memory-efficient deep learning structures have also been actively developed and tested.^206–210 With the advance of memory-efficient neural network design, a flexible configuration of complex deep learning architectures such as RCNNs can be implemented to fully characterize the dynamic image features in MR relaxometry. A deeper network with more convolutional layers and processing modules can also be made to improve the learning capability for MR relaxometry. The combination of these advances in both software and hardware is expected to substantially promote the use of deep learning in MR relaxometry.

Finally, there is a challenge to create a robust and generalizable deep learning model for MR relaxometry. Recent studies have reported that deep-learning-based MRI reconstruction might provide an inconsistent result when imaging parameters change from the network training step to the evaluation step.^82,211 As imaging parameters can vary across different times, scanners, coils, and protocols, there is a need to investigate the generalization of deep learning models against possible discrepancies of imaging parameters that often occur in a clinical setting. This might be achieved by embedding the variation of imaging parameters into the training of deep neural networks, so that different imaging parameters can be treated as extra information to allow joint learning with image features, similar to the recent demonstration in References 212–214. It is also important to perform regular model calibration to ensure consistent performance at different time points. Furthermore, deep learning models are expected to be robust against pathologies that are unseen in training datasets. Thus, careful clinical evaluation of a trained network on a large number of clinical examinations with a wide range of disease phenotypes is important to investigate whether it can be robust in detecting different abnormalities in the clinic.

In summary, deep learning holds great potential to address the current challenges associated with MR relaxometry and to deliver a rapid and efficient MR relaxometry framework that is clinically translatable. However, many challenges still exist, which require further careful investigation and rigorous research effort before clinical examinations can truly benefit from these new imaging methods.

Abbreviations:

BN

batch normalization network

CNN

convolutional neural network

CPU

central processing unit

CT

computed tomography

DeepT₁

deep learning for T₁ mapping

DESS

dual-echo steady-state sequence

FA

flip angle

FCN

fully connected neural network

FFT

fast Fourier transform

GAN

generative adversarial network

GPU

graphics processing unit

MANTIS

model-augmented neural network with incoherent k-space sampling

MANTIS-GAN

MANTIS with adversarial training

MOLLI

modified Look-Locker

MR

magnetic resonance

MRF

MR fingerprinting

MRF-Drone

MR fingerprinting deep reconstruction network

MRI

magnetic resonance imaging network

MRSR

MR super-resolution

MSCNN

model skipped convolutional neural network

nRMSE

normalized root mean square error

OLED

overlapping-echo detachment

PCA

principal coefficient analysis

RCNN

recurrent convolutional neural network

Relax-MANTIS

reference-free latent map extraction MANTIS

ReLU

rectified linear unit

RF

radiofrequency

SCQ

spatially-constrained tissue quantification

SNR

signal-to-noise ratio

SVD

singular value decomposition

TrueFISP

True Fast Imaging with Steady State Precession

T ₁

spin-lattice relaxation time

T _1ρ

spin-lattice relaxation in the rotating frame

T ₂

spin-spin relaxation time

T _E

echo time

T _R

repetition time

UTE

ultra-short echo time

VN

variational network