Abstract
Thiol dioxygenases are a subset of nonheme iron oxygenases that catalyze the formation of sulfinic acids from sulfhydryl-containing substrates and dioxygen. Among this class, cysteine dioxygenases (CDOs) and 3-mercaptopropionic acid dioxygenases (3MDOs) are the best characterized, and the mode of substrate binding for CDOs is well understood. However, the manner in which 3-mercaptopropionic acid (3MPA) coordinates to the nonheme iron site in 3MDO remains a matter of debate. A model for bidentate 3MPA coordination at the 3MDO Fe-site has been proposed on the basis of computational docking, whereas steady-state kinetics and EPR spectroscopic measurements suggest a thiolate-only coordination of the substrate. To address this gap in knowledge, we determined the structure of Azobacter vinelandii 3MDO (Av3MDO) in complex with the substrate analog and competitive inhibitor, 3-hydroxypropionic acid (3HPA). The structure together with DFT computational modeling demonstrates that 3HPA and 3MPA associate with iron as chelate complexes with the substrate-carboxylate group forming an additional interaction with Arg168 and the thiol bound at the same position as in CDO. A chloride ligand was bound to iron in the coordination site assigned as the O2-binding site. Supporting HYSCORE spectroscopic experiments were performed on the (3MPA/NO)-bound Av3MDO iron nitrosyl (S = 3/2) site. In combination with spectroscopic simulations and optimized DFT models, this work provides an experimentally verified model of the Av3MDO enzyme–substrate complex, effectively resolving a debate in the literature regarding the preferred substrate-binding denticity. These results elegantly explain the observed 3MDO substrate specificity, but leave unanswered questions regarding the mechanism of substrate-gated reactivity with dioxygen.
Keywords: thiol dioxygenase, nonheme iron, oxygenase, competitive inhibition, structure, DFT, computational modeling, iron-nitrosyl, FT-EPR, HYSCORE
Abbreviations: 2MA, 2-mercaptoanaline; 3HPA, 3-hydroxypropionic acid; 3MDO, 3-mercaptopropionic acid dioxygenase; 3MPA, 3-mercaptopropionic acid; 3SPA, 3-sulfinopropionic acid; ADO, cysteamine dioxygenase; Av3MDO, Azotobacter vinelandii 3MDO; CA, cysteamine (2-aminoethanethiol); CDO, cysteine dioxygenase; CSA, cysteine sulfinic acid; CW, continuous wave; CYS, L-cysteine; DFT, density-functional theory; DNIC, dinitrosyl iron complex; EPR, electron paramagnetic resonance; ET, ethanethiol; FT, Fourier transform; H-bond, hydrogen bond; HEPES, 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid; HT, hypotaurine; HYSCORE, hyperfine sublevel correlation spectroscopy; IPTG, isopropyl β-D-1-thiogalactopyranoside; MSDO, mercaptosuccinate dioxygenase; Pa3MDO, Pseudomonas aeruginosa 3MDO; PCO, plant cysteine oxidases; RnCDO, Rattus norvegicus CDO; SHY, Ser-His-Tyr; TPTZ, 2,4,6-tripyridyl-s-triazine; XRD, X-ray diffraction
Thiol dioxygenases are a subset of nonheme mononuclear iron oxygenases that catalyze the O2-dependent oxidation of thiol-bearing substrates to yield the corresponding sulfinic acid. Among this group, cysteine dioxygenase (CDO) (1, 2, 3, 4, 5) and cysteamine dioxygenase (ADO) (6, 7) are responsible for the biosynthesis of cysteine sulfinic acid (CSA) and hypotaurine (HT), respectively, which are precursors for the biosynthesis of taurine (1). Among bacteria, a number of other thiol dioxygenases have been identified, including mercaptosuccinate dioxygenase (MSDO) (8) and 3-mercaptopropionate dioxygenase (3MDO) (9, 10, 11, 12, 13, 14). Plant cysteine oxidases (PCO) catalyze the formation of an N-terminal cysteine sulfinic acid within ERF-VII transcription factors to initiate N-end rule degradation (15, 16). A similar function has recently been proposed for mammalian ADO in controlling regulators of G protein signaling (17).
Over the past decade, this class of enzymes has attracted considerable attention as imbalances in L-cysteine (CYS) metabolism are associated with neurological diseases (5, 18, 19). This observation suggests a correlation between impaired sulfur metabolism, oxidative stress, and neurodegenerative disease (20, 21). Consequently, enzymes involved in sulfur oxidation and transfer are increasingly being evaluated as potential drug targets (22, 23, 24, 25).
Across the domains of life, structurally characterized thiol dioxygenases share two major features: (1) a mononuclear nonheme iron active site coordinated by three protein-derived histidine residues and (2) a conserved sequence of outer Fe-coordination sphere amino acids (Ser-His-Tyr), the latter being adjacent to the iron site (∼3 Å). By analogy to the chymotrypsin-like serine proteases, the Ser-His-Tyr (“SHY”) network was previously referred to as a “catalytic triad” (5, 13, 14, 26, 27, 28, 29, 30). However, these residues appear to enhance the catalytic rate and efficiency but are not required for activity (31, 32, 33, 34). Consequently, we simply refer to this hydrogen-bonding network as the “SHY” motif. In eukaryotic CDOs, the “SHY” motif tyrosine (Tyr157) is covalently cross-linked with an adjacent cysteine residue (C93) to yield a C93-Y157 pair (35, 36), whereas bacterial forms utilize an unmodified Tyr-residue at this position.
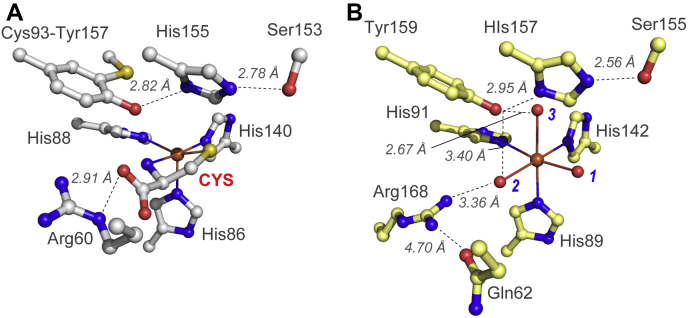
As shown in Figure 1A, the substrate-bound mammalian CDO reveals a bidentate coordination of CYS to the mononuclear Fe-site via thiolate and neutral amine (32, 37, 38). Both kinetic and spectroscopic studies demonstrate additional interactions between the CYS-bound Fe-site and outer sphere residues (Tyr157 and Arg60) within the CDO active site (27, 31). These multiple points of interaction are likely responsible for the high substrate specificity exhibited by this enzyme (35). To illustrate, cysteamine [2-aminoethanethiol, (CA)] is structurally similar to CYS, lacking only the α-carboxylate group. It is therefore reasonable that this substrate analogue could coordinate to the CDO Fe-site in a similar bidentate fashion as CYS. However, relative to CYS, a 10,000-fold decrease in kcat/KM was reported in steady-state reactions with CA (35). Therefore, removal of the CYS carboxylate has a profound impact on the formation of the CDO ES complex. More dramatically, no activity whatsoever is observed in reactions with similarly sized thiol substrates lacking an amine functional group. This observation demonstrates that coordination of the substrate amine to the CDO Fe-site is required for activity. By contrast, 3MDO (Fig. 1B) is capable of accommodating a variety of thiol-bearing substrates, such as 3-mercaptopropionic acid (3MPA), CYS, and CA to catalyze dioxygenation over a broad pH range (10, 11, 13, 14). While a modest decrease in kcat is observed in reactions with CA [0.29 ± 0.08 s−1] relative to 3MPA and CYS [1.0 ± 0.1 s−1], the vast difference in catalytic efficiency (kcat/KM) identifies 3MPA as the preferred substrate for MDO (14). Since 3MPA lacks an amine functional group, the first coordination sphere for the Av3MDO Fe-site cannot be equivalent to CDO.
Figure 1.
Structural comparison of mammalian CDO and Pseudomonas aeruginosa 3MDO active site.A, 1.6 Å X-ray diffraction structure of CYS-bound Rattus norvegicus CDO (PDB accession code 4IEV) (90). Selected atomic distances are designated by dashed lines. B, 2.14 Å X-ray diffraction structure of the Pseudomonas aeruginosa 3MDO active site (PDB 4TLF) (11). Fe-coordinated solvent ligands designated (1–3) for clarity.
To date, structures for the 3MPA-bound enzyme have been unavailable; however, two models for substrate binding at the Fe-site have been proposed. A bidentate model for 3MPA coordination to the Fe-site via substrate thiol and carboxylate functional groups was recently proposed by Jameson and Karplus (9). In this report, docking of 3MPA into the Pseudomonas aeruginosa 3MDO (Pa3MDO) crystal structure led to the conclusion that a salt bridge formed between the Arg168 guanidinium group and 3MPA carboxylate was catalytically essential (9, 10). Structurally, this model closely matches the CYS-bound mammalian CDO, although the relevant Arg group is in a position nonhomologous to that of mammalian CDO. The proposed salt bridge provided a reasonable explanation for the decreased affinity of the enzyme for amino-bearing substrates. However, the instability of Pa3MDO Arg168 variants precluded experimental validation of this model by site-directed mutagenesis.
Alternatively, we have previously argued that 3MPA Fe-coordination occurs via thiolate only based on the results of two key experiments (12). First, pH-dependent kinetic data for Av3MDO-catalyzed reactions with a substrate lacking a carboxyl group (cysteamine, CA) reveal only a modest decrease in kcat-values [v0/[E], 0.29 ± 0.08 s−1] relative to reactions performed with 3MPA and CYS [1.0–1.2 s−1] (14). Since both CDO and 3MDO exhibit an obligate-ordered binding of organic substrate prior to molecular oxygen, we conclude that Fe-coordination of the substrate–carboxylate group is not required to produce the O2-activating enzyme–substrate (ES) complex. Second, experiments using the O2-mimetic nitric oxide corroborate this argument. EPR spectroscopy verifies formation of a substrate-bound iron-nitrosyl species using thiol substrates lacking carboxylate groups [such as CA and ethanethiol (ET)] (14). Therefore, direct Fe-coordination of a substrate carboxylate is not required for converting the Fe(II) site into an NO-reactive state. These results clearly demonstrate that direct carboxylate coordination to the iron center is not obligatory to trigger oxygen activation.
In order to address this discrepancy in 3MDO substrate-binding models, we present the structure of Av3MDO in complex with the substrate analog and competitive inhibitor, 3-hydroxypropionic acid (3HPA). Using the Av3MDO-3HPA complex as a starting point, density functional theory (DFT) computations were performed to model the coordination of the native 3MPA substrate. Supporting HYSCORE experiments performed on the (3MPA/NO)-bound Av3MDO confirm the NO-binding site and corroborate bidentate 3MPA coordination in the substrate-bound iron-nitrosyl site. As suggested by Jameson and Karplus, these experiments support bidentate coordination of 3MPA with the substrate carboxylate group forming an additional interaction with Arg168 and the thiol bound at the same position as CDO.
Results
Crystal structure of Av3MDO in complex with 3HPA
Following extensive sparse matrix screening, we identified a condition giving rise to well-diffracting, rod-shaped Av3MDO crystals. The optimized crystals diffracted X-rays to ∼2.2 Å resolution and belonged to space group P31 (Table S1). Structure determination was initially complicated by the presence of tetartohedral twinning and pseudosymmetry (see Experimental procedures section for further details), but eventually the structure was solved by molecular replacement and refined against reflections extending to 2.25 Å resolution (Table S1). The polypeptide is clearly resolved except for the extreme N- and C termini, which are omitted from the final model. The asymmetric unit of the Av3MDO crystals consists of 12 monomers arranged in pairs of C2 symmetric dimers. The moderately hydrophobic dimer interface buries an average of ∼1260 Å2 (1199–1322 Å2 depending on the specific dimer pair) or ∼13% of the total monomer surface area (39) and is structurally similar to the dimers observed for 3MDOs from other bacteria (11, 26), all suggesting that it represents a physiologically relevant assembly. This finding contrasts with cysteine dioxygenases, which are monomeric proteins (37, 40).
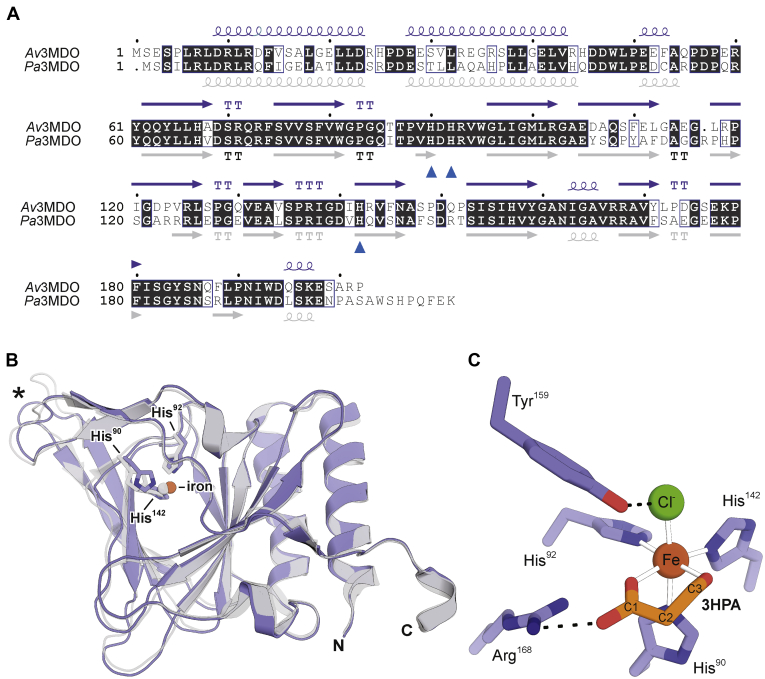
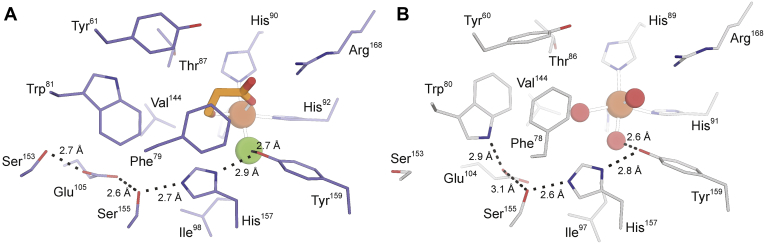
Av3MDO exhibits the classic thiol dioxygenase cupin fold consisting of three N-terminal alpha-helices followed by a series of 11 β-strands forming the cupin β-barrel structure that houses the enzymatic active site (Fig. 2A). Owing to the near uniformity in structure between the 12 monomers (Cα RMSD <0.4 Å), chain B was used as the representative monomer for structural comparisons. Among 3MDOs of known structure, Av3MDO exhibits greatest sequence and structural similarity to the 3MDO enzyme from P. aeruginosa (Pa3MDO, PDB accession code: 4TLF) with 70% sequence identity and a Cα RMSD of ∼1 Å. The largest main chain difference is found within the Leu113-Leu117 β hairpin where the insertion of an Arg in Pa3MDO results in a 5.8 Å shift at the tips of the β hairpins (Fig. 2B, asterisk). Like in Pa3MDO and other thiol dioxygenases (11, 26, 28), the iron center of Av3MDO is coordinated by three His residues (90, 92, and 142) contained within the conserved cupin motifs (Fig. 2C). Although the Av3MDO sample used for crystallization was ∼36% loaded with iron, the iron B-factors are similar to those of the surrounding His ligands when the metal is modeled at full occupancy, indicating the metal-loaded enzyme selectively crystallized (Table S1). Additionally, the metal is modeled as an Fe(III) ion given that a bulk of the iron in the enzyme sample used for crystallization was in the ferric oxidation state. However, some portion of the iron may have been photoreduced to Fe(II) during data collection. Analysis of residual electron density maps revealed two strong features near the Av3MDO iron center, which could not be successfully modeled with aquo ligands as was the case for Pa3MDO (11) (Fig. S1). As described in detail in the Experimental procedures section, we modeled these density features with chloride (trans to His90) and 3-hydroxypropionic acid (3HPA, trans to His 92 and 142), the latter being present as contaminant in the polyacrylate solution used for crystallization (Fig. 2C, Figs. S1 and S2).
Figure 2.
Structure of Av3MDO and its comparison to Pa3MDO.A, sequence alignment of Av3MDO and Pa3MDO with secondary structural elements colored in slate and gray, respectively. Curly lines, arrows, and “T” represent α-helices, β-strands, and β-turns, respectively. The iron-binding His residues are marked by blue arrows. B, structural superposition of Av3MDO (slate) and Pa3MDO (gray). Note the slight shift in His90, His92, and the iron cofactor as well as the conformational difference at the loop marked by an asterisk, which is due to a one residue deletion between residue 116 and 117 in Av3MDO. N and C mark the N- and C-termini, respectively. The superposition was performed using the “super” command in PyMOL. C, structure of the Av3MDO iron center (brown sphere) in complex with 3HPA (orange sticks) and chloride (green sphere). Dashed lines indicate H-bonding interactions.
3HPA binds to the iron center in a bidentate fashion via its hydroxyl and carboxylate oxygen atoms with metal–ligand bond distances of ∼2.1 to 2.2 Å (depending on the particular monomer). The carboxylate group simultaneously engages in an ionic interaction with Arg168, which is situated adjacent to the iron center. The 3HPA carboxylate oxygen is located ∼3.1 Å from the hydroxyl group of Tyr159, which is part of the “SHY” motif and is known to influence substrate binding to the iron center (12). Notably, we do not observe a significant interaction of 3HPA with Gln63, the distinguishing residue of the “Gln-type” thiol dioxygenases (26). These results indicate that the carboxylate-interacting Arg residue is relocated from position 61, as found in Arg-type thiol dioxygenases, to a nonhomologous position in the “Gln-type” thiol dioxygenases, as was previously suggested based on docking studies of 3MPA in Pa3MDO (9).
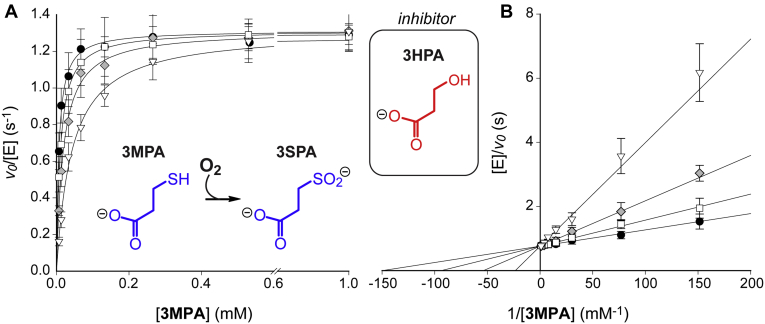
Despite the close structural resemblance of 3HPA to the native 3MPA substrate of 3MDOs (Fig. 3, inset), the influence of this compound on 3MDO activity has, to our knowledge, never been examined. Given its observed mode of binding to the iron center, we hypothesized that 3HPA could act as an inhibitor of Av3MDO. We tested this by carrying out Av3MDO steady-state assays in the presence of 3HPA (Fig. 3). We previously demonstrated that the initial rate of Av3MDO-catalyzed 3MPA reactions is independent of oxygen concentration down to ∼25 μM (13). Therefore, atmospheric oxygen concentration is sufficient to saturate the enzyme kinetics. Moreover, the consumption of oxygen per 3-sulfinopropionic acid (3SPA) produced is essentially stoichiometric (14). Crucially, no oxygen is consumed upon mixing enzyme with excess of 3HPA (10 mM). Therefore, the initial rate of oxygen consumption was used to monitor enzymatic inhibition as a function of inhibitor concentration. A Lineweaver–Burk plot of the activity data revealed an inhibition constant (Ki) of 280 ± 26 μM and intersection point at the ordinate consistent with the behavior of a classic competitive inhibitor. These results establish that 3HPA is an effective substrate analog and that its mode of binding to Av3MDO likely mirrors that of 3MPA.
Figure 3.
3-hydroxypropionic acid (3HPA) inhibition of Av3MDO-catalyzed 3MPA-reactions. Kinetic data were collected in the presence of 167 μM (white square), 500 μM (gray diamond), and 1500 μM (white triangle) 3HPA for comparison to the uninhibited enzyme (black circle). SigmaPlot was used to globally fit enzyme kinetics in either Michaelis–Menten (A) or Lineweaver–Burk (B) fashion assuming a fully competitive model of inhibition. The resulting least-square fits (solid-lines) are overlaid on kinetic data to obtain values for kcat, KM, and KI, as well as the error associated with each parameter [1.31 ± 0.01 s−1, 6.7 ± 0.4 μM, and 280 ± 26 μM, respectively]. Michaelis–Menten results (A) are presented with a gap ranging from 0.6 to 0.8 mM 3MPA to avoid data crowding at low concentration.
Chloride binds to the iron center trans to His90 at a distance of ∼2.4 Å and simultaneously contacts the hydroxyl moiety of Tyr159 forming a 2.7 Å ion–dipole interaction (Fig. 2C). This corresponds to the binding site for solvent 3 in the resting Pa3MDO structure (Fig. 1B). To distinguish this site from the other solvent-bound positions, we refer to this as the axial Fe-coordination site henceforth. Similar binding of chloride has been observed in structures of CDO (27, 41) but not in other “Gln-type” thiol dioxygenases determined to date. Activity studies carried out in the presence of increasing Cl− show a modest degree of inhibition (30%) at the 100 mM concentration found in the crystal (Fig. S3). However, EPR experiments demonstrated that Cl− concentration has no impact on the extent of NO binding to the 3MPA-bound enzyme; therefore, it is unlikely that this chloride inhibition reflects competition for O2 binding at the iron center (data not shown). It is possible that Cl− coordination is only significant for the ferric form of the enzyme, owing to its ability to provide charge balance to the Fe(III)-site. Regardless, the presence of an anionic ligand at the putative O2-binding site of the enzyme supports the idea that Tyr159 could facilitate the formation of an Fe(III)-superoxo intermediate during the Av3MDO catalytic cycle via hydrogen bonding (12).
Av3MDO active site accessibility
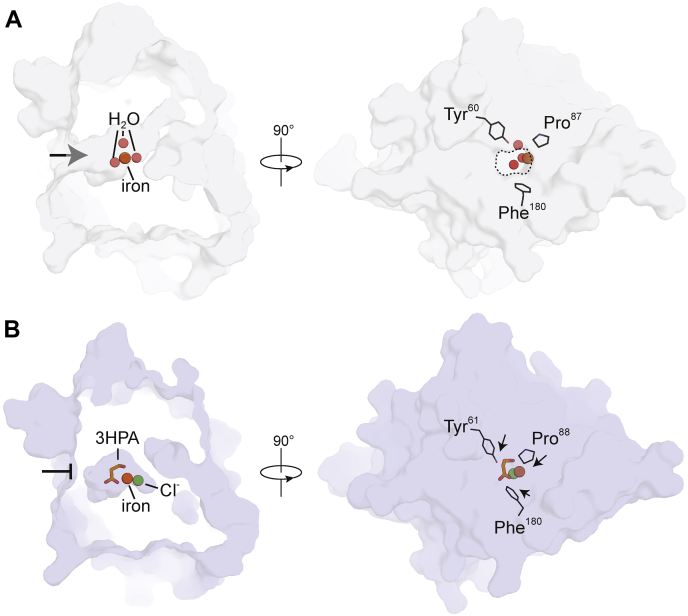
MDO homologs of Av3MDO, including Pa3MDO, exhibit active site openings on one side of the cupin beta barrel that presumably serves as the passageway for organic substrate diffusion (Fig. 4A, left). However, inspection of the Av3MDO structure revealed that its active site is completely sealed off to the bulk solvent (Fig. 4B, left). In comparison to the homologous residues of Pa3MDO, residues Tyr61, Pro88, and Phe180 of Av3MDO are shifted inward toward each other to occlude the potential passageway (Fig. 4, A and B, right panels). We observed additional variation within the active site of Av3MDO as compared with Pa3MDO including rotamer differences for Phe79 and Trp81 that were found in all 12 copies within the asymmetric unit (Fig. 5). Notably, the difference in Trp81 rotameric state results in different arrangements of the “SHY” motif between Av3MDO (Fig. 5A) and Pa3MDO (Fig. 5B). In the Pa3MDO structure, the Ser155 residue of this motif forms a hydrogen bond with Glu104, which simultaneously interacts with the Trp80 indole NH group. The alternative conformation of Trp81 as observed in the Av3MDO structure results in a ∼2.2 Å shift in Glu105 toward Ser153, which also has an altered conformation in the Av3MDO structure (Fig. 5), resulting in a new H-bond interaction with Ser153. These collective changes produce an extension of the “SHY” motif in Av3MDO.
Figure 4.
An occluded active site channel in 3HPA-bound Av3MDO. In contrast to the resting-state structure of Pa3MDO (A) in which the active site is readily accessible to organic substrate through a passageway marked by an arrow on the left view and a dashed circle on the right view, the active site of Av3MDO (B) is completely sealed to bulk solvent due to positional differences in Tyr61, Pro88, and Phe180 (directionality differences with respect to the corresponding residues in Pa3MDO indicated by arrows). The structures are shown as Connolly surfaces.
Figure 5.
Active site differences observed between 3HPA-bound Av3MDO and Pa3MDO. Comparison of the 3HPA-bound structure of Av3MDO (A) and the resting-state structure of Pa3MDO (B) reveals active site conformational differences in Phe79/Phe78 and Trp81/Trp80 and a rearrangement of the “SHY” H-bonding network with Glu105 interacting with Ser153 and Ser155 in the Av3MDO structure.
Because intrinsic structural differences between Av3MDO and Pa3MDO are expected to be small owing to their high sequence similarity (Fig. 2A), we considered the possibility that the observed active site differences could arise from the bound substrate mimetic in Av3MDO. To test this hypothesis, we identified alternative crystallization conditions to allow investigation of the resting-state structure of Av3MDO. Following further sparse matrix screening, we identified a crystallization condition containing a nonpolyacrylate precipitant (pentaerythritol propoxylate) as well as sodium thiocyanate that produced yellowish, rod-shaped crystals. The crystals diffracted X-rays to ∼3 Å resolution and belonged to space group P6122 with a pair of dimers (same conserved interface described above) in the asymmetric unit. Strong difference density in the equatorial positions of the iron center was adequately explained by two water molecules while the axial position contained an elongated difference peak that was too strong to represent only water or chloride (Fig. S4A). Placement of thiocyanate, a well-known Fe(III)-binding ligand present at > 0.3 M concentration in the crystal mother liquor, at this position adequately accounted for the density with reasonable refined B-factors (Table S1). Because thiocyanate is an ambivalent ligand, test refinements were carried out with the anion bound via either its nitrogen or sulfur atoms. Analysis of difference maps and refined B-factors provided strong evidence that coordination is through the nitrogen atom, which is consistent with the coordination preferences of Fe(III), a hard Lewis acid, and small-molecule crystallography results for high-spin, nonheme iron model compounds (42). Although this structure is not a true “resting-state” form of Av3MDO, it allowed us to address the question of whether the active site closure results from 3HPA binding.
Contrary to our hypothesis, we observed that the active site has maintained its closed state in this new crystal form (Fig. S4B). Hence, we conclude that the closed conformation is energetically favorable in crystallo and that active site closure is not strictly coupled to 3HPA coordination. Notable differences between the two Av3MDO crystal forms included a ∼40° rotation of the Phe79 Cβ-Cγ bond away from the iron center in the 3HPA-bound structure as well as rotamer differences for Gln63 and Ile98, which all are likely a consequence of steric factors involving the different metal-bound ligands (Fig. S4A). By contrast, the conformation of Trp81 is identical in every copy within the asymmetric units of the two Av3MDO structures, suggesting it represents an intrinsic structural difference as compared with Pa3MDO.
Computational modeling of the Av3MDO-3MPA complex
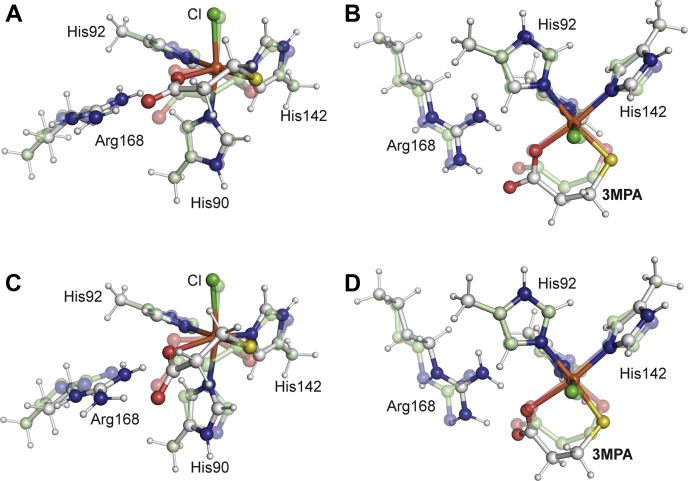
The structure of the Av3MDO-3HPA complex revealed a bidentate coordination of 3HPA to the Fe-site through the hydroxyl group and proximal oxygen of the carboxylate (Figs. 2C and 5A). Given the near structural equivalence of 3MPA and the competitive inhibitor 3HPA, a logical argument for bidentate 3MPA coordination within the enzymatic site can be made. Based on this hypothesis, we determined the optimal 3MDO Fe-site geometry for the bidentate Av3MDO-3MPA complex through DFT calculations using the coordinates from the 3HPA-bound Av3MDO crystal structure as a starting point. A truncated model for the inhibitor-bound active site, comprised of iron, His residues 90, 92, and 142, chloride, and Arg168, was generated and geometry-optimized with both 3HPA and 3MPA bound to the iron. Selected first-coordination sphere distances are presented in Table S2 for the Av3MDO-HPA complex, CYS-bound CDO, synthetic nonheme mononuclear iron model complexes, and our computational models. Although the bulk oxidation state observed for Av3MDO was ferric prior to crystallization, the possibility of reduction by the synchrotron source could not be ruled out.
The pKa of the 3HPA hydroxyl (14.4–15.1) is expected to be much higher than the 3MPA-thiol (∼8) (43). While it is unlikely that the Fe-bound 3HPA-hydroxyl is deprotonated, pKa values for metal-coordinated water can decrease by several pH units (44, 45). To corroborate the ionization state of the 3HPA inhibitor, optimized DFT models for the deprotonated (3HPA2−)- and protonated (3HPA1−)-hydroxyl group were made with ferric and ferrous iron for comparison to the crystallographic results (Table 1). While the overall structures were similar (Fig. S5), the protonated (3HPA1−)-bound model exhibited the lowest RMSD values relative to crystallographic coordinates. Moreover, optimized bond distances and angles closely match what is observed for the Av3MDO-3HPA complex. From this we conclude that the 3HPA-inhibitor coordinates bidentate to the Fe-site through carboxylate and neutral hydroxyl groups. For simplicity, all calculations and 3HPA-bound structures discussed henceforth refer solely to the 3HPA1− form in which the hydroxyl group is protonated. However, the calculated structural perturbations incurred by altering the oxidation state of the iron (+II versus +III) site fall within the inherent error (∼0.1 Å) of the crystal structure. Therefore, neither oxidation state can be ruled out on the basis of these calculations.
Table 1.
Selected distances (top) and angles (bottom) of the Av3MDO-3HPA complex (PDB accession code 6XB9) as compared with optimized DFT models of the iron active bound to 3HPA and 3MPA
| Selected geometric parameters | 6XB9 | Fe(III) 3HPA2− | Fe(III) 3HPA1− | Fe(III) 3MPA | Fe(II) 3HPA2− | Fe(II) 3HPA1− | Fe(II) 3MPA |
|---|---|---|---|---|---|---|---|
| RMSDa | - | 0.382 | 0.248 | 0.417 | 0.517 | 0.357 | 0.547 |
| Distance (Å) | |||||||
| Fe-O/S distance (Å) | 2.16 | 1.87 | 2.23 | 2.32 | 1.91 | 2.26 | 2.33 |
| Fe-O(carb)b (Å) | 2.17 | 2.14 | 1.97 | 2.08 | 2.55 | 2.25 | 2.51 |
| Fe-Cl (Å) | 2.36 | 2.36 | 2.28 | 2.36 | 2.60 | 2.38 | 2.47 |
| Fe-His(Ave) | 2.16 | 2.18 | 2.13 | 2.20 | 2.17 | 2.15 | 2.19 |
| Fe-H90 | 2.15 | 2.17 | 2.17 | 2.19 | 2.18 | 2.16 | 2.20 |
| Fe-H92 | 2.16 | 2.20 | 2.08 | 2.21 | 2.18 | 2.11 | 2.22 |
| Fe-H142 | 2.16 | 2.17 | 2.13 | 2.19 | 2.16 | 2.19 | 2.15 |
| Angles (°) | |||||||
| Fe-O/S-Cα | 92.5 | 120.6 | 113.0 | 96.7 | 117.7 | 111.6 | 98.4 |
| H90-Fe-Cl | 175.7 | 171.8 | 174.0 | 169.3 | 169.6 | 171.5 | 166.3 |
| H92-Fe-O/S | 171.1 | 177.9 | 174.1 | 171.9 | 168.2 | 179.3 | 175.9 |
| O(carb)-Fe-O/S | 101.1 | 92.1 | 85.1 | 96.4 | 82.6 | 88.6 | 88.8 |
| 3HPA/3MPA C1-C2-C3 | 114.6 | 116.9 | 115.6 | 119.3 | 116.5 | 117.8 | 117.6 |
The 3HPA-inhibitor was modeled as both the protonated and deprotonated alcohol (3HPA1− and 3HPA2−) for comparison.
Hydrogens and all constrained atoms were excluded from RMSD calculations.
Fe-O(carb) designates the distance separating the Fe(III)-site from the 3HPA (or 3MPA) carboxylate O-atom.
Given the ambiguous oxidation state of the iron site, 3MPA-bound structures were optimized in both the ferric and ferrous states. Figure 6 illustrates the Fe-sites for the Av3MDO-3HPA XRD structure and the DFT-optimized 3MPA-bound model. Selected bond distances and angles for both optimized structures are provided in Table 1 for comparison. DFT-optimized structures show a shorter bond length between the iron and 3HPA-hydroxyl than with the corresponding 3MPA-thiolate [2.23 versus 2.32 Å, respectively for ferric and 2.26 versus 2.33 Å for ferrous]. Similarly, the distance separating the substrate carboxylate O-atom from the Fe-site (Fe-Ocarbox) is closer for the ferric 3HPA-bound model [2.08 for 3MPA versus 1.97 Å for 3HPA]. The trend is more drastic in the ferrous state with 2.25 Å for 3HPA and 2.51 Å for 3MPA. The longer bond length for the 3MPA-bound structure can likely be attributed to (1) electrostatic interaction of the anionic carboxylate group with the adjacent cationic Arg168 and (2) inclusion of thee negative charges [Cl− and 3HPA2− (or 3MPA2−)] in the Fe(II) coordination sphere. However, charge neutrality is easily remedied by loss of a chloride ligand in the ferrous enzyme. For both ferric computational models, these distances are shorter than observed in the Av3MDO-3HPA complex (∼2.17 Å). By contrast, both ferrous models are longer, but well within the estimated coordinate error of the crystal structure (∼0.1 Å). Similarly, the average Fe-NHis and Fe-Cl bond lengths for the 3MPA-bound complex are largely invariant and any deviations observed fall well within the coordinate error of the Av3MDO-3HPA complex. For comparison, selected bond distances for thiolate-bound nonheme ferric thiol dioxygenase enzymes and model complexes are provided in Table S2.
Figure 6.
Overlay of 3HPA-bound Av3MDO complex (transparent-green) with a DFT optimized model (white) of the 3MPA-bound Av3MDO Fe(III)-site (RMSD, 0.417 Å). Shown from a side-on view (A) and following 90° rotation (B) through the bond of His142 (which is excluded from the image). These views are replicated in panels C and D for the ferrous optimized model. Selected distances, angles, and RMSD values are presented in Table 1 for comparison.
Regardless of iron oxidation state (+II or +III), all optimized structures modeled (3HPA2−, 3HPA1−, and 3MPA) predict a bidentate Fe coordination via a single carboxylate O-atom and terminal oxide/hydroxyl or thiolate. As predicted by Aloi et al. (9), this places the substrate carboxylate in a favorable position for electrostatic stabilization by cationic Arg168. Taken together with the XRD structure of the Av3MDO-3HPA complex, these optimized DFT structures infer that the native 3MPA substrate coordinates to the Av3MDO iron site in a bidentate fashion as well.
Modeling of the (3MPA/NO)-bound Av3MDO
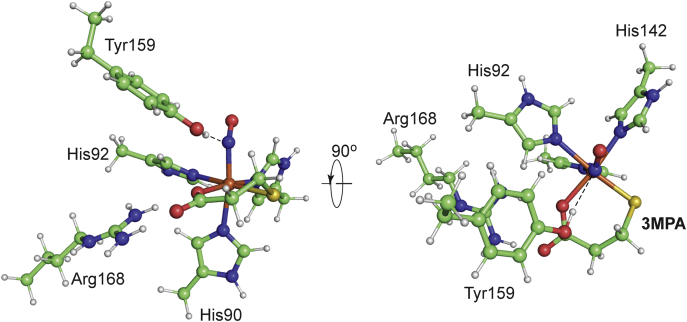
Nitric oxide is frequently used as a surrogate for molecular oxygen when characterizing nonheme iron oxidase/oxygenases. These experiments provide an excellent handle for EPR spectroscopy as the resulting iron-nitrosyl {FeNO}7 species is paramagnetic (S = 3/2). According to the Feltham–Enemark notation (46), the ground state S = 3/2 spin-manifold is produced by an antiferromagnetic coupling between a high-spin Fe(III) (S = 5/2) and a bound NO− anion (S = 1). Moreover, given the similarity of the NO electronic structure to O2, the resulting (3MPA/NO)-bound Av3MDO ternary complex likely provides insight into transient iron-oxo species produced during native turnover with oxygen. The 3MPA-bound iron nitrosyl form of Av3MDO has been extensively characterized by EPR and Mössbauer spectroscopies (12, 14). Such data provides an opportunity to validate computational models by comparing predicted spectroscopic properties to experimental values. To this end, we studied whether bidentate iron coordination of 3MPA is retained in the (3MPA/NO)-bound ternary complex. Starting from the optimized Av3MDO-3MPA model, a new structure for the (3MPA/NO)-bound Av3MDO active site was modeled and optimized. As shown in Figure 7, nitric oxide was placed in putative oxygen-binding site trans to His90, essentially displacing the axial chloride in previous models. This positioning of NO is also consistent with previous EPR experiments, which suggest that hydrogen bonding from Tyr159 stabilizes NO binding within the active site (12). The outer sphere Tyr159 was included in optimized models to account for this interaction.
Figure 7.
The optimized structure of the (3MPA/NO)-bound Av3MDO active site. The left panel displays a side view highlighting the axial nitric oxide ligand. The right panel rotates the structure to more clearly show bidentate coordination of 3MPA and Tyr159 hydrogen bond donation to the nitrogen of the NO ligand.
The precise orientation of hydrogen bonding between Tyr159 and Fe-bound nitric oxide is not known. Therefore, an energy surface (47, 48, 49) for Tyr159 hydrogen bonding was generated from the Av3MDO-3HPA complex to evaluate likely H-bond acceptors (Supporting Information). As shown in Fig. S6C, an energy minimum is observed for H-bond donation from Tyr159 to the Fe-bound Cl atom for both ferrous and ferric oxidation states. Potentially, substitution of the axial chloride ligand for NO could alter the direction of the Tyr159 H-bond to favor donation to H157. However, this would be inconsistent with the previous EPR and Mössbauer results. Moreover, as both chlorine and nitrosyl ligands have an equivalent formal charge (−1), a reasonable argument can be made that H-bond donation from Tyr159 would similarly favor axially bound NO over His157. Table S3 illustrates the influence of Tyr159 H-bond orientation on selected geometric parameters in the optimized (3MPA/NO)-bound Av3MDO Fe-site.
As an initial validation of the model, Mössbauer spectroscopic parameters were calculated for the optimized (3MPA/NO)-bound active site structures allowing comparison to the experimental values. As shown in Table S4, the isomer shift (δ) and quadrupole splitting (ΔEQ) observed for the (3MPA/NO)-bound enzyme are reasonably reproduced by all optimized models. In particular, ΔEQ is highly sensitive to the nature and symmetry of ligands directly coordinated to the Fe-site. Thus, the closeness of calculated ΔEQ-values strongly supports the hypothesis of a bidentate 3MPA coordination within the (3MPA/NO)-bound enzyme. Overall, the ΔEQ and asymmetry parameter (η) are best fit in optimized structures with Tyr159 donating a hydrogen bond to the N-atom of nitric oxide. However, the observed deviations among optimized structures largely fall within experimental error. Therefore, while the calculated Mössbauer parameters are entirely consistent with the optimized model shown in Figure 7, the orientation of Tyr159 hydrogen bond donation cannot be definitively assigned based solely on these results.
HYSCORE of the (3MPA/NO)-bound Av3MDO
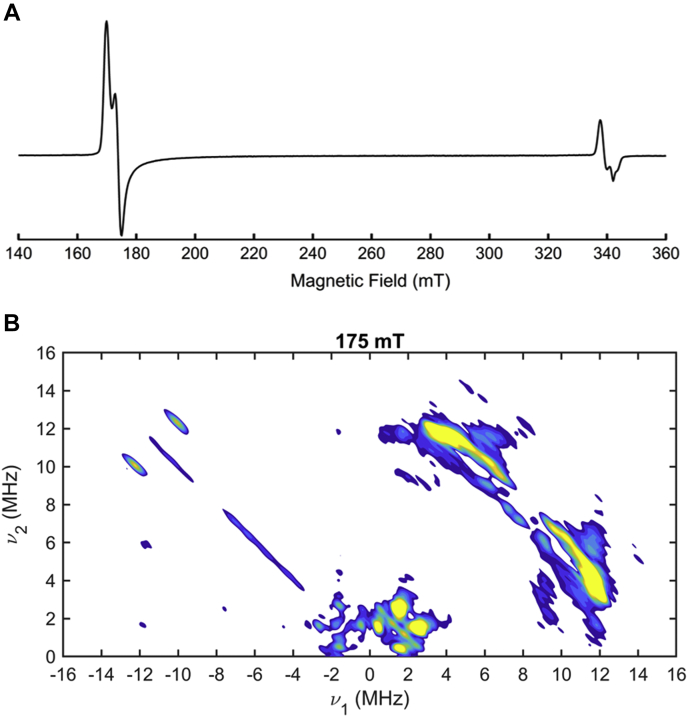
As noted above, we have previously reported the characterization of iron-nitrosyl produced by treating 3MPA-bound Av3MDO with nitric oxide using continuous-wave (CW) EPR spectroscopy (12). The CW EPR spectrum, shown in Figure 8 (panel A), has observed g-values of 4.06, 3.96, and 2.01 consistent with a nearly axial (E/D = 0.008) S = 3/2 iron-nitrosyl site. Further, the measured axial zero field splitting (D = 10 ± 2 cm−1) confirms that this signal is derived from a transition within the ground |ms = ± 1/2> doublet (38). These parameters are consistent with other spectroscopically and crystallographically characterized S = 3/2 iron-nitrosyl complexes (50, 51). Crucially, the observed CW spectrum is nearly homogeneous and exhibits only minor contributions from known dinitrosyl (DNIC) complexes localized near g = 2. As a result, this complex is ideal for further characterization by hyperfine sublevel correlation spectroscopy (HYSCORE).
Figure 8.
CW EPR (A) and HYSCORE (B) spectra of (3MPA/NO)-bound Av3MDO iron-nitrosyl. The instrumental parameters for (A) (previously reported) are described in detail elsewhere (12). The data in (B) were collected with the following instrumental parameters: microwave frequency, 9.78 GHz; field position of 175 mT; temperature, 5 K; pulse repetition rate, 1.25 kHz; τ, 120 ns. Additional instrumental parameters are described in detail in Experimental procedures.
HYSCORE is a two-dimensional, four-pulse EPR technique that directly probes magnetic nuclei coupled to paramagnetic centers. This is an exceptionally sensitive technique that has the resolution necessary to distinguish and characterize individual nuclei. The magnitude of coupling for each magnetic nucleus is highly dependent on the distance separating it from the paramagnetic center and its position relative to the magnetic axis. Similar HYSCORE experiments have been performed on a variety of nonheme enzymes to provide structural details about the (substrate/NO)-bound active site geometry (12, 51, 52, 53, 54, 55, 56). Moreover, relative to Mössbauer spectroscopy, HYSCORE is much more sensitive to subtle structural perturbations in the outer coordination sphere of the Fe-site, allowing for a more robust validation of the optimized (3MPA/NO)-bound Av3MDO structure.
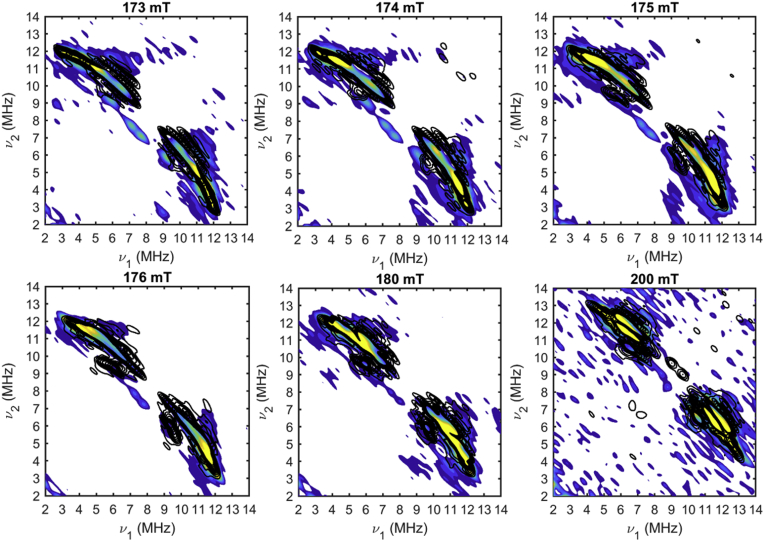
Figure 8 (panel B) shows a representative HYSCORE spectrum of the (3MPA/NO)-bound Av3MDO complex. This spectrum was measured at 175 mT near the low-field edge of the CW EPR spectrum (Fig. 8A) where there is no contribution from the small proportion of DNIC that appears near g = 2 (12, 38). The spectrum can be divided into two quadrants, the (−, +) quadrant, or the left half of the spectrum, and the (+, +) quadrant, or the right half of the spectrum. HYSCORE peaks appear in pairs that are reflected along the frequency diagonal at or near the nuclear Larmor frequency. The spectrum in Figure 8B encodes precise information about the nuclei coupled to the S = 3/2 center. The spectrum is comprised of multiple, overlapping peaks characteristic of coupled 14N and 1H from the coordinated histidine ligands, NO, 3MPA, and other nearby residues making up the second coordination sphere. The peaks in the (−, +) quadrant represent strongly coupled 14N nuclei; these peaks arise from nuclei where the hyperfine couplings are much greater than the 14N Larmor frequency at 175 mT, ∼0.54 MHz. These peaks are characteristic of what is observed for directly coordinated 14N from histidine ligands (53, 57). The (+, +) quadrant contains peak from weakly coupled nuclei, namely those where the 14N Larmor frequency is greater than the hyperfine coupling. Figure 8B shows several overlapping peaks in the (+, +) quadrant below ∼4 MHz; these peaks can be attributed to weakly coupled 14N. In general, the remote 14N of histidine ligands in metalloenzymes has a much weaker hyperfine coupling than the directly coordinated 14N (57). For example, the remote 14N in histidine residues coordinated to the diiron site of the hydroxylase component of methane monooxygenase was found to have an isotropic coupling of 0.8 MHz, whereas the coordinated nitrogen had a coupling of 13.0 MHz (58). Therefore, the peaks in the (+, +) quadrant below 4 MHz are likely the remote 14N on the three coordinated histidine ligands, although there could be a small contribution from second-sphere residues. In addition to 14N, the (+, +) quadrant reveals multiple pairs of coupled 1H peaks that are shifted from the 1H Larmor frequency by significant dipolar couplings. The most intense region of the 1H spectrum is an arc centered near (5, 12) MHz (ν1, ν2) that curves in toward the frequency diagonal. For simplicity, we refer to the coordinates of the peak that is on the high frequency side (larger ν2) of the diagonal since each peak is nearly symmetric about the diagonal. The arc consists of several underlying peaks with similar anisotropic hyperfine couplings. There are two additional sets of peaks with frequencies of (6, 7, 8, 9) MHz; these are more weakly coupled 1H as they appear closer to the 1H Larmor frequency along the diagonal.
In order to derive specific structural information from HYSCORE results, we carried out computational simulations for comparison to the experimental spectrum. In this case, the observed HYSCORE spectrum depends on several discrete factors. For an I = 1/2 nucleus like 1H, the peak positions are largely determined by the hyperfine coupling and the position of each nucleus with respect to the magnetic axis system. Beyond these parameters, additional complications arise for 14N (I = 1) quadrupole nuclei. For this reason, we chose to focus our attention solely on the 1H region of the spectrum. DFT calculations provide the geometry-optimized model from which distances and positions of each coupled 1H can be derived. As such, it is possible to simulate the HYSCORE spectrum by including all protons in the calculated model. However, the strongest couplings dominate the spectrum and the simulated intensity, which makes the intensity of weakly coupled protons difficult to distinguish. Accordingly, we focused on eight individual 1H with larger dipolar couplings (Ttotal derived from Equation 6, and listed in Table S5). These protons are located on the coordinated histidine residues and on C3 of 3MPA. Figure 9 shows HYSCORE spectra and simulations at magnetic fields spanning the low-field region of the EPR spectrum. The simulations take into account eight protons with axial hyperfine couplings, each with a hyperfine tensor and a set of angles that relate the Fe-1H vector and the magnetic axis system. Many of these peaks overlap due to the similarities in dipolar couplings. Figs. S7–S10 illustrate the individual contributions for each simulated 1H to the overall 1H HYSCORE spectrum. The hyperfine tensors and Euler angles, listed in Supporting Information (Table S5), were both derived directly from the DFT-optimized structure (see Experimental procedures for details).
Figure 9.
Comparison of (3MPA/NO)-bound Av3MDO HYSCORE data (1H region) collected at six field positions (173–200 mT) to simulations using parameters from the DFT optimized model. In each panel, experimental spectra are represented by the color contours, whereas simulations are overlaid in black contours. Data were collected from 173 to 200 mT using the following instrumental parameters: microwave frequency, 9.78 GHz; temperature, 5 K; pulse repetition rate, 1.25 kHz; τ, 120 ns. Additional instrumental parameters are described in detail in Experimental procedures.
The intensity of a 1H HYSCORE peak depends in part on measurement conditions, but the shape of the contours, or the peak “footprint,” shows the range of observed nuclear frequencies, which is largely independent of measurement conditions. Consequently, HYSCORE spectra are simulated by matching the peak locations and shapes rather than the intensities. The simulations in Figure 9, plotted as black contours, match the observed experimental contour shapes well. While the overlap of 1H peaks in the HYSCORE spectra limits our ability to optimize simulated contributions from individual 1H nuclei, the calculated parameters obtained from our computational model reasonably reproduce the entire 1H region of the observed spectra collected at multiple magnetic field positions. This later point is crucial as HYSCORE simulations are sensitive to changes in the hyperfine tensor and nuclear positions. To illustrate, Fig. S11 demonstrates how the simulated peaks for each 1H can shift considerably with relatively small changes in hyperfine coupling and/or its position relative to the magnetic axis. Accordingly, the fact that the simulations shown in Figure 9 reasonably overlay onto the experimental peaks across multiple magnetic fields confirms that the calculated model produces reasonable distances and locations for the 1H included in simulations. The protons in the optimized model that are not included in these simulations produce peaks that are too weak to resolve in the presence of the intense peaks from strongly coupled protons. The 3MPA protons on C2 fall into this category. We therefore performed deuterium exchange experiments as additional corroboration of bidentate 3MPA coordination. These experiments uniquely identify any solvent-based ligands that would be present in the case of monodentate 3MPA coordination. In principle, monodentate 3MPA coordination would be evident from the absence of strongly coupled 1H peaks in samples prepared in 2H2O-buffer. In order to test this, samples of (3MPA/NO)-bound AvMDO were prepared in 2H2O-buffer in order to observe Fe-coordinated solvent ligands and exchangeable protons via lost peaks in the 1H HYSCORE spectrum. However, as shown in Fig. S11, no such difference is observed in 2H2O samples. This observation is consistent with the absence of solvent-derived ligands directly coordinated to the Fe-site. Moreover, the observed nonexchangeable behavior is consistent with what is expected for each simulated group (Table S5).
Despite the inability to resolve the 1H peaks associated with 3MPA C2, a monodentate coordination of 3MPA can be reasonably ruled out as this would significantly alter the position and distance of the 3MPA C3 protons. Therefore, the ability to simulate the 1H HYSCORE spectra collected at multiple magnetic fields along with the absence of exchangeable Fe-bound solvent ligands provides ample validation of the optimized (3MPA/NO)-bound Av3MDO Fe-site model shown in Figure 7. Collectively, these results corroborate that the bidentate inhibitor coordination reflected in the Av3MDO-3HPA complex is retained in the 3MPA-bound ES-complex.
Discussion
Substrate coordination at the Av3MDO Fe-site
The structure of Av3MDO in complex with 3HPA and corroborating DFT computational modeling of the 3MPA-bound Fe-site are consistent with the bidentate substrate binding model proposed by Jameson and Karplus (9) where the substrate carboxylate group simultaneously interacts with iron as well as a nearby Arg168 residue. Interestingly, this Arg is nonhomologous to the Arg residue employed by CDO to bind the carboxylate group of CYS, demonstrating the phenomenon of active site plasticity within different lineages of thiol dioxygenases (59). Given the ambiguous oxidation state in the Av3MDO-3HPA complex, additional spectroscopic validation was performed to independently corroborate the nature of 3MPA coordination at the enzymatic Fe-site. Computationally predicted Mössbauer parameters (δ and ΔEQ) for the optimized (3MPA/NO)-bound Av3MDO site (Fig. 7) are consistent with reported experimental values, thereby providing support for a similar 3MPA coordination as present in the Av3MDO-3HPA complex. Moreover, the closeness of simulated HYSCORE 1H-couplings from coordinated His residues (His90, His92, and His142) and 3MPA C3 to observed spectra collected across multiple field positions makes a powerful argument for the validity of the optimized (3MPA/NO)-bound Av3MDO active site model. Further, since coordination of NO to the Fe-site defines the primary magnetic axis, 1H HYSCORE simulations also verify NO (and likely also dioxygen) binds to the axial Fe-site trans to His90. While 1H-peaks associated with 3MPA C2 are too weak to resolve, the absence of a difference in peaks between 2H2O/H2O HYSCORE spectra demonstrates that there are no solvent-derived ligands in the Av3MDO ES complex, further supporting the conclusion of bidentate coordination of the native 3MPA substrate at the enzymatic Fe-site. Collectively, the combined crystallographic, spectroscopic, and computational results provide an experimentally verified model for 3MPA binding within the Av3MDO active site resolving a debate in the literature regarding the denticity of substrate binding.
The chelate effect associated with bidentate 3MPA Fe coordination likely explains the ∼2000-fold increase in the KM value obtained in CA-reactions [0.013 ± 0.005 versus 26.5 ± 5 mM] (14). As mentioned in the start of the text, we previously disregarded this possibility on the basis of our kinetic and CW EPR studies performed on Av3MDO using multiple thiol-bearing substrates (3MPA, CYS, CA, and ET) (14). Taken together with the results presented here, it is evident that while bidentate coordination of the native 3MPA substrate is favored, it is not obligatory for catalysis or O2 activation. For substrates lacking a carboxylate functional group, only coordination of a thiolate (presumably trans to H92) is required for gating O2 activation. This behavior is unlike mammalian CDO, which is highly specific for the L-isomer of CYS (35). Despite the ability to activate oxygen, Av3MDO reactions with non-carboxylate-bearing substrates are significantly uncoupled. For instance, in assays with 3MPA and CYS, the consumption of molecular oxygen is essentially stoichiometric with formation of the sulfinic acid. However, in reactions with CA, the coupling efficiency decreased by more than half [40 ± 9%] (14). Similarly, in reactions with the aromatic substrate 2-mercaptoanaline (2MA), O2 consumption was observed without formation of a sulfinic acid product. Instead, the majority products of this reaction appear to be hydrogen peroxide and 2MA disulfide (60, 61). By contrast, no oxygen consumption is observed in Av3MDO reactions with inhibitor (3HPA) in the absence of substrate. Similarly, no formation of iron-nitrosyl species is observed by EPR upon addition of nitric oxide to Av3MDO in the presence of excess 3HPA. Therefore, thiol Fe coordination is essential for initiating O2 activation; however, coordination of the substrate carboxylate appears to attenuate nonproductive “off pathway” reactions following binding of O2 to the ES complex.
Orientation of hydrogen bonding network
The Av3MDO-3HPA structure reveals an apparent change in the directionality of the “SHY” proton relay network relative to the eukaryotic CYS-bound CDO. As shown in Fig. S6A, Trp77 of the mammalian CDO serves as an H-bond donor to Ser153 (W77 → S153). This dictates the direction of proton donation toward the Fe-site (dashed blue lines). By contrast, Glu105 of the Av3MDO-3HPA complex (Fig. S6B) is an H-bond acceptor, thus reversing (H157 → Ser155 → Glu105) hydrogen bond donation (dashed red lines). This leaves Tyr159 in a favorable position to donate a hydrogen atom to either His157 (red) or the axial Fe-bound chloride (blue). We have previously reported for both Av3MDO and Mus musculus CDO that perturbations within the “SHY” motif directly influence substrate specificity and denticity of Fe coordination, nitric oxide affinity, and the oxygen KM-value (12), as well as “coupling,” which is defined as the molar ratio of O2 consumed per sulfinic acid produced (35). Despite these observations, the functional role of this conserved proton relay network remains poorly understood. An obvious question is whether the orientation of the Tyr159 H-bond donation plays any role in gating O2 activation to coordination of the substrate at the Fe-site.
Energy surface scan calculations on the optimized Av3MDO-3HPA complex (Fig. S6C) predict that Tyr159 H-bond donation to the Fe-bound chloride ligand is more stable relative to the Tyr159 → His157 configuration. This conclusion is consistent with previously reported both EPR and Mössbauer studies verifying direct interaction between the SHY Tyr-residue and enzymatic Fe-site (12, 14, 31). However, the particular atom (N or O) receiving the hydrogen bond and how it would translate to catalytically relevant molecular oxygen remains unsettled. While attempts were made to directly observe and assign the Tyr159 hydroxyl proton by HYSCORE spectroscopy, the peaks overlapped with other weakly coupled 1H that had anisotropic hyperfine couplings of <1 MHz. These more distant 1H, which include the 1H on the remote nitrogen of the three histidine residues and the 1H on Arg168, overlap near the matrix 1H peak that occurs at the nuclear Larmor frequency along the diagonal (Shown in Fig. S13). Accordingly, the direction of the Tyr159 H-bond donation could not be corroborated spectroscopically.
Implications of the closed active site cavity observed for Av3MDO
A notable finding from our structural analysis of Av3MDO was its lack of a patent tunnel for substrate diffusion to the active site. This observation was consist across all crystallographically independent protomers of both Av3MDO crystal forms. This structural uniformity suggests that the closed conformation could be adopted in the solution form of the enzyme, although the fact that it is observed in both the presence and absence of 3HPA seems to rule out the possibility that active site closure could be triggered by substrate binding. Such a uniformly occluded conformation has not, to our knowledge, been observed for other thiol dioxygenases, although two of the four subunits of the Pa3MDO crystal structure do appear to be occluded. Clearly, the active site must communicate with the bulk solvent to allow organic substrate entry, and the tunnel described in Figure 4 is the best candidate for such a role given its appropriate size and orientation with respect to the iron center. Discerning the relevance of the closed conformation observed for Av3MDO to the thiol dioxygenase catalytic cycle will require further research.
Experimental procedures
Protein expression and purification
A detailed description for the expression and purification of this enzyme has been reported elsewhere (12, 14). Briefly, the Av3MDO expression vector was transformed into chemically competent BL21(DE3) E. coli (Novagen Cat. no. 70236-4) by heat shock and grown overnight at 37 °C on a LB-agar plate containing 100 mg/l ampicillin (Amp). A single colony was selected for training on antibiotic in liquid LB media prior to inoculation of the 10-L BF-110 fermenter (New Brunswick Scientific) at 37 °C. Cell growth was monitored by optical density at 600 nm (OD 600). Induction was initiated by adding 1.0 g isopropyl β-D-1-thiogalactopyranoside (IPTG), 78 mg ferrous ammonium sulfate, and 20 g casamino acids at an OD600 value of ∼4. During induction, the temperature of the bioreactor was decreased from 37 to 25 °C and agitation was set to maintain an oxygen concentration of 20% relative to air-saturated media. Four hours postinduction, cells were harvested and pelleted by centrifugation (Beckman-Coulter Avanti J-E, JA 10.5 rotor). The resulting cell paste was stored at −80 °C.
In a typical purification, ∼20 g frozen cell paste was added to extraction buffer [20 mM 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES), 50 mM NaCl, pH 8.0]. Lysozyme, ribonuclease, and deoxyribonuclease were added to the slurry for a final concentration of 10 μg/ml each and stirred slowly on ice prior to pulse sonication (Bronson Digital 250/450). The insoluble debris was removed from the cell-free extract by centrifugation at 48,000g for 1 h at 4 °C. The supernatant was diluted 1:1 with extraction buffer and then loaded onto a DEAE sepharose fast flow anion exchange column (GE Life Sciences #17070901) pre-equilibrated with 20 mM HEPES, 50 mM NaCl, pH 8.0. The column was washed with three column volumes of extraction buffer prior to elution in a linear NaCl gradient (50 mM–350 mM).
Fractions were collected overnight and pooled based on enzymatic activity and/or SDS PAGE as described elsewhere (12). The pooled enzyme solution was concentrated to ∼50 ml using an Amicon stir cell and YM-10 ultrafiltration membrane prior to thrombin protease (Biopharma Laboratories) cleavage to remove C-terminal His-tag from the expressed enzyme. Following overnight cleavage at 4 °C, the enzyme was dialyzed against 4 l of 20 mM HEPES, 20 mM NaCl at pH 8.0 to decrease the salt content. A second DEAE column separation in a linear gradient (50–250 mM NaCl) was used to separate the free (His)6-tag from the purified enzyme. Precrystallization desalting was performed by Sephadex G25 column equilibrated with 20 mM HEPES, 10 mM NaCl at pH 8.0 prior to concentrating drop freezing in liquid nitrogen and storage at −80 °C. Iron content was quantified spectrophotometrically for both ferric and ferrous concentration using 2,4,6-tripyridyl-s-triazine (TPTZ) in a method previously described (14, 38).
Enzyme assays
The rate of dioxygen consumption in activity assays was determined polarographically using a standard Clark electrode (Hansatech Instruments, Norfolk, England) in a jacketed 2.5 ml cell. Reaction temperatures were fixed at 25 °C ± 1 °C using a 5 l circulating water bath (Grant Instruments) and O2-electrode calibration was performed as described elsewhere (12, 31, 62). For all 3MPA concentrations [7–1000 μM], reactions were initiated by addition of 5.0 μM Fe(II)-Av3MDO. Steady-state kinetic parameters for the enzyme used in experiments were consistent with previously published values at 25 °C [kcat, 1.0 ± 0.1 s−1; KM, 13 ± 5 μM; kcat/KM, 72,000 ± 9200 M−1 s−1] (14).
Data analysis
Inhibition kinetic results were fit globally using the Enzyme Kinetics Add-On module of SigmaPlot ver. 14.0 (Systat Software Inc). In the presence of a competitive inhibitor, the Michaelis–Menten and Lineweaver–Burk equations take the form shown in Equations 1 and 2, respectively. From the analysis, kinetic parameters (Vmax, KM, and KI) as well as the error associated with each value were determined by nonlinear regression.
| (1) |
| (2) |
Av3MDO crystallization
Av3MDO crystallization conditions were identified through sparse matrix trials using a number of commercially available screens. The initial hit (crystal form A) was obtained in condition 2-42 of the MIDAS screen (Molecular Dimensions), which consists of 100 mM MES pH 6, 30% w/v poly(acrylic acid sodium salt) 5100, and 10% v/v ethanol. Two microliters of Av3MDO at a concentration of 40 mg/ml was mixed with 2 μl of the crystallization cocktail on a siliconized coverslip (Hampton Research), and the resulting drop was incubated over 500 μl of the same crystallization cocktail in a sealed chamber at 22 °C. Thin needle-shaped crystals with a tendency to grow in clusters were observed after a week of incubation. These initial crystals were replicated with independently prepared solutions and further optimized through streak seeding and inclusion of 50 mM MgCl2 in the crystallization cocktail. The optimized crystals grew as thin rods over the course of a week with approximate final dimensions of 50 × 50 × (100–800) μm. Most crystals exhibited a splitting defect along their long axis. The crystals were harvested directly from the mother liquor using elliptical Microloops (Mitegen) and flash frozen in liquid nitrogen.
To obtain an alternative Av3MDO crystal form, Av3MDO was further purified by anion exchange and gel filtration chromatography in the absence of reducing agents and then concentrated to 40 mg/ml. A second crystallization hit (crystal form B) was obtained in condition E4 of the MidasPLUS screen (MD1-107, Molecular Dimensions), which consists of 100 mM HEPES pH 7, 40% v/v pentaerythritol propoxylate (5/4 PO/OH), and 0.2 M sodium thiocyanate. Two microliters of Av3MDO at a concentration of 40 mg/ml was mixed with 2 μl of the crystallization cocktail on a siliconized coverslip (Hampton Research), and the resulting drop was incubated over 500 μl of the same crystallization cocktail in a sealed chamber at 22 °C. Yellowish, rod-shaped crystals with “feather-duster” growth defects on each end were observed after 2 to 5 days of incubation. The growth defects were minimized by changing the HEPES, pentaerythritol propoxylate, and sodium thiocyanate concentrations to 50 mM, 44%, and 0.6 M, respectively. Mature (150 × 150 × 600 μm) single crystals were harvested directly from the mother liquor using Microloops (Mitegen) and flash frozen in liquid nitrogen.
X-ray diffraction data collection, processing, and analysis
Av3MDO crystal diffraction data were collected using beamlines 17-ID-2 (FMX) at the National Synchrotron Light Source (NSLS)-II, beamline 12-2 at the Stanford Synchrotron Light Source (SSRL) and beamline 24-ID-E (NE-CAT) at the Advanced Photon Source (APS). All form A Av3MDO crystals examined were twinned to various degrees as described in more detail below. The microfocusing capability of the FMX 17-ID-2 beamline was used to collect data from small crystal volumes to minimize contributions from twin-related domains. Initial crystals diffracted to ∼2.7 Å resolution and the diffraction was somewhat anisotropic, being strongest along c∗. Weak diffuse scatter was observed between reflections in h-k planes of reciprocal space. Data were indexed, integrated, and scaled using XDS (63). The data were initially processed in space group P622 and examination of axial reflections along c∗ indicated the presence of a 62 or 64 screw axis. Analysis of the intensities with the L-test (64), as implemented in phenix.xtriage (65), provided strong indication that the data were twinned. The data were therefore reprocessed in space groups P321 and P3 with similar Rmerge values for each. H-tests (66) for the four possible unique twin operators in the latter point group indicated that the crystals were tetartohedrally twinned. Crystal streak seeding and the inclusion of MgCl2 in the crystallization cocktail substantially reduced crystal twinning and improved the data resolution to ∼2.25 Å. The optimized crystals remained partially merohedrally twinned with respect to operator (k, h, −l). The best crystals of crystal form B diffracted X-rays to ∼2.9 Å resolution. Data were processed in space group P6(1,5)22. While no twinning was detected in this crystal form, the native Patterson map suggested the presence of pseudotranslational symmetry. X-ray data collection statistics are shown in Table S1.
Structure refinement and analysis
Structure solution for crystal form A was carried out by molecular replacement in Phaser (67) using the coordinates of a related 3MDO protein (5) as a search model (PDB accession code 4TLF). Structure solution was attempted, unsuccessfully, in space groups P6(2, 4)22 before it was realized the data were twinned. Space groups P3(1, 2)12 were excluded from further consideration owing to poor merging statistics. MR trials in space groups P3(1, 2)21 led to a clear solution in space group P3121 with four molecules (a pair of dimers) per asymmetric unit and a solvent content of 64%. Amino acid substitutions and model adjustments were made using Coot (68) and the model was refined using Refmac (69). After several rounds of model building and refinement, Rfree plateaued at ∼37%. At this point, a majority of the strongest residual electron density was found within a large solvent channel, but it was largely uninterpretable. The possibility of rotational pseudosymmetry causing an elevation in the apparent crystal symmetry was considered and the partially refined Av3MDO coordinates were used as a search model for molecular replacement in space group P31. Phaser located 12 molecules in the asymmetric unit giving a solvent content of 47%. Refinement of this new model against the P31 processed data (with Rfree reflections transferred from the original data set after symmetry expansion to P31) resulted in an immediate reduction of Rfree to ∼28% and elimination of the residual density features noted above. RvR analysis (70) of the P31 data and calculated amplitudes as implemented in phenix.xtriage (65) revealed the presence of twofold rotational pseudosymmetry along the a and b axes together with partial merohedral twinning (k, h, −l with α ∼ 0.34). These features were also evident from inspection of Patterson self-rotation plots, which showed strong chi = 180° peaks along the “a” and “b” axes. Together, these features accounted for the similar Rmerge values for space groups P3121 and P31. The space group assignment was further validated using Zanuda (71) and labelit.check_pdb symmetry (72) as well as by manual inspection of the crystal packing environment for each of the monomers in the asymmetric unit. A monomer from the P31 model was then used as a model to solve crystal form B by molecular replacement in space group P6122 with four monomers in the asymmetric unit.
Refinement of both models was completed by alternating reciprocal space refinement in Refmac, using the amplitude-based twin refinement option in the case of crystal form A, and manual model improvements in Coot. Coordinate and dictionary files for the test ligands were generated using the GRADE server (Global Phasing LTD). In the case of crystal form A, inspection of residual density near the iron center revealed a large peak in the axial position and an elongated, continuous feature in the equatorial positions, indicative of a diffusible ligand set different from the three aquo complex modeled in the structure of Pa3MDO (Fig. S1A) (11). Indeed, placement of three water molecules poorly explained the residual density as shown in Fig. S1B. The density trans to His142 was flat and appeared to make a simultaneous interaction with Arg168, suggesting it could represent a carboxylate-containing ligand. Modeling of a bicarbonate at this position resulted in an excellent fit to the electron density map (Fig. S1C). However, the bicarbonate-H2O-H2O model resulted in residual positive density features at the axial position trans to His 90 as well as between bicarbonate and the water ligand trans to His92 in addition to an unacceptably close interaction (2.1 Å) between the nonaxial water and bicarbonate ligands (Fig. S1C). Replacing the axial water with a chloride ion, which was present in the crystal mother liquor at ∼100 mM concentration, fully quenched the residual density with a reasonable refined B-factor (Fig. S1D). Chloride binding at the equivalent site in CDO was previously reported (27, 41), which further supports the plausibility of our assignment. The difference map analysis described above suggested that the equatorial features represented a single carboxylate-containing compound. Since known components of the crystal mother liquor could not account for the electron density, we further considered possible contaminants that the density could represent. 3-hydroxypropionic acid is a known precursor and contaminant of the polyacrylate used for Av3MDO crystallization, which we confirmed by mass spectrometry, and was considered the most likely source of the electron density feature (73, 74). Additionally, 3HPA is a close analog of the 3MPA substrate of Av3MDO. Placement of 3HPA at this position completely quenched the residual density with refined B-factors closely matching those of iron and its other ligands (Fig. S1E and Table S1). We also attempted to model 3MPA into the density, but observed a residual density hole near the sulfur atom, which also exhibited an elevated B-factor relative to the remainder of the molecule (Fig. S1F).
The initial difference maps for the crystal form B model also revealed density in both the equatorial and axial positions. The equatorial features were interpreted as two coordinated water molecules while the axial density was elongated and not adequately satisfied by modeling either a single water or chloride ligand. The elongated density instead strongly suggested a bound thiocyanate ligand, which was modeled with its nitrogen atom directly coordinating the iron ion based on difference map analysis and refined B-factors computed with the ligand modeled in either orientation.
Structure validation was carried out with the Molprobity (75) and wwPDB (76) web servers. The final model statistics are shown in Table S1. The coordinates and structure factor amplitudes have been deposited in the Protein Data Bank under accession code 6XB9 (crystal form A) and 7KOV (crystal form B).
Mass spectrometry
Sodium polyacrylate 5100 solution (Hampton Research) was diluted to 10% (v/v) with Millipore water. In total, 100 μl of the resulting solution was mixed with 900 μl of HPLC-grade acetone to precipitate the acrylate polymer and the mixture was centrifuged at 17,000g for 15 min. The supernatant (10 μl) was diluted with 50% HPLC-grade methanol (90 μl), and 10 μl of the resulting solution was analyzed with LXQ Mass spectrometer (Thermo Scientific) coupled with an Ultimate 3000 HPLC system. 3HPA standard (Sigma-Aldrich) was prepared in an identical manner. Chromatography was performed with a Poroshell 120 EC C18 Column (2.7 μm, 4.6 mm × 50 mm, Agilent Technologies) using a gradient mobile phase of acetonitrile/2-propanol (1/1, v/v) in water from 20% to 98% over 20 min. The flow rate was 0.6 ml/min. Ions were detected in negative mode with a normalized collision energy of 35%.
Pulsed EPR measurements
HYSCORE measurements were made using an ELEXSYS E680 EPR spectrometer (Bruker-Biospin) equipped with a Bruker Flexline ER 4118 CF cryostat and an ER 4118X-MD4 ENDOR resonator. Measurements were made at 5 K with a nominal EPR frequency of 9.78 GHz and used a four-pulse sequence, π/2−τ−π/2−t1−π−t2−π/2−τ−echo. This sequence was repeated at a rate of 1.25 kHz with values of 16 ns and 32 ns for the π/2 and π pulses, respectively. The times t1 and t2 were varied independently from 48 ns to 3096 ns in increments of 24 ns for a total of 128 points in each dimension. The delay time τ was set to 120 ns to maximize resolution in the 1H region of the spectrum. HYSCORE spectra were processed using custom scripts in MATLAB (Mathworks, R2020a). Briefly, the complex raw data was phased to minimize the imaginary component, and the background decay was subtracted in each dimension by removing a second-degree polynomial. Then, a diagonal Blackman apodization function was applied to minimize noise at larger values of t1 and t2. The data were then zero-filled in both directions to 1024 points before calculating the two-dimensional Fourier transform. The absolute value of the real part of the Fourier transform is displayed. HYSCORE peaks are symmetric about the frequency diagonal; however, several factors, including interference from strong nuclear modulation, can affect the intensity of each peak. As a result, real peaks are roughly symmetric about the frequency diagonal, but they can have minor intensity variations. Noise, on the other hand, is not symmetric about the diagonal. Therefore, the spectra were left unsymmetrized in order to best distinguish between signal and noise. Spectra were simulated using the “saffron” function in EasySpin, a comprehensive EPR toolbox in MATLAB (77).
HYSCORE simulations on the 1H region are based off the spin Hamiltonian
| (3) |
where is the proton gyromagnetic ratio, and are the electron and nuclear spin operators, B is the magnetic field vector, and is the hyperfine coupling tensor. The proton couplings were modeled using an axial dipolar tensor,
| (4) |
where T is the anisotropic contribution of the hyperfine interaction. The tensor was considered purely dipolar due to the distance of the coupled 1H, which is consistent with other HYSCORE analyses of {FeNO}7 centers (52, 53, 54). The dipolar contribution, T, was calculated using the geometry-optimized DFT structure of 3MPA-bound Av3MDO treated with NO and spin-projection factors that take into account the electronic structure of the {FeNO}7 center (52, 54). In brief, distances between the Fe, the N, and the O of NO and each 1H were used to calculate a TFe, TN, and TO according to the point-dipole approximation.
| (5) |
where is the permittivity of free space, ge is the electronic g-value, gn is the nuclear g-value, βeis the electronic Bohr magneton, βn is the nuclear Bohr magneton, h is Planck’s constant, and r is the distance from the proton to the Fe, N, or O of the {FeNO}7 center. The dipolar contributions were then summed using spin projection factors.
| (6) |
where TFe, TN, and TO are the dipolar couplings resulting from the point-dipole approximation using the distance between the 1H and the Fe, N, and O of NO, respectively. The couplings for the 1H on His90 and His142 were varied by ±0.1 Å, which is the estimate of the precision of the atomic locations in the crystal structure. Equations 5 and 6 were used to transform the ±0.1 Å variation into the corresponding value in MHz. The other 1H couplings were left unvaried. For each 1H, the dipolar coupling between the 1H and the Fe dominates Equation 6; therefore, the vector connecting each 1H and Fe is a reasonable approximation of the hyperfine interaction (52). In addition to the hyperfine coupling, HYSCORE simulations take into account the transformation of the hyperfine tensor into the magnetic axis system. This transformation is defined by a set of Euler angles (α, β, γ) in EasySpin that follow the zy′z′ convention. In the case of an axial hyperfine interaction, only two angles are necessary. As with other {FeNO}7 centers, the principal axis of the zero field splitting (zfs) and the molecular z axis are nearly coincident (52, 53). As a result, these Euler rotations can be approximated using polar angles φ and ɵ, where φ is taken as the angle between the proton and the x-z plane, and ɵ defines the deviation from the z-axis defined by the Fe-NO bond. An illustration below Table S3 shows how these angles relate to structure for a 1H on 3MPA. All angles were measured based on the geometry-optimized structure using Chimera 1.14 (UCSF) (78). While simulations were not very sensitive to the value of φ, the value of ɵ was varied for His90 and His142 by <10% for the best fit.
Computational modeling
All calculations were performed using Orca version 4.2 (79). Starting coordinates for geometry optimizations were extrapolated from the crystal structure presented in this work and the crystal structure of Pa3MDO, PDB 4TLF. Optimizations were done by capping the alpha-carbons of each residue with a methyl group. Histidines directly coordinated to the iron were capped at the beta-carbon. Preliminary optimizations were done by optimizing only hydrogens and constraining the dihedral angles of capped methyl group hydrogens relative to the constrained main group atoms. These methyl groups were constrained in all geometry optimizations. Histidines coordinated to iron were protonated at the δ-position. Geometry optimizations utilized two methods. Most optimizations used the BP’86 functional with the Ahlrichs def2-tzvp basis set on iron and directly coordinated atoms and the def2-svp basis set on all other atoms (80, 81, 82). This method has been shown to work well for transition metal complexes (83). The nitroxide containing complexes used the B3LYP functional with the same basis set allocation as described earlier. B3LYP was chosen among other tested functionals (e.g., BP’86, TPSS, PBE, and PBE0), as it was the only functional that could reproduce the expected antiferromagnetically coupled S = 3/2 {FeNO}7 electronic structure with S = 5/2 for iron and S = −1 on the nitrosyl ligand. Additionally, the iron nitrosyl complexes used the “broken-symmetry” approach where the wavefunction was calculated as a high spin S = 7/2 system before flipping the sign of the spin on the nitrosyl atoms to converge to an S = 3/2 system (84). All calculations utilized Grimme’s D3 dispersion correction, a CPCM solvent model with ε = 4 to emulate a protein environment, and either the resolution of identity (RI) for BP’86 or resolution of identity and chain of sphere (RIJCOSX) approximation for B3LYP with def2/J auxiliary basis sets (85, 86, 87, 88).
Mössbauer parameters were calculated using the B3LYP functional with the CP(PPP) basis set for iron and def2-TZVP on all other atoms. Orca specific settings featured the radial integration accuracy raised to 7 for the iron atom and a TightSCF convergence threshold with Grid5 and FinalGrid7 for the whole structure. Quadrupole splitting (ΔEQ) and η were calculated directly in Orca using the electric field gradient on the iron nucleus. The isomer shift (δ) was determined from the method described by Remolt et al. (89) using the s electron density at the iron nucleus.
EPR parameters were calculated with the same method described for Mössbauer parameter, with the exception of the IGLO-II basis set used for sulfur and EPR-II used for all other atoms (CP(PPP) was still used for iron). The spin–orbit coupling part of the zero field splitting tensor was calculated with the coupled-perturbed method and the spin–spin part was calculated using the spin density of “UNO” orbitals (84). Isotropic and dipolar contributions of hyperfine coupling were calculated for the nitrogens of H90, H92, H142, and Arg168 and the hydrogens of H90, H92, H142, Arg168, 3MPA, and the phenol hydrogen of Tyr159.
Data availability
X-ray crystal structure data that support the findings of this study have been deposited in the Worldwide Protein Data Bank. The PDB accession codes for the Av3MDO complex with 3HPA and thiocyanate are 6XB9 and 7KOV, respectively.
Supporting information
This article contains supporting information (12, 13, 14, 31, 40, 47, 48, 49, 61, 91, 92).
Conflict of interest
The authors declare that they have no conflicts of interest with the contents of this article.
Acknowledgments
Data for this study were measured at beamline 17-ID-2 (FMX) of the National Synchrotron Light Source-II, which are supported by NIH grant GM111244 and the DOE Office of Biological and Environmental Research KP1605010. The NSLS-II is supported in part by the DOE Office of Science, Office of Basic Energy Sciences Program under contract number DE-SC0012704 (KC0401040). Use of beamlines 7-3 and 12-2 at the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the DOE Office of Biological and Environmental Research, and by the National Institutes of Health, National Institute of General Medical Sciences (P41GM103393). This work is based upon research conducted at the Northeastern Collaborative Access Team beamlines, which are funded by the National Institute of General Medical Sciences from the National Institutes of Health (P30 GM124165). The Eiger 16M detector on the 24-ID-E beam line is funded by a NIH-ORIP HEI grant (S10OD021527). This research used resources of the Advanced Photon Source, a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory under Contract No. DE-AC02-06CH11357. The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of NIGMS or NIH. We would also like to acknowledge Prof. Timothy Jackson (University of Kansas, Department of Chemistry) for useful conversations and advice on computational methods.
Author contributions
Protein purification, enzymology, kinetics: N. J. Y., S. S., and B. S. P. HYSCORE measurements and simulations: M. M. L. Computational modeling: N. J. Y. Crystallization, X-ray data collection and interpretation: N. K., W. S., R. E. S., and P. D. K. Mass spectrometry: J. Z. Drafting manuscript and revisions. B. S. P., P. D. K., N. J. Y., and M. M. L. All the authors have approved the final version of the article.
Funding and additional information
This work was supported by grants from the Department of Veterans Affairs (I01BX004939 to P. D. K.) and the National Institutes of Health (R01EY009339 to P. D. K.) and (2 R15 GM117511-01 to B. S. P.). P. D. K. acknowledges an unrestricted grant to the UC Irvine Department of Ophthalmology from Research to Prevent Blindness.
Edited by Ruma Banerjee
Contributor Information
Philip D. Kiser, Email: pkiser@uci.edu.
Brad S. Pierce, Email: bspierce1@ua.edu.
Supporting information
References
- 1.Stipanuk M.H. Sulfur amino acid metabolism: Pathways for production and removal of homocysteine and cysteine. Annu. Rev. Nutr. 2004;24:539–577. doi: 10.1146/annurev.nutr.24.012003.132418. [DOI] [PubMed] [Google Scholar]
- 2.Ewetz L., Sorbo B. Characteristics of the cysteinesulfinate-forming enzyme system in rat liver. Biochim. Biophys. Acta. 1966;128:296–305. doi: 10.1016/0926-6593(66)90176-7. [DOI] [PubMed] [Google Scholar]
- 3.Sorbo B., Ewetz L. The enzymatic oxidation of cysteine to cysteinesulfinate in rat liver. Biochem. Biophys. Res. Commun. 1965;18:359–363. doi: 10.1016/0006-291x(65)90714-x. [DOI] [PubMed] [Google Scholar]
- 4.Lombardini J.B., Singer T.P., Boyer P.D. Cysteine oxygenase. J. Biol. Chem. 1969;244:1172–1175. [PubMed] [Google Scholar]
- 5.Dominy J.E., Jr., Simmons C.R., Karplus P.A., Gehring A.M., Stipanuk M.H. Identification and characterization of bacterial cysteine dioxygenases: A new route of cysteine degradation for Eubacteria. J. Bacteriol. 2006;188:5561–5569. doi: 10.1128/JB.00291-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fernandez R.L., Dillon S.L., Stipanuk M.H., Fox B.G., Brunold T.C. Spectroscopic investigation of cysteamine dioxygenase. Biochemistry. 2020;59:2450–2458. doi: 10.1021/acs.biochem.0c00267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Dominy J.E., Simmons C.R., Hirschberger L.L., Hwang J., Coloso R.M., Stipanuk M.H. Discovery and characterization of a second mammalian thiol dioxygenase, cysteamine dioxygenase. J. Biol. Chem. 2007;282:25189–25198. doi: 10.1074/jbc.M703089200. [DOI] [PubMed] [Google Scholar]
- 8.Brandt U., Schürmann M., Steinbüchel A. Mercaptosuccinate dioxygenase, a cysteine dioxygenase homologue, from Variovorax paradoxus strain B4 is the key enzyme of mercaptosuccinate degradation. J. Biol. Chem. 2014;289:30800–30809. doi: 10.1074/jbc.M114.579730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Aloi S., Davies C.G., Karplus P.A., Wilbanks S.M., Jameson G.N.L. Substrate specificity in thiol dioxygenases. Biochemistry. 2019;58:2398–2407. doi: 10.1021/acs.biochem.9b00079. [DOI] [PubMed] [Google Scholar]
- 10.Fellner M., Aloi S., Tchesnokov E.P., Wilbanks S.M., Jameson G.N.L. Substrate and pH-dependent kinetic profile of 3-mercaptopropionate dioxygenase from Pseudomonas aeruginosa. Biochemistry. 2016;55:1362–1371. doi: 10.1021/acs.biochem.5b01203. [DOI] [PubMed] [Google Scholar]
- 11.Tchesnokov E.P., Fellner M., Siakkou E., Kleffmann T., Martin L.W., Aloi S., Lamont I.L., Wilbanks S.M., Jameson G.N.L. The cysteine dioxygenase homologue from Pseudomonas aeruginosa is a 3-mercaptopropionate dioxygenase. J. Biol. Chem. 2015;290:24424–24437. doi: 10.1074/jbc.M114.635672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Sardar S., Weitz A., Hendrich M.P., Pierce B.S. Outer-sphere tyrosine 159 within the 3-mercaptopropionic acid dioxygenase S-H-Y motif gates substrate-coordination denticity at the non-heme iron active site. Biochemistry. 2019;58:5135–5150. doi: 10.1021/acs.biochem.9b00674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Crowell J.K., Sardar S., Hossain M.S., Foss F.W., Jr., Pierce B.S. Non-chemical proton-dependent steps prior to O2-activation limit Azotobacter vinelandii 3-mercaptopropionic acid dioxygenase (MDO) catalysis. Arch. Biochem. Biophys. 2016;604:86–94. doi: 10.1016/j.abb.2016.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pierce B.S., Subedi B.P., Sardar S., Crowell J.K. The “Gln-type” thiol dioxygenase from Azotobacter vinelandii is a 3-mercaptopropionic acid dioxygenase. Biochemistry. 2015;54:7477–7490. doi: 10.1021/acs.biochem.5b00636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Weits D.A., Giuntoli B., Kosmacz M., Parlanti S., Hubberten H.-M., Riegler H., Hoefgen R., Perata P., van Dongen J.T., Licausi F. Plant cysteine oxidases control the oxygen-dependent branch of the N-end-rule pathway. Nat. Commun. 2014;5:3425. doi: 10.1038/ncomms4425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.White M.D., Klecker M., Hopkinson R.J., Weits D.A., Mueller C., Naumann C., O’Neill R., Wickens J., Yang J., Brooks-Bartlett J.C., Garman E.F., Grossmann T.N., Dissmeyer N., Flashman E. Plant cysteine oxidases are dioxygenases that directly enable arginyl transferase-catalysed arginylation of N-end rule targets. Nat. Commun. 2017;8:14690. doi: 10.1038/ncomms14690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Masson N., Keeley T.P., Giuntoli B., White M.D., Puerta M.L., Perata P., Hopkinson R.J., Flashman E., Licausi F., Ratcliffe P.J. Conserved N-terminal cysteine dioxygenases transduce responses to hypoxia in animals and plants. Science. 2019;365:65–69. doi: 10.1126/science.aaw0112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gordon C., Emery P., Bradley H., Waring H. Abnormal sulfur oxidation in systemic lupus erythematosus. Lancet. 1992;229:25–26. doi: 10.1016/0140-6736(92)90144-r. [DOI] [PubMed] [Google Scholar]
- 19.Heafield M.T., Fearn S., Steventon G.B., Waring R.H., Williams A.C., Sturman S.G. Plasma cysteine and sulfate levels in patients with motor neurone, Parkinson's and Alzheimer's disease. Neurosci. Lett. 1990;110:216–220. doi: 10.1016/0304-3940(90)90814-p. [DOI] [PubMed] [Google Scholar]
- 20.James S.J., Cutler P., Melnyk S., Jernigan S., Janak L., Gaylor D.W., Neubrander J.A. Metabolic biomarkers of increased oxidative stress and impaired methylation capacity in children with autism. Am. J. Clin. Nutr. 2004;80:1611–1617. doi: 10.1093/ajcn/80.6.1611. [DOI] [PubMed] [Google Scholar]
- 21.Deth R., Muratore C., Benzecry J., Power-Charnitsky V.-A., Waly M. How environmental and genetic factors combine to cause autism: A redox/methylation hypothesis. Neurotoxicology. 2008;29:190–201. doi: 10.1016/j.neuro.2007.09.010. [DOI] [PubMed] [Google Scholar]
- 22.Reddie K.G., Carroll K.S. Expanding the functional diversity of proteins through cysteine oxidation. Curr. Opin. Chem. Biol. 2008;12:746–754. doi: 10.1016/j.cbpa.2008.07.028. [DOI] [PubMed] [Google Scholar]
- 23.Winyard P.G., Moody C.J., Jacob C. Oxidative activation of antioxidant defence. Trends Biochem. Sci. 2005;30:453–461. doi: 10.1016/j.tibs.2005.06.001. [DOI] [PubMed] [Google Scholar]
- 24.Trachootham D., Alexandre J., Huang P. Targeting cancer cells by ROS-mediated mechanisms: A radical therapeutic approach? Nat. Rev. Drug Discov. 2009;8:579–591. doi: 10.1038/nrd2803. [DOI] [PubMed] [Google Scholar]
- 25.Behave D.P., Muse W.B., Carroll K.S. Drug targets in mycobacterial sulfur metabolism. Infect. Disord. Drug Targets. 2007;7:140–158. doi: 10.2174/187152607781001772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Driggers C.M., Hartman S.J., Karplus P.A. Structures of Arg- and Gln-type bacterial cysteine dioxygenase homologs. Protein Sci. 2015;24:154–161. doi: 10.1002/pro.2587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Driggers C.M., Kean K.M., Hirschberger L.L., Cooley R.B., Stipanuk M.H., Karplus P.A. Structure-based insights into the role of the Cys–Tyr crosslink and inhibitor recognition by mammalian cysteine dioxygenase. J. Mol. Biol. 2016;428:3999–4012. doi: 10.1016/j.jmb.2016.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Simmons C.R., Liu Q., Huang Q., Hao Q., Begley T.P., Karplus P.A., Stipanuk M.H. Crystal structure of mammalian cysteine dioxygenase: A novel mononuclear iron center for cysteine thiol oxidation. J. Biol. Chem. 2006;281:18723–18733. doi: 10.1074/jbc.M601555200. [DOI] [PubMed] [Google Scholar]
- 29.Davies C.G., Fellner M., Tchesnokov E.P., Wilbanks S.M., Jameson G.N.L. The Cys-Tyr cross-link of cysteine dioxygenase changes the optimal pH of the reaction without a structural change. Biochemistry. 2014;53:7961–7968. doi: 10.1021/bi501277a. [DOI] [PubMed] [Google Scholar]
- 30.Blaesi E.J., Fox B.G., Brunold T.C. Spectroscopic and computational investigation of the H155A variant of cysteine dioxygenase: Geometric and electronic consequences of a third-sphere amino acid substitution. Biochemistry. 2015;54:2874–2884. doi: 10.1021/acs.biochem.5b00171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Li W., Blaesi E.J., Pecore M.D., Crowell J.K., Pierce B.S. Second-sphere interactions between the C93-Y157 cross-link and the substrate-bound Fe site influence the O2-coupling efficiency in mouse cysteine dioxygenase. Biochemistry. 2013;52:9104–9119. doi: 10.1021/bi4010232. [DOI] [PubMed] [Google Scholar]
- 32.Ye S., Wu X.A., Wei L., Tang D., Sun P., Bartlam M., Rao Z. An insight into the mechanism of human cysteine dioxygenase: Key roles of the thioether-bonded tyrosine-cysteine cofactor. J. Biol. Chem. 2007;282:3391–3402. doi: 10.1074/jbc.M609337200. [DOI] [PubMed] [Google Scholar]
- 33.Dominy J.E., Hwang J., Guo S., Hirschberger L.L., Zhang S., Stipanuk M.H. Synthesis of amino acid cofactor in cysteine dioxygenase is regulated by substrate and represents a novel post-translational regulation of activity. J. Biol. Chem. 2008;283:12188–12201. doi: 10.1074/jbc.M800044200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Njeri C.W., Ellis H.R. Shifting redox states of the iron center partitions CDO between crosslink formation or cysteine oxidation. Arch. Biochem. Biophys. 2014;558:61–69. doi: 10.1016/j.abb.2014.06.001. [DOI] [PubMed] [Google Scholar]
- 35.Li W., Pierce B.S. Steady-state substrate specificity and O2-coupling efficiency of mouse cysteine dioxygenase. Arch. Biochem. Biophys. 2015;565:49–56. doi: 10.1016/j.abb.2014.11.004. [DOI] [PubMed] [Google Scholar]
- 36.Easson L.H., Stedman E. Studies on the relationship between chemical constitution and physiological action: Molecular dissymmetry and physiological activity. Biochem. J. 1933;27:1257–1266. doi: 10.1042/bj0271257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.McCoy J.G., Bailey L.J., Bitto E., Bingman C.A., Aceti D.J., Fox B.G., Phillips G.N., Jr. Structure and mechanism of mouse cysteine dioxygenase. Proc. Natl. Acad. Sci. U. S. A. 2006;103:3084–3089. doi: 10.1073/pnas.0509262103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Pierce B.S., Gardner J.D., Bailey L.J., Brunold T.C., Fox B.G. Characterization of the nitrosyl adduct of substrate-bound mouse cysteine dioxygenase by electron paramagnetic resonance: Electronic structure of the active site and mechanistic implications. Biochemistry. 2007;46:8569–8578. doi: 10.1021/bi700662d. [DOI] [PubMed] [Google Scholar]
- 39.Krissinel E., Henrick K. Inference of macromolecular assemblies from crystalline state. J. Mol. Biol. 2007;372:774–797. doi: 10.1016/j.jmb.2007.05.022. [DOI] [PubMed] [Google Scholar]
- 40.Driggers C.M., Stipanuk M.H., Karplus P.A. Mammalian cysteine dioxygenase. In: Scott R.A., editor. Encyclopedia of Inorganic and Bioinorganic Chemistry. John Wiley & Sons, Ltd; Hoboken, NJ: 2015. [Google Scholar]
- 41.Fellner M., Siakkou E., Faponle A.S., Tchesnokov E.P., de Visser S.P., Wilbanks S.M., Jameson G.N. Influence of cysteine 164 on active site structure in rat cysteine dioxygenase. J. Biol. Inorg. Chem. 2016;21:501–510. doi: 10.1007/s00775-016-1360-0. [DOI] [PubMed] [Google Scholar]
- 42.Abibat Salaudeen A., Kilner C.A., Halcrow M.A. Mononuclear and dinuclear iron thiocyanate and selenocyanate complexes of tris-pyrazolylmethane ligands. Polyhedron. 2008;27:2569–2576. [Google Scholar]
- 43.Silva A.M.N., Kong X., Hider R.C. Determination of the pKa value of the hydroxyl group in the α-hydroxycarboxylates citrate, malate and lactate by 13C NMR: Implications for metal coordination in biological systems. Biometals. 2009;22:771–778. doi: 10.1007/s10534-009-9224-5. [DOI] [PubMed] [Google Scholar]
- 44.Brines L.M., Coggins M.K., Poon P.C.Y., Toledo S., Kaminsky W., Kirk M.L., Kovacs J.A. Water-soluble Fe(II)–H2O complex with a weak O–H bond transfers a hydrogen atom via an observable monomeric Fe(III)–OH. J. Am. Chem. Soc. 2015;137:2253–2264. doi: 10.1021/ja5068405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Tyler L.A., Noveron J.C., Olmstead M.M., Mascharak P.K. Modulation of the pKa of metal-bound water via oxidation of thiolato sulfur in model complexes of Co(III) containing nitrile hydratase: Insight into possible effect of cysteine oxidation in co−nitrile hydratase. Inorg. Chem. 2003;42:5751–5761. doi: 10.1021/ic030088s. [DOI] [PubMed] [Google Scholar]
- 46.Enemark J.H., Feltham R.D. Principles of structure, bonding, and reactivity for metal nitrosyl complexes. Coord. Chem. Rev. 1974;13:339–406. [Google Scholar]
- 47.Dajnowicz S., Parks J.M., Hu X., Gesler K., Kovalevsky A.Y., Mueser T.C. Direct evidence that an extended hydrogen-bonding network influences activation of pyridoxal 5′-phosphate in aspartate aminotransferase. J. Biol. Chem. 2017;292:5970–5980. doi: 10.1074/jbc.M116.774588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bykov D., Plog M., Neese F. Heme-bound nitroxyl, hydroxylamine, and ammonia ligands as intermediates in the reaction cycle of cytochrome c nitrite reductase: A theoretical study. J. Biol. Inorg. Chem. 2014;19:97–112. doi: 10.1007/s00775-013-1065-6. [DOI] [PubMed] [Google Scholar]
- 49.Kampa M., Lubitz W., van Gastel M., Neese F. Computational study of the electronic structure and magnetic properties of the Ni–C state in [NiFe] hydrogenases including the second coordination sphere. J. Biol. Inorg. Chem. 2012;17:1269–1281. doi: 10.1007/s00775-012-0941-9. [DOI] [PubMed] [Google Scholar]
- 50.Brown C.D., Neidig M.L., Neibergall M.B., Lipscomb J.D., Solomon E.I. VTVH-MCD and DFT studies of thiolate bonding to {FeNO}7/{FeO2}8 complexes of isopenicillin N synthase: Substrate determination of oxidase versus oxygenase activity in nonheme Fe enzymes. J. Am. Chem. Soc. 2007;129:7427–7438. doi: 10.1021/ja071364v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Arciero D.M., Lipscomb J.D., Huynh B.H., Kent T.A., Münck E. EPR and Mössbauer studies of protocatechuate 4,5-dioxygenase. Characterization of a new Fe2+ environment. J. Biol. Chem. 1983;258:14981–14991. [PubMed] [Google Scholar]
- 52.McCracken J., Casey T.M., Hausinger R.P. 1H-HYSCORE reveals structural details at the Fe(II) active site of taurine:2-oxoglutarate dioxygenase. Appl. Magn. Reson. 2020 doi: 10.1007/s00723-020-01288-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.McCracken J., Eser B.E., Mannikko D., Krzyaniak M.D., Fitzpatrick P.F. HYSCORE analysis of the effects of substrates on coordination of water to the active site iron in tyrosine hydroxylase. Biochemistry. 2015;54:3759–3771. doi: 10.1021/acs.biochem.5b00363. [DOI] [PubMed] [Google Scholar]
- 54.Martinie R.J., Livada J., Chang W.-C., Green M.T., Krebs C., Bollinger J.M., Silakov A. Experimental correlation of substrate position with reaction outcome in the aliphatic halogenase, SyrB2. J. Am. Chem. Soc. 2015;137:6912–6919. doi: 10.1021/jacs.5b03370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Mitchell A.J., Dunham N.P., Martinie R.J., Bergman J.A., Pollock C.J., Hu K., Allen B.D., Chang W.-C., Silakov A., Bollinger J.M., Jr., Krebs C., Boal A.K. Visualizing the reaction cycle in an iron(II)- and 2-(Oxo)-glutarate-dependent hydroxylase. J. Am. Chem. Soc. 2017;139:13830–13836. doi: 10.1021/jacs.7b07374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Yu C.-P., Tang Y., Cha L., Milikisiyants S., Smirnova T.I., Smirnov A.I., Guo Y., Chang W.-C. Elucidating the reaction pathway of decarboxylation-assisted olefination catalyzed by a mononuclear non-heme iron enzyme. J. Am. Chem. Soc. 2018;140:15190–15193. doi: 10.1021/jacs.8b10077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Dikanov S.A., Davydov R.M., Gräslund A., Bowman M.K. Two-dimensional ESEEM spectroscopy of nitrogen hyperfine couplings in methemerythrin and azidomethemerythrin. J. Am. Chem. Soc. 1998;120:6797–6805. [Google Scholar]
- 58.Hendrich M.P., Fox B.G., Andersson K.K., Debrunner P.G., Lipscomb J.D. Ligation of the diiron site of the hydroxylase component of methane monooxygenase. An electron nuclear double resonance study. J. Biol. Chem. 1992;267:261–269. [PubMed] [Google Scholar]
- 59.Todd A.E., Orengo C.A., Thornton J.M. Plasticity of enzyme active sites. Trends Biochem. Sci. 2002;27:419–426. doi: 10.1016/s0968-0004(02)02158-8. [DOI] [PubMed] [Google Scholar]
- 60.Morrow W.P., Sardar S., Thapa P., Hossain M.S., Foss F.W., Pierce B.S. Thiol dioxygenase turnover yields benzothiazole products from 2-mercaptoaniline and O2-dependent oxidation of primary alcohols. Arch. Biochem. Biophys. 2017;631:66–74. doi: 10.1016/j.abb.2017.08.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Gordon J.B., McGale J.P., Prendergast J.R., Shirani-Sarmazeh Z., Siegler M.A., Jameson G.N.L., Goldberg D.P. Structures, spectroscopic properties, and dioxygen reactivity of 5- and 6-coordinate nonheme iron(II) complexes: A combined enzyme/model study of thiol dioxygenases. J. Am. Chem. Soc. 2018;140:14807–14822. doi: 10.1021/jacs.8b08349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Crowell J.K., Li W., Pierce B.S. Oxidative uncoupling in cysteine dioxygenase is gated by a proton-sensitive intermediate. Biochemistry. 2014;53:7541–7548. doi: 10.1021/bi501241d. [DOI] [PubMed] [Google Scholar]
- 63.Kabsch W. XDS. Acta Crystallogr. D Biol. Crystallogr. 2010;66:125–132. doi: 10.1107/S0907444909047337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Padilla J.E., Yeates T.O. A statistic for local intensity differences: Robustness to anisotropy and pseudo-centering and utility for detecting twinning. Acta Crystallogr. D Biol. Crystallogr. 2003;59:1124–1130. doi: 10.1107/s0907444903007947. [DOI] [PubMed] [Google Scholar]
- 65.Zwart P.H., Grosse-Kunstleve R.W., Lebedev A.A., Murshudov G.N., Adams P.D. Surprises and pitfalls arising from (pseudo)symmetry. Acta Crystallogr. D Biol. Crystallogr. 2008;64:99–107. doi: 10.1107/S090744490705531X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Yeates T.O. Detecting and overcoming crystal twinning. Methods Enzymol. 1997;276:344–358. [PubMed] [Google Scholar]
- 67.McCoy A.J., Grosse-Kunstleve R.W., Adams P.D., Winn M.D., Storoni L.C., Read R.J. Phaser crystallographic software. J. Appl. Crystallogr. 2007;40:658–674. doi: 10.1107/S0021889807021206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Emsley P., Lohkamp B., Scott W.G., Cowtan K. Features and development of Coot. Acta Crystallogr. D Biol. Crystallogr. 2010;66:486–501. doi: 10.1107/S0907444910007493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Murshudov G.N., Skubak P., Lebedev A.A., Pannu N.S., Steiner R.A., Nicholls R.A., Winn M.D., Long F., Vagin A.A. REFMAC5 for the refinement of macromolecular crystal structures. Acta Crystallogr. D Biol. Crystallogr. 2011;67:355–367. doi: 10.1107/S0907444911001314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Lebedev A.A., Vagin A.A., Murshudov G.N. Intensity statistics in twinned crystals with examples from the PDB. Acta Crystallogr. D Biol. Crystallogr. 2006;62:83–95. doi: 10.1107/S0907444905036759. [DOI] [PubMed] [Google Scholar]
- 71.Lebedev A.A., Isupov M.N. Space-group and origin ambiguity in macromolecular structures with pseudo-symmetry and its treatment with the program Zanuda. Acta Crystallogr. D Biol. Crystallogr. 2014;70:2430–2443. doi: 10.1107/S1399004714014795. [DOI] [PubMed] [Google Scholar]
- 72.Poon B.K., Grosse-Kunstleve R.W., Zwart P.H., Sauter N.K. Detection and correction of underassigned rotational symmetry prior to structure deposition. Acta Crystallogr. D Biol. Crystallogr. 2010;66:503–513. doi: 10.1107/S0907444910001502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Kumar V., Ashok S., Park S. Recent advances in biological production of 3-hydroxypropionic acid. Biotechnol. Adv. 2013;31:945–961. doi: 10.1016/j.biotechadv.2013.02.008. [DOI] [PubMed] [Google Scholar]
- 74.Jers C., Kalantari A., Garg A., Mijakovic I. Production of 3-hydroxypropanoic acid from glycerol by metabolically engineered bacteria. Front. Bioeng. Biotechnol. 2019;7:124. doi: 10.3389/fbioe.2019.00124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Williams C.J., Headd J.J., Moriarty N.W., Prisant M.G., Videau L.L., Deis L.N., Verma V., Keedy D.A., Hintze B.J., Chen V.B., Jain S., Lewis S.M., Arendall W.B., 3rd, Snoeyink J., Adams P.D. MolProbity: More and better reference data for improved all-atom structure validation. Protein Sci. 2018;27:293–315. doi: 10.1002/pro.3330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Read R.J., Adams P.D., Arendall W.B., 3rd, Brunger A.T., Emsley P., Joosten R.P., Kleywegt G.J., Krissinel E.B., Lutteke T., Otwinowski Z., Perrakis A., Richardson J.S., Sheffler W.H., Smith J.L., Tickle I.J. A new generation of crystallographic validation tools for the protein data bank. Structure. 2011;19:1395–1412. doi: 10.1016/j.str.2011.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Stoll S., Schweiger A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006;178:42–55. doi: 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
- 78.Pettersen E.F., Goddard T.D., Huang C.C., Couch G.S., Greenblatt D.M., Meng E.C., Ferrin T.E. UCSF Chimera—a visualization system for exploratory research and analysis. J. Comput. Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 79.Neese F. Software update: The ORCA program system, version 4.0. WIRES Comput. Mol. Sci. 2017;8:e1327. [Google Scholar]
- 80.Weigend F., Ahlrichs R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005;7:3297–3305. doi: 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- 81.Becke A.D. Density functional calculations of molecular bond energies. J. Chem. Phys. 1986;84:4524–4529. [Google Scholar]
- 82.Perdew J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B. 1986;33:8822–8824. doi: 10.1103/physrevb.33.8822. [DOI] [PubMed] [Google Scholar]
- 83.Bühl M., Kabrede H. Geometries of transition-metal complexes from density-functional theory. J. Chem. Theor. Comput. 2006;2:1282–1290. doi: 10.1021/ct6001187. [DOI] [PubMed] [Google Scholar]
- 84.Ye S., Price J.C., Barr E.W., Green M.T., Bollinger J.M., Krebs C., Neese F. Cryoreduction of the NO-adduct of taurine:α-Ketoglutarate dioxygenase (TauD) yields an elusive {FeNO}8 species. J. Am. Chem. Soc. 2010;132:4739–4751. doi: 10.1021/ja909715g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Vahtras O., Almlöf J., Feyereisen M.W. Integral approximations for LCAO-SCF calculations. Chem. Phys. Lett. 1993;213:514–518. [Google Scholar]
- 86.Kendall R.A., Früchtl H.A. The impact of the resolution of the identity approximate integral method on modern ab initio algorithm development. Theor. Chem. Acc. 1997;97:158–163. [Google Scholar]
- 87.Neese F., Wennmohs F., Hansen A., Becker U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009;356:98–109. [Google Scholar]
- 88.Grimme S., Antony J., Ehrlich S., Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010;132:154104. doi: 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- 89.Römelt M., Ye S., Neese F. Calibration of modern density functional theory methods for the prediction of 57Fe mössbauer isomer shifts: Meta-GGA and double-hybrid functionals. Inorg. Chem. 2009;48:784–785. doi: 10.1021/ic801535v. [DOI] [PubMed] [Google Scholar]
- 90.Driggers C.M., Cooley R.B., Sankaran B., Hirschberger L.L., Stipanuk M.H., Karplus P.A. Cysteine dioxygenase structures from pH4 to 9: Consistent Cys-persulfenate formation at intermediate pH and a Cys-bound enzyme at higher pH. J. Mol. Biol. 2013;425:3121–3136. doi: 10.1016/j.jmb.2013.05.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Fischer A.A., Miller J.R., Jodts R.J., Ekanayate D.M., Lindeman S.V., Brunold T.C., Fiedler A.T. Spectroscopic and computational comparisons of thiolate-ligated ferric nonheme complexes to cysteine dioxygenase: second-sphere effects on substrate (analogue) positioning. Inorg. Chem. 2019;58:16487–16499. doi: 10.1021/acs.inorgchem.9b02432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Fischer A.A., Stracey N., Lindeman S.V., Brunold T.C., Fiedler A.T. Synthesis, X-ray structures, electronic properties, and O2/NO reactivities of thiol dioxygenase acitve-site models. Inorg. Chem. 2016;55:11839–11853. doi: 10.1021/acs.inorgchem.6b01931. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
X-ray crystal structure data that support the findings of this study have been deposited in the Worldwide Protein Data Bank. The PDB accession codes for the Av3MDO complex with 3HPA and thiocyanate are 6XB9 and 7KOV, respectively.