Sequence-dependent cost for Z-form shapes the torsion-driven B–Z transition via close interplay of Z-DNA and DNA bubble

Abstract

Despite recent genome-wide investigations of functional DNA elements, the mechanistic details about their actions remain elusive. One intriguing possibility is that DNA sequences with special patterns play biological roles, adopting non-B-DNA conformations. Here we investigated dynamics of thymine-guanine (TG) repeats, microsatellite sequences and recurrently found in promoters, as well as cytosine–guanine (CG) repeats, best-known Z-DNA forming sequence, in the aspect of Z-DNA formation. We measured the energy barriers of the B–Z transition with those repeats and discovered the sequence-dependent penalty for Z-DNA generates distinctive thermodynamic and kinetic features in the torque-induced transition. Due to the higher torsional stress required for Z-form in TG repeats, a bubble could be induced more easily, suppressing Z-DNA induction, but facilitate the B–Z interconversion kinetically at the transition midpoint. Thus, the Z-form by TG repeats has advantages as a torsion buffer and bubble selector while the Z-form by CG repeats likely behaves as torsion absorber. Our statistical physics model supports quantitatively the populations of Z-DNA and reveals the pivotal roles of bubbles in state dynamics. All taken together, a quantitative picture for the transition was deduced within the close interplay among bubbles, plectonemes and Z-DNA.

Graphical Abstract

Graphical Abstract.

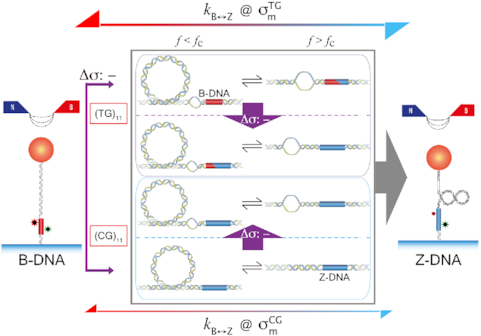
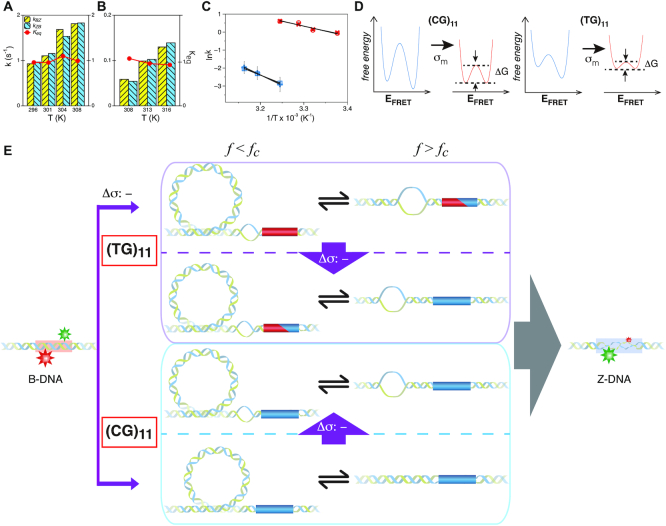
Dynamic interplay of bubble, supercoil and twisted B-DNA with the Z-DNA state of CG or TG repeats detected by smFRET under various mechanical (force and σ) conditions imposed by magnetic tweezers. TG repeats exhibit higher B–Z transition rates (k) than CG repeats at their respective midpoint σ values.

INTRODUCTION

Left-handed Z-DNA has attracted a great deal of attention over years due to its extraordinary structure and potential roles in biological processes(1–11). Z-DNA is a high-energy conformation of the double helix with a zigzag backbone; this structure can be formed in alternating purine-pyrimidine sequences by negative supercoiling induced by transcription or unwrapping of nucleosomes (8,9). The discovery of antibodies and enzymes that bind specifically to Z-DNA (12,13) has allowed the investigation of the biological significance of Z-DNA and the interdependence between transcription and Z-DNA formation (8,14–17). Other studies have aimed at understanding of mechanical and physical properties of Z-DNA (18). Thermodynamic, kinetic, and energetic properties for the B–Z transition have been measured for short oligomers or plasmids bearing suitable sequences (6,19–23). Lee et al. examined the mechanical and kinetic features of the B–Z transition occurring in cytosine-guanine (CG) repeat sequences at the single-molecule level (24): the authors discovered that a small degree of negative superhelicity is sufficient to trigger the B–Z transition in the presence of sub-picoNewton (pN) tension. Thus, from the physical standpoint, Z-DNA is an energetically attainable state under physiological conditions and may therefore be relevant to various biological phenomena. More recently, Oberstrass et al. investigated the B–Z transition as a sequence-specific cooperative transition in supercoiled DNA molecules containing CG repeat sequences in the high-tension regime, characterizing mechanical properties of Z-DNA (25,26).

Genome research has revealed that putative Z-DNA forming sequences are found in the regulatory regions of a multitude of genes (27,28). Although CG repeats, with the least propagation free energy in the B-to-Z transition (hence, free energy cost for Z-state relative to B-state) (19,29), have been the most extensively studied over the last three decades, thymine-guanine (TG) repeats, simple repeat sequence with the second least cost (29,30), exist more frequently in the gene regulatory regions of eukaryotes (28,31,32), e.g., near rodent globin, immunoglobulin, and galactokinase genes and the human globin and actin genes (27–29,33). TG repeats are mainly located upstream of the first expressed exons. Besides, TG repeats are the most frequent microsatellite sequences in plants and also common in other higher organisms. Microsatellite sequences have drawn much attention because they are recombination hotspots leading to genetic instability and serve as genetic markers (34). Expansion of microsatellites over generations is thought to aggravate the symptoms associated with genetic instabilities (32,35). Recently, the DNA fragility in the parallel evolution of pelvic reduction in stickleback fish has been attributed to Z-DNA formation by TG repeat sequences (36), which is, to date, the most straightforward evidence for biological functions of Z-DNA. Since the three seminal papers on the Z-DNA with TG repeats were published nearly four decades ago (37–39), the B–Z transition in TG repeats has been investigated from various aspects (29,40–43). Despite the prevalence of TG repeats in genomes and their potential biological significance, understanding of the energetics and dynamics of the B–Z transition remains elementary.

Here, we report distinctive dynamics of the Z-states by TG and CG repeats, their potential biological functions and the underlying picture for the overall phenomena. Despite general similarities, the Z-DNA by TG repeats is notably different from that by CG repeats in their mechanics and kinetics. We demonstrated via single-molecule manipulation that TG repeats also adopt Z-form in the presence of unwinding torsion, but with more negative superhelicity due to their larger energy cost for Z-form. We found that the tension, modulator of effective torsion in DNA, also plays crucial roles in the B–Z transition. The tension should exceed a threshold to induce a B–Z transition in a DNA molecule containing TG repeats (hereafter called TG molecule for brevity; likewise, a DNA molecule containing CG repeats is called CG molecule). The rate of the B–Z transition in a TG molecule is significantly higher than in a CG molecule at their respective midpoint torsion (torsion at which B- and Z-states have equal populations), indicating that the free energy barrier of the transition in the TG molecule is considerably smaller than that of the CG molecule because a denaturation bubble generated by more negative superhelicity within the TG molecule facilitates a nucleation step for the transition. The torsional softness of TG molecule due to a preformed bubble also accounts for the tension threshold or a Z-form saturation at the low tension. The dynamic B–Z transition observed under physiologically relevant tension and torsion indicates the physical advantage of Z-DNA, in particular, TG-repeat-based Z-DNA for its potential biological roles. As a sequence-specific nano-switch controlled by mechanical effects, TG repeats could control the torsion in the whole DNA molecule dynamically and facilitate Z-DNA-induced downstream processes, possibly transcription, via conformational transition or modulation of mechanical condition in DNA.

MATERIALS AND METHODS

Preparation of DNA samples

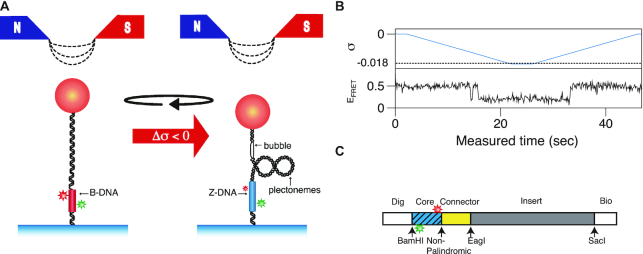
Sample preparation is described in detail elsewhere (24). We used one CG-repeat Core fragment (CG)₁₁ and three TG-repeat Core fragments, (TG)₁₁, (TG)₁₄ and (TG)₁₇, which contain 11, 14 and 17 repeats of a (TG/CA) di-nucleotide sequence, respectively, in which dyes are all separated by the same distance (14 bp). The sequences of these Core DNAs as well as (CG)₁₁ are given in Supplementary Table S1. DNA tethers were constructed as described elsewhere (24). The design of a DNA molecule and its tethering in the setup are depicted in Figure 1.

Figure 1.

Nano-scale conformation change associated with the B–Z transition (B-DNA (red) and Z-DNA (blue)) is monitored by smFRET. (A) Negative supercoiling (by magnetic tweezers) induces the B–Z transition in a DNA construct immobilized on surface by digoxigenin (Dig)/anti-Dig binding and attached to a magnetic bead by biotin (Bio)/NeutrAvidin binding. The negatively supercoiled molecule also displays schematically a denaturation bubble as well as plectonemes. The conformational state of the Core region is determined from the FRET state of the two dyes embedded therein (B-DNA: middle E_FRET; Z-DNA: low E_FRET). (B) Reversible B–Z transition in (TG)₁₁ controlled by negative supercoiling (σ: upper panel). Negative σ (< -0.01) triggers the B–Z transition revealed by smFRET (lower panel: E_FRET(B-DNA) ∼ 0.5 and E_FRET(Z-DNA) ∼ 0.2). (C) Design of the DNA tether molecule, which contains a Core fragment (blue, hatched) with a donor (Cy3, green) and an acceptor (Cy5, red) dye separated by 14 base pairs.

Experiment with the hybrid technique of single-molecule FRET and magnetic tweezers

The hybrid technique of single-molecule FRET (smFRET; for details of smFRET, see elsewhere (44)) and magnetic tweezers was developed and described previously (24). The FRET values in our experiment were determined by measurements of donor and acceptor fluorescence intensities and as their ratio (45). Alternatively, FRET values can be also determined by measurements of the lifetime of donor fluorescence (46). In the objective-type TIRF setup, workhorse for our smFRET assay, a green laser (532 nm DPSS laser, Coherent, USA) irradiates the sample chamber and fluorescence signals from Cy3 and Cy5 dyes were detected with an EMCCD (Andor IXON D897) to obtain the FRET efficiency (E_FRET). The magnetic tweezers module added above permits us to apply force and torque to DNA molecules tagged with magnetic beads. The beads’ images were acquired with an infrared LED (M850L2, Thorlabs) as a light source and a CCD camera (STC-CMC401PCL, Sentech America, USA) as a detector and the image data were analyzed to obtain the vertical position of the bead (and thus the extension of DNA). Singly tethered and torsionally constrained DNA molecules were chosen for experiments by checking the relationship between superhelicity σ and extension at various forces (1.4, 0.6, 0.4 and 0.3 pN). All experiments with the hybrid technique were performed at room temperature and with a physiological ionic condition ([Na⁺] = 100 mM) unless noted otherwise. The experimental arrangement is schematically given in Figure 1.

Determination of the energy barrier of the B–Z transition

By measuring the rate constants for the same molecule at various temperatures, we determined the energy barrier between the B- and Z-DNA states according to the Arrhenius equation. To establish the midpoint condition, the torsional stress was applied to a DNA molecule using magnetic tweezers. In the experiment, the DNA molecule was pulled at the tension of 1.4 pN. Under the midpoint condition, the E_FRET time trace was recorded, and the dwell time distribution was analyzed. The turn of the magnets for the midpoint condition differed at different temperatures, and the twist of DNA was carefully tuned to achieve the midpoint condition. We used four different temperatures for (TG)₁₁ (23, 28, 31 and 35°C) and three for (CG)₁₁ (35, 40 and 43°C).

RESULTS

Twisting of DNA induces the B–Z transition faithfully in TG repeats

TG repeats undergo the B–Z transition under unwinding torsional stress (38). Here we demonstrated the B–Z transition in TG repeats in the presence of well-defined superhelicity (σ ≡ ΔLk/Lk₀ = (Lk – Lk₀)/Lk₀ where Lk is the linking number of a DNA, Lk₀ the Lk value of the DNA in the relaxed state, and ΔLk their difference) and tension with magnetic tweezers (Figure 2). We characterized the behavior of TG repeats under torsion in comparison with that of CG repeats. The E_FRET values for B- and Z-DNA states are determined based on our previous smFRET measurements for the protein-induced B–Z transition (47). In the unwinding-driven B–Z transition (Figure 2), TG repeats are less responsive to external torque (from this work) than CG repeats (from a previous work) as shown in Figure 3A here and Supplementary Figure S3 in (24), similarly to the case of the protein-induced B–Z transition examined previously by smFRET assay (47).

Figure 2.

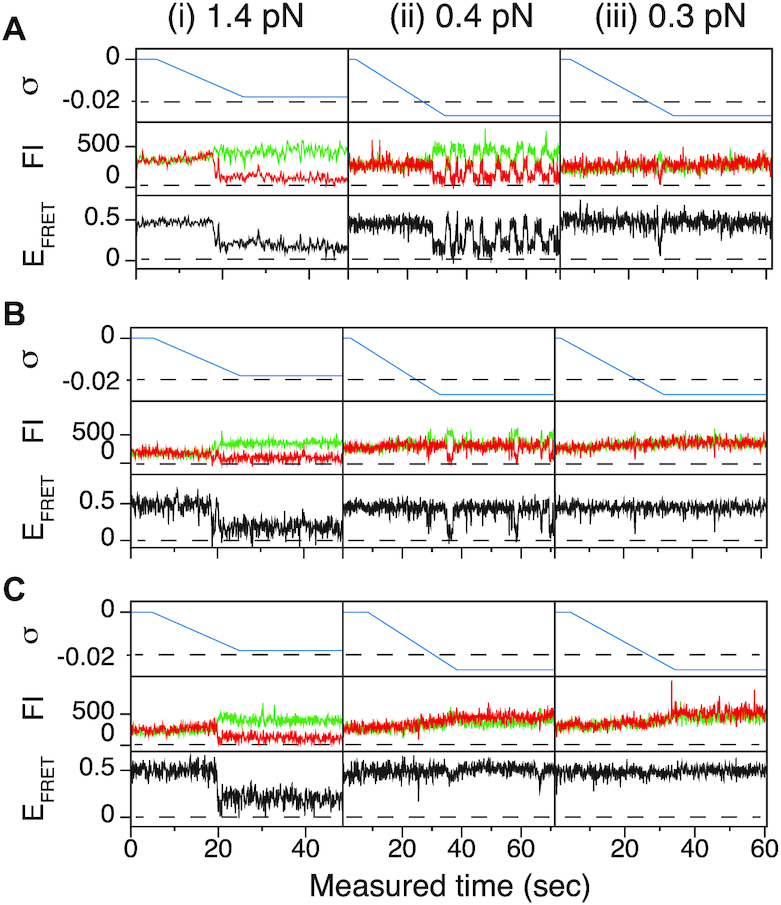
The B–Z transitions of TG repeats are sensitive to tension and torsion. FRET time traces for (A) (TG)₁₁, (B) (TG)₁₄ and (C) (TG)₁₇ molecules under various levels of tension and torsion. In the left, center, and right (i, ii, and iii) panels, DNA molecules were unwound until σ reached –0.018, –0.027 and –0.027 under the tension of 1.4, 0.4 and 0.3 pN, respectively. Each panel shows the state of supercoiling (top), fluorescence intensities (FI) of donor (green) and acceptor (red) dyes (middle) and E_FRET (bottom). Horizontal dashed guidelines in the top subpanels indicate σ of –0.02.

Figure 3.

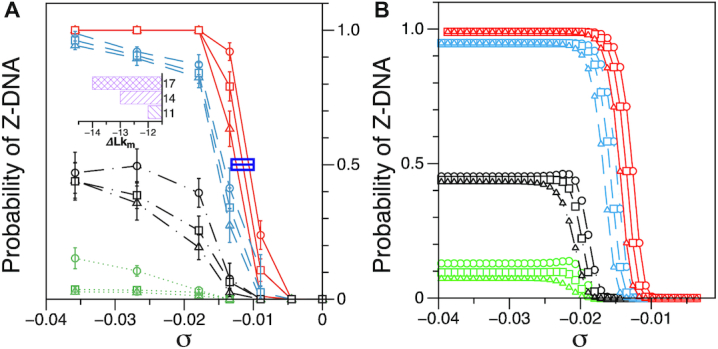
Probability of the Z-DNA state for TG molecules ((TG)₁₁, circle; (TG)₁₄, square; and (TG)₁₇, triangle) as a function of σ. (A) Experimental results. Data were obtained for four different tensions: 1.4 pN (red, solid), 0.6 pN (blue, dashed), 0.4 pN (black, dot-dashed), and 0.3 pN (green, dotted). The error bars are the standard errors of the sample proportions. Inset: midpoint 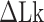(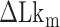) for three TG repeats at a tension of 1.4 pN (corresponding to the strip in main figure). (B) Theoretical estimates by the model prescribing the three states, plectonemes, Z-DNA, and twisted bubbles, with distinct free energy of 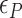, , 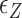and 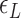, respectively. 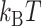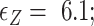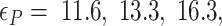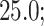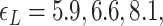Here, we set the following values of free energy in unit of : and and 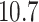for tension 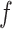= 0.3, 0.4, 0.6 and 1.4 pN, respectively. Figure symbols and conventions in (B) are the same as in (A).

The degree of supercoiling or superhelicity can be used to estimate the torsional stress because the torque is related to σ (τ = 2πC p⁻¹σ, where C is the torsional stiffness given by the torsional persistence length of DNA times thermal energy and p is the pitch of DNA) in the linear response regime. The critical torque for DNA buckling depends on the tensional force (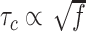) as the tension suppresses the formation of plectonemes, type of writhes relevant in our study (48). Negative supercoiling induced the E_FRET to change from 0.5 to 0.17 (Figure 2A–C), implying that the molecule adopted a Z-DNA conformation similar to the one assumed by the CG repeat (24). Traces (i, ii, iii) for three different tensions in Figure 2A (also B and C) were obtained from one and the same molecule to rule out any molecule-to-molecule variation. Other complete sets of traces are also shown in Supplementary Figure S1. We measured the population of Z-DNA at various mechanical conditions (σ and tension) and for different repeat lengths. Figure 3A summarizes the experimental results for relative populations of Z-state and a theoretical reconstruction of the results. From the theoretical modeling, the observed tension, torsion, and length-of-sequence dependences of Z-DNA population were reproduced and elucidated by taking account of three high-energy states, bubble, plectoneme, and Z-DNA, that compete with each other and twisted B-form in the presence of unwinding torsional stress. Our theoretical approach is described below in a separate sub-section and the intriguing interplay of these states revealed thereby is further discussed in Discussion. Clearly, the population of Z-DNA increases with negative σ, indicating that negative supercoiling facilitates the formation of Z-DNA. Each data point in Figure 3A was obtained by averaging data from 20 to 50 different molecules. The midpoint σ (σ_m) for a DNA molecule containing TG repeats (TG)₁₁ was larger than the one required for a (CG)₁₁ molecule (σ_m^TG and σ_m^CG vary from –0.011 to –0.027 and from –0.006 to –0.008, respectively, as the tension decreases from 1.4 to 0.4 pN; Figure 3A) but still smaller than the one necessary for bulk assays (σ_m,bulk = –0.03 to –0.09 (38–40,42)). In the presence of 1.4 pN’s tension, (TG)₁₁, (TG)₁₄ and (TG)₁₇ molecules underwent the B–Z transition at σ_m = –0.011, –0.012 and –0.013 (Figure 2A–C (i) and Figure 3A): one more negative turn was needed for each 6-bp expansion of the repeat (inset in Figure 3A). This indicates that the midpoint σ also depends on the length of repeats. This length dependence can be accounted for by noting that the applied torsional turns should be larger for the longer repeats in order to withstand the larger reduction of torsional stress taking place after the longer repeats undergo the B-to-Z transition completely. The length effect can be easily explained from a simple mechanical argument (see Supplementary Information) and further confirmed by the statistical physics modeling shown in Figure 3B. The change of length would merely shift the torsional stress required for Z-state saturation slightly regardless of sequence type as predicted from a pure mechanical model.

Tension exceeding a threshold is required for the Z-form by TG repeats to compete effectively with writhe

In Figure 2, we also note that the B–Z transition in TG repeats is sensitive to external tension, in contrast to the transition in CG repeats. Reduced tension impedes the B–Z transition driven by negative supercoiling, as observed with the three TG repeats ((TG)₁₁, (TG)₁₄ and (TG)₁₇) (Figure 2A–C and Supplementary Figure S1). The tension-facilitated Z-DNA formation is also shown in Figure 3A in this work and Figures 3, 4 and S3 in (24). One notable property of TG molecule is the existence of a transition threshold: small tension (<0.4 pN) suppresses the transition in TG repeats even at a large negative ΔLk (<–40) or σ ∼–0.036 (Figure 3A). The B–Z transition ensues in TG repeat sequences when the applied tension exceeds a threshold. This thresholding behavior is related to the higher onset negative σ for the B–Z transition in TG repeats than in CG repeats as discussed later. This higher onset negative σ falls beyond the values of superhelicity required for buckling transition and for bubble formation in AT-rich regions (49–53). At the level of tension lower than the threshold, the buckling transition sets in, prevailing over the B–Z transition. Then, the torsional stress in DNA is consumed by writhes rather than forming Z-DNA.

Figure 4.

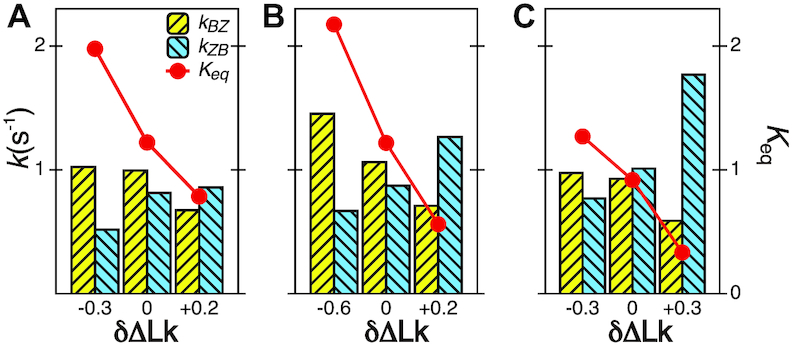
The B–Z transitions in TG repeats are dynamic and sensitive to 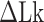. Rate constants for the B-to-Z and Z-to-B transitions, 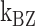(yellow, left-hatched) and 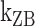(blue, right-hatched), and the equilibrium constant K_eq (red dot) are shown for various 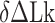with respect to 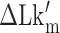. In the data shown, 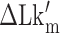values for (A) (TG)₁₁, (B) (TG)₁₄ and (C) (TG)₁₇ are –10.9, –12.8 and –15.8, respectively. The tension applied to DNA is 1.4 pN.

A statistical physics model for DNA mechanics can quantitatively elucidate the functional dependence of Z-DNA probability on both stretching tension and unwinding torsion in DNA

The probability of Z-DNA appears as a complex function of tension, torsion, and repeat length. We introduce a statistical physics model for quantitative analysis. In our model, we consider a DNA tether that has the potential for harboring plectonemes, denaturation bubbles, and non-B-form (here, Z-DNA) in the presence of twist (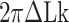). To our knowledge, these three conformations should be major modes that respond to negative torsional stress and would form to reduce the torsional stress in the physiological regime of tension and torsional angle (24,26,49). Therefore, we assume the three major modes (bubbles, plectonemes, and here Z-DNA) as excited states with the B-DNA as a reference state and rule out the possibility of other unessential exotic (non-B) structures. It is of note that the existence (and involvement) of bubbles is indirectly revealed due to ignorance of their exact locations and lack of means to detect them. The tether has a Core (Z-DNA forming sequence) embedded in a DNA molecule of random sequence. The elastic energy (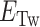) due to the residual negative turns remaining in B-form after formation of bubbles, Z-DNA, or plectonemes is given by 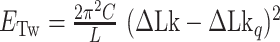with 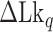the turns distributed to L-DNA (denaturation bubble by unwinding or torsionally melted DNA (54), depicted in Figure 1A and Figure 5E), Z-DNA, or plectonemes (where L is the total length of DNA). We then consider the grand partition function of DNA for a given number of 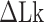and partition 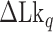into the aforementioned three modes (bubble, Z-DNA, and plectoneme). The onset 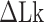or superhelicity for the B–Z transition turns out to be sensitive to the size of bubble and the effective torsional stiffness 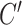, which hints at the existence of pre-formed L-DNA and the torsional softness of L-DNA featured by a very small 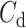, as discussed in Supplementary Information.

Figure 5.

Kinetics of the B–Z transition induced by supercoiling and molecular picture for the transition. Rate constants and equilibrium constants of the B–Z transition of (A) (TG)₁₁ and (B) (CG)₁₁ are shown for various temperatures (in Kelvin). Figure conventions are the same as in Figure 4. (C) ln k-versus-1/T graphs for (TG)₁₁ (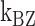: circle, 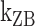: cross) and for (CG)₁₁ (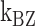: square, 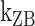: plus) at 100 mM NaCl. Lines are linear fits to data based on the Arrhenius equation. (D) Schematic free energy landscapes of (CG)₁₁ (left) and (TG)₁₁ (right) molecules in the absence (blue curve) or presence (red curve) of σ_m. The abscissa of the plot is E_FRET and the ordinate represents the free energy (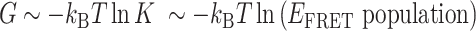) of the system. In each double-well potential, the left and right minima correspond to Z- and B-DNA states, respectively. The tension to DNA is 1.4 pN. (E) Molecular picture for the B–Z transition based on the interplay of Z-DNA, L-DNA, plectonemes and twisted B-DNA together with configurational states of CG and TG molecules under various mechanical conditions. The B-form DNA (red Core with middle E_FRET) in the absence of torsional stress (far left) undergoes the transition to the Z-form DNA (blue Core with low E_FRET) at sufficiently high negative torsion (far right) through various conformational states (middle) depending on type of sequence and mechanical conditions. The Z-form in TG molecules is preceded by other conformations depending on applied tension and torsion, and can compete with them beyond the tension threshold (f > f_c ∼ 0.3 pN) and a certain negative torsion while the Z-form in CG molecules can form at small negative torsion over the entire range of tension applied. High force (f > f_c) favors DNA bubble over plectonemes while low force (f < f_c) does the opposite in unwound DNA. In the middle panel, the red and blue Cores represent the B- and Z-forms, respectively. The red-blue Core represents the Core alternating between B- and Z-forms by trading turns with the rest of the molecules. The cartoon displays a denaturation bubble (separated strands) and plectonemes (DNA gyre), respectively. ‘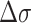: -’ implies additional unwinding of DNA and f_c indicates the critical tension for DNA buckling.

The free energy of each conformational state (relative to B-state) is of importance in the model and shall be expressed in terms of the (unit) free energy associated with one linking number change by the state (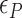, , 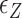and 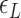for plectonemes, Z-DNA, and twisted bubbles, respectively) as the linking number is the quantity traded among the states during conformational transitions. The detailed formulation of the partition function is shown in Supplementary Information. For the three different lengths of TG repeats used (22, 28 and 34 bp long), three different (maximum) values of superhelical turns would be allocated to Z-DNA (assumed to be about –4, –5 and –6, respectively) in the case of complete conversion (To obtain low FRET signals, we expect that the whole TG repeats should adopt Z-state.).

The switching to Z-DNA occurs at the critical torque 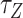, which is mainly determined by the free energy of Z-state, 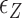. The free energy associated with the plectoneme state has a well-known tension dependence, 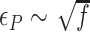, which is due to the energy penalty of forming a writhe against pulling force (48,53). The free energy of the L-DNA state also has a certain tension dependency as bubbles are more extended and less twisted under large tension. Furthermore, 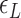has a range of values due to disorders in L-DNA harboring sequence, so the relevant 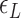should increase as L-DNA grows because denaturation of more stable base pairs should follow.

Far below the critical torque 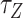, a stretch of L-DNA taking – 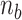( 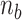> 0) turns can be formed at an AT-rich region (for example, our DNA tether has several AT-rich regions including a long AT-rich tract (…ATTTTTCTTTTTTTCATAAATT…)), the free energy of which is very small compared to 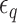of the all three modes under consideration. This picture is consistent with and well supported by several recent studies (25,26) and the critical torque measured therein is consistent with our interpretation of free energy cost in modelling L-DNA and Z-DNA in TG and CG sequences. Under the condition to form Z-DNA in TG repeats in the Core, the turns of 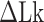+ 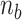are distributed to these states according to their Boltzmann weights. From the shift of the onset superhelicity for the B–Z transition, the size of precedent L-DNA (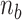) can be found together with .

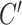By using the parameters (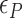,  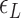and 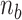) listed in Supplementary Table S2 for different levels of tension used in our study (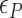: given for each tension with no adjustment; 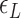: tuned for the best fit for the data within the justifiable range; 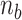: self-consistently determined within a reasonable range as a factor affecting both energy and effective torsional stiffness of DNA; for details, see Supplementary Information), we reached quantitative agreement with experimental data (Figure 3A) as shown in Figure 3B. The entropy of L-DNA (mainly associated with freed degrees of freedom of DNA) is already accounted for in the grand canonical function by considering the chemical potential of L-DNA. The theoretical curves (Figure 3B) were obtained by using the value of 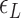strictly increasing with growing tension. An appropriate mean value 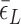permits us to match the asymptotic behavior (at large negative σ) of Z-DNA populations found in experiments. As we neglect the disorder in sequence, the transitions are rather sharp in the theoretical prediction of Z-DNA populations (Figure 3B), in contrast to those acquired experimentally. At low tension (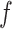< 0.3 pN) (53,55), the Core cannot take the Z-state as most of the added turns are spent for plectonemes, or the L-DNA of small 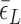( 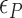< < 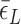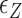). 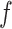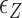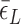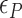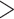In the intermediate range of tension (0.3 pN < < 0.9 pN), of TG repeats can be comparable to of comparable length of sequence ( 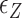∼ 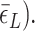In the presence of high tension (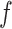> 0.9 pN), Z-DNA would be most favorable (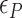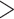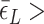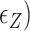. Naturally, we expect, the midpoint condition in the B–Z transition is fulfilled when 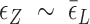. For CG repeats (shown in Supplementary Information), 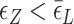is satisfied for almost the entire range of tension considered and thus Z-DNA forms before a torsional stress large enough to open bubbles is accumulated.

The B–Z transition in TG repeats is highly dynamic even at room temperature under certain mechanical settings

In our previous work, we found that a CG repeat sequence undergoes recurrent inter-conversions (<0.1 Hz) between the B- and Z-state at a physiological temperature (37°C). At room temperature, however, one-way transitions were observed due to a large free energy barrier between the states: The B-to-Z transition occurred at 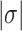sufficiently larger than 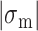, and the Z-to-B transition happened at 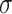close to zero. Here, TG repeats however exhibited highly dynamic inter-conversions with the transition rates of the order of 1 Hz even at room temperatures, with a certain set of mechanical conditions met (Figure 4 and Supplementary Figures S2, S3), suggesting a low free energy barrier between the states. To characterize the kinetics of the B–Z transition in TG molecules, we adjusted 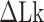towards 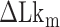until the average dwell times from B-to-Z and Z-to-B transitions converged. Due to several reasons (limited measurement time by dye bleaching, molecule-to-molecule variation, error in initial 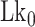, etc), the best experimental estimate of 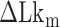for a given molecule (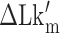) may deviate from true 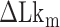. We then measured the equilibrium constant K_eq for various values of 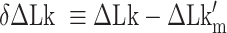: 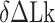of ± 0.2–0.3 resulted in 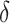K_eq of ± 35–60% (Figure 4A–C), indicating that the B–Z transition is indeed sensitive to supercoiling. Here, the rate constants from B- to Z-DNA and Z- to B-DNA ( 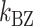and 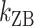) and K_eq were determined by analyzing FRET time traces (Figure 4A–C and Supplementary Figure S2). In summary, the Z-state can be accessible efficiently by TG repeats due to the small free energy barrier at the midpoint condition where the L-DNA state of similar free energy coexists as discussed earlier.

The energy barrier of the B–Z transition for TG repeats is significantly smaller than that for CG repeats at the midpoint condition

To estimate the energy barrier of the B–Z transition, we examined the kinetics of the transition at various temperatures in the presence of high tension (∼1.4 pN). Here and below, we refer to ‘energy barrier’ as the enthalpic barrier (ΔH) at the midpoint condition. The energy barrier can be determined from the temperature dependence of the rate constant. At different temperatures and their respective 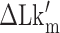, we obtained long FRET time traces (Figure 5A, B and Supplementary Figure S3). In Figure 5C, the logarithm of the rate constant is plotted as a function of 1/T. The (TG)₁₁ molecule exhibits the transition more frequently than the (CG)₁₁ molecule: at 308 K, 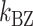(and 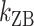) of (TG)₁₁ is >30 times larger than that of (CG)₁₁. Compatible with Arrhenius theory, the data are reasonably fitted by a linear function, the slope of which yields the value of the enthalpic barrier. From this analysis, we discovered the enthalpic barriers of the B–Z transitions in (TG)₁₁ and (CG)₁₁ repeats: the former is 10.5 ± 1.5 (s.d.) kcal/mol (Figure 5A, C) and the latter is, however, almost twice larger, 21.8 ± 4.1 (s.d.) kcal/mol (Figure 5B, C). From the kinetics data, we can also make an estimate of the difference of free energy barriers between the two sequences. Assuming a common value for the pre-exponential factor 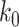, we can make the estimate of the difference of free energy barriers as follows. From 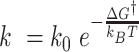, we get 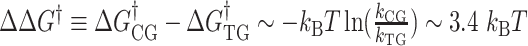. Thus, the free energy barrier of the CG molecule is about 2 kcal/mol higher than that of the TG molecule. Using the enthalpy values obtained above, the difference of entropic barriers at the transition state is given as: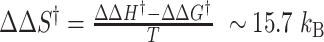. The interpretation for this analysis is given in next section.

DISCUSSION

Below, we provide both intuitive and quantitative understanding of the B–Z transition in TG as well as CG repeat sequences by comparing two cases systematically.

Negative supercoiling can induce the B–Z transition in TG repeats as in CG repeats. The torsional stress required for formation of Z-DNA in TG repeats is greater than that required in CG repeats as Z-DNA in TG repeats is less stable. For the DNA molecule (∼12 kb) used in this study, we have to apply additional five turns of negative twist to induce the B–Z transition in TG repeats pulled at 1.4 pN (|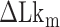| ∼ 6–7 for CG repeats and ∼10–12 for TG repeats, respectively). In response to torsional perturbation, the DNA molecule would gain considerably more energy by the five additional turns. Even though higher torsional stress (more negative superhelicity) is required to induce the B–Z transition in TG molecules, the level of superhelicity corresponding to this is about –0.01 to –0.02, still considerably less than physiological superhelicity (–0.03 to –0.09) inside cells (56).

One notable feature of the B–Z transition of TG repeats is the existence of a tension threshold. This can be also accounted for by the sequence-dependent energetics of Z-state. In contrast to CG repeats shown in Figure 4 of (24) (also in Supplementary Figure S5D of this work), a low level of tension (e.g. 0.3 pN) suppresses the B–Z transition over the large range of σ tested (from zero down to –0.036, which is physiological) as shown in Figure 3 because plectonemic supercoils are favored at the low tension as an easy mode to relax the torsional stress, the effective torsional stress is reduced in such a slack tether, and consequently, the onset σ for the B–Z transition in the TG molecule, already more negative than for the CG counterpart, is further shifted down to more negative values (50–53). At such large negative superhelicity, formation of L-DNA is turned on, which further suppresses formation of Z-DNA. Due to the clear switching response of plectoneme buckling, the B–Z transition also exhibits a similarly (inversely correlated) sharp transition with respect to the external tension.

The Z-DNA by TG repeats can compete with L-DNA in a complex manner. TG repeats require more unwinding turns than CG repeats. As seen from the statistical model a few stretches of L-DNA are already established in the range of supercoiling turns for Z-DNA formation in TG molecules. When the torsional stress in DNA is increased in the presence of intermediate to high tension, the L-DNA formed by a given number of unpaired base pairs cannot take the torsional stress as much as in the case of low tension because L-DNA is already stretched out and becomes tight. Besides, the growth of L-DNA into more stable flanking regions is more difficult to happen. The additional turns would favor Z-DNA rather than extending existing bubbles or creating a new bubble. Once Z-DNA is nucleated at the torsional stress large enough to overcome the junction penalty, the base pairs in the Core DNA switch between B-DNA and Z-DNA by trading unwinding turns from existing bubbles and the Z-DNA patch may absorb some torsional turns from L-DNA. Consequently, small L-DNA bubbles might be even closed (reducing the number of junctions). Although partial Z-DNA domain or its elongation in real time are challenging to capture definitely with smFRET and bead height measurements due to limited temporal and positional resolutions, experimental signature hinting at the existence of partial Z-DNA Core (intermediate E_FRET values lasting over several data points) or denaturation bubble (suggested by violated anti-correlation between Z-DNA and plectoneme states at low tension) can be readily found (see Supplementary Figure S4).

In the TG molecules, the B–Z transition at 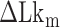occurs more frequently (<τ> ∼ 1 s) even at the room temperature (298 K), indicating the free energy barrier of the TG molecules is smaller than that of the CG molecule at the respective midpoint conditions while the free energy difference between the B- and Z-states of TG repeats is larger than that of CG repeats in the absence of torque as presented in the previous section. This situation is depicted schematically in Figure 5D. As noted, the kinetic rates of the B–Z transition in CG and TG repeats at their respective midpoints differ by a factor of ∼30, implying that their free energy barriers differ by ∼3.4 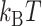. Using the enthalpic barriers deduced from the measured temperature dependence of the rates and assuming the same pre-factor of kinetic rate, we could estimate the entropic contribution to the barrier difference for T = 308 K and f = 1.4 pN.

The barrier crossing by the TG sequence involves a moderately smaller free energy barrier compared to the CG sequence while the enthalpic barrier is considerably larger in the CG molecule than in the TG molecule. This implies larger entropic gain for the transition state of the CG molecule while entropic contribution is not significant for TG molecules. Since the junction penalty is of enthalpic origin, the enthalpic barrier of the TG molecule (10.5 ± 1.5 (s.d.) kcal/mol), nearly equal to the junction penalty (∼10 kcal/mol), should arise from creation of the necessary junction structure for the B–Z transition. For the case of the CG molecule, the enthalpic barrier is approximately twice the junction penalty, so the rest must originate from opening of several base pairs to drive the B-to-Z transition. Larger entropic gain for the CG molecule in the barrier conformation must be related to freed degrees of freedom of chains into flexible single strands due to broken base pairs. On the other hand, the entropic gain of the TG molecule at the transition state is small, perhaps amounting to entropic gain achievable by breaking just additional one or two base pairs. This is consistent with our picture that there is a reservoir of unpaired DNA in nearby AT-rich regions. Since base unpairing can be fueled by nearly iso-energetic transfer of DNA unwinding in TG molecule, the enthalpic barrier as well as the entropic gain is small, and therefore the B–Z transition of the Core region occurs readily. The B–Z transition in CG repeats is kinetically more challenging at the low midpoint superhelicity because the molecule should create two junctions and at the same time open up several base pairs (or create de novo bubbles of size of several CG base pairs (∼5)). That is why the process is slow. Energetically, the junction penalty might be (partially) saved for the nucleation of the Z-DNA domain in the Core by being accommodated by a neighboring L-DNA patch, as hinted by a better fitting by a junction-less transition (e_j = 0) (Supplementary Figures S5 and S6). The distinct torsional responses of CG and TG molecules and their state dynamics are schematically depicted in Figure 5E.

Let's imagine a situation that chromatin remodelers knock off histones and disrupt nucleosomes in order to facilitate transcription. Once nucleosomes are disassembled, the negative supercoils once trapped by them are released. Disassembly of nucleosomes and accumulation of negative torsional stress may be continued in a processive manner. At this moment, there are at least four possible fates to face: (i) to open up bubbles in nearby AT-rich regions, (ii) to form plectonemes, (iii) to induce the B-to-Z transition in nearby CG or TG repeats or (iv) to restore nucleosomes. If there are CG repeats nearby to respond to the torsional stress, they will be converted to Z-form before forming bubbles in AT-rich regions. Any excess turns would be absorbed by CG repeats until all such sequences in B-form are exhausted. Bubbles begin to form afterwards. Restoration of B-form on such sequences would be possible when the torsional stress is sufficiently reduced. This implies that the Z-DNA by CG repeats serves as strong absorber of negative turns.

On the other hand, the torsional stress in a TG molecule would be continuously accumulated during nucleosome disassembly until Z-DNA by TG repeats or DNA bubbles are formed. Once the Z-DNA is formed, it can serve as a dynamic torsion buffer: The Z-DNA prevents the torsional stress in the DNA molecule from departing away from the value set at the phase transition, and thanks to the small transition barrier for the TG molecule, Z-DNA formation (and elimination) is highly dynamic even at room temperature and readily fulfilled as per cell's necessity.

Due to the similarity of the critical torques (i.e. free energy penalties) for bubbles of random sequence and Z-form in TG repeats, formation of bubbles, required for transcription initiation, would be a trivial task to conduct because the level of torsional stress already established for Z-DNA formation just matches the torque required to trigger bubble formation. Moreover, until Z-DNA disappears completely, the full potential for bubble generation is maintained even without the remodeler's activity to disrupt nucleosomes. Interestingly, the competition between Z-DNA and bubbles can work as a selection mechanism to create only a significant bubble, not auxiliary ones, which is perhaps a right one for accurate gene expression. Besides the aforementioned roles as torsion buffer and bubble selector, as proposed, it may also recruit various protein factors (such as Z-DNA binding proteins) via its unusual shape over the vast sea of B-form DNA.

The proposed roles of Z-DNA, which are based on our findings under the physiological, but simplified in vitro conditions, remain to be tested for more complex in vivo situations. Still, the roles of Z-DNA proposed here should be viable because the mechanical properties of Z-DNA shall remain in vivo.

In summary, we discovered that compared to a CG repeat, a TG repeat sequence requires more unwinding turns with a certain minimum tension for efficient Z-DNA formation. It displays a faster B–Z transition and a notably smaller enthalpic barrier dedicated for junction generation, along with small entropic cost worth holding just a few additional opened bases. The retarded onset and small-barrier transition of Z-DNA in TG repeats reveal the crucial involvement of L-DNA and the close interplay among Z-DNA, L-DNA, and plectonemes. Thus, TG repeats likely serve as a torsion buffer or bubble selector while CG repeats may work as a torsion absorber. Our work indicates that sequence-dependent energetics of Z-form dictates thermodynamic and kinetic features in the B–Z transition and demonstrates that the information encoded in a DNA sequence programs and plays active roles in its dynamical behaviors and biological function (57–60).

DATA AVAILABILITY

The data that support the findings of this study are available from the corresponding authors upon reasonable request.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Research Foundation (NRF) of Korea [NRF-2019R1A2C1089808, IBS-R023-D1]; S.H.K. and S.-C. H. also acknowledge the Global Research & Development Center Program [2018K1A4A3A01064272] through the NRF funded by the Ministry of Science and ICT. N.-K.L. acknowledges a NRF grant [NRF-2020R1A2B5B01002041]. Funding for open access charge: NRF [NRF-2019R1A2C1089808].

Conflict of interest statement. None declared.