Computational modelling of perivascular-niche dynamics for the optimization of treatment schedules for glioblastoma

Abstract

Glioma stem-like cells dynamically transition between a chemoradiation-resistant state (preferentially in the perivascular niche) and a chemoradiation-sensitive state (away from blood vessels). However, physical barriers in the tumour microenvironment restrict the delivery of chemotherapy to tumour compartments distant from blood vessels. Here we show that a computational stochastic model of the spatiotemporal dynamics of the perivascular niche that incorporates glioma stem-like cells, differentiated tumour cells, endothelial cells and stromal cells as well as relevant subcellular, cellular and tissue-level phenomena can be used to optimize the treatment schedules of chemoradiation and of standard radiation fractionation with the administration of temozolomide. In mice with platelet-derived-growth-factor-driven glioblastoma, the model-optimized treatment schedule increased the survival of the animals. For standard radiation fractionation in patients, the model predicts that chemotherapy may be optimally administered about an hour before the application of radiation. Massively parallel simulations of the spatiotemporal dynamics of the tumour microenvironment might predict tumour responses to a broader range of treatments and be used to optimize treatment regimens.

Reporting summary.

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Glioblastoma (GBM) is a devastating disease; despite multimodal treatment comprising surgery, radiotherapy and alkylating chemotherapy with temozolomide (TMZ) — the current standard of care for all patients following diagnosis¹ — the prognosis of GBM is invariably fatal, with a median overall survival of about one year^2,3. Clinical trials evaluating multiple different dose-escalation approaches based on the linear quadratic model of classical radiobiology have failed to increase survival⁴. Treatment strategies informed by an alternative approach explicitly modelling the mechanisms of treatment resistance and intratumor heterogeneity are necessary to achieve improved outcomes for patients.

Histologically, GBMs are characterized by extensive proliferation of disrupted microvessels⁵, which create a distinct microenvironment designated the perivascular niche (PVN)⁶. This PVN is defined by the spatial relation of cancer cells and endothelial cells⁶. Chemoradiation-resistant GBM stem-like cells (GSCs) preferentially reside in this PVN⁶, and localized signalling from the tumour microenvironment maintains and induces the stem-like phenotype of GSC through nitric oxide or Notch ligands^7,8. Although other cell types may contribute to these functional properties of the PVN, endothelial cells have been identified as the key mediators of stemness^6-8. GBM cells dynamically transition between a more stem-like chemoradiation-resistant and a more differentiated chemoradiation-sensitive state. Dedifferentiation of more differentiated cells to more stem-like cells occurs within hours following administration of radiation⁹. Accounting for this spatially explicit heterogeneity remains a challenge, with direct implications on the clinical management of this disease as physical barriers in the tumour microenvironment restrict chemotherapy delivery to tumour compartments distant from blood vessels.

We hypothesized that the use of a computational model quantifying how the spatial location of cells influences their sensitivity to therapy can be used to identify an optimized schedule for the administration of therapy for GBM that would maximize survival. To test this hypothesis, we developed a massively parallel, multiscale computational model of perivascular niche dynamics that links phenomena occurring at the subcellular, cellular, and tissue levels. Based on parameter values measured in mouse models of GBM, we identified a chemoradiation administration schedule predicted to optimize treatment efficacy. We validated our computational model predictions in a murine platelet-derived growth factor (PDGF)-driven GBM model, which shows that the optimized schedule indeed increased survival. This method identified a schedule that could be difficult to implement in the clinic due to the requirement to administer radiotherapy at specific times and multiple times a day. However, it elucidated the finding that a key driver in determining optimal scheduling was the time between administration of chemotherapy and radiotherapy. We then used our computational model to predict an optimal time for a single dose of each, administering TMZ 41 minutes before radiation given in standard fractionation, and show in a mouse model that optimizing timing between therapies improved survival. Using human pharmacokinetics parameters, we found an optimum time difference of 57 min between TMZ and radiation. Our findings lay the conceptual foundation for improved approaches for the clinical management of this disease.

Results

The aim of this work is to test the hypothesis that a computational model quantifying the effects of spatial location of cells on sensitivity to therapy can identify an optimized schedule for therapeutic administration for GBM that maximizes survival. To this end, we developed a spatially explicit, agent-based model to capture responses to different therapeutic regimens. We used the model to identify non-standard radiation-treatment schedules predicted to lead to optimal and suboptimal outcomes as measured by fractional volume changes of the tumour. Fractional volume change is defined here as the percent change in overall volume of the tumour. Efficacy was tested through use of a mouse GBM model. On the basis of this initial study, the optimal offset between radiotherapy and chemotherapy, using standard fractionation, was determined and validated in the mouse model as compared to current standard of care.

Development of a massively parallel computational model of GBM treatment response

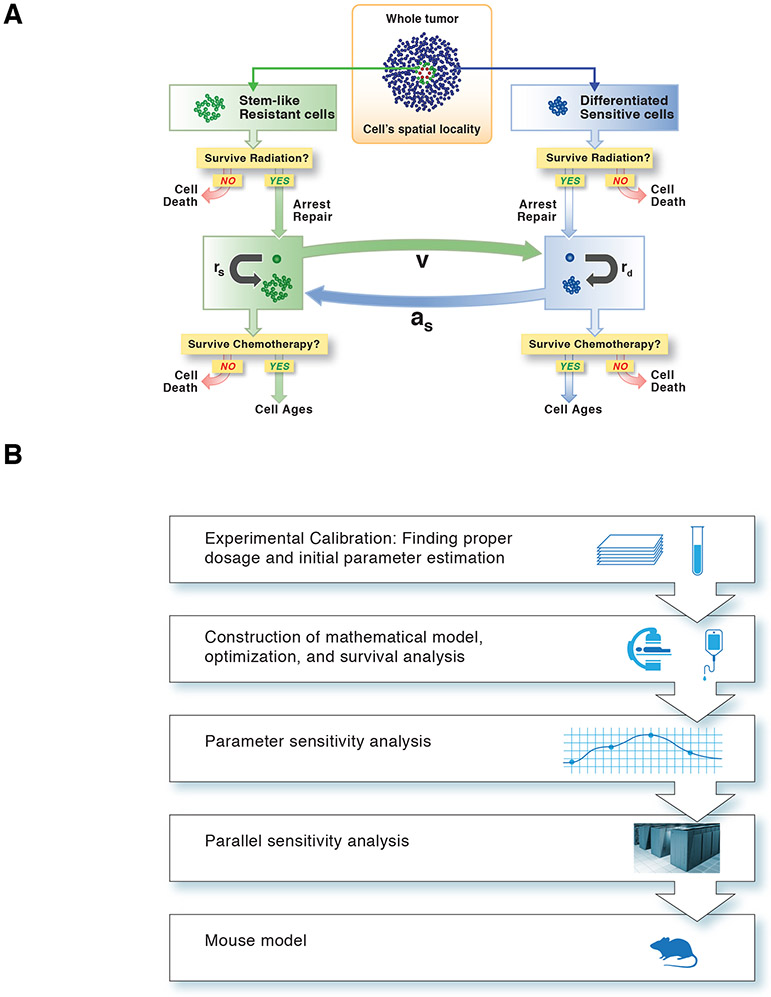
We developed a spatially explicit stochastic modelling approach to investigate the dynamics of GSC and differentiated glioma cells within the PVN (Figure 1A). In our framework, the PVN is modelled as a collection of autonomous decision-making agents that act independently in accordance to their individual environment and rules. We considered the PVN to be a cylindrical region in the brain and investigated two-dimensional cross-sections of the region for individual simulations. Our framework contains four cell types: endothelial cells, microenvironmental (stromal) cells, glioma stem-like cells (GSC) and differentiated tumour cells (DTC). The former two cell types are created at the initiation of the simulation and do not undergo division or death, but instead define the spatial structure of the PVN. Vascular remodelling upon chemoirradiation was not simulated because it typically occurs in the range of weeks after irradiation¹⁰ and thus is beyond the time-scale of our theoretical and experimental approach, whereas early post-irradiation endothelial cell apoptosis only occurs following single-dose supra-therapeutic irradiation¹¹ and radiation-induced recruitment of bone marrow-derived cells does not contribute to vasculogenesis, but rather supports endothelial cell survival¹⁰. By contrast, GSC divide asymmetrically to produce DTC that then divide symmetrically z times before terminally differentiating or dying. In addition, the model incorporates the possibility of differentiation, dedifferentiation, and cellular quiescence/arrest effects on cells that may depend on therapy or paracrine signals. The Methods contain further details of the model design, parameter estimation, and implementation of radiation and chemotherapy effects. Table S1 displays a list of parameters and their definitions as well as values estimated from GBM mouse models, while Figure 1A shows a schematic representation of the chemoradiation model. Figure 1B depicts the overall workflow of the project. An instantiation of the stochastic model for tumour growth is shown in Figure 2A. Our approach was implemented as a massively parallel simulation framework and computation for the mouse schedules was completed on the Vulcan supercomputer, an IBM Blue Gene/Q system, at Lawrence Livermore National Laboratory. To complete the necessary simulations, 36 million central processing unit (CPU) hours (4,109 years) on 131,072 cores were used. For the human studies, 500,000 CPU hours were used on the Duke compute Cluster and 2 million CPU hours were used on the Quartz supercomputer at Lawrence Livermore National Laboratory.

Fig. 1 ∣. A computational model of the GBM microenvironment.

(A) Schematic of the computational modelling approach used to describe the chemotherapeutic response. (B) Flow chart summarizing the workflow.

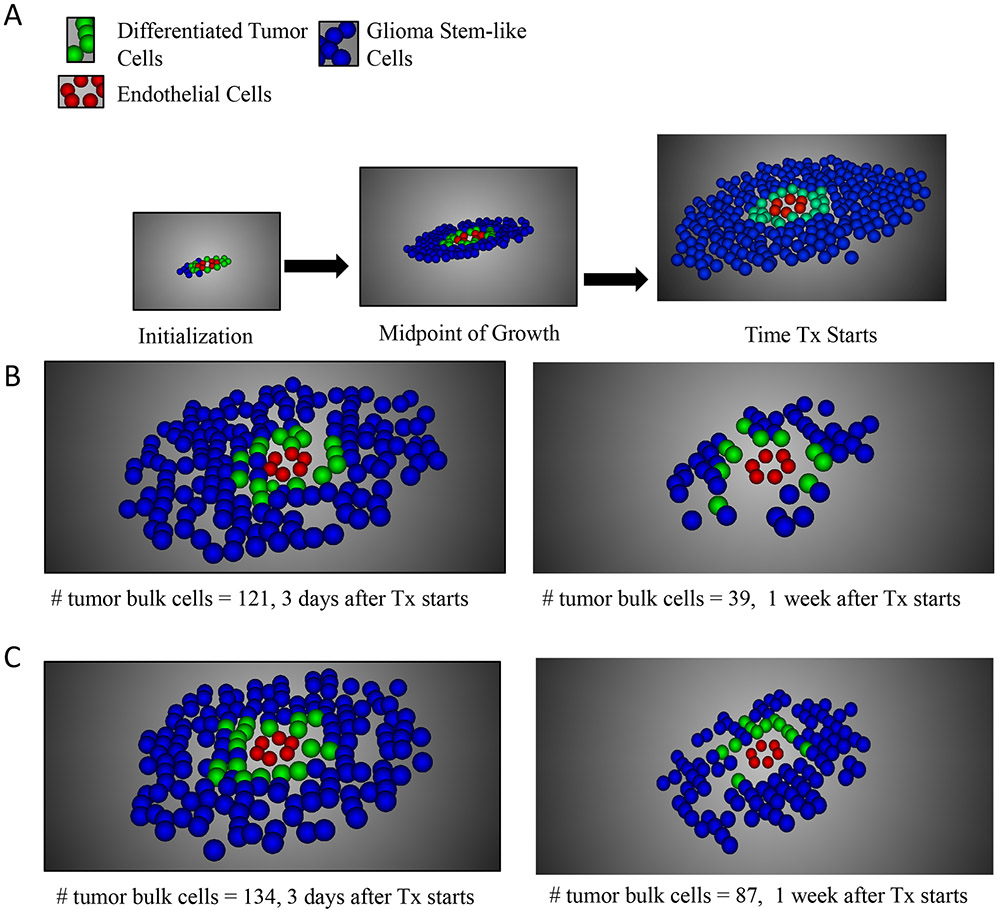
Fig. 2 ∣. Modelling GBM growth and treatment response.

(A) Results of one stochastic simulation of tumour growth for three time points. Our spatially explicit stochastic process model of the perivascular niche considers several distinct cell types: endothelial cells (red), glioma stem-like cells (GSC) adjacent to the blood vessel (green), and differentiated tumour cells (DTC, blue). (B) Results of one stochastic simulation of treatment response to chemoradiation administered according to the optimal schedule (Figure 3A) for two time points: 3 and 7 days after the start of treatment. (C) Results of one stochastic simulation of treatment response to chemoradiation administered according to the suboptimal schedule for two time points: 3 and 7 days after the start of treatment.

Optimizing the chemoradiotherapy administration schedule

The massively parallel model, together with simulated annealing, was used to derive an optimized radiation schedule in the presence of TMZ (see Methods). Parameters were selected that capture treatment response in the PDGF-driven mouse model (see Methods). We investigated five days of treatment with 10 Gy radiation total, with follow up until death. The administration of TMZ was fixed to occur every day (Monday – Friday) at 3pm. To determine an improved schedule, the time and fractionation of radiation was varied. Radiotherapy could be administered Monday to Friday between 8am and 5pm, on the hour. Even though the computational model was parameterized using mouse data and validated in a mouse study, constraints were derived from information of the Brigham and Women’s Hospital/Dana-Farber Cancer Institute radiation oncology clinic for potential clinical translation in the future. The constraints specify that there could be no more than 8 hours between the first and last dose per day, the maximum dose at one time was 3 Gy, and the maximum total dose per day was 4 Gy. There could be no more than three treatments per day and the maximum total dose over the course of treatment was set to 10 Gy.

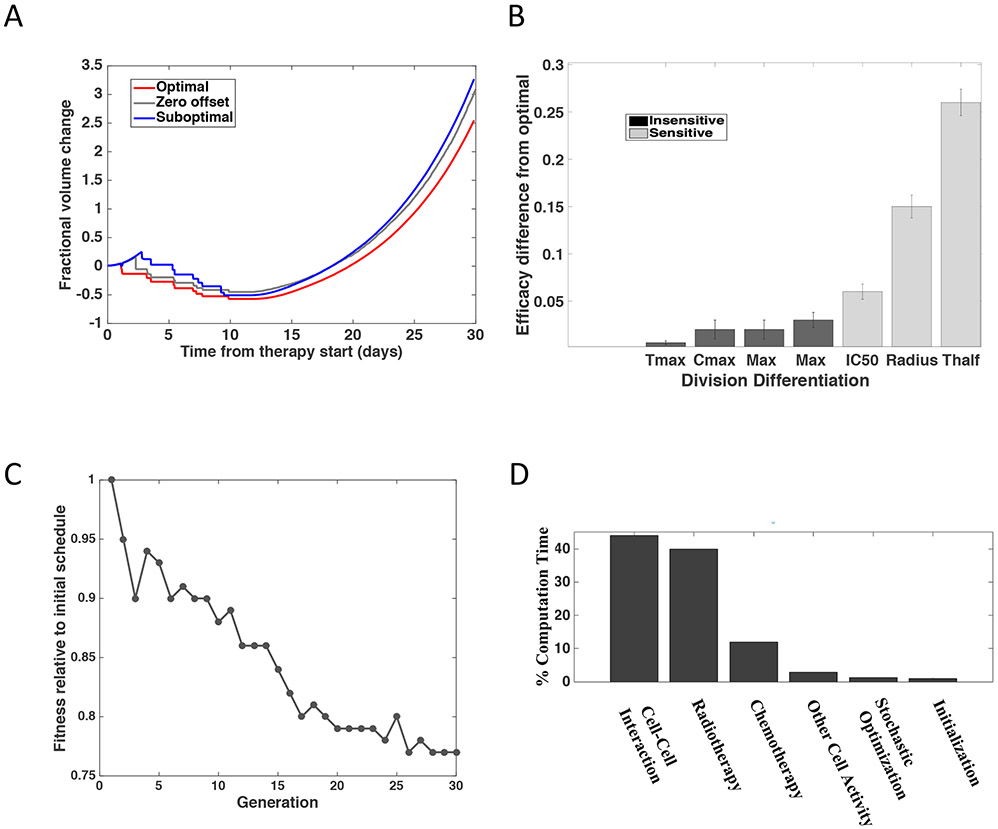
Using this approach, we predicted maximal survival time and investigated treatment response (shown in Figure 2B, C) under our identified, optimized radiation administration schedule, as well as a control sequence predicted to perform worse and a “zero offset” schedule designed to mimic standard of care treatment in patients (Table 1A). When performing the parallel, stochastic optimization routine, we compared the fitness (i.e. the number of tumor cells present 30 days after treatment conclusion, as compared to that of the initialization condition) of a range of schedules (1,024 in each generation) over 30 generations. In this case, generation is referring to the step or round of the simulated annealing heuristic. On average, when calculated for 128 instantiations of the stochastic simulation, we found that the predicted optimum schedule indeed led to slower expansion of DTCs than the suboptimum and zero offset schedules (Figure 3A). Since the suboptimum and zero offset schedules had similar predicted outcomes, we focus on the comparison between optimum and suboptimum schedules in the following analyses. The differences in expansion as defined by increase in fractional volume are significantly different between optimum and suboptimum schedules, with a mean fractional volume change of 3.67 for the optimal schedule and 4.72 for the suboptimal schedule (p < 0.0001, standard t-test). The observed variation is due to the stochasticity of the simulations and not due to uncertainties in the parameter values. We then performed sensitivity analysis to obtain information on the relative effects that changes in the parameter values have on outcome.

Table 1 ∣. Treatment arms.

Treatment arms used to predict responses to different chemoradiation schedules in both mice and humans. For the mouse schedules, the TMZ dosage was 50 mg/kg and for the human schedules, a dose of 75 mg/m² was used. For the mouse studies, three schedules were defined. The clinical RT SoC reflects current standard of care delivering 2Gy at 3pm. Our numerical model identifies an optimal RT fractionation and suboptimal RT fractionation schedule based on simulated fractional volume change. For the human studies, numerical models were used to determine the optimal offset or time between administration of TMZ and radiation. Four schedules were employed: (1) clinical RT standard of care, (2) the derived optimal offset, (3) zero offset in which radiation and TMZ are administered concurrently, and (4) when TMZ is administered at bedtime or 9 pm.

Group	Therapy schedule	Day 1	Day 2	Day 3	Day 4	Day 5
Mouse schedule TMZ 50 mg/Kg	Clinical RT SoC	2 Gy; 3 pm	2 Gy; 3 pm	2 Gy; 3 pm	2 Gy; 3 pm	2 Gy; 3 pm
	Optimal RT fractionation	No RT	1 Gy; 9 am 1 Gy; 4 pm	1 Gy; 8 am 2 Gy; 9 am	1 Gy; 9 am 2 Gy; 4 pm	1 Gy; 9 am 1 Gy; 5 pm
	Suboptimal RT fractionation	2 Gy; 1 pm	1 Gy; 1 pm 1 Gy; 5 pm	1 Gy; 2 pm 1 Gy; 3 pm	2 Gy; 8 am 1 Gy; 11 am	1 Gy; 5 pm
	All RT schedules	TMZ; 3pm	TMZ; 3pm	TMZ; 3pm	TMZ; 3pm	TMZ; 3pm
Human schedule TMZ 75 mg/m2	Clinical RT SoC	2 Gy; 3 pm	2 Gy; 3 pm	2 Gy; 3 pm	2 Gy; 3 pm	2 Gy; 3 pm
	Optimal offset (57 minutes)	TMZ; 2:03 pm	TMZ; 2:03 pm	TMZ; 2:03 pm	TMZ; 2:03 pm	TMZ; 2:03 pm
	Zero offset	TMZ; 3pm	TMZ; 3pm	TMZ; 3pm	TMZ; 3pm	TMZ; 3pm
	Bedtime chemotherapy	TMZ; 9pm	TMZ; 9pm	TMZ; 9pm	TMZ; 9pm	TMZ; 9pm

Fig. 3 ∣. Prediction of responses to different chemoradiation administration schedules.

(A) Prediction plots showing the expected fractional volume change over time for the optimized versus suboptimal and zero offset treatment schedules from (A). To account for stochasticity, the simulations were run 128 times to create the technical replicates required to account for stochasticity of the model. The dashed lines show the standard error. The differences in expansion as defined by increase in fractional volume are significantly different with a mean fractional volume change of 3.67 for the optimal schedule and 4.72 for the suboptimal schedule (p < 0.0001, two-sided t-test). (B) Sensitivity analysis of the model’s parameters, ranked from most to least sensitive, as determined by the sensitivity analysis in Figure S1. The variables that demonstrated a significant impact when varied +/− 30% are shown in light grey (p < 0.0001, two-sided t-test) whereas those with no significant impact are shown in black (p < 0.0001, two-sided t-test). (C) Relative fitness across stochastic optimization generations. Each generation consisted of 1024 different schedules being tested with 128 instances of each schedule. These instances provided the technical replicates required to account for stochasticity of the model. (D) Percent of time spent in each component of the 36 million compute hours on the IBM Blue Gene/Q supercomputer.

Computational model sensitivity

We conducted sensitivity studies to identify which parameters had the strongest influence on the results (Figure 3B, Figure S1). Throughout these studies, the parameters of our model were systematically changed and the effect on fractional volume change was measured. This approach was taken to address questions relating to different individuals reacting to the drug differently, but more importantly was used to derive an understanding of which parameters were influencing the outcome and why. We completed a series of uncertainty quantification tests to determine the effect of varying parameters such as the radius of the blood vessel, the maximum number of cell divisions before apoptosis, and the cutoff for the number of times a cell divides before terminally differentiating. The radius of the blood vessel demonstrated no significant impact on the results when the size was varied between 1.5 μm and 3 μm (Figure S1A), which is on par with the size of vessels found in this region^12,13. However, as the vessel radius increased beyond 3.5 μm, a significant change in relative fitness was observed. This observation is likely due to the influence of the diffusion of TMZ from the vessel wall being less substantial in larger vessels, reducing the role that the chemotherapy component of the schedule plays in determining cell behavior at the center of large vessels. Since the vessels in the mouse and human PVN have a radius of less than 3.5 μm, we concluded that a change in vessel size has no significant effect on the results. We also found that varying the number of times a DTC could divide before terminally dedifferentiating (z) and the cutoff for the number of times a cell could dedifferentiate (z_revert) led to no significant difference being observed (Figure S1B, C).

We also modeled the pharmacokinetic and pharmacodynamic parameters of TMZ at relevant tissue concentrations¹⁴ to identify if variability in these factors could influence our findings. These sensitivity studies (Figure 3B, Figure S1D-F) showed no significant impact (p < 0.0001, standard t-test) when the maximum concentration that the drug achieves, Cmax, or the time of the maximum concentration, T_max, were varied by plus or minus 30%. This range was selected to capture fluctuations derived from how the drug is processed in the body. Of note, these findings are in line with the clinical lack of benefit from dose-intensified versus standard dose TMZ regimens in patients with GBM^15,16. The concentration at which the response is reduced by half, IC₅₀, demonstrated a small effect on the relative efficacy of the chemoradiation schedule while the half-life of the drug, T_half, showed a significant effect. The efficacy of the schedule, as defined by fractional volume change 30 days from the time of treatment start, was also sensitive to the radius of the vessel at sizes above 3 μm. We found that the efficacy of the schedule was most sensitive to the drug’s half-life; if the drug takes longer to clear, it is able to diffuse further and thus not only influences cells over a longer time period, but also over a larger volume¹⁷. This information could play a key role in developing chemotherapeutics in the future.

The improvement in terms of fitness is shown in Figure 3C. The relative volume fraction specifying fitness is defined as the ratio of the fractional volume change at 30 days post treatment for the schedule tested in that generation compared to the fractional volume change at 30 days for the schedule initializing the stochastic optimization routine. The resulting number of differentiated tumor cells after treatment was typically smaller with each improved schedule. The schedule continued to be optimized until the same schedule was converged upon for over three generations. At this point, a local minimum was identified. To calculate the fitness of each schedule, a computationally expensive, parallel simulation was completed for 128 instances of each schedule. The breakdown of time spent in each computational function is shown in Figure 3D.

Investigating radiation and TMZ combination schedules

We then used our modeling approach to simulate five previously investigated schedules¹⁸; we found that, in the presence of TMZ, the standard dose of 2 Gy administered each day was predicted to be the optimal of these five schedules. Due to this observation, the standard schedule was used as the template schedule to seed the parallel simulated annealing simulation for identifying the global optimum of chemoradiation administration. We set the fitness function endpoint as the number of tumor cells present 30 days after treatment initiation. Mathematically determining the global optimal schedule was not computationally tractable due to the complex interdependencies of our model. We thus used the parallel simulated annealing model to identify an optimized combined therapeutic schedule as well as a suboptimal and zero offset schedule (Table 1A). Figure 3A depicts the outcome of these schedules in terms of the number of differentiated tumor cells, while Figure 2 shows examples of the spatial distribution of the different cell types at different time points for both the optimized and suboptimal schedules. Qualitatively, Figure 2 depicts that the optimized schedule has fewer differentiated tumor cells after treatment and the influence of chemotherapeutic diffusion from the vessel can be seen in the distribution of the remaining cells. These observations are further confirmed quantitatively in Figures 3A and 4. In Figure 3A, the tumor volume is significantly smaller after the optimized schedule as compared to that of the suboptimal schedule (mean difference 0.72 mm³, 95% CI 0.683 - 0.756, p < 0.0001) and in Figure 4A-B, the distance from the vessel of GSC vs. DTCs under each schedule is significantly greater (mean difference 81.85 μm 95% CI 81.511 - 82.198, p < 0.0001 for optimal and mean difference 25.7 μm, 95% CI 25.258 - 26.304, p < 0.0001 for suboptimal). The optimized vs. suboptimal schedule affected the distance from the vessel center that the DTCs were found at (mean difference 61 μm, 95% CI 60.13-61.87, p < 0.0001), as well as the location of the GSC (mean difference 0.07 mm, 95% CI 0.092 - 0.047, p < 0.0001).

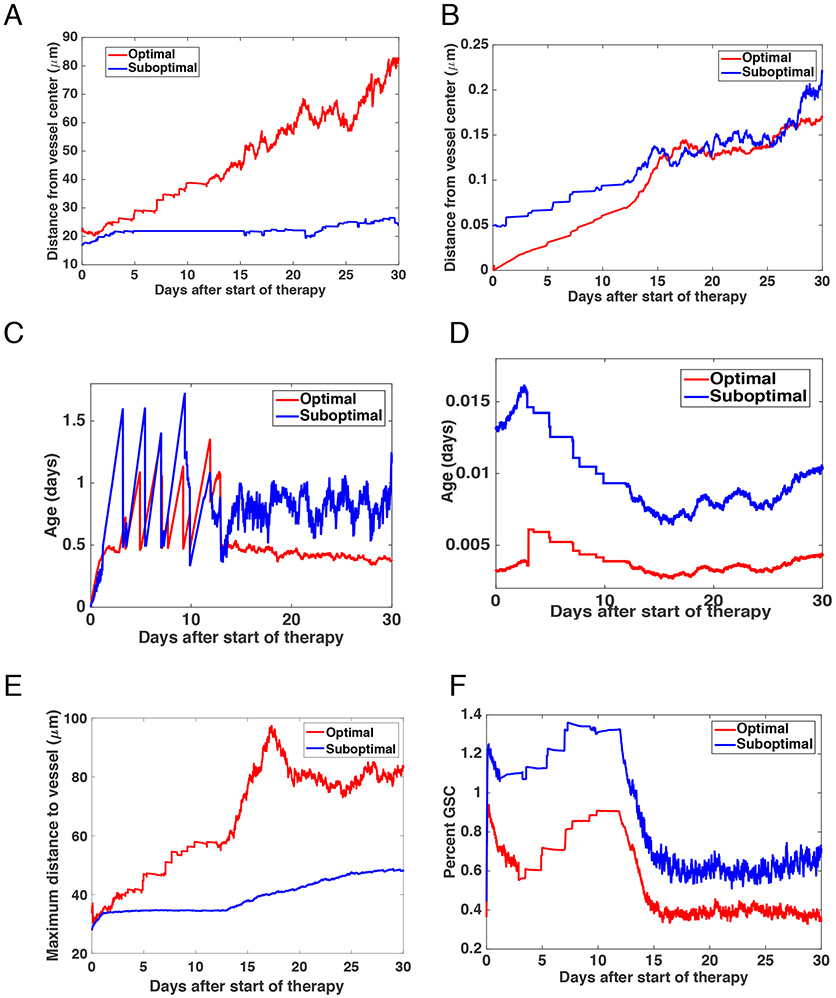
Fig. 4 ∣. Prediction of GBM growth and treatment response.

(A-B) Plots showing the average age of the cells at up to 30 days after the treatment started. (A) shows the results for DTCs and (B) GSCs. (C-D) Prediction plots showing the average distance of cells from the vessel centre up to 30 days after treatment commences. (C) shows the results for DTCs and (D) GSCs. (E) Maximum distance from the vessel that any of the cells travel up to 30 days after treatment commences. (F) Percent of cells that are GSC up to 30 days after treatment initiation.

We then undertook a series of tests to further investigate cellular response throughout the thirty days after treatment initiated. For this time duration from the start of the therapy to 30 days post treatment initiation, we determined the average age of GSCs (Figure 4C) and DTCs (Figure 4D), finding that GSCs were significantly older than DTCs (mean difference 0.993 days, 95% CI 0.795-1.191, p < 0.0001), whereas the age of GSCs had more variance. These findings primarily arose due to the proximate location of GSCs near to the vessel wall, and these cells thereby experiencing a greater effect of TMZ. Figure 4A-B shows the average distance from the vessel for both the GSCs and DTCs, demonstrating that GSCs tended to be much closer to the vessel over the course of the treatment, for example at 1 day after the start of therapy (mean difference in mm 22.9, 95% CI 20.99 – 24.93, p < 0.0001) and 7 days after the start of therapy (mean difference in mm 25.96, 95% CI 23.99 – 27.93, p < 0.0001). This localization pattern led to a fluctuation in distance as many of the cells present one day after treatment initiation were killed by therapy. The suboptimal schedule resulted in more DTC cells on average being located further from the vessel at one day than at seven days post treatment initiation (mean difference .025 μm, 95% CI 0.003 - 0.047, p < .001, an observation likely due to the higher concentration of the chemotherapeutic near the vessel and the associated relative increase in chemotherapy response. The maximum distance that all cells move away from the vessel is shown in Figure 4E, demonstrating that DTCs dictated the size of the cell population. The average cell distance from the vessel center was further as treatment progressed under both the optimal (mean difference −3.25 μm, 95% CI −3.35—3.14, p < 0.0001) and suboptimal schedules (mean difference, −6, 95% CI −6.1 to −5.9, p < 0.0001). The GSCs, however, moved further earlier on under the optimal schedule. The change was slight (0.81 μm to 0.58 μm) and, again, due to the spatial effects of the cell interaction with the chemotherapeutic. The composition of the cell population is shown in Figure 4F, visualizing the percentage of cells made up of GSCs at each daily time point. In all cases, GSCs made up less than 2% of the population. Under the optimal treatment schedule, this was further reduced from 0.82% to 0.486%, whereas under the control schedule, the percent GSC rose from 0.96% to 1.65%. With 128 instances, a t-test demonstrates that this is a significant difference (p < 0.0001) with the mean difference between the groups being −0.69 with a 95% confidence interval of this difference from −0.72 to −0.65. This change in percentage of the cells being GSCs was due to the cell interaction with TMZ.

Validation of model predictions in a genetically engineered mouse model of GBM

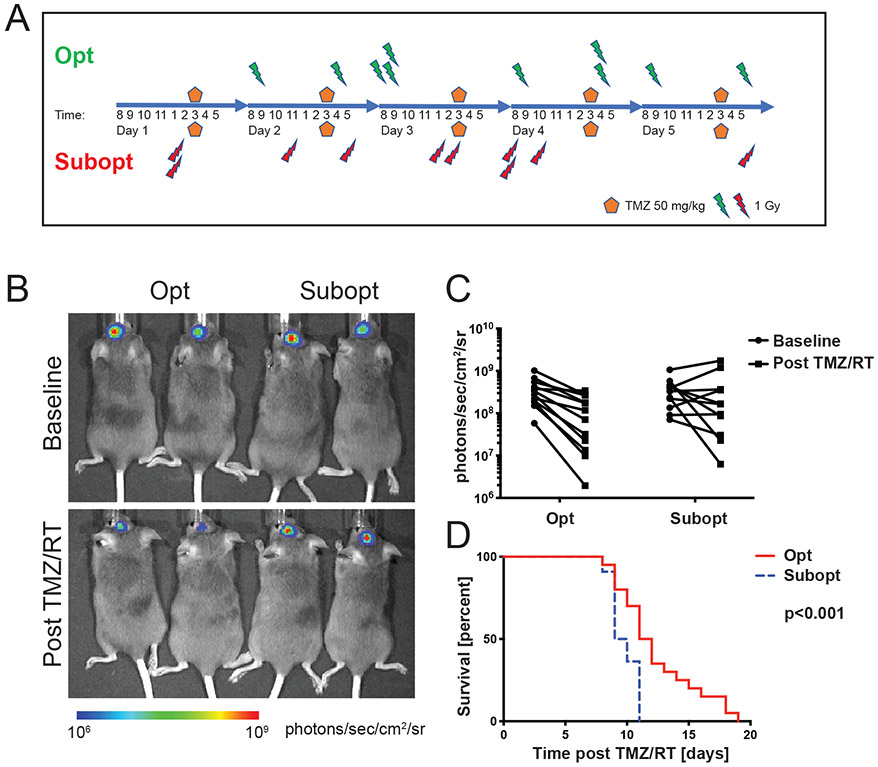
We then validated the mathematical modeling predictions using an RCAS (Replication-Competent ASLV [avian sarcoma-leukosis virus] long terminal repeat with a Splice acceptor)/tumor virus A (tva)-based platelet-derived growth factor (PDGF)-driven mouse model with a Ink4a/Arf^−/− germline mutation, which produces rapid and uniform gliomas, by randomizing tumor-bearing mice to receive either the optimized or the suboptimal treatment schedule (Figure 5A). Tumor formation prior to treatment was confirmed by bioluminescence imaging and changes recorded 72h after the last treatment dose (Figure 5B). These images provide insight into tumor volume growth as the radiance correlates with size. Radiance in both groups prior to treatment was similar (p = 0.95, unpaired t-test). The average bioluminescence signal after treatment was 34% of the baseline signal with the optimized schedule versus 105% with the suboptimal schedule (p = 0.008, unpaired t-test, Figure 5C). Median survival of mice in the optimized versus suboptimal groups was 11.5 versus 9.5 days (log rank hazard ratio 0.46, 95% confidence interval 0.24 - 0.87, p < 0.001, Figure 5D), thus validating the model predictions that the optimized schedule leads to superior outcomes.

Fig. 5 ∣. Validation of modelling predictions in a mouse model of GBM.

A) Schematic of chemoradiation schedules applied to N/t-va;Ink4a/Arf^−/−;PTEN^fl/fl;Luc^LSL/LSL:RCAS-PDGFB;Cre mouse GBMs. Opt, optimized schedule; subopt, suboptimal schedule; TMZ, temozolomide. (B) Representative images of mice at baseline and 72 hours after treatment with indicated chemoradiation schedules. Photographic images were overlain with a pseudocolor image to represent the spatial distribution of photon counts. Radiance in both groups prior to treatment was similar (p=0.95, unpaired t-test). (C) Quantification of radiance at baseline and 72 hours after indicated treatments. Two-tailed unpaired t-test at baseline and after combined chemoirradiation with temozolomide (TMZ/RT): p=0.95 versus p=0.008 using an unpaired t-test. (D) Post-treatment survival of mice treated with Opt (N=20) versus Subopt (N=2chemoradiationion schedules. The log-rank test was applied to compare survival times (log rank hazard ratio 0.46, 95% confidence interval 0.24 - 0.87, p < 0.001).

Optimization of the relative timing of chemotherapy and radiation administrations

When considering the mechanism of differential efficacy of the optimized versus suboptimal schedule, we noticed that the optimized schedule tended to have shorter time intervals between TMZ and radiation administrations compared to the suboptimal schedule. Therefore, we investigated whether the superior survival observed for the optimal schedule could be due to radiosensitization of glioma cells by TMZ. If the improved survival were due to TMZ-induced radiosensitization, then a survival improvement might be achieved through optimizing the time interval between TMZ and radiation administrations such that radiation is administered at the time of peak TMZ concentration. Therefore, the current standard of care administration schedule could be employed with the exception that a specific time interval between TMZ and radiation administration be prescribed. Unlike the previous optimal schedule, this strategy would be simple to translate to GBM patients.

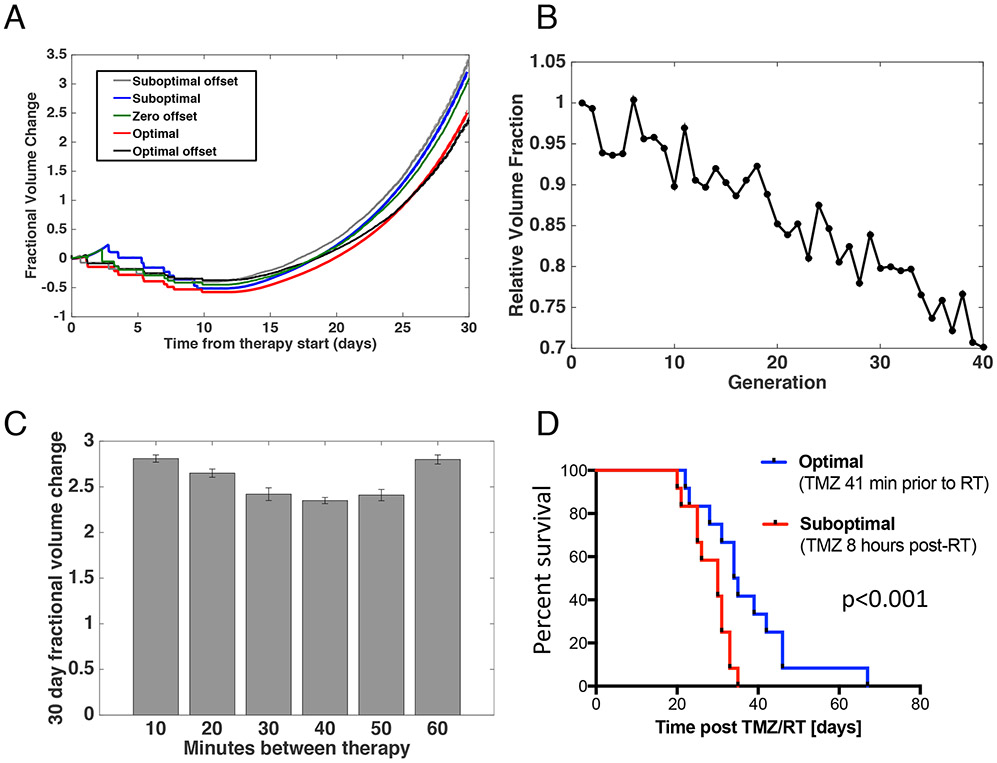
In order to test TMZ-induced radiosensitization, we used the same mouse genetic background as above and updated our computational model to include a TMZ concentration dependence to the radiation-induced cell kill (equation 7). Under these conditions, we first conducted a computational study to identify the optimal and suboptimal time intervals between administration of TMZ and radiotherapy. We again implemented stochastic optimization through the use of a simulated annealing strategy with the fractional volume change at 30 days post-therapy start as the defined fitness for each schedule. This systematic method identified the optimal time interval between administration of the two therapies to be 41 minutes when using mouse parameters. The 30-day fractional volume change for the identified schedules is shown in Figure 6A and the reduction in relative fitness achieved through the optimization technique is demonstrated in Figure 6B. Our findings demonstrated that the optimal and suboptimal offsets between therapies have a strong influence on overall outcome. The influence of the interval size is visualized in Figure 6C where fractional volume change is shown with a range of offsets around the identified optimum. Using just one dose of radiation per day, a similar behaviour is shown between schedules with optimal and suboptimal offsets and the derived optimal and suboptimal schedules discussed above. We further conducted a sensitivity analysis demonstrating that the results were robust to changes in the value of the radiosensitization parameter (Figure S2). To further assess cellular response in the first thirty days after treatment initiation, we also investigated the change in average age, distance from the vessel, and percent GSC (Figure S3).

Fig. 6 ∣. Identification of a combination schedule in mice by optimizing the offset between chemotherapy and radiotherapy.

(A) Prediction plots showing the expected fractional volume change over time for the originally identified optimal and suboptimal schedules as well as schedules with the suboptimal and optimal offsets between therapy administrations. (B) Relative fitness across stochastic optimization generations. Each generation consisted of 1024 different schedules being tested with 128 instances of each schedule, creating the required technical replicates to account for model stochasticity. (C) Fractional volume change under different offsets between radiotherapy and chemotherapy. Each schedule is simulated 50 times. Error bars, mean +/− s.d. (D) Survival of tumour-bearing mice from initiation of treatment with i.p. TMZ and daily whole brain irradiation with 2 Gy on 5 consecutive days (TMZ/RT). TMZ was administered 41 min prior to irradiation for the optimum-treated mice (N=12) and 8 hours post-irradiation for the suboptimum-treated mice (N=12).

To validate the predictions of our computational modelling of the time interval between TMZ and radiation treatment, we conducted a mouse trial in an Ink4a/Arf^wt/wt background with its extended survival and opportunity for increased treatment events. For this study, all mice received RT at the same time of day (2 Gy per day for 5 days) with the optimal group being administered TMZ 41 min prior to RT and the suboptimal group administered TMZ 8 hours post-RT; the latter choice was made since TMZ is usually taken at bedtime by patients. Median survival of mice in this optimized versus suboptimal radiotherapy fractionation schedule was 34.5 days versus 30 days (log rank hazard ratio 0.3925, 95% confidence interval 0.1613-0.9551, p < 0.001) (Figure 6D). The mouse study highlighted the importance of including radiosensitivity in the model considerations, as the survival time of the mice undergoing treatment with the optimized offset was slightly improved over the originally defined optimal schedule. The mouse trial thus validated our computational model predictions that the relative timing between TMZ and radiation administrations significantly affects survival.

The optimum schedule is robust when considering acquired resistance to chemoradiation

In order to assess the potential influence that the emergence of cells resistant to treatment due to the accumulation of (epi)genetic changes, we conducted a series of simulations with varying rates of appearance of resistant cells. Our model was modified to include a rate at which cells become resistant to chemoradiation, given by RR. Resistant cells were defined as cells impervious to both chemotherapy and radiotherapy. We then characterized the sensitivity of our results to the parameter RR. We varied its setting from 1x10⁻⁶ to 1x10⁻⁸ per cell division, as example rates at which resistance arises per cell division, and observed no significant change in the overall fractional volume change (p = 0.7280), percent of cells that were GSC (p = 0.2921), or the location of the cells (p = 0.9743) (Figure S4). As we observed no significant change in the fractional volume change when resistance was introduced, no impact on the emergent optimized schedules is expected as schedule fitness is defined based on the size of the DTCs. As resistance to both chemo- and radiotherapy leads to no substantive change in population fitness, the weaker implementation including a heterogeneous mix of radiotherapy-resistant and chemotherapy-resistant cells has even less impact. Similarly, in this model both GSCs and DTCs have the potential to generate resistant cells, providing a setup that would demonstrate maximal influence of the dynamics of emergence of resistant cells. Since no significant change was observed under these conditions, allowing only GSCs or DTCs to gain resistance results in an even smaller change. Here, the resistance rate RR was varied across two orders of magnitude and exhibited no measurable impact on the results; note that this finding might change if the rate is varied to a greater extent.

Translating the optimized administration schedule from mice to humans

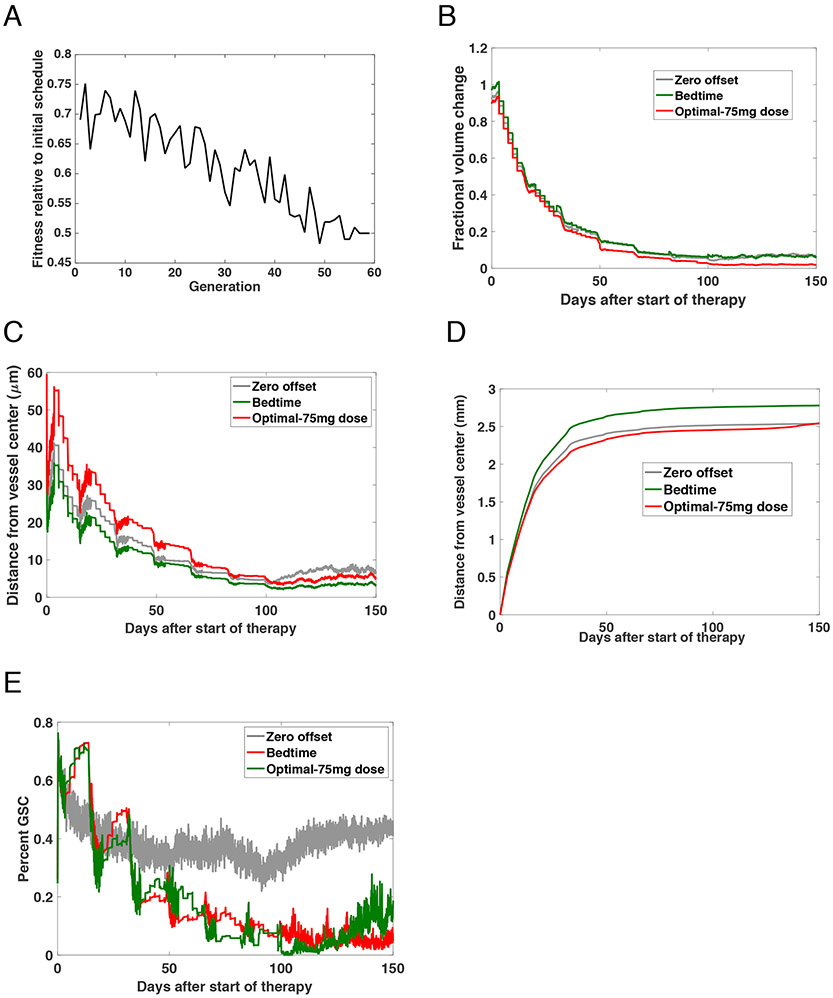
When optimizing the schedules, we found that considering chemotherapy radiosensitization influenced selection of the ideal offset between administration of chemotherapy and radiotherapy. All of the studies previously discussed had focused on mouse-derived PK/PD parameters. In order to understand how this work could be extrapolated to a future human study, we completed a large-scale computational study to identify the optimal offset under human-derived conditions. PK values were modified to match data for humans^19-21. Under these conditions, the half-life of TMZ was set to 1.8 hours, the dosage to 75 mg/m², Tmax to .7 hours, and Cmax to 3.7 mg/L. Treatment was undertaken for 6 weeks and we simulated 150 days from the start of therapy. We then used simulated annealing to identify the optimal offset, which we found to be 57 minutes. We then compared the identified optimal offset, zero offset in which both therapies are administered about the same time, and the schedule when radiation is administered at 3pm but TMZ given at bedtime, in this case 9pm. Table 1B presents the three assessed schedules: the derived optimum, the standard dosage of TMZ given at 3pm, and TMZ given at bedtime (9pm). Similar to the work described above for the mouse schedules, we used simulated annealing to identify the optimal schedule for human TMZ PK parameters. The fitness function was defined as the fractional volume change 150 days after the start of therapy. The optimization results are shown in Figure 7A. The routine was initially seeded with the standard schedule and during each generation, we randomly perturbed this schedule in 128 different ways that were simultaneously assessed. The schedule producing the minimal fractional volume change was then used to seed the next generation. We found that the optimal schedule administered TMZ 57 minutes before radiation. The fractional volume change over the 150 days for each schedule is shown in Figure 7B. We also assessed the distance from the vessel centre of both the DTCs (Figure 7C) and GSCs (Figure 7D). Finally, the percent of the overall cell population that were glioma stem-like cells is depicted in Figure 7E. Our model was thus able to predict schedules for potential testing in the clinic.

Fig. 7 ∣. Identification of an optimum schedule for human validation.

(A) Relative volume fraction at each generation of the stochastic optimization routine. Each generation consisted of 1024 different schedules being tested with 128 instances of each schedule, creating the required technical replicates to account for model stochasticity. (B) The fractional volume change from baseline to 150 days after the start of therapy under the zero offset, bed, and optimal-low dose schedules. (C-D) Plots showing the average distance of cells from the centre of the vessel up to 150 days post-treatment. (C) shows the results for DTCs and (D) GSC. (E) Percent of cells that are GSC up to 150 days after treatment commences.

Discussion

Gliomas are cellularly and spatially complex, consisting of multiple cell types with differing proliferation rates and sensitivities to DNA damage-based standard of care therapy. Previously, we showed that there is interconversion between cell types in vivo during the time course of radiotherapy²². This insight led to the ability to optimize a schedule for radiotherapy alone, mirroring the clinical scenario of salvage radiotherapy for recurrent GBM, which achieved a substantial survival benefit¹⁸ and is currently being tested in a clinical trial (NCT03557372). The various glioma cell types occupy specific locations within the tumours, with the least proliferative and treatment-responsive cells closest to the vessels. The standard-of-care therapy for newly diagnosed GBM is radiation, which delivers a uniform dose to all cells, and TMZ, which has time-and-distance-dependent concentration gradients relative to the blood vessels, leading to a complex dynamic therapeutic response. In order to identify optimal treatment strategies, models are required that can capture this spatiotemporal complexity.

Here we developed a massively parallel computational model of the GBM microenvironment to systematically investigate the effects of different treatment schedules on outcomes. In order to investigate how specific parameters influence the success of chemoradiation therapy, we developed a technique to sample the search space using large-scale stochastic optimization. We conducted one of the largest simulation studies of tumour treatment response to date, utilizing 36 million CPU hours on the Vulcan supercomputer. This allowed us to both examine the sensitivity of the treatment to TMZ pharmacokinetic and pharmacodynamic characteristics, and to study the relative efficacy of different administration schedules. Using this approach, we identified a chemoradiation schedule that was predicted to significantly improve survival compared to standard schedules. This treatment strategy was then tested in a GBM mouse model and was found to indeed lead to superior survival than the control schedule. Our approach is consistent with the hypothesis of spatial translocation of glioma stem-like cells (GSCs) upon cycling through a non-GSC state and the functional relevance of this process for resistance to chemoradiation.

When considering radiosensitivity, we identified that survival outcome could be improved by optimally timing the distance between the administration of chemotherapy and radiotherapy. By timing the radiotherapy shortly after the administration of TMZ, there was enough time for the drug to diffuse to and interact with the cells. The optimal time between therapies was found to be shortly after the time when the maximum concentration is reached.

In summary, our computational approach identified the close temporal association of TMZ treatment right before RT as paramount for improving the efficacy of this combination treatment. We reason that this temporal association of a synergistic effect of TMZ and RT may reflect not only the temporal restriction of the interconversion of GSC to a more chemosensitive state but also that this interconversion sets off early during the translocation of GSC away from blood vessels, while they are still exposed to TMZ. Of note, using tissue markers to track GSC in tissue has proven not to be feasible, likely because GSC lose the expression of these markers upon translocation away from the PVN.

Unfortunately, the necessary parameter values were not determined in one experiment by one lab for multiple individuals, and therefore there is uncertainty connected to these values. Similarly, we did not have the ability to orthogonally validate all parameters. Furthermore, we considered endothelial cells to be constant over time both in terms of number and spatial localization; therefore, changing blood vessels during angiogenesis are currently not considered in our work.

Our findings have clinically relevant implications for the treatment of GBM patients. Phase-III randomized clinical trials demonstrating a significant overall survival benefit from the addition of concurrent and adjuvant TMZ to radiation do not specify the time interval between TMZ and radiation administrations^23,24. However, many oncologists administer TMZ at bedtime due to nausea²⁵. This administration schedule is not supported by high quality evidence. The contribution of a synergistic interaction between radiation and TMZ to this improvement in survival is not known. However, a study of radiosensitization by TMZ in 20 different patient-derived orthotopic GBM xenografts showed that a subset of tumours exhibited synergy between radiation and TMZ when TMZ was administered 1 hour before radiation²⁶. Given that (i) a subset of patients could benefit from synergy between TMZ and radiation; (ii) no high quality evidence for the equivalence of bedtime administration of TMZ to administration shortly before radiotherapy exists; (iii) we have demonstrated, in mice, that administering TMZ shortly prior to radiotherapy improves overall survival compared with evening administration; we recommend that concurrent TMZ-radiotherapy for newly diagnosed GBM should use a 57 minute interval between administration of TMZ and radiation. We believe this time interval is driven by a combination of the time it takes for TMZ to reach its maximum concentration in a patient’s bloodstream and the time it takes for TMZ to diffuse away from the blood vessel into the tumour and take its effect. Since TMZ pharmacokinetics differ among patients and no data is available to investigate its variability within a population, we did not perform a sensitivity analysis to determine the range of time intervals that would be best for a patient population, but we expect that variation of the optimum time by 5-10 minutes will lead to very similar results. As TMZ pharmacokinetics¹⁹ predict a rapid absorption but slow decay, we expect earlier administration of TMZ relative to radiation (i.e. a bigger time interval than 57 min) to lead to smaller differences in outcome than later administration. A randomized clinical trial could be performed to directly test whether the administration time of TMZ affects overall survival.

However, the translation into clinical practice would need to take additional factors into account that affect therapeutic efficacy that might be present across a population of glioma patients and within any one glioma. For example, the immune cell compartment, which comprises almost exclusively macrophages, was modelled only on the stroma functional level, because the interplay of macrophages and GSC is widely elusive. In a rat glioma model, favourable modulation of the tumour-infiltrating lymphocyte composition by metronomic TMZ treatment schedules has been suggested²⁷, but translation of similar approaches to GBM patients did not alter outcome in the newly diagnosed¹⁵ or recurrent setting²⁸, likely reflecting the overall lack of tumour-infiltrating lymphocytes in GBM²⁹. Other variables which are currently not represented in these computational and mouse models which may, or may not, affect the optimal timing between TMZ and radiation include genetic alterations such as subclonal mutations in p53 or loss of PTEN^30-32, heterogeneity of expression patterns between³³ and within³⁴ tumours, and epigenetic heterogeneity³⁵. Future studies will incorporate such heterogeneity as well as immunotherapy response modelling.

Methods

Generation of mouse GBMs

All animal experiments were approved by the Institutional Animal Care and Use Committee of the Fred Hutchinson Cancer Research Center (protocol-ID 50842). Tumors were generated by injecting RCAS-transfected DF-1 cells into the brains of mice that express the t-va receptor under control of the nestin promoter (N/t-va). DF-1 cells were obtained from the American Type Culture Collection (ATCC, Manassas, VA, catalogue #CRL-12203) and grown in Dulbecco’s modified eagle medium containing 4 mM L-glutamine, 4.5 g/L glucose, 1 mM sodium pyruvate, and 1.5 g/L sodium bicarbonate supplemented with 10% fetal bovine serum (DMEM, ATCC, catalogue #30-2002) at 39°C without antibiotics. Transfections with custom-made RCAS-PDGFB-HA and RCAS-Cre was done using the Fugene 6 transfection kit (Roche, Basel, Switzerland, catalogue #11 814 443 001). 2x10⁵ transfected cells in 2 μl DMEM were injected into the brains of 6-8 weeks old male or female N/t-va;Cdkn2a^−/−;PTEN^fl/fl;Luciferase^LSL/LSL or Ntva;Cdkn2a^−/−;Pten^fl/fl mice. The bodyweight of the utilized mice was 20-25g. Mice were generated and bred in house, the genetic background being a mixture of 129/Sv, CJ7, C57BL6/J, FVB/N, and BALB/C³⁶. Hair at the site of surgery was removed utilizing an off-the-shelf clipper. Coordinates from the bregma were lateral 2 mm, anterior 0.75 mm, depth 2 mm. Upon developing symptoms such as lethargy, weight loss or pareses, mice were euthanized utilizing carbon dioxide.

Mouse chemoradiotherapy

Mice were treated 3 weeks after tumour initiation with TMZ (LKT laboratories, St. Paul, MN, catalogue #85622-93-1) 50 mg/kg body-weight daily for five days concomitant to whole brain irradiation with 2 Gy daily for five days. TMZ was freshly dissolved in phosphate-buffered saline with 0.5% dimethyl-sulfoxide prior intraperitoneal injection. Irradiation to the head was performed under anaesthesia with isoflurane using the X-RAD 320 Biological Irradiator from Precision X-Ray (North Branford, CT). Mice were monitored to check for tumour related symptoms such as lethargy, weight loss (15% body weight), seizure, hyperactivity, altered gait, poor grooming, macrocephaly, paralysis. Upon developing symptoms, mice were euthanized utilizing carbon dioxide.

Bioluminescence imaging

Tumour-bearing mice were anesthetized with isoflurane and retro-orbitally injected with 75 mg/kg body weight D-luciferin (Caliper, Hopkinton, MA, catalogue #122796). Images were acquired 3 minutes after injection of luciferin for 5 seconds utilizing the IVIS 100 imaging system (Caliper). A photographic image was overlain with the pseudocolor image to depict the spatial distribution of photon counts. A 1 cm² circular region centred manually between the ears was defined as region of interest for quantitation of radiance, defined as photons per second per cm² per steradian. Emission filters were set to 560 - 420 nm. No normalization or autofluorescence removal was performed. Mice were imaged before and 72 h after the last dose of treatment. Images of repeated measurements were set to the same scale. Hair removal was not performed prior to bioluminescence imaging, potentially limiting the accuracy of the in vivo imaging.

Anaesthesia

Isoflurane (Baxter, Deerfield, IL, catalogue #1001936060) was used for anaesthesia during surgery for tumour generation, irradiation of the brain and bioluminescence imaging. A VetFlo vaporizer (Kent Scientific, Torrington, CT, catalogue# VetFlo-1205S) at a concentration of 5% in oxygen for induction and 2% in oxygen for maintenance of sedation.

Sample size for survival experiments

Sample size for survival experiments was calculated to detect a 10% increase in median survival with the optimal vs suboptimal chemoradiation schedules with 90% power at a 5% alpha level. Assumptions included a standard deviation of survival of 10% for the first chemoradiation experiment, which was subsequently refined to 7.5%. Utilizing an open resource sample size calculator (www.clincalc.com), these assumptions yielded sample sizes per arm of N=20 and N=12 mice, respectively.

Computational modelling

We designed a spatially explicit stochastic process model to investigate the impact of spatial localization on an evolving, heterogeneous tumour population. Inspired by the cell setup process established in CHASTE³⁷, we considered a 2-D cross-section of the area surrounding a blood vessel (Figure 2). For each proliferating cell type τ, we defined a stochastic cell cycle period t ~ Uniform(t_min, t_max), after which the cell divides. For the initialization period before treatment, we enforce a shorter cell cycle to minimize setup time without influencing spatial locality or cell type. During the time of interest (during and after treatment), the range is set such to range from 0 to 24 hours, thus having the cell divide typically once per day. To model cellular quiescence, we extended the time until cell division for the affected cell. To simulate a differentiation event, the cell dropped one level in the differentiation cascade. For GSCs, this event transformed the cell into a DTC at differentiation level i = 1. For DTCs at differentiation level i ≠ z, the cells remained classified as DTCs, but became more differentiated, gaining one level of differentiation. DTCs at level z became terminally differentiated cells. Regardless of cell type, the recently differentiated cells restarted their cell cycles. However, if the cells were quiescent, they maintained their quiescent period. Dedifferentiation events were treated in a similar manner: we considered a differentiation level z_revert ≤ z above which cells could dedifferentiate. DTCs at levels 1 < i ≤ z_revert became more stem-like, losing a differentiation level. DTCs at differentiation level i = 1 became GSCs. Terminally differentiated cells and DTCs at differentiation levels z_revert < i ≤ z remained unaffected. Again, quiescence is also unaffected.

Spatial structure and interactions between cells

Each simulation was initialized with a blood vessel with a radius of d_radius cell radii and a single cell-thick layer of GSCs. The location of these endothelial cells is fixed throughout the simulation. Additionally, a fraction p_micro of cells within a distance d_micro near the blood vessel are microenvironment cells, such as stromal cells. These microenvironment cells do not move or divide, but do provide constraints on cellular motion and can provide cell signaling³⁸. Cells in the simulation each have a preferred cellular radius d and exert a force on other cells to ensure that cellular space. The cells naturally reside with their centres at a distance of two cell radii apart. Cell centres had a minimum distance of 2r apart at which they preferentially resided, and they exerted force on encroaching cells to ensure that spacing. The interaction stress between the cells is derived from the Lennard-Jones potential³⁹ . This stress is used to determine the force exerted on each cell and move the cells appropriately, thus ensuring that no two cells are too close together. Glial cells are estimated to be roughly circular with a fixed radius of approximately 2μm. This encapsulated the region that the glial cell and its appendages would occupy. Thus, in these 2D simulations each cell was defined physically as a circular area with a fixed radius r and defined a cell’s coordinates based off of the cell centre. We centred the simulation on the blood vessel; as such, the cells comprising of the blood vessel did not move. Microenvironmental cells were assumed to be fixed to an extracellular matrix and so are not pushed by other cells. Given the immobility of blood vessel and microenvironmental cells, all collision forces involving those cell types are propagated solely onto the colliding cell. We also assumed that GSCs were less motile than DTCs and so were less likely to move than the DTCs. Cells near the blood vessel are allowed to potentially change their phenotypes at a probability proportional to the distance to the blood vessel to simulate the effects of microenvironment factors. Thus, only a fraction f_STEM of the total collision force were absorbed by stem cells while the remainder of the force affected DTCs. Collisions between cells of the same type distributed the force between the cells evenly.

Motion in this system was primarily the result of cell division. Cell division-imposed forces between the resulting daughter cells. In stem cell niches, a gradient of soluble factors causes the spatial orientation of the offspring of stem cells⁴⁰. Therefore, when a stem cell divided, the division occurred such that the more differentiated daughter cell was oriented further away from the blood vessel, with a minimum separation distance imposed upon the cells. By contrast, non-stem divisions were randomly oriented. Once the division had occurred, normal collision resolution, as described above, was applied, separating the two daughter cells and propagating the motion to nearby cells. While we did include a small term of random noise in the motion of cells, we did not consider high cellular motility and assumed cells do not undergo high levels of either directed or undirected motion.

Radiotherapy

We considered the effects of radiotherapy to be independent of the spatial structure of the PVN—i.e., the region of interest is small enough such that edge effects of radiation are not significant. As such, cell death in response to radiation was modeled by two probabilities: one probability for GSCs and one probability for DTCs. For type τ, the probability of death from a single dose d of radiation was given by:

$$p_{⊺,\text{radio}}(d)=1\text{-}\text{exp}(\text{-}{{\alpha }_{⊺}}^{\ast }d\text{-}{{\beta }_{⊺}}^{\ast }{d}^2)$$ (1)

following the well-known and used linear-quadratic model of radiation response¹⁴. We related the two radiation-based death terms by the following equalities: α_GSC = ρ*α_TB and β_GSC = ρ*β_TB. Cells that did not die as a result of radiotherapy became quiescent for a type dependent period of time: we modeled radiation-induced quiescence as an exponentially distributed increase in cell cycle length Q_τ ~ Q_τ,min + Exponential(Q_τ,mean), where Q_τ,min is the minimum quiescent period for type τ and Q_τ,mean is the mean of the exponential distribution. Finally, radiotherapy is known to induce an increase in side population cells in gliomas¹⁸. As such, we considered a probability γ that a DTCs undergoes a dedifferentiation event as described earlier.

Temozolomide (TMZ)

In contrast to the spatially uniform dose distribution of radiotherapy, the TMZ concentration is spatially heterogeneous and dependent on the spatial structure of the PVN. TMZ enters the tumour through absorption into the blood followed by diffusion into the PVN. Thus, we model a dose of TMZ as a combination of two functions. The blood concentration of TMZ, C_blood(t), was modeled by exponential absorption of drug into the bloodstream until a maximum concentration C_max is reached, followed by an exponential decrease in drug concentration with half-life t_½:

$$C_{\mathsf{blood}}(t)=\{\begin{array}{cc}(\text{exp}(rt)-1)2^{-\frac{t}{t_{{}^1∕_2}}}\hfill & t<t_{\max }\hfill \\ C_{\max }{2}^{-\frac{t-t_{\max }}{t_{{}^1∕_2}}}\hfill & t\ge t_{\max }\hfill \end{array}\phantom{\}}$$ (2)

where $r=\frac{\text{ln}\left(\frac{C_{\max }}{2^{-\frac{t}{t_{{}^1∕_2}}}}+1\right)}{t_{\max }}$.

The parameter r in the above equation converts the known fixed point (t_max, C_max) into a rate of change of the drug concentration by solving the C_blood function. We based the functional form of the TMZ blood pharmacokinetic model on known pharmacokinetics of TMZ¹⁶. Diffusion of chemotherapeutic into the PVN was modeled by diffusion processes: we approximated the 2D diffusion partial differential equation:

$$\frac{\partial C}{\partial t}=D\left(\frac{{\partial }^{2}C}{\partial x^2}+\frac{{\partial }^{2}C}{\partial y^2}\right)$$ (3)

with the fundamental solution for the 2D diffusion equation given a single point source, positioned on the edge of the blood vessel:

$$C(t)=\frac{1}{4\pi D}{\int }_{\tau =0}^{\tau =t}\frac{1}{t-\tau }\text{exp}\left(\frac{x^2+y^2}{4D(t-\tau )}\right)d\tau .$$ (4)

As in the plasma, the temozolomide degrades in the tumour. We assumed the half-life in tumour tissue to be similar to the half-life in the blood:

$$C(t)=\frac{1}{4\pi D}{\int }_{\tau =0}^{\tau =t}\frac{C}{t-\tau }\text{exp}\left(\frac{x^2+y^2}{4D(t-\tau )}-\frac{t-\tau }{t_{{}^1∕_2}}\text{ln}2\right)d\tau .$$ (5)

To calculate the fraction of cells that die in a given time step at the given concentration, we set the EC50 value, the concentration at which the drug gives half-maximal response, for TMZ to 0.004268 mol/m³ based on experiments by Wedge et al.⁴² and calculate the EC_F value for the concentration using the following equation:

$${\mathsf{EC}}_{\mathsf{F}}={\left(\frac{\mathsf{F}}{100-\mathsf{F}}\right)}^{1∕\mathsf{H}}\cdot {\mathsf{EC}}_{50}$$ (6)

We set the Hill slope to 1.0 to represent a standard dose curve. We then stochastically determined if a cell is killed due to chemotherapy in a given time step due to the response to the existing concentration of the chemotherapeutic that diffused to that cell's spatial location. Note that the values for determining diffusion and response to the dose level of TMZ are based on parameters estimated from data from mouse models¹⁴. To adjust the model to humans, these parameters should be adjusted to those values found in Brock et al⁴³.

Radiosensitization by TMZ

We considered the effects of a potential synergistic interaction between TMZ and radiation through the introduction of a radiosensitization parameter based on local TMZ concentration. The calculation of the probability of cell death from a single dose d of radiation (equation 1) was modified to include a dependence on C(t), the concentration of the chemotherapeutic at the time of radiation administration and k_sens, a constant representing the magnitude of the radiosensitization:

$$p_{⊺,\text{radio}}(d)=1\text{-}\text{exp}(\text{-}{\alpha }_{⊺}{}^{\ast }(1+{k_{sens}}^{\ast }C(\mathrm{t}){)}^{\ast }d\text{-}{{\beta }_{⊺}}^{\ast }{d}^2).$$ (7)

This modification to equation 1 allowed us to account for exposure to TMZ to make it more likely for a cell to die due to subsequent radiation. The likelihood of dedifferentiation or time period of quiescence following radiation remained unchanged and modeled using the equations described above.

Parameter selection

Parameter estimates of cell cycle lengths for GSCs and non-stem-like cells were obtained from cell line experiments¹⁸. Estimation of z in GBMs is difficult, however, mouse experiments have determined a value z = 5 for normal brain glial cells¹⁸. The value of z_revert is unknown; we tested the effect of varying this parameter by conducting a sensitivity analysis. The number of DTCs only started to vary significantly when z_revert was less than 2 or greater than 14. We set z_revert to 7 for subsequent simulations.

Using this simulation model, we investigated a set of cellular interactions and environmental effects characterized by glioma biology. We allowed cells near the blood vessel to revert to less differentiated states at a probability proportional to their distance to the blood vessel to simulate the effects of microenvironmental factors such as endothelial nitric oxide (eNOS)³⁸. The diffusivity of eNOS has been experimentally determined⁴⁴: however, the necessary concentration to induce a stem-like phenotype remains unknown. We initially imposed a linear decrease in probability of reversion with decreasing concentration of eNOS. Additionally, we allowed for an outward migration of cells similar to the motility of oligodendrocytic progenitor cells by imposing a force f_move to each cell oriented away from the blood vessel. A probability p_death of random cell death was also included and allowed to vary across differentiation levels. Therapeutic intervention was addressed as a change in the death dynamics of the system. During radiotherapy, cells undergoing proliferation are preferentially targeted; other cells die at much lower rates and instead halt their cell cycles for a period of time. In contrast, TMZ preferentially targets cells closest to the blood vessel since there, the concentration of drug is largest: however, GSCs have lower rates of death compared to other cell types.

Schedule optimization and parallelization on a large-scale supercomputer

In order to derive optimized schedules, simulated annealing (SA)⁴⁵ was used. SA is a probabilistic algorithm drawing from statistical physics⁴⁶ and is used for a range of combinatorial optimization problems in which the goal is to identify, among many configurations, the one that minimizes a certain objective or fitness function; for instance, the fitness function could be dependent on the total number of tumour cells over time so that the best schedule is the one that minimizes that number. The method starts with a template input and creates small perturbations from this template. The fitness function is then calculated for the perturbed input. If the fitness for the perturbed input is greater than that for the template input, then the perturbed input will serve as the template in the next iteration. If the fitness is lower, stochasticity is introduced by accepting the perturbation over the template with a certain probability that is gated by a time-dependent parameter and degree of fitness degradation. At a fixed probability, the method will get a kick in which a randomly generated topology perturbation will be introduced. We defined the fitness function for minimization to be the number of DTCs.

We defined a parallel implementation of SA so that the search space could be maximized and the likelihood of staying in a local minimum reduced. The SA method was adapted to the problem of schedule optimization by starting with the standard of care set as the template schedule. Perturbations were then created that matched the constraints outlined above. For the parallel version, many different perturbations to the schedule were created for simultaneous testing. To address the stochasticity in the problem, 128 runs for each schedule were simultaneously modeled. The average fitness for each schedule was determined and that was used for comparison. This work was completed on the Vulcan supercomputer, an IBM Blue Gene/Q system, at Lawrence Livermore National Laboratory. To complete the necessary simulations, 36 million CPU hours (4,109 years) on 131,072 cores were used.

Data availability

The main data supporting the results in this study are available within the paper and its Supplementary Information. The raw and analysed datasets generated during the study are too large to be publicly shared, yet they are available for research purposes from the corresponding authors on reasonable request.