Sufficient sampling for kriging prediction of cortical potential in rat, monkey, and human μECoG

Abstract

Objective.

Large channel count surface-based electrophysiology arrays (e.g. μECoG) are high-throughput neural interfaces with good chronic stability. Electrode spacing remains ad hoc due to redundancy and nonstationarity of field dynamics. Here, we establish a criterion for electrode spacing based on the expected accuracy of predicting unsampled field potential from sampled sites.

Approach.

We applied spatial covariance modeling and field prediction techniques based on geospatial kriging to quantify sufficient sampling for thousands of 500 ms μECoG snapshots in human, monkey, and rat. We calculated a Probably Approximately Correct (PAC) spacing based on kriging that would be required to predict μECoG fields at ≤10% error for most cases (95% of observations).

Main Results.

Kriging theory accurately explained the competing effects of electrode density and noise on predicting field potential. Across five frequency bands from 4–7 Hz to 75–300 Hz, PAC spacing was sub-millimeter for auditory cortex in anesthetized and awake rats, and posterior superior temporal gyrus in anesthetized human. At 75–300 Hz, sub-millimeter PAC spacing was required in all species and cortical areas.

Significance.

PAC spacing accounted for the effect of signal-to-noise (SNR) on prediction quality and was sensitive to the full distribution of nonstationary covariance states. Our results show that μECoG arrays should sample at sub-millimeter resolution for applications in diverse cortical areas and for noise resilience.

1. Introduction

Electrocorticography (ECoG) is an intracranial electrophysiology tool often used clinically in neurosurgery following innovations in epilepsy treatment by Jasper and Penfield in the late 1940s [1]. The high signal amplitude and spatial precision resulting from direct cortical contact has provided neurophysiologists with an important tool for studying speech and skeletomotor systems [2, 3, 4, 5, 6, 7, 8, 9]. The centimeter scale geometry of ECoG grids has been prioritized for clinical usage. However, there is extensive evidence that sub-centimeter scale electrode arrays (i.e. millimeter scale contact size and spacing) can resolve finer topographical detail [10] and provide better discrimination for sensory input [11, 12], higher order language processing [13, 14, 15], and speech and motor output [16, 17, 18, 19].

Application of microfabrication technology has introduced a diverse set of sub-millimeter scale research electrode arrays collectively referred to as “micro” ECoG (μECoG) [20, 21, 22, 23, 24, 25, 26, 27]. μECoG arrays are typically produced with thin film polymers and one or more thin layers of conductive material that can fit over the curvature of neocortex with lower rigidity and bending stiffness than traditional silicon or metal microwire electrodes [28, 29]. μECoG arrays sample local field potential (LFP) at sub-millimeter intervals, revealing fine-scale sensory topologies consistent with intracortically mapped topologies in rat barrel cortex [30], rat auditory cortex [31, 23, 32], non-human primate (NHP) somatosensory cortex [33], cat visual cortex [34], and rat ocular dominance columns [35]. Improvements in the integration density of headstage and implanted neural amplifiers are expected to enable orders-of-magnitude scaling of μECoG sensor counts [27, 36, 37]. However, LFP, including surface potential, is spatially correlated for physical and physiological reasons, leading to the concern that high density sampling is redundant. Thus, the appropriate sampling resolution for μECoG remains an open question.

Prior studies linking primary visual cortex multiunit activity (MUA) to intracortical LFP through a Gaussian integration (point-spread) model have suggested Gaussian kernel scales of ~100 μm, measured via voltage sensitive dye [38], and between ~100 μm in layer 4 to ~200–300 μm in layers 5 and 2/3 in electrode recordings [39]. These (planar) integration models suggest that 95% of the sources contributing to the LFP are within a radius of 250–750 μm, and that the full width at half maximum of the point-spread function for a source is 230–700 μm. Modeling the impact of pairwise correlations on movement decoding from LFP recorded by arrays of microelectrodes suggests decoded performance is maximized with sub-millimeter spaced electrodes [40]. In an anatomically realistic simulation of field potential, the dynamic factor of synaptic input correlation modulated the spatial reach of source contributions between 100–1000 μm [41, 42].

The spatial reach of cellular sources on the surface potential has been studied using optogenetic methods. Optical stimulation resulted in μECoG-recorded potential profiles extending at least 1 mm in rodents and non-human primates [20, 43, 44, 45]. The point spread of surface potential has also been inferred by analyzing the spatial bandwidth of μECoG signals, with the conclusion that there is little spatial variation in cycle lengths lower than 0.5–0.7 mm in rat and rabbit, and 1–3 mm in human [46, 47, 48]. Recent correlogram studies that indexed pairwise correlations (or frequency-resolved coherence) by electrode distance suggest that the length scale of spatial correlation varies from 100s to 1000s of microns depending on electrode contact (epi- versus subdural) and brain state (anesthetized versus awake) [23], and is also highly dependent on the frequency band in question [49, 50, 51].

Results regarding characteristic length scales and spatial bandwidth have suggested spatial intervals at which field potential, on average, is no longer redundant. However, no report has discussed the confounding roles of process nonstationarity and signal to noise ratio (SNR) when interpreting auto-covariance functions, nor tested the efficacy of sampling at suggested length scales. We address these topics by using covariance kernel modeling and spatial prediction in a framework known as “kriging” in geospatial statistics [52, 53], and Gaussian processes more generally [54]. Kriging predicts the expected value of unobserved spatial field values conditional on several observed values, under the assumption that all field values are jointly Normal with spatially dependent covariance. As a statistical predictor, kriging also quantifies uncertainty in terms of the expected mean square error (MSE) of the predicted value.

We used kriging prediction error as the key figure of merit to delineate when μECoG spatial fields were sufficiently sampled. Based on analysis of theoretical kriging error, we established the competing roles of SNR and electrode spacing in determining the predictability of spatial field details. By manipulating the covariance model, we proposed sufficient electrode spacings required to predict spatial fields with an expected error of 10% of process variance. We tested the theoretical results in vivo with cross-validated analysis of kriging error for anesthetized rat auditory cortex μECoG recordings, using electrode arrays that were matched in geometry, but differed in noise levels. The different LFP prediction efficiency for the two arrays confirmed the theoretical trade-off between SNR and electrode spacing, and corresponded to the ability to decode sensory information, as measured by a tone frequency classification analysis. In subsequent results, we analyzed the spatial covariance and kriging error of μECoG in multiple bandpasses for awake rat, NHP, and anesthetized humans. Submillimeter electrode spacing was generally required for stable prediction at 10% error, although electrode spacing from 1–1.5 mm were sufficient for some human and NHP motor cortex bandpasses. Spacing at 600–850 μm was required in all species and cortical areas at the highest 75–300 Hz frequency band, even when recording noise was set to zero in the kriging model. The projected sufficient sampling based on expected kriging error accounted for the full range of covariance states surveyed in our datasets. Sufficient sampling for kriging prediction is easily tunable for stricter or looser tolerances in other settings, and can be estimated a priori given assumptions about LFP image statistics and measurement quality.

2. Methods

2.1. Electrophysiology

2.1.1. Electrode arrays

We measured epidural μECoG fields in rat with two types arrays (figure 1 “Rat Arrays”). One was a passively conducting (“passive”) array fabricated with gold conductors in liquid crystal polymer (LCP) insulator, manufactured by Dyconex Micro Systems Technologies (Bassersdorf, Switzerland [55]). The other was a custom fabricated “active” device with NMOS voltage buffering and multiplexing within the array. Gold electrode pads formed the biotissue interface, and were conductively coupled to back-side electronics via highly doped silicon nanomembranes (p⁺⁺-Si NM), which also functioned as a biofluid insulation material in chemical bond with the main insulation layer of thermally grown silicon-dioxide (t-SiO₂) [56]. Both devices had electrodes arrayed on an 8×8 grid. The active array had 64 rectangular electrodes of 360×360 μm² with 400 μm inter-electrode pitch (one electrode was excluded due to malfunction). The passive array included 61 channels (with 3 corners missing) of 229 μm diameter discs with 420 μm pitch. Impedance could not be measured for the active arrays as a result of their design, but conductor impedance measured with a test structure was ~450 kΩ at 1 kHz [56]. Typical in-vitro impedance values at 1 kHz for the passive arrays were 21–36 kΩ interquartile range (IQR). A 244-channel LCP and gold μECoG array (also manufactured by Dyconex) was used in the human and NHP recordings. These 229 μm disk electrodes were arrayed in a 16×16 grid with 762 μm pitch with typical in vitro impedance values at 1 kHz of 44–53 kΩ IQR (figure 1 “Human Array”).

Figure 1.

μECoG electrode arrays. Two μECoG arrays were designed for use in rat auditory cortex. The passively conducting array was fabricated with gold contacts (229 μm diameter) and interconnects insulated in liquid crystal polymer (LCP). The active array had gold contacts (360×360 μm₂) insulated by conductive silicon nanomembranes (p⁺⁺ Si NM). It was fabricated with active powered silicon transistors within the array that buffered and multiplexed field potential. The 61 passive electrodes and the 64 active electrodes were both arranged in an 8×8 grid with approximately 400 μm pitch. A second passive electrode array (shown at 1/2 the scale of the rat arrays) was designed for use in humans and non-human primates. This array was fabricated with LCP and gold using the same process as the rat array, and had an electrode pitch of 762 μm.

2.1.2. Acute auditory cortex recordings

All rat procedures were performed in accordance with National Institutes of Health standards and were conducted under a protocol approved by the Duke University Institutional Animal Care and Use Committee. Two female Sprague-Dawley rats weighing 260–280g were anesthetized with ketamine (80 mg kg⁻¹ intraperitoneal) and dexmedetomidine (0.125 mg kg⁻¹ intraperitoneal), and secured to a custom-built orbital clamp head mount. Craniotomies of approximately 6×6 mm² were made over temporal cortex, exposing right hemisphere auditory cortical areas. In acute recordings, active and passive μECoG arrays were sequentially implanted epidurally. Primary auditory cortex and anterior auditory field (collectively “auditory cortex”) were targeted by anatomical landmarks and the reversal of rostrocaudal tonotopic gradients. Neural field potential data from the active array was sampled and logged with a custom National Instruments data acquisition system [57] at an effective rate of 780 S/s per channel. Field potential from the passive rat array was amplified and sampled at 20 kS/s by an Intan RHD2164 64-channel board with high pass filtering at 0.1 Hz, and logged with the Open Ephys data acquisition system [58].

2.1.3. Chronic auditory cortex implants

Four female Sprague-Dawley rats weighing 225–275g were anesthetized with 5% isoflurane at 3L/min for induction and 1–3% at 0.5–1.0 L/min for maintenance. An identical surgical procedure to the acute preparation was carried out in sterile conditions for placement of passive LCP arrays. Additional procedures regarding surgery and implantation are detailed in [55]. Dexamethasone (0.3 mg/kg) and Baytril (0.5 mg/kg) were administered postoperatively for 3 days and 7 days respectively. The awake recordings were made with the animals awake and freely moving in their home cages and field potential was acquired in the same manner as acute passive array recordings.

2.1.4. Semi-chronic NHP implant

A semi-chronic recording chamber base was implanted in one adult male NHP (Macaca Mulatta), as described in [59]. In brief, the NHP was anesthetized during surgical implantation. The base was fixed to the skull with dental cement (MetaBond, Parknell Inc. and Simplex P, Stryker) and ceramic bone screws (Rogue Research). After the chamber base was affixed to the skull, chamber hardware was stacked on top of the base to a height that was tall enough to allow for seal testing of the chamber in vivo. After confirmation of chamber seals, a craniotomy and durotomy were performed to provide access to precentral gyrus, and an artificial dura molded with the 244-channel electrode array was implanted within the durotomy. All data collection occurred while the NHP was awake and seated quietly performing a center-out reach task [27]. All animal procedures were performed in accordance with National Institutes of Health standards and were approved by the New York University Animal Welfare Committee (UAWC). Neural data were sampled at 30 kS/s (NSpike NDAQ System, Harvard instrumentation Lab, x1 gain headstage, Blackrock Microsystems). Recordings were referenced to a metal screw implanted through the skull to make contact with the dura at a distant location. Of 242 of 244 electrodes that were recorded, we excluded 48 sites that were located across arcuate sulcus in the frontal eye field, and another 11 malfunctioning channels, leaving 183 precentral gyrus sites remaining that covered portions of dorsal premotor cortex and primary motor cortex (collectively “motor cortex”).

2.1.5. Human clinical procedure

Intraoperative recordings were made in two patients (subject A, female, age 20; subject B, female, age 22) undergoing resection surgery in left posterior superior temporal gyrus (pSTG) to treat drug resistant epilepsy. Clinical procedures were performed in accordance with National Institutes of Health standards and were conducted under a protocol approved by the Duke Institutional Review Board. Prior to surgery, each electrode array was pre-selected based on impedance measurements in saline solution. After selection, the electrode array was cleaned and impedance measurements were taken again in saline. The electrode array, electrode holder, and all cables were gas sterilized prior to use in the operating room. In the operating room, patients underwent general anesthesia with propofol (240 mg subject A, 150 mg subject B). Prior to resection, the surgeon placed the 244-channel μECoG electrode (either bare or molded in silicone) to record areas adjacent to the seizure onset zone. Recordings were made in pSTG for subject A (15 min) and motor cortex for subject B (6 min) during acoustic stimulation with words and non-words in vowel-consonant-vowel and consonant-vowel-consonant patterns. Neural responses were amplified and sampled at 20 kS/s using four Intan RHD2164 amplifiers held by a 3D printed mount and acquired through Open Ephys software.

2.2. Covariance modeling and kriging prediction

We modeled the μECoG signal x(s, τ), measured at location s and moment τ, as the sum of a spatially correlated neural field process η (variance λ μV²), uncorrelated measurement error ϵ(σ_n μV²), and a common spatial mode κ, which may be zero. Field covariance was estimated using the semivariogram (or variogram) which is half the variance of the difference in signal measured at two locations:

$${\gamma }_x(s,u)=\frac{1}{2}\mathrm{var}\left\{x_s-x_u\right\}$$ (1)

Due to finite signal energy and compact fields of view, we made the common simplifying assumption of spatially isotropic second-order stationarity, which reduces the variogram to a function of relative distance h = ||s – u||. We also assumed approximate process stationarity over short time windows, to estimate variances over time samples. Under these conditions, we link a field-plus-noise covariance model C_x(h) = C_η(h) + σ_nδ(h) to the variogram

$${\gamma }_x(h)=\underset{\text{neural}\text{field}}{\underbrace{C_{\eta }(0)-C_{\eta }(h)}}+\underset{\text{noise}}{\underbrace{{\sigma }_n(1-\delta (h))}}$$ (2)

We fit empirical variograms with a combination of a constant offset for noise (the “nugget”, per spatial statistics literature [60]) and the Matérn kernel [61] for the neural field covariance term. The Matérn kernel is parameterized by a length θ that scales the correlation range, and a unit-less shape parameter ν influences the smoothness of the field at short range. We summarized the noise-free spatial scale of neural fields with the Nyquist pitch, which is the sample spacing that would enable perfect interpolation for bandlimitted fields that are sampled with exact precision. We defined the effective Nyquist pitch as the reciprocal of the −30 dB bandwidth of the spatial power spectral density (Δ_nyq = BW⁻¹), calculated via the Fourier transform of the Matérn kernel. This interval corresponded to half of the smallest effective cycle length for a field process. See the supplemental discussion for extended details of the covariance and power spectrum models.

Once a covariance model was estimated, we could derive kriging predictions and errors for the μECoG field. Given a vector of μECoG measurements at n electrodes, $x={\left(x_1,\dots ,x_n\right)}^T$, the kriging predictor of a target site s′ is a linear predictor ${\widehat{\eta }}_{s^{\prime }}=w_{s^{\prime }}^{T}x$ that is optimized for error variance, conditioned on the spatial kernel model. The prediction error variance

$$\begin{gathered} {\sigma }_e=E\{{\left({\eta }_{s^{\prime }}-{\widehat{\eta }}_{s^{\prime }}\right)}^2\} \\ =\lambda -2w_{s^{\prime }}^T\mathrm{cov}\left\{x{\eta }_{s^{\prime }}\right\}+w_{s^{\prime }}^T{C}_x{w}_{s^{\prime }} \end{gathered}$$

is minimized by the filter $w_{s^{\prime }}=C_x^{-1}\mathrm{cov}\left\{x{\eta }_{s^{\prime }}\right\}$. Noting that the field and noise components of x are uncorrelated, the cross-covariance vector is computed from the neural field kernel absent the nugget $c\left(s^{\prime }\right)={\left(C_{\eta }\left(\Vert s_1-s^{\prime }\Vert \right),\dots ,C_{\eta }\left(\Vert s_n-s^{\prime }\Vert \right)\right)}^T$. The kriging predictor is a weighted sum of the sample data with coefficients that depend only on the covariance kernel

$${\widehat{\eta }}_{s^{\prime }}=c{\left(s^{\prime }\right)}^T{C}_x^{-1}x$$ (3)

Similarly, the prediction MSE depends only on the covariance model and not directly on the data sample itself

$${\sigma }_e\left(s^{\prime }\right)=\lambda -c{\left(s^{\prime }\right)}^T{C}_x^{-1}c\left(s^{\prime }\right)$$ (4)

The “simple” kriging predictor is the best unbiased linear predictor (BLUP) for a zero mean field. However, the presence of a spatial common mode does not affect the variogram modeling, and can be accommodated in the kriging predictor by constraining $w_{s^{\prime }}$ to sum to one. The “ordinary” kriging weights are an unbiased predictor of an unknown field value plus a constant mean, and the error has the standard form ${\sigma }_e\left(s^{\prime }\right)=\lambda -2w_{s^{\prime }}^{T}c\left(s^{\prime }\right)+w_{s^{\prime }}^T{C}_x{w}_{s^{\prime }}$ [53]. We used the ordinary kriging predictor for awake recordings, which tended to have more strongly correlated fields. We saw no justification for modeling spatially varying deterministic trends.

2.3. Cross-validated kriging

We quantified kriging error and critical sample spacing by modeling the covariance of μECoG field potential in short-time (500 ms) batches, to better approximate statistical stationarity on a per-batch basis. Empirical variogram clouds were computed from the sample variance of all pairwise electrode differences (figure 2(a)–(b)), and signal and shape parameters {λ, σ_n} ∪ {θ, ν} of the Matérn-plus-nugget model (eq 2) were estimated via nonlinear least squares fit to binned semivariance medians, weighted by bin count. Total signal variance ζ = λ + σ_n (the “sill”, per spatial statistics) was constrained to be within ±25% of the total signal sample variance. To account for a common mode variance, which is poorly estimated with the mean of correlated samples, total variance was computed after re-referencing the signal batch to the channel with minimum Euclidean distance to the channel average. Noise power was determined based on heuristic singular value thresholding [62]. Batches with poorly fit covariance were identified by smoothness values within 0.1 of the 0.3 < ν < 5 bounds, and were discarded.

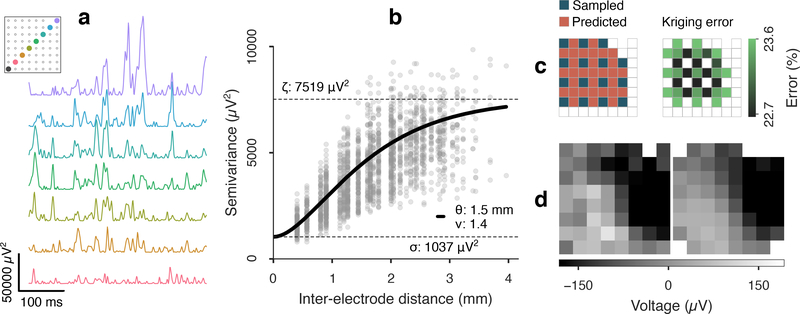
Figure 2.

Spatial variography and cross-validated kriging of inter-electrode μECoG samples. (a) Squared difference of cortical potential between a corner electrode (black) and electrodes along a diagonal transect of an 8×8 μECoG array. The physical distance of subtracted electrodes increases from bottom to top. (b) Semivariance (one-half the variance of differences) between all electrode pairs, ordered by inter-electrode distance. A Matérn variogram kernel (solid line) was fit with estimates for range (θ), smoothness (ν), noise (σ_n) and total signal variance (ζ). (c) One sampling-prediction pattern used for cross-validated kriging and the expected kriging error based on the variogram kernel in (b). Cortical potential was predicted (kriged) at the sites of the dropped electrodes without extrapolating. The electrode in position (1, 7) was excluded due to malfunction. (d) A μECoG frame (left) and the composite frame kriged from subsamples at alternate rows and columns (right). The cross-validation residual variance for this 500 ms batch was 1756 μV² MSE, or 23.4% MSE relative to the total power. The median expected value was 1754 μV² MSE, which included 717 μV² (9.5%) kriging error plus uncorrelated 1037 μV² (13.8%) noise power (eq 5). In this example, the kriging error for the interpolated frames is lower than the noise error in the raw frames, meaning the predicted frames were nearer to the true field potential than direct measurement.

Model prediction errors (eq 4) were cross-validated with residual errors from kriged μECoG fields, which were made by subsampling half of the array rows and columns and predicting interior sites (avoiding extrapolation, figure 2(c)). With this scheme, four sets of overlapping predictions could be made. The MSE of cross-validated residuals was computed using a 0.5% trimmed mean of square errors, which was robust to heavy-tail outliers [63]. Since the total cross-validated residual MSE included the noise variance of the reference sites, which was independent of the prediction error, we adjusted the total expected MSE to include estimated noise

$$E\{{\left|{\widehat{\eta }}_{s^{\prime }}-\left({\eta }_{s^{\prime }}+{ϵ}_{s^{\prime }}\right)\right|}^2\}={\sigma }_e+{\sigma }_n$$ (5)

The expected error was calculated per batch for all kriged sites and summarized by the median (figure 2(c)).

We used the Bhattacharyya coefficient (BC) to measure overlap of covariance parameter distributions on a 0–1 scale. Samples were histogrammed into density-normalized bins {P_i} and {Q_i} using the Freedman Diaconis rule and BC was calculated as ${\sum }_i{\left(P_i{Q}_i\right)}^{1/2}$. To find the hypothetical electrode spacing that would result in 10% kriging error–termed the “kriging resolution”–we computed Δ_10% = arg min_Δ |σ_e − 0.1| via line-search along inter-electrode pitch Δ while holding the covariance kernel parameters {θ, ν, σ_n/ζ} constant in eq 4.

2.3.1. Signal bandpasses

All recordings (except from the active array) were anti-alias filtered offline at 800 Hz and then resampled at 2 kS/s. We applied cross-validated kriging analysis to multiple commonly defined LFP frequency bands. We used approximately log-spaced frequency bands (following [50]): theta (4–7 Hz), alpha (7–14 Hz), beta (15–30 Hz), gamma (30–60 Hz). Additionally, we used a wide high frequency broadband (HFB) (75–300 Hz) in which power modulation has been linked to neuronal spiking rates [64, 65], and which includes high gamma (roughly 80–200 Hz) that is used for measuring stimulus- and behavior-related activity in human ECoG [2, 3, 4, 5, 6]. While broadband power fluctuations are technically a full-spectrum phenomenon, we use “HFB” to denote a bandpass generally free of narrow-band oscillatory activity [66].

A 4–300 Hz band was used to summarized the union of these frequency bands. However, due to the elevated transistor noise of the “active” electrode array, kriging analysis for the acute rat auditory cortex recordings was restricted to 5–100 Hz.

2.4. Tone stimulation and classification

Acute rat auditory cortex recordings were carried out in a sound-attenuated chamber. We played 60 repeats of tone pips for 13 frequencies (0.5–32 kHz, 0.5 octave spacing, 50 ms duration, 2 ms cosine-square ramps) at a rate of 1 s⁻¹ in pseudorandom sequence (780 trials). Acoustic stimuli were generated with custom MATLAB code through an NI 6289 DAC card, and delivered at 70 dB SPL through a free-field speaker (CR3, Mackie) calibrated to have a flat output over the frequency range used.

We analyzed the effect of electrode spacing on predicting auditory stimuli using a previously reported principal components analysis (PCA) and linear discriminants analysis (LDA) classification scheme [32, 55]. To vary electrode spacing in a continuous manner, we used Poisson Disc sampling [67] to generate subsets of the passive rat array that were approximately periodic in space: 10 subsets for spatial periods between 420–2000 μm in 25 μm steps. The effective inter-electrode distance was calculated as the square root of area per electrode: Δ = (A/n)^1/2, where A was derived by the electrode set’s convex hull (see figure 6(a)). The concatenated response from 50 ms post-stimulus μECoG on subset channels was used to form feature vector, and the SVD thresholding heuristic used for noise estimation [62] was used to determine the number of feature PCs to use in the LDA stage. Six-fold cross-validation was then used to produce tone frequency predictions for each trial.

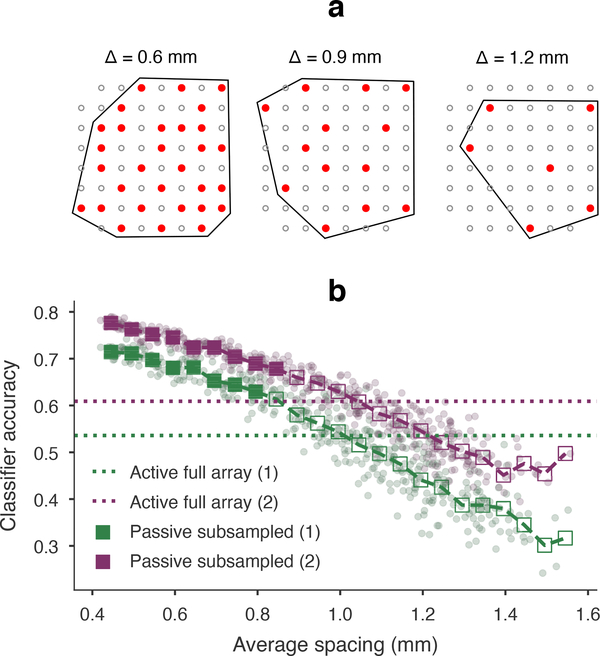
Figure 6.

Field predictability and μECoG information content. We created nearly periodic spatial samples of passive recordings, and computed tone frequency classification accuracy for each sample. (a) Three examples of subsampled electrodes (solid red) are shown at different spatial periods. The average spacing was calculated as (A/n)^1/2 for area A of the convex hull (traced in black) and n electrodes. (b) The reference accuracies based on fully sampled active arrays were 53.6% (rat 1) and 60.9% (rat 2). Chance accuracy was 7.7% for 13 frequencies. Purple and green points show classifier accuracy at each passive array subsample for rat 1 and rat 2, respectively. Accuracy results binned in 50 μm intervals (squares) were compared to reference accuracy (filled squares are significantly higher). Accuracy was not significantly higher than 400 μm spaced active electrodes starting at 845 μm for rat 1 and 895 μm for rat 2 (one-sided Z-test with binomial large sample Normal approximation, p = 0.003 threshold, false detection rate controlled at 0.05).

3. Results

3.1. Theoretical and in vivo analysis of sampling noise and density

The proposed electrode spacing requirements based on prediction loss followed from analytical results of kriging theory, which we outline here. We noted that optimal prediction loss (eq 4) was a function of 1) the length-scale and texture qualities of a spatial field, 2) the SNR of the measurements, and 3) the electrode array geometry vis-a-vis the location to be predicted. Since the expected loss was completely parameterized by the covariance model, we could compute results a priori in response to the three relevant geospatial and signal factors.

Using the Matérn covariance model (eq 2) with unit variance and zero noise, we calculated kriging errors on a 10×10 grid geometry with 1 mm pitch over a range of length scale and smoothness parameters (figure 3(a)). Error approached high levels (> 50% of process variance) for fine-scale models having short range and low smoothness, and was particularly affected by rough texture (low smoothness) fields at all length scales. Such rough spatial fields would be highly irregular within short-distance neighborhoods, regardless of the dominant spatial length scale indicated by θ. Error was monotonic with both spatial parameters, and we defined an error of 10% MSE relative to process variance (0.1 relMSE) to partition the range of covariance models into predictable and not-predictable subsets. The 1 mm pitch in this geometry implied that the covariance models along the predictability threshold had a Δ_10% “kriging resolution” of 1 mm.

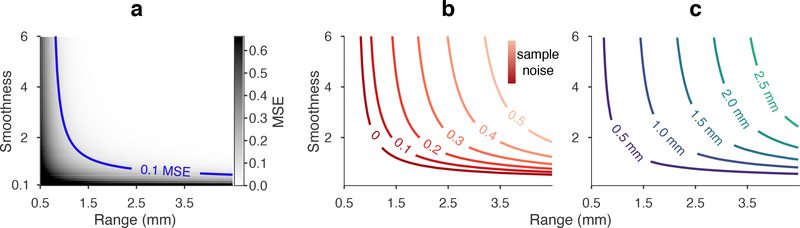
Figure 3.

Effects of covariance model parameters on expected prediction loss. (a) Kriging MSE (eq 4) was calculated for 1 mm spacing, unit variance, and zero noise over a Matérn parameter space. MSE was monotonic in both range and smoothness parameters. Our threshold for predictability was 10% MSE relative to process variance (blue isocontour). Predictability was limited by a low value of either parameter. Smoothness had a weak influence on predictability when range was below a limit, and vice-versa. (Exact limits depended on the sampling geometry.) (b) The 10% predictability threshold for 1 mm grid pitch was computed under increasing levels of sample noise. In higher noise, predictability was restricted to smoother and longer range fields. (c) Predictability thresholds at 20% noise and varied grid pitch from 0.5 to 2.5 mm. Increasing or decreasing pitch had a similar effect on predictability as increasing or decreasing noise. By reducing pitch to 0.5 mm, approximately the same fields were predictable in 20% noise as were predictable in 0% noise and 1 mm pitch.

We then repeated the prediction MSE calculations while introducing noise in the covariance kernel. Figure 3(b) depicts the predictability thresholds for noise levels at 10% increments overlaid in Matérn parameter space. The subset of predictable models at 1 mm spacing (equivalent to panel (a) at 0% noise) became increasingly lower resolution (smoother and longer range) with higher noise. In other words, 1 mm spacing had the same prediction efficiency for a finely featured (high resolution) field in low noise and a coarsely featured (low resolution) field in high noise.

We next explored how sample spacing affected the coverage of predictable models. Holding noise at 20%, we calculated prediction MSE for a 10×10 grid arrangement with electrode pitch in 0.5 mm increments. Predictability thresholds for all spacings are overlaid in figure 3(c). Comparing 3(b)–(c), increased noise and increased density (larger pitch) moved the predictability threshold in competing directions, such that the loss of coverage in higher noise was almost directly counteracted by higher density. Approximately the same subset of field models predictable at 10% MSE or lower in noiseless conditions was predictable in 20% noise by reducing electrode spacing from 1 mm to 0.5 mm.

We confirmed the theoretical effects of covariance model parameters on cross-validated prediction errors made from four paired epidural μECoG recordings of auditory cortex in two rats, using “active” and “passive” arrays that had similar geometry but different noise properties. Covariance modeling and kriging were carried out on 6540 (3459 active and 3081 passive) short-time 500 ms batches of signal in the 5–100 Hz bandpass (outlined in figure 2 and section 2.3). Extensive evaluation of kriging prediction with in vivo μECoG and simulated noise can be found in the supplemental materials (supplemental figure S3).

The spatial field and measurement signal statistics highlighted in the previous section accurately delineated predictable versus non-predictable μECoG batches. See figure 4 and supplemental videos S1–S4 for specific examples. In aggregate, the expected kriging errors based on covariance models were highly consistent with cross-validated kriging prediction errors. Ordinary least squares (OLS) regression of expected error (eq 5) from observed relMSE, normalized by the sill variance, resulted in slopes of 0.99 and 0.98 for active and passive batches, respectively (r² = 0.989, combined model using slopes only).

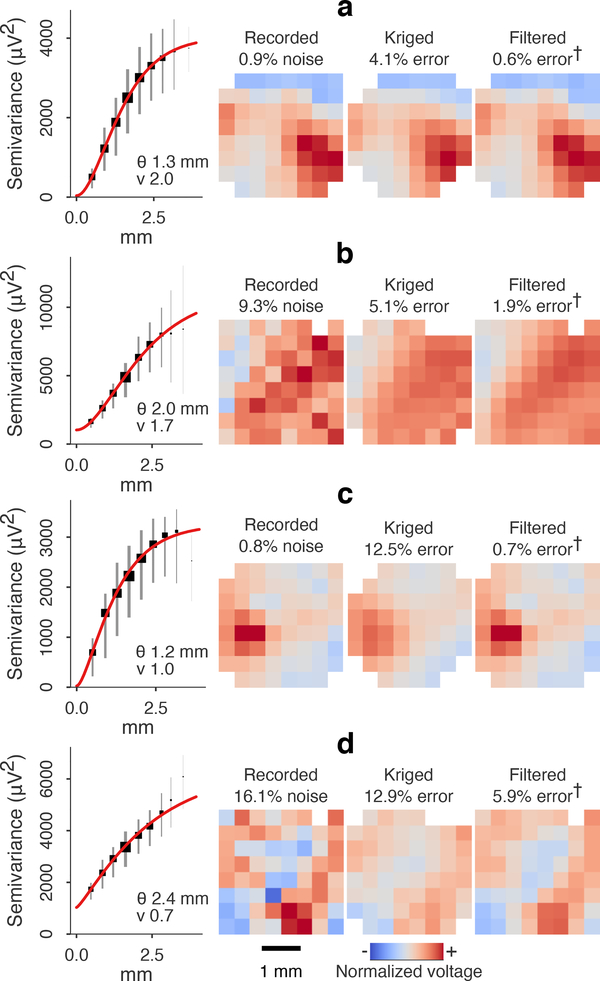
Figure 4.

Predictable and non-predictable frames in anesthetized rat auditory cortex. Variograms were binned at ^~0.4 mm intervals. Squares and vertical stripes are bin median and IQR scaled to bin count. (a)-(b) Longer range and smooth fields were predicted with errors of less than 10% of the signal variance in the spatially sub-sampled passive electrode (840 μm, a) and active electrode (800 μm, b). The kriging error (residual relMSE minus estimated noise) here was 4.1% and 5.1% for passive- and active-electrode, respectively. Interpolated frames in (a)-(b) were visually similar to the optimal prediction from all electrodes, i.e. filtered voltage. (Note that errors marked “†” are estimated since the true field potential was unknown.) (c) A rough field with (lower smoothness index) was not accurately predicted at 840 μm (passive array). The residual relMSE was 13.3%, with 12.5% due to kriging error. (d) A rough field with lower SNR was not predictable at 800 μm (active array), despite having a long covariance range. Residual error was 29.0% (12.9% kriging error and 16.1% noise). Kriging error in (c)-(d) was characterized by oversmoothing, compared to the optimally filtered frames.

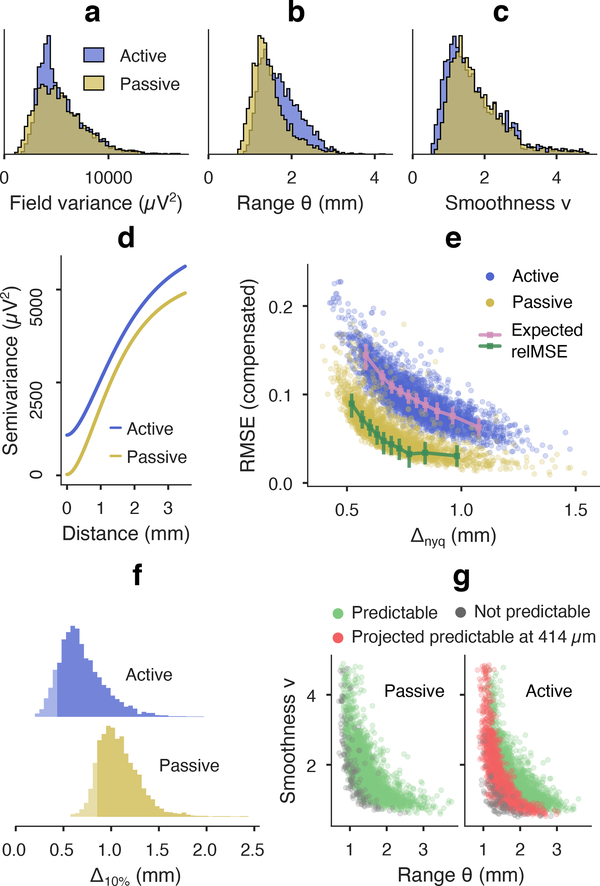
The covariance model parameters illustrated the distinction between “field” and “signal” properties of the two arrays (figure 5(a)–(c)). Statistics corresponding to the neural potential field, i.e. correlation range, smoothness, and field variance, were largely overlapping (smoothness BC=0.99; range BC=0.95; noise-compensated field variance BC=0.98). The larger covariance range estimated for the active array (1.65 mm median) versus passive array (1.38 mm median) may be explained by shorter edge-to-edge distances in the active array, which were 140 μm less than that of the passive array, and would likely increase correlation and bias the Matérn length scale.

Figure 5.

Kriging results for low and high noise recordings in anesthetized rat auditory cortex. (a)-(c) Variogram kernel parameter distributions from four paired auditory cortex recordings in two rats with low noise “passive” and high noise “active” electrodes (n=3081 passive signal batches, n=3459 active batches). Kernel parameters pertaining to the LFP process were consistent between devices (BC=0.98 noise-compensated field variance, BC=0.95 range, BC=0.99 smoothness). (d) Median variogram kernels are primarily distinguished by their noise floors: active 1037 μV² (18.5% signal power) and passive 26.5 μV² (0.5% power). (e) Noise compensated prediction relMSE was inversely related with spatial scale (summarized by Nyquist pitch Δ_nyq), and agreed with expected kriging error based on kernel parameters (OLS slope 0.99 and 0.98 for active and passive batches, respectively, r² = 0.989 combined). Error-bar plots show eq 4 kriging error median and IQR per decile of Δ_nyq. (f) Distributions of the projected spacing for 10% error (Δ_10% “kriging resolution”) for each μECoG snapshot. The 5th percentile probably approximately correct (PAC) spacing was 414 μm (active) and 844 μm (passive). (g) Predictability coverage over field batches is depicted in the Matérn parameter space. Green/gray dots mark fields at ≤ 10% and > 10% relMSE, respectively, at subsampled spacing. Red dots mark fields projected to become predictable with PAC spacing (414 μm) for the active electrode.

The buffering and multiplexing transistors in active arrays introduce 1/f and aliased wideband noise [27]. Median noise estimated by SVD [62] was 1037 μV² for the active array used here, which agreed with bench-top measurements of 992±308 μV² (mean ± SD, 5–100 Hz). The noise level was also consistent with the 870 μV² difference in median sill variance between active array and passive array batches. The separability of field and signal qualities was summarized by the average variograms for each device, which differ mainly by the vertical offset representing the noise floor of the active array (figure 5(d)).

Figure 5(e) depicts the inverse relationship between the Nyquist pitch Δ_nyq, and the noise-compensated prediction relMSE that is attributed to kriging prediction error. The increased error for smaller pitches echoed the tendency towards higher error for smaller model parameters in figure 3(a). Increased noise in the active array resulted in uniformly higher compensated relMSE, which shifted the 10% relMSE threshold to lower resolution fields, as in figure 3(b). Figure 5(e) also shows the extent to which imperfect measurement and lack of bandlimitting prevented lossless interpolation even when the subsampled electrode spacing was equal to or less than the effective Nyquist pitch. However, the prediction relMSE for active array fields (median 9.3%) was lower than the noise error (median 18.5%) in 3290/3459 (95.1%) of field snapshots, indicating that the interpolated fields were a better approximation of true cortical potential than the original measurements. We further validated denoising results for interpolated and in situ field prediction using controlled amounts of additive Gaussian white noise, summarized in supplemental figures S3 and S4.

We computed the empirical predictability “coverage”, at 0.1 compensated relMSE, for the two sub-sampled μECoG arrays. 95.2% of passive array snapshots were predictable at 840 μm, compared to 33.0% of active array snapshots at 800 μm. By manipulating the electrode spacing term in eq 4, we calculated the kriging resolution (Δ_10%) that would normalize prediction error to 10% MSE for each μECoG batch (Figure 5(f)). Due to the competing roles of electrode spacing and SNR, shorter electrode spacings would be needed for stable interpolation from active array measurements.

To concisely summarize uncertainty in both the range of model statistics and kriging prediction quality, we adopted the terminology Probably Approximately Correct to specify a single target for electrode spacing and prediction error (loosely based on the rigorous PAC learning theory, see [68] for a definition). For potential fields recorded with very low noise in anesthetized, epidural rat auditory cortex, 840 μm electrode spacing had a high probability (^~95% empirical rate) of enabling approximately correct (≤ 10% error) prediction of unseen field potential. However, the 95%−10% PAC electrode spacing for the same potential fields in a high noise scenario was projected at 414 μm, based on the 5th percentile of Δ_10% in active array batches. The projected expansion of predictability coverage from 800 μm to 414 μm is shown in Figure 5(g), echoing the recovery of predictability in the simulated results in Figure 3(c).

3.2. Field predictability and stimulus information content

We have observed previously [27] that, despite similar electrode geometry and recording conditions, auditory stimulus classification accuracy is lower using active array recordings compared to passive, due to increased noise. Here we used tone classification to test whether the hypothetical equivalence in active- and passive array sampling predictability corresponded to equivalent information content in the signals. We gradually reduced the effective inter-electrode distance of the passive array from 420 μm to ^~2000 μm to compare classifier accuracy with that from active arrays sampled at 400 μm (53.6% for rat 1 and 60.9% for rat 2, figure 6).

As expected, passive array classifier accuracy at full sampling (72.4% for rat 1 and 78.2% for rat 2) outperformed corresponding active arrays, and decreased fairly regularly as fields were sampled more sparsely. To determine where the subsampled accuracy rates intersected with the corresponding active array baselines, we binned results at every 50 μm and used the large-sample Normal approximation (with σ² = p(1 − p)/780) to calculate z-scored accuracy differences. The smallest electrode spacing bin with no significant difference in accuracy rates was 845 μm for rat 1 and 895 μm for rat 2 (one-sided Z-test, p < 0.003 with false detection rate controlled at 0.05). The equivalent spacing for stimulus information content agreed the hypothesized equivalent PAC spacings of 840 μm and 414 μm.

3.3. Kriging resolution in rat, NHP, and human μECoG

We analyzed spatial covariance in multiple bandpasses for μECoG recordings from one semi-chronically implanted NHP performing a center-out reach task, two intraoperatively implanted humans listening to word/non-word acoustic stimulation under anesthesia, and four chronically implanted rats listening to tone pips while awake and freely moving. We used four commonly defined oscillatory bandpasses (theta: 4–7 Hz, alpha: 7–14 Hz, beta: 15–30 Hz, gamma: 30–60 Hz) and a high frequency broadband (75–300 Hz) characterized by wide spectrum power fluctuations.

3.3.1. NHP motor cortex

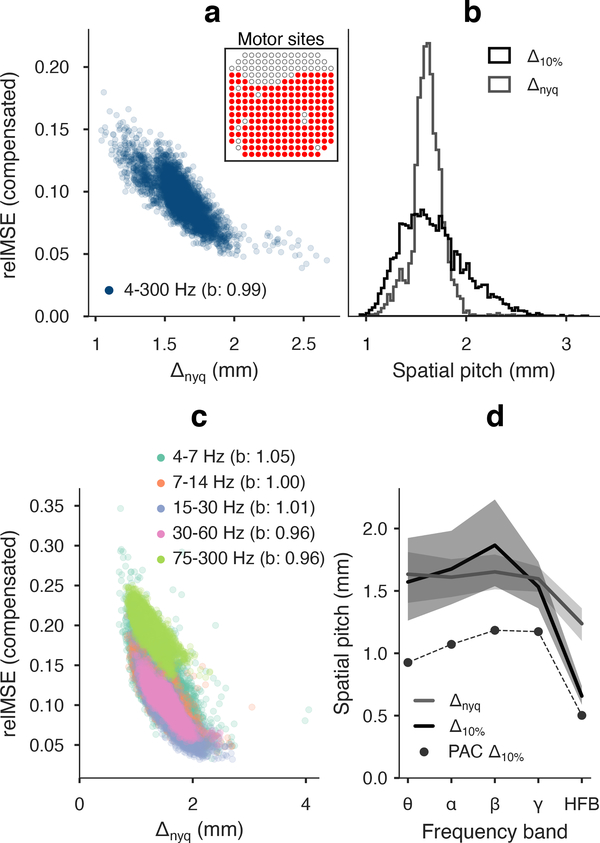
We recorded neural potentials from 183 of 244 electrodes with 762 mm pitch in motor cortex of a macaque performing a center-out reach task (figure 7(a) inset). Bandpassed and broadband spatial variance modeling of 4161 500 ms batches accurately predicted cross validated kriging error, with b = 0.99 in broadband signal and 0.96 < b < 1.05 among bandpasses. There was a lower degree of precision in the expected model error for broadband signal (r² = 0.842) versus bandpasses (r² = 0.952).

Figure 7.

Broadband and bandpass kriging results in awake NHP motor cortex (183 motor cortex electrode sites are shown inset). (a) Prediction relMSE worsened for fields with fine spatial pitch. Parametric kriging error explained residual errors with a slope of b = 0.99, r² = 0.842. (b) Nyquist pitch (1.61 mm median, 1.54–1.70 mm IQR) and kriging resolution (1.63 mm median, 1.44–1.87 mm IQR). The 5th percentile of kriging resolution (PAC electrode spacing) was 1.22 mm. (c) Prediction relMSE in bandpassed μECoG snapshots tended higher for decreasing Nyquist pitch and SNR (especially HFB). Expected kriging error was accurate within 5% of unity slope (r² = 0.952 combined). (d) Nyquist pitch (gray line) was consistent in theta through gamma bands (BC≥0.97 successive bands), but shifted to smaller values HFB (BC=0.84 gamma-HFB). Central tendency kriging resolution (black line, median and IQR) was similar to Nyquist pitch (gray line) in theta-gamma bands with median noise of 1.4–2.2%, but deviated in HFB due to higher 6.3% noise proportion. PAC spacing (black dots) was ^~1 mm for theta-gamma and 502 μm in HFB.

Broadband fields in awake NHP motor cortex had longer correlation range and rougher texture compared to anesthetized rat auditory cortex, with median Δ_nyq = 1.61 mm. The larger subsampled electrode spacing of 1.52 mm predicted 62.3% of field batches at 10% MSE or lower. The hypothetical kriging resolution for 95%−10% PAC coverage was 1.22 mm. At 2.1% median noise, the PAC sample spacing compared closely to the same 5% quantile of Nyquist pitch, which was 1.33 mm (figure 7(a)–(b)).

The spatial properties of bandpassed μECoG fields from theta to gamma were extremely consistent (note the overlapping sets in figure 7(c)). The Nyquist pitch distributions from theta to gamma (pairwise BC≥ 0.91) had median values highly consistent with the broadband 1.6 mm median. Noise was also similar at 1.4%−2.2% levels, but the actual 10% MSE predictability coverage at 1.52 mm was higher for alpha and beta bands (77.0% and 74.6%, respectively) than for theta and gamma (41.1% and 55.9%, respectively). PAC sample spacing was 0.93–1.18 mm in the theta to gamma bandpasses (figure 7(d)).

The combination of finer spatial scale (median Δ_nyq = 1.24 mm) and higher noise (median 6.3%) in HFB had a significant impact on kriging prediction error. The minimum compensated relMSE was 12.4%, meaning there was no predictability coverage at the 1.52 mm electrode spacing. We projected the 95%−10% PAC to be 502 μm in the HFB bandpass.

3.3.2. Human pSTG and motor cortex

We applied the kriging experiment to μECoG recorded from motor cortex in two human volunteers undergoing surgery for drug resistant epilepsy. The 244-channel electrode was implanted intraoperatively and field potential was recorded outside the seizure onset zone while subjects were anesthetized. Recordings were split into short-time batches (1560 subject A pSTG, 662 subject B motor). Model-based expected error was generally accurate explaining cross-validated kriging error for broadband (b = 1.00 for both subjects) and bandpassed fields (0.95 < b < 1.11 subject A, 0.92 < 1.03 subject B), with a difference in precision as noted in NHP fields (broadband r² = 0.898, bandpass r² = 0.982, combined factors models).

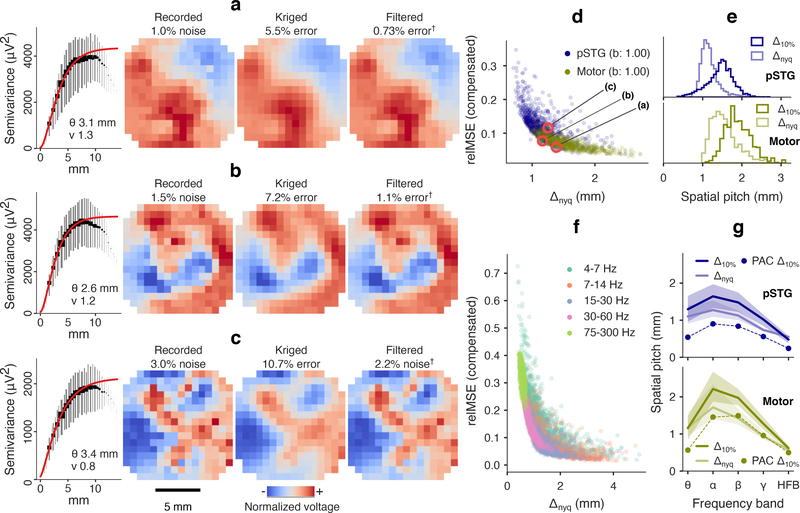
Examples of 4–300 Hz broadband fields from subject B with three different covariance characteristics are shown in figure 8(a)–(c) (and in animated form in supplemental videos S5–S7). The most predictable fields were those with smooth texture and large extents of equal polarity (e.g. figure 8(a)). As indicated by the analytical results, texture strongly affected the error of kriging predictors. Two field batches in figure 8(b)–(c) had dominant spatial cycle limits (Δ_nyq) of 1.16 mm and 1.25 mm, respectively, less than the subsampled pitch of 1.52 mm. However, the smoother texture in figure 8(b) led to recovery at 7.2% MSE, while more granular features in figure 8(c) were considered “not predictable,” at 10.7% MSE. In figure 8(a)–(c), the divergence of the empirical semivariogram from an asymptotic variance at long range is likely due to these points being the least reliable estimates of semivariance [69]. These points were down-weighted in the model fit, as indicated by the visual weight in the figures.

Figure 8.

Kriging results in anesthetized human pSTG and motor cortex. (a) Variography and prediction results for a low resolution/low error motor cortex field. Optimal predictions are also shown (“†” per figure 4). Long range and locally-regular (high smoothness index) patches of similar polarity were accurately predicted 1.52 mm subsampled spacing. Cross-validated kriging relMSE was 6.5% relMSE (1.0% noise and 5.5% kriging error). (b) A shorter range, but smooth field batch was predicted with 8.7% relMSE (1.5% noise and 7.2% kriging error). (c) A rough field batch was predicted at 13.7% relMSE (3.0% noise, 10.7% kriging error), which was above the 10% predictability threshold. The low smoothness index indicated texture detail that was lost to interpolation. (d) Noise-subtracted prediction error for broadband (4–300 Hz) fields was inversely related to spatial scale (Δ_nyq). The three snapshots in (a)-(c) are marked. Expected kriging error explained relMSE error with linear slopes of b = 1.00 (each subject), r² = 0.898 (combined). (e) Central tendencies of kriging resolution (pSTG: 1.48 mm median, motor: 1.87 mm median) exceeded Nyquist pitch (pSTG: 1.13 mm median, motor: 1.50 mm median), but approached similar values at the lower tails. PAC spacing was 829 μm in pSTG and 1.43 mm in motor cortex. (f) Grouped prediction error (relMSE combined subjects) for bandpass fields depended on Nyquist pitch, but tended higher in theta band due to rough texture, and at higher frequencies due to falling SNR. Per band and per subject, expected relMSE regressed actual kriging error with slopes 0.93 < b < 1.11 (combined model r² = 0.982). (g) Nyquist pitch (light lines, median and IQR) underestimated kriging resolution (dark lines) in bands with smoother fields and high SNR. PAC spacing was 240–902 μm in pSTG and 498 μm-1.49 mm in motor cortex.

Broadband motor cortex fields were of similar spatial scale in human (median Δ_nyq = 1.50 mm) as in NHP, while pSTG fields were smaller scale (median Δ_nyq = 1.13 mm). The difference in Nyquist pitch corresponded to 91.8% predictability coverage in motor cortex at the actual 1.52 mm electrode spacing, but only 42.7% predictability coverage in pSTG (figure 8(d)). PAC spacings were 1.43 mm and 829 μm respectively (figure 8(e)).

As a group, bandpassed human μECoG fields were predicted less effectively at smaller length scales (figure 8(e)). There was also greater variability between bands in both brain areas, compared to NHP motor cortex. Median Nyquist pitch peaked in the alpha band (1.27 mm, subj. A, 1.72 mm, subj. B), which may have been influenced by a moderate increase of coherent alpha rhythms in temporal areas during general anesthesia under propofol [70]. Median kriging resolution spacings exceeded the subsampled electrode spacing of 1.52 mm in bands with larger Nyquist pitches and lower noise proportions (figure 8(g). For generally stable prediction, we estimated the PAC spacing in pSTG to be between 902 μm (alpha band) and 240 μm (HFB), and in motor cortex between 1.49 mm (beta band) and 324 μm (HFB). See figure 9 for detailed PAC spacing and noise results. Supplemental videos S8–S13 show recorded, kriged, and filtered human μECoG snapshots for each bandpass.

Figure 9.

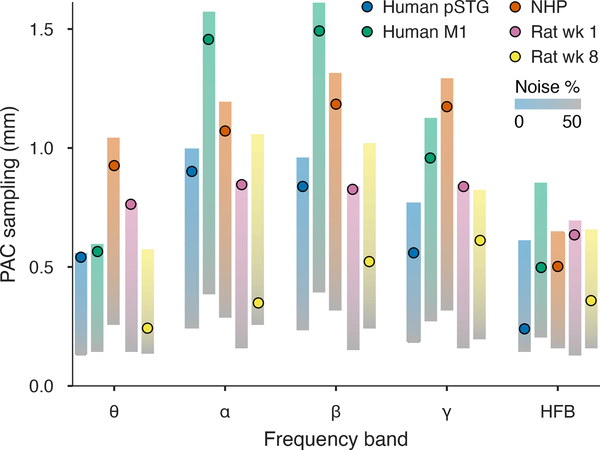
PAC spacing and signal statistics for human, NHP, and chronically implanted rat summarized across temporal bandpasses. PAC spacings per frequency band based on the observed noise conditions (dots) are placed in the context of the sufficient sampling projected for 0–50% noise (vertical gradients). PAC spacing was within 115 μm (mean) of the ideal case for electrodes that were placed per-session (human and NHP) or were recently implanted (rat week 1). Deteriorated SNR conditions at week 8 of implantation (near the peak of electrode impedance) decreased actual PAC sampling by 365 μm (mean) compared to zero noise. At 50% noise (gradient gray levels), all fields required sampling below 375 μm.

3.3.3. Combined effects of spatial scale and noise

To incorporate fields recorded in a chronic implantation setting, we also analyzed spatial field characteristics for a cohort of four rats implanted with the passive electrode array in auditory cortex [55]. We used recordings made in the first week and the eighth week of implantation, at which point the acute tissue response was presumed to have stabilized and electrode impedance was near peak levels.

In figure 9, we summarized the PAC sampling results in rat, NHP, and human in the context of the particular SNR that we observed in those recordings. After manipulating the electrode spacing term for the expected kriging error to find the PAC predictability boundary, we also varied the share of noise in covariance models on the boundary to project PAC spacings for 0–50% noise levels. PAC electrode spacings in the ideal scenario were uniformly submillimeter for HFB fields in all cortical areas and species. Spacings were approximately 1 mm or lower for auditory cortex in rat and pSTG in anesthetized human. Except in HFB and theta bands, motor cortex fields in both NHP and human were projected to be predictable at spacings between ^~1–1.5 mm.

In all cases, the compensatory balance of spatial oversampling in the presence of noise reduced estimation of the 95%−10% PAC spacing. Values for “new” implants (intraoperative human, semi-chronic NHP, and early rat electrodes) were within an average of 115 μm of ideal PAC spacings across bands. However, anesthetized human fields showed notable deviations from ideal PAC spacings at HFB of 371 μm (pSTG) and 354 μm (motor).

In the chronic implant setting, field statistics were relatively stable between week 1 and week 8, with overlap in Nyquist pitch having mean BC=0.90. By week 8, 1/f thermal noise from increased electrode impedance deteriorated signal quality at lower frequencies, raising median noise proportion from 1.2% to 9.2% mean across bands (mean BC=0.11). The signal properties had a significant effect on predictive sampling. At the first week of implantation, very low noise fields could be sampled effectively with 635–846 μm PAC spacing across bands, similar to results in anesthetized auditory cortex during the same acoustic tone stimulation. The PAC kriging resolution for week 8, as a product of SNR and field resolution, was 243–612 μm, which was lower than ideal by 200–700 μm (365 μm mean).

4. Discussion

In the preceding results, we analyzed sufficient spatial sampling of cortical surface potential with the objective of predicting continuous voltage fields with constrained loss of detail. From basic analytical results, we expected that predictability should depend on three independent factors: 1) the natural image statistics of the cortical field potential (the “field”), 2) the precision of measuring those potentials (the “signal”), and 3) the electrode sampling geometry. In particular, this analysis suggested that prediction loss induced by substantial noise or fine feature scale can be corrected with greater sampling density.

We established through covariance modeling and cross-validated predictions that the theoretically expected kriging error accurately explained prediction MSE across a range of field, signal, and electrode spacing conditions. Next, we extrapolated electrode spacings for each short-time batch that would normalize expected kriging error to 10% of the process variance (although a lower tolerance could be used in practice). Based on the distributions of spatial field statistics in a variety of regimes, we proposed electrode spacings that were “probably approximately correct”, i.e. resulting in ≤10% approximation error for ≥95% of the observed fields. The mathematically rigorous PAC learning framework [68] was only loosely adapted here, but the “probable” and “approximate” concepts succinctly described the task of seeking a sufficient sampling density to constrain loss under nonstationary conditions. In an experiment with controlled neural field statistics and electrode geometry, we found that different μECoG sampled at 95%−10% PAC predictability spacings generated approximately equivalent stimulus classification accuracy.

For the fields we observed, PAC sample spacing in ideal (noiseless) conditions was between about 570–1050 μm across bandpasses for rat auditory cortex. NHP and human motor cortex fields in the alpha, beta, and gamma bands could be predictably sampled in the 1–1.5 mm range, while human pSTG fields required sampling at approximately 600–1000 μm. HFB required sampling between 600–850 μm for all cortical areas and species, assuming noiseless conditions, while the 4–7 Hz theta band also required ^~500 μm sampling for human fields and rat fields at week 8, after implants had stabilized. Adjusted to the noise levels we observed, PAC sample spacing was, on average, 115 μm smaller than the ideal case for intraoperative or semi-chronic electrode placements, with the largest deviations occurring in HFB. In the long-term chronic case, increased thermal noise reduced PAC sampling 365 μm on average relative to the noiseless ideal.

Optimal linear combination techniques based on sensor covariance are commonly used for inverse problems in electro- and magnetoencephalography [71, 72, 73], and other spatial filters have been proposed to maximize spatial contrast [74]. To the best of our knowledge, this is the first study to rigorously apply optimal linear prediction methods to interpolate field potential based on spatial statistics. While other interpolation methods may yield a similar quality of predictions, a statistical interpolator forecasts the uncertainty of its prediction, i.e. eq 4. The model-based kriging error was the basis of our determination of sufficient sampling, but it also revealed the denoising benefit of correlated sampling. The kriging error for interpolated fields was often smaller than the estimated noise in the original recording. This result indicated that electrode spacing can be tuned for small approximation errors, even below the sensor noise limit, by sufficient over-sampling of correlated field potential.

We also made use of in situ prediction, as opposed to interpolation, to produce denoised views of neural fields (e.g. figure 8(a)–(c)). Any linear filter (e.g. Gaussian smoothing, spatial averaging, etc.) may enhance SNR in a correlated field with spatially independent noise. Kriging produces the best linear unbiased predictor, optimized conditional on the variance model, which tend to perform well compared to deterministic interpolators such as splines or inverse-weighted prediction [75]. Kriging is also adaptive to the field statistics, which vary in time. A more thorough analysis of denoising performance based on the approximately noise-free rat auditory field recordings is available in the supplemental material (supplemental figures S3 and S4). Since measurement noise may be an unavoidable consequence of electronics miniaturization, intentional spatial over-sampling coupled with spatial filtering is a promising strategy to recover high fidelity neural fields. Curves for hypothetical field coverage vis-a-vis electrode spacing and noise (as in figure 3(a)–(c)) could help guide electrode array design.

Prior investigations of neural signal correlation have made length scale inferences from either the correlogram or its dual, the spatial power spectrum. However, the analyses in these studies were device dependent. Recent results for ECoG in awake humans found electrode spacings at which correlation crossed a threshold of 1/2. One, using a parametric model, revealed length scales in STG ranging from 1.5 mm for gamma and high-gamma to > 4 mm for the lowest theta band [50]. Another, using spectral coherency profiles of microwire ECoG in motor cortex resulted in length scales from 0.8–1 mm at 150 Hz, and rising to 2.13–3.45 mm at low frequencies [49]. Raw correlogram profiles in STG recordings cross the 1/2 threshold between 1–3 mm in descending frequency bands [51]. Using device-independent covariance kernels (not scaled to signal or noise), we observed average half-correlation lengths with a minimum of ^~1.15 mm in the HFB range for both brain areas, and a maximum in the alpha band of ^~3 mm in pSTG and ^~4.25 mm in motor cortex. The discrepancy between motor area findings may partially be due to the lack of distinction between “field” and “signal” in the correlation coefficient and coherency estimators. Spatially independent noise lowers normalized correlation values at all inter-electrode distances. Correlograms from the same neural field, but measured with different noise power, would show threshold crossings at different inter-electrode distances. Another factor in the present results that likely impacted correlation range in alpha and HFB was the state of general anesthesia under propofol [70]. Spatial correlation profiles are also highly variable across time, as observed in [51] and confirmed in this study.

Previous spatial spectra analyses identified effective bandwidths where physiological spectra intersected noise floors, and determined sufficient sampling densities in terms of the bandwidth reciprocal. Our median results for spatial bandwidth resolution were similar to previous findings in human [47] and rat [48]. However, we found that a field’s texture, which had a large impact on predictability, had only a subtle impact on the power spectrum, making bandwidth an unreliable estimator of sufficient sample spacing. In addition, the bandwidth selection methodology in this report eliminated device dependence by discarding the noise floor. Estimating bandwidth based on the intersection of field and noise spectra leads to the counter-intuitive result of decreased bandwidth/increased electrode spacing in low SNR scenarios and increased bandwidth/decreased spacing for higher SNR, when the underlying field spectrum might be equal. Our basic results suggest the opposite result (see figure 3(b)–(c)). The same neural field can be predicted to the same accuracy in low noise using larger electrode spacing, or in high noise with smaller spacing.

The methodology we employed pre-supposed a need for correlated sampling, which is a requirement for spatial prediction. Another functional utility of redundant electrode signals was recently studied through the use of shared trial-to-trial variability in discriminating visual stimuli from V4 activity in NHP. Rather than being a nuisance, shared variability in LFP contributed substantially to decoding accuracy [76]. The logic of avoiding redundancy by setting electrode spacing based on spatial cycle limits was also challenged through a detection theory model that elucidated the impact of redundancy in both event-related signals of interest and background processes. High-density grids have greater detection power for spatially redundant event-related signals buried within a high-amplitude, low-correlation background process, or can conversely pick out spatially focal signals in the presence of highly correlated background activity [77]. The first result is directly analogous to our finding that field potential can be predicted to nominal precision in high noise with sufficiently dense sampling. The second result also relates to the need for dense sampling for highly textured (low smoothness) fields, even if the dominant correlation length scale is long range.

We attempted to adapt to nonstationarities in the field structure and SNR by operating in short-time batches. But there can be little doubt that our analysis smoothed over the most transient neural events such as evoked responses. We observed comparatively low fitness of our spatial prediction framework when kriging evoked response transients directly. Such events may plausibly be described by a the superposition of uncorrelated background and response field process with different spatial covariance kernels, and thus may benefit from a nested variogram model [53].

The present analysis was indifferent to spatio-temporal interactions in the covariance kernel, which were clearly demonstrated empirically in [49] and are also indicated by the cortical traveling wave phenomenon [78]. The framework of spatial prediction can be expanded using appropriate spatio-temporal covariance kernels [79, 80]. It is quite likely that coupled structure in space and time may provide more efficient field potential prediction and reduce the sufficient sampling density indicated in this study.

The 95% “probable” and 10% “approximate” figures were chosen as intuitively grasped quantities for the purpose of exposition. However, in light of the results relating sampling predictability to mutual information with sensory stimulation (figure 6), the 10% error tolerance may be too large for most applications. In fact, tone classification accuracy from the passive arrays continued to improve until the smallest testable electrode spacing (i.e. the fully sampled grid). Expected error for 95% of the observed fields at 420 μm spacing would be 3% or less, and the corresponding 95%−3% PAC sample spacing on the active array would be 69 μm. With these caveats in mind, the PAC sampling densities stated for multiple scenarios might be considered minimum starting points for electrophysiology in practice.

5. Conclusion

The present study attempted to rigorously address the problem of sufficient sampling in μECoG in terms of minimum MSE prediction of field potential. We introduced 1) a set of field covariance estimation techniques that improved upon common methodology in electrophysiology, and 2) a framework that quantified the relationship between prediction efficiency versus electrode spacing over a distribution of covariance and SNR conditions. Our prediction results suggested that sampling based on spatial bandwidth, as suggested in prior literature, can be a good rule of thumb for low frequency field potential and low noise conditions. However, using an single point estimate of bandwidth (i.e. the average) does not expose the full range of field statistics. Additional spatially over-sampling of the bandwidth-based pitch is required for rough textured fields, and can recover bandwidths beyond the noise floor in higher noise settings. We found that natural image statistics and SNR of field potential varied significantly within single recordings. Based on these distributions, we recommended sufficient sampling based on a high probability of low error predictions. These findings suggested that sufficient sample spacing for ≤10% MSE predictability in noiseless conditions ranged from lows of ^~500 μm across species, up to 1.5 mm in low frequency human and NHP motor cortex. Accounting for the most adverse chronic implant noise conditions, sufficient sample spacings were reduced by 200–700 μm. Importantly, the observed prediction errors were matched by the expected error, allowing sufficient sampling inferences to be made based on reasonable parameter assumptions prior to future electrode design.