Quantifying viscosity and surface tension of multicomponent protein-nucleic acid condensates

Abstract

Living cells organize their internal space into dynamic condensates through liquid-liquid phase separation of multivalent proteins in association with cellular nucleic acids. Here, we study how variations in nucleic acid (NA)-to-protein stoichiometry modulate the condensed phase organization and fluid dynamics in a model system of multicomponent heterotypic condensates. Employing a multiparametric approach comprised of video particle tracking microscopy and optical tweezer-induced droplet fusion, we show that the interfacial tension, but not viscosity, of protein-NA condensates is controlled by the NA/protein ratio across the two-phase regime. In parallel, we utilize fluorescence correlation spectroscopy to quantify protein and NA diffusion in the condensed phase. Fluorescence correlation spectroscopy measurements reveal that the diffusion of the component protein and NA within the condensate core is governed by the viscosity, and hence, also remains insensitive to the changes in NA-to-protein stoichiometry. Collectively, our results provide insights into the regulation of multicomponent heterotypic liquid condensates, reflecting how the bulk mixture composition affects their core versus surface organization and dynamical properties.

Significance

A quantitative study of the organization and dynamical properties of biomolecular liquid condensates requires the integration of experimental methodologies from soft matter physics and quantitative optical microscopy. In this letter, we employ a multiparametric approach to quantify viscosity, surface tension, and macromolecular diffusion of multicomponent protein-nucleic acid condensates by combining particle tracking microrheology, optical tweezer-induced droplet fusion, and fluorescence correlation spectroscopy. Our measurements of viscosity, surface tension, and diffusion shed light on the organization of the condensate core, the architecture of the condensate surface, and the protein and nucleic acid diffusion in the dense phase.

Introduction

Ribonucleoprotein (RNP) granules, such as stress granules, P bodies, and nucleoli, are fluid-like subcellular condensates formed through liquid-liquid phase separation of multivalent proteins in association with cellular nucleic acids (1,2). It is now well appreciated that these condensates carry essential intracellular functions as signaling hubs and storage compartments (3,4), and are conserved from bacteria to humans (5, 6, 7). The biophysical properties of cellular protein-nucleic acid (NA) condensates, such as molecular composition, surface tension, viscosity, and macromolecular diffusion, are important determinants of their cellular functions, whereas alterations in the same have been linked to various disease pathologies, such as neurological disorders and certain types of cancer (8, 9, 10, 11). Many of the pathological variants of cellular biomolecular condensates usually display altered condensate network structure and composition, which is believed to cause either a loss-of-function or a gain-in-toxicity phenotype (12, 13, 14).

Although many cellular NA-binding proteins can undergo homotypic condensation, heterotypic interactions with NAs constitute an important mode of regulation in this process (15, 16, 17). Recent evidence suggests several regulatory roles of cellular NAs in the formation of nucleoprotein granules, such as condensate-nucleating scaffolds (18,19), and in the autoregulation of RNP condensation through a reentrant phase transition (20,21). The RNA-mediated reentrant phase transition is marked by condensation and a subsequent decondensation of RNPs in response to increasing the RNA/protein mixing ratio (22). In addition, variations in mixture composition within the two-phase regime can produce distinct morphological transitions, such as the formation of hollow vesicle-like condensates in a binary protein-RNA mixture (23). These observations suggest that heterotypic multicomponent interactions are sensitively dependent on protein-NA stoichiometry, pointing to a nontrivial mechanism of composition-dependent condensation in multicomponent mixtures (24).

In this letter, we probe the effect of mixture composition on the viscosity and surface tension of protein-NA condensates. The polymer network structure within a condensate primarily determines the viscosity of the condensate (25). The viscosity directly influences the rate of molecular exchange within the condensate and is dependent on both the intermolecular interactions and the structural features of the constituting biopolymers (25). Surface tension, on the other hand, determines the shape of the condensate as well as its interactions with solid and liquid interfaces and is dependent on the surface composition and charge. To quantify the viscosity and surface tension of protein-NA condensates, we employ a multiparametric approach by combining video particle tracking (VPT) microscopy and optical tweezer-induced droplet fusion (OTF). As a model system, we utilized in vitro reconstituted condensates formed by a positively charged low-complexity disordered polypeptide containing Arg-Gly repeats ([RGRGG]₅) and a negatively charged homopolymeric single-stranded DNA (dT40). In parallel to determining viscosity and surface tension, we use fluorescence correlation spectroscopy (FCS) to quantify protein and nucleic acid diffusion in these condensates to explore how alterations in mixture composition impact biomolecular diffusion in the dense phase and how molecular diffusion compares with variations in the viscosity of the liquid condensates. Our results suggest that these heterotypic protein-NA condensates assume spatially organized structures in the mesoscale, in which the condensate surface, but not the condensate core, is responsive to alterations in the bulk mixture stoichiometry.

Results and discussion

A multiparametric approach to quantify molecular diffusion within and material properties of biomolecular condensates

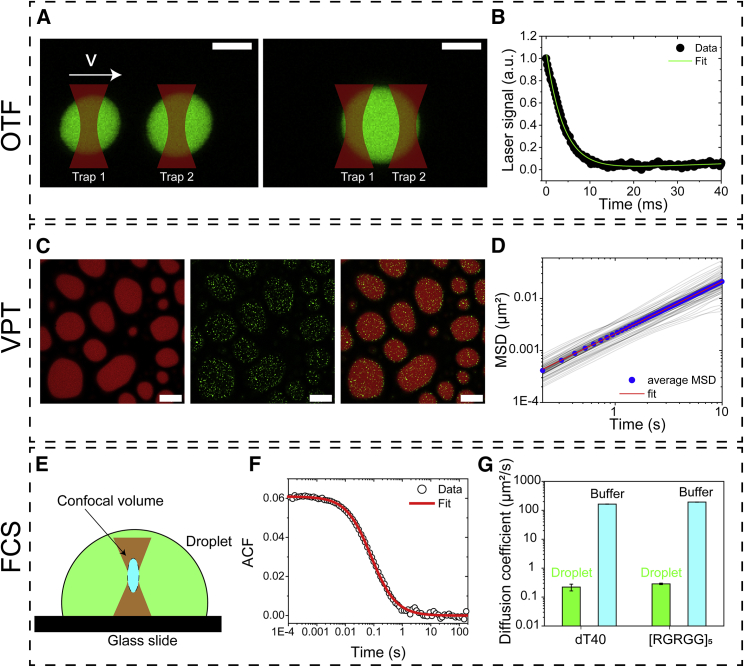
Previously, we and others have demonstrated that OTF of biomolecular condensates provides an improved and sensitive analysis of their fusion speed in vitro (26, 27, 28). Because the droplets are trapped in solution, spurious effects from surface drag force, as in the case of passive droplet fusion, are eliminated (29). In this assay, two condensates are trapped optically using a dual-trap optical tweezer coupled with a confocal fluorescence microscope. The optical trapping of the condensates is facilitated by the refractive index mismatch between the condensate and the coexisting dilute phase. The droplet fusion was initiated by the controlled movement of one droplet at a constant velocity toward another stationary droplet (Fig. 1 A). By analyzing the laser signal relaxation from the optical traps during the droplet fusion event, a fusion relaxation timescale τ is extracted (Fig. 1 B). For droplets displaying Newtonian fluid properties, this relaxation time is proportional to the ratio of the viscosity η over surface tension γ (30) and can be written as

$$\tau /l=\frac{\eta }{\gamma },$$ (1)

where l is the average diameter of the fusing droplets. Measurement of inverse capillary velocity (η/γ) alone does not provide any direct information on the viscosity and/or surface tension of condensates, unless an independent assay is used to measure one of these quantities (30). To this end, we employed VPT microscopy, which enables the determination of the viscosity of the same condensates (31). In brief, yellow-green polystyrene beads (200 nm) with carboxylate-modified surfaces (31,32) were passively embedded into these condensates and their motion was tracked using fluorescence VPT (Fig. 1 C). The polystyrene beads were premixed with the buffering solution before mixing the peptide and DNA to form condensates. By tracking the Brownian motion of a large number of beads inside the dense phase, we extracted their average mean squared displacement (MSD; Fig. 1 D). These MSD plots were used to estimate the diffusion coefficient of polystyrene beads. Subsequently, the condensate viscosity was obtained using the Stokes-Einstein relation (see below). Finally, by combining the measured inverse capillary velocity from the fusion experiments and the measured viscosity from VPT experiments, we used Eq. 1 to obtain the interfacial tension of the condensate.

Figure 1.

A multiparametric approach to quantify material properties of and molecular diffusion within biomolecular condensates. (A) Illustration shows optical tweezer-induced droplet fusion (OTF) assay using a dual-trap optical tweezer and correlative time-lapse imaging of condensates using confocal fluorescence microscopy. (B) A representative force relaxation curve from our OTF assay that is fitted using an appropriate model (see Supporting materials and methods for details) to extract inverse capillary velocity is shown. (C) Illustration is shown of video particle tracking (VPT) microscopy assay that shows fluorescently labeled condensates (red) and 200-nm polystyrene beads (green) within. Scale bars represent 10 μm. (D) MSDs of individual particles (light shade of gray) and the corresponding ensemble-averaged MSD (blue circles), which is fitted (red line) with MSD = 4Dt^α (α = 1 for Brownian particles; D = diffusion coefficients of the beads) are shown. These data were obtained by tracking 200-nm beads in dT40-[RGRGG]₅ condensates prepared at 0.4 [T]/[Arg] ratio. (E) The schematic diagram illustrates the positioning of the confocal volume inside a condensate for fluorescence correlation spectroscopy (FCS) analysis. (F) A typical autocorrelation curve for freely diffusing [RGRGG]₅ molecules (labeled with Alexa 594) within a condensate is shown. (G) A plot summarizing FCS-derived diffusion coefficients of the peptide and DNA molecules in dilute buffer solution and within phase-separated condensates is shown. All error bars represent ± 1 standard deviation.

To quantify the surface tension and viscosity of heterotypic protein-NA condensates, we utilized model condensates formed by a low-complexity Arg-Gly-rich polypeptide [RGRGG]₅ and a homopolymeric single-stranded DNA [dT]₄₀ (dT40). Before OTF and VPT experiments, we confirmed that the [RGRGG]₅-dT40 mixture displayed a reentrant phase behavior by using solution turbidity measurement and fluorescence microscopy with a fixed [RGRGG]₅ concentration (5.0 mg/mL) and variable DNA/peptide mixing ratio. The mixture turbidity displayed a peak around a [T]/[Arg] ratio of 0.4 ([nucleotide]:[Arg]) and considerably decreased beyond a ratio of 1.0, indicating that phase separation is maximal (largest number of interfaces and scattering amplitudes) around a [T]/[Arg] ratio of 0.4 (Fig. S1). This is corroborated by the fact that droplets at [T]/[Arg] ratio of 0.4 are significantly larger, and they cover more surface area on the coverslip (∼45% as judged by fluorescence microscopy) than those prepared at other mixing ratios (Fig. S1). For oppositely charged polymers, it is intuitive to expect that phase separation is maximal at their formal charge-neutral stoichiometry conditions ([T]/[Arg] = 1). However, this prediction may not hold for peptides and NAs because of a combined effect of uneven local charge distributions on the peptide chain (33), charge regulation effects (34,35), and the presence of short-range non-electrostatic interactions (22).

The [RGRGG]₅-dT40 condensates (prepared at a [T]/[Arg] ratio of 0.4) showed rapid fusion upon contact. Using our OTF assay, we measured the inverse capillary velocity of these condensates and found it to be ∼3.4 ± 0.2 ms/μm in a buffer containing 25 mM Tris-HCl, 25 mM NaCl (pH 7.5) (Video S3. OTF video showing that condensates prepared at [T]/[Arg] ratio of 1.6 do not undergo fusion when brought in contact with each other using the optical traps, Video S4. OTF video showing that condensates prepared at [T]/[Arg] ratio of 1.2 undergo rapid fusion when brought in contact with each other using the optical traps, Document S2. Article plus supporting material A). We note that passive fusion experiments on a Tween-coated microscope coverslip yielded a characteristic fusion relaxation time that is more than an order of magnitude higher (∼100 ms/μm), clearly pointing out the dominant effect of surface drag force on coalescence dynamics of these condensates (Fig. S2 B; Videos S1 and S2). Simultaneously, VPT experiments revealed that these [RGRGG]₅-dT40 condensates have a viscosity of ∼6 ± 1 Pa⋅s. We further confirmed that the bead size and concentration had no significant effects on the phase boundaries and the dynamics of these condensates (Fig. S3). Combining the two measurements, we estimate their surface tension to be ∼1.6 ± 0.4 mN/m. Although the viscosity value is qualitatively consistent with previous literature reports on heterotypic condensates formed by disordered protein and RNA mixtures (36), our estimated value of surface tension is higher than previously reported values of the same for biomolecular condensates (29). One reason for the observed difference could be that we are using salt concentrations that are lower than the physiological salt condition. The observed surface tension value, however, is similar to the previously reported values for complex coacervates (37).

Video S2. Passive fusion of two [RGRGG]₅-dT40 condensates residing on a Tween 20-coated microscope glass coverslip

These condensates are from the same sample as Video S1. Scale bar represents 5 μm.

The internal dynamics of protein-NA condensates (i.e., the mobility of individual polypeptide and NA molecules) can be probed using FCS. In contrast to a more traditional approach of fluorescence recovery after photobleaching, which yields diffusivity dynamics that is highly dependent on the choice of model to analyze the experimental data (38), FCS provides a more direct approach (39). Briefly, fluorescence time traces for the fluorescently labeled polypeptide or DNA molecules are recorded from a small confocal volume near the center of the condensates (Fig. 1 E). Signal fluctuations due to the diffusion of fluorescent molecules through the confocal volume are analyzed by means of calculating the autocorrelation function (Fig. 1 F). The characteristic decay time of the resulting autocorrelation curve provides direct information on their hydrodynamic properties (Fig. 1 F). Therefore, the knowledge of the confocal volume size and shape enables the determination of the diffusion coefficient D of a given fluorescent species. Because condensates are expected to have a higher index of refraction than water (as indicated by the feasibility of optical trapping), one key technical consideration is the sensitivity of confocal FCS to the refractive index mismatch between the solution under investigation and the immersion water. Previously, Sherman et al. characterized such an effect and observed that confocal FCS can be reliably used to accurately estimate diffusion coefficients of proteins and small molecules in solutions with refractive indices ranging from 1.33 to 1.46 (40). Consistent with their report, our FCS measurements provided a reliable determination of diffusion coefficients of particles in solvent media with refractive indices ranging from 1.33 to 1.41 (Fig. S4). In brief, we determined the diffusion coefficient of 20-nm fluorescent beads in 0–60% glycerol-water mixtures using FCS and estimated the viscosity of the medium utilizing the Stokes-Einstein relation: D = k_BT/6πηR_h (D = diffusion coefficient, k_B = Boltzmann constant, η = viscosity of the medium, R_h = hydrodynamic radius of the probe molecule). Our estimated values of solvent viscosity matched closely with the known values of solvent viscosity for various glycerol-water mixtures (Fig. S4).

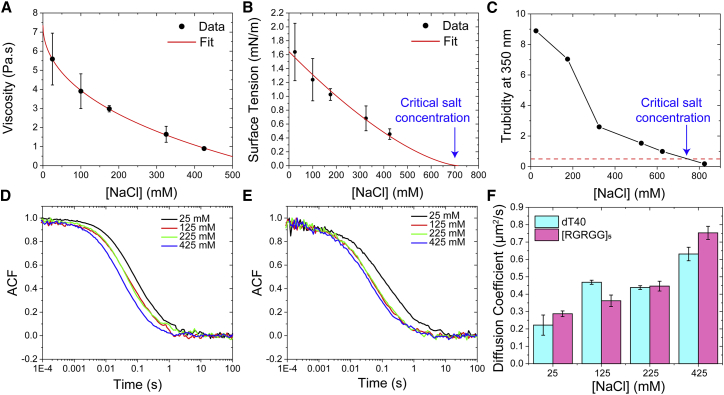
Using FCS, we obtained diffusion coefficients of [RGRGG]₅ polypeptide and dT40 DNA in the dense phase (condensates prepared at a [T]/[Arg] ratio of 0.4 in a buffer containing 25 mM Tris-HCl, 25 mM NaCl (pH 7.5)), which are ∼0.3–0.4 μm²/s. These values are ∼3 orders-of-magnitude lower than those for these molecules in the dilute buffer solution (Fig. 1 G). Next, to further validate our multiparametric approach, we performed the MSD analysis and droplet fusion experiments using condensates prepared at a fixed [T]/[Arg] ratio of 0.4 with varying NaCl concentrations. In parallel, we determined the diffusion coefficients of RGRGG-repeat polypeptide and dT40 molecules in the dense phase as a function of salt concentration using FCS. Increasing [NaCl] is expected to weaken the ionic attractions between [RGRGG]₅ and dT40 chains by decreasing the Debye length (41). Therefore, it is expected that the intermolecular network of these condensates would also weaken with increasing salt if ionic interactions contribute to the stability of these condensates (42). Indeed, we observed that the viscosity of [RGRGG]₅-dT40 condensates decreases from ∼6 Pa⋅s at 25 mM NaCl to ∼0.89 Pa⋅s at 425 mM NaCl (Fig. 2 A). Furthermore, our experimental results are consistent with previous reports that predicted a stretched exponential dependence of the viscosity of complex coacervates ($\eta \propto \text{exp}(-\sqrt{{\text{C}}_{salt}})$ on the salt concentration (43,44). The interfacial tension of [RGRGG]₅-dT40 condensates also decreases with increasing salt concentration (Fig. 2 B). These findings are in good agreement with previous experimental and theoretical reports on salt-mediated variations of viscosity and interfacial tensions of complex coacervates (37). We observed that the surface tension of peptide-DNA condensates approximately follows a well-known mean-field critical scaling (37): γ ∝ (C_salt − C_crit)^3/2 with an estimated critical salt concentration C_crit of 710 ± 50 mM (Fig. 2 B). To confirm the accuracy of the measured surface tension values, we next measured the turbidity of [RGRGG]₅-dT40 mixtures at variable salt concentrations and complemented these measurements with optical microscopy. Indeed, we observed that the phase separation of [RGRGG]₅-dT40 mixture vanishes at ∼700 mM salt concentration (Figs. 2 C and Document S1. Supporting materials and methods and Figs. S1–S13, Video S1. Passive fusion of two [RGRGG]5-dT40 condensates residing on a Tween 20-coated microscope glass coverslip These condensates are prepared at an [T]/[Arg] ratio of 0.4. Scale bar represents 5 μm. B), which is consistent with our power law fit to the interfacial tension data. In addition, in qualitative agreement with the VPT-derived viscosity data, we observed that both peptide and single-stranded DNA (ssDNA) diffusion coefficients increase ∼3-fold in response to an increase in the salt concentration from 25 mM NaCl to 425 mM NaCl (Fig. 2, D–F). These results suggest that the diffusivity dynamics of component molecules is correlated with the viscosity of the dense phase. This correlation is qualitatively consistent with the Stokes-Einstein relation, which implies that the product Dη is a constant at a fixed temperature and particle size. However, the peptide and ssDNA molecules are likely to undergo diffusion as complexes and not as free chains in the dense phase. The size distribution of these complexes may be sensitive to the ionic strength of the buffer, which may explain the observed discrepancy in the viscosity scaling with salt from our VPT assay (six-fold change) and the diffusion scaling with salt from the FCS experiments (three-fold change).

Figure 2.

Quantification of viscosity, surface tension, and biomolecular diffusion in [RGRGG]₅-dT40 condensates. (A) Variation of the condensate viscosity as a function of increasing [NaCl] is shown. The black points are the data and the red line is a fit using a stretched exponential function. The corresponding MSD plots are shown in Fig. S6. (B) Variation of the condensate surface tension as a function of increasing [NaCl] is shown. The black points are the data and the red line is a fit to a power law with exponent 3/2. The corresponding scaled relaxation times are shown in Fig. S7. The predicted critical value of [NaCl] is shown by a blue arrow. (C) Experimental determination of the critical [NaCl] for the same condensates as in (B) using the solution turbidity assay is shown. (D and E) Fluorescence autocorrelation curves are shown for the peptide and ssDNA chains at variable ionic strengths of the buffer, respectively (also see Fig. S5). (F) A plot summarizing FCS-derived diffusion coefficients of [RGRGG]₅ and dT40 as a function of [NaCl] within the dense phase is given. All error bars represent ± 1 standard deviation.

Effect of mixture stoichiometry on viscosity, biomolecular diffusion, and surface tension of [RGRGG]₅-ssDNA condensates

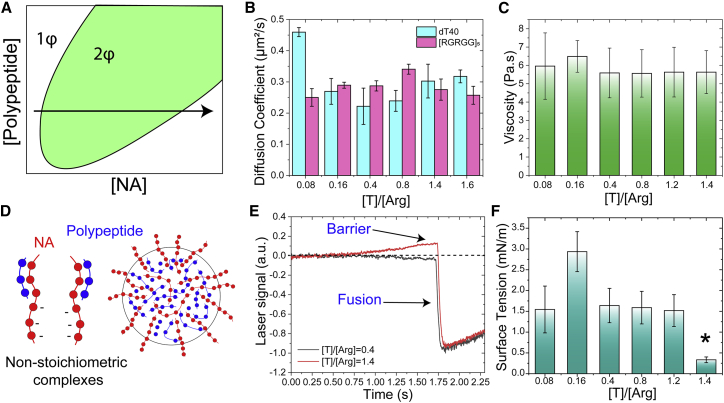
Reentrant phase transition is a result of a delicate interplay between attractive and repulsive forces that are sensitively dependent on the relative stoichiometry of protein and NA chains (Fig. 3 A; (22,45)). To probe how these multicomponent condensates are impacted by the changes in NA-to-protein mixture stoichiometry, we first measured the diffusivity dynamics of component molecules within the condensate using FCS. Remarkably, we found that the diffusion coefficients of the RGRGG-repeat polypeptide and dT40 DNA remained unaltered as we varied the nucleotide/Arg ratio from 0.08 to 1.6 in the bulk (Fig. 3 B). These data imply that the dynamics of the condensate core is not substantially impacted by the variations in bulk mixture composition. To complement these FCS-based diffusion measurements, we next estimated condensate viscosity using our VPT assay and observed an almost constant value within the same window of mixture composition (Fig. 3 C). Combining these two results, we observed that the product Dη stays almost unchanged across this entire range of mixing ratios. Considering that we have varied the mixture composition over more than one order of magnitude, our viscosity and diffusion measurements suggest that the core dynamics of [RGRGG]₅-ssDNA condensates is insensitive to variation in mixture composition.

Figure 3.

The role of mixture composition on the dynamical and surface properties of [RGRGG]₅-dT40 condensates. (A) Schematic of a reentrant phase diagram shows the formation and dissolution of heterotypic multicomponent condensates as the concentration of one component (nucleic acid) is continuously varied (horizontal black arrow), whereas the concentration of the other component (polypeptide) stays constant. (B) A plot summarizing FCS-derived diffusion coefficients of [RGRGG]₅ and dT40 in the dense phase as a function of DNA/peptide ratio. The corresponding autocorrelation plots are shown in Fig. S8. (C) Variation in condensate viscosity as a function of DNA/peptide ratio is shown. The corresponding MSD plots are shown in Fig. S9. (D) A schematic depiction is shown of nonstoichiometric partially charged peptide-NA complexes and their condensates with the surface decorated by the partially-complexed charged species. (E) Evidence of a kinetic barrier in the force relaxation curve (red) from the condensate fusion experiments for condensates formed at excess dT40 conditions (also see Video S4) is shown. Such a kinetic barrier was absent for nearly charged-matched condensates (black curve). (F) Variation of condensate surface tension as a function of DNA/peptide ratio is shown. The corresponding scaled relaxation times are shown in Fig. S10. The asterisk for the sample prepared at [T]/[Arg] ratio of 1.4 indicates the existence of a kinetic barrier of droplet coalescence. All error bars represent ± 1 standard deviation.

How do the surface properties of polypeptide-NA condensates vary with bulk mixture composition? Previously, we have shown that at mixture compositions far from the charged-matched stoichiometric conditions, partially condensed “tadpole-like” complexes are formed (23). These partially screened complexes are expected to have larger solvation volume and may prefer to occupy the surface of the condensates, where solvent exposure is warranted (Fig. 3 D; (46)). This phenomenon is expected to lower the interfacial tension of the condensate because of a surfactant-like action of the partially-screened tadpole-like complexes (Fig. 3 D). This model of reentrant condensation, originally proposed by Shklovskii and Zhang (47), therefore suggests that the condensates’ surface architecture is sensitively dependent on the mixture stoichiometry. Indeed, electrophoretic light scattering measurements previously revealed that these heterotypic condensates undergo a charge inversion as the NA/protein ratio increases in the bulk (22). These observations led us to hypothesize that the colloidal stability of the dispersed protein-NA droplets against coalescence increases far from stoichiometric conditions. To test this idea, we measured the surface tension of [RGRGG]₅-dT40 condensates at nucleotide/Arg ratios ranging from 0.08 to 1.4. We observed that unlike condensates formed at a low NA/protein ratio, condensates with excess dT40 ([T]:[Arg] = 1.4) resisted coalescence (Fig. 3 E) and showed a clear barrier in the laser signal preceding their coalescence, which is indicative of a repulsive force (48). These data are consistent with the aforementioned argument that the surfaces of protein-NA condensates are altered with mixture composition and that the surface tension is substantially lowered for condensates prepared at excess NA. Indeed, we observed that these condensates have ∼4-fold-lower interfacial tension as compared with condensates formed at ([T]:[Arg] = 0.4, Fig. 3 F). The observed barrier in the force relaxation curve during droplet coalescence at the single condensate level indicates that the condensate surface carries a net negative charge, which is consistent with the previously reported ensemble electrophoretic mobility measurements of peptide-RNA condensates prepared at a high RNA concentration (22). Additionally, increasing the nucleotide/Arg ratio to 1.6 ([T]:[Arg] = 1.6) resulted in condensates that did not undergo fusion, even under our optical traps (Video S3; also see Video S4).

Video S3. OTF video showing that condensates prepared at [T]/[Arg] ratio of 1.6 do not undergo fusion when brought in contact with each other using the optical traps

Scale bar represents 5 μm.

Video S4. OTF video showing that condensates prepared at [T]/[Arg] ratio of 1.2 undergo rapid fusion when brought in contact with each other using the optical traps

Scale bar represents 5 μm.

Because the polypeptide/DNA diffusion coefficient at the core of these condensates and the measured viscosity values remain unaltered for condensates prepared at an NA/peptide ratio of 1.4 as compared with the condensates formed at lower ssDNA, we conclude that the observed kinetic barrier in droplet coalescence at a relatively high NA concentration is not due to the increased viscosity but due to the decreased surface tension of [RGRGG]₅-dT40 condensates (Fig. 3, E and F; Videos S3 and S4). Taken together, our results suggest that a reentrant transition accompanies a nonmonotonic variation in the surface architecture of protein-NA condensates without being accompanied by drastic changes in the dynamical properties of the condensate core.

Conclusions

RNP LLPS in cell cytoplasm/nucleoplasm sensitively depends on the RNA/RNP ratio, giving rise to a rich nonmonotonic phase behavior that is best understood using the framework of reentrant phase transition (20,45) and is marked by a phase separation event at low RNA-to-RNP stoichiometry and the emergence of a homogenous single-phase at a high RNA/RNP ratio. The data reported here suggest that the composition of multicomponent heterotypic condensates plays a fundamental role not only in the formation and dissolution of these condensates but also in controlling their mesoscale structure. By quantifying the viscosity and surface tension of peptide-NA condensates, we find that the surfaces of these condensates are dependent on the bulk mixture composition, whereas the dynamical properties of the condensate core remain relatively independent thereof. The tunability in the surface properties of multicomponent heterotypic condensates provide a potential regulatory mechanism of condensate interactions with their surroundings and with each other in the subcellular space.

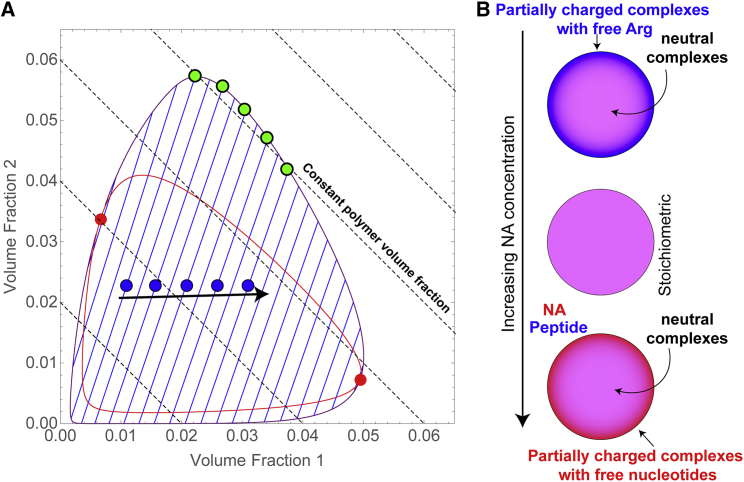
To construct a thermodynamic basis for our observation, we computed a phase diagram along with the equilibrium tie lines (that connect the dilute phase composition with that of the dense phase) for a multicomponent mixture with the use of a Flory-Huggins-type model (see Supporting materials and methods for further details) (24,45). From this model phase diagram (Fig. 4 A), which reveals a closed loop with two critical points, we see that as we increase the component 2 concentration at a fixed concentration of component 1, the total polymer concentrations in the dense phase do not change significantly if the upper end of the tie line closely follows a constant volume fraction line (Fig. 4 A). In such a case, the density and hence the viscosity of the condensates is expected to be insensitive to the variation in the bulk mixture composition. Therefore, our observation that the viscosity of the dense phase remains unaltered at varied mixture compositions is likely a manifestation of a near-constant total concentration of the peptide and ssDNA in the dense phase (Fig. 4 A), which is ultimately governed by the orientation of the equilibrium tie lines and regulated by the relative magnitudes of respective homotypic and heterotypic interactions in a multicomponent mixture (Fig. S13). We note that, although the scaling of viscosity with polymer volume fraction is still a subject of research in polymer dynamics, the proposition that variable volume fraction implies variable viscosity is well established (25). Surface tension, on the other hand, is determined by the proximity of the system to the nearest of the two critical points and also by the surface charge of the peptide-NA condensates. The accumulation of partially-charged complexes on the condensate surface becomes more significant as one moves further from the stoichiometric mixture composition (23). This scenario leads to the spatially organized core-shell structure of multicomponent protein-NA condensates that phase separate via heterotypic interactions (Fig. 4 B). Future studies can refine this thermodynamic model by measuring and modeling homotypic and heterotypic interactions in a multicomponent mixture. Finally, the application of frequency-dependent rheological measurements (42,49) will be valuable for probing the network structure of multicomponent biomolecular condensates and quantifying their viscous and elastic responses as a function of polypeptide/NA sequence composition and patterning. Such studies are currently underway.

Figure 4.

Proposed model of multicomponent phase separation and the formation of spatially organized condensates. (A) A closed-loop phase diagram computed using a Flory-Huggins-type free energy model, as described in the Supporting materials and methods. Spinodal curve and critical points are red, coexistence curve is purple and tie lines are blue. Dashed lines show constant solute volume fractions. The solid arrow indicates increasing the volume fraction of one component in the bulk while keeping the other component fixed (blue circles represent the bulk concentration of components). This results in changes in total polymer volume fraction in the dense phase in a very narrow range (green circles), as governed by the orientation of the tie lines. (B) A scheme showing that the surface of heterotypic protein-nucleic acid condensates is sensitively dependent on the bulk mixture composition, giving rise to tunable spatially-organized condensates that have low interfacial tensions at nonstoichiometric mixture compositions.

Author contributions

P.R.B. and I.A. conceived the idea and designed the experiments. I.A. performed the experiments and analyzed the data with help from P.R.B. G.M.T. performed the numerical simulations and calculated the theoretical phase diagram. All authors contributed to writing the manuscript.

Editor: Jason Kahn.

Supporting citations

References (50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64) appear in the Supporting materials and methods.