Sequence effects on internal structure of droplets of associative polymers

Abstract

Intrinsically disordered proteins (IDPs) can form liquid-like membraneless organelles, gels, and fibers in cells and in vitro. In this study, we propose a simple model of IDPs as associative polymers in poor solvent and explore the formation of transient liquid droplets and their transformation into solid-like aggregates. We use Langevin dynamics simulations of short polymers with two stickers placed symmetrically along their contour to study the effect of the primary sequence of these polymers on their organization inside condensed droplets. We observe that the shape, size, and number of sticker clusters inside the droplet change from a long cylindrical fiber to many compact clusters as one varies the location of stickers along the chain contour. Aging caused by the conversion of intramoleclular to intermolecular associations is observed in droplets of telechelic polymers but not for other sequences of associating polymers. The relevance of our results to condensates of IDPs is discussed.

Significance

Intrinsically disordered proteins (IDPs) are important ingredients of most biomolecular condensates in cells. The formation of these condensates is governed by liquid-liquid phase separation, in which IDPs condense into liquid droplets. Recent studies show that condensed liquid droplets of many IDPs, such as τ-proteins and nucleoporins, become solid-like aggregates (fibers and gels) after a long incubation time. Here, we model IDPs as associative polymers and explore the dependence of internal morphology of condensates on the primary structure of IDPs. Our model captures the phenomenon of aging in droplets of associative polymers.

Introduction

Membraneless subcellular compartments, such as P granules, nucleoli, cajal bodies, etc., perform specialized biochemical roles inside cells (1,2). The formation of these biomolecular condensates is governed by liquid-liquid phase separation, in which biopolymers such as proteins and nucleic acids condense into liquid droplets (3, 4, 5, 6). This phase separation depends on various factors, such as polymer-polymer, polymer-solvent, and solvent-solvent interactions, concentration of polymers in solvent, and environmental conditions such as temperature, pH, etc. A significant fraction of all proteins in a cell are flexible proteins that do not adopt a well-defined three-dimensional structure and are known as intrinsically disordered proteins (IDPs) (7). Studies have revealed that IDPs are important ingredients of most biomolecular condensates in cells (8, 9, 10). A characteristic feature of IDPs is that their backbone contains short sequences of hydrophobic amino acids that are strung together by flexible linkers that consist of hydrophilic amino acids (11). These hydrophobic segments facilitate phase separation and gelation of IDPs in solution and give rise to a variety of self-assembled structures, such as micelles (12).

Because of the presence of strongly associating sequences, IDPs can be considered as biological equivalents of associative polymers that contain segments or blocks of monomers known as stickers that promote aggregation of these polymers in selective solvents (13,14). Associative polymers undergo gelation by forming system-spanning polymer networks connected by physical cross-links between stickers at a sufficiently high concentration (15, 16, 17, 18, 19) and flowerlike micelles at a low concentration (20). One example of such associative polymers is telechelic polymers, which contain stickers at the two ends of the polymer chain. In aqueous solution, telechelic polymers with hydrophobic stickers form flowerlike micelles that are connected (bridged) by other telechelic polymers with two ends in two different micelles (21,22). Upon their formation, gels made of associative polymers cross-linked by clusters of stickers show aging behavior as they relax toward equilibrium (23, 24, 25), which is due to slow structural reorganization produced by interconversion of intermolecular and intramolecular associations between stickers (22).

If the average interpolymer attraction exceeds solvent-solvent and polymer-solvent interactions (poor solvent conditions), a solution of these associative polymers or IDPs undergoes phase separation into a polymer-rich phase that coexists with a dilute polymer solution (14,26). If the average polymer concentration is sufficiently small, the process will take place via formation of droplets of the polymer-rich minority phase that will grow by polymer exchange and by coalescence of droplets (27,28). Although this process has much in common with phase separation of homogeneous (i.e., made of identical monomers) polymers, the presence of strong associations between the stickers raises interesting questions about the internal morphology of these droplets. In particular, what are the sizes and the shapes of the clusters of stickers inside the droplets, and how is the connection between the internal morphology of the droplets and the sequence (primary structure) of the associative polymers or IDPs established? What is the kinetics of the droplet formation, and what is the temporal evolution of its internal structure? What happens on the molecular level, i.e., how does the balance between interchain and intrachain associations change with time after the onset of phase separation? Some of these issues were recently explored using computer simulations of a model very similar to ours (29).

To address these questions, in Methods, we introduce a simple model of associating polymers having two stickers symmetrically positioned along their contour. In Results, we use Langevin dynamics to simulate the relaxation of the dilute-associating polymer solution to equilibrium after a fast quench to poor solvent conditions. In experiments, such fast quench is attained by a change of temperature (23) or pH (30) or by rapid mixing in a microfluidic device (31). We study the evolution of internal structure of droplets (morphology of clusters of stickers) and the kinetics of interconversion between intramolecular and intermolecular associations for different sequences of our model polymers. In Discussion, we summarize our results on the polymer sequence dependence of the internal morphology and on the observed aging phenomena and discuss possible ramifications for experiments. Although this model is clearly an idealization and does not attempt to represent concrete experimental systems, it captures several important features of phase separation in solutions of IDPs, such as formation of dense droplets under poor solvent conditions, their internal structure (gel-like and fibrous aggregates), and change of conformation of IDPs during this phase transition.

Methods

We have performed implicit solvent simulations of a solution of M polymers of N = 10 monomers (beads) each. Beads interact with each other via Lennard-Jones (LJ) potential given by

$$U_{ij}^{LJ}\left(r\right)=4{\epsilon }_{ij}\left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right],$$ (1)

where ε_ij is the interaction strength between i^th and j^th beads, r is the distance between two beads, and σ determines the diameter of the beads. Equation 1 is truncated and shifted to 0 at cutoff distance $r_{ij}^{cut}$ such that

$$U_{ij}^{LJ}\left(r\right)=\{\begin{array}{cc}{U}_{ij}^{LJ}\left(r\right)-U_{ij}^{LJ}\left(r_{ij}^{cut}\right)& r\le r_{ij}^{cut}\\ 0& r>r_{ij}^{cut}\end{array}.$$ (2)

Each polymer contains two types of beads designated as stickers and nonstickers, respectively, such that ε_ij = ε_s if i^th and j^th beads are stickers and ε_ij = ε_ns if at least one of those beads is a nonsticker. Neighboring beads along the backbone of the chain interact via finitely extensible nonlinear elastic potential given by

$$U^{FENE}=-0.5K{R}_0^{2}ln\left[1-{\left(\frac{r}{R_0}\right)}^2\right],$$ (3)

where we take K = 30.0 and R₀ = 1.5. We use Large-scale Atomic/Molecular Massively Parallel Simulator (32) to carry out Langevin dynamics simulations in the NVT ensemble. The simulation is performed in a box of size 61 × 61 × 61 in units of σ, using periodic boundary conditions. The motion of each bead is given by the Langevin equation, neglecting hydrodynamic interactions:

$$m{\ddot{\mathbf{r}}}_i\left(t\right)=-\frac{\partial U}{\partial {\mathbf{r}}_i}-\zeta {\dot{\mathbf{r}}}_i\left(t\right)+{\eta }_i\left(t\right),$$ (4)

where U (sum over all U_ij), ζ, and η_i are the total potential energy, bead friction coefficient, and random thermal force because of the implicit solvent, respectively. The rms amplitude of the random noise is proportional to (ζk_BT/Δt)^1/2, where k_B, T, and Δt are Boltzmann’s constant, temperature, and integration time step, respectively. In the following, all the timescales are expressed in LJ time units τ_LJ = (mσ²/ε)^1/2 (mass m, particle diameter σ, interaction parameter ɛ, k_B, and temperature T are all set to 1). We set the integration time step to be Δt = 0.005 and friction coefficient ζ = 0.02. Each polymer contains two stickers symmetrically placed along its contour (see Fig. 1). To obtain an initially uniform polymer solution, we placed all the polymers in an array inside the simulation box and equilibrated the system under good solvent conditions. We then changed the interaction parameters to poor solvent conditions and continued to monitor the system through the processes of droplet formation and aging.

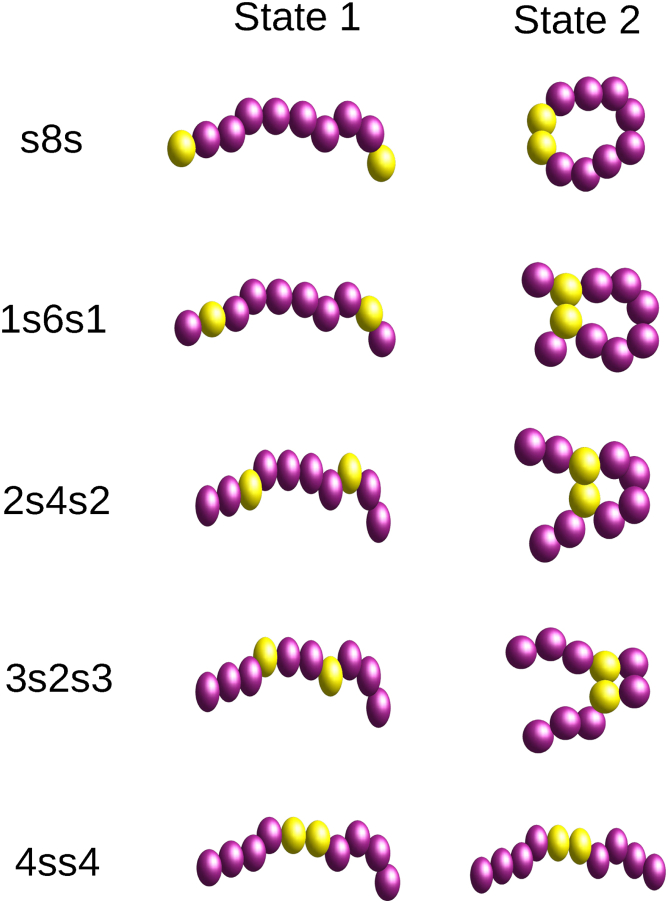
Figure 1.

Open and bound states of five different sequences of the N = 10 bead polymer, with two stickers symmetrically positioned along its contour. To see this figure in color, go online.

Results

We begin each simulation with dilute solution of M = 512 polymers in good solvent. The polymer volume fraction, ϕ = 0.011, is chosen to be below the overlap volume fraction ϕ^∗ ≈ 0.27, defined as the volume fraction of a single polymer in its pervaded volume. To ensure good solvent conditions in the state of preparation, we take ε_s = ε_ns = 0.8 with cutoff distance $r_{ij}^{cut}$ = 2^1/6σ, corresponding to purely repulsive interactions between all beads. Simulations are then performed starting with random initial configuration obtained by equilibrating the system under good solvent conditions.

We first examined the formation of a polymer droplet under poor solvent conditions assuming the same LJ interaction between all beads, ε_s = ε_ns, and carried out simulation for three different values, ε_s = ε_ns =1.0, 0.8, and 0.5. The potential is cut off at $r_{ij}^{cut}$ = 2.5σ, which corresponds to both short-range repulsion and long-range attraction between the beads. We observed that phase separation between polymers and solvent occurs and a spherical polymer droplet condenses out of solution for interaction parameter values 0.8 and 1.0 and not for 0.5 (see Figs. S1 and S2). In all the following simulations, we used the lower value of interaction strength between nonstickers for which phase separation takes place (in the ε_s = ε_ns case), i.e., ε_ns = 0.8.

Because our aim is to study the effect of primary sequence of associative polymers on their organization inside condensed droplets, we model each polymer as a chain of eight weakly attractive beads and two strongly attractive stickers and vary the location of the stickers along its contour. The five different symmetric sequences of such a polymer, shown in Fig. 1, range from the s8s sequence, which has two stickers at the ends and eight nonsticker beads in between (a telechelic polymer) to the 4ss4 sequence in which the two stickers at the center of the chain are flanked by four bead long tails. Here, s denotes a sticker, and the number specifies the length of a sequence of nonsticker beads. The two possible states of the polymers are depicted in Fig. 1, in which states 1 and 2 represent open and closed loop chain configurations, respectively. As shown in this figure, four of these sequences (s8s, 1s6s1, 2s4s2, and 3s2s3) can form loops because of the intramolecular bonds between the stickers, whereas the fifth one (4ss4) cannot.

We proceed to examine droplet formation in these associating polymer systems. After preparing a random initial state in good solvent, we increased the interaction parameter between the two stickers by a factor of five to ε_s = 4.0. The interaction parameter between the nonsticker beads and that between stickers and nonstickers remained ε_ns = 0.8, but all the cutoff distances were increased to $r_{ij}^{cut}$ = 2.5σ to include the attractive part of the LJ potential. The choice of ε_s-value that is five times larger than that of ε_ns was mainly dictated by our previous study of aging effects in thermoreversible gels of associating polymers (22) (we will show that the other choices of ε_s yield qualitatively similar results in the following). We monitored the evolution of the five systems corresponding to the different sequences shown in Fig. 1. Snapshots of one such system (the s8s sequence) from the state of preparation at t = 0 till t = 25,000 (in units of LJ time, τ_LJ) are shown in Fig. 2. Growth occurs by the coalescence of small droplets that are formed by aggregation of neighboring polymers immediately upon quenching the system to poor solvent conditions. This process continues until a single large droplet remains. All other sequences undergo a similar evolution process of droplet formation and growth through coalescence.

Figure 2.

Snapshots of the time evolution from the state of preparation till the formation of a single large droplet in the s8s system (ε_s = 4). Stickers and nonstickers are represented by yellow and purple spheres, respectively. To see this figure in color, go online.

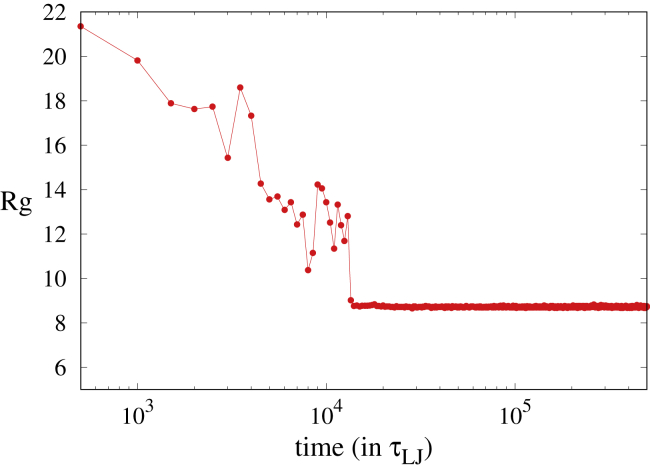
To characterize the formation of a single condensed polymer droplet from the randomly distributed polymers inside the simulation box, we monitored the radius of gyration of all the monomers in the system. We defined this radius of gyration as $R_g=\sum _{\left(i,j\right)}{\left({\mathbf{r}}_{\mathbf{i}}-{\mathbf{r}}_{\mathbf{j}}\right)}^2/2N^2$, where r_i is the position vector of the i^th monomer. Recall that the system contains 10M monomers, in which M is the number of polymers in the system. Fig. 3 shows the R_g vs. t plot for the s8s sequence. Initially, all the polymers are uniformly distributed in the entire simulation box, which gives a large value of R_g, but as time progresses, R_g decreases and eventually saturates at a plateau value that corresponds to the formation of a single large droplet that contains all the polymers in the system. The decrease in the R_g-value is nonmonotonic with time as the system evolves. This happens because of the presence of many droplets during intermediate times (see snapshots at t = 500 and t = 5000 in Fig. 2). The continuous random motion of these droplets leads to fluctuations of interdroplet distances and to nonmonotonic dependence of R_g on time before it saturates, as shown in Fig. 3. Similar time evolution is observed in all other systems with different polymer sequences, and in all cases, the time it takes a single droplet to form is below 20,000 (see Fig. S3).

Figure 3.

Plot of time evolution of the radius of gyration (R_g) of all monomers in the system for the s8s sequence (ε_s = 4). To see this figure in color, go online.

Having explored the dynamics of droplet formation, we proceed to study its internal structure to characterize the clustering of stickers and the competition between intra- and intermolecular associations of the polymers inside the droplets. To this end, droplets formed at some time ≤20,000 were further evolved till t = 300,000 (till t = 500,000 for the s8s system) to ensure equilibration. Clusters with very different structures were observed for different sequences (see Fig. 4). Clusters of stickers were defined operationally as follows: a sticker is assumed to belong to a cluster if it is found within a range of 1.5σ from any other sticker that belongs to this cluster.

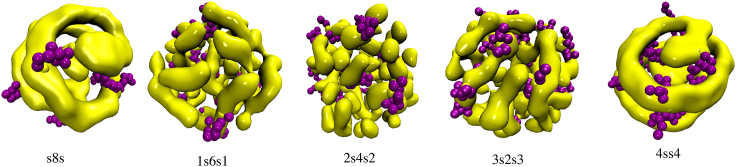
Figure 4.

Morphology of structures formed by stickers inside the droplet at t = 300,000 (shown in yellow). The nonsticker beads of several polymers are shown as purple spheres (ε_s = 4). To see this figure in color, go online.

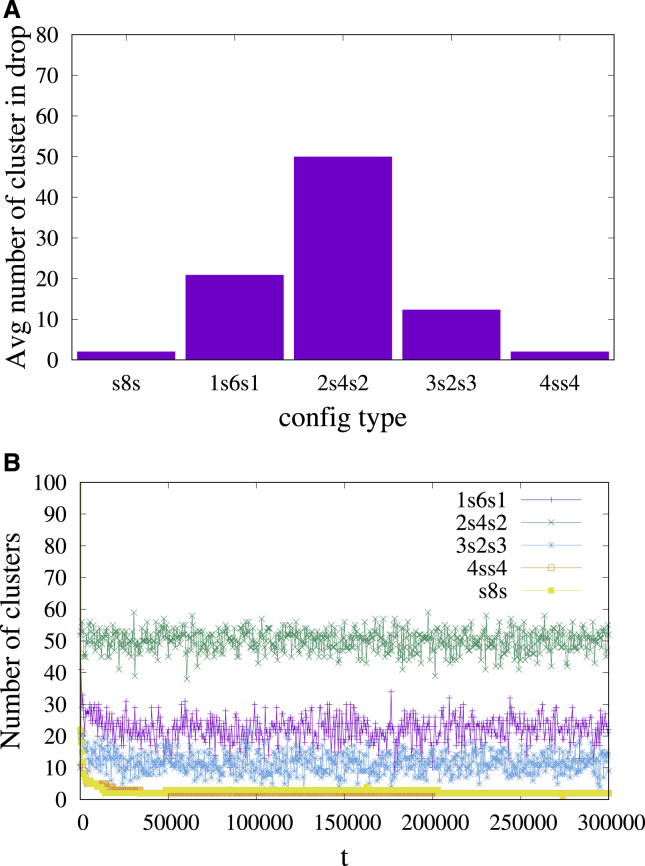
Inspection of the s8s droplet shows that almost all stickers belong to a single cluster that has the shape of a long cylindrical fiber that forms a spiral inside the droplet. A more thorough examination revealed the presence of another (smaller) compact cluster at the center of the droplet. A similar spiral fiber formed by the stickers is observed in the 4ss4 droplet. In the other three cases corresponding to 1s6s1, 2s4s2, and 3s2s3 sequences, many small elongated clusters, whose size and number depends on the sequence, are present in the equilibrium droplet (see Fig. 4). For example, the 2s4s2 sequence has smaller and more numerous clusters compared with sequences 1s6s1 and 3s2s3. Fig. 5 A shows a histogram of the time average number of clusters in a droplet for the five different sequences at time t = 300,000 (single stickers were excluded from the count). The time average was computed by recording the number of clusters after each time interval Δt = 500 between t = 300,000 − 20Δt and t = 300,000 and computing the average of these numbers. Fig. 5 B shows the number of clusters as a function of time for all sequences. The large fluctuations in the total number of stickers for 1s6s1, 2s4s2, and 3s2s3 sequences correspond to coalescence and breakup of clusters as the result of dissociation and association events between stickers. The corresponding droplets behave as physical gels, i.e., networks of chains that are cross-linked by compact clusters of stickers. Although the large-scale (on the scale of the droplet) equilibrium structure of the gel remains intact as the average number of clusters reaches a steady-state value in the early stages of droplet formation, on molecular scales, there are strong fluctuations as the result of dissociation and reassociation events. In case of s8s and 4ss4 sequences in which the stickers assemble into long fibers, fluctuations of the number of clusters are strongly suppressed (see Fig. 5 B). In all the cases, clusters of stickers are stabilized by the large energy required to dissociate a sticker from a cluster compared with the energy required to break a single bond between two isolated stickers (the equilibrium cluster size is determined by the interplay between this binding energy and the excluded volume repulsion between the nonsticker beads of the chains that emanate from the cluster) (22).

Figure 5.

(A) Histogram showing the average number of clusters for all five different sequences at t = 300,000. (B) The given plot shows the number of clusters as a function of time for all the sequences (ε_s = 4). To see this figure in color, go online.

To test the dependence of our results on polymer concentration, we performed simulations for polymer volume fraction ϕ = 0.006 and M = 256 for s8s and 2s4s2 sequences and did not observe any qualitative changes of the size and shape of clusters compared with the ϕ = 0.011 case shown in Fig. 4. We also tested the sensitivity of the organization of stickers inside the droplets to the strength of the interaction between stickers by performing simulations for ε_s = 3.0 and ε_s = 5.0. Although we did not find major qualitative differences in the organization of the stickers inside the droplets because ε_s was varied in the range 3–5, we observed a systematic variation of the shape, size, and number of clusters with varying ε_s. For example, in the case of s8s and 4ss4 arrangements, as ε_s increases, the width of the fiber increases as well, and for ε_s = 5, its cross section takes the shape of a planar bilayer (see Figs. S4 and S5).

Next, we studied the aging of a droplet starting from its formation and after the evolution of its internal structure on timescales that were several orders of magnitude larger than its formation time till it settled into equilibrium. Two types of structural rearrangements were monitored: on a mesoscopic scale, we followed the association and dissociation of clusters of stickers until a steady state was reached in which the average number and size of these clusters did not change with time. For all polymer sequences, we found that the system attains equilibrium with respect to the cluster number and size shortly after the formation of the droplet (see Fig. 5 B). On a molecular level, we followed the change of the distribution of polymer states (open and bound states in Fig. 1) with time. To this end, we computed the average (over all polymers in the droplet) distance between two stickers of the same polymer at different times.

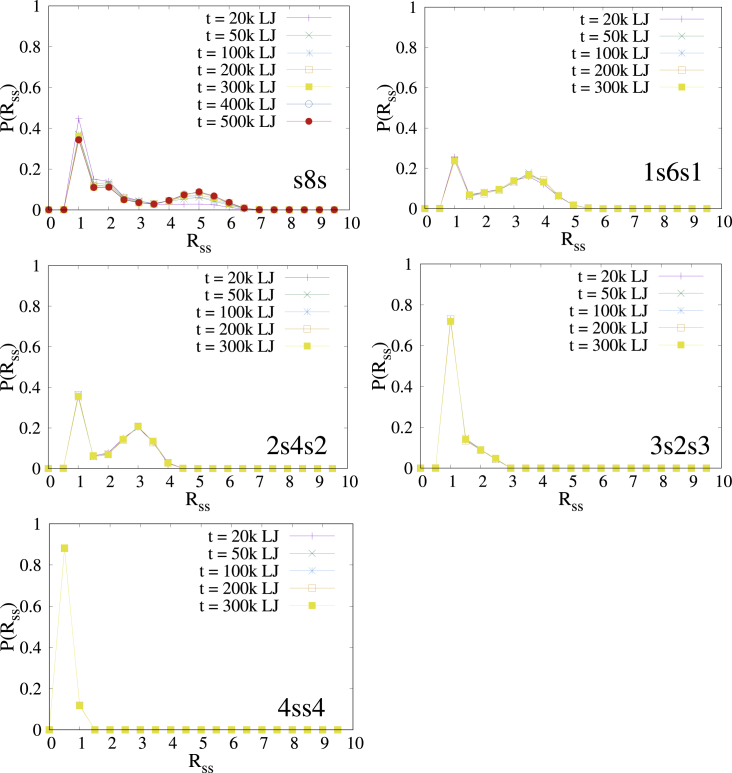
The distributions of averaged rms distance R_ss between two stickers on a polymer measured at different aging times are shown in Fig. 6, in which each of the five panels represents a different sequence. At all aging times, the distributions are bimodal for polymers with sequences s8s, 1s6s1, and 2s4s2 and unimodal for sequence 4ss4. The R_ss distribution for the 3s2s3 sequence has a single peak followed by a broad shoulder and is intermediate between the bimodal and the unimodal cases. In the bimodal case, the two peaks can be associated with open (large R_ss) and with bound (small R_ss) states of the corresponding polymer, with the latter peak located at R_ss ≈ 1, in agreement with expectations. The position of the second peak that corresponds to open chain configurations (state 1 in Fig. 1) is sequence dependent and increases with the length n of the sequence of beads between the two stickers. To understand the origin of this sequence dependence, note that the spatial separation between the stickers averaged over open chain conformations increases with the length n of the sequence of beads between the two stickers (for long sequences and no interaction between the beads, one expects the Gaussian chain result R_ss ∝ n^1/2), and therefore, the value of R_ss should monotonically decrease from s8s (n = 8) to 1s6s1 (n = 6) to the 2s4s2 (n = 4) sequence, as observed in Fig. 6. As expected, only open configurations are observed for the 4ss4 polymers that cannot form intramolecular loops, with a peak at R_ss ≈ 0.5 (the smaller value of R_ss is due to the attractive finitely extensible nonlinear elastic bond between neighboring stickers). A single smeared peak is observed for the 3s2s3 sequence because of the very small difference between the intersticker distances in the open (state 1) and bound (state 2) states.

Figure 6.

Distribution of rms distance R_ss between two stickers on a polymer inside the droplet at different aging times for five different sequences (ε_s = 4). To see this figure in color, go online.

Note that practically all the polymers are confined within the droplets, and most of their stickers are arranged in clusters. Therefore, the presence of loops and open chain configurations that correspond to the two peaks (for sequences s8s, 1s6s1, and 2s4s2) means that some of the polymers form intramolecular loops that bind together to a cluster, whereas other polymers form intermolecular bridges between points on the same or on different clusters (see Fig. 7). The numbers of intramolecular loops and intermolecular bridges depends on the sequence (compare the areas under the two peaks in the first three panels in Fig. 6).

Figure 7.

A snapshot of clusters of stickers for the s8s sequence. Several intramolecular loops and intermolecular bridges are shown (ε_s = 4). To see this figure in color, go online.

We now proceed to examine aging effects. Inspection of Fig. 6 shows that for four of the sequences, no significant molecular rearrangement is observed in the time interval 20,000–300,000. The only exception is the s8s sequence for which the number of intermolecular bridges increases monotonically with time at the expense of intramolecular loops and eventually saturates around t = 400,000. Even though polymers with the 4ss4 sequence form a single cylindrical fiber that is quite similar to that of the s8s sequence, no aging is observed for the 4ss4 sequence, presumably because it cannot form intermolecular bridges. Clearly, competition between intramolecular loops and intermolecular bridges is a necessary but not a sufficient condition for aging because it is not observed in 1s6s1 and 2s4s2 droplets, in which both open and closed polymer conformations (and multiple small clusters of stickers) are present.

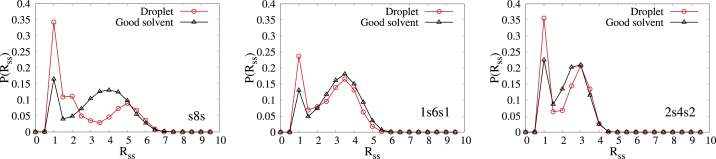
To get some intuition about the effects of intermolecular interactions on the conformation of associating polymers in the droplet, we proceed to compare the R_ss distribution of polymers inside the droplet to that of an isolated associative polymer in the poor and good solvents. We first simulated an isolated associative polymer in poor solvent, keeping all parameters the same as in the droplet case discussed above. For four of the five sequences, we observed a strong single peak at R_ss = 1 (at R_ss = 0.5 for the 4s4 sequence), with an extended shoulder for larger R_ss-values (see Fig. S6). This concurs with the expectation that open chain configurations are strongly suppressed and collapsed ones are enhanced for isolated polymers in poor solvent. Next, we simulated an isolated associative polymer in good solvent, with ε_s = 4.0 interaction between stickers and only repulsive interactions between the other beads (ε_ns = 0.8 with a cutoff at $r_{ij}^{cut}$ = 2^1/6σ). The results are shown in Fig. 8, in which the R_ss distribution of a polymer in a droplet is compared with that in good solvent for the s8s, 1s6s1, and 2s4s2 sequences. In all these cases, a bimodal distribution is observed, and the probability of the bound state formation is higher in a droplet than in good solvent. For the 1s6s1 and 2s4s2 sequences, the open chain peaks are quite similar in amplitude and position in the droplet and in good solvent, but for the s8s sequence, the droplet peak is lower and is shifted to higher intersticker distances compared with the good solvent. A tentative explanation is that in the 1s6s1 and 2s4s2 cases, there are multiple small clusters of stickers inside the droplet, and intermolecular bridges can form between clusters whose separation happens to coincide with the average end-to-end distance of a free polymer chain. In the s8s case, the stickers form a long helical fiber that is folded inside the droplet, and the chains have to stretch to form intermolecular bridges between neighboring turns of the fiber. Because at t = 0 we begin with a dilute solution of associating polymers in poor solvent in which most of the chains contain intramolecular bonds between their stickers, the observation of a second peak that corresponds to intermolecular bridges means that major molecular rearrangement takes place inside droplets formed by polymers with the s8s, 1s6s1, and 2s4s2 sequences. The fact that significant aging after the formation of a large droplet is observed only for the s8s sequence implies that for the 1s6s1 and 2s4s2 sequences, the distance between the stickers is optimized by a partial conversion from intramolecular to intermolecular associations already during the growth of smaller droplets and is completed by the time the large droplet is formed by their coalescence.

Figure 8.

Comparison of R_ss distribution of polymer chains inside droplets with that of isolated associating polymers in good solvent for the s8s, 1s6s1, and 2s4s2 sequences (ε_s = 4). To see this figure in color, go online.

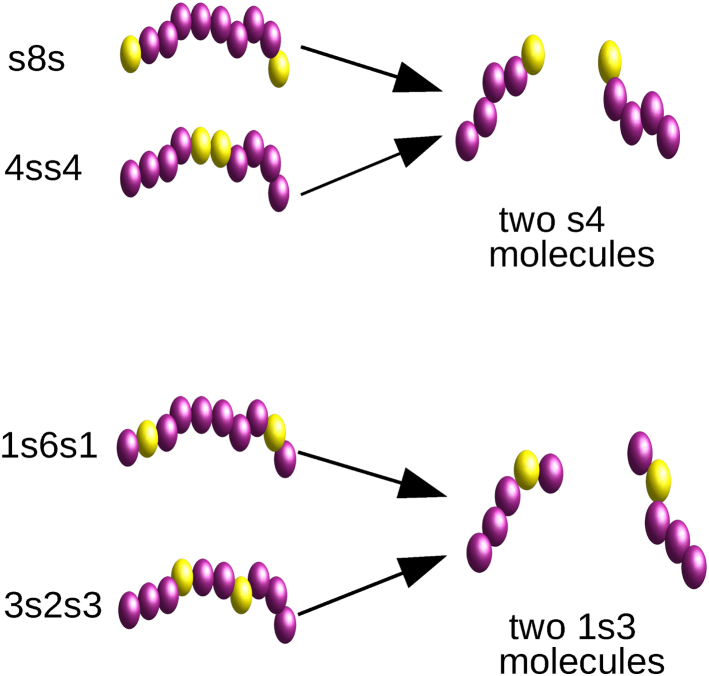
An inspection of Figs. 4 and 5 A shows remarkable similarity between the internal droplet morphologies (size, shape, and number of clusters of stickers) of the sequences s8s and 4ss4 and of the sequences 1s6s1, and 3s2s3. To understand the origin of this similarity, we split each of the 10-long polymer sequences in the middle to yield two identical sequences of length five, with one sticker each (see Fig. 9). Clearly, both s8s and 4ss4 consist of two identical s4 repeat units, and both 1s6s1 and 3s2s3 contain two 1s3 repeat units. To check whether an N = 5 polymer with a single sticker produces similar internal droplet morphology to the corresponding N = 10 polymer with two stickers, we performed simulations of droplet formation and aging in dilute solutions of N = 5 polymers, keeping the volume fraction of polymers and other simulation parameters the same as in the N = 10 case. In accord with expectations, we obtained droplets with similar internal morphology to those of the corresponding N = 10 sequence (see Fig. S7). We therefore conclude that the number, size, and shape of clusters is controlled mainly by the sequence of the repeat unit (“monomer”) of the associating polymer (e.g., s4) and not by the way these repeat units are joined together to form a polymer (i.e., s8s or 4ss4). Note, however, that even though the internal structure of droplets is similar for the corresponding N = 5 and N = 10 sequences, there are profound differences between the two cases at the molecular level. Although the formation of intramolecular loops and intermolecular bridges is strictly forbidden in droplets formed by single-sticker N = 5 polymers (e.g., s4 sequence), it can be either forbidden or allowed in clusters formed by the corresponding N = 10 chains, depending on the way they are joined together (forbidden for 4ss4 and allowed for s8s).

Figure 9.

Correspondence between N = 10 polymers with two stickers and their one-sticker N = 5 repeat units. To see this figure in color, go online.

Discussion

In this work, we modeled IDPs as short associative polymers with two stickers and studied the effect of the primary sequence of IDPs on their organization inside condensed droplets. We considered all five possible sequences of the N = 10 long polymer with two stickers symmetrically positioned along its contour and observed that growth of condensed droplets occurs via coalescence until a single large spherical droplet is formed in all the systems. We found a striking dependence of the morphology of clusters of stickers on the sequence: although a long helical fiber was observed for both s8s and 4ss4 sequences, many small compact (and somewhat elongated) clusters were seen for the other three sequences. We also found that the morphology of the clusters is determined mostly by the repeat unit of the associating polymer: both s8s and 4ss4 (1s6s1 and 3s2s3) sequences are formed from the s4 repeat unit, and both have a similar internal morphology (a similar conclusion applies to the 1s6s1 and 3s2s3 sequences that have a common 1s3 repeat unit).

For three of the sequences (s8s, 1s6s1, and 2s4s2), we found that the average spatial distance R_ss between the two stickers of a polymer inside the condensed droplet has a bimodal distribution such that one of the peaks corresponds to intramolecular bonds and the other to intermolecular bridges between clusters (or between different parts of a long fiber of stickers). Only a single peak that corresponds to intramolecular associations between stickers was observed for the other two sequences, 3s2s3 and 4ss4, in accord with the expectation that intermolecular bridges can form only for sequences that have sufficiently long spacers between stickers.

Telechelic polymers (but no other sequences in our study) exhibited a slow evolution of the distribution of intersticker distances inside the droplet as the peak corresponding to the small (large) values of R_ss decreased (increased) with time. We identified this “aging” phenomenon with molecular rearrangement, in which loops formed by intramolecular association open up to form intermolecular bridges between different folds of the helical fiber of the stickers inside the droplet. The evolution from intramolecular to intermolecular associations in droplets of telechelic polymers in poor solvent should be contrasted with the opposite phenomenon that was observed in gels produced by self-assembly of telechelic polymers in good solvent (22).

Finally, we would like to comment on the relevance of our results to biomolecular condensates of IDPs. One limitation of our results is that to reduce the simulation time, we have used a relatively small system size (512 polymers), and one could argue that the properties of our system can be affected by finite size effects. We believe that because the shape of the clusters depends mainly on the sequence and on interaction strength, the internal structure of the droplets is only weakly affected by size effects as long as it contains a large number of polymer chains. Next, because we use a coarse-grained model in which each bead may represent an arbitrary sequence of amino acids, it can be used to represent both IDPs and short peptides (33). Clearly, our simple model misses many of the molecular details of real IDPs, such as hydrogen bonding and electrostatic interactions between amino acids and the formation of a partial secondary structure (such as α-helices and β-strands). Still, it does capture some of the generic feature of flexible proteins, such as their ability to change their conformation to associate with other macromolecules (in our model, this is illustrated by the replacement of intramolecular by intermolecular associations between stickers). It also captures, albeit qualitatively, the phenomenon of aging of liquid-like IDP droplets and, in particular, their tendency to form strong gels and fibers. Such phenomena have been observed in the liquid droplets of τ-proteins (34) and of nucleoporin domains (31,35). Another similarity between our associative polymer model and IDPs is illustrated by the fact that, just like in our simple model, fibril formation by amyloid peptides (36), formation of stress granules of low complexity domains that drive fibrillization during liquid-liquid phase separation (37), formation of nanostructures via self-assembly of short peptides (38), and nanoscale organization of nucleoporins in the nuclear pore complex (39) strongly depend on their sequence.

Author contributions

K.S. and Y.R. designed the research. K.S. carried out all simulations. K.S. and Y.R. analyzed the results and wrote the article.

Editor: Monika Fuxreiter.