A unified framework for cross-population trait prediction by leveraging the genetic correlation of polygenic traits

Summary

The development of polygenic risk scores (PRSs) has proved useful to stratify the general European population into different risk groups. However, PRSs are less accurate in non-European populations due to genetic differences across different populations. To improve the prediction accuracy in non-European populations, we propose a cross-population analysis framework for PRS construction with both individual-level (XPA) and summary-level (XPASS) GWAS data. By leveraging trans-ancestry genetic correlation, our methods can borrow information from the Biobank-scale European population data to improve risk prediction in the non-European populations. Our framework can also incorporate population-specific effects to further improve construction of PRS. With innovations in data structure and algorithm design, our methods provide a substantial saving in computational time and memory usage. Through comprehensive simulation studies, we show that our framework provides accurate, efficient, and robust PRS construction across a range of genetic architectures. In a Chinese cohort, our methods achieved 7.3%–198.0% accuracy gain for height and 19.5%–313.3% accuracy gain for body mass index (BMI) in terms of predictive R² compared to existing PRS approaches. We also show that XPA and XPASS can achieve substantial improvement for construction of height PRSs in the African population, suggesting the generality of our framework across global populations.

Introduction

In the past 15 years, genome-wide association studies (GWASs) have been performed on a wide spectrum of complex traits and diseases, providing an unprecedented opportunity to stratify the general population into different risk groups. With the availability of large-scale GWAS data, polygenic risk scores (PRSs) have been constructed to estimate the genetic predisposition of complex phenotypes by collecting contributions of many single-nucleotide polymorphisms (SNPs). The accurate construction of PRSs holds promise in disease risk prediction, personalized healthcare guidance, disease screening, and therapeutic intervention.¹ As one example, it was shown that an appropriately constructed PRS can identify 8% of the population with three-fold increased risk of coronary artery disease (CAD), while monogenic mutations with comparable risk can only cover 0.4% of the population.² In terms of the area under the receiver operator curve (AUC), the PRS’s accuracy in predicting CAD onset can be as high as 0.81 based on 288,978 independent testing participants from the UK Biobank.³ More recently, a significant improvement of AUC (from 0.73 to 0.80) was achieved in glaucoma prediction by incorporating PRSs in the traditional risk prediction model without genetic information.⁴

Despite the great promise of PRSs, one major limitation for its broader applications is the fact that most GWASs have been performed on samples with European (EUR) ancestry.^{5, 6, 7, 8, 9, 10, 11} According to the GWAS diversity monitor,⁸ about 89% of GWAS participants to date are from European ancestry, while less than 8% of the participants are from East Asian (EAS) ancestry and less than 0.45% are from African (AFR) ancestry. Despite the wealth of GWAS findings derived from Europeans, such an unbalanced sample makeup across global populations may exacerbate the disparities in genetic studies of non-Europeans.⁶ Recent studies have reported that the PRSs derived from European samples are often less accurate when applied to other populations.^12,13 It remains unclear how much the genetic discovery from the European population can be transferred to non-European populations.

The challenges of transferable genetic studies arise from three aspects. First, SNPs with biologically important roles in the non-European populations may be neglected in GWASs if they are absent or have very low allele frequencies in Europeans.^14,15 Second, the same SNP may have different effect sizes on the same phenotype across different populations,^10,14 limiting the extrapolation value of GWAS findings and the GWAS-derived PRS power in non-discovery populations. Third, the linkage disequilibrium (LD) patterns vary across populations,^{12,16, 17, 18, 19, 20} exacerbating the bias in extrapolating the PRS for risk prediction.

PRSs can be constructed by using either individual-level or summary-level GWAS data. The individual-level methods construct PRSs by directly taking the genotype and phenotype data as their input. Well-known individual-level approaches include best linear unbiased predictor (BLUP),²¹ LASSO,²² BayesR,^23,24 and BayesS.²⁵ These methods have their limitations in construction of PRS in the trans-ancestry setting. First, they are often too time consuming or memory consuming to be applicable for the biobank-scale GWAS data. While the recently proposed snpnet²⁶ method implements LASSO in a memory-efficient manner, it does not provide much gain in computational efficiency. Second, these methods cannot be easily extended to integrate datasets from heterogeneous ethnic backgrounds, since they do not account for different genetic architectures. While the bivariate BLUP (bvBLUP) is useful to reconcile the different genetic effects, the most popular bvBLUP approach provided by the GCTA software (GCTA-bvBLUP)²⁷ is not scalable to the biobank-scale dataset, and thus cannot fully utilize the large-scale datasets to improve prediction performance. Different from individual-level methods, summary-level PRS methods use only summary statistics (e.g., z-scores or marginal effect size estimates) that are widely available for large-scale GWASs to approximate the prediction of individual-level methods. Therefore, they are more flexible, efficient, and easily scalable to well-powered GWAS data. Notable summary-level methods include P+T procedure,²⁸ LDpred,²⁹ and lassosum.³⁰ By taking the advantage of large sample size, existing PRS models have proved informative in predicting genetic risk of European ancestry. However, in view of the imbalanced population composition and the different genetic structures across populations, existing PRS approaches that do not take the heterogeneous genetic architectures into account may not be easily applied in trans-ancestry genetic prediction, leading to sub-optimal prediction accuracy for under-represented populations. The recently proposed MTAG approach³¹ provides an effective data integration framework to combine GWAS summary data of multiple phenotypes, which has been proved useful to improve power of association mapping or construction of PRSs in the same population. Despite the success of MTAG, its performance in the construction of PRSs across populations remains largely unknown. To generate more accurate PRSs by leveraging trans-ancestry information from large-scale European GWASs, a pioneer approach, XP-BLUP,³² was recently proposed, which generalizes BLUP by introducing an extra variance component to model the effect sizes of significant SNPs derived from well-powered GWASs of the auxiliary population. The underlying assumption is that the significant SNPs from the auxiliary population are more useful for improving PRS accuracy in the under-represented populations. However, as XP-BLUP only incorporates information from significant SNPs, its improvement in prediction accuracy is limited. Therefore, there is a great need for a comprehensive investigation on the transferability of genetic study in the PRS construction among global populations.

With our innovations in data structure and algorithm design, XPA is able to handle bio-bank scale individual-level datasets and achieves the accurate prediction with the computational cost nearly linear to the SNP number and sample size. To demonstrate the effectiveness of our methods, we considered the data collected from about 33,000 Chinese participants through a direct-to-customer platform. For two anthropometric traits, height and body mass index (BMI), we applied XPA to integrate the Chinese training dataset (about 20,000 participants) with the UKBB dataset and evaluated its prediction accuracy on an independent Chinese testing dataset (about 13,000 participants). XPA achieved R² = 18.92% for height and R² = 6.06% for BMI. Compared to the runner up, XPA improved the relative prediction accuracy by 7.3% for height and 19.5% for BMI. We also evaluated XPASS and other related methods that only use summary statistics. Given the summary statistics obtained from the same individual-level GWAS data as its input, XPASS is slightly worse than XPA as expected, but it is more broadly applicable when individual-level data are not accessible. Since the ancestry profiles of Japanese and Chinese are close to each other, summary statistics from a larger East Asian GWAS, the BioBank Japan (BBJ) project,^33,34 was used as the training data to construct PRSs for testing dataset. By integrating summary data from BBJ with UKBB, XPASS was able to further improve the prediction accuracy for height with R² = 19.54%, offering 12.7% relative improvement compared to training with Chinese and UKBB summary data. We also demonstrated that our proposed methods was able to improve the construction of PRSs in African population by integrating UKBB.

Material and methods

Method overview: XPA and XPASS

Due to the polygenicity of human complex traits, it is challenging to construct accurate PRSs for an under-studied target population. On one hand, the PRSs constructed using samples from EUR ancestry becomes less accurate when it is applied to non-European samples. On the other hand, the accuracy of PRSs constructed only using samples from the under-represented target population is limited by the sample size. By integrating small-scale or medium-scale data from the target population with existing large-scale data resources from EUR ancestry, our methods can robustly improve the PRS prediction performance. The key idea of our methods is based on the observed substantial genetic correlation that largely remains for the same trait between populations due to the shared genetic basis. Therefore, a large amount of information in the biobank-scale data of EUR ancestry can be utilized for risk prediction in the under-represented ancestry. By taking individual-level GWAS data as input, XPA offers analytic estimate for the SNP effect sizes using shared information across populations. With our innovations in data structure and algorithm design, such as Boolean representation^35,36 and stochastic approximation,³⁷ the analytic SNP effect size estimates can be computed efficiently, allowing us to construct PRSs in the target population accurately. Because of the unavailability of individual-level data for many traits, we have extended XPA to XPASS which requires only the GWAS z-scores and SNP correlation matrices from the target and auxiliary populations, where the SNP correlation matrices can be approximated using block-diagonal correlation matrices from a genotype reference panel of the two populations. The computational complexity of XPA and XPASS is approximately linear to the number of SNPs and sample size, making our framework appealing in cross-population risk prediction with biobank-scale data.

XPA statistical framework

Consider a GWAS dataset {G₁,Z₁,y₁} from an under-represented ancestry, where G₁ is an n₁ × p genotype matrix, Z₁ is an n₁ × c₁ matrix collecting all covariates (e.g., age, sex, and principal components), and y₁ is an n₁ × 1 phenotype vector. Due to the polygenicity of complex traits, the accuracy of risk prediction is limited by the sample size. Now suppose a biobank-scale dataset {G₂,Z₂,y₂} from European ancestry is also available, where G₂ is an n₂ × p genotype matrix, Z₂ is an n₂ × c₂ covariate matrix, y₂ is an n₂ × 1 phenotype vector, and $n_2\gg n_1$. Since we are mainly interested in improving risk prediction in the under-represented population, we shall regard it as the target population and the biobank-scale data from European ancestry as the auxiliary dataset. To reconcile the difference of allele frequencies in the two populations, XPA assumes that the SNP effect sizes in both the target and auxiliary populations increase as the allele frequencies decrease³⁸ and works with standardized genotype matrices. Specifically, let ${\mathbf{g}}_{1j}\in {\mathbb{R}}^{n_1}$ and ${\mathbf{g}}_{2j}\in {\mathbb{R}}^{n_2}$ denote the j-th column of G₁ and G₂, respectively. The corresponding column means and standard deviations are given as ${\overline{\mathbf{g}}}_{1j}$ and ${\overline{\mathbf{g}}}_{2j}$, $s_{1j}$ and $s_{2j}$, respectively. Then we have the corresponding standardized genotype matrices as ${\mathbf{X}}_1=[{\mathbf{x}}_{11},{\mathbf{x}}_{12},\dots ,{\mathbf{x}}_{1p}]\in {\mathbb{R}}^{n_1\times p}$ and ${\mathbf{X}}_2=[{\mathbf{x}}_{21},{\mathbf{x}}_{22},\dots ,{\mathbf{x}}_{2p}]\in {\mathbb{R}}^{n_2\times p}$, where the j-th column of X₁ and X₂ is given as ${\mathbf{x}}_{1j}=\left({\mathbf{g}}_{1j}-{\overline{\mathbf{g}}}_{1j}\right)/\left(s_{1j}\sqrt{p}\right)$ and ${\mathbf{x}}_{2j}=\left({\mathbf{g}}_{2j}-{\overline{\mathbf{g}}}_{2j}\right)/\left(s_{2j}\sqrt{p}\right)$, respectively. In such a way, each column of X₁ and X₂ has mean 0 and variance 1/p. We relate genotypes and phenotypes using the following linear models:

$$\begin{array}{l}{\mathbf{y}}_1={\mathbf{Z}}_1{\mathit{\omega }}_1+{\mathbf{X}}_1{\mathit{\beta }}_1+\mathrm{\epsilon },\\ {\mathbf{y}}_2={\mathbf{Z}}_2{\mathit{\omega }}_2+{\mathbf{X}}_2{\mathit{\beta }}_2+\mathit{\xi },\end{array}$$ (Equation 1)

where ${\mathit{\omega }}_1\in {\mathbb{R}}^{c_1}$ and ${\mathit{\omega }}_2\in {\mathbb{R}}^{c_2}$ are fixed effects of covariates, ${\mathit{\beta }}_1={[{\beta }_{\mathrm{1,1}},{\beta }_{\mathrm{1,2}},\dots ,{\beta }_{1,p}]}^T\in {\mathbb{R}}^p$ and ${\mathit{\beta }}_2={[{\beta }_{\mathrm{2,1}},{\beta }_{\mathrm{2,2}},\dots ,{\beta }_{2,p}]}^T\in {\mathbb{R}}^p$ are vectors collecting the SNP effect sizes from the two populations, and $\mathrm{\epsilon }\sim \mathcal{N}\left(0,{\sigma }_{\epsilon }^2{\mathbf{I}}_{n_1}\right)$ and $\mathit{\xi }\sim \mathcal{N}\left(0,{\sigma }_{\xi }^2{\mathbf{I}}_{n_2}\right)$ are independent errors. Of note, the two datasets do not share samples because they are from different populations. Therefore, we can assume that the residual vectors $\mathrm{\epsilon }$ and $\mathit{\xi }$ are independent. To model the polygenic effects and their correlation between two populations, we introduce the following probabilistic structures on ${\mathit{\beta }}_1$ and ${\mathit{\beta }}_2$:

$$\left(\begin{array}{l}{\beta }_{1,j}\hfill \\ {\beta }_{2,j}\hfill \end{array}\right)\sim \mathcal{N}\left(0,{\mathbf{\Sigma }}_{\beta }\right)=\mathcal{N}\left(\left(\begin{array}{l}0\hfill \\ 0\hfill \end{array}\right),\left(\begin{array}{ll}{\sigma }_1^2\hfill & \rho {\sigma }_1{\sigma }_2\hfill \\ \rho {\sigma }_1{\sigma }_2\hfill & {\sigma }_2^2\hfill \end{array}\right)\right),j=1,\dots ,p,$$ (Equation 2)

where ${\sigma }_1^2$ and ${\sigma }_2^2$ are the variance components characterizing the polygenic effects in the two populations, respectively, ρ is the trans-ancestry genetic correlation of the same trait across population, and $\delta :=\rho {\sigma }_1{\sigma }_2$ is the corresponding covariance. XPA computes the posterior mean of ${\mathit{\beta }}_1$ by combining the target dataset with the auxiliary dataset through their genetic correlation, and therefore constructs an improved genetic prediction when the genetic correlation ρ is nonzero. In contrast to XP-BLUP,³² XPA leverages genome-wide information by using all SNPs rather than only the top SNPs from the auxiliary population. While the inclusion of all SNPs from the biobank-scale auxiliary dataset introduces challenges in computation and data storage, we show that they can be properly addressed by the novel data structure and algorithm design in XPA.

XPA₊ for capturing population-specific effects

The XPA framework can incorporate population-specific genetic effects to improve prediction performance. To see this, we denote ${\mathbf{Z}}_{c1}\in {\mathbb{R}}^{n_1\times c_1}$ and ${\mathbf{Z}}_{c2}\in {\mathbb{R}}^{n_2\times c_2}$ as matrices collecting all the covariates, and ${\mathbf{X}}_{l1}\in {\mathbb{R}}^{n_1\times l_1}$ and ${\mathbf{X}}_{l2}\in {\mathbb{R}}^{n_2\times l_2}$ as the standardized genotype matrices of SNPs with large effects in populations one and two, respectively. By constructing Z₁ and Z₂ in Equation 1 as ${\mathbf{Z}}_1=[{\mathbf{Z}}_{c1},{\mathbf{X}}_{l1}]$ and $[{\mathbf{Z}}_{c2},{\mathbf{X}}_{l2}]$, respectively, we can re-write Equation 1 as:

$$\begin{array}{l}{\mathbf{y}}_1={\mathbf{Z}}_{c1}{\mathit{\omega }}_{c1}+{\mathbf{X}}_{l1}{\mathit{\gamma }}_1+{\mathbf{X}}_1{\mathit{\beta }}_1+\mathrm{\epsilon },\\ {\mathbf{y}}_2={\mathbf{Z}}_{c2}{\mathit{\omega }}_{c2}+{\mathbf{X}}_{l2}{\mathit{\gamma }}_2+{\mathbf{X}}_2{\mathit{\beta }}_2+\mathit{\xi },\end{array}$$ (Equation 3)

where ${\mathit{\gamma }}_1\in {\mathbb{R}}^{l_1}$ and ${\mathit{\gamma }}_2\in {\mathbb{R}}^{l_2}$ are fixed effects of the pre-selected SNPs, ${\mathit{\omega }}_{c1}\in {\mathbb{R}}^{c_1}$ and ${\mathit{\omega }}_{c2}\in {\mathbb{R}}^{c_2}$ are fixed effects of covariates, and ${\mathit{\omega }}_1={[{\mathit{\omega }}_{c1}^T,{\mathit{\gamma }}_1^T]}^T$, ${\mathit{\omega }}_2={[{\mathit{\omega }}_{c2}^T,{\mathit{\gamma }}_2^T]}^T$. SNPs in ${\mathbf{X}}_{l1}$ and ${\mathbf{X}}_{l2}$ are selected by applying the P+T procedure to the GWAS summary statistics of the target and the auxiliary populations, respectively. Because $l_1\ll n_1$ and $l_2\ll n_2$ in practice, the vectors of fixed effects ${\mathit{\gamma }}_1\in {\mathbb{R}}^{l_1}$ and ${\mathit{\gamma }}_2\in {\mathbb{R}}^{l_2}$ can be accurately estimated.

This flexible model structure can accommodate polygenic effects across population and large population-specific effects. On one hand, the probabilistic structures of ${\mathit{\beta }}_1$ and ${\mathit{\beta }}_2$ capture the polygenic effects that are correlated between populations, allowing the auxiliary samples to be effectively utilized. On the other hand, ${\mathit{\gamma }}_1$ and ${\mathit{\gamma }}_2$ capture the large population-specific genetic effects, which further boost the prediction performance. We call this extension of XPA as XPA₊. When no SNPs with large population-specific effects are selected, XPA₊ is equivalent to XPA. Once the large-effect SNPs have been selected, the parameters can be estimated in the same way as in XPA.

Parameter estimation in XPA

To obtain the posterior mean of ${\mathit{\beta }}_1$, we first need to estimate the unknown parameters $\left\{{\sigma }_1^2,{\sigma }_2^2,\delta ,{\sigma }_{\epsilon }^2,{\sigma }_{\xi }^2\right\}$. For convenience, we define $\mathbf{y}=\left[\begin{array}{l}{\mathbf{y}}_1\hfill \\ {\mathbf{y}}_2\hfill \end{array}\right]$, $\mathbf{Z}=\left[\begin{array}{ll}{\mathbf{Z}}_1\hfill & 0\hfill \\ 0\hfill & {\mathbf{Z}}_2\hfill \end{array}\right]$, $\mathbf{X}=\left[\begin{array}{ll}{\mathbf{X}}_1\hfill & 0\hfill \\ 0\hfill & {\mathbf{X}}_2\hfill \end{array}\right]$, $\mathit{\omega }=\left[\begin{array}{l}{\mathit{\omega }}_1\hfill \\ {\mathit{\omega }}_2\hfill \end{array}\right]$, and ${\mathbf{\Sigma }}_e=\left[\begin{array}{ll}{\sigma }_{\epsilon }^2{\mathbf{I}}_{n_1}\hfill & 0\hfill \\ 0\hfill & {\sigma }_{\xi }^2{\mathbf{I}}_{n_2}\hfill \end{array}\right]$. The marginal distribution of $\mathbf{y}$ can be obtained by combining Equations 1 and 2 and taking integration over $\mathit{\beta }$:

$$\mathbf{y}\sim \mathcal{N}\left(\mathbf{Z}\mathit{\omega },\mathbf{\Omega }\right),\mathbf{\Omega }=\mathbf{X}\left({\mathbf{\Sigma }}_{\beta }\otimes {\mathbf{I}}_p\right){\mathbf{X}}^T+{\mathbf{\Sigma }}_e,$$ (Equation 4)

where $\mathbf{X}\left({\mathbf{\Sigma }}_{\beta }\otimes {\mathbf{I}}_p\right){\mathbf{X}}^T=\left[\begin{array}{ll}{\sigma }_1^2{\mathbf{K}}_1\hfill & \delta {\mathbf{K}}_{12}\hfill \\ \delta {\mathbf{K}}_{12}^T\hfill & {\sigma }_2^2{\mathbf{K}}_2\hfill \end{array}\right]$, ${\mathbf{K}}_1={\mathbf{X}}_1{\mathbf{X}}_1^T$, ${\mathbf{K}}_2={\mathbf{X}}_2{\mathbf{X}}_2^T$, and ${\mathbf{K}}_{12}={\mathbf{X}}_1{\mathbf{X}}_2^T$. To estimate unknown parameters $\left\{{\sigma }_1^2,{\sigma }_2^2,\delta ,{\sigma }_{\epsilon }^2,{\sigma }_{\xi }^2\right\}$, we get rid of the covariates by multiplying Equation 4 with the projection matrix $\mathbf{M}\equiv \left[\begin{array}{ll}{\mathbf{M}}_1\hfill & 0\hfill \\ 0\hfill & {\mathbf{M}}_2\hfill \end{array}\right]={\mathbf{I}}_{n_1+n_2}-\mathbf{Z}{\left({\mathbf{Z}}^T\mathbf{Z}\right)}^{-1}{\mathbf{Z}}^T$, which leads to $\mathbf{M}\mathbf{y}\sim \mathcal{N}\left(0,\mathbf{M}\mathbf{X}\left({\mathbf{\Sigma }}_{\beta }\otimes {\mathbf{I}}_p\right){\mathbf{X}}^T\mathbf{M}+\mathbf{M}{\mathbf{\Sigma }}_e\right)$. For convenience, we use $\tilde{\mathbf{A}}$ to denote MA for any matrix A involved in our notation, hence we have $\tilde{\mathbf{y}}\sim \mathcal{N}\left(0,\tilde{\mathbf{\Omega }}\right),\text{ where }\tilde{\mathbf{\Omega }}=\tilde{\mathbf{X}}\left({\mathbf{\Sigma }}_{\beta }\otimes {\mathbf{I}}_p\right){\tilde{\mathbf{X}}}^T+{\tilde{\mathbf{\Sigma }}}_e.$ The method of moments (MoM) offers a computationally efficient estimator of $\mathit{\theta }=\left\{{\sigma }_1^2,{\sigma }_2^2,\delta ,{\sigma }_{\epsilon }^2,{\sigma }_{\xi }^2\right\}$ by matching the second-order moment based on the criterion of least-squares: ${\text{argmin}}_{\mathit{\theta }}\left|\right|\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T-\tilde{\mathbf{\Omega }}|{|}_F^2$. Taking derivatives of the objective function w.r.t $\mathit{\theta }$ and setting them to zero leads to the estimating equations (see Appendix A):

$$\underset{\mathbf{S}}{\underbrace{\left[\begin{array}{lllll}\text{tr}\left({\tilde{\mathbf{K}}}_1^2\right)\hfill & \text{tr}\left({\tilde{\mathbf{K}}}_1\right)\hfill & 0\hfill & 0\hfill & 0\hfill \\ \text{tr}\left({\tilde{\mathbf{K}}}_1\right)\hfill & \text{tr}\left({\mathbf{M}}_1\right)\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & \text{tr}\left({\tilde{\mathbf{K}}}_2^2\right)\hfill & \text{tr}\left({\tilde{\mathbf{K}}}_2\right)\hfill & 0\hfill \\ 0\hfill & 0\hfill & \text{tr}\left({\tilde{\mathbf{K}}}_2\right)\hfill & \text{tr}\left({\mathbf{M}}_2\right)\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & \text{tr}\left({\tilde{\mathbf{K}}}_{12}{\tilde{\mathbf{K}}}_{12}^T\right)\hfill \end{array}\right]}}\underset{\mathit{\theta }}{\underbrace{\left[\begin{array}{l}{\sigma }_1^2\hfill \\ {\sigma }_{\epsilon }^2\hfill \\ {\sigma }_2^2\hfill \\ {\sigma }_{\xi }^2\hfill \\ \delta \hfill \end{array}\right]}}=\underset{\mathbf{q}}{\underbrace{\left[\begin{array}{l}{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{K}}}_1{\tilde{\mathbf{y}}}_1\hfill \\ {\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{y}}}_1\hfill \\ {\tilde{\mathbf{y}}}_2^T{\tilde{\mathbf{K}}}_2{\tilde{\mathbf{y}}}_2\hfill \\ {\tilde{\mathbf{y}}}_2^T{\tilde{\mathbf{y}}}_2\hfill \\ {\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{K}}}_{12}{\tilde{\mathbf{y}}}_2.\hfill \end{array}\right]}}$$ (Equation 5)

The bottle neck of solving Equation 5 is computing the traces of squared kinship matrices, which has a computational complexity $\mathcal{O}\left(\text{max}{\left(n_1,n_2\right)}^{2}p\right)$. This computational overhead can become very large when dealing with biobank-scale data. Instead of computing the traces exactly, we apply a stochastic approximation to derive unbiased estimates of the trace terms.³⁷ Given a matrix $\mathbf{A}\in {\mathbb{R}}^{n\times n}$ and a vector of random variables $\mathbf{d}\in {\mathbb{R}}^n$ with $\mathbb{E}\left(\mathbf{d}\right)=0$ and $\text{Cov}\left(\mathbf{d}\right)={\mathbf{I}}_n$, we have the identity $\mathbb{E}\left({\mathbf{d}}^T\mathbf{A}\mathbf{d}\right)=\text{tr}\left(\mathbf{A}\right)$. Using this identity, we can construct the following estimates:

$$\begin{array}{l}{\mathbf{L}}_{B_1}\equiv \stackrel{ˆ}{\text{tr}\left({\tilde{\mathbf{K}}}_1^2\right)}=\stackrel{ˆ}{\text{tr}\left({\tilde{\mathbf{K}}}_1{\tilde{\mathbf{K}}}_1^T\right)}=\frac{1}{B}\stackrel{B}{\sum _{b=1}}{\mathbf{d}}_b^T{\tilde{\mathbf{K}}}_1{\tilde{\mathbf{K}}}_1^T{\mathbf{d}}_b=\frac{1}{B}\stackrel{B}{\sum _{b=1}}\Vert {\tilde{\mathbf{X}}}_1{\tilde{\mathbf{X}}}_1^T{\mathbf{d}}_b{\Vert }_2^2,\\ {\mathbf{L}}_{B_2}\equiv \stackrel{ˆ}{\text{tr}\left({\tilde{\mathbf{K}}}_2^2\right)}=\frac{1}{B}\stackrel{B}{\sum _{b=1}}\Vert {\tilde{\mathbf{X}}}_2{\tilde{\mathbf{X}}}_2^T{\mathbf{d}}_b{\Vert }_2^2,{\mathbf{L}}_{B_{12}}\equiv \stackrel{ˆ}{\text{tr}\left({\tilde{\mathbf{K}}}_{12}{\tilde{\mathbf{K}}}_{12}^T\right)}=\frac{1}{B}\stackrel{B}{\sum _{b=1}}\Vert {\tilde{\mathbf{X}}}_1{\tilde{\mathbf{X}}}_2^T{\mathbf{d}}_b{\Vert }_2^2,\end{array}$$ (Equation 6)

where ${\mathbf{d}}_1,\dots ,{\mathbf{d}}_B$ are B random vectors drawn independently from a distribution with zero mean and identity covariance matrix ${\mathbf{I}}_p$. The stochastic approximation in Equation 6 requires a computational complexity of $\mathcal{O}\left(\text{max}\left(n_1,n_2\right)pB\right)$. In practice, we found that the traces can be effectively approximated with $B\sim 50$. Replacing $\text{tr}\left({\tilde{\mathbf{K}}}_1^2\right)$, $\text{tr}\left({\tilde{\mathbf{K}}}_2^2\right)$, and $\text{tr}\left({\tilde{\mathbf{K}}}_{12}{\tilde{\mathbf{K}}}_{12}^T\right)$ by ${\mathbf{L}}_{B_1}$, ${\mathbf{L}}_{B_2}$, and ${\mathbf{L}}_{B_{12}}$, respectively, we obtained $\hat{\mathit{\theta }}={\mathbf{S}}^{-1}\mathbf{q}$. Then heritablities of the given phenotype in the target and auxiliary populations are estimated as ${\hat{h}}_1^2=\frac{{\hat{\sigma }}_1^2}{{\hat{\sigma }}_1^2+{\hat{\sigma }}_{\epsilon }^2}$ and ${\hat{h}}_2^2=\frac{{\hat{\sigma }}_2^2}{{\hat{\sigma }}_2^2+{\hat{\sigma }}_{\xi }^2}$, respectively. The shared genetic basis between the two populations can be quantified by the estimated trans-ancestry genetic correlation, computed as $\hat{\rho }=\frac{\hat{\delta }}{{\hat{\sigma }}_1{\hat{\sigma }}_2}$, which is the key to utilizing information from the biobank-scale EUR data for risk prediction in the target population.

PRS construction in XPA

Given the estimated parameters $\hat{\mathit{\theta }}=\left\{{\hat{\sigma }}_1^2,{\hat{\sigma }}_2^2,\hat{\delta },{\hat{\sigma }}_{\epsilon }^2,{\hat{\sigma }}_{\xi }^2\right\}$, the fixed effects in Equation 1 are estimated by:

$$\hat{\mathit{\omega }}\equiv \left[\begin{array}{l}{\hat{\mathit{\omega }}}_1\hfill \\ {\hat{\mathit{\omega }}}_2\hfill \end{array}\right]={\left({\mathbf{Z}}^T{\hat{\mathbf{\Omega }}}^{-1}\mathbf{Z}\right)}^{-1}{\mathbf{Z}}^T{\hat{\mathbf{\Omega }}}^{-1}\mathbf{y},$$ (Equation 7)

where $\hat{\mathbf{\Omega }}=\mathbf{X}\left({\hat{\mathbf{\Sigma }}}_{\beta }\otimes {\mathbf{I}}_p\right){\mathbf{X}}^T+{\hat{\mathbf{\Sigma }}}_e,{\hat{\mathbf{\Sigma }}}_{\beta }=\left[\begin{array}{ll}{\hat{\sigma }}_1^2\hfill & \hat{\delta }\hfill \\ \hat{\delta }\hfill & {\hat{\sigma }}_2^2\hfill \end{array}\right],{\hat{\mathbf{\Sigma }}}_e=\left[\begin{array}{ll}{\hat{\sigma }}_{\epsilon }^2{\mathbf{I}}_{n_1}\hfill & 0\hfill \\ 0\hfill & {\hat{\sigma }}_{\xi }^2{\mathbf{I}}_{n_2}\hfill \end{array}\right]$.

The posterior mean of ${\mathit{\beta }}_1$ can be derived as (see Appendix A):

$${\hat{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}}={\left[\begin{array}{l}{\hat{\sigma }}_1^2{\mathbf{X}}_1\hfill \\ \hat{\delta }{\mathbf{X}}_2\hfill \end{array}\right]}^T\underset{{\hat{\mathbf{\Omega }}}^{-1}\in {\mathbb{R}}^{\left(n_1+n_2\right)\times \left(n_1+n_2\right)}}{\underbrace{{\left[\begin{array}{ll}{\hat{\sigma }}_1^2{\mathbf{X}}_1{\mathbf{X}}_1^T+{\hat{\sigma }}_{\epsilon }^2{\mathbf{I}}_{n1}\hfill & \hat{\delta }{\mathbf{X}}_1{\mathbf{X}}_2^T\hfill \\ \hat{\delta }{\mathbf{X}}_2{\mathbf{X}}_1^T\hfill & {\hat{\sigma }}_2^2{\mathbf{X}}_2{\mathbf{X}}_2^T+{\hat{\sigma }}_{\xi }^2{\mathbf{I}}_{n2}\hfill \end{array}\right]}^{-1}}}\left[\begin{array}{l}{\mathbf{y}}_1-{\mathbf{Z}}_1{\hat{\mathit{\omega }}}_1\hfill \\ {\mathbf{y}}_2-{\mathbf{Z}}_2{\hat{\mathit{\omega }}}_2\hfill \end{array}\right].$$ (Equation 8)

Obviously, when the genetic correlation $\rho \ne 0$ (i.e., $\delta \ne 0$), information could be borrowed from the auxiliary population to the target population to improve the posterior mean estimates.

Finally, to obtain the effect size of dosage genotypes ${\tilde{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}}\in {\mathbb{R}}^p$, we need to re-scale the posterior mean by ${\tilde{\mathit{\mu }}}_{1j}^{\mathbf{X}\mathbf{P}\mathbf{A}}={\hat{\mathit{\mu }}}_{1j}^{\mathbf{X}\mathbf{P}\mathbf{A}}/\left(s_j\sqrt{p}\right)$, for $j=1,\dots ,p$. When a new observation of genotype ${\mathbf{g}}_{1,new}\in {\mathbb{R}}^p$ is available, the associated PRS can be computed by its inner product with ${\tilde{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}}$, i.e., ${\text{PRS}}_{new}={\mathbf{g}}_{1,new}^T{\tilde{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}}$. If the covariates of the new observation ${\mathbf{z}}_{1,new}\in {\mathbb{R}}^{c_1}$ are also available, we can predict the phenotype at its original scale by ${\hat{y}}_{new}={\text{PRS}}_{new}+{\mathbf{z}}_{1,new}^T{\hat{\mathit{\omega }}}_1-\sum _j{\tilde{\mu }}_{1j}^{\mathbf{X}\mathbf{P}\mathbf{A}}{\overline{\mathbf{g}}}_{1j}$.

For XPA ₊, we note that by constructing ${\mathbf{Z}}_1=[{\mathbf{Z}}_{c1},{\mathbf{X}}_{l1}]$ and ${\mathbf{Z}}_2=[{\mathbf{Z}}_{c2},{\mathbf{X}}_{l2}]$, the effect sizes of the pre-selected SNPs ${\mathit{\gamma }}_1$ and ${\mathit{\gamma }}_2$ can be estimated jointly with ${\mathit{\omega }}_{c1}$ and ${\mathit{\omega }}_{c2}$ in Equation 7, and the posterior mean in the target population ${\hat{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}{\mathbf{A}}_{+}}$ can be computed in the same way as in Equation 8. Similarly, the posterior mean ${\tilde{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}{\mathbf{A}}_{+}}$ should be re-scaled in the same way as in XPA and the estimated effects of large-effect SNPs should be re-scaled by ${\tilde{\mathit{\gamma }}}_{1j}^{\mathbf{X}\mathbf{P}{\mathbf{A}}_{+}}={\hat{\mathit{\gamma }}}_{1j}^{\mathbf{X}\mathbf{P}{\mathbf{A}}_{+}}/\left(s_j\sqrt{p}\right)$, for $j=1,\dots ,l_1$. Then, the PRSs associated with the new observation ${\mathbf{g}}_{1,new}$ is computed as ${\text{PRS}}_{new}={\mathbf{g}}_{l1,new}^T{\tilde{\mathit{\gamma }}}_1^{\mathbf{X}\mathbf{P}{\mathbf{A}}_{+}}+{\mathbf{g}}_{1,new}^T{\tilde{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}{\mathbf{A}}_{+}}$, where ${\mathbf{g}}_{l1,new}\in {\mathbb{R}}^{l_1}$ is the sub-vector of ${\mathbf{g}}_{1,new}$ corresponding to the SNPs with large effects.

Despite the simple form of Equation 8, it is highly nontrivial to obtain the posterior mean in biobank-scale data due to the challenges in both data storage in computer memory and computation. To boost the computational speed, we solve the large-scale linear system in Equation 8 (i.e., $\left(n_1+n_2\right)\times \left(n_1+n_2\right)$) using the efficient conjugate gradient (CG) method. Because the classical CG requires storing the whole $\hat{\mathbf{\Omega }}$ matrix, which is infeasible for bio-bank scale dataset, we developed a memory-efficient strategy (as described in the following section) for storing standardized genotype matrices, and designed a highly efficient CG algorithm (see Appendix A). Our CG algorithm has the time complexity of $\mathcal{O}\left(p\left(n_1+n_2\right)\left(c_1+c_2+1\right)\sqrt{\kappa }\right)$, where κ is the condition number of $\hat{\mathbf{\Omega }}$. Because κ is usually small, the CG algorithm offers substantial computational improvement in solving the linear system.

Data storage for large genotype matrices in XPA

In practice, the sample size of the auxiliary dataset can be very large (e.g., $n_2\approx \mathrm{400,000}$ for UKBB), producing both computation and data storage problems. To address this difficulty, we apply the memory-efficient Boolean representation proposed in our previous work BOOST³⁵ and the hash table data structure³⁶ to store the standardized genotypes.

Suppose that we are handling a standardized biobank-scale genotype matrix of 400,000 × 3,000,000, the memory usage of storing such a matrix in double-precision floating-point format is 8 bytes$\times \mathrm{400,000}\times \mathrm{3,000,000}=9.6\times {10}^{12}$ bytes $\approx 8.7$ Tb. Therefore, directly storing such a large matrix is usually impractical. However, we note that each genotype only takes 4 possible values even after standardization: $\frac{0-{\overline{\mathbf{g}}}_j}{s_j}$,$\frac{1-{\overline{\mathbf{g}}}_j}{s_j}$,$\frac{2-{\overline{\mathbf{g}}}_j}{s_j}$, and ${\tilde{\mathbf{g}}}_j$, where ${\overline{\mathbf{g}}}_j$ is the mean genotype value at SNP j, s_j is the standard deviation of the genotype j, and ${\tilde{\mathbf{g}}}_j$ is the value to be filled in for the missing genotypes. For each SNP, we index the standardized genotype values using a Boolean representation. Specifically, we can use 00 to index $\frac{0-{\overline{\mathbf{g}}}_j}{s_j}$, 01 to index $\frac{1-{\overline{\mathbf{g}}}_j}{s_j}$, 10 to index $\frac{2-{\overline{\mathbf{g}}}_j}{s_j}$, and 11 to index ${\tilde{\mathbf{g}}}_j$. We then save 4 consecutive individual’s genotypes at a time using the 8-digit Boolean representation, which has 2⁸ = 256 combinations. This constructs a hash table of size 256×4, where each cell contains a standardized genotype value in double precision. The total size of this hash table is 256×4×8 bytes = 8,192 bytes. Finally, we need to construct such a hash table for all 3,000,000 SNPs, which amounts to 8,192 bytes ×3,000,000 = 24.576 Gb. In addition to the hash tables, we need to save the Boolean representations for retrieving genotypes, which takes 400,000 × 3,000,000 / 4 = 3 × 10¹¹ bytes $\approx 280$ Gb. In total, this memory-efficient storing strategy requires only 305 Gb for storing the UKBB genotype matrix.

Constructing PRS using summary statistics by XPASS

We consider the datasets $\left\{{\mathbf{z}}_1,{{\mathbf{G}}_1}^{\text{′}},{{\mathbf{Z}}_1}^{\text{′}}\right\}$ and $\left\{{\mathbf{z}}_2,{{\mathbf{G}}_2}^{\text{′}},{{\mathbf{Z}}_1}^{\text{′}}\right\}$ from the two populations. The vectors ${\mathbf{z}}_1={[z_{11},\dots ,z_{1j},\dots ,z_{1p}]}^T\in {\mathbb{R}}^p$ and ${\mathbf{z}}_2={[z_{21},\dots ,z_{2j},\dots ,z_{2p}]}^T\in {\mathbb{R}}^p$ contain the z-scores derived from the two populations, where $z_{1j}=\frac{{\left({\mathbf{x}}_{1j}^T{\mathbf{x}}_{1j}\right)}^{-1}{\mathbf{x}}_{1j}^T{\mathbf{y}}_1}{\sqrt{{\hat{\sigma }}_{1j}^2{\left({\mathbf{x}}_{1j}^T{\mathbf{x}}_{1j}\right)}^{-1}}}$ and $z_{2j}=\frac{{\left({\mathbf{x}}_{2j}^T{\mathbf{x}}_{2j}\right)}^{-1}{\mathbf{x}}_{2j}^T{\mathbf{y}}_2}{\sqrt{{\hat{\sigma }}_{2j}^2{\left({\mathbf{x}}_{2j}^T{\mathbf{x}}_{2j}\right)}^{-1}}}$, ${\hat{\sigma }}_{1j}^2$ and ${\hat{\sigma }}_{2j}^2$ are the residual variance of regressing ${\mathbf{y}}_1$ on ${\mathbf{x}}_{1j}$ and ${\mathbf{y}}_2$ on ${\mathbf{x}}_{2j}$, respectively. Following Vilhjálmsson et al.,²⁹ we assume the z-scores are derived from GWAS datasets with phenotype vectors ${\mathbf{y}}_1$ and ${\mathbf{y}}_2$ standardized to have mean of zero and standard deviation of one. The first few PCs of the reference genotypes from the two populations are given in ${{\mathbf{Z}}_1}^{\text{′}}\in {\mathbb{R}}^{m_1\times c{\text{′}}_1}$ and ${{\mathbf{Z}}_2}^{\text{′}}\in {\mathbb{R}}^{m_2\times c{\text{′}}_2}$. Similar to XPA, we first standardize the reference genotype matrices ${{\mathbf{G}}_1}^{\text{′}}$ and ${{\mathbf{G}}_2}^{\text{′}}$ to obtain the corresponding ${{\mathbf{X}}_1}^{\text{′}}$ and ${{\mathbf{X}}_2}^{\text{′}}$ that have column means zero and variances 1/p.

In real applications, the individual-level GWAS data may not be easily accessible. To effectively make use of publicly available GWAS summary statistics, we extend the XPA method as XPASS which requires only the z-scores from GWAS results and reference genotypes from the target and auxiliary populations. For XPASS, we consider the vectors ${\mathbf{z}}_1$ and ${\mathbf{z}}_2$ of the z-scores for p SNPs derived from the target and auxiliary populations, respectively, and the m₁ × p matrix ${{\mathbf{X}}_1}^{\text{′}}$ and m₂ × p matrix ${{\mathbf{X}}_2}^{\text{′}}$ being the standardized reference genotype matrices from the corresponding populations. With these summary-level data, we show that XPASS approximates the posterior mean of SNP effect sizes in XPA as (see Appendix A):

$$\left[\begin{array}{l}{\hat{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}\mathbf{S}}\hfill \\ {\hat{\mathit{\mu }}}_2^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}\mathbf{S}}\hfill \end{array}\right]={[\left[\begin{array}{ll}{n}_1{\hat{\mathbf{R}}}_1\hfill & 0\hfill \\ 0\hfill & n_2{\hat{\mathbf{R}}}_2\hfill \end{array}\right]+{\left[\begin{array}{ll}\frac{{\hat{h}}_1^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_{12}}{1-{\hat{h}}_2^2}\hfill \\ \frac{{\hat{h}}_{12}}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_2^2}{1-{\hat{h}}_2^2}\hfill \end{array}\right]}^{-1}\otimes {\mathbf{I}}_p]}^{-1}\left[\begin{array}{l}\sqrt{\frac{n_1}{p}}{\mathbf{z}}_1\hfill \\ \sqrt{\frac{n_2}{p}}{\mathbf{z}}_2\hfill \end{array}\right],$$

where $\otimes$ denotes the Kronecker product, ${\hat{h}}_1^2$ and ${\hat{h}}_2^2$ are estimates of heritabilities $h_1^2$ and $h_2^2$ for the two populations, respectively, ${\hat{h}}_{12}$ is the estimate of co-heritability $h_{12}:=\rho h_1{h}_2$ between two populations, and ${\hat{\mathbf{R}}}_1={\mathbf{X}}_1^{\text{′}T}{\mathbf{X}}_1^{\text{′}}/m_1$ and ${\hat{\mathbf{R}}}_2={\mathbf{X}}_2^{\text{′}T}{\mathbf{X}}_2^{\text{′}}/m_2$ are the LD matrices of target and auxiliary populations, respectively. The parameter estimates ${\hat{h}}_1^2$, ${\hat{h}}_2^2$, and ${\hat{h}}_{12}$ can be computed using the summary-level datasets (Appendix A).^39,40 Again, the information is shared across populations through the genetic correlation. In practice, XPASS takes the heterogeneous LD patterns into account by computing the LD matrices using $\mathbf{X}{\text{′}}_1$ and $\mathbf{X}{\text{′}}_2$ from either subsamples of ${\mathbf{X}}_1$ and ${\mathbf{X}}_2$ or external reference genotypes from the two populations. Because the LD between SNPs decreases exponentially with their distance, we approximate the LD matrices using block diagonal matrices by assuming the SNPs between LD blocks are approximately independent.⁴¹ The heterogeneous LD patterns result in different LD partitions across populations. Therefore, we build the approximated LD matrices using partitions derived from either the target or the auxiliary population. The application of XPASS to real datasets suggests that our method is insensitive to the partition strategy. To obtain the dosage scale effect size, we compute ${\tilde{\mathit{\mu }}}_{1j}^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}\mathbf{S}}={\hat{\mathit{\mu }}}_{1j}^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}\mathbf{S}}/\left(s_j\sqrt{p}\right),j=1,\dots ,p$. When the genotypes of a new sample is available, we can obtain the PRS by ${\text{PRS}}_{new}={\mathbf{g}}_{1,new}^T{\tilde{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}\mathbf{S}}$.

XPASS₊ for capturing large population-specific effects

Similarly to XPA₊, we extend XPASS as XPASS₊ to incorporate large population-specific effects to improve prediction performance. We denote $\mathbf{X}{\text{′}}_{l1}\in {\mathbb{R}}^{m_1\times l_1}$ and $\mathbf{X}{\text{′}}_{l2}\in {\mathbb{R}}^{m_1\times l_2}$ as the standardized genotype matrices collecting the columns of $\mathbf{X}{\text{′}}_1$ and $\mathbf{X}{\text{′}}_2$ that correspond to the SNPs with large effects, and ${\mathbf{z}}_{l1}\in {\mathbb{R}}^{l_1}$ and ${\mathbf{z}}_{l2}\in {\mathbb{R}}^{l_2}$ as sub-vectors of ${\mathbf{z}}_1$ and ${\mathbf{z}}_2$ corresponding to the SNPs with large effects, respectively. The large genetic effects can be estimated by XPASS₊ as (see Appendix A):

$$\begin{array}{c}\left[\begin{array}{l}{\hat{\mathit{\gamma }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}{\mathbf{S}}_{+}}\hfill \\ {\hat{\mathit{\gamma }}}_2^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}{\mathbf{S}}_{+}}\hfill \end{array}\right]={\left(\left[\begin{array}{ll}{n}_1{\hat{\mathbf{R}}}_{l1}\hfill & 0\hfill \\ 0\hfill & n_2{\hat{\mathbf{R}}}_{l2}\hfill \end{array}\right]-\left[\begin{array}{ll}{n}_1{\hat{\mathbf{R}}}_{ls1}\hfill & 0\hfill \\ 0\hfill & n_2{\hat{\mathbf{R}}}_{ls2}\hfill \end{array}\right]{\left({\left[\begin{array}{ll}\frac{{\hat{h}}_1^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_2^2}\hfill \\ \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_2^2}{1-{\hat{h}}_2^2}\hfill \end{array}\right]}^{-1}\otimes {\mathbf{I}}_p+\left[\begin{array}{ll}{n}_1{\hat{\mathbf{R}}}_1\hfill & 0\hfill \\ 0\hfill & n_2{\hat{\mathbf{R}}}_2\hfill \end{array}\right]\right)}^{-1}\left[\begin{array}{ll}{n}_1{\hat{\mathbf{R}}}_{sl1}\hfill & 0\hfill \\ 0\hfill & n_2{\hat{\mathbf{R}}}_{sl2}\hfill \end{array}\right]\right)}^{-1}\\ \left(\left[\begin{array}{l}\sqrt{\frac{n_1}{p}}{\mathbf{z}}_{l1}\hfill \\ \sqrt{\frac{n_2}{p}}{\mathbf{z}}_{l2}\hfill \end{array}\right]-\left[\begin{array}{ll}{n}_1{\hat{\mathbf{R}}}_{ls1}\hfill & 0\hfill \\ 0\hfill & n_2{\hat{\mathbf{R}}}_{ls2}\hfill \end{array}\right]{\left({\left[\begin{array}{ll}\frac{{\hat{h}}_1^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_2^2}\hfill \\ \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_2^2}{1-{\hat{h}}_2^2}\hfill \end{array}\right]}^{-1}\otimes {\mathbf{I}}_p+\left[\begin{array}{ll}{n}_1{\hat{\mathbf{R}}}_1\hfill & 0\hfill \\ 0\hfill & n_2{\hat{\mathbf{R}}}_2\hfill \end{array}\right]\right)}^{-1}\left[\begin{array}{l}\sqrt{\frac{n_1}{p}}{\mathbf{z}}_1\hfill \\ \sqrt{\frac{n_2}{p}}{\mathbf{z}}_2\hfill \end{array}\right]\right),\end{array}$$ (Equation 9)

where ${\hat{\mathbf{R}}}_{l1}={\mathbf{X}}_{l1}^{\text{′}T}\mathbf{X}{\text{′}}_{l1}/m_1$ and ${\hat{\mathbf{R}}}_{l2}={\mathbf{X}}_{l2}^{\text{′}T}\mathbf{X}{\text{′}}_{l2}/m_2$ are the LD matrices of large-effect SNPs and ${\hat{\mathbf{R}}}_{ls1}={\mathbf{X}}_{l1}^{\text{′}T}\mathbf{X}{\text{′}}_1/m_1$ and ${\hat{\mathbf{R}}}_{ls2}={\mathbf{X}}_{l2}^{\text{′}T}\mathbf{X}{\text{′}}_2/m_2$ are the SNP correlation matrices between large-effect SNPs and all SNPs from the two populations, respectively. With the estimated fixed effects given in Equation 9, the posterior means can be computed as:

$$\left[\begin{array}{l}{\hat{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}{\mathbf{S}}_{+}}\hfill \\ {\hat{\mathit{\mu }}}_2^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}{\mathbf{S}}_{+}}\hfill \end{array}\right]={[\left[\begin{array}{ll}{n}_1{\hat{\mathbf{R}}}_1\hfill & 0\hfill \\ 0\hfill & n_2{\hat{\mathbf{R}}}_2\hfill \end{array}\right]+{\left[\begin{array}{ll}\frac{{\hat{h}}_1^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_{12}}{1-{\hat{h}}_2^2}\hfill \\ \frac{{\hat{h}}_{12}}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_2^2}{1-{\hat{h}}_2^2}\hfill \end{array}\right]}^{-1}\otimes {\mathbf{I}}_p]}^{-1}\left[\begin{array}{l}\sqrt{\frac{n_1}{p}}{\mathbf{z}}_1-{\hat{\mathbf{R}}}_{sl1}{\hat{\mathit{\gamma }}}_1\hfill \\ \sqrt{\frac{n_2}{p}}{\mathbf{z}}_2-{\hat{\mathbf{R}}}_{sl2}{\hat{\mathit{\gamma }}}_2\hfill \end{array}\right].$$ (Equation 10)

Finally, to obtain the effect sizes for the dosage genotypes, we re-scale both the posterior mean and the estimated fixed effects by ${\tilde{\mathit{\mu }}}_{1j}^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}{\mathbf{S}}_{+}}={\hat{\mathit{\mu }}}_{1j}^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}{\mathbf{S}}_{+}}/\left(s_j\sqrt{p}\right)$, for $j=1,\dots ,p$ and ${\tilde{\mathit{\gamma }}}_{1j}={\hat{\mathit{\gamma }}}_{1j}^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}{\mathbf{S}}_{+}}/\left(s_j\sqrt{p}\right)$, for $j=1,\dots ,l_1$, respectively. When a new observation with genotype ${\mathbf{g}}_{1,new}\in {\mathbb{R}}^p$ is available, its PRS can be computed as ${\text{PRS}}_{new}={\mathbf{g}}_{1,new}^T{\tilde{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}{\mathbf{S}}_{+}}+{\mathbf{g}}_{l1,new}^T{\tilde{\mathit{\gamma }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}\mathbf{S}{\mathbf{S}}_{+}}$, where ${\mathbf{g}}_{l1,new}\in {\mathbb{R}}^{l_1}$ is the vector of dosage genotypes corresponding to the SNPs with large effects.

Simulation design

We conducted a comprehensive simulation study to compare the performance of XPA and XPASS with other PRS approaches for individual-level data and summary data, respectively. For individual-level approaches, we investigated the prediction accuracy of XPA and XPA₊ in comparison with three scalable PRS models, including BLUP and bvBLUP implemented in the GCTA,²¹ LASSO,²² and XP-BLUP.³² The BLUP and bvBLUP were fitted using the GCTA software v.1.93 (GCTA-BLUP and GCTA-bvBLUP). The LASSO was fitted using the R package glmnetPlus. For single-population-base approaches, GCTA-BLUP and LASSO, we trained them with either only the target dataset or only the auxiliary dataset. In addition, we trained GCTA-BLUP with the combined dataset obtained by directly merging the target and the auxiliary data (GCTA-BLUP-combine). For GCTA-bvBLUP, we followed the instruction from the GCTA forum for integrating two independent samples. For XP-BLUP, we considered 6 settings of p value threshold for selecting candidate SNPs from the auxiliary GWAS results: 5 × 10⁻⁶, 1 × 10⁻⁶, 5 × 10⁻⁷, 1 × 10⁻⁷, 5 × 10⁻⁸, 1 × 10⁻⁸. We revised the original XP-BLUP script to allow for the support of multi-threading computation. For XPA₊, we selected the large-effect SNPs by applying the P+T procedure to the target dataset with LD threshold r² = 0.1 and p value threshold 1 × 10⁻⁶.

For summary-level approaches, we compared XPASS and XPASS₊ with three alternative summary-level PRS models: P+T procedure, LDpred-inf,²⁹ and lassosum.³⁰ As the performance of non-infinitesimal LDpred is often similar to lassosum,^30,42 we only considered LDpred-inf, a special case of LDpred with closed form solution. The LDpred-inf was computed using the ldpred software v.1.0.11 with LD radius set at the recommended value 300,000/3,000 = 100. For P+T procedure, we set the region size as 1,000 kb and the LD threshold as 0.1 and considered 10 p value thresholds according to a previous study:⁴³ 5 × 10⁻⁸, 1 × 10⁻⁶, 1 × 10⁻⁴, 0.001, 0.01, 0.05, 0.1, 0.2, 0.5, and 1. We used R package ieugwasr to compute effect sizes in P+T procedure. The lassosum was fitted using the R package v.0.4.4 with default tuning parameter settings. Because these summary-level methods cannot handle multi-ancestry datasets, we trained these models with either only the target dataset or only the auxiliary dataset. To assess the prediction utility of MTAG, we applied MTAG to combine the datasets from the target and auxiliary populations, and then applied LDpred-inf to construct PRS (MTAG+LDpred-inf). For XPASS₊, we selected the large-effect SNPs by applying the P+T procedure to the target dataset with LD threshold r² = 0.1 and p value threshold 1 × 10⁻⁶.

To mimic realistic LD patterns, we used the genotypes from the Chinese and UKBB samples to generate the target and auxiliary individuals, respectively. For the target population, 5,000 samples were randomly drawn from the Chinese dataset. For the auxiliary population, we explored seven different sample sizes using random samples from the UKBB dataset: 0, 5,000, 10,000, 30,000, 50,000, 70,000, and 90,000. We included 300,000 SNPs in total by selecting the first 30,000 SNPs from each of chromosomes 1 to 10. Given these SNPs, we simulated their effect sizes with heritability $h_1^2=h_2^2=0.5$ and generated the phenotypes in both populations. To investigate a wide spectrum of genetic architectures, we varied the proportion of non-zero genetic effects and the genetic correlation between the two populations. Specifically, we set the proportion of non-zero genetic effects to be 0.9, 0.01, or 0.001, corresponding to the highly polygenic scenario, the moderately sparse scenario, and the sparse scenario, respectively. We considered three settings of the overall genetic correlation ρ: 0, 0.4, and 0.8, corresponding to no, moderate, and high genetic correlation, respectively. As the effect sizes may not be correlated for all SNPs, we generated the nonzero effects by simulating 80% of them from the bi-variate normal distribution $\mathcal{N}\left(0,\left[\begin{array}{ll}\frac{h_1^2}{p}\hfill & \frac{\rho h_1{h}_2}{0.8p}\hfill \\ \frac{\rho h_1{h}_2}{0.8p}\hfill & \frac{h_2^2}{p}\hfill \end{array}\right]\right)$ and the rest from two independent normal distributions $\mathcal{N}\left(0,\frac{h_1^2}{p}\right)$ and $\mathcal{N}\left(0,\frac{h_2^2}{p}\right)$ for populations one and two, respectively, where p is the number of nonzero effects. By the combinatorial configurations of the proportion of non-zero effects and genetic correlation, nine scenarios were considered in our analysis. To evaluate the prediction performance, we sampled 3,000 additional individuals from the Chinese dataset serving as the test set of the target population. For each simulation setting, we computed the averaged prediction R² from 10 replications.

Among the individual-level methods considered, XPA, GCTA-BLUP, GCTA-bvBLUP, and XP-BLUP support multi-threading computation. To examine the computational and memory efficiency of these methods, we further evaluated their CPU time and memory usage when different numbers of SNPs were included in the model: 100,000, 200,000, and 300,000. The analyses were performed with 16 threads on the platform of Intel Xeon Gold 6152 CPU.

Application of XPA and XPASS to predict height and BMI in the Chinese population

Following the simulation studies, we applied XPA and XPASS to construct PRSs for height and BMI in the Chinese population by integrating European samples from UKBB and Asian samples from Chinese cohort and BBJ. In the individual-level PRS analysis, we split the Chinese data into the training and testing sets and only included the SNPs overlapping with UKBB. For height, we used 21,069 samples for training and held out 11,852 samples for testing. After quality control and overlapping, 3,776,575 SNPs were used to fit the model. For BMI, we used 18,575 samples for training and 10,572 for testing. After quality control and overlapping, 3,777,871 SNPs were used to fit the model. For Chinese population, we included age, sex, and first 10 principal components as covariates. For UKBB, we used the top 20 principal components, age, squared age, sex, genotyping arrays, and sequencing platforms as covariates.

To benchmark the performance of XPA and XPA₊ with existing approaches, we compared the predictive R² of XPA and XPA₊ with six other PRS models. Four of the six methods are designed only for single population analysis, including BLUP, which serves as a baseline model; snpnet, a memory-efficient LASSO implementation for large-scale genetic prediction based on R packages glmnetPlus and glmnet;²⁶ BayesR, a hierarchical Bayesian mixture model;^23,24 and BayesS, which accounts for the impact of natural selection.²⁵ We trained all these four models on the Chinese dataset, and additionally trained BLUP on the UKBB dataset using our efficient implementation. The fifth method, GCTA-bvBLUP, was trained with all Chinese samples and 150K subsamples randomly drawn from the UKBB dataset because the large memory requirement of GCTA-bvBLUP makes it infeasible to include more UKBB samples (see the results section for details). We also included a recently proposed approach for cross-population prediction,³² XP-BLUP, in our comparison. We implemented the conventional BLUP method in our XPA software, making it more efficient and scalable to biobank-scale data. Since parameter-tuning is required in snpnet, we randomly took one-third of training samples as validation set and fitted the LASSO model on the rest of the training samples. The GCTB v2.0 was used to fit the BayesR and BayesS models with 25,000 MCMC iterations in total and 5,000 burn-in iterations. We set the initial value of heritability at 0.3 for height and 0.15 for BMI. In BayesS, we set the initial value of the proportion of non-zero effects at 0.05 for both height and BMI. The XP-BLUP requires a list of candidate SNPs selected from the UKBB GWAS results by taking a threshold of p values. We considered eight thresholds for selecting SNPs: 5 × 10⁻⁶, 1 × 10⁻⁶, 5 × 10⁻⁷, 1 × 10⁻⁷, 5 × 10⁻⁸, 1 × 10⁻⁸, 5 × 10⁻⁹, and 1 × 10⁻⁹. After tuning, the optimal thresholds were found at 1 × 10⁻⁸ and 5 × 10⁻⁷ for height and BMI, respectively. For XPA₊, we set the LD threshold at r² = 0.1 and the p value threshold at 5⁻⁸.

In the summary-level PRS analysis, we obtained the summary statistics of the Chinese dataset and UKBB using the BOLT-LMM software³⁶ and additionally included summary statistics from BBJ (∼170,000 Japanese samples)^33,34 as an alternative training data from the target population. We took the intersection of SNPs in the Chinese dataset, UKBB and BBJ, leading to 3,621,504 SNPs to be included in height and 3,562,502 SNPs to be included in BMI, respectively. We first randomly sub-sampled 2,000 individuals form both UKBB and the Chinese dataset as the LD reference panels for the two populations.

Here we mainly compared XPASS and XPASS₊ with LDpred and P+T because other related methods with different assumptions on effect sizes, such as SBayesR,⁴³ are expected to have very minor improvement, as shown in the aforementioned individual-level analysis. Because LDpred and P+T were developed for single-population analysis, we considered two ways for training the PRS models. The first way was to train the models separately using the Chinese cohort, BBJ, or UKBB. The second way was to first combine the target and auxiliary datasets using MTAG and then train the models with the combined datasets. When MTAG was applied, a covariance matrix of the estimation error should be first constructed and provided as an input.³¹ Because the two datasets were from different populations, we applied LD score regression to estimate the intercepts of the Chinese cohort and UKBB summary datasets with their corresponding reference genotypes, respectively. After that, the estimated intercepts were used to construct the diagonal elements of the covariance matrix. The off-diagonal elements of the covariance matrix were set to zero because there was no sample overlap between populations. For XPASS and XPASS₊, we considered two configurations of the training sets, i.e., Chinese + UKBB and BBJ + UKBB. Assuming only the SNPs within the same LD block are correlated, XPASS approximates the LD matrices by partitioning the genome into nearly independent blocks. Because the LD block partition is not aligned in EAS and EUR,⁴¹ we used the LD block partition derived from both EAS and EUR to construct PRS and then evaluated the sensitivity of PRS to the two of LD block partition strategies.

Because both LDpred and P+T have tuning parameters, we considered a number of parameter settings and determine the optimal values by evaluating prediction performance on the test set. For LDpred, we considered nine settings of the proportion of non-zero effects: 1 × 10⁻⁴, 5 × 10⁻⁴, 1 × 10⁻³, 5 × 10⁻³, 1 × 10⁻², 5 × 10⁻², 1 × 10⁻¹, 5 × 10⁻¹, and 1. For height, the optimal values turned out to be 5 × 10⁻² in Chinese, 1 in BBJ, 1 in UKBB, 10⁻¹ in MTAG-Chinese, and 1 in MTAG-UKBB (Figures S25 and S29). For BMI, the optimal values were 1 × 10⁻³ in Chinese, 5 × 10⁻¹ in BBJ, 1 in UKBB, 5 × 10⁻¹ in MTAG-Chinese, and 1 in MTAG-UKBB (Figures S26 and S30).

For P+T procedure, we set the LD threshold at r² = 0.1 and considered ten settings of the proportion of p value threshold: 5 × 10⁻⁸, 1 × 10⁻⁶, 1 × 10⁻⁴, 1 × 10⁻³, 1 × 10⁻², 5 × 10⁻², 1 × 10⁻¹, 2 × 10⁻¹, 5 × 10⁻¹, and 1. For height, the optimal values turned out to be 1 × 10⁻⁴ in Chinese, 1 × 10⁻³ in BBJ, 1 × 10⁻⁴ in UKBB, 5 × 10⁻² in MTAG-Chinese, and 1 × 10⁻² in MTAG-UKBB (Figures S25 and S29). For BMI, the optimal values were 1 × 10⁻⁶ in Chinese, 5 × 10⁻² in BBJ, 1 × 10⁻² in UKBB, 1 × 10⁻¹ in MTAG-Chinese, and 1 × 10⁻² in MTAG-UKBB (Figures S26 and S30). Since the parameter tuning process involved the testing data, the performance of LDpred and P+T reported here could be slightly optimistic.

When XPASS₊ was applied, we set the LD threshold r² = 0.1 and varied the p value threshold at {10⁻⁵,10⁻⁶,10⁻⁷,10⁻⁸} to include large population-specific effects. The selected SNPs are treated as covariates only in the target population. As shown in Figure S33, the prediction performance of XPASS₊ was insensitive to the p value threshold. Therefore, we reported the results obtained with p value threshold at 10⁻⁶ and used 10⁻⁶ as the default setting in the XPASS software.

We used the prediction R² to examine the prediction performance. Given a test set $\left\{{\mathbf{y}}_{new},{\mathbf{G}}_{new},{\mathbf{Z}}_{new}\right\}$, we used the predictive R² to evaluate the performance of PRS. The PRS for the testing samples is constructed by ${\text{PRS}}_{new}={\mathbf{G}}_{new}{\tilde{\mathit{\mu }}}_1$, where ${\tilde{\mathit{\mu }}}_1$ is the posterior mean of the effect sizes on the dosage genotypes. Then, the predictive R² of PRS was defined as the squared correlation between PRS_new and the residual obtained by regressing ${\mathbf{y}}_{new}$ on ${\mathbf{Z}}_{new}$, denoted as ${\mathbf{y}}_{res}$:

$$R_{\text{PRS}}^2=corr{\left({\mathbf{y}}_{res},{\text{PRS}}_{new}\right)}^2.$$

When the covariates were taken into account, XPA generated prediction on the original scale of phenotype: ${\hat{\mathbf{y}}}_{new}={\text{PRS}}_{new}+{\mathbf{Z}}_{1,new}{\hat{\mathit{\omega }}}_1-\sum _j{\tilde{\mu }}_{1j}^{\mathbf{X}\mathbf{P}\mathbf{A}}{\overline{\mathbf{g}}}_{1j}$. In this case, we evaluated the R² by computing the squared correlation between ${\mathbf{y}}_{new}$ and ${\hat{\mathbf{y}}}_{new}$:

$$R_{\hat{\mathbf{y}}}^2=corr{\left({\mathbf{y}}_{new},{\hat{\mathbf{y}}}_{new}\right)}^2.$$

Collection, genotyping, and imputation of Chinese sample

To evaluate the prediction performance of our framework, we have collected genotypes of Chinese individuals from the WeGene platform and participants have signed the consent form. The study was reviewed and approved by the Committee on Research Practices of HKUST in strict compliance with regulations regarding ethical considerations and personal data protection. To comply with the regulations of the Human Genetic Resources Administration of China (HGRAC), all Chinese genotypic and phenotypic data were processed and analyzed in a server located in Shenzhen, China. Researchers who request access to the summary statistics from the Chinese samples must get permission from Ministry of Science and Technology of the People’s Republic of China.

DNA extraction and genotyping were performed on saliva samples. A total of 35,908 Chinese participants were genotyped on the Illumina or Affymetrix platforms. Among all participants, 21,830 were genotyped on the Affymetrix WeGene V1 Arrays covering 596,744 SNPs at the WeGene genotyping center, Shenzhen. The WeGene V1 Array optimized the identification of all known paternal and maternal lineages through adding EAS-relevant 18,963 Y chromosome and 4,448 mtDNA phylogenetic SNPs.⁴⁴ The remaining 14,078 individuals were genotyped on Illumina WeGene V2 Arrays with a total of about 700,000 SNPs at the WeGene genotyping center, Shenzhen. The WeGene V2 array was designed based on the Illumina Infinium Global Screening Array.

Imputation of unobserved genetic variants was performed using the 1000 Genomes Project Phase 3 reference panel.¹⁵ All datasets were phased by SHAPEIT2⁴⁵ and imputed by IMPUTE2⁴⁶ using regular steps and parameters. SNP-level (INFO score$>$0.5) and genotype-per-participant-level (genotype probability$>$0.9) filters were used to exclude poorly imputed variants.

Sample description of the Chinese cohort

The 35,908 genotyped Chinese participants in the Chinese cohort cover 33 out of 34 administrative divisions and 43 out of 56 ethnic groups in China, with the majority of samples from the Southeastern area (Figure S2). Among the 28,796 participants with self-reported ethnic information, there are 26,953 (93.6%) Han Chinese, 440 (1.5%) Manchu, 385 (1.3%) Hui, 201 Mongols (0.7%), and 817 (2.8%) from other minority ethnic groups.

To explore the population structure of the Chinese cohort, we first combined genotypes data from the Chinese cohort and the 1000 Genomes Project and performed a principal component analysis (PCA). As shown in Figure S2, the Chinese samples are overlapped with EAS from the 1000 Genomes Project, while its variance is larger because it is comprised of both Han Chinese and multiple minority groups. We then carried out PCA within Chinese to study differentiation across minority ethnic groups in China. Since the Han Chinese dominates the sample makeup, directly applying PCA to all samples fails to capture the variation among minority groups. Therefore, we first obtained the PC loadings from a subset of samples that included 500 randomly selected Han Chinese (roughly matching the number of Manchu people) and then computed the PC scores of all samples using these PC loadings (Figure S2). The first two principal components represent the latitudinal and longitudinal differentiation behind Chinese population structure. The Han Chinese differs substantially along the latitudinal gradient, while less differentiation is found along the longitude direction, which is consistent with previous reports.^{47, 48, 49} Among the minority ethnic groups, Manchus are genetically closest to the Han Chinese in the northeastern China. In the same area, Koreans in China are more distant to Han Chinese compared to Manchus. The most differentiated groups are Mongols, Hui, and Tibetan from the northwestern area. In the South China, Zhuang people also differ substantially from Han Chinese.

We considered two anthropometric phenotypes in our analysis, height and BMI. After quality control of genotype and phenotype data (see supplementary note), there were 32,921 samples with self-reported height and 29,147 samples with BMI computed from height and weight. For both phenotypes, there are slightly fewer males than females (15,406 compared to 17,515 for height and 13,721 compared to 15,426 for BMI). The overall distributions of height and BMI are summarized in Figure S1. Regarding the geometric distribution, the Northern Chinese are generally higher in both males and females (Figures S2 and S4). A similar latitudinal differentiation is observed in BMI, where the individuals from the north have higher obesity indices than those from the south (Figures S2 and S6). Besides, the older people are generally shorter and tend to have higher BMI (Figures S5 and S7).

Sample description of UKBB data

The UKBB genotype and phenotype data were obtained from the UK Biobank Access Management System (see web resources). We used the measured height phenotype extracted from Data Field 50 and the BMI value constructed from height and weight from Data Field 21001. To restrict the samples within EUR ancestry, we identified the individuals with self-reported ethnic background as “white” in Data Field 21000 and included only these samples for analysis. After phenotype and genotype quality control (see supplemental note), the UKBB data contain genotype information of 3,776,575 SNPs for 429,312 individuals in the analysis of height and 3,777,818 SNPs for 428,864 individuals in the analysis of BMI. We obtained the summary statistics of the UKBB datasets using the BOLT-LMM software³⁶ with age, squared age, sex, and the first 20 genomic PCs as covariates. The same set of covariates was included in the construction of PRS when applying XPA.

Sample description of GWAS data from African population

To demonstrate the generality of our framework to other populations, we applied XPA and XPASS to two GWAS datasets comprising thousands of samples from African ancestry: Institute for Personalized Medicine (IPM) BioMe biobank¹⁰ (phs000925.v1.p1) and UKBB. IPM BioMe biobank aimed to study clinical care processes, with 28% samples of which were African Americans. The African participants from the IPM BioMe cohort were genotyped on Illumina Human OmniExpressExome Chip with a total of about 500K SNPs that passed an initial quality control (QC) process. Imputation of unobserved genetic variants was performed using the 1000 Genomes Project Phase 3 reference panel. All datasets were phased by SHAPEIT2 and imputed by Minimac4^46,50 using regular steps and default parameters.

After removing ancestry and phenotype outliers and samples with ambiguous sex (see supplemental note), 5,491 confirmed African participants from IPM were included in our study. For UKBB, 3,323 participants with self-reported African ancestry were also included, after the same procedure of sample QC, 2,931 samples remained for our analysis. By projecting the genotypes of IPM and UKBB samples to the PC coordinates derived from the 1000 Genomes Project, we found that the Africans from both datasets overlapped with the AFR samples from the 1000 Genomes Project (Figure S3). We observed similar phenotypic distributions for height between IPM and UKBB Africans, before or after we regressed the covariates (e.g., age, squared age, sex, first 20 genomic PCs) out.

To evaluate the performance of PRS approaches, we combined the African samples from IPM and UKBB, leading to a total of 8,422 African samples with 2,690,737 overlapping SNPs. Then, we randomly selected 1K samples as testing data and used the remaining 7.4K samples as training data. We obtained the summary statistics of the training set using the BOLT-LMM software³⁶ with age, squared age, sex, and the first 20 genomic PCs as covariates. The same set of covariates was included in the construction of PRSs when applying XPA.

Results

Simulation study

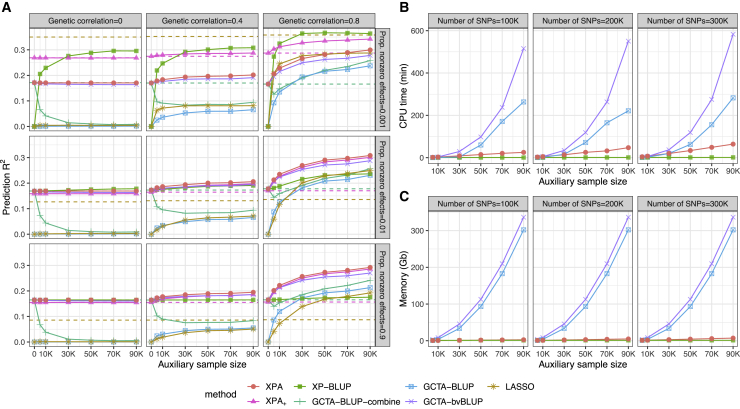
With data simulated as described above, we investigated the prediction accuracy of XPA in comparison with alternative methods. To gain some intuition, we first considered the single-population-based methods, such as BLUP and LASSO. These predictive models can be trained using samples from either the target population or the auxiliary population. The performance of BLUP and LASSO trained on the target population can serve as the reference results (dashed lines in Figure 1A). When the genetic correlation was zero, the prediction accuracy of BLUP and LASSO trained on the auxiliary dataset could not be improved regardless of the auxiliary sample size. When the genetic correlation became moderate ($\rho =0.4$) or strong ($\rho =0.8$), the prediction accuracy of BLUP and LASSO trained on the auxiliary dataset steadily improved as the auxiliary sample size increased. It is worthwhile to note that BLUP and LASSO trained on the auxiliary dataset were more accurate than those trained on the target population when the correlation was strong and the auxiliary sample size was large.

Figure 1.

Comparison of individual-level approaches in simulation studies

(A) Mean predictive R² of XPA, XPA₊, GCTA-BLUP, LASSO, and XP-BLUP in each of nine simulation scenarios. The dashed lines show the R² obtained by training with target dataset only. For XPA, XPA₊, XP-BLUP, and GCTA-bvBLUP, the solid lines show the R² obtained by combining both target and auxiliary datasets. For GCTA-BLUP-combine, the solid line shows the R² obtained by merging the target and auxiliary datasets. For GCTA-BLUP and LASSO, the solid lines show the R² obtained by training with auxiliary dataset only.

(B) CPU timings for XPA, XP-BLUP, and GCTA-BLUP are shown for increasing auxiliary sample size based on different numbers of SNPs.

(C) Memory usages for XPA, XP-BLUP, and GCTA-BLUP are shown for increasing auxiliary sample sizes based on different numbers of SNPs. Results are summarized from ten replicates.

Among the methods that combine both datasets, GCTA-BLUP-combine had the worst performance in most settings. As expected, when there was no genetic correlation, the inclusion of auxiliary dataset led to worse performance than using only the target dataset. When the genetic correlation was nonzero, the predictive R² first dropped and then increased with increasing auxiliary sample size. When the auxiliary sample size was large enough (e.g., n₂ > 30K), the performance of GCTA-BLUP-combine gradually converged to GCTA-BLUP. For GCTA-bvBLUP, it had similar predictive R² with XPA when the auxiliary sample size was comparable with the target sample size (i.e., $n_2\in \left\{\mathrm{0,5}K,10K\right\}$). However, GCTA-bvBLUP does not account for the allele frequency difference between two populations. Therefore, as we can expect, its prediction accuracy became worse than XPA when the auxiliary sample size was large (i.e., n₂ > 30K). Between the cross-population methods XPA and XP-BLUP, XPA was clearly the overall winner, as shown in Figure 1A. When the genetic correlation became moderate ($\rho =0.4$) or strong ($\rho =0.8$), the prediction accuracy of XPA steadily improved as the sample size of auxiliary population increased, suggesting that XPA was able to leverage the trans-ancestry genetic correlation for constructing PRSs. When either the genetic correlation or the auxiliary sample size approached zero, XPA reduced to BLUP which was trained on the target dataset, as no information could be borrowed from the auxiliary population in these cases. For XP-BLUP, it assumes that the top SNPs from the auxiliary dataset are more likely to have non-zero effects in the target population, but it does not model the correlation of effect sizes between populations. Therefore, it was worse than XPA in the polygenic and moderately sparse settings, but had better performance in the setting of highly sparse effects. However, in the highly sparse setting, XPA₊ extension achieved comparable performance with XP-BLUP by incorporating large population-specific effects. We also noted that the causal SNPs between the target and auxiliary populations largely overlapped in our simulation setting, which was preferred by XP-BLUP. We expect the performance of XPA₊ will be better than XP-BLUP when the causal SNPs with large effects are not largely overlapping between the two populations.

Among methods with the support of multi-threading computation (Figure 1B), XP-BLUP had the lowest computational cost and memory usage, as its computation was mostly based on the target dataset. While GCTA-BLUP, GCTA-bvBLUP, and XPA all had increased computational cost as the scale of the auxiliary dataset became larger, the CPU time of XPA was nearly linear in the sample size, providing higher efficiency than GCTA-BLUP and GCTA-bvBLUP when the auxiliary sample size was larger than 50,000. In addition, because we have adopted a memory-efficient strategy in storing genotypes, the memory cost of XPA was also linear in the auxiliary sample size and the number of SNPs. However, the memory cost of GCTA-BLUP and GCTA-bvBLUP increased quadratically with the sample size, limiting its usage in the biobank-scale data analysis.

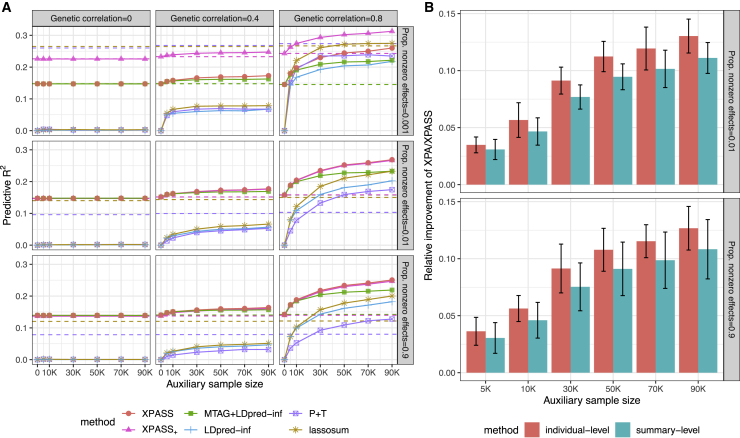
Next, we compared XPA with XPASS which takes the summary-level data as its input. When the auxiliary data are not available, XPA and XPASS reduce to their special cases, BLUP and LDpred-inf, respectively. When the auxiliary sample size increased in our simulation, we measured the relative improvement of individual-level and summary-level approaches as the difference of prediction R² between XPA and BLUP, and that of XPASS and LDpred-inf, respectively. As shown in Figure 2B, XPA was slightly better than XPASS, suggesting that XPASS can provide comparable prediction improvement using only summary-level datasets. The advantage of XPA became more apparent as the auxiliary sample size increased, suggesting the importance of developing methods to handle biobank-scale individual-level data. These observations highlight the value of XPA and XPASS in different practical scenarios: XPASS provides well-powered PRSs using cross-population information based on summary-level datasets while XPA can achieve higher accuracy with the availability of individual-level datasets.

Figure 2.

Comparison of summary-level approaches in simulation studies

(A) Mean prediction R² in each of nine simulation scenarios. Compared methods include XPASS, XPASS₊, LDpred-inf, MTAG+LDpred-inf, P+T procedure, and lassosum. The dashed lines show the R² obtained by training with target dataset only. For XPASS, XPASS₊, and MTAG+LDpred-inf, the solid lines show the R² obtained by combining both target and auxiliary datasets. For other methods, the solid lines show the R² obtained by training with auxiliary dataset only.

(B) Relative improvement in predictive R² of XPA and XPASS as compared to GCTA-BLUP and LDpred-inf, respectively. Results are summarized from ten replications. Error bars represent ±1.96 of the standard error.

As a promising approximation to XPA, XPASS also outperformed existing summary-level PRS models. As shown in Figure 2, XPASS had nearly the same performance with LDpred-inf when either the genetic correlation was zero or the auxiliary dataset was unavailable, consistent with previous observations for individual-level methods. With the availability of the auxiliary dataset and non-zero genetic correlation, XPASS achieved the highest prediction R² among all compared methods in the polygenic and moderately sparse settings. In the highly sparse setting, its extension XPASS₊ had the best performance when the genetic correlation was high ($\rho =0.8$) and was comparable to alternative approaches with smaller genetic correlation ($\rho =0$ and 0.4). The prediction accuracy of both XPASS and XPASS₊ increased with larger auxiliary sample size and stronger genetic correlation. Of note, the improvement of XPASS had a very similar pattern in both the sparse scenario and the polygenic scenario, suggesting the robustness of XPASS to different genetic architectures.⁵¹ For models trained on the auxiliary dataset, P+T procedure had the lowest prediction accuracy, followed by LDpred-inf. Because lassosum adopts an elastic net model, it had comparable R² to LDpred-inf in the sparse scenario and outperformed LDpred-inf with larger sample size.

Construction of PRS for the Chinese population by XPA using the individual-level data from the Chinese cohort and UKBB

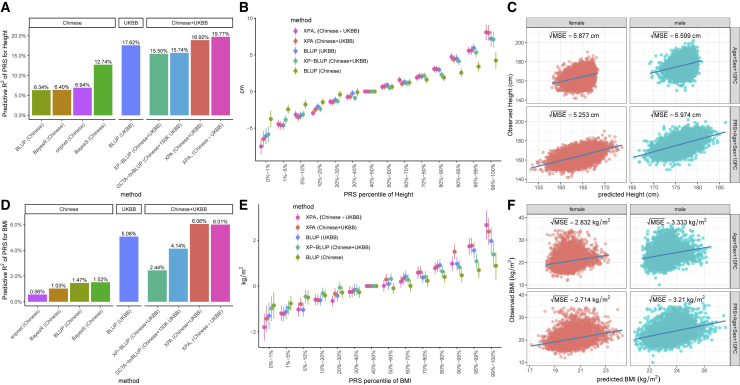
To study the performance of XPA and XPASS in real applications, we applied our approaches to construct PRSs for height and BMI in the Chinese population by integrating Chinese and UKBB data. We first investigate the performance of XPA using the individual-level data from Chinese and UKBB. To benchmark the performance of XPA with existing approaches, we compared the predictive R² of XPA with five other PRS models. XPA estimated the genetic correlations between Chinese and UKBB as 0.71 for height (${\hat{h}}_{\text{Chinese}}^2=33.6\text{\%}$ with SE = 1.8%, ${\hat{h}}_{\text{UKBB}}^2=41.2\text{\%}$ with SE = 0.7%) and 0.66 for BMI (${\hat{h}}_{\text{Chinese}}^2=16.7\text{\%}$ with SE = 1.7%, ${\hat{h}}_{\text{UKBB}}^2=18.1\text{\%}$ with SE = 0.1%), suggesting substantial genetic sharing between the two populations. As summarized in Figures 3A and 3D, regarding the overall performance, XPA had the highest accuracy for both height and BMI, with a substantial improvement compared to the baseline BLUP model trained on the Chinese data only. XPA outperformed the runner up (BLUP trained on UKBB) by 7.3% and 19.5% improvements for height and BMI, respectively. In contrast, both XP-BLUP and GCTA-bvBLUP, the two methods that integrated Chinese and UKBB datasets, had lower predictive R² than XPA. XP-BLUP was only slightly better than the methods trained on the Chinese data, but inferior to both XPA and BLUP trained on the UKBB only. This is because XP-BLUP only includes information from the significant SNPs in UKBB while XPA can borrow information from UKBB across the whole genome. Due to the memory bottleneck, GCTA-bvBLUP failed to include all UKBB samples, and so could not further improve the prediction accuracy (see Figure S23 for details of comparing the memory usage and computational time). GCTA-bvBLUP took 75.8 h and required 1.07 Tb to integrate 150K UKBB samples with all Chinese samples and achieved its best performance for constructing PRSs with predictive R² = 15.74%. In contrast, XPA used only 54.5 h (including 9 h for loading data, 3 h for estimating variance components, and 42.5 h for computing the posterior means and estimating fixed effects) and 385 Gb to analyze all Chinese and UKBB samples while achieving 20.2% and 46.4% improvement compared to GCTA-bvBLUP for height and BMI, respectively. When the population-specific large-effect SNPs were utilized by XPA₊, we found the predictive R² further increased to 19.72% in height and remained roughly the same with XPA in BMI.

Figure 3.

Prediction performance of XPA and related individual-level methods for height and BMI in the Chinese population

Predictive R² for height and BMI are shown in (A) and (D). Stratification ability of compared methods for height and BMI are shown in (B) and (E). Error bars represent ±1.96 of the standard error. (C) and (F) show the comparison of XPA with traditional risk factor models in height and BMI.

In clinical applications, it is critical to stratify individuals into different genetic risk groups. In our discussion, we use ‘risk’ as a generic term to describe a trait. To measure the ability of risk stratification, we compared the observed phenotypic values of individuals from the top PRS quantiles with those from the reference group (i.e., 40%–50% quantile in our analysis). For both height and BMI, XPA was most effective in screening individuals with high genetic risk (Figures 3B and 3E). Compared to their reference groups, the individuals in the top 1% of PRS were 8.04 cm (SE = 0.54 cm) taller in height and 2.38 kg/m² larger in BMI. When XPA₊ was applied, the stratification ability was further improved, with 8.27 cm increased height and 2.67 kg/m² larger BMI for the individuals in the top 1% of PRSs. By incorporating covariates, such as age, sex, and first 10 principal components, XPA can construct prediction on the original phenotypic scale. Compared to the risk prediction model using these covariates only, XPA achieved a three-fold improvement of R² in height and two-fold improvement of R² in BMI for both males and females. In terms of the square root of mean squared error ($\sqrt{\text{MSE}}$), XPA achieved a 10% improvement in height and 4% improvement in BMI for both males and females (Figures 3C and 3F), respectively. We also found XPA can improve the stratification ability of PRSs for different ethnic groups in the Chinese population (see supplemental note and Figure S24). These results suggest that the prediction accuracy in a target population can be greatly improved by XPA which can effectively incorporates trans-ancestry genetic information.

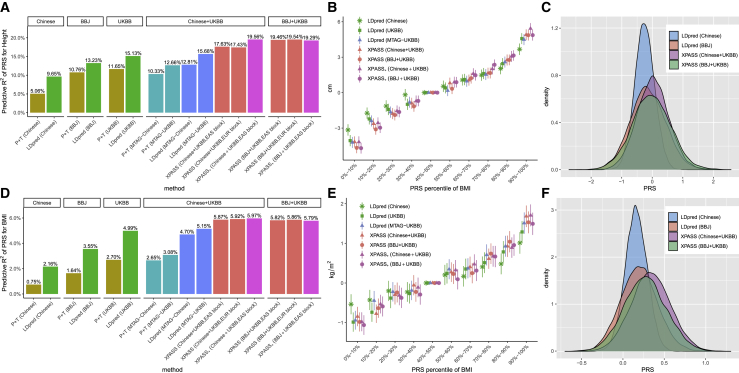
Construction of PRSs for the Chinese population by XPASS using the summary-level data from trans-ancestry groups

When the individual-level GWAS data are not accessible, XPASS can take summary statistics as its input to construct PRSs. As estimated by XPASS, the genetic correlation between Chinese and UKBB was 0.78 for height (${\hat{h}}_{\text{Chinese}}^2=35.0\text{\%}$ with SE = 2.4%, ${\hat{h}}_{\text{UKBB}}^2=43.6\text{\%}$ with SE = 2.3%) and 0.68 for BMI (${\hat{h}}_{\text{Chinese}}^2=16.7\text{\%}$ with SE = 1.9%, ${\hat{h}}_{\text{UKBB}}^2=19.4\text{\%}$ with SE = 0.7%), comparable to those estimated by XPA. For the genetic correlations between BBJ and UKBB, the estimated genetic correlation computed by XPASS was 0.71 for height (${\hat{h}}_{\text{BBJ}}^2=36.7\text{\%}$ with SE = 1.9%) and 0.68 for BMI (${\hat{h}}_{\text{BBJ}}^2=13.0\text{\%}$ with SE = 0.5%). Given the substantial genetic correlations, XPASS could effectively leverage the UKBB summary data to improve prediction accuracy in the Chinese population. As summarized in Figures 4A and 4D, the PRSs derived by XPASS largely outperformed LDpred and P+T trained with the training set from a single population. When XPASS was trained on Chinese+UKBB, the predictive R² for height increased from 9.65% (LDpred trained on the Chinese data only) to 17.6%. By either applying XPASS₊ or using BBJ+UKBB as training set, the predictive R² further increased to 19.5%, achieving $\left(19.5\text{\%}-15.1\text{\%}\right)/15.1\text{\%}\approx 29\text{\%}$ improvement compared to the best method using a single population. XPASS also outperformed MTAG with $\left(19.5\text{\%}-15.7\text{\%}\right)/15.7\text{\%}\approx 24\text{\%}$ improvement in terms of R², when the MTAG output was used as training data for LDpred and P+T. A similar trend of improvement was observed for BMI (R² = 5.9% for XPASS compared to R² = 2.16% for LDpred trained on Chinese and R² = 5.15% for LDpred trained on MTAG-UKBB), although the amount of improvement for BMI was less than that of height. This can be attributed to the lower heritability of BMI. We found that the choice of LD block partitions in XPASS had little effect on its performance, suggesting that XPASS is quite robust to the partitioning strategy.

Figure 4.

Prediction performance of XPASS and related summary-level methods for height and BMI in the Chinese population

Compared methods include XPASS, XPASS₊, LDpred, and P+T. For LDpred and P+T, one of the five sets of GWAS summary statistics were used as training set: Chinese only, BBJ only, UKBB only, improved Chinese and UKBB summary statistics obtained by combining the two datasets using MTAG (MTAG-Chinese and MTAG-UKBB). Predictive R² for height and BMI are shown in (A) and (D). Panels in (A) and (D) represent the datasets used for training. Stratification ability of XPASS and LDpred for height (B) and BMI (E). Error bars represent ±1.96 of the standard error. The distributions of PRSs constructed by XPASS and LDpred for height (C) and BMI (F).

When the PRS was used to stratify individuals, we found XPASS is more effective in identifying the groups with extreme genetic values (Figures 4B and 4E), consistent with the analyses conducted on the individual-level data. By comparing the PRS distributions (Figures 4C and 4F), we observed that PRSs derived by XPASS from the larger training sets often had broader distribution than those derived by LDpred from the smaller training sets. We note that this observation is consistent with the stratification analysis, since the model with higher stratification ability pulls individuals with extreme PRSs farther away from its mean value.

Influence of the auxiliary sample size on prediction performance

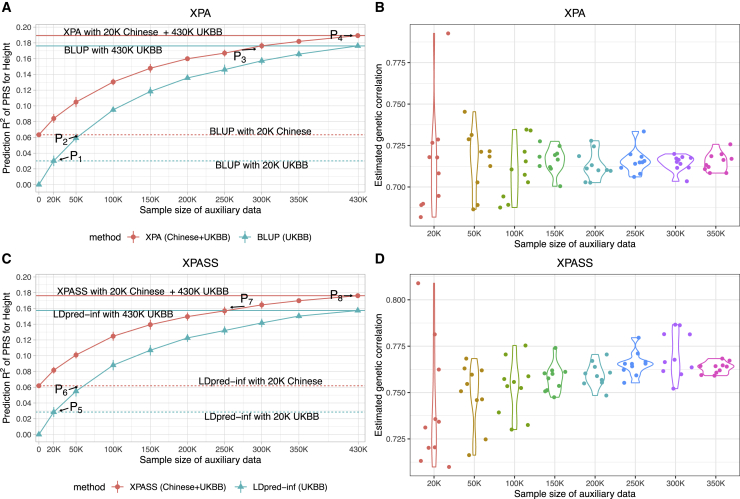
As we can observe in the simulation analyses, a large auxiliary dataset is critical for the performance of cross-population prediction. To systematically investigate how the sample size of auxiliary dataset influences the predictive performance of XPA, we randomly subsampled 20,000–300,000 UKBB individuals as an auxiliary dataset to construct a PRS for height in the Chinese population and evaluated the predictive R². We also trained BLUP using only auxiliary datasets as benchmark. As expected, due to the population difference between EAS and EUR, BLUP trained on 20,000 sample from UKBB was significantly inferior to that trained on 20,000 samples from Chinese (point P₁ in Figure 5A). When the UKBB sample size became larger than 50,000 (point P₂ in Figure 5A), it achieved better performance than the model trained on 20,000 samples from Chinese. In contrast, XPA provided stable estimate of genetic correlation (Figure 5B) regardless of the auxiliary sample size, so it always outperformed BLUP and effectively improved the prediction accuracy with the inclusion of more UKBB samples. It is also worth noting that XPA used only 20,000 Chinese and 300,000 Europeans to achieve the comparable performance with BLUP that was trained using all 430,000 European samples (point P₃ in Figure 5A), highlighting the importance of including samples from the target population in PRS construction. Comparing XPASS with its special case LDpred-inf²⁹ led to similar conclusions (Figures 5C and 5D). When 250,000 samples were included in the auxiliary dataset, XPASS achieved comparable performance with LDpred-inf using all 430,000 UKBB samples (point P₇ in Figure 5C). When XPASS₊ was applied, it further improved the performance and outperformed LDpred-inf when only 150,000 UKBB samples were included (Figure S34). By contrasting Figures 5A and 5C, we found individual-level approaches were generally better than summary-level approaches, which is consistent with our simulation results.

Figure 5.

Influence of the auxiliary sample size on the prediction performance of XPA and XPASS for predicting height

Predictive R² of XPA and XPASS are shown in (A) and (C). The corresponding trans-ancestry genetic correlations estimated by XPA and XPASS in each replicate are shown in (B) and (D). We trained XPA and XPASS by integrating 21,069 Chinese training samples with 20,000–300,000 random subsamples drawn from UKBB, where samples from UKBB could be viewed as the auxiliary dataset. The results are summarized from ten replications. Dashed horizontal lines in (A) and (C) mark the BLUP/LDpred-inf results obtained by using 20,000 samples from Chinese (red) and UKBB (cyan). Solid horizontal lines in (A) and (C) mark the results obtained by using all UKBB samples with (red) or without (cyan) Chinese. Points P₁−P₄ in (A) represent the situations where the auxiliary sample size achieves 20,000 (P₁), BLUP trained on about 50,000 UKBB samples achieves equivalent performance with that trained on 20,000 Chinese samples (P₂), XPA achieves identical performance with BLUP trained on all UKBB samples (P₃), and XPA is trained with all UKBB samples (P₄). Points P₅−P₈ in (C) represent the similar situations for summary-level approaches XPASS and LDpred-inf. Error bars represent ±1.96 of the standard error.

Construction of PRS for the African population by XPA and XPASS

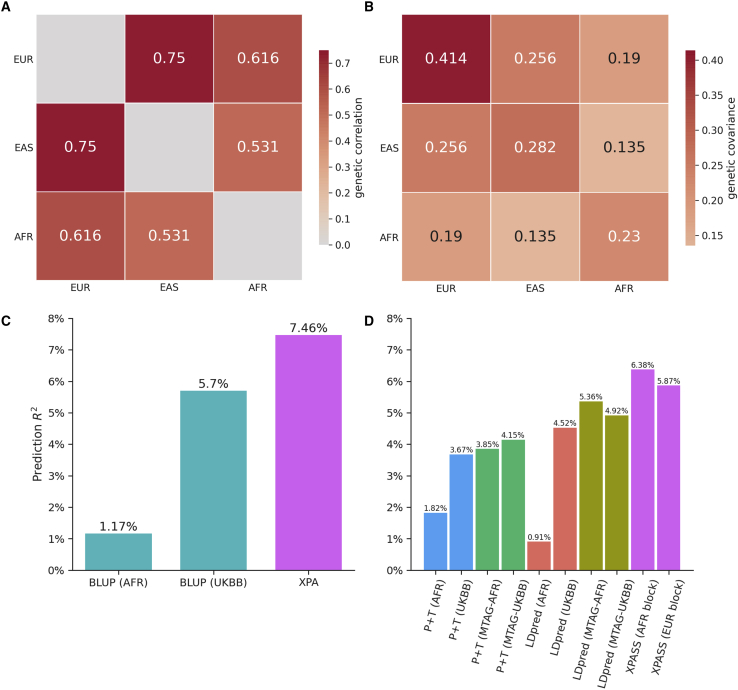
To demonstrate the generality of our framework to other populations, we compared the prediction performance of XPA and XPASS with existing approaches using GWAS data from the African population. First, we estimated the trans-ancestry genetic correlation among European, African, and East Asian populations for height. Our results suggest that trans-ancestry genetic correlations of East Asian and European populations are often stronger than those of African and European populations (Figure 6A), consistent with a previous report.⁵² To construct PRSs, we applied XPA and XPASS to integrate 7.4K African training samples with 430K European samples from UKBB. The prediction accuracy was evaluated on the 1K testing African samples. Clearly, both XPA (Figure 6C) and XPASS (Figure 6D) outperformed BLUP and LDpred and effectively improved the prediction accuracy with the inclusion of UKBB samples. The replication of better prediction performance by combining African and well-powered auxiliary European populations reassures us that, despite the more significant genetic distance, our XPA and XPASS framework still achieved state-of-the-art performance when compared to alternative methods.

Figure 6.

Application of XPA and XPASS for predicting height in the African population

Trans-ancestry genetic correlation (A) and genetic covariance (B) among European, African, and East Asian populations for height. (C) Prediction performance of XPA and BLUP for height measured by predictive R². (D) Prediction performance of XPASS, LDpred, and P+T for height measured by predictive R². For LDpred and P+T, one of the four sets of GWAS summary statistics were used as training set: African only, UKBB only, improved African and UKBB summary statistics obtained by combining the two datasets using MTAG (MTAG-AFR and MTAG-UKBB). For XPASS, we used the LD reference from either AFR or EUR population to construct independent LD blocks (AFR block and EUR block).

Discussion

The genetic architectures of various human traits have been mostly studied in samples with European ancestry, while non-European populations are still under-represented. Whether the genetic discoveries derived from Europeans can be transferred to non-Europeans remains unclear. In this study, we have proposed a unified framework for cross-population analysis (XPA and XPASS) to improve genetic prediction of under-represented populations by leveraging their trans-ancestry genetic correlations with a large and well-powered auxiliary GWAS dataset from another population. By combining the individual-level UKBB samples and Chinese samples, we were able to construct improved PRSs for height and BMI in the Chinese population, demonstrating the utility of trans-ancestry genetic prediction. We also showed that XPASS can achieve comparable prediction performance while only requiring summary-level data. When XPASS was trained using the summary-level BBJ and UKBB data, it produced even better prediction performance than XPA trained with the individual-level UKBB and Chinese data. As we do not have access to the individual-level BBJ data, XPASS offers an effective strategy to make use of existing data resources. We also observed improved prediction accuracy of PRSs in the African population when we applied XPA and XPASS to combine AFR and EUR GWAS data, suggesting the generality of our framework across global populations. When XPA₊ and XPASS₊ were applied, the population-specific effects can also be incorporated, leading to higher prediction accuracy in height. Because of the better performance and robustness to the choice of p value threshold, we recommend XPA₊ and XPASS₊ in practice.

Existing studies^53,54 have established the connection between the prediction accuracy of PRSs and various parameters from the theoretical perspective, including heritability, sample size, genetic correlation, and the effective number of chromosome segments. These theoretical properties have been supported by practical evidence. For example, Truong et al.⁵⁵ showed that the prediction accuracy of PRSs increased when individuals with higher-level relatedness were included in the analysis, which was due to the decreasing number of effective chromosome segments. Our work mainly focuses on the side of practice, aiming to develop a scalable and accurate method for the construction of PRSs in the cross-ancestry setting. We have observed that higher genetic correlation and inclusion of more target samples in the training set can improve prediction performance, which is consistent with the theory.⁵³

In real applications, by taking the advantage of widespread pleiotropy among phenotypes, many successful multi-trait models^{56, 57, 58} have been developed to produce powerful PRSs with increased prediction accuracy. While these approaches have been widely used in risk prediction within a single population, they may not be easily applied to integrate datasets from multi-ancestry backgrounds, since they do not take the heterogeneous genetic architectures into account. Our XPA framework, as compared to existing multi-trait models, provides a scalable solution to effectively combine multi-ancestry datasets by leveraging the stable estimate of trans-ancestry genetic correlation while accounting for the heterogeneous LD structure between populations. The success of XPA sheds light on the transferable genetic basis among global populations and demonstrates the benefits of integrating multi-ancestry datasets in genetic prediction.

While we have mainly focused on the anthropometric traits in this study, it is worth noting that XPA and XPASS can be applied to a wide class of phenotypes, such as complex diseases and molecular phenotypes. Due to the binary nature of diseases, their relationships with genotypes are often better captured by the liability threshold model (LTM). When the individual relatedness is low, the uni-variate linear mixed model (LMM) can be viewed as an approximation of the LTM.²⁷ A recent study⁵⁹ found that the bi-variate LMM can approximate the bi-variate LTM and produce consistent genetic correlation estimate for binary responses, suggesting the potential of applying XPA and XPASS to predict disease risks.

Our XPA framework needs more investigation in the following directions. First, XPA could be improved by allowing more flexible assumptions on SNP effect sizes. XPA assumes that, for a given population, the variance of the effect sizes of standardized genotypes is a constant, implicitly assuming that the SNP effect sizes increase as the allele frequencies decrease at the rate $1/\sqrt{2f\left(1-f\right)}$, where f is the allele frequency (AF). This assumption was also adopted in the previous trans-ancestry analysis.⁶⁰ Some recent studies have suggested that the effect sizes may not keep increasing when the allele frequency is small due to the negative selection.^25,61,62 It was shown that the prediction can benefit from introducing a selection parameter in BayesS (Figure 3A).

Second, the trans-ancestry genetic correlation may not be homogeneous across the genome. The differential selection pressure between populations can induce differences in their AF.^34,63 By sorting the SNPs according to the normalized AF difference between EAS and EUR, we estimated the genetic correlation of the effect sizes corresponding to the SNPs with the largest AF differences. As shown in the Figure S35, the trans-ancestry genetic correlation decreases as the AF difference increases. To assess the effect of AF difference on the prediction accuracy, we extended the XPASS model to include an additional genetic component that captures the effects of SNPs with large AF differences across populations (see supplemental note). From our real data analysis, we did not observe significant enrichment of heritability among these SNPs. As a result, we did not obtain a better PRS by modeling the effect sizes of these SNPs as an additional variance component in the extended model (see Table S1). Our results suggest that modeling the effect sizes of SNPs with large AF difference may not be the key to improve PRSs.

Third, the integration of multiple GWASs across populations may further improve the prediction accuracy of XPA and XPASS. It has been shown that jointly modeling multiple genetically correlated phenotypes can produce more accurate prediction within EUR population.^{56, 57, 58} By applying XPASS to estimate genetic correlations for a wide spectrum of phenotypes between EUR and EAS, we found that many genetically correlated traits discovered in EUR studies are replicated between EAS and EUR (supplemental note). Therefore, when a number of correlated phenotypes are simultaneously available in both populations, a more flexible model that jointly considers these phenotypes may further increase the prediction power.

Fourth, functional annotations may also be included to inform the prediction. The SNPs with biological functions, such as gene regulatory elements,^{64, 65, 66} epigenomic regulations,^40,67,68 and tissue-specific functional pathways, are usually enriched for the heritability of complex traits.^{69, 70, 71, 72, 73} Recent studies suggest that leveraging the functional annotations in prediction models trained on the EUR datasets produced PRSs with higher accuracy in both EUR^74,75 and EAS,⁷⁶ indicating the substantial overlap of functionally important variants across populations. Hence, integrating functional information to prioritize biologically relevant SNPs in complex traits can potentially increase the prediction accuracy of the XPA framework.

Declaration of interests

The authors declare no competing interests.

Published: March 25, 2021

Appendix A

Derivation of normalEquation 5

Note $\tilde{\mathbf{y}}\sim \mathcal{N}\left(0,\tilde{\mathbf{\Omega }}\right)$ has its first-order moment as zero. Thus, the MoM estimator is then obtained by matching the second-order moment based on the criterion of least-squares:

$${\text{argmin}}_{{\sigma }_1^2,{\sigma }_2^2,\delta ,{\sigma }_{\epsilon }^2,{\sigma }_{\xi }^2}\left|\right|\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T-\left(\tilde{\mathbf{X}}\left({\mathbf{\Sigma }}_{\beta }\otimes {\mathbf{I}}_p\right){\tilde{\mathbf{X}}}^T+{\tilde{\mathbf{\Sigma }}}_e\right)|{|}_F^2.$$ (Equation A1)

Knowing the fact that $\left|\right|\mathbf{B}|{|}_F=\sqrt{\text{tr}\left(\mathbf{B}{\mathbf{B}}^T\right)}$, the OLS objective function in Equation A1 can be re-written as

$${[\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T-\left(\tilde{\mathbf{X}}\left({\mathbf{\Sigma }}_{\beta }\otimes {\mathbf{I}}_p\right){\tilde{\mathbf{X}}}^T+{\tilde{\mathbf{\Sigma }}}_e\right)]}^T=\text{tr}[\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T+\tilde{\mathbf{X}}\left({\mathbf{\Sigma }}_{\beta }\otimes {\mathbf{I}}_p\right){\tilde{\mathbf{X}}}^T\tilde{\mathbf{X}}\left({\mathbf{\Sigma }}_{\beta }\otimes {\mathbf{I}}_p\right){\tilde{\mathbf{X}}}^T+{\tilde{\mathbf{\Sigma }}}_e{\tilde{\mathbf{\Sigma }}}_e-2\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T\tilde{\mathbf{X}}\left({\mathbf{\Sigma }}_{\beta }\otimes {\mathbf{I}}_p\right){\tilde{\mathbf{X}}}^T-2\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T{\tilde{\mathbf{\Sigma }}}_e+2\tilde{\mathbf{X}}\left({\mathbf{\Sigma }}_{\beta }\otimes {\mathbf{I}}_p\right){\tilde{\mathbf{X}}}^T{\tilde{\mathbf{\Sigma }}}_e]=\text{tr}[\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T+\left[\begin{array}{ll}{\sigma }_1^2{\tilde{\mathbf{K}}}_1\hfill & \delta {\tilde{\mathbf{K}}}_{12}\hfill \\ \delta {\tilde{\mathbf{K}}}_{12}^T\hfill & {\sigma }_2^2{\tilde{\mathbf{K}}}_2\hfill \end{array}\right]{\left[\begin{array}{ll}{\sigma }_1^2{\tilde{\mathbf{K}}}_1\hfill & \delta {\tilde{\mathbf{K}}}_{12}\hfill \\ \delta {\tilde{\mathbf{K}}}_{12}^T\hfill & {\sigma }_2^2{\tilde{\mathbf{K}}}_2\hfill \end{array}\right]}^T+\left[\begin{array}{ll}{\sigma }_{\epsilon }^2{\mathbf{M}}_1\hfill & 0\hfill \\ 0\hfill & {\sigma }_{\xi }^2{\mathbf{M}}_2\hfill \end{array}\right]{\left[\begin{array}{ll}{\sigma }_{\epsilon }^2{\mathbf{M}}_1\hfill & 0\hfill \\ 0\hfill & {\sigma }_{\xi }^2{\mathbf{M}}_2\hfill \end{array}\right]}^T]+\text{tr}[-2\left[\begin{array}{ll}{\tilde{\mathbf{y}}}_1{\tilde{\mathbf{y}}}_1^T\hfill & {\tilde{\mathbf{y}}}_1{\tilde{\mathbf{y}}}_2^T\hfill \\ {\tilde{\mathbf{y}}}_2{\tilde{\mathbf{y}}}_1^T\hfill & {\tilde{\mathbf{y}}}_2{\tilde{\mathbf{y}}}_2^T\hfill \end{array}\right]\left[\begin{array}{ll}{\sigma }_1^2{\tilde{\mathbf{K}}}_1\hfill & \delta {\tilde{\mathbf{K}}}_{12}\hfill \\ \delta {\tilde{\mathbf{K}}}_{12}^T\hfill & {\sigma }_2^2{\tilde{\mathbf{K}}}_2\hfill \end{array}\right]-2\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T\left[\begin{array}{ll}{\sigma }_{\epsilon }^2{\mathbf{M}}_1\hfill & 0\hfill \\ 0\hfill & {\sigma }_{\xi }^2{\mathbf{M}}_2\hfill \end{array}\right]+2\left[\begin{array}{ll}{\sigma }_1^2{\tilde{\mathbf{K}}}_1\hfill & \delta {\tilde{\mathbf{K}}}_{12}\hfill \\ \delta {\tilde{\mathbf{K}}}_{12}^T\hfill & {\sigma }_2^2{\tilde{\mathbf{K}}}_2\hfill \end{array}\right]\left[\begin{array}{ll}{\sigma }_{\epsilon }^2{\mathbf{M}}_1\hfill & 0\hfill \\ 0\hfill & {\sigma }_{\xi }^2{\mathbf{M}}_2\hfill \end{array}\right]={\tilde{\mathbf{y}}}^T\tilde{\mathbf{y}}{\tilde{\mathbf{y}}}^T\tilde{\mathbf{y}}+{\left({\sigma }_1^2\right)}^2\text{tr}\left[{\tilde{\mathbf{K}}}_1^2\right]+{\left({\sigma }_2^2\right)}^2\text{tr}\left[{\tilde{\mathbf{K}}}_2^2\right]+2{\delta }^2\text{tr}\left[{\tilde{\mathbf{K}}}_{12}{\tilde{\mathbf{K}}}_{12}^T\right]+{\left({\sigma }_{\epsilon }^2\right)}^2\text{tr}\left[{\mathbf{M}}_1\right]+{\left({\sigma }_{\xi }^2\right)}^2\text{tr}\left[{\mathbf{M}}_2\right]-2{\sigma }_1^2{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{K}}}_1{\tilde{\mathbf{y}}}_1-4\delta {\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{K}}}_{12}{\tilde{\mathbf{y}}}_2-2{\sigma }_2^2{\tilde{\mathbf{y}}}_2^T{\tilde{\mathbf{K}}}_2{\tilde{\mathbf{y}}}_2-2{\sigma }_{\epsilon }^2{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{y}}}_1-2{\sigma }_{\xi }^2{\tilde{\mathbf{y}}}^T{\tilde{\mathbf{y}}}_2+2{\sigma }_1^2{\sigma }_{\epsilon }^2\text{tr}\left[{\tilde{\mathbf{K}}}_1\right]+2{\sigma }_2^2{\sigma }_{\xi }^2\text{tr}\left[{\tilde{\mathbf{K}}}_2\right].$$

Taking derivatives of the objective function with respect to $\mathit{\theta }=\left\{{\sigma }_1^2,{\sigma }_2^2,\delta ,{\sigma }_{\epsilon }^2,{\sigma }_{\xi }^2\right\}$ and setting them to zero leads to estimating Equation 5.

Derivation of posterior mean (Equation 8)

Given the estimates of parameters $\left\{{\hat{\sigma }}_1^2,{\hat{\sigma }}_2^2,\hat{\delta },{\hat{\sigma }}_{\epsilon }^2,{\hat{\sigma }}_{\xi }^2\right\}$ and fixed effects $\hat{\mathit{\omega }}$, the posterior means of $\mathit{\beta }$ are given as:

$$\left[\begin{array}{l}{\mathit{\beta }}_1\hfill \\ {\mathit{\beta }}_2\hfill \end{array}\right]|{\mathbf{Z}}_1,{\mathbf{X}}_1,{\mathbf{y}}_1,{\mathbf{Z}}_2,{\mathbf{X}}_2,{\mathbf{y}}_2\sim \mathcal{N}\left({\hat{\mathit{\mu }}}^{\mathbf{X}\mathbf{P}\mathbf{A}},\mathbf{\Sigma }\right),$$ (Equation A2)

with

$$\begin{array}{l}\mathbf{\Lambda }={\mathbf{\Sigma }}^{-1}=\left[\begin{array}{ll}\frac{{\mathbf{X}}_1^T{\mathbf{X}}_1}{{\hat{\sigma }}_{\epsilon }^2}\hfill & 0\hfill \\ 0\hfill & \frac{{\mathbf{X}}_2^T{\mathbf{X}}_2}{{\hat{\sigma }}_{\xi }^2}\hfill \end{array}\right]+\left({\hat{\mathbf{\Sigma }}}_{\beta }^{-1}\otimes {\mathbf{I}}_p\right),\\ \hat{\mathit{\mu }}\equiv \left[\begin{array}{l}{\hat{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}}\hfill \\ {\hat{\mathit{\mu }}}_2^{\mathbf{X}\mathbf{P}\mathbf{A}}\hfill \end{array}\right]=\mathbf{\Sigma }\left[\begin{array}{l}\frac{1}{{\hat{\sigma }}_{\epsilon }^2}{\mathbf{X}}_1^T\left({\mathbf{y}}_1-{\mathbf{Z}}_1{\hat{\mathit{\omega }}}_1\right)\hfill \\ \frac{1}{{\hat{\sigma }}_{\xi }^2}{\mathbf{X}}_2^T\left({\mathbf{y}}_2-{\mathbf{Z}}_2{\hat{\mathit{\omega }}}_2\right)\hfill \end{array}\right],\end{array}$$

where ${\hat{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}}$ and ${\hat{\mathit{\mu }}}_2^{\mathbf{X}\mathbf{P}\mathbf{A}}$ are the posterior means of ${\mathit{\beta }}_1$ and ${\mathit{\beta }}_2$, respectively. Note that directly working on this form of posterior mean ${\mathit{\mu }}^{\mathbf{X}\mathbf{P}\mathbf{A}}$ requires solving a $2p\times 2p$ linear system, which is intractable since p is in the order of millions. Here, we derive an equivalent form that computes ${\mathit{\mu }}^{\mathbf{X}\mathbf{P}\mathbf{A}}$ by solving only an $\left(n_1+n_2\right)\times \left(n_1+n_2\right)$ linear system:

$${\mathit{\mu }}^{\mathbf{X}\mathbf{P}\mathbf{A}}={\mathbf{\Lambda }}^{-1}{\left(\left[\begin{array}{ll}{\hat{\sigma }}_{\epsilon }^2\hfill & 0\hfill \\ 0\hfill & {\hat{\sigma }}_{\xi }^2\hfill \end{array}\right]\otimes {\mathbf{I}}_p\right)}^{-1}{\mathbf{X}}^T\left(\mathbf{y}-\mathbf{Z}\hat{\mathit{\omega }}\right)={[\left[\begin{array}{ll}{\mathbf{X}}_1^T{\mathbf{X}}_1\hfill & 0\hfill \\ 0\hfill & {\mathbf{X}}_2^T{\mathbf{X}}_2\hfill \end{array}\right]+\hat{\mathbf{\Delta }}\otimes {\mathbf{I}}_p]}^{-1}{\mathbf{X}}^T\left(\mathbf{y}-\mathbf{Z}\hat{\mathit{\omega }}\right),={[{\mathbf{X}}^T\mathbf{X}+\hat{\mathbf{\Delta }}\otimes {\mathbf{I}}_p]}^{-1}{\mathbf{X}}^T\left(\mathbf{y}-\mathbf{Z}\hat{\mathit{\omega }}\right)=\left({\hat{\mathbf{\Delta }}}^{-1}\otimes {\mathbf{I}}_p\right){\mathbf{X}}^T{\left({\mathbf{I}}_{n_1+n_2}+\mathbf{X}\left({\hat{\mathbf{\Delta }}}^{-1}\otimes {\mathbf{I}}_p\right){\mathbf{X}}^T\right)}^{-1}\left(\mathbf{y}-\mathbf{Z}\hat{\mathit{\omega }}\right),$$ (Equation A3)

where $\hat{\mathbf{\Delta }}=\left[\begin{array}{ll}{\hat{\sigma }}_{\epsilon }^2\hfill & 0\hfill \\ 0\hfill & {\hat{\sigma }}_{\xi }^2\hfill \end{array}\right]{\left[\begin{array}{ll}{\hat{\sigma }}_1^2\hfill & \hat{\delta }\hfill \\ \hat{\delta }\hfill & {\hat{\sigma }}_2^2\hfill \end{array}\right]}^{-1}=\left[\begin{array}{ll}\frac{{\hat{\sigma }}_{\epsilon }^2{\hat{\sigma }}_2^2}{{\hat{\sigma }}_1^2{\hat{\sigma }}_2^2-{\hat{\delta }}^2}\hfill & -\frac{{\hat{\sigma }}_{\epsilon }^2\hat{\delta }}{{\hat{\sigma }}_1^2{\hat{\sigma }}_2^2-{\hat{\delta }}^2}\hfill \\ -\frac{{\hat{\sigma }}_{\xi }^2\hat{\delta }}{{\hat{\sigma }}_1^2{\hat{\sigma }}_2^2-{\hat{\delta }}^2}\hfill & \frac{{\hat{\sigma }}_{\xi }^2{\hat{\sigma }}_1^2}{{\hat{\sigma }}_1^2{\hat{\sigma }}_2^2-{\hat{\delta }}^2}\hfill \end{array}\right]$ and the last equation is granted by the Woodburry matrix identity. XPA computes the posterior mean of the target population by:

$${\hat{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}}={\left[\begin{array}{l}{\hat{\sigma }}_1^2{\mathbf{X}}_1\hfill \\ \hat{\delta }{\mathbf{X}}_2\hfill \end{array}\right]}^T{\left[\begin{array}{ll}{\hat{\sigma }}_1^2{\mathbf{X}}_1{\mathbf{X}}_1^T+{\hat{\sigma }}_{\epsilon }^2{\mathbf{I}}_{n1}\hfill & \hat{\delta }{\mathbf{X}}_1{\mathbf{X}}_2^T\hfill \\ \hat{\delta }{\mathbf{X}}_2{\mathbf{X}}_1^T\hfill & {\hat{\sigma }}_2^2{\mathbf{X}}_2{\mathbf{X}}_2^T+{\hat{\sigma }}_{\xi }^2{\mathbf{I}}_{n2}\hfill \end{array}\right]}^{-1}\left[\begin{array}{l}{\mathbf{y}}_1-{\mathbf{Z}}_1{\hat{\mathit{\omega }}}_1\hfill \\ {\mathbf{y}}_2-{\mathbf{Z}}_2{\hat{\mathit{\omega }}}_2\hfill \end{array}\right]\equiv {\hat{\mathbf{\Omega }}}^{-1}\left(\mathbf{y}-\mathbf{Z}\hat{\mathit{\omega }}\right),$$

Computation of posterior means and fixed effects with the CG algorithm

The fixed effects and posterior means are given as

$$\hat{\mathit{\omega }}\equiv \left[\begin{array}{l}{\hat{\mathit{\omega }}}_1\hfill \\ {\hat{\mathit{\omega }}}_2\hfill \end{array}\right]={\left({\mathbf{Z}}^T{\hat{\mathbf{\Omega }}}^{-1}\mathbf{Z}\right)}^{-1}{\mathbf{Z}}^T{\hat{\mathbf{\Omega }}}^{-1}\mathbf{y},$$

and

$${\hat{\mathit{\mu }}}_1^{\mathbf{X}\mathbf{P}\mathbf{A}}={\left[\begin{array}{l}{\hat{\sigma }}_1^2{\mathbf{X}}_1\hfill \\ \hat{\delta }{\mathbf{X}}_2\hfill \end{array}\right]}^T\underset{{\hat{\mathbf{\Omega }}}^{-1}\in {\mathbb{R}}^{\left(n_1+n_2\right)\times \left(n_1+n_2\right)}}{\underbrace{{\left[\begin{array}{ll}{\hat{\sigma }}_1^2{\mathbf{X}}_1{\mathbf{X}}_1^T+{\hat{\sigma }}_{\epsilon }^2{\mathbf{I}}_{n1}\hfill & \hat{\delta }{\mathbf{X}}_1{\mathbf{X}}_2^T\hfill \\ \hat{\delta }{\mathbf{X}}_2{\mathbf{X}}_1^T\hfill & {\hat{\sigma }}_2^2{\mathbf{X}}_2{\mathbf{X}}_2^T+{\hat{\sigma }}_{\xi }^2{\mathbf{I}}_{n2}\hfill \end{array}\right]}^{-1}}}\left[\begin{array}{l}{\mathbf{y}}_1-{\mathbf{Z}}_1{\hat{\mathit{\omega }}}_1\hfill \\ {\mathbf{y}}_2-{\mathbf{Z}}_2{\hat{\mathit{\omega }}}_2\hfill \end{array}\right]={\left[\begin{array}{l}{\hat{\sigma }}_1^2{\mathbf{X}}_1\hfill \\ \hat{\delta }{\mathbf{X}}_2\hfill \end{array}\right]}^T\left({\hat{\mathbf{\Omega }}}^{-1}\mathbf{y}-{\hat{\mathbf{\Omega }}}^{-1}\mathbf{Z}\hat{\mathit{\omega }}\right),$$

respectively. Both quantities involve solving the linear systems $\mathbf{U}={\hat{\mathbf{\Omega }}}^{-1}\mathbf{Z}$ and $\mathbf{v}={\hat{\mathbf{\Omega }}}^{-1}\mathbf{y}$. Therefore, we can compute the estimates of fixed effects and the posterior means at the same time while only solving the linear systems once. Specifically, we first construct a working matrix $\mathbf{W}=[\mathbf{y},\mathbf{Z}]$ and apply the conjugate gradient approach to solve the combined linear systems $[\mathbf{v},\mathbf{U}]={\hat{\mathbf{\Omega }}}^{-1}\mathbf{W}$, as summarized in Algorithm 1.

Algorithm 1. Conjugate Gradient algorithm for solving [v,U]=Ωˆ−1W.

At each iteration of the CG algorithm, we need to compute

$$\hat{\mathbf{\Omega }}{\mathbf{P}}_j=\hat{\mathbf{\Omega }}\left[\begin{array}{l}{\mathbf{P}}_{1j}\hfill \\ {\mathbf{P}}_{2j}\hfill \end{array}\right]=\left[\begin{array}{l}{\hat{\sigma }}_1^2{\mathbf{X}}_1{\mathbf{X}}_1^T{\mathbf{P}}_{1j}+{\hat{\sigma }}_{\epsilon }^2{\mathbf{P}}_{1j}+\hat{\delta }{\mathbf{X}}_1{\mathbf{X}}_2^T{\mathbf{P}}_{2j}\hfill \\ {\hat{\sigma }}_2^2{\mathbf{X}}_2{\mathbf{X}}_2^T{\mathbf{P}}_{2j}+{\hat{\sigma }}_{\xi }^2{\mathbf{P}}_{2j}+\hat{\delta }{\mathbf{X}}_2{\mathbf{X}}_1^T{\mathbf{P}}_{1j}\hfill \end{array}\right],$$

where ${\mathbf{P}}_{1j}\in {\mathbb{R}}^p$ and ${\mathbf{P}}_{2j}\in {\mathbb{R}}^p$ are column vectors. With entries of ${\mathbf{X}}_1$ and ${\mathbf{X}}_2$ decoded from the Hash table, we first compute ${\mathbf{X}}_1^T{\mathbf{P}}_{1j}$ and ${\mathbf{X}}_2^T{\mathbf{P}}_{2j}$ and then multiply ${\mathbf{X}}_1$ and ${\mathbf{X}}_2$ on their left to obtain the corresponding terms. This operation is highly efficient since it only involves matrix-vector multiplication. The final time complexity of the CG algorithm is $\mathcal{O}\left(p\left(n_1+n_2\right)\left(c_1+c_2+1\right)\sqrt{\kappa }\right)$, where κ is the condition number of $\hat{\mathbf{\Omega }}$. Because κ is usually small, the CG algorithm offers substantial computational improvement in solving the linear system.

Assumptions for XPASS model

We consider the datasets $\left\{{\mathbf{z}}_1,{{\mathbf{G}}_1}^{\text{′}},{{\mathbf{Z}}_1}^{\text{′}}\right\}$ and $\left\{{\mathbf{z}}_2,{{\mathbf{G}}_2}^{\text{′}},{{\mathbf{Z}}_1}^{\text{′}}\right\}$ from the two populations. The vectors ${\mathbf{z}}_1={[z_{11},\dots ,z_{1j},\dots ,z_{1p}]}^T\in {\mathbb{R}}^p$ and ${\mathbf{z}}_2={[z_{21},\dots ,z_{2j},\dots ,z_{2p}]}^T\in {\mathbb{R}}^p$ contain the z-scores derived from the two populations, where $z_{1j}=\frac{{\left({\mathbf{x}}_{1j}^T{\mathbf{x}}_{1j}\right)}^{-1}{\mathbf{x}}_{1j}^T{\mathbf{y}}_1}{\sqrt{{\hat{\sigma }}_{1j}^2{\left({\mathbf{x}}_{1j}^T{\mathbf{x}}_{1j}\right)}^{-1}}}$ and $z_{2j}=\frac{{\left({\mathbf{x}}_{2j}^T{\mathbf{x}}_{2j}\right)}^{-1}{\mathbf{x}}_{2j}^T{\mathbf{y}}_2}{\sqrt{{\hat{\sigma }}_{2j}^2{\left({\mathbf{x}}_{2j}^T{\mathbf{x}}_{2j}\right)}^{-1}}}$ and ${\hat{\sigma }}_{1j}^2$ and ${\hat{\sigma }}_{2j}^2$ are the residual variance of regressing ${\mathbf{y}}_1$ on ${\mathbf{x}}_{1j}$ and ${\mathbf{y}}_2$ on ${\mathbf{x}}_{2j}$, respectively. Following Vilhjálmsson et al.,²⁹ we assume the z-scores are derived from GWAS datasets with phenotype vectors ${\mathbf{y}}_1$ and ${\mathbf{y}}_2$ standardized to have mean of zero and standard deviation of one. The first few PCs of the reference genotypes from the two populations are given in ${{\mathbf{Z}}_1}^{\text{′}}\in {\mathbb{R}}^{m_1\times c{\text{′}}_1}$ and ${{\mathbf{Z}}_2}^{\text{′}}\in {\mathbb{R}}^{m_2\times c{\text{′}}_2}$. Similar to XPA, we first standardize the reference genotype matrices ${{\mathbf{G}}_1}^{\text{′}}$ and ${{\mathbf{G}}_2}^{\text{′}}$ to obtain the corresponding ${{\mathbf{X}}_1}^{\text{′}}$ and ${{\mathbf{X}}_2}^{\text{′}}$ that have column means zero and variances $1/p$.

Parameter estimation in XPASS

To derive the normal equations using the summary-level datasets, we start by eliminating the ${\sigma }_{\epsilon }$ and ${\sigma }_{\xi }$ in Equation 5, which leads to

$$\left[\begin{array}{lll}\text{tr}\left({\tilde{\mathbf{K}}}_1^2\right)-\frac{{\text{tr}}^2\left({\tilde{\mathbf{K}}}_1\right)}{n_1}\hfill & 0\hfill & 0\hfill \\ 0\hfill & \text{tr}\left({\tilde{\mathbf{K}}}_2^2\right)-\frac{{\text{tr}}^2\left({\tilde{\mathbf{K}}}_2\right)}{n_2}\hfill & 0\hfill \\ 0\hfill & 0\hfill & \text{tr}\left({\tilde{\mathbf{K}}}_{12}{\tilde{\mathbf{K}}}_{12}^T\right)\hfill \end{array}\right]\left[\begin{array}{l}{\sigma }_1^2\hfill \\ {\sigma }_2^2\hfill \\ \delta \hfill \end{array}\right]=\left[\begin{array}{l}{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{K}}}_1{\tilde{\mathbf{y}}}_1-\frac{{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{y}}}_1\text{tr}\left({\tilde{\mathbf{K}}}_1\right)}{n_1}\hfill \\ {\tilde{\mathbf{y}}}_2^T{\tilde{\mathbf{K}}}_2{\tilde{\mathbf{y}}}_2-\frac{{\tilde{\mathbf{y}}}_2^T{\tilde{\mathbf{y}}}_2\text{tr}\left({\tilde{\mathbf{K}}}_2\right)}{n_2}\hfill \\ {\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{K}}}_{12}{\tilde{\mathbf{y}}}_2\hfill \end{array}\right].$$

By dividing the three equations by $n_1^2$, $n_2^2$ and $n_1{n}_2$, the estimating Equation 5 became:

$$\left[\begin{array}{lll}\frac{\text{tr}\left({\tilde{\mathbf{K}}}_1^2\right)-\frac{{\text{tr}}^2\left({\tilde{\mathbf{K}}}_1\right)}{n_1}}{n_1^2}\hfill & 0\hfill & 0\hfill \\ 0\hfill & \frac{\text{tr}\left({\tilde{\mathbf{K}}}_2^2\right)-\frac{{\text{tr}}^2\left({\tilde{\mathbf{K}}}_2\right)}{n_2}}{n_2^2}\hfill & 0\hfill \\ 0\hfill & 0\hfill & \frac{\text{tr}\left({\tilde{\mathbf{K}}}_{12}{\tilde{\mathbf{K}}}_{12}^T\right)}{n_1{n}_2}\hfill \end{array}\right]\left[\begin{array}{l}{\sigma }_1^2\hfill \\ {\sigma }_2^2\hfill \\ \delta \hfill \end{array}\right]=\left[\begin{array}{l}\frac{{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{K}}}_1{\tilde{\mathbf{y}}}_1}{n_1^2}-\frac{{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{y}}}_1\text{tr}\left({\tilde{\mathbf{K}}}_1\right)}{n_1^3}\hfill \\ \frac{{\tilde{\mathbf{y}}}_2^T{\tilde{\mathbf{K}}}_2{\tilde{\mathbf{y}}}_2}{n_2^2}-\frac{{\tilde{\mathbf{y}}}_2^T{\tilde{\mathbf{y}}}_2\text{tr}\left({\tilde{\mathbf{K}}}_2\right)}{n_2^3}\hfill \\ \frac{{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{K}}}_{12}{\tilde{\mathbf{y}}}_2}{n_1{n}_2}\hfill \end{array}\right].$$ (Equation A4)

Note that the summary statistic of the j-th SNP $z_{1j}=\frac{{\left(x_{1j}^T{x}_{1j}\right)}^{-1}{x}_{1j}^{T}y}{\sqrt{{\hat{\sigma }}_j^2{\left(x_{1j}^T{x}_{1j}\right)}^{-1}}}=\frac{x_{1j}^{T}y}{\sqrt{{\hat{\sigma }}_j^2\frac{n}{p}}}\approx \frac{x_{1j}^{T}y}{\sqrt{{\sigma }_{y_1}^2\frac{n}{p}}}$, where the first equation is derived from the assumption that $x_j$ has mean 0 and variance $1/p$, and the approximation is granted by the assumption that each SNP only contributes a small proportion of the total phenotypic variance. Similarly, $z_{2j}\approx \frac{x_{2j}^{T}y}{\sqrt{{\sigma }_{y_2}^2\frac{n}{p}}}$. Therefore, we can approximate the terms in the right-hand side of Equation A4 by

$$\begin{array}{l}\frac{{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{X}}}_1{\tilde{\mathbf{X}}}_1^T{\tilde{\mathbf{y}}}_1}{n_1^2}=\stackrel{p}{\sum _{j=1}}{\left(\frac{{\tilde{\mathbf{x}}}_{1j}^T{\tilde{\mathbf{y}}}_1}{n_1}\right)}^2\approx \stackrel{p}{\sum _{j=1}}{\left(z_{1j}\sqrt{\frac{{\sigma }_{y_1}^2}{n_{1}p}}\right)}^2=\frac{{\sigma }_{y_1}^2}{n_{1}p}\stackrel{p}{\sum _{j=1}}{z}_{1j}^2,\\ \frac{{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{y}}}_1\text{tr}\left({\tilde{\mathbf{K}}}_1\right)}{n_1^3}\approx \frac{n_1^2{\sigma }_{y_1}^2}{n_1^3}=\frac{{\sigma }_{y_1}^2}{n_1},\\ \frac{{\tilde{\mathbf{y}}}_2^T{\tilde{\mathbf{X}}}_2{\tilde{\mathbf{X}}}_2^T{\tilde{\mathbf{y}}}_2}{n_2^2}=\stackrel{p}{\sum _{j=1}}{\left(\frac{{\tilde{\mathbf{x}}}_{2j}^T{\tilde{\mathbf{y}}}_2}{n_2}\right)}^2\approx \stackrel{p}{\sum _{j=1}}{\left(z_{2j}\sqrt{\frac{{\sigma }_{y_2}^2}{n_{2}p}}\right)}^2=\frac{{\sigma }_{y_2}^2}{n_{2}p}\stackrel{p}{\sum _{j=1}}{z}_{2j}^2,\\ \frac{{\tilde{\mathbf{y}}}_2^T{\tilde{\mathbf{y}}}_2\text{tr}\left({\tilde{\mathbf{K}}}_2\right)}{n_2^3}\approx \frac{n_2^2{\sigma }_{y_2}^2}{n_2^3}=\frac{{\sigma }_{y_2}^2}{n_2},\\ \frac{{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{X}}}_1{\tilde{\mathbf{X}}}_2^T{\tilde{\mathbf{y}}}_2}{n_1{n}_2}=\stackrel{p}{\sum _{j=1}}{\left(\frac{{\tilde{\mathbf{y}}}_1^T{\tilde{\mathbf{x}}}_{1j}{\tilde{\mathbf{x}}}_{2j}^T{\tilde{\mathbf{y}}}_2}{\sqrt{n_1{n}_2}}\right)}^2\approx \frac{{\sigma }_{y_1}{\sigma }_{y_2}}{\sqrt{n_1{n}_2}p}\stackrel{p}{\sum _{j=1}}{z}_{1j}{z}_{2j}.\end{array}$$

In the left-hand side of Equation A4, ${\tilde{\mathbf{y}}}_1$ and ${\tilde{\mathbf{y}}}_2$ are not involved, and the terms involving ${\tilde{\mathbf{X}}}_1$ and ${\tilde{\mathbf{X}}}_2$ can be approximated using the reference genotypes ${{\mathbf{X}}_1}^{\text{′}}$ and ${{\mathbf{X}}_2}^{\text{′}}$. For example, $\frac{\text{tr}\left({\tilde{\mathbf{K}}}_1^2\right)-\frac{{\text{tr}}^2\left({\tilde{\mathbf{K}}}_1\right)}{n_1}}{n_1^2}$ can be approximated by $\frac{\text{tr}\left({\tilde{\mathbf{K}}}_1^{\text{′}2}\right)-\frac{{\text{tr}}^2\left(\tilde{\mathbf{K}}{\text{′}}_1\right)}{m_1}}{m_1^2}$, where ${{\tilde{\mathbf{K}}}_1}^{\text{′}}=\mathbf{M}{\text{′}}_1\mathbf{X}{\text{′}}_1{\left(\mathbf{M}{\text{′}}_1\mathbf{X}{\text{′}}_1\right)}^T$ and $\mathbf{M}{\text{′}}_1={\mathbf{I}}_{m_1}-\mathbf{Z}{\text{′}}_1{\left({\mathbf{Z}}_1^{\text{′}T}\mathbf{Z}{\text{′}}_1\right)}^{-1}{\mathbf{Z}}_1^{\text{′}T}$. Other terms in the left-hand side can be approximated in the same way. Using these approximations, the final normal equation is given as

$$\left[\begin{array}{lll}\frac{\text{tr}\left({\tilde{\mathbf{K}}}_1^{\text{′}2}\right)-\frac{{\text{tr}}^2\left(\tilde{\mathbf{K}}{\text{′}}_1\right)}{m_1}}{m_1^2}\hfill & 0\hfill & 0\hfill \\ 0\hfill & \frac{\text{tr}\left({\tilde{\mathbf{K}}}_2^{\text{′}2}\right)-\frac{{\text{tr}}^2\left(\tilde{\mathbf{K}}{\text{′}}_2\right)}{m_2}}{m_2^2}\hfill & 0\hfill \\ 0\hfill & 0\hfill & \frac{\text{tr}\left(\tilde{\mathbf{K}}{\text{′}}_{12}{\mathbf{K}}_{12}^{\text{′}T}\right)}{m_1{m}_2}\hfill \end{array}\right]\left[\begin{array}{l}{h}_1^2\hfill \\ h_2^2\hfill \\ h_{12}\hfill \end{array}\right]=\left[\begin{array}{l}\frac{1}{p}\sum _{j=1}^p\frac{z_{1j}^2-1}{n_1}\hfill \\ \frac{1}{p}\sum _{j=1}^p\frac{z_{2j}^2-1}{n_2}\hfill \\ \frac{1}{p}\sum _{j=1}^p\frac{z_{1j}{z}_{2j}}{\sqrt{n_1{n}_2}}\hfill \end{array}\right],$$ (Equation A5)

where ${{\tilde{\mathbf{K}}}_2}^{\text{′}}=\mathbf{M}{\text{′}}_2\mathbf{X}{\text{′}}_2{\left(\mathbf{M}{\text{′}}_2\mathbf{X}{\text{′}}_2\right)}^T$, ${{\tilde{\mathbf{K}}}_{12}}^{\text{′}}=\mathbf{M}{\text{′}}_1\mathbf{X}{\text{′}}_1{\left(\mathbf{M}{\text{′}}_2\mathbf{X}{\text{′}}_2\right)}^T$, $\mathbf{M}{\text{′}}_2={\mathbf{I}}_{m_2}-\mathbf{Z}{\text{′}}_2{\left({\mathbf{Z}}_2^{\text{′}T}\mathbf{Z}{\text{′}}_2\right)}^{-1}{\mathbf{Z}}_2^{\text{′}T}$, $h_1^2:=\frac{{\sigma }_1^2}{{\sigma }_1^2+{\sigma }_{\epsilon }^2}$ and $h_2^2:=\frac{{\sigma }_2^2}{{\sigma }_2^2+{\sigma }_{\xi }^2}$ are heritabilities for the two populations, respectively, and $h_{12}:=\rho h_1{h}_2$ is the co-heritability between two populations. Note that all terms in Equation A5 depend only on the z-scores and reference panels. Solving Equation A5 leads to the parameter estimates $\left\{{\hat{h}}_1^2,{\hat{h}}_2^2,{\hat{h}}_{12}\right\}$.

Given the parameter estimates $\left\{{\hat{h}}_1,{\hat{h}}_2,{\hat{h}}_{12}\right\}$, the genetic correlation can be estimated by $\hat{\rho }={\hat{h}}_{12}/{\hat{h}}_1{\hat{h}}_2$. To test for $H_0:\rho =0$ using summary statistics, we estimate the standard error of $\hat{\rho }$ by applying the jackknife resampling method, with a leaving-one-chromosome-out strategy.

Derivation ofEquations 9and10

With the model in Equation 3, the estimates of fixed effects and the posterior means are given as

$$\begin{array}{l}\left[\begin{array}{l}{\hat{\mathit{\gamma }}}_1\hfill \\ {\hat{\mathit{\gamma }}}_2\hfill \end{array}\right]={\left({\left[\begin{array}{ll}{\mathbf{X}}_{l1}\hfill & 0\hfill \\ 0\hfill & {\mathbf{X}}_{l2}\hfill \end{array}\right]}^T{\hat{\mathbf{\Omega }}}^{-1}\left[\begin{array}{ll}{\mathbf{X}}_{l1}\hfill & 0\hfill \\ 0\hfill & {\mathbf{X}}_{l2}\hfill \end{array}\right]\right)}^{-1}{\left[\begin{array}{ll}{\mathbf{X}}_{l1}\hfill & 0\hfill \\ 0\hfill & {\mathbf{X}}_{l2}\hfill \end{array}\right]}^T{\hat{\mathbf{\Omega }}}^{-1}\mathbf{y},\\ \left[\begin{array}{l}{\mathit{\mu }}_1\hfill \\ {\mathit{\mu }}_2\hfill \end{array}\right]={\left({\left[\begin{array}{ll}\frac{{\hat{h}}_1^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_2^2}\hfill \\ \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_2^2}{1-{\hat{h}}_2^2}\hfill \end{array}\right]}^{-1}\otimes {\mathbf{I}}_p+\left[\begin{array}{ll}{\mathbf{X}}_1^T{\mathbf{X}}_1\hfill & 0\hfill \\ 0\hfill & {\mathbf{X}}_2^T{\mathbf{X}}_2\hfill \end{array}\right]\right)}^{-1}{\left[\begin{array}{ll}{\mathbf{X}}_1\hfill & 0\hfill \\ 0\hfill & {\mathbf{X}}_2\hfill \end{array}\right]}^T\left[\begin{array}{l}{\mathbf{y}}_1-{\mathbf{Z}}_1{\hat{\mathit{\omega }}}_1-{\mathbf{X}}_{l1}{\hat{\mathit{\gamma }}}_1\hfill \\ {\mathbf{y}}_2-{\mathbf{Z}}_2{\hat{\mathit{\omega }}}_2-{\mathbf{X}}_{l2}{\hat{\mathit{\gamma }}}_2\hfill \end{array}\right].\end{array}$$

By taking the advantage of the Woodbury matrix identity to compute the matrix inversion of ${\hat{\mathbf{\Omega }}}^{-1}$, we obtain

$$\begin{array}{c}\left[\begin{array}{l}{\hat{\mathit{\gamma }}}_1\hfill \\ {\hat{\mathit{\gamma }}}_2\hfill \end{array}\right]={\left(\left[\begin{array}{ll}{n}_1{\mathbf{R}}_{l1}\hfill & 0\hfill \\ 0\hfill & n_2{\mathbf{R}}_{l2}\hfill \end{array}\right]-\left[\begin{array}{ll}{n}_1{\mathbf{R}}_{ls1}\hfill & 0\hfill \\ 0\hfill & n_2{\mathbf{R}}_{ls2}\hfill \end{array}\right]{\left({\left[\begin{array}{ll}\frac{{\hat{h}}_1^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_2^2}\hfill \\ \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_2^2}{1-{\hat{h}}_2^2}\hfill \end{array}\right]}^{-1}\otimes {\mathbf{I}}_p+\left[\begin{array}{ll}{n}_1{\mathbf{R}}_1\hfill & 0\hfill \\ 0\hfill & n_2{\mathbf{R}}_2\hfill \end{array}\right]\right)}^{-1}\left[\begin{array}{ll}{n}_1{\mathbf{R}}_{sl1}\hfill & 0\hfill \\ 0\hfill & n_2{\mathbf{R}}_{sl2}\hfill \end{array}\right]\right)}^{-1}\\ \left(\left[\begin{array}{l}{\mathbf{X}}_{l1}^T{\mathbf{y}}_{l1}\hfill \\ {\mathbf{X}}_{l2}^T{\mathbf{y}}_{l2}\hfill \end{array}\right]-\left[\begin{array}{ll}{n}_1{\mathbf{R}}_{ls1}\hfill & 0\hfill \\ 0\hfill & n_2{\mathbf{R}}_{ls2}\hfill \end{array}\right]{\left({\left[\begin{array}{ll}\frac{{\hat{h}}_1^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_2^2}\hfill \\ \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_2^2}{1-{\hat{h}}_2^2}\hfill \end{array}\right]}^{-1}\otimes {\mathbf{I}}_p+\left[\begin{array}{ll}{n}_1{\mathbf{R}}_1\hfill & 0\hfill \\ 0\hfill & n_2{\mathbf{R}}_2\hfill \end{array}\right]\right)}^{-1}\left[\begin{array}{l}{\mathbf{X}}_1^T{\mathbf{y}}_1\hfill \\ {\mathbf{X}}_2^T{\mathbf{y}}_2\hfill \end{array}\right]\right),\\ \left[\begin{array}{l}{\mathit{\mu }}_1\hfill \\ {\mathit{\mu }}_2\hfill \end{array}\right]={\left({\left[\begin{array}{ll}\frac{{\hat{h}}_1^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_2^2}\hfill \\ \frac{{\hat{h}}_{12}^2}{1-{\hat{h}}_1^2}\hfill & \frac{{\hat{h}}_2^2}{1-{\hat{h}}_2^2}\hfill \end{array}\right]}^{-1}\otimes {\mathbf{I}}_p+\left[\begin{array}{ll}{n}_1{\mathbf{R}}_1\hfill & 0\hfill \\ 0\hfill & n_2{\mathbf{R}}_2\hfill \end{array}\right]\right)}^{-1}{\left[\begin{array}{ll}{\mathbf{X}}_1\hfill & 0\hfill \\ 0\hfill & {\mathbf{X}}_2\hfill \end{array}\right]}^T\left[\begin{array}{l}{\mathbf{y}}_1-{\mathbf{Z}}_1{\hat{\mathit{\omega }}}_1-{\mathbf{X}}_{l1}{\hat{\mathit{\gamma }}}_1\hfill \\ {\mathbf{y}}_2-{\mathbf{Z}}_2{\hat{\mathit{\omega }}}_2-{\mathbf{X}}_{l2}{\hat{\mathit{\gamma }}}_2\hfill \end{array}\right],\end{array}$$ (Equation A6)

where ${\mathbf{R}}_1={\mathbf{X}}_1^T{\mathbf{X}}_1/n_1$ and ${\mathbf{R}}_2={\mathbf{X}}_2^T{\mathbf{X}}_2/n_2$ are the LD matrices of all SNPs, ${\mathbf{R}}_{l1}={\mathbf{X}}_{l1}^T{\mathbf{X}}_{l1}/n_1$ and ${\mathbf{R}}_{l2}={\mathbf{X}}_{l2}^T{\mathbf{X}}_{l2}/n_2$ are the LD matrices of large-effect SNPs, and ${\mathbf{R}}_{ls1}={\mathbf{R}}_{sl1}^T={\mathbf{X}}_{l1}^T{\mathbf{X}}_1/n_1$ and ${\mathbf{R}}_{ls2}={\mathbf{R}}_{sl2}^T={\mathbf{X}}_{l2}^T{\mathbf{X}}_2/n_2$ are the SNP correlation matrices between large-effect SNPs and all SNPs from the two populations, respectively.

With the reference genotype matrices, we can approximate the LD matrices in Equation A6 with ${\mathbf{R}}_1\approx {\hat{\mathbf{R}}}_1={\mathbf{X}}_1^{\text{′}T}\mathbf{X}{\text{′}}_1/m_1$, ${\mathbf{R}}_2\approx {\hat{\mathbf{R}}}_2={\mathbf{X}}_2^{\text{′}T}\mathbf{X}{\text{′}}_2/m_2$, ${\mathbf{R}}_{ls1}\approx {\hat{\mathbf{R}}}_{ls1}={\mathbf{X}}_{l1}^{\text{′}T}\mathbf{X}{\text{′}}_1/m_1$, and ${\mathbf{R}}_{ls2}\approx {\hat{\mathbf{R}}}_{ls2}={\mathbf{X}}_{l2}^{\text{′}T}\mathbf{X}{\text{′}}_2/m_2$. In addition, the terms involving $\mathbf{y}$ can be approximated by ${\mathbf{X}}_{l1}^T{\mathbf{y}}_{l1}\approx \sqrt{\frac{n_1}{p}}{\mathbf{z}}_{l1}$, ${\mathbf{X}}_{l2}^T{\mathbf{y}}_{l2}\approx \sqrt{\frac{n_2}{p}}{\mathbf{z}}_{l2}$, ${\mathbf{X}}_1^T{\mathbf{y}}_1\approx \sqrt{\frac{n_1}{p}}{\mathbf{z}}_1$, and ${\mathbf{X}}_2^T{\mathbf{y}}_2\approx \sqrt{\frac{n_2}{p}}{\mathbf{z}}_2$, where ${\mathbf{z}}_{l1}\in {\mathbb{R}}^{l_1}$ and ${\mathbf{z}}_{l2}\in {\mathbb{R}}^{l_2}$ are sub-vectors of ${\mathbf{z}}_1$ and ${\mathbf{z}}_2$ corresponding to the large-effect SNPs. Replacing the relevant terms with corresponding approximations leads to Equations 9 and 10.

Data and code availability

The publicly available GWAS summary statistics for estimating genetic correlations were obtained from the links summarized in Table S2. Access to genome-wide summary statistics from the Chinese data has to be approved by the contact authors (see Table S2). Researchers who wish to gain access to the data are required to submit the data request by sending an email to the contact authors. GWAS summary statistics from other studies can be accessed using the links provided in Table S2. The UKBB data are available through the UK Biobank Access Management System. The IPM BioMe biobank data are accessible on dbGap with accession number phs000925.v1.p1. The C++ software for XPA and the R package for XPASS are available online.

Web resources

• ANNOVAR, http://annovar.openbioinformatics.org/en/latest/

• BOLT-LMM, https://alkesgroup.broadinstitute.org/BOLT-LMM

• C++ software for XPA, https://github.com/YangLabHKUST/XPA

• dbGaP, https://www.ncbi.nlm.nih.gov/gap

• GCTA, https://cnsgenomics.com/software/gcta/#Overview

• GCTB, https://cnsgenomics.com/software/gctb/#Overview

• glmnetPlus, https://github.com/junyangq/glmnetPlus

• lassosum, https://github.com/tshmak/lassosum

• LDSC, https://github.com/bulik/ldsc

• LDpred, https://github.com/bvilhjal/ldpred

• PLINK, https://www.cog-genomics.org/plink/

• Popcorn, https://github.com/brielin/Popcorn

• R package for XPASS, https://github.com/YangLabHKUST/XPASS

• snpnet, https://github.com/junyangq/snpnet

• UKBB, https://www.ukbiobank.ac.uk