On the use of direct-coupling analysis with a reduced alphabet of amino acids combined with super-secondary structure motifs for protein fold prediction

Abstract

Direct-coupling analysis (DCA) for studying the coevolution of residues in proteins has been widely used to predict the three-dimensional structure of a protein from its sequence. We present RADI/raDIMod, a variation of the original DCA algorithm that groups chemically equivalent residues combined with super-secondary structure motifs to model protein structures. Interestingly, the simplification produced by grouping amino acids into only two groups (polar and non-polar) is still representative of the physicochemical nature that characterizes the protein structure and it is in line with the role of hydrophobic forces in protein-folding funneling. As a result of a compressed alphabet, the number of sequences required for the multiple sequence alignment is reduced. The number of long-range contacts predicted is limited; therefore, our approach requires the use of neighboring sequence-positions. We use the prediction of secondary structure and motifs of super-secondary structures to predict local contacts. We use RADI and raDIMod, a fragment-based protein structure modelling, achieving near native conformations when the number of super-secondary motifs covers >30–50% of the sequence. Interestingly, although different contacts are predicted with different alphabets, they produce similar structures.

INTRODUCTION

Protein structure is conserved through evolution, as protein function is structure dependent (1). The reason for such conservation is due to energetically favorable interactions between specific protein residues, which implies that there must be a certain degree of coevolution between the residues responsible for both the function and fold of all the members of a protein family (2). In the last decade, several authors developed the mean field approximation for direct-coupling analysis (DCA), either by solving an inverse covariance matrix (3) or by using a pseudo-likelihood-based approach (4,5) to compute direct information (DI) values (6) and detect correlated positions of the sequence (for a review see (7)). The implementation of an L2-regularized pseudo-likelihood to compute the DI between amino acid positions of protein sequences has also implied a large reduction of the computational time (8). These correlations are reflected by co-evolution and are potentially due to the spatial proximity of the residues, thereby helping to infer the contact map of a protein family (9). This has been used to improve protein models (10,11), predict the structure of proteins (12,13) or predict the structure of homo-dimers (14). The theory underlying DCA is based on the Potts model (15) and recent studies have shown that the number of Potts states can be compressed without affecting the quality of reconstruction (16). Furthermore, the compression of the alphabet has been used to include the three-body interaction terms on the calculation of DCA, reducing not only the time but also the amount of memory required (17,18). Here we propose a modification of the DCA algorithm for proteins using a compression that reduces the number of sequences required for the multiple-sequence alignment (MSA) and it is still useful to model the structure. Instead of analyzing every mutation in the protein, we ignore the mutations occurring within certain subsets of amino acids with equivalent physicochemical properties. We transform the sequences of an MSA of a protein family into a simplified alphabet of equivalent residues, and if the information of the alignment is still enough, we calculate the top-ranking pairs of positions with high values of DI. Pairs of positions of a protein sequence with high values of DI are potential contacts of the protein conformation and are used as restrictions to model its structure. However, many contacts are necessary to produce an accurate model. Local contacts can be predicted using the prediction of secondary structure, but the connection and interaction between secondary structures is still necessary. Previous works have shown that proteins can be constructed on a modular fashion, using templates of fragments of the sequence (19,20). Furthermore, distance restraints can be extracted from experimental data (i.e. NMR) to finally construct a model using short templates formed by super-secondary structures (21). In this work we will use ArchDB14 (22), a dataset of classified super-secondary structures formed by two regular structures (sMotifs). The structure of a protein will be constructed using the predicted contacts calculated with different alphabets, the prediction of secondary structure and the structures of sMotifs from ArchDB14 used as templates.

MATERIALS AND METHODS

DI values are computed using a modification of the DCA algorithm, which we have named reduced alphabet DI (RADI). We denote by q the number of different symbols (i.e. alphabet) in the MSA.

Multiple-sequence alignments

MSAs are created using the script ‘buildmsa.py’ included in the RADI Git repository. First, the script builds a profile of the query searching for similar sequences in the uniref50 database with MMseqs2 (23). Next, it uses the query profile to find more sequence relatives in the uniref100 database. Then, the script builds a MSA of the query and the identified sequences (up to 100 000) with FAMSA (24). Finally, it removes the columns of the MSA with gaps in the query. Note that MMseqs2 is executed with options ‘-s 7.5’ and ‘–max-seq-id 1.0’ for a more sensitive search.

Reduced alphabet

RADI simplifies the computation of DI values by transforming the entire alphabet of q = 21 symbols (i.e. the 20 different amino acids plus the gap) into a reduced alphabet. For instance, using an alphabet of q = 21 (henceforth named RA0) in RADI is equivalent to using the original DCA algorithm. We create three reduced alphabets (henceforth named RA1, RA2, and RA3) by grouping amino acids based on different physicochemical properties (Table 1). We also define the number of effective sequences as the number of sufficiently different sequences (i.e. <80% of sequence identity) after removing the columns with more gaps than a threshold, which varies between 15% and 75% of the total number of sequences. Specifically, this threshold is set to the smallest percentage that would result in either 1000 or the maximum number of effective sequences. The limit at 1000 sequences is selected following Morcos et al. sensitivity analysis of the performance of DCA (9), as larger alignments would not significantly change the results. Finally, we calculate the frequencies of symbols and weight them by the corresponding number of effective sequences at each position to calculate the mutual or direct information (9), correcting the entropic effects with the Average Product Correlation (APC) (25).

Table 1.

Classification of amino acids into groups for the three reduced alphabets RA1, RA2 and RA3. The second column shows the number of q symbols of the corresponding reduced alphabet

Type	Q	Amino acid groups
RA1	9	Positively charged: {Arg, His, Lys}. Negatively charged: {Asp, Glu}. Polars: {Ser, Thr, Asn, Gln}. Aliphatics: {Ala, Ile, Leu, Met, Val}. Aromatics: {Phe, Trp, Tyr}. Single groups: {Cys}, {Gly}, {Pro} and the gap
RA2	5	Polar: {Arg, His, Lys, Asp, Glu, Ser, Thr, Asn, Gln, Cys}. Non-polar: {Ala, Ile, Leu, Met, Val, Phe, Trp, Tyr}. Single groups: {Gly}, {Pro} and the gap
RA3	3	Polar: {Arg, His, Lys, Asp, Glu, Ser, Thr, Asn, Gln, Cys, Gly}. Non-polar: {Ala, Ile, Leu, Met, Val, Phe, Trp, Tyr, Pro}. Single groups: gap

Analysis

Two residues are in contact if: (i) at least two atoms, one of each residue, are at a distance <5Å; (ii) the distance between their Cα atoms is <15Å or (iii) the distance between their Cβ atoms is <8Å. We define the contact-map of a protein as the set of pairs of residues in contact. We only analyze the top DI pairs where the residues belong to two different secondary structures. We consider that two pairs, say (i,j) and (n,m), are equivalent if one of them is in the vicinity of the other defined by a [9 × 9] square (i.e. (i,j) is in the set of pairs [n - 4, n + 4] × [m - 4, m + 4]). Then, true positive contacts are top DI pairs equivalent to pairs of residues in the contact map. Top DI pairs using one of the RADI approaches (RA1, RA2, RA3) are similar to the original DCA method if they are equivalent to a pair predicted in RA0. We have used a similar definition for the comparison of equivalent pairs between RADI approaches (RA0,RA1,RA2,RA3) and the top DI pairs obtained using an L2-regularized pseudo-likelihood approach with the program CCMPred (8).

Fragment-based modeling of protein structure using DI information

We use the following approach to model the structures of protein based on DI contact prediction and sMotifs (22). Firstly, we map the secondary structure predicted with SABLE (26) on the sequence of the target and predict the type of super-secondary structures (i.e. two consecutive secondary structures) defined as sMotifs and classified in ArchDB14 (22). ArchDB is a structural classification of sMotifs, formed by clusters of similar structures. The similarity between sMotifs is based on the alignment of (ϕ,ψ) angles of the backbones of the loop regions (i.e. between two secondary structures) and the 3D orientation of the secondary structures. Interestingly, specific residues are often preserved in certain positions of the sMotifs in a class/cluster (often in the loop or in its regions at the stems with regular secondary structure). These sequence-profiles are used to detect and align the target sequence with the sMotif structural templates.

The sequence of the proteins is used to compute the DI and select for each alphabet the top 40 pairs of residues with the higher correlation. The structures of sMotifs aligned to the target sequence are used as templates for homology modelling with MODELLER (27). We add distance restraints between the pairs of amino acids selected, constrain the secondary structure predicted with SABLE and generate 10000 structural models that are subsequently clustered and scored. The protocol to run MODELLER is as follows: (i) we use as templates the structures of the predicted sMotifs; (ii) apply constrains at 8Å using a Gaussian potential on the Cβ-Cβ atoms of the selected residue-pairs with highest correlation; and (iii) we force the type of secondary structure as mapped by the prediction of secondary structure. Finally, we rank the models with DOPE (28) and cluster them by similar structure, evaluate the quality of the models with Prosa2003 (29) and select the best scored structures. The scripts to automate the search of sMotif templates and construct the inputs for fragment-based modelling with MODELLER are accessible in https://github.com/structuralbioinformatics/raDIMod.

Hardware

To enable the benchmarking, RADI has been tested on the queues of a cluster with the same CPU: 2 AMD Opteron 4226 hexacore of 2.9 Ghz CPU with 64 GB RAM. The same CPU has been used for the comparison with CCMPred.

RESULTS

The modification of the alphabet results in different matrices of DI values. Nevertheless, we show that regardless of the alphabet, the top 40 pairs similarly hit equivalent residueñresidue contacts with all three alphabets, while reducing the number of symbols (q) reduces the execution time and reduces the number of sequences of the MSA (after reducing the alphabet many sequences become redundant and are removed from the alignment). We selected a limit of 40 top pairs as in the work of Morcos et al. (9), although for the comparison with CCMPred (8) often no >30 pairs are automatically selected (i.e. the maximum by default).

Comparison of top DI and MI pairs with respect the contact map

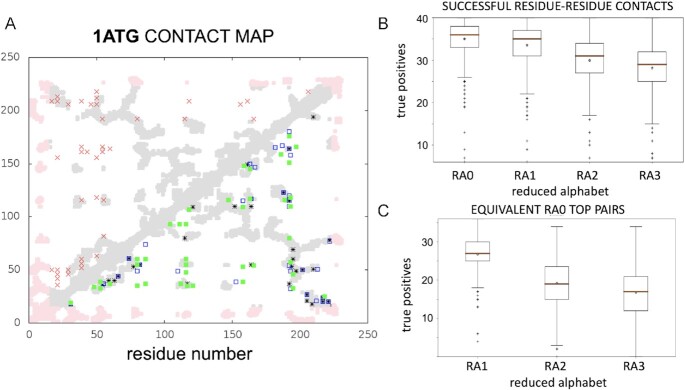
We compare both RADI and the original DCA algorithm on the same set of 509 different proteins from (3), hereafter defined as benchmark. The benchmark contains 78 different protein families from 50 different folds in SCOP (30). Protein sequences and three-dimensional structures are downloaded from the RCSB Protein Data Bank (PDB) (31). As an example, Figure 1A shows the contact map for molybdate binding protein (PDB code 1ATG), compared with the top 40 DI (and MI) values using the original DCA algorithm (i.e. RA0) and the reduced alphabets RA1 and RA3.

Figure 1.

(A) Example of residue-residue contact predictions for Molybdate binding protein (PDB code: 1ATG). Real contacts are shown in grey (or pink if not sufficiently covered by the MSA). Red crosses show the top 40 pairs sorted by MI values using RA0. Under the diagonal are shown the top 40 pairs sorted by DI values using different amino acid alphabets: RA0 (black stars); RA1 (unfilled blue squares); and RA3 (green squares). (B) Boxplots of the distribution of the number of true positive contacts within pairs of positions with top 40 DI values. The boxplots show the distributions obtained by RADI with alphabets RA0, RA1, RA2 and RA3. (C) Boxplots of distribution of the number of residue-residue pairs in the top 40 DI values (for RA1, RA2 and RA3) equivalent to ones among the top 40 DI values with RA0.

For the whole benchmark (see details in Supplementary Data), we compare the distribution of the number of true positive contacts (Figure 1B). The average of true positives across the 509 proteins varies between 29 (for RA3) and 35 (for RA0) and, although all distributions are significantly different, alphabets with RA0 and RA1 classifications are only slightly better than RA2 and RA3. Furthermore, the average number of similar top pairs of classifications RA1, RA2 and RA3 with respect to RA0 varies between 19 and 29, with >20 equivalent pairs between RA1 and RA0 for most proteins of the benchmark (Figure 1C).

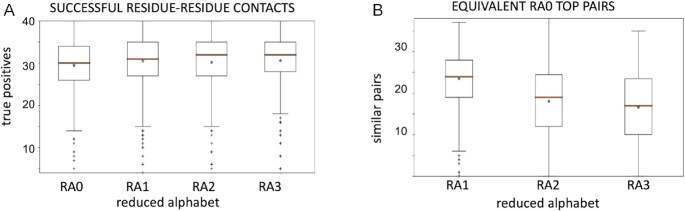
In Figure 2 we compare the success of contact predictions using MI with alphabets RA0, RA1, RA2 and RA3 (Figure 2A) and the number of residue-residue pairs among the top 40 MI values using RA1, RA2 and RA3 equivalent to the pairs among the top 40 MI results when using RA0 (Figure 2B). We conclude that the number of correct contact predictions using MI is similar for all alphabets (the average is around 30 correct pairs) but lower than the number obtained with DI and RA0, while the distributions of equivalent pairs between the entire alphabet RA0 and any of the alphabets RA1, RA2, RA3 are similar to those obtained with DI. Interestingly, the success of MI contact predictions with RA2 and RA3 is higher than using DI for the same alphabet. However, the distribution of pairs ranked at the top of MI along the sequence of each protein are clustered in in local regions, i.e. short range restraints, which is not as helpful as long-range restraints for structural modelling purposes (see supplementary contact maps provided in the GitHub repository and models in the supplementary files of the manuscript).

Figure 2.

(A) Boxplot of the distribution of the number of true positive contacts within pairs of positions with the 40 top MI values. (B) Boxplots of the distribution of the number of residue–residue pairs in the 40 top MI values (for RA1, RA2 and RA3) equivalent to ones among the top 40 DI values with RA0.

Protein structure model building

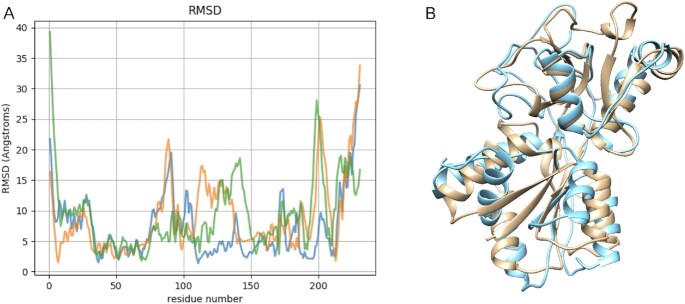
One important applications of the calculation of co-evolving residues is using the highly correlated pairs to define contact constraints and thereby model the structure of a protein. As a proof of concept, we use the 40 top pairs of residues with higher DI values using alphabets RA0, RA1, RA2, RA3 to model the structures of Molybdate binding protein (with PDB code: 1ATG). We use a total of 26 template sMotifs covering 68% of the total sequence (see details in Supplementary Material). The structural superposition of the models of Molybdate binding protein and the crystallographic structure show the quality of the models, which can be quantified per residue by the RMSD of Cα atoms (see Figure 3). We note that all models are significantly good and similar to the crystallographic structure (TM-score around 0.5), although they are generated with different distance restrictions obtained using either RA0, RA1 or RA3 alphabets (see Supplementary Table S1 in Supplementary Material). The total RMSD with TM-align (32) also quantifies the structural similarity, proving deviations of around 5Å for the three models. The RMSD of Cα atoms is also below 5Å in a core region of the three models.

Figure 3.

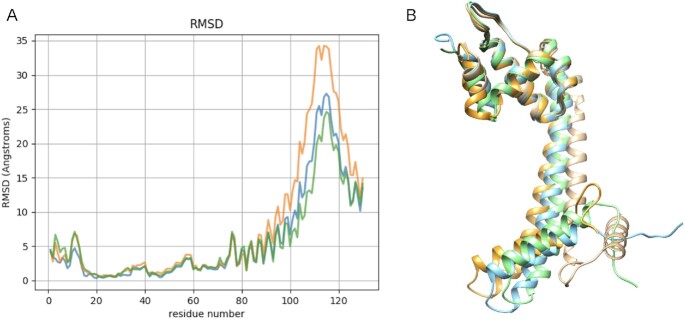
(A) RMSD of Cα atoms between the modelled structures of Molybdate binding protein on the crystal structure using distance restraints obtained with alphabets RA0 (blue), RA1 (orange) and RA3 (green). (B) Superimposition of the modelled structures of Molybdate binding protein obtained with different alphabets RA0 (blue) on the crystal structure (sand color).

Encouraged by the positive outcome, we apply the same approach on a much larger set composed of proteins from 50 different folds of the benchmark and analyzed the quality of the models (see details in Supplementary Table S1 and the set of models in the Supplementary Material). The RMSD of 10 selected models from the benchmark (5 best and 5 worst out of 50 examples) obtained with restraints derived by RA0, RA1 or RA3 alphabets are shown in Table 2. We also indicate the number of sMotif-templates, the percentage of the target sequence covered by them and the Z-score calculated with ProSa2003.

Table 2.

Comparison of selected models with the crystallographic structures: five best (in green background) and five worst (in red background) models out of 50 different folds from the benchmark (the remaining set is shown in Supplementary Table S1). Columns 2–7 show the ProSa2003 Z-score of each model, the RMSD and the TM-score between the model and the crystallographic structure, calculated with TM-align (32). Models are built with spatial restraints derived from the 40 top DI values using RA0 and RA3 alphabets. The last three columns show the length (L) and percentage (C) of the target sequence covered by templates from the classification of sMotifs and the total number of sMotifs used (M)

	RA0			RA3
PDB	TM RMSD	TM Scr	Prosa Z-scr	TM RMSD	TM Scr	Prosa Z-scr	L	C	M
1N9L	1.4	0.9	-6.3	1.7	0.9	-5.8	109	0.95	61
1H98	1.6	0.8	-7.0	1.8	0.8	-6.5	77	0.88	15
1FR3	2.1	0.8	-4.4	2.1	0.7	-5.0	67	0.70	5
1LSS	2.6	0.8	-7.6	2.3	0.9	-7.8	132	0.96	25
1C02	3.0	0.7	-6.0	3.6	0.4	-4.0	166	0.53	4
1G60	5.8	0.2	-1.6	5.6	0.2	-0.3	238	0.37	8
1FEP	7.8	0.2	-1.6	8.4	0.2	-2.4	669	0.52	45
1B7E	7.1	0.2	0.9	7.0	0.3	-1.1	372	0.45	12
1A0P	5.2	0.2	2.4	7.3	0.2	0.0	271	0.16	4
1QKS	6.9	0.2	-2.3	7.5	0.2	-2.5	559	0.05	3

As expected, Table 2 shows that the best results are obtained with a large coverage of the sequence by sMotifs. There is a small but significant correlation between the quality of the models and the coverage of the sequence by sMotifs. This is expected because it follows from the classical approach of homology modelling based on templates, even if they are only applied to local fragments. Nevertheless, this correlation is <0.5 for alphabets RA0 and RA3 (see Supplementary Figure S1). Some examples show that we achieved a reliable model with only around 50% of the target sequence covered by sMotifs thanks to the distance restraints derived by DI. As shown in detail in Supplementary Table S1, for 16 out of 50 folds the approach achieves good quality models deviating<5Å and with a TM-score >0.5 (32). Only 4 models present a TM-score <0.2, which is considered a random solution. Many wrong models are also detected by ProSa2003, being able to select the best model for each target. In the Supplementary Material, we include the models obtained with all other restraints (40 top correlated pairs of residues for each alphabet) and the results for all targets selected covering the total set of different 50 folds of the benchmark. It is also noteworthy that models produced with distance restraints obtained with alphabets RA3 and RA1 were of similar quality to those obtained with RA0. TM-scores of the structures modelled using the entire alphabet, RA0, ranged mostly between 0.2 and 0.9, while models with alphabets RA3 or RA1 were in the same range. As expected, good quality models obtained with alphabet RA0 correspond to good quality models obtained with RA3 or RA1. We conclude that the relationship between the quality of the models and the coverage of sMotifs is almost independent of the alphabet (the Least Square fitting lines in Supplementary Figure S1 are very similar for models obtained using restraints derived by RA0 and RA3 alphabets).

Figure 4 compares the quality of the folds between models obtained using restraints derived with the RA0 alphabet and with RA3. Interestingly, some models obtained with distances derived with alphabet RA3 have better quality than using RA0 (e.g. the comparison with the crystallographic structure of the model for 1QSA produces a TM score of 0.59 with alphabet RA3, while this is 0.49 with RA0). This is also observed in Figure 4, some models obtained with alphabet RA3 have TM-score >0.5, while the model obtained with alphabet RA0 have lower scores. The fitting line shown in Figure 4 has slope close to 1 (approximately 0.84), proving that the quality of the models, using restrains obtained with either RA0 or RA3 alphabets is very similar. Similar correlation is obtained in the comparison of Z-scores calculated with Prosa2003 (see Supplementary Figure S2). Nevertheless, although some models obtained with restraints using alphabet RA3 have better quality than using the whole alphabet (RA0), this is within the range of variability expected by the method. The distribution of the differences of TM scores (ΔTM) between models obtained with different distance-restraints (i.e. using RA0 and RA3 alphabets) shows a standard deviation of 0.09 around an average of 0.02 (see Supplementary Figure S3). The distribution of TM scores of models obtained with restraints using alphabets RA0 and RA3 are practically the same (both are non-significantly different in a paired Student’s T test, with P-value > 0.1, see Supplementary Figure S4). Furthermore, there is no correlation between the quality of the models and the number of effective sequences, neither for models obtained with full (RA0) nor reduced (RA3) alphabets (see Supplementary Figure S5).

Figure 4.

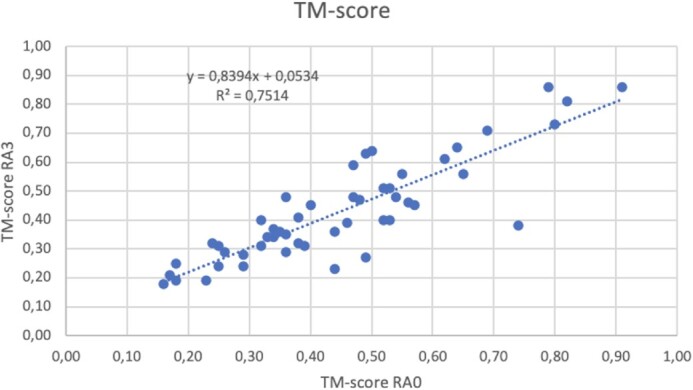
Correlation between TM-scores of models obtained using restraints derived with alphabets RA0 (horizontal axis) and RA3 (vertical axis). The R factor and parameters of a fitting line are shown in the upper left corner.

One of the advantages of reducing the alphabet is that the number of effective sequences is reduced, increasing the applicability to MSAs with <50 non-redundant sequences in a highly compressed alphabet (RA3). Figure 5 compares the number of effective sequences with the original number of sequences obtained with MMseq2. The number of effective sequences for each target studied is also available in Supplementary Table S1. Furthermore, due to the compression of the alphabet, the time of computation is also reduced, although this is not significant in comparison with other new and recent approaches (8). The calculation of the pseudoinverse of a matrix is a computationally expensive step of DCA, whose dimensions depend on the length of the protein (L) and the number of symbols (q) in the MSA alphabet. Reducing the alphabet from RA0 to RA1 speeds 32-fold the computation time of our approach for a protein of L  ≈ 900, while the computation time is reduced ∼2500-fold when reducing the alphabet from RA0 to RA3 (see Supplementary Figure S6 and the comparison with CCMPred). Details of the computational times to calculate DI by RADI and CCMpred for the different folds used for modelling are shown in Supplementary Table S1. A good example is the calculation of DI for chain A of 1QSA, with a length of >600 residues and >3000 sequences in the MSA (>1000 effective): CCMPred reduces the computational time from 3.1e⁴ s (with RADI using alphabet RA0) to 4.5e³ s, like alphabet RA1 (3.5e³ s), while alphabets RA2 and RA3 reduce the time to 4 s. However, we note that CCMPred is prepared to run with several GPU cores, thus surpassing the speed of RADI.

Figure 5.

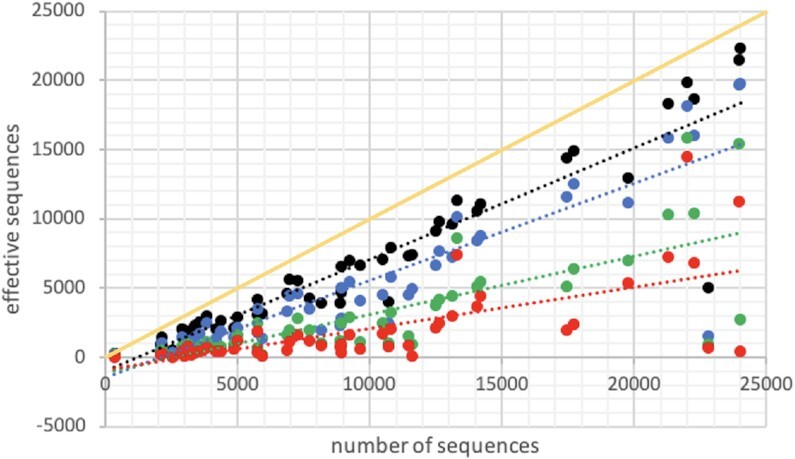
Number of effective sequences in the MSA using the entire alphabet RA0 (in black), or any of the compressed alphabets RA1 (blue), RA2 (green) and RA3 (red) with respect to the original number of similar sequences in the MSA. The least-square fitting lines help to compare the reduction on the number of effective sequences produced by the compression of the alphabet. The yellow line shows the diagonal with exactly the number of sequences in the MSA.

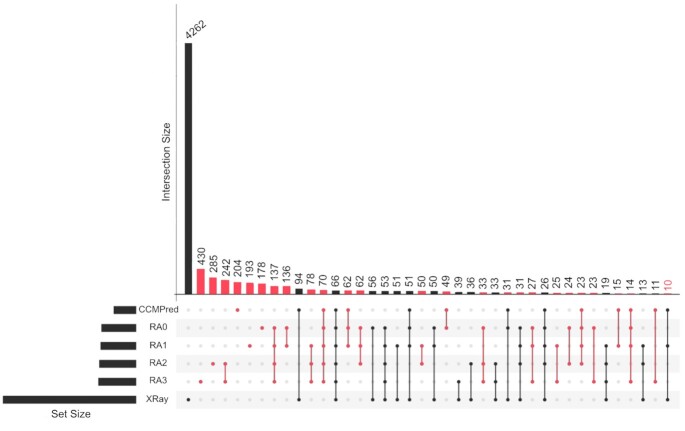
We have compared the residue-residue pairs with top DI obtained by RADI and by CCMPred of the modelled folds of the benchmark (details of the results are provided in the Supplementary Files). The maximum number of pairs selected by CCMPred is 30, and 15 to 20 out of them are equivalent to those selected by RADI with alphabet RA0 (see Supplementary Figure S7). The number of equivalent pairs drops to <10 with alphabets RA2 and RA3. The number of equivalent pairs detected by RADI and CCMPred that correspond to real contacts in the structures is around 5 (using alphabets RA2 and RA3) and 15–20 (using alphabets RA1 and RA0, respectively). However, we noticed that RADI with alphabets RA0 and RA1 detected real contacts different than those found with CCMPred. Figure 6 shows in detail the intersection of different approaches with real contacts (Supplementary Figure S8 shows the Venn diagram of these intersections). The UpSet plot (33) shows that there is a relevant number of false predictions by independent or combined methods that needs to be further analyzed. However, the combination of RADI, using several alphabets, and CCMpred produces a relevant number of correct predictions and their difference is small (i.e. 105 with CCMpred and 102 with all alphabets of RADI). The ratio of true-positive and coverage of the predictions for the combination of approaches can be obtained from the UpSet plot (Figure 6) and the Venn diagram (Supplementary Figure S8). Table 3 shows the average of true-positive and coverage ratios obtained per protein and the ratios of the accumulated predictions. Although the accuracy of CCMpred is higher than RADI, the coverage of RADI with most alphabets is better than CCMPred.

Figure 6.

UpSet plot of the intersection of residue-residue pairs of real and predicted contacts obtained with Intervene tool (33). The number of coincident and non-coincident contacts, either real or predicted by one or more methods, are calculated using interval-squares of 9 × 9 positions of the two-dimensional contact-map centered around each pair with a real or a predicted contact. The number of 1 × 1 squares predicted by one or more approaches, or obtained by real contacts, are accumulated for all folds of the benchmark and the final number is normalized by 81 (i.e. the total number of squares around each position in the 2D map). The UpSet plot shows only individual or combined sets with >14 contacts. Contacts predicted with RADI use the original alphabet (RA0), or other alphabets (RA1, RA2 and RA3).

Table 3.

Coverage and true positive ratio of predictions. The coverage and true-positive ratios of CCMPred and RADI with alphabets RA0, RA1, RA2 and RA3 are calculated for the proteins of the benchmark used in Table 2 (a total of 50 different folds). The first two rows contain the average and standard deviation (in parenthesis) of coverage and true-positive ratios. The last two rows contain the ratios of the total of accumulated predictions. Note: Details per protein are in Supplementary Table S2

		CCMPred	RA0	RA1	RA2	RA3
Average	TPR	0.91 (0.13)	0.84 (0.12)	0.80 (0.13)	0.67 (0.12)	0.61 (0.11)
	COV	0.006 (0.0057)	0.0072 (0.0068)	0.0068 (0.0067)	0.0058 (0.0059)	0.0055 (0.0060)
Cumulative	TPR	0.91	0.84	0.80	0.67	0.61
	COV	0.003	0.004	0.004	0.003	0.003

These results are interesting because they proof the advantages of using RADI with different alphabets: (i) it helps to predict other potential contacts different than CCMPred (or RADI with the standard RA0 alphabet) and increase the coverage, and (ii) it reinforces the prediction of contacts of those pairs detected by CCMPred and RADI because the largest percentage of these equivalent pairs correspond to real contacts.

Sources of errors

Morcos et al. showed that a potential source of error was caused by the homodimerization of a protein (9): when a protein dimerizes with itself and two residues from different chains of the dimer are in contact with each other, this results in a high correlation (or high value of DI) which does not correspond to an intrachain but an interchain interaction. Constraining the distance between both residues within the same chain results in a deformation of the structure of the model, and thereby gives rise to an erroneous prediction.

To illustrate this issue we have modelled the structure of a transcriptional regulator of the MerR family from Bacillus cereus (code 3HH0 of PDB), a homo-tetramer, using the restraints obtained with alphabets RA0, RA1 and RA3, and the sMotif of templates covering 100% of the sequence (see details in Supplementary Material). This is an interesting example because although the structure of a single chain is a single domain, the region at the N-tail is structured as a bundle of helices far from the C-tail, which is formed by a single helix, and both are connected through a large helix. Consequently, distance restraints between N-tail and C-tail are unexpected and still necessary to properly orient both regions. Figure 7 shows the tetramer quaternary structure of 3HH0, the contact map of a single chain sequence and the top 40 pairs with highest DI for various alphabets.

Figure 7.

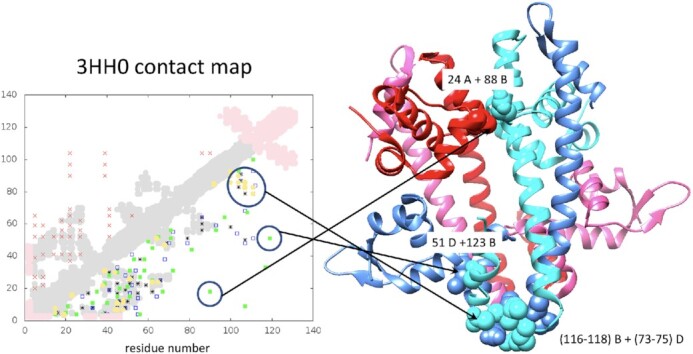
Residue-residue contact predictions for a single domain of the transcription regulator of the MerR family with code 3HH0 in the PDB is shown in the left: real contacts and 40 top pairs with higher MI and DI values are shown as in legend of Figure 1, adding in yellow circles the top pairs detected by CCMPred. The quaternary structure of the tetramer complex of 3HH0 is shown in the right: chain A in red, chain B in light blue, D in blue and C in magenta at the rear. Side-chains of the pair of residues with high DI (encircled in the contact map) are shown in spheres (light blue in chain B, blue in chain D and red in chain A) and the correspondence is identified by arrows and by the sequence positions of pairs labelled in the ribbon plot of the structure. The group of contacts between residues 116–118 of chain B and 73–75 of chain D were found by RADI using all alphabets and by CCMPred.

As shown in the contact map highlighted by circles, there are two pairs of residues with high DI obtained with alphabet RA3 that do not correspond to intrachain contacts but to interchain ones. The correlation between residues 116–118 and 73–75, also encircled in Figure 7, is similarly associated with interchain contacts. This is consistent with the fact that in the quaternary structure of the protein, the two amino acids of both pairs are facing each other but from different protein chains (or monomers). The contact is produced between the side-chains of the residues in different chains (the correspondence is shown in Figure 7). The contacts predicted by DI are wrong if they are considered as part of a pair of residues within a single chain, but are correct when taking into account the complete quaternary structure. Interestingly, the contacts between residues 116–118 and 73–75 of two different chains are detected by CCMPred and RADI (with all alphabets), while the interchain contacts between positions 51–123 and 24–88 are only detected with RADI using alphabet RA3. This example shows how different alphabets help to detect correlations associated with structural contacts that were unnoticed by the standard alphabet.

Thus, when modeling the conformation of 3HH0, the restraints between residues that only occur in the quaternary structure may deform the model. In addition, it is not possible to define as constraints large distances between the last helix at C-tail and the bundle of helices in the N-tail. Therefore, the orientation of the C-tail helix is wrong, and this cannot be detected neither by the restraints derived with DI nor from the analysis of the energy of the final models with Prosa2003. Figure 8 compares the model of a single chain with the crystallographic structure and the RMSD profile of the Cα atoms along the sequence after forcing the superposition on the first 90 residues, highlighting the deviation at the C-tail. The TM-score is 0.66 and the RMSD with TM-align is 3.33 Å for the comparison between the model obtained with restraints of RA0 and the crystal structure. Interestingly the Z-score with Prosa2003 is not good (about -2.65), mostly due to the addition of the surface scores of Prosa2003, which is already an indication of the potential oligomerization of the protein.

Figure 8.

(A) RMSD of Cα atoms between the modelled structures of the transcription regulator of the MerR family with code 3HH0 in the PDB and the crystal structure of a single chain. Color labels are as in Figure 4. (B) Superimposition of the modelled structures of 3HH0 obtained with different alphabets (RA0 blue, RA1 orange and RA3 green) on the crystal structure (sand color).

DISCUSSION

Pairs of residues with top DI values can be used to predict the contact map of a protein structure, regardless of the alphabet. In addition, pairs ranked at the top of MI values give rise to similar number of successful contacts independent of the alphabet, but the time saved by reducing the size of the alphabet is not as significant as that for DI calculation. We must note two additional relevant conclusions: First, the simplification of the system produced by the reduction in the number of symbols is still representative of the physicochemical nature that characterizes the protein structure. This holds for the calculation of both DI and MI. Second, the number of sequences required to calculate the MSA is reduced, as many sequences become redundant after simplifying the alphabet from RA0 to RA3, helping to apply the approach on proteins that appeared late in evolution if enough sequences described by polar/non-polar symbols are still available. We notice that the minimum number of sequences of the MSA in our study was 49. Although certainly the reduction of sequences of the MSA decreases the computational time, it is more important to notice that it helps to widen the applicability because if the variability of sequences allows for alignments with a small number of sequences after the reduction, then we can apply the approach to many more proteins (i.e. those that appeared late in evolution, which are important for human). Also, correlated pairs after changing the alphabet will highlight correlated physicochemical features. Finally, the contact predictions with a reduced alphabet (RA3) are as valuable for the prediction of protein structure as with the entire alphabet (RA0). We have shown that the quality of the models obtained with restraints derived from amino acid covariations is similar when using either the full list or any of the reduced alphabets, if they are combined with a significant information of the local structures. Local conformations are modelled with short templates covering fragments of the protein sequence. These fragments are identified as regular super-secondary structure motifs (sMotifs) in the classification of ArchDB14 (22). The coverage of the protein sequence by sMotifs is important, but not critical. We achieve near native structures with the combination of long-distance restraints obtained by the coupling analysis and short/medium-distance restraints from local templates of sMotifs, even when the coverage of these templates is <50%. Still, the quality of each model is better when the coverage of the sequence by sMotifs is larger. Interestingly, the compression of the amino acid sequence into a sequence of polar/non-polar or polar/hydrophobic residues had been applied since the early studies of the mechanisms of protein-folding (34) and in Lattice-model examples (35). The approach followed by us operates in a similar manner, by modeling mini-folded super-secondary structures and then applying spatial restraints derived from amino acid covariation. Finally, we hypothesize that recent advances achieved in ab initio fold prediction (36,37) could also benefit from the use of a simplified alphabet, not only on the speed of some of the steps, but by reinforcing or adding new predictions with the use of multiple sequence alignments processed by self-attention (38).

Note: The program and results for the sequences of the benchmark are available at https://github.com/structuralbioinformatics/RADI. For the construction of structural models, it is necessary to align the sequence of the query target with structural fragments (sMotifs). The script is available at https://github.com/structuralbioinformatics/archdbmap. For the construction of the models, we use the program MODELLER. The scripts to combine the fragment-based modeling and distance restraints from RADI are available at https://github.com/structuralbioinformatics/raDIMod.

DATA AVAILABILITY

RADI is available at https://github.com/structuralbioinformatics/RADI and raDIMod at https://github.com/structuralbioinformatics/raDIMod

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

Spanish Ministry of Economy MINECO [BIO2014-57518-R, BIO2017-83591-R (FEDER, UE), BIO2017-85329-R (FEDER, UE)]; Generalitat de Catalunya [SGR17-1020].

Conflict of interest statement. None declared.