Enzyme dynamics: Looking beyond a single structure

Abstract

Conventional understanding of how enzymes function strongly emphasizes the role of structure. However, increasing evidence clearly indicates that enzymes do not remain fixed or operate exclusively in or close to their native structure. Different parts of the enzyme (from individual residues to full domains) undergo concerted motions on a wide range of time-scales, including that of the catalyzed reaction. Information obtained on these internal motions and conformational fluctuations has so far uncovered and explained many aspects of enzyme mechanisms, which could not have been understood from a single structure alone. Although there is wide interest in understanding enzyme dynamics and its role in catalysis, several challenges remain. In addition to technical difficulties, the vast majority of investigations are performed in dilute aqueous solutions, where conditions are significantly different than the cellular milieu where a large number of enzymes operate. In this review, we discuss recent developments, several challenges as well as opportunities related to this topic. The benefits of considering dynamics as an integral part of the enzyme function can also enable new means of biocatalysis, engineering enzymes for industrial and medicinal applications.

Graphical Abstract

Last two decades have seen intense debate about the role of protein dynamics in enzyme catalysis. Evidence from a wide variety of techniques and for an increasing number of enzyme complexes has already been collected, and a better picture has emerged about how internal motions and conformational fluctuations are important contributors to the catalytic efficiency of enzymes. This review discusses new opportunities in fundamental understanding of biocatalysis as well as enzyme engineering and applications.

INTRODUCTION

A long list of observations, made possible by a century of careful investigations, collectively emphasize the role of a single native protein structure in enzyme catalysis (1). Biochemistry textbooks typically depict enzymes with a single three-dimensional structure defined with fixed bonds, angles and other geometric parameters. Several important aspects of enzyme catalysis can be understood using this single-structure protein model, including active-site shape and charge complementarity. However, many enzymes have been shown to speed up chemical reactions on millisecond time frames (or even faster) when the uncatalyzed reactions normally take billions of years to occur. Several efforts to dissect the high catalytic efficiency of enzymes based on the single-structure model have concluded with limited success. Further, it is unclear why enzymes require large and complex three-dimensional structures when their reactive centers (or active-site) are relatively small. Individual residues, particularly those located away from the active-site, appear to play significant roles besides stabilizing a three-dimensional architecture. In this review, we describe recent progress in the field of investigations related to the role of internal residue motions and conformational fluctuations in enzyme catalysis. We also highlight the technical challenges associated with the topic and also discuss the potential benefits of emerging view in enzyme engineering.

Enzyme function involves a series of steps that include binding of substrate(s) (and other reaction participants such as cofactors), the chemical conversion, as well as the release of products and spent cofactor. Both the entry of substrate(s) into the reactive center and product release intrinsically involve motions of protein residues occurring on several time-scales, which typically range from picoseconds to several seconds depending on the enzyme. However, a relevant and important question remains whether the rate of specific residue motions (and other structural motifs) determines the rate of overall catalysis, and therefore catalytic efficiency, much like the speed of people moving through automated revolving doors is determined by the speed of the door’s rotation. Increasing evidence suggests that the rate of transitions between conformational sub-states (green arrows in Figure 1) is related to the rate of proceeding through steps of the catalytic cycle (2). The largest energy barrier would correspond to the slowest, or rate-determining step (3). Sampling of these conformational transitions has been shown to act as an intrinsic property of the protein fold, where residues involved in catalysis sample the proper alignment at a rate coinciding with the rate of observed substrate conversion; a rate also observable in apo enzymes (a phenomenon known as conformational selection) (4). Obtaining information about the motions of individual enzyme residues as well the conformational transitions associated with the rate-determining step have proved to be extremely challenging.

Figure 1. Schematic representation of conformational landscape associated with steps of enzyme catalysis.

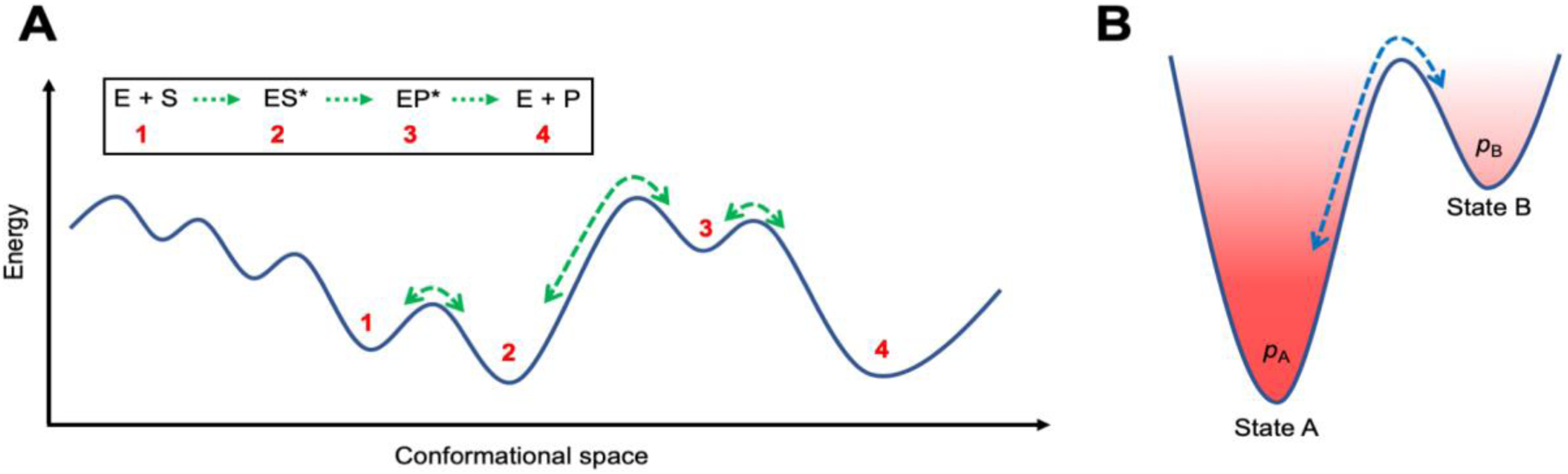
(A) Enzymes do not stay fixed in their ‘native’ structures, but instead undergo conformational motions. Conformational changes experienced by the protein on several time-scales facilitate the different steps of substrate (and/or cofactor) binding, reactant ground state stabilization, chemical step of conversion, and product release along the catalytic cycle of an enzyme. The green arrows over the barriers in the conformational landscape correspond to the rate of transitions between the distinct sub-states. The rates of these conformational transitions are intrinsic properties of an enzyme topology and can be reproducibly measured with appropriate experimental techniques (2, 4). (B) Interconversion between two conformational states A and B. A is the lower energy state compared to state B (excited state), therefore, the conformational populations and associated probability p_A will be higher than p_B.

At first glance, a direct approach whereby each protein residue is mutated to all other amino acid possibilities could be envisioned as the ideal experiment to investigate the role of dynamics on enzyme activity. Emerging automation in library design and high-throughput screening methodologies certainly aid in data generation and collection. However, such an approach is expected to face execution challenges for several reasons, including physical limitations of experimental screening and combinatorial explosion in library design (5). In addition to affecting dynamical properties, the primary structure controls many aspects of a protein’s fate and function, including foldability, three-dimensional structure, oligomerization, and activity. In more complex cases, it also affects cell localization and interactions with other biomolecules. As a result, mutations can alter many aspects of a protein function, in addition to affecting expression and purification yields. Even when mutant enzymes can be expressed, purified and kinetically characterized, an additional level of complexity arises. Since structure and dynamics are closely interrelated, changes in primary structure might not solely lead to changes in protein dynamics, but in three-dimensional structure as well. Therefore, teasing apart the role of each residue and concretely characterizing their dedicated role on protein dynamics has been extremely challenging to achieve, although new and promising techniques have been developed to overcome some of these limitations.

In this article, we review some of the ongoing challenges as well as related opportunities that have recently been uncovered as a result of the new paradigm of enzymes as dynamical assemblies. In section 1, we briefly summarize the current understanding of enzyme dynamics. A number of reviews have already covered many aspects of protein dynamics in relation to enzyme catalysis (6), and the interested reader is directed to these reviews for a comprehensive view of the topic. This review focuses on a number of other aspects that have not been covered elsewhere. In section 2, we discuss new experimental and computational techniques that are enabling a better understanding of the roles played by dynamics, with focus on techniques which connect dynamics to the rate-determining step in enzyme catalysis. The vast majority of literature on enzyme studies is based on laboratory-scale studies, which are performed in dilute aqueous conditions. However, in cells, enzymes operate in crowded environments that are remarkably different from such idealized conditions. Section 3 discusses the potential impact of solvent and surrounding conditions on enzyme dynamics, and therefore function. In section 4, we review a powerful technique that enables lab-scale evolution and design to fine tune enzyme dynamics to catalyze new reactions. Finally, section 5 describes some perspectives, challenges and opportunities associated with this topic. As this area has already benefited from a long list of pioneering investigations on well-characterized systems, the reader will also be directed to relevant published studies and other reviews at appropriate places throughout the article.

1. The emerging paradigm of Enzyme Dynamics

Cellular machinery relies on assembling diverse enzymes from a list of only twenty amino acids, aided by post-translational modifications and sometimes inclusions of uncommon amino acids. The length and sequence of the protein determines the structures of enzymes, and these diverse enzymes catalyze hundreds of biochemical reactions at varying speeds ranging from once per minute to billions of times per second. What factors enable enzymes to recognize their substrate(s) with high accuracy and work with high efficiency? The search has been ongoing for many decades now. A number of theories have been proposed and successfully used to explain multiple aspects, which are covered in many other quality reviews (1, 6a, 7).

Enzyme dynamics refers to internal motions that occur from femtosecond (fs) to second (s) time-scales (8). Faster motions are associated with localized structure, while slower motions that occur on longer time-scales are associated with the conformational fluctuations occurring over large domains or full enzyme structure (9). It has been suggested that localized motions play a role, especially in the active-site, by forming direct interactions with the reactants, to control the precise interactions that enable progress along the reaction coordinates (6d, 6f, 6m). On the other hand, a number of studies have suggested that conformational dynamics on longer time-scales enable enzymes to sample sub-states that contain the functionally important features required for the various sub-steps along the catalytic cycle (2). Dynamical networks of conserved residues have been discovered in many enzymes that connect dynamical surface residues to the active-site, which have been shown to be critical for function (9). Mutations of these residues lead to loss of efficiency or even complete abrogation of activity, providing some validation for the importance of dynamics in enzyme catalysis. New engineering solutions with photo-activation of conformations and cross-linking within dynamical residue networks have also been designed to improve enzyme catalysis and design de novo function (10). Further, loop engineering of dynamical surface residues to increase catalysis has also provided new means of validation (11).

A number of recent reviews have summarized the information obtained about enzyme dynamics from a variety of techniques as well as their relevance in catalysis. Hammes-Schiffer and coworkers proposed a model incorporating flexibility and conformational changes that explains how enzymes can robustly follow multiple pathways between the reactant and product states, on a multi-dimensional free energy surface (6g). Klinman and Kohen focus on findings that pertain to enzyme motions that control donor and acceptor distance in enzyme-catalyzed hydride transfer, creating an ensemble of conformations suitable for hydrogen-tunneling (12). In another review, Kohen addresses the substantial versus semantic controversies in the field (6j). Providing examples, this review summarizes systems where enzyme dynamics enables shifting of conformational ensemble upon binding; then via thermal search of the conformational space toward the reaction’s transition-state and the rare event of the barrier crossing toward products, which is likely to be on faster time scales than the first and following events; and finally via the dynamics associated with release of products, which are rate-limiting for many enzymatic reactions. In an alternate view, Warshel and coworkers have summarized evidence that does not favor enzyme dynamics in promoting catalysis, rather that the majority of rate-promoting contributions can be explained based on electrostatic effects and particularly preorganization effects (6e, 6k). Chennubhotla and Agarwal summarized studies indicating that the enzyme ability to sample conformational sub-states and populations in functionally important states are tied to the overall rate of enzyme catalysis (4). A review by Schramm includes discussions on the relevance of enzyme dynamics and transition states (6l). Another excellent article by Schwartz builds a consensus view emerging from experimental and computational techniques, particularly on the role of fast motions in enzyme reactions (6m). Agarwal also summarized a biophysical model of enzymes based on enzyme and solvent dynamics with focus on pathways of energy transfer between the dynamical surface loop regions and the active-site of several enzymes (6n).

In addition to dynamics, a number of other factors are also important contributors to enzyme catalysis. In particular, the role of electrostatic effects has been widely acknowledged. The local structure of the active-site allows the electronic environment to be controlled to optimally facilitate the progression of the chemical reaction being catalyzed. Long-range electrostatics have also been acknowledged in fine-tuning the enzyme behavior for various steps along the catalytic cycle (substrate binding, chemical turnover and product release), and also the important preorganization of the active-site. Collectively, the overall protein fold, local structural organization, electrostatic effects and dynamical effects allow enzymes to strike the functional balance and achieve the required efficiency for the targeted chemical reaction to occur.

2. New and promising techniques to investigate enzyme dynamics

The effects of structural changes on the biological functions of proteins have been acknowledged for some time, mainly through conformational changes observed at the molecular level from X-ray structure of proteins subjected to mutation and/or ligand binding (13). Internal protein motions span at least 12 to 15 orders of magnitude in time, preventing the use of a single technique to capture information on all relevant time-scales (6b). A number of past reviews have already discussed a variety of techniques and methodologies employed to study protein dynamics (6g, 6i, 13b, 14). In this section, we discuss recent advancements that primarily interrogate protein dynamics occurring on time-scales relevant to enzyme catalysis, which typically occur on the millisecond-to-second (ms-s) time frames. Beyond these observations, a critical link has also been suggested between dynamic events experienced by enzymes on several time-scales and their functional effects on substrate specificity, ligand binding, release, and/or catalysis. Over the past several years, however, our understanding of how exactly these enzyme conformational dynamics enable or affect catalysis has remained elusive, if not sometimes purely incidental. A number of now established experimental methods have been developed to investigate protein dynamics on several time frames, among which the most informative remains nuclear magnetic resonance (NMR), specifically the relaxation dispersion experiments.

2.1. NMR relaxation-dispersion CPMG and chemical exchange saturation transfer (CEST)

The conventional Carr-Purcell-Meiboom-Gill (CPMG) NMR sequence is a powerful tool for the investigation of conformational exchange in proteins. Since 1972 (15), it has been used to probe exchange phenomena occurring on time-scales that approximately range between 300 μs and 10 ms (k_ex ~100 to ~3000 s⁻¹)(16), and has since been extensively reviewed (16–17). This technique allows the determination of an exchange rate (k_ex) and chemical shift difference (Δω) between the major conformer and the excited state of a protein in solution, in addition to extracting population ratios (p_A and p_B; Figure 1B) of both states. Primarily recorded as a series of ¹⁵N-HSQC experiments, the technique has extremely good atomic-scale resolution, allowing the investigation of specific protons and other relevant atoms on selected residues in any protein or enzyme amenable to NMR investigation. The chemical shift of the investigated atoms can then be determined by combining Δω with information obtained from an HMQC spectrum (18), which in turn can be used to determine the solution structure of the excited state (19). More recently, modified CPMG sequences have allowed broadening of the time-scales available to probe conformational exchange in proteins down to ~25 μs phenomena (k_ex ~40000 s⁻¹)(20), or to gather additional information on the structure of the metastable states, such as residual dipolar couplings (RDC)(21), residual chemical shift anisotropy (CSA)(21b), order parameters (22), and diffusion constants (23).

In 2011, a pulse sequence called dark-state exchange saturation transfer (DEST) was used to study amyloid-β, which undergoes an exchange process between soluble monomers and massive protofibrils (24). The particular innovation of this experiment was its use for the first time to analyze a protein normally undetectable by solution NMR. This pulse sequence was then refined into a two-dimensional chemical exchange saturation transfer (¹⁵N-CEST) experiment, which provides similar information as CPMG (k_ex, Δω, p_A and p_B), but for time-scales ranging between ~2.5 ms and ~50 ms (k_ex ~20 to ~400 s⁻¹), with the added benefits of directly extracting the chemical shift of the excited state from a single magnetic field (25). The full physical details of the pulse sequences and equations that allow parameter determination lie outside of the scope of the present review and have been recently reviewed (25b).

Modifications to the CEST sequence were successful in extracting the values of various parameters in the invisible state of a protein, such as histidine side chain pKa values (26), conformer-specific hydrogen exchange rates (26), paramagnetic resonance enhancements (PRE)(27), or pseudocontact shifts (28). Recently, an altered version of the same pulse sequence managed to reduce acquisition time of the spectrum, at the expense of overlap in resonances exchanging between states separated by a large Δω. This method has been developed independently by two groups. Traaseth and coworkers dubbed it multiple frequency CEST (MF-CEST)(29), while Bouvignies and coworkers named it DANTE-CEST (D-CEST) after the selective excitation scheme used in their study (30). Typically, all of these experiments and variants provide information on exchanging backbone ¹⁵N atoms, although they can also readily be adapted to investigation of ¹³C atoms (31). Protons are trickier to study using CEST, as an NOE-based dip can be observed on standard CEST sequence-based ¹H spectra, which can easily be mixed with the minor state dip (32). To circumvent this issue, a pseudo-4D CEST pulse sequence was recently developed to collect information on exchanging ¹H^N atoms while cancelling out the undesired dip (25b, 33). All of these variations nevertheless illustrate the versatility of the CEST technique, allowing the user to extract a wide variety of dynamic information from their protein of interest.

Classical CPMG equations typically account for two-state conformational exchange (16), which in many cases is an oversimplification of actual exchange phenomena. Additionally, one of the drawbacks of this experiment stems from the fact that it can be difficult to observe more complex exchange processes solely from CPMG relaxation dispersion profiles. CEST profiles, however, have the advantage of directly providing the chemical shift of the minor state, and can even illustrate when more than one minor state exists in equilibrium with the basal state. For instance, in the Bacillus subtilis arsenate reductase (ArsC), the active-site P-loop alternates between three different conformations in its reduced form, which is one of the four conformations observed during its full catalytic cycle (34). While the CEST equations might be impossible to solve for a three-state exchange process, the CEST profile manages to provide a general idea of the more complex nature of the exchange processes occurring in many enzyme systems.

Despite the aforementioned limitations, CPMG and CEST NMR relaxation experiments have shed significant light on the conformational mechanisms governing function in several protein and enzyme systems. For instance, exchanging proteins appear to be involved in the infection cycle of HIV, as both HIV protease (17c) and NCp7 nucleocapsid (31b) undergo conformational exchange in solution. While the existence of movements in HIV protease flap regions have been acknowledged for a relatively long time (35), the dynamic model for their exact role in virus replication has been proposed only recently, based on CPMG and CEST characterization of a complex between the protease and its substrate, the precursor Gag polyprotein (36). The authors described that flap closure would lengthen the lifetime of the complex, thus raising the likelihood of Gag cleavage into the three proteins it contains, while flap closure would not be efficiently stabilized in nonspecific substrate binding to allow this lifetime extension (36). CEST and CPMG experiments have also managed to explain the elusive mechanism of mercaptobenzamide thioesters, a promising drug class which only targets one of the two NCp7 zinc knuckles. This was illustrated by showing that the C-terminal zinc knuckle undergoes conformational exchange involving the Zn²⁺-coordinating residues, which allows thioesters to access those residues and subsequent acylation of the protein (31b).

The study of conformational exchange was also extremely useful to understand the mechanisms of action of intrinsically disordered proteins (IDPs) and their role in enzymatic regulation. For instance, a combination of ¹⁵N-CEST, ¹⁵N-CPMG and R_1ρ experiments has been used to characterize the recognition mechanism between the mitogen-activated protein kinase (MAPK) p38α and the intrinsically disordered regulatory domain of the MAPK kinase (MKK) MKK4, which provides MKK4 specificity for p38α (37). Another example is the activation of the bacterial chaperone histone-like nucleoid structuring-dependent expression A (HdeA) through acid-driven structure loss, which was characterized by ¹⁵N-CEST, paramagnetic relaxation enhancement (PRE), and H-D exchange (38). These experiments revealed that acid activation of the protein exposes hydrophobic patches that permit client protein recognition and binding. Interestingly, CEST even found applications in the medical field through MRI. Indeed, using the weak B₁ field to saturate labile protons on a specific compound of interest, a contrast can be obtained, thus leading to vital physiological and pathological information in a patient (39).

2.2. Millisecond ‘kinetic’ mass spectrometry: Time-Resolved ElectroSpray Ionization with Hydrogen/Deuterium eXchange (TRESI-HDX)

Hydrogen-deuterium exchange (HDX) is a principle that allows the identification of solvent-exposed labile ¹H atoms that are not involved in hydrogen bonding. The basic principle involves exposing an unlabeled protein to a deuterated aqueous solvent, as time incubation allows exchange between labile ¹H in the protein and deuterons from the solvent (40). This allows for identification of transiently solvent-exposed ¹H atoms since deeply buried ¹H will either not exchange or exchange on a much slower time-scale than exposed ¹H atoms. As a result, this technique can be significantly useful to investigate slow time-scale conformational exchange experienced by active enzymes and proteins. Among other examples, this principle has been applied in NMR to determine the stabilization of mouse galectin-2 following S-nitrosylation of Cys57 (41), changes to domain stability in human galectins 1 and 8 upon lactose binding (42), or hydrogen bond strength in the chicken α-spectrin SH3 domain.(43) HDX was also combined with mass spectrometry (MS) to study, among many other examples, the structural effects of steroid-binding to apolipoprotein-D (44), misfolding of a cystic fibrosis transmembrane conductance regulator mutant (45) or identification of an allosteric modulation in the KDM5A histone demethylase (46).

Because of technical limitations, HDX was historically only usable to study exchange phenomena occurring on the time-scale of minutes or slower (47). Recently, a clever use of microfluidics circumvented some of these technical limitations and allowed the collection of HDX data using MS on subsecond time-scales (48). These developments, which have been termed TRESI-HDX, effectively allowed the study of enzyme systems as they undergo catalysis by stopping the reaction at various time points, providing specific dynamic information on the conformational landscape of the enzyme as it moves along reaction coordinates. This methodology also provides significant advantages over other techniques. For instance, although NMR still provides unrivaled atomic-scale resolution relative to MS (which is typically secluded to an area of about 5 residues on the sequence), NMR remains limited by the fact that signal build-up requires several minutes/hours of instrument acquisition time. This typically prevents real-time investigation of fast, non-equilibrium enzyme reactions without the requirement of stable reaction intermediates, a rather rare occurrence in active enzyme kinetics. Additionally, although significant improvements have been achieved in specific isotopic labeling schemes (49), NMR techniques somewhat remain constrained to the study of smaller protein complexes.

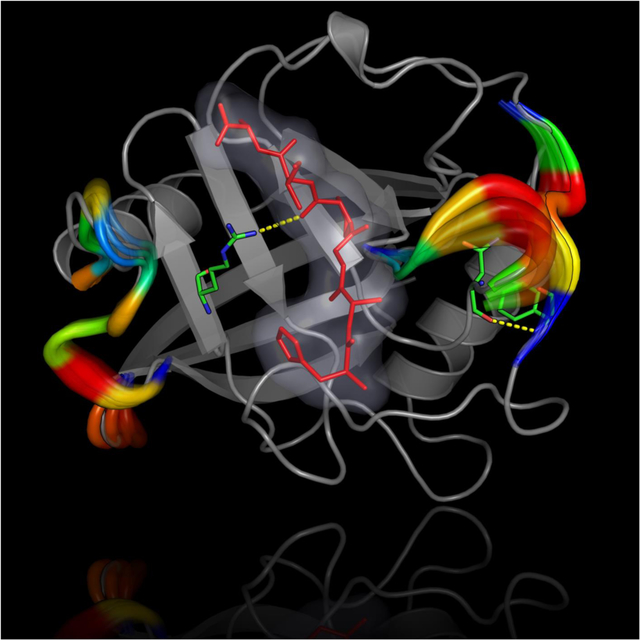
As a relatively straightforward method, TRESI-HDX uses a microfluidic ESI-MS spectrometer apparatus to follow the time evolution of a catalytic system by mixing the enzyme of interest in D₂O in presence of a relevant ligand (substrate, inhibitor, analogue, etc.)(48). The catalytic reaction is followed in real time, with HDX occurring at exposed conformational sites sampled by the working enzyme, after which deuteration is terminated by acid quenching, followed by proteolysis and ESI-MS analysis of the peptides (Figure 2A). Among other examples, the Wilson group has recently used this methodology to illustrate specific dynamic modes and changes in enzyme dynamics associated with substrate/inhibitor binding and turnover in the active TEM-1 β-lactamase (50). Their results illustrate that specific dynamic modes experienced by TEM-1 only occur in presence of certain penicillin substrates or the clavulanate inhibitor. For instance, rigidification of the S4/S5 loop (residues 250–257) suggests a previously unknown long-distance effect of this loop on the deacylation step of the reaction. Similarly, their results also illustrate that the C-terminal alpha helix of TEM-1 (residues 273–284) requires flexibility for catalytic function, as rigidification of this structural motif is a unique event only observed in the presence of the clavulanate inhibitor. Turnover would thus be associated with a high degree of flexibility in this region, with dynamic alteration considerably perturbing the rate of the essential deacylation step of the catalytic reaction (Figure 2B). Interestingly, this region was also previously associated with a number of long-range mutations observed in laboratory and clinical isolates of this enzyme, which are specifically associated with resistance to inactivation by clavulanate. As pointed out by the authors, our ability to acquire such detailed pictures of catalysis-linked dynamics has real implications for allosteric drug development, namely by targeting previously hidden dynamic modes that control the function of physiologically and therapeutically important enzymes.

Figure 2. Schematic depiction of the millisecond time frame sampled by TRESI-HDX.

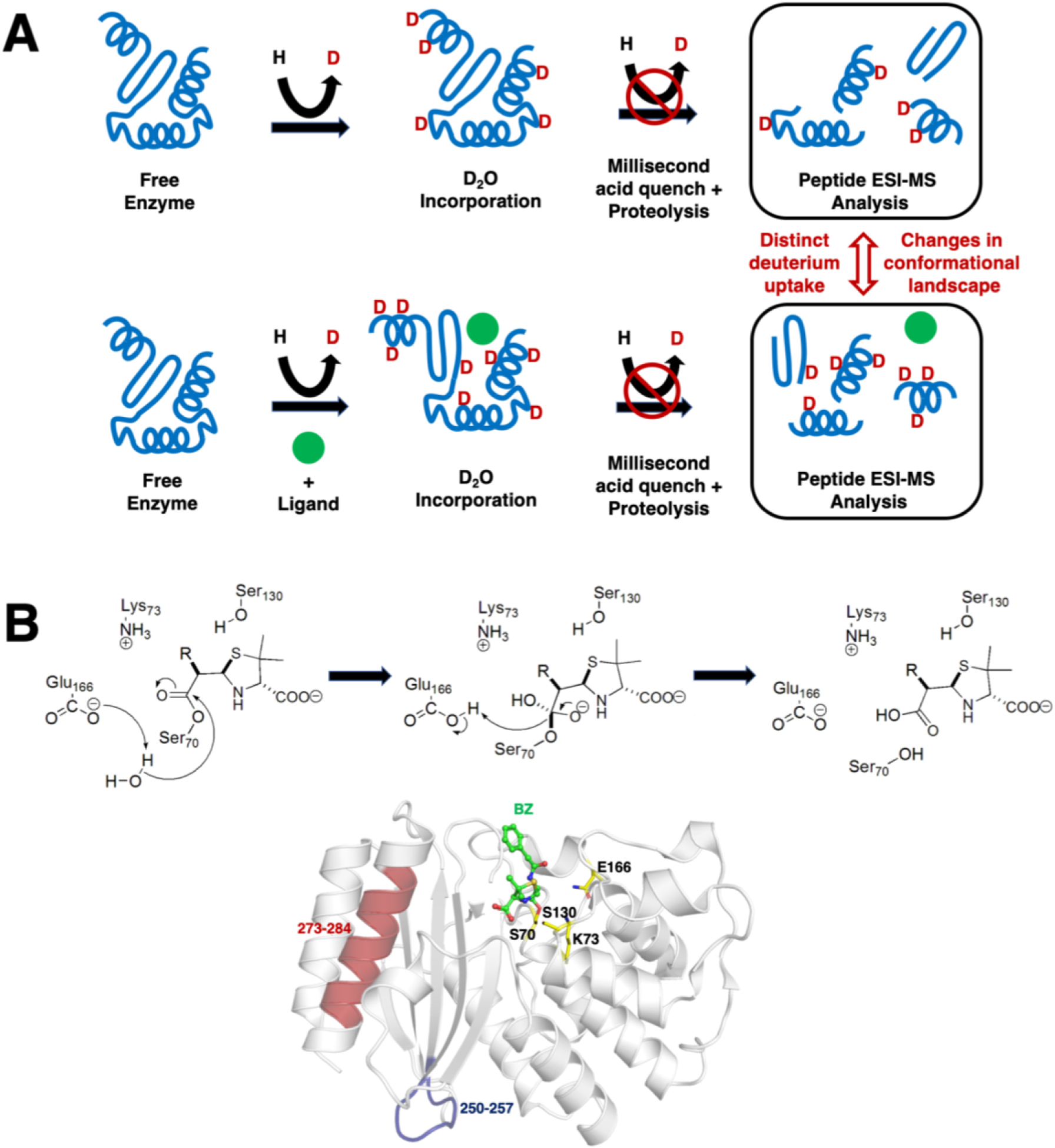
A) The experiment allows comparative analysis of changes in conformational dynamics experienced by a working enzyme during catalysis. The enzyme is first subjected to deuterium incorporation in absence (top) and presence (bottom) of a ligand of interest. To isolate unique dynamic modes associated to specific states of a catalytic cycle, broad ligand diversity can be a significant comparative asset (good or bad substrate affinity, inhibitor, analog, product, etc.). As the protein samples different dynamic modes in its working state, labile/exposed ¹H on the structure are replaced by deuterium from the solvent. Deuterium incorporation is further stopped by acid quenching after a given period of time (in this case, milliseconds) and the protein is subjected to proteolysis before peptide ESI-MS analysis. Differences in deuterium uptake effectively allows extraction and comparison of the conformational landscape sampled by the enzyme under the influence of different ligands along the reaction. Figure adapted from ref. (50). B) Catalytic mechanism of deacylation in TEM-1 β-lactamase, whereby Glu166 abstracts a proton from a strictly conserved water molecule to initiate breakdown of the acyl-enzyme intermediate and regenerate the free enzyme. The typical benzylpenicillin (BZ) substrate is illustrated as example, with labeling and mapping of catalytic residues S70, K73, S130 and E166 (yellow carbon coloring) on the crystal structure of the acylated form of TEM-1 with BZ (green carbon coloring). Long-range rigidification of the S4/S5 loop (residues 250–257, in blue) and C-terminal alpha helix of TEM-1 (residues 273–284) have been shown to affect deacylation in TEM-1, possibly through a previously uncharacterized allosteric mechanism (50).

2.3. Conformational sub-state identification based on anharmonic conformational analysis

Computational modeling using molecular dynamics (MD) simulations offer the advantage of obtaining atomic-level insights into enzyme motions on a wide range of time-scales. A large set of reports based on computational investigations of protein dynamics and its impact on enzyme catalysis can be found in the literature. Arguably, such reports have been largely met with skepticism, particularly in cases where investigations are performed without any experimental validation and/or results are difficult to reproduce or inconsistent with other techniques. Nonetheless, correctly applied computational methods have emerged as extremely powerful and valuable techniques to provide atomic level details on multiple time-scales, particularly when complementing experimental investigations. Up until a few years ago, available computational resources allowed modeling of only picosecond-to-nanoseconds time-scale. However, recent advances in computer hardware and software, most importantly graphics processing units (GPUs), have allowed access to microsecond and longer time-scale MD trajectories on a regular basis (51). The recent advances in MD for protein and enzyme modeling have been covered in a number of publications (52).

One of the challenges of using MD data is to identify and quantitatively characterize the motions and conformational states related to enzyme function (Figure 1). A number of groups have spent a significant amount of efforts over decades analyzing MD data using dimensionality reduction, including methods such as principal component analysis (PCA), independent component analysis and identification of metastable states based on Markov State models, particularly for applications in protein folding simulations (53). However, application of these methods to characterize functionally relevant enzyme motions faces an important challenge. As discussed above, the rate of enzyme function typically falls on the time-scale of milliseconds (or slower), which is still difficult to obtain by single MD trajectories on a routine basis. Further, the conformational relaxation identified by CPMG/CEST and other experimental techniques often describe two (or more) conformational sub-states. One of the features of the conformational sub-states important for enzyme catalysis is their unique structural and geometric properties (such as active-site distances and angles) and, more broadly, the higher energy of their excited states. Second-order methods such as principal component analysis, normal mode analysis, and quasi-harmonic analysis (among others) have shown limited success in the identification of conformational states with homogeneous properties (Figure 3)(54).

Figure 3: Higher-order statistical methods are required to correctly identify slower motions and conformational sub-states in proteins.

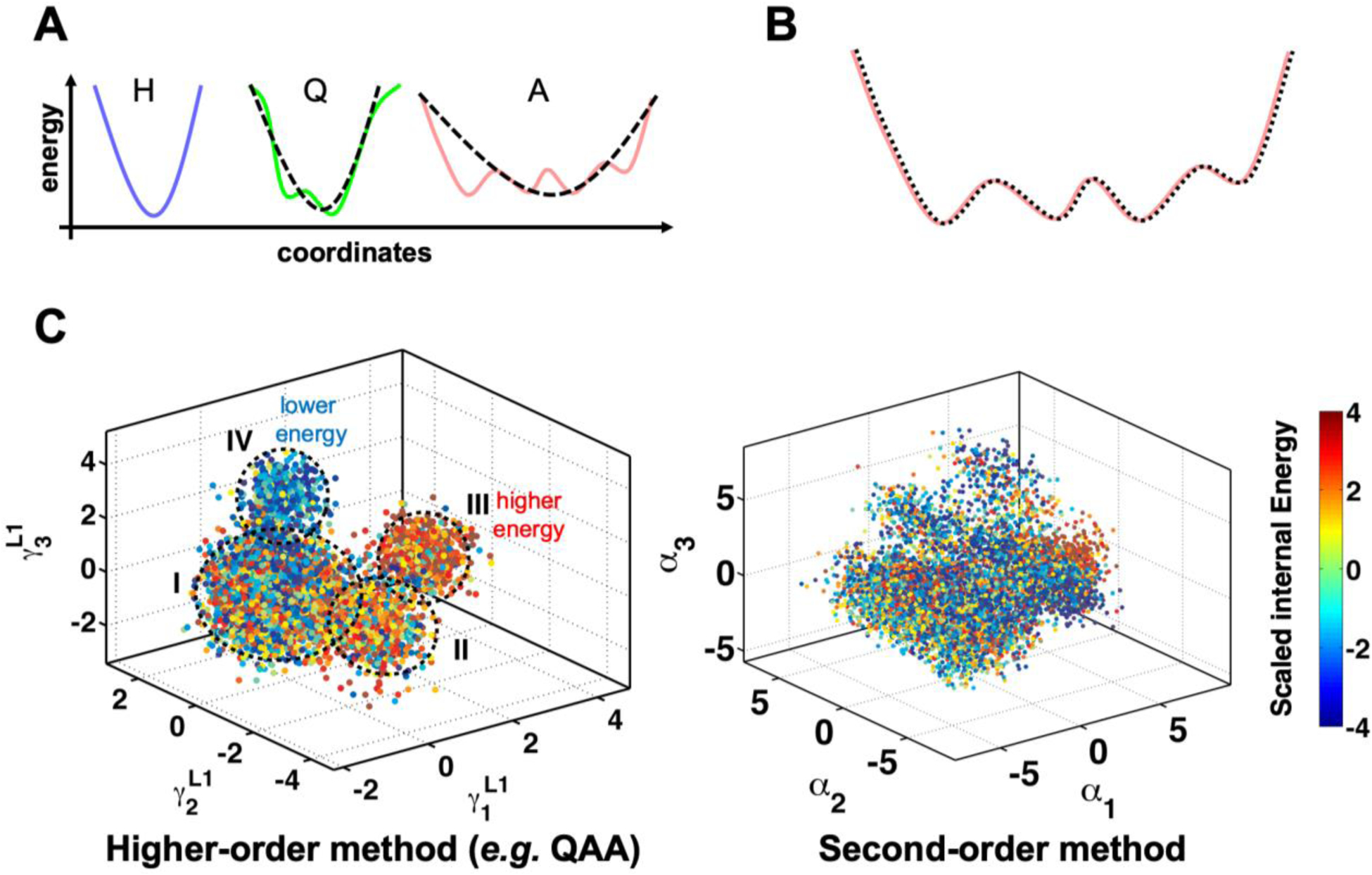
(A) Motions can be harmonic (indicated by blue curve and marked by H), quasi-harmonic (green curve, Q) or anharmonic (pink, A). Second order methods such as principal component analysis and normal mode analysis are based on fitting a quadratic equation such as the one shown by black dashed line. Good fits for H and Q can be obtained with second-order methods. However, for anharmonic motions, the second-order methods provide poor approximations. (B) Higher-order methods such as quasi-anharmonic analysis (QAA)(54b) equate to fitting higher-order polynomials (indicated by dashed black line) to the protein anharmonic motions. (C) Conformational heterogeneity in protein conformational sub-states as identified by higher-order methods provides homogeneous separation, while second-order methods fail to provide this separation. Each dot represents a single protein conformation, which is colored by internal energy (the conformations can also be classified by any other property such as distance or angles). Note that the QAA-based method correctly identifies the lower energy (IV) and higher energy (III) states relative to the other two sub-states (I and II) with mixed energy conformations.

The reason for this is that enzyme motions are anharmonic on longer time-scales (55), particularly the ones relevant for enzyme catalysis. Although this has been known and acknowledged for a long time, and even pursued in developing analysis methods, the computational cost of performing such characterization has always been prohibitive. Recently, higher order statistics-based methods such as quasi-anharmonic analysis (QAA) has provided the ability to identify and characterize functionally relevant conformational sub-states associated with enzyme catalysis. The multilevel hierarchy of protein conformations sampled using MD simulations can be delineated using QAA. The mathematical description of this methodology is beyond the scope of this review, and the interested reader is directed to the original publication describing this method (54b). In brief, this decomposition of the complex protein conformational hierarchy is made possible by a framework built on higher-order statistical analysis of the atomic deviations. The use of fourth order terms allows capturing conformational fluctuations which are anharmonic, which are required as a higher-order term is needed to correctly capture the anharmonic landscapes. Note that the use of a quadratic equation (such as those used in second-order methods) can only accurately describe conformational fluctuations with one well (Figure 3A). The use of higher order statistics (corresponding to polynomial with higher than second degree terms) allows accurate capturing of fluctuations that cover multiple wells. Further, multilevel QAA decomposition of conformational wells with mixed populations allows separation into further sub-states, such that ultimately states with homogeneous populations can be achieved. Interestingly, the lower levels of QAA correspond to local motions (smaller energy wells), while higher levels correspond to global motions, covering full protein or large domain motions (large conformational wells). QAA has successfully allowed identification of functionally relevant conformational sub-states related to catalysis in a number of enzymes including human cyclophilin A, adenylate kinase, E. coli dihydrofolate reductase (54b, 56). But QAA is limited by the input set of conformations, and regular MD simulations are not able to collect sampling at long time-scales and even single long trajectories do not provide statistically meaningful results. The reader should note that a single MD trajectory corresponds to watching a single enzyme molecule behavior over time, however, the experimentally measured properties correspond to an ensemble average of the molecules present in the test-tube.

Ways to address the inefficiency of MD to sample the catalytically relevant time-scale include using multiple MD trajectories, along with reaction pathway methods, including potential of mean force, umbrella sampling and other enhanced sampling methods (57). Further a collection of MD trajectories can be combined to collect statistically meaningful results. The conformations sampled in the collection of MD trajectories can then be combined with methods such as QAA to identify conformational fluctuations and conformational sub-states. However, this also leads to an additional challenge. As mentioned above, a single MD simulation describes enzyme behavior evolution over time equivalent to a single enzyme molecule being observed in experiments on the MD time-scale (ns-μs). The use of multiple combined trajectories or biased sampling pathway methods cause the time information to be lost. How the behavior of multiple molecules from different MD simulations, or a single molecule from different MD simulations (corresponding to different paths of the reaction coordinates) relates to the behavior of a single enzyme molecule over longer time-scales is an important question to be addressed. Time-analysis based methods which combine conformational state (and principal component analysis) with the time information from MD simulations have also been developed, which is discussed in next section.

2.4. Time-structure-based independent component analysis (tICA)

Time structure-based (or time-lagged) Independent Component Analysis (tICA) is a technique developed to allow clustering by time-scale. Its advantages include identification of the slowest movements corresponding to conformational fluctuations at longer time-scales, in order to tease apart Brownian movements (58). To achieve this, tICA analyzes the displacement of each simulation frame from the average position and compares it to the displacement of a frame that occurs a certain time later (58). This method has the advantage of providing an easier sampling of metastable states in comparison to traditional MD (59). The usefulness of tICA was validated using lysine-, arginine-, ornithine-binding protein (LAO) as a model, the authors managing to reduce the system dimensionality from 706 to 6 degrees of freedom that portrayed the protein as two mostly rigid domains separated by a flexible linker (58a). Following their original development of the method, the same group extended their investigation of LAO movements to its backbone dynamics and managed to pinpoint four different local movements that happen on a slower time-scale compared to the Brownian movements, in addition to a large-scale twisting inter-domain motion (60).

The movements identified by tICA occur slowly. But discriminating an exchange between two (or more) conformations from a simple large-scale harmonic fluctuation around a single structure might not be straightforward. It is however possible following a dimensionality reduction by tICA to elegantly present the various conformations as energy landscapes (61). This method was recently used to explain the ability of epoxide hydrolase from Bacillus megaterium (BmEH) to hydrolyze various epoxide substrates, including its acceptance of bulky substrates (62). Four accessible conformations were identified, three of which shared a bigger active-site cavity, which allows the bulkier substrates access to the active-site, with one remaining catalytically unproductive. However, this latter conformation is separated from the other three by a 3 kcal/mol energy barrier. The authors also uncovered that two mutants which can process bulkier substrates use partial unfolding of both the lid domain and the α helix bearing the catalytic Tyr144 in order to increase the volume of the catalytic pocket even further than the WT enzyme (62).

2.5. Techniques for conformational heterogeneity and ensemble characterization

Recent advances in a number of other techniques have also allowed for characterization of protein conformational heterogeneity and information about structure ensembles. Techniques such as small angle X-ray/neutron scattering (SAXS/SANS)(14b, 14d), ambient temperature X-ray crystallography (63), and cryo-EM (64) have continued to improve and show promise for future studies. While some of these techniques can only handle large protein/enzyme complexes, the low-resolution information they provide can nevertheless be combined with computational algorithms to fit a structure ensemble into the molecular envelope or other measured quantities (such as radius of gyration). SAXS/SANS offer the unique advantage that characterization can be performed in solution phase, without the need to obtain crystals and work with small amounts of protein. There is significant excitement about the ability of cryo-EM to handle large biomolecular assemblies such as ribosomes or multimeric proteins (65). However, cryo-EM resolution remains relatively low relative to other atomic-scale techniques, and information about time-scales remains unavailable. Nevertheless, given the potential of further improvements in Cryo-EM resolution, the technique offers a unique advantage; since this technique can provide information about individual molecules instead of data averaged over a population (like X-ray diffraction and NMR), it would be foreseeably possible to use cryo-EM to study small enzymes and proteins, or even extract details from more than one conformation from a single sample (64). More detailed information about these techniques are available in other reviews (64).

3. Cellular environment and solvent effects on functional enzyme dynamics

The cell is a crowded environment and molecules do not operate in conditions similar to the laboratory conditions of dilute aqueous conditions (66). The concentration of cellular components is suggested to range from 300–400 mg/mL depending on whether the cells are prokaryotic or eukaryotic (67). In addition to required participants such as substrate and cofactors, enzymes also interact with a wide variety of cellular components. It has been suggested that proteins and ligands experience non-specific (quinary) interactions as they move around in the cellular milieu, and the free volume available to proteins is decreased as compared to dilute solutions (68). It has already been demonstrated that these effects affect how ligands interact with the enzymes compared to when they are in dilute aqueous conditions. Therefore, the crowded environment of the cell, where a variety of molecules are present in close vicinity of enzymes, could also be expected to impact how proteins and enzymes sample conformations (Figure 4)(66b, 68a). Unfortunately, these effects are difficult to explore directly, as efforts to mimic the cellular conditions to reaction solutions, through addition of either selected proteins or even cell lysates (66a), has offered only little benefits.

Figure 4: Impact of non-aqueous conditions and cellular milieu on enzyme dynamics and activity.

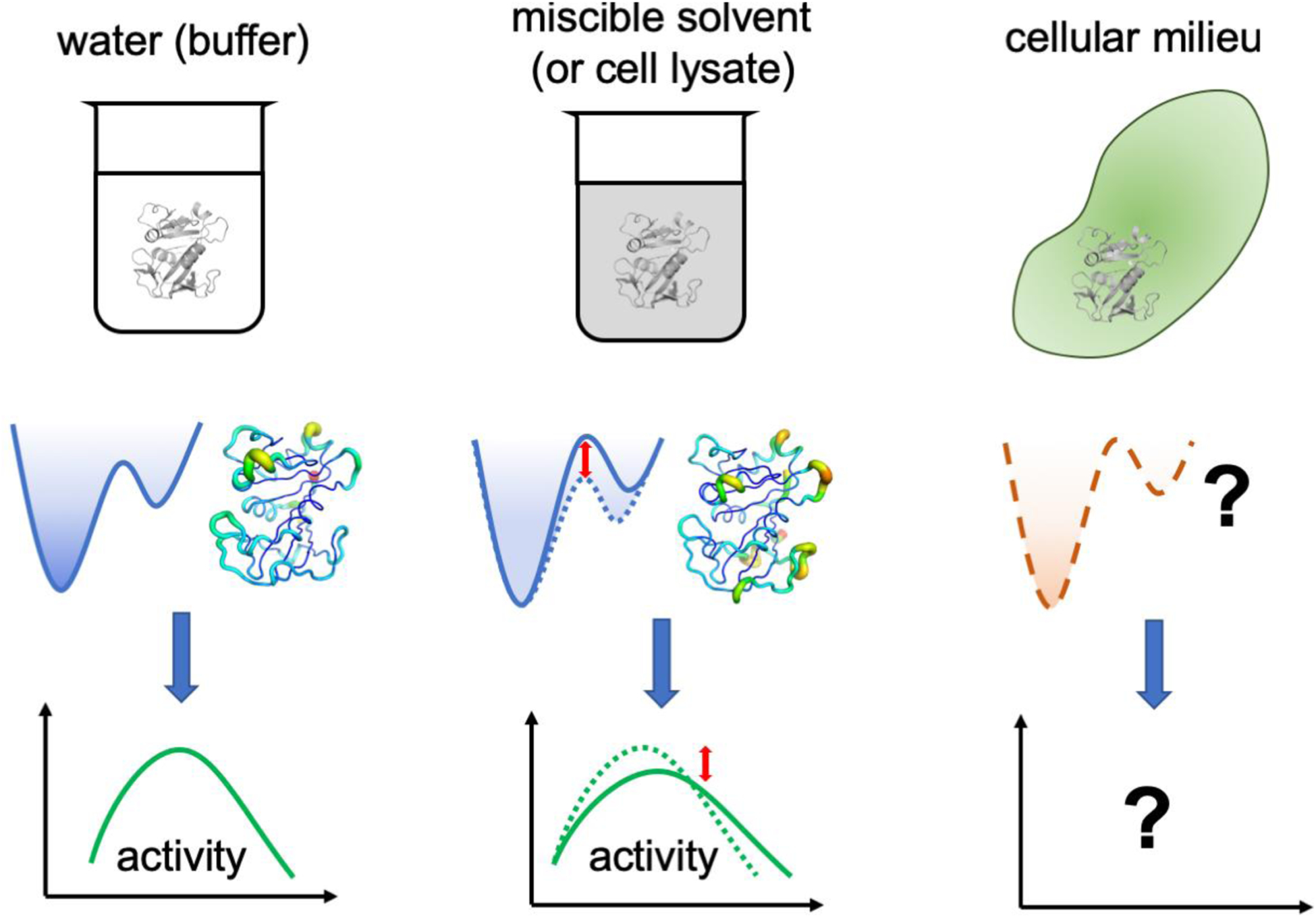
Laboratory experiments are usually performed in dilute aqueous conditions, considerably different than the complex environment of the cellular milieu. The effects of such environment on enzyme dynamics and activity remains elusive. Miscible organic solvents and crowding agents (including inert proteins) have been used as non-aqueous conditions. The effects of altered solvation have already been shown to change the conformational energy landscape and how the enzyme samples the functionally relevant motions, in turn altering the enzyme activity.

Evidence continues to build suggesting that enzymes may not operate in environments where they are surrounded only by water molecules or even random molecules, rather enzymes associated with some metabolic pathways may be co-localized and operate as multi-enzyme complexes (69). The proposed advantage of such complexes is to increase local concentration of substrates as the product(s) from the preceding enzyme in the biochemical pathway do not diffuse out into the solvent but are instead directed (or channeled) into the active-site of the subsequent enzyme in the pathway (69). The purinosome is an example of a such complex which has been characterized (70). The presence of other biomolecules in close vicinity is expected to influence how the enzyme moves or samples its internal motions, and in turn the functionally important dynamics could also be different in these complexes relative to the enzyme in solution, where it is free to move unhindered. Suggestions have already proposed that the crowding from cellular components could be uniformed or structured, impacting enzyme dynamics and function (71). It has been difficult to investigate enzymes in laboratory scale under conditions which correspond to the cellular milieu. Inert polymers, including polyethylene glycols (PEGs) and dextrans, have been most commonly used as crowding effect mimics (66b). While the secondary structure of enzymes does not behave significantly differently in presence of these crowding agents, one of the repeated observations from different enzyme systems is the possible effect of how surface water interacts with the enzymes (72).

The possible effect of cellular milieu components on enzyme conformations assumes great significance, as the most flexible regions of enzymes are known to be surface loops, which are regions more likely to come in contact with other molecules. There is a long (and increasing) list of enzyme systems where the dynamics of surface loops (even located at considerable distances from the reaction center) are closely tied to the rates and outcome of enzyme chemistry (2, 73). For several decades, the pioneering work of Frauenfelder and coworkers indicated that hydration shell solvent motions have a direct and strong influence on internal protein residue motions (74). Driven by the temperature-associated fluctuations, the motions of solvent molecules at surface enslave the motions of protein surface residues protein, which in turn influences how the longer time-scale motion sampling occurs (6n, 75).

Altering solvent conditions could help dissecting the relationship between structure and dynamics of enzyme mechanisms (Figure 4). Organic solvents have long been used to affect enzyme stability and more recently enzyme activity (76), the reason being attributed to various effects, including changes in conformational dynamics (77). Recently, activity measurements of E. coli dihydrofolate reductase in binary aqueous mixtures of isopropanol has provided insights into how conformational sampling of functional sub-states is related to the overall rate kinetics of enzyme function (56b). X-ray crystallographic studies revealed that the enzyme structure in water (buffer) and 20% isopropanol-water was practically unchanged, and computational studies showed that both the transition state structure and the electrostatic effects in the active-site were identical. Nevertheless, stopped-flow kinetics measurement of hydride transfer under rate-limiting conditions (pH > 8.5) indicated a 2.2 fold decrease in k_cat with 20% isopropanol. Quasi-elastic neutron scattering indicated that under non-aqueous conditions (20% and 25% isopropanol), the overall motions of the enzyme were suppressed. Computational modeling and analysis (based on QAA) indicated that the presence of isopropanol altered the conformational landscape of the enzyme and considerably impeded the enzyme’s ability to sample the conformational sub-states where the cofactor and substrate are structurally and dynamically positioned to achieve the transition sub-state. At 20% isopropanol, computational modeling predicted a ~3 fold decrease in the number of frames visiting the sub-states in the vicinity of transition state, coinciding with the 2.2-fold decrease in the observed rate. The approach of altering solvent conditions is general and could be used more broadly for investigating other enzymes as well as investigating changes in activity by adding osmolytes and other crowding agents.

From an applied point of view, altered or engineered solvent conditions assumes an important role in industrial applications. Enzyme stability is inter-related to dynamics and solvent conditions (77–78). A number of enzyme systems have been designed by altering dynamical regions to improve the thermal stability, and in combination with use of specialized solvent conditions, engineered enzymes can be used to improve the speed and/or outcome of industrial reactions (79).

4. Evolving and engineering enzymes based on dynamics

If it is important for function then it is conserved, has been one of the golden rules of structural enzymology. Active-site residues which directly participate in the chemistry, and other residues that control entry of reactants and release of products are known to be conserved at the primary structure level. At a higher levels, functionally important beta strands and helices, which provide optimal electrostatic environment and/or structural positioning of substrate/cofactor, are also conserved as a part of the enzyme fold. Similarly, function-promoting dynamics has also been shown to be conserved as part of the enzyme architecture in regions near and distal to the active-site (9). What other features are conserved as a part of enzyme fold evolution? Recent evidence indicates that dynamical regions are also conserved to preserve protein function (Figure 5). In enzyme folds catalyzing the same chemical reaction, surface loops often see their dynamical motions preserved from bacteria to humans, despite the lack of primary structure conservation. In a superfamily of enzymes such as ribonucleases, where the chemical function of cleaving the phosphodiester bond in RNA substrates is associated with diverse biological functions (80), the dynamics is conserved within sub-family members, yet remains distinct between subfamilies with different biological function (81).

Figure 5: Evolving new enzyme activity by controlling dynamics.

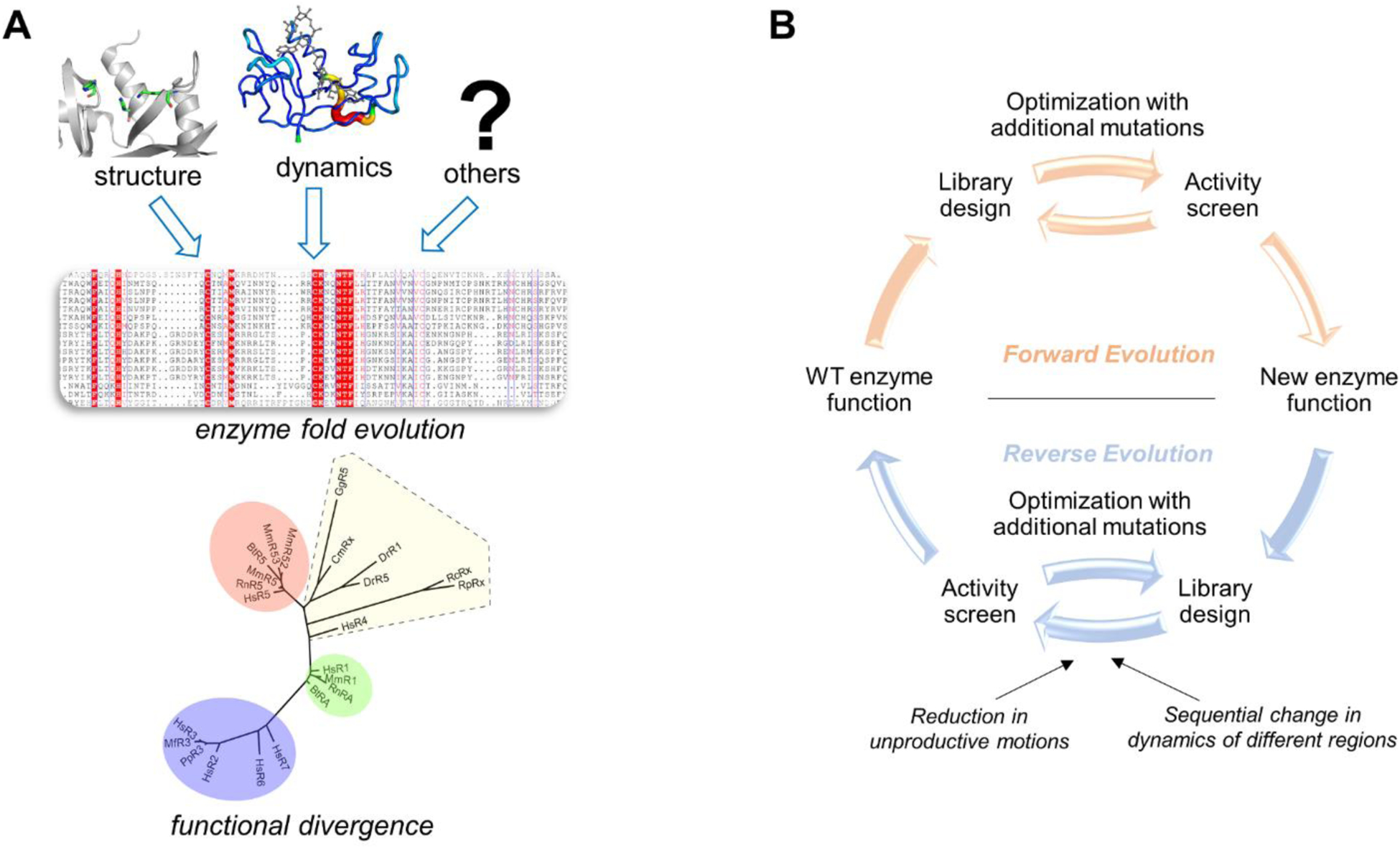
(A) Multiple factors promoting enzyme function are conserved as a part of the enzyme fold. In addition to the active-site residues for structural role, distal residues are also preserved as part of the enzyme architecture. Recent study of ribonucleases (81) has provided insights into how the dynamics of a common fold shared by the super-family is fine-tuned for different biological activity of the sub-families. (B) Schematic overview of the approach used by Jackson and coworkers for developing new enzyme activity on an existing enzyme fold (86).

Functional dynamics tweaking is already being used to design more efficient enzymes or enzymes that catalyze new chemistry. The simplest way to envision this flexibility-function protein engineering is to mutate dynamical residues to optimize the rate-limiting step of the catalytic reaction. However, novel ways have also been used to engineer constructs through the covalent addition of either small molecules or full enzyme domains which can be activated by external stimulus such as light and pH. Azobenzene, a small molecule which rapidly interconverts between two conformations based on the frequency of activating light signals, has been attached on multiple enzymes, including PvuII restriction endonuclease and lipase B (10b, 82). This provided a molecular mechanism to enable the interconversion rate of enzyme conformations by exposure to light of appropriate frequency (82–83). In a more interesting application, a chimeric construct of DHFR and photoactivated LOV domain allowed the signal to be transferred allosterically from the LOV domain to the catalytic center of DHFR through a previously identified network of protein promoting motions (10a). Further discussion and other interesting examples have been discussed in a recent review by Boehr and coworkers (84). The possible implications of enzyme dynamics conservation as a part of enzyme fold opens up new possibilities of evolving enzymes at laboratory scale by changing or controlling their internal dynamics. A number of recent examples are only starting to test the potential of this approach, some of which are discussed below.

4.1. Evolving new chemical function with optimization of enzyme dynamics

Directed evolution of new enzyme activity:

Mutating enzyme active-site residues to alter substrate selectivity and even catalyze new chemical function have been previously described (85). In a very interesting series of experiments, Jackson and coworkers observed the role of protein dynamics in the ability to catalyze new chemistry (86). Starting from an enzyme fold exhibiting phosphotriesterase activity (i.e. organophosphate hydrolysis (PTE)), the investigators used directed evolution to evolve arylesterase activity (i.e. aromatic ester hydrolysis (AE)). The group obtained AE activity in 22 generations (labeled R0 to R22), and further successfully reversed this process in 12 generations (labeled Rev1 to Rev12) (Figure 5B and 6).

Figure 6: Changes in enzyme dynamics and function over evolutionary trajectory.

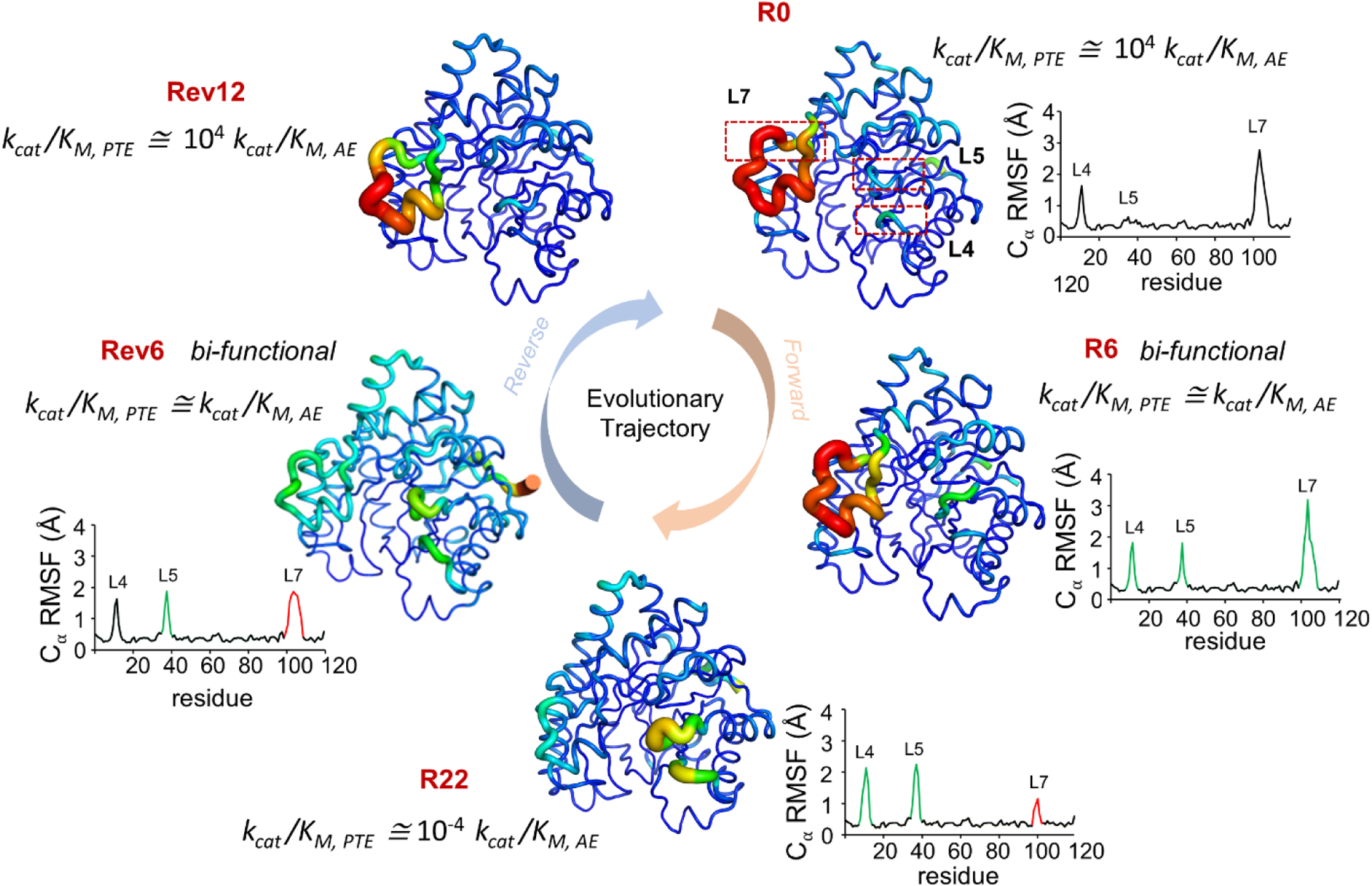
Jackson and coworkers (86) investigated development of arylesterase activity (AE) by an enzyme which had native phosphotriesterase (PTE) activity. They reported increase in dynamics of loops L4 and L5, while decrease in dynamics of L7 during the evolution of new function (from R0 with native PTE activity to R22 with primarily AE activity). While in the reverse evolution trajectory, the dynamics of L7 increases while dynamics of L4 and L5 is reduced. R0 and Rev12 showed ~10⁴ higher catalytic efficiency (k_cat/K_M) for PTE, while R22 shoed s ~10⁴ higher k_cat/K_M for AE. Bifunctional intermediates R6 and Rev6 have equivalent efficiency for both functions, and sample conformations similar to both start and end points of the evolutionary trajectory. Increasing B-factor of individual residue is represented as width of the cartoon putty. RMSF of C_α atom of each residue is plotted, green peaks represent increase in dynamics while red peaks represent decrease in dynamics as compared to R0. k_cat/K_M ratio of PTE to AE activity is reported. Figure adapted from (86).

Structural and dynamical analysis of the enzyme variants obtained over successive generations revealed an interplay between enzyme structure, dynamics and function. Interestingly, the catalytic efficiency (k_cat/K_M) ratio of the the primary and secondary enzyme activities for the starting (PTE/AE for R0) and ending (AE/PTE for R22) variants was 10⁴ in both cases. The R6 and Rev6 intermediates, corresponding to forward and reverse evolutionary trajectories respectively, were bi-functional enzymes with nearly identical k_cat/K_M for both PTE and AE functions. Despite the significant changes in catalytic efficiencies, the starting (R0 PTE), ending (R22 AE) and restored (Rev12 PTE) enzyme variants shared ~90% sequence identity and had nearly identical X-ray structures with a maximum root-mean-square-deviation of only 0.4 Å. While enzyme backbone remained the same, substantial changes were observed in the conformations of functionally important loops (loops 4, 5 and 7). Changes in loop 5 (L5) conformation provided additional room for substrate binding, while conformational changes in loop 7 (L7) is known to be rate limiting for PTE activity (87). Active-site substitutions important for substrate specificity change (Phe306, Leu271 and His254) occurred early in the trajectory (R1-R5), contributing to introduction of charged groups and reshaping of the substrate binding pocket. However, these active-site substitutions accounted for only ~1% increase in the catalytic efficiency of the newly evolved enzymes, suggesting that evolution of new enzyme function involves changes in distal regions. Interestingly, substitutions occurring in the later part of the trajectory (R6-R22) were located at/near the surface, with these second- and third-shell substitutions contributing to specialization of new activity by dramatically reorganizing the internal interaction network in the R6-R22 enzymes.

Further conformational changes in three important regions (Arg254, L5 and L7) were analyzed for additional variant intermediates (R1, R2, R6, R8 and R18). The first mutation in this evolutionary trajectory was the His254Arg replacement, where Arg254 was observed in bent and extended conformations in R1 and R2 enzymes. Both conformations are compatible with PTE function, while only the bent conformation is catalytically productive for AE activity. The subsequent Asp233Glu mutation stabilized the bent conformation by formation of a salt bridge between Arg254 and Glu233, in addition to shifting conformational equilibrium. Analysis of the structural densities revealed that the occupancy of bent conformation increased during the evolutionary trajectory (61% in R1 to 100% in R6). This was interpreted as a non-productive extended conformation of Arg254 and was frozen out by new substitutions.

Evolution during these generations also governed the mobility of the loops (Figure 6). In R1, loop L7 was observed to be in a closed conformation essential for PTE activity, forming an electrostatic interaction with the bent conformation of Arg254. Formation of Arg254-Glu233 salt bridge in R2 reduced the interaction of Arg254 with L7, in turn increasing disorder in L7. The nonproductive open conformation and dynamics of L7 was reduced by gain of additional interaction networks in the second half of the trajectory (R6-R22). Slight changes in dynamics of loop L5 was observed from R0-R6. However, in the latter half of the trajectory (R6-R18), mutations resulted in loss of interactions that destabilized L5, increasing its dynamics/fluctuations and corresponding to the specialization of the enzyme for AE. These progressive changes correlate with the functional shift of the enzymes, suggesting that mobility detrimental to the new activity is hampered by evolutionary pressure.

The bifunctional intermediates, R6 and Rev6, exhibited high flexibility in the surface loop regions and could sample conformations unique to both R0 and R22 conformations. Activity specialization in subsequent generations was achieved by minimization of unnecessary dynamics and catalytic promiscuity. Additionally, the authors also introduced rationally designed distal epistatic mutations in a sequential manner to gradually optimize the conformational landscape of catalytically important regions, which suggested that the dynamic nature of these enzymes is responsible for gradual evolutionary transitions. Taken together, these results establish that, in addition to mutations in the active-site, dynamic enrichment of preexisting conformations can evolve new function and that modification of the conformational landscape is essential for evolution of enzyme function.

Ancestral reconstruction:

Jackson and coworkers further extended the concept for imparting new enzyme activity to a non-catalytic solute-binding protein (88). Starting from an amino acid binding protein from Wolinella succinogenes (AABP), they created variants with enzyme activity to catalyze a cofactor-independent Grob-type fragmentation of prephenate to phenylpyruvate and L-arogenate to L-phenylalanine (cyclohexadienyl dehydratase, CDT). The investigators used the approach of ancestral reconstruction to obtain 5 proteins between W. succinogenes AABP (Ws0279) and Pseudomonas aeruginosa CDT (PaCDT), which share the same structural fold (periplasmic binding protein-like II fold) but only show 26% sequence identity. Ancestral reconstruction is based on determining critical branching points (ancestors) through sequence level phylogenetic analysis, followed by recombinantly synthesizing and characterizing these ancestor proteins in the lab for comparative evolutionary analysis (89). The substrate binding and CBT activity profiles of the 5 proteins (called AncCDT-1 to AncCDT-5) along this evolutionary trajectory revealed several interesting observations. AncCDT-1 showed that the amino acid binding activity was lost before the ancestral reconstructs along the trajectory started gaining CDT activity. The second ancestral protein (AncCDT-2) demonstrated neither CDT activity nor binding affinity toward amino acids; interestingly, this intermediate showed affinity for carboxylic acid group, a functional group found in the substrates of PaCDT.

Structural characterization based on X-ray crystallography showed that the evolution of this new binding function coincided with incorporation of desolvated general acid into the binding site and its reshaping. In subsequent points along the trajectory (AncCDT-3 to AncCDT5), optimization of the active-site was perfected by enabling transition state stabilization through tailoring hydrogen-bonding networks that precisely positioned catalytic residues.

Developing enzymes de novo in laboratory with catalytic efficiency close to the natural counterparts is not an easy task. The AABP to CDT evolution trajectory also provided unique insights into the role of enzyme dynamics into gaining catalytic efficiency. In addition to reshaping of the binding pocket to accommodate the substrate, positioning of the general acid, and optimization for complementarity to the transition state, additional changes outside the active-site were also observed at remote locations, i.e. in second- and third-shell residues. Computational analysis revealed that these residues were instrumental in optimizing conformational sampling to favor catalytically relevant conformations. The investigators suggested that evolution seemed to play a role in minimizing unproductive sampling of the noncatalytic conformations. Collectively, this work provides unique insights into the evolution of chemical activity, coinciding with developing correct active-site features and the ability of enzymes to sample relevant conformations. In addition to opening the possibilities of lab-scale enzyme engineering, the work of Jackson and coworkers also provides support to the suggestion that dynamics also plays a role in the natural evolution of binding proteins gaining enzyme activity.

Thermal stability and enzyme dynamics:

Dalby and coworkers recently described their experience of epistatic (non-additive) effects from mutations located in distal parts of E. coli transketolase (TK) while attempting to improve its thermal stability (90). Starting from the wild-type enzyme, the investigators created several TK variants with single, double, triple and quadruple mutations. The activity and thermal stability (based on melting temperature T_m, and aggregation temperature, T_agg) of the variants were measured. TK is a homodimer formed by two 70 kDa monomers, with beneficial distal mutations at residues H192, A282, I365, and G506 located between 10 to 30 Å from each other. Selection of these mutational locations were based on past experience in improving TK activity and stability. Different combinations (paths) of triple and quadruple variants based on different starting points of single or double mutations (called parents) allowed insights into the epistatic nature of the activity and thermal stability. Results indicated that the triple and quadruple variants retained higher TK activity and deactivated (denatured) more slowly with increase in temperature than the WT and single-mutant parents. Further, these triple and quadruple mutants demonstrated substrate binding (K_M) and enzyme activity (k_cat) similar to the WT at higher temperatures. The effects of these distant mutations on protein stability were not always found to be additive, which the investigators referred to as epistasis or epistatic effect. Mutations located far away from each other were expected to show additive effect in activity and/or thermal stability (for example, double mutants should exhibit changes which are the sum of the two single-parent mutations). To understand the basis of epistasis, MD simulations were performed on the various mutants and dynamic cross-correlation matrix were analyzed. Detailed analysis of the cross-correlation matrices indicated that these mutations interacted via a network in the enzyme and produced distinct long and short-range epistasis. Comparison of short- and long-range epistasis indicated a complex interdependence between the dynamics around each mutation, which not only caused changes in the local dynamics, but sometimes also altered the dynamics of certain other (often distant) regions. The investigators proposed that the epistasis-mediated mechanism between distant mutations could therefore be exploited in future enzyme-engineering strategies.

5. Perspectives, Challenges and Opportunities

The identification of functional dynamics in enzyme catalysis opens up broad opportunity with wide implications for the fields of fundamental and applied research, including discovery of better medicine and enzyme engineering. A few challenges and opportunities are discussed below.

5.1. In vivo characterization of enzyme dynamics

Dilute aqueous solution conditions of laboratory experiments are known to affect many aspects of enzyme function. As tools and techniques emerge for investigating enzyme function in vivo (91), it would be useful to characterize enzyme dynamics in the context of various cellular environments (92). Techniques which allow the in vivo investigation of large complexes such as purinosomes (70) with emphasis on enzyme dynamics would reveal new information. However, it is envisioned that the development of such techniques is expected to face challenges on multiple experimental fronts.

5.2. Dynamics-based de novo enzyme design

Designing proteins that bind to substrates and/or transition states as an approach to designing enzymes for catalyzing a desired chemistry is now becoming increasingly possible (93). While these proteins exhibit high binding affinity for reactant participants, their catalytic efficiency still remains several orders of magnitude lower than their natural counterparts. Several suggestions on what could be missing factors include electrostatic contributions of distal residues (particularly the second layer), as well as the ability of enzymes to readjust in the presence of substrate(s), as the original design approach does not necessarily account for all side-chain rotamers, although efforts are being made on this front (93c). In addition to these factors, approaches that include the function-promoting design into enzyme design from start rather than as an afterthought would be worth exploring. In other words, instead of first designing a protein fold with high substrate affinity and then changing residues to allow for increased motions in the binding pocket, an alternate approach worth investigating would be to understand the functional dynamics of each enzyme fold and identifying the distal residues and regions that are directly connected to the mechanism catalyzed chemistry. Once this understanding is fully developed, changing the associated active-site residues to incorporate other substrates and facilitate the desired chemistry would be possible. Efforts in this direction are already underway (94), and have been reviewed recently (95). It should also be emphasized that approaches that allow selected residues to move as a means to engineer dynamics, is fundamentally different than identifying rate-limiting conformations and designing better enzymes through conformational modulation (10b).

5.3. Industrial implications

In addition to improved catalytic efficiency (through increased substrate turnover and/or better substrate binding), improved enzyme stability and increased substrate selectivity are also important features which are routinely on the list of desired features for industrial applications (96). Evidence favoring the role of dynamics of surface loops located far away from the active-site continues to emerge for an increasing number of enzyme systems (97). These findings assume significance for large scale applications, as the dynamics of surface loop regions also impacts stability of the systems under different conditions, including increased temperature, altered pH and different solvent conditions (including organic solvents) which are used for storage. Differences in dynamics and changes in the sequence of surface loops are connected to differences in the stability and activity profiles of thermophilic and mesophilic enzymes with the same fold (98). Preliminary investigations indicate that changes in loop sequences can change the thermal stability of enzymes as well as the temperature range for optimal activity (99). Similarly, dynamics-based design of substrate selection also continues to emerge. Inclusion of dynamics into the enzyme engineering processes provides great opportunities for improving the list of design features sought in industrial applications.

5.4. Enzymes as therapeutic treatments

For applications in health, looking beyond small molecule design to inhibit enzymes, designing new enzymes (and possibly even applying current enzymes) to remove toxic and or unwanted metabolites have started to gain popularity (100). Unfortunately, the delivery challenges of enzymes at the site of application would also need to be addressed but given the unique ability of enzymes to bind to small molecules as well as DNA/RNA fragments and even other proteins with high specificity, as well as the ability of enzymes to catalyze the desired chemistry, offer new opportunities for using enzymes as therapy. A short list of disorders and diseases for potential use of enzyme as therapeutic agents to remove unwanted metabolites include galactosemia (101), Gaucher’s disease (102), gout (103), hyperammonemia (104), Lesch-Nyhan syndrome (105), phenylketonuria (106), and Tay-Sachs disease (107). Thinking more broadly, our improving knowledge of enzymes, including the role of dynamics in catalysis, offers unique avenues of developing enzymes as therapeutic agents.

CONCLUSIONS

The understanding of factors that contribute to various aspects of enzyme mechanisms, including their phenomenal abilities to recognize substrate with high specificity and catalyze the desired reaction at extremely high rates, have been sought for a long time. In addition to the roles of structure, solvent, and electrostatic effects, the role of conformational fluctuations on different time-scales (commonly referred to as enzyme dynamics) is also becoming established. The topic has been somewhat controversial due to lack of clear definition of the term dynamics. These conformational fluctuations occur over 12–15 orders of magnitude in time, making it difficult for a single experimental or computational technique to provide concrete answers. Therefore, a combination of techniques is needed. As we are starting to learn more about how enzymes operate in their native environment (including the complex cellular milieu), more challenges lie ahead but opportunities also exist for investigating the role of enzyme dynamics in these conditions. The benefits of including enzyme dynamics as a design parameter offers new opportunities for applications in industry as well as medicine.

Biographies

Dr. Pratul K. Agarwal is a Professor in the Department of Physiological Sciences at Oklahoma State University (OSU). He is also the Assistant Vice President of Research for Cyber-Infrastructure, and the Director of High-Performance Computing Center at OSU. Previously, he held positions at University of Tennessee, Knoxville and Oak Ridge National Laboratory. For over 15 years he has studied enzymes and proteins using computational models and other techniques.

Dr. David N. Bernard is currently a postdoctoral fellow at the Centre Armand-Frappier Santé Biotechnologie of the Institut National de la Recherche Scientifique (INRS), specialized in NMR spectroscopy and structural biology, which he has been studying for over 10 years.

Dr. Khushboo Bafna is a postdoctoral research associate at Rensselaer Polytechnic Institute. In 2019, she received a PhD from University of Tennessee, Knoxville. Her interest includes studying protein structure-function relationship using computer simulations and experimental techniques (including NMR).

Prof. Nicolas Doucet joined the faculty of the Montreal-based Centre Armand-Frappier Santé Biotechnologie of the Institut National de la Recherche Scientifique (INRS) in 2010, where he has been full professor since 2019. His research is interdisciplinary in nature and draws upon the tools of directed evolution and protein NMR to illustrate the power of ‘flexibility-function’ analyses in protein design. His lab explores the conservation of conformational dynamics among structural protein homologs to highlight and exploit evolutionary conservation of atomic motion in protein and enzyme engineering.