Sensitivity to geometric shape regularity in humans and baboons: A putative signature of human singularity

Significance

Determining the cognitive differences between human and nonhuman primates is a central goal of cognitive neuroscience. We show that intuitions of geometry are present in humans but absent in baboons. A simple intruder task in which subjects must find which of six geometric shapes is different reveals an effect of geometric regularity in all human groups regardless of age, education, and culture, yet this effect is absent in baboons. Models of the ventral visual pathway for object recognition predict baboons’ performance, but a symbolic model is needed to account for human performance. Our results underline the human propensity for symbolic abstraction, even in an elementary shape perception task, and provide a challenge for neural network models of human shape perception.

Abstract

Among primates, humans are special in their ability to create and manipulate highly elaborate structures of language, mathematics, and music. Here we show that this sensitivity to abstract structure is already present in a much simpler domain: the visual perception of regular geometric shapes such as squares, rectangles, and parallelograms. We asked human subjects to detect an intruder shape among six quadrilaterals. Although the intruder was always defined by an identical amount of displacement of a single vertex, the results revealed a geometric regularity effect: detection was considerably easier when either the base shape or the intruder was a regular figure comprising right angles, parallelism, or symmetry rather than a more irregular shape. This effect was replicated in several tasks and in all human populations tested, including uneducated Himba adults and French kindergartners. Baboons, however, showed no such geometric regularity effect, even after extensive training. Baboon behavior was captured by convolutional neural networks (CNNs), but neither CNNs nor a variational autoencoder captured the human geometric regularity effect. However, a symbolic model, based on exact properties of Euclidean geometry, closely fitted human behavior. Our results indicate that the human propensity for symbolic abstraction permeates even elementary shape perception. They suggest a putative signature of human singularity and provide a challenge for nonsymbolic models of human shape perception.

[The universe] is written in mathematical language, and its characters are triangles, circles, and other geometric figures, without which it is impossible to humanly understand a word.

The Assayer, Galileo Galilei

Among primates, humans are unique in their ability to develop formal symbolic systems that capture regularities in the external world, such as the language of mathematics. A great variety of nonexclusive hypotheses have been proposed to account for human singularity, including the emergence of evolved mechanisms for social competence (1), pedagogy (2), natural language (3, 4), and recursive structures across multiple domains such as language, music, and mathematics (5–8). To explore these hypotheses, experimental paradigms that afford a direct comparison of human and nonhuman primate behavior using the exact same methods are the most informative (9–14). Here we present a paradigm for investigating the differences between humans and baboons in the domain of geometry and, more specifically, the visual perception of quadrilaterals such as squares, rectangles, and parallelograms. We show that all humans, regardless of culture or education, are sensitive to the presence of geometric regularities such as right angles, parallelism, and symmetry and perform very differently from baboons in an elementary visual perception task.

Prehistoric records suggest that the appreciation of regular geometric shapes is as ancient as humanity itself. Parallel lines, circles, squares, and spirals are omnipresent in human art and architecture. The earliest engravings attributed to Homo sapiens, consisting of a triangular mesh of parallel lines, are estimated to be ∼73,000 y old (15). Even Homo erectus already drew abstract patterns ∼540,000 y ago (16). Paleoanthropologists do not question the human origins of such drawings because when given the opportunity to draw, other nonhuman primates never produce structured figures (17). By contrast, the diversity and abstraction of young children’s drawings are striking (18, 19). Prior research has established that even kindergartners and adults with no formal education from the Amazon already possess sophisticated intuition for geometry (20, 21), forming an intuitive mathematical “language of thought” (22). Those prior results suggest, but do not prove, that humans possess a more symbolic level of understanding of the abstract properties of geometry at the perception level compared with other primates. Here our goal was to design a simple empirical test capable of probing this hypothesis.

We reasoned that if humans are spontaneously attuned to the major properties of Euclidean geometry (i.e., lines, length, parallelism, perpendicularity, and symmetry) and their combinations, then they might exhibit a geometric regularity effect, with a better and faster perception of regular shapes, such as a square, than of irregular shapes. This hypothesis is in line with a long tradition in the psychology of perception pioneered by Wundt, Tichener, and then the Gestaltists (23); Leeuwenberg’s visual grammar (24, 25); and Leyton’s generative theory of shape (26), which posits that the shapes that elicit the most compact internal representations also tend to be judged as the most regular or elegant. Several previous experiments, both within and outside the domain of geometry, have shown that whenever regularities are present, humans use them to compress information in working memory and achieve a smaller “minimal description length,” thus facilitating memorization, anticipation, and outlier detection (22, 27–30).

Crucially, the domain of visual shape perception is simple enough for probing the sensitivity of human and nonhuman animals to the same mathematical properties. Indeed, a previous study demonstrated that humans can perceive visual patterns with nested symmetries, while pigeons cannot (31). Here we opted for an even simpler intruder test, in which a participant must simply find the outlier shape within a set of six, which has been previously used to explore human intuitions of geometry (20, 32). We used it to test a large number of humans and baboons with the very same stimuli.

Results

Design of the Geometric Intruder Task.

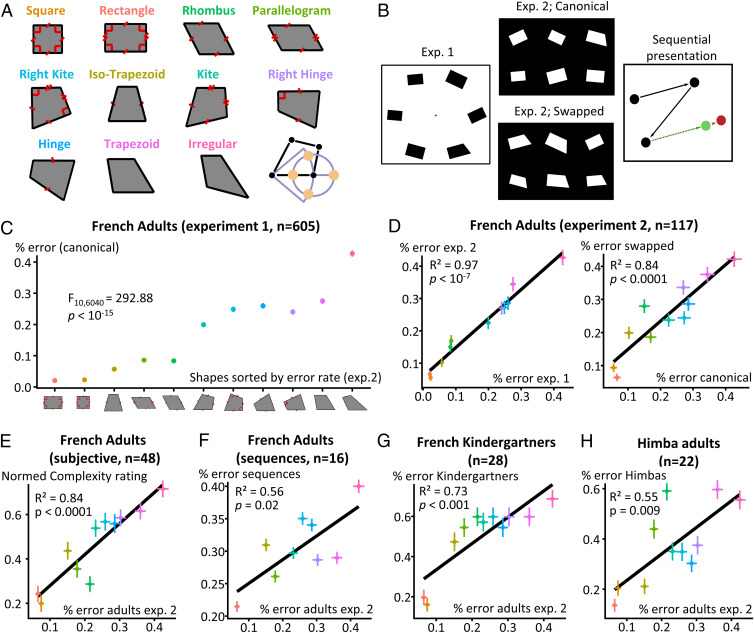
We focused on four geometrical properties of polygons: the presence of parallel lines, equal sides, equal angles, and right angles. Our hypothesis was that the perceived geometric regularity of a shape would be directly related to its number of its geometrical properties. On this basis, we selected 11 quadrilaterals ranging from highest regularity (a square) to full irregularity (an arbitrary quadrilateral devoid of any of these properties). The 11 shapes, ordered by predicted regularity, are depicted in Fig. 1A and described in SI Appendix, Table S1. For each such reference shape, four deviant versions were generated by changing the position of the bottom-right vertex by a constant distance, either along the bottom side or along a circle centered on the bottom-left vertex (thereby violating either distance or parallelism). All deviants departed from their reference shape by the same amount, and all 11 reference shapes were matched for average distances between vertices (SI Appendix). On each trial of the intruder task, we selected one of the 11 possible reference shapes and presented five instances of it, varying in scale and orientation (e.g., five rectangles), together with a single deviant (in this case, a non-rectangle with the bottom-right vertex displaced). The location of this outlier was randomized, and six levels of shape rotation and shape scale were distributed pseudorandomly among the six shapes. The participants’ task was to click on the outlier shape as fast and accurately as possible (Fig. 1B).

Fig. 1.

Geometric regularity effect in humans. (A) Stimuli. We selected 11 quadrilaterals, here ordered according to their number of geometrical regularities (parallelism, equal sides, equal angles, or right angles). For each quadrilateral, four deviants were generated by moving the bottom right corner by a fixed distance, thus shortening, lengthening, or rotating the bottom side. (B) Examples of intruder-task displays. (Left) Circular display used in experiment 1. Participants had to tap the intruder. (Center) Rectangular display used in experiment 2 and subsequently. In the canonical presentation, five shapes exemplified a fixed quadrilateral, with variations in size and orientation, and the remaining shape was a deviant. In the swapped presentation, those two shapes were swapped. In either case, participants had to tap the intruder. (Right) Sequential presentation, unfolding from top to bottom and from left to right over a span of 1.8 s. Participants had to answer “correct” for properly placed dots (in green) and “incorrect” for deviant dots (example in red). (C) Geometric regularity effect in experiment 1. The error rate varied massively with shape regularity in French adults. Shapes are ordered by performance, and each is labeled with a color that is consistent across graphs, including A. Error bars represent the SE pooled over all participants; in this figure, it is smaller than dot size. (D–H) Replications of the geometric regularity effect with swapped vs. canonical trials in French adults (D), subjective judgments of shape complexity on a scale of 1 to 100 (E), sequential presentation of the four corners (F), French kindergartners (G), and uneducated Himba adults from rural Namibia (H).

Intruder Task in Educated Adults.

In experiment 1, with 605 French adults, we observed that error rates in the intruder task varied dramatically with the reference shape, from 2% to 40% (Fig. 1C; univariate type III repeated-measures ANOVA: F_{10, 6,040} = 292.88, P < 10⁻¹⁵; explained variance evaluated by generalized eta squared [η²_G] = 0.27). Average performance was well predicted by the total number of geometrical regularities (linear regression on 11 points: r² = 0.64, P = 0.0031) and showed a consistent, though imperfect, ordering from regular to irregular (Fig. 1C). Since the regularity of symmetrical figures, such as the isosceles trapezoid, was underestimated by our theoretical measure, in subsequent experiments we used the error rate from experiment 2 as an empirical measure of regularity.

In contrast to the major effect of shape, the size, rotation, and position of the outlier had significant but only minor effects (size: F_{5, 3,020} = 4.46, P = 0.0005, η²_G = 0.005; rotation: F_{5, 3,020} = 21.19, P < 0.0001, η²_G = 0.021; position: F_{5, 3,020} = 4.96, P = 0.0001, η²_G = 0.005). Response times were tightly correlated with error rates (linear regression: r² = 0.92, P < 0.0001) and thus also exhibited a large geometric regularity effect (SI Appendix, Fig. S1).

In experiment 1, the intruder was always a deviant shape and thus was more irregular than the reference shape. Thus, participants could have responded by selecting the most irregular shape among the six shapes on display. To avoid this confound, in experiment 2 and all subsequent experiments, one-half of the displays were canonical (five instances of one of the 11 reference shapes, plus a single deviant) and the other half were swapped (five deviants, identical up to a rotation or scale change, plus a single reference shape; examples in Fig. 1B). As previously, participants were simply asked to click on the shape that differed from the others. In a new group of 117 French adults, the geometric regularity effect was replicated (differences between shapes: F_{10, 1,160} = 70.96, P < 10⁻¹⁵, η²_G = 0.25; correlation with experiment 1: r² = 0.97; P < 10⁻⁷; Fig. 1D), while size, position, and rotation effects again had either insignificant or very small effects (size: F_{5, 580} = 2.16, P = 0.056, η²_G = 0.008; rotation: F_{5, 580} = 9.66, P < 0.0001, η²_G = 0.031; position: F_{5, 580} = 2.26, P = 0.047, η²_G = 0.008). Response times also yielded a large geometric regularity effect (correlation with error rate: r² = 0.95, P < 0.00001). Error rates were strongly correlated across the two display types (r² = 0.84, P < 0.0001; Fig. 1D).

Subjective Ratings of Complexity.

Three additional experiments investigated the origins of the geometric regularity effect. First, we asked whether geometric regularity was consciously accessible and thus could be directly reported using subjective ratings. Twenty-seven French adults rated the subjective complexity, 21 rated the subjective regularity of each reference shape on a scale of 1 to 100 scale. Both subjective ratings correlated tightly with error rates in the intruder task (complexity, r² = 0.88; regularity, r² = 0.76; r² = 0.84 after aggregating the two conditions by averaging complexity and 1 – regularity; all P < 0.0001; Fig. 1E). Since what characterizes complex stimuli at the early visual stages of object recognition is thought to be largely inaccessible to introspection (33), the finding that humans have correct intuition that some geometric shapes are simpler than others suggests that this effect arises at a level of representation beyond early vision.

Visual Search.

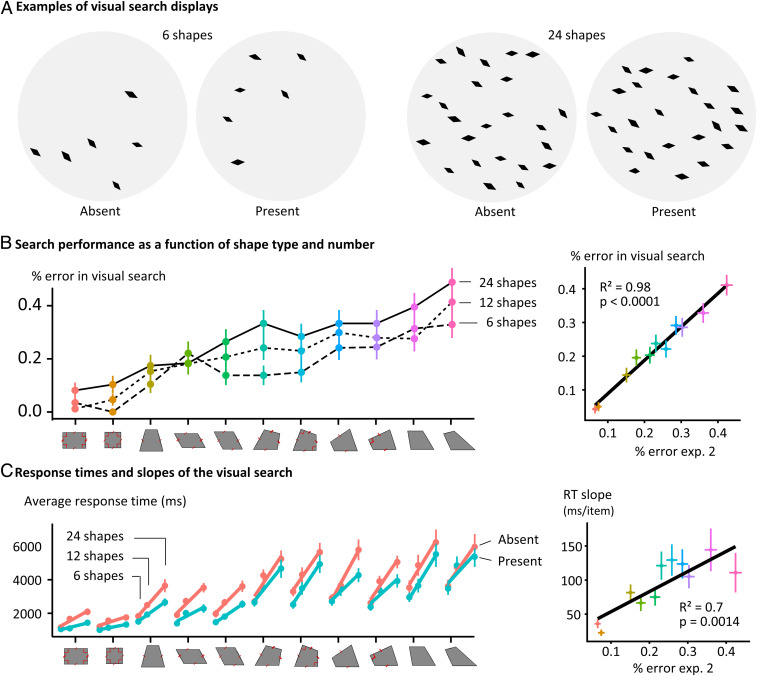
We tested this idea further by probing whether the search for geometric regularity engages parallel (“pop-out”) or serial processes. Eleven French adults engaged in a classic task of a visual search for an outlier in arrays of 6, 12, or 24 shapes. Response times showed that search was always serial for all 11 shapes, yet with a slope and an error rate that again correlated linearly with geometric regularity (P < 0.0001, r² = 0.98; Fig. 2); a detailed analysis of the effects of number of items and item presence is provided in SI Appendix. This finding shows that the regularity effect does not arise from an early preattentive pop-out, even for the simplest shapes such as squares and rectangles, but rather, geometric shape perception involves an attention-dependent stage whose speed increases with geometric regularity.

Fig. 2.

Visual search paradigm. (A) Examples of visual search displays. In the visual search task, 6, 12, or 24 shapes were randomly positioned inside a circle, and the participant had to decide whether all the shapes were identical, irrespective of rotation and scaling, or whether there was one that differed from the others. They gave their binary present/absent response by pressing one of two possible keys on the keyboard. (B) Error rates in the visual search task. Errors rates increased with both the number of shapes and their complexity (geometric irregularity). The latter effect closely correlated with the average error rate in the intruder task. (C) Search times. (Left) Slope of the visual search as a function of the number of displayed items, the presence or absence of an outlier, and the shape. (Right) Correlation between the slope of the visual search on present trials and the error rates of the intruder task (experiment 2).

Sequential Presentation of Shapes.

As a further test of the perceptual stage at which the geometric regularity effect arises, we asked whether this effect would still be present if the shapes could not be perceived in one glance but had to be mentally reconstructed for a sequential display of their vertices. Sixteen 16 French adults participated in an experiment in which the shapes were broken down into a sequence of four dots, one for each vertex location, in a systematic order. By having the sequence unfold over a time span of 1.8 s, thus largely exceeding the time window for integration within the ventral visual recognition system (34, 35), our goal was to prevent classical bottom-up shape recognition mechanisms but still allow subjects to grasp the geometric relationships between the four vertices. The experiment was run in small blocks, each with reference shapes. In the first six trials of a given block, the four dots always traced a fixed quadrilateral (e.g., rectangle), with variations in size and orientation. Then, on each subsequent trial, the first three dots continued to trace the same quadrilateral (again with variations in size and orientation), but on one-half of the trials, the fourth dot was displaced to one of the four possible deviants shown in Fig. 1A. Participants were asked to indicate if the last dot was correctly or incorrectly located. Even under this sequential condition, the geometric regularity effect was replicated; the error rate still varied dramatically across shapes (F_{8, 120} = 10.1, P < 10⁻⁹, η²_G = 0.16), and the effect correlated with the geometric regularity effect observed for static shapes (r² = 0.56; P = 0.02; Fig. 1F). Thus, the effect arises from a level of representation at which geometric properties can be ascertained even when they are not simultaneously present in the stimulus.

Probing the Influence of Education: Himbas and Young Children.

We next investigated the dependence of the effect on age, education, and culture. One possibility is that the effect arises from formal education in mathematics, for instance, because regular shapes are also familiar, nameable, and taught at school. To address this concern, we turned to human populations with little or no formal schooling. First, we tested French kindergartners (n = 28; mean age 5 y, 4 mo; range, 4:11 to 5:10). To shorten the duration of the experiment, children were tested solely with canonical displays. One hundred fifty-six first graders were also tested; retailed results are shown in SI Appendix Fig. S2. Second, because those Western children could have been introduced to shape names, we also tested 22 uneducated Himba adults, a pastoral people of northern Namibia whose language contains no words for geometric shapes, who receive little or no formal education, and who, unlike French subjects, do not live in a carpentered world (36).

In both populations, the geometric regularity effect was replicated (Fig. 1 G and H). SI Appendix, Table S2 outlines a systematic investigation of the significance and effect size of each predictor on each population. Error rates varied more dramatically in the French kindergartners than in the educated French adults across the 11 shapes. They remained below 20% for the square and rectangle, were ∼50% for the isosceles trapezoid, and continued to climb up to 60 to 70% for more irregular quadrilaterals. The correlation of French children’s and adults’ performance was strong and remained significant even when excluding the two simplest shapes, square and rectangle (SI Appendix, Fig. S2D). Similarly, the performance of Himba adults varied with geometrical regularity and was correlated with that of both French adults (r² = 0.55) and French kindergartners (r² = 0.59). Both findings converge with previous work (20, 22) to suggest that the geometric regularity effect reflects a universal intuition of geometry that is present in all humans and is largely independent of formal knowledge, language, schooling, and environment.

Can Baboons Pass the Intruder Test?

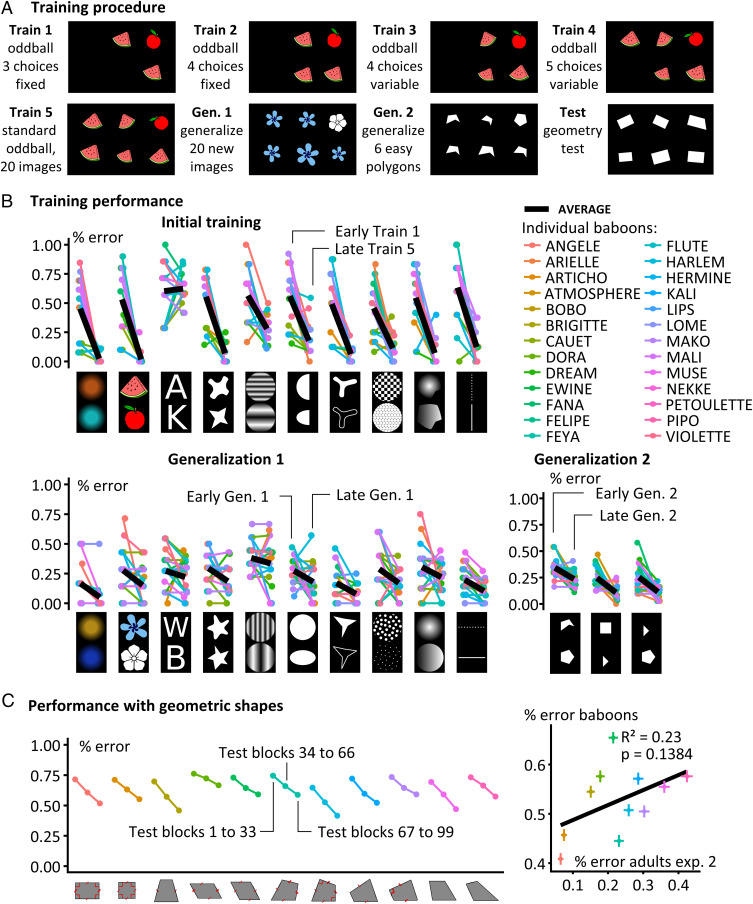
We next investigated whether the effect was also present in a nonhuman primate species, the guinea baboon (Papio papio). The baboon’s visual system is largely similar to that of humans, and they perform similarly in some shape recognition tasks (37). We capitalized on a large facility where baboons can freely access testing booths with touch screens (38). Twenty-six baboons received individualized training on the intruder task using a wide variety of images and textures (Fig. 3). Details of each subject’s learning history and performance are provided in SI Appendix, Fig. S3. A full dataset was obtained from 20 animals who completed 1) an initial series of training stages on the intruder task with 10 nongeometric image pairs with a progressively increasing number of available choices (Fig. 3A; 20 animals met the criterion, at an average of 5,200 trials (range, 1,000 to 14,500 trials); 2) a first generalization to 10 novel nongeometric image pairs, indicating that they understood the intruder task (tested in only 18 animals; average of 272 trials; range, 100 to 700); 3) a second generalization to black-and-white geometric shapes, where a simple nongeometric parameter sufficed to respond (e.g., pick a small triangle amid large pentagons; average of 220 trials; range, 100 to 600); and finally 4) generalization and further retraining with the complete set of quadrilaterals identical to human participants (average of 6,305 trials; range, 704 to 8,712).

Fig. 3.

The geometric regularity effect is absent in baboons. (A) Training procedure. Each animal was trained for thousands of trials on the intruder task, first with a small number of fixed images (three; training stage 1), then with a larger number of images (up to six; training stage 5) and with variations in size and orientation. Mastery of the task was verified through two generalization tests using novel images. Each baboon moved from one stage to the next only when the error rate fell below 20%. (B) Summary of baboon training performance (first and last blocks of 88 trials each). Each color represents one baboon. Most animals attained the criterion on the 10 pairs of shapes used for training (Top) and successfully generalized to 10 new pairs of shapes (Bottom Left) and to three pairs of easily distinguishable polygons (Bottom Right; chance: 83.3% errors with six shapes). (C) performance in the geometric intruder task. (Left) Average performance for each geometric shape at three stages: the first 33 test blocks, the middle 33 test blocks, and the last 33 test blocks. Each block contained 88 trials, and baboons took at most 99 blocks. (Right) correlation between the average error rate in baboons and in French adults taking the same test (experiment 2).

Twenty of the 26 animals showed a clear understanding of the intruder task, because after training with 20 nongeometric images, they showed immediate first-trial generalization to new such images and/or to easily distinguishable polygons (Fig. 3B). However, when presented with the 11 quadrilaterals, their performance collapsed, suggesting that they found all of them equally similar (Fig. 3C). Their performance was close to chance on the first test block (error rate, 76.2%; SE, 1%; chance, 83.3%) and progressed slowly on subsequent days. Eleven animals continued performing the geometrical task for 8,000 or more trials, eventually reaching a 53% error rate (SD, 6.7%) on blocks 81 to 99. Note that this performance was comparable to that of the kindergartners and first graders, who achieved error rates of 51% (SD, 14%) and 48% (SD, 16%), respectively. Yet even in the latter blocks, for the 11 baboons who reached that stage and thus had received substantial training, no geometric regularity effect was observed. Although error rates differed across the 11 shapes (F_{10, 100} = 24.68, P < 10⁻¹⁴, 0.0001, η²_G = 0.44), with a consistent ordering across baboons (SI Appendix, Fig. S4) and a tight correlation with their response times (SI Appendix, Fig. S1), they correlated weakly and nonsignificantly with the geometric regularity effect found in human populations (Fig. 3C). Rather, the baboons’ performance was impacted, at least in part, by visual properties that had little to no impact on human participants, such as outlier rotation and outlier type (SI Appendix, Table S2). Thus, baboons performed poorly with quadrilaterals and were insensitive to their geometric regularities.

Models of Human and Baboon Performance.

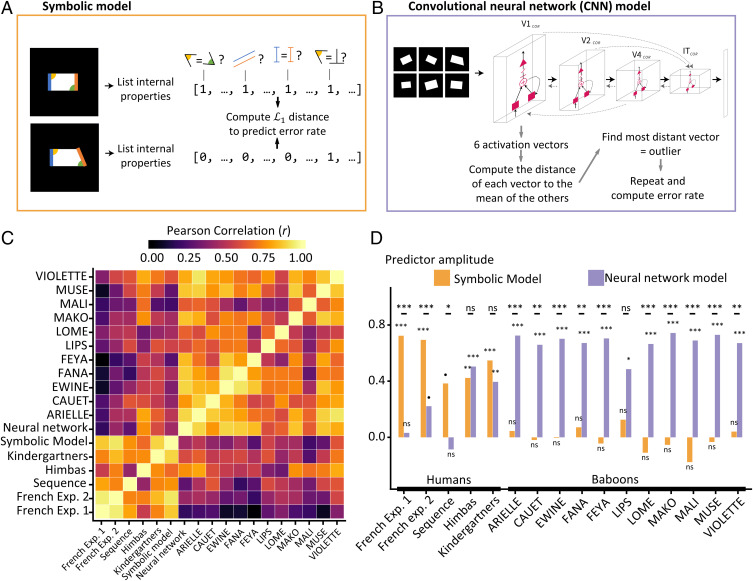
To shed light on the dissociated performance of humans and baboons, we contrasted two classes of models of the intruder task (Fig. 4). The first class assumes that quadrilaterals are processed by standard image recognition mechanisms in the ventral visual pathway, while the second assumes an additional level of discrete, symbolic processing of nonaccidental geometrical properties.

Fig. 4.

A double dissociation in geometric shape perception. (A) Symbolic model. Each shape is coded by a vector of discrete geometric properties (equal angles, parallel sides, equal lengths, and right angles; each relationship is assumed to be detected with a tolerance of 12.5%). The distance between the standard and outlier vectors is then used as a predictor of the ease of intruder detection. (B) Neural network model (modified from ref. 58, with permission from the authors). CORnet, a model of the ventral visual pathway for image recognition, is used to encode each of the six shapes of a given trial by an activation vector in inferotemporal cortex (IT). The shape whose vector is the most distant (L₂-norm) from the average of the five others is taken as the network’s intruder response. The predicted error rate is obtained by averaging across hundreds of trials. (C) Simple correlation matrix across shapes between the performance of individual baboons (names in capitals; Top), the predictions of the two models (Middle), and various human groups (Bottom). Color indicates the correlation coefficient, r. (D) Standardized regression weights (β) in a multiple regression of the data from various human and nonhuman primate groups across 44 data points (11 shapes × 4 outlier types) using the symbolic and neural network models as predictors. Stars indicate significance level (●P < 0.05; *P < 0.01; **P < 0.001; ***P < 0.0001).

We modeled the ventral visual pathway using CORnet, one of the top-scoring convolutional neural networks (CNNs) on brain-score.org, a platform that compares computational models with behavioral and neural observations (39); other CNNs gave identical results (SI Appendix). This model was pretrained to label photographs on ImageNet, a large set of images featuring natural and man-made items. To determine whether this model could successfully simulate the outlier task, we fed the network, without retraining, with each of the six images actually presented to the participants on a given trial, collected the corresponding activation vectors in each CNN layer, and defined the image whose vector differed most from the mean of the others as the intruder. When averaging across trials, this process yielded a predicted error rate for each shape, separately for each layer in the model.

A second class of model, capitalizing on the prior demonstration of categorical perception for parallels and perpendicularity (32), assumes that quadrilaterals are mentally encoded as a symbolic list of discrete geometric properties. For each shape, the model loops over all pairs of sides and angles and generates a vector of 0s and 1s for the presence or absence of equal angles, equal sides, parallelism, and right angles (with a tolerance fitted to 12.5%, although this parameter had little impact; SI Appendix, Fig. S5). The difficulty of spotting the intruder is then predicted to be inversely related to the L₁ distance (Manhattan distance) between the symbolic vectors coding for the reference and deviant shapes.

Fig. 4C shows the matrix of correlation over the 11 shapes between the error rates for each human population and for each of the 11 well-trained baboons, along with the predictions of the two models. Two squares are apparent. First, all baboons were intercorrelated, and their performance was well predicted by the last layer of the CNN model, putatively corresponding to the ventral inferior temporal cortex (IT; mean across animals: r = 0.81, SE = 0.03). However, the CNN model was a poor predictor of human performance (mean across human groups: r = 0.48, SE = 0.10; the two distributions were significantly different: t test, P = 0.024) and reached significance only for Himbas and kindergartners (P = 0.005 and 0.048, respectively). Second, conversely, all human groups were well predicted by the symbolic model (mean r = 0.84, SE = 0.05; SI Appendix, Table S3 provides a breakdown of the effect of each symbolic property), but that model is a poor predictor of baboon behavior (mean r = 0.44, SE = 0.04; the two distributions are significantly different: t test, P < 0.001).

This double dissociation was confirmed by a two-parameter multiple regression in which the predictions of the two models were put in competition to predict 44 data points (11 shapes × 4 deviants) per population (Fig. 4D). The three experiments with French adults who received formal education were captured almost exclusively by the symbolic regressor, and each baboon’s data were captured almost exclusively by the neural network regressor. Interestingly, uneducated populations (Himba adults and French kindergartners) showed significant contributions of both models.

Thus, the modeling suggests that two strategies are available to solve the intruder task and may coexist in humans (36, 40): 1) an early visual capacity, shared with other nonhuman primates, to recognize shapes in the ventral visual pathway and use this code to detect a salient deviation in shape and 2) a higher-level universal human capacity to grasp abstract geometric properties. The former may exploit a variety of early and late visual cues, since further analysis of the CNN’s performance showed some degree of predictability of the baboons’ behavior by the V1 layer already or by the surface area of the stimuli (SI Appendix, Fig. S6). The abstract strategy appears to be out of reach of such simple perceptual models, however—indeed, without further assumptions, the neural networks would have been incapable of passing the sequence version of the task, as humans did.

We verified that several other similar neural networks, such as DenseNet and ResNet, were similarly unable to fit human behavior (SI Appendix, Fig. S7). It could be argued that the geometric shape fell too far off the training space to elicit uninterpretable results; however, the model trained to label the ImageNet dataset did attribute a highly consistent label, mostly “envelopes”, to each geometric shape (SI Appendix, Table S4). To test the effect of the training space, we modified the network with extra output units and trained it to label our reference shapes (SI Appendix, Fig. S8). Four training strategies were tried, depending on whether we trained the network to label all 11 shapes or just the shapes with names in English, and whether all layers were allowed to change or just the final layer (SI Appendix). Nevertheless, all four manipulations failed to increase the predictive power of the CNN for any human population and either worsened the predictive power for the baboon behavior or left it unchanged. Since CNNs are far from perfect in capturing human behavior, even for natural stimuli (41–43), we also tested variational autoencoders (VAEs) (44). VAE architecture enforces the unsupervised learning of a low-dimensionality representation of a set of data by jointly learning to encode and decode to/from a bottleneck layer. In that sense, a VAE “compresses” information and thus may be more suited to the task of encoding regular shapes. A classical VAE was successfully trained to encode and decode our reference shapes (SI Appendix, Fig. S9A); however, it also did not exhibit the geometric regularity effect. First, its loss function varied very little across the 11 shapes (SI Appendix, Fig. S9B). All shapes were learned similarly across training epochs, and the loss did not correlate well with either the human behavior or the baboon behavior (SI Appendix, Fig. S9C). Second, using the same methodology as for CNNs, we probed whether the internal compressed representation of the model could be used to spot the outlier; again, it proved to be predictive of neither the humans’ nor the baboons’ behavior (SI Appendix, Fig. S9D).

Discussion

Using the geometric intruder test, regardless of the human populations that we tested, we observed a replicable geometric regularity effect: Finding an intruder among six quadrilaterals is much easier when either the reference or the deviant shape is highly regular. This effect was already present in young children (kindergartners and first graders) and was also replicated in uneducated adults from a remote non-Western population with reduced access to education, suggesting that the effect does not depend on age, culture, and education. Additionally, we found that this effect was replicable using different presentation modes (by presenting the entire shape at once or the four vertices sequentially) and different tasks (intruder, serial search, or subjective complexity rating).

Given this apparent universality in humans, it is noteworthy that the baboons did not share this effect. Their performance was initially quite poor with all quadrilaterals, but even when it later improved to the level of human children and showed significant variations across shapes, it still did not correlate with the geometrical regularity effect. This striking difference occurred even though the baboons clearly understood the demands of the intruder task, having reached a threshold of ≥80% correct on a first set of stimuli (where chance is 16.7% correct) and then generalized to new nongeometrical stimuli. It also cannot come from a lack of motivation; while a few baboons did not complete the training, the 20 on which we collected data spontaneously performed an average of 867 geometrical trials per day (first quartile, 278 trials; median, 641 trials; third quartile, 1,332 trials).

An empiricist could argue that the difference was due to the different environments in which humans and baboons live. The “carpentered world” hypothesis (45) proposes that an increased sensibility for right angles and parallel lines arises naturally from a Western lifestyle in a world full of rectilinear shapes (e.g., objects, buildings, books). Indeed, this was the dominant environment for most of our participants. However, several arguments refute this idea. First and foremost, the effect was present in the Himba people but not in baboons, yet the rural settlements of the Himba are quite unlike industrialized societies, and their environment is relatively free of rectilinear objects. Conversely, the baboons that we tested were not wild animals but grew up and lived in an environment comprising a mixture of natural objects (trees and rocks) and man-made rectilinear objects (e.g., buildings, doors, computer screens) that was arguably as “carpentered” as the Himbas’ environment (SI Appendix).

Second, even in a carpentered world, after projection in two dimensions, irregular shapes are arguably more frequent than regular shapes on the retina, because the observers are rarely perfectly aligned with their environment for a rectilinear projection to occur. Parallelograms are also rare in our environment, and yet they figured among the shapes with few errors. Thus, it is not clear how frequency in the environment would explain our result. Finally, we directly tested this empiricist hypothesis by training artificial neural networks with a dataset (ImageNet) that featured many man-made rectilinear image categories, such as envelopes, binders, band-aids, and lampshades (labels that they readily applied to our quadrilaterals; SI Appendix, Table S4). Even more crucially, we retrained them with our geometric shapes (SI Appendix, Fig. S8). Neither type of training sufficed for the neural networks to predict human behavior.

The dissociated performance of humans and baboons suggests that the intruder task can be solved using two strategies: a perceptual strategy, well captured by current neural network models of the ventral visual pathway, in which geometric shapes are encoded using the same feature space also used to recognize any image (e.g., faces, objects), and a symbolic strategy in which geometric shapes are encoded by their discrete nonaccidental regularities, such as right angles and parallel sides. The latter strategy seems to be available to all humans whether in Paris or in rural Namibia. It is tempting to speculate that it may be available only to humans, as suggested by the failure of all the baboons we tested. At the moment, however, this proposal remains tentative, because we only tested a limited number of humans and a single nonhuman primate species. Baboons also responded much faster than humans (∼2 s vs. ≥5 s; SI Appendix, Fig. S1), possibly preventing the deployment of a more abstract strategy. Both facets of our proposal will have to be submitted to further tests, for instance, by contrasting human infants, who are known to be born with sophisticated symbolic abilities (46), and chimpanzees, who may lack a logical or hierarchical mode of data analysis (8).

The present results converge with prior research using more complex geometric displays and tasks indicating that all humans, even young or uneducated ones, possess intuitions for geometry (20–22) and automatically apply a symbolic, language-like formalism to geometric data (22, 47). Brain imaging has shown that this “language of geometry” rests primarily on dorsal and inferior sectors of the prefrontal cortex (47). These regions are activated whenever humans reason about mathematical concepts and recombine them algebraically (48–50). While they are located outside of classical language areas, their surface area is strikingly expanded in the human lineage (51, 52), and thus they are good candidates for the emergence of novel human capacities in evolution, including symbolic mathematics. Previous work has shown that proto-mathematical core knowledge is present in other nonhuman primates, such as numerosity in macaque monkeys (53, 54) and spatial navigation in baboons (55). However, what these species may lack is the capacity to discretize those representations and recombine them in larger language-like combinatorial expressions, such as “four equal sides” (5–8), which are needed to conceive of a square and draw it. In the future, it would be informative to test whether chimpanzees who received “language training,” that is, learned to use visual tokens to label numbers and objects (56, 57), would show the geometric regularity effect. There are reasons to doubt it, since careful analyses suggest that unlike young children, chimpanzees do not use these tokens in productive combinations (11).

A parallel issue is how could the neural networks that we tested be modified to eventually pass the geometrical intruder test? Classical convolutional neural networks mimic only part of the human visual recognition capability (43). They roughly correspond to the first, bottom-up pass of invariant visual object recognition (58), but much more sophisticated recurrent top-down architectures are required to attain human-level performance in slower perceptual decision making tasks (59, 60). It will be interesting to examine whether those newer models pass the present test or, as we tentatively suggest, whether yet another level of symbolic representation, perhaps based on symbolic tree-based generative models and program inference (61–63), is needed.

In summary, the present results suggest a new putative human cognitive universal: the capacity to perceive the regularity of a geometric shape, such as a square. They hint at the exciting possibility that humans differ from other primates in cognitive mechanisms that are much more basic than language comprehension or theory of mind and involve a rapid grasp of mathematical regularities in their environment. Those findings also provide a challenge for artificial intelligence, as none of the classical neural network models that we tested so far could capture human behavior.

Materials and Methods

Reference Shapes.

All experiments relied on a single set of 11 fixed reference shapes, all of which were quadrilaterals (Fig. 1A; the coordinates of their vertices are listed in SI Appendix, Table S1). We matched most reference shapes for two parameters. First, the average distance between all pairs of vertices (i.e., the mean of six distances) was the same across the 11 shapes. This ensured that the reference shapes had the same overall size. Second, the bottom edge was of fixed length across 9 of the 11 shapes. This was particularly important for the sequence experiment, in which this segment was the last to appear on the screen and was the only one that could contain an outlier. The square and the rhombus were the only exceptions; they were only matched to other shapes on the average of distances. This was necessary because the square had only 1 degree of freedom and the rhombus otherwise would have been either too similar to the square or utterly flat.

For some shapes (e.g., rectangle), this set of constraints led to a single choice for the specific shape. For others, we selected a shape that satisfied the constraints while being maximally different from the shapes in other categories. For instance, the specific quadrilateral that we selected for the “irregular” category made it maximally obvious that it did not have equal sides, parallel sides, equal angles, or right angles.

The constraints that we adopted implied that the shapes were not strictly equalized in other dimensions, such as surface or perimeter. Such residual differences might explain why the performance of neural networks and baboons varied slightly across shapes but, crucially, they were uncorrelated with shape regularity (SI Appendix).

Deviant Shapes.

For each reference shape, we generated four deviant shapes by changing the position of the bottom-right vertex. All deviant vertices were equidistant from the correct vertex location. Two deviant vertices were positioned along the bottom edge, either lengthening it or shortening it (Fig. 1A). The two other deviant positions preserved the correct distance from the bottom-left vertex, and thus the length of the bottom edge, but changed its orientation. The distance of the deviant position from the correct position was fixed for all experiments and was common to all shapes. It was computed as a proportion of the (fixed) average distance between all pairs of vertices (55% for the sequence experiment; 30% for all other experiments).

Variations in Orientation and Size.

In their default presentation, the shapes were centered on their center of mass, and their top edge was horizontal. We then rotated the six shapes by a random permutation of the following angles: [−25°, −15°, −5°, 5°, 15°, 25°]. We avoided 0° rotation to prevent participants from relying on parallelism with the edges of the computer screen, and we avoided larger angles to sidestep the fact that some shapes had rotational symmetry (e.g., a 45° rotated square is identical to a −45° rotated square, but the same does not hold for a trapezoid). We also scaled the shapes by a random permutation of the following scaling factors applied to the edge lengths: [0.875, 0.925, 0.975, 1.025, 1.075, 1.125].

Participants and Experimental Procedures.

Details of the participants, study design, procedures, Ethical Committee approvals, and analyses specific to each experiment are presented in SI Appendix. All experiments involving French subjects were approved by the Ethical Committee of Université Paris-Saclay. The experiment involving Himba adults was approved by the Ethical Committee of Goldsmiths University of London. All subjects or their legal guardians provided informed consent.

In brief, 612 French adults were recruited for online experiment 1, 117 were recruited for online experiment 2, and 48 were recruited for online subjective ratings. For the sequence and visual search experiments, we tested 16 and 11 participants, respectively, in individual isolated testing booths. Twenty-eight French kindergartners (mean age, 64 mo; range, 59 to 70 mo; 15 boys, 13 girls) from two classrooms were tested individually in their school. Finally, 44 native Himba adults were recruited onsite in small individual villages of northern Namibia (southern Africa). All were monolingual native speakers of Otjihimba, a dialect of the Otjiherero language, which does not have vocabulary for most geometric shapes. Among these, we report data for the 22 participants who did not attend a single year of schooling. Additional analyses of the effect of schooling are provided in SI Appendix.

Baboons (26 P. papio; 18 females; age range, 1.5 to 23 y; mean age, 11 y) were tested at the CNRS primate facility in Rousset-sur-Arc, France. Baboons lived in a 700-m² outdoor enclosure with access to indoor housing and could, on a voluntary basis, at any time enter 10 automated learning devices for monkeys equipped with a 19-inch touch screen, a food dispenser, and a radio-frequency identification (RFID) reader that could identify the animals

Data Availability

The data for all experiments, as well as both the neural network and the symbolic models, are available in the Open Science Framework at https://osf.io/w5pzf/.