Emergence of hierarchy in networked endorsement dynamics

Significance

Hierarchies structure the lives of many social animals, including humans. We propose a generative model of time-varying networks in which endorsements between individuals give rise to enduring hierarchies. For several network-based ranking functions, our model possesses a distinct, analytically tractable, critical transition between egalitarian and hierarchical states. We also use our model to explore hierarchical structures in empirical data on hiring patterns among mathematicians, dominance relations among parakeets, and friendships among members of a fraternity, observing several persistent patterns. Overall, our model enables data-informed modeling of hierarchical networks in social and biological systems.

Abstract

Many social and biological systems are characterized by enduring hierarchies, including those organized around prestige in academia, dominance in animal groups, and desirability in online dating. Despite their ubiquity, the general mechanisms that explain the creation and endurance of such hierarchies are not well understood. We introduce a generative model for the dynamics of hierarchies using time-varying networks, in which new links are formed based on the preferences of nodes in the current network and old links are forgotten over time. The model produces a range of hierarchical structures, ranging from egalitarianism to bistable hierarchies, and we derive critical points that separate these regimes in the limit of long system memory. Importantly, our model supports statistical inference, allowing for a principled comparison of generative mechanisms using data. We apply the model to study hierarchical structures in empirical data on hiring patterns among mathematicians, dominance relations among parakeets, and friendships among members of a fraternity, observing several persistent patterns as well as interpretable differences in the generative mechanisms favored by each. Our work contributes to the growing literature on statistically grounded models of time-varying networks.

Hierarchies—stable sets of dominance relationships among individuals (1–3)—structure many human and animal societies. Among animals, hierarchical rank may determine access to resources such as food, grooming, and reproduction (4). Among humans, rank shapes the epistemic capital and employment prospects of researchers (5, 6), susceptibility of adolescents to bullying (7), messaging patterns in online dating (8), and influence in group decision-making (9).

A central question concerns how enduring hierarchies shape and are shaped by interactions between individuals. Empirical studies have indicated the presence of a “winner effect”: An individual who participates in a favorable interaction, such as winning a fight or receiving an endorsement, increases their likelihood of being favored in future interactions (10, 11). Both theoretical work (12–20) and controlled experiments in humans (21) suggest that winner effects are sufficient (though not necessary) to form stable hierarchies. Mechanistic explanations of winner effects vary. A common approach postulates that each individual possesses an “intrinsic strength,” which may depend on factors such as size, skill, or aggression levels. For instance, physiological mechanisms, such as changes in hormone levels following confrontational interactions (22), can alter an individual’s strength, causing the strong to get stronger.

However, intrinsic strengths are not necessary to produce winner effects. If a politician endorses a rival candidate, the latter does not become intrinsically more fit for office; instead, the endorsee builds support for their candidacy that may lead to future endorsements. The fame of the endorser is key: The better-known the endorser, the more valuable the endorsement. We refer to such prestige by proxy as “transitive prestige.” Since transitive prestige enables hierarchical rank to flow through interactions between individuals, networks provide a natural lens through which to study its role. Recent empirical studies have emphasized the networked nature of hierarchy in biological and social groups (2, 3, 23–25). Several theoretical studies (26–29) have also investigated reinforcing hierarchy using time-varying network models called “adaptive networks” (30, 31). In this class of models, edges, representing interactions, evolve in response to node states and vice versa. Edges tend to accrue to important or highly central nodes, leading to self-reinforcing hierarchical network structures. Despite their recent uses, adaptive networks are often difficult to analyze analytically or compare to empirical data.

We present a flexible adaptive network model of social hierarchy that addresses these challenges. Winner effects in our model are driven entirely by social reinforcement, rather than intrinsic strengths. We allow arbitrary matrix functions to determine rank or prestige of nodes in the network and introduce parameters governing the behavior of individuals in response to rank. A key feature of our model is that it is amenable both to mathematical analysis and to statistical inference. We analytically characterize a critical transition separating egalitarian and hierarchical model states for several choices of ranking function. We also explore hierarchical patterns in four biological and social datasets, using our model to perform principled selection between competing ranking methods in each dataset, and highlight persistent macroscopic patterns. We conclude with a discussion of potential model extensions and connections to recent work on centrality in temporal networks.

Modeling Emergent Hierarchy

In our adaptive network model, new directed edges are formed based on existing, node-based hierarchy, after which they decay over time. We conceptualize a directed edge $i\to j$ as an “endorsement,” in which $i$ affirms that $j$ is fit, prestigious, or otherwise of high quality. For example, endorsements could capture contests won by $j$ over $i$, retweets of $j$ by $i$, or comparisons in which a third party ranks $j$ above $i$. We collect endorsements in a weighted directed network on $n$ nodes summarized by its adjacency matrix $\mathbf{A}\in {\mathbb{R}}^{n\times n}$, where entry $a_{ij}$ is the weighted number of interactions $i\to j$. The matrix $\mathbf{A}$ evolves in discrete time via the iteration

$$\mathbf{A}\left(t+1\right)=\lambda \mathbf{A}\left(t\right)+\left(1-\lambda \right)\mathit{\Delta }\left(t\right)\hspace{0.17em}.$$ [1]

Here, the “update matrix” $\mathit{\Delta }\left(t\right)$ contains new endorsements at time $t$. The “memory parameter” $\lambda \in \left[\mathrm{0,1}\right]$ represents the rate with which memories of old endorsements decay; the smaller the value of $\lambda$, the more quickly previous endorsements are forgotten.

The new endorsements in $\mathit{\Delta }\left(t\right)$ depend on previous endorsements through a ranking of the $n$ nodes, which we call the “score vector” (or simply “score”) $\mathbf{s}\in {\mathbb{R}}^n$. The score vector is the output of a “score function” $\sigma :\mathbf{A}\mapsto \mathbf{s}\in {\mathbb{R}}^n$, which may be any rule that assigns a real number to each node.

We consider three score functions chosen for analytical tractability and relevance in applications. Let ${\mathbf{D}}^{\text{in}}$ and ${\mathbf{D}}^{\text{out}}$ be diagonal matrices whose entries are the weighted in- and out-degrees of the network, i.e., ${\mathbf{D}}_{ii}^{\text{in}}={\sum }_j{\mathbf{A}}_{ij}$ and ${\mathbf{D}}_{ii}^{\text{out}}={\sum }_j{\mathbf{A}}_{ji}$. First, the Root-Degree score is the square root of the in-degree—the weighted number endorsements—of each node $i$, defined as $s_i=\sqrt{{\mathbf{D}}_{ii}^{\text{in}}}$. The Root-Degree score function does not model transitive prestige, since only the number of endorsements is considered, not the prestige of the agents from which they come. Second, PageRank (32) is a recursive notion of rank, in which high-rank nodes are those whose endorsers are numerous, and themselves high rank. The foundational algorithm used by Google in ranking web pages, PageRank computes a value for each node interpretable as the proportion of time that a random surfer following the network of endorsements would spend on that node. We define PageRank score $\mathbf{s}$ as the PageRank vector of ${\mathbf{A}}^T$, which is the unique solution to the system

$$\left[{\alpha }_p{\mathbf{A}}^T{\left({\mathbf{D}}^{\text{out}}\right)}^{-1}+\left(1-{\alpha }_p\right)n^{-1}\mathbf{e}\hspace{0.17em}{\mathbf{e}}^T\right]\mathbf{s}=\mathbf{s}$$ , [2]

up to scalar multiplication. Here, ${\alpha }_p\in \left[\mathrm{0,1}\right]$ is the so-called teleportation parameter, for which we use the customary value ${\alpha }_p=0.85$. We normalize the PageRank vector so that ${\mathbf{e}}^T\mathbf{s}=n$, where $\mathbf{e}$ is the vector of ones. Finally, SpringRank (33) is another recursive definition of rank, in which endorsers are ranked one unit below endorsees, and disagreements are resolved by using an analogy to a physical system of springs: The ranking of nodes minimizes the total energy of the system. Mathematically, the SpringRank score $\mathbf{s}$ is the unique solution to the linear system (33)

$$\left[{\mathbf{D}}^{\text{in}}+{\mathbf{D}}^{\text{out}}-\left(\mathbf{A}+{\mathbf{A}}^T\right)+{\alpha }_s\mathbf{I}\right]\mathbf{s}=\left[{\mathbf{D}}^{\text{in}}-{\mathbf{D}}^{\text{out}}\right]\mathbf{e}\hspace{0.17em},$$ [3]

with the identity matrix $\mathbf{I}$ and a regularization parameter ${\alpha }_s>0$, which ensures the uniqueness of $\mathbf{s}$. Unlike the Root-Degree score, both PageRank and SpringRank scores model transitive prestige: The impact of an endorsement depends on the prestige of the endorser. These three score functions can all be interpreted as rankings or centrality measures, although this property is not required of score functions in our model.

Given score vector $\mathbf{s}$, new endorsements $\mathit{\Delta }$ are chosen using a random utility model, a standard framework in discrete choice theory that has recently been applied in models of growing networks (34). At time step $t$, node $i$ is selected uniformly at random. We suppose that endorsing $j$ has utility $u_{ij}\left(\mathbf{s}\right)$ for $i$, which depends on the current scores. In this work, we focus on utilities of the functional form

$$u_{ij}\left(\mathbf{s}\right)={\beta }_1{s}_j+{\beta }_2{\left(s_i-s_j\right)}^2\hspace{0.17em},$$ [4]

where we generally assume that ${\beta }_1>0$ and ${\beta }_2<0$. The parameter ${\beta }_1$ captures a “preference for prestige”; a positive value of ${\beta }_1$ indicates a tendency to endorse others with high scores. The parameter ${\beta }_2$ captures a “preference for proximity”; a negative value of ${\beta }_2$ indicates a tendency to endorse others with scores relatively similar to their own. Many other choices of utility functions are possible; we prove a stability theorem for a large class of these functions in SI Appendix.

In the random utility model, node $i$ observes all possible utilities subject to noise. Traditionally, this noise is chosen to be Gumbel-distributed, in which case the probability that endorsing $j$ yields the greatest utility is given by the multinomial logit (35)

$$p_{ij}\left(\mathbf{s}\right)=\frac{e^{u_{ij}\left(\mathbf{s}\right)}}{\sum _{j=1}^n{e}^{u_{ij}\left(\mathbf{s}\right)}}\hspace{0.17em}.$$ [5]

We collect $m\in \mathbb{N}$ endorsements in an update matrix $\mathit{\Delta }$, where the entry ${\mathit{\Delta }}_{ij}$ gives the number of times that $i$ endorses $j$ in the time step. More complex random utility models can lead to more realistic structures in networks with a growing number of nodes (36); we do not pursue these complications here because our model does not focus on network growth and because these complications obstruct analytical insight.

Eq. 5 can also be derived from an alternative model, in which node $i$ makes a randomized choice among $n$ nodes to endorse. In this model, the option to endorse $j$ is assigned a deterministically observed weight proportional to $e^{u_{ij}\left(\mathbf{s}\right)}$. In this case, ${\beta }_1$ and ${\beta }_2$ signify inverse temperatures that tune the degree of randomness in this choice, with lower values corresponding to greater randomness. Although this alternative model—in which node $i$ makes a noisy choice between deterministically observed utilities—and the random utility model—in which node $i$ makes a deterministic choice between noisily observed utilities—are mathematically equivalent, the two formulations can lead to different interpretations of system behavior. In the case of institutional faculty hiring discussed below (Hierarchies in Data), the random utility model assumes that a hiring committee makes imperfect observations of the utilities of the institutions from which they could hire and then deterministically chooses the highest of these imperfectly observed qualities. In contrast, the alternative framework assumes that the committee makes a perfect observation of the utilities, but then chooses among them with some degree of randomness, which may reflect dissension on the hiring committee, search-specific priorities, or other factors.

Eqs. 1 and 5 capture key features of our model. First, the dynamics in Eq. 1 imply that past interactions decay geometrically at rate $\lambda$. This global, gradual decay contrasts with another rank-based relinking model, in which single edges fully disappear within each time step (26). Second, Eq. 5 implies that the likelihood of a node being endorsed at a given time step depends only on the distribution of previous endorsements and not on intrinsic strength or desirability. Those who receive more endorsements and therefore obtain higher scores are more likely to be endorsed in the future—a mechanistic instantiation of winner effects via social reinforcement.

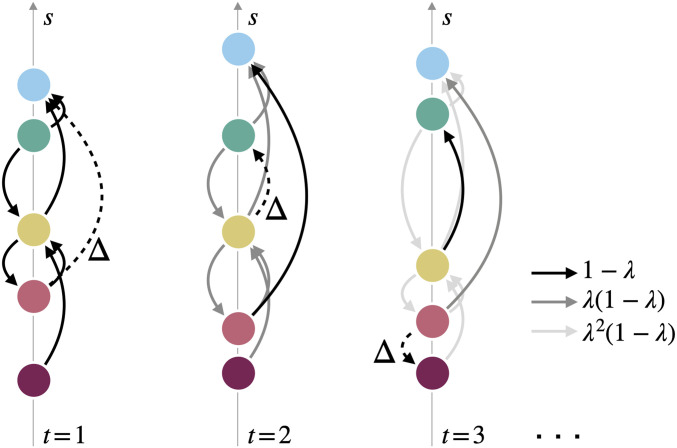
Fig. 1 schematically illustrates model dynamics with $m=1$ endorsement per time step. At time $t=1$, the model is initialized with a small number of endorsements logged in $\mathbf{A}$. The score function takes $\mathbf{A}$ as an input and outputs the score vector $\mathbf{s}$, which, in turn, determines a new interaction according to Eq. 5. Logged in $\mathit{\Delta }$, this new interaction is weighted by $1-\lambda$ and added to the previous endorsements, which are discounted by $\lambda$. This process repeats over time with new endorsements gradually replacing old ones in the system’s memory, sequentially updating the score vector $\mathbf{s}$. Fig. 1 also depicts in stylized fashion the operation of both a winner effect (${\beta }_1>0$), in which endorsements tend to flow in the direction of increasing score, and a proximity effect (${\beta }_2<0$), in which endorsements tend to flow between nodes of similar scores. The net effect is that most endorsements are “short hops” up the hierarchy. As we will discuss, this is a common pattern in empirical data.

Fig. 1.

Schematic illustration of our model dynamics. Nodes are initialized at time $t=1$ with a set of pre-existing endorsements logged in $\mathbf{A}$ (solid arrows), and the score $\mathbf{s}=\sigma \left(\mathbf{A}\right)$ is computed (vertical axis). Then, a new edge logged in $\mathit{\Delta }$ is added (dashed line). In the next time step $t=2$, old interactions decay by a factor of $\lambda$ (gray arrows). The new endorsement and decay of previous endorsements lead to an updated score function, which then informs the next time step.

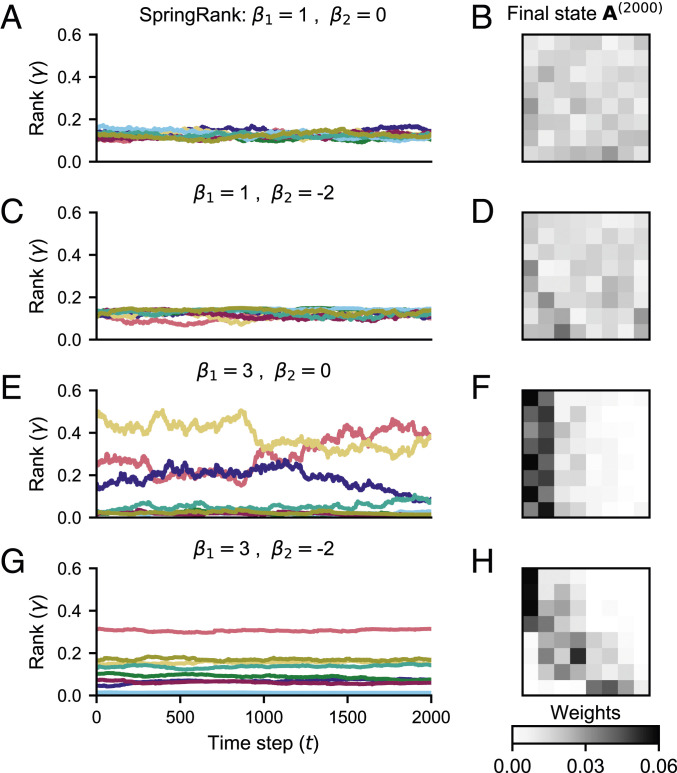
Despite its simplicity, the model displays a wide range of behaviors. To observe them, we define a “rank vector” $\mathit{\gamma }$, whose $j$th entry ${\gamma }_j=n^{-1}{\sum }_i{p}_{ij}$ gives the likelihood that a new endorsement flows to $j$. We say that the system state is “egalitarian” when all ranks ${\gamma }_j$ are equal and “hierarchical” otherwise. Fig. 2 illustrates representative behaviors when the SpringRank score is used. When ${\beta }_1$ is relatively small, winner effects are overtaken by noise, and the system settles into an approximately egalitarian state (Fig. 2 A and B). When ${\beta }_1$ is relatively large, persistent hierarchies emerge (Fig. 2 C–F). Moreover, the distribution and stability of ranks depend on the strength of proximity effects, modeled by the quadratic term in the utilities. For ${\beta }_2=0$ (no proximity preference), a single node garners more than half of endorsements in a hierarchy with significant fluctuations (Fig. 2 C and D). Adding a proximity preference leads to a marginally more equitable hierarchy with ranks that are nearly constant in time (Fig. 2 E and F).

Fig. 2.

Representative dynamics of the proposed model. Each column shows a population of $n=8$ nodes simulated for 2,000 time steps using the SpringRank score function with $m\hspace{0.17em}=\hspace{0.17em}1$ update per time step, varying the preference parameters ${\beta }_1$ and ${\beta }_2$. A, C, E, and G show the simulated rank vector $\mathit{\gamma }$ over time; different colors track the ranks of different nodes. B, D, F, and H show the adjacency matrix $\mathbf{A}$ at time step t = 2,000 for the corresponding parameter combinations. See SI Appendix, Fig. S1 for additional examples with SpringRank; SI Appendix, Fig. S2 for examples with PageRank; and SI Appendix, Fig. S3 for examples with Root-Degree. See SI Appendix, Fig. S4 for the dependence of rank variance on ${\beta }_1$ and ${\beta }_2$ jointly. Parameters: $\lambda \hspace{0.17em}=\hspace{0.17em}0.995$, ${\alpha }_s\hspace{0.17em}=\hspace{0.17em}10^{-8}$.

The Long-Memory Limit

The behavior observed in Fig. 2 suggests the presence of qualitatively distinct regimes depending on prestige preference ${\beta }_1$. For small ${\beta }_1$ (Fig. 2A), the winner effect is weak, and approximate egalitarianism prevails. For larger ${\beta }_1$, a stronger winner effect enforces a stable hierarchy. We characterize the boundary between these regimes analytically in the “long-memory limit” $\lambda \to 1$ by defining a function $\mathbf{f}$, which is analogous to a deterministic time-derivative for the dynamics of our discrete-time stochastic process. Let

$$\mathbf{f}\left(\mathbf{s},\mathbf{A}\right)=\underset{\lambda \to 1}{lim}\frac{\mathbb{E}\left[\sigma \left(\lambda \mathbf{A}+\left(1-\lambda \right)\mathit{\Delta }\right)\right]-\mathbf{s}}{1-\lambda }\hspace{0.17em},$$ [6]

where the expectation is taken with respect to $\mathit{\Delta }$. If $\mathbf{f}\left(\mathbf{s},\mathbf{A}\right)=0$ for all $\mathbf{A}$, the score vector $\mathbf{s}$ is a fixed point of the model dynamics in expectation. Our choices of Root-Degree, PageRank, and SpringRank score functions admit closed-form expressions for $\mathbf{f}$, allowing us to analytically derive the conditions for the stability of egalitarianism in the limit of long memory.

Theorem 1. For each of the Root-Degree, PageRank, and SpringRank score functions, $\mathbf{f}$ has a unique egalitarian root. This root is linearly stable if and only if ${\beta }_1<{\beta }_1^c$, where

$${\beta }_1^c=\left\{\begin{array}{cc}2\sqrt{\frac{n}{m}}\hspace{1em}\hfill & \hspace{1em}\text{Root}-\text{Degree},\hfill \\ 1/{\alpha }_p\hspace{1em}\hfill & \hspace{1em}\text{PageRank},\hfill \\ 2+{\alpha }_s\frac{n}{m}\hspace{1em}\hfill & \hspace{1em}\text{SpringRank}.\hfill \end{array}\right.$$

In SI Appendix, we prove Theorem 1, as well as a generalization to arbitrary smooth utility functions. In each case, the proof of uniqueness exploits the algebraic structure of the score function, and the critical value ${\beta }_1^c$ is obtained via the linearization of $\mathbf{f}$ about the egalitarian state. Interestingly, only ${\beta }_1$ plays a role in the stability of the egalitarian root. While proximity preference ${\beta }_2$ does not determine where the hierarchical regime begins, it does influence the structure of and the transient dynamics toward nonegalitarian equilibria (Fig. 2 E and G).

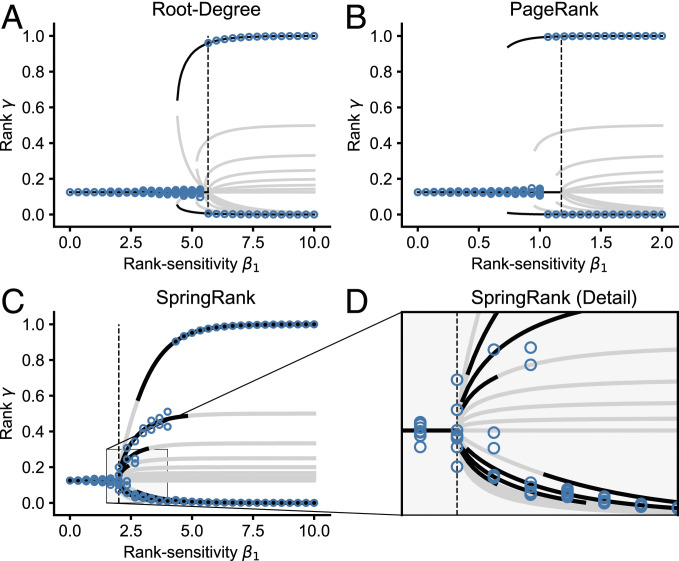
Fig. 3 illustrates the destabilization of egalitarianism predicted by Theorem 1 in the case of $n=8$ nodes. Although not required by Theorem 1, we fix ${\beta }_2=0$ for simplicity. Curves show fixed points of the model dynamics in the long-memory limit. We show only fixed points in which nodes separate into two groups, each of which have identical rank. For ${\beta }_1<{\beta }_1^c$, the egalitarian regime is stable, and the long-run state deviates from egalitarianism only slightly. For ${\beta }_1>{\beta }_1^c$, in contrast, the long-run state switches to an inegalitarian, stable fixed point.

Fig. 3.

Bifurcations in models with Root-Degree (A), PageRank (B), and SpringRank (C and D) score functions with ${\beta }_2=0$ and $m=1$ update per time step. Points give the value of the rank vector $\mathit{\gamma }$ averaged over the final 500 time steps of a $5\times 10^4$-step simulation with $n=8$ nodes, memory parameter $\lambda =0.9995$, and varying ${\beta }_1$ specified by the horizontal axis. Solid curves show stationary points of the long-memory dynamics obtained by numerically solving the equation $\mathbf{f}\left(\mathbf{s},\mathbf{A}\right)=\mathbf{0}$, subject to the restriction that nodes separate into two groups with identical ranks in each. Black curves are linearly stable, while gray curves are unstable. Stability was determined by studying the spectrum of the Jacobian matrix of $\mathbf{f}$. Vertical lines give the critical value ${\beta }_1^c$, at which the egalitarian solution becomes linearly unstable, according to Theorem 1. Parameters: ${\alpha }_p=0.85$, ${\alpha }_s=10^{-8}$.

In the Root-Degree and PageRank models, there is a single stable inegalitarian equilibrium with one node absorbing nearly all endorsements (Fig. 3 A and B). Interestingly, there is a bistable regime in which both egalitarian and inegalitarian states are attracting. Whether the system converges to one or the other depends on initial conditions. The SpringRank model displays qualitatively distinct behavior (Fig. 3 C and D). Past ${\beta }_1^c$, we observe staggered multistable regimes. As ${\beta }_1$ increases, equilibria with multiple elite (i.e., highly ranked) nodes become sequentially unstable until eventually only a single elite node remains. The long-term behavior of the system again depends on initial conditions, but now there are many more possible stable states. This behavior would seem to make the SpringRank score function especially appropriate for modeling empirical systems with multiple distinct hierarchical regimes and sensitivity to initial conditions, an intuition that we confirm empirically in the following section.

Hierarchies in Data

In addition to being amenable to analytical treatment, our model has a tractable likelihood function, described in SI Appendix. This allows us to study hierarchical structures in empirical data using principled statistical inference. The likelihood function not only supports maximum-likelihood parameter estimates of $\lambda$, ${\beta }_1$, and ${\beta }_2$, but also enables direct comparisons of different score functions in a statistically rigorous framework: Score functions with higher likelihoods provide more predictive low-dimensional summaries of observed interactions. This, in turn, allows us to explore the relative value of competing mechanistic explanations of observed data.

Several mathematical features of the model facilitate the exploration of real data. First, the predictive distribution Eq. 5 is in the linear exponential family, making the estimation of $\mathit{\beta }$ a convex optimization with a unique solution. Second, the estimation problem in $\widehat{\lambda }$ is, in general, nonconvex, but can be tractably solved via first-order optimization methods with multiple starting points. Finally, while model likelihoods evaluated on training data may, in principle, be inflated due to overfitting, our model uses only three parameters to fit hundreds or thousands of observations, suggesting that overfitting is not a major concern.

We conducted a comparative study of model behavior on four datasets: an academic exchange network in math, two networks of parakeet interactions, and a network of friendships among members of a fraternity. The Math PhD Exchange dataset is extracted from The Mathematics Genealogy Project (37–39). Nodes are universities. An interaction $i\to j$ at time $t$ occurs when a mathematician who received their degree from university $j$ at time $t$ supervises one or more PhD theses at university $i$. This event is a proxy for university $i$ hiring a graduate from university $j$ at a time near $t$. We view this as an endorsement by $j$ that graduates of $i$ are of high quality (5). We restricted our analysis to the activity of the 70 institutions that placed the most graduates between 1960 and 2000. Doing so helped to avoid singularities produced by institutions with no placements early in the time period and to minimize temporal boundary effects associated with the beginning and end of data collection.

The two Parakeet datasets (3, 40) record aggression events in two distinct groups of birds studied over four observation quarters (weeks). An interaction $i\to j$ at time $t$ occurs when parakeet $i$ loses a fight to parakeet $j$ in period $t$. Since there are just four observation periods, estimates of the memory parameter $\lambda$ should be approached with caution.

Lastly, the Newcomb Fraternity dataset was collected by the authors of refs. 41 and 42 and accessed via the KONECT network database (43, 44). The dataset documents friendships among members of a fraternity at the University of Michigan. Each week during a fall semester, excluding a week for fall break, each of 17 cohabiting brothers ranked every other brother according to friendship preference, with ranks 1 and 16 referring to that brother’s most and least preferred peers, respectively. An endorsement $i\to j$ is logged when brother $i$ ranks $j$ among his top $k=5$ peers (small changes to $k$ did not significantly alter the results). While friendship is often viewed as a symmetric relationship, expressed friendship preferences may be asymmetric (45).

We studied these data using the Root-Degree, PageRank, and SpringRank score functions. Table 1 summarizes our results, including parameter estimates, SEs (obtained by inverting the numerically calculated Fisher information matrix), and optimized log-likelihoods for each combination of score and dataset. Several features stand out. In all four datasets and across all three score functions, we find ${\widehat{\beta }}_1>0$ and ${\widehat{\beta }}_2<0$. This suggests a persistent pattern in time-dependent hierarchies: While endorsements do flow upward (${\widehat{\beta }}_1>0$), nodes are more likely to endorse those close to them in rank (${\widehat{\beta }}_2<0$). Endorsements tend to flow a few rungs up the ladder—not directly to the top. The reasons for this pattern likely vary across datasets. In the Math PhD Exchange, this may indicate that low-ranked schools struggle to recruit graduates of high-ranked ones due to a limited supply of elite candidates. In parakeet populations, proximal aggression may facilitate inference of dominance hierarchies through transitive inference (3). In Newcomb’s Fraternity, we postulate that implicit social norms may encourage friendships between those of similar standing. Similar results have been reported in static social-network data among adolescents (24). Thus, while we do not attribute this pattern in the parameter estimates to a universal mechanism, we suggest its persistence as an interesting observation worthy of future study.

Table 1.

Parameter estimates and likelihood scores using each of three score functions for the four datasets described in Hierarchies in Data

	Root-Degree	PageRank	SpringRank
Math PhD Exchange
(N = 6,019)
$\widehat{\lambda }$	0.87 (0.01)	0.96 (0.01)	0.91 (0.01)
${\widehat{\beta }}_1$	1.28 (0.02)	0.74 (0.01)	2.99 (0.04)
${\widehat{\beta }}_2$	−0.18 (0.01)	−0.07 (0.00)	−1.12 (0.04)
$\mathcal{L}$	−14,379	−15,001	−14,927
Parakeets (G1)
(N = 838)
$\widehat{\lambda }$	0.97 (0.08)	0.59 (0.08)	0.67 (0.14)
${\widehat{\beta }}_1$	0.84 (0.05)	1.82 (0.08)	3.03 (0.16)
${\widehat{\beta }}_2$	−0.12 (0.01)	−0.50 (0.03)	−1.74 (0.12)
$\mathcal{L}$	−1,106	−1,053	−964
Parakeets (G2)
(N = 961)
$\widehat{\lambda }$	0.42 (0.07)	0.13 (0.03)	0.40 (0.06)
${\widehat{\beta }}_1$	0.62 (0.03)	0.82 (0.04)	2.86 (0.14)
${\widehat{\beta }}_2$	−0.06 (0.01)	−0.12 (0.01)	−1.46 (0.12)
$\mathcal{L}$	−975	−1,029	−924
Newcomb Fraternity
(N = 1,428)
$\widehat{\lambda }$	0.56 (0.13)	0.81 (0.19)	0.71 (0.14)
${\widehat{\beta }}_1$	0.95 (0.05)	1.21 (0.07)	2.33 (0.14)
${\widehat{\beta }}_2$	−0.08 (0.03)	−0.25 (0.05)	−0.86 (0.16)
$\mathcal{L}$	−1,850	−1,865	−1,841

Parenthetical values are SEs for each parameter estimate. For each dataset, the largest log-likelihood $\mathcal{L}$ is indicated in bold. All parameter estimates are statistically distinct from zero at 95% confidence. N gives the total number of interactions in the data. See SI Appendix, Fig. S5 for simulated trajectories with the inferred parameters.

Because different score functions capture distinct qualitative features of the data, quantitative comparisons yield insights into the generating mechanisms at work. In general, parameters from models using differing score functions should not be directly compared, since these parameters are sensitive to the scale of the score vector. However, we can compare models on the basis of their likelihoods. In the Math PhD Exchange, the Root-Degree model was strongly favored over either SpringRank or PageRank. In the context of this dataset, the Root-Degree score is a measure of faculty production: A school that places more candidates has a higher score, regardless of the prestige of the institutions at which the candidates land. The strong fit from the Root-Degree score is consistent with previous findings that raw faculty production plays a major role in structuring the hierarchy of academic hiring within computer science, business, and history (5). As the authors of ref. 5 note, transitive prestige also plays an important role. It would be of significant interest to extend our study to include multiple score functions, enabling an inferential analysis of the relative roles of production and transitive prestige.

In contrast, the SpringRank score was favored by large margins in both Parakeet datasets and by a smaller margin in the Newcomb Fraternity dataset, suggesting that transitive prestige plays a more prominent role. Among parakeets, it may matter not only how many confrontations one wins, but also against whom, with victories over high-ranking birds counting more toward one’s own prestige. This finding is consistent with those of ref. 3, which found, using different methodology, that parakeet behavior suggests the ability to draw sophisticated, transitive inferences about location in the hierarchy. Similarly, in Newcomb’s Fraternity, friendships with highly ranked brothers may confer greater prestige than those with lower-ranked ones.

In addition to the likelihoods, we can also compare the memory estimate $\widehat{\lambda }$ across models and datasets. Since the model assumes that the impact of past endorsements decays at rate $\lambda$, the quantity $t_{1/2}=-\log \left(2\right)/\log \left(\widehat{\lambda }\right)$ represents the half-life of system information according to the inferred dynamics, in units of observation periods. In the Math PhD data, the favored Root-Degree score gave a half-life of $t_{1/2}\approx 5$ y. In the Parakeets data, the half-life estimated under SpringRank is $t_{1/2}\approx 1.7$ wk for the first group and $t_{1/2}\approx 0.8$ wk for the second. The small number of observation periods implies that these estimates should be approached with caution. Finally, in the Newcomb Fraternity data, the SpringRank half-life was $t_{1/2}\approx 2$ wk. This suggests that the friendships in this dataset evolved on timescales much shorter than the full semester. This likely reflects the fact that the brothers did not know each other prior to data collection, requiring them to form their social relationships from scratch. An important caveat in interpreting these estimated half-lives is that the indirect influence of an interaction may extend far beyond its direct influence. In the Math PhD data, for instance, while the half-life indicates that only a quarter of hiring events will be directly “remembered” in the system after a decade, those events will have influenced 10 cycles of hiring, which may further reinforce the patterns established by the earlier events.

As described in Theorem 1, in the long-memory limit, our model has distinct egalitarian and hierarchical regimes, separated by a critical value ${\beta }_1^c$. The model’s estimate of ${\beta }_1$ allows us to roughly locate empirical systems within these regimes. There are two necessary points of caution. First, when the estimate $\widehat{\lambda }$ is far from the idealized long-memory limit, hierarchical and egalitarian regimes may not be sharply distinguished. Second, in the Math PhD and Parakeet data, the number of updates $m$ varies between time steps. Here, a reasonable approximation is to use the average number of updates $\overline{m}$ per time step. Using this average and Theorem 1, we computed an approximate long-memory critical value ${\beta }_1^c$ for each empirical system.

Comparing the data-derived preference estimates ${\widehat{\beta }}_1$ to the approximate critical values ${\beta }_1^c$ reveals that all four empirical systems are in or near the hierarchical regime (Table 2). The Root-Degree estimates of ${\beta }_1$ tend to be very close to the approximate critical point. For the Math PhD data, in which Root-Degree is the preferred model, the estimate of ${\beta }_1$ is slightly, but statistically significantly, below the critical value. In each of the other three datasets, the estimate is slightly above the critical value, and significantly so in the two Parakeet groups. Given the presence of a bistable regime in the Root-Degree model (Fig. 3A), the estimate of ${\beta }_1$ for the Math PhD data is consistent with persistent hierarchy, despite the fact that the estimate falls slightly below the critical threshold. Indeed, simulations with the inferred parameters produce persistent hierarchical structure similar to that observed in the data (SI Appendix, Fig. S5). The PageRank estimates behave similarly to Root-Degree, although the finding in Parakeets (G2) is reversed. The presence of a bistable regime in the PageRank model (Fig. 3B) indicates that these findings are consistent with persistent hierarchy in any of these datasets (see SI Appendix, Fig. S5 for simulated dynamics). Finally, in the SpringRank model, which obtains the highest likelihood for both Parakeet datasets and the Newcomb Fraternity dataset, the estimated values of ${\beta }_1$ significantly exceed the estimated critical values and tend to lie in or near the range $\left[\mathrm{2,3}\right]$. In summary, all three models suggest that the system corresponding to each dataset is in or near the regime of self-reinforcing hierarchy.

Table 2.

Estimates of ${\beta }_1$ (identical to those in Fig. 1) compared to the mean critical value ${\beta }_1^c$ for each system

	Root-Degree	PageRank	SpringRank
Math PhD Exchange
${\beta }_1^c$	1.36	1.18	2.00
${\widehat{\beta }}_1$	1.28* (0.02)	0.74* (0.01)	2.99† (0.04)
Parakeets (G1)
${\beta }_1^c$	0.55	1.18	2.00
${\widehat{\beta }}_1$	0.84† (0.05)	1.82† (0.08)	3.03† (0.16)
Parakeets (G2)
${\beta }_1^c$	0.49	1.18	2.00
${\widehat{\beta }}_1$	0.62† (0.03)	0.82* (0.04)	2.86† (0.14)
Newcomb Fraternity
${\beta }_1^c$	0.89	1.18	2.00
${\widehat{\beta }}_1$	0.95 (0.05)	1.21 (0.07)	2.33† (0.14)

We calculate ${\beta }_1^c$ as in Theorem 1, using as m the mean number of interactions per time-step in the observed data. As in Table 1, the parameters corresponding to the highest log-likelihood are shown in bold. SI Appendix, Fig. S5 for simulated trajectories using the inferred parameters.

^*Estimates that are smaller than the approximate critical value by two SEs

^†Estimates that exceed the approximate critical value by two SEs

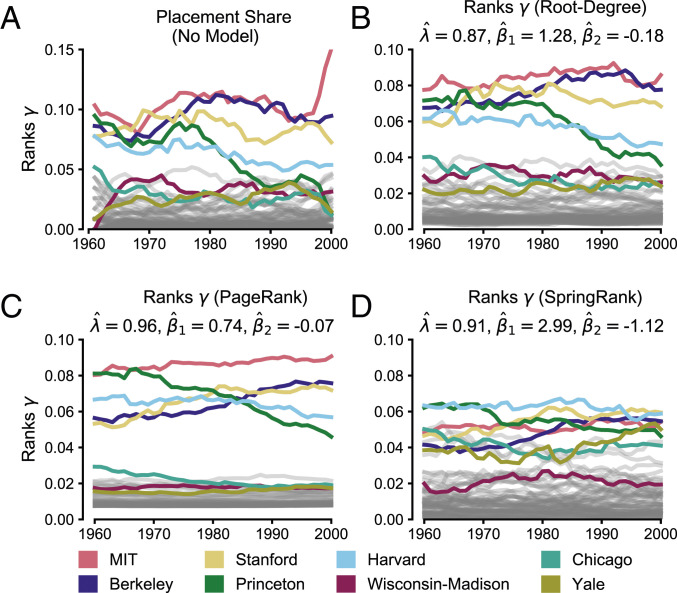
Our model also assigns interpretable, time-dependent ranks to empirical data (Fig. 4). For the Math PhD Exchange network, for example, the raw placement share (Fig. 4A) and Root-Degree model (Fig. 4B) show strong qualitative agreement, with institutions that place the most candidates occupying higher ranks. Due to the relatively large estimates $\widehat{\lambda }$, both the Root-Degree and PageRank models (Fig. 2 B and C) produce smoother rank trajectories than the purely descriptive placement share with 8-y rolling average. In contrast, the SpringRank score generates qualitatively different trajectories that are less sensitive to raw volume (Fig. 4D). For instance, SpringRank places Harvard at the top over most of the time period, while the other scores prefer MIT. This difference reflects SpringRank’s sensitivity to where Harvard’s graduates were placed, a consideration that Root-Degree entirely ignores. Similarly, SpringRank places Chicago and Yale noticeably higher than Wisconsin–Madison, despite all three having similar numbers of placements.

Fig. 4.

Visualization of evolving ranking functions in the Math PhD Exchange. (A) Fraction of all placements (number of graduates hired) from each school, shown as a moving average with bin-width 8 y for visualization purposes. (B) Inferred rank vector $\mathit{\gamma }$ as a function of time using the Root-Degree score function. (C and D) As in B, with PageRank and SpringRank score functions, respectively. Parameters for B–D are shown in the first section of Table 1.

Discussion

We have proposed a simple and flexible model of persistent hierarchy as an emergent feature of networked endorsements with feedback. When the preference for high status exceeds a critical value, egalitarian states destabilize, and hierarchies emerge. The location of this transition depends on the structure of the score function and of the node’s preferences. Our findings emphasize that winner effects do not require internal, rank-enhancing feedback mechanisms. Social reinforcement through prestige preference is sufficient to generate social hierarchies.

Crucially, our model has a tractable likelihood function, supporting principled statistical inference of parameters—for both preferences and memory strength—from empirical data. In the four datasets analyzed, we found that links are typically formed in alignment with the hierarchy (${\widehat{\beta }}_1>0$), but that they are preferentially created to other nodes with similar ranks (${\widehat{\beta }}_2<0$). The likelihood also opens the door to model selection to determine relevant score functions. We found that networked ranking methods that capture transferable prestige are preferred over nonnetworked methods in some, but not all, systems. Due to its flexibility, our framework can be applied to additional datasets, score functions, and/or preference models to test the generality of these empirical observations.

There are limitations to our approach. First, we specified a fixed parametric form for the utilities with Eq. 4 and Gumbel-distributed noise with Eq. 5. Other choices may be more justified in particular applications, ideally informed by domain-specific considerations. Importantly, our inferential framework allows for quantitative evaluation and comparison of these choices. Taking advantage of this, future work could systematically explore the most appropriate functional forms in systems from diverse scientific domains. Second, our model assumes that all nodes use identical preference parameters ${\beta }_1,{\beta }_2$ and score vector $\mathbf{s}$ when computing utilities. The latter is an especially strong assumption, since it requires each node to have global knowledge of the endorsement network, or at least of the score vector. This is unlikely to be true in real systems and should be regarded as a modeling device. Future work, along the lines of ref. 3, could explore the interplay between the cognitive capabilities of individuals represented by nodes and the information available to them in the formation of social hierarchies.

Our model points to several other avenues for further work. A crucial step would be to extend extant network-based models (26, 27, 29) so that their parameters could be statistically learned from data. This would enable comparative validation of different modeling frameworks. Studies of the relationship between measures of time-dependent centralities (38, 46, 47) and dynamic models of hierarchy would also be valuable. In particular, the theory of time-dependent centralities faces an important methodological issue: Different reasonable ranking methods can yield directionally different orderings of nodes when applied to the same dataset (48). Their performance on external validation tasks, such as the prediction of central nodes in spreading processes (49), may also vary significantly. Because the theories of centrality and generative networks have evolved largely separately, evaluating the suitability of a centrality metric for a given dynamic system can be difficult. Our inferential approach offers a candidate validation task to overcome this challenge: Good centrality metrics are those that most effectively predict the future evolution of the system. This approach enables us to not only compare different score and utility functions in a principled manner, but also explore their relative importance in observed networks. For instance, one could study the relative influence of degree-based and SpringRank scores by incorporating both into our model and then analyzing their distinct coefficients. Further work in this direction could reveal how different forms of centrality combine to govern the evolution of interaction networks. We anticipate that a fruitful dialogue between centrality theory and generative models of time-varying networks will deepen our understanding of the feedback mechanism between local interactions and hierarchical structures.

Data Availability

A repository containing all data used in our analyses, model implementation, and figure-generation scripts is available at GitHub (50). Raw data are available at https://sites.google.com/site/danetaylorresearch/data (Math PhD Exchange), https://datadryad.org/stash/dataset/doi:10.5061/dryad.p56q7 (Parakeets G1 and G2), and http://vlado.fmf.uni-lj.si/pub/networks/data/ucinet/ucidata.htm#newfrat (Newcomb Fraternity).