Significance
We investigated the relationship between cooperativity and epistasis and found low cooperativity results in high epistasis between nonnative contacts, whereas high cooperatively results in epistasis mainly between native contacts. This provides a mechanistic explanation for why epistasis measurements can be used to reconstruct protein structure. The structure of GB1 protein has been successfully reconstructed using epistasis measurements, and we calculated its epistasis distribution for a cooperative and a noncooperative model. The structure of the native state is clearly mapped out in the cooperative model but becomes obscured in the noncooperative model due to the presence of a folding intermediate. We thus conclude that using epistasis measurements to reconstruct the native state of proteins with stable intermediates may not be appropriate.
Keywords: protein folding, protein structure prediction
Abstract
Epistasis and cooperativity of folding both result from networks of energetic interactions in proteins. Epistasis results from energetic interactions among mutants, whereas cooperativity results from energetic interactions during folding that reduce the presence of intermediate states. The two concepts seem intuitively related, but it is unknown how they are related, particularly in terms of selection. To investigate their relationship, we simulated protein evolution under selection for cooperativity and separately under selection for epistasis. Strong selection for cooperativity created strong epistasis between contacts in the native structure but weakened epistasis between nonnative contacts. In contrast, selection for epistasis increased epistasis in both native and nonnative contacts and reduced cooperativity. Because epistasis can be used to predict protein structure only if it preferentially occurs in native contacts, this result indicates that selection for cooperativity may be key for predicting structure using epistasis. To evaluate this inference, we simulated the evolution of guanine nucleotide-binding protein (GB1) with and without cooperativity. With cooperativity, strong epistatic interactions clearly map out the native GB1 structure, while allowing the presence of intermediate states (low cooperativity) obscured the structure. This indicates that using epistasis measurements to reconstruct protein structure may be inappropriate for proteins with stable intermediates.
Two mutations have an epistatic interaction if their combined effect on a trait is not equal to the sum of their independent effects (1). The effect may be on fitness, function, or a physical property such as stability. Epistasis has been demonstrated many times experimentally. It has been found to impact the rate of adaptation (2), to constrain mutational trajectories leading to drug resistance (3, 4), and to impact yeast metabolism (5). It has been observed in the evolution of influenza (6, 7), between beneficial mutations in an evolving population of Escherichia coli (8), during the evolution of RNA viruses (9), and in the evolution of new enzyme activity (10, 11). Epistasis influences the amino acid preferences at different sites (12) and can have a substantial impact on protein evolution by restricting certain evolutionary pathways and by opening up new ones, resulting in sequences and functions that were not previously available (13). It has been suggested that epistasis is highly pervasive, affecting up to 90% of substitutions (14).
Experimentally measured epistasis can be used to predict the three-dimensional (3D) native structure of a protein. For example, Olson et al. (15) measured the epistasis between the majority of possible residue pairs of the guanine nucleotide-binding protein (GB1), which was used by Rollins et al. (16) to predict the protein’s 3D structure. Such prediction methods assume that the majority of epistatic pairs are in contact in the native state, an assumption supported by experimental evidence (15). In the native state structure, the side chains of residues in contact interact, and so they no longer behave independently. This can result in nonadditivity in terms of protein properties such as stability. However, native contacts are not the only interactions that determine protein properties. Mutations in contacts present in intermediate states and unfolded state structures that alter the stability of those states relative to the native state will impact properties such as stability. It is therefore unclear why experimental evidence suggests that mostly native contacts interact epistatically.
Cooperativity in Protein Folding
Proteins are under evolutionary pressures to fold and unfold cooperatively (17), where breaking a small number of interactions leads to complete unfolding. When proteins fold cooperatively, they move from the unfolded to the folded state, avoiding the intermediate state. The disadvantage of stable intermediate states is that they are prone to aggregation and can lead to misfolding, which is known to play a role in many diseases, including amyloid diseases such as Alzheimer’s and Parkinson’s (18–20). Many small, single-domain proteins, for example, display highly cooperative two-state folding (21, 22), in which only the native and fully unfolded states are occupied, due to the instability of any intermediate states. In contrast, larger, multidomain proteins, often fold stepwise via the formation of partially unfolded forms (PUFs), where each PUF is made up of one or more cooperative structural units known as foldons (19). Cooperativity of folding is also observed in macromolecular complexes, and strong coevolutionary preferences have been observed between cooperative proteins composing part of a macromolecular complex, where the components display a conserved self-assembly order (23).
Cooperative folding requires the presence of unfavorable destabilizing interactions at structurally important sites in partially folded states and/or highly favorable interactions that stabilize the native state, while not overstabilizing those intermediate states in which the stabilized native contact is present. This was demonstrated by Yadahalli and Gosavi (24) when the designed noncooperative protein Top7 was made to fold cooperatively by introducing stabilizing mutations at a set of native contacts and destabilizing mutations at residue pairs that were found to stabilize intermediate states.
Cooperativity and epistasis thus both involve sometimes strong interactions among adjacent amino acid residues in the native structure. It seems possible that selection for one might drive the other, or vice versa, but how they influence each other is unknown. We chose to investigate this by simulating protein evolution using a mechanistic model based in thermodynamics and statistical mechanics that has been shown to be able to reproduce many important features of protein evolution such as epistasis and coevolution (12, 25). We evolved a protein under different levels of selection for cooperativity to explore how and why epistasis differs between cooperative and noncooperative sequences.
To investigate how selection for cooperativity impacts 3D structure reconstruction using epistasis data, we simulated the evolution of the GB1 protein for a two-state (containing native and unfolded states) and three-state (containing native, unfolded, and intermediate states) model and determined the distribution of epistasis between all pairs of residues.
Results
We performed 10 evolutionary simulations for 50,000 generations of a protein sequence based on the structure of a cysteine-free variant of E. coli ribonuclease H (RNase H). For these simulations we calculated the fitness based on the probability that a protein would be in its native state at thermal equilibrium. We also included a fitness penalty that reduced the fitness of proteins with folding intermediates, allowing us to tune the impact of this penalty using a cooperativity tuning coefficient, . The folding pathway of RNase H has been determined at near amino acid resolution (26). We generated a series of intermediate partially folded states based on the stepwise folding pathway, in which the folded regions of the proteins were fixed to their position in the folded structure and the unfolded regions were modeled as a freely joined chain defined by the position of the atoms, with bond lengths between 3 and 7 Å. We also included an excluded volume term prohibiting atoms from being closer than 3 Å (see SI Appendix for more detail).
We carried out simulations for four different values of the cooperativity tuning coefficient : no selection for cooperativity () and low (), medium (), and high selection for cooperativity () (Eq. 7).
Two-state folding generally results in sharp sigmoidal melting curves and a peak in the heat capacity at the melting temperature , although multistate transitions can also show such behavior (27, 28). The level of cooperativity is determined experimentally by calculating the ratio of the van’t Hoff enthalpy change evaluated at to the calorimetric enthalpy change of the entire transition (29, 30). The van’t Hoff enthalpy change is calculated purely from the difference in the enthalpy of the native and unfolded states, while the calorimetric enthalpy change is the experimentally measured enthalpy change during the unfolding transition. If the system is purely two-state, the calorimetric enthalpy change is equal to the difference between the enthalpies of the native and the unfolded state, and so the ratio equals 1. Values of are observed for many globular proteins (31–33). For folding simulations where the distribution of the protein states is available, we can directly distinguish two-state folding by examining the underlying populations of intermediate states during the folding transition. In this case lower occupation of intermediates indicates higher levels of cooperativity.
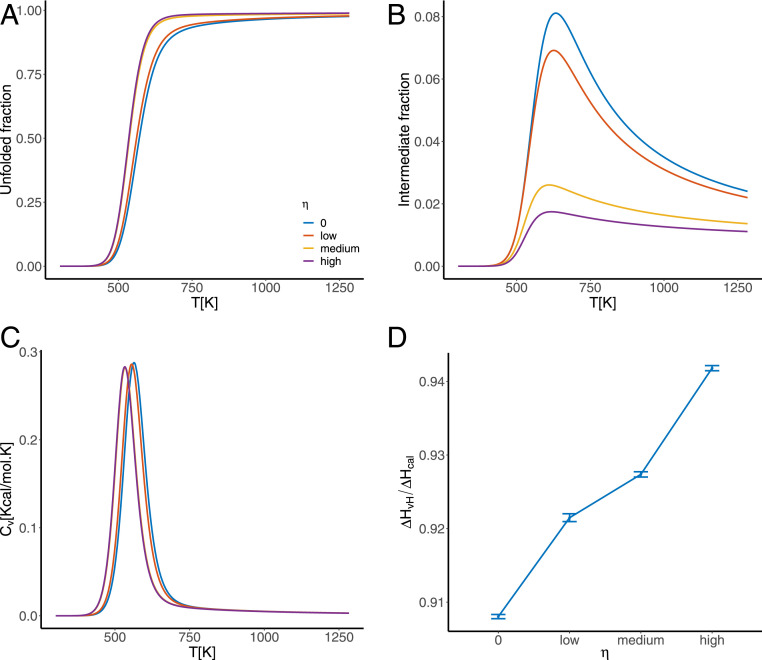
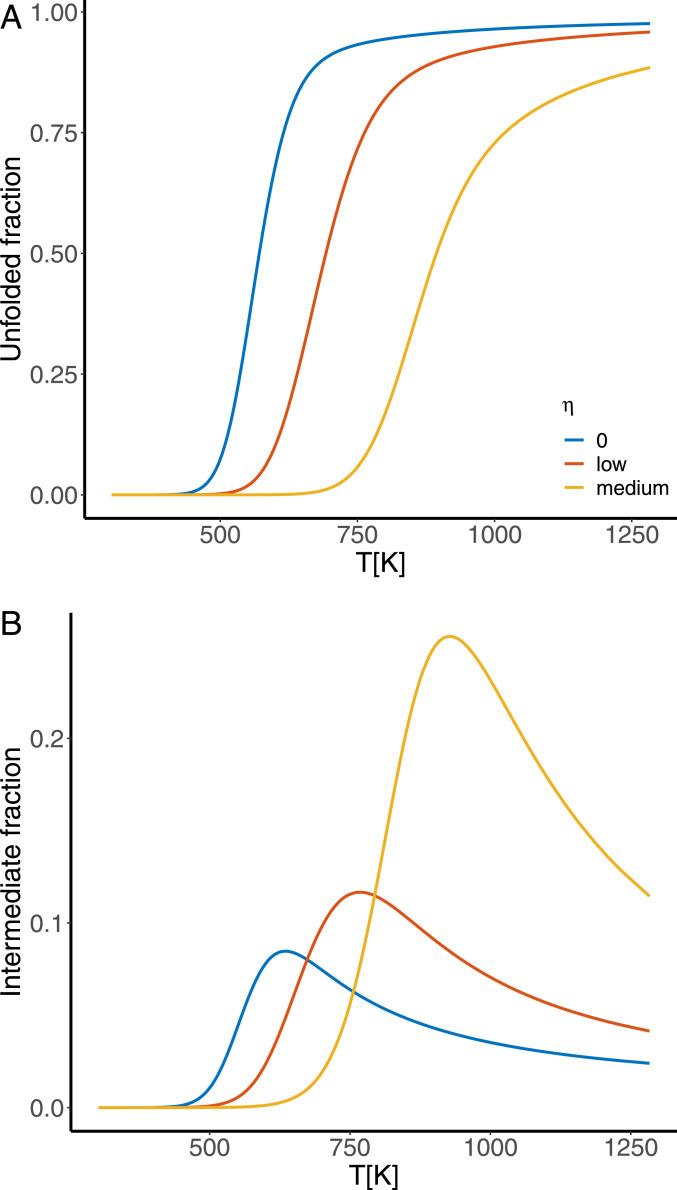
Multiple lines of evidence indicate that our selection for cooperativity is effective in increasing the cooperativity of the folding transition in our simulations. First, the sharpness of the sigmoidal melting curves increases as the value of the cooperativity tuning coefficient increases (Fig. 1A). Second, the value of the van’t Hoff criterion increases with selection for cooperativity from in the absence of selection for cooperativity, to for high selection (Fig. 1D). Finally, we consider the total fraction of the population occupying the intermediate states (i.e., the fraction of the population not in either the native or the fully unfolded states), which shows that as selection for cooperativity increases, the fraction in the intermediate states decreases (Fig. 1B).
Fig. 1.
Investigating the cooperativity of sequences evolved under zero, low, medium, and high values of the tuning coefficient by considering (A) the fraction of the system found in the fully unfolded state during denaturation under increased temperature; (B) the fraction in the ensemble of intermediate states during the unfolding transition; (C) heat capacity curves during the unfolding transition, the area under which is the enthalpy change associated with the transition; and (D) the van’t Hoff ratio of the unfolded transition associated with each value of the cooperativity tuning coefficient . All values are averaged over the set of 1,000 most evolved sequences for each evolutionary simulation.
Selection for Cooperativity Causes Epistasis to Increase between Native Contacts but Decrease between Nonnative Contact Pairs.
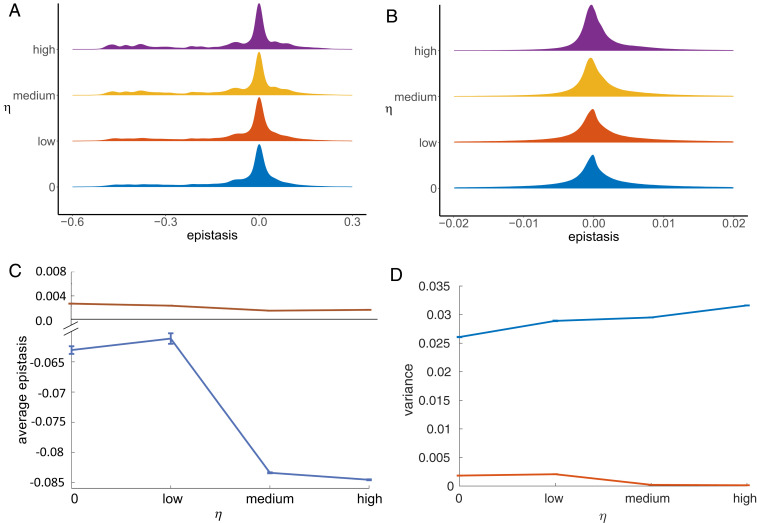
We then calculated the epistasis in protein stability (Eq. 15) between each possible pair of residues in the protein for the final 2,000 generations of the 50,000 generations simulated and calculated the mean epistasis between each pair of residues averaged over all simulations, for the different values of selection for cooperativity. We investigated the distribution of epistasis between pairs of residues in contact in the native state (Fig. 2A) and pairs of residues not in contact in the native state (Fig. 2B). The sign convention we adopted for defining stability is in the direction of folding (Eq. 5), and so negative epistasis, for example, occurs when wild-type residues at positions and mutually stabilize each other compared to the mutant “noninteracting” residues.
Fig. 2.
The distribution of epistasis as the selection coefficient increases. (A and B) The normalized distribution of the epistasis in protein stability between (A) native contacts and (B) nonnative contacts when evolving proteins under varying degrees of selection for cooperativity. As selection for cooperativity increases, more native contacts experience higher-magnitude (more negative) epistasis, while more nonnative contacts experience very low levels of epistasis. The area under each curve sums to 1. (C and D) The mean of the epistasis distributions (C) and the variance of the epistasis distribution (D) of the final 2,000 generations of the 50,000 generations simulated, averaged over all 10 simulations for native contacts (blue) and nonnative contacts (red). The error bars represent the variance of these values across the 10 simulations. The average of the epistasis distribution at the native contacts becomes more negative as the value of the selection coefficient increases and the variance in the distribution increases. The average of the epistasis distribution at the nonnative contacts goes to zero as the selection coefficient increases, and the variance decreases.
As selection for cooperativity increases, the epistasis distribution between native contacts becomes less peaked around zero and the average of the distribution becomes more negative, while the variance of the distribution increases (blue line in Fig. 2 C and D, respectively).
In contrast, for the nonnative contacts the average epistasis goes toward zero and the variance decreases. In other words, the more cooperative sequences display higher magnitudes of negative epistasis between pairs of native contacts, but smaller magnitudes of epistasis between the nonnative pairs compared with sequences associated with lower cooperativity in protein folding.
Selection for Epistasis at Native Contacts Leads to a Decrease in Cooperativity.
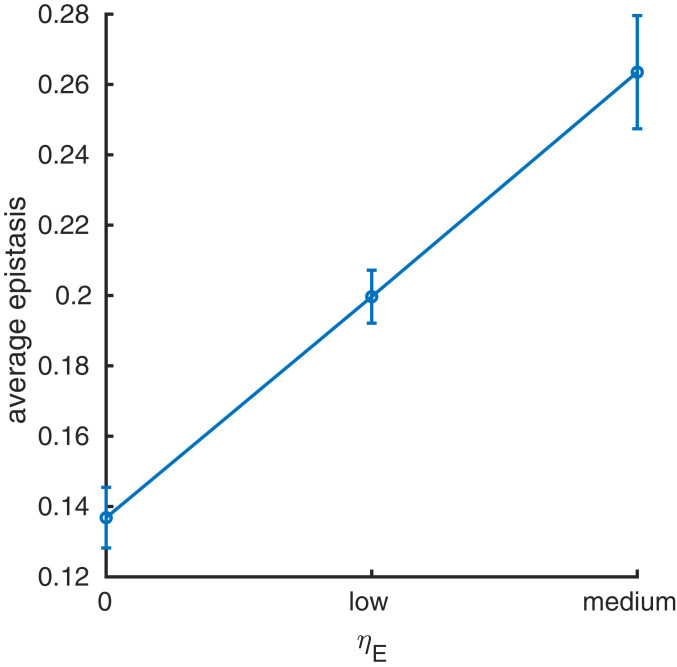
If cooperativity increases epistasis at native contacts, is the converse true? As a thought experiment, we investigated this question by directly selecting for epistasis between native contacts, although we do not expect this sort of selection in nature. The coefficient increases selection for sequences with large epistasis at native contacts (Eq. 8). We performed 10 evolutionary simulations for three values of the tuning coefficient : no selection (), low selection (), and medium selection (), and determined the average epistasis between each pair of native contacts during the evolutionary process. Selecting for the average epistasis between native contacts was much more computationally expensive than selection for cooperativity, and therefore we chose to simulate evolution for just 5,000 generations. To enable a fair comparison between the epistasis distributions for selection for stability only () and the two levels of selection for epistasis ( and ), we considered only the first 5,000 generations of the simulations presented in the previous section. To determine the epistasis distributions for each value of , we calculated the epistasis in protein stability (Eq. 15) between each possible pair of residues in the protein for the final 2,000 generations of the 5,000 generations simulated and calculated the mean epistasis between each pair of residues, averaged over all simulations. As selection for epistasis increases, the average magnitude of epistasis per native contact per substitution increases (Fig. 3), demonstrating that the selection works as intended.
Fig. 3.
The mean absolute epistasis in protein stability (y axis), averaged over all 10 simulations, between each pair of native contacts when evolving proteins under increasing selection ( = 0, low, medium) for the absolute epistasis in protein stability at the native contacts (x axis). The error bars depict the variance in the mean. The average absolute epistasis between native contacts increases as the value of the selection coefficient increases.
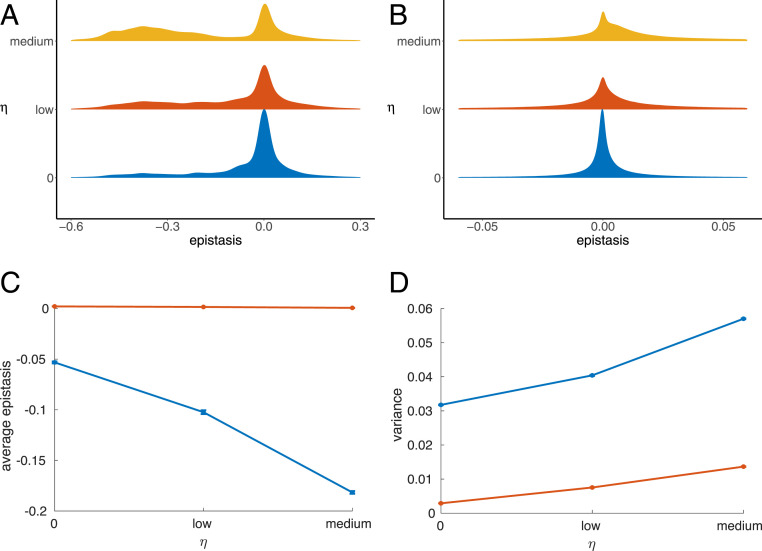
The effect on the distribution of mean epistasis among native contact pairs is similar to what was observed for cooperativity, but the effect is stronger (Fig. 4A). However, there was also more epistasis at nonnative contact pairs, although epistasis between these pairs was not directly selected for (Fig. 4B). The average epistasis at native contacts becomes sharply more negative (blue line in Fig. 4C), while for the nonnative contacts the average is unchanged (red line in Fig. 4C) but the variance, and thus the levels of both positive and negative epistasis, increases (red line in Fig. 4D).
Fig. 4.
The distribution of epistasis as the selection coefficient increases. (A and B) The normalized distributions of epistasis between (A) native and (B) nonnative contacts when evolving sequences under different magnitudes of selection for the average magnitude of epistasis between the native contacts. As the value of the selection coefficient increases, a higher number of native contacts experience greater magnitude negative epistasis, while a higher number of nonnative contact pairs experience nonzero epistasis. The area under the curves sums to 1. (C and D) The mean of the epistasis distributions (C) and the variance of the epistasis distribution (D), of the final 2,000 generations of the 5,000 generations simulated, averaged over all 10 simulations for native contacts (blue) and nonnative contacts (red). The error bars represent the variance of these values across the 10 simulations. The average of the epistasis distribution at the native contacts becomes more negative as the value of the selection coefficient increases and the variance in the distribution increases. The average of the epistasis distribution at the nonnative contacts remains roughly constant as the selection coefficient increases, but the variance in the distribution increases.
We investigated the cooperativity of the evolved sequences via the protein’s melting curves and the fraction of the system in the intermediate states during unfolding, because this is sufficient to determine cooperativity. Although we observed earlier that selection for cooperativity induces epistasis at native contacts, the inverse is not true. Instead, selection for epistasis at native contacts results in less cooperativity. The melting curve becomes less sharp and shifts to the right (Fig. 5A), indicating the protein passes through more stable intermediate states as it unfolds. The fraction of the ensemble of intermediate states also increases (Fig. 5B). Thus, although selecting for cooperativity induces epistasis at the native contacts, selecting for epistasis at the native contacts does not induce cooperativity, but instead decreases it.
Fig. 5.
Investigating the cooperativity of the unfolding transition with increased selection for the average magnitude of epistasis at the native contacts, by considering (A) the fraction of the population in the unfolded state during denaturation and (B) the fraction of the population in the ensemble of partially folded states during denaturation. As the value of the selection coefficient increases, the unfolding transition becomes less sharp and the fraction of the population in the intermediate states increases, showing the folding is becoming less cooperative.
The Intermediate and Unfolded Ensemble Approaches the Unfolded State Distribution for Selection for Cooperativity.
To understand why selection for higher cooperativity increases epistasis between native contacts and decreases epistasis between nonnative contacts, we considered how epistasis arises in the model and how the stability of each state impacts our epistasis calculations. We can rewrite Eq. 15, the epistasis between residues and , as , where is the epistasis in the free energy of the native state, and is the epistasis in the free energy of the intermediate and unfolded ensemble, , where denotes the intermediate states and denotes the unfolded state. For native contacts, the epistasis is determined by both the epistasis in the native state and the intermediate and unfolded ensemble, and whether epistasis is positive or negative is determined by a trade-off between the two values. For nonnative contacts, the epistasis in the free energy of the native state, , is zero. Therefore positive epistasis at nonnative contacts arises when is negative, and negative epistasis at the nonnative contacts arises when is positive.
From Eq. 1 we can see that the epistasis between residues and in the free energy of a single structure is , where is the contact potential between amino acids at residues and , and is equal to 1 if residues are in contact and 0 otherwise. Therefore, the epistasis between two residues and is equal to the contact potential between the two amino acids if they are in contact in the native state and zero otherwise.
The free energy of each state in the intermediate and unfolded ensemble was determined using a large number of dummy structures. From Eq. 3 the epistasis between residues and in one of the intermediate states , or the unfolded state , is , where is the average probability of residues and being in contact in the ensemble of the chosen intermediate or unfolded state, denoted .
Epistasis in the free energy of one of these states, between residues i and j, arises when a large fraction of dummy structures contain this contact, and so is large, resulting in changes to the average and variance of the free energy of the state in question. If a particular pair has a high probability of contact in several intermediate states, this can lead to epistasis in the free energy of the intermediate and unfolded ensemble.
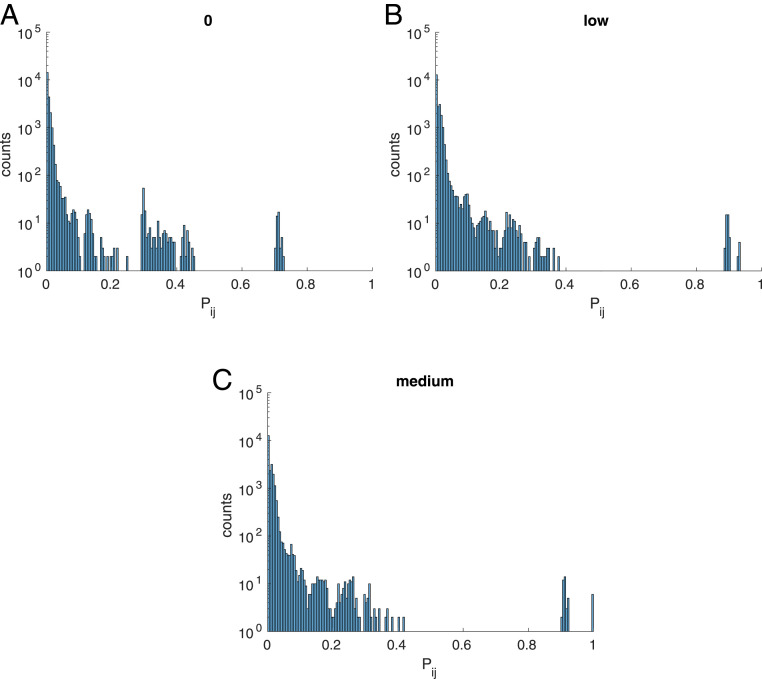
To understand why epistasis between nonnative contacts decreases as selection for cooperativity increases, we consider the distribution of the probability that residues i and j are in contact in the intermediate and unfolded ensemble, (Eq. 16). For one of the intermediate or unfolded states, the average probability that residues and are in contact, , will be a number between 0 and 1; i.e., it is the fraction of structures in the ensemble of state that contains the - contact. When selection for cooperativity is imposed, the intermediate states are destabilized and as selection increases the probability of being in any of the intermediate states goes to zero. This results in the distribution of contact probabilities becoming more concentrated around lower values (Fig. 6), demonstrating the contact probabilities of the intermediate and unfolded ensemble are becoming more like those of the unfolded state.
Fig. 7.
Histogram of the distribution of contact probabilities between site and site when evolving proteins under selection for epistasis between native contacts, when is set to (A) 0, (B) low, and (C) medium.
Because the probability that any pair of residues and are in contact in the unfolded state is small, the corresponding epistasis in the intermediate and unfolded ensemble will be small. Therefore, as selection for cooperativity increases, the epistasis in the intermediate and unfolded ensemble decreases. Because the unfolded ensemble contains mostly nonnative contacts, there is a decrease in epistasis at nonnative contacts as selection for cooperativity increases. Similarly, given the equation for epistasis between residues and , , we can see that as goes to zero, for native contacts , explaining the increase in the magnitude of the epistasis between native contacts as cooperativity increases.
Sequences under selection for the average magnitude of epistasis between native contacts display broad epistasis distributions at both native and nonnative contacts (Fig. 4). Under this selection regime, intermediate states are stabilized (Fig. 5B). This happens because selection for epistasis at native contacts selects for pairs of residues with large contact potentials since , and so those intermediate state ensembles containing native contacts will be stabilized. This results in a decrease in cooperativity and an increase in the variance in the epistasis between both native and nonnative contacts.
If we again consider the distribution of contact probabilities in the partially folded and unfolded ensemble, we observe that as selection for epistasis at native contacts increases, the distribution of probabilities spreads out, with some pairs of residues having a contact probability between 0.8 and 1 (Fig. 7). This happens because some of the intermediate states, which are being stabilized relative to the unfolded state, have highly structured areas with contact probabilities of 1 or almost 1. In other words, the distributions of contact probabilities in the intermediate and unfolded ensemble are becoming more like the native state contact probabilities and less like the unfolded state contact probabilities. As mentioned earlier, epistasis in the intermediate and unfolded ensemble arises when a particular pair has a high probability of contact in this ensemble. Therefore, the larger number of high-probability contacts in the intermediate and unfolded ensembles suffices to explain the broader distribution of epistasis between nonnative contacts when there is high selection for epistasis at native contacts.
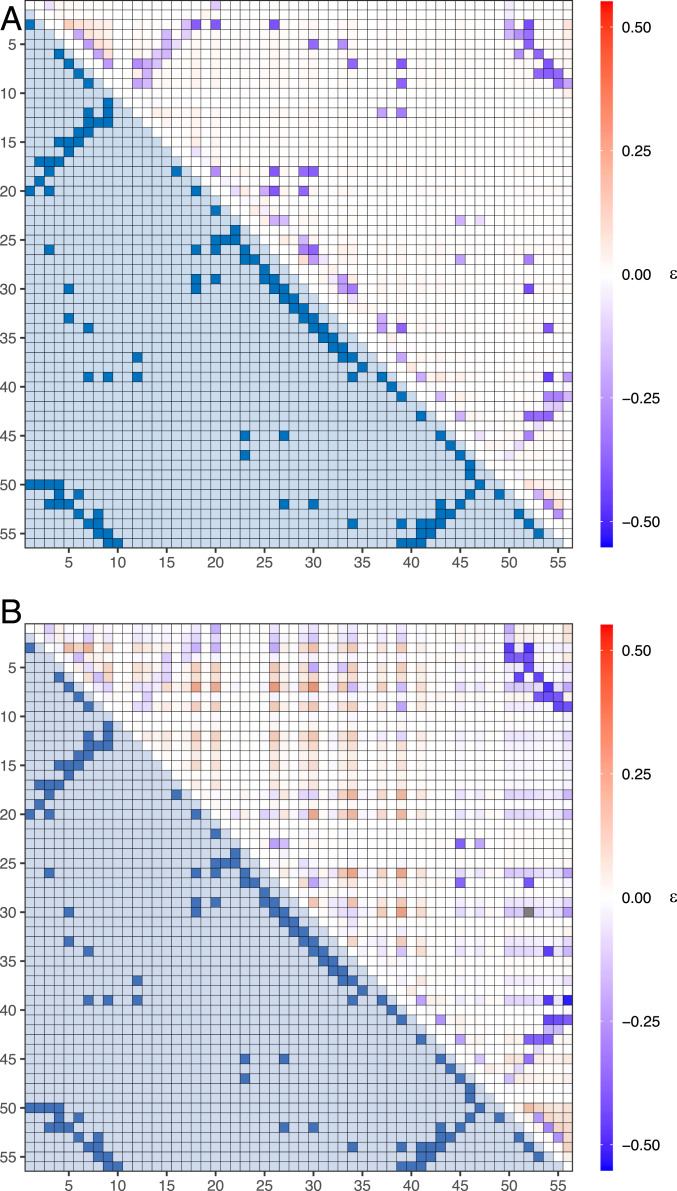
Fig. 8.
The average epistasis between each possible pair of residues for (A) a two-state and (B) a three-state system. The upper triangle of each heat map is the calculated epistasis, and the lower triangle is the contact map for the GB1 protein, where a value of 1 means the residues are in contact in the native state. The epistasis for the two-state system accurately maps out the structure of the GB1 protein, with the majority of native contacts experiencing high magnitudes of negative epistasis. For the three-state system, the native contact map becomes obscured by high levels of positive epistasis at nonnative contacts. These results suggest epistatic measurements work well when reconstructing the native state of two-state systems, but are less successful for multistate systems.
The 3D Structure of Multistate Proteins Cannot Be Predicted Using Epistasis.
Methods for inferring 3D protein structure using measured epistasis rely on the assumption that the largest-magnitude epistasis occurs between native contacts. In the previous section we observed the distribution of epistasis between nonnative contact pairs became broader as the protein became less cooperative. Therefore, it is possible that native structure inference methods using epistasis measurements may not be suitable for proteins with stable intermediate states. To examine this hypothesis, we simulated the evolution of the GB1 domain of streptococcal protein G, (Protein Data Bank [PDB] ID 1PGA) (34) for a cooperative system and a noncooperative system. The cooperative system was composed of the native and the fully unfolded state, where the free energy of the unfolded state ensemble was approximated using a large number of dummy structures generated by a random coil model. The noncooperative system had an additional ensemble of intermediate states in which beta sheets 3 and 4 (residues 40 to 56) were unstructured. The free energy of the intermediate state ensemble was approximated using the same method as for the unfolded state ensemble. The systems were evolved under selection for stability alone, and so the fitness of the protein was determined exclusively by the fraction in the folded state.
We calculated the epistasis in protein stability between all pairs of residues for both the cooperative and noncooperative systems (Fig. 8 A and B, respectively) for 100 sequences over 10 runs and averaged for each pair. For the cooperative system high magnitudes of negative epistasis occurred almost exclusively at native contacts and, when compared with the known GB1 native structure, the epistasis accurately mapped out the structure to a high degree of accuracy. Many of the highly epistatic pairs predicted by the model correspond to the measured highly epistatic pairs used to reconstruct the 3D structure of GB1 by Rollins et al. (16).
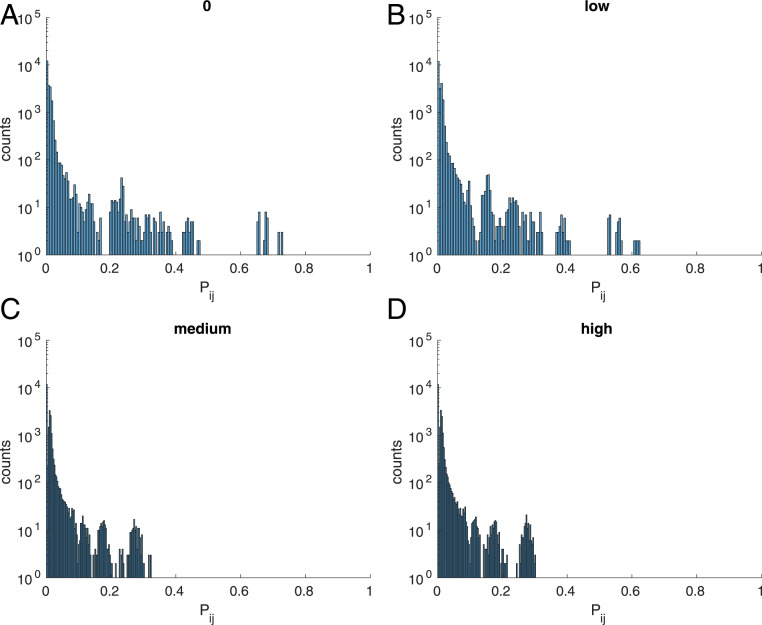
Fig. 6.
Histogram of the distribution of contact probabilities between site and site when evolving proteins under selection for cooperativity, when is set to (A) 0, (B) low, (C) medium, and (D) high.
For the noncooperative system, however, the magnitude of the negative epistasis at the majority of the native contact pairs decreased. Some contacts continued to have large negative epistasis (e.g., 1 to 10, 40 to 56, and 50 to 56), but the overall structure is less evident. Furthermore, more contacts display strong positive epistasis compared to the cooperative system.
Discussion
We observed that selection for cooperativity in protein folding changes the distribution of epistasis in simulated proteins. Proteins with higher cooperativity were associated with more epistasis between native contacts and less epistasis between nonnative contacts compared to less cooperative proteins. Conversely, we observed that selection for epistasis at native contacts results in less cooperativity as selection increases.
This leads us to conclude that selection for cooperativity is not equivalent to selection for epistasis at native contacts and suggests that high levels of epistasis at nonnative contacts are detrimental to cooperative folding and could lead to the aggregation of partially folded states. It is likely therefore that highly cooperative proteins will display epistasis only between native contacts. Because a large number of proteins fold cooperatively, these results provide a possible explanation for experimental observations that have found the majority of epistatic pairs to be native contacts.
We would thus expect that natural proteins with stable intermediates in their unfolding transition would display greater epistasis between nonnative contacts than natural proteins that have two-state transitions. This suggests that the use of epistasis measurements to reconstruct the native state of these noncooperative proteins, under the assumption that epistasis occurs only at native contacts, may be problematic.
We gained further support for this theory by simulating the evolution of the GB1 protein for a cooperative and a noncooperative system. The highest-magnitude negative epistasis in the cooperative system occurred between native contact pairs and the pattern of high-magnitude negative epistasis traced out the native structure well. The inclusion of an intermediate state in the noncooperative system, however, reduced the magnitude of the negative epistasis between those native contacts present in the intermediate state and introduced strong positive epistasis at nonnative contacts.
The intermediate state contains the majority of the native state contacts, as only residues 40 to 56 are unfolded. These native contacts are in contact in 100 of the intermediate dummy structures, and so the probability of them being in contact in the unfolded and intermediate ensemble is high, meaning epistasis in the free energy of this ensemble of states for these native state contacts will be relatively large.
The large epistasis between these native contacts in the free energy of the unfolded and intermediate ensemble acts to partially cancel out the epistasis between these pairs in the native state (), resulting in lower-magnitude epistasis for the native contacts contained in the intermediate state. As a result, it may be more difficult to infer the native state structure.
GB1 is a small protein and so it is unlikely to have intermediate states like the artificial one created for the purposes here. Therefore, it is likely that the structure of smaller proteins will be better inferred using measured epistasis than that of larger proteins that have folding intermediates.
Olson et al. (15) noted, however, that positive epistasis occurred between a cluster of conformationally correlated residues. Otwinowski (35) sought to explain the epistasis observed by Olson et al. (15), using a two- and three-state model of protein–ligand binding, but neither model could explain the presence of the positive epistasis, and they suggested that a model including additional conformational states might capture this epistasis better. Therefore, even small proteins such as GB1 may have additional states or correlation in residue dynamics that might obscure prediction of the native state structure using measurements of epistasis.
Coevolution between both native and nonnative contact pairs may occur in noncooperative proteins. For cooperative proteins, however, we expect that coevolution occurs almost exclusively between pairs that interact in the native structure. It should be noted, however, that while epistasis is a prerequisite to coevolution, strong epistasis can prevent either site involved from changing and so there might be no observable coevolution.
Furthermore, Sailer and Harms (36) investigated the predictability of evolutionary trajectories using a lattice protein model and found the presence of additional conformational ensembles in the model made evolution unpredictable. They observed pairwise epistasis in a two-state model and higher-order epistasis in a three-state model in the evolutionary trajectories of a small 12-amino-acid protein. The pairwise epistasis in the two-state model was due to direct contact between residues, while higher-order epistasis in the three-state model resulted from the redistribution of the relative probabilities of structures in the ensemble. While we did not consider higher-order epistasis in this work, we did observe that the epistasis associated with nonnative contacts was the result of epistasis in the free energies of the nonnative ensembles and that this epistasis was more prevalent in less cooperative proteins. Therefore, it is likely that we would observe prevalent higher-order epistasis in our model under lower selection for cooperativity and little higher-order epistasis under higher selection for cooperativity.
Sailer and Harms (36) also found that a pairwise model was able to perfectly predict evolutionary trajectories for the two-state model but not the three-state model and that predictions could not be improved even when including higher-order epistasis. Therefore, from their observations, we may hypothesize that it may be easier to use sequence data to predict protein structure for proteins that evolved under selection for cooperativity than for those that did not, due to the large number of intermediate ensembles.
Wells (37) remarked that the simple additive behavior between many pairs of mutants is surprising given the highly cooperative nature of protein folding, but provides a few examples to the contrary where epistasis arises between contacting residues. We propose that it is because protein folding is highly cooperative that few residue pairs exhibit epistasis unless they are in contact in the native state.
Materials and Methods
Protein Model.
The free energy of an amino acid sequence , where is the length of the protein, in a specific structure can be calculated using a simple contact potential
| [1] |
where is the contact potential between amino acids and in positions and , respectively, determined by Miyazawa and Jernigan (38), and is equal to one if residues and are in contact and zero otherwise. Two amino acids are considered to be in contact if their atoms ( in the case of glycine) are within of one another.
The free energy of the native state was calculated using the structure of a cysteine-free variant of E. coli RNase H, a 155-residue mixed protein (PDB designation 1F21) (39), using Eq. 1. The unfolded and intermediate states will each be associated with an ensemble of possible structures, and the free energy of each structure can be calculated using Eq. 1. The number of possible structures within each ensemble is incredibly high, and therefore an approximate to the distribution of energies is required. We used a random coil model (40, 41) to produce random structures of sequences 152 amino acids long and obtained thousands of possible structures for each partially folded ensemble, , where denotes the individual intermediate states, and fully unfolded state . For each intermediate or unfolded state, , we used these structures to parameterize a Gaussian distribution with mean and variance , to approximate the degeneracy of states (i.e., the number of states [or structures] within the ensemble that have the same energy). An identical procedure was carried out for the GB1 protein (PDB designation 1PGA) (34) to approximate the free energy associated with the unfolded state ensemble for the two-state model and both the unfolded and intermediate state ensembles in the three-state model.
The partition function of each intermediate or unfolded ensemble is given as
| [2] |
where is the Boltzmann constant, is the temperature in kelvins, and is the total number of possible structures in the partially unfolded state or the unfolded state . For each state was set to equal , where is the number of conformations per residue and is the number of unfolded residues in the state.
The free energy of each intermediate state or the unfolded state can be found using the relation :
| [3] |
We can write the partition function of the system containing both the native state and the ensemble of partially folded and unfolded states as
| [4] |
The stability of the native state is then given by the difference between the native state free energy and the free energy of the intermediate and unfolded ensemble, :
| [5] |
The stability is in the direction of folding, and so the more negative the stability the more stable the protein. The fraction of sequences in the native state at equilibrium, , was computed using
| [6] |
Selection for Cooperative Folding.
The fitness of a sequence was set to equal the fraction of sequences in the native state minus a penalty for noncooperative folding, , which was set to equal the average number of folded residues multiplied by a factor . The fitness of a sequence was therefore calculated as
| [7] |
where the purpose of is to tune the level of cooperativity; i.e., a larger value of would require selection for mutations which destabilize the intermediate states , leading to greater cooperativity in folding.
Selection for Epistasis.
To select for mutations which are highly epistatic among native contacts, the fitness of a sequence was set to equal the fraction folded minus a penalty for sequences with little epistasis between native contacts, :
| [8] |
Here, is the average magnitude of the epistasis, , between each pair of native contacts, . Therefore, the larger the value of is, the lower the fitness penalty. is calculated using Eq. 15.
Quantifying Cooperativity.
Cooperativity in the protein-folding transition is determined experimentally using the van’t Hoff criterion, defined as the ratio of the van’t Hoff enthalpy, , evaluated at , to the calorimetric enthalpy of the entire transition.
The calorimetric enthalpy, , is the enthalpy change during the observed unfolded transition and can be calculated from the area under the heat capacity curve, with a baseline correction (42–44), between the temperature at which the majority if the system is in the native state and the temperature at which the majority of the system is in the unfolded state ,
| [9] |
where is the heat capacity of the system; and are the fraction of the system in the native and the fully unfolded state, respectively; and and are the hypothetical heat capacities of the pure native and pure fully unfolded states, respectively.
The heat capacity was calculated as the differential with respect to temperature of the average enthalpy of the system, . The average enthalpy, , of the system at temperature was calculated as the differential of system partition function (Eq. 4) with respect to temperature, ,
| [10] |
where denoting a sum over all states of the system. The van’t Hoff enthalpy is found from the effective equilibrium constant , which is the ratio of the fraction of the population in the unfolded state, , to the fraction in the remaining states, . The van’t Hoff enthalpy can then be calculated using the van’t Hoff equation:
| [11] |
The van’t Hoff criterion can then be found as
| [12] |
If the value of , then the transition can be considered to be two-state, whereas for multistate processes .
Evolutionary Simulations.
We simulated the evolution of a 155-amino-acid protein, where the initial nucleic acid sequence was constructed by choosing a set of codons at random, and the fitness of the sequence was equal to Eq. 7. Mutations in the nucleic acid would be made following the K80 mutation model with equal nucleotide frequencies and a ratio of transition to transversion probabilities of 2.0, where mutations resulting in stop codons were rejected. When a mutation is introduced, the probability of fixation of this mutation depends upon its impact on protein fitness, where we can calculate the selective advantage of a mutant using
| [13] |
where is the fitness of the premutation wild type and is the fitness of the mutated sequence. The selective advantage can be zero, positive, or negative, indicating the mutation to be synonymous, advantageous, or deleterious.
At each generation we consider all possible mutations to the nucleic acid sequence and calculate the probability of fixation of each mutation using Kimura’s expression for diploid organisms (45),
| [14] |
where is the effective population size which is due to mating behavior and population structure is in general smaller than the true population size and here was set to equal . We then chose a mutation to accept with a probability proportional to the probability of fixation given in Eq. 14.
Quantifying Epistasis.
Epistasis occurs between two mutations when the sum of their independent effects on a trait () is larger or smaller than their combined effect on the trait, . To determine the epistasis between the amino acids at sequence positions and , for a given wild-type sequence with stability , we determine the stability of the structure if we substitute a noninteracting amino acid at residue . Similarly, we substitute a noninteracting amino acid into the wild-type sequence at residue to determine the stability . For the double mutation , we substitute a noninteracting amino acid at both positions and simultaneously. We then calculate epistasis for stability between two sites and within the protein as
| [15] |
where for each pair or single mutation , where is the stability following the mutation(s) . The epistasis between a pair of residues can be either positive or negative. Positive epistasis occurs when the combined impact of two mutations at residues and on protein stability is greater than the sum of their individual impact . Negative epistasis occurs when is less than .
Calculating the Probability That a Pair of Residues i and j Are in Contact in the Ensemble of Partially Folded and Fully Unfolded States.
For any pair of residues i and j, we can calculate the contact probability in the ensemble of partially folded and fully unfolded states as
| [16] |
is the probability of being in intermediate state , is the average probability that residues and are in contact in intermediate state , and is the average probability they are in contact in the unfolded state.
Supplementary Material
Acknowledgments
R.A.G. and R.C.E. are funded by UK Biotechnology and Biological Sciences Research Council Grant BB/P007562/1, and D.D.P. is funded by NIH Grant GM083127.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2010057118/-/DCSupplemental.
Data Availability
All study data are included in this article and/or SI Appendix.
References
- 1.Starr T. N., Thornton J. W., Epistasis in protein evolution. Protein Sci. 25, 1204–1218 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Chou H. H., Chiu H. C., Delaney N. F., Segrè D., Marx C. J., Diminishing returns epistasis among beneficial mutations decelerates adaptation. Science 332, 1190–1192 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Weinreich D. M., Delaney N. F., DePristo M. A., Hartl D. L., Darwinian evolution can follow only very few mutational paths to fitter proteins. Science 312, 111–114 (2006). [DOI] [PubMed] [Google Scholar]
- 4.Salverda M. L. M., et al. , Initial mutations direct alternative pathways of protein evolution. PLoS Genet. 7, e1001321 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Segrè D., DeLuna A., Church G. M., Kishony R., Modular epistasis in yeast metabolism. Nat. Genet. 37, 77 (2004). [DOI] [PubMed] [Google Scholar]
- 6.Gong L. I., Suchard M. A., Bloom J. D., Stability-mediated epistasis constrains the evolution of an influenza protein. eLife 2, e00631 (2013).23682315 [Google Scholar]
- 7.Kryazhimskiy S., Dushoff J., Bazykin G. A., Plotkin J. B., Prevalence of epistasis in the evolution of influenza A surface proteins. PLoS Genet. 7, e1001301 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Khan A. I., Dinh D. M., Schneider D., Lenski R. E., Cooper T. F., Negative epistasis between beneficial mutations in an evolving bacterial population. Science 332, 1193–1196 (2011). [DOI] [PubMed] [Google Scholar]
- 9.Sanjuán R., Cuevas J. M., Moya A., Elena S. F., Epistasis and the adaptability of an RNA virus. Genetics 170, 1001–1008 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wang X., Minasov G., Shoichet B. K., Evolution of an antibiotic resistance enzyme constrained by stability and activity trade-offs. J. Mol. Biol. 320, 85–95 (2002). [DOI] [PubMed] [Google Scholar]
- 11.Miton C. M., Tokuriki N., How mutational epistasis impairs predictability in protein evolution and design. Protein Sci. 25, 1260–1272 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pollock D. D., Thiltgen G., Goldstein R. A., Amino acid coevolution induces an evolutionary Stokes shift. Proc. Natl. Acad. Sci. U.S.A. 109, E1352–E1359 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Weinreich D. M., Watson R. A., Chao L., Harrison R., Perspective: Sign epistasis and genetic constraint on evolutionary trajectories. Evolution 59, 1165–1174 (2005). [PubMed] [Google Scholar]
- 14.Breen M. S., Kemena C., Vlasov P. K., Notredame C., Kondrashov F. A., Epistasis as the primary factor in molecular evolution. Nature 490, 535 (2012). [DOI] [PubMed] [Google Scholar]
- 15.Olson C., Wu N., Sun R., A comprehensive biophysical description of pairwise epistasis throughout an entire protein domain. Curr. Biol. 24, 2643–2651 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rollins N. J., et al. , 3D protein structure from genetic epistasis experiments. Nat. Genet. 51, 1170–1176 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Watters A. L., et al. , The highly cooperative folding of small naturally occurring proteins is likely the result of natural selection. Cell 128, 613–624 (2007). [DOI] [PubMed] [Google Scholar]
- 18.Dobson C. M., The structural basis of protein folding and its links with human disease. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 356, 133–145 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dobson C. M., Protein folding and misfolding. Nature 426, 884 (2003). [DOI] [PubMed] [Google Scholar]
- 20.Thomas P. J., Qu B. H., Pedersen P. L., Defective protein folding as a basis of human disease. Trends Biochem. Sci. 20, 456–459 (1995). [DOI] [PubMed] [Google Scholar]
- 21.Jackson S., Folding of chymotrypsin inhibitor 2. 1. Evidence for a two-state transition. Biochemistry 30, 10428–10435 (1991). [DOI] [PubMed] [Google Scholar]
- 22.Zwanzig R., Two-state models of protein folding kinetics. Proc. Natl. Acad. Sci. U.S.A. 94, 148–150 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Mallik S., Akashi H., Kundu S., Assembly constraints drive co-evolution among ribosomal constituents. Nucleic Acids Res. 43, 5352–5363 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yadahalli S., Gosavi S., Designing cooperatively into the designed protein Top7. Proteins 82, 364–374 (2014). [DOI] [PubMed] [Google Scholar]
- 25.Pollock D. D., Pollard S. T., Shortt J. A., Goldstein R. A., “Mechanistic models of protein evolution” in Evolutionary Biology: Self/Nonself Evolution, Species and Complex Traits Evolution, Methods and Concepts,” P. Pontarotti, Ed. (Springer International Publishing, Cham, Switzerland), pp. 277–296 (2017). [Google Scholar]
- 26.Hu W., et al. , Stepwise protein folding at near amino acid resolution by hydrogen exchange and mass spectrometry. Proc. Natl. Acad. Sci. U.S.A. 110, 7684–7689 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chan H., Bromberg S., Dill K., Models of cooperativity in protein folding. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 348, 61–70 (1995). [DOI] [PubMed] [Google Scholar]
- 28.Tsong T. Y., Baldwin R. L., McPhie P., Elson E. L., A sequential model of nucleation-dependent protein folding: Kinetic studies of ribonuclease A. J. Mol. Biol. 63, 453–469 (1972). [DOI] [PubMed] [Google Scholar]
- 29.Savo L., Physiochemical Aspects of Protein Denaturation (John Wiley & Sons, 1979). [Google Scholar]
- 30.Privalo P., Stability of proteins: Small globular proteins. Adv. Protein Chem. 33, 167–241 (1979). [DOI] [PubMed] [Google Scholar]
- 31.Saboury A., Moosavi Movahedi A., Clarification of calorimetric and van’t Hoff enthalpies for evaluation of protein transition states. Biochem. Mol. Biol. Educ. 22, 210–211 (1994). [Google Scholar]
- 32.Privalo P., Stability of proteins: Proteins which do not present a single cooperative system. Adv. Protein Chem. 35, 1–104 (1982). [PubMed] [Google Scholar]
- 33.Chan H., Modelling protein density of states: Additive hydrophobic effects are insufficient for calorimetric two-state cooperativity. Proteins 40, 543–571 (2000). [DOI] [PubMed] [Google Scholar]
- 34.Gallagher T., Alexander P., Bryan P., Gilliland G.L., Two crystal structures of the B1 immunoglobulin-binding domain of streptococcal protein G and comparison with NMR. Biochemistry 33, 4271–4729 (1994). [PubMed] [Google Scholar]
- 35.Otwinowski J., Biophysical inference of epistasis and the effects of mutations on protein stability and function. Mol. Biol. Evol. 35, 2345–2354 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sailer Z., Harms M., Molecular ensembles make evolution unpredictable. Proc. Natl. Acad. Sci. U.S.A. 114, 11938–11943 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Wells J. A., Additivity of mutational effects in proteins. Biochemistry 29, 8509–8517 (1990). [DOI] [PubMed] [Google Scholar]
- 38.Miyazawa S., Jernigan R., An empirical energy potential with a reference state for protein fold and sequence recognition. Proteins 36, 357–369 (1999). [PubMed] [Google Scholar]
- 39.Goedken E. R., Keck J. L., Berger J. M., Marqusee S., Divalent metal cofactor binding in the kinetic folding trajectory of Escherichia coli ribonuclease HI, Protein Sci. 9, 1914–1921, (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Flory P. J., Principles of Polymer Chemistry (Cornell University Press, 1953). [Google Scholar]
- 41.Flory P. J., Statistical Mechanics of Chain Molecules (Hanser Gardner Publications, 1989). [Google Scholar]
- 42.Zhou Y., Hall C., Karplus M., The calorimetric criterion for a two state process revisited. Protein Sci. 8, 1064–1074 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Takahashi K., Sturtevant J., Thermal denaturation of streptomyces subtilisin inhibitor, subtilisin BPN’, and the inhibitor-subtilisin complex. Biochemistry 20, 6185–6109 (1981). [DOI] [PubMed] [Google Scholar]
- 44.Sturtevant J., Biochemical applications of differential scanning calorimetry. Annu. Rev. Phys. Chem. 38, 463–488 (1987). [Google Scholar]
- 45.Kimura M., On the probability of fixation of mutant genes in a population, Genetics 47, 713–719 (1962). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in this article and/or SI Appendix.