Tree-structured Subgroup Analysis of Receiver Operating Characteristic Curves for Diagnostic Tests

Abstract

Rationale and Objectives

Multiple diagnostic tests are often available for a disease. Their diagnostic accuracy may depend on the characteristics of testing subjects. This paper proposed a new tree-structured data-mining method that identifies subgroups and their corresponding diagnostic tests to achieve the maximum area under the receiver operating characteristic curves (AUC).

Materials and Methods

The Osteoporosis and Ultrasound Study (OPUS) is a prospectively designed population-based European multicenter observational study to evaluate state-of-the-art diagnostic methods for assessing osteoporosis. A total 2837 female participants had dual X-ray absorptiometry (DXA) and quantitative ultrasound (QUS) measured. Prevalent vertebral fractures were determined by a centralized radiology laboratory based on radiographs. Our data mining algorithm includes three steps: defining the criteria for node splitting and selection of the best diagnostic test based on AUC; using a random-forest to estimate the probability of DXA being the preferred diagnosis for each participant; and building a single regression tree to describe subgroups for whom either DXA or QUS is more accurate test or for whom the two tests are equivalent.

Results

For participants with weight equal or below 54.5kg, QUS had higher AUC in identifying prevalent vertebral fracture. For participants whose weight is above 58.5kg but height equal or below 167.5cm, DXA scan was better; and for the remaining participants, DXA and QUS had comparable accuracy and could be used interchangeably.

Conclusion

The proposed tree-structured subgroup analysis successfully defines subgroups and their best diagnostic tests. The method can be used to develop optimal diagnostic strategies in personalized medicine.

Introduction

Multiple diagnostic tests are commonly available for the same disease. Their diagnostic accuracy may depend on the characteristics of the testing subjects. For example, bone mineral density (BMD) measured by dual X-ray absorptiometry (DXA) scanners and speed of sound (SOS) by quantitative ultrasound (QUS) devices are continuous diagnostic markers for osteoporosis. Compared to DXA, QUS has the advantages of low cost, portability and absence of radiation exposure but it may be less accurate. A recent prospective multicenter epidemiological study (Schott et al., 2004) [1] pointed that age may influence the choice of quantitative bone assessment techniques in elderly women. In the era of personalized medicine, proper methods are needed to find subgroups with their corresponding optimal diagnostic strategy.

The area under a receiver operating characteristic (ROC) curve (AUC) is a measure of diagnostic accuracy (Metz 1978; Samuelson et al. 2011)[2,3]. A higher AUC reflects higher diagnostic accuracy. Differences between AUCs not only depend on the tests themselves but also the population tested. Recent regression approach of ROC analysis (Pepe 1998)[4] detects the interactions between the diagnostic performance and covariates and assess diagnostic utility after adjusting for covariate effects. Because of possible complex interactions, in particular when the number of covariates is large, modeling based on regression approaches may be difficult to answer the question who should take what test. Ciampi ea al. (1995) [5] proposed a tree-structured subgroup analysis for survival data based on a Cox model with interaction terms in order to find subgroups of patients for which one treatment is preferable to the other. Negassa et al. (2005) [6] investigated a model selection in tree structured subgroup analysis based on Ciampi et al. (1995)[5]. These tree-based methods demonstrated efficiency to handle large number of covariates and identify operational subgroups of patients.

In this paper, we extend tree-based methods to development of evidence based decision rules to choose the most accurate diagnostic test according to easily collected covariates of a subject and apply this new approach to BMD and QUS in diagnosis of prevalent osteoporotic fractures.

Materials and Methods

Description of the Study Data

The Osteoporosis and Ultrasound Study (OPUS) (Glüer et al. 2004)[7] is a population-based European multicenter prospectively designed observational study to evaluate state-of-the-art diagnostic methods for assessing osteoporosis. Population based random samples were selected from five participating study centers in the United Kingdom, France, and Germany. All investigations were conducted in accordance with the Declaration of Helsinki and were approved by the appropriate institutional human research committee at each participating center. Of 2837 women participating, 463 (16%) were 20–39 years old, and 2374 (84%) were 55–79 years old. Techniques evaluated in this study included spine and hip BMD by dual x-ray absorptiometry (DXA) using bone densitometers manufactured by GE Lunar (Madison, WI, USA) and Hologic (Bedford, MA, USA), broadband ultrasound attenuation (BUA) and speed of sound (SOS) measured by DTU–one (OSI/Osteometer Meditech, Hawthorne, CA, USA) and UBIS 5000 (Diagnostic Medical Systems, Montpellier, France). Baseline x-ray films were taken from all the study participants and used to evaluate prevalent vertebral fractures at a centralized radiology laboratory. Women with 20% or more height reduction from the young population mean height were considered fractured.

In our particular application, the gold standard of clinical event is the prevalent vertebral fracture defined by the baseline radiographs. The diagnostic tests to be compared are the baseline DXA measurement hip BMD (test 1, T₁) and QUS measurement speed of sound (SOS) measured by DTU (test 2, T₂). Of 2322 elderly participants with complete hip BMD and DTU-SOS information, 371 (16%) had prevalent vertebral fractures, whereas 1951 (84%) had no fractures. The characteristic variables for subgroup construction include age, height, weight, body mass index (BMI). Table 1 summarizes the data.

Table 1.

Summary statistics of diagnostic measurements and covariates

	Non-fractured Subjects (n0=1951)	Fractured Subjects (n1=371)
Diagnostic tests	Mean ± SD§	Mean ± SD
Hip BMD (DXA)	878.85 ± 140.03	802.11 ± 149.59
SOS (QUS)	1546.33 ± 10.53	1541.98 ± 10.29
Continuous covariates
age	66.42 ± 6.86	69.18 ± 7.10
Height(cm)	160.64 ± 6.31	159.61 ± 6.30
Weight(kg)	68.71 ± 12.38	67.72 ± 12.41
BMI	26.61 ± 4.51	26.56 ± 4.42

^§SD=Standard Deviation

Description of Recursive Partitioning Tree Algorithm and Random Forest

A recursive partitioning tree algorithm, also known as classification and regression tree (CART) (Breiman et al. 1984)[8], consists of a sequence of splits of a group of subjects into two subgroups according to values of covariates. These splits form branches to generate a tree. Subjects before a split form a parent node. The resulted subgroups are its daughter nodes. Because there are many ways to split a node into two daughter nodes, a utility function needs to be defined for selecting the best split among all the possible binary splits. Typically, subjects in a study are divided randomly into the training and validation data. A tree grows based on the training data such that the utility is homogenous within nodes but maximally different between nodes. The splitting step grows a large tree. Using a cost-complex function of CART (Breiman et al. 1984)[8], a nested sequence of sub-trees

$${Tr}_0\succ {Tr}_1\succ {Tr}_2\succ \cdots \succ {Tr}_1=\mathit{Root}$$ (1)

is identified that represents the optimal choices of trees at different size. Here, Tr₀ is the largest tree, and Tr_l is the smallest tree that has everyone in it. The validation data is used to determine which one of these subtrees has the best utility value in an independently collected data set. The use of validation data is to assure that the final tree does not overly fit the training data because the splitting step is data dependent.

An alternative method to consider sampling variation is the random forest approach (also known as bootstrap aggregating, or bagging) proposed by Breiman (1996)[9]. In this approach, m bootstrap samples are generated from original data as new training sets and m trees are fully grown based on the bootstrap samples. Thus there are m trees generated to form a random forest. Such a forest accounts the effect of sampling variations in tree constructions. As a result, different trees may have different decision rules that choose different diagnostic tests as the best one for the same subject. Note that a random forest is a “committee of experts”. Because trees in the forest have different decision rules, there is not a simple way to explain the underlying rationale driving the combined predictions. Rather, a forest predicts the best decision for each individual.

Description of Subgroup Analysis Algorithm

We used both a classification tree algorithm and a random forest to develop our subgroup analysis algorithm. First we defined the splitting criterion for decision tree growth and selection of the best diagnostic test for the subgroups based on AUCs of ROC curves (Appendix A). Second, we use a random-forest to estimate the probability of DXA being the preferred diagnosis for each participant (Appendix B). To explain the black-box-like relationship between the preference score and predictors, we built a single regression tree as a super-expert to substitute the “expertise” from the forest that achieves the maximum agreement in decision while maintaining a clear explanation of decision rationales. Our last step of a single regression tree described subgroups for whom either DXA or QUS is more accurate test or for whom the two tests are equivalent (Appendix C).

In the AUC-based tree growth procedure, AUCs and their covariance matrix can be estimated parametrically (Metz, 1986; Metz,et al., 1998, ROCFIT)[10,11,12], semiparametrically (Pesce et al. 2011)[13] or non-parametrically (Delong et al. 1982)[14]. In this paper, we developed R programs based on the non-parametric AUC and covariance estimates of [14].

Selection of Non-inferiority Margin

DXA is the most completely developed, reliable and popular bone densitometry technique in use, the “gold standard” and the “reference standard”. Quantitative ultrasonometry of bone is a safe, simple, free of radiation, portable, cost-effective and therefore QUS may be preferred when its performance is comparable. Thus, we may choose QUS if its AUC is non-inferior to that of BMD, i.e, θ̂₁ − θ̂₂ ≤ δ_θ, where δ_θ is a pre-specified positive non-inferiority margin, θ̂₁ and θ̂₂ are estimated AUCs for T₁ and T₂ respectively. If no preference between the two tests is observed, δ_θ can be set as 0. Based on Jin and Lu [15], we selected an inferiority margin of δ = 0.1 after Fisher transformations of AUCs, and the AUC inferiority margin δ_θ is determined by δ and θ₁, the AUC of standard test, ${\delta }_{\theta }={\theta }_1-\frac{1+{\theta }_1-(1-{\theta }_1)e^{\delta }}{1+{\theta }_1+(1-{\theta }_1)e^{\delta }}$.

Results

The overall AUCs for hip BMD and SOS were 0.653 and 0.623 respectively, which difference was greater than δ_θ = 0.029. Thus, DXA was a better test for the entire data set. So for the root node with 1951 (84%) non-fractured and 371 (16%) fractured study participants, the decision d = T₁ and the corresponding AUC was 0.653. The tree growing began with the split of a root node into two daughter nodes. After searching among all covariates and cut-off values, the combination of variable “Weight” and its cut-off value 58.5 kg provided the largest standardized AUC gain and thus it was selected as the best split. According to “Weight ≤ 58.5kg” or “Weight > 58.5kg”, participants in the root node were separated into two daughter nodes with the best test of T₂ (QUS) and T₁ (DXA), respectively. Then the two daughter nodes were split recursively in the same way, and so on. We stopped splitting when the number of fractured or non-fractured in the node was less than 20 or no further improvement by splitting the nodes could be achieved.

We generated a random forest of 100 fully grown decision trees from 100 bootstrap samples. A preference score was obtained for each subject. Taking preference score as the outcome or response variable, and the covariates age, height, weight and BMI as predictors, a usual regression tree was generated by CART to construct subgroups. The fully grown regression tree (Tr₀) for original overall data had 18 terminal nodes. There were 15 nested subtrees {Tr_k, k = 1, ···, 15} from usual cost-complexity pruning step.

Figure 1 displays the correlation coefficients between the preference score v from the random forest with the standardized non-inferiority AUC differences (st), i.e., cor(v, st|Tr_k), and the mean prevalence score v̂, i.e, cor(v, v̂|Tr_k), for the fully grown tree and all 15 nested subtrees (k = 0, 1, ···,15). As it shows, the fully grown regression tree Tr₀ with size 18 had the highest correlation cor (v, v̂|Tr_k) of 0.955, but was not the best tree for cor(v, st|Tr_k), which was 0.684. Instead, the subtree Tr₁₃ with size 4 provided the maximal correlation between preference score and AUC difference (cor(v, st|Tr₁₃) =0.849) and reasonably high correlation between the observed and predicted preference scores (cor (v, v̂|Tr₁₃) = 0.865). So the subtree Tr₁₃ with size 4 was selected as the final tree and displayed by Figure 2.

Figure 1.

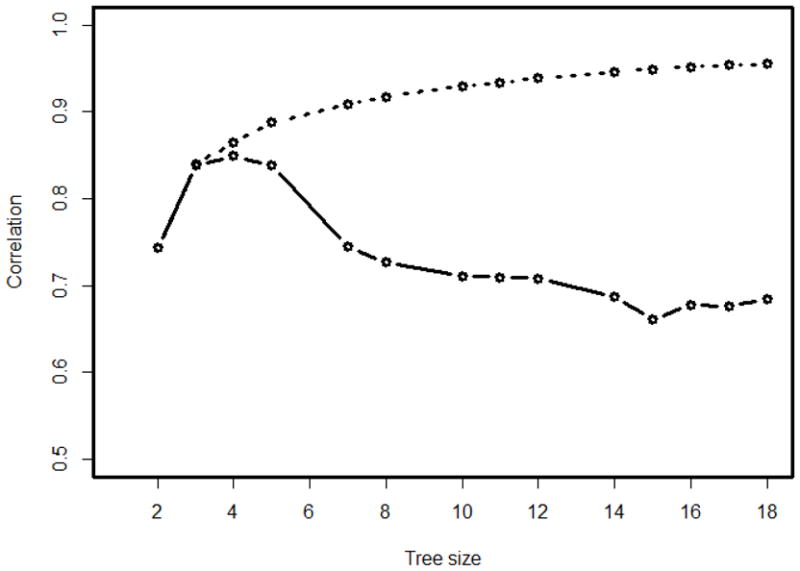
Correlations between the preference score v and the predicted preference score (v̂) (dashed line) or the inferiority statistic st (solid line) for the OPUS data

Figure 2.

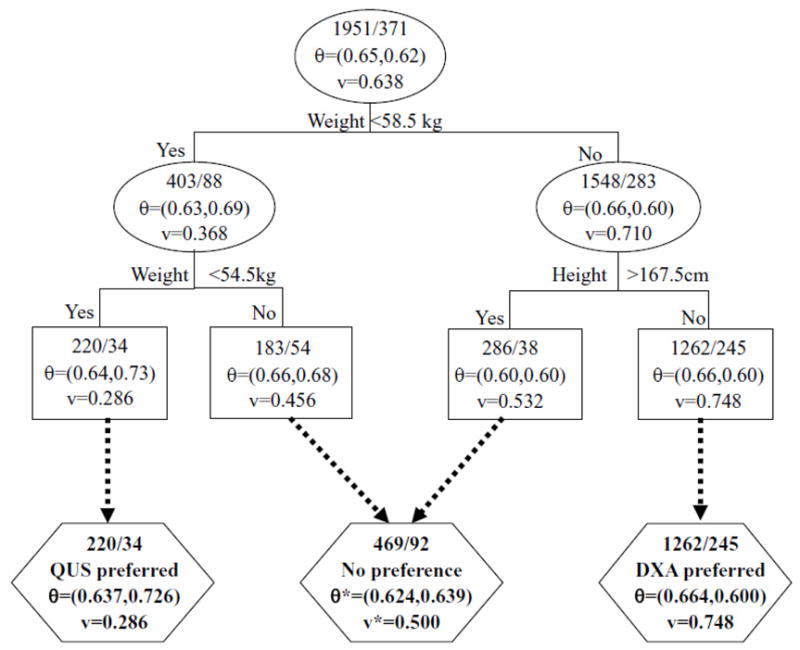
The selected regression tree for preference score prediction

In Figure 2, internal nodes are shown in oval, and the terminal nodes are shown in rectangular. The subgroups formed are shown in hexagon. The top numbers in each node are the number of non-fractured and number of fractured participants. AUC or preference score values shown in subgroups are corresponding weighted values if the subgroup contains 2 or more nodes.

Figure 3 gives the diagnostic accuracy and the preference score level in four terminal nodes of the final tree. Node 1 had 254 (11%) women, of whom 220 (87%) non-fractured and 34 (13%) fractured, with a preference score level 0.286 and an AUC difference −0.089 (Standard Error (SE)=0.057). So participants belonging to this node were better to undergo QUS examinations. Node 4 had 1507 (65%) women, of whom 1262 (84%) non-fractured and 245 (16%) fractured, with a preference score 0.748 and an AUC difference 0.064 (SE=0.021), and therefore participants belonging to this group were better to undergo DXA examinations. The remaining 2 nodes had 561 (24%) women in total, of whom 469 (84%) non-fractured and 92 (16%) fractured, with preference scores 0.456 and 0.532, respectively for nodes 2 and 3. Their AUC differences were −0.022 (SE=0.042) and −0.008(SE=0.043), respectively. Therefore these nodes were combined as one decision group without any preference to either DXA or QUS, with combined AUC difference of −0.015 (SE=0.030).

Figure 3.

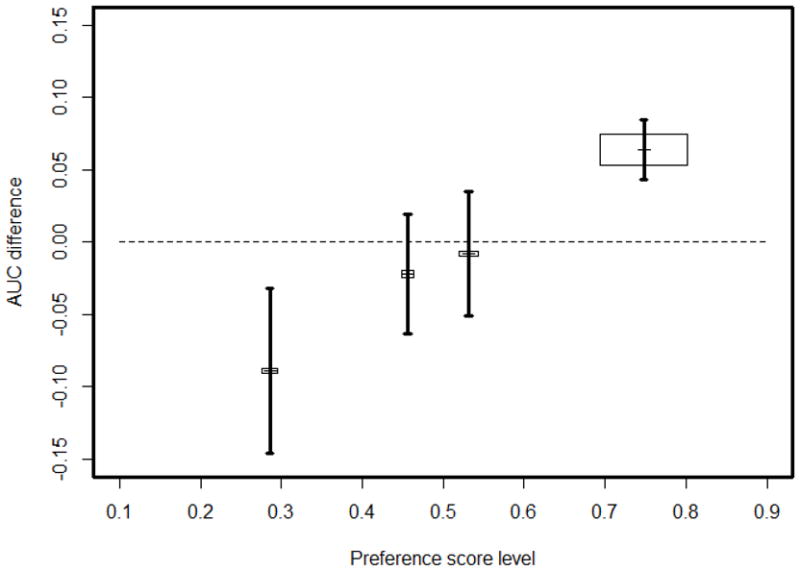
The AUC differences, standard error (SE) and predicted preference score in 4 terminal nodes of the final tree. The center coordinates of the box for node h are (v̂,Δθ̂) in h, the height and width are proportional to n₀ (h) and n₁ (h), the area of the box is weight in weighted stratified AUC calculation; the vertical line cross the box is the interval (Δθ̂ − SE, Δθ̂ +SE).

As a consequence of the aforementioned findings, we proposed a decision rule as follows: for women with weight equal or below 54.5kg SOS by QUS is more accurate; for women whose weight is above 58.5kg but height at most 167.5cm, BMD assessment by DXA has a better accuracy; and the remaining women can take either of the examination since they have comparable accuracy.

Table 2 summaries the information of 4 terminal nodes and combined decision groups. For the QUS preferred subgroup, the AUCs of DXA and QUS were 0.637 and 0.726, respectively, with a non-inferiority test statistic st= −2.037 and a p value of 0.021 to reject H₀: Δλ ≥ δ. For the DXA preferred subgroup, the AUCs of DXA and QUS were 0.664 and 0.600, respectively. The test statistic st was 1.699 and, thus, rejected H₀: Δλ ≤ δ with at p value of 0.045. For the combined no preference subgroup, the weighted AUCs of DXA and QUS were 0.624 and 0.639, respectively, and an insignificant test statistic st = −1.484.

Table 2.

Summary statistics of the terminal nodes, decision groups and combinations in the final tree

Node h	Node information	Sample size nh =(nh0, nh1)	Preference score† v̂ ± SE‡	AUCs‡ (θ̂ = (θ̂1, θ̂2)	AUC difference Δ θ̂ ± SE	st
QUS preferred subgroup (node 1)		(220, 34)	0.286 ± 0.006	(0.637, 0.726)	−0.089 ± 0.057	−2.037
1	Weight<54.5	(220, 34)	0.286 ±0.006	(0.637, 0.726)	−0.089 ± 0.057	−2.037
No preference subgroup (nodes 2~3 combined)		(469, 92)	0.500 ± 0.003	(0.624, 0.639)	−0.015 ± 0.030	−1.484
2	54.5≤Weight<58.5	(183, 54)	0.456 ± 0.007	(0.656, 0.678)	−0.022 ± 0.042	−1.195
3	Weight≥58.5, Height≥167.5	(286, 38)	0.532 ± 0.005	(0.595, 0.603)	−0.008 ± 0.043	−0.924
DXA preferred subgroup (node 4)		(1262, 245)	0.748 ±0.002	(0.664, 0.600)	0.064 ± 0.021	1.699
4	Weight≥58.5, Height<167.5	(1262, 245)	0.748 ± 0.002	(0.664, 0.600)	0.064 ± 0.021	1.699
Total (nodes 1~4 combined)		(1951, 371)	0.484 ±0.004	(0.653, 0.623)	0.030 ± 0.016	0.013

^†When 2 or more nodes are combined, the weighted AUC or preference score are reported in the table.

^‡SE=Standard Error.

Figure 4 graphically illustrates the decisions by plotting the weighted ROC curves for decision subgroups. We can see that the ROC curve for DXA was always higher than that for QUS within the DXA preferred subgroup, especially in reasonably high specificity in (50%, 100%). However, within the QUS preferred subgroup, two ROC curves were mixed together for specificity within 90% to 100% and then the QUS ROC curve showed a higher sensitivity then that for DXA for specificities ranging between 0% to 90%. Within the no preference subgroup, the empirical weighted ROC curves were mixed together.

Figure 4.

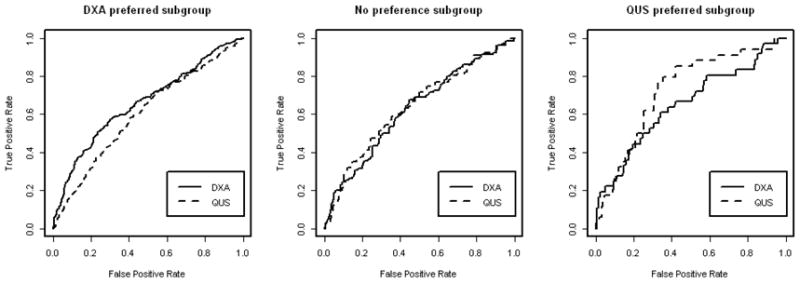
Weighted ROC curves for three decision subgroups.

In addition, we use data from the Study of Osteoporotic Fractures (SOF, http://sof.ucsf.edu/Interface/) [16,17] to cross-validate our results. SOF is a multicenter observational study of 10,000 elderly white women in US. At SOF Visit 4, the surviving white women aged 69 years or older total hip BMD by DXA scanners and SOS by QUS were measured. Instead of prevalent vertebral fracture, we compared the two tests for their ability to predict hip fracture in the subsequent 5 year follow-up. The overall dataset contains 246 (5%) woman who had hip fracture and 4917 (95%) women who didn’t. The AUCs for BMD and SOS were 0.748 and 0.638, respectively, with the difference 0.110 (SE=0.018) for the complete data set. The QUS preferred subgroup defined by OPUS had 714 (92%) non-fractured and 66 (8%) fractured participants with AUC 0.741 and 0.700, respectively, for DXA and QUS. The AUC difference was 0.041 (SE=0.032), much lower than that of the complete data set. The DXA preferred subgroup had 3277 (96%) non-fractured and 138 (4%) fractured participants with AUC 0.740 and 0.588, respectively, for DXA and QUS. The difference was 0.152 (SE=0.026), much higher than the overall difference. The no-preference subgroup had 887 (96%) non-fractured and 40 (4%) fractured participants with AUCs of 0.707 and 0.624, respectively, for DXA and QUS. The difference was 0.082 (SE=0.048), a little bit lower than the overall difference. This suggests that our decision rule works in consistent directions in a very different population for a completely different endpoint.

Discussion

A tree method can show complex interactions of covariates that may be difficult or impossible to discover using traditional regression techniques. In addition, no assumptions are made regarding the underlying distribution of variables and linearity relationship. Borrowing the idea “the split provides a gain in invariability or purity” from CART, we have developed an AUC gain function as our splitting criterion.

Because tree based algorithm perform exhaustive search to develop the model, it depends on the selected training samples. To account for the impact of sample variation, we use a random-forest to account for sampling variations in tree constructions. The preference score from the generated votes gives an empirical estimate of the probability that the DXA method is the preferred diagnosis for each subject.

One important note is that our method separates study participants according to their best diagnostic strategies not their risk of fractures. The QUS preferred subgroup (11% of study participants), no preference subgroup (24%) and DXA preferred subgroup (65%) had fracture risk of 13%, 16%, and 16% respectively, with a p-value of 0.4884. This is different from most of the tree algorithm with the goal to find subgroups with different risks or disease severities (Lu et al. 2003; Jin et al. 2004; Jin et al. 2004)[18,19,20] and other machine learning or decision algorithm in previous radiology literature for construction of the optimal diagnosis (Liu et al. 2011; Paquerault et al. 2010)[21,22].

The proposed tree-structured subgroup analysis successfully defines subgroups of participants with different preferred diagnostic tests. Our findings are in agreement with several other studies [23, 24] that suggest body weight have a significant effect on QUS measurements. Body weight modifies the relationships between QUS and DXA measurements of the hip and calcaneus. Higher weight may influence bone and soft tissue properties and this may have a greater effect on SOS. Accuracy as well as precision of QUS measurements is decreased by anatomically inconsistent placement and by variability in bone width, soft tissue thickness and marrow composition of the measurement region (Glüer 1997) [25]. In addition, DXA is a two-dimensional measurement technique to evaluate a three-dimensional structure that is affected by soft tissue composition. QUS is also a two-dimensional technique but the impact of body composition is different, for technical reasons and because one is measuring a different site. Thus differences in performance between the techniques depending on body composition are plausible and in agreement with observations in clinical practice.

However, the decision rule and exact cutoff points to decide individualized optimal diagnostic test were empirically developed based on our algorithm and the OPUS data. From a physics point of view body weight or height will influence QUS and DXA results in different ways, providing room for optimized selection criteria. However, the specific cutoff-values derived have not yet been validated either through clinical practice or studies. In this paper, we performed an ad hoc examination based on a different dataset and a different endpoint. The resulted AUC differences between decision groups were consistent with the directions proposed in the paper, supporting likely external validity of our findings. The most rigorous validation of our decision model would be a prospectively designed and well controlled imaging diagnostic trial, which should be performed in future follow-up research.

The method described here can be used to develop optimal diagnostic strategy in personalized medicine for other similar clinical problems. Although we only considered two tests in our application, our method also works for multiple diagnostic tests by comparing the AUCs across multiple tests to select the best splits and diagnostic tests. If the performance restricted in a high specificity range is of interests, the partial AUC can be used to develop utility functions in our subgroup analysis algorithm.

Appendix A: Criterion for Splitting and Diagnostic Test Selection

Let n₀ be the number of non-diseased and n₁ be the diseased subjects in training data with data form $\left(Y_i^{(1)},Y_i^{(2)},D_i,Z_i\right)$, i =1, 2, …, n. Here the subscript i indicates the ith subject; $Y_i^{(1)}$ and $Y_i^{(2)}$ are her test results of Test 1 and Test 2; D_i is the disease status with 1 for diseased and 0 otherwise; Z_i = (Z_1i, Z_2i,· · ·, Z_pi) is a vector of p covariates; and n = n₀ + n₁. The covariates can be continuous, ordinal or nominal, and may have missing values for some subjects. The overall AUCs can be estimated parametrically (Metz, 1986; Metz,et al., 1998)[10,11] or non-parametrically (Delong, Delong and Clark-Pearson, 1982)[12] for T₁ and T₂, denoted as θ̂_k for k=1, 2.

For each node, there are two decision options to choose: either to use T₁ (BMD) if T₂ (SOS) is inferior to T₁, i.e., θ̂₁ − θ̂₂ > δ_θ, or to use T₂ (SOS) if it is non-inferior to T₁ (BMD). i.e., θ̂₁ − θ̂₂ ≤ δ_θ, where δ_θ is a pre-specified positive non-inferiority margin. So the decision made at node h is

$$d(h)=T_{1}I({\widehat{\theta }}_1-{\widehat{\theta }}_2>{\delta }_{\theta })+T_{2}I({\widehat{\theta }}_1-{\widehat{\theta }}_2\le {\delta }_{\theta }),$$ (A1)

where I(E) is the binary indication function of the event E.

In a splitting step, subjects in a node are separated into two daughter nodes according to either “≤” or “>” of a potential cutoff value for a continuous or ordinal covariate, or according to whether they are “in” or “out” of an observed category for a nominal variable. We first consider a possible splitting s for node h. Node h contains a subsample with n(h) subjects. For a split s, the data at node h are divided into left (“L”) and right (“R”) daughter nodes $h_s^{(L)}$ and $h_s^{(R)}$, with $n(h_s^{(L)})=n_0(h_s^{(L)})+n_1(h_s^{(L)})$ and $n(h_s^{(R)})=n_0(h_s^{(R)})+n_1(h_s^{(R)})$ subjects respectively. We can calculate AUCs for these daughter nodes based on different tests, denoted as ${\widehat{\theta }}_k(h_s^{(L)})$ and ${\widehat{\theta }}_k(h_s^{(R)})$ in $h_s^{(L)}$ and $h_s^{(R)}$ for test k (k=1, 2), respectively. We define an AUC gain due to splitting as

$$\begin{array}{l}g(s,h\mid {\delta }_{\theta })=w(h_s^{(L)})[{\widehat{\theta }}_{d(h_s^{(L)})}(h_s^{(L)})-{\widehat{\theta }}_{d(h)}(h_s^{(L)})]+w(h_s^{(R)})[{\widehat{\theta }}_{d(h_s^{(R)})}(h_s^{(R)})-{\widehat{\theta }}_{d(h)}(h_s^{(R)})]\\ +w(h_s^{(L)})[I(d(h_s^{(L)})=T_2)-I(d(h)=T_2)]{\delta }_{\theta }+w(h_s^{(R)})[I(d(h_s^{(R)})=T_2)-I(d(h)=T_2)]{\delta }_{\theta },\end{array}$$ (A2)

where $w(h_s^{(L)})$ and $w(h_s^{(R)})$ are weights on daughter nodes $h_s^{(L)}$ and $h_s^{(R)}$ is given by

$$w(h_s^{(L)})=\frac{n_0(h_s^{(L)})n_1(h_s^{(L)})}{n_0(h_s^{(L)})n_1(h_s^{(L)})+n_0(h_s^{(R)})n_1(h_s^{(R)})}\text{and}w(h_s^{(R)})=\frac{n_0(h_s^{(R)})n_1(h_s^{(R)})}{n_0(h_s^{(L)})n_1(h_s^{(L)})+n_0(h_s^{(R)})n_1(h_s^{(R)})}.$$

It is easy to see by its definition that g (s, h |δ_θ) ≥ 0 and g (s, h |δ_θ) = 0 if and only if d(h) = d(h^(L)) = d(h^(R)).

The optimal split s_h is selected from all possible splits at node h such that it maximizes the standardized AUC gain

$$s_h=\underset{s}{argmax}\{\frac{g(s,h\mid {\delta }_{\theta })}{\sqrt{\text{v}\widehat{\text{a}}\text{r}(g(s,h\mid {\delta }_{\theta })}}\mid g(s,h\mid {\delta }_{\theta })>0\}$$ (A3)

vâr(g(s, h|δ_θ) can be derived by the covariance matrix of AUC estimators from ROCFIT [12] for binormal models or Delong’s non-parametric estimates [14].

Appendix B: Construction of the Random Forest

The tree growing begins with the split of a root node into two daughter nodes. Then the two daughter nodes are split recursively in the same way, and so on. We’ll stop splitting the node when the case or control size in the node is small (less than a pre-specified number, e.g. 20) or the gain function is zero for all splits.

Using the criterion of diagnostic test selection in Equation (A1) and the criterion for splitting in Equation (A3), we can generate a large tree for which the terminal nodes form patient subgroups with their best diagnostic test determined by Equation (A1). Using a random forest approach, we generate m trees. For a subject i, different trees may assign different optimal diagnostic tests. Let V_i trees vote T₁ as the best diagnostic test 0 ≤ V_i ≤ m), the proportion v_i = V_i/m is the preference score that measures the subject i’s preference of T₁ over T₂.

The simplest way to determine the best diagnostic test for an individual is based on v_i. If v_i >0.5, then T₁ is the preferred diagnostic test. If v_i = 0.5, two tests are exchangeable. Otherwise, T₂ is preferable. However, this approach doesn’t reveal why and when T₁ is a better choice than T₂ nor when the difference is strong enough to warrant avoiding the unfavorable test.

Appendix C: Construction of Final Regression Decision Tree

To answer the above questions and reveal the decision rationale, we further perform a regression tree analysis of the preference score v. Using the standard CART algorithm, we can derive the nested sequence of optimal trees as specified in Equation (1). Because the preference score v is generated by the random forest algorithm and represents the best individual choices, we want to select a final tree in the sequence whose terminal nodes recommend diagnostic tests in a high agreement with those by v‘s. In addition, we want the tree terminal nodes be stable enough so that the AUC differences between the recommended and alternative diagnostic tests in its terminal nodes also have the highest correlation with v.

We use the statistic $st=({\widehat{\lambda }}_1-{\widehat{\lambda }}_2-\delta )/\sqrt{\text{v}\widehat{\text{a}}\text{r}({\widehat{\lambda }}_1-{\widehat{\lambda }}_2)}$ (Jin and Lu, 2008)[15] to measure AUC improvement in each terminal node. All subjects in a terminal node will use the st value of the terminal as individual measure of AUC differences. Here λ̂_k = ln[(1 + θ̂_k)/(1 − θ̂_k)] for k=1, 2, the variance of λ̂₁ − λ̂₂ is estimated from the covariance matrix of (θ̂₁, θ̂₂) by the delta method, and δ is an inferiority margin after Fisher transformation. The Fisher transformation of AUC improves the normality overall and, in particular, when the AUC is close to 1.

For each terminal node in a given subtree Tr_k, we can get the preference score v and the non-inferiority statistic st value for individual subjects. We select the optimal subtree that maximizes {cor(v, st|Tr_k), k 0,1, 2, · · ·, l}, the correlations of preference score and st. The regression tree can then replace the “committee of experts” by a super-expert if it preserves the agreement cor (v, st) well.

The terminal nodes with a significantly higher preference score can be combined to the “test 1 preferred subgroup.” Those with a significantly lower preference score level can be combined to the “test 2 preferred subgroup.” Those with preference scores levels around 0.5 can be combined to the “no preference group”. We use weighted measurements ${\widehat{\theta }}_1^{\ast },{\widehat{\theta }}_2^{\ast },{\mathit{ROC}}_1^{\ast },{\mathit{ROC}}_2^{\ast }$, and v̂^* to summarize and compare the diagnostic accuracies of the tests for the subgroup formed with J terminal nodes h₁, h₂, ··· h_j, with the weights $w_j(h_j)=\frac{n_0(h_j)n_1(h_j)}{{\displaystyle \sum _{j=1}^J}{n}_0(h_j)n_1(h_j)}$.