Memory is key in capturing COVID-19 epidemiological dynamics

Abstract

SARS-CoV-2 virus has spread over the world rapidly creating one of the largest pandemics ever. The absence of immunity, presymptomatic transmission, and the relatively high level of virulence of the COVID-19 infection led to a massive flow of patients in intensive care units (ICU). This unprecedented situation calls for rapid and accurate mathematical models to best inform public health policies.

We develop an original parsimonious discrete-time model that accounts for the effect of the age of infection on the natural history of the disease. Analysing the ongoing COVID-19 in France as a test case, through the publicly available time series of nationwide hospital mortality and ICU activity, we estimate the value of the key epidemiological parameters and the impact of lock-down implementation delay.

This work shows that including memory-effects in the modelling of COVID-19 spreading greatly improves the accuracy of the fit to the epidemiological data. We estimate that the epidemic wave in France started on Jan 20 [Jan 12, Jan 28] (95% likelihood interval) with a reproduction number initially equal to 2.99 [2.59, 3.39], which was reduced by the national lock-down started on Mar 17 to 24 [21, 27] of its value. We also estimate that the implementation of the latter a week earlier or later would have lead to a difference of about respectively $-$13k and $+$50k hospital deaths by the end of lock-down.

The present parsimonious discrete-time framework constitutes a useful tool for now- and forecasting simultaneously community incidence and ICU capacity strain.

1. Introduction

In Dec 2019, an increasing number of ‘pneumonia of unknown etiology’ cases were reported in Wuhan, China (Li et al., 2020a). The causal agent was rapidly identified as a new coronavirus named SARS-Cov-2 (Coronaviridae Study Group of the ICTV, 2020). Because of its relatively large basic reproduction number (${\mathcal{R}}_0\approx 2.2$ in the Wuhan outbreak (Li et al., 2020a)) and the high proportion of undetected cases (Nishiura et al., 2020, Li et al., 2020b, He et al., 2020), the virus rapidly spread in mainland China and then all over the world. The sizeable virulence of the so-called COVID-19 infection – the fatality ratio of which was estimated to approx. 1% in China (Verity et al., 2020) – and the important proportion of severe cases requiring hospitalisation rapidly made it the primary health concern worldwide.

The COVID-19 pandemic provides an opportunity to develop adequate tools for the short-term forecasting and potential management of this and future epidemics. In the absence of any prophylactic or curative pharmaceutical solution, the nations and their healthcare systems face two major challenges. The first one is blocking the transmission chains in the community with measures such as social distancing, school closure, mask-wearing, tracking and quarantine, along with massive testing (Flaxman et al., 2020). The second one is caring for the hospitalised patients with severe complications, especially within intensive care units (ICU) (Bouadma et al., 2020).

At the early stage of the epidemic, and until a very restrictive non-pharmaceutical intervention (NPI) such as national lock-down is implemented, the incidence is growing exponentially. Consequently, both the means of prevention (mask stocks, PCR reagents, tracking logistics) and the ICU bed capacity can be rapidly overloaded, exposing health systems to a major crisis. The optimal allocation of these limited resources over time is therefore crucial (Halpern, 2011, Djidjou-Demasse et al., 2020) and require models to predict short-term dynamics as accurately as possible (Weissman et al., 2020).

The vast majority of epidemiological models relies on ordinary differential equations (ODEs) (Keeling and Rohani, 2008). Although these models have useful analytical properties when analysed over a long time period, they perform poorly on short time scales. One reason for this is that they are essentially Markovian, i.e. ‘memoryless’. This means for instance that an individual that has been infected for 10 days has the same probability to clear the infection as e.g. an individual infected less than a day ago.

In this work, we develop an original discrete-time method that combines the advantages of individual-based approaches and the law of large numbers, to best analyse ICU activity and hospital mortality time series, both being particularly informative because of their high and homogeneous sampling rate (i.e. few cases are missed). This is done by introducing a parsimonious model supported by an original statistical treatment that best reproduces chronologically the natural history of disease. Using the French epidemics as a test case we show that, contrary to its memory-less counterpart, the model can very accurately capture the ICU admission, occupancy, and mortality peaks. It can thus be used to forecast epidemics and evaluate potential disease control implementations.

2. Methods

2.1. Model structure and dynamics

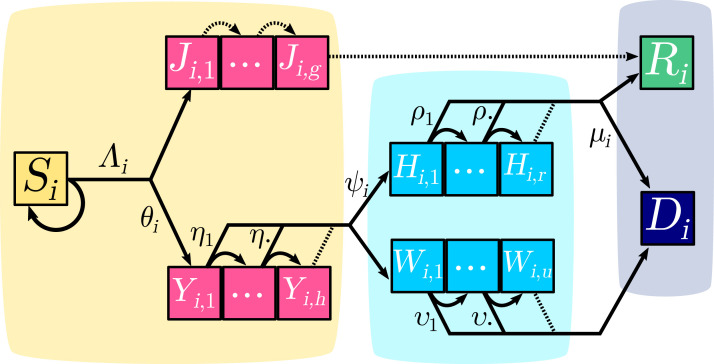
As classically done (Kermack and McKendrick, 1927, Keeling and Rohani, 2008), we group individuals with the same epidemiological contribution into compartments whose densities are tracked over time. Given that many COVID-19 clinical outcome proportions are age-dependent – e.g. the infection fatality ratio (IFR) (Verity et al., 2020) – we further split each compartment into an arbitrary number of age groups, denoted by index $i$. This allows us to adjust nationwide averages and capture demographic effects by matching demography to age-stratified hospital data.

The structure of the system is shown in Fig. 1. Initially, all individuals in group $i$ belong to the susceptible compartment, the density of which is denoted $S_i$. These individuals can be infected with a daily probability called the force of infection, the expression of which is

$${\Lambda }_i\left(t\right)={\left(1+{\left({\mathcal{R}}_0\frac{k_i\left(t\right)}{k_i\left(0\right)}\sum _j\frac{k_j\left(t\right)}{k_j\left(0\right)}\sum _{\tau }{\zeta }_{\tau }{\pi }_{j,\tau }\left(t\right)\right)}^{-1}\right)}^{-1}$$ (1)

where ${\pi }_{j,\tau }$ is the prevalence of $j$-individuals infected since $\tau$ days, $k_j$ the per capita contact rate and ${\zeta }_{\tau }$ the discretised serial interval distribution, i.e. the relative contribution of each day upon infection to the individual force of infection (see Appendix S2.2 for the derivation).

Fig. 1.

COVID-19 epidemic discrete-time model structure. Each square represents a group of individuals who share the same clinical kinetics and who contribute equally to the epidemic dynamics. Contiguous squares form a day after day progression sequence which captures the memory effects of the infection age. Pink boxes correspond to infected individuals in the community (yellow area). Light blue boxes represent critical cases cared for in hospitals (blue area). The grey area corresponds to removed compartments that do not contribute to the epidemic. Arrows between boxes correspond to the daily flow of individuals. Dotted arrows depict transitions that occur with probability $1$. For the sake of simplicity, only one age group $i$ is here depicted and only one of the two probabilities is shown for each bifurcating transition. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Upon infection, a fraction $1-{\theta }_i$ of the individuals will develop non-critical infections and move to the $J_{i,\cdot }$ compartment, where the second subscript indicates the age of the infection (in days). At each time step, an individual in the compartment $J_{i,k}$ moves to the compartment $J_{i,k+1}$ and after $g$ days of infection it moves to the recovered (and assumed lastingly immunised) compartment $R_i$.

A fraction ${\theta }_i$ of infections will lead to critical complications (typically acute respiratory distress syndrome (Bouadma et al., 2020)), and move to the $Y_{i,1}$ compartment. On day $k$, individuals in the $Y_{i,k}$ subgroup have a probability ${\eta }_k$ to be hospitalised and a complementary probability $1-{\eta }_k$ to move to the $Y_{i,k+1}$ subgroup. As detailed in Appendix S2.5, two groups of hospitalised critical patients are considered. Upon hospitalisation, a proportion ${\psi }_i$ of them have a substantial chance, $1-{\mu }_i$, to recover and benefit from a long stay in an ICU; they are denoted by $H_{i,\cdot }$. Their length of stay is captured by probabilities ${\rho }_k$ ($k$ denoting the number of days since hospitalisation) (Santé Publique France, 2020a). Those who will die, either after a short stay in ICU or in another ward, are denoted by $W_{i,\cdot }$. Time to death for this latter compartment is captured by the sequence of ${\upsilon }_k$.

2.2. Memory effects

The daily probability for a key transition in the natural history of COVID-19 to occur is likely to increase with elapsed time. This has been documented for the onset of contagiousness and the respiratory complications, which are likely to arise in narrow time windows respectively around the 4th day since infection (Nishiura et al., 2020) and a week after symptom onset (Linton et al., 2020, Bouadma et al., 2020). To capture this ’ageing property’, which is lacking in the exponential distributions implicitly used by ODE models, we used Weibull distributions (Bolker, 2008) with shape parameters greater than $1$ in the parameterisation of the time distributions involved in the model, as detailed in Appendix S2.6. For the sake of parsimony, we assume that these distributions are identically distributed across age classes.

Importantly, our model does not require an incubation or a latency period to be specified explicitly. Instead, the contribution of each individual to the force of infection is weighted by the discretised empirical distribution of the serial interval estimated by Nishiura et al. (2020), according to the age of its infection. This modelling approach eventually recovers a classical SIR model for the non-critical cases, capturing the empirical and effective non-homogeneous infectiousness period without recourse to additional arbitrary compartments (such as a latent/exposed $E$, and convalescent densities) and their corresponding parameters.

2.3. Data and estimation

All statistical analyses and numerical integration were conducted in R (R Core Team, 2020). The system was initialized as a fully susceptible population according to the French population pyramid (Institut National de la Statistique et des Études Économiques, 2020) from which the residents of nursing homes (Muller, 2017) have been excluded, to focus on the general population viral circulation. Parameter inference was performed using nationwide daily ICU admissions, current ICU bed occupancy, as well as the cumulative number of deaths, all available on the French government data repository (Santé Publique France, 2020b). These time series were 7-day rolling averaged beforehand in order to correct for under-reporting during week-ends.

We first located the region of highest likelihood using initial parameter values estimated from data or compatible with the literature (see Appendix S1 for details). Then, the maximum likelihood estimates (MLE) and associated 95%-intervals were stepwise calculated (Bolker and Giné-Vázquez, 2020) with respect to daily ICU admissions, ICU discharges, and daily mortality time series, assuming a Gaussian noise around the prediction. The median and 95% confidence intervals of the model’s output are finally calculated as the daily sample quantiles across runs from 1000 randomly drawn parameter sets with statistically equivalent likelihoods (Wilks, 1938). Details on times series, parameter estimation and output calculations can be found in Appendix S2.4, S2.7, and S2.8 respectively. Moreover, we ran the fitting procedure using an alternative set of initial age-stratified IFRs (Salje et al. (2020) instead of Ferguson et al. (2020)) and show that our key estimates are robust to the uncertainty on this parameter (Appendix S3.2) .

3. Results

3.1. Memoryless approach

To illustrate the ability of our discrete model to capture COVID-19 short-term dynamics, we first explored the best outcome of parameter inference for a Markovian (memory-less) model.

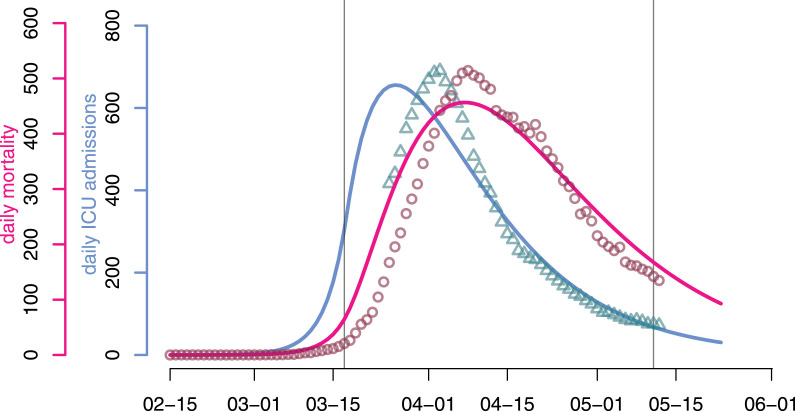
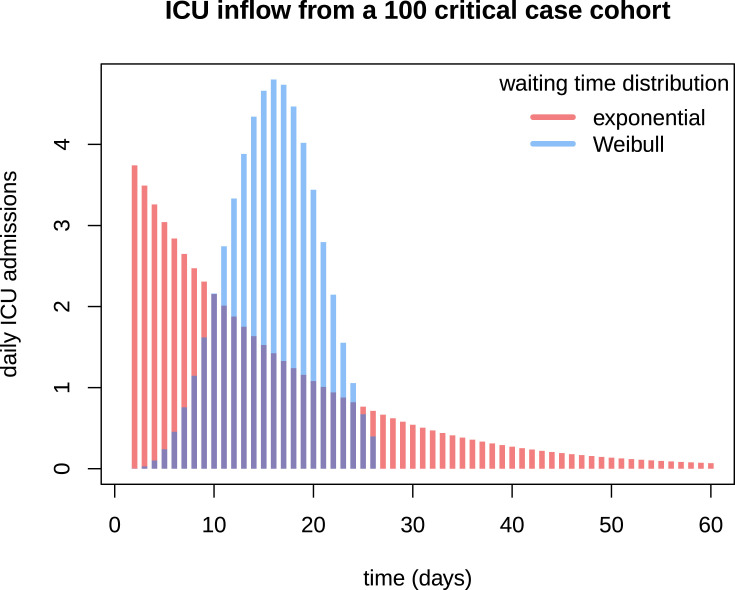
As shown in Fig. 2, in spite of one additional degree of freedom compared to the focal model (see Appendix S2.9 for more details), the best fit performs poorly on the daily ICU admissions and mortality. Indeed, the model cannot capture both time series (respectively in blue and red). Furthermore, for each of the time series the decline phase after the lockdown (on Mar 17 for France) is underestimated. This can be explained by the fact that memoryless/Markovian models implicitly assume exponentially distributed waiting times that essentially cannot reproduce peaked dynamics, as shown by Fig. 3.

Fig. 2.

Predicted (plain line) and observed (dots) dynamics with (classical) memory-less processes. The continuous-time memory-less analog of the focal model poorly reproduces the observed trends in daily ICU admissions (turquoise triangles) and mortality (red circles) in France. Vertical lines indicate the beginning and end of the national lockdown.

Fig. 3.

Flow through time shape comparison between Markovian and non-Markovian dynamics. 100 individuals assumed to develop respiratory complications are infected the same day. The bars represent the number of daily ICU admissions related to this virtual cohort. Time between infection and admission follows either an exponential (in red) or a Weibull (in blue) distribution. Both distributions have the same mean, about 14.5 days. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

While this comparison shows that memory effects associated with contagiousness and critical symptom onset are essential to the epidemiological dynamics, preliminary fitting attempts have on the other hand shown that those associated with post-hospitalisation events (namely the distributions of ${\rho }_k$ and ${\upsilon }_k$) are weaker. Precisely, exponentially-distributed hospitalisation to ICU discharge or death intervals (namely ${\rho }_k$ and ${\upsilon }_k$) appear to be more parsimonious.

3.2. Epidemic parameter values estimation

Maximum likelihood estimates and 95% likelihood intervals (hereafter indicated by square brackets) were found for all parameters except those determining the generation time distribution (kept fixed following Nishiura et al., 2020). The basic reproduction number was estimated to 2.99 [2.59–3.39]. The effect of the lock-down is estimated to a 75.9% [72.9–78.7] reduction of the reproduction number. The estimates for the other parameters are all in line with official reports of average values. The epidemic wave is estimated to have started around Jan 20. This result is in agreement with early phylogenetic analyses on sequence data sampled in France (Danesh et al., 2020). Estimates and intervals for the other parameters are summarised in Table S-5.

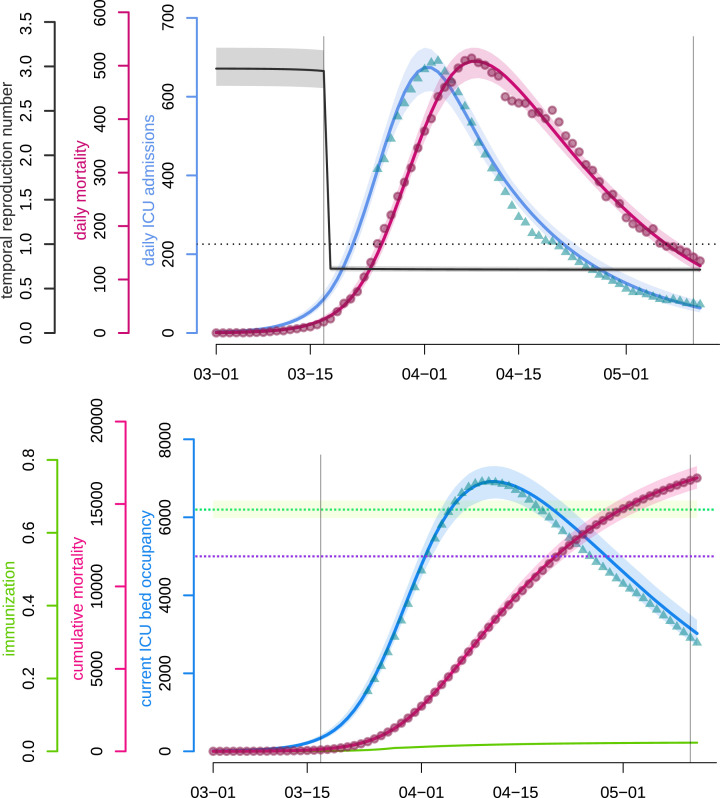
The fitted non-Markovian discrete-time model accurately captures the dynamics of both the daily hospital mortality and the daily number of ICU admissions since most of the data points fall into the 95% confidence intervals. As can be observed in Fig. 4(top), the model correctly approaches the number of daily admissions in the vicinity of the peak, which is crucial for hospital management at both local and national levels.

Fig. 4.

COVID-19 epidemic wave in France fitted by a non-Markovian discrete-time model.Top panel. The blue and pink curves respectively represent the median daily ICU admissions and the median daily (hospital) mortality as generated by the fitted model. Turquoise triangles and red circles are the (rolling 7-day average) data counterparts. The black curve shows the median daily temporal reproduction number calculated from the simulated epidemic. The dotted horizontal line shows the reproduction number threshold value, i.e. $1$. Bottom panel. The blue and pink curves respectively represent the median number of occupied beds in ICU nationwide and the median cumulative (hospital) mortality as generated by the fitted model. The turquoise triangles and red circles are the (rolling 7-day average) data counterparts. The purple dotted horizontal line shows the initial French ICU capacity, ca. 5000 beds. The green curve shows the median proportion of the population that has recovered (and is assumed to be immune). The green dotted horizontal line corresponds to the median herd immunity threshold $1-{\mathcal{R}}_0^{-1}$. The two vertical lines show respectively (from left to right) the beginning and the end of the French national lock-down. Shaded areas correspond to 95% confidence intervals. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

We also present the temporal reproduction number (${\mathcal{R}}_t$), which rapidly drops below unity following the onset of the national lock-down and was equal to 0.71 $\left[0.69,0.74\right]$ by May 11 according to the model. Notice that ${\mathcal{R}}_t$ started to decrease before the lock-down onset, due to density-dependent effects. In a model with strong host heterogeneity and so-called ‘super-spreaders’, this effect would be even more pronounced. Other explanations include local saturation, staggered implementation of pre-containment measures, such as health communication campaigns, or improved patient management as diagnosis and therapy became more effective. However, neither the structure of the model nor the level of detail in the available data makes it possible to identify the isolated impact of each measure on epidemiological dynamics.

Fig. 4(bottom) illustrates that the model also accurately captures the post-ICU admission dynamics (though with a slight tendency to overestimate the declining ICU bed occupancy), which is essential in assessing the risk of saturation of such hospital units, which would lead to excess-mortality. The fit to these data points could be improved with access to non-aggregated patient data or distributions of ICU residency time. The cumulative mortality curve is fitted with great accuracy, which allows us to use it as a comparison criterion between control strategies in further analyses. Finally, the figure also shows that the level of population immunisation, the median of which we estimate at 2.37% ($\left[2.27,2.48\right]\text{\%}$ 95%-CI) by May 11, is far below the classical group immunity threshold (ETE Modelling Team, 2020).

3.3. Timing of the estimation

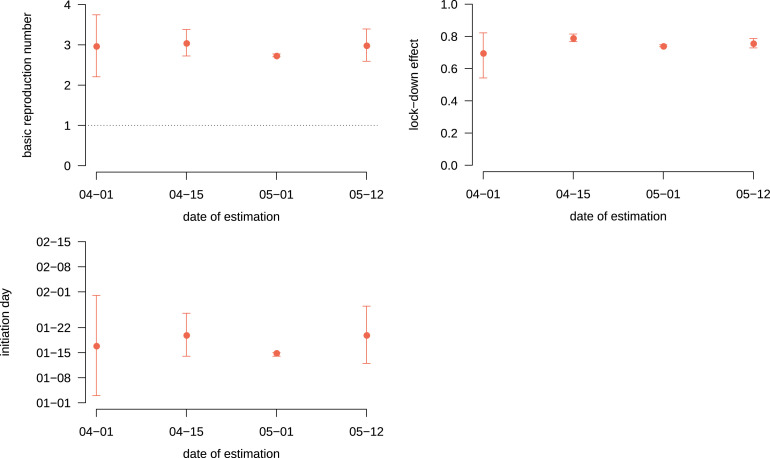
This model was applied to the early phase of the epidemic and its adequation to the data greatly improved on April 23, when French data on ICU residency time was made public. To illustrate the ability of the model to perform accurate parameter value estimations early in the epidemics, we performed the inference by censoring the data to the right.

As shown in Fig. 5, estimates with censoring on April 15, that is one month before the final data point shown in Fig. 4, were already accurate. Estimates with an earlier censoring are qualitatively correct but the confidence intervals larger. The enlargement of the last confidence intervals can be explained by a wider range of parameter sets having close likelihoods: either by fitting well the peak or the final slow decrease, possibly affected by improved care of hospitalised patients two months after the outbreak. As a supplementary result, we also provide in Appendix S3.3 the model forecast of the hospital time series based on the data available from Mar 18 to Apr 7 2020. With less than three weeks of daily figures, our framework was able to anticipate the following week trajectory and to capture the trend of the hospital dynamics for more than a month ahead.

Fig. 5.

Basic reproduction number, lock-down effect and initiation day estimates as a function of the date of censoring. Each dot represents the maximum likelihood estimate of the basic reproduction number ${\mathcal{R}}_0$ (top left), the lock-down effect $\kappa$ (top right) and the initiation day $t_0$ (top right) calculated from data truncated at the corresponding date on the $x$-axis. Bars shows 95% likelihood intervals.

3.4. Response date impact

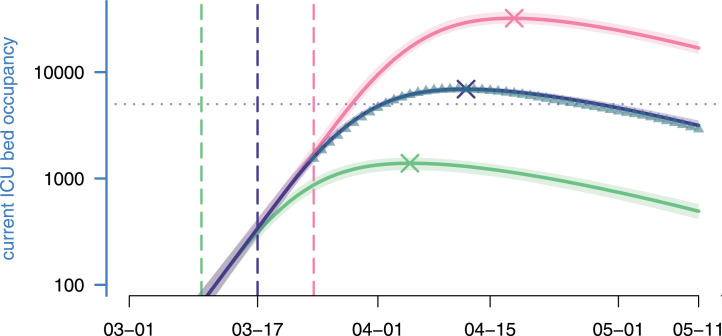
Using our estimated parameters, we then explored the effects of implementing the national lock-down a week earlier or a week later. As shown in Fig. 6, the peak was reached on Apr 8, with $7019$ ICU beds occupied (the model estimates it to Apr 12 and $6920$ beds). Enforcing the lock-down a week earlier (in green) would have led to an earlier and smaller epidemic peak with less than $1500$ ICU beds occupied on Apr 5. Conversely, another week of delay (in red) would have led to a peak above $32000$ beds occupied in ICU on Apr 18, which is largely above the ICU capacity at the time (ca. $5000$ beds). Overall, in the range studied, each elapsed week multiplies ICU occupancy peak by more than 4.5, while delaying it by 3 weeks.

Fig. 6.

Lock-down implementation date effect and ICU bed occupancy. Each curve represents the median current ICU bed occupancy as generated by the model according to a given lock-down scenario, while their surrounding shaded areas correspond to their 95% confidence intervals. From bottom to top: the green scenario simulates an early national lock-down (on March 10th); the purple scenario is the realised one (lock-down beginning on Mar 17); the pink scenario simulates a late lock-down (on Mar 24th). Vertical lines indicate lock-down implementation dates. Crosses indicate the median ICU peak activity. Triangles represent the data and the dotted line the maximum ICU bed capacity in France. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

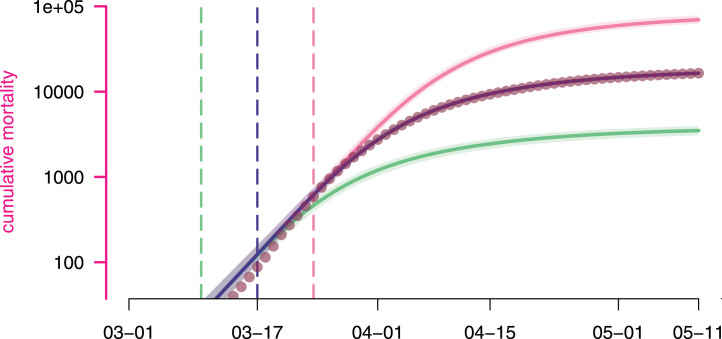
These differences also translate in terms of mortality. According to the model, implementing the lock-down a week earlier could have led to $13300$ [$12900$–$13700$] less deaths, while waiting for an additional week could have claimed $52800$ [$45800$–$61500$] more lives (Fig. 7).

Fig. 7.

Estimated lock-down date effect on cumulative mortality. Each curve represents the median cumulative (hospital) mortality as generated by the model according to a given lock-down scenario, while their surrounding shaded areas correspond the their 95% confidence intervals. The scenarios are as detailed in Fig. 6. Dots represent the data.

4. Discussion

COVID-19 is not an unusually lethal or contagious infectious disease. On the other hand, the large proportion of transmission attributable to individuals with few or no symptoms makes it redoubtably difficult to control compared to e.g. SARS (Fraser et al., 2004). In the absence of a massive and homogeneous screening effort, the dynamics of COVID-19 can only be studied through hospitalisations induced by complications, which are rare and occur on average two weeks after infection. The marginal, indirect, and delayed nature of these events justifies the use of statistical analyses and mathematical modelling in the short-term epidemiological management of this unprecedented health crisis. However, given the magnitude of the risks at stake, the diversity of fields involved, and the number of unknowns (such as climate effects, immunity duration), mathematical modelling predictions should be handled with caution in the decision process.

Informing decision-making processes is challenging because most mathematical modelling in epidemiology relies on ordinary differential equations. These offer a wide palette of analytical tools, but they also become less accurate on short time scales. Conversely, stochastic models, whether agent-based or not, offer a much more precise picture of the early stages of the epidemics. However, they become less necessary once the outbreak threshold has been crossed and epidemic dynamics become essentially deterministic.

We therefore developed an original framework at the crossroads of individual-centred and compartmental modelling approaches, tailored to the COVID-19 natural history, which has two great advantages. First, its discrete time structure, shared with that of common epidemiological data, allows us to assume any distribution for model processes, therefore introducing what is known in the literature as memory effects (or ‘non-Markovian’ processes), related to the age of the infection. As a result, we obtain a much better fit than classical memory-less (or ‘Markovian’) models on intermediate timescales (weeks or months). Second, the deterministic nature of the model allows us to perform extremely fast simulations, especially compared to agent-based modelling that requires the drawing of millions of random numbers for a single simulation. The computational performance combined with the great parsimony, that still allows it to accurately fit the observed epidemiological dynamics, makes this model a relevant tool that can be easily transposed and deployed to other settings, countries or scales, even with solely aggregated publicly available data — as it is the case in the present work, while the extension to age-stratified data sets is straightforward.

First, we used our model to infer three key parameters of the epidemics. Our estimate of ${\mathcal{R}}_0$ is comparable to that already computed in France based on their 95% confidence interval (Di Domenico et al., 2020, Salje et al., 2020). We also estimate the temporal reproduction number ${\mathcal{R}}_t$ after the lock-down to 0.71, in line with the estimates of other studies (Salje et al., 2020, Hoertel et al., 2020, Forien et al., 2020), and the number of lives potentially saved (more than $50000$) compared to a lock-down implemented a week later.

The model makes several strong assumptions, the strongest being the mean-field approximation: the population is supposed to be well-mixed. This limitation can become strong if the epidemic grows in size to infect a large proportion of the population. Nonetheless, earlier works have shown that non spatially structured models produce conservative estimates from a public health viewpoint, while their parsimony and tractability outweighs the greater precision provided by finer models (Keeling, 1999, Trapman et al., 2016). Second, there is no specification of the public health control measures implemented: all the options (quarantine of confirmed cases, adoption of barrier measures, social distancing: closing of schools and universities, banning of gatherings, etc.) are combined to reduce the contact rate. We also neglected fomite transmission (see Ferretti et al., 2020 for an example) and assumed perfect and lifelong immunity against reinfection due to currently insufficient data on immunity. One simplifying assumption we made is that mortality probabilities do not vary over time, whereas in practice hospital saturation could affect mortality, whether related to COVID-19 or not.

In terms of outlook, the model can straightforwardly be extended to formally take into account any kind of finer stratification, e.g. age, sex, and comorbidities simultaneously and take advantage of a discrete implicit spatial structure. This work has laid the foundation for two epidemic surveillance and projection online applications, respectively at the national (Reyné et al., 2020) (published in Jul 2020) and infra-national level (Boennec et al., 2021) (published in Feb 2021 and currently referenced by the French government data and app repository). Future work includes taking into account possible changes in parameter values with time, mainly detecting and estimating seasonal effects. If these are of significant impact, model fitting could be adapted, either by estimating parameters within defined time windows or by left-censoring the data as time goes by. Beyond the ongoing pandemic, this framework can be easily adapted and deployed as a now- and forecasting tool in future outbreaks.

CRediT authorship contribution statement

Mircea T. Sofonea: Conceptualization, Methodology, Software, Formal analysis, Investigation, Visualization, Writing - original draft, Validation. Bastien Reyné: Data curation, Software, Validation. Baptiste Elie: Data curation, Validation. Ramsès Djidjou-Demasse: Resources, Writing - review & editing, Validation. Christian Selinger: Resources, Writing - review & editing, Validation. Yannis Michalakis: Writing - original draft, Validation. Samuel Alizon: Writing - original draft, Supervision, Validation.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Mathematical notations, model details and supplementary results

The following is the Supplementary material related to this article.