A Multisite Study of a Breast Density Deep Learning Model for Full-Field Digital Mammography and Synthetic Mammography

Abstract

Purpose

To develop a Breast Imaging Reporting and Data System (BI-RADS) breast density deep learning (DL) model in a multisite setting for synthetic two-dimensional mammographic (SM) images derived from digital breast tomosynthesis examinations by using full-field digital mammographic (FFDM) images and limited SM data.

Materials and Methods

A DL model was trained to predict BI-RADS breast density by using FFDM images acquired from 2008 to 2017 (site 1: 57 492 patients, 187 627 examinations, 750 752 images) for this retrospective study. The FFDM model was evaluated by using SM datasets from two institutions (site 1: 3842 patients, 3866 examinations, 14 472 images, acquired from 2016 to 2017; site 2: 7557 patients, 16 283 examinations, 63 973 images, 2015 to 2019). Each of the three datasets were then split into training, validation, and test. Adaptation methods were investigated to improve performance on the SM datasets, and the effect of dataset size on each adaptation method was considered. Statistical significance was assessed by using CIs, which were estimated by bootstrapping.

Results

Without adaptation, the model demonstrated substantial agreement with the original reporting radiologists for all three datasets (site 1 FFDM: linearly weighted Cohen κ [κ_w] = 0.75 [95% CI: 0.74, 0.76]; site 1 SM: κ_w = 0.71 [95% CI: 0.64, 0.78]; site 2 SM: κ_w = 0.72 [95% CI: 0.70, 0.75]). With adaptation, performance improved for site 2 (site 1: κ_w = 0.72 [95% CI: 0.66, 0.79], 0.71 vs 0.72, P = .80; site 2: κ_w = 0.79 [95% CI: 0.76, 0.81], 0.72 vs 0.79, P < .001) by using only 500 SM images from that site.

Conclusion

A BI-RADS breast density DL model demonstrated strong performance on FFDM and SM images from two institutions without training on SM images and improved by using few SM images.

Supplemental material is available for this article.

Published under a CC BY 4.0 license.

Summary

A breast density deep learning model showed strong performance on digital and synthetic mammographic images from two institutions without training on synthetic mammographic images and improved with adaptation by using few synthetic mammographic images.

Key Points

• ■ A Breast Imaging Reporting and Data System breast density deep learning (DL) model achieved substantial agreement with the original interpreting radiologists for full-field digital mammography (FFDM) examination data from site 1 (linearly weighted Cohen κ [κ_w] = 0.75 [95% CI: 0.74, 0.76]).

• ■ Without modification, the DL model trained on FFDM images demonstrated substantial agreement with the original reporting radiologists for a test set of synthetic two-dimensional mammographic (SM) images, which were generated as part of digital breast tomosynthesis examinations (site 1: κ_w = 0.71 [95% CI: 0.64, 0.78]).

• ■ Without modification, the DL model also demonstrated close agreement for a test set of SM images obtained from a different institution than that of the training data (site 2: κ_w = 0.72 [95% CI: 0.70, 0.75]). Adaptation techniques requiring few SM images were able to further improve performance (eg, site 2: κ_w = 0.79 [95% CI: 0.76, 0.81]; P < .001).

Introduction

Breast density is an important risk factor for breast cancer (1–3). Additionally, areas of higher density can mask findings within mammograms, leading to lower sensitivity (4). Many states have passed breast density notification laws requiring clinics to inform women of their breast density (5). Radiologists typically assess breast density by using the Breast Imaging Reporting and Data System (BI-RADS) lexicon, which divides breast density into four categories: A, almost entirely fatty; B, scattered areas of fibroglandular density; C, heterogeneously dense; and D, extremely dense (examples are presented in Fig E1 [supplement]) (6). Unfortunately, radiologists exhibit intra- and interreader variability in the assessment of BI-RADS breast density, which can result in differences in clinical care and estimated risk (7–9).

Deep learning (DL) has previously been used to assess BI-RADS breast density for film (10) and full-field digital mammographic (FFDM) images (11–16), with some models demonstrating closer agreement with consensus estimates than individual radiologists (14). To realize the promise of the use of these DL models in clinical practice, two key challenges must be met. First, because digital breast tomosynthesis (DBT) is increasingly used in breast cancer screening (17) due to improved reader performance (18–20), DL models should be compatible with DBT examinations. To aid in radiologist interpretation of breast cancer and breast density, DBT examinations contain two-dimensional images in addition to three-dimensional images. These two-dimensional images may be either FFDM images or synthetic two-dimensional mammographic (SM) images derived from the three-dimensional images. Figure E2 (supplement) shows the differences in image characteristics between FFDM and SM images. The relatively recent adoption of DBT at many institutions means that the datasets available for training DL models are often fairly limited for DBT examinations compared with FFDM examinations. Second, DL models must offer consistent performance across sites, where differences in imaging technology, patient demographics, or assessment practices could impact model performance. To be practical, this should be achieved while requiring limited additional data from each site.

In this study, we present a BI-RADS breast density DL model that offers close agreement with the original reporting radiologists for both FFDM and DBT examinations at two institutions. A DL model was first trained to predict BI-RADS breast density by use of a large-scale FFDM dataset from one institution. The model was then evaluated on a test set of FFDM images and SM images generated as part of DBT examinations acquired from the same institution and from a separate institution. Adaptation techniques, requiring few SM images, were explored to improve performance in the two SM datasets.

Materials and Methods

This retrospective study was approved by an institutional review board for each of the two sites where data were collected (site 1, internal institutional review board; and site 2, Western Institutional Review Board, Puyallup, Wash). Informed consent was waived, and all data were handled according to the Health Insurance Portability and Accountability Act. This work was supported in part by funding from Whiterabbit. Washington University has equity interests in Whiterabbit and may receive royalty income and milestone payments from a collaboration and license agreement with Whiterabbit to develop a technology evaluated in this research.

Datasets

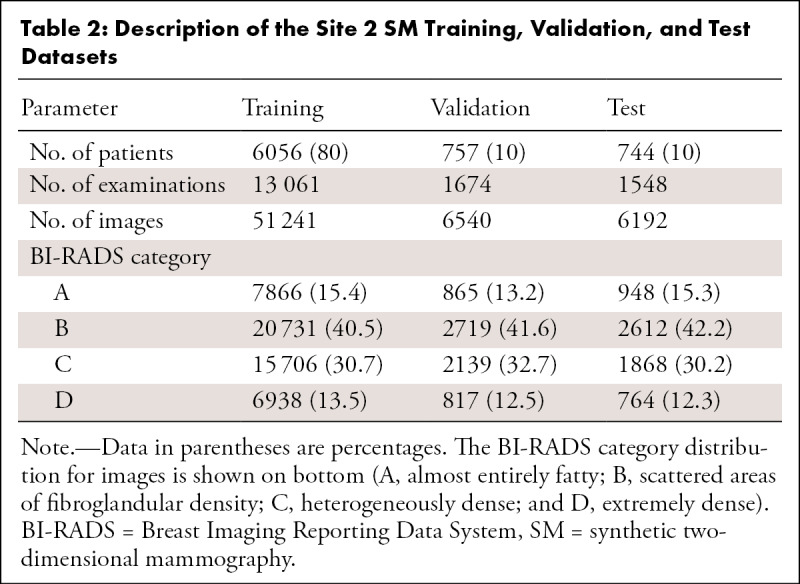
Mammography examinations were collected from two sites: site 1, an academic medical center located in the Midwestern United States, and site 2, an outpatient radiology clinic located in Northern California. For site 1, FFDM and SM datasets were collected, whereas for site 2, only a SM dataset was collected. The site 1 FFDM dataset consisted of 187 627 examinations acquired from 2008 to 2017, the site 1 SM dataset consisted of 3866 examinations acquired from 2016 to 2017, and the site 2 SM dataset consisted of 16 283 examinations acquired from 2015 to 2019. The FFDM images were acquired on Selenia and Selenia Dimensions imaging systems (Hologic), whereas the SM images were acquired on Selenia Dimension imaging systems (C-View; Hologic). The two sites serve different patient populations. The patient cohort from site 1 was 59% White, non-Hispanic (34 192 of 58 397), 23% Black, non-Hispanic (13 201 of 58 397), 3% Asian (1630 of 58 397), and 1% Hispanic (757 of 58 397); the patient cohort from site 2 was 58% White, non-Hispanic (4350 of 7557), 1% Black, non-Hispanic (110 of 7557), 21% Asian (1594 of 7557), and 7% Hispanic (522 of 7557). The distribution of ages is similar for the two sites (site 1, 55 years ± 16 [standard deviation]; site 2, 56 years ± 11).

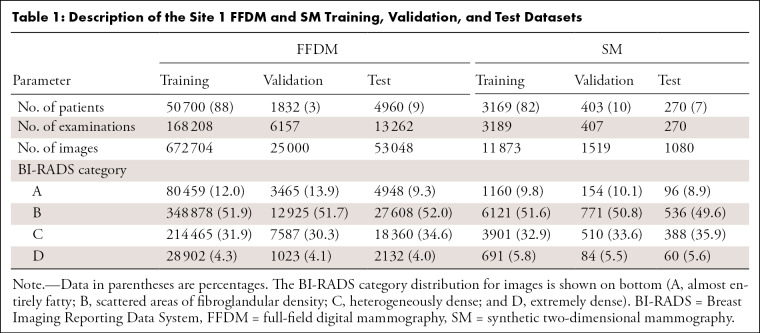
The examinations were interpreted by one of 11 radiologists (breast imaging experience ranging from 2 to 30 years) for site 1 and by one of nine radiologists (experience ranging from 10 to 41 years) for site 2. The BI-RADS breast density assessments of the radiologists were obtained from each site’s mammography reporting software (site 1: Magview 7.1, Magview; site 2: MRS 7.2.0, MRS Systems). Patients were randomly selected for training, validation, and testing at ratios of 80%, 10%, and 10%, respectively. Because the split was performed at the patient level, the images for a given patient (in particular, all FFDM and SM images for site 1) appear in only one of these sets. All examinations with a BI-RADS breast density assessment were included. No explicit filtering was performed for implants or prior surgery. For the FFDM validation set, only the first 25 000 images were used in order to accelerate the training process (evaluation on the validation set occurs after each training epoch). For the test sets, examinations were required to have exactly the four standard screening mammographic images (the mediolateral oblique and craniocaudal views of both breasts). This restriction led to the elimination of nearly all examinations for patients with implants because of the presence of implant-displaced views. Following these restrictions, the distribution of patients was as follows: training (FFDM, 50 700 patients [88%]; site 1: SM, 3169 [82%] patients; site 2: SM, 6056 [80%] patients), validation (FFDM, 1832 patients [3%]; site 1: SM, 403 patients [10%]; site 2: SM, 757 patients [10%]), and testing (FFDM, 4960 patients [9%]; site 1: SM, 270 patients [7%]; site 2: SM, 744 patients [10%]). The distribution of the BI-RADS breast density assessments for each set are presented in Table 1 (site 1) and Table 2 (site 2).

Table 1:

Description of the Site 1 FFDM and SM Training, Validation, and Test Datasets

Table 2:

Description of the Site 2 SM Training, Validation, and Test Datasets

DL Model

The DL model and training procedure were implemented by using the PyTorch DL framework (version 1.0; https://pytorch.org). The base model architecture is a preactivation ResNet-34 (21–23), which accepts as input a single image corresponding to one of the views from a mammographic examination and produces estimated probabilities that the image belongs to each of the BI-RADS breast density categories. The model was trained by use of the FFDM dataset following the procedure described in Appendix E1 (supplement).

Domain-Adaptation Methods

The goal of domain adaptation is to take a model trained on a dataset from one domain (source domain) and transfer its knowledge to a dataset in another domain (target domain), which is typically much smaller in size. Features learned by DL models in the early layers can be general (ie, domain and task agnostic) (24). Depending on the similarity of domains and tasks, even deeper features learned from one domain can be reused for another domain or task.

In our work, we explored approaches for adapting the DL model trained on FFDM images (source domain) to SM images (target domain) that reuse all the features learned from the FFDM domain. First, inspired by the work of Guo et al (25), we considered the addition of a small linear layer following the final fully connected layer where either the 4 × 4 matrix is diagonal (vector calibration) or the 4 × 4 matrix is allowed to vary freely (matrix calibration). Second, we retrained the final fully connected layer of the ResNet-34 model on samples from the target domain (fine-tuning). More information on these methods can be found in Appendix E2 (supplement).

To investigate the impact of the target domain dataset size, the adaptation techniques were repeated for different SM training sets across a range of sizes. The adaptation process was repeated 10 times for each dataset size with different training data to investigate the uncertainty arising from the selection of the training data. For each realization, the training images were randomly selected, without replacement, from the full training set. As a reference, a ResNet-34 model was trained from scratch (ie, random initialization) for the largest number of training samples for each SM dataset.

Statistical Analysis

To obtain an examination-level assessment, each image within an examination was processed by the DL model and the resulting probabilities were averaged. Several metrics were computed from these average probabilities for the four-class BI-RADS breast density task and the binary dense (BI-RADS C and D) versus nondense (BI-RADS A and B) task: accuracy, estimated on the basis of concordance with the original reporting radiologists, the area under the receiver operating characteristic curve (AUC), and Cohen κ (scikit version 0.20.0; https://scikit-learn.org). CIs were computed by non-Studentized pivotal bootstrapping of the test sets for 8000 random samples (26). For the four-class problem, macroAUC, the average of the four AUC values from the one class versus others tasks and linearly weighted Cohen κ (κ_w) are reported. For the binary density task, the predicted dense and nondense probabilities were computed by summing the probabilities for the corresponding BI-RADS density categories. For comparisons of accuracy and Cohen κ before and after adaptation, P values were calculated by using a two-sided z test with an α of .05 (SciPy version 1.1.0, https://scipy.org; statsmodels version 0.11.1, https://www.statsmodels.org) (27).

Results

Examination-level Performance on FFDM Images

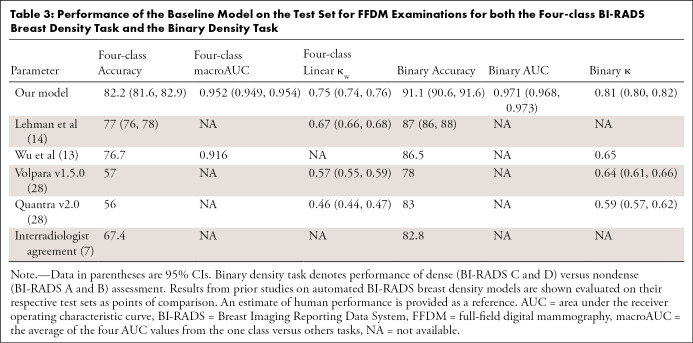
The trained model was first evaluated on a large held-out test set of FFDM examinations from site 1 (4960 patients, 13 262 examinations, 53 048 images; mean age, 57 years [age range, 23–97 years]). In this case, the images were from the same institution and of the same image type (FFDM) as those used to train the model. The BI-RADS breast density distribution predicted by the DL model (A, 8.5%; B, 52.2%; C, 36.1%; D, 3.2%) was similar to that of the original reporting radiologists (A, 9.3%; B, 52.0%; C, 34.6%; D, 4.0%). A more detailed comparison of the density distributions can be found in Appendix E3 (supplement). The DL model exhibited close agreement with the radiologists for the BI-RADS breast density task across a variety of performance measures (Table 3), including accuracy (82.2% [95% CI: 81.6, 82.9]) and κ_w (0.75 [95% CI: 0.74, 0.76]). A high level of agreement was also observed for the binary breast density task (accuracy, 91.1% [95% CI: 90.6, 91.6]; AUC, 0.971 [95% CI: 0.968, 0.973]; κ = 0.81 [95% CI: 0.80, 0.82]). As demonstrated by the confusion matrices shown in Figure 1, the DL model is rarely off by more than one breast density category (eg, calls an extremely dense breast scattered), in total, 0.03% of examinations (four of 13 262).

Table 3:

Performance of the Baseline Model on the Test Set for FFDM Examinations for both the Four-class BI-RADS Breast Density Task and the Binary Density Task

Figure 1:

Confusion matrices for the, A, Breast Imaging Reporting and Data System (BI-RADS) breast density task and the, B, binary density task (dense [BI-RADS C and D] vs nondense [BI-RADS A and B]) evaluated on the full-field digital mammography test set. The number of test samples (examinations) within each bin is shown in parentheses. DL = deep learning.

To place the results in the context of previous work, the performance on the FFDM test set was compared with results from academic centers (13,14), with commercial breast density software (28) and with an estimate of human performance (7) (Table 3). Although there are limitations in comparing results evaluated on different datasets with different readers, our DL model appears to offer competitive performance for FFDM examinations.

Examination-level Performance on SM Images

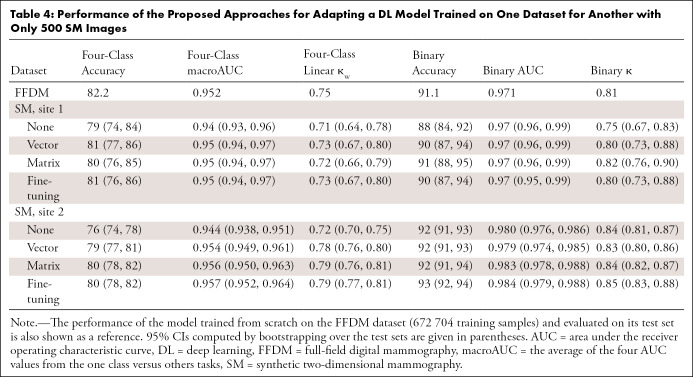
Site 1 results.—Results are first reported for the site 1 SM test set (270 patients; 270 examinations; 1080 images; mean age, 55 years [age range, 28–72 years]) because this avoids any differences that may occur between the two sites. Without adaptation, the model demonstrates close agreement with the original reporting radiologists for the BI-RADS breast density task (accuracy, 79% [95% CI: 74, 84]; κ_w = 0.71 [95% CI: 0.64, 0.78]; Table 4). The DL model slightly underestimates breast density for SM images (Fig 2), producing a BI-RADS breast density distribution (A, 10.4%; B, 57.8%; C, 28.9%; D, 3.0%) with more nondense cases and fewer dense cases relative to the radiologists (A, 8.9%; B, 49.6%; C, 35.9%; D, 5.6%). A more detailed comparison of the density distributions can be found in Appendix E3 (supplement). Agreement for the binary density task is also high without adaptation (accuracy, 88% [95% CI: 84, 92]; κ = 0.75 [95% CI: 0.67, 0.83]; AUC, 0.97 [95% CI: 0.96, 0.99]).

Table 4:

Performance of the Proposed Approaches for Adapting a DL Model Trained on One Dataset for Another with Only 500 SM Images

Figure 2:

Confusion matrices evaluated on the site 1 synthetic two-dimensional mammography (SM) test set without adaptation, for the, A, Breast Imaging Reporting and Data System (BI-RADS) breast density task, and the B, binary density task (dense [BI-RADS C and D] vs nondense [BI-RADS A and B]). Confusion matrices evaluated on the site 1 SM test set with adaptation by matrix calibration for 500 site 1 SM training samples for the, C, BI-RADS breast density task and the, D, binary density task (dense vs nondense). The number of test samples (examinations) within each bin is shown in parentheses. DL = deep learning.

After adaptation by matrix calibration with 500 site 1 SM images, the density distribution is slightly more similar to that of the radiologists (A, 5.9%; B, 53.7%; C, 35.9%; D, 4.4%), whereas overall agreement is about the same (accuracy, 80% [95% CI: 76, 85], P = .75; κ_w = 0.72 [95% CI: 0.66, 0.79], P = .80). Accuracy for the two dense classes is improved at the expense of the two nondense classes (Fig 2). A larger, although not statistically significant, improvement is seen for the binary density task, where Cohen κ rose from 0.75 (95% CI: 0.67, 0.83) to 0.82 (95% CI: 0.76, 0.90 [P = .16]; accuracy, 91% [95% CI: 88, 95], P = .20).

Site 2 results.—Close agreement between the DL model and the original reporting radiologists was also observed for the site 2 SM test set (744 patients, 1548 examinations, 6192 images [mean age, 55 years; age range, 30–92 years]) without adaptation (accuracy, 76% [95% CI: 74, 78]; κ_w = 0.72 [95% CI: 0.70, 0.75]; Table 4). The BI-RADS breast density distribution predicted by the DL model (A, 5.7%; B, 48.8%; C, 36.4%; D, 9.1%) was similar to the distributions found in the site 1 datasets. The predicted density distribution does not appear to be skewed toward low density estimates, as seen for site 1 (Fig 3). Agreement for the binary density task was especially strong (accuracy, 92% [95% CI: 91, 93]; κ = 0.84 [95% CI: 0.81, 0.87]; AUC, 0.980 [95% CI: 0.976, 0.986]).

Figure 3:

Confusion matrices evaluated on the site 2 synthetic two-dimensional mammographic (SM) test set without adaptation for the, A, Breast Imaging Reporting and Data System (BI-RADS) breast density task and, B, the binary density task (dense [BI-RADS C and D] vs nondense [BI-RADS A and B]). Confusion matrices evaluated on the site 2 SM test set with adaptation by matrix calibration for 500 site 2 SM training samples for the, C, BI-RADS breast density task and the, D, binary density task (dense vs nondense). The number of test samples (examinations) within each bin is shown in parentheses.

With adaptation by matrix calibration with 500 site 2 SM training samples, performance for the BI-RADS breast density task in the site 2 SM dataset substantially improved (accuracy, 80% [95% CI: 78, 82], P < .001; κ_w = 0.79 [95% CI: 0.76, 0.81], P < .001). After adaptation, the predicted BI-RADS breast density distribution (A, 16.9%; B, 43.3%; C, 29.4%; D, 10.4%) was more similar to that of the radiologists (A, 15.3%; B, 42.2%; C, 30.2%; D, 12.3%). Less improvement was seen for the binary breast density task (accuracy, 92% [95% CI: 91, 94], P = .69; κ = 0.84 [95% CI: 0.82, 0.87], P = .79).

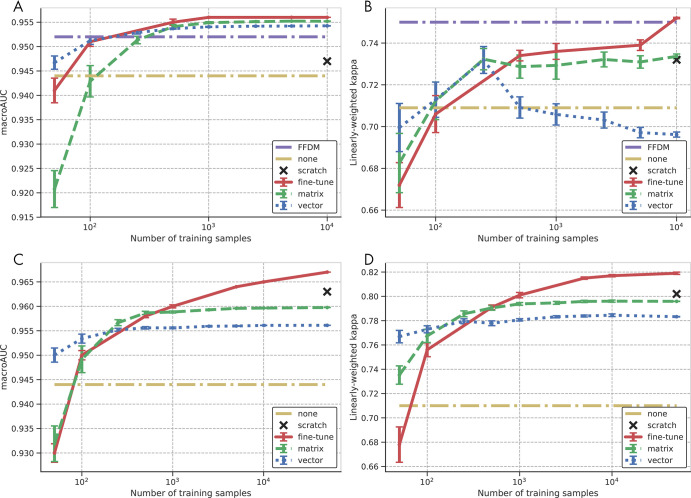
Impact of dataset size on adaptation.—The preferred adaptation method will depend on the number of training samples available for the adaptation, with more training samples benefiting methods with more parameters. Figure 4 shows the impact of the amount of training data on the performance of the adaptation methods, measured by κ_w and macroAUC, for both the site 1 and site 2 SM datasets. Each adaptation method has a range of the number of samples at which it offers the best performance, with the regions ordered by the corresponding number of parameters for the adaptation methods (vector calibration, eight parameters; matrix calibration, 20 parameters; fine tuning, 2052 parameters). This demonstrates the trade-off between the performance of the adaptation method and the amount of training data that must be acquired. When the number of training samples is small (eg, <100 images), some adaptation methods negatively impact performance. Even at the largest dataset sizes, the amount of training data was too limited for the ResNet-34 model trained from scratch on SM images to exceed the performance of the models adapted from FFDM data.

Figure 4:

Impact of the number of site-specific training samples in the target domain on the performance of the adapted model for the site 1 synthetic two-dimensional mammographic (SM) test set measured by, A, macroAUC, the average of the four areas under the curve (AUC) values from the one class versus others tasks and, B, linearly weighted Cohen κ; and for the site 2 SM test set as measured by, C, macroAUC and, D, linearly weighted Cohen κ. Results are shown for vector and matrix calibration and for retraining the last fully connected layer (fine tuning). Error bars indicate the standard error of the mean computed over 10 random realizations of the training data. Performance prior to adaptation (none) and training from scratch are shown as references. For the site 1 SM studies, the full-field digital mammography (FFDM) performance serves as an additional reference. Note that each graph is shown with its own full dynamic range to facilitate comparison of the different adaptation methods for a given metric and dataset.

Discussion

BI-RADS breast density can be an important indicator of breast cancer risk and radiologist sensitivity, but intra- and interreader variability may limit the effectiveness of this measure. DL models for estimating breast density can reduce this variability while still providing accurate assessments. However, to be a useful clinical tool, DL models need to demonstrate that they can be applied to DBT examinations and generalize across institutions. To overcome the limited training data for DBT examinations, a DL model was trained on a large set of FFDM images. The model showed close agreement with the radiologists’ reported BI-RADS breast density for a test set of FFDM images (site 1: κ_w = 0.75 [95% CI: 0.74, 0.76]) and for two datasets of SM images, which are generated as part of DBT examinations (site 1: κ_w = 0.71 [95% CI: 0.64, 0.78]; site 2: κ_w = 0.72 [95% CI: 0.70, 0.75]). The strong performance on the SM datasets from different institutions suggests that the DL model may generalize to DBT examinations and multiple sites. Further adaptation of the model for the SM datasets led to no improvement for site 1 (κ_w = 0.72 [95% CI: 0.66, 0.79]) and a more substantial improvement for site 2 (κ_w = 0.79 [95% CI: 0.76, 0.81]). The investigation of the impact of dataset size suggests that these adaptation methods could serve as practical approaches for adapting DL models if a model must be updated to account for site-specific differences.

When assessments of radiologists are accepted as the ground truth, interreader variability may limit the performance that can be achieved for a given dataset. For example, the performance obtained on the site 2 SM dataset following adaptation was higher than that obtained on the FFDM dataset used to train the model. This is likely a result of more consistency in the ground-truth labels for the site 2 SM dataset due to over 80% of the examination data having been read by two readers.

Unlike previous studies, our BI-RADS breast density DL model was evaluated on SM images from DBT examinations and on data from multiple institutions. Further, when evaluated on the FFDM images, the model appeared to offer competitive performance compared with previous DL models and commercial breast density software (κ_w = 0.75 [95% CI: 0.74, 0.76] vs Lehman et al, 0.67 [95% CI: 0.66, 0.68]; Volpara Health, 0.57 [95% CI: 0.55, 0.59]; and Hologic Quantra, 0.46 [95% CI: 0.44, 0.47]) (14, 28). Estimates of the model performance appear comparable, or even superior, to previous estimates of interradiologist variability for the BI-RADS breast density task (7). For each automated breast density method, results are reported on their respective test sets, which may be more or less challenging because of varying levels of interreader variability or other factors. Additionally, many performance metrics, such as accuracy and Cohen κ, depend on the prevalence of the BI-RADS breast density categories. Whether the model is evaluated against the assessments of individual radiologists or a consensus of multiple radiologists may also impact the apparent performance of the model. The provided performance numbers from our work and previous work are on the basis of the assessments of individual radiologists.

Other measures of breast density, such as volumetric breast density, were estimated previously by automated software for DBT examinations (29–31). Thresholds can be chosen to translate these measures to BI-RADS breast density, but this may result in lower levels of agreement than direct estimation of BI-RADS breast density (eg, κ_w = 0.47) (31). Here, BI-RADS breast density is estimated from two-dimensional SM images instead of from the three-dimensional tomosynthesis volumes because this simplifies transfer learning from the FFDM images. This is also the manner in which breast radiologists assess density for DBT examinations.

Our study had several limitations. First, the proposed domain-adaptation approaches may be less effective when the differences between domains are larger. In this work, adaptation was from two types of mammographic images acquired using equipment from the same manufacturer. Second, the FFDM data from site 1 was collected over a period covering the transition from BI-RADS version 4 to BI-RADS version 5, during which the criteria for assessing BI-RADS breast density changed. Third, the test set included multiple examinations of the same patient, which may have led to underestimation of the variance for the given performance measures. Fourth, the reference standard was breast density assessed by the original interpreting radiologist, which is known to have inter- and intrareader variation. Fifth, when a DL model is adapted for a new institution, adjustments may be made for differences in image content, patient demographics, or the interpreting radiologists. This last adjustment may result in a degree of interreader variability between the original and adapted DL models, although this variability would likely be lower than the individual interreader variability if the model learned the consensus of each group of radiologists. As a result, the improved performance after adaptation for the site 2 SM dataset could have been from differences in patient demographics or radiologist assessment practices compared with the FFDM dataset. The weaker improvement for the site 1 SM dataset may have been from similarities in these same factors.

The broad use of BI-RADS breast density DL models holds great promise for improving clinical care. The success of the DL model without adaptation suggests that the features learned by the model are largely applicable to both FFDM images and SM images from DBT examinations and to different readers and institutions. A BI-RADS breast density DL model that can generalize across sites and image types could lead to rapid and more consistent estimates of breast density for women.