The transient outward potassium current plays a key role in spiral wave breakup in ventricular tissue

Abstract

Spiral wave reentry as a mechanism of lethal ventricular arrhythmias has been widely demonstrated in animal experiments and recordings from human hearts. It has been shown that in structurally normal hearts spiral waves are unstable, breaking up into multiple wavelets via dynamical instabilities. However, many of the second-generation action potential models give rise only to stable spiral waves, raising issues regarding the underlying mechanisms of spiral wave breakup. In this study, we carried out computer simulations of two-dimensional homogeneous tissues using five ventricular action potential models. We show that the transient outward potassium current (I_to), although it is not required, plays a key role in promoting spiral wave breakup in all five models. As the maximum conductance of I_to increases, it first promotes spiral wave breakup and then stabilizes the spiral waves. In the absence of I_to, speeding up the L-type calcium kinetics can prevent spiral wave breakup, however, with the same speedup kinetics, spiral wave breakup can be promoted by increasing I_to. Increasing I_to promotes single-cell dynamical instabilities, including action potential duration alternans and chaos, and increasing I_to further suppresses these action potential dynamics. These cellular properties agree with the observation that increasing I_to first promotes spiral wave breakup and then stabilizes spiral waves in tissue. Implications of our observations to spiral wave dynamics in the real hearts and action potential model improvements are discussed.

NEW & NOTEWORTHY Spiral wave breakup manifesting as multiple wavelets is a mechanism of ventricular fibrillation. It has been known that spiral wave breakup in cardiac tissue can be caused by a steeply sloped action potential duration restitution curve, a property mainly determined by the recovery of L-type calcium current. Here, we show that the transient outward potassium current (I_to) is another current that plays a key role in spiral wave breakup, that is, spiral waves can be stable for low and high maximum I_to conductance but breakup occurs for intermediate maximum I_to conductance. Since I_to is present in normal hearts of many species and required for Brugada syndrome, it may play an important role in the spiral wave stability and arrhythmogenesis under both normal condition and Brugada syndrome.

INTRODUCTION

The leading cause of sudden cardiac death (SCD) is ventricular arrhythmias (1), in which focal excitations and reentry are the main abnormal electrical activities in the ventricular muscle of the heart (2, 3). Although the exact forms of electrical dynamics responsible for ventricular arrhythmias are still debatable (4–7), spiral waves (also called “rotors”) as a form of functional reentry have been widely demonstrated in experiments of animal hearts (8–21) and recordings from human hearts (22–24). In most of the cases, ventricular arrhythmias manifest as multiple spiral waves or rotors. Moreover, the number of spiral waves does not remain constant but is highly variable over time (8, 14, 25). Because of this spatiotemporal irregularity in spiral wave dynamics, the resulting pseudo-ECG is also highly irregular. In clinical settings, polymorphic ventricular tachycardia (VT) and ventricular fibrillation (VF), two dangerous forms of arrhythmia, also exhibit irregular ECGs. This indicates that unstable spatiotemporal spiral wave dynamics may indeed be responsible for these lethal forms of human ventricular arrhythmias.

It is well known that complex spatiotemporal spiral wave dynamics can be caused by either tissue heterogeneities or by voltage or calcium (Ca²⁺)-driven dynamical instabilities, or interactions of both (2, 26). In early computer simulations using simple action potential (AP) models, such as the Noble model (27, 28), the Beeler–Reuter model (29–32), the 1991 Luo–Rudy (LR1) model (33), and other simplified AP models (34–37), it has been shown that the slope of the AP duration (APD) restitution curve is a major parameter determining spiral wave stability. One can change the slope of the APD restitution curve and thus the spiral wave stability by adjusting the maximum conductance of some ionic currents, in particular the maximum conductance of the L-type calcium (Ca²⁺) current (I_Ca,L) or the potassium (K⁺) currents (33, 38). The roles of APD restitution in spiral wave stability have also been demonstrated in many experiments (10, 39–43). However, more recent computer simulations (44–47) have shown that many of the second-generation physiologically detailed AP models (48–52) give rise to stable spiral waves in tissue, whereas only a few of them (53–55) result in unstable spiral wave dynamics. The major reason that the spiral waves are stable in these models is that the slopes of the APD restitution curves are small (46), which may be a result of the much faster kinetics of I_Ca,L in the second-generation AP models (49). Note that these AP models were developed based on experimental data from ventricular myocytes of normal hearts. The fact that the spiral waves are stable in tissue with the myocytes described by these AP models disagrees with the observation that spiral waves are highly variable and short-lived during ventricular arrhythmias in normal hearts.

In this study, we seek to investigate spiral wave stability in tissues with the electrophysiological behaviors of the myocytes described by the second-generation AP models. We hypothesize that the transient outward K⁺ current (I_to) is a key current promoting spiral wave instability in cardiac tissue. The rationale for this hypothesis is that it has been widely shown that I_to can promote dynamical instabilities resulting in complex APD dynamics in cardiac myocytes (56–59). These cellular instabilities may also promote spiral wave instabilities in the tissue scale to result in spiral wave breakup. I_to is primarily present in the right ventricle and the epicardial layer of left ventricle (59–61). Moreover, I_to is a current required for J-wave syndrome and Brugada syndrome (62, 63), which can give rise to phase-2 reentry (64, 65). Therefore, the objectives of this study are twofold: 1) to understand the role of I_to in promoting spiral wave instabilities and thus its role in arrhythmogenesis in J-wave syndrome and Brugada syndrome, and 2) to examine if spiral wave breakup can be promoted in the second-generation AP models by increasing the maximum I_to conductance (G_to). We carry out simulations of two-dimensional (2-D) homogeneous tissue models using several widely used second-generation ventricular AP models. We show that spiral wave breakup is promoted by increasing G_to; however, the spiral waves become stable when G_to is large enough. To better understand the underlying mechanisms by which I_to promotes spiral wave breakup, we carry out simulations using the simple LR1 model. We show that in the absence of I_to, speeding up the I_Ca,L kinetics (one of the major improvements made in the second-generation AP models) stabilizes spiral waves, but spiral wave breakup can still be promoted by increasing the maximum conductance of I_to. Implications of our observations to spiral wave dynamics in the real heart and improvements of the AP models are discussed.

METHODS

Mathematical Models

We carried out single-cell and two-dimensional (2-D) tissue simulations with different ventricular myocyte AP models. The differential equation for voltage for single-cell simulations is as follows:

$$\frac{dV}{dt}=\left(-I_{\mathrm{ion}}+I_{\mathrm{sti}}\right)/C_{\mathrm{m}},$$ (1)

where C_m = 1 µF/cm² is the membrane capacitance, I_ion the ionic current density, and I_sti the external stimulus current density. The differential equation for voltage of 2-D tissue is as follows:

$$\frac{\partial V}{\partial t}=-\frac{I_{\mathrm{ion}}}{C_{\mathrm{m}}}+D\left(\frac{{\partial }^{2}V}{\partial x^2}+\frac{{\partial }^{2}V}{\partial y^2}\right),$$ (2)

where D is the diffusion constant. We used the following AP models: 1) the 1991 Luo and Rudy (LR1) guinea pig ventricular AP model (66); 2) the 1994 Luo and Rudy (LRd) guinea pig ventricular AP model with later modifications (49, 67); 3) the Mahajan et al. rabbit ventricular AP model (68); 4) the O’Hara et al. (ORd) human ventricular AP model (50); and 4) the 2004 ten Tusscher et al. (TP04) human ventricular AP model (52). Except for the LR1 model, computer codes of the single-cell AP models were downloaded from the websites of the original authors to ensure originality of the models. These single-cell models were implemented in 2-D tissue using Eq. 2. We used D = 0.00154 cm²/ms for the TP04 model, the original value used by ten Tusscher et al. (52). We used D = 0.001 cm²/ms for the other models, which gives rise to a conduction velocity around 0.55 m/s for the LR1 model with a maximum I_Na conductance of 16 mS/cm² (38). No-flux boundary conditions were used.

Simulation Methods

We used the typical cross-field protocol to induce a single spiral wave in the 2-D tissue. The initial conditions were set as follows. A single cell (Eq. 1) was paced at a pacing cycle length (PCL) of 500 ms for 1,000 beats to remove transient behaviors. The values of all the variables were recorded at the end of the pacing and they were used as the initial conditions for all the cells in the 2-D tissue. The entire left boundary of cells in the tissue was then paced, triggering a wave propagating toward the center of the tissue. Once the propagated wave repolarizes at the center of the tissue, all cells in the bottom half of the tissue were depolarized by fixing their voltages to −30 mV for 2 ms. Afterward, Eq. 2 was integrated for 5–10 s. APD and the spiral wave cycle length (CL) were calculated from a cell located at (3.2 cm, 3.2 cm) in the tissue. APD was defined as the time period in which V remains above −75 mV.

For all the models, the 2-D tissue was discretized as Δx = Δy = 0.0125 cm, with 2,048 × 2,048 discretized cells for all models except for the LR1 model. A 1,024 × 1,024 cells were used for the LR1 model. A time-adaptive forward Euler method was used with a time step of Δt = 0.0025 ms if the change in voltage ΔV > 0.1 mV in a time step, otherwise the time step is Δt = 0.025 ms. Simulations were performed on Tesla and GeForce GPUs (NVIDIA corporation) using C++ programs in CUDA, a programming language designed for graphical processing units.

RESULTS

I_to Promotes Spiral Wave Breakup in Tissue Using the LRd Model

The LRd model is an AP model for guinea pig ventricular myocytes developed in 1994 by Luo and Rudy (49); in this study, we used the later modified version by Faber and Rudy (67) with an I_to formulation given by Gima and Rudy (69). We first simulated spiral wave dynamics in the LRd model with different G_to. A spiral wave in 2-D tissue using the original LRd model is stable with small variations in CL and APD (Fig. 1A). In this case, the maximum I_to conductance is G_to = 0.5 mS/cm² which was set as the control value. When G_to is two times of the control value (Fig. 1B), spiral wave breakup occurs with CL and APD varying in large ranges and irregularly. When G_to is five times of the control value (Fig. 1C), spiral wave breakup still occurs but the wavelength becomes apparently shorter. APD remains below 40 ms and CL around 60 ms but can be occasionally large (APD ∼100 ms and CL ∼150 ms). When G_to is 6.5 times of the control value, spiral wave breakup occurs initially with large CL but small APD variations. The CL and APD eventually become unchanged (Fig. 1D). In this case, after the initial chaotic spiral wave breakup phase, the spiral waves become stable, and thus the spiral wave pattern, although spatially irregular, is temporally periodic. When G_to is 10 times of the control value (Fig. 1E), no breakup occurs, and the spiral wave is completely stable with a much shorter APD and CL compared with control. We replotted the values of APD and CL from the aforementioned cases in a single panel (Fig. 1F) to compare the APD and CL variations.

Figure 1.

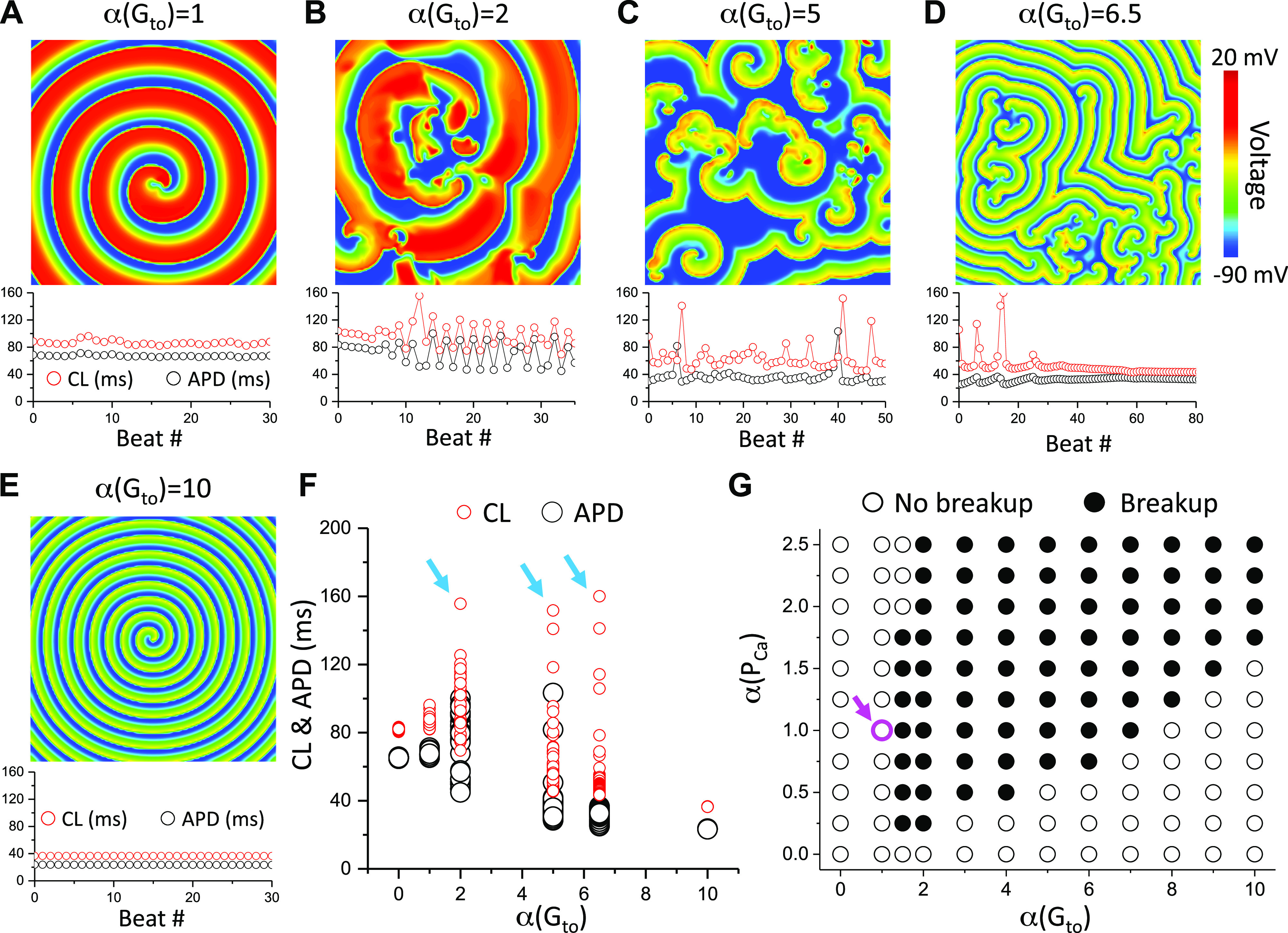
Effects of the maximum I_to conductance on spiral wave breakup in two-dimensional (2-D) tissue with the 1994 Luo and Rudy (LRd) model. A–E: voltage snapshots (upper) and CL and APD vs. beat # (lower) for the original (control) LRd model (A), two times of the control G_to (B), five times of the control G_to (C), 6.5 times of the control G_to (D), and 10 times of the control G_to (E). F: APD and CL vs. α(G_to) replotted from data shown in A–E. Cyan arrows indicate the G_to with spiral wave breakup. G: spiral wave behaviors versus α(P_Ca) and α(G_to). The magenta circle and arrow mark the parameter set of the original LRd model (control). The control G_to is 0.5 mS/cm².

We systematically explored the spiral wave behaviors for different maximum I_Ca,L conductance (P_Ca, which was used in the AP models to describe the strength of I_Ca,L, proportional to the maximum conductance) and G_to while maintaining other parameters at their control values, summarized in Fig. 1G. We used the cross-field protocol described in methods to induce a single spiral wave in the tissue. If this spiral wave remained intact without breakup, we labeled the point as “no breakup” (open circles). If the spiral wave did not remain intact, but degenerated into multiple spiral waves, whether they finally became stable (such as the case in Fig. 1D) or unstable (such as the cases in Fig. 1, B and C), we labeled the point as “breakup” (solid circles). As shown in Fig. 1G, spiral wave breakup occurs in a wide range of parameters when I_to is present. When I_to is absent (G_to = 0) or at its control value, no spiral wave breakup occurs for P_Ca ranging from 0 to 2.5 times of its control value. When G_to is larger than its control value, spiral wave breakup occurs in a wide range of P_Ca. When G_to is too large, the spiral wave becomes stable again. Note that at the left boundary from no breakup to breakup, a larger P_Ca prevents breakup (see the third column from the left). At the right boundary from breakup to no breakup, a larger P_Ca promotes breakup.

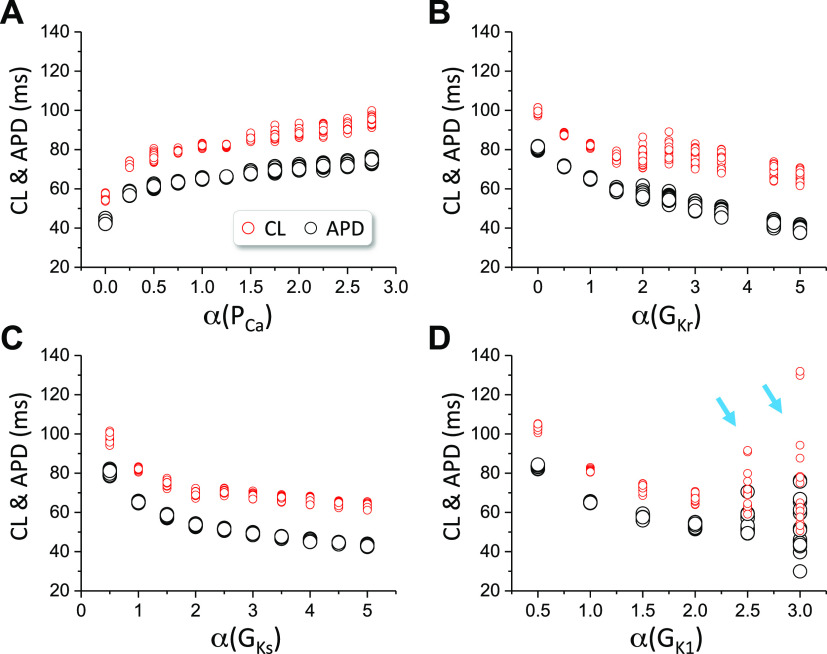
As shown in Fig. 1, I_to plays a critical role in spiral wave breakup in the LRd model. We then test whether spiral wave breakup can occur in the LRd model in the absence of I_to. We set G_to = 0 and varied the maximum conductance of other ionic currents to assess the spiral wave dynamics. Figure 2 plots APD and CL for different fold changes of the maximum conductance of I_Ca,L (Fig. 2A), I_Kr (Fig. 2B), I_Ks (Fig. 2C), and I_K1 (Fig. 2D). We did not observe spiral wave breakup for P_Ca from 0 to 2.75 times of its control value, for G_Kr from 0 to 5 times of its control value, for G_Ks from 0.5 to 5 times of its control value, or for G_K1 from 0.5 to 2 times of its control value. However, when G_K1 is larger than 2.5 times of its control value, spiral wave breakup occurs (indicated by arrows in Fig. 2D). Therefore, in the LRd model and in the absence of I_to, no spiral wave breakup can occur in wide ranges of parameters away from their control values.

Figure 2.

Spiral wave dynamics in two-dimensional (2-D) tissue with the Luo and Rudy (LRd) model in the absence of I_to. cycle length (CL) and action potential duration (APD) of spiral waves vs. the fold change (α) of the maximum conductance of different ionic currents. G_to=0. The 2-D tissue simulations were done the same way as in Fig. 1. A: P_Ca. B: G_Kr. C: G_Ks. D: G_K1. Cyan arrows indicate that breakup occurs.

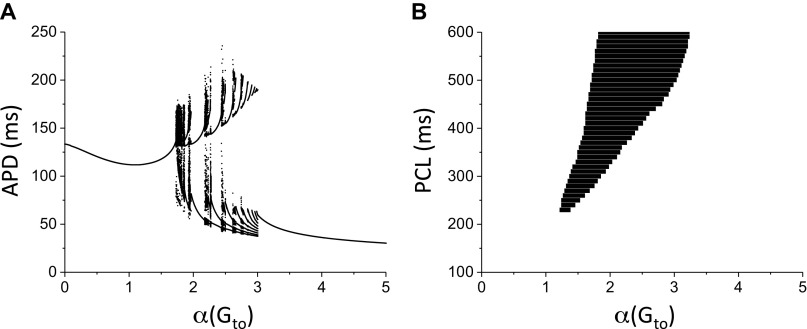
To gain some insights into I_to promoting APD instabilities in the LRd model, we carried out single-cell simulations. Figure 3A shows a bifurcation diagram showing APD versus G_to for PCL = 500 ms. When G_to is small, APD is stable, that is, APD is the same from beat to beat. As G_to is increased to certain value, APD instabilities occur, in which APD changes from beat to beat, such as APD alternans and chaos. As G_to increases further, APD becomes stable again but becomes much shorter. Figure 3B shows the APD behaviors for different PCL and G_to. For the control G_to [α(G_to) = 1], APD is stable for any PCL, which agrees with the observation that there is no spiral wave breakup in the control LRd model. For very large G_to, APD becomes stable again, which also agrees with the observation that spiral wave is stable when I_to conductance is large enough.

Figure 3.

Effects of I_to on action potential duration (APD) dynamics in a single Luo and Rudy (LRd) cell. A: bifurcation diagram showing APD vs. α(G_to) for pacing cycle length (PCL) = 500 ms. For each α(G_to) value, 100 APDs were plotted. B: region of APD instability for different G_to and PCL. The black region is the unstable region in which APD varies from beat to beat, including APD alternans and chaos.

I_to Promotes Spiral Wave Breakup in Tissue Using Other Ventricular AP Models

We carried out simulations in 2-D tissue using three other AP models for spiral wave stability: the rabbit ventricular myocyte model by Mahajan et al. (68), the TP04 human ventricular myocyte model (52), and the ORd human ventricular myocyte model (50). For each model, we showed voltage snapshots for G_to = 0, control G_to, an intermediate G_to causing spiral wave breakup, and a very large G_to resulting in a stable spiral wave. We also investigated spiral wave stability in the absence of I_to by varying the maximum conductance of other currents.

Figure 4 shows the results for the Mahajan et al. model. We varied the maximum conductance of the fast I_to (I_to,f) in this model. The spiral wave is stable for G_to = 0 and the control G_to (0.11 mS/cm²), breaks up when G_to is two times of its control value, and becomes stable when G_to is four times of its control value (in Fig. 4A, left). The right panel plots APD and CL for the four cases, which show when spiral wave breakup occurs, both APD and CL varied in wide ranges. In the absence of I_to (Fig. 4B), spiral wave breakup occurs when P_Ca is 1.5 times its control value or larger or when G_Ks is reduced by half. Therefore, I_to promotes spiral breakup but is not required in this model.

Figure 4.

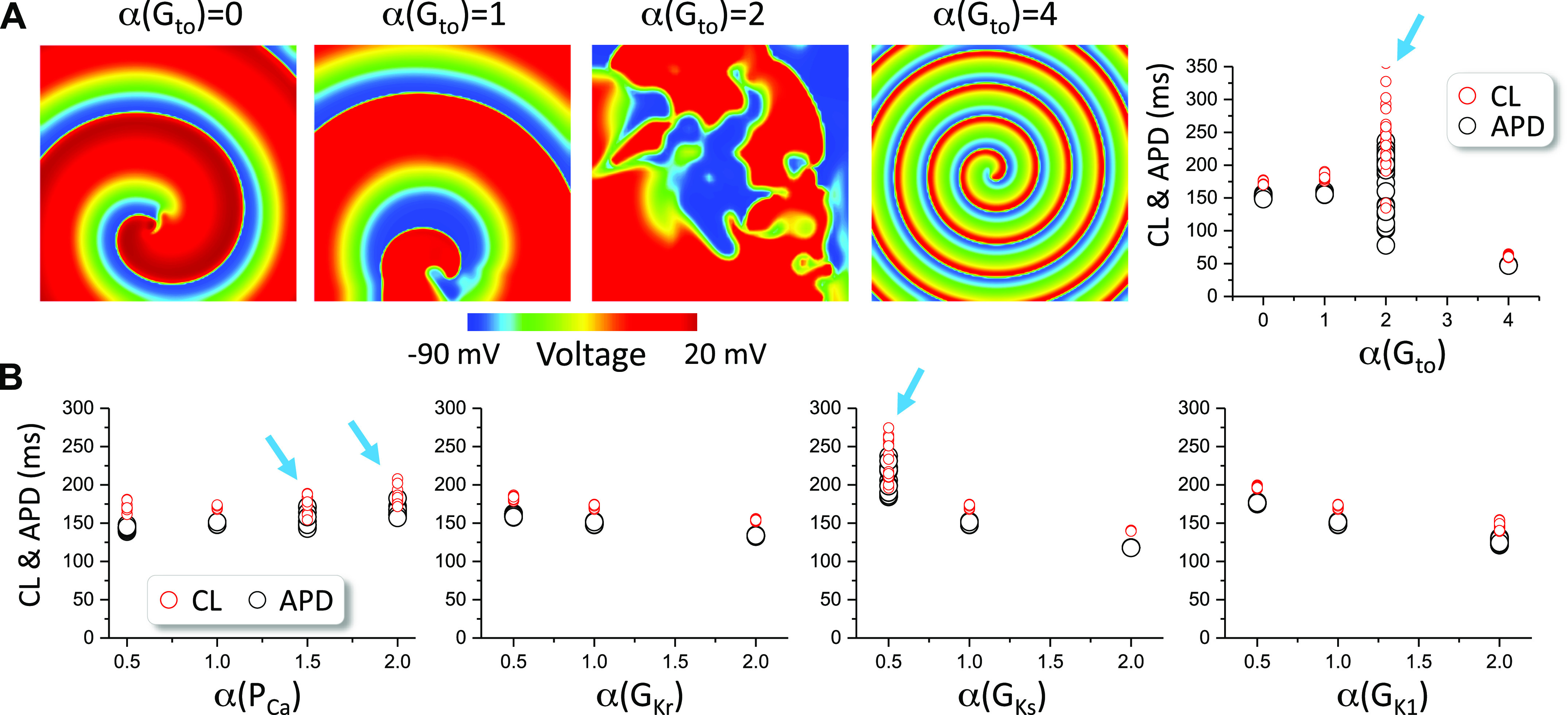
Spiral wave dynamics in two-dimensional (2-D) tissue with the Mahajan et al. model. A: left four panels: voltage snapshots of spiral waves at different G_to levels. Right panel: action potential duration (APD) and cycle length (CL) vs. G_to for the four G_to levels. B: APD and CL vs. the fold change (α) of the control maximum conductance of I_Ca,L, I_Kr, I_Ks, and I_K1 in the absence of I_to (G_to = 0). Arrows indicate the cases of spiral wave breakup. The control G_to is 0.11 mS/cm². Only the fast component (I_to,f) was altered.

Figure 5 shows the results for the TP04 model. The spiral wave is stable for G_to = 0 and control G_to (0.294 mS/cm²), breaks up when G_to is 20 times of its control value, and becomes stable when G_to is 100 times of its control value (in Fig. 5A, left). APD and CL vary in wide ranges when spiral breakup occurs (in Fig. 5A, right). However, in the absence of I_to, no spiral wave breakup occurs in this model when the maximum conductance of the selected ionic currents is doubled or halved (Fig. 5B).

Figure 5.

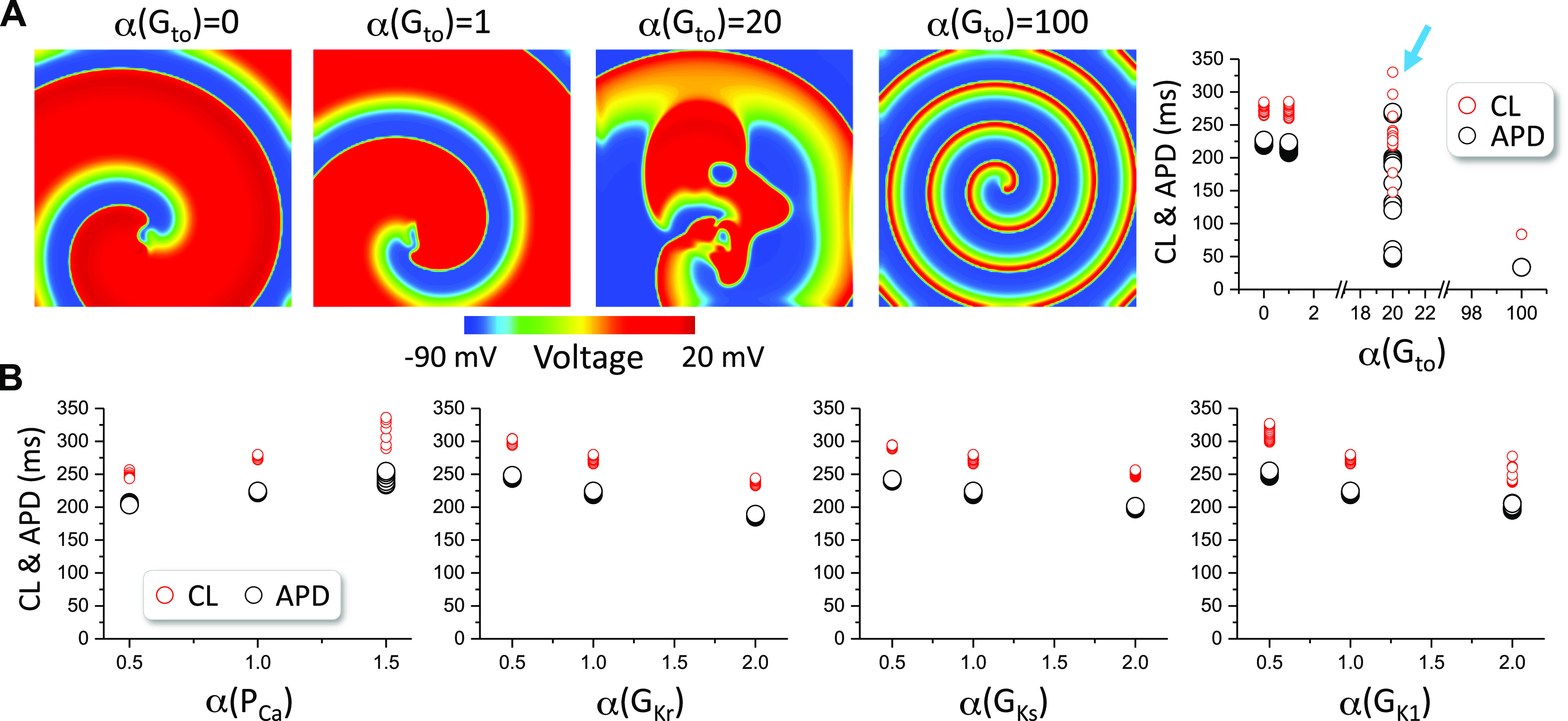
Spiral wave stability in two-dimensional (2-D) tissue with the TP04 model. A: left four panels: voltage snapshots of spiral waves at different G_to levels. Right panel: action potential duration (APD) and cycle length (CL) vs. G_to for the four G_to levels. B: APD and CL vs. the fold change (α) of the control maximum conductance of I_Ca,L, I_Kr, I_Ks, and I_K1 in the absence of I_to (G_to = 0). Arrows indicate the cases of spiral wave breakup. The control G_to is 0.294 mS/cm². TP04, 2004 ten Tusscher et al.

We observed the same spiral wave behaviors for the ORd model (Fig. 6). That is, the spiral wave is stable for G_to = 0 and control G_to (0.08 mS/cm²), breaks up in intermediate G_to, and becomes stable when G_to is very large. In the absence of I_to, no breakup occurs when the maximum conductance of other currents is doubled or halved.

Figure 6.

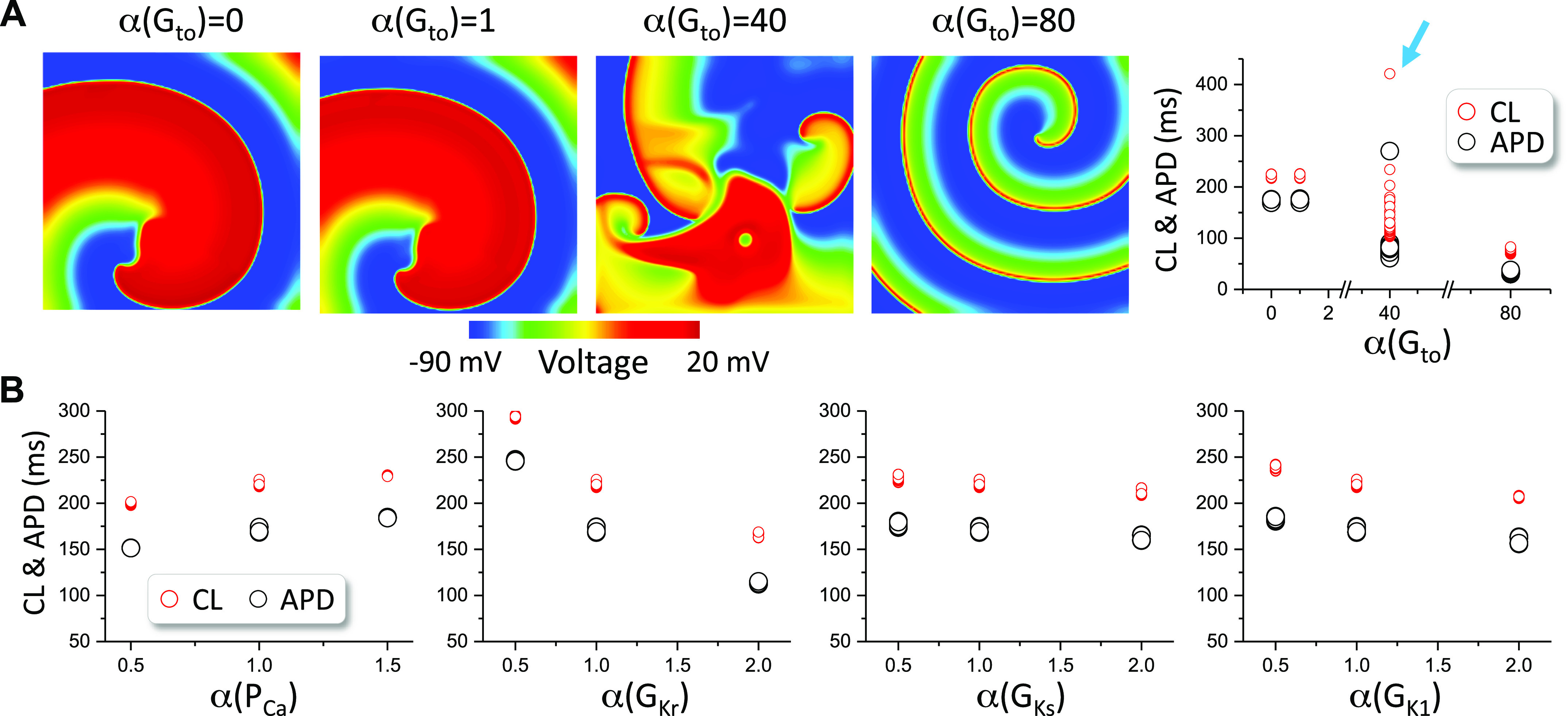
Spiral wave stability in two-dimensional (2-D) tissue with the O’Hara et al. (ORd) model. A: left four panels: voltage snapshots of spiral waves at different G_to levels. Right panel: action potential duration (APD) and cycle length (CL) vs. G_to for the four G_to levels. B: APD and CL vs. the fold change (α) of the control maximum conductance of I_Ca,L, I_Kr, I_Ks, and I_K1 in the absence of I_to (G_to = 0). Arrows indicate the cases of spiral wave breakup. The control G_to is 0.08 mS/cm².

L-type Ca²⁺ Channel Kinetics and I_to Conductance on Spiral Wave Breakup: Insights from the Simple LR1 Model

As shown in the simulation results above, I_to plays a critical role in spiral wave stability. In particular, for the LRd model, the spiral wave remains stable for a wide range of parameters when I_to is absent. One of the major changes of the LRd model from the previous models, such as the LR1 model (66) and the Beeler–Reuter model (70), was the reformulation of I_Ca,L based on patch clamp experimental data that show much faster kinetics (49). It has been widely shown that I_Ca,L and its kinetics play a key role in spiral wave stability (29, 30, 33, 38, 71, 72), the reformulation of I_Ca,L is the most likely cause for stable spiral wave in the LRd model and other second-generation AP models. As shown in our simulations, altering other currents cannot cause spiral wave breakup (except the Mahajan et al. model) but increases in I_to can promote spiral wave breakup in all the AP models. Furthermore, the spiral wave becomes stable when I_to is very large. However, the underlying mechanism is not well understood. To gain more mechanistic insights into the effects of I_to on promoting spiral wave breakup, we used a relatively simple AP model, the LR1 model, to investigate the interactions of I_Ca,L and I_to. We added an I_to [I_to,f from the Mahajan et al. model (68)] to the model. As shown in many previous studies (33, 47, 73), spiral waves in 2-D tissue with cells described by the LR1 model are unstable. In the LR1 model, I_Ca,L was called slow inward current (I_si) because of the slow kinetics adopted from the Beeler–Reuter model (70). Previous studies (29, 38, 72) have shown that speeding up the kinetics of I_si in the Beeler–Reuter model or the LR1 model, flattens APD restitution and stabilizes the spiral waves. We simulated two cases: the original slow I_si kinetics and a speedup I_si kinetics (70% reduction of both the activation and inactivation time constants).

In the case of the original I_si kinetics (Fig. 7A), spiral wave breakup occurs in the original model, but breakup is prevented by reducing G_si and/or increasing G_to (the lower right region). In the case of the speedup I_si kinetics (Fig. 7B), spiral waves are stable when G_si is large and G_to is small. As G_to increases, spiral wave breakup occurs. When G_to is even larger, spiral wave becomes stable again. Representative voltage snapshots from these three regions are shown in Fig. 7C. This behavior is very similar to that of the LRd model (compare Fig. 7B with Fig. 1G).

Figure 7.

Spiral wave dynamics in two-dimensional (2-D) tissue with the 1991 Luo and Rudy (LR1) model. A: spiral wave behaviors vs. G_si and G_to with the original I_si kinetic. The magenta circle and arrow mark the parameter set of the original LR1 model (control). B: spiral wave behaviors vs. G_si and G_to for a speedup I_si kinetics. To speed up the kinetics of I_si, the time constants of the activation and inactivation gates were reduced by multiplying a factor 0.3, i.e., ${\tau }_d\to 0.3{\tau }_d$ and ${\tau }_f\to 0.3{\tau }_f$. C: voltage snapshots showing spiral waves for the speedup I_si kinetics for G_si = 0.09 mS/µF and different G_to as indicated on each panel.

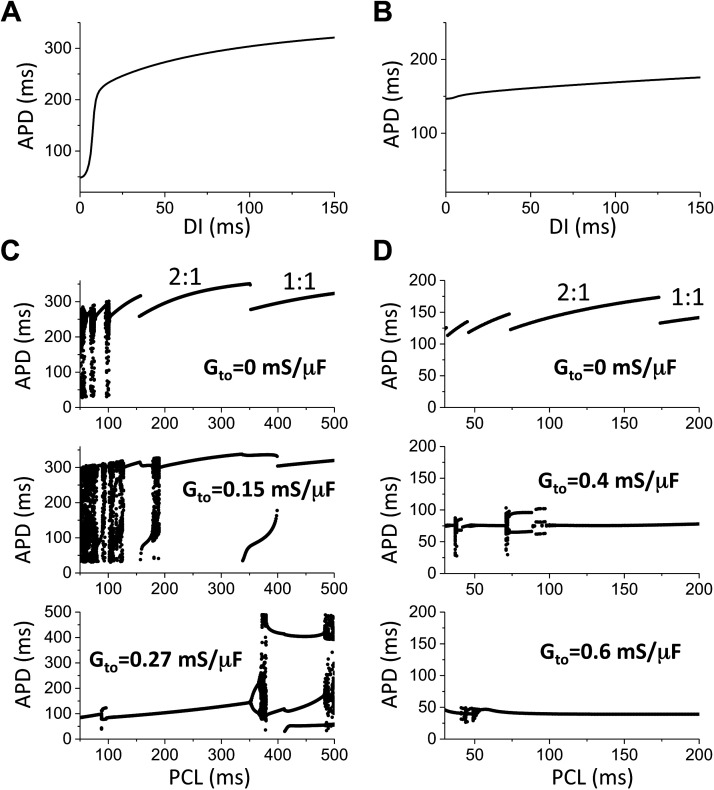
To gain more mechanistic insights into the effects of I_to on spiral wave stability in the LR1 model, we carried out single-cell simulations to investigate the effects of I_to on AP dynamics. Speeding up the I_si kinetics results in a flattened APD restitution curve (Fig. 8, A and B), agreeing with the fact that speeding up the I_si kinetics stabilizes the spiral wave. For the control kinetics, when G_to = 0, complex APD dynamics occurs at very fast pacing (Fig. 8C). As G_to increases, APD instabilities occur at longer PCL. As G_to increases further, APD become stable at short PCLs. This agrees with the observation that spiral wave becomes stable as the maximum conductance of I_to increases (note that the CL of spiral waves corresponds to the short PCL range). For the speedup kinetics, when G_to = 0, the APD is stable for all PCLs (Fig. 8D). However, as G_to increases to a certain level, unstable APD dynamics can be observed, indicating that I_to promoted dynamical instabilities. As G_to increases even further the APD become stable again. This agrees with the observation that spiral wave breakup occurs in the intermediate range of G_to in the case of speedup I_si kinetics.

Figure 8.

Effects of I_to on action potential duration (APD) dynamics in the 1991 Luo and Rudy (LR1) model. A: APD restitution curve for the control I_si kinetics. B: APD restitution curve for the speedup I_si kinetics. C: bifurcations showing APD vs pacing cycle length (PCL) for G_to values marked on each panel for the control I_si kinetics. D: bifurcations showing APD vs. PCL for G_to values marked on each panel for the speedup I_si kinetics.

DISCUSSION

In this study, we carried out simulations to investigate the roles of I_to in spiral wave dynamics in 2-D cardiac tissue. We simulated five ventricular AP models and investigated the spiral wave stability of each model by varying the maximum conductance of I_to and those of other major ionic currents. Our major finding is that the maximum I_to conductance and the I_Ca,L kinetics are the two key parameters for spiral wave breakup in cardiac tissue. In this study, we discuss the mechanisms of spiral wave breakup and the mechanisms by which I_to promotes spiral wave breakup.

Mechanisms of Spiral Wave Breakup and the Role of I_ca,L Recovery

Different mechanisms of spiral wave breakup in cardiac tissue have been proposed (21, 27, 33, 35, 36, 73), including: 1) dynamical instabilities; 2) fibrillatory conduction block caused by repolarization heterogeneities; and 3) low and heterogeneous excitability. Note that repolarization or excitability heterogeneities are required for the latter two mechanisms but not for the first mechanism. Spiral wave breakup caused by dynamical instabilities can occur in homogeneous tissue, and a steep slope of the APD restitution curve is well-known to promote dynamical instabilities. Spiral wave breakup occurs when the slope is greater than one in a wide diastolic interval (DI) range (38). The roles of APD restitution in spiral wave stability have also been demonstrated in many experiments (10, 39–43). APD restitution results from the incomplete recovery of ion channels. Although changing the conductance and kinetics of any of the currents affects APD as well as APD restitution, different currents exhibit different effects, making the effects of some currents more profound compared with others in spiral wave stability. For example, the Na⁺ channel recovers quickly, and incomplete recovery of the Na⁺ current at very short DIs shortens APD, contributing to the steepness of the APD restitution curve at very short DIs. Therefore, the Na⁺ channel plays a very important role in spiral wave meandering (38). The L-type Ca²⁺ channels recover more slowly than the Na⁺ channels, and thus affect APD restitution at longer DIs compared with that of Na⁺ channels. Because of this, I_Ca,L recovery plays a key role in spiral wave breakup (33, 38, 71). K⁺ channels recover in a wide range of DIs and thus affect the APD restitution at a wide range of DIs, which also affect spiral wave stabilities.

I_Ca,L was first formulated by Beeler and Reuter (70) and adopted in the LR1 model (66). However, the kinetics of this formulation is slow, and thus the current was called the slow-inward current (I_si). A major reason for the development of the LRd model (49) is to reformulate I_Ca,L based on single-cell and single-channel experiments, which show much faster activation and inactivation kinetics. Similar I_Ca,L kinetics were implemented in other second-generation AP models. Speeding up the kinetics flattens the APD restitution curve (Fig. 8) and thus prevents spiral wave breakup (see Fig. 7). For the same reason, the spiral wave in the LRd model is stable. As shown by Elshrif and Cherry (46), the slopes of the APD restitution curves are small in many of the second-generation AP models, which are likely caused by the fast I_Ca,L kinetics and the major cause for stable spiral waves for these models (44–47) (also see Figs. 5 and 6).

On the other hand, in the Mahajan et al. model (68) which uses a Markovian formulation to model the proper recovery kinetics of I_Ca,L, spiral wave breakup can occur by increasing the maximum conductance of I_Ca,L or reducing the maximum conductance of the K⁺ currents (see Fig. 4). It has been shown that spiral waves are unstable and break up in tissues using the canine ventricular AP model by Hund and Rudy (44). I_Ca,L in the Hund and Rudy model (53) was reformulated to result in a slower recovery by introducing a new gating variable with a slower time constant. I_Ca,L was also reformulated in the 2006 version of the ten Tusscher et al. model (55) to slow the recovery, which can then exhibit APD alternans and spiral wave breakup. These modeling studies further demonstrate that the kinetics of I_Ca,L recovery plays a key role in promoting dynamical instabilities for spiral wave breakup.

Mechanism by Which I_to Promotes Spiral Wave Breakup

A well-known effect of I_to is to promote a so-called spike-and-dome AP morphology. As the maximum conductance of I_to increases (58, 74), APD initially increases but then suddenly decreases once the maximum conductance reaches a certain value. This same effect can exhibit a large effect on APD restitution properties as shown in computer simulations (58) and experiments (59, 75). However, as shown in our recent studies (57, 58), I_to unmasks/exacerbates the effects of memory, resulting in a strong dependence of the APD restitution properties on the prior pacing history. Because of the memory effects, the slope of the APD restitution curve is not a good predictor of the APD instability, and memory has to be taken into account. Instead of calculating the APD restitution curves, we carried out simulations to show dynamical instabilities promoted by I_to in single cells (Figs. 3 and 8).

Based on our simulations of the LR1 model, I_to is not required for spiral wave breakup, and increasing the maximum I_to conductance can stabilize the spiral wave. Speeding up the I_Ca,L kinetics flattens the APD restitution curve and stabilizes the spiral wave. However, under this condition, spiral wave breakup can be promoted by increasing the maximum I_to conductance. This insight can explain why the spiral waves are stable but breakup is promoted by I_to in tissue using the second-generation AP models. In other words, the fast I_Ca,L kinetics results in stable spiral waves, but I_to promotes instabilities to cause spiral wave breakup. As shown in our simulations of the AP models, in the absence of I_to, it becomes difficult to promote spiral wave breakup by altering the maximum conductance of the other ionic currents, indicating a distinct role of I_to in promoting spiral wave instabilities. Note that I_to exhibits a fast and a slow component (abbreviated as I_to,f and I_to,s, respectively). In our simulations, only the effect of I_to,f (even though they are denoted as I_to in the AP models) was investigated. However, since I_to,s recovers very slowly with a time constant ∼3 s (76), it remains mostly inactivated when the heart rate is fast. Therefore, it may not exhibit a large effect for spiral wave stability because the spiral wave CL (<300 ms) is much shorter than the recovery time of I_to,s. Moreover, besides its maximum conductance, the activation and inactivation kinetics of I_to,f and its recovery time may still play an important role in spiral wave stability because the spiral wave CL is short.

We are not aware of any direct experiments demonstrating the role of I_to in spiral wave stability. In one experimental study (77), 4-AP, a selective blocker of I_to, converted VF to VT. This may agree with our simulation results suggesting that increasing I_to conductance promotes spiral wave breakup (e.g., VT to VF) and blocking I_to stabilizes spiral waves (VF to VT). In the optical mapping experiments of arrhythmias in Brugada syndrome by Aiba et al. (75), they observed VT and VF in different animals, and VT occurred in the ones with shortened APD and flattened APD restitution curves. This can be explained by the fact that a stronger I_to shortens APD and stabilizes spiral wave reentry as seen in our simulations.

Potential Caveats in the AP Models

As shown in previous simulations (44–47) and the current study, many of the second-generation AP models (48–52) give rise to stable spiral waves in a homogeneous tissue. Considering the experimental observations that spiral waves are unstable in normal undiseased hearts, one may assume that spiral wave breakup should occur in these AP models if the unstable spiral wave behaviors are caused by dynamical instabilities. This disagreement might lead one to argue that there are potential caveats in these AP models that prevent spiral wave breakup. One potential caveat is that too little I_to was included in these models and spiral wave breakup is caused by I_to in the real hearts. Although I_to may be present in many species (78), some species may not exhibit much I_to. For example, there is little I_to in the guinea pig ventricles (79). With no or a small I_to, the spiral wave is stable in the LRd guinea pig ventricular model, disagreeing with the experimental observations that spiral waves are unstable in guinea pig hearts. As we discussed above, stabilization of the spiral waves is due to the fast kinetics of I_Ca,L in the models that have incorporated better patch-clamp experimental data. On the other hand, the recovery of I_Ca,L of the Mahajan et al. model, the Hund and Rudy model, and 2006 ten Tusscher et al. model were slowed, spiral wave breakup then occurs in these models (44, 55, 71). Therefore, we argue that I_to may play a key role in spiral wave breakup in certain species and the recovery kinetics of I_Ca,L in some of the AP models might need to be slowed to allow spiral wave breakup.

Limitations

Several limitations of the current study need to be mentioned. The maximum I_to conductance needed for spiral wave breakup or stabilizing the spiral wave is different for different AP models. For example, the maximum I_to conductance needed for spiral wave breakup in the LRd model and the Mahajan et al. model is roughly in the physiological range [see the literature survey in Nguyen et al. (78)]. However, the maximum I_to conductance needed for spiral wave breakup and stabilization in the TP04 model and the ORd model is very large. The difference may attribute to the different mathematical formulations of the AP models, which could be caveats in the AP models, as we discussed in the last section in DISCUSSION. On the other hand, there are other transient outward currents such as the small conductance Ca²⁺-activated K⁺ current (80, 81) and the Ca²⁺-activated chloride current (82, 83). These currents may work in synergy with I_to to affect spiral wave stability.

In our simulations, we altered the maximum conductance of other ionic currents in the absence of I_to to investigate their contributions to spiral wave stability. Our conclusions may be biased due to the limited number of simulations and the choice of parameter ranges. Ideally, one may perform a parameter sensitivity analysis (84–87) to reveal the differential contribution of each ionic current to spiral wave stability, but due to the extremely high computational demand of tissue simulations, it is unrealistic to carry out the large number of simulations needed for regression analyses.

Unstable spiral wave dynamics observed in the real hearts can also be caused by spontaneous Ca²⁺ release. However, all AP models simulated in this study lack spontaneous Ca²⁺ release, whose role in spiral wave breakup needs to be modeled using more detailed cell models (88) and multiscale computational methods (89).

Finally, we did not alter the I_Ca,L recovery properties of other models but the activation and inactivation time constants of I_si in the LR1 model to investigate the role of I_Ca,L recovery on spiral wave stability. However, changing both time constants changes not only the recovery but also other properties, such as the conductance of I_Ca,L, and thus the stabilization of the spiral wave may not only be attributed to I_si recovery. As we mentioned in detail in the section of the LR1 model in RESULTS, one of the major improvements of the second-generation AP models is the speedup of the I_Ca,L kinetics, which results in stable spiral waves for these models. On the other hand, spiral wave stability in a homogeneous tissue is a dynamical property that can be affected by many parameters (maximum conductance, time constants, and ion concentrations, etc.), and parameter sensitivity analyses may be needed to pinpoint the differential contributions of the parameters. Nevertheless, based on the previous studies, I_Ca,L recovery is a key parameter for spiral wave stability and our findings show that I_to conductance is another key parameter for spiral wave stability in cardiac tissue.

Conclusions

Besides I_Ca,L recovery kinetics, the maximum I_to conductance is another key parameter that can promote spiral wave breakup in cardiac tissue. It may contribute to the unstable spiral wave dynamics observed in experiments of normal hearts and may play important roles in promoting the transition from VT to VF in Brugada syndrome.

GRANTS

This study was supported by National Institutes of Health Grants R01 HL139829, R01 HL134709, and F30 HL140864; Zhejiang Province Commonweal Projects Grant LGF18A050001 (to X.Y.); and China Scholarship Council Grant No. 201708330401 (to X.Y.).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

J.L., P-S.C., and Z.Q. conceived and designed research; J.L. and X.Y. performed experiments; J.L. and Z.Q. analyzed data; J.L., X.Y., and Z.Q. prepared figures; J.L. and Z.Q. drafted manuscript; J.L., P-S.C., and Z.Q. edited and revised manuscript; J.L., X.Y., P-S.C., and Z.Q. approved final version of manuscript.