Homology of process: developmental dynamics in comparative biology

Abstract

Comparative biology builds up systematic knowledge of the diversity of life, across evolutionary lineages and levels of organization, starting with evidence from a sparse sample of model organisms. In developmental biology, a key obstacle to the growth of comparative approaches is that the concept of homology is not very well defined for levels of organization that are intermediate between individual genes and morphological characters. In this paper, we investigate what it means for ontogenetic processes to be homologous, focusing specifically on the examples of insect segmentation and vertebrate somitogenesis. These processes can be homologous without homology of the underlying genes or gene networks, since the latter can diverge over evolutionary time, while the dynamics of the process remain the same. Ontogenetic processes like these therefore constitute a dissociable level and distinctive unit of comparison requiring their own specific criteria of homology. In addition, such processes are typically complex and nonlinear, such that their rigorous description and comparison requires not only observation and experimentation, but also dynamical modelling. We propose six criteria of process homology, combining recognized indicators (sameness of parts, morphological outcome and topological position) with novel ones derived from dynamical systems modelling (sameness of dynamical properties, dynamical complexity and evidence for transitional forms). We show how these criteria apply to animal segmentation and other ontogenetic processes. We conclude by situating our proposed dynamical framework for homology of process in relation to similar research programmes, such as process structuralism and developmental approaches to morphological homology.

1. Introduction: why process homology?

It has long been recognized that biology is best conducted in a comparative mode. The evolved diversity of life is a massive natural experiment, and hypotheses about its causes can be generated and tested through the use of comparative methods [1]. Distinguishing fundamental regulatory principles of ontogeny from accidental and contingent features also requires us to compare developmental systems across multiple evolutionary lineages. In addition, our ability to generalize insights gained from specific experimental model systems must be based on comparative principles, given that the number of evolutionary lineages to be studied vastly outnumbers our capacity to investigate each of them individually. Finally, a comparative approach to development in particular is essential for our understanding of the process of evolution itself, since changes in morphological traits are necessarily mediated by changes in the processes that generate them (e.g. [2–4]; see also [5], and historical references therein).

At the heart of comparative biology lies the concept of homology. In the words of David Wake: ‘Homology is the central concept for all biology. Whenever we say that a mammalian hormone is the “same” as a fish hormone, that a human sequence is the “same” as a sequence in a chimp or a mouse, that a HOX gene is the “same” in a mouse, a fruit fly, a frog, and a human—even when we argue that discoveries about a roundworm, a fruit fly, a frog, a mouse, or a chimp have relevance to the human condition—we have made a bold and direct statement about homology’ [6, p. 268]. With the advent of evolutionary developmental biology, or evo-devo, developmental biology has become an increasingly comparative discipline, and ‘once a field becomes comparative, it must reckon with the idea of homology’ [7].

Homology can hold between entities at many different levels of organization. Classical perspectives focus on the relationships of morphological characters, guided by Owen's [8] definition of a homologue as ‘the same organ in different animals under every variety of form and function’. After Darwin, ‘the same organ’ was generally interpreted as ‘a feature of two or more taxa […] derived from the same (or a corresponding) feature of their common ancestor’ [9, p. 45; 10]. The transformation of ‘homology’ into an evolutionary and ultimately phylogenetic concept led biologists to appreciate that almost any kind of characteristic could be homologized by being embedded in a comparative-phylogenetic framework [11].

In the late 1960s and early 1970s, homology was extended and applied to molecular genes, identified by their degree of sequence similarity [12]. Homology has also been extended to gene regulatory networks [13,14] and organismic behaviours [15–17]. An important category of trait that has received much less attention is that of developmental processes, including gene expression dynamics, morphogenesis and cell differentiation, as well as processes that characterize life cycles, such as metamorphosis or metagenesis. Following Striedter [18] as well as Gilbert & Bolker [19], we argue that processes can and should be homologized, and this paper explores how this can be done.

There are two major reasons why homology between ontogenetic processes¹ remains neglected: (i) persistent assumptions of one-to-one genotype–phenotype mapping and (ii) the difficulties of using processes as characters in phylogenetic analysis.

First, as long as we assume that genotypes uniquely map onto phenotypes in a one-to-one fashion then neither ontogenetic processes nor morphological traits can vary independently of genetic changes. There is little point in establishing homology criteria for processes if processes are fully traceable in terms of gene homology. Over the past two decades, however, an increasing amount of evidence has accumulated indicating that evolution at different levels of organization is highly dissociable. Homologous morphological traits are often generated by processes involving non-homologous genes (developmental system drift), while homologous genes are often co-opted in the generation of non-homologous traits (deep homology) [20–24]. We now know that the relationship between evolution at the genotypic and the phenotypic levels is surprisingly fluid, degenerate, multi-level and complex (see [24–26]). As a result, homology between processes cannot always be traced in terms of homology between genes. Therefore, phylogenetic comparison of ontogenetic processes requires criteria specific to those processes.

Second, the most standard and successful methods for resolving phylogenies, such as congruence testing based on parsimony or probabilistic analysis, work with sets of morphological and especially molecular characters (see [27]). Characters that are useful for purposes of mapping phylogenies are easy to identify, evolve only once rather than repeatedly and vary quasi-independently of other characters [28–30]. Processes are not very good characters in this sense. They are more difficult to identify and individuate as units of homology than the more clearly bounded morphological characters and genes. It has been pointed out, for example, that homology at the level of regulatory network structure is difficult to trace or resolve [13,20], a problem exacerbated by the widespread presence of developmental system drift [21,23,31,32]. Finally, it is not clear how much adding process characters into phylogenetic reconstructions would improve the quality of the resulting phylogenetic trees.

Even if processes are not the most tractable characters for phylogenetic reconstruction, and may not be essential for arriving at congruent phylogenies, the main biological use for process homology lies elsewhere. Phylogenetic approaches to homology allow us to resolve evolutionary patterns, but do not address the underlying causal processes that generate them (see [2,4,5]; see also [33]). However, such a causal understanding is ultimately required if we are interested in reconstructing the evolutionary origins and history of a specific character. Since ontogenetic processes generate phenotypic characters, they determine the probability of the evolutionary transitions that a given character can undergo, thus influencing the relative probabilities of homoplasy and homology.

Beyond the causal reconstruction of character phylogenies, process homology also has a more general role in explanations of evolutionary change. To explain how a lineage gets from one state to a later state—rather than merely describing the sequence of states—it is often not enough to rely on simple statistical models of genetic architecture and linear genotype–phenotype mapping [25]. Because the genotype–phenotype map is degenerate, and most traits are generated by nonlinear hierarchical regulatory processes, bridging the gap between genotype and phenotype calls for a causal understanding of complex dynamic mechanisms [25,26,34].

Process homology has two roles in this context of mechanistic evolutionary research.² First, when changes in ontogeny are used to explain evolutionary changes, it is essential that these changes are placed in their actual historical sequence [38]. Obviously, an ontogenetic process can only explain some morphological trait if the two are historically contemporaneous. This requires establishing phylogenies (and thus homologies) of processes. Second, such explanations can potentially be generalized to different lineages through the notion of process homology.

Explanations of how traits within a lineage transition from one state to another due to changes in the underlying ontogenetic mechanisms/processes are called lineage explanations [39] (figure 1a). We call the generalization of a lineage explanation to a different lineage a cross-lineage explanation (figure 1b). Cross-lineage explanations require the ability to trace both the focal trait and the ontogenetic process that produces it back along different branches of the phylogenetic tree to corresponding features in a common ancestor.

Figure 1.

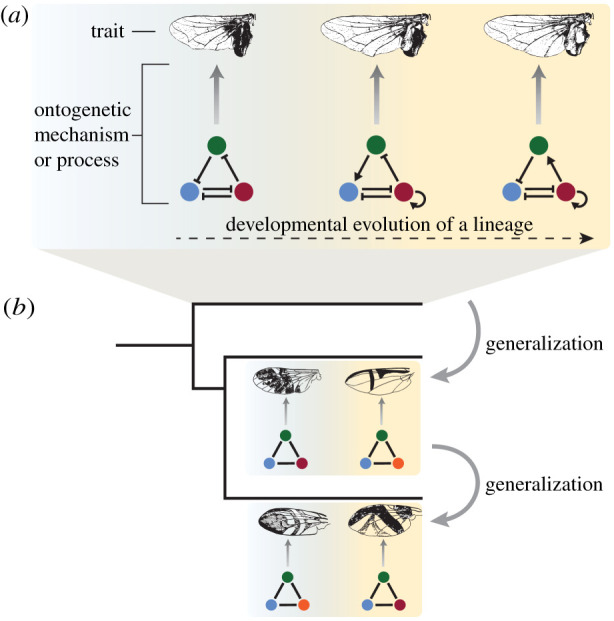
Lineage and cross-lineage explanations. (a) Lineage explanations resolve how changes in ontogenetic mechanisms/processes cause phenotypic change within an evolutionary lineage. (b) Cross-lineage explanations generalize a lineage explanation to several evolutionary lineages, tracing both morphological characters and the ontogenetic processes that generate them back to the corresponding features in a common ancestor.

In this paper, we aim to develop a conceptual model of process homology that is suitable for grounding cross-lineage explanations in the presence of widespread genetic co-option and developmental system drift. In §2, we illustrate the general problem using the examples of vertebrate somitogenesis and insect segmentation. Section 3 presents the core of the argument: we describe six complementary criteria for establishing homology between ontogenetic processes, illustrating each criterion with specific examples. We conclude the paper by discussing the relation of our account to other approaches to homology, and the broader evolutionary implications of our proposal.

2. The homology of animal segmentation processes

Most difficulties with homology arise from the combined facts that it occurs at different levels of organization, and that evolution at different levels is dissociable to some degree. Three examples—all processes involved in animal body segmentation—demonstrate such evolutionary dissociation between levels.

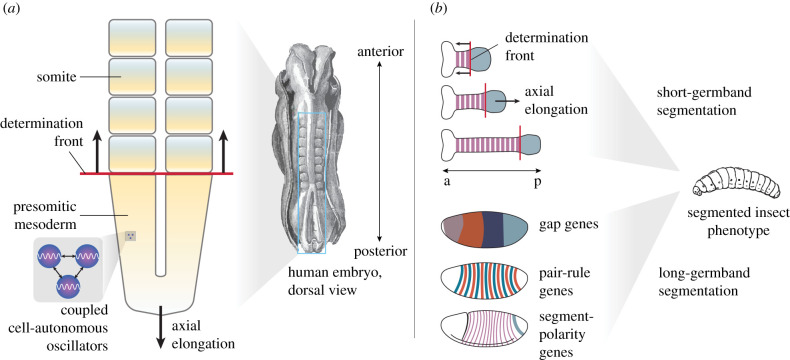
Our first example is somitogenesis, the process by which body segments are formed in vertebrates [40–45] (figure 2a). Following the current literature on the subject, we define this process as involving the posterior growth of a tissue called the paraxial or presomitic mesoderm, and a regulatory network with three functionally distinguishable ‘dynamical modules’³ [33,46]: (i) a cell-autonomous oscillator (the ‘segmentation clock’), (ii) cell–cell signalling between neighbouring cells that maintains and/or synchronizes cell-autonomous oscillations across the tissue, and (iii) a graded long-range modulation of the clock period (often called ‘the wavefront’⁴) causing it to slow down and eventually stop at some distance away from the posterior end of the tissue. The coordinated interaction of these dynamical modules results in periodic waves of gene expression travelling ‘up’ the presomitic mesoderm towards the anterior, which results in transient blocks of mesodermal tissue forming sequentially along the antero-posterior axis of the embryo. These blocks are called somites [40]. Different subregions of the somites ultimately give rise to vertebrae, rib cage, skeletal muscle, as well as cartilage and dermis. Somites, as well as the activities of all three dynamical modules, are highly conserved across vertebrates, from fishes to birds to mammals (see [43]).

Figure 2.

Animal body segmentation processes. (a) Vertebrate somitogenesis is the process that generates body segments (somites) through posterior growth of a tissue called the presomitic mesoderm during axis elongation. This process involves three functionally distinguishable dynamical modules: (i) Cells within the presomitic mesoderm contain a cell-autonomous genetic oscillator (the ‘segmentation clock’). (ii) Neighbouring cells signal to each other to maintain and/or synchronize their oscillations. (iii) Cellular oscillations slow down and eventually stop as cells leave the presomitic mesoderm anteriorly, constituting a determination front (the ‘wavefront’). This results in a stationary periodic spatial pattern of gene expression, which determines the morphological boundaries of the somites. (b) Short-germband (top) versus long-germband (bottom) segment determination in insects. Similar to somitogenesis, short-germband segment determination occurs through posterior tissue growth and a clock-and-wavefront mechanism, predominantly after gastrulation has occurred. In orthopteran insects, such as grasshoppers and crickets, for example, this leads to the sequential addition of segments as the embryo extends and grows posteriorly. By contrast, long-germband segmentation does not require tissue growth, and predominantly happens before gastrulation. In D. melanogaster, for example, the embryo is subdivided by a hierarchical genetic cascade, initiated by gradients of maternal morphogens (not shown), which activate the zygotic gap, pair-rule and segment-polarity genes. These genes form the distinct layers of the segmentation hierarchy; genes within each layer regulate each other and are regulated by layers above but not below them (with a few notable exceptions). Segment-polarity genes form a molecular pre-pattern that leads to the formation of morphological segments later in development. Both short- and long-germband segment determination result in a conserved segmented bauplan. See text for details.

However, the underlying molecular and genetic mechanisms differ in many details. Segmentation clocks are all based on negative auto-regulation by members of the Hes/Her transcription factor family, but there seems to be some redundancy built into the oscillatory mechanism, and the identity of the hes/her paralogues involved differs between lineages [43]. Similarly, cell–cell signalling in the presomitic mesoderm is always based on the Notch-Delta pathway, but different post-translational modifications of signalling components lead to different functional roles: in zebrafish, Notch-Delta signalling serves as an escapement mechanism that coordinates cell-autonomous oscillations, while in mice and chicks, it is required for the initiation and maintenance of the oscillations and alters their period [50]. In addition, there is surprisingly little overlap among the sets of genes that oscillate in different species, particularly in components of the Fgf and Wnt pathways, which suggests significant functional differences in the mechanisms that govern the gradual slowdown of expression waves [51]. Finally, the oscillation period of the clock differs drastically between evolutionary lineages [52].

In this example, there is enough phylogenetic evidence to establish homology between vertebrate somitogenesis processes without a detailed understanding of the underlying molecular and genetic mechanisms. However, such understanding is required for explaining the evolution of somitogenesis mechanisms, and to distinguish which aspects of this evolutionary process are adaptive, and which are due to neutral or compensatory developmental system drift [24]. Because the molecular and genetic components of the underlying processes have diverged substantially in different lineages, a cross-lineage explanation for the evolutionary persistence of somites and somitogenesis as a process should include evidence at levels other than the molecular-genetic. In vertebrate somitogenesis, the ‘causality horizon’ (the lowest level at which the causes of the same phenotypic feature are conserved) lies at the relatively high level of the dynamics of the process rather than the lower level of the underlying detailed molecular-genetic interactions [25,50,53]. Thus, we should ask not only what aspects of the mechanism are conserved, but also what aspects of the activity of the system are conserved (and which ones are not). Stabilizing or positive selection can act on different aspects of the oscillatory dynamics (oscillatory period, for example). Also relevant to understanding the conservation of the process are entrenched interdependencies between somites, somitogenesis, and other characters and processes, such as axis elongation and tissue maturation [50,54,55].

Our second and third examples concern invertebrate body segmentation. Insects exhibit a highly conserved bauplan, with stereotypical numbers and arrangements of head, thoracic and abdominal segments [56]. However, different orders of insects use what appear to be wildly divergent modes of segment determination to specify the position of their body segments [57–61] (figure 2b).

These divergent modes of segment determination can be arranged along a spectrum with many intermediate forms. At one end of this spectrum lies what is thought to be the ancestral mode of segment determination. It occurs in lineages with short-germband embryos (reviewed in [57]). These insects form their body segments sequentially, mostly after gastrulation occurs, through tissue extension and growth at the posterior end of the embryonic anlage. Paradigmatic examples of short-germband insects are crickets and grasshoppers (Orthoptera). The process of segment determination in short-germband insects is strikingly similar (although not homologous) to the process of somitogenesis, involving equivalent clock-and-wavefront dynamics⁵ [65,66], as well as a three-tiered dynamic modularity with a cell-autonomous clock, cell–cell synchronization and expression changes at a longer time scale that cause the slowing down of the clock in the anterior part of the segment-addition zone [61] (figure 2b).

At the other extreme of the spectrum, long-germband insects determine their segments (almost) simultaneously, by subdividing their bodies into distinct regions of gene expression during early embryogenesis, predominantly before the onset of gastrulation (figure 2b). No tissue growth is required for this process. Long-germband segment determination only occurs in holometabolous insects.⁶ Examples include bees and wasps (Hymenoptera), some beetle species (Coleoptera), as well as flies, midges and mosquitoes (Diptera). Many intermediate forms exist—in true bugs (Hemiptera), or certain beetle species, for example—where anterior segments form simultaneously, while posterior ones form sequentially [61,67].

In this example, it is ostensibly only the outcome of the process—an embryonic stage called the segmented germband—that is highly conserved [57], while the overall dynamics and many of the genes involved in the segment determination process (especially maternal activators and gap genes) differ between insect lineages [61,68]. This would initially suggest that the two modes of segmentation are non-homologous, but the answer depends on the phylogenetic scope of comparison [69]. On the one hand, long-germband segmentation only occurs within the superorder of the Holometabola, and could be considered an evolutionary novelty compared to segment determination modes outside this clade. At this scale, it is not homologous to short-germband segment determination. On the other hand, long-germband segment determination clearly derives from a short-germband process in the common ancestor of all insects [57,59,61]. Thus, across the entire class of Insecta, long- and short-germband segment determination must be considered transformational homologues of the same ancestral segmentation process. Because the dynamics have significantly diverged between the two modes of segment determination, a lineage explanation is needed for establishing a plausible transformation sequence between them—and thus homology. Since the transformation from short- to long-germband modes has occurred multiple times independently in different holometabolous lineages [59,61], such a lineage explanation can be generalized into a cross-lineage explanation (we will revisit this point in §3.6).

Our third example concerns segment determination within a much narrower phylogenetic range of insects: different lineages of cyclorrhaphan flies⁷ [56,70]. These flies all exhibit some form of long-germband segment determination. In this phylogenetic context, not only are the general dynamics and the outcome of the process highly conserved, but also the qualitative structure of the underlying genetic mechanism. Despite such high conservation down to the genetic level, it is surprising that the molecular details of gene regulation still differ: the sequences of cis-regulatory elements that govern the expression of segmentation genes show very little conservation even across closely related dipteran species (see [71,72]). The underlying sequence changes are mostly neutral or affect the strength of specific regulatory interactions, while the overall qualitative topology of the network remains unchanged [73,74].

Our three examples of process homology are summarized in table 1. Segment determination in cyclorrhaphan flies is conserved at the level of the outcome (the segmented germband), the dynamics or activity of the process, the nature of the underlying genetic interactions, but not at the molecular level of regulatory sequences. Vertebrate somitogenesis is conserved at the level of the outcome (somites), the overall dynamics or activity of the process, but only partially at the level of the underlying genetic interactions. Little is known about the molecular mechanisms at the level of regulatory sequence in this case. Segment determination across different orders of insects shows conservation of outcome (the segmented germband), but not at the level of dynamics/activity (short- versus long-germband segmentation), while there is partial conservation of the underlying genetic and molecular mechanisms.

Table 1.

Summary of examples. Ontogenetic processes represent a distinctive level of organization (highlighted in italics). The distinctive pattern of conservation across these examples indicates that evolution at this ‘process’ level is (at least partially) dissociable from evolution at other levels, and is thus amenable to classification in terms of process homology.

conservation/homology at level	vertebrate somitogenesis	insect segmentation	cyclorrhaphan segmentation	sea urchin larval skeleton
phenotypic outcome	yes	yes	yes	no
ontogenetic process	yes	yes or noa	yes	yes
genetic network	partial	partial	yes	yes
individual genes	partial	partial	partial	yes
sequence level	unknown	no	no	unknown

^aDepending on phylogenetic scope (see text).

In addition to the above, we need to mention examples of gene regulatory network co-option [22,75–78]. Such co-option events are thought to underlie the evolutionary origin of beetle horns and butterfly wing spots, which are both based on a developmental process originally involved in insect limb formation [79–81]. Similarly, the conserved regulatory network responsible for adult skeletogenesis across echinoderms got recruited into embryonic development in sea urchins, where it is responsible for generating the larval skeleton of the pluteus larva, which only occurs in this particular lineage [82–84]. In both of these cases, the morphological outcome of the process is clearly not homologous to the original trait whose underlying network was co-opted,⁸ but there is homology at the level of process dynamics as well as genetic and molecular components (table 1, and also §3.2).

What do these examples tell us about the requirements for an account of process homology? One immediate conclusion we can draw, even from such a preliminary and limited sample of examples, is that evolution is dissociable at different levels of organization. If we include the examples of network co-option—which do not have a conserved outcome—it is evident that none of the levels depicted in table 1 show a consistent pattern of conservation across all examples. In fact, we can think of no good example where the homology of a complex generative process is fully conserved at all levels of organization across a significant phylogenetic distance. It seems that some amount of network drift and dissociability are the norm in evolution. Therefore, an account of process homology must be consistent with these phenomena: we need criteria of homology for each level that is dissociable from other levels, and cannot simply collapse the sub-morphological levels down to genetic homology.

This points to a major limitation of the earlier account of process homology provided by Gilbert & Bolker [19,85]. According to these authors, ‘the homology of process' is ‘the relationship between pathways that are composed of homologous proteins’ [19, p. 3]. Their account relies on conserved structural properties of the underlying genetic signatures as its only criterion for homology. Accordingly, Gilbert & Bolker [19] use conserved intercellular signalling pathways—such as the Wnt pathway—as their primary examples of process homologues. For this reason, we refer to their account as ‘pathway homology’. Pathway homology ends up collapsing homology of process onto the genetic level. It is only applicable to processes in which the underlying genetic components are conserved, but not to those that are affected by developmental system drift, where pathway components have been exchanged during the course of evolution. Furthermore, it is not able to deal with transformational homologies, such as the different modes of insect segment determination, where the dynamics of the process have evolved as well. This means that the pathway approach will miss many true cases of process homology (table 1). The following section presents criteria for recognizing process homology that are consistent with the evolutionary dissociability of levels.

3. Homology of processes

To develop an understanding of how ontogenetic processes can stand in relations of homology, we focus on relatively well-defined examples like somitogenesis and segmentation and attempt to reach more general insights in a bottom-up fashion. However, it may be unavoidable to consider more general questions about biological processes from the start. Specifically, one might worry that it is necessary to know how to demarcate processes in general prior to assessing their homology. Whether or not two characters are homologous is sensitive to the way we draw boundaries around them, and this is clearly true of ontogenetic processes as well. Does a model of process homology, therefore, need to provide a background ‘ontology’ of processes, then?

To address this issue, consider that biologists successfully establish homologies without having a clear definition or theory of ‘characters’, even though homology relations depend on the identification of characters. This is possible because context-specific information about the particular characters at issue does part of the work of demarcation. It is also because the dependence is not one way: character identification and homology assessment have a mutually revising, iterative relationship. For example, whether bat wings and the pectoral fins of a given teleost are homologous certainly depends on how we define ‘wings’ and ‘fins’, but the phylogeny of these characters also tells us that any such homology would be at the very coarse level of osteichthyan paired appendages, which does not include tetrapod skeletal articulations such as the stylopod, zeugopod and autopod. Success in applying the criteria of homology shows that the characters are well defined enough that the process of assessing homology and revising character boundaries can get off the ground without requiring a foundationalist basis [86]. This is the approach we take to the demarcation of processes here—namely, to allow the applicability of the proposed criteria of process homology to distinguish the processes that are well defined enough to be homologized from those that are not. A more general ontology of biological processes would, like a theory of characters, be a helpful addition to this project but is not a necessary precondition for it (for some existing resources, see [86–89]).

It is also important to note the limits of criteria for recognizing and inferring homology. Phylogenetic relations of homology can never be fixed with absolute certainty because the evidence used to infer them is based on finite and open-ended empirical research. As a consequence, homology judgements are always hypotheses. They may be more or less well confirmed in different cases, but, like other empirical claims, they are always revisable in the light of new evidence. Given also that the sources of evidence for establishing homology are diverse and sometimes indirect, there is not going to be a simple and informative definition of process homology beyond the generic phylogenetic one (homology as sameness due to derivation from a shared common ancestor). Instead, establishing homology between processes will involve multiple evidential criteria, which together are indicative of phylogeny, but none of which is necessary or sufficient for homology.

We propose that the evidential criteria for process homology include the following:

• 1. sameness of the parts or components involved in a process,
• 2. sameness of the phenotypic outcome,
• 3. sameness of topological position,
• 4. sameness of dynamical properties,
• 5. dynamical complexity, and
• 6. evidence of transitional forms of the process.

Several of these (1–3) are also criteria of homology for ‘character identity mechanisms’ [34]. Criteria 3–6 are loosely based on established criteria of homology for morphological characters [90], but are adapted specifically for the tools of dynamical modelling, which is where our main contribution lies. The main results of this discussion are summarized in table 2 at the end of this section.

Table 2.

Criteria of process homology based on various features of processes (see text for details).

feature of process	evidential criteria of process homology
parts	gene orthology; homology of cell types, tissues, organs (carries more weight for simple processes than complex processes)
	violated by: developmental system drift
outcome	homology criteria for structural features [90]: similarity (in special qualities), topological position, evidence of transitional forms
	violated by: co-option of processes into new roles
topological position	sameness of spatio-temporal position and relations with other processes within a life cycle
	violated by: heterochrony, heterotopy, serial homology
dynamical properties	morphological processes: same as ‘outcome’ above, but for temporally extended series of structural features
	morphogenetic processes: equivalence classes of configuration space topologies
	violated by: dynamically dissimilar but homologous processes
dynamical complexity	complexity of outcome (see ‘outcome’ above); phase space dimensionality; topological complexity of phase portrait; number of parts, number of dynamical modules
	violated by: dynamically simple homologous processes
transitional forms	plausible connectability of actually realized processes by trajectories in the same configuration space
	violated by: transitions not actually realized

3.1. Parts

Ontogenetic processes are causal activities that are performed by parts or components, such as genes, proteins, cells and tissues. The parts that are causally involved in a process constitute its participant structure [91]. Somitogenesis, for example, has a complicated participant structure that includes cyclic oscillatory genes such as Hes/Her-family transcription factors, the signalling molecules and receptors in the Delta-Notch pathway, Notch signalling-modulator Lunatic fringe (Lfng) and tissue-level components such as the cells of the presomitic mesoderm [43,50]. Although the overall dynamics and the outcome of the process are conserved across vertebrates, the participant structure of somitogenesis has diverged significantly between different lineages [50,51] (table 1, §2). This example shows how having the same parts is a useful but fallible guide to homology of the overlying ontogenetic process. A good default assumption is that the participant structure of a process will be highly conserved in recently diverged lineages, but this conservation will tend to degrade with increasing phylogenetic distance even if the process stays the same.

One reason why somitogenesis can be traced and homologized quasi-independently of underlying gene homologies is that it is a complex process involving the interaction between numerous parts, many of which are functionally redundant and replaceable in evolution. This points to a distinction between two kinds of processes that is important for assessing homology (see [34], for more detail). A simple process is an activity or behaviour of a single unified entity. A complex process like somitogenesis or segmentation, in contrast, is the result of interactions between multiple entities, without there being a unified entity that covaries with the process on the same spatio-temporal scales. Complex processes include expression dynamics of gene regulatory networks, tissue morphogenesis based on cell movements and excitation dynamics in neural networks. Simple processes include the DNA-binding activity of a transcription factor, the migration of individual cells and behaviours of whole organisms (such as locomotion). The distinction between complex and simple is not absolute but is partly relative to a level of organization and grain of description. Complex processes can be decomposed into multiple simple processes whose integration often introduces nonlinear emergent dynamics. In turn, simple activities such as transcription factor binding can be further decomposed into a biochemically complex process, involving interactions of multiple molecular parts.

The relevance of this distinction comes from the fact that a trait must possess evolutionary individuality in order to stand in homology relations: it must be traceable across generations and lineages, and should be capable of varying quasi-independently of other traits. A simple activity is unlikely to have a meaningful degree of quasi-independence from the entity that performs it. As a result, simple activities are less interesting processes to homologize for comparative developmental biology, and can be traced (if desired) in terms of the homology of the performing entity (gene, cell type, etc.). Complex activities, by contrast, often do possess quasi-independence from the interacting entities involved [34]. Many ontogenetic processes are robust to perturbations in their participant structure and evolve with high functional redundancy among genetic components [92]. This makes complex processes more interesting to trace in comparative biology, but also makes their homology more challenging to assess.

3.2. Phenotypic outcome

As with the parts involved in a process, sameness of the outcome, product or end state of two processes is indicative of their homology. If the outcome of a process is a morphological trait—including cell types, tissues and organs—sameness of outcome can be established using existing criteria of morphological homology. Our examples of somitogenesis and segmentation both involve conserved morphological characters (somites, segments) that provide evidence for the homology of the ontogenetic processes that generate them.

As is the case for all the other criteria, homology of morphological outcome should not be viewed as necessary for homology of process. The main reason is that processes (just like gene networks) can be co-opted into novel developmental roles (see §2). Larval skeletogenesis in sea urchins provides an excellent example: although the developmental context of the process differs radically, the intrinsic activity of building a skeleton remains remarkably similar in larvae and adults [82–84]. If processes were only identified by their role or outcome, the undesirable result would follow that any co-opted process ceases to be homologous to the same process before co-option. This threatens to make co-option a meaningless biological category. A better alternative is to hold that the sameness of outcome is a defeasible (potentially violable) criterion of homology, which no longer applies when homologous processes are redeployed for different functions. When this happens, one should rely on other criteria to identify homologies between ontogenetic processes.

This discussion highlights that phenotypic outcomes and ontogenetic roles are closely associated with the notion of biological function. For instance, it is the function of skeletogenesis to produce a skeleton (larval or adult). Function, however, is a factor that is supposed to have no bearing on homology. According to Owen's classical definition, homologues are the same ‘under every variety of form and function’ [8]. For instance, the ontogenetic processes generating insect appendages and beetle horns or butterfly wing spots can be homologous without serving the same function [79–81]. A similar example is provided by the life cycle of cnidarians, which often involves a process of metagenesis called strobilation, during which a series of medusae segment and detach from a sessile polyp. In cubozoans, however, this metagenetic process has been transformed into a form of metamorphosis, as each polyp only produces one medusa [93]. Here, homologous processes play different roles, and thus fulfil different functions, as part of the life cycle [94]. The problems related to mixing homology judgements with considerations of function or outcomes only arise if homologous processes cannot be identified independently of their outcome. Our examples illustrate that this is not the case.

A different question concerns whether processes themselves are functions (as opposed to having functions). If this is the case, then processes would seem to be inappropriate candidates to stand in relations of homology. The assumption that processes are functions and are, therefore, not homologizable has been a long-standing source of confusion (see [19,95], for further discussion). On this point, we note that there are multiple notions of ‘function’, most of which are not synonymous with ‘process’ as we use the term (see [34,95–98]). The key distinction is between ‘function’ understood as something external to the process—its adaptive effect, ontogenetic role or phenotypic outcome—versus ‘function’ understood as the process itself—its inherent operation, activity or ‘functioning’. It is the former kind of extrinsic function that was excluded by Owen's classic definition of homology. Yet, as others have argued (especially [95,98]), there is no reason to prohibit homologizing the latter kind of functions as long as it is fruitful to do so. Whether these are called ‘functions’, ‘activity-functions’ or simply ‘processes’ (as we call them) does not matter. What matters is that they can be identified not only by their outcomes or developmental roles but by their intrinsic characteristics. We will show how this is done in §3.4.

3.3. Topological position

Perhaps the most important criterion of homology before the arrival of evolutionary theory was the topological position of a character relative to other characters in the organism. Early comparative anatomists such as Geoffroy Saint-Hilaire and Richard Owen noted that the topology of the character was more invariant across diverse taxonomic groups than properties like size, shape, form and use-function, and that it could be successfully used as a basis for establishing classifications of characters such as elements of the vertebrate skeleton [99]. This criterion has generally been preserved as homology was applied to characters at other levels of organization. Genes, for example, are homologized based on sequence similarity as well as location—the relative position of nucleotides within the gene, and the gene's syntenic location on chromosomes [12,100].

Many of the ontogenetic processes that can be homologized are active in restricted regions of the organism and exhibit specific spatio-temporal relations to other processes. Having the same topological position relative to other processes is evidence that two ontogenetic processes are homologous. Temporal position in ontogenetic sequences is also a useful criterion and is essential for establishing the identity of developmental stages in particular [101]. Stage identity informs the way that rearrangements of stages—such as pedomorphosis and other forms of heterochrony—are classified in comparative research.

Like sameness of phenotypic outcome, the sameness of topological position in space and time is defeasible, and can be violated by heterochrony as well as heterotopy, which occur when there is co-option and redeployment of ontogenetic processes for different developmental roles. For example, segment determination and gastrulation are related in very different ways in long- and short-germband insects. While the former determine most or all body segments before the onset of gastrulation, the latter do so mostly after gastrulation has occurred (see [57,59,61]). Therefore, segment determination has been heterochronically shifted to an earlier developmental stage in long-germband insects, a fact that will become important when (re)considering the homology of the process in §3.6. Similarly, larval skeletogenesis in sea urchins occurs at an earlier stage and in a different developmental context than adult skeletogenesis [82]. Nevertheless, the two processes are clearly homologous. In such cases of co-option, again, one must rely on other criteria of homology.⁹

3.4. Dynamical properties

An important consequence of the limitations of the previous three criteria is that homology of process must, at least in part, be based on intrinsic characteristics of the processes or activities themselves. We call these characteristics ‘dynamical properties’. The activities of most ontogenetic processes can be identified and described as regular sequences of changes—for example, the distinctive sequence of gene expression changes and tissue movements that occur during gastrulation or neurulation. This initial characterization tends to be followed by experimental investigations of the regulatory mechanisms that account for the orderliness of these sequences. Homology for such processes can be established by applying the traditional morphological similarity criteria not only to end states (e.g. the neural tube) but to the entire sequence of changes leading to those end states (neurulation) (see [102]). When the underlying mechanisms guiding such changes are identified, this may further inform and corroborate judgements of homology for the overlying phenotypic processes.

However, in many cases, it is impossible to identify dynamic mechanisms by observation and experiment alone, because complex ontogenetic processes involve nonlinear interactions of many different parts across multiple levels of organization. This is why dynamical systems modelling is required to understand and trace the orchestrated overall activities of such processes [25,26,103–105]. In addition, dynamical systems theory reveals a whole range of further dynamic properties that can be used for the classification and characterization of processes, going beyond simple sequences of changes and qualitative regulatory interactions.

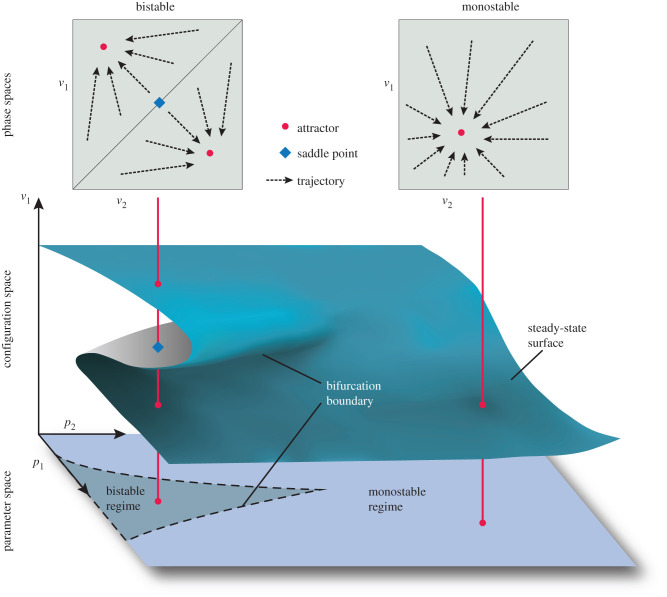
A dynamical model of an ontogenetic process formalizes its regulatory structure as a set of (differential) equations.¹⁰ These equations describe the underlying rules that govern the observed patterns of change in state variables such as concentrations of metabolites, proteins or signalling molecules, cell number, shape or size, membrane potentials, or factors such as pH that affect the intracellular milieu. They represent the time evolution of an ontogenetic process along a trajectory from an initial state to an end state in phase space (sometimes also called state space), an abstract mathematical construct whose dimensions are given by the state variables and whose points consist of specific states of the system (figure 3, top). The sum total of all trajectories in a phase space defines the phase portrait. Points at which trajectories end (and the state of the system no longer changes) are known as steady states. Some states in the phase portrait are more stable than others. These stable states or regions of a phase portrait are known as attractors, where trajectories from many initial states converge on a point or on a trajectory (cyclical or aperiodic) located in a restricted subvolume of phase space. The subset of trajectories that converge on a particular attractor are called its basin of attraction (figure 3, top left). The number, type and relative position of these attractors and their basins with regard to each other define the topology of a phase space, which in turn determines the repertoire of dynamical behaviours a system can generate starting from a given range of initial states [103,105,111].

Figure 3.

Concepts of dynamical systems theory. Top: the phase or state space of a system is defined by its state variables (v₁ and v₂). The totality of trajectories in this space defines the phase portrait of the system. Examples of bistable and monostable phase portraits are shown, in which trajectories (indicated by arrows) converge towards two attractors or one attractor (indicated by circles), respectively. The bistable phase portrait also has a saddle point (diamond), which lies on a separatrix that forms the border between its two basins of attraction. Bottom: the parameter space of a system is defined by its parameters (p₁ and p₂). Bifurcation boundaries separate bistable and monostable dynamical regimes. Middle: phase and parameter space together form the configuration space of the system. The steady-state value of one of the variables (v₁) is shown as a folded sheet. The fold and its cusp within the sheet represent the bifurcation boundaries. Steady states in the phase portraits map onto specific cross-sections of configuration space (as indicated by vertical lines). Steady states that map onto the upper surface of the folded sheet are attractors, steady states that map onto folds of the sheet are saddle points. See text for details.

Dynamical systems models are defined not only by their state variables, but also by their parameters, which describe aspects such as rates of production, diffusion and decay for molecular components, rates of cell division at the tissue level or the level of random fluctuations to which a regulatory process is exposed. A special set of parameters, called the boundary conditions of the system, delimit the spatio-temporal domain across which a process is active. Like the state variables, the parameters of a process can change during ontogenesis and/or evolution (e.g. [111]). For instance, the shape and size of the spatial domain of the system can change through tissue rearrangements or growth, diffusion rates can be altered through changes in the extracellular matrix or through the cellularization of a tissue, or the structure of a gene regulatory network itself can be modified by environmental influences and mutational processes. The parameters of the system define the dimensions of its parameter space, whose points consist of specific phase portraits of the system (figure 3, bottom). Parameter values typically change over a longer time scale than variables, but the separation between the two is somewhat arbitrary and highly problem-dependent. Changing the parameters of a system renders its structure time-variable, and changes its dynamical repertoire. Attractors are created, altered and annihilated through bifurcations, which transform the topology of the phase portrait when the system crosses a bifurcation boundary in parameter space. The configuration space of a system combines its phase and parameter spaces (figure 3, middle). Each point in this abstract space represents a specific set of state variables and parameters (a specific system configuration). The topology of configuration space consists of the phase space topologies within it, plus the bifurcation boundaries and the dynamical regimes they separate (figure 3).

Thom [112] established that complex morphogenetic processes can be rigorously and systematically classified based on the topological properties of their configuration spaces. The core idea is to define equivalence classes for configuration space topologies that correspond to the same kinds of processes. One such class, the cusp-and-fold, is shown in figure 3. We extend his framework by noting that the geometrical arrangement of sets of attractors and their bifurcations (which Thom called ‘catastrophes’) defines not only their dynamical properties, but also their evolutionary potential. The dynamical properties systematically capture the intrinsic characteristics of a process: the state variables, their functional interdependencies and the temporal sequence of states that follows from a given range of system configurations. These properties contain much more information than either the outcome, which corresponds to end states only, or the structural description of the components involved in the process. The evolutionary potential of a process, in turn, is described in the model by the way dynamical properties can change and generate different phenotypic transitions with different probabilities. Thus, for example, a dynamical model of a process can illuminate how a process can remain the same despite changing components and interactions. Furthermore, the topology of configuration space indicates whether the dynamics of a process are sensitive to changes in its configuration. If a system is resilient to a certain type of such changes, it can be said to be structurally stable with regard to the affected variables and parameters [112].¹¹ Structural stability is a formal measure for the robustness of the process. Replacement of parts or changes in the number or kind of interactions are less likely to lead to qualitative differences in overall activity to the extent that a system is structurally stable. Because models can capture not only the dynamical regime of an ontogenetic process but also its stability, they can significantly contribute to explaining the persistence of a process through developmental system drift, both qualitative and quantitative (see [74]).

If two ontogenetic processes can be placed in equivalence classes of configuration space topologies, according to empirically validated dynamical models, this is strong evidence of their homology. Belonging to such classes is what it means for processes to have the ‘same dynamics’, from within the formalism of dynamical systems theory. Of course, this criterion—shared dynamical properties, for short—must be combined with the other criteria in assessing homology.

An important way in which this dynamical perspective differs from other criteria of homology is that it is not restricted to the properties of a system or character that are actually realized. The states and parameters represented by points in configuration space may be actual configurations of real systems, or possible configurations that are accessible to those systems via changes in parameters or initial states. This provides a powerful exploratory tool to study the space of possible dynamical properties of ontogenetic processes and their equivalence relations, which goes far beyond the reach of experimental studies. We will revisit this important issue in §3.6 and the conclusions (§4).

3.5. Dynamical complexity

The trouble with similarity-based criteria of homology, including shared dynamical properties, is that similarity can arise from convergent evolution rather than common descent. It is for this reason that Remane [90] refined the generic criterion of similarity to similarity in ‘special quality’—structural details of a character not explained by its adaptive role. The more complex those structural details are, the less likely they are to be products of convergent evolution (see [54]). In a phylogenetic framework, the complexity of a character is proportional to the number of subcharacters it contains, under the assumption that each distinct subcharacter constitutes an independent piece of evidence of phylogeny.

Similar considerations apply when the character under consideration is an ontogenetic process. The complexity of a process, as represented in a dynamical model, is proportional to the following factors:¹²

• 1. complexity of morphological outcome (assessed by morphological criteria, e.g. number and diversity of subcharacters, such as cell types and tissues),
• 2. number of variables and parameters (the dimensionality of configuration space),
• 3. topological complexity of configuration space, i.e. number and diversity of types of attractors and bifurcations,
• 4. number and diversity of types of parts involved, and
• 5. number and diversity of types of dynamical modules (see below).

For two processes under comparison, having shared dynamical properties carries more phylogenetic signal to the extent that those processes are complex, as determined by factors 1–5. Evaluating these factors requires a more advanced understanding of the process than criteria like topological position, so considerations of complexity are more appropriate to later stages of comparative research, such as providing plausible transformation sequences through cross-lineage explanations (see §3.6).

Dynamical modules (factor 5) are causally distinct subprocesses or activities within a larger process, analogous to subcharacters within a morphological character (e.g. phalanges within the autopod) [33,46]. Like structural parts, processes can be ‘modular’ in the sense that subprocesses exhibit some autonomy relative to the rest of the system combined with some kind of internal causal cohesion. For example, the Hes/Her-driven oscillations that occur during somitogenesis are cell-autonomous behaviours: cells isolated from the presomitic mesoderm continue to oscillate for a while without Delta-Notch synchronization and the wavefront mechanism, though the oscillation is unstable and has a longer period [50,113–115]. These oscillators (the ‘segmentation clock’) constitute one of three dynamical modules in the somitogenesis process, along with Delta-Notch signalling and the wavefront modulation of the clock (as introduced in §2). Because these three modules are causally dissociable to some degree, their joint presence in different vertebrate lineages adds extra evidence to the hypothesis that somitogenesis is homologous across vertebrates.

Since dynamical modules are activities that make up a coherent overlying process, we can think of processes as occupying higher or lower levels of organization (see [116]; and also [98]). Often, these dynamical levels roughly correspond to the compositional levels of parts or components of a process. For instance, complex transcriptional processes can frequently be subdivided into dynamical modules that occur at the level of the underlying gene regulatory network. An example is provided by the segmentation gene system of dipteran insects, which can be subdivided into maternal, gap, pair-rule and segment-polarity subnetworks, each generating a characteristic type of gene expression pattern (figure 2b in §2).

However, dynamical and compositional levels can come apart when the participants in a dynamical module lack structural modularity, or when the same parts are involved in multiple processes. For example, the gap gene network generates multi-stable (switch-like) expression dynamics in the anterior, and (damped) oscillatory expression dynamics in the posterior of the embryo [117–120]. These different dynamical regimes can be mapped onto different subsets of genes and interactions within the network, but these subsets show extensive overlap in composition with regard to each other (see [121]; reviewed in [122]). Moreover, there is a subnetwork that is active in the middle of the embryo, which generates both switch-like and oscillatory behaviours. Clearly, there is no simple mapping between activity and structure here. In such cases, dynamical modularity can be used to identify modules of parts—a ‘decomposition under a process'—in a way that reveals a non-trivial correspondence of dynamical and compositional levels (see [86]; see also [33,46]). Like statistically derived variational modules [14,123,124], dynamical modules and levels can be viewed as comprising quasi-independent units of developmental evolution.

3.6. Transitional forms in configuration space

Characters do not have to be complex to be homologous, but they also do not even need to be similar. Well-known examples of dissimilar homologues include the transformation of the jaw joint of reptiles into inner ear ossicles of mammals, and the transformation of the parietal eye in lower vertebrates to the mammalian pineal gland. The existence of transitional forms is part of the reason these characters can be recognized as homologous despite their dissimilarity. According to Remane [90], two characters that cannot be homologized using the criteria of topological position and special quality can still be homologous if they can be connected in a transformation series in which each adjacent character can be homologized using those criteria (see [125]; cf. [126, p. 93]). The same considerations apply to homology between ontogenetic processes.

Unfortunately, our capacity to construct transformation series using actual transitional forms will always be limited, especially in the case of ontogenetic processes, which are incredibly difficult to reconstruct from evidence in the fossil record. This capacity is significantly enhanced by the use of dynamical models that provide hypothetical or inferred transformations based on a reconstruction of the space of possible variations for a given actual process (see [105,127]; see also [128]). As we have seen, ontogenetic processes that actually occur in an organism can be represented as specific trajectories within a phase portrait, or in the larger context of a configuration space (figure 3). On top of this, the configuration space of a dynamical model includes the set of all possible trajectories for a process across a given range of configurations, not only the ones that are presently actualized (see §3.4). Accordingly, transitional forms may correspond to possible but yet-unrealized trajectories that lie between actual trajectories in configuration space. If our hypothesis is right that homologies of process map to equivalence classes of configuration space topologies, which are structurally stable with regard to certain changes in values of state variables and parameters, then it follows that any realistic transformation series must correspond to realizable evolutionary trajectories through configuration space.

Configuration space provides a probabilistic ‘map of the possible’ for how the causal structure of an ontogenetic process might change under various kinds of perturbations, even when counterfactual states are not directly accessible experimentally or observationally. Such a ‘map of the possible’ reveals how probable (or improbable) it is for a given transition to happen in evolution. Some dramatic phenotypic changes may turn out to reflect rather subtle tweaking of the configuration of the system. Insect segmentation, once again, provides an example. The processes of short- and long-germband segment determination differ considerably in their components, dynamic properties and topological relations (figure 2b and table 1 in §2). However, it takes surprisingly few and subtle mutations and fate map changes to convert one into the other (cf. [61,120,121,129,130]).

We have seen in §3.5 how a subnetwork of the gap gene system can generate both switch-like and damped oscillatory behaviours observed in long-germband segmentation. An analysis of its configuration space reveals that the damped oscillatory regime in turn lies in the vicinity of sustained oscillations typical for short-germband segmentation. In other words, short- and long-germband segmentations are much closer together on the map of the possible than previously thought, which makes transitions between them much more probable [121]. Another consequence of the damped oscillatory regime is that it is required for proper positioning of shifting pair-rule stripes in the posterior of the embryo [129]. In contrast with the gap network, the role of pair-rule genes in segmentation is highly conserved across insects [61]. When comparing their expression dynamics between long- and short-germband embryos, a previously undiscovered similarity between the two modes of segment determination becomes apparent [131]: pair-rule genes undergo a dynamic transition in their regulatory regime in the segment-addition zone during sequential segmentation, leading to the stabilization of expression waves. This transition also occurs in long-germband insects, albeit before gastrulation and simultaneously along the entire length of the embryo. Once reassessed in terms of their dynamic regimes, both long- and short-germband segmentation processes become simple spatio-temporal transformations of each other, rather than being separated by a seemingly unbridgeable evolutionary gap [61]. Transitions between the modes of segmentation are revealed to be much more probable than expected, which is evidence of their transformational homology.

Similar modelling analyses uncovering surprising equivalences between seemingly diverse patterning processes have been performed for the evolution of mammalian teeth [132–134] and the fin-to-limb transition in vertebrate evolution [135,136]. In this way, dynamical modelling can contribute substantially to homology judgements by providing indirect evidence for transitional forms and probabilities of transformations, for both ontogenetic processes and their phenotypic outcomes.

A particularly relevant application of this dynamical ‘map of the possible’ concerns the problem of distinguishing homology and homoplasy. As is well known, distinct lineages that evolve under the same developmental or functional constraints are prone to evolve the same traits independently. For example, similar topological and functional constraints on tetrapod limbs have been hypothesized to cause homoplastic similarities in their appendicular musculature [137]. A map of configuration space not only allows us to assign probabilities to possible evolutionary transitions, but also enables us to explore how large the range of possible solutions to a problem is to begin with. The space of possibilities for body segmentation, for example, is developmentally and functionally highly constrained. Ultimately, there are only two viable ways of segmenting a body axis—by serial addition (short-germband) or simultaneous subdivision (long-germband). This should make it unsurprising that these segmentation modes are subject to repeated homoplastic evolution, especially since transitions between these modes are highly likely and can occur in a gradual manner along the embryo's axis, generating the many intermediate forms we observe between the two extremes [61]. The capacity of dynamical systems approaches to model the ‘space of possibilities' for an evolving character gives them a distinct advantage for comparative research compared to most other methods of investigating the causes of evolution—including traditional mechanistic research that describes only the actual, qualitative causal structure of some process [138]. Obviously, one does not exclude the other, and the two approaches are best used in a complementary way.

In this section, we have provided a number of mutually reinforcing criteria for identifying and classifying homologous ontogenetic processes, which are summarized in table 2. The criteria are intended to be indicative of relationships of phylogenetic continuity, and can be combined as needed with existing phylogenetic methods (such as congruence testing). This indicative role of the six criteria also provides a basis for resolving conflicts that arise when some criteria are met but others are not. In general, when a given criterion is not met, the process can only be homologized if other criteria collectively give sufficient evidence of phylogenetic continuity. What counts as ‘sufficient’ evidence and how the different criteria are to be weighted are questions that must be informed by what is known about the developmental and evolutionary biology of the specific process under consideration. We have seen how this works for processes like echinoderm skeletogenesis, insect segmentation and vertebrate somitogenesis, each of which fails some of the criteria for process homology but nonetheless is judged to be a homologous process within the relevant monophyletic group. Further progress on the general problem of how to establish process homology is unlikely to come in the form of an algorithmic inference procedure operating on the evidential criteria (which would be a roundabout way of giving necessary and sufficient conditions for process homology). Instead, it is more likely to come in the form of empirically validated theoretical principles that explain how and when the features targeted by the criteria (e.g. sameness of parts, outcome and dynamical properties) stick together and when they come apart in evolution [24,34]. Understanding these principles is a major open task for empirical investigation in developmental evolutionary biology.

4. Discussion and conclusion

The homology of process has been recognized previously as an important notion for comparative and evolutionary biology [2,4,95,101,139–142], yet there have been few attempts to explicitly develop criteria for process homology and show what work the notion can do. Striedter's [18] epigenetic concept of homology describes homology in terms of the recurring attractor states that determine their outcome. Our criteria for process homology can be seen as an elaboration of this approach, which focuses less on the outcome and more on the intrinsic dynamics of the processes themselves. Another is the account of pathway homology put forward by Gilbert & Bolker [19]. In contrast with this account, we focus on a wider range of homology-supporting criteria that go beyond conserved genetic composition and structure.

As our examples from §2 show, ontogenetic processes constitute a dissociable level in evolution that cannot be reduced or traced exclusively in terms of features at other levels (such as genes or morphological characters). Thus, ontogenetic processes must be seen as quasi-independent units of evolutionary comparison just like genes or morphological characters, and we need to know what it means to be ‘the same’ process—in the sense of common evolutionary ancestry—just as we need to know what it means to be the same gene or the same body part.

More specifically, homology of process plays two major roles in evolutionary research: (i) it is required to shift from characterizing phylogenetic patterns of phenotypic change to causally explaining how phenotypic transitions occur in a lineage in terms of changes in the underlying generative processes; and (ii) it allows us to generalize such ‘lineage explanations' [25,39] across taxa, yielding ‘cross-lineage explanations’ (see Introduction). An example of (i) is the repeated transformation of the ancestral short-germband mode of segment determination into derived long-germband modes in various holometabolous insect lineages that include model organisms such as the jewel wasp Nasonia vitripennis, or the vinegar fly Drosophila melanogaster. An example of (ii) is the generalization of that explanation to lineages not studied in detail (i.e. non-model insects) on the basis of homology between the segmentation processes under comparison. These roles for process homology are not satisfied by existing phylogenetic approaches working on morphological and/or molecular traits. To put it simply, phylogenetic approaches are useful for resolving evolutionary patterns, but they tell us little about the underlying processes—and therefore also little about the evolutionary patterns of those processes.

The two roles for process homology we have discussed are not the only potentially fruitful uses of the concept.¹³ That being said, it is probably not a lack of appreciation that an account of process homology would be useful that has caused its historical neglect. It is more likely due to uncertainties about how to approach the problem methodologically. From classical anatomy to contemporary molecular biology, the concept of homology has traditionally had more affinity to stable structures—the ‘building blocks’ of the phenotype [143]—rather than transient activities or generative processes.

We have explored a way of overcoming these obstacles that combines existing criteria of homology (sameness of parts, phenotypic outcome and topological position) with the formal concepts of dynamical systems theory. The latter yield additional criteria of homology—shared dynamical properties, dynamical complexity and transitional forms in configuration space—that allow developmental processes to be precisely categorized and compared in the context of data-driven dynamical modelling. Generic, vaguely defined processes such as ‘tissue growth’ or ‘convergent extension’ will not have determinate homology relations as evaluated by the first three criteria. Such generic processes do not have specific identifiable parts, outcomes or relations to other processes. In these cases, it will also be difficult to construct a dynamical model of the process which can be validated against experimental evidence to characterize its particular dynamical properties. In this way, the six proposed criteria illuminate which instances of the seemingly nebulous category of ‘processes’ are homologizable and which are not. The central conceptual insight of our proposed dynamical framework is to show that processes can be homologized in terms of equivalence classes of configuration space topologies. This is crucial for providing an intrinsic description of ontogenetic processes as units of homology that does not collapse them into structural ‘building blocks’ at other levels, such as molecular components and phenotypic outcomes. In turn, our framework sets the groundwork for a comparative biology of developmental dynamics that is consistent with widespread developmental system drift and co-option of ontogenetic processes into novel roles and contexts.

The general idea of establishing homology by means of a systematic categorization of developmental dynamics amounts to a modern reincarnation of ‘process structuralism’. As a research programme, process structuralism sought to revive the pre-Darwinian tradition of establishing a ‘rational taxonomy’ for organismic form (reviewed in [4,144–146]). Rational taxonomies provide ahistorical systems of morphological classification based on possible transformations between different forms. In the process-structuralist version of this project, rational taxonomy is based on transformations between the processes that generate morphologies [2–4,127]. It assumes that the space of possible forms is small enough that they can be ordered into something like a ‘periodic table’ for ontogeny [2]. Homology, according to Goodwin, is ‘an equivalence relation over the members of a set, defined by a transformation that takes any member into any other member within the set’ (see [139, p. 233]; see also [2]). Fish fins and tetrapod limbs, for example, ‘fall within particular parameter domains of the same generative space’ and can be transformed into one another by modification of the generative rules that are generic to limb-forming processes [139, p. 238].¹⁴ A central aim of this generative classification programme is to determine the probability of phenotypic transitions in evolution based on the size of dynamic attractors in the space of possible morphologies (see [139]; see also [4]). In this way, it is similar to Striedter's [18] epigenetic approach.

Although there are obvious parallels, our approach differs in significant ways from this project. Process structuralists pointed to some of the same explanatory limitations of purely historical or pattern-based approaches to evolution as we do, but reacted by embracing the even stricter limitations of ‘ahistorical’ biology rather than attempting to synthesize the two.¹⁵ Without placing generative processes and forms in their actual phylogenetic sequence, our capacity to construct lineage explanations will remain limited to evolutionary changes that are currently observable. These extremely (and unnecessarily) restricted cases cannot then be generalized to other lineages via shared evolutionary history, but only via abstract ‘transformations’ in parameter space. This notion of transformation is not historical or evolutionary, but is essentially the notion of transformation from mathematical group theory.

Although we agree that the presence of possible transitional forms in configuration space influences the probabilities of evolutionary change (§3.6), these formal representations need to be embedded within historical reconstructions of phylogeny. This way, they can serve as a guide to understand actual historical transformations—which have an evolutionary ‘polarity’ or ‘historicity’—rather than speculative abstract transformations which are the same forwards and backwards in time (despite the fact that, for example, tetrapod limbs never transformed back into fish fins). The problem is that the space of biological possibilities is incredibly vast (and impossible to pre-state, see [147]), which means that evolution is highly non-ergodic. It explores only a tiny fraction of all possible configurations, which means that historical accidents will always play a key role in evolutionary explanations (see [148]; see also [149]). Because of this, it is more productive to combine the resources from historical and ‘generative’ approaches, both pattern and process, for understanding developmental dynamics in comparative biology. This requires a notion of process homology that is based on both evolutionary history and abstract modelling.¹⁶

It is important to emphasize another key difference. The project of rational taxonomy aimed to provide a system of classification for forms, or morphologies, and the process-structuralist version of this project does this in terms of generative processes. The aim of a framework for process homology, by contrast, is to classify the processes themselves, not the resulting forms.¹⁷ If it is true that processes and forms (‘phenotypic outcomes’, as we have called them) are dissociable in evolution—through co-option events, for example—then attempting to reduce morphological homology to process homology would be ill-advised in many cases. The idea of process homology does not revise existing criteria of homology for morphological characters, but rather complements them by extending the homology relation to an additional level of organization.

This point is also critical for understanding the relationship between process homology and developmental approaches to homology [14,141,151–157]. Developmental approaches aim to explain patterns of morphological homology in terms of shared underlying developmental mechanisms, constraints or pathways. This project is sometimes interpreted as an alternative conceptualization or definition of homology compared to phylogenetic views, but it can also be interpreted as a source of explanations for patterns of homology identified by phylogenetic methods [24,158]. A recent articulation of the latter project by Wagner and co-workers [34] is the model of ‘Character Identity Mechanisms' (ChIMs)—conserved modules that are hypothesized to control the identity of individualized morphological characters, including cell types, tissues and organs. Here again, the investigative target is morphological homology, but the proposed developmental model ultimately requires establishing homology criteria at the level of the underlying generative mechanisms themselves (ChIMs). The idea of process homology complements but only partially overlaps with the ChIM research programme. Homology between processes is not hypothesized to explain morphological character identity. Because ChIMs do have this explanatory role, they are not dissociable from their outcomes as ontogenetic processes are. Accordingly, ChIMs represent a special subset of the broader category of developmental mechanisms [37]—i.e. those mechanisms that can play this role of underwriting character identity (see [34]; cf. [156]). Ontogenetic processes are, therefore, a broader category that includes activities that do not have that role and are not ChIM-like: for example, segmentation clocks, vascular morphogenesis, life cycle traits and transient embryonic processes (see [34]). Both frameworks align in the broad project of comparative-mechanistic biology, of developing causal explanatory models of homology at the neglected intermediate levels between genes and morphology (see also [25,26]).

This project is a forward-looking one that still largely remains to be carried out. But the tools for doing so are now within our reach. The comparative study of ontogenetic processes will usually require that researchers have substantial background knowledge of the systems under study—not just genomic or phylogenetic data, but appropriate validated models of complex nonlinear regulatory processes. Therefore, it is no accident that our central examples are drawn from well-studied model systems. However, as evidence on the homology of ontogenetic processes increasingly accumulates in non-model organisms at multiple levels of organization, it is useful to have a theoretical framework that can be used both to interpret the existing data and to guide the trajectory of future research.

Data accessibility

This article has no additional data.

Authors' contributions

Both authors contributed equally to the content and the writing of this paper. J.D. conceived the ideas and wrote the paper; J.J. conceived the ideas and wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

J.D. gratefully acknowledges the Research Foundation—Flanders (FWO) for financial support (grant no. 41277). J.J. is currently the recipient of a six-month fellowship—the D'Alembert Research Chair 2020/21—jointly sponsored by the Université Paris Saclay and the Institut d’Études Avancées (IEA) in Paris.