Abstract
Motivation
Protein fold recognition is a key step for template-based modeling approaches to protein structure prediction. Although closely related folds can be easily identified by sequence homology search in sequence databases, fold recognition is notoriously more difficult when it involves the identification of distantly related homologs. Recent progress in residue–residue contact and distance prediction opens up the possibility of improving fold recognition by using structural information contained in predicted distance and contact maps.
Results
Here we propose to use the congruence coefficient as a metric of similarity between maps. We prove that this metric has several interesting mathematical properties which allow one to compute in polynomial time its exact mean and variance over all possible (exponentially many) alignments between two symmetric matrices, and assess the statistical significance of similarity between aligned maps. We perform fold recognition tests by recovering predicted target contact/distance maps from the two most recent Critical Assessment of Structure Prediction editions and over 27 000 non-homologous structural templates from the ECOD database. On this large benchmark, we compare fold recognition performances of different alignment tools with their own similarity scores against those obtained using the congruence coefficient. We show that the congruence coefficient overall improves fold recognition over other methods, proving its effectiveness as a general similarity metric for protein map comparison.
Availability and implementation
The congruence coefficient software CCpro is available as part of the SCRATCH suite at: http://scratch.proteomics.ics.uci.edu/.
Supplementary information
Supplementary data are available at Bioinformatics online.
1 Introduction
Computational approaches for protein structure prediction generally follow one of two broad strategies (Kryshtafovych et al., 2019; Kuhlman and Bradley, 2019): template-free (or ab-initio) modeling and template-based modeling, which uses known protein structures as templates for the structural modeling of the unknown protein structure. While closely related templates can easily be detected by using protein sequence search methods, the detection of distantly related templates needs more sophisticated fold recognition strategies. Popular approaches make use of sequence profiles, predicted secondary structure and solvent accessibility, and exploit diverse computational methods, such as linear programming, dynamic programming, hidden Markov models as well as other machine learning methods (Jones and Thornton, 1993; Lemer et al., 1995). However, despite considerable progress, remote homology detection remains a challenging problem.
The most recent Critical Assessment of Structure Prediction experiment (CASP13) held in 2018 reported a dramatic improvement in protein structure prediction for both template-free and template-based modeling (Kryshtafovych et al., 2019). This improvement has been driven primarily by the successful applications of deep-learning approaches (Di Lena et al., 2012; Kandathil et al., 2019) and direct coupling analysis (De Juan et al., 2013) to predict intra-residues distances and contacts (Hou et al., 2019; Shrestha et al., 2019; Senior et al., 2019; Xu and Wang, 2019; Zheng et al., 2019).
The recent progress in intra-residue distance and contact prediction opens up the possibility to further improve fold recognition by database searches using predicted distance/contact maps. This requires addressing two distinct problems: (i) developing efficient two-dimensional alignment procedures for map comparison and (ii) developing a good scoring function to measure the fitness between target maps and templates.
In this work, we deal explicitly with the second problem, and partially with the first problem, by exploiting the congruence coefficient (Burt, 1948) as a measure of similarity between aligned maps. The congruence coefficient bears some similarity to the Pearson’s correlation coefficient, since its value lies in the interval and it is insensitive to multiplication (but not addition) by a constant factor. However, unlike Pearson’s correlation coefficient, its normalization factor is invariant with respect to any alignment between two maps, which makes it particularly suitable as an objective function for alignment procedures.
We prove some interesting statistical properties of the congruence coefficient, such as a measure of statistical significance and polynomial-time formulas for computing both the exact mean and variance of the coefficient over all possible (exponential number of) alignments between two symmetric matrices. Such statistical properties are complementary. The statistical significance of the congruence coefficient can be used to detect statistically significant similarities between two aligned maps, which improves template ranking for predicted target maps. Conversely, the mean and variance of the congruence coefficient over all possible alignments can be used to compute the alignment Z-scores, which give indications on the quality of the alignments.
We test the fold recognition performances of the congruence coefficient by recovering predicted maps from the last two CASP editions and over 27 000 structural templates from the ECOD database (Cheng et al., 2014) that do not share sequence similarity with the CASP targets. In detail, for performance assessment with predicted contact maps, we use residue–residue predictions at CASP12 and CASP13 and three contact map alignment software: AlEigen (Di Lena et al., 2010), EigenTHREADER (Buchan and Jones, 2017) and Map_Align (Ovchinnikov et al., 2017). All three tools return an alignment between two input maps together with a similarity score. Keeping fixed the alignments, we compute the congruence coefficient between target and structural templates. Performances have been then assessed by comparing fold recognition accuracy with the congruence coefficient versus the original similarity score. A statistical analysis of alignment quality is also provided in order to evaluate to which extend alignment quality affects fold recognition performances. Since there is no CASP category for predicted distance maps and there are no standalone tools for distance map alignment, we assess fold recognition accuracy by using regular protein structure predictions at CASP and structural alignment tools CE (Shindyalov and Bourne, 1998) and TM-align (Zhang and Skolnick, 2005). In this case, we recover predicted distance maps from predicted structures, use the structural alignments to induce alignments between distance maps and then compute the congruence coefficient between the aligned maps. Performance assessment is achieved by comparison of fold recognition accuracy with the congruence coefficient versus the specific structural alignment similarity scores. Also in this case, alignment Z-scores are used to assess alignment quality and its impact on fold recognition performances. Although fold recognition with distance maps recovered from structural predictions may appear artificial, it provides a fair evaluation of fold recognition by protein distance maps. Overall our tests provide a benchmark to compare the congruence coefficient to other structural alignment metrics, in both contact-based and distance-based fold recognition.
As a general conclusion, fold recognition with predicted contact maps is significantly improved by using the congruence coefficient score as a fitness function. In comparison to structural alignment metrics, the congruence coefficient shows comparable or better fold recognition accuracy, proving its potential as general similarity metric for protein map comparisons.
2 Materials and methods
2.1 Congruence coefficient
2.1.1 Definition
The congruence coefficient was first introduced in Burt (1948), with the name of unadjusted correlation, as a measure of similarity in factor analysis.
Definition 2.1
Let be two real matrices. The congruence coefficient between X, Y is defined by:
(1) The rc score is between −1 and +1, with rc = 1 representing the highest degree of similarity. Although the congruence coefficient appears quite similar to the Pearson’s correlation coefficient, the latter measures the deviations from the mean whereas the congruence coefficient measures the deviations from zero. Like the correlation coefficient, the congruence coefficient is insensitive to the multiplication of the matrices X, Y by constant factors different from zero. Unlike the correlation coefficient, it is sensitive to the addition of constant factors.
Although the rc coefficient can be computed for non-square matrices, here we focus on protein contact and distance maps, which are both represented by square (symmetric) matrices. Typically, contact and distance maps of different proteins have different sizes determined by the protein sequence lengths, thus the rc coefficient between two contact/distance maps can be computed only if an alignment between the two matrices is provided. Aligned matrices can be simply obtained by introducing rows and (respective) columns of zeroes in the original symmetric matrices, which correspond to gaps in the alignments. Since zero (gap) rows/columns do not contribute in the trace of the products in Equation (1), an equivalent and simpler formulation of the congruence coefficient with respect to some alignment can be obtained by leaving unchanged the X matrix and by removing all rows/columns in the Y matrix that match a gap row/column in the aligned X matrix (Section 3 in Supplementary Material). In this way, we can just recode the Y matrix as follows.
Definition 2.2
A partial function is an alignment if such that and then:
where means that α is not defined on i. Given a matrix and an alignment , we define the new matrix by:
Now, let be two symmetric matrices and an alignment. We define (Section 3 in Supplementary Material) the congruence coefficient with respect to the alignment α by
(2)
Note that, the normalization factor in Equation (2) is invariant with respect to any possible alignment α. Such property does not hold for Pearson’s correlation which measures the deviation from the mean value and is thus affected by the number of zero rows and columns introduced in the alignment. The alignment that maximizes the rc coefficient in Equation (2) is thus simply the alignment that maximizes the trace of the product between the two aligned matrices.
2.1.2 Statistical properties of the congruence coefficient
Here we show that the congruence coefficient has several desirable mathematical properties: its statistical significance can be rigorously assessed, and its mean and variance can be estimated in polynomial time. The details of our proofs are given in the Supplementary Material.
Statistical hypothesis testing of the congruence coefficient between two aligned maps, under the null hypothesis that the coefficient is zero, can be reframed as a statistical hypothesis testing on the angle between two unitary vectors on some N-dimensional unit sphere, under the null hypothesis that the two vectors are orthogonal. The dimension N depends on the size and topology of the two input matrices. The P-value can be then computed as the ratio between the volume of the N-dimensional unit sphere and the volume of the hyper-spherical cap (Li, 2011) identified by the angle between the two unitary vectors. In summary, let and be two symmetric matrices with zero main diagonal, and an alignment. Then (Section 6 in Supplementary Material) the right-tailed P-value of the congruence coefficient is given by:
| (3) |
where I is the regularized incomplete beta function, , and the degree of freedom N is the number of non-zero elements in the upper (or lower) triangular portion of X. Given any symmetric matrix , Equation (3) gives the probability of uniformly sampling a random symmetric matrix (with zero main diagonal), such that . We can symmetrically use Equation (3) with known Y, where the degree of freedom N is the number of non-zero elements in the upper triangular portion of Y. The condition of having zero main diagonal is necessary, and trivially satisfied by distance maps, as well as contact maps (contacts between adjacent residues are typically ignored). In database searches, we use Equation (3) to assess whether two aligned matrices are significantly similar. That is, given a target matrix X, a template matrix Y and an alignment α between X and Y, we ignore template Y if or , where t is the Bonferroni-corrected P-value cutoff 0.05.
The exact mean and variance of the rc score under all possible alignments can be used to test the quality of a given alignment between two maps (i.e. Z-score). Given two symmetric matrices and , the expected value of the congruence coefficient between X and Y with respect to all possible alignments α is given by (Section 4.2 in Supplementary Material):
| (4) |
where is the expectation matrix, that averages all matrices. The expectation matrix can be computed from Y and m, without the need of X. Equivalently, the variance of the congruence coefficient between X and Y with respect to all possible alignments α is given by (Section 4.3 in Supplementary Material):
| (5) |
where ⊗ is the Kronecker product and: is the variance–covariance matrix of random matrices . The variance–covariance matrix can also be computed using only Y and m. The computational time for the expectation matrix in Equation (4) is quadratic in the product of the lenghts mn, which is reasonably fast for native contact/distance maps. Instead, the computational time for the variance–covariance matrix in (5) is quartic in mn, which is challenging for large matrices. However, an ad hoc sampling of alignments (i.e. proportional to the fraction of alignments of a given size) provides an almost exact estimation of the variance (Section 7.3 in Supplementary Material).
In addition, following the combinatorial approach described in Kazi-Aouala et al. (1995), we can derive closed expressions for the expectation and variance of the congruence coefficient between two symmetric maps X and Y over all possible permutations of Y, and with respect to all possible alignments between X and Y (Section 5 in Supplementary Material). We tried to exploit permutation statistics as a fast approach for approximating variance calculations over all possible alignments. However, tests on real protein contact/distance maps show that both expectation and variance over permutations poorly approximate expectation and variance over all possible alignments (Section 7.3 in Supplementary Material). Thus the formula obtained does not seem to have an immediate application in protein map comparison, although they have intrinsic theoretical interest and may be useful in other contexts.
2.2 Template and benchmark data
Benchmark datasets were obtained from the CASP repository (Section 7.1 in Supplementary Material). For contact-based fold recognition assessment, we selected all residue–residue contact predictions submitted to the CASP12 and CASP13 experiments. For distance-based fold recognition assessment, we decided to simulate predicted distance maps by recovering them from the structural predictions at CASP12 and CASP13. This was necessary since distance map predictions were used as an intermediary step, rather than as a standalone problem, and such predictions were not available. We considered only the CASP targets for which the experimentally determined structure was available in the Protein Data Bank (PDB) and the fold annotation was available in the Evolutionary Classification Of protein Domains (ECOD) classification (Cheng et al., 2014).
Template data were obtained from the ECOD database (Section 7.1 in Supplementary Material). ECOD protein domains are classified with respect to four groups: the F-group (Family level) groups domains with significant sequence similarity; the T-group (Topology level) groups domains with similar topological connections; the H-group (Homology level) groups domain that are considered homologous based on different attributes (e.g. functional similarity, literature); and the X-group (Possible Homology level) groups domains that are potentially homologous although there is not yet adeguate evidence to support their homology relationship. We downloaded the ECOD pre-filtered subset at 40% sequence identity. In order to prevent any sequence homology bias in our tests, we removed from the ECOD dataset all protein domains found by hmmsearch (Eddy, 2011) and HHsearch (Steinegger et al., 2019) scans of the CASP12 and CASP13 targets against the ECOD database. Such scans filtered-out all the ECOD domains at the Family level of similarity with the CASP targets. In order to identify a subset of hard targets, we matched the FM (free modeling) domains of the CASP targets with the domains identified in ECOD. Native contact and distance maps were extracted from the ECOD pdb domain files.
The exact number of ECOD templates used in our experiments, as well as the targets and FM targets in the two CASP benchmark datasets, are shown in Table 1.
Table 1.
Benchmark dataset
| Dataset | #Targets (#FM) | #RR Pred | #REG Pred | #ECOD templates |
|---|---|---|---|---|
| CASP12 | 34 (12) | 1109 | 2567 | 27 077 |
| CASP13 | 23 (8) | 956 | 1842 | 27 112 |
Note: Benchmark set statistics. #Targets: number of CASP targets with fold annotation; #FM: number of targets containing FM domains; RR Pred: residue–residue contact predictions; REG Pred: regular structure predictions; #ECOD templates: number of sequence homology-free ECOD templates.
2.3 Benchmark tools
2.3.1 Contact maps
We considered three contact map alignment tools for performance comparison (Section 7.2 in Supplementary Material): AlEigen (Di Lena et al., 2010), EigenTHREADER (Buchan and Jones, 2017) and Map_Align (Ovchinnikov et al., 2017). We used the three tools to first align target and template maps and then to rank the templates: (i) using the tool-specific scores and (ii) using the congruence coefficient with respect to the alignments returned by the tools.
2.3.2 Distance maps
Unlike contact map alignment, the standalone distance map alignment problem has received little or no attention in the literature. For this reason, for performance comparison, we decided to use two popular structural alignments tools (Section 7.2 in Supplementary Material), CE (Shindyalov and Bourne, 1998) and TM-align (Zhang and Skolnick, 2005), and recover the distance map alignments from the structural alignments computed by both tools. Also in this case we rank the templates: (i) using the tool-specific scores and (ii) using the congruence coefficient with respect to the alignments returned by the tools.
Our choice of alignment tools has been driven mainly by speed considerations due to the very large number of comparison performed in our tests: a total of 57M contact map comparisons, and 122M structure comparisons, per method (see Table 1). The average running times of the benchmarked methods are summarized in Table 2.
Table 2.
Average running time per prediction
| Method | Average time CASP12 | Average time CASP13 |
|---|---|---|
| EigenTHREADER | 41 min | 52 min |
| AlEigen | 2.8 h | 3.9 h |
| Map_Align | 6 days | 8.7 days |
| CE | 4.7 days | 4.9 days |
| TM-align | 2.2 h | 2.2 h |
3 Results
3.1 Fold recognition with predicted contacts
For performance comparison, we search all residue–residue contact predictions submitted at CASP for a single target against the ECOD templates. This implies a maximum number of 38 predictions per target at CASP12 and 46 at CASP13, corresponding to the number of residue–residue prediction groups in the two CASP editions. More precisely, for a given CASP target, the ECOD database scan returns a list of mappings of the form:
<CASP prediction ID, ECOD template ID, similarity score >,
where the similarity score is specific to the alignment method used for the search. Such list of mappings is sorted according to the similarity score in order to obtain a similarity ranking of the ECOD templates against the CASP target. Each ECOD template is ranked according to the first position in which it appears in the sorted list. Such multiple map approach for fold recognition has been chosen in order to avoid having to make an a priori selection of the best predictor(s), or best contact prediction(s), information that is not available in a realistic blind test. True positive rate (TPR) fold recognition performances are assessed by selecting the top-1, top-5, top-10 and top-20 templates identified by the search with multiple predicted maps. For each top-k set, the TPR score is computed by counting the fraction of targets for which at least one template with similar fold is in the top-k hits. We assess the TPR performances separately for the three ECOD classes: Topology Level (T), Homology Level (H) and Possible Homology Level (X). This implies that, for example, for TPR assessment at the Topology Level we consider only the CASP targets that have been annotated at the Topology Level in ECOD. The TPR performances on the CASP12 and CASP13 benchmark datasets, for the three map alignment tools AlEigen, EigenTHREADER and Map_Align are summarized in Table 3. The table compares the performances of the three tools with their specific scoring schemes against those obtained using the congruence coefficient, indicated by AlEigen + rc, EigenTHREADER + rc and Map_Align + rc, respectively.
Table 3.
Fold recognition performances with predicted contacts
| Method | Benchmark set | Top-1 hit |
Top-5 hits |
Top-10 hits |
Top-20 hits |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | H | X | T | H | X | T | H | X | T | H | X | ||
| AlEigen | CASP12 | 0.07 | 0.07 | 0.06 | 0.07 | 0.07 | 0.09 | 0.07 | 0.10 | 0.12 | 0.07 | 0.10 | 0.15 |
| AlEigen + rc | 0.18 | 0.27 | 0.29 | 0.25 | 0.30 | 0.35 | 0.25 | 0.33 | 0.44 | 0.39 | 0.43 | 0.53 | |
| EigenTHREADER | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.09 | 0.04 | 0.03 | 0.09 | 0.11 | 0.10 | 0.15 | |
| EigenTHREADER + rc | 0.21 | 0.27 | 0.29 | 0.39 | 0.40 | 0.50 | 0.46 | 0.50 | 0.62 | 0.50 | 0.53 | 0.62 | |
| Map_Align | 0.07 | 0.07 | 0.06 | 0.07 | 0.07 | 0.06 | 0.07 | 0.10 | 0.12 | 0.11 | 0.10 | 0.15 | |
| Map_Align + rc | 0.43 | 0.43 | 0.50 | 0.46 | 0.50 | 0.56 | 0.50 | 0.53 | 0.65 | 0.64 | 0.67 | 0.71 | |
| AlEigen | CASP13 | 0.11 | 0.20 | 0.26 | 0.17 | 0.25 | 0.35 | 0.22 | 0.30 | 0.43 | 0.22 | 0.30 | 0.43 |
| AlEigen + rc | 0.28 | 0.30 | 0.43 | 0.33 | 0.35 | 0.61 | 0.50 | 0.50 | 0.65 | 0.56 | 0.55 | 0.70 | |
| EigenTHREADER | 0.11 | 0.10 | 0.13 | 0.11 | 0.20 | 0.26 | 0.17 | 0.20 | 0.30 | 0.22 | 0.25 | 0.35 | |
| EigenTHREADER + rc | 0.33 | 0.35 | 0.52 | 0.50 | 0.60 | 0.70 | 0.61 | 0.65 | 0.74 | 0.61 | 0.65 | 0.78 | |
| Map_Align | 0.28 | 0.35 | 0.48 | 0.28 | 0.35 | 0.48 | 0.33 | 0.40 | 0.52 | 0.44 | 0.45 | 0.57 | |
| Map_Align + rc | 0.39 | 0.40 | 0.48 | 0.56 | 0.60 | 0.65 | 0.61 | 0.65 | 0.74 | 0.72 | 0.75 | 0.78 | |
Note: TPR fold recognition performances on CASP12 and CASP13 benchmark sets. Comparison of TPR performance achieved by AlEigen, EigenTHREADER and Map_Align with their own scoring system against those obtained by using statistically significant congruence coefficient, AlEigen + rc, EigenTHREADER + rc and Map_Align + rc, respectively. The TPR performances are assessed with respect to the top-1, top-5, top-10 and top-20 ranked hits. ECOD hierarchy: (T) Topology Level (28 targets in CASP12, 18 targets in CASP13), (H) Homology Level (30 targets in CASP12, 20 targets in CASP13), (X) Possible Homology Level (34 targets in CASP12, 23 targets in CASP13). Best TPR performances per column on CASP12 and CASP13 benchmark sets are highlighted in bold.
Fold recognition performances with predicted contact maps are influenced by three main factors: (i) contact map prediction accuracy; (ii) accurate alignments between target and templates; and (iii) proper scoring of the fitness between target and templates. The influence of a good scoring function is particularly evident for fold recognition performances in the CASP12 benchmark set (see Table 3), where the fold recognition precision is dramatically improved by the usage of the congruence coefficient for fitness ranking. We remark that for the computation of the rc coefficient we use the alignments returned by the three packages, thus the low TPR performances of the three tools with their specific fitness functions are not an immediate consequence of poor contact map predictions or poor alignments. The improvement in fold recognition accuracy with rc scoring can be observed also on the CASP13 benchmark set (see Table 3). In this case, the improvement is still significant, although less pronounced, since all the three methods show overall better performances with their own scoring functions in comparison to those achieved for CASP12. To a large extent, this can be imputed to better contact predictions for CASP13, which compensate for the lack of a good scoring function. In fact, if we restrict our tests to contact predictions submitted only by the top-ranked predictors (using the official CASP rankings), we notice a general improvement in fold recognition accuracy for all methods (Section 7.4.1 in Supplementary Material). Interestingly, the improvement is almost negligible or absent for rc ranking performances, which indicates that the congruence coefficient can filter out most of the noisy similarities. This is partially a consequence of the statistically significant P-value cutoff applied to the rankings (Section 7.4.4 in Supplementary Material).
For each CASP target in our benchmark set there is a highly variable number of related (i.e. similar) templates in ECOD. In particular, the number of related templates per target varies from 2 to 3373 for CASP12 targets, and from 46 to 1444 for CASP13 targets. In Table 3, we assess fold recognition performances by considering only the top-scored templates, but this does not tell us how all the templates related to a given target are ranked during a search. In Figure 1, we show the ranking distributions of all the templates related to the CASP12 and CASP13 targets. The probability density functions in Figure 1 are estimated from the observed rankings in our tests for both CASP12 and CASP13 targets, using the density function available in R. In order to detect whether there is a statistically significant difference in template rankings with or without the congruence coefficient, we use the Wilcoxon paired signed-rank test to compare the template ranks obtained with an alignment tool’s own scoring function against the ranks obtained with the congruence coefficient. In all three cases (i.e. AlEigen + rc versus AlEigen, EigenTHREADER + rc versus EigenTHREADER and Map_Align + rc versus Map_Align) the Wilcoxon’s test detects that the median rank obtained with the congruence coefficient is significantly shifted to the left (i.e. lower ranks) with P-value <2.2e−16. In fact, by observing Figure 1, it is clear that the congruence coefficient shifts the ranking distribution of related templates closer toward 1, uniformly for all methods. However, in Figure 1 we can see that the peak of the rc-related distributions is around ranking position 607, which is still quite far from the top-20 interval considered in Table 3. To this extent, it is interesting to ask how much fold recognition performances are affected by inaccurate contact predictions. In order to answer this question, we tested fold recognition accuracy by using only the top-ranked contact predictions per target, using the official CASP rankings (Section 8 in Supplementary Material). Consistently with the observations reported by restricting to top-ranked predictors, we notice an overall improvement in fold recognition performances, particularly for the three alignment methods with their own scoring functions. More generally, we can observe an overall good correlation between prediction accuracy and template rankings (Section 8 in Supplementary Material). However, while highly accurate predictions generally enhance fold recognition, there are also several cases of inaccurate predictions (according to CASP evaluation) that still provide good fold recognition performances (Section 8 in Supplementary Material).
Fig. 1.
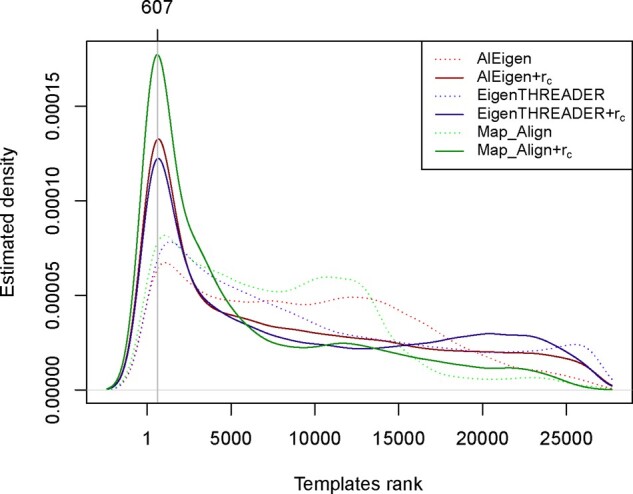
Estimated ranking distribution of templates searched with predicted contacts. Comparison of the ranking distribution for templates related to the target proteins in CASP12 and CASP13. Probability density function estimated from observed rankings in CASP12 and CASP13 benchmark sets. The Wilcoxon paired signed-rank test detects a statistically significant shift (P-value < 2.2e−16) to the left of the median rank obtained with the congruence coefficient for all three comparisons AlEigen + rc versus AlEigen, EigenTHREADER + rc versus EigenTHREADER and Map_Align + rc versus Map_Align
A more stringent analysis of the fold recognition performances can be done on CASP targets that contain at least one FM domain. There the fold recognition performances are assessed only for the FM domains of such targets. The TPR performances are summarized in Table 4. To improve readability, we show only the results for the top-20 recovered templates (complete results in Section 7.4.1 in Supplementary Material). With Map_Align + rc we can exceed 40% fold recognition accuracy on FM targets at the Topology level for both CASP12 and CASP13. While leaving room for improvements, such performance is still interesting. Recall that for both CASP12 and CASP13, the ECOD database was pre-filtered by removing all domains that share a significant sequence similarity with the CASP targets. Hence, although we do not have many FM targets in our benchmark sets, the results in Table 4 suggest that contact prediction is at a sufficiently high level of accuracy to improve fold recognition for distantly related homologs.
Table 4.
Fold recognition performances with predicted contacts on FM targets (top-20 hits)
| Method | CASP12 |
CASP13 |
||||
|---|---|---|---|---|---|---|
| T | H | X | T | H | X | |
| AlEigen | 0.14 | 0.12 | 0.08 | 0.17 | 0.29 | 0.25 |
| AlEigen + rc | 0.29 | 0.38 | 0.42 | 0.50 | 0.43 | 0.62 |
| EigenTHREADER | 0.00 | 0.00 | 0.17 | 0.17 | 0.14 | 0.12 |
| Eigen THREADER + rc | 0.29 | 0.38 | 0.42 | 0.50 | 0.43 | 0.62 |
| Map_Align | 0.14 | 0.12 | 0.08 | 0.17 | 0.29 | 0.25 |
| Map_Align + rc | 0.43 | 0.50 | 0.42 | 0.50 | 0.57 | 0.50 |
Note: Comparison of TPR performance achieved on FM targets by AlEigen, EigenTHREADER and Map_Align with their own scoring system against those obtained by using statistically significant congruence coefficient, AlEigen + rc, EigenTHREADER + rc and Map_Align + rc, respectively. ECOD hierarchy: (T) Topology Level (7 targets in CASP12, 6 targets in CASP13), (H) Homology Level (8 targets in CASP12, 7 target in CASP13), (X) Possible Homology Level (12 targets in CASP12, 8 targets in CASP13). Best TPR performances per column are highlighted in bold.
Finally, we look at the quality of the alignments provided by the three methods. We measure the alignment quality through the Z-score of the congruence coefficient between two aligned maps, where the mean and standard deviation are computed over all possible alignments between the two maps. The alignment quality measure is independent of the similarity between the two maps being aligned: optimal alignments can be computed for two unrelated maps and poor alignments can be computed for similar maps, which may affect fold recognition performances. In Figure 2, we plot the Z-score distribution of all the alignments between CASP12/CASP13 targets and templates maps. The Z-scores are computed using the true mean of the congruence coefficient over all possible alignments, and the sampled standard deviations (Section 7.3 in Supplementary Material). The Z-score distributions are computed separately for all the alignments between a target map and all its related templates in ECOD, and between a target map and all unrelated templates. First of all, in Figure 2 we can notice that, independently of the chosen method, the alignment Z-score distribution is similar for related and unrelated templates. This indicates that the alignment quality of each method is independent of the similarity between the two input maps, i.e. on average one cannot expect to see better alignments for related maps than for unrelated maps. Overall, Map_Align provides better alignments than the two other methods. This is consistent with the performances reported in Table 3, where Map_Align, especially with the correlation coefficient as its scoring function, achieves overall best fold recognition accuracy. In contrast, EigenTHREADER provides on average lower quality alignments. In particular, in a non-trivial number of cases the rc scores with respect to the alignments computed by EigenTHREADER are lower that the expected mean. However, EigenTHREADER’s fold recognition performances are no dramatically affected when coupled with the congruence coefficient. This is further evidence that the congruence coefficient provides an effective measure of map similarity.
Fig. 2.
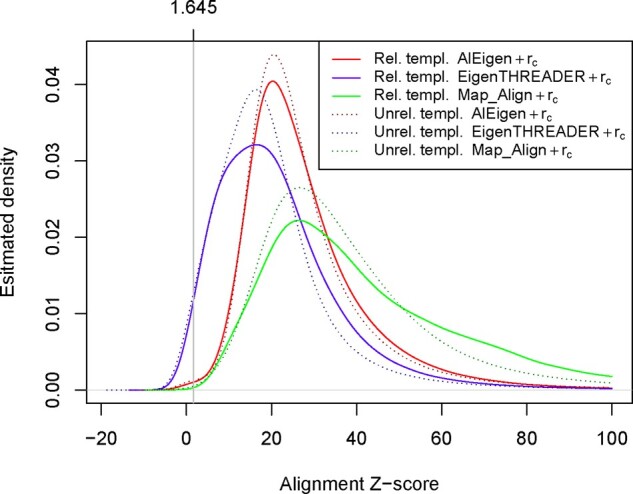
Estimated Z-score distribution of contact map alignments for templates related and unrelated to the target proteins in CASP12 and CASP13. The alignment Z-score distribution is similar for related and unrelated templates for every alignment method. Map_Align provides the most accurate alignments, EigenTHREADER the lower quality alignments
EigenTHREADER’s fold recognition performances in Table 3 are somewhat disappointing in comparison to those reported in Buchan and Jones (2017). This may be due to the specific characteristics of the CASP benchmark dataset, which contains several inaccurate predictions of multi-domain proteins. In contrast, the EigenTHREADER’s original benchmark dataset contains highly accurate predictions of single-domain proteins. Furthermore, the EigenTHREADER’s scoring function has been fitted on single-domain proteins only. In order to further test the congruence coefficient, we assessed fold recognition performances on the EigenTHREADER’s dataset (Section 7.4.3 in Supplementary Material), consisting of 150 single-domain proteins with their associated contacts predicted (with high accuracy) by MetaPSICOV (Jones et al., 2015) and 13k fold library domains recovered from SCOP (Structural Classification of Proteins) 1.75 (Andreeva et al., 2020). Overall, these comparison tests confirm what was already reported in Buchan and Jones (2017): when homology is present in the fold library, sequence-based methods (in particular HHsearch) outperform contact-based fold recognition tools. Conversely, in a low homology setting, map alignment tools outperform sequence-based fold recognition methods. Consistently with the results of our tests on the CASP benchmark dataset, when homology is present, the congruence coefficient provides little or no improvement (Section 7.4.3 in Supplementary Material). However, when low or no homology is present in the fold library, the congruence coefficient fitness function helps to improve fold recognition performances on the EigenTHREADER’s benchmark dataset for all the map alignment tools.
3.2 Fold recognition with predicted distances
For distance maps, we run tests similar to those performed with contact maps. Here we use two structural alignment tools, CE and TM-align. Also here we compare the fold recognition capabilities of CE and TM-align with their own scoring schemes, CE’s Z-score and TM-score, respectively, against those obtained by using the congruence coefficient, CE + rc and TM-align + rc, respectively. The goal of these tests is to show whether the congruence coefficient is suitable also for distance map comparisons and thus for distance map-based fold recognition. Furthermore, this provides a preliminary comparison between contact-based versus distance-based fold recognition.
The TPR performances on the CASP12 and CASP13 sets are summarized in Table 5, while performances on the FM targets are in Table 6 (Section 7.4.2 in Supplementary Material for the complete table). Unlike the contact results, in these tests fold recognition capabilities are mainly affected by the quality of the predicted structures. In particular, the overall fold recognition performance for CASP13 is better than for CASP12, a direct consequence of the improvements in protein structure prediction reported at CASP13. Furthermore, the restriction to structural predictions by the top-performing methods overall does improve fold recognition on CASP12, and for some methods also on CASP13 (Section 7.4.2 in Supplementary Material). We observe exactly the same trend if we restrict to top predictions (Section 8 in Supplementary Material). Furthermore, and consistently with our observations for contact-based fold recognition, although better predictions improve fold recognition accuracy there are several cases of inaccurate structural predictions—as evaluated in CASP—that still yield good fold recognition performances (Section 8 in Supplementary Material).
Table 5.
Fold recognition performances with predicted distances/structures
| Method | Benchmark set | Top-1 hit |
Top-5 hits |
Top-10 hits |
Top-20 hits |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | H | X | T | H | X | T | H | X | T | H | X | ||
| CE | CASP12 | 0.29 | 0.37 | 0.35 | 0.43 | 0.53 | 0.56 | 0.43 | 0.53 | 0.56 | 0.46 | 0.53 | 0.56 |
| CE + rc | 0.36 | 0.40 | 0.35 | 0.43 | 0.47 | 0.50 | 0.54 | 0.57 | 0.56 | 0.54 | 0.57 | 0.56 | |
| TM-align | 0.21 | 0.33 | 0.35 | 0.39 | 0.43 | 0.53 | 0.54 | 0.57 | 0.59 | 0.61 | 0.60 | 0.62 | |
| TM-align + rc | 0.36 | 0.40 | 0.35 | 0.43 | 0.50 | 0.47 | 0.50 | 0.53 | 0.53 | 0.54 | 0.60 | 0.59 | |
| CE | CASP13 | 0.33 | 0.40 | 0.43 | 0.39 | 0.50 | 0.57 | 0.44 | 0.55 | 0.65 | 0.50 | 0.55 | 0.65 |
| CE + rc | 0.39 | 0.45 | 0.48 | 0.56 | 0.60 | 0.61 | 0.61 | 0.65 | 0.70 | 0.61 | 0.65 | 0.74 | |
| TM-align | 0.50 | 0.55 | 0.61 | 0.50 | 0.60 | 0.70 | 0.56 | 0.65 | 0.74 | 0.56 | 0.65 | 0.74 | |
| TM-align + rc | 0.39 | 0.45 | 0.48 | 0.56 | 0.60 | 0.61 | 0.56 | 0.60 | 0.65 | 0.61 | 0.65 | 0.70 | |
Note: TPR fold recognition performances on CASP12 and CASP13 benchmark sets. Comparison of TPR performance achieved by CE and TM-align with their own scoring system against those obtained by using statistically significant congruence coefficient, CE + rc and TM-align + rc, respectively. The TPR performances are assessed with respect to the top-1, top-5, top-10 and top-20 ranked hits. ECOD hierarchy: (T) Topology Level (28 targets in CASP12, 18 targets in CASP13), (H) Homology Level (30 targets in CASP12, 20 targets in CASP13), (X) Possible Homology Level (34 targets in CASP12, 23 targets in CASP13). Best TPR performances per column on CASP12 and CASP13 benchmark sets are highlighted in bold.
Table 6.
Fold recognition performances with predicted distances/structures on FM targets (top-20 hits)
| Method | CASP12 |
CASP13 |
||||
|---|---|---|---|---|---|---|
| T | H | X | T | H | X | |
| CE | 0.00 | 0.12 | 0.17 | 0.33 | 0.43 | 0.50 |
| CE + rc | 0.29 | 0.38 | 0.42 | 0.33 | 0.43 | 0.50 |
| TM-align | 0.29 | 0.38 | 0.33 | 0.33 | 0.43 | 0.50 |
| TM-align + rc | 0.29 | 0.38 | 0.33 | 0.33 | 0.43 | 0.50 |
Note: Comparison of TPR performance achieved on FM targets by CE and TM-align with their own scoring system against those obtained by using statistically significant congruence coefficient, CE + rc and TM-align + rc, respectively. ECOD hierarchy: (T) Topology Level (7 targets in CASP12, 6 targets in CASP13), (H) Homology Level (8 targets in CASP12, 7 target in CASP13), (X) Possible Homology Level (12 targets in CASP12, 8 targets in CASP13).
In terms of fold recognition performances, the congruence coefficient is comparable to TM-score and CE’s Z-score, two metrics adopted by CASP. In some cases, the congruence coefficient achieves slightly better accuracy. However, we do not observe significantly strong differences between the TM-Align versus CE and TM-score/Z-score versus congruence coefficient, since no approach is overall better than another in all cases. This is consistent with what we observe in Figure 3, which shows that the ranking distributions of related templates are practically undistinguishable among all benchmarked approaches. However, the Wilcoxon paired signed-rank test detects a positive shift of the median rank toward the left for the comparison CE + rc versus CE with P-value = 7.106e−05 and with P-value <2.2e−16 for the TM-align + rc versus TM-align comparison.
Fig. 3.
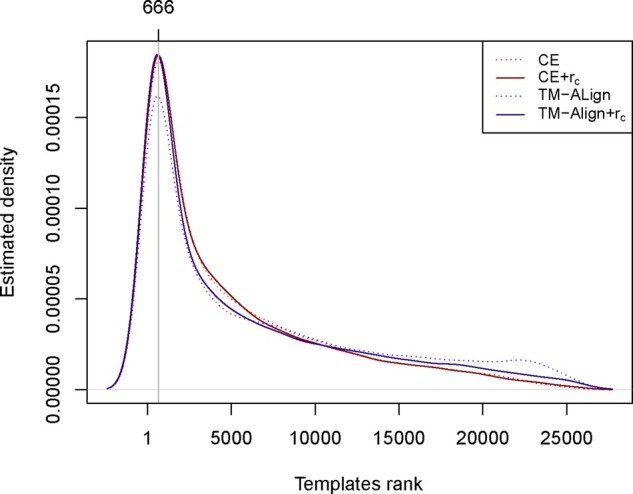
Estimated ranking distribution of templates searched with predicted structures/distances. Comparison of the ranking distribution for templates related to the target protein. Probability density function estimated from observed rankings in CASP12 and CASP13 benchmark sets. The Wilcoxon paired signed-rank test detects a statistically significant shift to the left of the median rank obtained with the congruence coefficient for the comparisons CE + rc versus CE (P-value = 7.106e−05) and TM-align + rc versus TM-align (P-value < 2.2e−16)
In Figure 4, we show the Z-scores distributions of the alignments provided by CE and TM-align. Unlike map alignment tools, structural alignment tools tend to compute slightly better alignments between a target and its related templates than against unrelated templates. However, not surprisingly, in most of the cases the rc coefficients related to such alignments are lower than the expected coefficient over all possible alignments. This is because CE and TM-align perform local alignments, while the maximum rc score between two maps is achieved by performing a global alignment. Specific distance map alignment tools may provide better global alignments and may further improve fold recognition with predicted distances. Although most of the local alignments computed by CE and TM-align are not optimal global alignments, the rc P-value is generally statistically significant, due to the large degree of freedom associated with distance maps. Thus, unlike the case of contact-based searches, the P-value cutoff for distance maps does not seem to improve database searches.
Fig. 4.
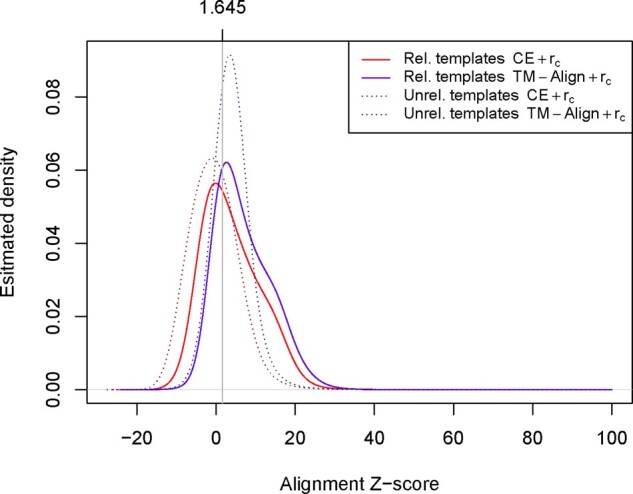
Estimated Z-score distribution of contact map alignments for templates related and unrelated to the target proteins in CASP12 and CASP13. The alignment quality is slightly better for related templates than for unrelated templates with both alignment methods
Finally, distance-based fold recognition does not outperform contact-based fold recognition. If anything, the converse is true when looking at Tables 4 and 6 summarizing fold recognition performances on FM targets. While the limited number of targets in our benchmark sets does not allow one to draw strong conclusions, these tests at least confirm that contact map comparison is a valuable approach for detecting protein structure similarities.
4 Conclusion
We exploited the congruence coefficient as a measure for detecting map similarities. We proved that the congruence coefficient has several important mathematical properties allowing one to rigorously assess its statistical significance and efficiently compute its average and standard deviation. We compared contact map-based and distance map-based fold recognition performances of the congruence coefficient against those of contact map alignment and structural alignment tools. Overall, the congruence coefficient score improves the fold recognition accuracy, particularly for contact-based fold recognition, proving its effectiveness as a general similarity metric for protein map comparisons. Furthermore, contact-based fold recognition accuracy is comparable or better than distance/structure-based fold recognition, suggesting its potential as a general approach for improving the detection of protein structure similarities.
Funding
This work was partially supported by the EU Horizon 2020 research and innovation programme under Marie Curie grant [777822 to P.D.L.] and NIH grant [GM123558 to P.B.].
Conflict of Interest: none declared.
Supplementary Material
Contributor Information
Pietro Di Lena, Department of Computer Science and Engineering, University of Bologna, Bologna 40126, Italy.
Pierre Baldi, Department of Computer Science, University of California, Irvine, CA 92697, USA; Institute for Genomics and Bioinformatics, University of California, Irvine, CA 92697, USA.
References
- Andreeva A. et al. (2020) The SCOP database in 2020: expanded classification of representative family and superfamily domains of known protein structures. Nucleic Acids Res., 48, D376–D382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchan D.W.A., Jones D.T. (2017) EigenThreader: analogous protein fold recognition by efficient contact map threading. Bioinformatics, 33, 2684–2690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burt C. (1948) Factor analysis and canonical correlations. Math. Stat. Psychol., 1, 95–106. [Google Scholar]
- Cheng H. et al. (2014) ECOD: an evolutionary classification of protein domains. PLoS Comput. Biol., 10, e1003926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Lena P. et al. (2010) Fast overlapping of protein contact maps by alignment of eigenvectors. Bioinformatics, 26, 2250–2258. [DOI] [PubMed] [Google Scholar]
- Di Lena P. et al. (2012) Deep architectures for protein contact map prediction. Bioinformatics, 28, 2449–2457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Juan D. et al. (2013) Emerging methods in protein co-evolution. Nat. Rev. Genet., 14, 249–261. [DOI] [PubMed] [Google Scholar]
- Eddy S.R. (2011) Accelerated profile HMM searches. PLoS Comput. Biol., 7, e1002195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hou J. et al. (2019) Protein tertiary structure modeling driven by deep learning and contact distance prediction in CASP13. Proteins, 87, 1165–1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemer C. et al. (1995) Protein structure prediction by threading methods: evaluation of current techniques. Proteins, 23, 337–355. [DOI] [PubMed] [Google Scholar]
- Jones D., Thornton J. (1993) Protein fold recognition. J. Comput. Aided Mol. Des., 7, 439–456. [DOI] [PubMed] [Google Scholar]
- Jones D.,T. et al. (2015) MetaPSICOV: combining coevolution methods for accurate prediction of contacts and long range hydrogen bonding in proteins. Bioinformatics, 31, 999–1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kandathil S.M. et al. (2019) Recent developments in deep learning applied to protein structure prediction. Proteins, 87, 1179–1189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kazi-Aouala F. et al. (1995) Refined approximations to permutation tests for multivariate inference. Comput. Stat. Data Anal., 29, 643–656. [Google Scholar]
- Kryshtafovych A. et al. (2019) Critical assessment of methods of protein structure prediction (CASP)? Round XIII. Proteins, 87, 1011–1020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuhlman B., Bradley P. (2019) Advances in protein structure prediction and designAdvances in protein structure prediction and design. Nat. Rev. Mol. Cell Biol., 20, 681–697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li S. (2011) Concise formulas for the area and volume of a hyperspherical cap. Asian J. Math. Stat., 4, 66–70. [Google Scholar]
- Ovchinnikov S. et al. (2017) Protein structure determination using metagenome sequence data. Science, 355, 294–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senior A.W. et al. (2019) Protein structure prediction using multiple deep neural networks in the 13th Critical Assessment of Protein Structure Prediction (CASP13). Proteins, 87, 1141–1148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shindyalov I.N., Bourne P.E. (1998) Protein structure alignment by incremental combinatorial extension of the optimum path. Protein Eng., 11, 739–747. [DOI] [PubMed] [Google Scholar]
- Shrestha R. et al. (2019) Assessing the accuracy of contact predictions in CASP13. Proteins, 87, 1058–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinegger M. et al. (2019) HH-suite3 for fast remote homology detection and deep protein annotation. BMC Bioinformatics, 20, 473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y., Skolnick J. (2005) TM-align: a protein structure alignment algorithm based on TM-score. Nucleic Acids Res., 33, 2302–2309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng W. et al. (2019) Deep-learning contact-map guided protein structure prediction in CASP13. Proteins, 87, 1149–1164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu J., Wang S. (2019) Analysis of distance-based protein structure prediction by deep learning in CASP13. Proteins, 87, 1069–1081. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


