Abstract
Massively parallel reporter assays (MPRAs) are useful tools to characterize regulatory elements in human genomes. An aspect of MPRAs that is not typically the focus of analysis is their intrinsic ability to differentiate activity levels for a given sequence element when placed in both of its possible orientations relative to the reporter construct. Here, we describe pervasive strand asymmetry of MPRA signals in data sets from multiple reporter configurations in both published and newly reported data. These effects are reproducible across different cell types and in different treatments within a cell type and are observed both within and outside of annotated regulatory elements. From elements in gene bodies, MPRA strand asymmetry favors the sense strand, suggesting that function related to endogenous transcription is driving the phenomenon. Similarly, we find that within Alu mobile element insertions, strand asymmetry favors the transcribed strand of the ancestral retrotransposon. The effect is consistent across the multiplicity of Alu elements in human genomes and is more pronounced in less diverged Alu elements. We find sequence features driving MPRA strand asymmetry and show its prediction from sequence alone. We see some evidence for RNA stabilization and transcriptional activation mechanisms and hypothesize that the effect is driven by natural selection favoring efficient transcription. Our results indicate that strand asymmetry is a pervasive and reproducible feature in MPRA data. More importantly, the fact that MPRA asymmetry favors naturally transcribed strands suggests that it stems from preserved biological functions that have a substantial, global impact on gene and genome evolution.
Spatiotemporal and quantitative control of transcript levels is a crucial aspect of essentially all biological processes in humans (Plank and Dean 2014; Schoenfelder and Fraser 2019). As such, finding the sequence elements that regulate transcription in human genomes and understanding the rules governing their effects are fundamental goals in human biology. For decades, these goals have driven a large amount of work, including both technology development (Dekker et al. 2002; Johnson et al. 2007; Patwardhan et al. 2009; Kwasnieski et al. 2012; Arnold et al. 2013; Gordon et al. 2020) and applications of those technologies to systematically find regulatory elements, including promoters, enhancers, silencers, and insulators (Ashe et al. 1997; Bell et al. 1999; Visel et al. 2009a; The ENCODE Project Consortium 2012; Moore et al. 2020).
One key technological advance has been the development of “massively parallel reporter assays” (MPRAs), in which numerous sequence fragments are assayed in a single experiment for their ability to alter transcript levels. MPRAs take a variety of forms but typically include the cloning of a diverse collection of short (∼200-bp to ∼1.5-kb) DNA elements into transcriptional reporter plasmid libraries (for review, see Klein et al. 2020). These libraries are then transfected into cells that are subsequently subjected to high-throughput sequencing.
One version of an MPRA, self-transcribing active regulatory region sequencing (STARR-seq), places sequence elements within the 3′ UTR portion of a gene in a plasmid construct that also includes a promoter (Arnold et al. 2013). The transcriptional enhancer effects of a given element, in a location that is downstream from the transcription start site (TSS) of the reporter DNA, can be directly quantified as each one contributes to its own abundance within the pool of plasmid-derived RNA. Another mode of MPRA, “survey of regulatory elements” (SuRE), involves placement of sequence elements in an upstream location relative to a gene in a promoter-free plasmid (Van Arensbergen et al. 2019). These elements are linked to barcodes within the transcribed reporter, and their effects are quantified by measuring the abundance of their transcribed barcodes.
MPRAs of various types, including STARR-seq and SuRE, are primarily designed to identify “active” sequences that increase transcription of the reporter. However, the “strandedness” of the test elements, namely, their 5′-3′ orientation relative to the transcribed reporter, is a potential contributor to the activity level of any given element. In experiments using libraries built from fragmented genomic DNA, for instance, fragments representing the same genomic location will randomly be cloned into individual reporter plasmid molecules in both orientations at a near equal rate. These experiments then yield activity measurements for both orientations separately. Thus, with sufficiently complex libraries, such that each orientation is sampled at a given location multiple times, and deep sequencing, such that the functional effects of any given element are measured robustly, even relatively subtle differences in activities between the two possible orientations of a given element might be detectable.
Potential asymmetric sequence effects are often largely ignored or assumed to impact only a limited number of loci (Muerdter et al. 2015; Liu et al. 2017; Barakat et al. 2018; Schöne et al. 2018; Wang et al. 2018; Sun et al. 2019; Ramaker et al. 2020). However, the case for strand asymmetry of DNA function within MPRAs is, in general, strong. Indeed, gene transcription, perhaps the most fundamental of all biological functions encoded in DNA, is inherently stranded. Promoter activity is often directional, and even in cases in which the activity is bidirectional, there is generally a bias toward one strand (Almada et al. 2013; Andersson et al. 2015; Duttke et al. 2015). Other properties, such as mutational correction, have also been shown to be strand-biased (Green et al. 2003). Furthermore, MPRAs may have features within their designs that predispose to strand asymmetry from nonregulatory effects. For example, in STARR-seq, the tested regulatory element is itself transcribed, implying that any sequence elements with strand-specific effects on RNA stability will lead to strand asymmetry in the data.
Thus, we hypothesized that asymmetry would exist in MPRAs and be widely distributed. We sought to analyze both previously published and newly generated MPRA data from multiple reporter configurations and in multiple cell types. We also sought to test whether strand asymmetry is reproducible for specific sequences or correlated with genomic features. Such asymmetry might reflect both the sensitivity and power of MPRAs and point to features relevant to both sequence function and genomic evolution.
Results
Strand asymmetry is pervasive in MPRA signal
We considered four MPRA data sets in our analyses. We generated a STARR-seq (Arnold et al. 2013) library with a super-core promoter (SCP) (Addgene 71509) from sonicated bacterial artificial chromosomes (BACs) spanning an ∼1.2-Mb locus around the HTT gene (Supplemental Table 1). We assayed this library in four cell types: A549, BE(2)-C, HepG2, and K562 (Methods). We also generated a STARR-seq library using the promoter-less STARR-seq vector (Addgene 99296) from BACs in the SORT1 gene locus in HepG2 cells (Methods).
In addition to these experiments conducted in our laboratories, we also obtained data from the NCBI Sequence Read Archive (SRA; https://www.ncbi.nlm.nih.gov/sra) for a STARR-seq experiment using a fragmented whole-genome library in A549 cells treated with dexamethasone for various durations (Johnson et al. 2018). Lastly, we obtained SuRE data from a reporter with the test element upstream of a promoter-less gene using libraries from four fragmented whole genomes in HepG2 and K562 cells (Van Arensbergen et al. 2019).
For the three STARR-seq experiments, we aligned and processed the FASTQ files retaining both the alignment position and the strand orientation using a uniform pipeline (Methods; Fig. 1). Because of the complexity of associating test elements to barcodes in the Van Arensbergen et al. data from FASTQ files, we instead obtained stranded signal values from the bigWig files provided by the investigators (NCBI Gene Expression Omnibus [GEO; https://www.ncbi.nlm.nih.gov/geo/] accession GSE128325). All data sets were then mapped to a common set of 290-bp bins spanning the autosomes (Methods). To avoid ambiguity from terms such as “plus” or “minus” and to avoid confounding genic strands with reference strands, we defined signal derived from reads matching the human genome reference strand as “Reference” and those aligning to the reference reverse complement as “Complement.” From these signals, we calculated a value termed “Reference minus Complement (RMC)” (Fig. 1A). We derived RMC by calculating the read-depth normalized RNA to read-depth normalized DNA ratio for the Reference strand and for the Complement strand separately. We then subtract the Complement RNA-to-DNA ratio from the Reference ratio to obtain a simple measure of asymmetric strand signal.
Figure 1.
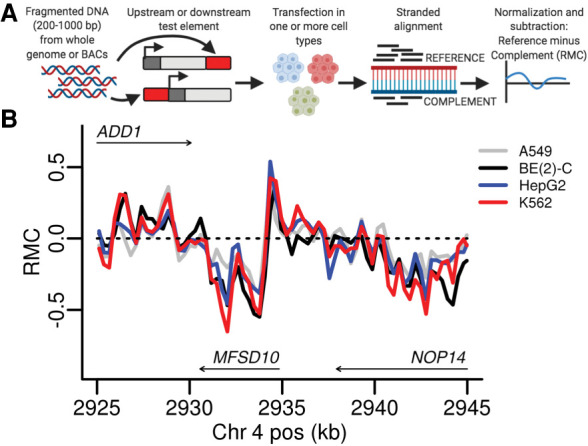
Derivation and example of RMC data. (A) DNA test elements from either BACs or whole-genome fragmentation are cloned downstream from or upstream of the TSS in different experiments. After transfection in one or more cell types, reporter-derived RNA and DNA are harvested and sequenced. The reads are mapped retaining strandedness and the normalized signal Reference strand signal minus the Complement strand signal (RMC) is calculated (created with BioRender.com). (B) RMC data from four cell lines are shown on a 20-kb portion of Chromosome 4 (hg38 coordinates). The arrows mark gene bodies and the direction of stable transcription.
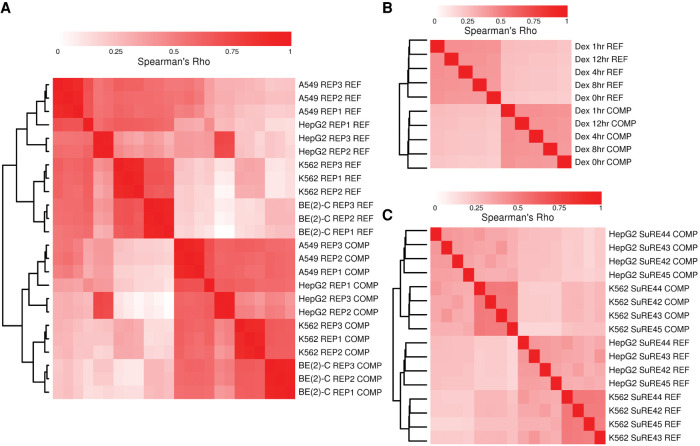
We noticed that the RMC from BAC-derived data in the HTT locus was consistent across the four cell types (Fig. 1B). We explored whether this effect was pervasive across this data set and the others, including those spanning the whole genome, as well as the BAC-derived library targeting the SORT1 locus. For each experiment group (treatment, cell type, replicate) within each data set, we calculated the reporter signal from the two strands separately. We then calculated, within a data set, the correlation between all strand–experiment group pairs (Methods). Finally, we clustered stranded reporter signal correlations for each data set (Fig. 2). The strand of the signal segregated with the first cluster clade, before even cell type (Fig. 2A,C), technical replicates (Fig. 2A; Supplemental Fig. 1), dexamethasone treatment duration (Fig. 2B), or genome donor (Fig. 2C). We ruled out that biases in input reporter construct pools could be responsible for the strand asymmetry by comparing the sequenced DNA counts assigned to the two strands, finding high correlation (Supplemental Fig. 2). Thus, strand asymmetry is the predominant feature driving global patterns of similarity of signals from MPRA data sets, being more prominent than any other technical (e.g., replicates) or biological (e.g., cell type) factor.
Figure 2.
Clustering of MPRA signal by strand. Hierarchical clustering of Spearman's correlation coefficients is shown for MPRA signal from (A) a pooled BAC-derived STARR-seq library spanning HTT gene in four cell types, (B) a whole-genome-derived STARR-seq library in A549 cells from Johnson et al., and (C) whole-genome libraries from four donors in a promoter-less reporter system with an upstream test element in two cell types from Van Arensbergen et al. All comparisons were made from binned data (see Methods).
In the Johnson et al. data, dexamethasone treatment is proposed to activate regulatory regions, namely, glucocorticoid response elements. We observed the same strand-driven clustering behavior both within and after excluding likely regulatory regions defined by activating histone marks (Supplemental Fig. 3A,B). Although the Van Arensbergen et al. reporter aims to find promoter activity, we similarly observed strand-driven clustering in this data set both within and after excluding promoter regions, defined as −2000 to +500 bp from annotated TSSs (Supplemental Fig. 4). We were not able to find any genome segmentation, based on features like histone marks, promoters, or gene bodies, that removed the strand-driven clustering in either of the whole-genome data sets. In fact, a randomly selected set of 1 million bins shows the same clustering pattern in both data sets (Supplemental Figs. 3E, 4C).
MPRA strand asymmetry correlates with gene bodies
Given the pervasiveness of the MPRA strand asymmetry, we sought to compare it with other genomic features displaying strand-specific effects. We first considered, as the most obvious stranded genomic feature, gene bodies (defined by GTEx v8, including noncoding transcripts). Although the MPRA signal continues to cluster by strand both within and after excluding gene bodies (Supplemental Fig. 3C,D), we hypothesized that RMC values would tend to favor a gene's transcribed strand within gene bodies. For example, RMC should be positive in Reference genes (transcript sense to reference) and negative in Complement genes. To evaluate this, we divided autosomes into Reference gene bodies, Complement gene bodies, intergenic regions, or regions where transcripts from both strands overlap (Methods). By using linear regression, we found significant enrichment for positive RMC values in Reference gene bodies and negative values in Complement gene bodies compared with intergenic regions across the three genome-wide data sets (all P < 2.2 × 10−16) (Table 1; Supplemental Fig. 5A–C). We found no significant difference between regions with transcripts on both strands and intergenic regions.
Table 1.
MPRA strand asymmetry shows significant and concordant association with gene body types
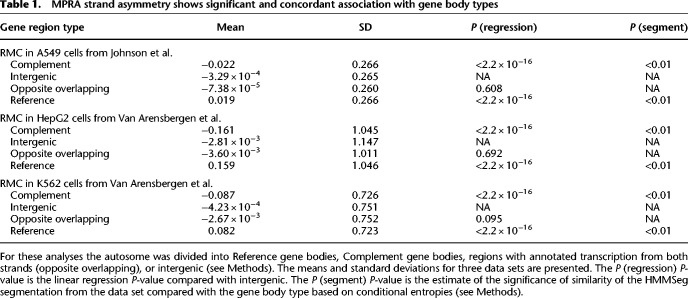
To further explore the association of MPRA strand asymmetry with gene bodies, we tested whether a segmentation of the genome by RMC would be consistent with gene bodies. We used the HMMSeg tool (Day et al. 2007), segmenting into high (Reference-like) and low (Complement-like) states, at a range of transition probabilities, in all of the considered data sets (Methods). The resulting segmentations appear visually consistent with gene bodies across multiple data sets and cell types in the HTT locus (Fig. 3A,B; Supplemental Fig. 6A–C) and in the SORT1 locus (Supplemental Fig. 6D).
Figure 3.
MPRA strand asymmetry is consistent with gene bodies. Values are plotted in the HTT locus for (A) RMC for STARR-seq signal from a library generated from BACs spanning the HTT locus in K562 cells or (B) RMC from Van Arensbergen et al. whole genome also in K562 cells. Gray dots are average RMC value for 5-kb windows. Pink and blue blocks were assigned to Reference and Complement, respectively, using HMMSeg on each data set with a transition probability of 0.3 (see Methods).
To robustly evaluate the agreement with gene bodies genome-wide, we compared the HMMSeg-derived autosome segmentations from the Johnson et al. and Van Arensbergen et al. data sets to gene bodies using a conditional entropy approach (Methods) (Haiminen et al. 2007). All data sets produced segmentations more similar to gene bodies than 1000 randomly shuffled segmentations across a range of transition probabilities (Table 1; Supplemental Fig. 7). Although the segmentations did not match gene bodies perfectly, they classified a high fraction of Reference regions and Complement gene bodies correctly (Supplemental Fig. 5D–F). Intergenic regions and regions with transcripts on both strands were nearly evenly split between Reference and Complement segmentations (Supplemental Fig. 5D–F). In effect, genome-wide MPRA strand asymmetry data are able to accurately predict which strand is genic, including across intronic regions.
Independent mobile element insertions are consistently strand-biased
Another strand-oriented genomic feature is repetitive regions derived from retrotransposons, which move through a transcriptional intermediate as part of their replication cycle. The most abundant such element in human genomes is the Alu element, present at more than 1 million copies in the reference human genome (Deininger 2011). We first examined the distribution of RMC values within Reference and Complement strand-oriented Alu regions in the Johnson et al. data set and found a clear correlation (Fig. 4), reminiscent of the genic strand bias (i.e., Reference transcribed Alu strand tends to have positive RMC).
Figure 4.
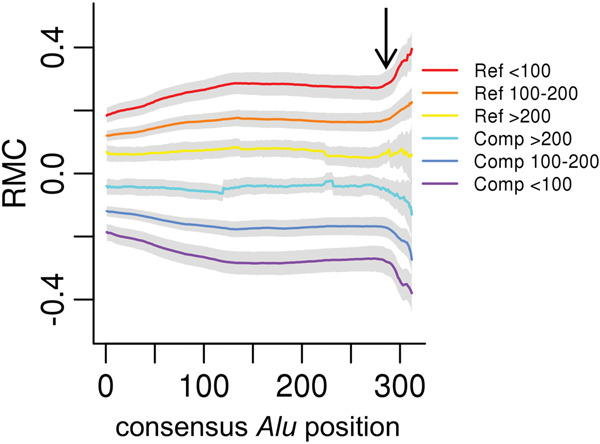
Alu divergence level effects strand asymmetry. From the Johnson et al. data, the genome-wide median RMC (y-axis) for each annotated Alu consensus position (x-axis) is plotted for Reference (Ref)- or Complement (Comp)-oriented Alu insertions, grouped by levels of divergence (indicated in respective colors) measured by milliDiv units (e.g., <100 corresponds to <10% divergence from the ancestral consensus; see Methods). The gray bands represent two standard deviations from the median. The black arrow indicates the start of the A-tail sequence.
We furthermore exploited the fact that Alus provide, in a sense, “biological replicates” of one another, being independently sampled genomic fragments that share similar sequence content. Within an annotated Alu, the genomic position can be mapped to a position within the Alu ancestral consensus sequence. We mapped each annotated Alu genomic base pair in data from Johnson et al. to positions in the Alu consensus sequence as determined by RepeatMasker (Jurka et al. 1996).
In the Johnson et al. data set, the resulting distributions of RMC values as a function of Alu consensus position indicate a clear pattern across the length of Alu sequences, with opposite strand orientation Alu-consensus positions mirroring one another. The 3′ end of Alu insertions are composed of an A-tail, a feature that we see tends to intensify the degree of RMC in favor of the transcribed strand in this data set. Additionally, Alus are silenced after insertion, and their sequence diverges from the ancestral sequence as mutations accumulate and are fixed over evolutionary time. We binned the Alu-RMC data by Alu divergence level and observed more intense effects from younger, less diverged Alu sequences (Fig. 4). This observation is consistent with the sequence-specific nature of RMC within Alus. Younger, less divergent Alus are more similar to one another, and thus show more consistent effects, in contrast with older, more divergent, and dissimilar Alus.
We also applied this analysis to data sets derived from two cell types from Van Arensbergen et al. We did not see the effect of Alu orientation and ancestral sequence conservation in data from K562 cells, with most data points scattering near zero (Supplemental Fig. 8A). In HepG2 cells, test elements that are highly similar to ancestral Alu sequence do display RMC concordant with Alu orientation similar to that seen in the Johnson et al. data (Supplemental Fig. 8B). However, test elements with more diverged Alu sequence also have near zero RMC in the HepG2 data. Furthermore, the A-tail appears to have opposite effects in both Van Arensbergen et al. data sets compared with the Johnson et al. data. We present and discuss the differing effects of very A-rich test elements in the Johnson et al. versus Van Arensbergen et al. data sets below.
Genomic sequence drivers of MPRA strand asymmetry
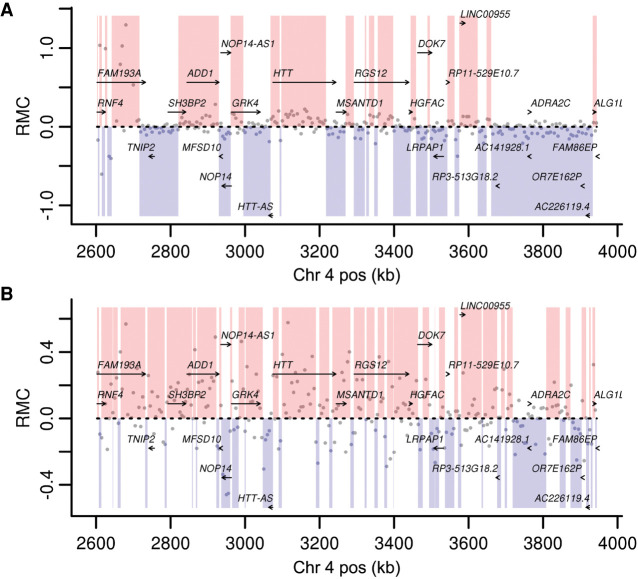
To find sequence features that might be predictive of strand asymmetry, we evaluated the correlation of monomer, dimer, and octamer frequencies within autosomal bins to RMC values separately for the Johnson et al. and both Van Arensbergen et al. data sets (three total analyses). We selected the significantly correlated k-mers from each regression and constructed linear models trained on data from Chromosome 1 (see Methods). Each of the three models predicts with significant agreement its corresponding RMC data on Chromosome 2 (all P < 2.2 × 10−16) (Fig. 5A–C). Next, we used a sequence-based predictive model of transcriptional activity using convolutional neural networks, Xpresso (Agarwal and Shendure 2020), to the HTT locus. We chose this smaller locus owing to computational practicality. Xpresso-predicted values significantly correlate to RMC data in that locus in four cell types (R2 = 0.11 to 0.46) (Supplemental Fig. 9). Lastly, we used gkmSVM analysis (Ghandi et al. 2014, 2016) to subsets of the Johnson et al. and Van Arensbergen et al. data sets (Methods). The generated models significantly predicted RMC from sequence inputs (Pearson R 0.27 − 0.40, all P < 2.2 × 10−16) (Supplemental Fig. 10). We also present the hyperplane distances of the 1000 k-mers most distal from the SVM hyperplane from each of the three whole-genome data sets (Supplemental Data 3).
Figure 5.
Sequence drivers of RMC. A linear model based on monomer, dimer, and octamer frequencies was trained on Chromosome 1 for three data sets. Model-predicted RMC values for Chromosome 2 are plotted versus actual values for (A) Johnson et al. A549, (B) Van Arensbergen et al. K562, and (C) Van Arensbergen et al. HepG2 cells. The Pearson's R for each model is indicated. Red line represents the model fit. (D) The linear regression t-statistic (effect size) for 3491 octamers (union of 2000 most significant in each data set) is plotted as columns and hierarchically clustered in a heatmap. Each row represents one of three labeled data sets. A positive t-statistic (red in the heatmap) indicates the octamer is associated with positive RMC values, and a negative t-statistic (blue) is associated with negative RMC values. The black box indicates an A-rich cluster of octamers associated with negative RMC in all data sets.
Consistent with the strand asymmetry in RMC, a given k-mer's reverse complement should have an equal but opposite effect. As expected, in linear models trained on only a single k-mer's frequencies, k-mer performance closely matched that of its reverse complement, in opposite directions for all three analyses (Supplemental Fig. 11). No palindromes yielded significant association, an important confirmation of the validity of the analytical techniques.
We sought to compare the k-mer regression results across the three data sets that derive from upstream and downstream test element configurations and different cell types. Because reverse complement pairs always have opposite and nearly equal effect sizes, we consider the pairs to be reducible to a single data point. We used a sequence similarity clustering approach seeded by alphabetical ordering to choose the representative sequence and effect direction (see Methods).
Among monomers, the A/T pair (represented by A) has a significant (P < 2.2 × 10−16) negative association with RMC in all three data sets (Supplemental Data 1). This means that the A monomer is associated with lower Reference strand signal compared with Complement strand signal. The C/G pair (represented by C) only has significant effects (P < 2.2 × 10−16) in the two Van Arensbergen data sets, both with negative effect directions. The dimer data largely reinforce this observation. Most A-containing dimers (excluding palindromes) associate negatively with RMC in all three data sets. The CC dimer associates negatively with RMC similar to the C monomer in the Van Arensbergen et al. data. In the Johnson et al. data, however, CC associates significantly positively with RMC (Supplemental Data 1).
To explore more complex sequence features driving RMC in the data sets, we clustered the regression t-statistic (variance normalized effect size) across the union of the top 2000 most significant octamers in each of the three data sets (3491 total octamers) (Fig. 5D). Many of the octamers show agreement across all three data sets. The Van Arensbergen K562 and Johnson et al. A549 data show the closest agreement, despite being from MPRAs with upstream and downstream test element configurations. Although we extensively analyzed subclusters for octamer sequence commonality, we were unable to find enrichment for any complex sequence motifs. The cluster of common negative association of the octamers with RMC (highlighted by black box in Fig. 5D) is composed of A-rich octamers, consistent with the monomer and dimer observations.
Though A-rich sequence is negatively associated with RMC in all three data sets, we observed that very A-rich octamers (eight or seven A's) positively associate with RMC in the Johnson et al. data only (Supplemental Fig. 12). Octamers with six or fewer A's have the negative association with RMC observed for A-rich monomers and dimers. We speculate that because the test element is transcribed in the Johnson et al. MPRA configuration, the oligo(dT) beads used in RNA enrichment in their protocol may preferentially bind these transcripts, enriching them over their reverse complement. However, our analysis indicates this only appears to occur in these very A-rich test elements and does not affect the vast majority of the data (Supplemental Fig. 12).
We annotated significantly predictive octamers by comparison to RNA-binding protein (RBP) and transcription factor (TF) motifs using FIMO (Grant et al. 2011). We found significant matches to RBP and TF motifs for some highly RMC-predictive octamers (Supplemental Data 2). However, motif matches were not found for most significantly predictive octamers.
Discussion
In MPRA data generated from both fragmented whole-genome DNA or targeted BAC pools, in STARR-seq vectors with and without the SCP, and in SuRE vectors with an upstream, nontranscribed test element, we see pervasive and highly reproducible strand asymmetry in reporter signal. The effect persists over multiple cell types, from multiple donor genomes, and in differing drug treatments. Strand asymmetry is the predominant driver of clustering in all these data sets (Fig. 2; Supplemental Figs. 1, 3, 4).
The presence of strand asymmetry might be considered as merely an artifact of MPRAs were it not for its correlation to well-established stranded genomic features. Test elements derived from Reference-sense-strand genes have significantly positive RMC values, whereas the converse is true for Complement-sense-strand genes in data sets derived from whole-genomic DNA (Table 1). Regions where stable transcription products are annotated on both strands yield RMC values near zero, perhaps indicating equilibrium between competing forces. Although MPRA strand asymmetry is pervasive, it appears to be organized coherently in gene bodies, allowing for segmentations via HMMSeg that are significantly similar to gene bodies (Fig. 3A,B; Supplemental Figs. 6, 7).
Test elements derived from Alu sequence show pronounced MPRA strand asymmetry, especially in the Johnson et al. data (Fig. 4). In data from Van Arensbergen et al., we do not observe the effect in K562 but do see it in elements with high similarity to ancestral Alu sequence in HepG2 (Supplemental Fig. 8). We are not certain why the data sets differ. We believe that high read coverage of the Alu positions is required to resolve the effect, which was present in the Johnson et al. data. For the Van Arensbergen et al. data, we obtained the strand signal from the provided bigWig files and did not measure the underlying read depth. We also observe opposing effects of the Alu A-tail in the Johnson et al. data versus that of Van Arensbergen et al. We believe that the oligo(dT) purification effect, which is only relevant to the Johnson et al. data, is likely to explain this discrepancy.
Ancestral Alu sequence has active retrotransposon activity that depends on transcription and interaction with LINE-produced proteins (Mills et al. 2007; Deininger 2011). As Alus tend to degenerate after insertion and accumulate fixed changes over evolutionary time, they provide a natural mutagenesis experiment by allowing simultaneous assessment of about 1 million independently inserted and evolved sequence fragments. We find that RMC values are clearly nonrandomly distributed with respect to the transcribed Alu strand. Further, younger Alu elements, which are more similar to the consensus, display a greater magnitude of RMC at every Alu consensus position (Fig. 4).
It is expected that the data from Van Arensbergen et al. display strand asymmetry. The investigators intended to detect promoter activity in their experiments, and promoters are usually more active in one direction (Van Arensbergen et al. 2019). We also note that because we used their bigWig files instead of processing FASTQs through the common pipeline used in all other presented data sets, the Van Arensbergen et al. data may be less comparable to the other data sets. Nevertheless, the Van Arensbergen et al. data show significant correlation with gene bodies similar to the Johnson et al. STARR-seq data despite the test element not being transcribed (Table 1). Also, segmentations by HMMSeg of the Van Arensbergen et al. data are significantly similar to gene bodies, showing comparable regional coherence to that seen in the Johnson et al. STARR-seq data (Fig. 3B; Supplemental Figs. 6B, 7D,E). Furthermore, the Johnson et al. data and Van Arensbergen et al. data show similar associations with sequence k-mers and RMC (Fig. 5D). We speculate that in an upstream reporter configuration, gene body fragments increase the recruitment of RNA polymerase or other transcription initiators in a manner matching their genomic orientation. Previous research has highlighted the similarities between enhancer activity, enhancer transcription, and promoter activity, and it is possible that the effects we describe here are related to these phenomena (Mikhaylichenko et al. 2018).
Overall, we have shown that fragments of genomic sequence (∼200 bp to ∼1.1 kb in the presented data sets) from gene bodies or Alus retain their strand asymmetry in an artificial reporter construct away from their native context of broader genomic organization, chromatin structure, nuclear localization, and three-dimensional conformation. This strongly suggests that the strand asymmetry is driven by sequence, as no other information is carried through to the reporters. Overall, A-rich sequence is associated with lower Reference strand MPRA signal compared with that of Complement. C-rich sequence appears to affect upstream and downstream MPRAs differently. However, we could not find more complex sequence motifs among the RMC-associated octamers. We do find some octamers significantly similar to RBP motifs and others to TF motifs (Supplemental Data 2). However, we found no “smoking gun” sequence element able to explain a large portion of the effect. Applying Xpresso, a tool that accurately predicts transcription level from genomic sequence only (Agarwal and Shendure 2020), yields predictions significantly correlated with RMC (Supplemental Fig. 9). Also, gkmSVM analysis produces significantly correlated predictions (Supplemental Fig. 10). All sequence-driven models that we tested, although highly significant, are able to explain only a fraction of the total variance in RMC.
We believe it is likely that both mechanisms that depend on the test element as a template for transcription (e.g., those related to splicing, pre-mRNA stabilization, and poly(A) tail generation) and those that depend on its ability to recruit and activate transcriptional complexes are involved (Supplemental Data 2). The strong strand asymmetry seen from the Alu sequence that contains both RNA stability and RNA polymerase promoter sequences is consistent with this hypothesis. Further, the concordance of RMC between STARR and SuRE also supports this hypothesis. That said, it is possible that at least some portion of the test elements in SuRE may in fact be transcribed and thereby contribute to some degree of mechanistic overlap, in terms of RMC, with STARR-seq. In particular, if test elements cloned into the SuRE plasmid harbor promoter driving sequences within their most upstream portions, transcription may begin in the middle of the element, leading to inclusion of a downstream portion of that element into the resultant transcript. Synthetic mutagenesis of strongly asymmetric sequences in multiple reporter configurations and locations may be helpful in future studies of specific mechanisms that may contribute to RMC.
The SuRE assay used by Van Arensbergen et al. measures promoter-like activity, and in these data, the absolute value of RMC strongly correlates with mean signal of the strands (Supplemental Fig. 13B,C). This correlation means that as total signal in the SuRE assay increases, the magnitude of its asymmetry also increases, as is expected given that many promoters are active in only one direction. However, in the STARR-seq assay used by Johnson et al., the same correlation is much weaker, although still significant (P < 2.2 × 10−16) (Supplemental Fig. 13A). Thus, although strand asymmetry is clearly present in STARR-seq-derived data, it tends to be a small fraction of the total signal at any given locus. As such, for enhancer sequences with high activity, the differences between the two orientations, although reproducibly detectable, are small relative to the total activity level of the element. This observation is consistent with the general hypothesis that enhancers are thought to be orientation independent (Andersson et al. 2014) and the fact that many individual enhancers have been shown to be approximately equally effective in both orientations in heterologous reporter assays (Visel et al. 2009b; Andersson et al. 2014; Dao et al. 2017; Mikhaylichenko et al. 2018; Klein et al. 2020). This is particularly true when considering enhancer measurements from experiments, like luciferase reporter assays, in which technical precision in measuring activity is much lower than that afforded by MPRAs. Generally, although we believe that the processing of raw MPRA data should be performed in strand-aware fashion because of the added information obtained from modestly more complex processing, ignoring strand asymmetry in STARR-seq data will not have a large effect on the measure of total enhancer activity for most loci.
Our results make clear that MPRA data detect a biological phenomenon that, although often subtle for a given sequence, is highly reproducible and pervasive across human genomes. The vast multiplexing and deep sequencing inherent in MPRA technology has enabled the robust measurements required to find these effects. Although further characterization is required, the fact that strand asymmetry is driven by primary sequence and correlates with gene body and Alu element orientation strongly suggests that, whatever the underlying mechanisms are, they are factors relevant to gene and genome evolution.
Methods
Targeted BAC-derived STARR-seq assays
We constructed STARR-seq libraries from 14 BACs spanning the HTT locus (Supplemental Table 1). We grew each BAC separately in Escherichia coli and purified BAC DNA separately according to standard BAC preparation protocols. We sheared each BAC DNA (5 μg) separately using a Biorupter pico (Diagenode) to a 100- to 500-bp size, then ran on 1% agarose gel, manually selected 250- to 350-bp size, purified by Qiagen gel extraction, and eluted. Each BAC fragment library separately underwent end repair, dA addition, and paired-end adapter ligation (Illumina). Each BAC fragment library separately served as a template for PCR with primers FragF (5′-TAGAGCATGCACCGGACACTCTTTCCCTACACGACGCTCTTCCGATCT-3′) and FragR (5′-GGCCGAATTCGTCGACGGTCTCGGCATTCCTGCTGAACCGCTCTTCCGATCT-3′), for seven or nine cycles, enough to generate a visible band at target size (∼400 bp). We purified the PCR amplicon libraries by Ampure SPRI beads (Beckman Coulter) and cloned by in-fusion cloning (Takara) into the pSTARR-seq_human (Addgene 71509) backbone digested with AgeI and SalI (NEB) according to the manufacturer's protocols. We transformed assembled plasmids by electroporation (Bio-Rad MicroPulser) into MegaX DH10B cells (Thermo Fisher Scientific) in four electroporations for each BAC. After recovery, we combined the four cultures for each BAC and grew them overnight in 500 mL LB broth. We purified plasmids by the Qiagen plasmid maxi kit. We then pooled plasmid libraries representing each BAC by size of BAC and DNA concentration for equal representation across the locus.
We grew and maintained all cell lines according to ATCC guidelines. For each technical replicate, we transfected 40 million cells with 133 µg of reporter plasmid pool. We performed three replicates per cell type. We used FuGENE (Promega) as the transfection reagent for the A549, BE(2)-C, and HepG2 cells. For K562 cells, we used Lipofectamine PLUS (Invitrogen). After 48 h, we washed the cells with PBS and lysed using RLT buffer (Qiagen). We extracted RNA from the lysate using the total RNA purification kit (Norgen), using four spin columns per replicate and using a lysate volume equivalent to 2 million cells per column. DNA was prepped in a similar manner using the DNeasy kit (Qiagen). We purified mRNA from the total RNA preps using the DynaBeads poly(A) selection kit (Invitrogen). We removed contaminating DNA from the mRNA preps using TURBO DNase I (Ambion). We performed targeted reverse transcription of reporter RNA using a primer specific to the reporter sequence (5′-CAAACTCATCAATGTATCTTATCATG-3′). Following RNase treatment, we performed junction PCR for 15 cycles targeting a splice created in the reporter mRNA with the following primers: F, 5′-GGGCCAGCTGTTGGGGTG*T*C*C*A*C-3′, and R, 5′-CTTATCATGTCTGCTCG*A*A*G*C-3′, with asterisks indicating phosphorothioate bonds. We prepared sequencing libraries using PCR with Illumina-compatible primers and the junction PCR product as a template. We generated DNA libraries in the same manner as for RNA except that the DNA entered after the reverse transcription step. We sequenced all libraries on the Illumina NextSeq platform using paired-end 50-bp reads, generating approximately 40 million reads per replicate on average.
For the SORT1 locus, we prepped two BACs (Supplemental Table 1) according to standard BAC protocols. We sheared the BAC DNA using a Covaris ultrasonicator, and each underwent end repair, dA addition, and ligation to custom adaptors:
Left—Starr-adapt-3A, 5′-TTGAATTAGATTGATCTAGAGCATGCACCGG*T-3′, and Starr-adapt-3C, 5′-CCGGTGCATGCTCTAGATCAATC-3′;
Right—Starr-adapt-2A, 5′-ATGTCTGCTCGAAGCGGCCGGCCGAATTCG*T-3′, and Starr-adapt-2C, CGAATTCGGCCGGCCGCTTCGAGC.
We size-selected ligated fragment on an agarose gel, aiming for 1-kb fragments. After gel extraction, we subjected the product to 14 cycles of PCR using Starr-adapt-3A and Starr-adapt-2A as primers. We digested the STARR-seq ORI vector (Addgene 99296) with AgeI and SalI restriction enzymes (NEB) and inserted fragments via NEBuilder HiFi assembly (NEB). For each BAC library, we transformed into NEB 3020 electrocompetent cells and prepped the entire transformation with a Chargeswitch midi kit (Invitrogen).
We transfected HepG2 cells with each BAC-derived library using Lipofectamine (Invitrogen). After 48 h, we harvested RNA and DNA using the Qiagen AllPrep kit (Qiagen). We purified mRNA using the mRNA mini kit (Oligotex). We removed contaminating DNA from the mRNA preps using TURBO DNase I (Ambion). For RNA, we performed reverse transcription adding a UMI with P7-StarrBAC-umi-r, 5′-CAAGCAGAAGACGGCATACGAGATNNNNNNNNNNCAAACTCATCAATGTATCTTATCATG-3′. This primer also served as the reverse primer for PCR of both the cDNA and prepped DNA. The forward primer was P5-StarrBAC-i#, 5′-AATGATACGGCGACCACCGAGATCTACAC##########TGTTGAATTAGATTGATCTAG-3′, where “#” indicates an indexing sequence. We performed the first round of PCR for three cycles and purified the reactions with Ampure XP beads (Beckman-Coulter). We then performed a second round of PCR with primers targeting the P5 and P7 sequences only: P5, 5′-AATGATACGGCGACCACCGAGATCTACA-3′, and P7, 5′-CAAGCAGAAGACGGCATACGAGAT-3′, for 19 to 20 cycles. We sequenced the libraries on an Illumina NextSeq, generating paired-end 100-bp reads using the custom primers:
StarrBAC-R1, 5′-TGTTGAATTAGATTGATCTAGAGCATGCACCGGT-3′;
StarrBAC-ind1, 5′-GAGCAGACATGATAAGATACATTGATGAGTTTG-3′;
StarrBAC-ind2, 5′-ACCGGTGCATGCTCTAGATCAATCTAATTCAACA-3′; and
StarrBAC-R2, 5′TCATGTCTGCTCGAAGCGGCCGGCCGAATTCGT-3′.
Sequencing data processing and MPRA signal calculation
We acquired raw FASTQ files from SRA from Johnson et al. (2018) (SRP144640), using SRA Toolkit (v2.9.6-1). We aligned raw paired-end Illumina reads either to genome (hg38) subsets corresponding to the regions of BAC coverage for BAC-derived libraries or to the whole genome using Bowtie 2 (v 2.2.5) (Langmead and Salzberg 2012). For BAC-derived libraries, we also included the E. coli genome (K-12 MG1655) in the reference to filter out E. coli genomic DNA contaminants and assess BAC prep purity. By using the alignment positions and flag sum in the aligned BAMs, we constructed BED files of the sequenced fragment, including its orientation to reference using SAMtools v 1.8 (Li et al. 2009) and a custom Perl script. We have included the scripts that take FASTQs to fragment BED files in the Supplemental Files. We refer to fragments aligning to the reference as “Reference” and those to the reference reverse complement as “Complement.”
We created a set of 290-bp nonoverlapping bins spanning the autosome using the R version 3.6.1 (R Core Team 2019) package GenomicRanges v1.36 (Lawrence et al. 2013). We picked 290 bp because it was the median fragment size of the BAC-derived libraries. For BAC-derived libraries, we reduced the bins to only those that overlapped the BAC-covered regions to facilitate computation. We converted the sequencing data fragment BED files to GenomicRanges objects using the R package rtracklayer v1.44.3 (Lawrence et al. 2009). We found overlaps of Reference and Complement fragments separately for each bin, generating bin counts from each strand. We supply the scripts for generating bin counts in the Supplemental Files.
Each experiment had DNA counts corresponding to reporter input levels and RNA counts corresponding to transcripts derived from the reporters. We normalized the raw counts of each pair of DNA and RNA versus strand by dividing by the sum of each count type across all bins. We then calculated the reporter activity for each strand by dividing the normalized RNA counts by the normalized DNA counts. To measure strand asymmetry, we subtracted the Complement strand signal from the Reference strand signal to yield RMC.
The reporter data from Van Arensbergen et al. used barcodes associated by a separate sequencing run with upstream elements (Van Arensbergen et al. 2019). Because of the complexities of associating barcodes to test elements in an unfamiliar experimental design we did not perform ourselves, we instead downloaded the stranded reporter signal bigWigs from the metadata in the GEO submission (GSE128325). These bigWigs are also hg19-referenced, so we mapped, with the import function in rtracklayer, the bigWig values to the autosome bin set that we had lifted from hg38 to hg19 using the UCSC Genome Browser liftOver tool (Kent et al. 2002). We assigned signal from the bigWigs labeled “plus” to the Reference strand and those labeled “minus” to the Complement strand in accordance with the investigators’ description of their processing. After mapping, we back-converted to hg38 so that these data would be comparable to the other data sets. We calculated RMC for these data as above but noticed outliers of very high absolute RMC. HMMSeg assumes a Gaussian underlying distribution, and these outliers interfered with the segmentation calculations. Accordingly, we removed bins whose signal value in either strand was exactly zero and those that were above the 99th percentile in signal intensity. This modest trimming of outliers produced RMC values that met HMMSeg assumptions.
Hierarchical clustering and association with gene bodies
To create heatmaps of data hierarchically clustered by similarity, we calculated Spearman's correlation coefficient, rho, between each sample within an experiment. We then calculated the Euclidean distance between each sample and clustered using the R functions dist and hclust. We created heatmaps with the indicated saturation color ranges.
For the Johnson et al. data, we observed agreement in strand asymmetry across dexamethasone-treatment duration. To have more accurate genome-wide data, we summed the sequencing bin counts across all dexamethasone-treatment durations to a single RMC measurement for the data set. We filtered out bins with fewer than 57 summed DNA counts, which we calculated would yield 10 RNA counts from each strand for a neutral test element, on average. For the Van Arensbergen et al. data, we noticed similar agreement across donor genomic DNA. For these data, we took the median signal across the donors and calculated a single RMC for each cell type.
To compare these data to gene bodies, we constructed a GenomicRanges object for gene models obtained from GTEx v8 without limiting to protein coding or any other filter. All regions of the autosome without an annotated gene model we labeled “intergenic.” We labeled regions, calling sense transcripts matching reference “Reference.” Those with sense transcripts matching the reverse complement of reference we labeled “Complement.” Wherever there were annotated gene models on both strands, we labeled them “opposite overlapping.” In this way, we divided the entire autosome into four categories. To evaluate the correlation of RMC with these gene body categories, we calculated the overlap of each autosome bin to each category. By using the category as the independent variable and the RMC as the dependent variable, we performed linear regression using the R function lm. Boxplots were made in a similar fashion.
To create segmentations of the RMC values, we used a hidden Markov model approach via the HMMSeg software package (Day et al. 2007). For all data, we used a two-state model. For the whole-genome data sets, the emission means and variances were calculated from the means and variances of the data in Complement and Reference genes, respectively. Because the BAC-derived data sets encompassed smaller regions containing a small number of gene models, we used the emission means and variances of the Johnson et al. data in the segmentation models of these. For all data sets, we tested a range of transition probabilities from 0.05 to 0.5. We present data from a representative subset of these. To evaluate the similarity of the calculated segmentations to gene body classes, we used a conditional entropy approach (Haiminen et al. 2007). We calculated the conditional entropy (H) of the HMMSeg segmentation (P) given a stranded gene body class, for example, Reference genes (Q), based on the lemma H(P|Q) = H(U) – H(Q) provided by Haiminen et al. (2007), where U is the union of all segment borders in both P and Q. We then isentropically shuffled P (maintaining the width and number of segments but shuffling start positions) 1000 times and calculated H(P|Q) of each shuffle. We evaluated significance by comparing the actual value of H(P|Q) to the distribution of values from shuffles. We used the process separately to Reference and Complement genes, considering both P-values in our evaluation of significance.
Calculation of Alu sequence effect
We downloaded the complete BED file of RepeatMasker tracks from the UCSC Genome Browser (Kent et al. 2002). By using a custom Perl script (Supplemental Files), we processed this file to pull out Alu positions, creating a BED file of every Alu base with genomic position, position within the Alu consensus sequence, strand, and divergence (in milliDiv units). To this Alu reference, we then counted overlaps of the fragment BED files from the Johnson et al. data in the same process used for the autosome bins. For the Van Arensbergen et al. data sets, we queried the signal bigWig files at each Alu base pair (1-bp-wide genomic ranges) using a custom R-script (Supplemental Files). Again, we filtered out values that were exactly zero and those above the 99th percentile. RMC was calculated by subtracting the Complement base values from the Reference base values. Many (about 1 million) genomic positions map to each Alu consensus base. We split each consensus base into three blocks of divergence by milliDiv thresholds of less than 100, 100–200, and more than 200. Then we summed stranded counts from genomic positions to their Alu consensus position/milliDiv group for the Johnson et al. data. In this case, we kept the dexamethasone-treatment sets separate in order to estimate variance and because the subsequent collapsing to consensus sequence yields sufficiently numerous counts. From these collapsed counts, we calculated median RMC at each Alu consensus position/milliDiv group set, as well as the standard deviation across dexamethasone-treatment durations. For the Van Arensbergen et al. data, we took the median of signal across the genomic positions to their Alu consensus position/milliDiv group. We kept data from each donor genome separate in order to estimate variance. We calculated the RMC at each Alu consensus position/milliDiv group as well as the standard deviation across donor genomes.
Sequence-based modeling of MPRA asymmetry
To build a linear model relating sequence content to RMC, we first counted the frequency of all monomers, dimers, and octamers in each bin across the genome, allowing k-mer overlaps. For each k-mer, we then performed a genome-wide Spearman's correlation for the Johnson et al. A549 data and the Van Arensbergen et al. K562 and HepG2 between RMC and k-mer count on three genome bin sets: All bins, the combination of top 1% and bottom 1% RMC bins, and the middle 80% RMC bins. To avoid overfitting and make a linear model computationally tractable, we reduced the set of octamers to fewer than 1000 octamers by selecting the strongest P-value between the three correlations for each octamer and picking the 1000 most significant. We then used the counts for each of these octamers, all dimers, and all monomers (for a total of 956 k-mers) as predictor variables in a linear model of RMC ∼ k-mer counts. The model was trained on all data from Chromosome 1 and tested on all data from Chromosome 2. Additionally, we created a model for each individual k-mer using that k-mer's count as the sole independent variable to determine individual r2 values. For comparison to RBP and TF motifs within the Cis-BP database (Weirauch et al. 2014), we identified all octamers that were found significant in the linear model. We saved these octamers as a FASTA file and used the FIMO function (Grant et al. 2011) of the MEME suite (version 5.1.0), using default parameters.
We ran Xpresso using a pretrained convolutional neural network model intended to predict median gene expression levels across cell types (Agarwal and Shendure 2020; https://xpresso.gs.washington.edu/). We computed the predicted RMC as the difference between the predicted value of Xpresso run on the Reference versus Complement strand, centered upon the same intervals used to calculate RMC from MPRA data.
We used gkmSVM (Ghandi et al. 2014, 2016) with the Johnson et al. and Van Arensbergen et al. data sets. For each of the three data sets, we identified all regions with RMC > 0 as a positive set and all regions with RMC < 0 as a negative set. We sampled 10,000 regions in each, as well as an additional, independent 20,000 regions as a test set from the full RMC data. We then ran gkmsvm_kernel with addRMC = F, gkmsvm_trainCV with default parameters, and gkmsvm_classify with addRC = F.
To compare k-mers across the three data sets, we found all pairs of reverse complements. Initially, we chose the sequence that was alphabetically first among the two to represent the pair. For octamers, we selected the top 2000 most significant for each of the three data sets and took the union, resulting in 3491 octamers. We calculated the pairwise alignment score between all of these octamers (ShortRead R package). We then symmetrically clustered the octamers by pairwise alignment score using the R functions dist() and hclust(). We split the octamers into two subclusters and then chose the sequence to represent a reverse complement pair by finding the one that produced the best mean alignment score to the other octamers in its subcluster. With each octamer pair's representative sequence chosen, we assigned t-statistics to each pair based on the chosen sequence. These t-statistics were hierarchically clustered using the dist() and hclust() functions.
Data access
All raw and processed sequencing data generated in this study have been submitted to the NCBI Gene Expression Omnibus (GEO; https://www.ncbi.nlm.nih.gov/geo/) under accession number GSE156857.
Supplementary Material
Acknowledgments
We thank the Tim Reddy laboratory at Duke University and the Bas van Steensel laboratory at the Netherlands Cancer Institute for their generation of high-quality MPRA data sets. This work was supported by the CHDI Foundation grant A-15607 (to R.M.M.) and the Leo Fund at HudsonAlpha and National Institutes of Health (NIH) grants 1UM1HG009408 and 1R01HG009136 (to J.S.). J.S. is an investigator of the Howard Hughes Medical Institute.
Footnotes
[Supplemental material is available for this article.]
Article published online before print. Article, supplemental material, and publication date are at https://www.genome.org/cgi/doi/10.1101/gr.270751.120.
Competing interest statement
The authors declare no competing interests.
References
- Agarwal V, Shendure J. 2020. Predicting mRNA abundance directly from genomic sequence using deep convolutional neural networks. Cell Rep 31: 107663. 10.1016/j.celrep.2020.107663 [DOI] [PubMed] [Google Scholar]
- Almada AE, Wu X, Kriz AJ, Burge CB, Sharp PA. 2013. Promoter directionality is controlled by U1 snRNP and polyadenylation signals. Nature 499: 360–363. 10.1038/nature12349 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson R, Gebhard C, Miguel-Escalada I, Hoof I, Bornholdt J, Boyd M, Chen Y, Zhao X, Schmidl C, Suzuki T, et al. 2014. An atlas of active enhancers across human cell types and tissues. Nature 507: 455–461. 10.1038/nature12787 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson R, Chen Y, Core L, Lis JT, Sandelin A, Jensen TH. 2015. Human gene promoters are intrinsically bidirectional. Mol Cell 60: 346–347. 10.1016/j.molcel.2015.10.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold CD, Gerlach D, Stelzer C, Boryń ŁM, Rath M, Stark A. 2013. Genome-wide quantitative enhancer activity maps identified by STARR-seq. Science 339: 1074–1077. 10.1126/science.1232542 [DOI] [PubMed] [Google Scholar]
- Ashe HL, Monks J, Wijgerde M, Fraser P, Proudfoot NJ. 1997. Intergenic transcription and transinduction of the human β-globin locus. Genes Dev 11: 2494–2509. 10.1101/gad.11.19.2494 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barakat TS, Halbritter F, Zhang M, Rendeiro AF, Perenthaler E, Bock C, Chambers I. 2018. Functional dissection of the enhancer repertoire in human embryonic stem cells. Cell Stem Cell 23: 276–288.e8. 10.1016/j.stem.2018.06.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bell AC, West AG, Felsenfeld G. 1999. The protein CTCF is required for the enhancer blocking activity of vertebrate insulators. Cell 98: 387–396. 10.1016/S0092-8674(00)81967-4 [DOI] [PubMed] [Google Scholar]
- Dao LTM, Galindo-Albarrán AO, Castro-Mondragon JA, Andrieu-Soler C, Medina-Rivera A, Souaid C, Charbonnier G, Griffon A, Vanhille L, Stephen T, et al. 2017. Genome-wide characterization of mammalian promoters with distal enhancer functions. Nat Genet 49: 1073–1081. 10.1038/ng.3884 [DOI] [PubMed] [Google Scholar]
- Day N, Hemmaplardh A, Thurman RE, Stamatoyannopoulos JA, Noble WS. 2007. Unsupervised segmentation of continuous genomic data. Bioinformatics 23: 1424–1426. 10.1093/bioinformatics/btm096 [DOI] [PubMed] [Google Scholar]
- Deininger P. 2011. Alu elements: know the SINEs. Genome Biol 12: 236. 10.1186/gb-2011-12-12-236 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dekker J, Rippe K, Dekker M, Kleckner N. 2002. Capturing chromosome conformation. Science 295: 1306–1311. 10.1126/science.1067799 [DOI] [PubMed] [Google Scholar]
- Duttke SHC, Lacadie SA, Ibrahim MM, Glass CK, Corcoran DL, Benner C, Heinz S, Kadonaga JT, Ohler U. 2015. Human promoters are intrinsically directional. Mol Cell 57: 674–684. 10.1016/j.molcel.2014.12.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- The ENCODE Project Consortium. 2012. An integrated encyclopedia of DNA elements in the human genome. Nature 489: 57–74. 10.1038/nature11247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghandi M, Lee D, Mohammad-Noori M, Beer MA. 2014. Enhanced regulatory sequence prediction using gapped k-mer features. PLoS Comput Biol 10: e1003711. 10.1371/journal.pcbi.1003711 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghandi M, Mohammad-Noori M, Ghareghani N, Lee D, Garraway L, Beer MA. 2016. gkmSVM: an R package for gapped-kmer SVM. Bioinformatics 32: 2205–2207. 10.1093/bioinformatics/btw203 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon MG, Inoue F, Martin B, Schubach M, Agarwal V, Whalen S, Feng S, Zhao J, Ashuach T, Ziffra R, et al. 2020. lentiMPRA and MPRAflow for high-throughput functional characterization of gene regulatory elements. Nat Protoc 15: 2387–2412. 10.1038/s41596-020-0333-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant CE, Bailey TL, Noble WS. 2011. FIMO: scanning for occurrences of a given motif. Bioinformatics 27: 1017–1018. 10.1093/bioinformatics/btr064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Green P, Ewing B, Miller W, Thomas PJ, Thomas J, Touchman J, Blakesley R, Bouffard G, Beckstrom-Sternberg S, McDowell J, et al. 2003. Transcription-associated mutational asymmetry in mammalian evolution. Nat Genet 33: 514–517. 10.1038/ng1103 [DOI] [PubMed] [Google Scholar]
- Haiminen N, Mannila H, Terzi E. 2007. Comparing segmentations by applying randomization techniques. BMC Bioinformatics 8: 171. 10.1186/1471-2105-8-171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson DS, Mortazavi A, Myers RM, Wold B. 2007. Genome-wide mapping of in vivo protein–DNA interactions. Science 316: 1497–1502. 10.1126/science.1141319 [DOI] [PubMed] [Google Scholar]
- Johnson GD, Barrera A, McDowell IC, D'Ippolito AM, Majoros WH, Vockley CM, Wang X, Allen AS, Reddy TE. 2018. Human genome-wide measurement of drug-responsive regulatory activity. Nat Commun 9: 5317. 10.1038/s41467-018-07607-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jurka J, Kapitonov VV, Klonowski P, Walichiewicz J, Smit AF. 1996. Identification of new medium reiteration frequency repeats in the genomes of Primates, Rodentia and Lagomorpha. Genetica 98: 235–247. 10.1007/BF00057588 [DOI] [PubMed] [Google Scholar]
- Kent WJ, Sugnet CW, Furey TS, Roskin KM, Pringle TH, Zahler AM, Haussler D. 2002. The human genome browser at UCSC. Genome Res 12: 996–1006. 10.1101/gr.229102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein JC, Agarwal V, Inoue F, Keith A, Martin B, Kircher M, Ahituv N, Shendure J. 2020. A systematic evaluation of the design and context dependencies of massively parallel reporter assays. Nat Methods 17: 1083–1091. 10.1038/s41592-020-0965-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwasnieski JC, Mogno I, Myers CA, Corbo JC, Cohen BA. 2012. Complex effects of nucleotide variants in a mammalian cis-regulatory element. Proc Natl Acad Sci 109: 19498–19503. 10.1073/pnas.1210678109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B, Salzberg SL. 2012. Fast gapped-read alignment with Bowtie 2. Nat Methods 9: 357–359. 10.1038/nmeth.1923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence M, Gentleman R, Carey V. 2009. rtracklayer: an R package for interfacing with genome browsers. Bioinformatics 25: 1841–1842. 10.1093/bioinformatics/btp328 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawrence M, Huber W, Pagès H, Aboyoun P, Carlson M, Gentleman R, Morgan MT, Carey VJ. 2013. Software for computing and annotating genomic ranges. PLoS Comput Biol 9: e1003118. 10.1371/journal.pcbi.1003118 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Handsaker B, Wysoker A, Fennell T, Ruan J, Homer N, Marth G, Abecasis G, Durbin R, 1000 Genome Project Data Processing Subgroup. 2009. The Sequence Alignment/Map format and SAMtools. Bioinformatics 25: 2078–2079. 10.1093/bioinformatics/btp352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Yu S, Dhiman VK, Brunetti T, Eckart H, White KP. 2017. Functional assessment of human enhancer activities using whole-genome STARR-sequencing. Genome Biol 18: 219. 10.1186/s13059-017-1345-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikhaylichenko O, Bondarenko V, Harnett D, Schor IE, Males M, Viales RR, Furlong EEM. 2018. The degree of enhancer or promoter activity is reflected by the levels and directionality of eRNA transcription. Genes Dev 32: 42–57. 10.1101/gad.308619.117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mills RE, Bennett EA, Iskow RC, Devine SE. 2007. Which transposable elements are active in the human genome? Trends Genet 23: 183–191. 10.1016/j.tig.2007.02.006 [DOI] [PubMed] [Google Scholar]
- Moore JE, Purcaro MJ, Pratt HE, Epstein CB, Shoresh N, Adrian J, Kawli T, Davis CA, Dobin A, Kaul R, et al. 2020. Expanded encyclopaedias of DNA elements in the human and mouse genomes. Nature 583: 699–710. 10.1038/s41586-020-2493-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muerdter F, Boryń ŁM, Arnold CD. 2015. STARR-seq—principles and applications. Genomics 106: 145–150. 10.1016/j.ygeno.2015.06.001 [DOI] [PubMed] [Google Scholar]
- Patwardhan RP, Lee C, Litvin O, Young DL, Pe'Er D, Shendure J. 2009. High-resolution analysis of DNA regulatory elements by synthetic saturation mutagenesis. Nat Biotechnol 27: 1173–1175. 10.1038/nbt.1589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plank JL, Dean A. 2014. Enhancer function: mechanistic and genome-wide insights come together. Mol Cell 55: 5–14. 10.1016/j.molcel.2014.06.015 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramaker RC, Hardigan AA, Goh ST, Partridge EC, Wold B, Cooper SJ, Myers RM. 2020. Dissecting the regulatory activity and sequence content of loci with exceptional numbers of transcription factor associations. Genome Res 30: 939–950. 10.1101/gr.260463.119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team. 2019. R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna. https://www.R-project.org/. [Google Scholar]
- Schoenfelder S, Fraser P. 2019. Long-range enhancer–promoter contacts in gene expression control. Nat Rev Genet 20: 437–455. 10.1038/s41576-019-0128-0 [DOI] [PubMed] [Google Scholar]
- Schöne S, Bothe M, Einfeldt E, Borschiwer M, Benner P, Vingron M, Thomas-Chollier M, Meijsing SH. 2018. Synthetic STARR-seq reveals how DNA shape and sequence modulate transcriptional output and noise. PLoS Genet 14: e1007793. 10.1371/journal.pgen.1007793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, He N, Niu L, Huang Y, Shen W, Zhang Y, Li L, Hou C. 2019. Global quantitative mapping of enhancers in rice by STARR-seq. Genomics Proteomics Bioinformatics 17: 140–153. 10.1016/j.gpb.2018.11.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Arensbergen J, Pagie L, FitzPatrick VD, de Haas M, Baltissen MP, Comoglio F, van der Weide RH, Teunissen H, Võsa U, Franke L, et al. 2019. High-throughput identification of human SNPs affecting regulatory element activity. Nat Genet 51: 1160–1169. 10.1038/s41588-019-0455-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visel A, Blow MJ, Li Z, Zhang T, Akiyama JA, Holt A, Plajzer-Frick I, Shoukry M, Wright C, Chen F, et al. 2009a. ChIP-seq accurately predicts tissue-specific activity of enhancers. Nature 457: 854–858. 10.1038/nature07730 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visel A, Rubin EM, Pennacchio LA. 2009b. Genomic views of distant-acting enhancers. Nature 461: 199–205. 10.1038/nature08451 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X, He L, Goggin SM, Saadat A, Wang L, Sinnott-Armstrong N, Claussnitzer M, Kellis M. 2018. High-resolution genome-wide functional dissection of transcriptional regulatory regions and nucleotides in human. Nat Commun 9: 5380. 10.1038/s41467-018-07746-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weirauch MT, Yang A, Albu M, Cote AG, Montenegro-Montero A, Drewe P, Najafabadi HS, Lambert SA, Mann I, Cook K, et al. 2014. Determination and inference of eukaryotic transcription factor sequence specificity. Cell 158: 1431–1443. 10.1016/j.cell.2014.08.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.