Optimized sample selection for cost-efficient long-read population sequencing

Abstract

An increasingly important scenario in population genetics is when a large cohort has been genotyped using a low-resolution approach (e.g., microarrays, exome capture, short-read WGS), from which a few individuals are resequenced using a more comprehensive approach, especially long-read sequencing. The subset of individuals selected should ensure that the captured genetic diversity is fully representative and includes variants across all subpopulations. For example, human variation has historically focused on individuals with European ancestry, but this represents a small fraction of the overall diversity. Addressing this, SVCollector identifies the optimal subset of individuals for resequencing by analyzing population-level VCF files from low-resolution genotyping studies. It then computes a ranked list of samples that maximizes the total number of variants present within a subset of a given size. To solve this optimization problem, SVCollector implements a fast, greedy heuristic and an exact algorithm using integer linear programming. We apply SVCollector on simulated data, 2504 human genomes from the 1000 Genomes Project, and 3024 genomes from the 3000 Rice Genomes Project and show the rankings it computes are more representative than alternative naive strategies. When selecting an optimal subset of 100 samples in these cohorts, SVCollector identifies individuals from every subpopulation, whereas naive methods yield an unbalanced selection. Finally, we show the number of variants present in cohorts selected using this approach follows a power-law distribution that is naturally related to the population genetic concept of the allele frequency spectrum, allowing us to estimate the diversity present with increasing numbers of samples.

In recent years it has become increasingly clear that structural variants (SVs) play a key role in evolution, diseases, and many other aspects of biology across all organisms (Lupski 2015; Sudmant et al. 2015; Alonge et al. 2020). It is less well known, however, whether the evolutionary forces shaping SV diversity are analogous or distinct from those influencing single-nucleotide variants (SNVs). Genome-wide inferences of human evolutionary relationships (The 1000 Genomes Project Consortium 2015) and key population genetic parameters such as θ (Watterson 1975), π (Nei and Li 1979), and Tajima's D (Tajima 1989) have largely focused on SNVs but not SVs. Similarly, genome-wide scans of human SNV data have revealed positive and/or balancing selection targeting genomic regions including lactase, the ABO blood group, and the HLA immune complex (Fu 2014), but the role of SVs in human adaptation remains poorly understood. Performing population genetic research using structural variants will require better methods that identify SVs in a more cost-effective way. Short-read sequencing is currently the most widely used approach for identifying SVs, although it suffers from limited accuracy (Chaisson et al. 2015; Sedlazeck et al. 2018). Long reads, such as those from Pacific Biosciences (PacBio) and Oxford Nanopore Technologies, provide greater sensitivity and lower false discovery rates, but their higher costs hinder widespread application in large sequencing studies. Another related question with large cohorts is how to efficiently validate a large number of SVs from the short read–based calls. Traditional methods such as PCR/Sanger sequencing are costly and labor intensive, necessitating careful consideration of variants and samples to validate for further study. Thus, these methods are often limited to hundreds of SVs that can be validated out of an average of 20,000–23,000 SVs present in a healthy individual (Mahmoud et al. 2019).

Here, we present SVCollector, an open-source method (MIT license) to optimally rank and select samples based on variants that are shared within a large population. By default, the optimal ranking strives to capture as much genetic population diversity as possible in a fixed number of samples. As a consequence of this approach, the selected samples will include most common variants plus as many rare and private variants as possible. Alternatively, it can optimize the selection by weighting the variants by their allele frequency, which further enriches for common variants in the population. Naive methods to select samples include picking a random selection or picking the samples which individually have the most variants. These methods do not account for the fact that variants may be shared across multiple samples in the selection.

Instead, SVCollector uses an optimized greedy approach to identify a set that collectively spans as many variants as possible. Thus, SVCollector allows for both a more cost-efficient way to validate a large number of common SVs, along with an improved resequencing approach to discover SVs that were initially missed by short-read sequencing. In the analysis, SVCollector reports the cumulative number of distinct variants present for each individual selected. By extrapolating out to larger collections of genomes, SVCollector estimates the number of individuals that would need to be sequenced to obtain a given fraction of the total population-specific diversity.

Results

SVCollector overview

SVCollector is implemented in C++ and computes a ranked list and diagnostic plots of the samples listed in a multisample VCF file. It uses an iterative approach to minimize the memory footprint, and requires <2 MB of RAM even when ranking thousands of samples with tens of thousands of variants each. In the first iteration, it parses the VCF file, counts the total number of variants, and generates a temporary file storing the sample IDs associated with each variant. For subsequent iterations, it reads the temporary file and deletes variants that were present in the previously selected sample.

SVCollector has two major ranking modes: topN and greedy (Fig. 1), as well as a simple random selection model. For the topN mode, it picks samples in the order of the number of variants they contain, irrespective of whether the variants are shared with other samples. In the default greedy mode, SVCollector finds an optimal subset of samples that collectively contain the largest number of distinct variants. SVCollector can be used to optimize for all types of variants (SNVs, SVs, etc.) listed in a VCF file.

Figure 1.

topN versus greedy methods. (A) Presence/absence matrix for three samples and four variants. (B) When picking the two most diverse samples, the topN algorithm selects A and B because they are the individuals with the greatest number of variants. However, this selection only includes three of the four variants. (C) The greedy algorithm on the other hand selects A and C because it accounts for the fact that the variants covered by B have already been included by A. The greedy selection includes all four variants.

We assessed the results of SVCollector based on simulated data (Supplemental Note S1; Supplemental Figs. S1, S2) and two large short-read sequencing projects involving 2504 and 3024 samples each (Fig. 2). For each cohort, we focused on selecting an optimal set of 100 diverse samples. Using SVCollector, the individuals that are identified span all subpopulations, whereas the naive topN approach concentrates the selection in a few subpopulations. For all cohorts, the runtime and memory requirements were minimal. For example, for the 1000 Genomes Project VCF file of 2504 samples over 66,555 distinct SVs (Sudmant et al. 2015), SVCollector computed the top 100 samples in 67 sec using 1.7 MB memory. Each of the modes had a similar runtime and RAM requirements.

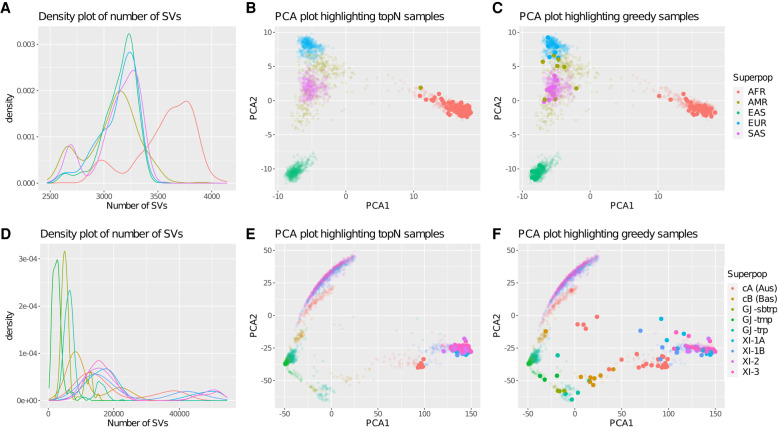
Figure 2.

Density and PCA plots of the 1000 Genomes Project and the 3000 Rice Genomes Project. (A) Density plot of the number of SVs reported per person for each of the five superpopulations in the 1000 Genomes Project. The variants include all nonreference alleles, with both homozygous and heterozygous variants considered equally. The peak for the African (AFR) superpopulation occurs around 3750 SVs per person, whereas the peaks for the other superpopulations occur around 3250 SVs per person. (B,C) PCA plots of the 1000 Genome Project samples colored by superpopulation highlighting the 100 most diverse samples chosen by the topN or greedy approaches, respectively. The topN method oversamples from superpopulations with a greater number of SVs, whereas the greedy method picks a representative sampling across all the superpopulations. (D) Density plot of the number of SVs per sample for each of the nine populations in the 3000 Rice Genomes Project. (E,F) PCA plots of the 3000 Rice Genome Project samples constructed by using variants with an allele frequency >5%. The PCA plots are colored by population and highlight the 100 most diverse samples chosen by the topN or greedy approaches, respectively. The topN method oversamples from populations with a greater number of SVs, whereas the greedy method picks a representative sampling across all the populations.

Sample selection based on SVs from 2504 human genomes

We assessed SVCollector based on 2504 human genomes from the 1000 Genomes Project (Sudmant et al. 2015). For our analyses, we used the phase 3 variant callset (The 1000 Genomes Project Consortium 2015) for Chromosomes 1 through 22 with all children removed. Figure 2 shows a summary of the results and Supplemental Note S2, Supplemental Figure S3, and Supplemental Table S1 list the details. We first investigated the distribution of the 100 samples selected by SVCollector across the five superpopulations (Supplemental Table S2). The naive topN approach selects 99 African samples and one American sample, whereas SVCollector's optimal greedy approach covers all five superpopulations containing 57 African, 14 East Asian, 14 South Asian, eight American, and seven European samples and represents 25 of the 26 subpopulations, excluding only GBR (Fig. 2B,C). The topN approach oversamples from the African superpopulation because it has a greater number of SVs than the other superpopulations (Fig. 2A).

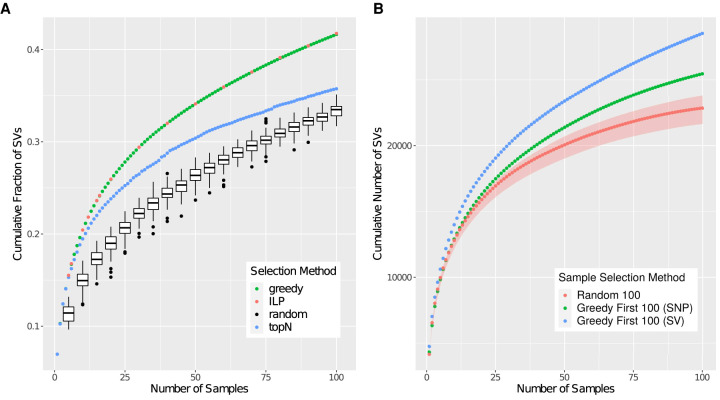
We next investigated the fraction of SVs covered by the 100 samples selected by SVCollector. We compared SVCollector's greedy method to the naive topN method, to a random method, and to the exact algorithm using integer linear programming (ILP) (Fig. 3A). The ILP approach allowed us to establish a ground truth so that we could assess the accuracy of the much faster greedy heuristic (Methods). In the random approach, samples are drawn from a uniform random distribution of samples across the whole cohort. The random selection was run 100 times per cohort, and we report a box plot of the percent of SVs identified. We gave the ILP solver the greedy solution as a starting point, ran it for 24 h, and chose the best solution at this time. SVCollector's fast greedy approach (20.43% of SVs) slightly outperforms the naive topN approach (19.47% of SVs) and equals the ILP solution (20.43% of SVs) when investigating the top 10 ranked samples in terms of SVs captured. However, when extending the selection to 100 genomes, the greedy approach (41.65% of SVs) more substantially outperforms the topN approach (35.75% of SVs) and only slightly underperforms the ILP solution (41.75% of SVs) by 74 SVs. Across all the values we tested (k = 5, 6, 10, 12, 15, 16, 20, 30, 40, 50, 60, 70, 80, 90, 100, 120, 140, 160, 180, 200), we find that the greedy approach takes only seconds to run and underperforms the ILP solution by at most 74 variants (0.11% of SVs).

Figure 3.

Comparison of various sample selection methods. (A) Cumulative fraction of SVs covered for a given number of samples chosen by the ILP, greedy, topN, and random approaches. SVCollector's greedy approach approximates the true ILP solution and exceeds the topN and random approaches at recovering unique SVs. (B) Number of SVs covered using three sample selection methods. In red is the median number of SVs covered over 100 trials of a random sample of 100 individuals. The red ribbon comprises the minimum and maximum number of SVs covered over the 100 trials. In green is the number of SVs covered using the 100 best ranked (greedy) individuals from the SNV data, and in blue is the number of SVs covered using the 100 best ranked individuals (greedy) from the SV data. Data are from the 1000 Genomes Project (The 1000 Genomes Project Consortium 2015).

We also found that a balanced random selection performs worse than a uniform random selection on these data. Specifically, we performed 100 trials of a balanced random selection of 100 samples (i.e., a random sample of 20 individuals within each of the five superpopulations). The median fraction of SVs recovered by these trials was 31.71355%, which is less than the median fraction of SVs recovered by 100 trials of a uniform random selection of 100 samples (33.4944%). On reflection, this result is expected because a balanced random selection will be under-selecting samples from the more diverse African superpopulation. Recall that the greedy solution chooses 57 African samples. However, the balanced random selection will only choose 20 African samples, but the uniform random solution on average will choose 26 African samples based on the distribution of samples in the superpopulations.

By default, SVCollector maximizes the count of distinct variants, without taking into account the allele frequency of the variants. This often leads to an enrichment of rare or private variants in the identified set, potentially at the expense of capturing more common variants. However, SVCollector can also be run in a mode that takes allele frequency into account. In this mode, SVCollector also uses a greedy approach but optimizes for common variants in the population by weighting variants by their observed allele frequency. We assessed SVCollector in this allele frequency mode to choose the most diverse set of 10 samples in the 1000 Genomes Project. In the allele frequency mode, SVCollector selects samples that cover 92.47% of the total weighted SV diversity, whereas in the normal mode SVCollector selects samples that cover 91.25%. We also compared the two modes when choosing the most diverse set of 100 samples. In the allele frequency mode, SVCollector selects samples that cover 98.96% of the total weighted SV diversity, but in the normal mode the samples selected cover 98.89%. Furthermore, SVCollector chooses 51 African, 14 East Asian, 13 European, 12 South Asian, and 10 American samples. Thus, even in the allele frequency mode SVCollector chooses a representative selection of samples across all subpopulations.

Sample selection based on SNVs from 2504 human genomes

Next, we investigated the relationship between SNVs and SVs, especially to measure if SNV calls can be used as an approximation of SV diversity. For this, we used the 1000 Genomes Project data and compared three different methods for picking a sample of 100 individuals to optimize the total number of SVs covered. Overall we find that SVCollector is effective at optimizing sample selection to maximize the number of distinct SVs, even in the absence of SV calls (Fig. 3B).

First we analyzed 100 trials each consisting of 100 randomly picked individuals. Out of the 100 trials, the SVs covered ranged from 21,627 to 23,792 with a median of 22,839.5 SVs. Next, we ran SVCollector in the greedy mode on the SNV data from the 1000 Genomes Project and picked the best ranked 100 individuals. The number of SVs contained in this sample was 25,459. Comparing this to the greedy selection of SVCollector based on SVs resulted in only 3070 fewer SVs. Thus, selecting the best ranked individuals from the SNV data is an improvement over a random sample and approaches the upper limit of SVs covered.

Sample selection based on SVs from 3024 rice genomes

We also assessed SVCollector based on 3024 genomes from the 3000 Rice Genomes Project (The 3,000 Rice Genomes Project 2014). Figure 2 summarizes the results, and Supplemental Table S3 lists the details. We first investigated the distribution of the 100 samples selected by SVCollector across the populations, using the 2223 samples that can be confidently classified into one of the nine populations (Supplemental Table S4; Wang et al. 2018). The topN approach selects 42 XI-3, 31 XI-2, 16 XI-1A, 7 cA, and 4 XI-1B samples, but no cB, GJ-subtrp, GJ-tmp, or GJ-trp samples. The greedy approach on the other hand selects a representative sample consisting of all nine subpopulations (24 XI-3, 23 cA, 17 XI-2, 9 XI-1A, 8 cB, 8 XI-1B, 5 GJ-trp, 3 GJ-subtrp, 3 GJ-tmp) (Fig. 2E,F). The topN approach oversamples the XI-3, XI-2, and XI-1A populations because they have a greater number of SVs than the other populations (Fig. 2D). We next investigated the fraction of SVs covered by the 100 samples selected by SVCollector. SVCollector's greedy approach (19.2%) outperformed the topN approach (17.0%) when investigating the first 10 ranked samples. When extending the selection to 100 genomes, the greedy approach (45.4%) outperforms the topN approach (37.8%).

Estimating total population-specific diversity

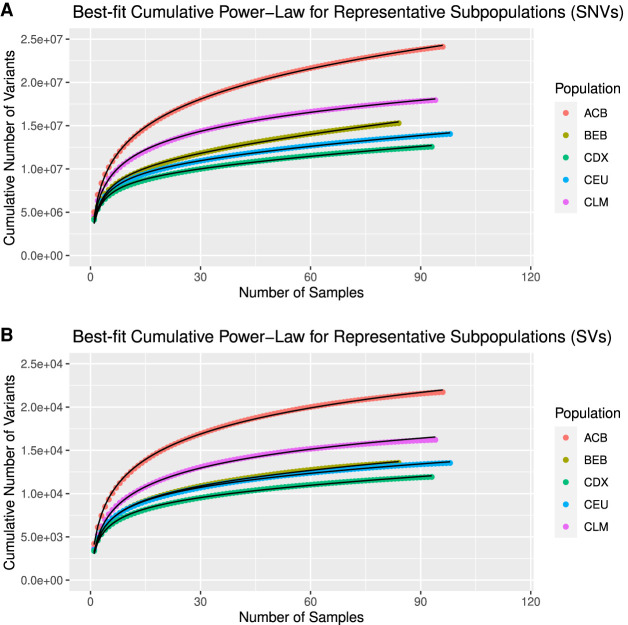
SVCollector creates a diagnostic plot of population diversity in which the y-axis is the cumulative count of variants up to the chosen sample, and the x-axis is the number of samples (Fig. 4). These SVCollector curves (when produced using the greedy mode) allow us to visualize the rate at which the cumulative number of variants increases as individuals are optimally added. Indeed, this rate is a function of the genetic diversity of the population under consideration. To see this, consider a population consisting of individuals with a constant positive number of personal variants, but with zero shared variants between each other. In this case, the rate of change in the cumulative number of variants will remain constant as individuals are added. Now consider a population consisting of individuals with shared variants. A higher prevalence of shared variants across individuals will result in a faster decrease in the rate of change of cumulative variants as individuals are added.

Figure 4.

SVCollector curves and best-fit cumulative power-law models for SNVs (A) and SVs (B). Data are shown for one representative subpopulation for each superpopulation in the 1000 Genomes Project.

We found that these curves are modeled well by a power-law distribution (Supplemental Figs. S4–S29). This is true for both SNVs (Fig. 4A) and SVs (Fig. 4B). These curves can be constructed for each population in a cohort, and a corresponding population-specific best-fit power-law curve can be modeled. The power-law distribution has been found to underlie many natural phenomena and arises from situations involving a preferential attachment process (i.e., new items are preferentially distributed among individuals according to how many items they already have) (Mitzenmacher 2004). The underlying power-law equation that describes these curves and a more in-depth analysis of the interpretation of these curves are described in Methods.

The central advantage of fitting a mathematical model to these curves is that the model can then be extrapolated to larger numbers of samples to estimate the total population-specific diversity that is present. These extrapolations can then be used to determine the extent to which the pan-genome is open and to determine how many individuals would need to be sequenced to obtain a given proportion of the variants shared by at least two individuals. Fully capturing private variants unique to a single individual would require sequencing every individual.

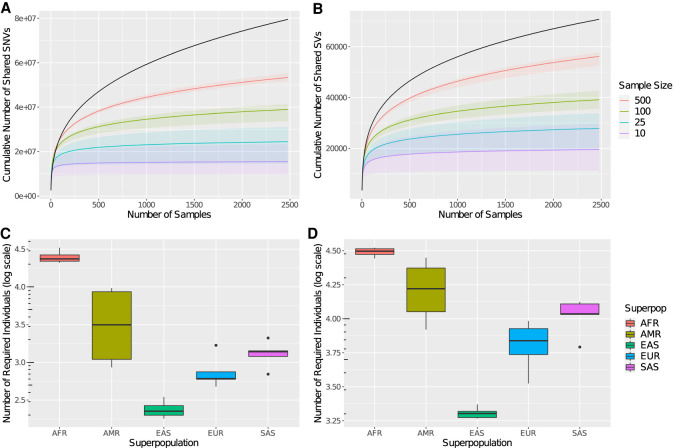
To test the robustness of these extrapolations with varying numbers of samples, we first perform subsampling on the entire 1000 Genomes Project data set, fit a best-fit curve to each subsample, and extrapolate to the full data set. We run 100 trials each for subsamples of 10, 25, and 100 random individuals (Fig. 5A,B). As is expected, the extrapolation from subsampling produces an underestimation in the amount of diversity because the subsample would have to include exactly the most diverse individuals for the extrapolated diversity to match the actual diversity on the entire data set. Consequently, increasing the sample size improves the accuracy of the extrapolation.

Figure 5.

The 1000 Genomes Project extrapolated superpopulation diversity. (A,B) Extrapolating the number of shared variants covered with subsamples. In black is the shared diversity of the full data set. The lines represent the median number of covered variants over 100 trials of the given sample size. The ribbons represent the minimum and maximum number of covered variants over 100 trials of the given sample size. The left panel is calculated on SNVs, and the right panel is calculated on SVs. (C,D) Box plots of subpopulation diversity by superpopulation. For each subpopulation, the predicted total amount of shared variants for 100,000 individuals is calculated. Then, the number of sequenced individuals necessary to obtain 90% of this diversity is calculated. Finally, box plots of the number of required individuals (log scale) are plotted for the corresponding subpopulations in each superpopulation. The left panel is calculated on SNVs, and the right panel is calculated on SVs.

Finally, for each subpopulation in the 1000 Genomes Project data, we extrapolate the best-fit power-law curve out to 100,000 individuals to estimate a lower bound on the total number of variants shared by at least two individuals. Then, we calculate the number of sequenced individuals necessary to obtain 90% of this diversity. We find that relatively fewer East Asian individuals would need to be sequenced and relatively more African individuals would need to be sequenced (Fig. 5C,D). For example, only 180 Chinese Dai (CDX) individuals are needed to capture 90% of the shared SNVs of 100,000 CDX individuals, but at least 32,978 Luhya (LWK) individuals are needed to capture 90% of the shared SNVs of 100,000 LWK individuals. Because these estimates are lower bounds, we conclude that many more individuals need to be sequenced, especially of African descent, to fully capture the diversity of human variants.

Discussion

SVCollector is a fast and powerful method to quantitatively and optimally select samples for long-read resequencing or optical mapping based on their genomic variation (SNV and/or SV) shared in the population. SVCollector's greedy mode substantially outperforms the naive topN or random selections both in the representativeness across populations and in the number of SVs captured. These gains will in turn translate to cost savings for resequencing and validation experiments. Indeed, SVCollector has already been applied to larger sequencing projects such as a detailed study of 11 human genomes and 100 tomato genomes sequenced with long reads (Alonge et al. 2020; Shafin et al. 2020).

We found that SNV variant callsets can be used to choose a sample of individuals that maximizes the number of distinct SVs. In the 1000 Genomes Project data set, this method results in only 3070 fewer SVs captured than when using the SV variant callset directly. Additionally, in the human data sets, female samples often contributed more SVs than male samples because of the extra heterozygous SVs on the X Chromosome. Depending on the application, researchers may want to exclude the sex chromosomes before analysis as we did in our analyses.

We found that plots of the cumulative number of variants included in a selection versus the number of samples in the selection follow a power-law curve. By constructing these plots for each population in a cohort, information can be extracted to estimate the total population-specific diversity that would be captured by sequencing increasing numbers of individuals. We show that the human pan-genome is very diverse, and that capturing 90% of the total shared diversity would require the sequencing of many more individuals than has been done in any long-read cohort to date.

An important consideration for these analyses is that the definition of a population is often arbitrary and based on geographic origins, whereas real populations show varying levels of structure as well as admixture. It is thus important that population genetic studies be designed in ways that are tailored to particular downstream goals, and that experts such as anthropologists are consulted in such decisions where appropriate. Decisions about sample grouping will in turn influence the power-law curves, just as they do the allele frequency spectrum. For example, if many closely related individuals are sampled, there will be an excess of common alleles in the samples, and additional relatives will not result in the discovery of many novel variants. Power-law curves should thus be interpreted in the context of any known selection biases.

It remains challenging to create a population-wide variant callset as the selection clearly depends on the quality of the initial SV callset. Nevertheless, given a low quality (i.e., overrepresentation of false positive SVs) variation callset, SVCollector also overrepresents false positives, which will help with the detection and negative validation of these SV calls. We show that SVCollector is robust in the presence of false positive calls (Supplemental Table S5). In the case when an SV callset is limited in the detection of SVs, SVCollector will still rank the samples, but it is unclear what minimal sensitivity rate would be needed to accurately represent the population.

Overall, we showcase a cost-efficient yet comprehensive way to use long-read sequencing at population scale. This is particularly important for population projects (CCDG, TOPMed, 1000 Genomes Project, etc.) where genotyping data are available. We show that SVCollector identifies the optimal subset of samples for further examination and at the same time provides population-specific insights. Given the current many-fold price differences between long-read sequencing and Illumina sequencing, together with the abundance of population studies (exons, arrays, etc.), SVCollector will remain useful for quite some time.

Methods

Data sets

The 22 autosome SNV VCF files for the 1KGP project can be downloaded at ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/release/20130502/. The 22 autosome SV VCF files for the 1KGP project can be downloaded at ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/phase3/integrated_sv_map/. The data used to generate the SV VCF files for the 3000 Rice Genome Project Large Structural Variants Dataset can be downloaded at https://snp-seek.irri.org/_download.zul.

Integer linear programming

SVCollector ranks a list of samples in a multisample VCF file to provide a selection maximizing the variants included. Solving this problem exactly is computationally demanding as it is a version of the well-known NP-hard maximum coverage problem. We implement the following integer linear programming (ILP) formulations of the problem to solve it exactly, although this requires an excessively long run time even for relatively small data sets.

The input for the ILP maximum coverage optimization problem is represented by an n × m binary matrix A = [a_i,j] ∈ {0, 1}^n×m, in which every entry a_i,j ∈ {0, 1} determines if in sample i the variant j is present or absent. Given a matrix A and 1 ≤ k ≤ n, we define an optimization problem as a search for a subset I⊆{1, 2, …, n} of samples with |I| ≤ k, such that the total number of variants present across all samples in I is maximized.

We formulate the following ILP to solve the aforementioned optimization problem. First, we define the decision variables in our ILP formulation:

$$\mathrm{\forall }i\in [1,2,\dots ,n]:x_i\in \{0,1\}$$ (1a)

$$\mathrm{\forall }j\in [1,2,\dots ,m]:y_j\in \{0,1\}$$ (1b)

where a variable x_i encodes whether or not a sample i is selected to be present in the problem solution I, and a variable y_j encodes whether or not a variant j is going to be represented in the problem solution (i.e., present in at least one sample from I).

We now define the constraints for the ILP formulation. We start with the constraint that ensures that no more than k samples are selected:

$$\sum _i{x}_i\le k$$ (2)

We then define constraints that ensure that when a variable y_j = 1, at least one sample x_i in which variant j is present is selected:

$$\mathrm{\forall }j\in [1,2,\dots ,m]:\sum _i{x}_i\cdot a_{i,j}\ge y_j$$ (3)

Finally, we define an objective function for our optimization ILP, forcing the maximum number of variants to be represented in the desired solution:

$$\underset{x_i,y_j}{max}\sum _j{y}_j$$ (4)

Although these ILP formulations solve the maximum coverage problem exactly, they are inefficient. Conversely, the greedy algorithm provides an efficient polynomial time solution that closely approximates the optimal solution (Feige 1998). Consequently, SVCollector uses a greedy approximation that starts with the sample with the largest number of variants, and then iteratively picks the sample containing the largest number of variants not yet included in the subset. It also has a random mode that mimics an arbitrary selection process and is helpful for evaluating the diversity of the topN or greedy approaches.

Additionally, SVCollector has a mode in which the user may supply a file of sample names and weighted factors. In this way, a user can up-weight or down-weight whether to include particular samples based on external factors. These weighted factors can be set in terms of sample accessibility, breeding phenotypes, or other factors unique to the particular experiment. For each mode, SVCollector reports the rank, sample name, its unique contribution of SVs, the cumulative sum of SVs up to the chosen sample, and the cumulative percentage compared to the total number of SVs in the input VCF file.

Interpreting the power-law curves

We examined the distribution in the number of distinct variants present for each individual selected by SVCollector and found that it follows a power-law distribution. Similar analyses of the cumulative population diversity in samples have been performed in the context of determining the extent to which the pan-genome of a bacterial species is open or closed (Medini et al. 2005). In this analysis, the pan-genome includes the “core” genome that is shared among all individuals in a population and a “dispensable” genome that is either shared between a subset of individuals (accessory genome) or is unique to a single individual (unique genome). Here, we define the “shared” genome as the union of the core and accessory genomes. In one study, the pan-genome of Streptococcus agalactiae was concluded to be open owing to mathematical extrapolation of the plot of the cumulative number of genes present versus number of strains added (Tettelin et al. 2005).

To model the SVCollector curves, we fit the following equation:

$$f(n)=\sum _{i=1}^n(\alpha {(i)}^{\beta }+\gamma )$$ (5)

where n is the number of individuals included in the selection, f (n) is the cumulative number of variants present after the nth individual is added, α is a population diversity metric that scales with the total number of variants in the population, β is a population diversity metric that describes the diversity of the population, and γ is a variable that relates to the number of personal variants for each individual. To determine the parameter values of the model that best-fit the data, SVCollector uses nonlinear optimization. Specifically, the nlsLM function in R is used (R version 3.6.3) (R Core Team 2020), which implements the Levenberg-Marquardt algorithm (Moré 1978), whereby an iterative procedure is performed to update the initial estimate.

In this model, α measures the population mutation rate, and β measures the extent to which variants are shared across individuals in the population. A larger α value corresponds to a higher mutation rate, and a smaller α value corresponds to a lower mutation rate. A less negative β (i.e., closer to 0) corresponds to a relative excess of rare variants in the population, and a more negative β corresponds to a relative lack of rare variants in the population. Thus, we would expect more genetically heterogeneous populations to have a less negative β and more homogeneous populations to have a more negative β.

To gain a deeper understanding of these curves, we sought to interpret their shapes in light of existing population genetic theory and metrics. To connect the parameters from our power-law curve to well-established theory, we compare the α parameter of our model to Watterson's θ and the β parameter of our model to Tajima's D. Watterson's θ and Tajima's D are summary statistics derived from the allele frequency spectrum (Fisher 1931; Wright 1938). The allele frequency spectrum considers counts of the number of samples possessing each variant. SVCollector instead considers counts of the number of variants contained within each sample. As we have shown, the central advantage to using the counts of the number of variants is that it is straightforward to extrapolate the number of variants we would expect to see as the number of individuals in the sample is increased.

For each of the 26 subpopulations in the 1000 Genomes Project data, we calculated the value of α, β, Watterson's θ, and Tajima's D over the autosomes (Supplemental Tables S6, S7). We calculated one set of values on the SNV data and another on the SV data. The program scikit-allel (https://github.com/cggh/scikit-allel) was used to determine the values for Watterson's θ and Tajima's D. From this analysis, we find that the parameters from the power-law curves are correlated with these previously existing diversity metrics. We first compared the α parameter to Watterson's θ, which is used to determine the population mutation rate. We find that α is highly correlated with Watterson's θ both using SNV data and using SV data (Supplemental Fig. S30A,C). The correlations also hold when performing a localized analysis of individual chromosomes, although with varying levels of correlation with r² varying from 0.7812 (Chromosome 14) to 0.9026 (Chromosome 19). We next compared the β parameter to Tajima's D, which is often used to test for deviations from neutrality or demographic equilibrium. Specifically, it compares the mean number of pairwise differences to the number of segregating sites. We find that β is highly correlated with Tajima's D both using SNV data and using SV data (Supplemental Fig. S30B,D). The correlations also hold when performing a localized analysis of individual chromosomes, with r² varying from 0.7738 (Chromosome 2) to 0.8683 (Chromosome 21).

To better understand whether the population structure of structural variants within a population is similar to that of small variants, we compared the values of each metric calculated using SV data for each subpopulation to the values calculated using SNV data for each subpopulation (Supplemental Fig. S31). We find high correlation between the SV and SNV values for all four metrics with r² values of 0.8941, 0.9387, 0.9932, and 0.9459 for α, β, Watterson's θ, and Tajima's D, respectively. These results indicate that the population structures of structural variants and small variants are highly analogous, providing further evidence to support previous findings (Sudmant et al. 2015).

Population substructure and signatures of selection

One consequence of this population genetic interpretation of the power-law curves is that the β parameter can be used to compare the genetic diversity of subpopulations. For example, after comparing the values of β for each of the 26 subpopulations, we find β is least negative (indicating a relative excess of rare variants) for the seven African populations and most negative (indicating a relative lack of rare variants) for the five East Asian populations, as expected (Fig. 6A). This comports with previous analyses of intrapopulation diversity showing the African superpopulation to be the most genetically diverse and the East Asian superpopulation to be the least genetically diverse (The 1000 Genomes Project Consortium 2015) as a result of serial founder effects during ancient human dispersal across the globe (Deshpande et al. 2009).

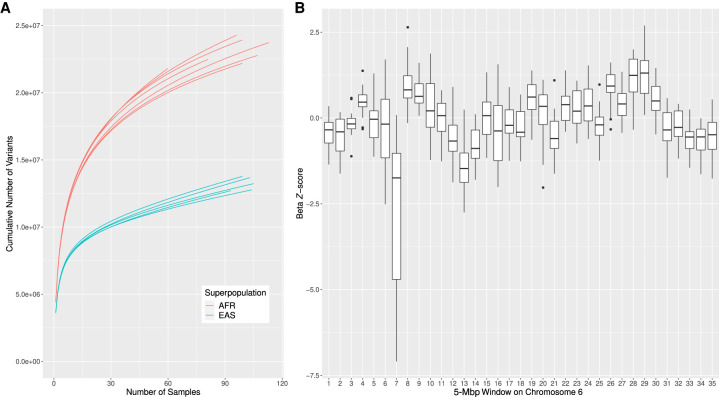
Figure 6.

Subpopulation diversity and selective sweeps. (A) SVCollector curves for the most and least diverse human subpopulations (SNVs). The seven African subpopulations are the most diverse, and the five East Asian subpopulations are the least diverse according to their corresponding β values. (B) Selective sweep on Chromosome 6. For each 5-Mbp window on Chromosome 6, the β Z-scores for the 26 populations are plotted as a box plot. Window 7 corresponds to the HLA region and shows a strong signal for selective pressure acting in this region.

Furthermore, the β parameter can be used to find regions of the genome showing signatures of positive or balancing selection. To perform a genome-wide scan for such signatures, we calculated β over small genomic regions (5-Mbp nonoverlapping windows). Specifically, for each of the 26 subpopulations, we calculated β over each window using only the corresponding SNVs. On average, there were 28,760 SNVs per window. Then, for each subpopulation, we computed the β Z-score across all windows to allow for comparisons across the different subpopulations. For each window, we then constructed a box plot of the β Z-scores across the 26 subpopulations. We find that for the 26 subpopulations, the genomic region spanning the HLA immune complex (window 7 on Chromosome 6) has a more negative β value than all other regions. This indicates a relative lack of rare variants in this region, which is a signal of balancing/diversifying selection (Fig. 6B; Hughes and Yeager 1998).

Finally, the β parameter can be used to discover regions of the genome targeted by historical local adaptation, whereby positive selection generated strong frequency differences across human populations. For example, we would expect that Northern European populations, but not East Asian populations, would show signatures of positive selection targeting the lactase gene (LCT) (Bersaglieri et al. 2004; Bayless et al. 2017). Indeed we find that the British in England and Scotland (GBR) population has the most negative β Z-score (−0.920) for this region, but none of the East Asian populations have a negative β Z-score. The limited number of SVs in the 1000 Genomes Project data set, with an average of only 26 SVs per 5-Mbp window, limits similar selective sweep analyses using SVs. However, using our mathematical model we have reaffirmed previously known facts about human population genetics. This validates that our method can be used to discover new information about less well-characterized populations.

Software availability

The SVCollector source code is available at GitHub (https://github.com/fritzsedlazeck/SVCollector) and as Supplemental Code.

Competing interest statement

The authors declare no competing interests.