Significance
Federated learning (FL) is an emerging paradigm that enables multiple devices to collaborate in training machine learning (ML) models without having to share their possibly private data. FL requires a multitude of devices to frequently exchange their learned model updates, thus introducing significant communication overhead, which imposes a major challenge in FL over realistic networks that are limited in computational and communication resources. In this article, we propose a communication-efficient FL framework that enables edge devices to efficiently train and transmit model parameters, thus significantly improving FL performance and convergence speed. Our proposed FL framework paves the way to collaborative ML in large-scale networking systems such as Internet of Things networks.
Keywords: machine learning, federated learning, wireless communications
Abstract
Federated learning (FL) enables edge devices, such as Internet of Things devices (e.g., sensors), servers, and institutions (e.g., hospitals), to collaboratively train a machine learning (ML) model without sharing their private data. FL requires devices to exchange their ML parameters iteratively, and thus the time it requires to jointly learn a reliable model depends not only on the number of training steps but also on the ML parameter transmission time per step. In practice, FL parameter transmissions are often carried out by a multitude of participating devices over resource-limited communication networks, for example, wireless networks with limited bandwidth and power. Therefore, the repeated FL parameter transmission from edge devices induces a notable delay, which can be larger than the ML model training time by orders of magnitude. Hence, communication delay constitutes a major bottleneck in FL. Here, a communication-efficient FL framework is proposed to jointly improve the FL convergence time and the training loss. In this framework, a probabilistic device selection scheme is designed such that the devices that can significantly improve the convergence speed and training loss have higher probabilities of being selected for ML model transmission. To further reduce the FL convergence time, a quantization method is proposed to reduce the volume of the model parameters exchanged among devices, and an efficient wireless resource allocation scheme is developed. Simulation results show that the proposed FL framework can improve the identification accuracy and convergence time by up to 3.6% and 87% compared to standard FL.
Machine learning (ML) uses data to realize intelligent and autonomous decision-making and inference. ML algorithms have been used in a wide variety of areas, such as computer vision, natural language processing, medical imaging, and communications (1–4). Data are often collected on devices at the edges of networks: Images and text messages are often generated and stored on smartphones; biomedical signals are collected by medical and wearable devices, and often stored on hospital servers; various forms of signals are recorded by Internet of Things systems and sensors.
As massive amounts of data are typically required to train an ML model, such as deep neural networks, centralized ML algorithms must collect training data from edge devices for training purposes. For example, to train an ML model for medical diagnosis, a central controller (CC) must collect the medical data from multiple hospitals. Nonetheless, in some applications, such as the aforementioned example of training an ML diagnosis system for medical data, the edge devices may not be willing to share their data, due to privacy concerns and regulations. Furthermore, conveying large volumes of aggregated data by many mobile devices may induce a notable burden on the communication infrastructure. These considerations gave rise to the need for ML algorithms that train an ML model in a distributed fashion, such that edge devices can contribute to the learning procedure without sharing their data.
Federated learning (FL) proposed in ref. 5 is a distributed learning algorithm that enables edge devices to jointly train a common ML model without being required to share their data. The FL procedure relies on the ability of each device to train an ML model locally, based on its data, while having the devices iteratively exchanging and synchronizing their local ML model parameters with each other in a manner orchestrated by a CC unit (6). Due to its unique features, FL has been applied in a wide variety of practical applications such as mobile keyboard prediction [e.g., Google (7)], speaker and command recognition [e.g., Apple (8)], and data silos for insurance companies [e.g., WeBank (9)].
However, implementation of FL in practical applications faces several challenges which stem from its distributed operation, which is fundamentally different from traditional centralized ML algorithms (10). These challenges include 1) communication overhead induced by the repetitive model parameter exchanges; 2) device hardware heterogeneity, as each device may have different computational capabilities; 3) data heterogeneity, as each device can access a relatively small and personalized dataset and may thus train an ML model which is biased toward its own data; and 4) privacy and security issues, which follow from the fact that the learning procedure is carried out over multiple individual devices. Among these challenges, the communication overhead constitutes a major bottleneck due to the following reasons. First, FL is trained by an iterative process, and hence the time it takes to learn, that is, the convergence time, depends on both the optimization procedure, for example, the number of training steps, as well as the FL parameter transmission delay per training step. Second, FL training is potentially implemented by millions of edge devices, and each device must iteratively share its large-size FL parameters with a CC. Therefore, for FL implemented over a realistic network with limited computational and communication resources, its FL parameter transmission delay may be much larger than the time it takes the devices to train their local ML models. Therefore, it is necessary to design a communication-efficient FL framework that can significantly improve both convergence speed and model accuracy, thus allowing its application to training large-scale ML models over millions of edge devices.
A number of existing works, including refs. 11–23, have studied the design of communication-efficient FL algorithms. However, the majority of these works focus on optimization of FL in a single aspect such as device selection and scheduling (11–13), FL model parameter update and transmission (14–18), or network resource management (20–22). In this study, we propose a communication-efficient FL framework that tackles multiple causes for communication delay, by jointly optimizing the device selection, FL model parameter transmission, and network resource management. In particular, we first propose a probabilistic device selection scheme which allows the devices that can significantly improve the convergence speed and training loss to have higher probabilities for ML model transmission. Then, a quantization method is designed to reduce the data size of the ML parameters exchanged among devices, thus improving FL convergence speed. In addition, for the selected devices, a wireless resource allocation scheme is developed to further improve their transmission data rates, thus reducing the FL transmission delay at each learning step. Finally, we analyze the convergence of our proposed FL framework. Simulation results based on real-world data demonstrate the performance of our proposed FL framework and its ability to allow accurate and fast collaborative training of multiple edge devices in a federated manner.
Communication-Efficient FL
Basic Concepts of FL.
Before introducing the proposed FL framework, we first explain the basic FL training process. Consider a set of devices and a CC cooperatively implementing an FL algorithm (see SI Appendix, section 1 for further details). Letting be the model parameters, the objective of FL is given as follows:
| [1] |
Here, is a set of training data samples of each device , where each training data sample of device consists of an input vector and output vector , is a local objective function, and is the total number of training samples. FL tackles the problem in Eq. 1 using iterative distributed optimization orchestrated by the CC.
A common FL optimization algorithm is the local stochastic gradient descent (SGD) method (24), where, at every FL iteration, each device uses SGD iterations to train its local model . In particular, the update process at iteration begins with the CC sharing the global model with the devices, which first set their local models to , followed by local SGD steps,
| [2] |
where is the local FL model of device at local updates of FL iteration , is the learning rate, is the training dataset of user at local SGD step of iteration , which consists of training samples randomly selected from the local training dataset , and is the gradient of the objective function with respect to the model parameters.
When each device completes steps of local FL training via Eq. 2, it transmits its trained local FL model parameters, , to the CC. The CC aggregates the received local FL parameters of all of the participating devices into a global FL model as follows:
| [3] |
The local SGD algorithm implements multiple iterations of the local FL model update in Eq. 2 and global FL model update in Eq. 3. At convergence, we have .
Communication Model.
From the FL training process, we can see that the devices and the CC must iteratively exchange their FL parameters over wireless links.
The devices communicate with the CC over an uplink wireless channel, which comprises resource blocks (RBs), for example, frequency bins, each of bandwidth . We consider frequency flat fading channels with Gaussian noise and interference. Let be the signal transmitted by device , and let be the corresponding channel output at the CC. When RB is assigned to device , the channel input–output relationship is given by
| [4] |
Here, is the channel gain between device and the CC, where is the distance between device and the CC, and is the Rayleigh fading parameter, assumed to be known to each device and the CC; is additive white Gaussian noise with power spectral density ; and is the interference over RB , whose energy is . Finally, the channel input is constrained to maximal transmit power of .
The channel model in Eq. 4 implies that FL is carried out over wireless channels which are limited in energy and bandwidth, as well as subject to noise and interference. The ML models conveyed over the channel in FL typically comprise a very large number of parameters, particularly when representing deep neural networks. Combining this with the limited wireless resources, such as energy and bandwidth, implies that the convergence time of FL implemented over realistic wireless networks depends not only on the number of iterations but also on the FL parameter transmission time per iteration. Therefore, it is necessary to design a communication-efficient FL algorithm that trains accurate models using minimal convergence time.
Next, we introduce our proposed communication-efficient FL algorithm that consists of three components: 1) probabilistic device selection for limiting the number of participating devices, 2) universal FL parameter compression method for reducing the volume of data conveyed at each FL iteration, and 3) a resource allocation scheme for optimizing the usage of the wireless channel.
Probabilistic Device Selection Scheme.
Due to limited network resource and energy-constrained devices, only a subset of devices can participate in FL at each iteration. Hence, it is necessary to design a device selection method that selects the devices that can significantly improve convergence speed and training loss to execute the FL. To introduce the proposed device selection scheme, we first define
| [5] |
Then, at each iteration, the proposed selection method consists of the following three steps: 1) Each device calculates and its norm , 2) device sends to the CC, and 3) the CC determines the device connection probability, which is given by
| [6] |
where is the distance between device and the CC, and .
Using the model updates to determine the participation probability of each device in Eq. 6 implies that users with increased contribution to the global model are more likely to participate. This is because captures the change in the local FL model of device at learning step . Consequently, the proposed setting is expected to increase the convergence speed of the global FL model to the optimal global FL model compared to uniform selection as in ref. 5. Furthermore, determines the FL parameter transmission distance, thus affecting transmission delay. As a result, the second term in Eq. 6 accounts for the transmission delay per learning step. The balance between these two terms is dictated by the setting of the hyperparameter : Increasing enables the CC to select the devices that are more likely to contribute toward faster FL model updates, while decreasing implies that the CC is expected to select the devices that transmit their parameters with reduced delay.
The CC determines the devices that transmit their model updates, based on the probability distribution . The proposed device selection method guarantees all devices have a chance to participate in the FL training process, which enables the proposed FL algorithm to find the optimal FL model. Since the connection probability of each device at iteration depends on both its expected contribution to the global model and its transmission delay, a device with a large connection probability is likely to improve both convergence speed and training loss. An additional term that affects the convergence speed and is not accounted for in Eq. 6 is the time required by each device to carry out its local update. While this duration can change considerably between devices, the FL parameter transmission time, which is accounted for in Eq. 6, tends to be the dominant cause of delay in FL carried out over resource-constrained wireless networks. It is noted, however, that one can decrease the number of local SGD updates to further decrease the time used for local FL model updating, although possibly affecting the convergence accuracy, as discussed in ref. 25.
Universal FL Model Parameter Compression.
Due to limited energy and bandwidth resources, devices may not be able to directly transmit the large-sized FL parameters to the CC. This gives rise to the need to compress the local FL model updates transmitted from the devices to the CC, and, particularly, to represent their updates using a limited number of bits, such that the CC can still accurately generate the global model via Eq. 3. However, due to the heterogenous nature of the training data available at the users, a priori knowledge of the underlying distribution of the local FL model parameters is not available at the device side, which motivates compressing the local FL model as a form of universal quantization. In addition, the fact that the CC and the users communicate repeatedly allows them to share a source of common randomness, for example, a random seed, enabling the participating users to implement low-distortion discretization in a universal manner via random lattice quantization (15, 26).
The resulting model compression scheme consists of the following steps: As a preliminary step, an -dimensional lattice is fixed. Upon FL model parameter transmission, each device normalizes its local FL model parameter by times its norm, where is a given scaling factor. The normalization result is divided into -sized vectors, to which the users add a random dither signal randomized in an independent and identically distributed fashion from a uniform distribution over the basic cell of the lattice. The dithered signal is discretized by projecting to the nearest lattice point, and the discrete quantity is further compressed prior to transmission, using lossless entropy coding. The CC decompresses the model updates by recovering the lattice point, and subtracting the dither signal from it. The fact that the devices and the CC can generate the same dither signals relies upon their ability to share a source of common randomness, that is, a random seed (see SI Appendix, section 2 for further details).
Network Resource Management Scheme.
Since the compressed local FL models must be transmitted over wireless links, we also optimize the wireless resource allocation in order to further reduce transmission time. To that aim, recall that the total number of uplink RBs is , which implies that only devices can participate in the FL training process at each iteration. The data rate of device transmitting its compressed local FL model to the CC is . Here, is the RB allocation index, with implying that RB is allocated to device at iteration ; otherwise, we have , and . Then, the transmission delay at each FL iteration is given by , where is the subset of devices that transmit their compressed local FL model parameters to the CC at iteration , which is determined by . Let denote the number of bits that are used to represent the FL parameters that each device needs to transmit to the CC. Hence, the transmission delay minimization problem can be formulated as
| [7] |
| [7a] |
| [7b] |
| [7c] |
where is the set of RBs. To solve this optimization problem, we first transform it to an equivalent integer linear programming problem (see SI Appendix, section 3 for further details). Then, we solve it using interior-point methods (27), to obtain the optimized allocation.
Convergence Analysis.
To analyze the convergence of the proposed FL algorithm, we first assume that the local loss functions satisfy the following conditions: 1) The expected squared norm of the random vector , is bounded by some ; 2) the local loss functions are -smooth and -strongly convex; and 3) the probabilistic device selection scheme selects the set of devices, such that and is uniformly distributed over all -sized subsets of . While assumptions 1 through 3 may not accurately reflect practical FL systems, particularly when training deep models, and can even be in conflict (28), they are often employed in distributed learning studies (24, 25). Therefore, analyzing the convergence of our proposed scheme when these assumptions are satisfied facilitates identifying the contribution of the introduced methods for improving communication efficiency to the convergence profile, compared to FL carried out over ideal communication channels, as studied in refs. 24 and 25.
We let be the normalized second-order moment of the lattice (29), and define the heterogeneity mismatch as , where , and is the target optimal global FL model that minimizes the objective function in Eq. 1. The resulting convergence bound of the proposed communication efficient FL is stated in the following theorem:
Theorem 1. Set and consider local SGD with local iterations, step-size , and mini-batch size . Under this setting, when assumptions 1 through 3 are satisfied, it holds that
| [8] |
where .
The proof of Theorem 1 is detailed in SI Appendix, section 4. Theorem 1 proves that the asymptotic convergence rate of our proposed communication efficient FL is . This is observed by noting that the nominator in Eq. 8 comprises constants which are determined by the FL scheme, and do not change with , and thus the overall bound decays asymptotically as , which is the same as FL over ideal error-free channels (e.g., ref. 25, theorem 1). This indicates the ability of the proposed communication-efficient FL scheme to overcome the challenges associated with the need to communicate over shared noisy and throughput-limited channels. Comparing the instantaneous bound in Eq. 8, that is, for a fixed , to the corresponding bound for FL over ideal links in ref. 25, theorem 1, reveals the effect of the components of our proposed communication-efficient FL scheme on the convergence profile. In particular, each component induces an additive term to the constant , which can be written as . Increasing is translated to a decrease in the convergence rate. For instance, the requirement to limit the number of participants induces the additive term proportional to , that is, , whose contribution decreases as the number of participating devices increases. Quantizing the local FL model parameters results in the term proportional to , namely, , which is smaller for denser lattices, that is, when more bits are allowed to be conveyed. It is also observed that the quantization error is mitigated by averaging the local FL models at the CC side. This follows from the fact that this error term vanishes as grows when the datasets are of similar sizes, and, particularly, when as . Finally, by repeating the arguments in ref. 25, it can be shown that the number of communication rounds required to achieve a given accuracy, which dictates the convergence speed and is reduced by the proposed scheme for improving communication efficiency, has a finite minimum with respect to the number of local SGD steps .
Extensions.
The device selection scheme, universal FL model parameter compression method, and RB allocation technique are designed for learning via the federated averaging algorithm introduced from Eqs. 1–3. An interesting extension of the proposed communication-efficient FL scheme would be to adopt the proposed techniques for alternative distributed optimization algorithms such as in refs. 11 and 30–37. Furthermore, one can also consider the queuing delays and FL parameter transmission for the FL algorithms implemented over communication networks. A further extension involves enhancing the proposed device selection scheme for scenarios with additional forms of diversity among the devices which may faithfully reflect some FL applications. Such scenarios include 1) devices with varying computational power, 2) devices which can be clustered based on the distribution of their local data as in ref. 17, and 3) devices implementing different numbers of local SGD updates. In particular, to extend the proposed device selection scheme for scenario 3, one only needs to consider the devices that complete the local model update in Eq. 6. Finally, an analysis of how the value of the hyperparameter in Eq. 6 affects FL convergence and how to optimize to improve FL performance is an interesting topic for further study.
Results
Next, we evaluate our proposed FL method for handwritten digit identification, object recognition, and finger movement detection. For comparison purposes, we use two baselines: baseline a, an FL algorithm that uses the proposed device selection and resource allocation schemes without the compression of local FL model parameters; and baseline b, a standard FL algorithm in ref. 6 that randomly determines device selection and resource allocation without compressing the local FL model parameters of each device. All simulation settings are detailed in Materials and Methods.
Handwritten Digit Identification.
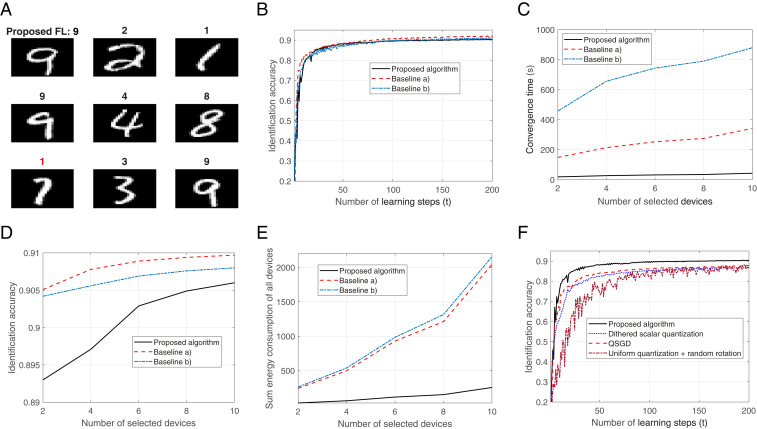
We first evaluate the proposed communication-efficient FL scheme by identifying handwritten digits from 0 to 9, as shown in Fig. 1. In particular, Fig. 1A shows an example of implementing the proposed FL method for handwritten digit identification. In Fig. 1A, the black digits are the identification results of the proposed FL scheme, while the red digit is the wrong identification result. From Fig. 1A, we can see that the proposed FL algorithm can correctly identify the handwritten digits. Fig. 1B shows how the identification accuracy changes as the number of FL learning steps increases. From Fig. 1B, we can see that the identification accuracy achieved by the proposed algorithm is slightly lower than that of baselines a and b. This is because our proposed quantization-based FL transmission slightly affects the identification accuracy. In Fig. 1C, we show how the convergence time changes as the number of selected devices varies. From Fig. 1C, we can see that, as the number of selected devices increases, the convergence time of all considered FL algorithms increases. This is because the FL model transmission delay at each learning step depends on the device with the largest transmission delay. As the number of selected devices increases, the maximum transmission delay among all devices increases.
Fig. 1.
Implementation of FL for handwritten digit identification. (A) An example of implementing FL for handwritten digit identification. (B) Identification accuracy changes as the number of learning steps varies. (C) Convergence time changes as the number of selected devices varies. (D) Identification accuracy changes as the number of selected devices varies. (E) Sum energy consumption of all devices changes as the number of selected devices varies. (F) Convergence of the FL algorithms with various quantization methods.
From Fig. 1 B and C, we can also see that baseline a achieves better identification accuracy and convergence time than baseline b. This is due to the fact that the proposed device selection scheme can select the most appropriate devices to join the FL training process. We also observe, in Fig. 1 B and C, that, although the proposed scheme achieves lower identification accuracy, it significantly reduces the convergence time by up to 85% and 87% compared to baselines a and b. These gains stem from the fact that the proposed FL uses advanced quantization methods specifically tailored for its distributed operation to compress the local FL model parameters, thus significantly reducing the size of the local FL model that is transmitted over wireless links. Fig. 1C also shows that, for a simple handwritten digit identification task, the standard FL (baseline b) needs more than 800 s to converge, which further illuminates the need for designing a communication-efficient FL algorithm.
Fig. 1D shows how the identification accuracy changes as the number of selected devices varies. From Fig. 1D, we can see that baseline a can achieve better performance than baseline b. This is because baseline a uses the proposed device selection scheme, thus improving identification accuracy. Fig. 1D also shows that, as the number of selected devices increases, the gap between the proposed FL and baseline a decreases. This is due to the fact that, as the number of selected devices increases, the effects of compression errors on the global FL model update decrease, which verifies the analytical observation made based on Theorem 1.
In Fig. 1E, we show how the sum energy consumption of all devices changes as the number of selected devices varies. From Fig. 1E, we see that the proposed FL significantly reduces the energy that all devices used for FL parameter transmission. This is because we jointly optimize wireless resource allocation, device selection, and FL parameter compression.
Fig. 1F shows the convergence of the FL algorithms that use various quantization methods. Our scheme with two-dimensional lattices is compared to its implementation with conventional scalar quantizers, the Quantized SGD (QSGD) FL algorithm proposed in ref. 38, and the combination of uniform quantization with random rotations proposed in ref. 39. From Fig. 1F, we see that the proposed algorithm outperforms the other quantization-based FL methods. This is because the proposed FL algorithm implements substractive dithered lattice quantization, which reduces the distortion induced by quantizing the FL model parameters and mitigates its effect on the aggregated global model.
Object Recognition in Images.
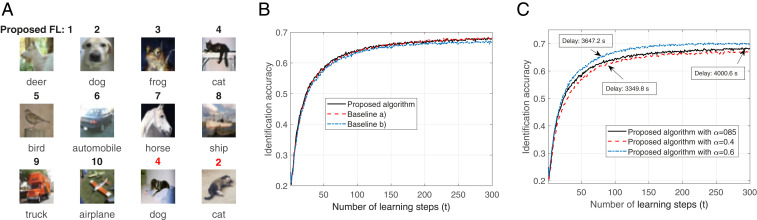
Next, we demonstrate how the proposed FL algorithm identifies 10 class objects in images, as shown in Fig. 2. Fig. 2A shows an example of implementing the proposed FL for 10-class object identification. In this figure, the digits are the labels used to represent each class of objects. The black digits are the correct identification results, while the red digits are the wrong identification results. For example, for the last object, the proposed FL identifies a cat (label 4) as a dog (label 2). Fig. 2B shows how the identification accuracy changes as the number of learning steps varies. From Fig. 2B, we can see that the proposed FL algorithm achieves almost the same identification accuracy as baseline a, which is different from the case in Fig. 1B, that the proposed FL algorithm has a lower identification accuracy compared to baseline a. This is due to the fact that the size of weight matrices of a neural network model used for object recognition is much larger than that of a neural network model used for handwritten digit identification. As the size of the weight matrices of a neural network increases, the weight bias caused by quantization method decreases.
Fig. 2.
Implementation of FL for object recognition. (A) An example of implementing FL for object recognition. (B) Identification accuracy changes as the number of learning steps varies. (C) Convergence of the proposed FL changes as the value of in Eq. 6 varies.
Fig. 2C shows how FL convergence changes as the value of in Eq. 6 varies. From this figure, we see that the identification accuracy and convergence time both depend on . In particular, as decreases, FL convergence time decreases. This is because the CC prefers to select the devices that can improve transmission time. However, identification accuracy does not decrease as decreases. In particular, when , the proposed FL algorithm achieves a better identification accuracy compared to the proposed FL, with or .
From Figs. 1C and 2C, we see that the convergence time of the FL algorithm used for objective identification is much larger than that of the FL algorithm used for handwritten digit identification. This is because the FL model used for objective identification is a convolutional neural network (CNN) that consists of 17 layers, while the FL model used for handwritten digit identification is a shallow neural network.
Finger Movement Detection.
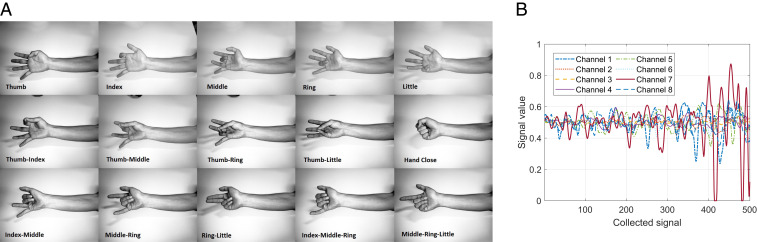
Next, we introduce the use of the proposed FL method for processing actual medical data. In particular, the proposed FL method is implemented for detecting 15-class finger movements, as shown in Fig. 3A. Fig. 3B shows the signal samples used to represent the hand closed movement. In Fig. 3B, the signals have been processed by the windowing method, and, hence, the number of the signal samples used to represent each finger movement is 500.
Fig. 3.
Implementation of FL for finger movement detection. (A) Fifteen-class finger movements. (B) Signal samples used to represent the hand closed movement.
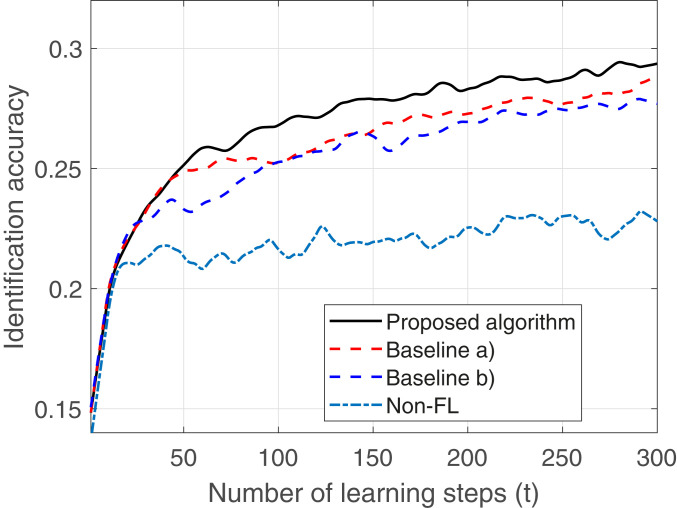
Fig. 4 shows the convergence of the FL methods used for finger movement detection. In this figure, non-FL is a method in which each device trains its ML model using its own dataset, and each device will not share its ML model with the CC. From Fig. 4, we can see that the proposed FL algorithm can improve the identification accuracy by up to 3.6%, 3.9%, and 30% compared to baseline a, baseline b, and non-FL algorithm. The 30% gain implies that using the FL algorithm can significantly improve the identification accuracy of an ML model.
Fig. 4.
Convergence of FL used for finger movement detection.
Materials and Methods
In our simulations, we consider a circular network area having a radius m with one CC at its center servicing uniformly distributed devices. The CC can allocate a total of RBs to all devices for local FL model transmission, and thus only 10 devices can transmit their trained local FL models to the CC at each FL iteration. Lattice quantization is carried out by setting to be the two-dimensional hexagonal lattice (40), using four bits per sample, with a scale parameter of . The interference over RBs is given by . The bandwidth of each RB is 2 MHz, the transmit power of each device is 1 W, and the noise power spectral density dBm/Hz. Optimal RB allocation vector is found by the Matlab intlinprog function. All simulations are implemented using Matlab 2018b. Neural networks used for data analysis are generated using Matlab machine learning toolbox. Identification accuracy, which is defined as the portion of training data samples that each device can correctly identify, is used to capture the FL performance. All code required to reproduce the results reported in this paper is available online at https://github.com/mzchen0/Communication-Efficient-Federated-Learning and https://code.ihub.org.cn/projects/4394/repository/revisions/master/show/PNAS. Next, we introduce the setup for the proposed FL and the simulation settings for all of the learning tasks.
Handwritten Digit Identification.
For handwritten digit identification, each device trains a fully connected neural network (FNN) that consists of 50 neurons (see SI Appendix, section 5 for further details) using 1,000 training data samples from MNIST dataset (41, 42). The 1,000 training data samples are distributed sequentially among the devices; that is, the first device has the first 1,000 samples in the dataset, while the second device has the second 1,000 samples, thus resulting in an uneven heterogeneous division of the labels of the devices. For example, device 1 has 100 digit 1, while device 2 may have 200 digit 1. Each device’s FNN is generated by the Matlab patternnet function. At each FL iteration, each device updates its local FL model using the SGD method with one epoch. The entire testing dataset is used to measure the identification accuracy.
Object Recognition in Images.
For 10-class object recognition, CIFAR-10 dataset (43, 44) is used to train FL models. The 50,000 training images are evenly allocated to 16 devices, and each device will have the same number of images of each object. Here, among these 16 devices, one of eight devices has 3,130 training data samples, and the number of training data samples of each object is 313. One of another eight devices has 3,120 training data samples, and the number of training data samples of each object is 312. The local FL model of each device is a CNN which is generated by the Matlab Layer and Option functions. The detailed architecture of the CNN is shown in SI Appendix, section 6. At each FL iteration, the CNN of each device is updated using the Adam method. One epoch with batch size 50 is adopt for each local FL model update. The entire testing dataset is used to measure the identification accuracy.
Finger Movement Detection.
For 15-class finger movement detection, each device trains its CNN using the electromyogram dataset 2 (45, 46). The electromyogram dataset 2 is collected from eight subjects that were asked to participate in 15-class finger movements, and hold each movement for a period of 20 s in each trial. Each figure movement is performed by a total of three trials. In our simulations, we only use 5-s data collected from each finger movement. Since the signal sampling frequency is 4,000 Hz, the number of signal samples collected by one sensor from each finger movement is 20,000. Since eight sensors are used to collect signals, the size of input vector of the local FL model will be 20,000 × 8. Hence, it is impractical to directly use all signal samples as one training sample to train the local FL model. In consequence, the windowing method in ref. 44 is used to process the original raw data. The size of each window is 500, and the increment is 50. Using the windowing method, the size of the input vector is , and the size of the output vector is 15. Meanwhile, we assume that each device has 15-class finger movement data collected from one subject within one trial, and, hence, each device will have 391 training data samples for each finger movement and 5,865 data samples in total. The testing dataset consists of all 15-class finger movement data samples collected from eight subjects in one trial. The detailed architecture of the CNNs is shown in SI Appendix, section 7. Each device trains its CNN using Adam method. During each FL iteration, one epoch with batch size 75 is adopted for training each CNN.
Supplementary Material
Acknowledgments
The work was supported, in part, by the Key Area R&D Program of Guangdong Province Grant 2018B030338001, the National Key R&D Program of China with Grant 2018YFB1800800, Shenzhen Outstanding Talents Training Fund, Guangdong Research Project 2017ZT07X152, the European Union’s Horizon 2020 research and innovation program under Grant 646804-ERC-COG-BNYQ, Israel Science Foundation Grant 0100101, and US NSF Grant CCF-1908208.
Footnotes
The authors declare no competing interest.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2024789118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or SI Appendix. All code required to reproduce the results reported in this paper is available online at GitHub (https://github.com/mzchen0/Communication-Efficient-Federated-Learning) and iHub (https://code.ihub.org.cn/projects/4394/repository/revisions/master/show/PNAS).
References
- 1.Voulodimos A., Doulamis N., Doulamis A., Protopapadakis E., Deep learning for computer vision: A brief review. Comput. Intell. Neurosci. 2018, 1–13 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Jurafsky D., Martin J. H., Speech and Language Processing: An Introduction to Speech Recognition, Computational Linguistics and Natural Language Processing (Prentice-Hall, Upper Saddle River, NJ, 2008). [Google Scholar]
- 3.van Sloun R. J., Cohen R., Eldar Y. C., Deep learning in ultrasound imaging. Proc. IEEE 108, 11–29 (2019). [Google Scholar]
- 4.Chen M., Challita U., Saad W., Yin C., Debbah M., Artificial neural networks-based machine learning for wireless networks: A tutorial. IEEE Commun. Surv. Tutor. 21, 3039–3071 (2019). [Google Scholar]
- 5.McMahan B., Moore E., Ramage D., Hampson S., y Arcas B. A., Communication-efficient learning of deep networks from decentralized data. Proc. Machine Learning Res. 54, 1273–1282 (2017). [Google Scholar]
- 6.Bonawitz K., et al. , Towards federated learning at scale: System design, in Proceedings of the 2019 11th International Conference on Systems and Machine Learning (Association for Computing Machinery, 2019). Accessed 2 October 2020. [Google Scholar]
- 7.McMahan B., Ramage D., “Federated learning: Collaborative machine learning without centralized training data.” Google AI Blog (2020). https://ai.googleblog.com/2017/04/federated-learning-collaborative.html. Accessed 2 October 2020. [Google Scholar]
- 8.Hao K., “How Apple personalizes Siri without hoovering up your data.” Technology Review (2020). https://www.technologyreview.com/2019/12/11/131629/apple-ai-personalizes-siri-federated-learning/. Accessed 2 October 2020. [Google Scholar]
- 9.Li T., “WeBank, Swiss Re in federated learning deal.” Shine (2020). https://www.shine.cn/biz/company/1905235275/. Accessed 2 October 2020. [Google Scholar]
- 10.Li T., Sahu A. K., Talwalkar A., Smith V., Federated learning: Challenges, methods, and future directions. IEEE Signal Process. Mag. 37, 50–60 (2020). [Google Scholar]
- 11.Chen T., Giannakis G., Sun T., Yin W., Lag, “Lazily aggregated gradient for communication-efficient distributed learning” in Proceedings of Advances in Neural Information Processing Systems, S. Bengio et al., Eds. (Neural Information Processing Systems Foundation, 2018), p. 2440. [Google Scholar]
- 12.Yang H. H., Liu Z., Quek T. Q. S., Poor H. V., Scheduling policies for federated learning in wireless networks. IEEE Trans. Commun. 68, 317–333 (2020). [Google Scholar]
- 13.Ren J., et al. , Scheduling for cellular federated edge learning with importance and channel awareness. IEEE Trans. Wireless Commun. 19, 7690–7703 (2020). [Google Scholar]
- 14.Amiri M. M., Gunduz D., “Machine learning at the wireless edge: Distributed stochastic gradient descent over-the-air” in Proceedings of 2019 IEEE International Symposium on Information Theory (ISIT), (Institute of Electrical and Electronics Engineers, 2019), pp. 1432–1436. [Google Scholar]
- 15.Shlezinger N., Chen M., Eldar Y. C., Poor H. V., Cui S., UVeQFed: Universal vector quantization for federated learning. IEEE Trans. Signal Process. 69, 500–514 (2021). [Google Scholar]
- 16.Sery T., Shlezinger N., Cohen K., Eldar Y. C., Over-the-air federated learning from heterogeneous data. arXiv [Preprint] (2020). https://arxiv.org/abs/2009.12787. Accessed 2 October 2020. [Google Scholar]
- 17.Shlezinger N., Rini S., Eldar Y. C., “The communication-aware clustered federated learning problem” in Proceedings of 2020 International Symposium on Information Theory (ISIT) (Institute of Electrical and Electronics Engineers, 2020), pp. 2610–2615. [Google Scholar]
- 18.Liu Y., et al. , “A communication efficient vertical federated learning framework” in Proceedings of Advances in Neural Information Processing Systems Workshop on Federated Learning for Data Privacy and Confidentiality (WeBank, 2019). [Google Scholar]
- 19.Wang S., et al. , Adaptive federated learning in resource constrained edge computing systems. IEEE J. Sel. Area. Commun. 37, 1205–1221 (2019). [Google Scholar]
- 20.Li T., Sanjabi M., Beirami A., Smith V., “Fair resource allocation in federated learning” in Proceedings of the International Conference on Learning Representations (ICLR, 2020). [Google Scholar]
- 21.Yang Z., Chen M., Saad W., Hong C. S., Shikh-Bahaei M., Energy efficient federated learning over wireless communication networks. IEEE Trans. Wireless Commun. 20, 1935–1949 (2021). [Google Scholar]
- 22.Chen M., Poor H. V., Saad W., Cui S., Convergence time optimization for federated learning over wireless networks. IEEE Trans. Wireless Commun., 10.1109/TWC.2020.3042530 (2021). [Google Scholar]
- 23.Reisizadeh A., Mokhtari A., Hassani H., Jadbabaie A., Pedarsani R., FedPAQ: A communication-efficient federated learning method with periodic averaging and quantization. Proc. Machine Learning Res. 108, 2021–2031 (2020). [Google Scholar]
- 24.Stich S. U., “Local SGD converges fast and communicates little” in Proceedings of the International Conference on Learning Representations (ICLR, 2019). [Google Scholar]
- 25.Li X., Huang K., Yang W., Wang S., Zhang Z., “On the convergence of FedAvg on Non-IID data” in Proceedings of the International Conference on Learning Representations (ICLR, 2020). [Google Scholar]
- 26.Zamir R., Feder M., On universal quantization by randomized uniform/lattice quantizers. IEEE Trans. Inf. Theor. 38, 428–436 (1992). [Google Scholar]
- 27.Boyd S., Vandenberghe L., Convex Optimization (Cambridge University Press, 2004). [Google Scholar]
- 28.Nguyen L., et al. , “SGD and Hogwild! convergence without the bounded gradients assumption” in Proceedings of the International Conference on Machine Learning, J. Dy, A. Krause, Eds. (PMLR, 2018), pp. 3750–3758. [Google Scholar]
- 29.Zamir R., Feder M., On lattice quantization noise. IEEE Trans. Inf. Theor. 42, 1152–1159 (1996). [Google Scholar]
- 30.Kairouz P., et al. , Advances and open problems in federated learning. Found. Trend. Mach. Learn. (Vol. 14, No. 1, 2021). [Google Scholar]
- 31.Wang H., Yurochkin M., Sun Y., Papailiopoulos D., Khazaeni Y., “Federated learning with matched averaging” in Proceedings of the International Conference on Learning Representations (ICLR, 2020). [Google Scholar]
- 32.Vogels T., Karimireddy S. P., Jaggi M., PowerSGD, “Practical low-rank gradient compression for distributed optimization” in Proceedings of Advances in Neural Information Processing Systems (Neural Information Processing Systems Foundation, 2019). [Google Scholar]
- 33.Sun J., Chen T., Giannakis G., Yang Z., Vancouver, “Communication-efficient distributed learning via lazily aggregated quantized gradients” in Proceedings of Advances in Neural Information Processing Systems (Neural Information Processing Systems Foundation, 2019). [Google Scholar]
- 34.Lin T., Stich S. U., Patel K. K., Jaggi M., “Don’t use large mini-batches, use local SGD” in Proceedings of the International Conference on Learning Representations (ICLR, 2020). [Google Scholar]
- 35.Yu H., Yang S., Zhu S., “Parallel restarted SGD with faster convergence and less communication: Demystifying why model averaging works for deep learning” in Proceedings of the AAAI Conference on Artificial Intelligence, (Association for the Advancement of Artificial Intelligence, 2019). [Google Scholar]
- 36.Karimireddy S. P., Rebjock Q., Stich S., Jaggi M., “Error feedback fixes SignSGD and other gradient compression schemes” in Proceedings of the International Conference on Machine Learning (PMLR, 2019), pp. 3252–3261. [Google Scholar]
- 37.Alistarh D., et al. , “The convergence of sparsified gradient methods” in Proceedings of Advances in Neural Information Processing Systems (Neural Information Processing Systems Foundation, 2018). [Google Scholar]
- 38.Alistarh D., Grubic D., Li J., Tomioka R., Vojnovic M., “QSGD: Communication-efficient SGD via gradient quantization and encoding” in Proceedings of Advances in Neural Information Processing Systems (Neural Information Processing Systems Foundation, 2017). [Google Scholar]
- 39.Konečnỳ J., et al. , Federated learning: Strategies for improving communication efficiency. arXiv [Preprint] (2016) https://arxiv.org/abs/1610.05492 (Accessed 10 October 2020). [Google Scholar]
- 40.Kirac A., Vaidyanathan P., Results on lattice vector quantization with dithering. IEEE Trans. Circuits Syst. II Analog Digit. Signal Process. 43, 811–826 (1996). [Google Scholar]
- 41.Lecun Y., Bottou L., Bengio Y., Haffner P., Gradient-based learning applied to document recognition. Proc. IEEE 86, 2278–2324 (1998). [Google Scholar]
- 42.LeCun Y., Cortes C., Burges C. J. C., The MNIST Database. MNIST. http://yann.lecun.com/exdb/mnist. Accessed 5 October 2020.
- 43.Krizhevsky A., Hinton G., “Learning multiple layers of features from tiny images. Citeseer” (Tech Rep. 7, 2009). [Google Scholar]
- 44.Krizhevsky A., The CIFAR-10 dataset. CIFAR-10. https://www.cs.toronto.edu/∼kriz/cifar.html. Accessed 10 October 2020.
- 45.Khushaba R. N., Kodagoda S., “Electromyogram (EMG) feature reduction using mutual components analysis for multifunction prosthetic fingers control” in Proceedings of the International Conference on Control Automation Robotics Vision (ICARCV) (2012).
- 46.Khushaba R. N., Kodagoda S., Detecting individual and combined fingers movements. EMG Datasets Repository. https://onedrive.live.com/?authkey=%21Ar1wo75HiU9RrLM&id=AAA78954F15E6559%21312&cid=AAA78954F15E6559&sc=Photos. Accessed 20 October 2020.
- 47.Jia G., Lam H. K., Liao J., Wang R., Classification of electromyographic hand gesture signals using machine learning techniques. Neurocomputing 401, 236–248 (2020). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All study data are included in the article and/or SI Appendix. All code required to reproduce the results reported in this paper is available online at GitHub (https://github.com/mzchen0/Communication-Efficient-Federated-Learning) and iHub (https://code.ihub.org.cn/projects/4394/repository/revisions/master/show/PNAS).